Optimization of a Dual-Channel Water-Cooling Heat Dissipation System for PMSM in Underwater Unmanned Vehicles Using a Multi-Objective Genetic Algorithm
Abstract
1. Introduction
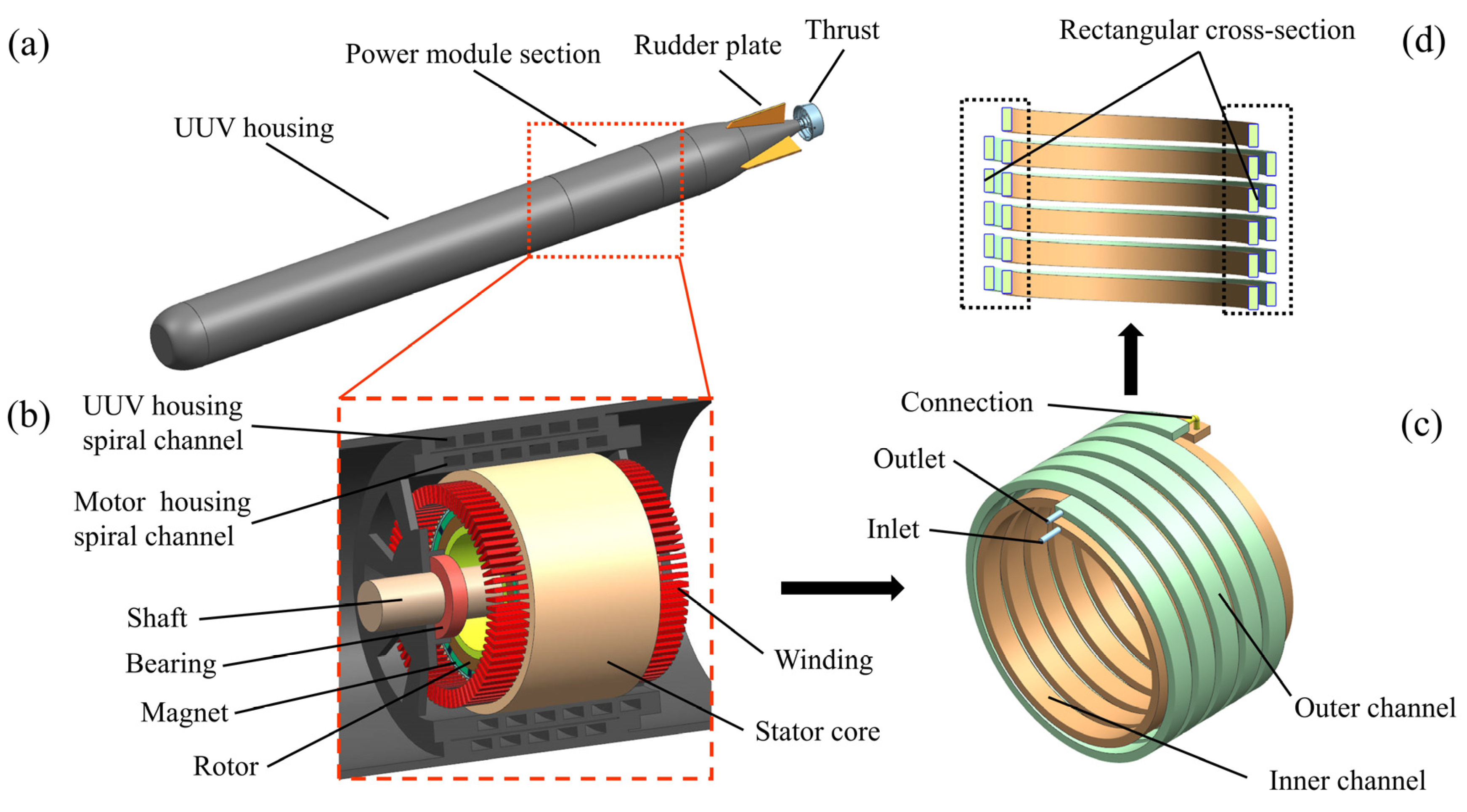
2. Problem Description
2.1. Motor Model and System Parameter
2.2. Mathematical Model
2.2.1. Control Equations
2.2.2. Multi-Objective Optimization
3. CFD Coupling Simulation
3.1. Numerical Conditions and Grid
3.2. Numerical Validation
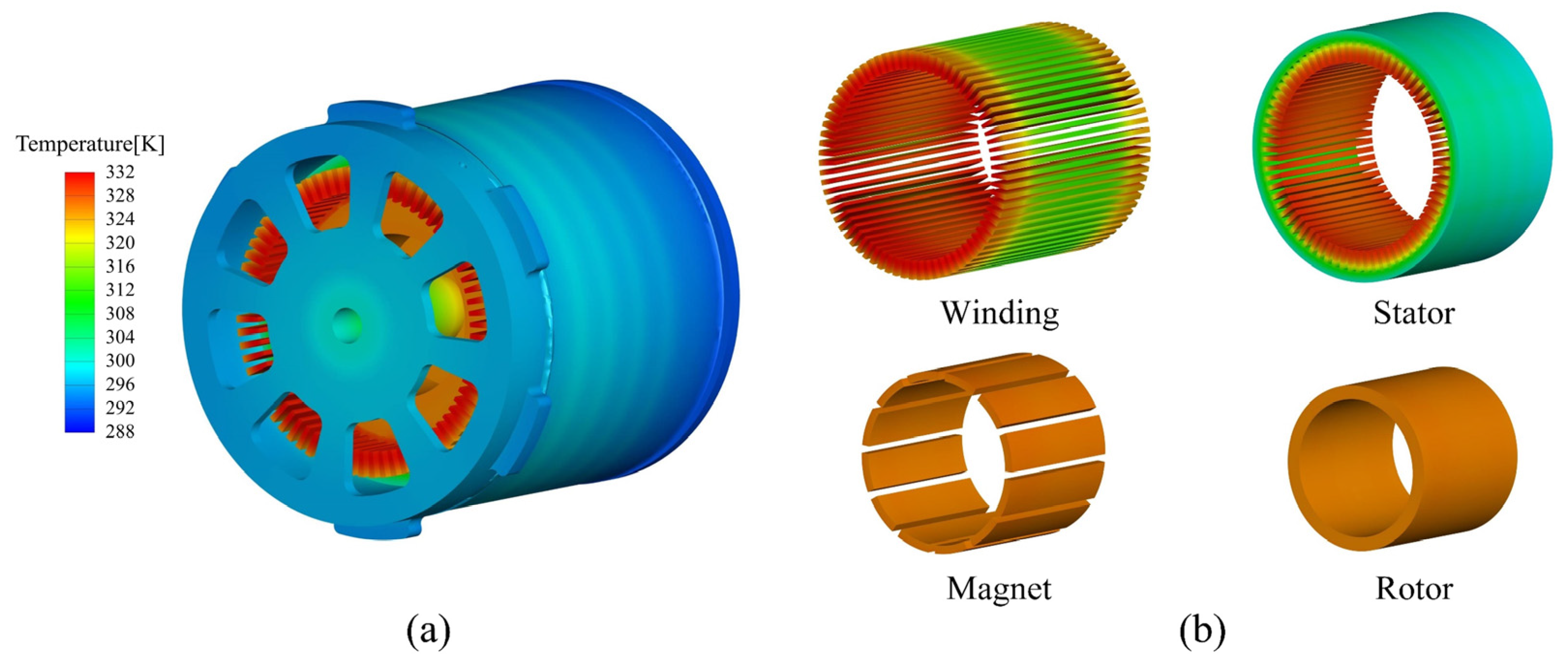
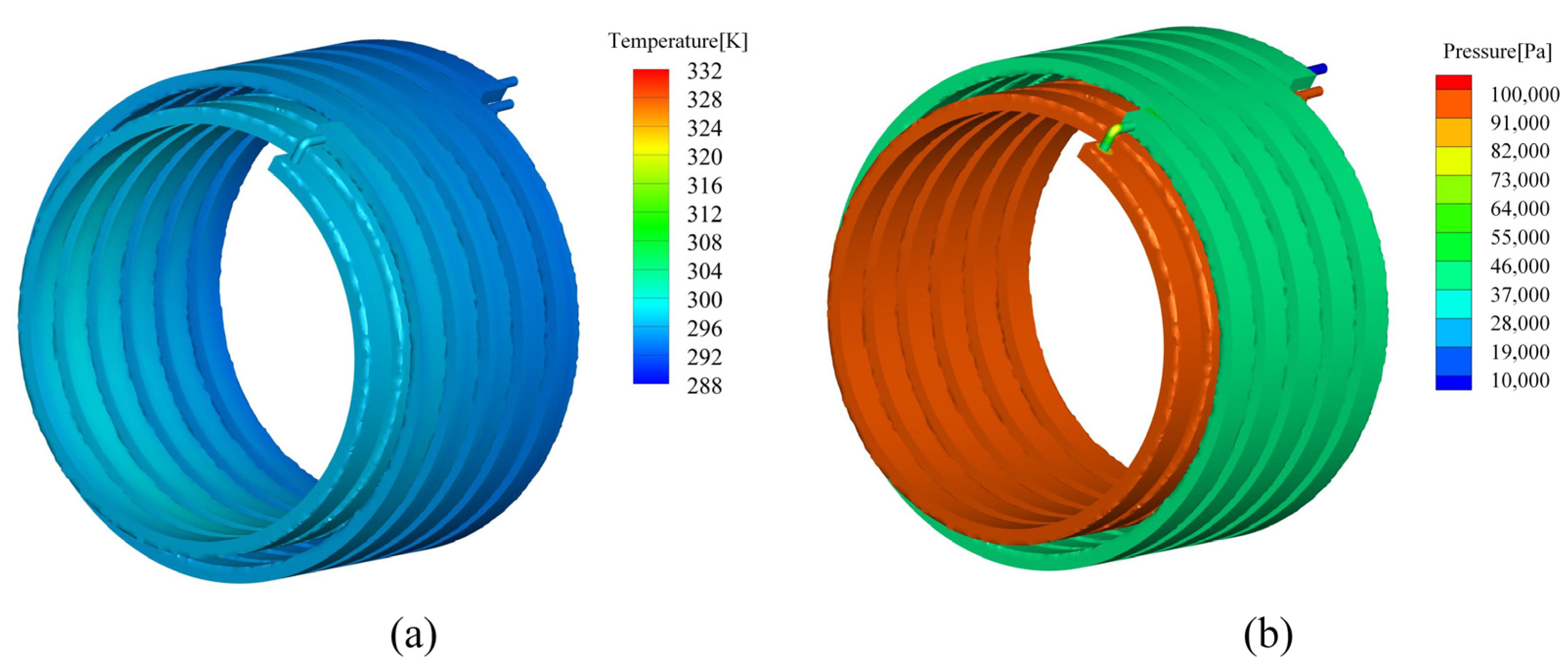
3.3. Numerical Results
4. Sensitivity Analysis
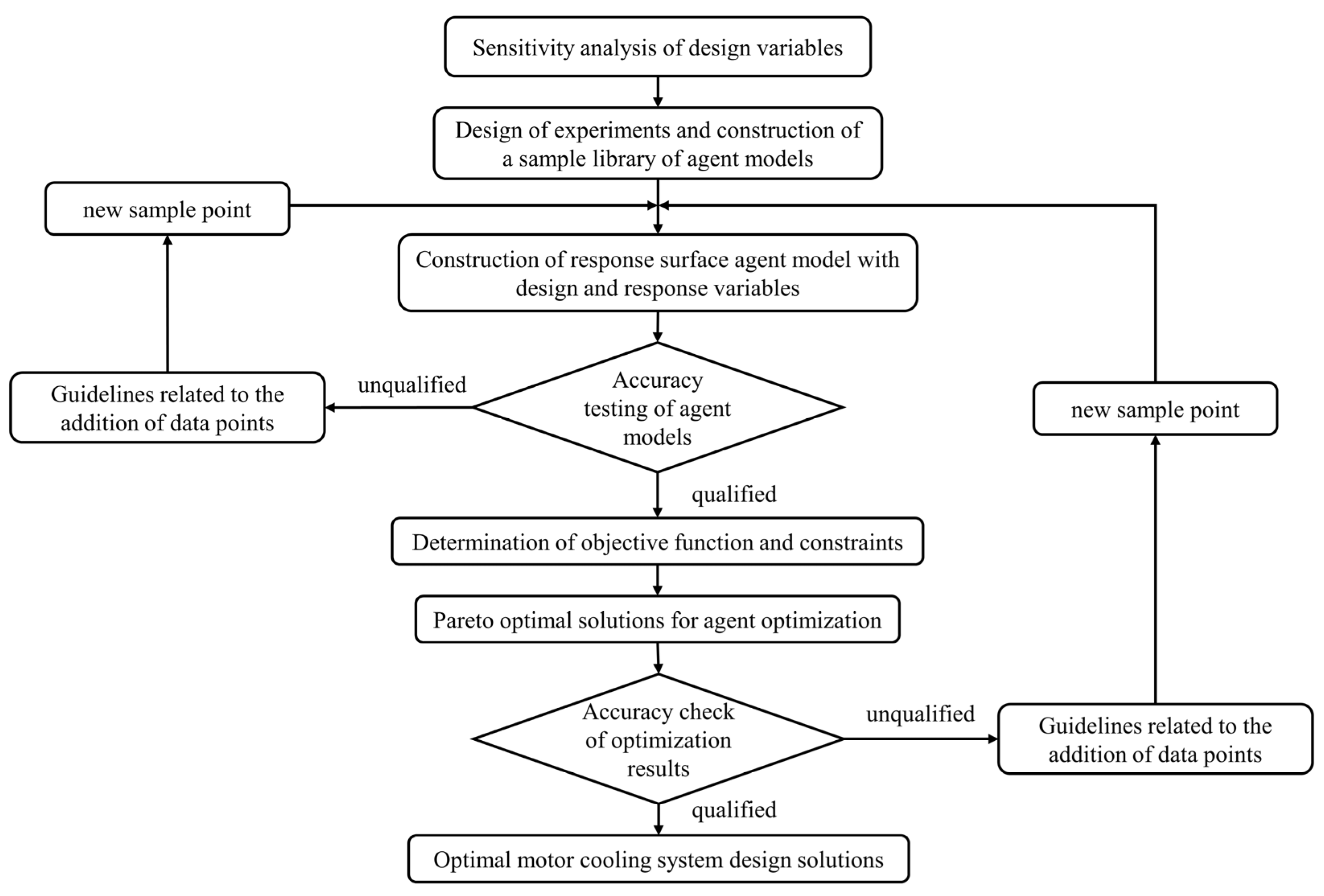
5. Construction and Validation of the Agent Model
5.1. Construction of RSM
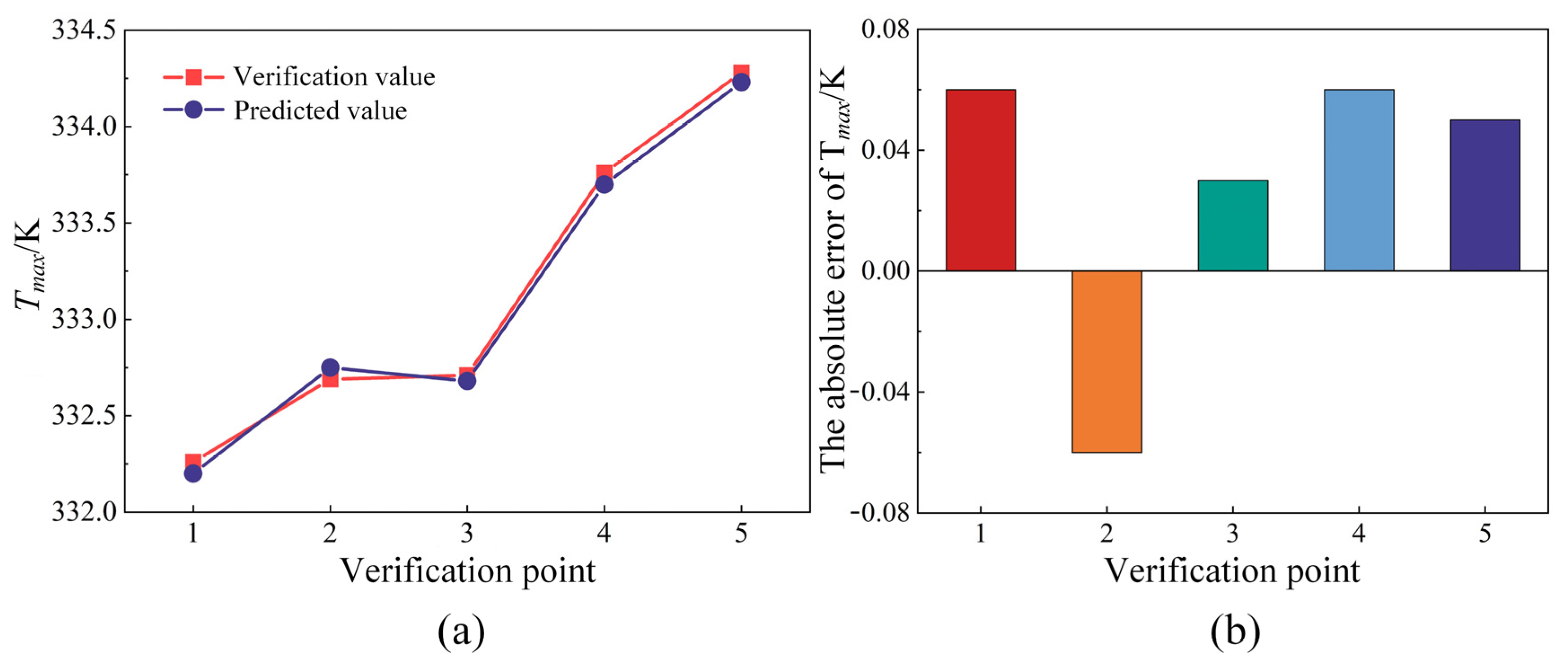
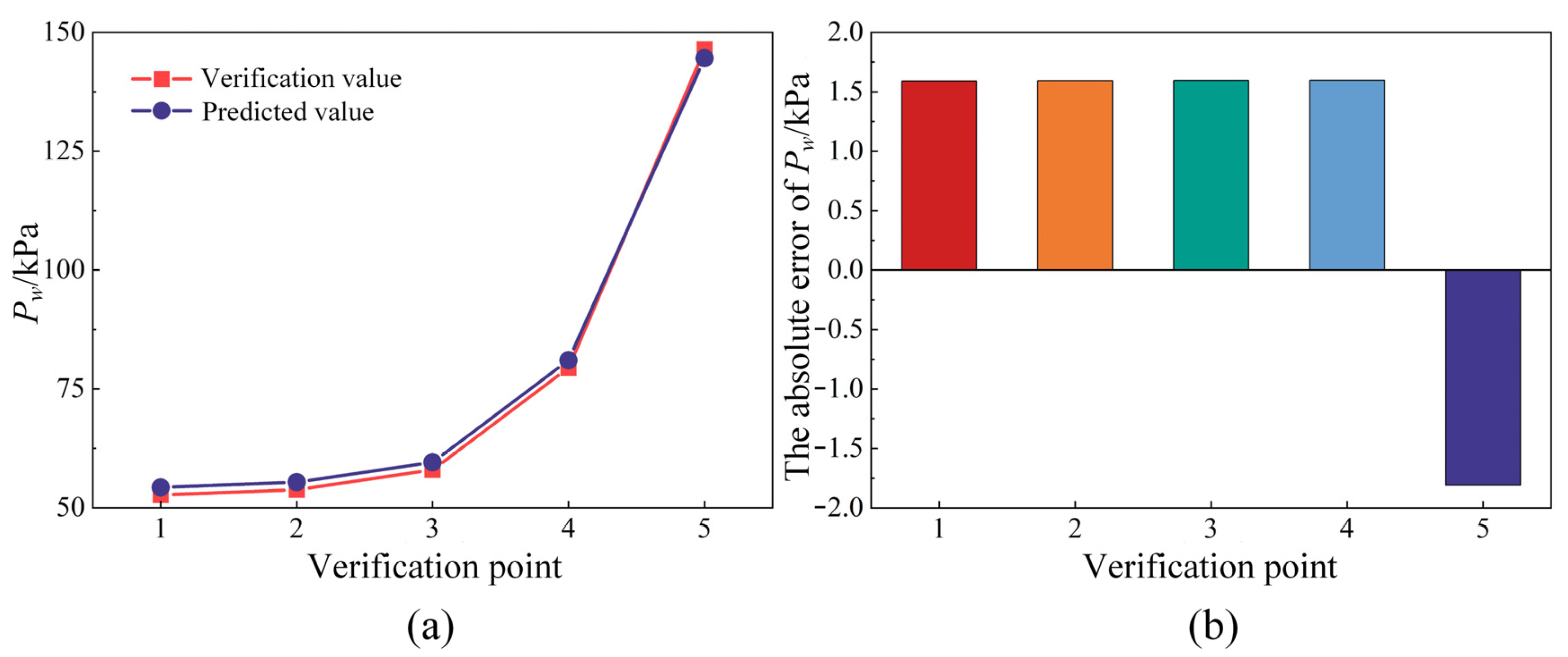
5.2. Validation of RSM
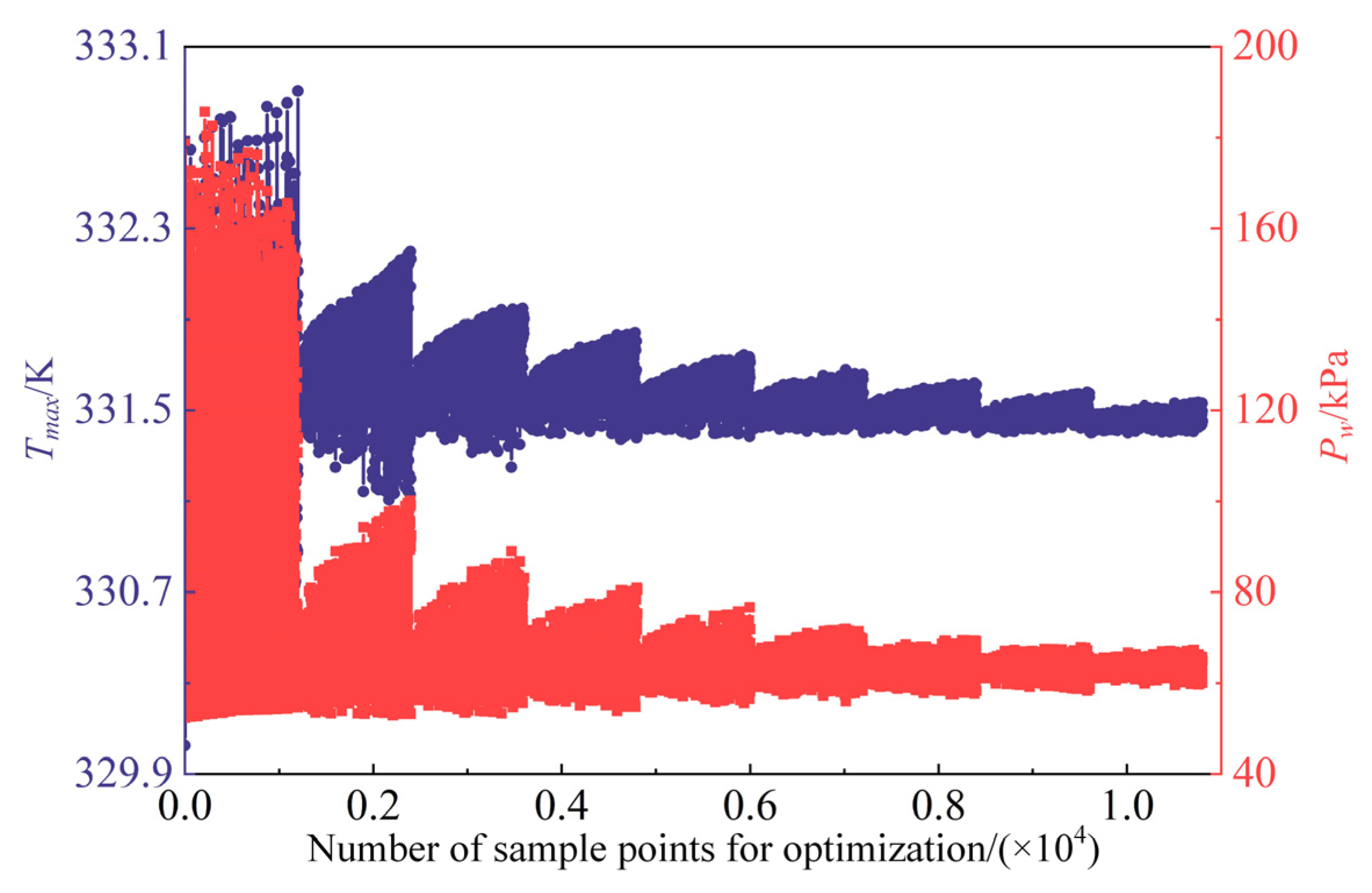
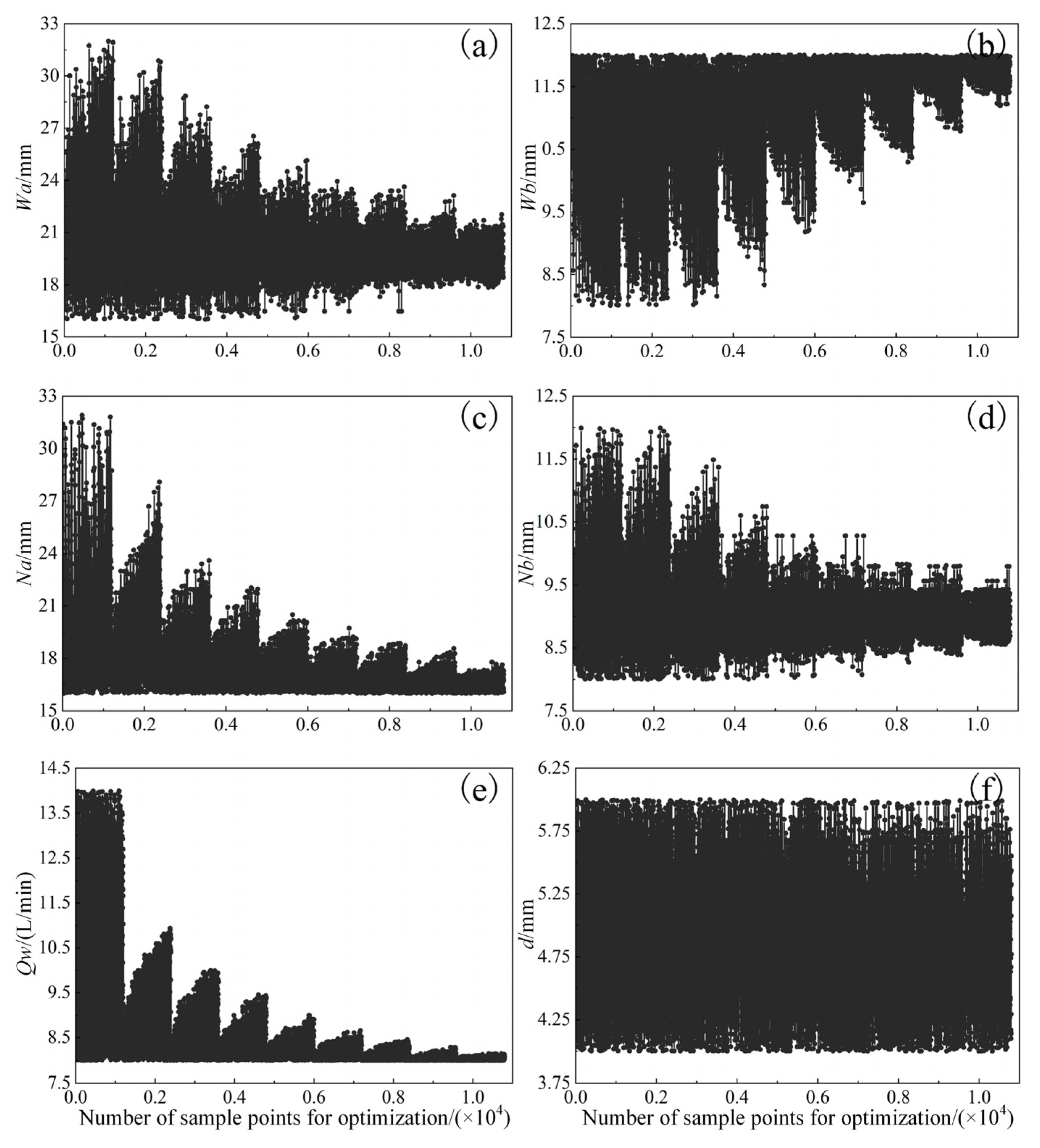
6. Optimization Results Analysis
7. Conclusions
- (1)
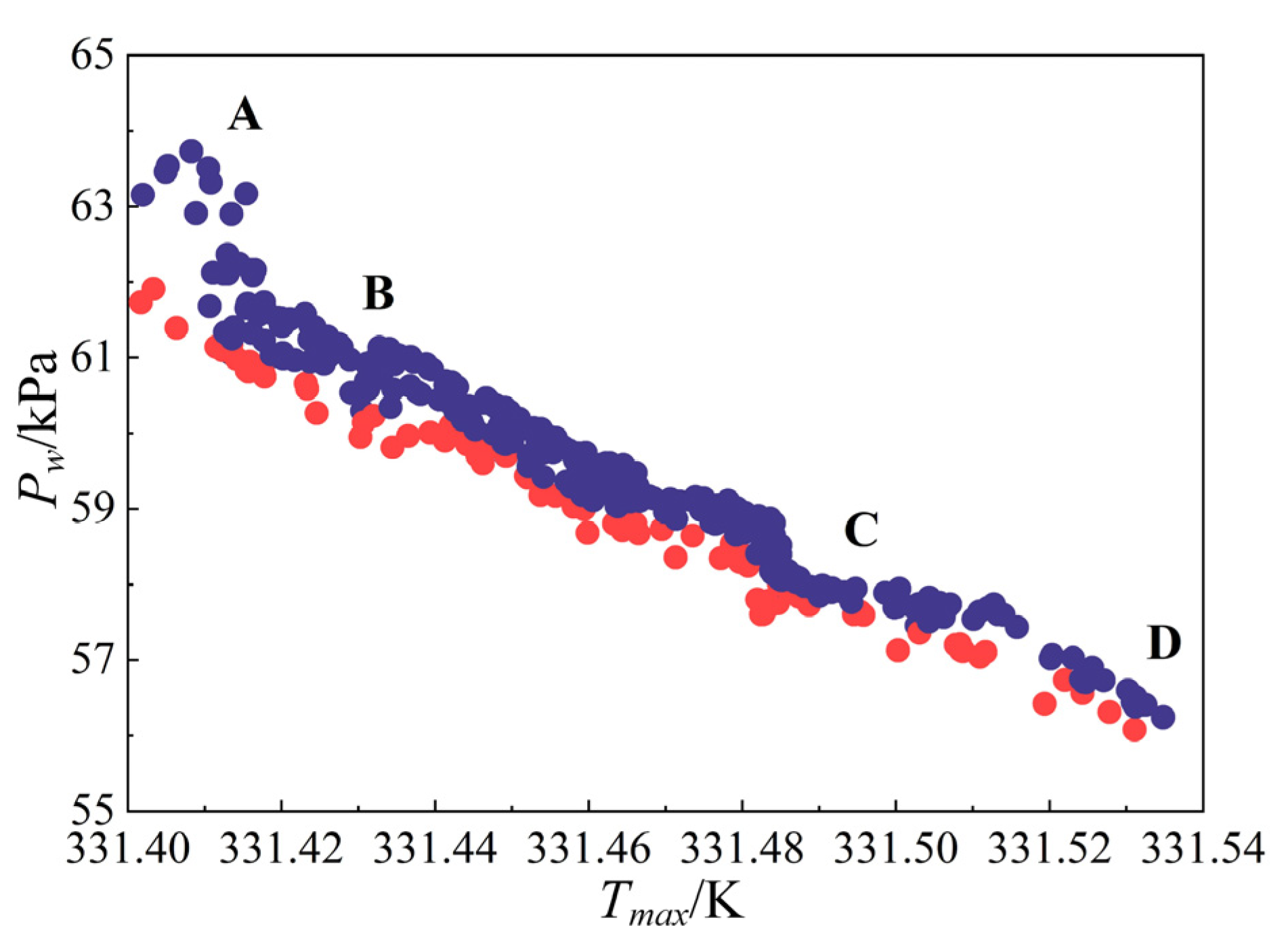
- The sensitivity analysis results indicate that the cooling water flow rate Qw has the most significant impact on both Tmax and Pw, with sensitivities of 77.79% and 99.84%, respectively. In contrast, the sensitivity of the cross-sectional dimensions of the inner and outer channel on Tmax was approximately 20%, while their effects on Pw were relatively minor, generally below 10%.
- (2)
- For the multi-objective optimization of the motor cooling system design, the response surface agent model was constructed using Latin hypercube sampling. The prediction accuracy was validated through test samples, revealing an average error of less than 1% between the predicted and verification values, which proved the validity and reliability of this agent model in the optimization of motor cooling systems.
- (3)
- Sample points were selected from the Pareto solution set and their comparison with CFD simulations revealed that the maximum absolute errors of the response variables were all below 1%. The optimized design variables for the cooling structure were [Wa, Wb, Na, Nb, d, Qw] = [20.33 mm, 11.92 mm, 17.78 mm, 9.10 mm, 5.13 mm, 9.62 L/min]. Compared to the initial parameters, the maximum temperature of the motor decreased from 332.86 K to 331.46 K. The flow loss of the water-cooling structure decreased from 100.02 kPa to 59.58 kPa, achieving a maximum improvement rate of 40.43%, demonstrating a significant overall optimization effect.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Wa | width of the water channel outside the UUV housing |
| Wb | height of the water channel outside the UUV housing |
| Na | width of the water channel inside the motor housing |
| Nb | height of the water channel inside the motor housing |
| d | groove depth of the inner water channel in the motor housing |
| Qw | volume flow rate of cooling water |
| Tmax | maximum temperature of the motor |
| Pw | flow loss of water-cooled structure |
| x | x-direction scale in 3D coordinate system |
| y | y-direction scale in 3D coordinate system |
| z | z-direction scale in 3D coordinate system |
| t | time scale |
| u | velocity of the fluid in the x-direction |
| v | velocity of the fluid in the y-direction |
| w | velocity of the fluid in the z-direction |
| ρ | density of the fluid |
| P | pressure on the fluid |
| μα | effective viscosity of the fluid |
| constant pressure specific heat capacity of the fluid | |
| T | temperature of the fluid |
| thermal conductivity of the fluid | |
| k | turbulent kinetic energy |
| ω | specific dissipation rate |
| turbulence generation term | |
| β | empirical constant of the turbulent kinetic energy transport equation |
| molecular viscosity | |
| turbulent viscosity | |
| Prandtl number of turbulent kinetic energy | |
| model constant | |
| Prandtl number of turbulent specific dissipation rate | |
| blending function | |
| S | strain rate |
| Q | thermal conductivity flow per unit time |
| A | thermal conductivity area |
| thermal conductivity | |
| temperature gradient | |
| heat transfer per unit area | |
| h | convective heat transfer coefficient |
| temperature of the shell surface | |
| Tw | temperature of the cooling water |
| ks | thermal conductivity of the solid material |
| Ts | temperature of the solid region |
| q | calorific value per unit volume of the solid |
| SAi | sensitivity of a design variable to a response variable |
| fmax(xi) | maximum value of the response variable within the range of value |
| fmin(xi) | minimum value of the response variable within the range of value |
| n | total number of samples |
| response variable | |
| xi | design variable |
| constant term for response surface model | |
| linear coefficient for response surface model | |
| quadratic coefficient for response surface model | |
| interaction term coefficient for response surface model | |
| ξ | error term in response surface model |
| R2 | coefficient of determination |
| MAE | maximum absolute error |
| RMSE | root mean square error |
| yi | actual simulation value for test sample point |
| predicted value of the agent model | |
| average of actual simulation | |
| ntest | number of test sample |
| f(x) | the set of objective function to be solved |
| m | number of objective function |
| gi(x) | inequality bound function |
| hj(x) | linear equation constraint function |
| p | the number of inequality constraint function |
| u | the number of linear equation constraint function |
| decision variable | |
| Tr | maximum temperature of the motor rotor |
| Tm | maximum temperature of the motor magnet |
| Ts | maximum temperature of the motor stator |
| Tw | maximum temperature of the motor winding |
References
- Cheng, B.; Qin, D.; Hu, Z. Research on the propulsion motor cooling by the coupled flow field of unmanned underwater vehicles. Appl. Therm. Eng. 2024, 237, 121797. [Google Scholar] [CrossRef]
- Zhang, B.; Ji, D.; Liu, S.; Zhu, X.; Xu, W. Autonomous Underwater Vehicle navigation: A review. Ocean Eng. 2023, 273, 113861. [Google Scholar] [CrossRef]
- Mondal, K. Autonomous Underwater Vehicles: Recent Developments and Future Prospects. Int. J. Res. Appl. Sci. Eng. Technol. 2019, 7, 215–222. [Google Scholar] [CrossRef]
- Li, W.; Cao, Z.; Zhang, X. Thermal Analysis of the Solid Rotor Permanent Magnet Synchronous Motors With Air-Cooled Hybrid Ventilation Systems. IEEE Trans. Ind. Electron. 2022, 69, 1146–1156. [Google Scholar] [CrossRef]
- Repecho, V.; Bin Waqar, J.; Biel, D.; Dòria-Cerezo, A. Zero Speed Sensorless Scheme for Permanent Magnet Synchronous Machine Under Decoupled Sliding-Mode Control. IEEE Trans. Ind. Electron. 2022, 69, 1288–1297. [Google Scholar] [CrossRef]
- Kim, K.; Lee, M.; Lee, S.; Jang, G. Optimal design and experimental verification of fluid dynamic bearings with high load capacity applied to an integrated motor propulsor in unmanned underwater vehicles. Tribol. Int. 2017, 114, 221–233. [Google Scholar] [CrossRef]
- Lei, S.; Xin, S.; Liu, S. Separate and integrated thermal management solutions for electric vehicles: A review. J. Power Sources 2022, 550, 232133. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, Y.; Niu, S.; Zhao, X. Advances in Thermal Management Technologies of Electrical Machines. Energies 2022, 15, 3249. [Google Scholar] [CrossRef]
- Wu, P.-S.; Hsieh, M.-F.; Cai, W.L.; Liu, J.-H.; Huang, Y.-T.; Caceres, J.F.; Chang, S.W. Heat transfer and thermal management of interior permanent magnet synchronous electric motor. Inventions 2019, 4, 69. [Google Scholar] [CrossRef]
- Yu, W.; Hua, W.; Zhang, Z. Cooling Analysis of High-Speed Stator-Permanent Magnet Flux-Switching Machines for Fuel-Cell Electric Vehicle Compressor. IEEE Trans. Veh. Technol. 2022, 71, 210–219. [Google Scholar] [CrossRef]
- Chen, W.; Mao, Z.; Tian, W. Water cooling structure design and temperature field analysis of permanent magnet synchronous motor for underwater unmanned vehicle. Appl. Therm. Eng. 2024, 240, 122243. [Google Scholar] [CrossRef]
- Park, J.; An, J.; Han, K.; Choi, H.-S.; Seouk Park, I. Enhancement of cooling performance in traction motor of electric vehicle using direct slot cooling method. Appl. Therm. Eng. 2022, 217, 119082. [Google Scholar] [CrossRef]
- Wan, Z.; Sun, Y.; Hu, L.; Yu, H. Dynamic softening behavior and microstructural characterization of TiAl-based alloy during hot deformation. Mater. Charact. 2017, 130, 25–32. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Q.; Wang, X.; Zhao, S.; Shah, S.W.A. Reynolds number based optimization on liquid cooling system for permanent magnet synchronous motor of electric vehicle. Case Stud. Therm. Eng. 2024, 60, 104720. [Google Scholar] [CrossRef]
- Ou, H.; Hu, Y.; Tian, W.; Mao, Z.; Cheng, B.; Li, B. Investigation of self-adjusting cooling system for the autonomous underwater vehicle propulsion motor. Appl. Therm. Eng. 2024, 238, 121972. [Google Scholar] [CrossRef]
- Chen, W.; Luo, Q.; Cai, Z.; Wang, C. Temperature field analysis and cooling structure optimization of permanent magnet linear synchronous motor. Therm. Sci. Eng. Prog. 2024, 50, 102532. [Google Scholar] [CrossRef]
- Lee, Y.; Choi, H.; Park, P.; Lee, H. Multi-objective optimization of a U-shaped water jacket with a guide vane for improving the thermal performance of 20kW in-wheel motor. Case Stud. Therm. Eng. 2024, 53, 103927. [Google Scholar] [CrossRef]
- Li, C.; Guan, Z.; Li, J.; Zhao, B.; Ding, X. Optimal design of cooling system for water cooling motor used for mini electric vehicle. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–4. [Google Scholar]
- Baojun, G.; Jiong, Z.; Tao, D. Temperature prediction and cooling structure optimization of explosion-proof high pressure water-cooled double speed motor. Energy Rep. 2022, 8, 3891–3901. [Google Scholar] [CrossRef]
- Jha, P.; Hussain, M.; Khan, M.K. Numerical evaluation of nanofluid-based indirect liquid cooling of a Li-ion battery pack using equivalent circuit model under static and dynamic loading conditions. Int. Commun. Heat Mass Transf. 2024, 159, 108079. [Google Scholar] [CrossRef]
- Kumar Srinivasan, N.; Ponnusamy, C. Stability, thermal and solidification behaviour of oxygen functionalized GNPs–CuO/water-based hybrid nanofluid phase change materials for cool thermal energy storage system. J. Energy Storage 2024, 98, 113107. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.; Kang, D.G.; Kim, M.S. Motor cooling method using flow boiling of two-phase refrigerant and its analysis with lumped parameter thermal model. Int. J. Therm. Sci. 2023, 192, 108458. [Google Scholar] [CrossRef]
- Li, M.; Ma, C.; Liu, J. Topology optimization design of cooling water jacket structure for highspeed spindle-bearing system. J. Manuf. Process. 2023, 102, 1–22. [Google Scholar] [CrossRef]
- Zaniewski, D.; Klimaszewski, P.; Klonowicz, P.; Witanowski, Ł.; Lampart, P.; Jędrzejewski, Ł.; Suchocki, T. Organic Rankine cycle turbogenerator cooling–Optimization of the generator water jacket heat exchange surface. Appl. Therm. Eng. 2023, 223, 120041. [Google Scholar] [CrossRef]
- Zhu, G.; Li, L.; Mei, Y.; Liu, T.; Xue, M. Design and Analysis of a Self-Circulated Oil Cooling System Enclosed in Hollow Shafts for Axial-Flux PMSMs. IEEE Trans. Veh. Technol. 2022, 71, 4879–4888. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, B.; Zhao, F.; Yan, T.; Li, C. Research on enhancing power plant net power by integrating modeling heat transfer and operation optimization of once-through cooling water system. Case Stud. Therm. Eng. 2024, 61, 104966. [Google Scholar] [CrossRef]
- Ye, W.; Liu, Y.; Wu, G.; Wu, Q.; Chen, Z.; Chen, Z.; Li, Z.; Cao, Z. Design optimization and manufacture of permanent magnet synchronous motor for new energy vehicle. Energy Rep. 2022, 8, 631–641. [Google Scholar] [CrossRef]
- Xia, T.; Zhang, C.; Li, H. Optimizing coolant loop design across the stator core: A research study. Heliyon 2024, 10, e36865. [Google Scholar] [CrossRef]
- Liu, H.; Xie, J.; Ma, X. Multi-objective optimization analysis of air-cooled heat dissipation coupled with thermoelectric cooling of battery pack based on orthogonal design. Appl. Therm. Eng. 2024, 249, 123402. [Google Scholar] [CrossRef]
- Ahmed, S.; Grabher, C.; Kim, H.-J.; Koseki, T. Multifidelity Surrogate Assisted Rapid Design of Transverse-Flux Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2020, 67, 7280–7289. [Google Scholar] [CrossRef]
- Rafiee, V.; Faiz, J. Robust Design of an Outer Rotor Permanent Magnet Motor Through Six-Sigma Methodology Using Response Surface Surrogate Model. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Xu, L.; Xu, Y.; Gong, J. Analysis and Optimization of Cogging Torque in Yokeless and Segmented Armature Axial-Flux Permanent-Magnet Machine with Soft Magnetic Composite Core. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Bittner, F.; Hahn, I. Kriging-Assisted Multi-Objective Particle Swarm Optimization of permanent magnet synchronous machine for hybrid and electric cars. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 15–22. [Google Scholar]
- Chen, S.; Arabkoohsar, A.; Yang, Y.; Zhu, T.; Nielsen, M.P. Multi-objective optimization of a combined cooling, heating, and power system with subcooled compressed air energy storage considering off-design characteristics. Appl. Therm. Eng. 2021, 187, 116562. [Google Scholar] [CrossRef]
- Mi, S.; Liu, J.; Cai, L.; Xu, C. Multi-objective optimization of two-phase ice slurry flow and heat transfer characteristics in helically coiled tubes with RSM and NSGA-II. Int. J. Therm. Sci. 2024, 199, 108942. [Google Scholar] [CrossRef]
- Zhang, Z.; He, H.; Quan, S.; Chen, J.; Han, R. Multi-parameter and multi-objective optimization of dual-fuel cell system heavy-duty vehicles: Sizing for serial development. Energy 2024, 308, 132857. [Google Scholar] [CrossRef]
- Pandya, S.B.; Jangir, P.; Mahdal, M.; Kalita, K.; Chohan, J.S.; Abualigah, L. Optimizing brushless direct current motor design: An application of the multi-objective generalized normal distribution optimization. Heliyon 2024, 10, e26369. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Garg, A.; Gao, L.; Li, W. Heat dissipation analysis and multi-objective optimization of a permanent magnet synchronous motor using surrogate assisted method. Case Stud. Therm. Eng. 2021, 27, 101203. [Google Scholar] [CrossRef]
- Hendre, O.; Kale, P.; Gore, R.; Pardeshi, N. Numerical study of water cooling jacket of a diesel engine using coupled field analysis. Mater. Today Proc. 2023, 77, 739–747. [Google Scholar] [CrossRef]
- Song, X.G.; Kang, S.H.; Park, Y.C. Thermal Performance Prediction and Optimization of Heat Sink with Jet Impingement Based on Adaptive Surrogate Model. In AIP Conference Proceedings-American Institute of Physics; AIP: Las Vegas, NV, USA, 2012; pp. 420–427. [Google Scholar]
- Saleem, A.; Hyeon Park, M.; Ambreen, T.; Chul Kim, S. Optimization of oil flow distribution inside the in-wheel motor assembly of electric vehicles for improved thermal performance. Appl. Therm. Eng. 2022, 201, 117753. [Google Scholar] [CrossRef]
- Yu, Y.; Liang, C.; Zeng, D.; Hu, Y.; Yang, J. Multi-objective optimization of IPMSM for electric vehicles based on the combinatorial surrogate model and the hierarchical design method. Int. J. Electr. Power Energy Syst. 2024, 162, 110245. [Google Scholar] [CrossRef]
- Keshavarzzadeh, A.H.; Maleki Zanjani, A.; Gharali, K.; Dusseault, M.B. Multi-objective evolutionary-based optimization of a ground source heat exchanger geometry using various optimization techniques. Geothermics 2020, 86, 101861. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, S.; Chen, G.; Tang, Y.; Liang, F. Experimental and numerical investigation on a novel heat pipe based cooling strategy for permanent magnet synchronous motors. Appl. Therm. Eng. 2020, 170, 114970. [Google Scholar] [CrossRef]
- Zhang, D.; Li, H.; Tian, Y.; You, R.; Zhang, X.; Wu, A. Effects of a high Reynolds number and rotation on the leading-edge heat transfer of a ribbed cooling channel with a cross-section consisting of a semicircle and a rectangle. Int. J. Heat Mass Transf. 2022, 188, 122646. [Google Scholar] [CrossRef]
- Chang, B.; Yuan, T.; Wang, Y.; Guo, H.; Li, Z.; Zhao, L.; Zhang, C.; Peng, S.; Deng, J. Cooling performance enhancement of electric vehicle film capacitor for ultra-high temperatures using micro-channel cold plates thermal management system. Int. J. Heat Mass Transf. 2024, 233, 126037. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, Q.; Zhang, H.; Wu, X.; Yu, D. Optimized design of liquid-cooled plate structure for flying car power battery system. J. Energy Storage 2024, 97, 112720. [Google Scholar] [CrossRef]
- Chang, M.; Lai, B.; Wang, H.; Bai, J.; Mao, Z. Comprehensive efficiency analysis of air-cooled vs water-cooled electric motor for unmanned aerial vehicle. Appl. Therm. Eng. 2023, 225, 120226. [Google Scholar] [CrossRef]
- Lin, X.; Lin, Z.; Wei, S. Multi-objective optimized driving strategy of dual-motor EVs using NSGA-II as a case study and comparison of various intelligent algorithms. Appl. Soft Comput. 2021, 111, 107684. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.; Xing, P.; Gao, H.; Song, Y.; Zhang, H. Numerical calculation and experimental investigation of the dynamic alignment of ship propulsion shafting based on Latin hypercube stochastic finite element. Ocean Eng. 2024, 296, 116935. [Google Scholar] [CrossRef]
- Liu, H.; Niu, W.; Guo, Y. Direct torque control for PMSM based on the RBFNN surrogate model of electromagnetic torque and stator flux linkage. Control Eng. Pract. 2024, 148, 105943. [Google Scholar] [CrossRef]







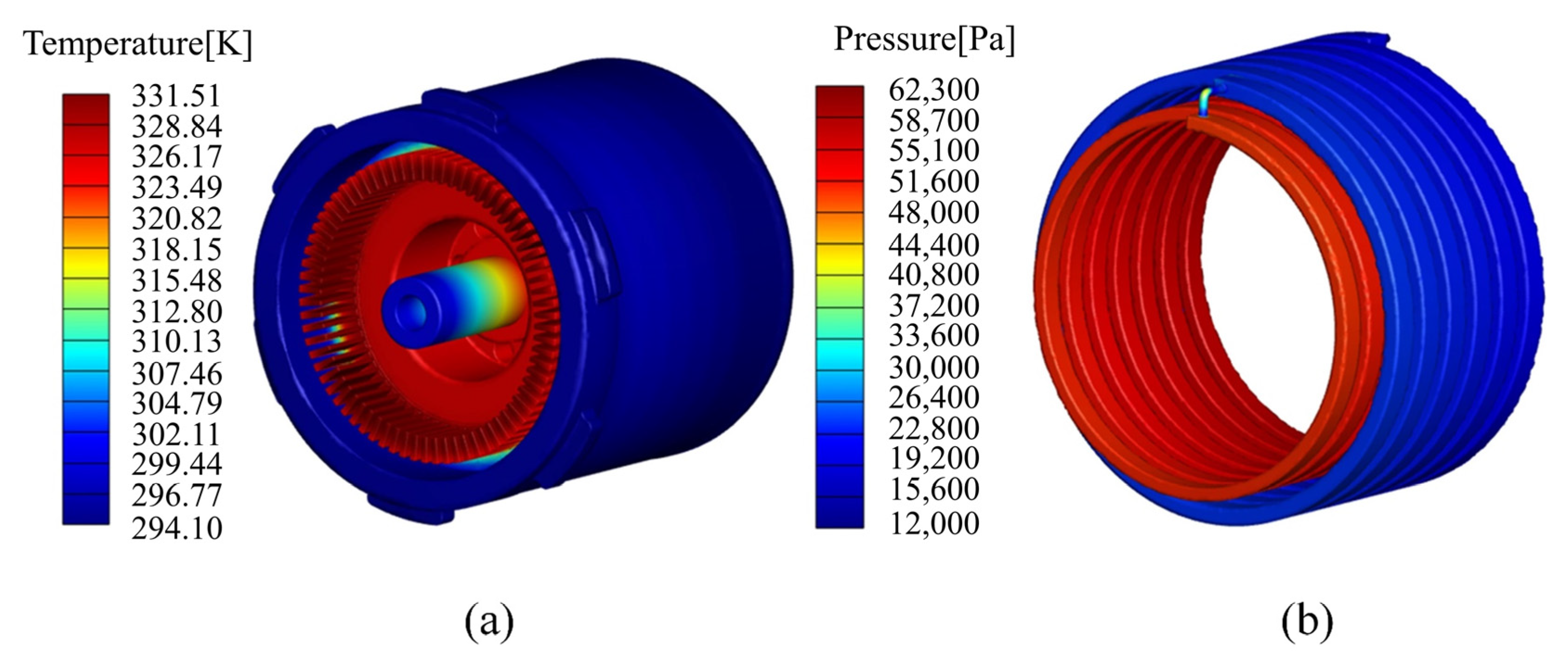
| Parameter | Values | Parameter | Values |
|---|---|---|---|
| Rated power (kW) | 90 | Rated speed (rpm) | 3000 |
| Stator inner diameter (mm) | 177 | Rotor inner diameter (mm) | 129 |
| Stator outer diameter (mm) | 237 | Rotor outer diameter (mm) | 156 |
| Stator length (mm) | 150 | Air gap length (mm) | 2.5 |
| Slots | 72 | Winding pitch | 5 |
| Magnet thickness (mm) | 8 | Parallel branches | 2 |
| Magnet width (mm) | 37.5 | Pole pairs | 6 |
| Pole-arc coefficient | 0.83 | Turns | 2 |
| Motor Components | Material | Specific Heat (J/kg⋅K) | Density (kg/m3) | Thermal Conductivity (W/m⋅K) |
|---|---|---|---|---|
| Winding | Copper | 390 | 8978 | Axial: 233 Radial: 2.82 Tangential:2.82 |
| Stator | 50WW350 | 460 | 7800 | Axial: 1.97 Radial: 25 Tangential:25 |
| Rotor | Stainless steel | 502 | 8030 | 16.27 |
| Magnet | Nd2Fe14B | 460 | 7500 | 7.60 |
| Potting insulation | Epoxy resin | 1500 | 1200 | 0.22 |
| Air gap | Air | 1000 | 1.29 | 0.15 |
| Motor housing | Aluminum | 924 | 2790 | 193 |
| Motor Component | Loss (W) | Effective Volume (m3) | Heat Generation Rate (kW/ m3) |
|---|---|---|---|
| Stator | 967.70 | 0.00206 | 469.89 |
| Rotor | 0.17 | 0.00087 | 0.19 |
| Winding | 2781.27 | 0.00129 | 2156.27 |
| Magnet | 2.30 | 0.00051 | 4.49 |
| Number of Grids (×106) | Tr (K) | Tm (K) | Ts (K) | Tw (K) | Pw (kPa) |
|---|---|---|---|---|---|
| 2 | 317.112 | 318.771 | 328.381 | 328.727 | 12.053 |
| 3 | 317.838 (0.73) | 319.550 (0.78) | 329.854 (1.47) | 329.593 (0.87) | 12.449 (0.396) |
| 4 | 318.501 (0.66) | 320.669 (1.12) | 330.645 (0.79) | 331.280 (1.69) | 13.155 (0.706) |
| 4.5 | 319.636 (1.14) | 321.195 (0.53) | 331.801 (1.16) | 333.762 (2.48) | 13.978 (0.823) |
| 5 | 319.851 (0.22) | 321.628 (0.43) | 331.931 (0.13) | 334.009 (0.25) | 14.283 (0.305) |
| 5.5 | 319.896 (0.05) | 321.714 (0.09) | 332.110 (0.18) | 334.082 (0.07) | 14.292 (0.009) |
| Evaluation Indicator | R2 | MAE | RMSE |
|---|---|---|---|
| Tmax | 0.9952 | 0.0586 | 0.0552 |
| Pw | 0.9984 | 4.5847 | 370.6325 |
| Parameter | Value |
|---|---|
| Initial sample size | 6000 |
| Number of samples per cycle | 1200 |
| Maximum allowable Pareto percentage | 30 |
| Maximum number of cycles | 20 |
| Maximum number of candidate points | 5 |
| Cross-probability | 0.9 |
| Mutation probability | 0.1 |
| Optimization Variable | Initial Design Value | Candidate Point 1 | Candidate Point 2 | Candidate Point 3 | Candidate Point 4 | Candidate Point 5 | Maximum Improvement Rate |
|---|---|---|---|---|---|---|---|
| Wa (mm) | 24 | 20.33 | 18.86 | 18.04 | 19.32 | 18.89 | −15.29% |
| Wb (mm) | 10 | 11.92 | 11.89 | 11.99 | 11.92 | 11.78 | +19.20% |
| Na (mm) | 24 | 17.78 | 17.08 | 17.00 | 17.22 | 17.39 | −25.92% |
| Nb (mm) | 10 | 9.10 | 9.25 | 9.05 | 9.43 | 9.08 | −9.00% |
| D (mm) | 5 | 5.13 | 5.70 | 5.42 | 4.77 | 5.66 | +2.62% |
| Qw (L/min) | 11 | 9.62 | 9.63 | 9.66 | 9.67 | 9.69 | −12.55% |
| Tmax (K) | 332.86 | 331.46 | 331.48 | 331.49 | 331.48 | 331.49 | −0.42% |
| Pw (kPa) | 100.02 | 59.58 | 59.92 | 59.81 | 59.73 | 59.74 | −40.43% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Zhang, C.; Mao, Z.; Cheng, B. Optimization of a Dual-Channel Water-Cooling Heat Dissipation System for PMSM in Underwater Unmanned Vehicles Using a Multi-Objective Genetic Algorithm. J. Mar. Sci. Eng. 2024, 12, 2133. https://doi.org/10.3390/jmse12122133
Tian W, Zhang C, Mao Z, Cheng B. Optimization of a Dual-Channel Water-Cooling Heat Dissipation System for PMSM in Underwater Unmanned Vehicles Using a Multi-Objective Genetic Algorithm. Journal of Marine Science and Engineering. 2024; 12(12):2133. https://doi.org/10.3390/jmse12122133
Chicago/Turabian StyleTian, Wenlong, Chen Zhang, Zhaoyong Mao, and Bo Cheng. 2024. "Optimization of a Dual-Channel Water-Cooling Heat Dissipation System for PMSM in Underwater Unmanned Vehicles Using a Multi-Objective Genetic Algorithm" Journal of Marine Science and Engineering 12, no. 12: 2133. https://doi.org/10.3390/jmse12122133
APA StyleTian, W., Zhang, C., Mao, Z., & Cheng, B. (2024). Optimization of a Dual-Channel Water-Cooling Heat Dissipation System for PMSM in Underwater Unmanned Vehicles Using a Multi-Objective Genetic Algorithm. Journal of Marine Science and Engineering, 12(12), 2133. https://doi.org/10.3390/jmse12122133




