Graphics Processing Unit-Accelerated Propeller Computational Fluid Dynamics Using AmgX: Performance Analysis Across Mesh Types and Hardware Configurations
Abstract
1. Introduction
1.1. Background
1.2. Current Status of GPU-Accelerated CFD Research
1.3. Current Status of CFD Research on Propellers
1.4. Outline of This Work
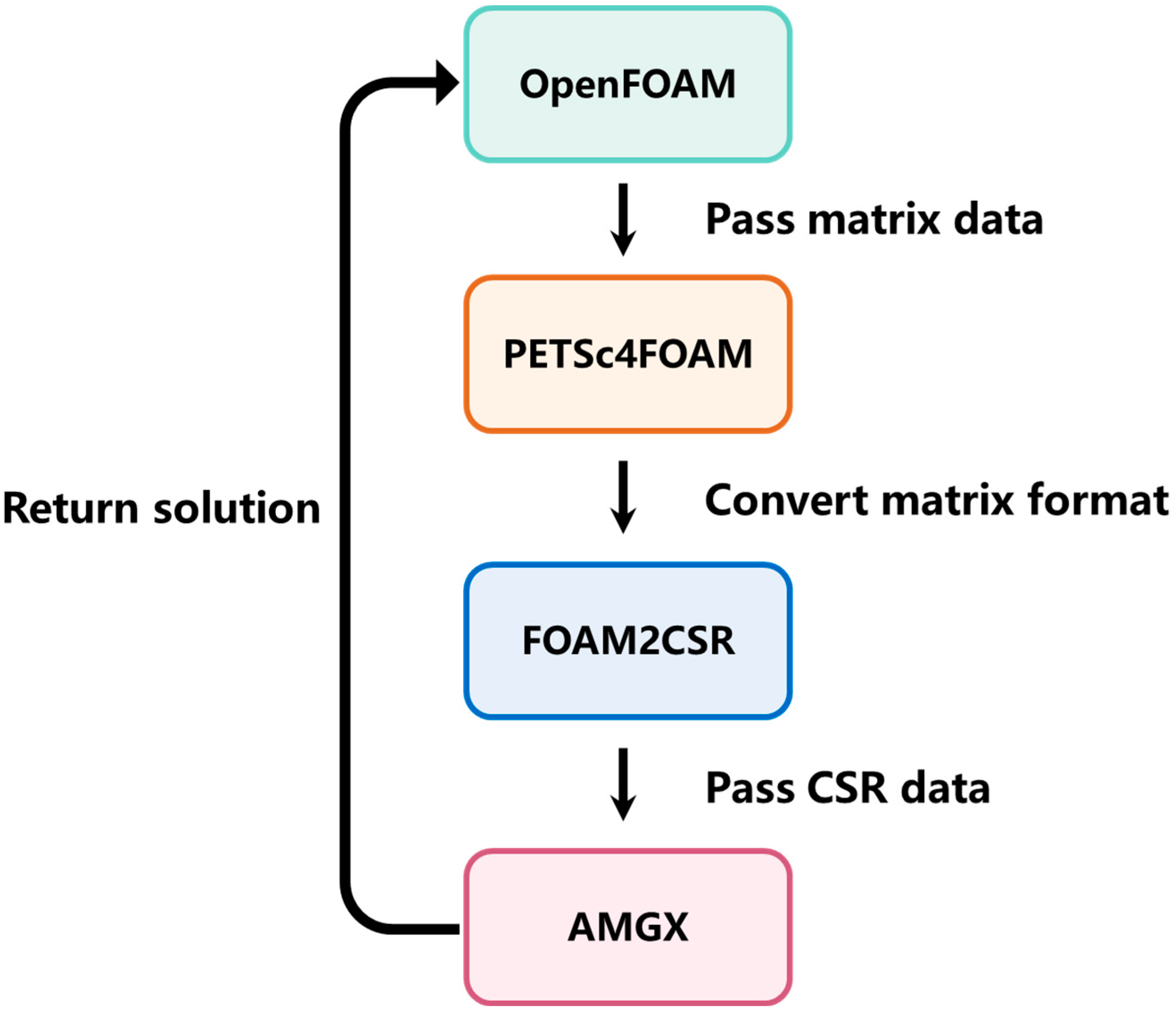
2. GPU-Accelerated OpenFOAM Implementation Based on AmgX Library
2.1. Integration Strategy of AmgX Library with OpenFOAM
2.2. Algebraic Multigrid Method in the AmgX Library
2.3. Implementation of AmgX Library in OpenFOAM
3. CFD Simulation
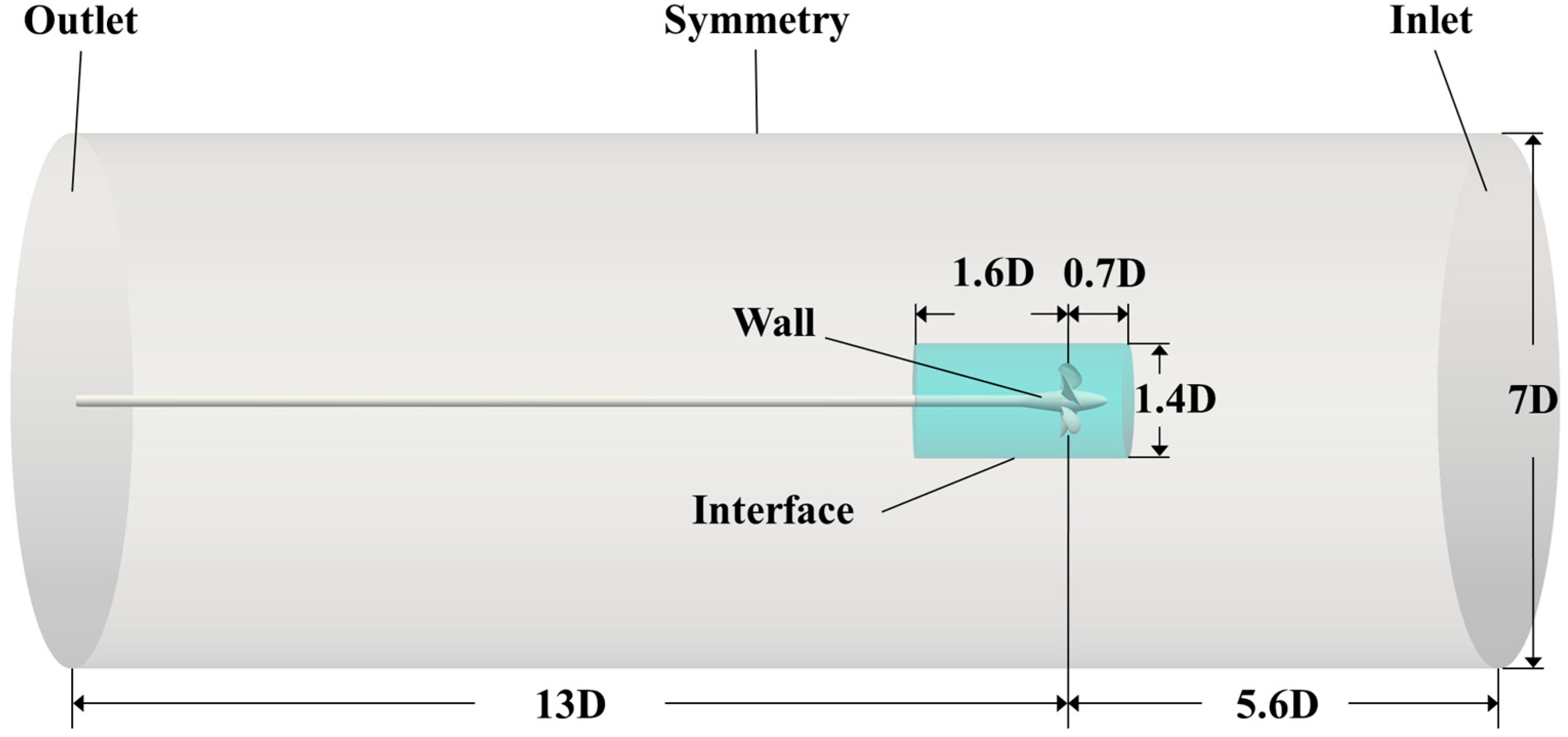
3.1. VP 1304 Parameters and Computational Domain Setup
3.2. Governing Equation
3.3. Simulation Setup
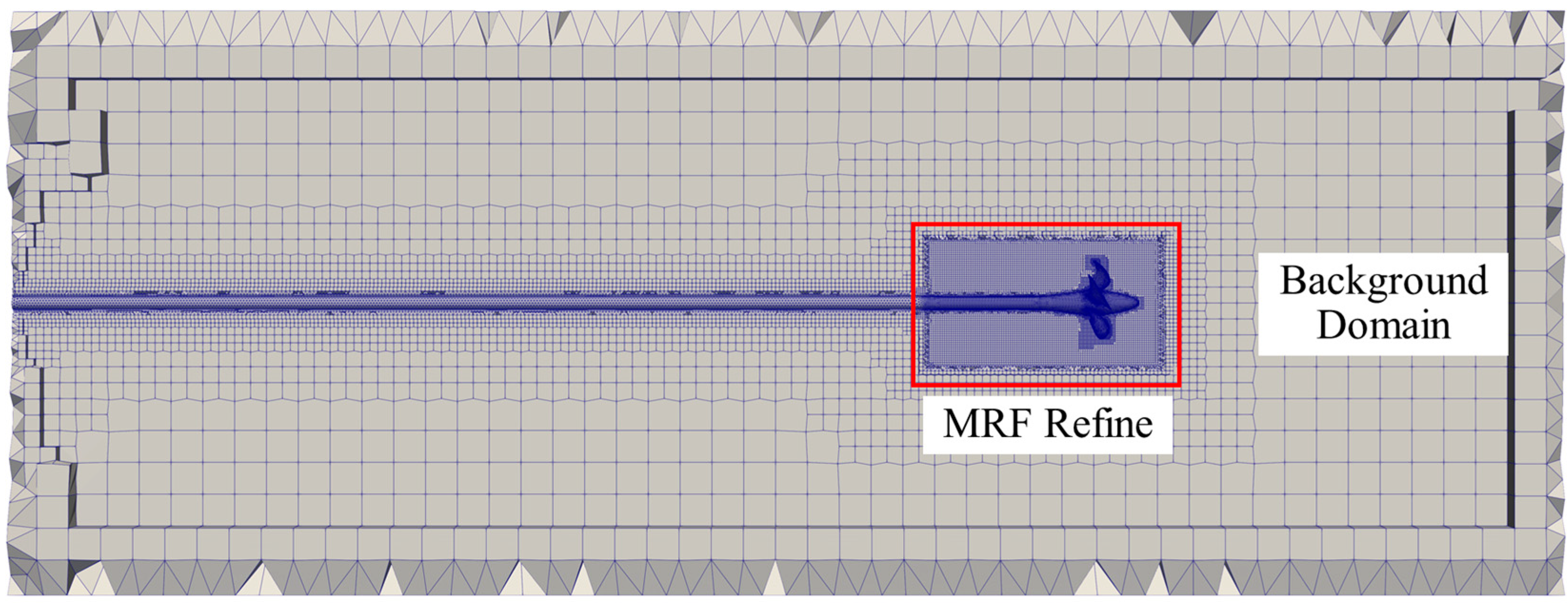
3.4. Grid Size Independence Analysis
3.5. Hardware and Computational Conditions
4. Results and Discussion
4.1. Impact of GPU Solver and Mesh Type on Computational Outcomes
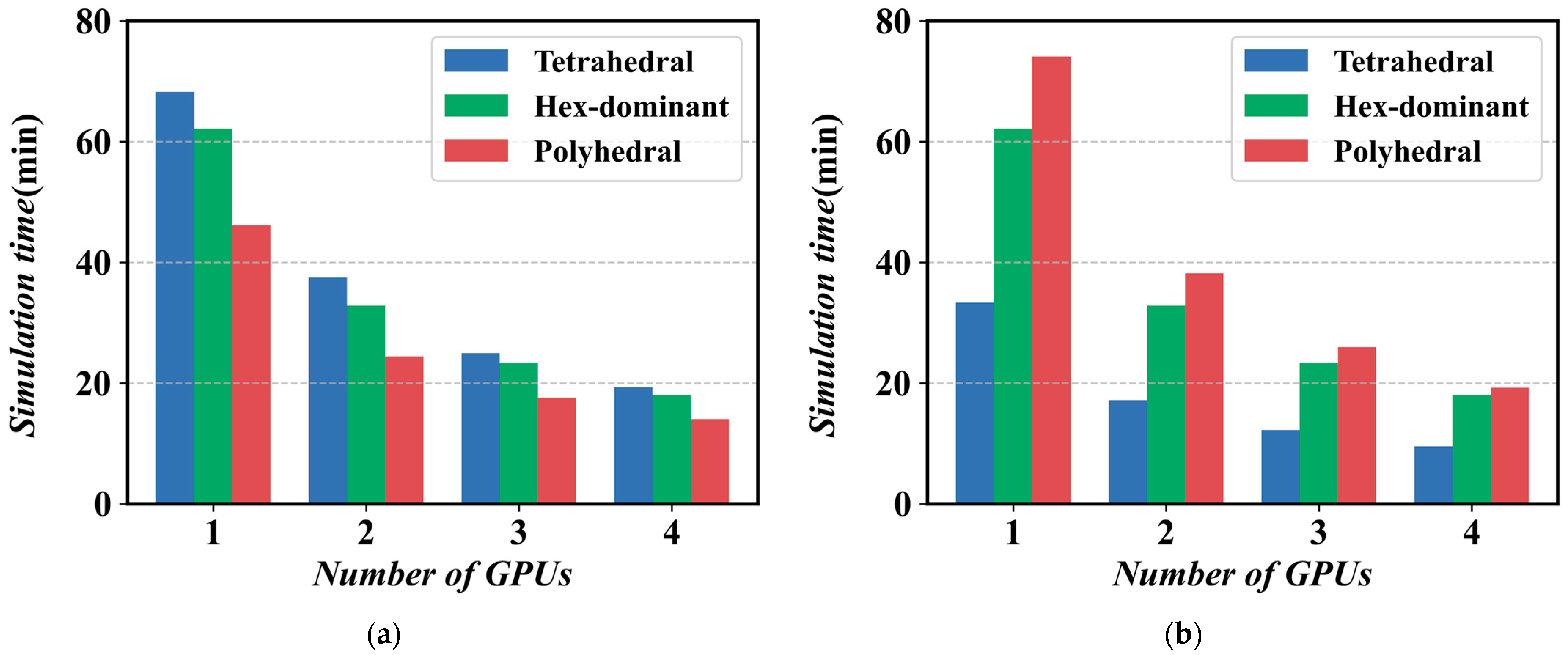
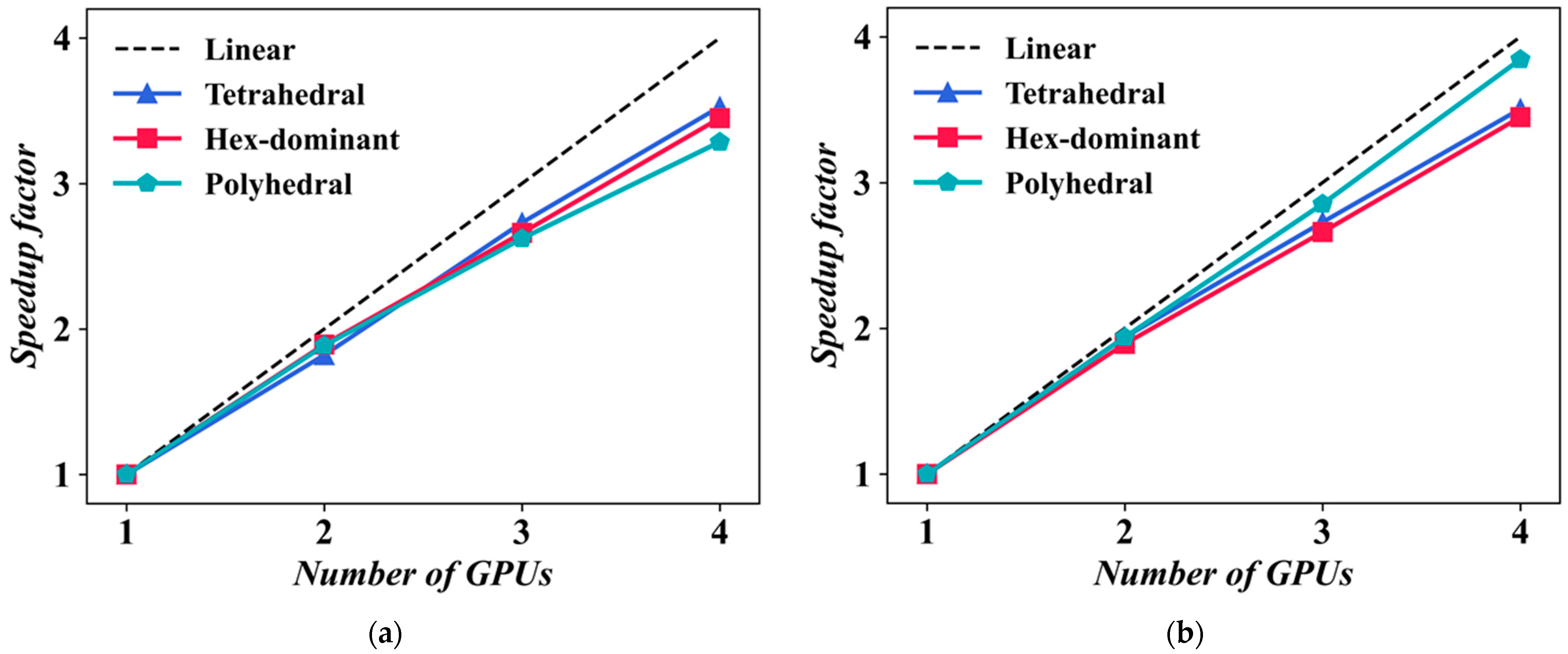
4.2. Native CPU Solver Parallel Efficiency
4.3. GPU Solver Parallel Efficiency
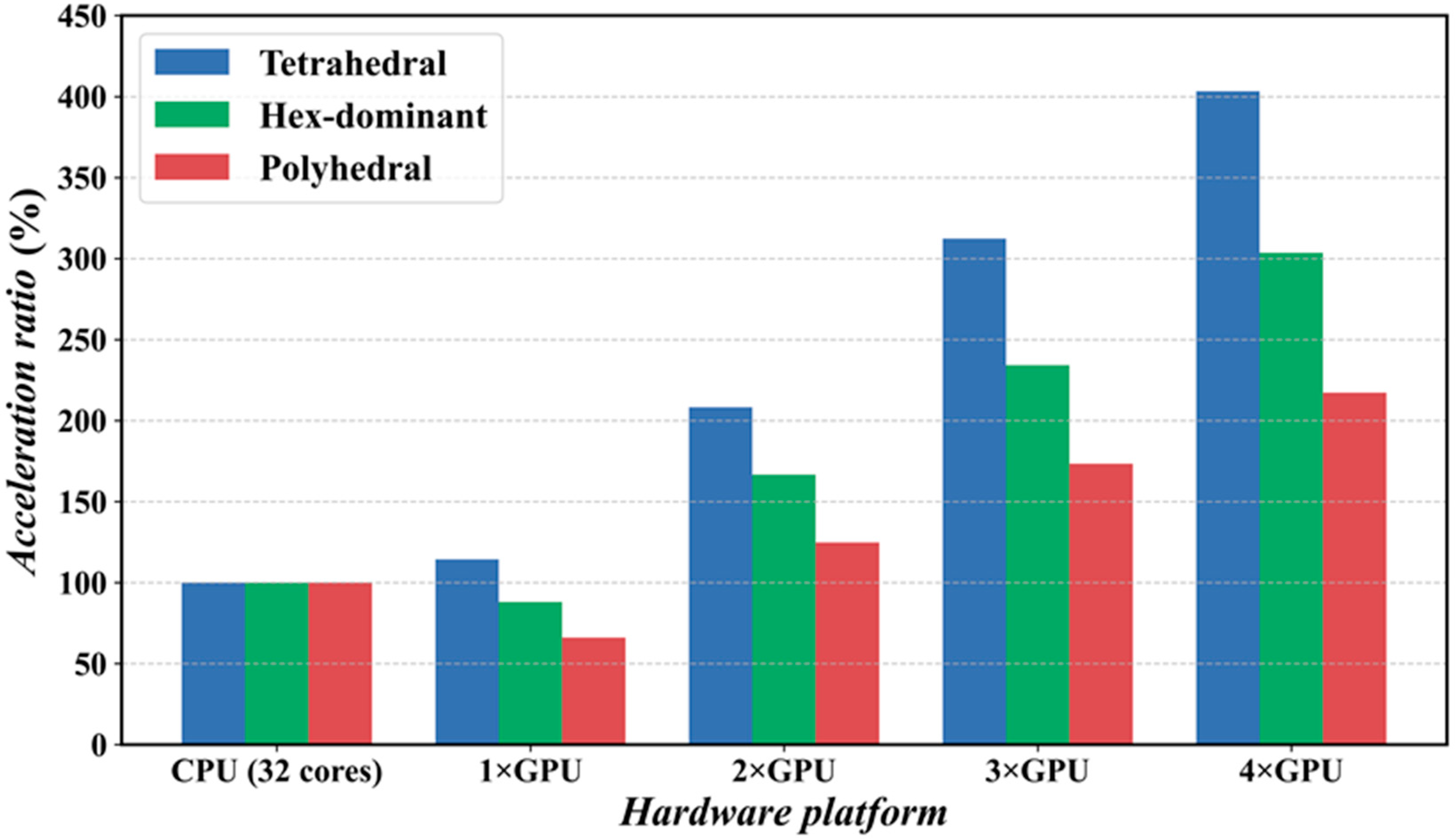
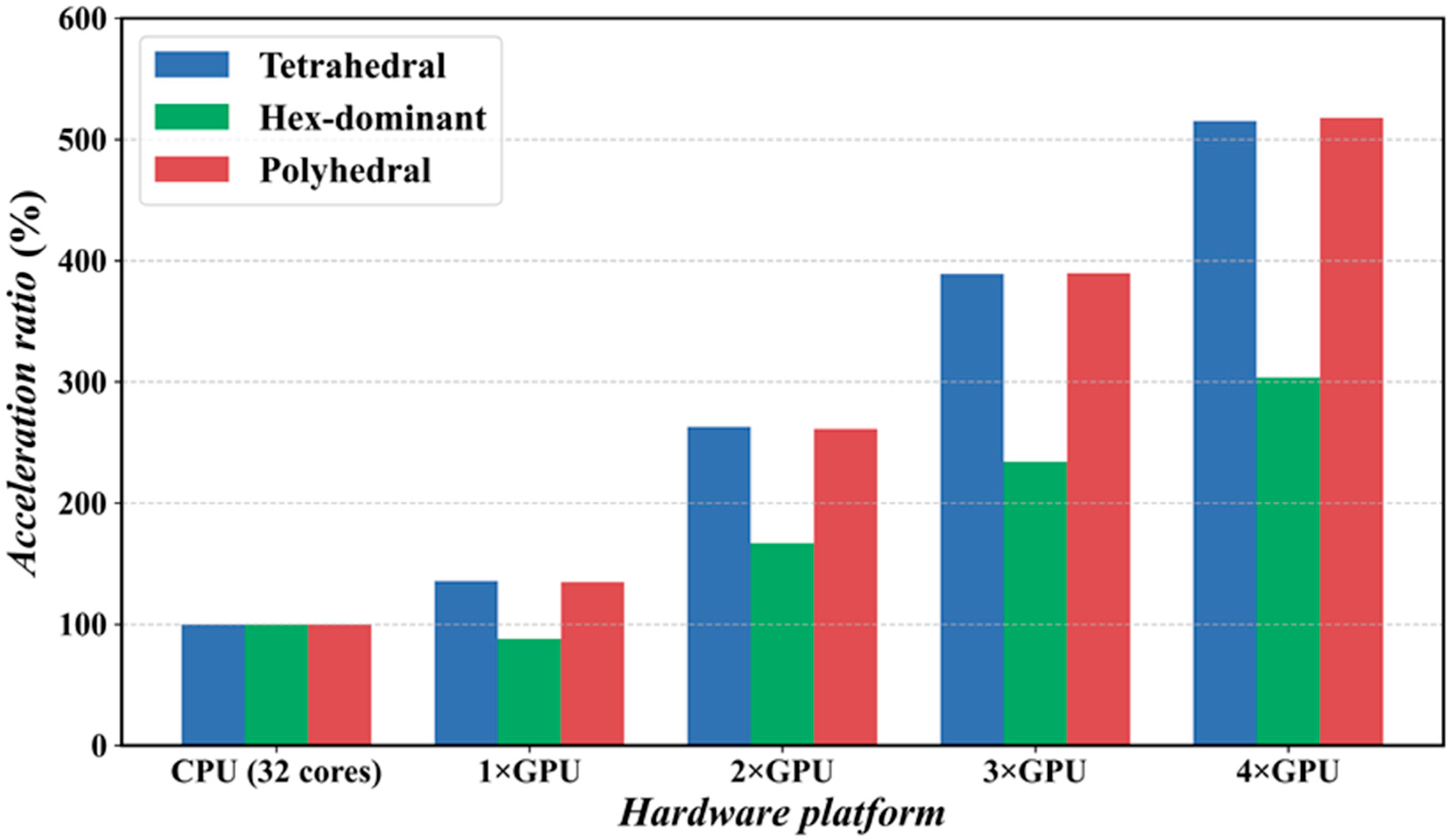
4.4. Acceleration Effect of GPU Compared to CPU Solvers
5. Conclusions
- 1.
- GPU acceleration substantially enhanced the computational efficiency of propeller CFD simulations. In a 4 GPU setup, tetrahedral meshes achieved more than 400% speedup, while polyhedral meshes exceeded 500% speedup under fixed grid count conditions. This suggests that GPU acceleration techniques have the potential to dramatically reduce propeller design and optimization timelines.
- 2.
- The type of mesh significantly influences the effectiveness of GPU acceleration. For fixed grid sizes, tetrahedral meshes showed the highest acceleration, whereas for fixed grid counts, polyhedral meshes demonstrated optimal performance. This discovery offers valuable insights for refining mesh strategies in GPU-accelerated CFD simulations.
- 3.
- The efficiency of GPU acceleration is strongly correlated with the scale of the problem. For large-scale problems, GPUs show more significant advantages, suggesting they are especially well-suited for computationally demanding, large-scale CFD simulation tasks. Results from GPU and CPU computations show high consistency and good agreement with experimental data, confirming the reliability of GPU acceleration methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gropp, W.D.; Kaushik, D.K.; Keyes, D.E.; Smith, B.F. Latency, Bandwidth, and Concurrent Issue Limitations in High-Performance CFD; Argonne National Lab: Lemont, IL, USA, 2000. [Google Scholar]
- Bandi, A.; Adapa, P.V.S.R.; Kuchi, Y.E.V.P.K. The Power of Generative AI: A Review of Requirements, Models, Input–Output Formats, Evaluation Metrics, and Challenges. Future Internet 2023, 15, 260. [Google Scholar] [CrossRef]
- Majumder, P.; Maity, S. A Critical Review of Different Works on Marine Propellers over the Last Three Decades. Ships Offshore Struct. 2022, 18, 391–413. [Google Scholar] [CrossRef]
- Grlj, C.G.; Degiuli, N.; Tuković, Ž.; Farkas, A.; Martić, I. The Effect of Loading Conditions and Ship Speed on the Wind and Air Resistance of a Containership. Ocean Eng. 2023, 273, 113991. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Tomljenović, I.; Martić, I. Numerical Investigation of Interference Effects for the Delft 372 Catamaran. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2024, 238, 385–394. [Google Scholar] [CrossRef]
- Kim, K.-W.; Paik, K.-J.; Lee, J.-H.; Song, S.-S.; Atlar, M.; Demirel, Y.K. A Study on the Efficient Numerical Analysis for the Prediction of Full-Scale Propeller Performance Using CFD. Ocean Eng. 2021, 240, 109931. [Google Scholar] [CrossRef]
- Agrawal, S.; Kumar, M.; Roy, S. Demonstration of GPGPU-Accelerated Computational Fluid Dynamic Calculations. In Proceedings of the Intelligent Computing and Applications; Mandal, D., Kar, R., Das, S., Panigrahi, B.K., Eds.; Springer: New Delhi, India, 2015; pp. 519–525. [Google Scholar]
- Pickering, B.P.; Jackson, C.W.; Scogland, T.R.W.; Feng, W.-C.; Roy, C.J. Directive-Based GPU Programming for Computational Fluid Dynamics. Comput. Fluids 2015, 114, 242–253. [Google Scholar] [CrossRef]
- Niemeyer, K.E.; Sung, C.-J. Recent Progress and Challenges in Exploiting Graphics Processors in Computational Fluid Dynamics. J. Supercomput. 2014, 67, 528–564. [Google Scholar] [CrossRef]
- Trimulyono, A.; Atthariq, H.; Chrismianto, D.; Samuel, S. Investigation of sloshing in the prismatic tank with vertical and t-shape baffles. Brodogradnja 2022, 73, 43–58. [Google Scholar] [CrossRef]
- Wu, E.; Liu, Y.; Liu, X. An Improved Study of Real-Time Fluid Simulation on GPU. Comput. Animat. Virtual 2004, 15, 139–146. [Google Scholar] [CrossRef]
- Harris, M. Fast Fluid Dynamics Simulation on the GPU. In Proceedings of the ACM SIGGRAPH 2005 Courses on—SIGGRAPH ’05, Los Angeles, CA, USA, 31 July–4 August 2005; ACM Press: Los Angeles, CA, USA, 2005; p. 220. [Google Scholar]
- Stam, J. Stable Fluids. In Seminal Graphics Papers: Pushing the Boundaries; Whitton, M.C., Ed.; ACM: New York, NY, USA, 2023; Volume 2, pp. 779–786. ISBN 9798400708978. [Google Scholar]
- Jespersen, D.C. Acceleration of a CFD Code with a GPU. Sci. Program. 2010, 18, 564806. [Google Scholar] [CrossRef]
- Brandvik, T.; Pullan, G. Acceleration of a Two-Dimensional Euler Flow Solver Using Commodity Graphics Hardware. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 1745–1748. [Google Scholar] [CrossRef]
- Brandvik, T.; Pullan, G. Acceleration of a 3D Euler Solver Using Commodity Graphics Hardware. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit; American Institute of Aeronautics and Astronautics, Reno, NV, USA, 7 January 2008. [Google Scholar]
- Brandvik, T.; Pullan, G. An Accelerated 3D Navier-Stokes Solver for Flows in Turbomachines. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea and Air, Orlando FL, USA, 8–12 June 2009. [Google Scholar]
- Dyson, J. GPU Accelerated Linear System Solvers for OpenFOAM and Their Application to Sprays. Ph.D. Thesis, Brunel University of London, London, UK, 2018. [Google Scholar]
- Piscaglia, F.; Ghioldi, F. GPU Acceleration of CFD Simulations in OpenFOAM. Aerospace 2023, 10, 792. [Google Scholar] [CrossRef]
- Grlj, C.G.; Degiuli, N.; Farkas, A.; Martić, I. Numerical Study of Scale Effects on Open Water Propeller Performance. J. Mar. Sci. Eng. 2022, 10, 1132. [Google Scholar] [CrossRef]
- Dong, X.-Q.; Li, W.; Yang, C.-J.; Noblesse, F. RANSE-Based Simulation and Analysis of Scale Effects on Open-Water Performance of the PPTC-II Benchmark Propeller. J. Ocean. Eng. Sci. 2018, 3, 186–204. [Google Scholar] [CrossRef]
- Permadi, N.V.A.; Sugianto, E. CFD Simulation Model for Optimum Design of B-Series Propeller Using Multiple Reference Frame (MRF). CFD Lett. 2022, 14, 22–39. [Google Scholar] [CrossRef]
- Van-Vu, H.; Le, T.-H.; Thien, D.M.; Tao, T.V.; Ngoc, T.T. Numerical Study of the Scale Effect on Flow Around a Propeller Using the CFD Method. Pol. Marit. Res. 2024, 31, 59–66. [Google Scholar] [CrossRef]
- Liu, Y.; Wan, D. Energy Saving Mechanism of Propeller with Endplates at Blade Tips. In Proceedings of the International Conference on Computational Methods ICCM 2019, Beijing, China, 9–14 June 2019. [Google Scholar]
- Bahatmaka, A.; Kim, D.-J.; Zhang, Y. Verification of CFD Method for Meshing Analysis on the Propeller Performance with OpenFOAM. In Proceedings of the 2018 International Conference on Computing, Electronics & Communications Engineering (iCCECE), University of Essex, Southend, UK, 16–17 August 2018; pp. 302–306. [Google Scholar]
- Vargas Loureiro, E.; Oliveira, N.L.; Hallak, P.H.; De Souza Bastos, F.; Rocha, L.M.; Grande Pancini Delmonte, R.; De Castro Lemonge, A.C. Evaluation of Low Fidelity and CFD Methods for the Aerodynamic Performance of a Small Propeller. Aerosp. Sci. Technol. 2021, 108, 106402. [Google Scholar] [CrossRef]
- Yurtseven, A.; Aktay, K. The Numerical Investigation of Spindle Torque for a Controllable Pitch Propeller in Feathering Maneuver. Brodogradnja 2023, 74, 95–108. [Google Scholar] [CrossRef]
- Dubbioso, G.; Muscari, R.; Mascio, A.D. CFD Analysis of Propeller Performance in Oblique Flow. In Proceedings of the Third International Symposium on Marine Propulsors, Launceston, Australia, 5–8 May 2023. [Google Scholar]
- Rhee, S.H.; Joshi, S. CFD Validation for a Marine Propeller Using an Unstructured Mesh Based RANS Method. In Proceedings of the ASME/JSME 2003 4th Joint Fluids Summer Engineering Conference, Honolulu, HI, USA, 6–10 July 2003; Volume 1: Fora, Parts A, B, C and D, pp. 1157–1163. [Google Scholar]
- Lee, B.-S.; Jung, M.-S.; Kwon, O.-J.; Kang, H.-J. Numerical Simulation of Rotor-Fuselage Aerodynamic Interaction Using an Unstructured Overset Mesh Technique. Int. J. Aeronaut. Space Sci. 2010, 11, 1–9. [Google Scholar] [CrossRef]
- Naumov, M.; Arsaev, M.; Castonguay, P.; Cohen, J.; Demouth, J.; Eaton, J.; Layton, S.; Markovskiy, N.; Reguly, I.; Sakharnykh, N.; et al. AmgX: A Library for GPU Accelerated Algebraic Multigrid and Preconditioned Iterative Methods. SIAM J. Sci. Comput. 2015, 37, S602–S626. [Google Scholar] [CrossRef]
- Stone, C.P.; Walden, A.; Zubair, M.; Nielsen, E.J. Accelerating Unstructured-Grid CFD Algorithms on NVIDIA and AMD GPUs. In Proceedings of the 2021 IEEE/ACM 11th Workshop on Irregular Applications: Architectures and Algorithms (IA3), St. Louis, MO, USA, 15 November 2021; pp. 19–26. [Google Scholar]
- Rathnayake, T.; Jayasena, S.; Narayana, M. Openfoam on GPUS Using AMGX. In Proceedings of the 25th High Performance Computing Symposium, Virginia Beach, VA, USA, 23–26 April 2017. [Google Scholar]
- Bna, S.; Spisso, I.; Olesen, M.; Rossi, G. PETSc4FOAM: A Library to Plug-in PETSc into the OpenFOAM Framework. Zenodo, 6 June 2020. Available online: https://www.semanticscholar.org/paper/PETSc4FOAM%3A-a-library-to-plug-in-PETSc-into-the-Bn%C3%A0-Spisso/0234a490ba9a3647a5ed4f35bee9a70f07cb2e49 (accessed on 24 September 2024).
- openfoam/FOAM2CSR·GitLab. Available online: https://gitlab.hpc.cineca.it/openfoam/foam2csr (accessed on 24 September 2024).
- SVA_report_3752. Available online: https://www.sva-potsdam.de/wp-content/uploads/2016/04/SVA_report_3752.pdf (accessed on 24 September 2024).
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New Inflow Boundary Conditions for Modelling the Neutral Equilibrium Atmospheric Boundary Layer in Computational Wind Engineering. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- Sawant, N.; Yamakawa, S.; Singh, S.; Shimada, K. Automatic Hex-Dominant Mesh Generation for Complex Flow Configurations. SAE Int. J. Engines 2018, 11, 615–624. [Google Scholar] [CrossRef]
- Zhang, R.; Lam, K.P.; Zhang, Y. Conformal Adaptive Hexahedral-Dominant Mesh Generation for CFD Simulation in Architectural Design Applications. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 928–942. [Google Scholar]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-319-99691-2. [Google Scholar]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Comprehensive Approach to Verification and Validation of CFD Simulations—Part 1: Methodology and Procedures. J. Fluids Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Wilson, R.V.; Stern, F.; Coleman, H.W.; Paterson, E.G. Comprehensive Approach to Verification and Validation of CFD Simulations—Part 2: Application for Rans Simulation of a Cargo/Container Ship. J. Fluids Eng. 2001, 123, 803–810. [Google Scholar] [CrossRef]
- Duan, R.; Liu, W.; Xu, L.; Huang, Y.; Shen, X.; Lin, C.-H.; Liu, J.; Chen, Q.; Sasanapuri, B. Mesh Type and Number for the CFD Simulations of Air Distribution in an Aircraft Cabin. Numer. Heat. Transf. Part B Fundam. 2015, 67, 489–506. [Google Scholar] [CrossRef]
- Chawner, J.R.; Dannenhoffer, J.; Taylor, N.J. Geometry, Mesh Generation, and the CFD 2030 Vision. In Proceedings of the 46th American Institute of Aeronautics and Astronautics AIAA Fluid Dynamics Conference, Washington, DC, USA, 13 June 2016. [Google Scholar]
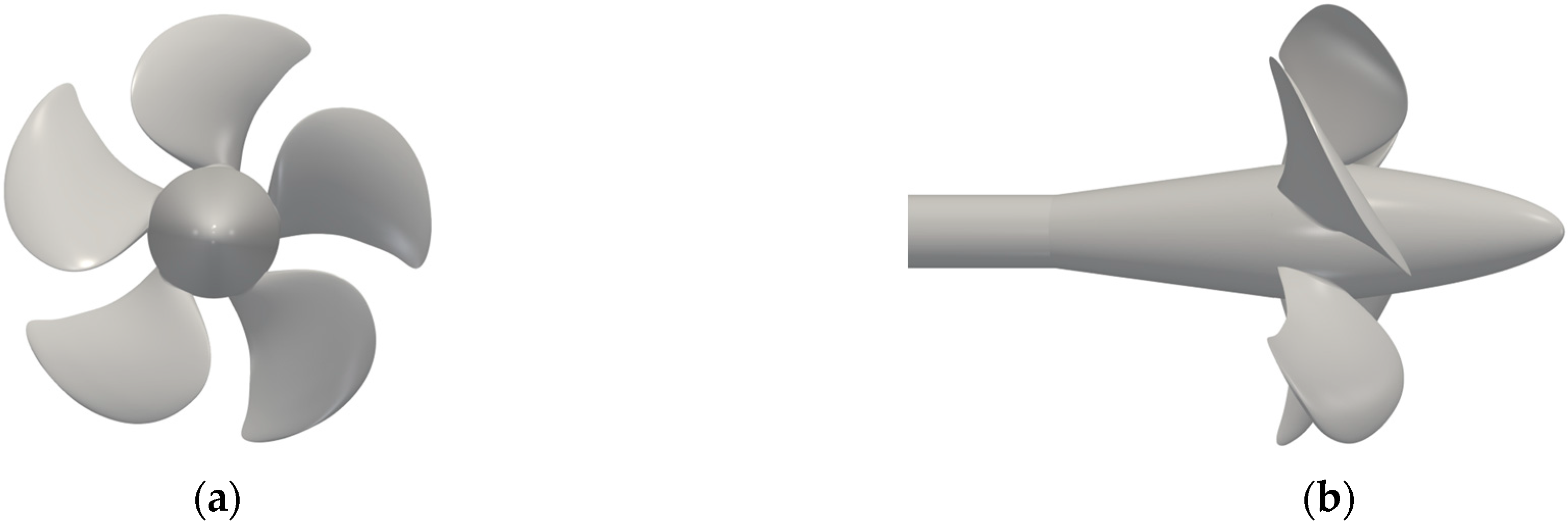
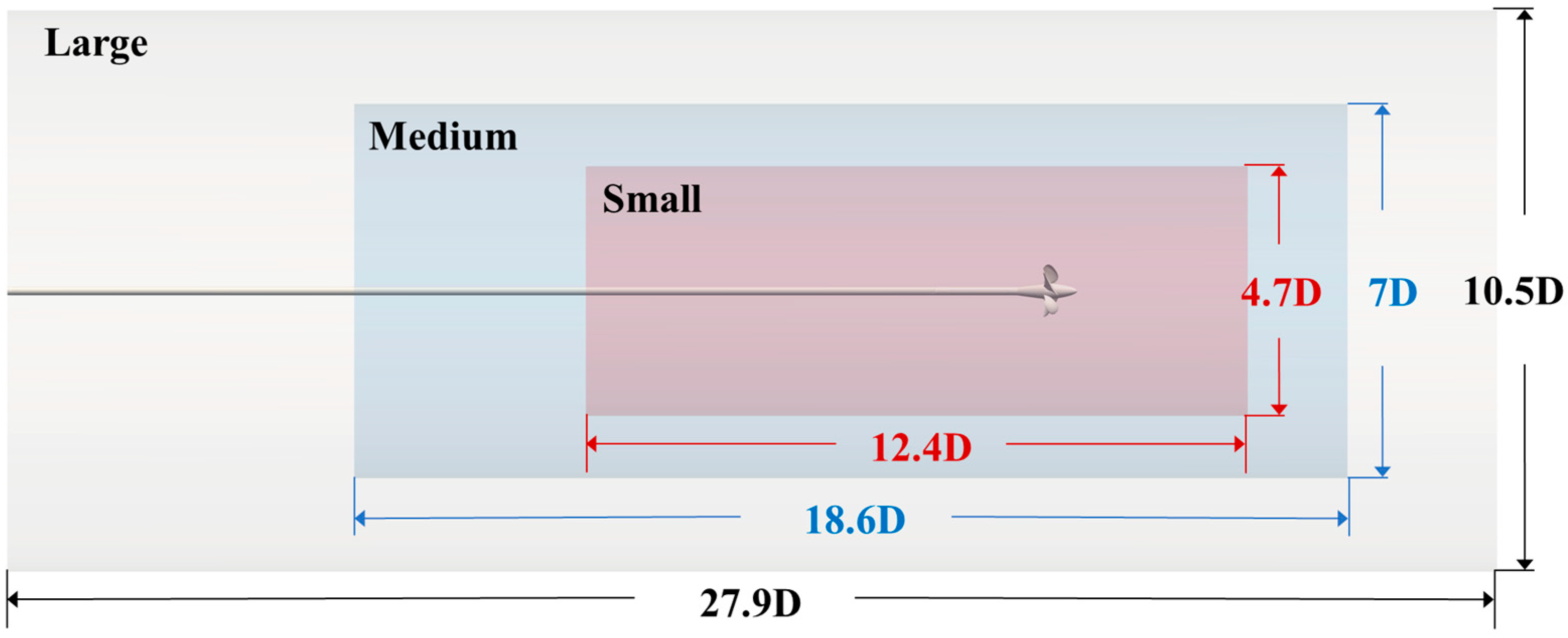



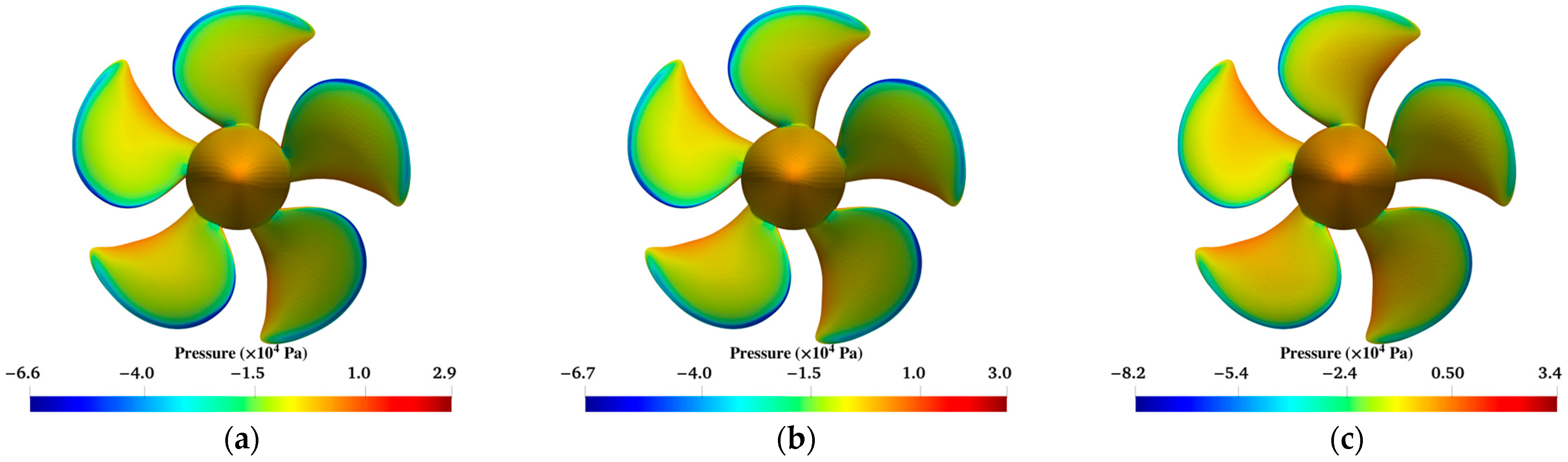


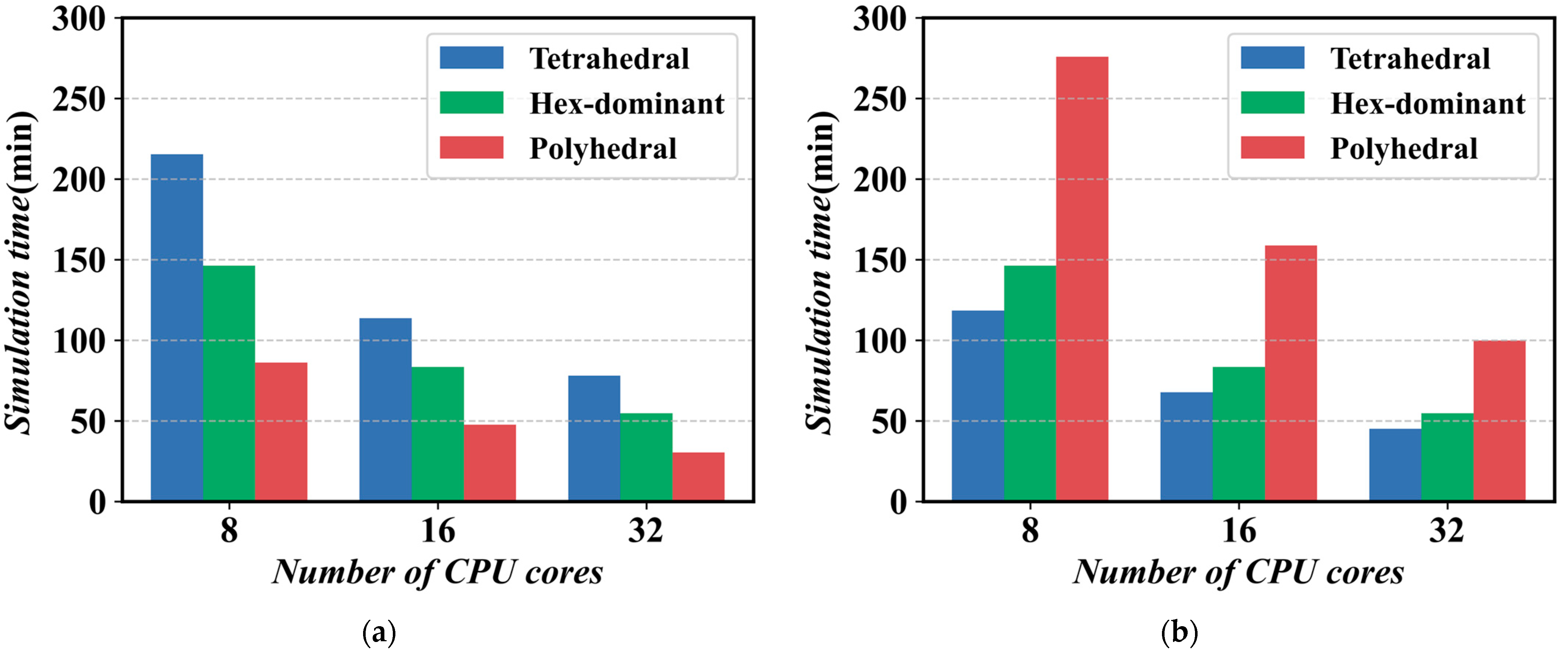
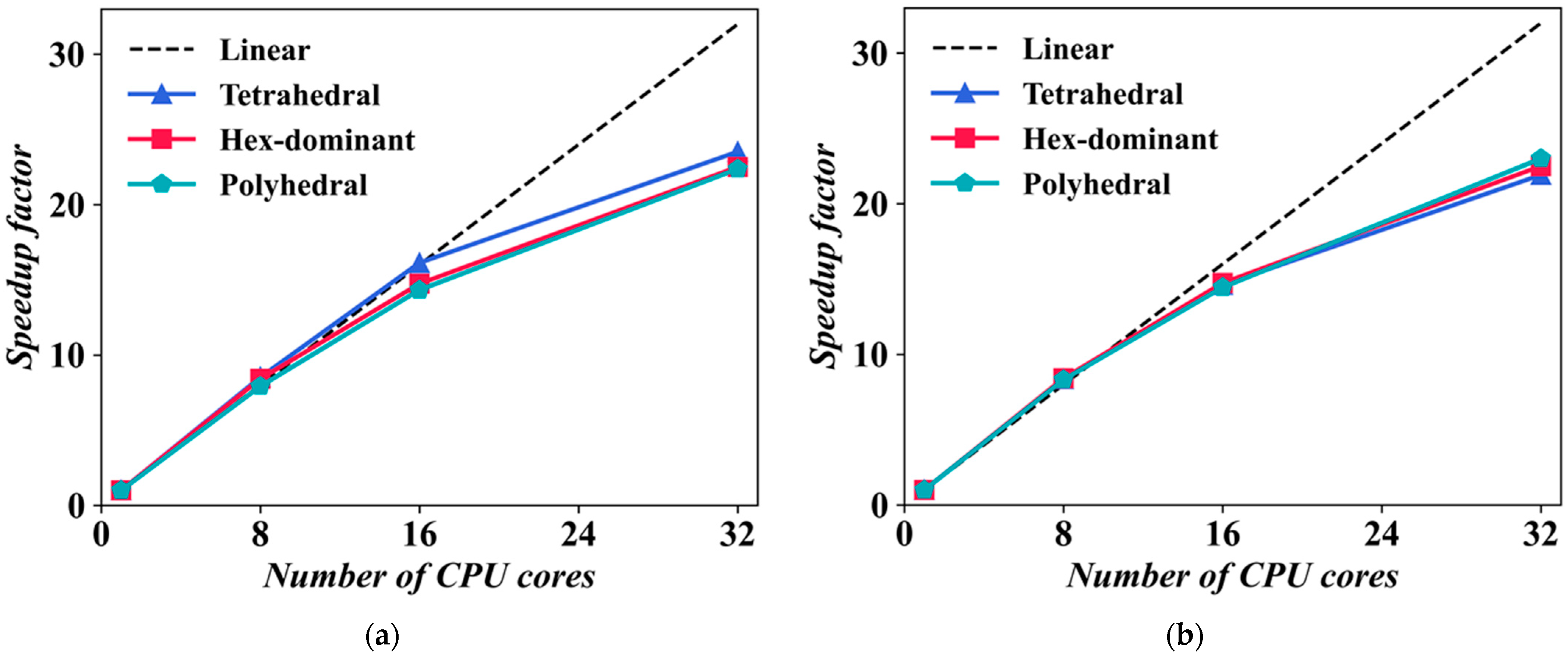
| Parameter | Unit | Value |
|---|---|---|
| Propellel diameter | m | 0.25 |
| Chord length (0.75 R) | m | 0.106 |
| Pitch ratio | 1.635 | |
| Skew angle | ° | 18.837 |
| Aera ratio | 0.779 | |
| Number of blades | 5 |
| J | KT | 10 KQ | η0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp | Grid Size (mm) | Exp | Grid Size (mm) | Exp | Grid Size (mm) | |||||||
| 3.15 | 4.5 | 6.3 | 3.15 | 4.5 | 6.3 | 3.15 | 4.5 | 6.3 | ||||
| 0.6 | 0.629 | 0.619 | 0.607 | 0.617 | 1.396 | 1.439 | 1.440 | 1.444 | 0.430 | 0.411 | 0.409 | 0.402 |
| 0.8 | 0.510 | 0.500 | 0.496 | 0.501 | 1.178 | 1.211 | 1.213 | 1.220 | 0.551 | 0.525 | 0.525 | 0.518 |
| 1.0 | 0.399 | 0.384 | 0.381 | 0.387 | 0.975 | 0.992 | 0.993 | 1.005 | 0.652 | 0.615 | 0.615 | 0.604 |
| 1.2 | 0.295 | 0.272 | 0.270 | 0.275 | 0.776 | 0.774 | 0.775 | 0.787 | 0.726 | 0.670 | 0.670 | 0.656 |
| 1.4 | 0.188 | 0.158 | 0.152 | 0.162 | 0.559 | 0.538 | 0.538 | 0.552 | 0.749 | 0.655 | 0.652 | 0.613 |
| εAvg | - | 6.22% | 6.36% | 7.64% | - | 2.31% | 2.37% | 2.52% | - | 6.99% | 7.2% | 9.56% |
| J | KT | 10 KQ | η0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp | Simulation Domain | Exp | Simulation Domain | Exp | Simulation Domain | |||||||
| S | M | L | S | M | L | S | M | L | ||||
| 0.6 | 0.629 | 0.615 | 0.617 | 0.622 | 1.396 | 1.447 | 1.440 | 1.433 | 0.430 | 0.406 | 0.409 | 0.410 |
| 0.8 | 0.510 | 0.497 | 0.500 | 0.503 | 1.178 | 1.216 | 1.213 | 1.206 | 0.551 | 0.521 | 0.525 | 0.525 |
| 1.0 | 0.399 | 0.381 | 0.384 | 0.384 | 0.975 | 0.991 | 0.993 | 0.985 | 0.652 | 0.612 | 0.615 | 0.615 |
| 1.2 | 0.295 | 0.268 | 0.272 | 0.270 | 0.776 | 0.769 | 0.775 | 0.765 | 0.726 | 0.667 | 0.670 | 0.670 |
| 1.4 | 0.188 | 0.154 | 0.157 | 0.153 | 0.559 | 0.525 | 0.538 | 0.527 | 0.749 | 0.652 | 0.652 | 0.650 |
| εAvg | - | 7.3% | 6.36% | 6.64% | - | 3.08% | 2.37% | 2.63% | - | 7.66% | 7.2% | 7.19% |
| Platform | Hardware Model | Processor Cores | Memory Size | Number |
|---|---|---|---|---|
| CPU | EPYC 7551p | 32 (Physical) | 128 GB | 1 |
| GPU | Tesla M40 | 3072 (CUDA) | 24 GB | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Gan, J.; Lin, Y.; Wu, W. Graphics Processing Unit-Accelerated Propeller Computational Fluid Dynamics Using AmgX: Performance Analysis Across Mesh Types and Hardware Configurations. J. Mar. Sci. Eng. 2024, 12, 2134. https://doi.org/10.3390/jmse12122134
Zhu Y, Gan J, Lin Y, Wu W. Graphics Processing Unit-Accelerated Propeller Computational Fluid Dynamics Using AmgX: Performance Analysis Across Mesh Types and Hardware Configurations. Journal of Marine Science and Engineering. 2024; 12(12):2134. https://doi.org/10.3390/jmse12122134
Chicago/Turabian StyleZhu, Yue, Jin Gan, Yongshui Lin, and Weiguo Wu. 2024. "Graphics Processing Unit-Accelerated Propeller Computational Fluid Dynamics Using AmgX: Performance Analysis Across Mesh Types and Hardware Configurations" Journal of Marine Science and Engineering 12, no. 12: 2134. https://doi.org/10.3390/jmse12122134
APA StyleZhu, Y., Gan, J., Lin, Y., & Wu, W. (2024). Graphics Processing Unit-Accelerated Propeller Computational Fluid Dynamics Using AmgX: Performance Analysis Across Mesh Types and Hardware Configurations. Journal of Marine Science and Engineering, 12(12), 2134. https://doi.org/10.3390/jmse12122134








