Global Mean Sea Level Change Projections up to 2100 Using a Weighted Singular Spectrum Analysis
Abstract
1. Introduction
2. Methods and Employed Datasets
2.1. Weighted Singular Spectrum Analysis
- (1)
- The time series is defined by
- (2)
- The numbers form the M terms of the recurrent forecast. Thus, recurrent forecasting is performed using the linear recurrence relation with coefficients .
2.2. Evaulation Indices
2.3. Employed Datasets
3. Results and Analysis
3.1. Prediction of Global Mean Sea Level Changes with Simulation Cases
3.2. Analysis of Global Mean Sea Level Changes from 1880 to 2023
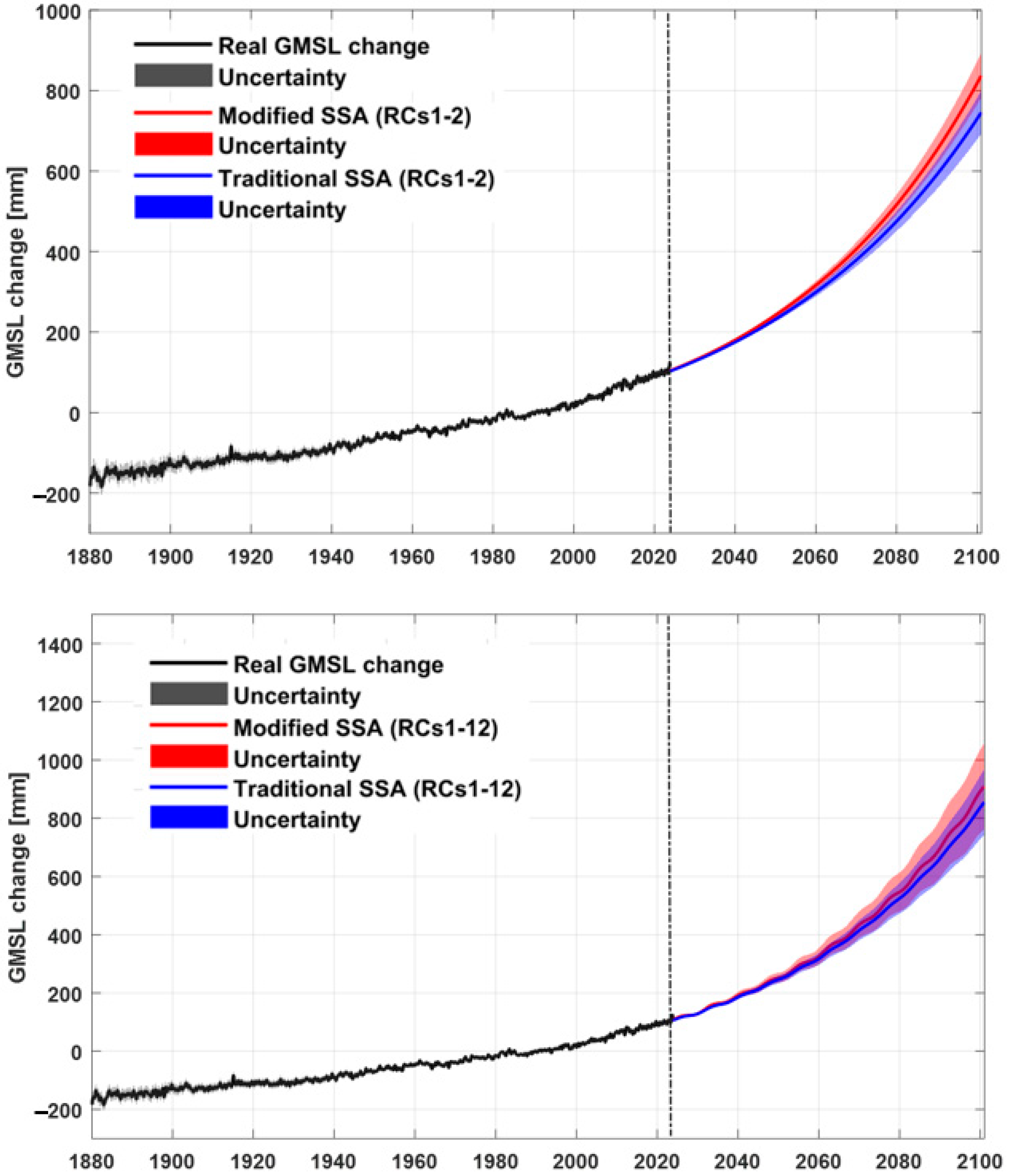
3.3. Prediction of Global Mean Sea Level Changes from 2024 to 2100
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellison, A.M.; Farnsworth, E.J. Anthropogenic disturbance of Caribbean Mangrove Ecosystems: Past impacts, present trends, and future predictions. Biotropica 1996, 28, 549–565. [Google Scholar] [CrossRef]
- Cronk, J.K.; Fennessy, M.S. Wetland Plants: Biology and Ecology; CRC Press LLC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Anthoff, D.; Nicholls, R.J.; Tol, R.S.; Vafeidis, A.T. Global and Regional Exposure to Large Rises in Sea-Level: A Sensitivity Analysis. Tyndall Centre for Climate Change Research-Working Paper 96. 2006. Available online: http://www.tyndall.ac.uk/sites/default/files/wp96_0.pdf (accessed on 20 May 2024).
- Hoegh-Guldberg, O.; Bruno, J.F. The impact of climate change on the world’s marine ecosystems. Science 2010, 328, 1523–1528. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Cazenave, A.; Hamlington, B.; Horwath, M.; Barletta, V.R.; Benveniste, J.; Chambers, D.; Döll, P.; Hogg, A.E.; Legeais, J.F.; Merrifield, M.; et al. Observational Requirements for Long-Term Monitoring of the Global Mean Sea Level and Its Components over the Altimetry Era. Front. Mar. Sci. 2019, 6, 582. [Google Scholar] [CrossRef]
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- IPCC AR6. Monitoring and Projections of Global and Regional Sea Level Change. 2022. Available online: https://www.ipcc.ch/report/sixth-assessment-report-cycle/ (accessed on 20 May 2024).
- Moorhead, K.K.; Brinson, M.M. Response of Wetlands to Rising Sea Level in the Lower Coastal Plain of North Carolina. Ecol. Appl. 1995, 5, 261–271. [Google Scholar] [CrossRef]
- Vecchio, A.; Anzidei, M.; Serpelloni, E. Sea level rise projections up to 2150 in the northern Mediterranean coasts. Environ. Res. Lett. 2023, 19, 014050. [Google Scholar] [CrossRef]
- Vaziri, M. Predicting Caspian Sea surface water level by ANN and ARIMA models. J. Waterw. Port Coast. Ocean Eng. 1997, 123, 158–162. [Google Scholar] [CrossRef]
- IPCC AR5. Climate Change 2013, IPCC Fifth Assessment Report. 2013. Available online: http://www.ipcc.ch/report/ar5/ (accessed on 25 March 2024).
- Pfeffer, W.T.; Harper, J.T.; O’Neel, S. Kinematic constraints on glacier contributions to 21st century sea-level rise. Science 2008, 321, 1340–1343. [Google Scholar] [CrossRef]
- Rahmstorf, S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef]
- Domingues, C.M.; Church, J.A.; White, N.J.; Gleckler, P.J.; Wijffels, S.E.; Barker, P.M.; Dunn, J.R. Improved estimates of upper-ocean warming and multi-decadal sea-level rise. Nature 2008, 453, 1090–10931093. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Reconstructing sea level from paleo and projected temperatures 200 to 2100 AD. Clim. Dyn. 2009, 34, 461–472. [Google Scholar] [CrossRef]
- Church, J.; White, N. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- GSFC. Global Mean Sea Level Trend from Integrated Multi-Mission Ocean Altimeters TOPEX/Poseidon, Jason-1, OSTM/Jason-2, and Jason-3 Version 5.1. Ver. 5.1 PO.DAAC, CA, USA, 2021. Available online: https://doi.org/10.5067/GMSLM-TJ151 (accessed on 20 May 2024).
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer: Berlin/Heidelberg, Germany, 2013; p. 119. [Google Scholar] [CrossRef]
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef]
- Elneel, L.; Zitouni, M.S.; Mukhtar, H.; Al-Ahmad, H. Examining sea levels forecasting using autoregressive and prophet models. Sci. Rep. 2024, 14, 14337. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics with applications to paleoclimatic time series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Wang, F.; Shen, Y.; Li, W.; Chen, Q. Singular spectrum analysis for heterogeneous time series by taking its formal errors into account. Acta Geodyn. Geomater. 2018, 15, 395–403. [Google Scholar] [CrossRef]
- Li, W.; Shen, Y. The Consideration of Formal Errors in Spatiotemporal Filtering Using Principal Component Analysis for Regional GNSS Position Time Series. Remote Sens. 2018, 10, 534. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, F.; Chen, Q. Weighted multichannel singular spectrum analysis for post-processing GRACE monthly gravity field models by considering the formal errors. Geophys. J. Int. 2021, 226, 1997–2010. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy, chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Livezey, R.E.; Chen, W.Y. Statistical Field Significance and its Determination by Monte Carlo Techniques. Mon. Weather. Rev. 1983, 111, 46–59. [Google Scholar] [CrossRef]
- Davis, J.L.; Mitrovica, J.X. Glacial isostatic adjustment and the anomalous tide gauges record of eastern North America. Nature 1996, 379, 331–332. [Google Scholar] [CrossRef]
- Garner, G.G.; Hermans, T.; Kopp, R.E.; Slangen, A.B.A.; Edwards, T.L.; Levermann, A.; Nowikci, S.; Palmer, M.D.; Smith, C.; Fox-Kemper, B.; et al. IPCC AR6 Sea-Level Rise Projections. Version 20210809. PO.DAAC, CA, USA, 2021. Available online: https://podaac.jpl.nasa.gov/announcements/2021-08-09-Sea-level-projections-from-the-IPCC-6th-Assessment-Report (accessed on 18 June 2024).
- Chen, J.; Wilson, C.; Chambers, D.; Nerem, R.; Tapley, B. Seasonal global water mass budget and mean sea level variations. Geophys. Res. Lett. 1998, 25, 3555–3558. [Google Scholar] [CrossRef]
- Nerem, R. Measuring global mean sea level variations using TOPEX/POSEIDON altimeter data. J. Geophys. Res. Ocean. 1995, 100, 25135–25151. [Google Scholar] [CrossRef]
- Chambers, D.; Merrifield, M.; Nerem, R. Is there a 60-year oscillation in global mean sea level? Geophys. Res. Lett. 2012, 39, L18607. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, Y.; Xiao, C.; Hua, L.; Yan, Z. Interpretation of IPCC AR6 report: Monitoring and projections of global and regional sea level change. Adv. Clim. Chang. Res. 2022, 18, 12–18. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Sebesvari, Z. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2019; pp. 321–445. [Google Scholar] [CrossRef]
- Oelsmann, J.; Marcos, M.; Passaro, M.; Sanchez, L.; Dettmering, D.; Dangendorf, S.; Seitz, F. Regional variations in relative sea-level changes influenced by nonlinear vertical land motion. Nat. Geosci. 2024, 17, 137–144. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Hewitt, H.T.; Xiao, C.; Aðalgeirsdóttir, G.; Drijfhout, S.S.; Edwards, T.L.; Golledge, N.R.; Hemer, M.; Kopp, R.E.; Krinner, G.; et al. Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; Chapter 9. [Google Scholar]
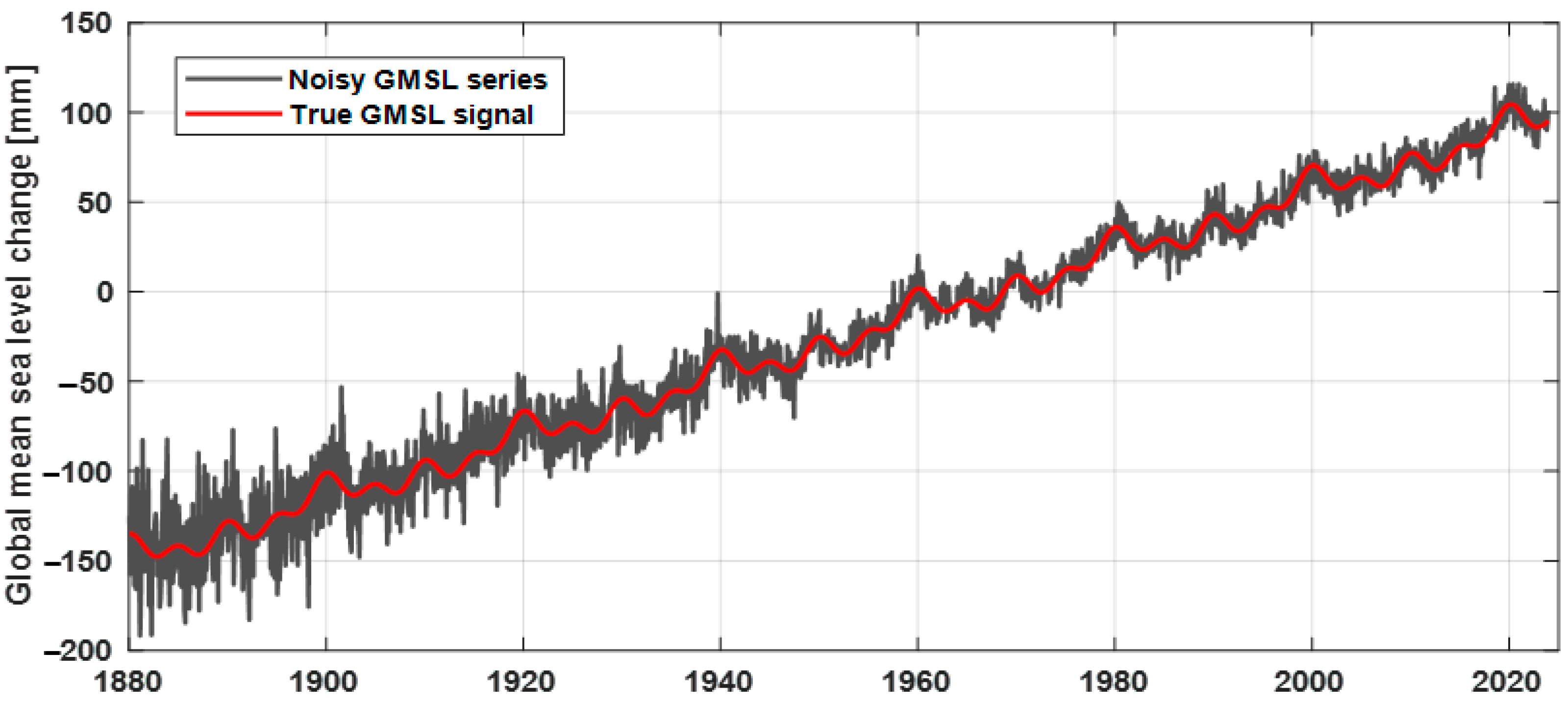

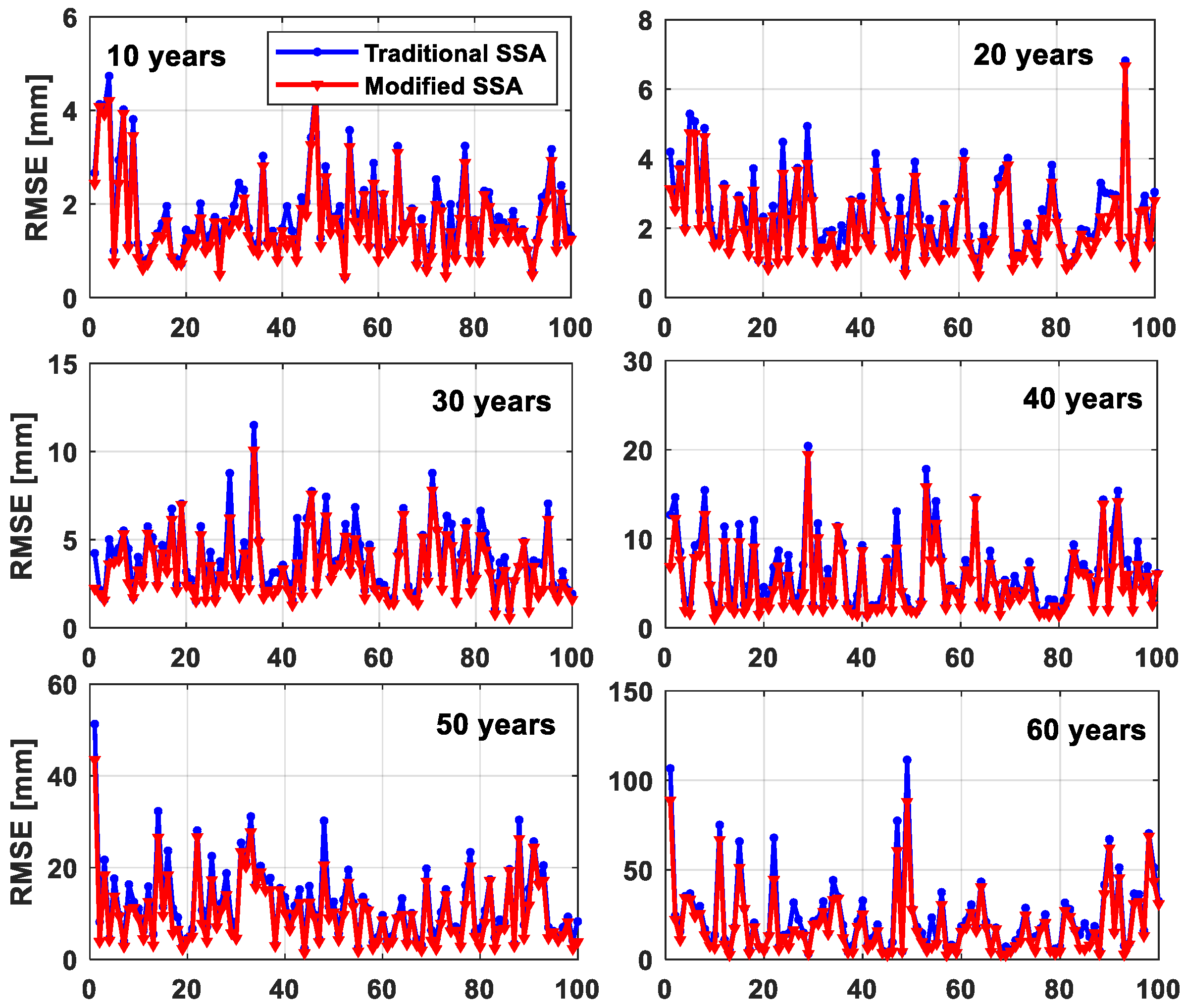
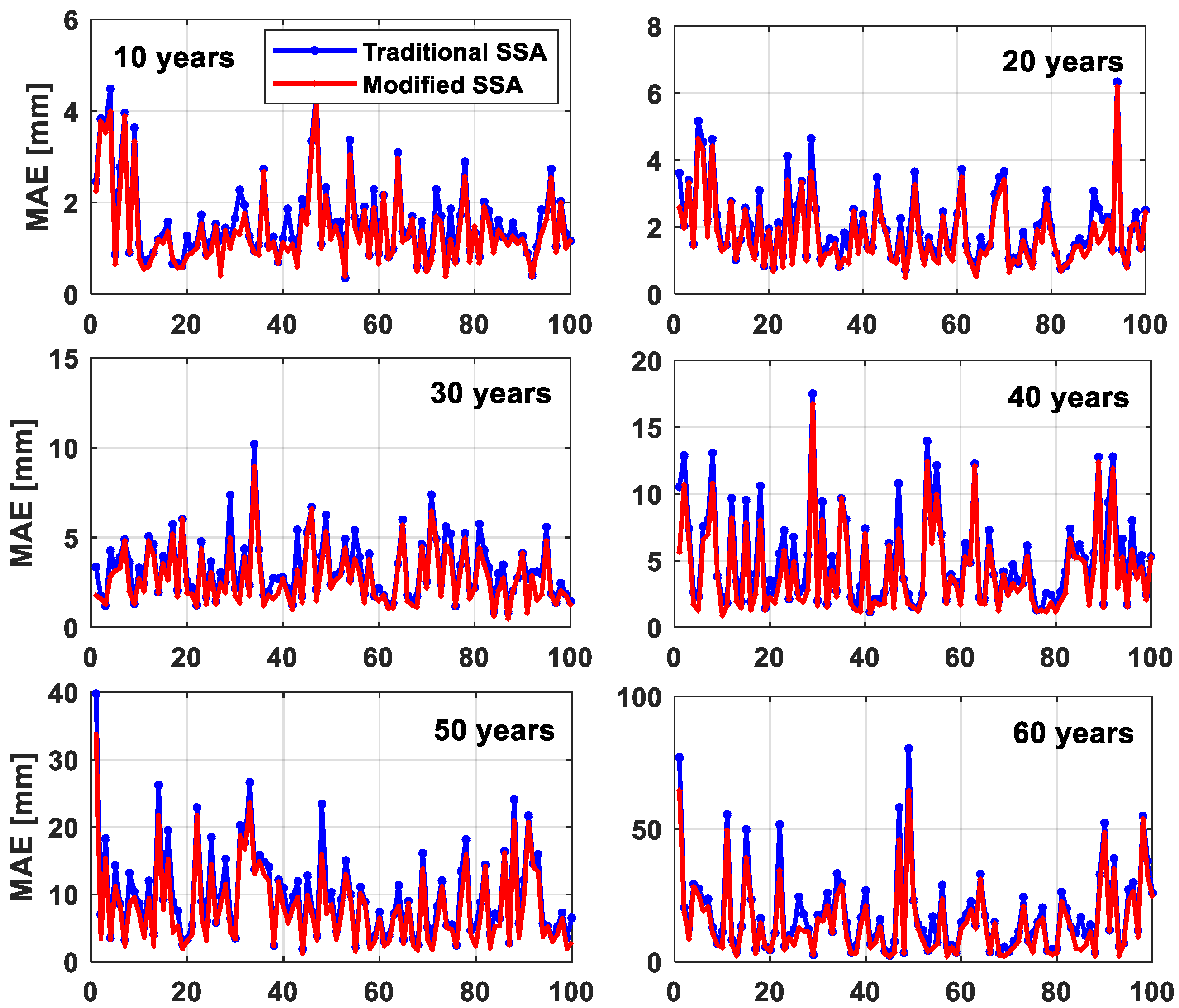

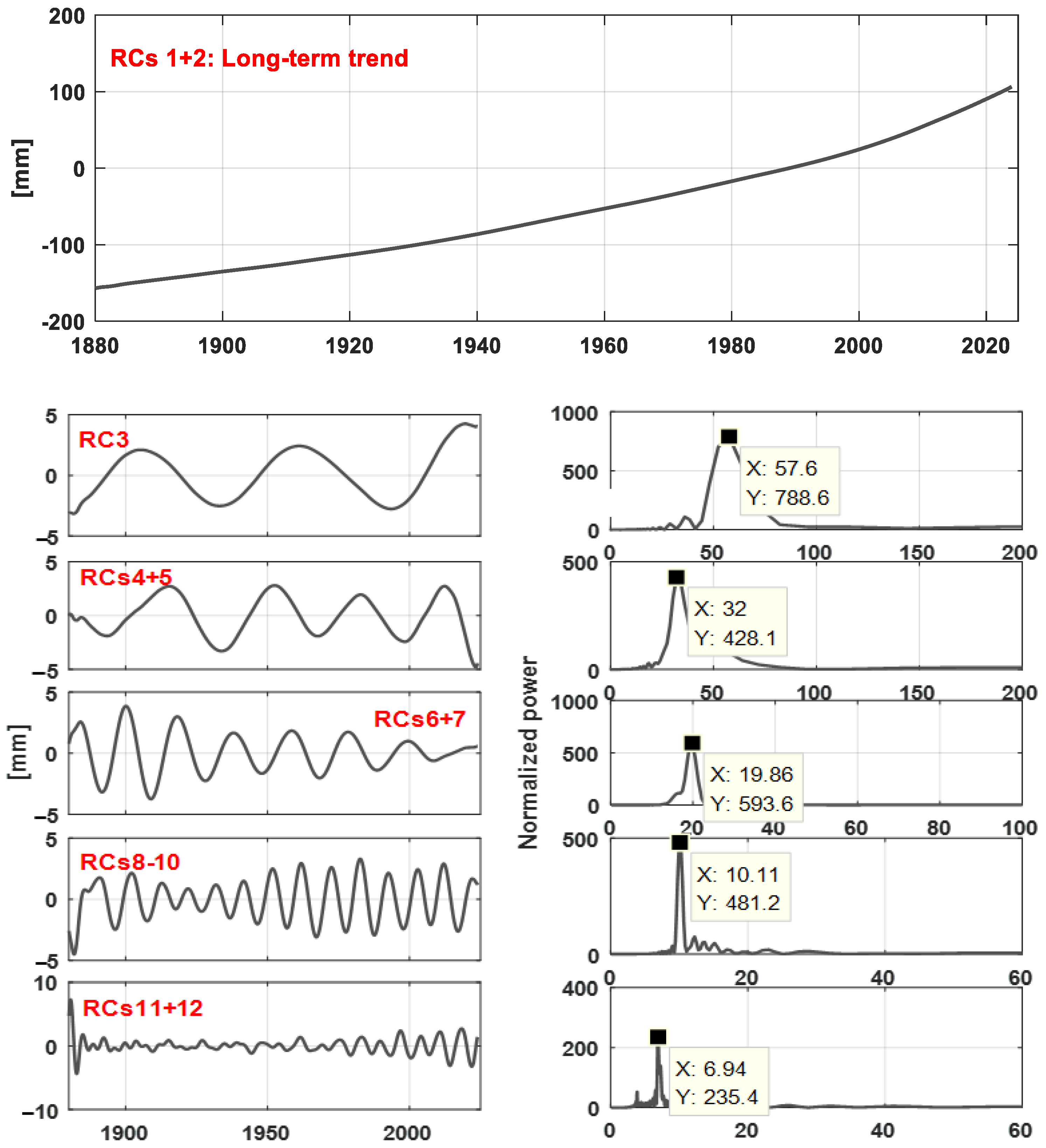
| Prediction Length [Years] | RMSE/mm | MAE/mm | ||
|---|---|---|---|---|
| Traditional SSA | Weighted SSA | Traditional SSA | Weighted SSA | |
| 10 | 1.96 | 1.64 | 1.58 | 1.37 |
| 20 | 2.58 | 2.07 | 2.37 | 1.90 |
| 30 | 4.48 | 2.54 | 3.62 | 2.00 |
| 40 | 6.80 | 4.25 | 5.52 | 3.38 |
| 50 | 10.72 | 7.81 | 8.94 | 6.42 |
| 60 | 19.13 | 12.10 | 14.65 | 8.83 |
| Prediction Length [Years] | RMSE/mm | MAE/mm | ||||
|---|---|---|---|---|---|---|
| Traditional SSA | Weighted SSA | IMP/% | Traditional SSA | Weighted SSA | IMP/% | |
| 10 | 1.80 | 1.59 | 11.67 | 1.59 | 1.40 | 11.95 |
| 20 | 2.36 | 2.07 | 12.29 | 2.02 | 1.77 | 12.38 |
| 30 | 3.94 | 3.30 | 16.24 | 3.28 | 2.74 | 16.46 |
| 40 | 6.18 | 5.05 | 18.28 | 5.11 | 4.18 | 18.20 |
| 50 | 12.20 | 10.08 | 17.38 | 9.82 | 8.12 | 17.31 |
| 60 | 23.20 | 18.98 | 18.19 | 18.02 | 14.76 | 18.09 |
| Index | Year | Traditional SSA | Weighted SSA | IPCC AR6 | ||
|---|---|---|---|---|---|---|
| RCs1-2 | RCs1-12 | RCs1-2 | RCs1-12 | Medium Confidence SSP5-8.5 | ||
| Validation | 2020 | 54.01 ± 0.81 | 54.51 ± 1.02 | 55.13 ± 0.79 | 54.15 ± 1.32 | 51.0 ± 6.99 |
| Prediction | 2030 | 91.86 ± 2.01 | 94.46 ± 3.88 | 94.60 ± 1.94 | 95.90 ± 5.50 | 102.0 ± 14.59 |
| 2040 | 140.01 ± 3.86 | 152.30 ± 8.60 | 145.81 ± 3.76 | 158.07 ± 12.35 | 163.0 ± 24.52 | |
| 2050 | 197.83 ± 6.74 | 210.97 ± 13.54 | 208.50 ± 6.62 | 215.17 ± 17.38 | 243.0 ± 36.96 | |
| 2060 | 266.20 ± 11.01 | 287.05 ± 21.90 | 284.03 ± 10.93 | 298.09 ± 29.64 | 325.0 ± 52.11 | |
| 2070 | 347.43 ± 17.16 | 385.11 ± 35.73 | 375.54 ± 17.22 | 404.27 ± 47.11 | 427.0 ± 71.93 | |
| 2080 | 445.53 ± 25.78 | 495.70 ± 54.72 | 488.39 ± 26.17 | 516.21 ± 69.65 | 541.0 ± 96.02 | |
| 2090 | 563.64 ± 37.62 | 638.62 ± 79.34 | 627.02 ± 38.66 | 677.40 ± 103.49 | 674.0 ± 122.22 | |
| 2100 | 705.25 ± 53.73 | 814.62 ± 112.84 | 796.75 ± 55.92 | 868.90 ± 147.42 | 830.0 ± 152.42 | |
| Year | Rate [mm/year] | Acceleration [mm/year2] | ||
|---|---|---|---|---|
| RCs1-2 | RCs1-12 | RCs1-2 | RCs1-12 | |
| 1880–2023 | 1.70 ± 0.02 | 1.70 ± 0.02 | 0.015 ± 0.001 | 0.016 ± 0.001 |
| 2024–2100 | 9.14 ± 1.28 | 9.92 ± 1.79 | 0.180 ± 0.040 | 0.206 ± 0.120 |
| 1880–2100 | 3.72 ± 0.26 | 3.54 ± 0.74 | 0.052 ± 0.008 | 0.056 ± 0.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Shen, Y.; Geng, J.; Chen, Q. Global Mean Sea Level Change Projections up to 2100 Using a Weighted Singular Spectrum Analysis. J. Mar. Sci. Eng. 2024, 12, 2124. https://doi.org/10.3390/jmse12122124
Wang F, Shen Y, Geng J, Chen Q. Global Mean Sea Level Change Projections up to 2100 Using a Weighted Singular Spectrum Analysis. Journal of Marine Science and Engineering. 2024; 12(12):2124. https://doi.org/10.3390/jmse12122124
Chicago/Turabian StyleWang, Fengwei, Yunzhong Shen, Jianhua Geng, and Qiujie Chen. 2024. "Global Mean Sea Level Change Projections up to 2100 Using a Weighted Singular Spectrum Analysis" Journal of Marine Science and Engineering 12, no. 12: 2124. https://doi.org/10.3390/jmse12122124
APA StyleWang, F., Shen, Y., Geng, J., & Chen, Q. (2024). Global Mean Sea Level Change Projections up to 2100 Using a Weighted Singular Spectrum Analysis. Journal of Marine Science and Engineering, 12(12), 2124. https://doi.org/10.3390/jmse12122124







