Next Article in Journal
Incorporating Non-Equlibrium Ripple Dynamics into Bed Stress Estimates Under Combined Wave and Current Forcing
Next Article in Special Issue
Pervasive Millennial-Scale Interstadial/Interglacial Climate Variability in the High-Latitude Northern Hemisphere
Previous Article in Journal
Bionic Raft Design and Performance Investigation of a Two-Raft Wave Energy Converter
Previous Article in Special Issue
Application of Multiple Geophysical Exploration Methods in the Exploration of Marine Sand Resources in the Northern Offshore Waters of the South China Sea
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 12
Issue 12
10.3390/jmse12122115
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Controlling Factors and Prediction of Deep-Water Mass Transport Deposits in the Pliocene Qiongdongnan Basin, South China Sea

by
Jiawang Ge
1,2,*,
Xiaoming Zhao
1,2,*,
Qi Fan
1,
Weixin Pang
1,
Chong Yue
2,3 and
Yueyao Chen
2
1
State Key Laboratory of Offshore Natural Gas Hydrates, CNOOC Research Institute, Beijing 102209, China
2
College of Geosciences and Technology, Southwest Petroleum University, Chengdu 610500, China
3
PetroChina Tarim Oilfield Company, Korla 841000, China
*
Authors to whom correspondence should be addressed.
J. Mar. Sci. Eng. 2024, 12(12), 2115; https://doi.org/10.3390/jmse12122115
Submission received: 31 August 2024 / Revised: 17 October 2024 / Accepted: 19 October 2024 / Published: 21 November 2024
(This article belongs to the Special Issue Recent Developments and Advances in Geological Oceanography and Ocean Observation in the Pacific Ocean and Its Marginal Basins)
Browse Figures
Versions Notes

Abstract

:
Large-scaled submarine slides or mass transport deposits (MTDs) widely occurred in the Pliocene Qiongdongnan Basin, South China Sea. The good seismic mapping and distinctive topography, as well as the along-striking variation in sediment supply, make it an ideal object to explore the linkage of controlling factors and MTD distribution. The evaluation of the main controlling factors of mass transport deposits utilizes the analysis of terrestrial catastrophes as a reference based on the GIS-10.2 software. The steepened topography is assumed to be an external influence on triggering MTDs; therefore, the MTDs are mapped to the bottom interface of the corresponding topography strata. Based on detailed seismic and well-based observations from multiple phases of MTDs in the Pliocene Qiongdongnan Basin (QDNB), the interpreted controlling factors are summarized. Topographic, sedimentary, and climatic factors are assigned to the smallest grid cell of this study. Detailed procedures, including correlation analysis, significance check, and recursive feature elimination, are conducted. A random forest artificial intelligence algorithm was established. The mean value of the squared residuals of the model was 0.043, and the fitting degree was 82.52. To test the stability and accuracy of this model, the training model was used to calibrate the test set, and five times 2-fold cross-validation was performed. The area under the curve mean value is 0.9849, indicating that the model was effective and stable. The most related factors are correlated to the elevation, flow direction, and slope gradient. The predicted results were consistent with the seismic interpretation results. Our study indicates that a random forest artificial intelligence algorithm could be useful in predicting the susceptibility of deep-water MTDs and can be applied to other study areas to predict and avoid submarine disasters caused by wasting processes.

1. Introduction

Mass transport deposits (MTDs) widely occur worldwide [1,2,3,4,5] and are unstable transport caused by various controlling factors (high sedimentation rates, paleo–marine landslides and mass failures, sea level fluctuations, volcanism, water temperatures, ocean currents, tsunamis, storms, hurricanes, tides, earthquakes, gas-hydrate dissociation, glaciation, etc.) on deep-water, shelf-margins or slopes, canyons, uplifted tectonic flanks, and channel sidewalls [6,7,8,9,10,11,12,13]. Sediments are deformed along the transport, and the processes mainly include slides, slumps, and debris flow [14,15,16]. The log responses typically demonstrate elevated resistivity, compressional velocity, density, and porosity. Concurrently, geotechnical measurements reveal an increase in shear strength, accompanied by a reduction in void ratio and water content [17,18]. Sometimes, the related deposits are sand-prone and have good porosity and permeability as reservoirs [18,19,20]. MTDs could be one of the major natural hazards in deep-water areas of both lacustrine and ocean settings. When the shear strength of continental slope sediments is significantly reduced at the location of future basal sliding surfaces or shear zones, submarine slope instability occurs; this may cause damage to submarine stability [21]. Carter (2010) counted approximately 430 cable breaks worldwide from 1996 to 2006 as being affected by this process; large submarine slides have resulted in severe tsunami catastrophes, causing massive loss of life and property damage [22,23,24,25,26]. Serious engineering accidents (e.g., energy pipeline, production platform, and deep-water drilling failure or instability) caused by submarine geological disasters have also been mentioned in previous studies [27,28].
The triggering mechanisms of landslides are complex and challenging to monitor, with seismic activity, rapid sedimentation, fluid escape, and climatic events being hot topics [29,30,31]. Extensive discussions have been promoted on the following aspects: (1) Static slope analysis using the limit equilibrium method and the finite element method [32] to observe the influence of weak layers on the stability of slopes under different phases before, during, and after earthquakes; (2) sensitivity mapping of submarine landslides using inverse distance weighting and Geographic Information System (GIS) techniques to establish safety factors for slope stability, and studies showing that transverse waves are more destructive to submarine slopes than longitudinal waves, and the weaker the strength of the submarine soil the greater the effect of earthquakes on slopes [33]; (3) numerical sedimentation simulations to discuss the effect of overpressure from rapid sediment deposition on slope stability, which showed that large-scale damage to slopes consisting of homogeneous low-permeability sediments is in some cases not generated by rapid sediment loading alone (possibly due to lateral fluid flow to the foot of the slope) [34,35,36]. (4) Discussing the effects of climate on sediment supply and glacier-generated overpressure on submarine slopes [37,38]; (5) analysis of debris flow mobility under different lithologies, which showed that clastic rocks are the most landslide active and basalt and flint are the least active [39]. In summary, the development of new techniques has greatly contributed to the understanding of the prediction of MTDs, and, especially, the tool of GIS has allowed for the integration of geophysical and 3D imagery in spatial analysis. However, the application of GIS and the numerical instability of controlling factors (i.e., topography, sediment supply) on offshore oceanic settings are relatively less reported.
In this paper, topographic, sedimentary, and climatic data are mapped to the bottom interface of MTDs in the Pliocene Qiongdongnan Basin (QDNB). Utilizing high-density seismic data and well data, these controlling factors of MTDs are digitized using GIS software. The principal controlling factors of MTDs are subsequently screened through correlation analysis and recursive feature elimination. Furthermore, the Random forest artificial intelligence algorithm is employed to elucidate the intricate relationships between these controlling factors and the propensity for MTD occurrence, ultimately discerning the most influential factors.

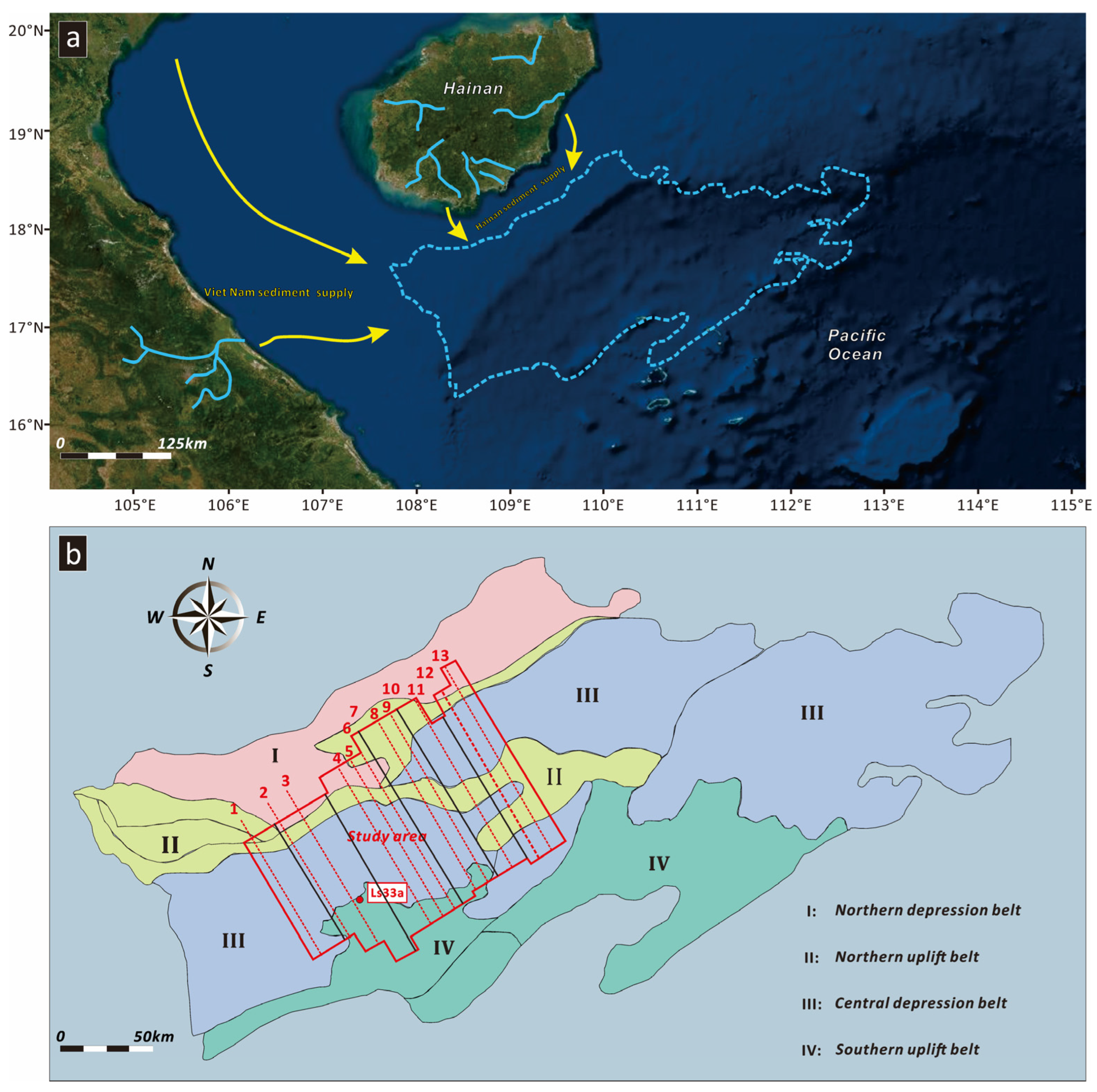
2. Geological Setting

The QDNB is located in the north-western part of the South China Sea, connected to Hainan Island in the north, adjacent to the Yinggehai Basin in the west, and bordering the Pearl River Mouth Basin in the east and the Xisha Uplift in the south. The QDNB is of an overall NE–SW orientation and about 290 km long and 181 km wide, with a total area of about 4.5 × 104 km2 [40,41] (Figure 1a). The QDNB consists of four primary tectonic units, including the northern depression belt, the northern uplift belt, the central depression belt, and the southern uplift belt [42]. The Cenozoic tectonic evolution of the QDNB is divided into three stages [43,44]: (1) Early Eocene–Oligocene fault subsidence, which experienced a history of evolution from weak to strong and finally weak fault activity; (2) Early–Middle Miocene post-rifting thermal subsidence period when the basin entered the thermal subsidence phase and was subject to mantle magma thermal action basin subsidence; (3) Late Miocene–present accelerated thermal subsidence as the tectonic activity of the basin tends to stabilize. The study area is located in the central part of QDNB, covering about 1.56 × 104 km2; the study area contains part of the Lingshui Depression, Lingsnan Low Bulge, Beigao Depression, Songnan Low Bulge and Songnan Baodao Depression, and other secondary tectonic units (Figure 1b).

3. Data and Potential Controlling Factors

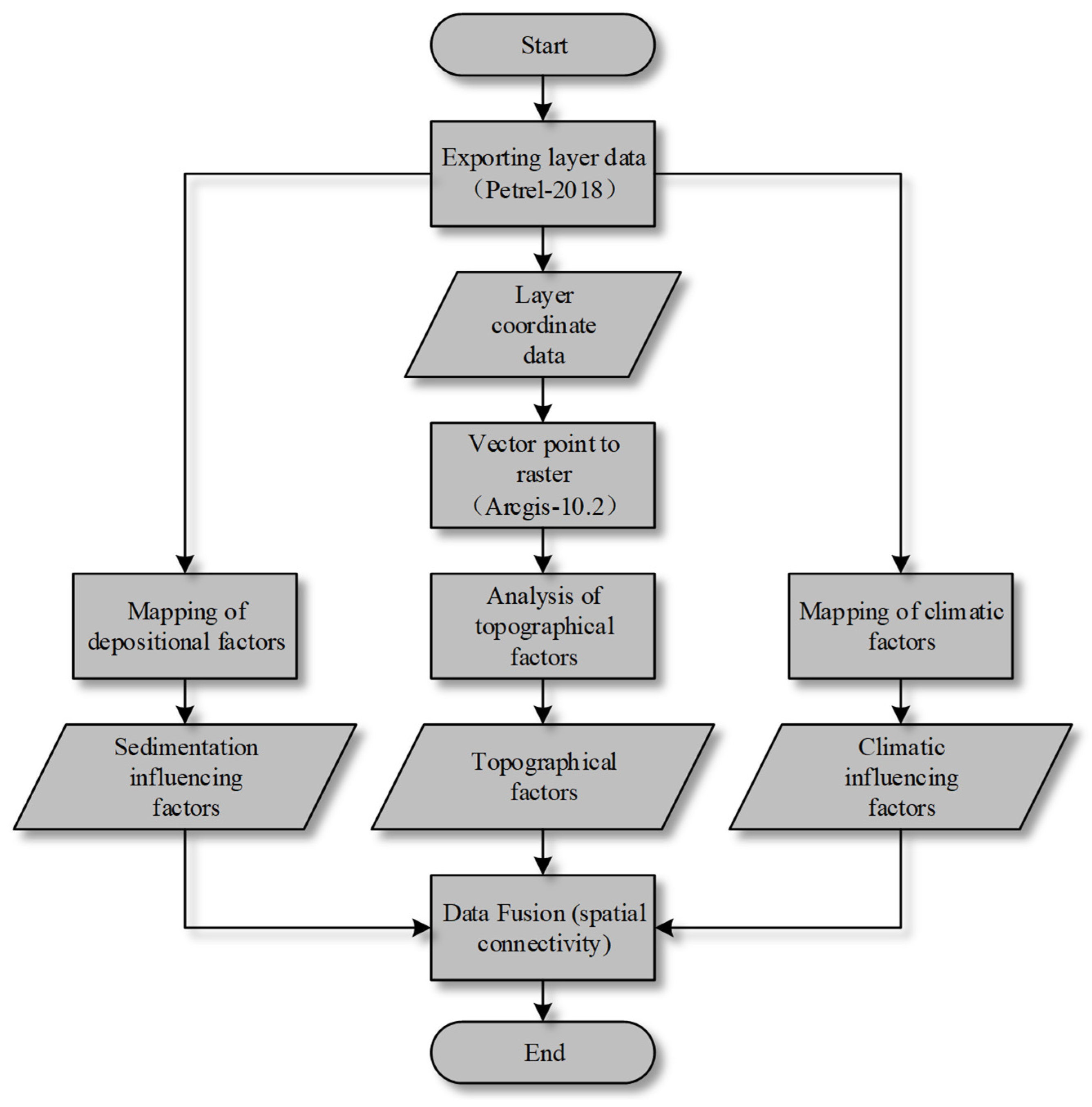
3.1. Data

MTD data were obtained from high-density 2D seismic data and well data as well as published data, including 2D seismic data (2 km × 2 km) with a 2 ms vertical sampling rate, and processed as a zero-phase profile, with a seismic main frequency of about 30 Hz and a vertical resolution of about 20 m. Based on the seismic–well tie, the depth and age of the sequence interface in the QDNB were determined [45,46].
The controlling factor analysis of MTDs is based on the terrestrial geotechnical analysis as a reference, and MTDs are mapped to the bottom interface of the corresponding sequence. Two major sequence stratigraphic surfaces (namely, T30 and T20) are identified at the top and bottom of the Pliocene Yinggehai Formation. Three secondary stratigraphic interfaces (namely, T29, T28, and T27) can be identified. The above surfaces are aged as 5.5 Ma (T30), 4.2 Ma (T29), 3.2 Ma (T28), 2.7 Ma (T27), and 1.8 Ma (T20) (Figure 2). Based on the seismic characteristics of the MTDs, the MTDs in the study area were divided into 11 packages, named 1~11 (Figure 3 and Figure 4; Table 1); the largest and smallest packages of MTDs occurred with planar distribution areas of about 5200 km2 and 1000 km2, respectively (Figure 4; Table 1).

3.2. Potential Controlling Factors of MTDs

(1)
Narrow and Negative Topography
Topographic factors are closely related to MTD triggering and mostly occur in submarine canyons and shelf margins or slopes [47,48,49]. In this paper, topographic elements will be analyzed for the seismically interpreted sequence interfaces, which include elevation, slope gradient, slope direction, profile curvature, plane curvature, flow direction, and flow rate.
The elevation is the distance from a point along the plumb line direction to the absolute base surface (sea level). The elevation is an important controlling factor for MTD occurrences, and the elevation in the article is the real elevation data obtained from the time-depth conversion of the seismic interface.
The slope gradient is the angle between the tangent plane of a point on the surface and the horizontal ground; the slope direction is the angle between the projection of the normal vector of the tangent plane of a point on the surface in the horizontal plane and the due north direction of the point, both of which affect the rate of source supply and fluid state, and are important influencing factors for MTDs.
Profile curvature is the component of ground curvature in the vertical direction (the direction where gravity acts most) and the measure of the rate of change of ground elevation along the direction of maximum slope gradient drop (a negative curvature indicates that the image element is convex upward, a positive curvature indicates that the image element is concave downward, and a zero curvature indicates that the surface is flat), and profile curvature affects the acceleration and deceleration of MTDs flowing over a surface.
Plane curvature (often called surface curvature) is the component of the direction perpendicular to the maximum slope (negative curvature indicates that the image element is convex upward, positively indicates that the image element opening is concave downward, and zero indicates that the surface is flat), and plane curvature is related to whether MTDs flowing over a surface converge or disperse. The flow direction is calculated from the elevation around the surface of the terrain, which may control the erosion direction of the ocean and the flow direction of the MTDs. The flow rate is analyzed based on the flow direction results correlative to the cumulative flow of topographic units that may be flowed through by other areas, and the flow may change the topography and thus affect the distribution of MTDs.
(2)
Sedimentary factors
The sediment stacking and transporting architecture and its material composition directly influence the morphology of shelf-edge slopes, which, in turn, affects the occurrence of MTDs [50,51,52]. For clinoforms, parameters such as accretion, progradation, the ratio of accretion to progradation, and net sediment fluxes at the shelf edge need to be calculated for further sediment supply (Figure 5).
The equations for accretion rate (Ra), progradation rate (Rp), and net sediment fluxes (Fc) are as follows [53]:
R a = A T
R p = P T
F c = R p × A × 10
where Ra, Rp, and Fc are in units of m/Ma, m/Ma, and m2/Ma, respectively; T is the time in units of Ma.
To facilitate the following study, the study area is divided into six calculated zones; these zones are bounded by seismic profiles 1, 2–3, 4–6, 7–9, 10–11, and 12–13, as shown in Figure 1b. Sedimentary factors are mainly based on the results of the survey line section statistics within the study area and the average of the survey line section statistics within the six zones.
(3)
Climate factors
The magnitude, as well as the rate of climate–sea level fluctuations, are important controlling factors for submarine landslides [54,55]. Sea level fluctuations affect sediment transport and deposition processes at the shelf edge and determine the stability state of the shelf-edge deposits. When the rate of sea level fluctuation increased, it often caused the occurrence of large-scale MTDs by landslides on the shelf edge and slope. Here, the amplitude of sea level fluctuation is calculated by referring to the reported sea level change curve [56], and the sea level fluctuation rate is displayed based on its ability to participate in the evaluation of the susceptibility of MTDs.
(4)
Data mapping
The interpreted layer data and MTDs are mapped and ArcGIS-10.2 is used for further data processing (Figure 6): (a) exporting layer data and MTDs (point data in 3D coordinates); (b) converting layer and MTD data to raster data; (c) converting layer data to time-depth; (d) converting raster data of MTDs to vector surfaces; (e) analyzing topographic influences based on the layer (elevation, slope gradient, slope direction, profile curvature, plane curvature, flow direction, flow rate); (f) conversion of layer data to vector point data; (g) estimating sedimentary factors from relevant data (accretion rate, progradation rate, sediment fluxes) and sea level fluctuation amplitude to layer data [56]; (h) data fusion (spatial linkage) of topographic influences and MTD distribution.
In the digitizing of the controlling factors for MTDs in the QDNB, the study area was divided into 405,958 grid cells. As the smallest study cell, each grid cell was assigned to each influence factor and occupied an area of 38,427.6 m2, where the area of the observed MTDs was assigned a value of 1; otherwise, it was assigned a value of 0 (Table 2).
The elevation is calculated in milliseconds in our study. The slope gradient is the angle with the horizontal plane calculated from the topographic elevation data, with data ranging from 0 to 90 degrees. The slope direction is measured clockwise with north as the reference direction and is expressed by positive degrees between 0 and 360 degrees. Section curvature and plane curvature greater than 0 means that the surface is convex upwards, negative means that the surface opening is recessed upwards, and 0 means that the surface is flat. Flow direction is modeled as D8, dividing the flow direction into eight categories (1 for east, 2 for southeast, 4 for south, 8 for southwest, 16 for west, 32 for northwest, 64 for north, and 128 for northeast). Flow is the cumulative runoff from the smallest study unit counted with a minimum value of 0. Sedimentary factors are obtained from the statistics of slope-fold unit parameters with a variable range of values. The units of accretion rate and progradation rate are m/Ma, and the unit of sediment fluxes is m2/Ma. The sea level fluctuation rate is a measure of sea level fluctuation per unit of time, and its unit is m/Ma.

4. Methodology

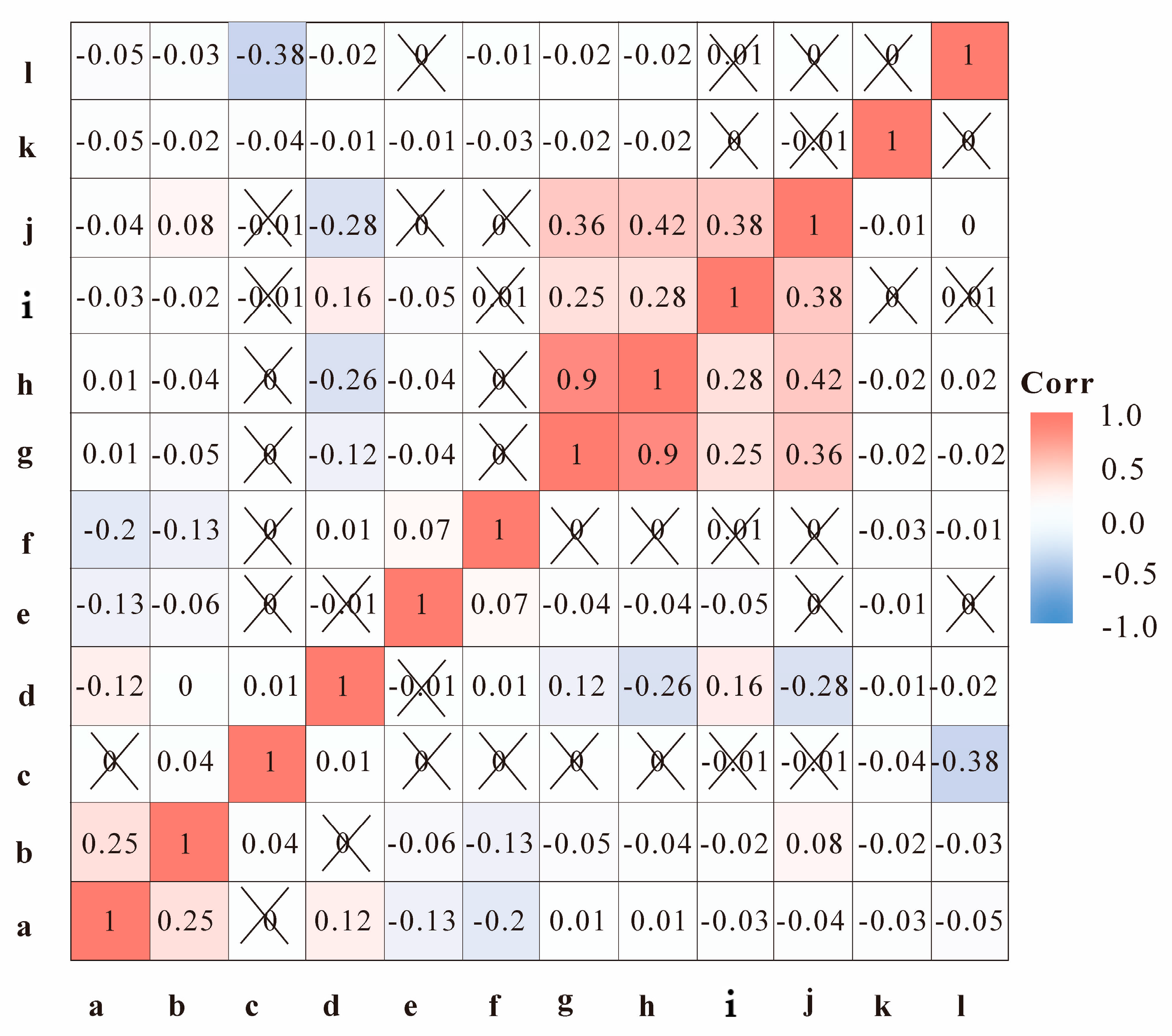
4.1. Correlation and Significance Checks

Correlation analysis can be used to describe relationships between variables and is widely applied to hazard prediction [57,58,59,60,61]. In this paper, the Pearson correlation coefficient was used to analyze the correlation relationship between the influencing factors of MTDs. The values of the correlation coefficient ranged between −1 and 1; it directly reflects the degree of correlation strength. The correlation coefficient calculation formula is as follows:
C o r ( X , Y ) = c o v ( X , Y ) σ X σ Y = E [ X − μ X Y − μ Y ] ∑ i = 1 n ( X i − μ X ) 2 ∑ i = 1 n ( Y i − μ Y ) 2
In the formula, C o r ( X , Y ) is the covariance of X and Y ; σ X , σ Y is the standard deviation of X and Y ; X and Y are series groups; X i , Y i are the groups of series values; μ X , μ Y are the mean of X and Y .
After calculating the Pearson correlation coefficients, the reliability of the Pearson correlation coefficients is also examined based on the significance check. The p-value is the probability that a more extreme result of the obtained sample observation will occur when the original hypothesis is true. If this occurs, it is reasonable to reject the original hypothesis according to the probability principle [59,60,61]. If the p-value is low, it means that the probability of the occurrence of the original hypothesis is low; alternatively, a lower p-value corresponds to a more significant result. Statistics based on the p-value are obtained by the significance test method. Generally, p < 0.05 indicates a moderate statistical difference, while p < 0.01 suggests a significant statistical difference. However, p < 0.001 reflects an extremely significant statistical-related variance.

4.2. Recursive Feature Elimination

A good alternative for selecting important features is the Recursive Feature Elimination (RFE) method, which was proposed by Guyon et al. (2002) [62]; this method is based on the principle of filtering the best feature parameters and ranking their feature parameters through model iterations. Nowadays, the related algorithm is widely applied in geology [63,64,65], and RFE is processed by three main steps: (1) constructing the model on the training dataset and estimating the importance of features on the test dataset; (2) maintaining the priority of the most important variables by constructing iterations of the model for a given subset size, i.e., a subset of the most important predictor variables identified from step 1; the ranking of the predictor variables is thus recalculated in each iteration; (3) comparing the performance of the models with different subset sizes to arrive at the optimal number and list of final predictor variables.

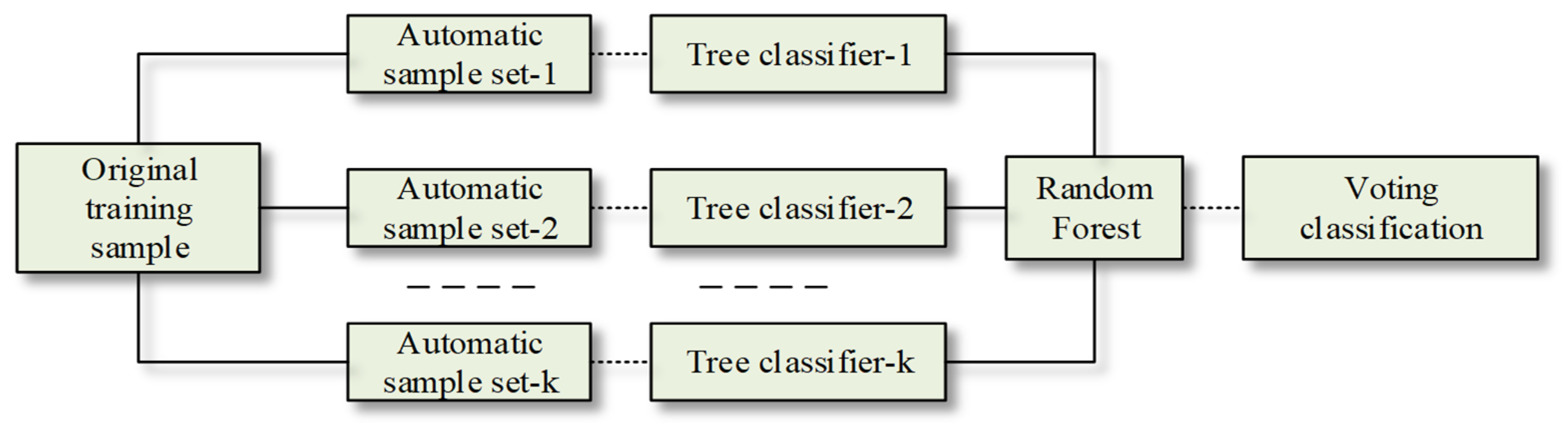
4.3. Random Forest Regression Algorithm

First proposed by Breiman (1996) and Cutler et al. (2006) [66,67], the random forest regression algorithm (RFRA) is a classifier integration algorithm based on decision trees, in which the decision tree relies on a random vector, and the vectors in the forest are independently and identically distributed. RFRA is widely applied in various industries and fields. The RFRA obtains the output of the random forest by constructing decision trees for different data subsets and then voting on the judgment results of each decision tree. When constructing decision trees using data subsets, elements of different data subsets can be repeated (i.e., with put-back sampling); otherwise, there is no correlation between decision trees with each other. Not all features are accepted as final candidate variables during the binary classification of data. In this sense, features are optimally selected afterward as candidate variables to increase the diversity of decision trees and, thus, improve the quality of the data classification performance.
In RFRA, N denotes the number of samples in the original training set, and M represents the number of variables. The number of variable nodes in the decision tree is m, where m should be less than M. The steps of RFRA construction are shown as follows (Figure 7):
(1)
The bootstrap sampling technique is used in the random forest, and k new sample sets are randomly selected with put-back to build k decision trees; the samples that are not selected form k out-of-bag data.
(2)
A single decision tree is generated for each self-sample set.
(3)
Predict the data based on the results of the generated decision tree classifier to derive the category with the highest number of votes for the voting results of the decision tree.

4.4. Model Validation Methods

(1)
Cross-validation
The cross-validation method is extensively used to evaluate the model validation. The original data sample is divided into two parts based on this method: one part is selected as the training set for building the model, and the other part is used as the testing set for the model. Afterward, the different data sets are applied for the error estimation, which can increase the generalization ability as well as the stability of the model.
K-fold cross-validation is widely used in remote sensing, communication, and geology [68,69]. The original data are divided into K copies using this method. One copy is selected as the testing set, and the remaining K-1 copies of data are used as the training set; afterward, the K models are obtained. The cross-validation method is useful for the limited data, and the evaluation results can be as close as possible to the performance of the model on the test set and can be used as an indicator for model optimization.
(2)
Receiver Operating Characteristic (ROC)
Leshowitz (1969) applied the Receiver Operating Characteristic (ROC) curve to evaluate radar signal reception capability [70]. In the ROC curve, the horizontal coordinate is the false positive rate (FPR), the vertical coordinate is the true positive rate (TPR), and the area under the ROC curve is the Area Under Curve (AUC) value. Usually, the value of the AUC is between 0.5 and 1.0. A higher AUC value represents the better performance of the selected method. An AUC value of less than 0.5 indicates the poor ability of the model prediction. AUC values of 0.5–0.7 imply an averaged prediction model, while values of 0.7–0.9 suggest a good model prediction ability. AUC values higher than 0.9 denote an excellent prediction model.

5. The Main Controlling Factor for Triggering MTDs

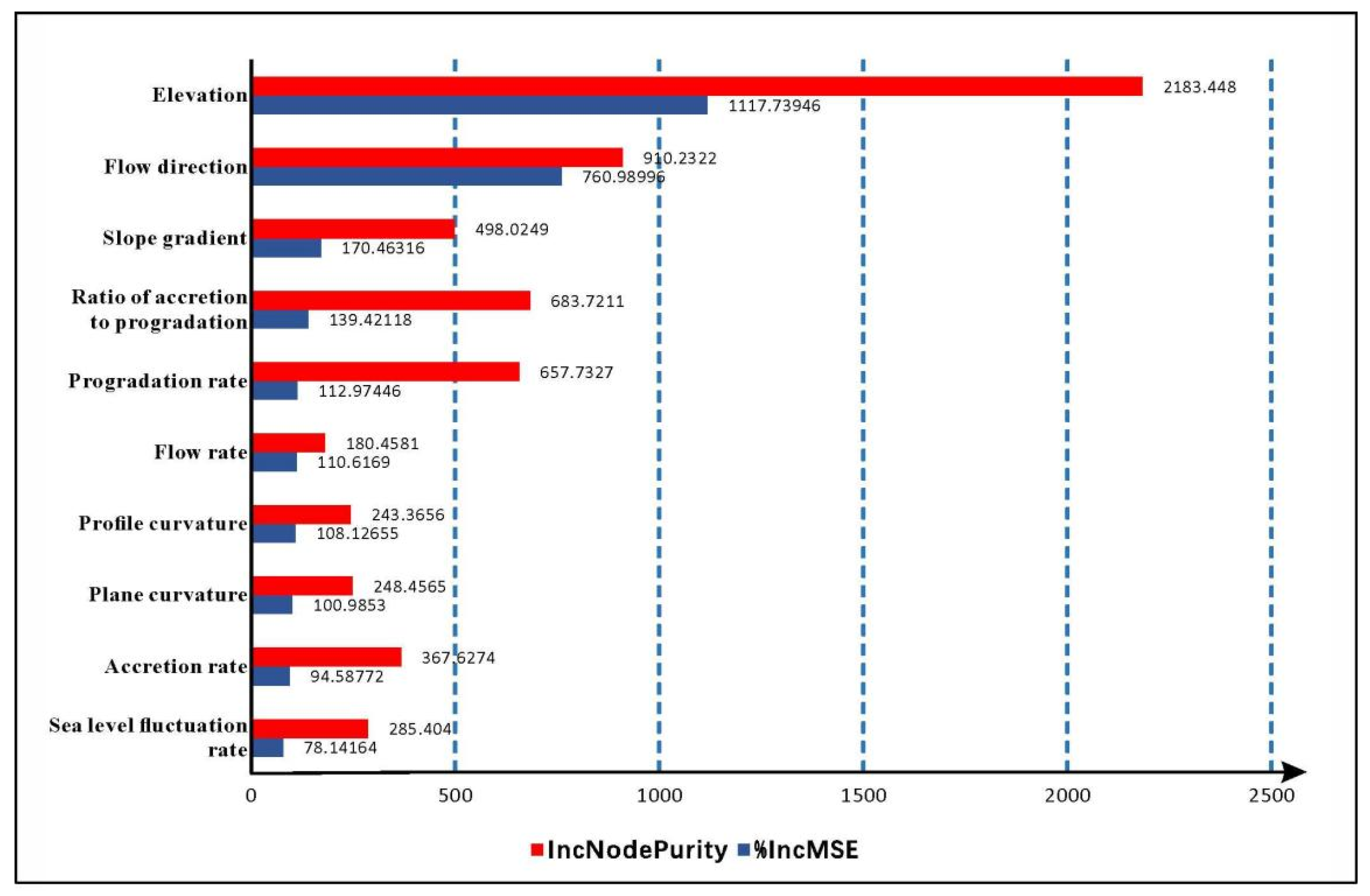
5.1. Screening of the Main Controlling Factors

In order to screen out the most dominant controlling factors, the data of four sequence interfaces of the Yinggehai Formation were diluted, and 2% of the data points were randomly extracted for this study, which was analyzed in 4 × 8119 study units. In this paper, correlation analysis was conducted for influencing factors analysis of 11 packages of MTDs.
If the absolute value of the correlation coefficient was greater than 0.95, the correlation was very high, 0.8~0.95 was a high correlation, 0.8~0.5 was a moderate correlation, 0.5~0.3 was a low correlation, and less than 0.3 was identified as no correlation. The correlation analysis was followed by a significance check to examine the reliability of the correlation, and a p-value equal to 0.05 was used as the cut-off for the significance level (Figure 8). The results of the correlation analysis and significance check showed that most of the factors influencing MTDs had low correlations; among them, the correlation between progradation rate and sediment fluxes was high and highly significant. The above analysis shows that the correlation between progradation rate and sediment fluxes is high, where sediment fluxes are converted from the formula of progradation rate and accretion rate; so, the sediment fluxes are excluded in this study.
A subsequent random forest model is applied to reduce the number of controlling factors and reduce the complexity of data processing. RFE was used to further analyze the MTD controlling factors, and RFRA was used for feature screening (Table 3, Figure 9). The above analysis reduced the 12 factors to 10 factors, including topographic factors (elevation, slope gradient, profile curvature, flow rate, plane curvature, and flow direction), sedimentary factors (accretion rate, progradation rate, and ratio of accretion to progradation), and climatic factors (sea level fluctuation rate).

5.2. MTD Occurrence Analysis

The RFRA model was built according to the above 10 MTD controlling factors, in which the number of trees was 1000, and the node variable was 5. The diluted data were divided into a 20% testing set and an 80% training set. The training data-based RFRA model revealed that the mean value of the model squared residual was 0.043. The goodness of fit was 82.52; this indicated that the random forest regression simulation result was good. The importance and ranking of the controlling factors were analyzed by the constructed random forest regression model (Figure 10). The %IncMSE and IncNodePurity in the importance analysis indicated that three influencing factors, including elevation, flow direction, and slope gradient, were the most important (Figure 10).
To discriminate the effect of the random forest regression model, the prediction of the testing data-based RFRA model was calibrated, and its ROC curve was plotted according to the prediction results (Figure 11). The related AUC value is as high as 0.987, indicating the model is very good. The optimal threshold cut point for MTDs was scored as 0.495, the specificity of the prediction model could reach 0.951, and the sensitivity was up to 0.936 (Figure 11). To verify the stability of the model, two-fold cross-validations were performed five times. The results yielded AUC values of 0.9847, 0.9849, 0.9847, 0.9853, and 0.9851, respectively. The mean AUC value is 0.9849, which indicates a good and stable modeling result.
The RFRA model was established with a diluted dataset, and four complete sets of layer-bounded data of the Yinggehai Formation in the QDNB were used as the predicted datasets to predict the likelihood of MTD (Figure 12). The probability of the MTDs being valued between 0 and 1, and the susceptibility of MTDs are graded according to their values. The predicted results are divided into five levels, namely, very low (less than 0.1), low (0.1–0.3), medium (0.3–0.6), high (0.6–0.85), and very high (greater than 0.85). It is suggested that the prediction results of the RFRA model are mostly consistent with the observation results. Moreover, the distribution of predicted MTDs is characterized by irregular geometries. The prediction results are well correlated with the distribution pattern of the observed MTD elements, which may be caused by the discontinuity of the values of the sedimentary elements according to the block assignment (Figure 4 and Figure 12). The model indicates that high susceptibilities of MTDs are localized in areas where they are not found in the seismic data interpretation. There is a clear transition in the boundaries of the high-susceptibility areas, which indicates that the model delineation is effective.

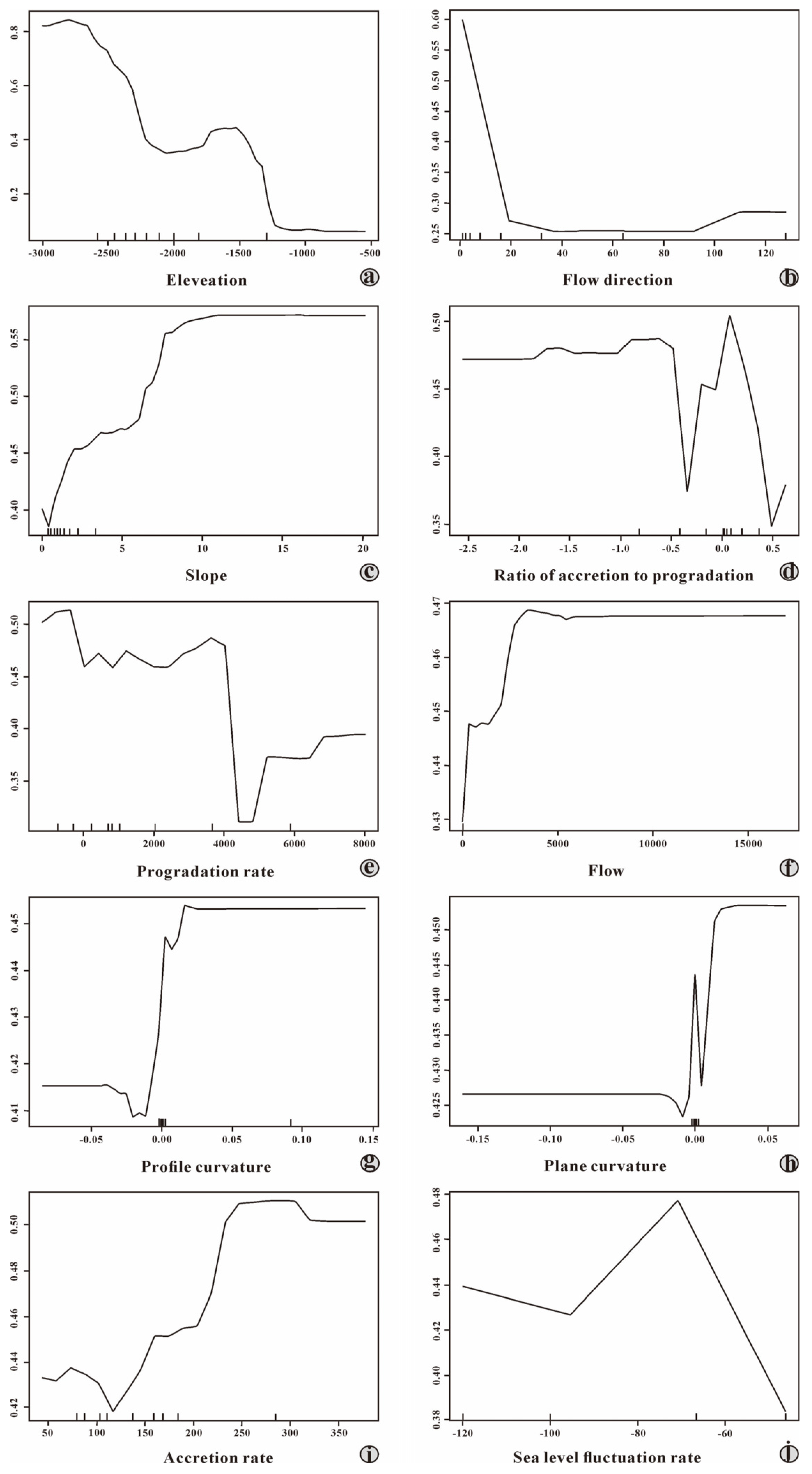
6. Partial Dependency Evaluation of Controlling Factors

There are regional differences in the factors controlling MTD, and many previous studies have been carried out. On the western continental margin of the Ulleung Basin, it was proposed that gas charging appears to be the major preconditioning factor, most likely aided by earthquakes associated with tectonic activity [71]. During the Plio–Quaternary in the Gela Basin (Strait of Sicily, Mediterranean Sea), a combination of long-term tectonic activity, climate change, and shifts in oceanographic regime affected where and when MTDs were emplaced [72]. As for the study area, three triggering mechanisms are proposed, including the combined action of slope gradient and overpressure, global environmental changes, and tectonic events. Among them, the type caused by the first set of mechanisms covers the least extent, and the frequency, inversely, is the highest [73].
The above analysis shows that the topographic and sedimentary factors are more closely related to the controlling factors of MTDs than the climatic factors (Figure 8 and Figure 10). The controlling factors are limited by the data, and the influence of tectonic factors (earthquakes) on MTDs is not added in this study. In this study, the integrated rate of sea level rise and fall in different evolutionary periods is considered and calculated. In this paper, three controlling factors, namely, accretion rate, progradation rate, and the ratio of accretion to progradation, are added. It is shown that MTDs of the Yinggehai Formation in the QDNB are mainly associated with the sediment retro-gradational stages [74]. The supply of clastic sediment sources was sufficient, and the shelf-edge-related clinoforms advanced rapidly toward the basin and resulted in fewer MTD observations (Figure 4d).
A total of 10 factors were screened in this study, among which topographic and sedimentary factors have the most prominent controls on MTD distributions. Due to the limitation of data and the lack of climatic factors caused by the difficulty of quantification, only the influence of climatic factors (sea level fluctuation rate) on MTDs was analyzed. To figure out the effects of individual controlling factors on MTDs, a random forest regression model was established with 20% of the sampling dilution data, and the marginal effects of individual controlling factors, when compared with the occurrence of MTDs, were analyzed using partial dependence plots (Figure 13).
About eleven large-scale sets of MTDs of the Yinggehai Formation widely occurred in the QDNB. These MTDs gravity-originated on the shelf edge and were transported to the abyssal plain. The partial dependence map of the elevation shows that the MTDs are mainly distributed at 1250 m below the sea level, while the occurring possibility of MTDs in other areas is very low (Figure 13a). The transport direction of MTDs is highly overlapping with the topographic flow direction (Figure 13b).
The slope gradient and the possibility of MTDs are closely correlated [71]. The steepened slope gradient will more likely trigger the MTDs, and the possibility of MTDs significantly increases during the intervals of 0.2°~2° and 5°~10°, as revealed in the partial dependence map of slope (Figure 13c). This implies that MTDs mainly occurred correlative to high-value stages of the ratio of accretion to progradation (Figure 13d). When the rate of progradation is greater than the rate of accretion, however, the possibility of MTDs decreases (Figure 13d) for the reason that a progradation exceeding accretion could, in theory, decrease slope gradients and, as such, is prone to favor stability. In detail, the least possibility of MTDs will occur during the low (<4000 m/Ma) progradation rate conditions. The partial dependence map of flow reflects the dynamic changes in the occurrence of MTDs. It is revealed that the transport capacity decreases when the flow of the topographic surface is greater than 5000, and the possibility of MTDs is stable (Figure 13f).
The partial dependence map of plane curvature reflects that MTDs mainly occur when the surface is convex (Figure 13h). There is a sudden change in the possibility of MTDs in the flattened area compared to that in the convex areas. It is suggested that a higher accretion rate would promote the possibility of MTDs, especially when the accretion rate is more than 120 m/Ma (Figure 13i).
The previous study found that there is a strong coincidence between the occurrences of slope failure and the climatically induced change in relative global sea level [6]. In Figure 13j, it is implied that the high rates of sea level dropping will trigger the possibility of MTD occurrences. This is correlative to the fact that the shelf edge will lower the sea level, leading to reduced hydrostatic pressure and, thus, destabilized deposits [75] (Figure 13j).
Here, an example of the application of RFRA models to deep water is reported, and the prediction results are well correlated with the distribution pattern of the observed MTD elements. This study indicates that the RFRA models are effective in deep-water MTD evaluation and could be applied in geological hazard prediction in the South China Sea and other similar areas worldwide. This paper presents a new methodology to understand how a bivariate statistical model of AI-based predicting responds to marine mass movements using data derived from seismic volumes. This study highlights the application of GIS used in the offshore oceanic MTD distribution possibilities.

7. Conclusions

(1) The correlation analysis of the controlling factors of MTDs in the Yinggehai Formation of the QDNB shows that the correlation between sediment fluxes and accretion rate is extremely high; ten controlling factors with the greatest influence on the controlling factors of MTDs are selected by recursive feature elimination.
(2) The analysis of the importance of controlling factors indicates that the elevation, flow direction, and slope gradient are selected as the three most important controlling factors. The MTDs in the Yinggehai Formation of the QDNB mostly occur in the shelf-margin and slope areas below 1250 m below sea level.
(3) The flow direction directly determines the transport direction of MTDs; MTDs positively occur on the condition that the slope gradient is in the intervals of 0.2°~2° and 5°~10°.
(4) The RFRA model is identified as an effective method for MTD prediction in the Pliocene QDNB and can also be extended to landslide prediction in other similar geological areas.

Author Contributions

Conceptualization, J.G.; methodology, X.Z.; software, C.Y.; validation, Y.C.; formal analysis, J.G.; investigation, Q.F. and W.P.; resources, Q.F.; data curation, X.Z.; writing—original draft preparation, J.G.; writing—review and editing, J.G.; visualization, C.Y.; supervision, X.Z.; project administration, Q.F. and W.P.; funding acquisition, J.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by [Open Fund Project of National Key Laboratory of Natural Gas Hydrates in 2022] grant number [2022-KFJJ-SHW], [Natural Science Foundation of Sichuan—Sichuan Science and Technology Program] grant number [No. 2023NSFSC0810], the [National Natural Science Foundation of China] grant number [No. 42072183] and [Open Fund of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University)] grant number [PLN2022-41]. And the APC was funded by [Open Fund Project of National Key Laboratory of Natural Gas Hydrates in 2022] grant number [2022-KFJJ-SHW].

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to this data may involve a potential future petroleum company.

Acknowledgments

We are grateful to the Guangdong Provincial Laboratory of Southern Marine Science and Engineering (Zhanjiang) for their generous help in providing the seismic data and drilling information.

Conflicts of Interest

Author Chong Yue was employed by the company PetroChina Tarim Oilfield Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

  1. Tappin, D.R.; Watts, P.; McMurtry, G.M.; Lafoy, Y.; Matsumoto, T. The Sissano, Papua New Guinea tsunami of July 1998—Offshore evidence on the source mechanism. Mar. Geol. 2001, 175, 1–23. [Google Scholar] [CrossRef]
  2. Gaullier, V.; Loncke, L.; Droz, L.; Basile, C.; Maillard, A.; Patriat, M.; Carol, F. Slope instability on the French Guiana transform margin from swath-bathymetry and 3.5 kHz echograms. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 569–579. [Google Scholar]
  3. Alves, T.M. Submarine slide blocks and associated soft-sediment deformation in deep-water basins: A review. Mar. Petrol. Geol. 2015, 67, 262–285. [Google Scholar] [CrossRef]
  4. Krastel, S.; Wynn, R.B.; Georgiopoulou, A.; Geersen, J.; Henrich, R.; Meyer, M.; Schwenk, T. Large-scale mass wasting on the Northwest African continental margin: Some general implications for mass wasting on passive continental margins. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2012; Volume 31, pp. 189–199. [Google Scholar]
  5. Zhou, Q.; Li, X.; Zhou, H.; Liu, L.; Xu, Y.; Gao, S.; Ma, L. Characteristics and genetic analysis of submarine landslides in the northern slope of the South China Sea. Mar. Geophys. Res. 2019, 40, 303–314. [Google Scholar] [CrossRef]
  6. Maslin, M.; Owen, M.; Day, S.; Long, D. Linking continental-slope failures and climate change: Testing the clathrate gun hypothesis. Geology 2004, 32, 53–56. [Google Scholar] [CrossRef]
  7. Canals, M.; Lastras, G.; Urgeles, R.; Casamor, J.L.; Mienert, J.; Cattaneo, A.; De Batist, M.; Haflidason, H.; Imbo, Y.; Laberg, J.S.; et al. Slope failure dynamics and impacts from seafloor and shallow sub-seafloor geophysical data: Case studies from the COSTA project. Mar. Geol. 2004, 213, 9–72. [Google Scholar] [CrossRef]
  8. Weimer, P.; Slatt, R.; Bouroullec, R.; Fillon, R.; Pettingill, H.; Pranter, M.; Tari, G. Introduction to the petroleum geology of deepwater setting. Geology 2006, 32, 53–56. [Google Scholar]
  9. Moscardelli, L.; Wood, L. New classification system for mass transport complexes in offshore Trinidad. Basin Res. 2008, 20, 73–98. [Google Scholar] [CrossRef]
  10. Liapidevskii, V.Y.; Dutykh, D.; Gisclon, M. On the modelling of shallow turbidity flows. Adv. Water Resour. 2018, 113, 310–327. [Google Scholar] [CrossRef]
  11. Wu, S.G.; Qin, Z.L.; Wang, D.W.; Peng, X.C.; Wang, Z.J. Seismic characteristics and triggering mechanism analysis of mass transport deposits in the northern continental slope of the South China Sea. Chin. J. Geophys. 2011, 54, 3184–3195. [Google Scholar]
  12. He, Y.L. The Characteristics and Mechanism of Sediment Gravity Flow in Slope Area in Qiongdongnan Basin. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2012. [Google Scholar]
  13. Qin, Z.L. Sedimentary Process, Distribution and Mechanism of Mass Transport Deposits, the Slope Area of Northern South China Sea; Institute of Oceanology, Chinese Academy of Sciences: Qingdao, China, 2012. [Google Scholar]
  14. Moscardelli, L.; Wood, L.; Mann, P. Mass-transport complexes and associated processes in the offshore area of Trinidad and Venezuela. AAPG Bull. 2006, 90, 1059–1088. [Google Scholar] [CrossRef]
  15. Shanmugam, G. New Perspectives on Deep-Water Sandstones: Origin, Recognition, Initiation, and Reservoir Quality; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
  16. Qin, Y.Q.; Wan, L.K.; Ji, Z.F.; Xu, H.L.; Ba, D. Progress of research on deep-water mass-transport deposits. Oil Gas Geol. 2018, 39, 140–152. [Google Scholar]
  17. Pirmez, C.; Marr, J.; Shipp, C.; Kopp, F. Observations and numerical modeling of debris flows in the Na Kika Basin, GulfofMexico. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. [Google Scholar]
  18. Shipp, R.C.; Nott, J.A.; Newlin, J.A. Physical characteristics and impact of mass transport complexes on deepwater jetted conductors and suction anchor piles. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. [Google Scholar]
  19. Meckel, L.D.; Angelatos, M.; Bonnie, J.; McGarva, R.; Almond, T.; Marshall, N.; Bourdon, L.; Aurisch, K. Reservoir characterization of sand-prone mass-trans-port deposits within slope canyons. In Mass-Transportdeposits in Deepwater Settings: SEPM Special Publication; Shipp, R.C., Weimer, P., Posamentier, H.W., Eds.; Tulsa: Claremore, OK, USA, 2011; Volume 96, pp. 391–421. [Google Scholar]
  20. Wang, D.W.; Wu, S.G.; Lu, F.L.; Wang, B.W. Mass transport deposits and its significance for oil & gas exploration in deep-water regions of South China Sea. J. China Univ. Pet. (Ed. Nat. Sci.) 2011, 35, 14–19. [Google Scholar]
  21. Alves, T.M.; Kurtev, K.; Moore, G.F.; Strasser, M. Assessing the internal character, reservoir potential, and seal competence of mass-transport deposits using seismic texture: A geophysical and petrophysical approach. AAPG Bull. 2014, 98, 793–824. [Google Scholar] [CrossRef]
  22. Carter, L. Submarine Cables and the Oceans: Connecting the World; UNEP/Earthprint: Nairobi, Kenya, 2010. [Google Scholar]
  23. Bardet, J.P.; Synolakis, C.E.; Davies, H.L.; Imamura, F.; Okal, E.A. Landslide tsunamis: Recent findings and research directions. Landslide Tsunamis Recent Find. Res. Dir. 2003, 160, 1793–1809. [Google Scholar]
  24. Ramadan, K.T.; Omar, M.A.; Allam, A.A. Modeling of tsunami generation and propagation under the effect of stochastic submarine landslides and slumps spreading in two orthogonal directions. Ocean Eng. 2014, 75, 90–111. [Google Scholar] [CrossRef]
  25. Feng, X.; Yin, B.; Gao, S.; Wang, P.; Bai, T.; Yang, D. Assessment of tsunami hazard for coastal areas of Shandong Province, China. Appl. Ocean Res. 2017, 62, 37–48. [Google Scholar] [CrossRef]
  26. Sassa, S.; Takagawa, T. Liquefied gravity flow-induced tsunami: First evidence and comparison from the 2018 Indonesia Sulawesi earthquake and tsunami disasters. Landslides 2019, 16, 195–200. [Google Scholar] [CrossRef]
  27. Locat, J.; Ten Brink, U.S.; Chaytor, J.D. The block composite submarine landslide, southern New England slope, USA: A morphological analysis. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2010; Volume 28, pp. 267–277. [Google Scholar]
  28. Ma, L.W.; Wu, S.G.; Liu, Y.R.; Sun, J.; Min, O.Y.; Li, Q.P.; Qin, Y.P.; Wang, D.W. Slope Instability Analysis of the Qiongdongnan Basin in the Northern Part of the South China Sea: Implications for the Risk Evaluation of Deepwater Drilling. J. Ocean Univ 2023, 22, 393–409. [Google Scholar] [CrossRef]
  29. Masson, D.G.; Harbitz, C.B.; Wynn, R.B.; Pedersen, G.; Løvholt, F. Submarine landslides: Processes, triggers and hazard prediction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2009–2039. [Google Scholar] [CrossRef]
  30. Talling, P.J.; Clare, M.; Urlaub, M.; Pope, E.; Hunt, J.E.; Watt SF, L. Large submarine landslides on continental slopes: Geohazards, methane release, and climate change. Oceanography 2014, 27, 32–45. [Google Scholar] [CrossRef]
  31. Kremer, K.; Usman, M.O.; Satoguchi, Y.; Nagahashi, Y.; Vadakkepuliyambatta, S.; Panieri, G.; Strasser, M. Possible climate preconditioning on submarine landslides along a convergent margin, Nankai Trough (NE Pacific). Prog. Earth. Planet. Sci. 2017, 4, 20. [Google Scholar] [CrossRef]
  32. Rodríguez-Ochoa, R.; Nadim, F.; Hicks, M.A. Influence of weak layers on seismic stability of submarine slopes. Mar. Pet. Geol. 2015, 65, 247–268. [Google Scholar] [CrossRef]
  33. Nian, T.K.; Guo, X.S.; Zheng, D.F.; Xiu, Z.X.; Jiang, Z.B. Susceptibility assessment of regional submarine landslides triggered by seismic actions. Appl. Ocean Res. 2019, 93, 101964. [Google Scholar] [CrossRef]
  34. Urlaub, M.; Zervos, A.; Talling, P.J.; Masson, D.G.; Clayton, C.I. How do∼2° slopes fail in areas of slow sedimentation? A sensitivity study on the influence of accumulation rate and permeability on submarine slope stability. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2012; pp. 277–287. [Google Scholar]
  35. Liu, F.; Tan, L.; Crosta, G.; Huang, Y. Spatiotemporal destabilization modes of upper continental slopes undergoing hydrate dissociation. Eng. Geol. 2020, 264, 105286. [Google Scholar] [CrossRef]
  36. Yang, S.; Choi, J.C.; Vanneste, M.; Kvalstad, T. Effects of gas hydrates dissociation on clays and submarine slope stability. Bull. Eng. Geol. Environ. 2018, 77, 941–952. [Google Scholar] [CrossRef]
  37. Llopart, J.; Urgeles, R.; Camerlenghi, A.; Lucchi, R.G.; Mol, B.D.; Rebesco, M.; Pedrosa, M.T. Slope instability of glaciated continental margins: Constraints from permeability-compressibility tests and hydrogeological modeling off Storfjorden, NW Barents Sea. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 95–104. [Google Scholar]
  38. Gales, J.A.; Mckay, R.M.; De Santis, L.; Rebesco, M.; Laberg, J.S.; Shevenell, A.E.; Harwood, D.; Leckie, R.M.; Kulhanek, D.K.; King, M.; et al. Climate-controlled submarine landslides on the Antarctic continental margin. Nat. Commun. 2023, 14, 2714. [Google Scholar] [CrossRef]
  39. Bessette-Kirton, E.K.; Coe, J.A.; Schulz, W.H.; Cerovski-Darriau, C.; Einbund, M.M. Mobility characteristics of debris slides and flows triggered by Hurricane Maria in Puerto Rico. Landslides 2020, 17, 2795–2809. [Google Scholar] [CrossRef]
  40. Zhu, H.; Yang, X.; Liu, K.; Zhou, X. Seismic-based sediment provenance analysis in continental lacustrine rift basins: An example from the Bohai Bay Basin, China. AAPG Bull. 2014, 98, 1995–2018. [Google Scholar] [CrossRef]
  41. Zhu, W.L. Discrepancy tectonic evolution and petroleum exploration in China offshore Cenozoic Basins. Earth Sci. Front. 2015, 22, 88–101. [Google Scholar]
  42. Zhu, W.L.; Zhang, G.C.; Gao, L. Geological characteristics and exploration objectives of hydrocarbons in the northern continental margin basin of South China Sea. Acta Pet. Sin. 2008, 29, 1–9. [Google Scholar]
  43. Clift, P.D.; Sun, Z. The sedimentary and tectonic evolution of the Yinggehai-Song Hong basin and the southern Hainan margin, South China Sea: Implications for Tibetan uplift and monsoon intensification. J. Geophys. Res. Solid Earth 2006, 111, B6. [Google Scholar] [CrossRef]
  44. Leloup, P.H.; Lacassin, R.; Tapponnier, P.; Schärer, U.; Zhong, D.; Liu, X.; Trinh, P.T. The Ailao Shan-Red river shear zone (Yunnan, China), tertiary transform boundary of Indochina. Tectonophysics 1995, 251, 3–84. [Google Scholar] [CrossRef]
  45. Du, T.J. Sequence Stratigraphic and Deep Water Sedimentaiy Characteristic in the Qingdongnan Basin. Master’s Thesis, Ocean University of China, Qingdao, China, 2013. [Google Scholar]
  46. Liu, X.F.; Sun, Z.P.; Liu, X.Y.; Liu, D.S.; Zhai, S.K.; Long, H.Y.; Jiang, L.J.; Bi, D.J. Chronostratigraphic Framework based on Micro-paleontological Data from Drilling LS33a in Deep Water Area of Northern South China Sea. Acta Sedimentol. Sin. 2018, 36, 890–902. [Google Scholar] [CrossRef]
  47. Li, W.; Alves, T.M.; Rebesco, M.; Sun, J.; Li, J.; Li, S.; Wu, S. The Baiyun Slide Complex, South China Sea: A modern example of slope instability controlling submarine-channel incision on continental slopes. Mar. Pet. Geol. 2020, 114, 104231. [Google Scholar] [CrossRef]
  48. Zhang, K.; Song, H.; Sun, S.; Gao, J. Distribution and genesis of submarine landslides in the northeastern South China Sea. Geol. J. 2021, 56, 1187–1201. [Google Scholar] [CrossRef]
  49. Gamboa, D.; Omira, R.; Terrinha, P. Spatial and morphometric relationships of submarine landslides offshore west and southwest Iberia. Landslides 2022, 19, 387–405. [Google Scholar] [CrossRef]
  50. Yang, S.L.; Solheim, A.; Forsberg, C.F.; Kvalstad, T.; Feng, X.L.; Li, A.L.; Urgeles, R. Geotechnical properties of river-fed sediments compared with glacier-fed sediments. Mar. Georesources Geotechnol. 2009, 27, 281–295. [Google Scholar] [CrossRef]
  51. Lucchi, R.G.; Pedrosa, M.T.; Camerlenghi, A.; Urgeles, R.; De Mol, B.; Rebesco, M. Recent submarine landslides on the continental slope of Storfjorden and Kveithola Trough-Mouth Fans (north west Barents Sea). In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2012; Volume 31, pp. 735–745. [Google Scholar]
  52. Stoecklin, A.; Friedli, B.; Puzrin, A.M. Sedimentation as a control for large submarine landslides: Mechanical modeling and analysis of the Santa Barbara Basin. J. Geophys. Res. Solid Earth 2017, 122, 8645–8663. [Google Scholar] [CrossRef]
  53. Helland-Hansen, W.; Hampson, G.J. Trajectory analysis: Concepts and applications. Basin Res. 2009, 21, 454–483. [Google Scholar] [CrossRef]
  54. Joh, M.H.; Yoo, D.G. Plio-Quaternary seismic stratigraphy and depositional history on the southern Ulleung Basin, East Sea. Sea: J. Korean Soc. Oceanogr. 2009, 14, 90–101. [Google Scholar]
  55. Yi, Y.M.; Yoo, D.G.; Kang, N.K.; Yi, B.Y. Distribution and origin of quaternary mass transport deposit in the Ulleung Basin, East Sea. Geophys. Geophys. Explor. 2014, 17, 74–87. [Google Scholar] [CrossRef]
  56. Lisiecki, L.E.; Raymo, M.E. Correction to “A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records”. Paleoceanogr. Paleoclimatology 2005, 20, 1–17. [Google Scholar] [CrossRef]
  57. Revell, L.J.; Harrison, A.S. PCCA: A program for phylogenetic canonical correlation analysis. Bioinformatics 2008, 24, 1018–1020. [Google Scholar] [CrossRef] [PubMed]
  58. Melnykov, A.V.; Hall, K.B. Revival of high-order fluorescence correlation analysis: Generalized theory and biochemical applications. J. Phys. Chem. B 2009, 113, 15629–15638. [Google Scholar] [CrossRef]
  59. Witt, A.; Malamud, B.D.; Rossi, M.; Guzzetti, F.; Peruccacci, S. Temporal correlations and clustering of landslides. Earth Surf. Process. Landf. 2010, 35, 1138–1156. [Google Scholar] [CrossRef]
  60. Strauss, L.G.; Koczan, D.; Seiz, M.; Tuettenberg, J.; Schmieder, K.; Pan, L.; Dimitrakopoulou-Strauss, A. Correlation of the Ga-68-bombesin analog Ga-68-BZH3 with receptors expression in gliomas as measured by quantitative dynamic positron emission tomography (dPET) and gene arrays. Mol. Imaging Biol. 2012, 14, 376–383. [Google Scholar] [CrossRef]
  61. Geitner, R.; Fritzsch, R.; Popp, J.; Bocklitz, T.W. corr2D-implementation of two-dimensional correlation analysis in R. arXiv 2018, arXiv:1808.00685. [Google Scholar] [CrossRef]
  62. Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
  63. Naghavi, H.; Fallah, A.; Shataee, S.; Latifi, H.; Soosani, J.; Ramezani, H.; Conrad, C. Canopy cover estimation across semi-Mediterranean woodlands: Application of high-resolution earth observation data. J. Appl. Remote Sens. 2014, 8, 083524. [Google Scholar] [CrossRef]
  64. Bachofer, F.; Quénéhervé, G.; Hochschild, V.; Maerker, M. Multisensoral topsoil mapping in the semiarid Lake Manyara region, northern Tanzania. Remote Sens. 2015, 7, 9563–9586. [Google Scholar] [CrossRef]
  65. Sorenson, P.T.; Kiss, J.; Bedard-Haughn, A.K.; Shirtliffe, S. Multi-Horizon Predictive Soil Mapping of Historical Soil Properties Using Remote Sensing Imagery. Remote Sens. 2022, 14, 5803. [Google Scholar] [CrossRef]
  66. Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  67. Cutler, A.; Stevens, J.R. random forests for microarrays. Methods Enzymol. 2006, 411, 422–432. [Google Scholar] [PubMed]
  68. Gholinejad, S.; Naeini, A.A.; Amiri-Simkooei, A. Robust particle swarm optimization of RFMs for high-resolution satellite images based on k-fold cross-validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 2594–2599. [Google Scholar] [CrossRef]
  69. Al-Mukhtar:, M. Random forest, support vector machine, and neural networks to modeling suspended sediment in Tigris River-Baghdad. Environ. Monit. Assess. 2019, 191, 673. [Google Scholar] [CrossRef]
  70. Leshowitz, B. Comparison of ROC Curves from One- and Two-Interval Rating-Scale Procedures. J. Acoust. Soc. Am. 1969, 46, 399–402. [Google Scholar] [CrossRef]
  71. Cukur, D.; Kim, S.-P.; Kong, G.-S.; Bahk, J.-J.; Horozal, S.; Um, I.-K.; Lee, G.-S.; Chang, T.-S.; Ha, H.-J.; Völker, D.; et al. Geophysical evidence and inferred triggering factors of submarine landslides on the western continental margin of the Ulleung Basin, East Sea. Geo-Mar Lett. 2016, 36, 425–444. [Google Scholar] [CrossRef]
  72. Gauchery, T.; Rovere, M.; Pellegrini, C.C.; Cattaneo, A.; Campiani, E.; Trincardi, F. Factors controlling margin instability during the Plio-Quaternary in the Gela Basin (Strait of Sicily, Mediterranean Sea). Mar. Pet. Geol. 2021, 123, 104767. [Google Scholar] [CrossRef]
  73. Wang, W.W.; Wang, D.W.; Wu, S.G.; Völker, D.; Zeng, H.L.; Cai, G.Q.; Li, Q.P. Submarine landslides on the north continental slope of the South China Sea. J. Ocean Univ. China 2018, 17, 83–100. [Google Scholar] [CrossRef]
  74. Yue, C.; Zhao, X.M.; Ge, J.W.; Ma, C.; Liao, J.; Song, P.; Fang, X.Y.; Fan, T.E. Evolution and Main Controlling Factors of Continental Shelf-edge Trajectory in Yinggehai Formation, Qiongdongnan Basin. Acta Sedimentol. Sin. 2023, 41, 110–125. [Google Scholar] [CrossRef]
  75. Rothwell, R.G.; Thomson, J.; Kähler, G. Low-sea-level emplacement of a very large late Pleistocene “megaturbidite” in the Western Mediterranean Sea. Nature 1998, 392, 377–380. [Google Scholar] [CrossRef]
Jmse 12 02115 g001
Figure 1. Location of QDNB in the South China Sea (a) and tectonic unit as well as the well location of the study area (b). The black line indicates six secondary blocks named from 1 to 6 in the study area from west to east.
Figure 1. Location of QDNB in the South China Sea (a) and tectonic unit as well as the well location of the study area (b). The black line indicates six secondary blocks named from 1 to 6 in the study area from west to east.
Jmse 12 02115 g001
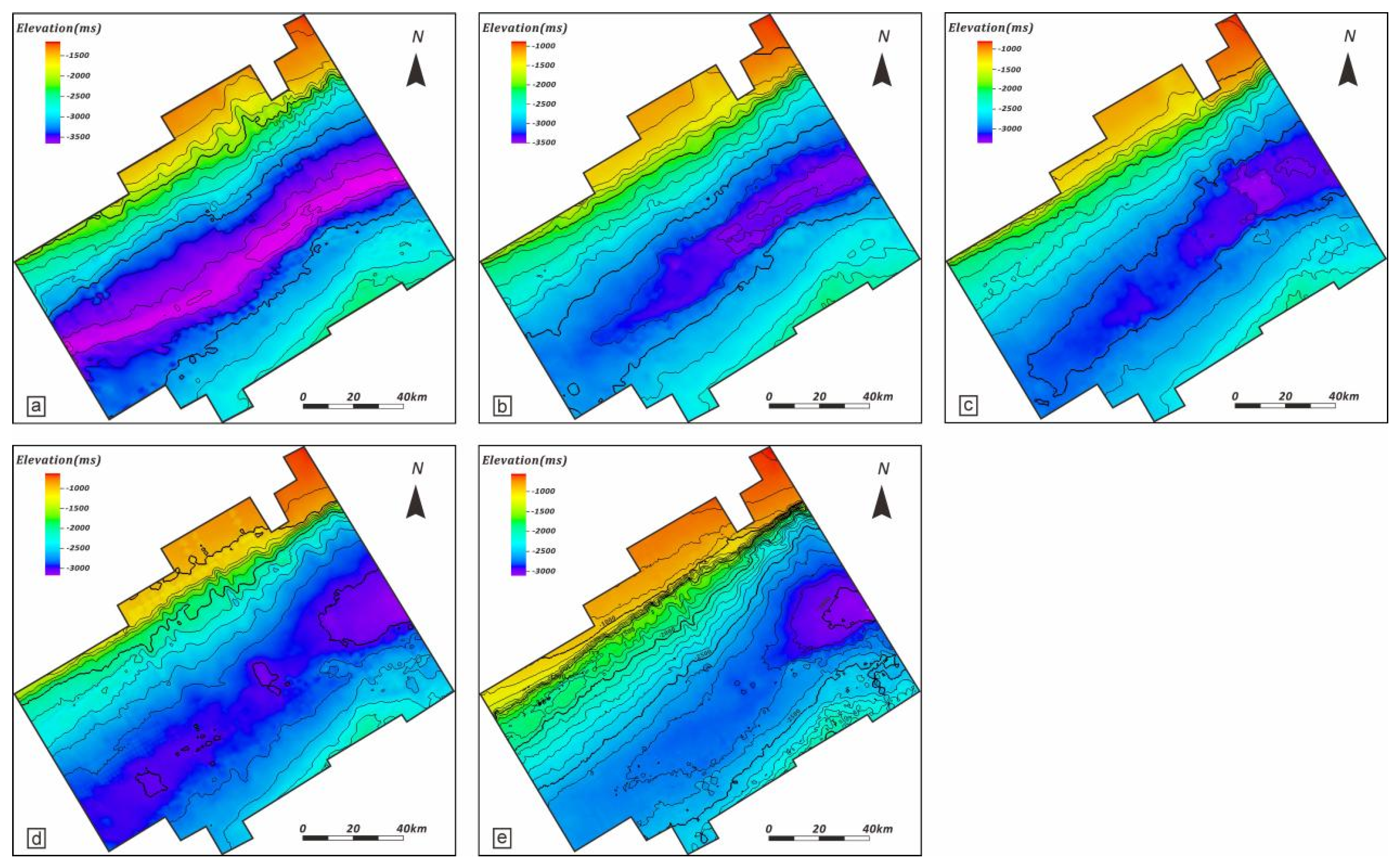
Jmse 12 02115 g002
Figure 2. Elevation maps of the main surfaces, including T30 (a), T29 (b), T28 (c), T27 (d), and T20 (e) of the Pliocene Yinggehai Formation in the Qiongdongnan Basin, South China Sea.
Figure 2. Elevation maps of the main surfaces, including T30 (a), T29 (b), T28 (c), T27 (d), and T20 (e) of the Pliocene Yinggehai Formation in the Qiongdongnan Basin, South China Sea.
Jmse 12 02115 g002
Jmse 12 02115 g003aJmse 12 02115 g003b
Figure 3. Seismic profiles 3, 10, and AA’ showing the MTDs identified from T30 to T29. TWT: two-way travel time; MTDs: mass-transport deposits. See locations in Figure 1b.
Figure 3. Seismic profiles 3, 10, and AA’ showing the MTDs identified from T30 to T29. TWT: two-way travel time; MTDs: mass-transport deposits. See locations in Figure 1b.
Jmse 12 02115 g003aJmse 12 02115 g003b
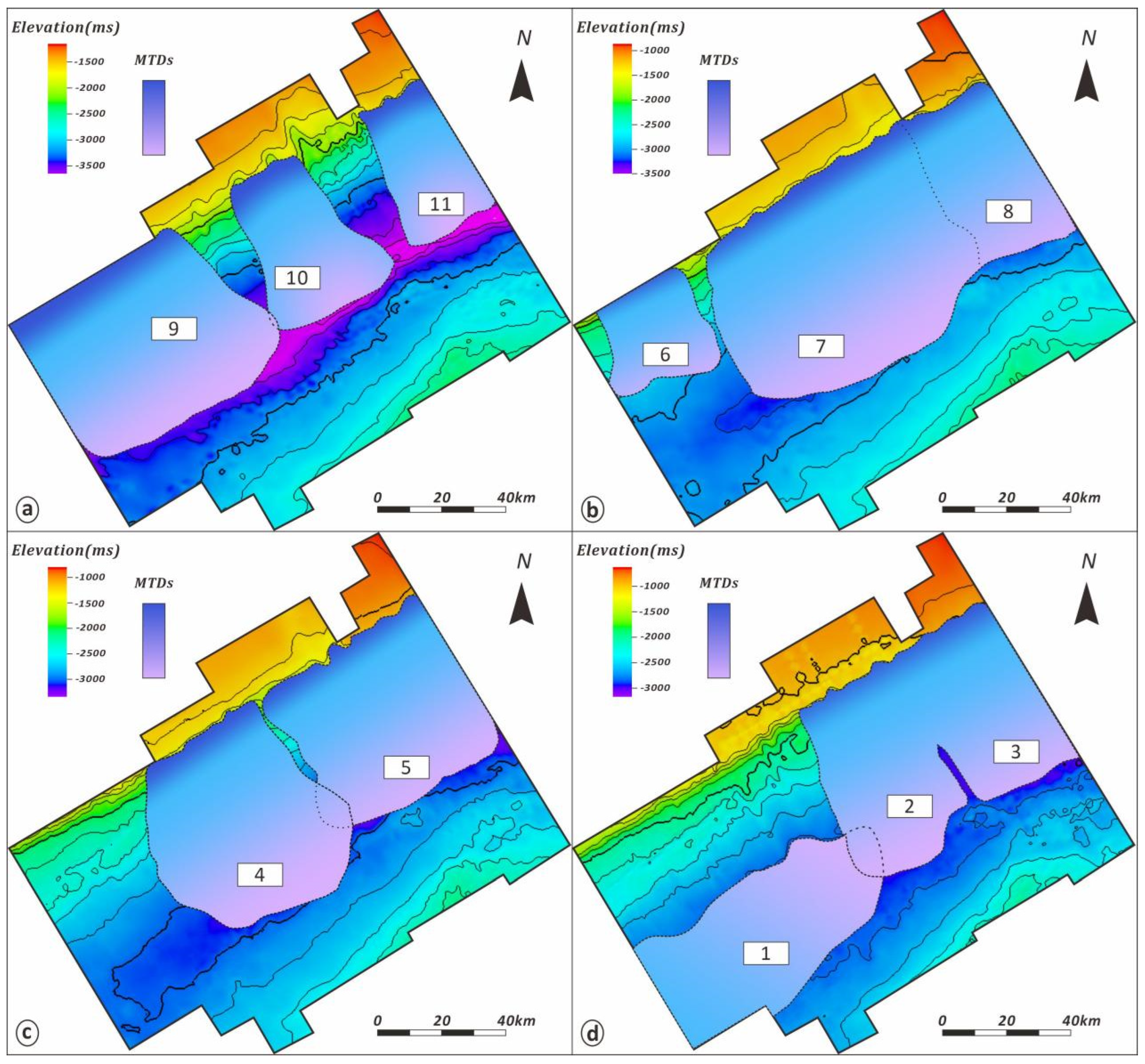
Jmse 12 02115 g004
Figure 4. MTD plane distribution map in four sequences ((a) T30-T29, (b) T29-T28, (c) T28-T27, (d) T27-T20) of Yinggehai Formation in Qiongdongnan Basin, South China Sea.
Figure 4. MTD plane distribution map in four sequences ((a) T30-T29, (b) T29-T28, (c) T28-T27, (d) T27-T20) of Yinggehai Formation in Qiongdongnan Basin, South China Sea.
Jmse 12 02115 g004
Jmse 12 02115 g005
Figure 5. Schematic diagram of morphological characteristics and geometric parameters of slope topography [53].
Figure 5. Schematic diagram of morphological characteristics and geometric parameters of slope topography [53].
Jmse 12 02115 g005
Jmse 12 02115 g006
Figure 6. Digital flow chart of MTD controlling factors. The numerical process of MTD controlling factors is described in detail.
Figure 6. Digital flow chart of MTD controlling factors. The numerical process of MTD controlling factors is described in detail.
Jmse 12 02115 g006
Jmse 12 02115 g007
Figure 7. The specific steps of random forest. Describe the algorithm flow of random forest in detail.
Figure 7. The specific steps of random forest. Describe the algorithm flow of random forest in detail.
Jmse 12 02115 g007
Jmse 12 02115 g008
Figure 8. Correlation and visibility of MTD trigger factors. a: Elevation; b: Slope gradient; c: Profle curvature; d: Accretion rate; e: Slope direction; f: flow direction; g: Sediment fluxes; h: Progradation rate; i: Ratio of accretion to progradation; j: Sea level fluctuation rate; k: flow rate; l: Plane curvature.
Figure 8. Correlation and visibility of MTD trigger factors. a: Elevation; b: Slope gradient; c: Profle curvature; d: Accretion rate; e: Slope direction; f: flow direction; g: Sediment fluxes; h: Progradation rate; i: Ratio of accretion to progradation; j: Sea level fluctuation rate; k: flow rate; l: Plane curvature.
Jmse 12 02115 g008
Jmse 12 02115 g009
Figure 9. The recursive feature elimination root mean square error trend diagram of MTD controlling factors.
Figure 9. The recursive feature elimination root mean square error trend diagram of MTD controlling factors.
Jmse 12 02115 g009
Jmse 12 02115 g010
Figure 10. The importance ranking of MTD controlling factors. The controlling factors are ranked by importance analysis. Notice that the elevation, flow direction, and slope gradient rank high.
Figure 10. The importance ranking of MTD controlling factors. The controlling factors are ranked by importance analysis. Notice that the elevation, flow direction, and slope gradient rank high.
Jmse 12 02115 g010
Jmse 12 02115 g011
Figure 11. Random forest model receiver operating characteristics reflected the high accuracy of the model.
Figure 11. Random forest model receiver operating characteristics reflected the high accuracy of the model.
Jmse 12 02115 g011
Jmse 12 02115 g012
Figure 12. MTD prediction results in four third-order sequences ((a) T30-T29; (b) T29-T28; (c) T28-T27; (d) T27-T20) of Pliocene in QDNB, South China Sea. Notice that the results were consistent with the facts presented in Figure 4.
Figure 12. MTD prediction results in four third-order sequences ((a) T30-T29; (b) T29-T28; (c) T28-T27; (d) T27-T20) of Pliocene in QDNB, South China Sea. Notice that the results were consistent with the facts presented in Figure 4.
Jmse 12 02115 g012
Jmse 12 02115 g013
Figure 13. Partial dependency map of MTD controlling factors: Eleveation (a), Flow direction (b), Slope gradient (c), Ratio of accretion to progration (d), Progradation rate (e), Flow rate (f), Profile curvature (g), Plane curvature (h), Accretion rate (i) and Sea level fluctuation rate (j).
Figure 13. Partial dependency map of MTD controlling factors: Eleveation (a), Flow direction (b), Slope gradient (c), Ratio of accretion to progration (d), Progradation rate (e), Flow rate (f), Profile curvature (g), Plane curvature (h), Accretion rate (i) and Sea level fluctuation rate (j).
Jmse 12 02115 g013
Table 1. The geomorphologic parameters of each described MTD in the Pliocene to Early Pleistocene successions of the study area.
Table 1. The geomorphologic parameters of each described MTD in the Pliocene to Early Pleistocene successions of the study area.
SequenceNumberLocations in the Study AreaLength (km)Width (km)
SQ4
(T27-T20)		1Southwest89.7633.18
2North central64.2737.50
3Northeast60.6936.62
SQ3
(T28-T27)		4North central66.0949.34
5Northeast56.0963.26
SQ2
(T29-T28)		6Northwest35.7228.51
7Central66.7278.12
8Central–Northeast58.4848.06
SQ1
(T30-T29)		9Northwest57.7175.53
10North central53.2231.44
11Northeast48.6827.83
Table 2. Statistical table of MTD controlling factors of the Pliocene Qiongdongnan Basin, South China Sea.
Table 2. Statistical table of MTD controlling factors of the Pliocene Qiongdongnan Basin, South China Sea.
Factor CategoryVariablesData TypeNumber RangeUnit
Topographic factorsElevationContinuous[−2552.011~−54.627]m
SlopeContinuous[0~17.603]°
Slope directionContinuous[1, 2, 3, 4, 5, 6, 7, 8]-
Profile curvatureContinuous[−0.085~0.141]-
Plane curvatureContinuous[−0.161~0.03]-
Flow directionCategorical[1, 2, 4, 8, 16, 32, 64, 128]-
FlowContinuous[0, 1, 2~16,970]-
Sedimentary factorsAccretion rateContinuous[43.801~377.153]m/Ma
Progradation rateContinuous[−1175~8.13.889]m/Ma
Ratio of accretion to progradationContinuous[−2.557~0.628]-
Sediment fluxesContinuous[−348.101~1632.94]m2/Ma
Climatic factorsSea level fluctuation rateContinuous[−120~−46.15]m/Ma
Table 3. Recursive feature elimination screening table of MTD controlling factors.
Table 3. Recursive feature elimination screening table of MTD controlling factors.
VariablesSerial NumberRMSERsquaredMAERMSESDRsquaredSDMAESDSelected
Elevation10.51290.08690.39350.00450.00840.0056√
Slope20.43490.24620.34510.03620.10860.0374√
Progradation rate30.31050.61520.22050.01250.03120.0175√
Ratio of accretion to progradation40.30940.62540.22980.00460.01320.0031√
Flow50.31110.62780.23930.00440.01270.0034√
Profile curvature60.28730.66950.18930.00740.01730.0069√
Accretion rate70.28810.67030.19580.00540.01310.0039√
Plane curvature80.28790.67300.20010.00480.01150.0040√
Sea level fluctuation rate90.23740.76980.13570.03490.06830.0374√
Flow direction100.20900.82530.10820.00490.00840.0025√
Slope direction110.20940.82490.10980.00510.00870.0030
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ge, J.; Zhao, X.; Fan, Q.; Pang, W.; Yue, C.; Chen, Y. The Controlling Factors and Prediction of Deep-Water Mass Transport Deposits in the Pliocene Qiongdongnan Basin, South China Sea. J. Mar. Sci. Eng. 2024, 12, 2115. https://doi.org/10.3390/jmse12122115

AMA Style

Ge J, Zhao X, Fan Q, Pang W, Yue C, Chen Y. The Controlling Factors and Prediction of Deep-Water Mass Transport Deposits in the Pliocene Qiongdongnan Basin, South China Sea. Journal of Marine Science and Engineering. 2024; 12(12):2115. https://doi.org/10.3390/jmse12122115

Chicago/Turabian Style

Ge, Jiawang, Xiaoming Zhao, Qi Fan, Weixin Pang, Chong Yue, and Yueyao Chen. 2024. "The Controlling Factors and Prediction of Deep-Water Mass Transport Deposits in the Pliocene Qiongdongnan Basin, South China Sea" Journal of Marine Science and Engineering 12, no. 12: 2115. https://doi.org/10.3390/jmse12122115

APA Style

Ge, J., Zhao, X., Fan, Q., Pang, W., Yue, C., & Chen, Y. (2024). The Controlling Factors and Prediction of Deep-Water Mass Transport Deposits in the Pliocene Qiongdongnan Basin, South China Sea. Journal of Marine Science and Engineering, 12(12), 2115. https://doi.org/10.3390/jmse12122115

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop