Incorporating Non-Equlibrium Ripple Dynamics into Bed Stress Estimates Under Combined Wave and Current Forcing

Abstract

We present direct measurements of seafloor ripple dimensions, near-bed mean flow Reynolds stresses and near-bed turbulent sediment fluxes on a sandy inner shelf subjected to strong wave and tidal current forcing. The measurements of ripple dimensions (height, wavelength) and Reynolds stresses are used to evaluate the performance of a methodology for the incorporation of non-equilibrium ripple dynamics into the calculations of the drag exerted by the bed on the overlying flow (i.e., the bed stress) using a boundary layer model for wave–current interaction. The methodology is based on the simultaneous use of existing models for the time-dependent evolution of ripple geometry and for the wave–current boundary layer that enable a continuous feedback between bottom drag and small-scale seabed morphology, which determines seabed roughness. The model-data comparison shows good agreement between modeled and measured bed stresses and bedform dimensions. Moreover, the proposed methodology is shown to give better results than combining the wave–current interaction model and standard equilibrium ripple predictors, both in terms of bed stresses and ripple dimensions. The near-bed turbulent vertical sediment fluxes show good correlation with the combined wave–current stresses and are used as a proxy for the resuspension of fine sediments (d < 64 μm) from the sandy seabed matrix. Implications for the modeling of the resuspension processes and erosional fluxes are discussed in light of our findings.

1. Introduction

Sediment transport processes are of interest for a variety of ecological problems in coastal ocean environments. For example, the transport of fine sediments is related to the fate of contaminants and water quality issues, as well as the inhibition of primary production and hypoxia [1]. Engineering practices are often conditioned to the natural pathways of suspended sediments, as they can impair the optimal functioning of coastal projects. Human intervention, such as dredging or beach nourishment, may lead to enhanced suspended sediment concentrations and undesirable effects on the functioning of harbors and navigation channels [2]. Thus, a better understanding of the physical processes that determine sediment mobilization and accumulation zones is essential to improve our capability of sustainably managing coastal areas.

Sediment mobilization and transport rates in coastal seas are largely determined by the magnitude of the bed shear stress, which controls both the amount and the size of the particles that are entrained into the water column [3]. In coastal seas subjected to strong wave and current forcing, the bed shear stress is the result of the non-linear combination of wave and current effects and the bed conditions [4,5,6]. The enhanced turbulence within the wave boundary layer increases the effective roughness that the current feels, which increases the drag between the bed and the overlying flow [4]. Measuring the bed shear stress under wave and current forcing is a difficult task since measurements need to be taken within the wave-boundary layer, which is only a few centimeters thick [4,7]. As a result, the bed shear stress under combined wave and current forcing is usually estimated using parametric models that rely on bulk wave parameters such as bottom wave orbital velocity, wave period and wave direction, the measurement of near-bottom currents (which are relatively easy to measure) and estimates of bed roughness (e.g., refs. [4,7,8,9]).

Among all the parameters involved in the computation of the bed shear stresses, bed roughness is often the most challenging to estimate [6,10]. Sandy seabeds in shelf seas (with or without contents of fine sediments) are often covered with small scale bedforms (ripples) that result from the action of waves, currents or the combination of both [11,12,13]. These small-scale ripples have important effects in bottom boundary layer dynamics and the generation of near-bed turbulence [6,14,15,16]. Bed roughness is usually incorporated into bottom boundary layer models in terms of the ripple geometry as $k_B\sim {\eta }^2/\lambda$, where $\eta$ is the ripple height, and $\lambda$ is the ripple wavelength (e.g., refs. [17,18,19]). The ripple dimensions needed to estimate bed roughness are, in turn, obtained from small-scale bedform predictors that are based on parameters related to the wave or current forcing and the grain size of bed sediments [12,17,18,20]. There are several proposed formulations to estimate ripple height and wavelength; an extensive review of such predictors is provided in Nelson et al. [21]. One of the most commonly used models is that of Wiberg and Harris [20], which provides estimates of $\eta$ and $\lambda$ based on the ratio of near-bed wave orbital diameter to grain size. Other predictors, for example, rely on the use of the Shields parameter (e.g., ref. [17]), the mobility number (e.g., ref. [18]) and the Reynolds number (e.g., ref. [22]), among other parameters. Bed roughness can be readily incorporated into boundary layer models using any of the predictors available (e.g., refs. [6,10]).

Most small-scale bedform predictors assume that bedforms are in equilibrium with the forcing conditions, which is only true if enough time has lapsed for bedforms to adjust to the hydrodynamic forcing [21,23]. If that is not the case, bedforms will actively change their dimensions, and if the forcing conditions change continuously, the transient character of the bedforms will persist in time [24,25]. Laboratory and field experiments have found that the adjustment time of bedforms can be longer than the time over which the forcing changes, highlighting the transient character of ripple formation and evolution [26,27]. A few models that account for the time-dependent adjustment of ripple dimensions have been proposed, in which a differential equation for ripple evolution is solved at each time step (e.g., refs. [13,27,28]). Soulsby et al. [13] proposed a fully time-evolving model that predicts the height, wavelength and orientation of bedforms on sandy seabeds generated by currents, waves or both, including processes such as the initiation of motion, bedform wash-out and biological degradation. Models of this type (e.g., refs. [13,27,28]) incorporate time-dependent coefficients and temporally variable adjustment time scales and thus allow for delays between the hydrodynamic forcing and changes in ripple morphology [27].

Non-equilibrium ripple dynamics can result in large spatio-temporal variations in bottom drag [6] and, consequently, need to be accounted for when estimating bottom stresses in sediment transport studies to adequately evaluate processes such as sediment resuspension and erosional fluxes. In this work, we present a simple methodology to incorporate time-evolving ripple dynamics in the estimation of bed shear stress under combined wave and current forcing. The methodology is based on the simultaneous use of a wave–current boundary layer model [4] and a ripple evolution model [13]. The modeled bed stresses and ripple geometry are compared against direct measurements of seafloor ripple dimensions ($\eta$, $\lambda$) and near-bed Reynolds stresses collected on a predominantly sandy inner shelf region along the Dutch coast, with favorable results. The proposed methodology is also shown to perform better than the use standard bedform predictors (that assume equilibrium ripple conditions) to estimate bed roughness and bed stresses. Implications for the modeling of erosional processes are discussed in light of our findings and turbulence measurements, with a focus on the empirical determination of the critical stress for erosion and the resuspension constant (e.g., refs. [29,30]). The paper is organized as follows: The model equations are presented in Section 2, and a description of the study site and field measurements is presented in Section 3. The results and discussion are presented in Section 4 and Section 5, respectively. Finally, a summary and conclusions are presented in Section 6.

2. Model Equations

2.1. Wave–Current Interaction

The Grant and Madsen [4] model is a wave–current interaction model that allows for the specification of a dynamic bed roughness, which feeds the model hydrodynamics. In this section, we present the basic assumptions and the core model equations, which are common to many other boundary layer models (e.g., refs. [9,31]).

One of the main assumptions of the model is the existence of a constant stress layer where the bottom stress is approximately equal to the turbulent Reynolds stress. If no waves are present, the velocity profile in the bottom boundary layer $U\left(z\right)$ is logarithmic and it scales with the friction velocity $u_{\ast c}=\sqrt{{\tau }_b/{\rho }_0}$, where ${\tau }_b$ is the bottom shear stress, and ${\rho }_0$ is the density of seawater,

$$U\left(z\right)={\displaystyle \frac{u_{\ast c}}{\kappa }}log\left({\displaystyle \frac{z}{z_0}}\right)$$

(1)

where $\kappa \approx 0.4$ is the von Karman constant, and $z_0$ is the hydrodynamic roughness where velocity goes to zero. The hydrodynamic roughness is included as a Nikuradse roughness, $z_0=k_B/30$, where $k_B$ is the physical roughness of seabed irregularities such as small-scale ripples.

The influence of the waves is modeled as an increase in the eddy viscosity in the wave boundary layer, which is assumed to scale with the combined wave–current friction velocity ($u_{\ast cw}$) that characterizes the maximum shear stress associated with the combined effect of waves and currents. The wave–current friction velocity $u_{\ast cw}$ is obtained as

$$u_{\ast cw}=u_{\ast w}{\left[1+2{\left({\displaystyle \frac{u_{\ast c}}{u_{\ast w}}}\right)}^{2}cos\theta +{\left({\displaystyle \frac{u_{\ast c}}{u_{\ast w}}}\right)}^4\right]}^{1/4}$$

(2)

where $\theta$ is the angle between waves and currents, and $u_{\ast w}$ is the friction velocity associated with the wave stresses, obtained as

$$u_{\ast w}=\sqrt{{\displaystyle \frac{1}{2}}{f}_w}{u}_b$$

(3)

where $f_w$ is a wave friction factor [4,19,31], and $u_b$ is the bottom wave orbital velocity.

2.2. Bedform Geometry Predictors

Because of their importance to bottom boundary layer dynamics and sediment transport processes, a vast number of studies aiming to predict ripple dimensions $\eta$ and $\lambda$ (ripple height and wavelength, respectively) have been conducted both in laboratory and field conditions (see a complete review of such models in [21]). In this work, we test the performance of three ripple predictors in the prediction of bottom stresses using the Grant and Madsen [4] model (hereafter GM79) and compare the results to those obtained using the GM79 model in combination with the Soulsby et al. [13] non-equilibrium ripple model (see Section 2.3). The three bedform predictors were chosen based on the use of different sets of parameters to estimate ripple dimensions, and are described in the following paragraphs.

The Wiberg and Harris [20] predictor (hereafter WH94) is based on the near-bed wave orbital excursion normalized by the median sediment particle size, $d_0/D_{50}$. The original WH94 formulation involves iteration; however, Malarkey and Davies [32] presented a modification that facilitates its implementation:

$$\begin{array}{cc}\hfill {\lambda }_{orb}& =0.62d_0\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\lambda }_{ano}& =535D_{50}\hfill \end{array}$$

(5)

$$\begin{array}{cc}{\lambda }_{sub}& =535D_{50}exp\left[-{\displaystyle \frac{log\left({\lambda }_{orb}/{\lambda }_{ano}\right)log\left(0.01d_0\right)}{log\left(5\right)}}\right]\hfill \end{array}$$

(6)

$$\begin{array}{cc}\eta & ={\displaystyle \frac{d_0}{exp\left[B_2-\sqrt{B_3-B_{1}log\left(\frac{d_0}{\lambda }\right)}\right]}}\hfill \end{array}$$

(7)

where $B_1=10.526$, $B_2=7.59$ and $B_3=33.6$. Wavelength subscripts indicate orbital, anorbital and suborbital ripples. For the orbital ripples, the wavelength scales with $d_0$ and they occur for small values of $d_0/D_{50}$. The ripple wavelength for anorbital ripples scales with $D_{50}$ and they occur for large $d_0/D_{50}$ values. The limits for orbital, suborbital and anorbital ripples are given by $d_0/D_{50}<1754$, $1754<d_0/D_{50}<5587$ and $d_0/D_{50}>5587$, respectively.

Grant and Madsen [17] (hereafter GM82) proposed a parameterization based on the Shields parameter,

$${\theta }_w={\displaystyle \frac{{\tau }_w}{(s-1)g{D}_{50}}}$$

(8)

where ${\tau }_w$ is the wave-induced shear stress. Their predictor gives increasing wavelengths for increasing Shields parameter up to a limiting value, given by

$${\theta }_B=1.8{\theta }_{cr}{\left({\displaystyle \frac{D_{\ast }^{1.5}}{4}}\right)}^{0.6}$$

(9)

where ${\theta }_{cr}$ is the critical Shields parameter for sediment movement, and $D_{\ast }$ is the non-dimensional particle diameter,

$$D_{\ast }=D_{50}{\left({\displaystyle \frac{g(s-1)}{{\nu }^2}}\right)}^{1/3}$$

(10)

where $\nu$ is the kinematic viscosity of sea water, and s is the submerged weight of sediment particles.

For ${\theta }_{cr}<\theta \le {\theta }_B$, ripple heights and wavelength are given by

$$\begin{array}{cc}\hfill \hspace{1em}\eta & =0.22{\left({\displaystyle \frac{\theta }{{\theta }_{cr}}}\right)}^{-0.16}{A}_w\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \lambda & ={\displaystyle \frac{\eta }{0.16{\left(\frac{\theta }{{\theta }_{cr}}\right)}^{-0.04}}}\hfill \end{array}$$

(12)

whereas for $\theta >{\theta }_B$,

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\eta & =0.48{\left({\displaystyle \frac{D^{1.5}}{4}}\right)}^{0.8}{\left({\displaystyle \frac{\theta }{{\theta }_{cr}}}\right)}^{-1.5}{A}_w\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill \lambda & ={\displaystyle \frac{\eta }{0.28{\left(\frac{D^{1.5}}{4}\right)}^{0.6}{\left(\frac{\theta }{{\theta }_{cr}}\right)}^{-1}}}\hfill \end{array}$$

(14)

where $A_w$ is the wave orbital amplitude. ${\theta }_{cr}$ can be obtained from Soulsby [19] as

$${\theta }_{cr}={\displaystyle \frac{0.3}{1+1.2D_{\ast }}}+0.055\left(1-exp(-0.02D_{\ast })\right)$$

(15)

Pedocchi and Garcia [33] (hereafter PG09) suggested that ripple dimensions are related to the ratio of wave orbital velocity to particle settling velocity, $U_w/w_s$. They proposed expressions for $\eta$ and $\lambda$ for three different grain size regimes, based on the particle Reynolds number, $R{e}_p=\sqrt{(s-1)g{D}_{50}^3}/\nu$. Considering the median particle size of bed sediments at our field site (see Section 3.1), here, we use the expression for the $9\le R{e}_p<13$ range. This range corresponds to a particle size interval between 177 and 220 μm. The equations for ripple height and wavelength are given by

$$\begin{array}{cc}\hfill \eta & =0.1d_0{\left[{\left(0.055U_w/w_s\right)}^4+1\right]}^{-1}\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \lambda & =0.65d_0{\left[{\left(0.040U_w/w_s\right)}^2+1\right]}^{-1}\hfill \end{array}$$

(17)

The settling velocity $w_s$ can be obtained following Soulsby [19] as

$$w_s={\displaystyle \frac{\nu }{d_{50}}}\left[{\left(10.{36}^2+1.049D_{\ast }^3\right)}^{1/2}-10.36\right]$$

(18)

2.3. Prediction of Time-Evolving Ripple Dynamics

Soulsby et al. [13] presented a fully time-evolving model for predicting the dimension of ripples generated by waves, currents or a combination of both. The model includes a vast number of equations in order to specify adjustment time scales and equilibrium morphology values for ripple heights and wavelengths, for both wave-dominated and current-dominated ripple conditions. The reader is referred to Soulsby et al. [13] for a complete description of the model equations.

In the Soulsby et al. [13] model (hereafter S12), the time evolution of ripple properties under a varying forcing field is modeled as a perturbation from its equilibrium value. The equation governing the time-evolution of bedform dimensions is given by

$${\displaystyle \frac{d\eta }{dt}}={\displaystyle \frac{\beta }{T_e}}\left({\eta }_{eq}-\eta \right)$$

(19)

where $T_e$ is a characteristic timescale, $\beta$ is a coefficient that governs the rate of change of $\eta$, ${\eta }_{eq}$ is the equilibrium value, and $\eta =\eta \left(t\right)$ is the time-dependent bedform height. In general, $T_e$, $\beta$ and ${\eta }_{eq}$ are functions of time. Equivalent equations are used for the time evolution of bedform wavelength and orientation. Soulsby et al. [13] provide expressions for ${\eta }_{eq}$ and ${\lambda }_{eq}$, which are based on an extensive review of the available formulations. In their formulation, Soulsby et al. [13] provide equations for both current- and wave-dominated ripples. The criterion to establish wave or current dominance is based on the skin friction Shields parameter,

$$\begin{array}{cc}{\displaystyle {\theta }_w=\frac{(1/2)f_w{U}_w^2}{g(s-1)D_{50}},}\hfill & {\displaystyle {\theta }_c=\frac{C_D{U}^2}{g(s-1)D_{50}}}\hfill \end{array}$$

(20)

such that if ${\theta }_w>{\theta }_c$, the ripples are wave dominated, and if ${\theta }_c>{\theta }_w$, the ripples are current dominated. For wave-dominated ripples, equilibrium heights and wavelengths are given by

$$\begin{array}{cc}{\displaystyle \frac{\lambda }{A}}& ={\left[1+1.87·{10}^{-3}\Delta \left(1-exp\{-{(2.0·{10}^{-4}\Delta \}}^{1.5}\right)\right]}^{-1}\hfill \end{array}$$

(21)

$$\begin{array}{cc}{\displaystyle \frac{\eta }{\lambda }}& =0.15\left[1-exp\{-{(5000/\Delta )}^{3.5}\}\right]\hfill \end{array}$$

(22)

where $\Delta =A/D_{50}$, with A being the orbital amplitude and $D_{50}$ the median particle size diameter. For current-dominated conditions, equilibrium heights and wavelengths are based on empirical expressions for the maximum ripple height and wavelengths,

$$\begin{array}{cc}\hfill {\eta }_{max}& =d_{50}202D_{\ast }^{-0.554}1.2<D_{\ast }<16\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}{\lambda }_{max}& =d_{50}\left(500+1881D_{\ast }^{-1.5}\right)1.2<D_{\ast }<16\hfill \end{array}$$

(24)

where $D_{\ast }={[g(s-1)/{\nu }^2]}^{1/3}{D}_{50}$ is the non-dimensional particle size, and $\nu$ is the kinematic viscosity of water. The effect of wash-out ripples and sheet flow at large current speed is also included by applying a linear reduction in ripple height according to limits based on the Shields parameter,

$$\begin{array}{cc}\hfill {\theta }_{wo}& =1.66D_{\ast }^{-1.6}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\theta }_{sf}& =2.26D_{\ast }^{-1.3}\hfill \end{array}$$

(26)

where the subscripts $wo$ and $sf$ refer to wash-out and sheet flow. Expressions for the ripple height are then given by

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {\eta }_{eq}& =\mathrm{pre}-\mathrm{existing} \mathrm{value}\mathrm{for}0<{\theta }_c<{\theta }_{cr}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}{\eta }_{eq}& ={\eta }_{max}\mathrm{for}{\theta }_{cr}<{\theta }_c<{\theta }_{wo}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} {\eta }_{eq}& ={\eta }_{max}\left({\displaystyle \frac{{\theta }_{sf}-{\theta }_c}{{\theta }_{sf}-{\theta }_{wo}}}\right)\mathrm{for}{\theta }_{wo}<{\theta }_c<{\theta }_{sf}\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\eta }_{eq}& =0\mathrm{for}{\theta }_c>{\theta }_{sf}\hfill \end{array}$$

(30)

where ${\theta }_{cr}$ is the critical Shields parameter for motion initiation. Wavelengths are assumed to be unaffected by wash-out. For both wave- and current-dominated ripples, the evolution of height and wavelength occurs only if $\theta >{\theta }_{cr}$, that is, if the threshold for motion is achieved. Otherwise, the model assumes that ripples are not modified (relict ripples). The parameters controlling the time evolution of ripple dimensions ($T_e$ and $\beta$) are also specified for wave-dominated or current-dominated conditions, as the timescales for waves and currents are intrinsically different. For wave-dominated conditions, the timescale $T_e$ is set to be equal to the wave period. The $\beta$ parameter for wave dominated conditions is given by

$${\beta }_w={\displaystyle \frac{2.996{\psi }^{1.07}}{21700+{\psi }^{1.07}}}$$

(31)

where $\psi =U_w^2/\left(g(s-1)D_{50}\right)$ is the wave mobility parameter. The timescale for currents is less obvious than that of the waves and is assumed to be related to the time that it takes for the volume per unit of a ripple to be delivered by the volumetric bedload transport rate. The expression for $T_c$ is given by

$$T_c={\displaystyle \frac{{\eta }_{max}{\lambda }_{max}}{{\left[g(s-1)D_{50}^2\right]}^{1/2}}}$$

(32)

Laboratory experiments [34] showed that for current-generated ripples, bedform height evolved faster than the wavelength; hence, different $\beta$ parameters are required. These are given by

$$\begin{array}{cc}\hfill {\beta }_{\eta }& ={\displaystyle \frac{20{({\theta }_c-{\theta }_{cr})}^{1.5}}{2.5+{({\theta }_c-{\theta }_{cr})}^{1.5}}}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\beta }_{\lambda }& ={\displaystyle \frac{12{({\theta }_c-{\theta }_{cr})}^{1.5}}{2.5+{({\theta }_c-{\theta }_{cr})}^{1.5}}}\hfill \end{array}$$

(34)

For further details on the derivation of these empirical expressions, the reader is referred to Soulsby et al. [13]. The time stepping procedure involves solving the differential equation given by Equation (19), which can be carried out using a Runge–Kutta scheme of the fourth order. At each time step, wave or current dominance has to be established, the equilibrium values, $T_e$ and $\beta$ coefficients have to be computed and the equation for ${\eta }_{t+1}$ (or ${\lambda }_{t+1}$) has to be solved. If $\theta <{\theta }_{cr}$, then ${\eta }_{t+1}={\eta }_t$. The critical Shields parameters can be obtained from the expression proposed by Soulsby et al. [35] (Equation (15)).

3. Methods

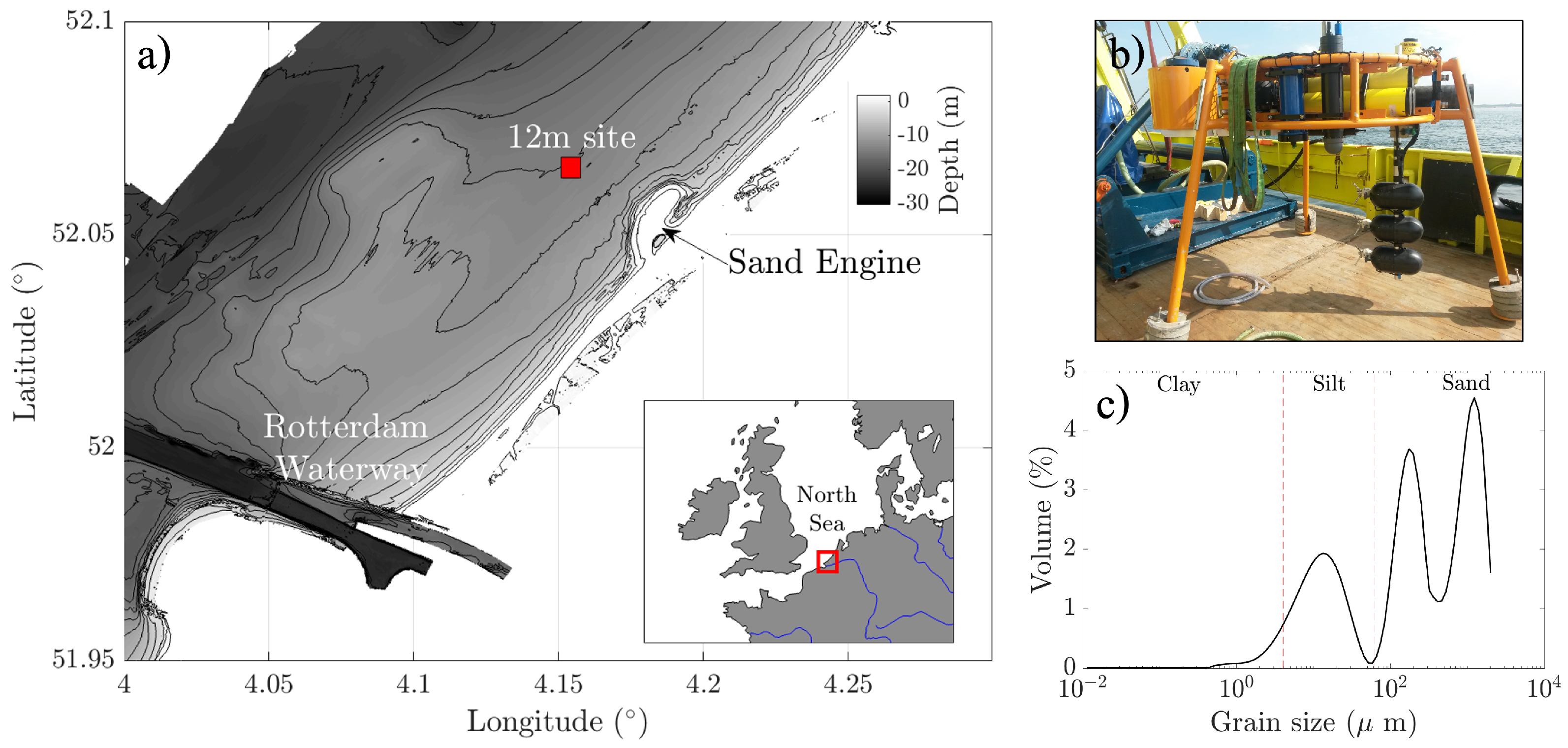
3.1. Data Collection

The stratification impacts on nearshore sediment transport (STRAINS) experiment [36,37,38] made hydrodynamic and sediment transport measurements in the Rhine region of freshwater influence along the Dutch coast in the fall of 2014. Instruments were deployed in 12 m and 18 m of water, 10 km north of the Rhine River mouth and in the vicinity of the Sand Engine (Figure 1a), a mega-nourishment pilot project that aims to protect the Dutch coast from risks of flooding and sea-level rise [39,40].

Near-bottom hydrodynamics, turbulence and bed characteristics were measured using a benthic frame deployed in 12 m of water (Figure 1b). Three-dimensional flow velocities were measured using three synchronized 6 MHz Sontek acoustic Doppler velocimeters (ADVs), sampling at 16 Hz and located at 0.25, 0.5 and 0.75 m above the bottom. The ADVs were mounted on an arm away from the frame to avoid turbulent perturbations due to the frame itself (Figure 1b). The ADVs recorded 10-min bursts every 15 min, for a total of 2990 data bursts. Fast-sampling optical backscatter sensors (OBS) were deployed to measure near-bottom concentrations of suspended sediments. These instruments sampled at 16 Hz and were collocated and synchronized with the ADVs to obtain the turbulent fluxes of sediment (see Section 3.2.1).

The bedform data used here were processed and first published by Meirelles et al. [41]. These data correspond to hourly three-dimensional seabed images acquired by an acoustic ripple profiler (ARP) that provided bed elevation over a circular area of approximately 12 m², operating at 1.1 MHz. The echo intensity recorded by the ARP was converted into bed elevation, interpolated to a regular Cartesian grid, detrended and corrected for tilt variations of the benthic frame. The final seafloor image resolution was 1.95 cm per pixel, which provides the lower limit of the horizontal features that can be detected. The ripple parameters are extracted from the seafloor images using discrete 2D Fourier analysis, following the procedure outlined in Perron et al. [42].

The Dutch coast is predominantly sandy, although finer sediments (silts and clays) are also found in lower proportions [40,43]. Bed material cores were taken on deployment day at different water depths while in transit from the 18 m isobath to the 12 m deployment site. Samples were taken from the cores and sized using a Malvern size analyzer to obtain particle size distribution. All sites showed a mixture of fine sands and silts and very small proportions of clay-sized material. A substantial increase in coarseness was not observed between the 18 m and the 12 m site, even though medium-to-coarse sands were observed at the 12 m site in small proportions (5–10%). Median particle size at the 12 m site was $d_{50}=200$ μm, with a fraction of silts and sands of approximately $20\%$ and $80\%$, respectively (Figure 1c).

3.2. Data Processing

3.2.1. Near-Bottom Currents, Reynolds Stresses and Turbulent Fluxes

The raw ADV data were quality controlled and de-spiked using the three-dimensional phase space algorithm of Goring and Nikora [44]. After the initial quality control, very few spikes were observed in the ADV velocities, and the data were considered to be reliable. Near-bottom mean tidal velocities were estimated by time averaging over a 10-min period, and turbulent velocity components $u^{\prime }$, $v^{\prime }$ and $w^{\prime }$ were obtained by removing the tidal trend.

The shallowness of the field site and the presence of large waves during storms required the use of a wave-turbulence separation method to obtain reliable estimates of the Reynolds stresses and fluxes, since wave motions were likely to penetrate all the way to the seabed. To reduce the wave-induced bias on the Reynolds stresses, we used the linear filtration technique proposed by Shaw and Trowbridge [45], which relies on the identification of coherent motions between two independent sensors. The sensors have to be separated by a vertical distance larger than the length scale of the turbulent eddies (which scale with the vertical distance from the bottom) but smaller than the correlation scale of wave motion. Here, we have used a vertical separation between instruments of $\Delta z=0.5$ m, using our lowest and highest ADVs.

The measured Reynolds stresses are used to obtain a current-induced friction velocity $u_{\ast c}$ as

$$u_{\ast c}=\sqrt{{\overline{u^{\prime }{w}^{\prime }}}_{filt}^2+{\overline{v^{\prime }{w}^{\prime }}}_{filt}^2}$$

(35)

where the subscript filt indicates that the Reynolds stresses were previously wave-filtered to eliminate wave bias. The measured current friction velocities $u_{\ast c}$ are compared to the modeled current friction velocity from the Grant and Madsen [4] model in order to assess model performance. We implement the GM79 model using different methods to estimate bottom roughness (see Section 4.3).

The vertical turbulent sediment fluxes were estimated using the eddy correlation method [46,47,48]. Typically, both $c^{\prime }$ and $w^{\prime }$ are determined from high frequency ADV measurements, where the ADV backscatter is properly calibrated to yield suspended sediment concentrations [49,50]. Fugate and Friedrichs [50] showed the validity of this approach for cohesive sediments in an estuarine environment. Alternatively, we compute the turbulent sediment fluxes using a combination of collocated fast-sampling ADVs and OBSs. Since the OBSs are more sensitive to the smaller particle sizes [51], our estimates of the turbulent sediment fluxes are more representative of the fine sediment dynamics. The vertical component of the near-bed turbulent sediment fluxes, $\overline{w^{\prime }{c}^{\prime }}$, is assumed to represent the resuspension of fine sediment, i.e., the erosional flux (e.g., Ref. [47]).

3.2.2. Wave Parameters

Representative wave parameters at our 12 m site were computed using the high-frequency ADV flow velocity measurements. The representative bottom orbital velocity ($u_{br}$) and the representative wave frequency associated with $u_{br}$ were obtained from the frequency spectra of horizontal velocities, following Madsen [31] and Wiberg and Sherwood [52] as

$$u_{br}=\sqrt{2\int \left(S_{uu}+S_{vv}\right)df}$$

(36)

$$f_{br}={\displaystyle \frac{{\displaystyle \int f{S}_{uu}df}}{{\displaystyle \int S_{uu}df}}}$$

(37)

where $S_{uu}$ and $S_{vv}$ are the spectra of the horizontal velocities u and v. The spectra was calculated after performing the wave-turbulence separation method, thus avoiding the inclusion of turbulence energy into the calculations of wave parameters.

4. Results

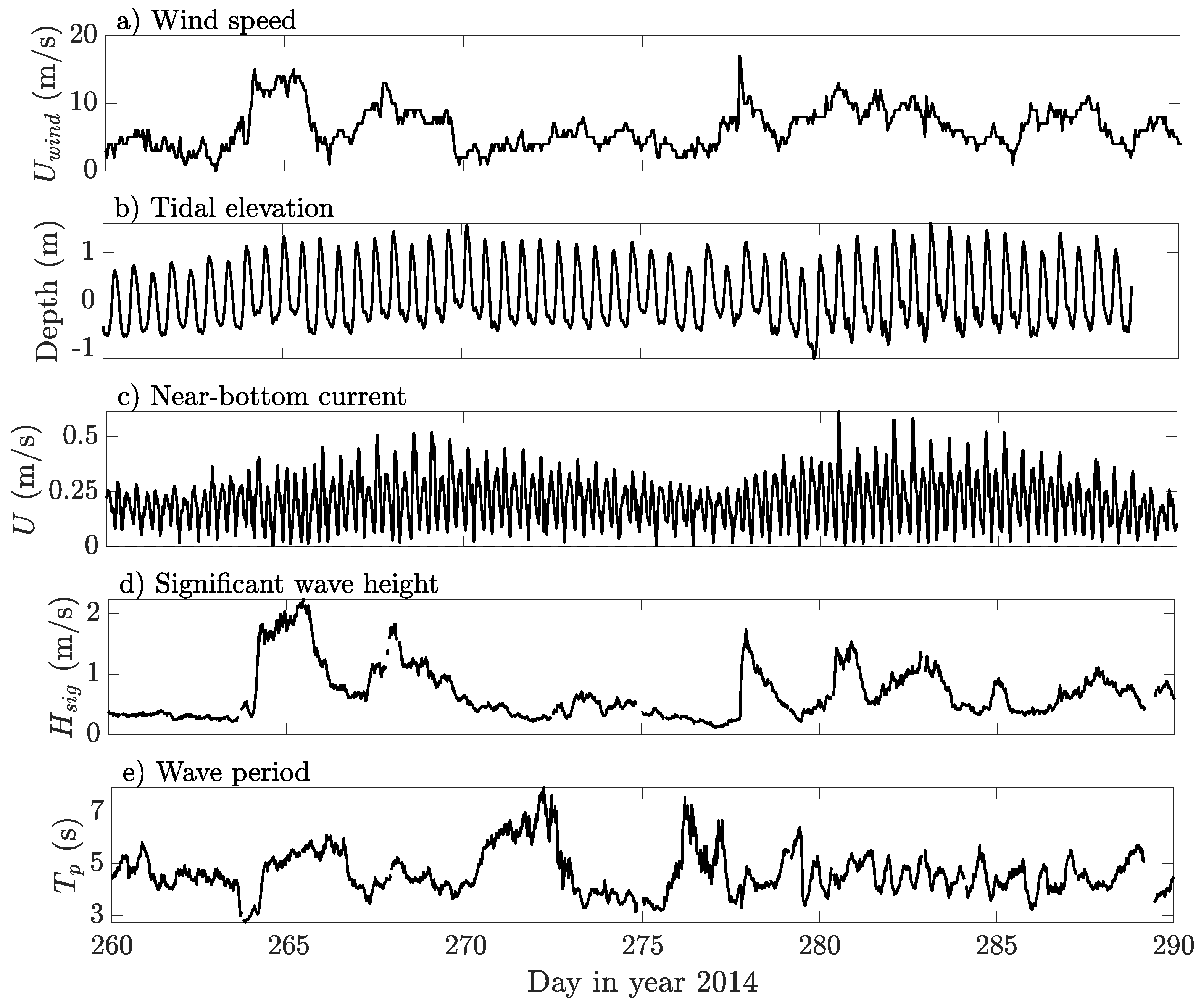
4.1. Experimental Conditions

An overview of the forcing conditions is presented in Figure 2. The mean wind speed was approximately 6.4 ms⁻¹, but variability was high throughout the deployment (Figure 2a). Sustained wind speeds of nearly 15 ms⁻¹ occurred during a big storm on days 264 to 266. Towards the middle of the deployment, wind speed ranged between 3 and 7 ms⁻¹; however, an acute peak of 17 ms⁻¹ was observed on day 278. Wind speeds on the order of 10 ms⁻¹ were persistently observed on days 280–284 and 286–288.

Tides along the Dutch coast are semidiurnal (M2-dominated) with amplitudes typically ranging between 1 and 2 m (Figure 2b). In this region of the North Sea, the tide behaves as a progressive Kelvin wave such that tidal elevation is in phase with the tidal currents; maximum flood (northeast) currents occur at high water, whereas maximum ebb currents (southwest) occur at local low water [53,54,55]. Maximum near-bottom currents at 0.25 mab (meters above the bed) were typically on the order of 0.25–0.3 ms⁻¹, although peaks of approximately 0.5 ms⁻¹ were frequently observed during spring tides (Figure 2c).

The wave statistics shown in Figure 2d,e were measured by a WaveRider buoy located 1 km southwest of our deployment site. Wave heights followed the wind forcing closely (Figure 2a,d), and several wave events with significant wave heights greater than 1 m occurred throughout the experiment. Peak significant wave height was approximately 2.5 m during the storm of days 264–266. Wave periods were variable, but typically below 6 s (Figure 2e).

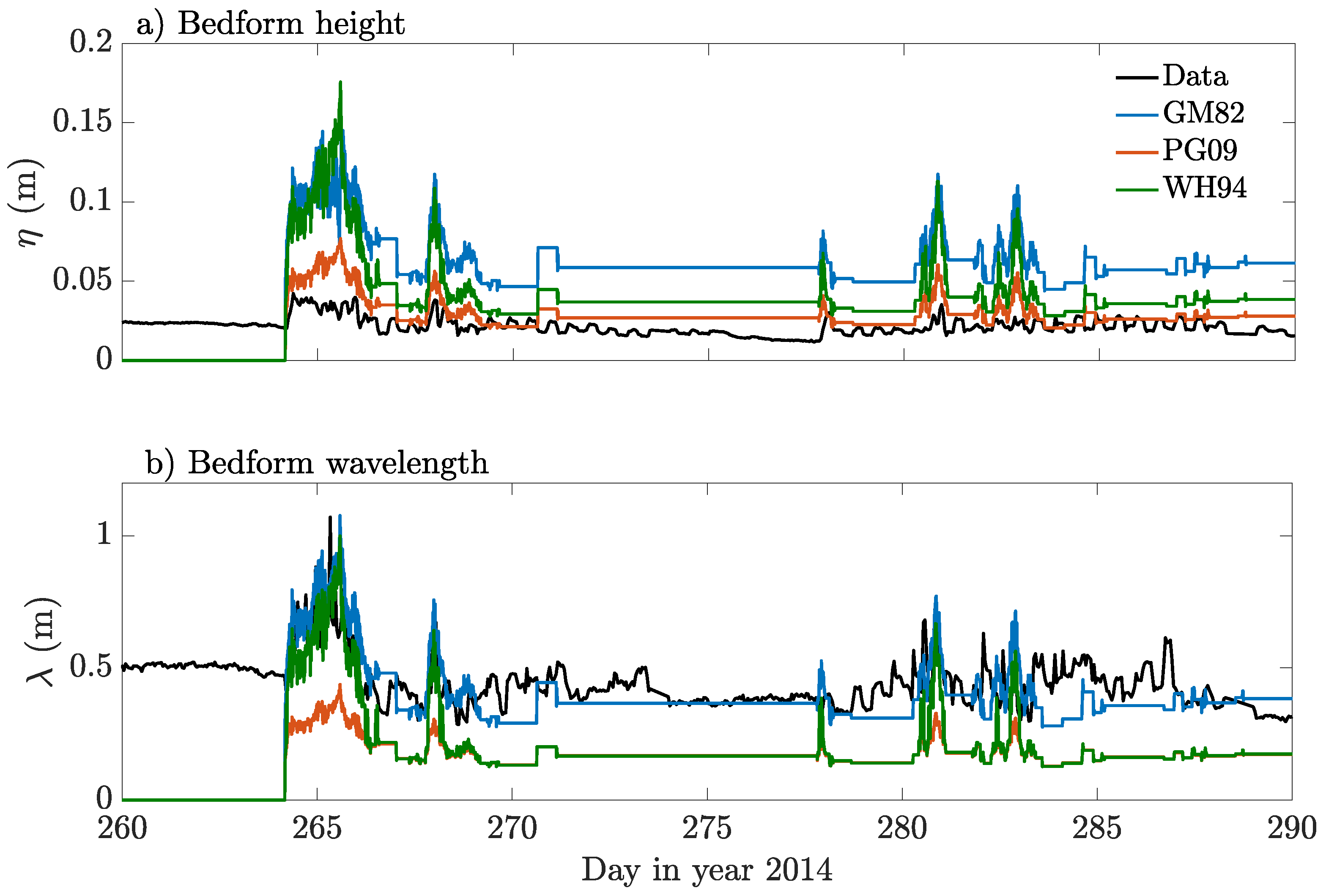
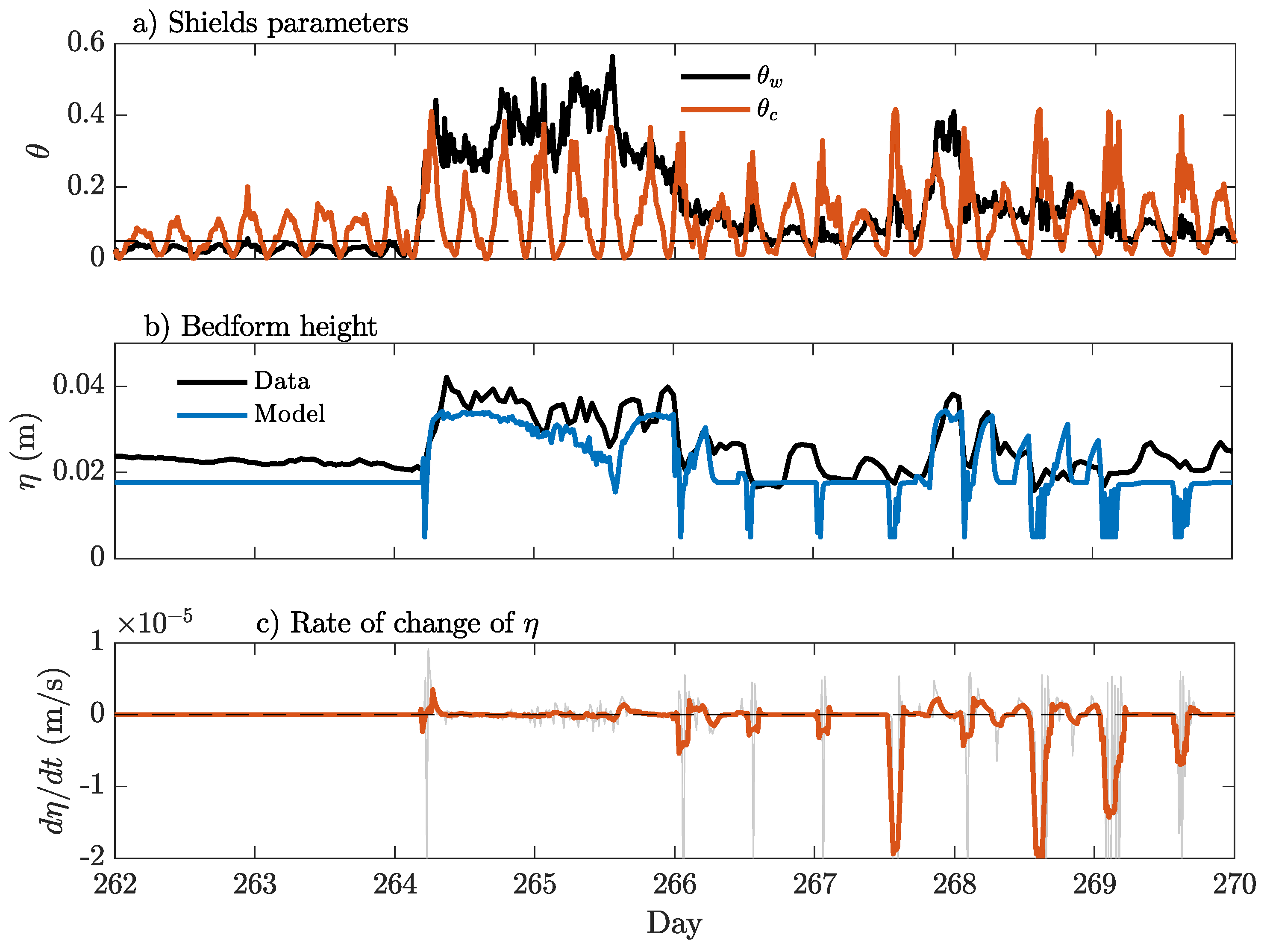
4.2. Bedforms

The representative wave parameters derived from the ADVs and the bedform dimensions derived from the acoustic ripple profiler are shown in Figure 3. Bedforms were always present during the deployment and show a relatively stable background level with bedform height of $\eta \approx 2$ cm and wavelength $\lambda \approx 0.5$ m (Figure 3a,b) during weak forcing conditions (neap tide and low waves, e.g., days 260–264 and 275–277). We observe a strong correlation between bedform dimensions and bottom wave orbital velocity (Figure 3a,b,d), with bedform heights and wavelengths rapidly increasing during the storm on days 264–266. During this storm, bottom wave orbital velocities peaked at 0.4 ms⁻¹, and bedform heights and wavelengths reached $\eta =4$ cm and $\lambda =1$ m, respectively. The wave events of days 268, 278 and 281 are also reflected in an increase in bedform height; however, bedform wavelength seems to be less sensitive to wave orbital velocity (e.g., day 278). Two-dimensional bedforms are observed when the wave forcing is strong (e.g., Figure 3f,g,i), whereas irregular 3D bedforms are present when waves are low and the forcing is current-dominated (Figure 3h,j). Bedform steepness is relatively low (Figure 3c), with values in the range of $\eta /\lambda =0.05-0.08$ and with no clear relation to the wave forcing. Tidal currents are also able to modify bedform dimensions; when wave forcing is low, tidal currents during spring tides result in variations in both bedform height and wavelength (e.g., days 270–273). On the other hand, neap tide currents do not seem to induce clear variations in bedform dimensions (e.g., days 260–264 and 273–278), most likely because the threshold for motion initiation was not exceeded.

Bedform heights and wavelengths obtained from the GM82, WH94 and PG09 equilibrium models are shown in Figure 4. None of the predictors are able to capture the measured variability in $\eta$ or $\lambda$, and all of them show a clear tendency to overestimate the bedform height. We note that when the bed stress is less than the threshold of motion ($\tau <{\tau }_c$), bedform dimensions from these predictors are chosen to remain unchanged (e.g., days 272–277). From the three predictors, PG09 gives the best results with respect to $\eta$; however, values are typically overestimated by 2 to 4 cm during periods of high wave forcing (Figure 4a). Wavelengths are better predicted by the GM82 and WH94 models, particularly during periods of strong wave forcing (Figure 4b). These two predictors accurately predict the wavelengths during the first storm of days 264–266, reproducing wavelengths on the order of 1 m. The wave event of day 267 is also well reproduced by these two predictors in terms of the bedform wavelength. During the periods of high wave forcing, both WH94 and GM82 give bedform heights and wavelength that result in $\eta /\lambda \sim 0.15-0.17$, which is typically thought to be the equilibrium steepness value for orbital ripples [20].

The non-equilibrium ripple behavior is clearly seen in the differences between the measurements and the equilibrium predictors. When the wave forcing is low or decreasing, ripples stop adjusting, leaving behind relict ripples that have large wavelengths that cannot be reproduced by the equilibrium predictors (e.g., days 260–264 and 273–280). Furthermore, both ripple heights and wavelengths lag the equilibrium predictors, particularly at times of rapid variations in the forcing conditions. Similar observations were reported by Scully et al. [6], using the WH94 model in a sandy inner shelf location along the east coast of the U.S.

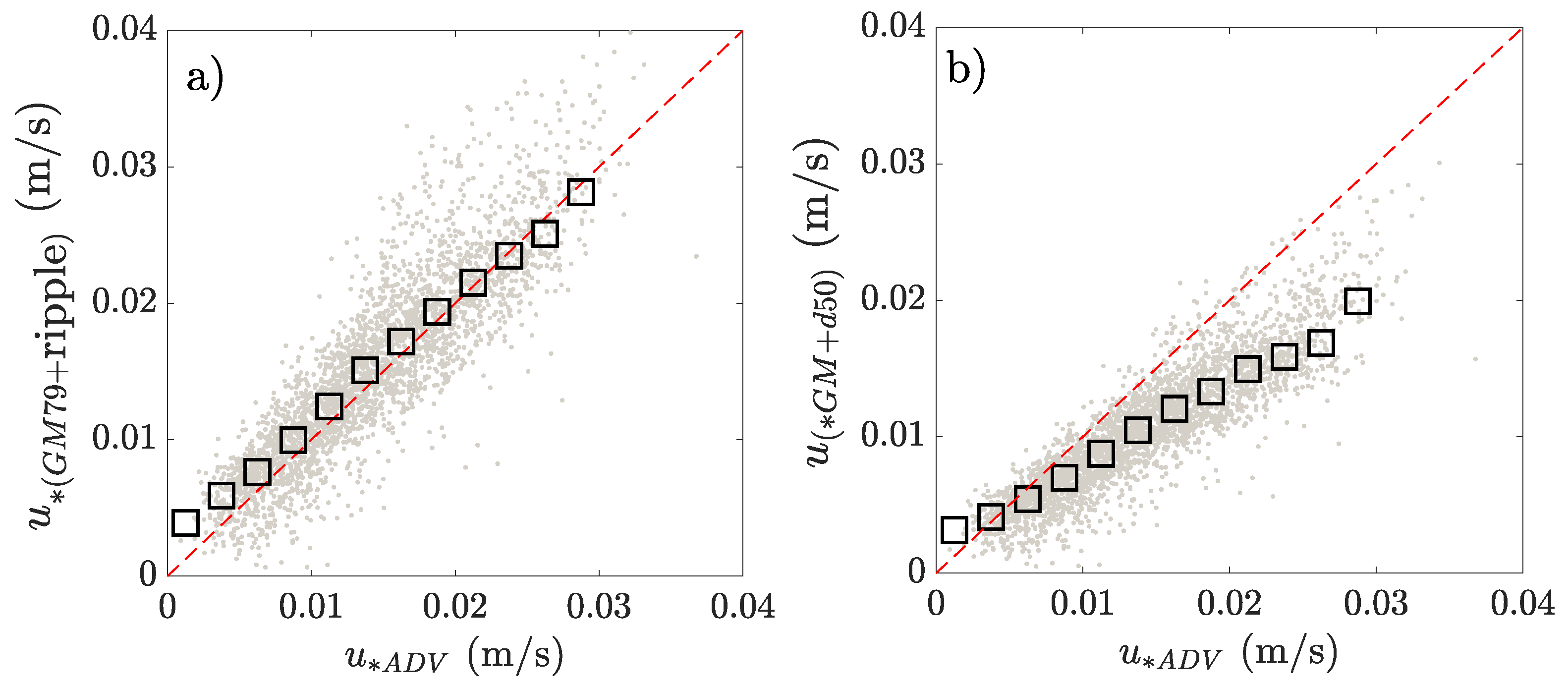
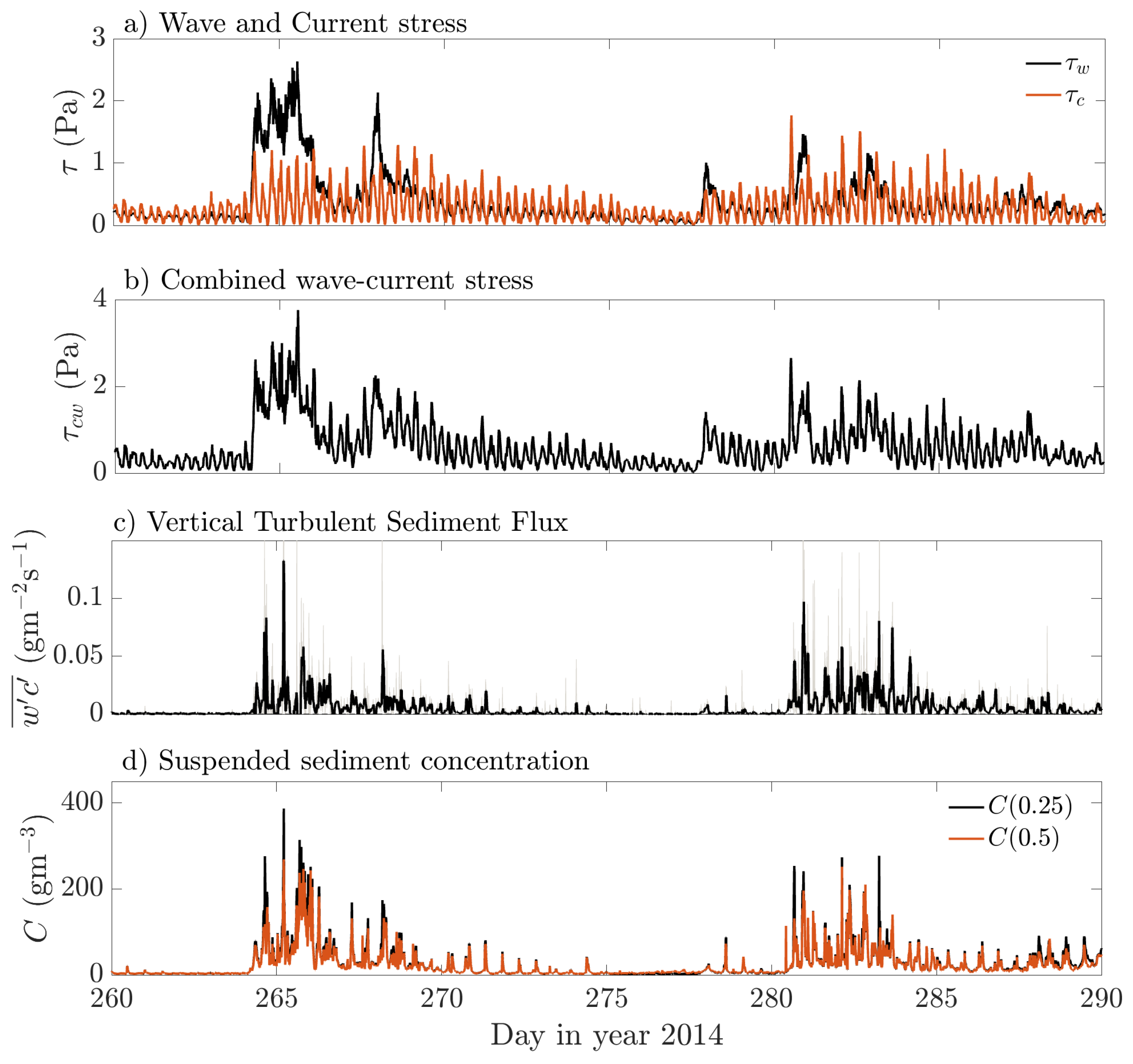
4.3. Bed Stress

4.3.1. Measured Bedforms Versus Flat Bottom

We compare field estimates of $u_{\ast c}$ against predictions from the Grant and Madsen [4] bottom boundary layer model (Figure 5). The model calculations were performed using bottom roughness values derived from field measurements of bedform dimensions. For comparison, in Figure 5, we have also included model estimates where we have used a constant bottom roughness derived from the particle size of bed sediments, $k_B=2.5D_{50}$ (e.g., ref. [56]). This comparison is valuable since in many cases, $D_{50}$ might be the only information available regarding seabed conditions in sediment transport studies.

The modeled current friction velocities $u_{\ast c}$ agree well with the wave-filtered turbulence measurements when measured ripple heights and wavelengths are used to estimate bottom roughness (Figure 5a). While there is dispersion in the data, the agreement is excellent when considering the binned-averaged values ($R^2=0.95$). This shows the consistency of the boundary layer model when bottom roughness is accounted for properly. The modeled current friction velocities obtained using $K_B=2.5D_{50}$ show a clear underestimation of the bottom stresses, particularly in the large $u_{\ast c}$ range (Figure 5b). This suggests that the use of $D_{50}$ only might be justified in low energy cases, when bed stresses are low and the seabed is expected to remain approximately flat.

4.3.2. Bedform Predictors and Time-Evolving Ripple Dynamics

The comparison of measured and modeled friction velocities for cases where bottom roughness was derived from the GM82, WH94 and PG09 predictors is shown in Figure 6. All three models show a consistent overestimation of bed stresses for the entire range of measured values, with the overestimation increasing for large $u_{\ast c}$ values. This clearly results from the overprediction of bedform heights at times of strong wave forcing (Figure 4). The fact that the PG09 model gives the best results from all three models tested is explained by the better estimates of bedform height the model provides (Figure 4), considering that bottom roughness is included as ${\eta }^2/\lambda$.

The model-data comparison of $u_{\ast c}$ improves considerably when using the Grant and Madsen [4] boundary layer model and the S12 ripple evolution model simultaneously (Figure 7c). Opposite to what is observed for the equilibrium bedform predictors (Figure 6), the agreement between modeled and observed $u_{\ast c}$ improves as $u_{\ast c}$ increases (Figure 7c). This approach computes bed stresses and bedform dimensions simultaneously and results in a much better reproduction of the bedform height, particularly during the strong wave forcing periods (Figure 7a). However, the agreement in wavelength predictions is very poor (Figure 7b). Wavelength dimensions are severely underpredicted during times of high waves and remain more or less stable during periods of low wave forcing. Despite the latter, the overall agreement in the reproduction of friction velocities is very good and much better than the agreement achieved with any of the equilibrium bedform predictors we tested (Figure 6). Similarly to what is observed in Figure 6c for the PG09 predictor, the fact that good $u_{\ast c}$ predictions are obtained with a poor reproduction of $\lambda$ suggests that bedform height controls bottom roughness. It is worth noting that even though the S12 model accounts for current-dominated bedforms, the bedform dimensions during times of low wave activity are not well reproduced (e.g., days 273–278).

In order to evaluate whether bed stress and bedform dimension predictions can be further improved, we use the Grant and Madsen [17] model as the equilibrium predictor in the S12 time-dependent formulation, thus replacing the predictor proposed in their study (Figure 8). Estimates of $u_{\ast c}$ are greatly improved with respect to the case shown in Figure 6a, where only the equilibrium predictor was used, and we did not include time-dependent ripple dynamics. We observe a substantial improvement in the ripple height predictions (Figure 8a); however, this improvement seems to be at the expense of the wavelength predictions (Figure 8b). Similar calculations using the PG09 predictor showed that bedform height predictions were also improved but that changes are not significant during high wave forcing periods. The difference in response between both predictors is explained by the fact that the GM82 formulation uses the wave-induced stress to obtain the equilibrium bedform dimensions, such that there is a feedback loop between bed roughness and the model hydrodynamics. An important advantage of the combined boundary layer and ripple dynamics approach is that the equilibrium predictor in the S12 model can be easily interchanged. This allows for (i) the use of equilibrium predictors that are based on hydrodynamic parameters, such as bed stress, and (ii) the use of equilibrium predictors that have been shown to work satisfactorily at a specific field site.

4.4. Turbulent Sediment Fluxes

The near-bed vertical turbulent sediment fluxes, sediment concentrations and bed stresses are shown in Figure 9. In Figure 9, bed stresses correspond to those estimated using the Grant and Madsen [4] model and measured bedform data (our best estimate). Both the near-bottom turbulent sediment fluxes (Figure 9c) and suspended sediment concentrations (Figure 9d) follow the wave forcing closely (Figure 9a,b), with the highest concentrations and vertical turbulent fluxes occurring during the storms on days 264–266 and days 281–284. During these times, we observe strong gradients in the near-bed suspended sediment concentrations (Figure 9d). Tidal variability in the near-bed sediment concentration and turbulent fluxes is observed primarily during spring tides (e.g., days 267–270 and 285–288). During neap tides and low wave forcing, the threshold of motion is not reached, such that both sediment concentrations and turbulent fluxes are very low (Figure 9c,d).

5. Discussion

5.1. Non-Equilibrium Ripple Dynamics

Non-equilibrium ripple dynamics affect bottom drag and bed stresses, thus directly influencing coastal circulation patterns in continental shelves [6]. Accounting for the time-dependent development of ripple dimensions (height, wavelength) was shown to improve the estimates of bed stresses with respect to the traditional approach of using equilibrium ripple predictors to obtain bottom roughness (Figure 5 and Figure 6).

The S12 model [13] uses Equation (19) to solve for the time-dependent ripple dynamics. Evidently, if $\eta \left(t\right)={\eta }_{eq}$, then $d\eta /dt=0$, and the bedforms are in equilibrium with the forcing conditions. The time evolution of $d\eta /dt$ for a subset of the data is shown in Figure 10, which allows for the identification of equilibrium and non-equilibrium bedform conditions. We observe that the predicted bedform dynamics rapidly reach a state that is close to equilibrium ($d\eta /dt\approx 0$) shortly after the start of the big storm on days 264–266 (Figure 10a,c). This is consistent with the laboratory observations showing that ripple dimensions rapidly attain equilibrium dimensions under strong wave forcing [26,57]. Non-equilibrium conditions are typically observed under lower energy conditions, either under decaying wave forcing (e.g., day 266) or current-dominated conditions (Figure 10a,c). In particular, ripple dynamics are frequently predicted to be out of equilibrium at times close to peak flood tide, when current stresses (Shields parameter, ${\theta }_c$) exceed both the wave stresses and the critical stress for sediment movement (Figure 10a,c). Under these conditions, the model predicts decreasing bedform height as the current Shields number exceeds the washout limit (${\theta }_c>{\theta }_{wo}$) (Figure 10b). Ripple heights quickly recover after peak flood, reaching $\eta ={\eta }_{max}$ for the current-dominated conditions (Figure 10b). This suggests that the limits given by Equation (30) may not apply to this specific field site or, alternatively, that the grain size may not be appropriately characterized, as it is expected to continuously vary throughout the deployment.

5.2. Fine Sediment Resuspension

In what follows, we assume that the vertical turbulent fluxes $\overline{w^{\prime }{c}^{\prime }}$ provide a good estimate of fine sediment resuspension (e.g., ref. [47]). This assumption neglects horizontal processes and assumes that the very near-bed sediment concentrations are determined by a vertical balance. The assumption that $\overline{w^{\prime }{c}^{\prime }}$ provides a good estimate of fine sediment resuspension is supported by Figure 9, which shows a clear correlation between the turbulent fluxes, sediment concentrations and bed stresses.

The erosional flux of fine sediment, E (kgm⁻²s⁻¹), is typically modeled using a linear formulation [29,30,58],

$$E=M{\left({\tau }_b-{\tau }_{cr}\right)}^k$$

(38)

where M and k are empirical constants, ${\tau }_b$ is the bottom shear stress (considering waves and currents, that is ${\tau }_{cw}$), and ${\tau }_{cr}$ is the critical stress. M, k and ${\tau }_{cr}$ can vary widely between sites as they depend on sediment material properties such as grain size and porosity [48,58,59]. Typically, researchers have opted to use a linear relationship by setting $k=1$ (e.g., ref. [58]). The accurate estimation of the erosional fluxes relies on the accurate prediction of the bed stresses, which results from the hydrodynamic feedback between flow hydrodynamics and seabed morphology but also on a good estimation of the resuspension parameter M and the critical stress for erosion, ${\tau }_{cr}$. These parameters are extremely difficult to estimate directly in the field as they require high resolution measurements at (or very close to) the seabed. Numerical models, such as ROMS or COAWST, usually require M and ${\tau }_{cr}$ to be specified by the user for sediment transport calculations (e.g., refs. [55,60]).

Field estimates of M and ${\tau }_{cr}$ have been obtained by setting $E=\alpha \overline{w^{\prime }{c}^{\prime }}$, where $\alpha$ is a proportionality constant that is a function of the distance above the bed [48]. As we did not have the information to estimate $\alpha$, we have chosen to set $\alpha =1$, which may lead to a slight underestimation of the erosional fluxes. A least-squares linear regression between $\overline{w^{\prime }{c}^{\prime }}$ and ${\tau }_{cw}$ then provides estimates of M and ${\tau }_{cr}$. Evidently, both M and ${\tau }_{cr}$ vary according to the bed stresses that are used as input in Equation (38). We consider that the bed stresses obtained using measured bedform dimensions provide the best estimates of M and ${\tau }_{cr}$.

Linear fits to Equation (38) are shown in Figure 11 for cases where the bottom stresses (${\tau }_{cw}$) were computed using measured bedform geometry (black squares), $D_{50}$ (red squares) and for the GM79+S12 approach (blue squares). While dispersion is observed regarding the instantaneous ${\tau }_{cw}$ and $\overline{w^{\prime }{c}^{\prime }}$ values (see dashed lines in Figure 11), a linear relation is indeed observed for the binned values, particularly at high values of ${\tau }_{cw}$. The linear regressions to Equation (38) are performed using the binned values, and the values we obtained are shown in

Table 1. Fitted M and ${\tau }_{cr}$ parameters.

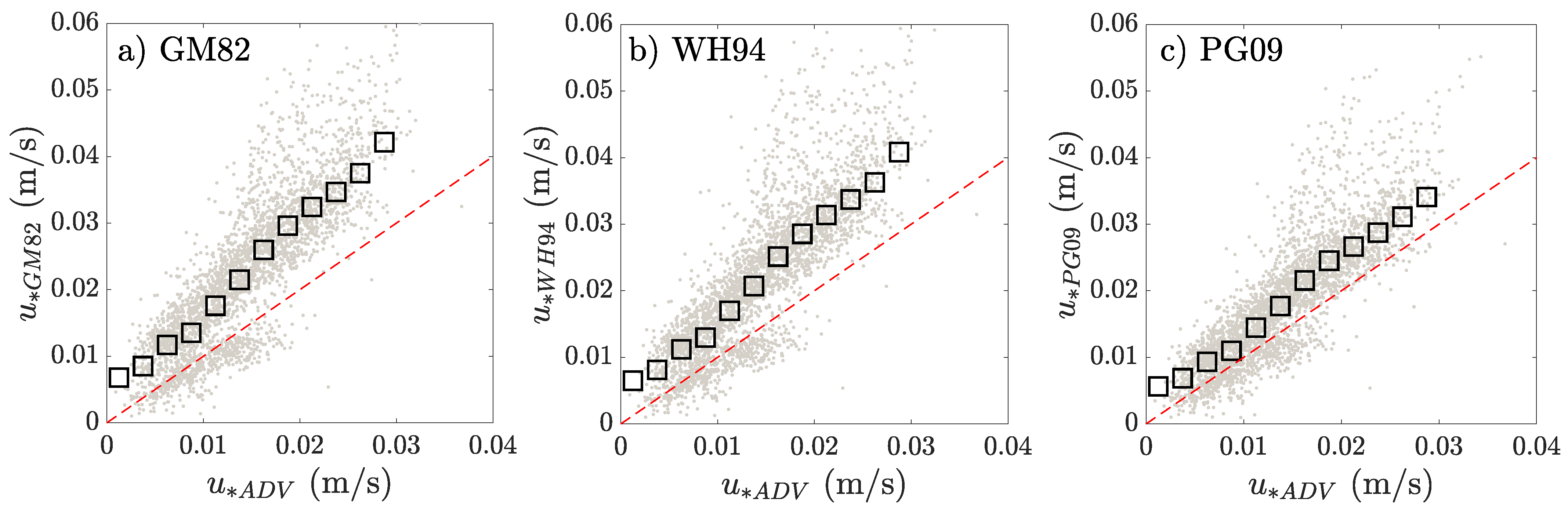
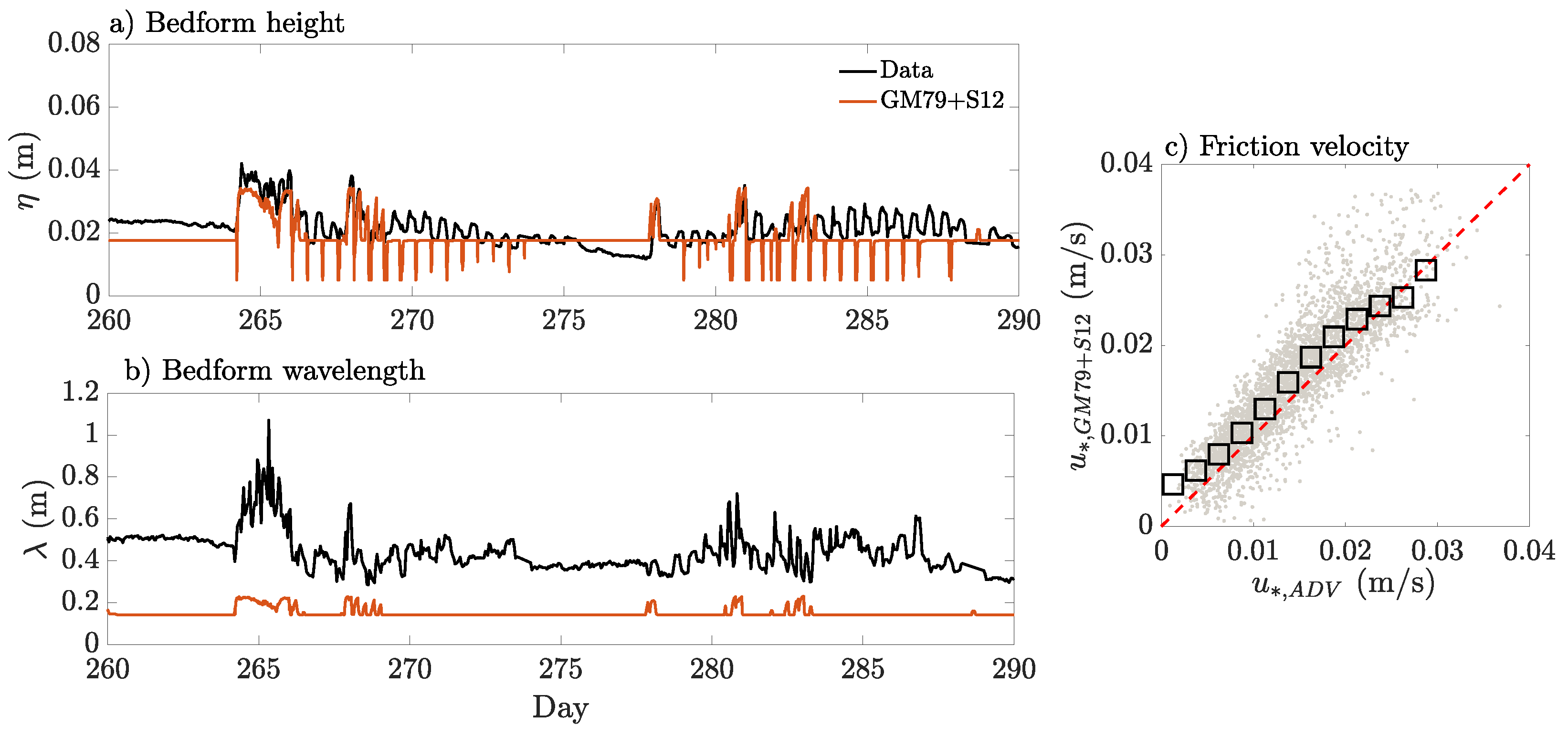
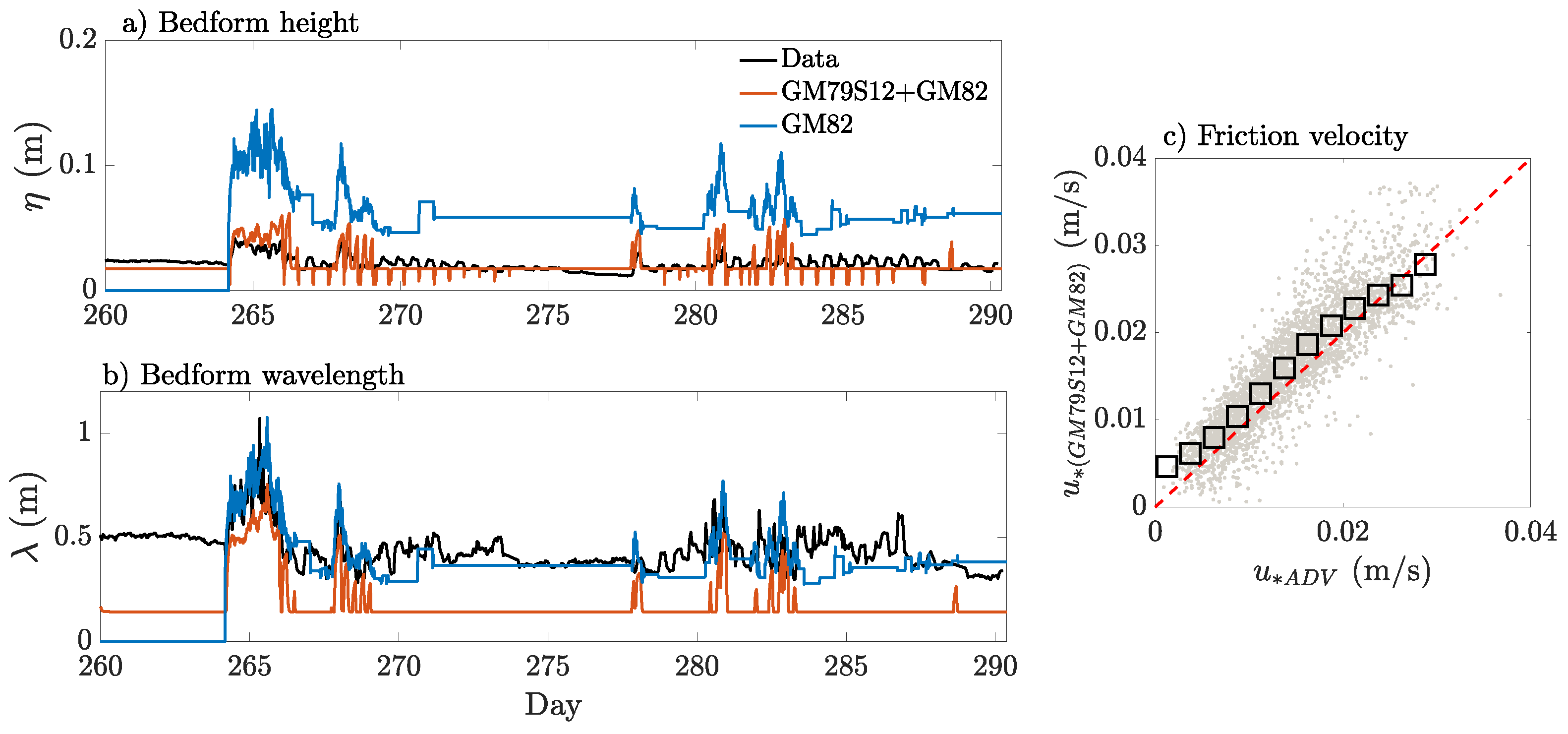
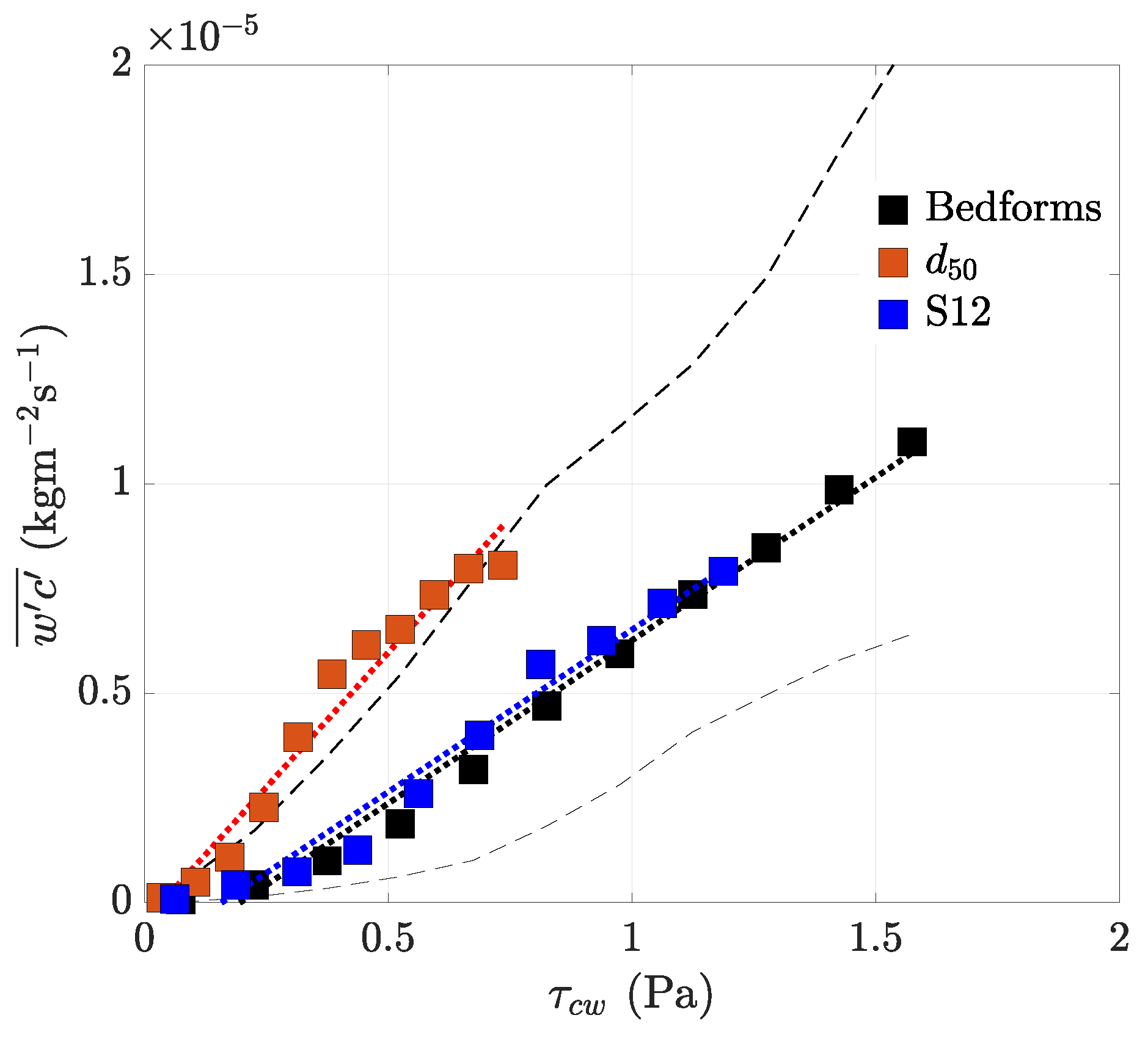
Case	M (kg/m−2s−1Pa−1)	${\mathit{\tau }}_{\mathbf{cr}}$ (Pa)
Bedforms	7.78 × ${10}^{-6}$	0.19
d50	1.28 × ${10}^{-5}$	0.03
S12	7.74 × ${10}^{-6}$	0.15
GM82	2.94 × ${10}^{-6}$	0.3
WH94	3.27 × ${10}^{-6}$	0.32
PG09	4.08 × ${10}^{-6}$	0.13

. Table 1 also shows values obtained for cases where the GM82, WH94 and PG09 were used to estimate bottom roughness. We observe that fitted values of both M and ${\tau }_{cr}$ are very similar for the cases of bed stresses computed using measured bedform dimensions and for the case where we used the Soulsby et al. [13] model, as both of these approaches resulted in very good estimates of the bed stresses (Figure 5a and Figure 8c). This further confirms that the GM79+S12 approach provides a robust method for the estimation of the bed stresses. We see that the use of $D_{50}$ results in a severe overestimation of the M parameter, which is twice as high as the value obtained when the measured bedform was used to estimate bed stresses (Figure 11). The opposite is true with respect to ${\tau }_{cr}$, as the value obtained for the $D_{50}$ case is substantially lower. M and ${\tau }_{cr}$ values for cases where the GM82, WH94 and PG09 predictors were used in the estimation of stresses are shown in Table 1, where it can be appreciated that ${\tau }_{cr}$ is clearly overestimated. Overall, we see that these values are in general agreement (order of magnitude) with the values presented in the literature [58] and the values used along the Dutch coast [61]. However, a direct comparison of the values found in this study with values found in other field sites or in the laboratory is not possible due to all the factors that affect the erodibility of fine sediments.

Estimates of the resuspension parameter M and ${\tau }_{cr}$ were shown to be very sensitive to the approach followed to estimate bed roughness (Figure 11 and Table 1). In Figure 11, we used the complete dataset (30 days) to estimate M and ${\tau }_{cr}$ in order to obtain values that are representative of a wide range of forcing conditions. The M and ${\tau }_{cr}$ values are thus expected to be highly influenced by the periods of high wave forcing that occurred during the storms, which led to the highest turbulent sediment fluxes (Figure 9). A fit to Equation (38) for a period with current-dominated conditions (low wave forcing) results in $M=1.06\times {10}^{-5}$ (kgm⁻²s⁻¹Pa⁻¹) and ${\tau }_{cr}=0.03$ Pa. These values are very different from those obtained with the use of the complete data set. The critical stress for erosion decreases almost by an order of magnitude in response to the lower stresses observed during current-dominated conditions, and its value aligns much better with what can be expected for the critical stress of fine (silt-sized) sediments. A possible interpretation of this is that during current-dominated conditions, fine sediment resuspension results from the erosion of a fluff layer that forms during slack tides when tidal currents cease and fine sediments are allowed to settle. This fluff layer erodes easily, and thus the critical stress for erosion is very low.

This contrasts with the results shown in Figure 11 and Table 1 for the cases where bottom roughness was obtained from measured bedform data or the S12 approach, as the inferred critical stress is more representative of fine sands rather than silts. This is found to be consistent with studies suggesting that fine sediment erosion during high energy periods is dominated by the release of fines that are stored within the sandy matrix [61]. Since the big storm on days 264–266 was the first storm of the fall season in 2014, an alternative explanation for the elevated critical stresses is that the bed sediments may have presented a large degree of consolidation, as they were allowed to consolidate for a long period of time during the calm summer months. The critical stress for erosion has been shown to depend on a wide variety of factors, such as the proportion of sands and fines, geochemical properties (mineralogy, PH) and organic content and biological properties [59,62]. From our measurements, we cannot really differentiate between all the processes that might lead to differences in ${\tau }_{cr}$.

6. Summary and Conclusions

In this work, we proposed a methodology to include time-dependent ripple dynamics into bed stress calculations under combined wave and current forcing. The approach combines the use of the Grant and Madsen [4] wave–current boundary layer model and the Soulsby et al. [13] bedform evolution model and was shown to improve bed stress estimates when compared to those obtained from the use of standard ripple geometry predictors. The bedform dimensions obtained by this approach were also improved; however, discrepancies with the field data were large at times, particularly for current-dominated conditions. The combination of these models presents three main advantages; first, it does not require additional information with respect to that required by standard bedform predictors (e.g., WH94, PG09) and the Grant and Madsen [4] model. Second, the approach allows for the feedback between the bed stresses and bottom roughness, as bed stresses participate in determining the evolution of the bedforms and, in turn, the bedforms participate in setting the magnitude of the stresses via the bottom roughness. Third, since the Soulsby et al. [13] model relies on equilibrium ripple predictors to compute the time-dependent ripple dimensions, the predictor can be adapted to use an equilibrium formulation that gives good results at any specific field site.

The dynamics observed regarding the resuspension of fine sediment highlight the importance of waves and storms in the sediment transport dynamics along the Dutch coast. The vertical turbulent sediment flux data were incorporated into a linear erosion formulation and used to obtain field estimates of the resuspension parameter M and the critical stress for erosion ${\tau }_{cr}$. These parameters were shown to be highly sensitive to the quality of the bed stresses used in the calculations. When using the best stress estimate (using measured bedform data), the critical stress for erosion was found to be ${\tau }_{cr}\approx 0.2$ (Pa). This value is more representative of fine sands than fine sediments, supporting the hypothesis that the entrainment of fines primarily occurs when sands are being mobilized during storms. Values of M are within an order of magnitude of the previously reported values and might serve to inform sediment transport models in the Dutch coast region along the southern North Sea.