Numerical Simulation of Seismoacoustic Wave Transformation at Sea–Land Interface
Abstract
1. Introduction
2. Full-Scale Experiment and Realistic Model of the Environment
3. Numerical Model
3.1. Finite Element Mesh for Realistic Model
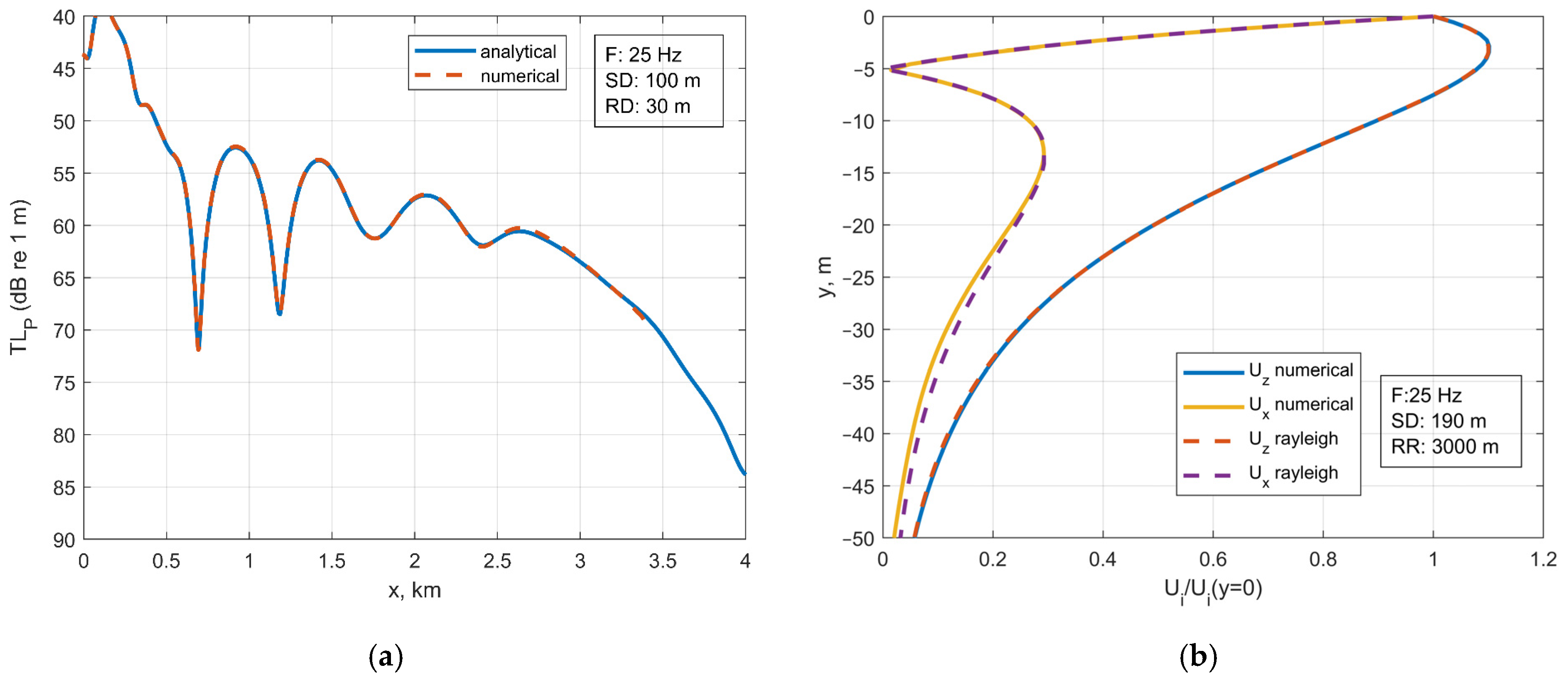
3.2. Verification and Validation of the Numerical Model
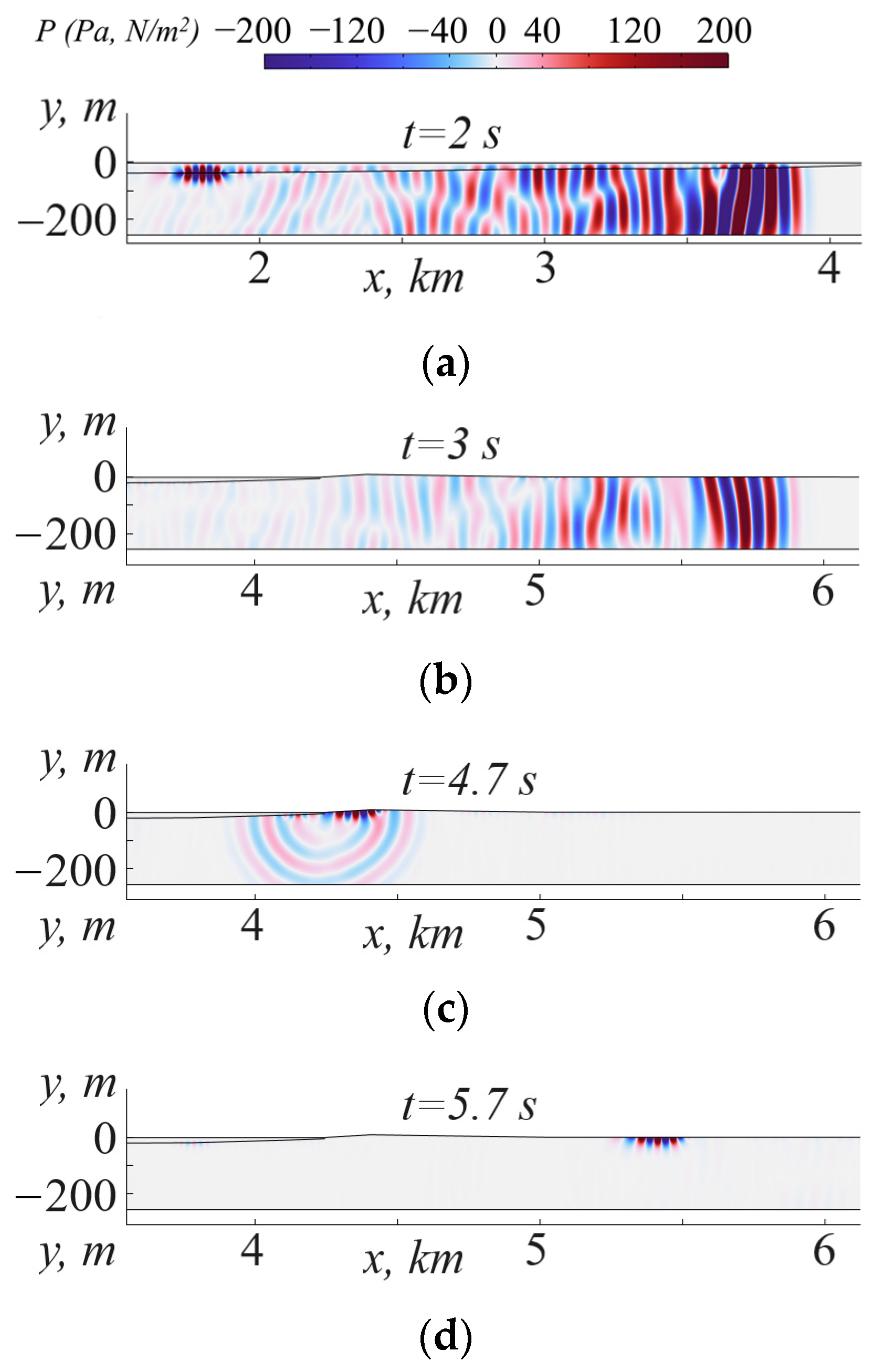
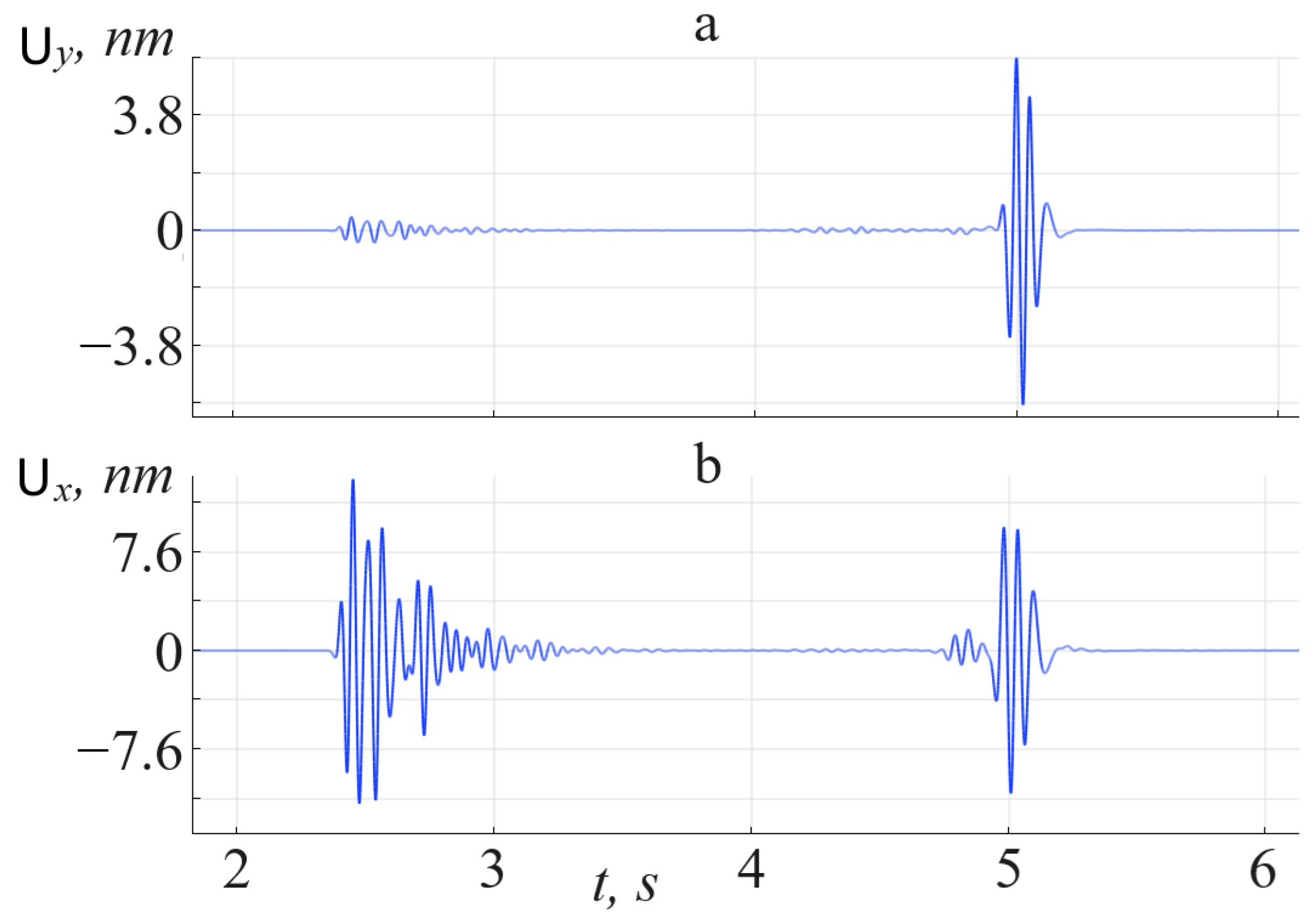
4. Numerical Results of Wave Propagation and Seismic Effects
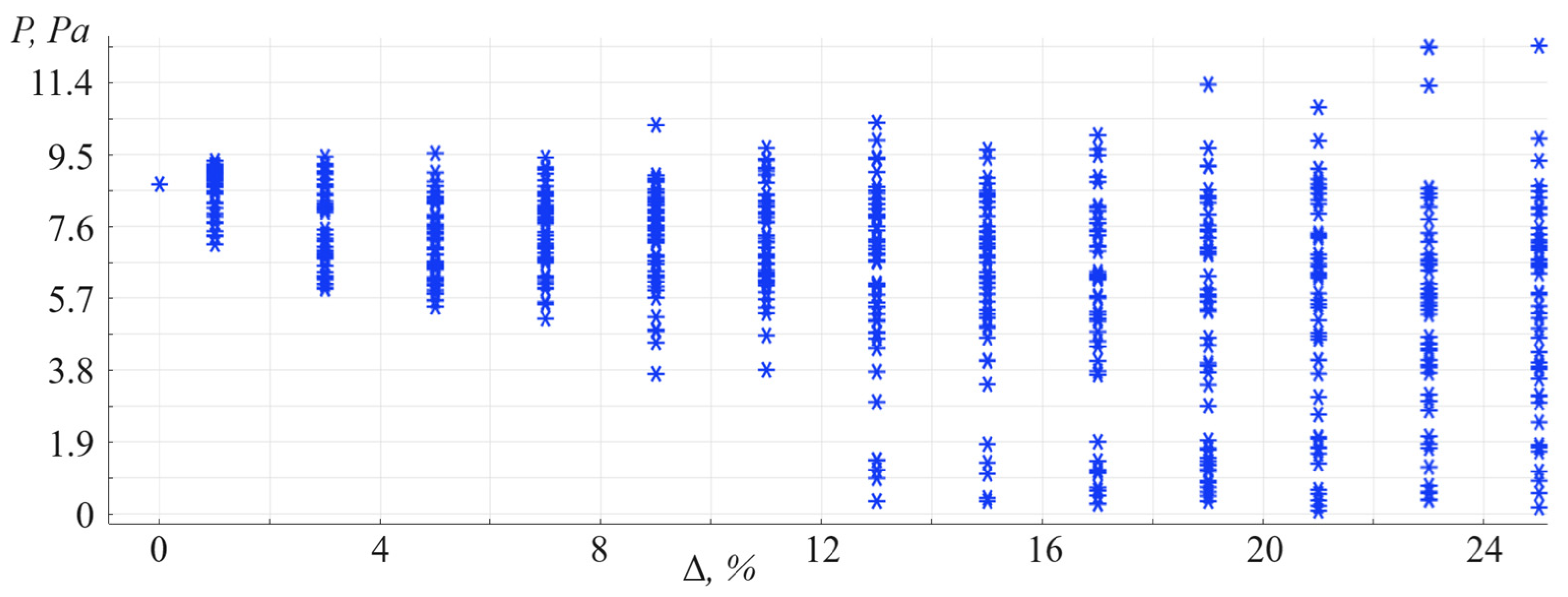
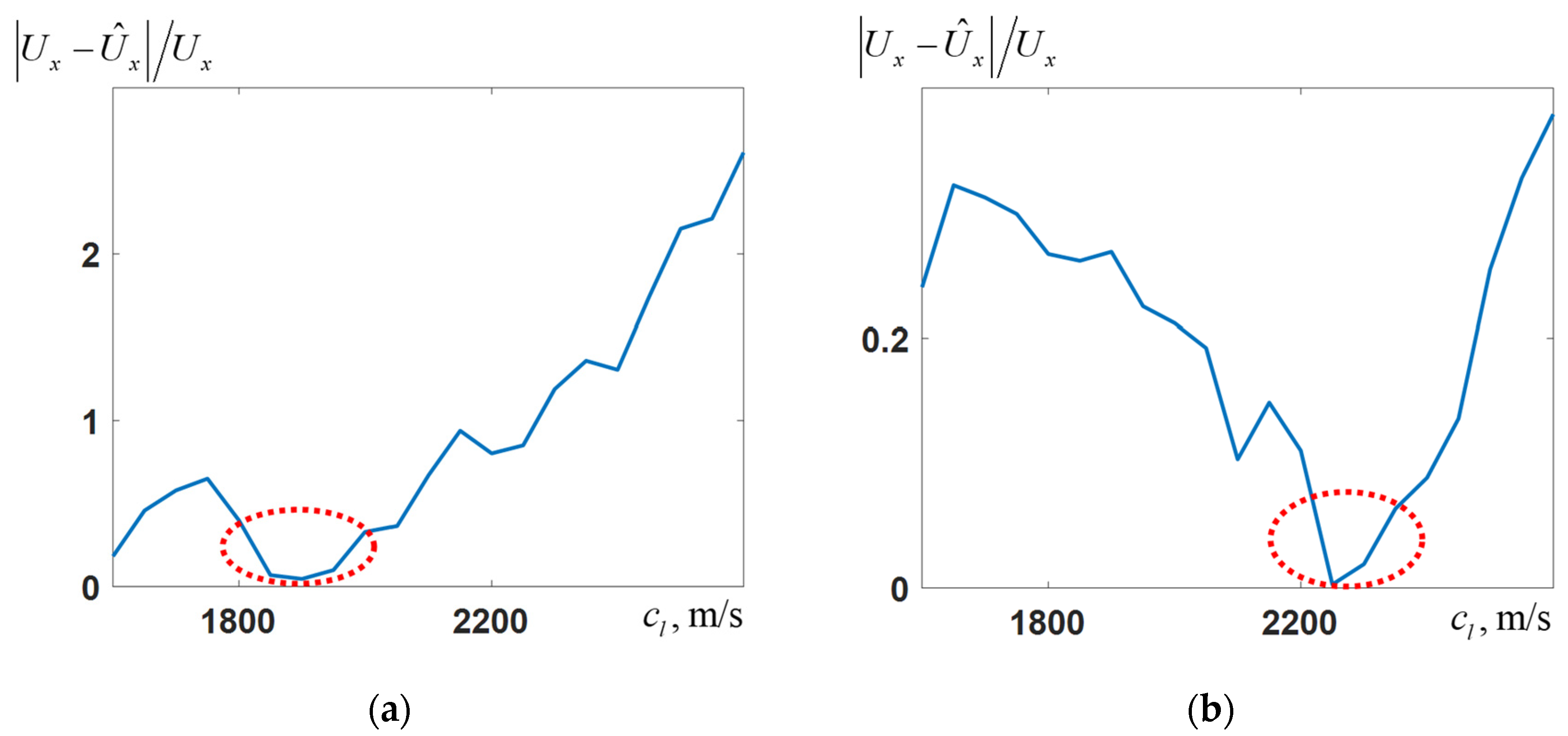
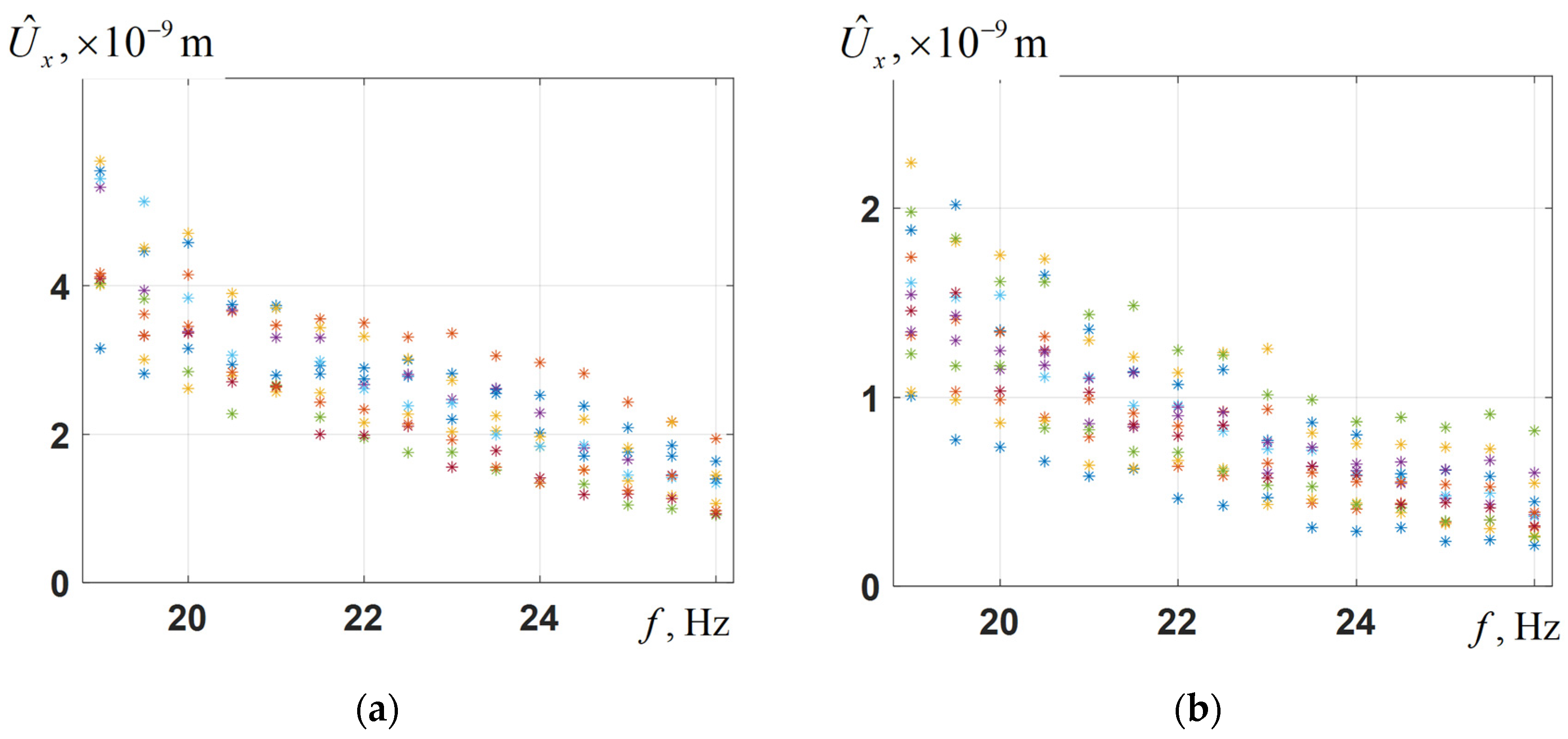
5. Investigation of Seismic Signal Sensitivity to Coastal Wedge Parameters
6. Conclusions
- It was shown that it is possible to accurately model acoustic–elastic propagation at the transition between sea and land using a finite element method, after validation against known analytical solutions.
- This study demonstrates that the shore displacement field is highly sensitive to the radiation efficiency of body waves, while the Scholte surface wave transforms during coastal landfall.
- It is shown that the results of numerical modeling adequately describe the obtained experimental data, and it is established that the bottom sediment parameters—in particular, the velocities of elastic waves—have a crucial influence on the seismic signal value on the shore.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buehler, J.S.; Shearer, P.M. T phase observations in global seismogram stacks. Geophys. Res. Lett. 2015, 42, 6607–6613. [Google Scholar] [CrossRef]
- de Groot-Hedlin, C.D.; Orcutt, J.A. Excitation of T-phases by seafloor scattering. J. Acoust. Soc. Am. 2001, 109, 1944–1954. [Google Scholar] [CrossRef] [PubMed]
- Okal, E.A. The generation of T waves by earthquakes. Adv. Geophys. 2008, 49, 1–65. [Google Scholar] [CrossRef]
- Adushkin, A.V.; Burchik, V.N.; Goncharov, A.I.; Kulikov, V.I.; Khristoforov, B.D. Seismic, Hydroacoustic, and Acoustic Action of Underwater Explosions. Combust. Explos. Shock Waves 2004, 40, 707–713. [Google Scholar] [CrossRef]
- Vedenev, A.I.; Kochetov, O.Y.; Lunkov, A.A.; Shurup, A.S.; Kassymbekova, S.S. Air–borne and Underwater Noise Produced by a Hovercraft in the North Caspian Region: Pressure and Particle Motion Measurements. J. Mar. Sci. Eng. 2023, 11, 1079. [Google Scholar] [CrossRef]
- Garagash, I.A.; Lobkovsky, L.I. Deformation tectonic waves as a possible trigger mechanism for the activation of methane emissions in the Arctic. Arct. Ecol. Econ. 2021, 11, 42–50. [Google Scholar] [CrossRef]
- Antonovskaya, G.; Konechnaya, Y.; Morozova, E.; Mikhailova, Y.; Shakhova, E. Potential of the Arkhangelsk seismic network for European Arctic monitoring. Earthq. Sci. 2024, 37, 1–11. [Google Scholar] [CrossRef]
- Kulchin, Y.N.; Kamenev, O.T.; Petrov, Y.S.; Romashko, R.V. Developing Physical Bases for Low-Frequency Acoustic Tomography in the Arctic Shelf Using Fiberoptic Geophones. Bull. Russ. Acad. Sci. Phys. 2018, 82, 487–490. [Google Scholar] [CrossRef]
- Sobisevich, A.L.; Presnov, D.A.; Shurup, A.S. Fundamentals of passive seismohydroacoustic methods for Arctic shelf investigation. Acoust. Phys. 2021, 67, 62–82. [Google Scholar] [CrossRef]
- Katsnelson, B.; Petnikov, V.; Lynch, J. Fundamentals of Shallow Water Acoustics; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics, 2nd ed.; Springer: New York, NY, USA, 2011; pp. 337–380, 420. [Google Scholar]
- Fatyanov, A.G.; Terekhov, A.V. High-performance modeling acoustic and elastic waves using the parallel dichotomy algorithm. J. Comput. Phys. 2011, 230, 1992–2003. [Google Scholar] [CrossRef]
- Kozitskiy, S. Coupled-Mode Parabolic Equations for the Modeling of Sound Propagation in a Shallow-WaterWaveguide with Weak Elastic Bottom. J. Mar. Sci. Eng. 2022, 10, 1355. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, Y.; Zhu, X.; Liu, W.; Lan, Q.; Xiao, W. Parallel optimization of three-dimensional wedge-shaped underwater acoustic propagation based on MPI+OpenMP hybrid programming model. J. Supercomput. 2021, 77, 4988–5018. [Google Scholar] [CrossRef]
- Stevens, J.L.; Hanson, J.; Nielsen, P.; Zampolli, M.; Le Bras, R.; Haralabus, G. Calculation of Hydroacoustic Propagation and Conversion to Seismic Phases at T-Stations. Pure Appl. Geophys. 2021, 178, 2579–2609. [Google Scholar] [CrossRef]
- Rutenko, A.N.; Manul’chev, D.S.; Kozitskii, S.B. Study of Acoustic Signal Propagation from Sea to Land. Acoust. Phys. 2019, 65, 279–287. [Google Scholar] [CrossRef]
- Budrin, S.; Dolgikh, G.; Chupin, V.; Dolgikh, S. Some Peculiarities of Low-Frequency Hydroacoustic Signals Behavior in Tomographic Studies of “Sea-Land-Sea” System. J. Mar. Sci. Eng. 2022, 10, 1550. [Google Scholar] [CrossRef]
- Li, G.; Wang, J.; Meng, X.; Hua, Q.; Kan, G.; Liu, C. Seafloor Sediment Acoustic Properties on the Continental Slope in the Northwestern South China Sea. J. Mar. Sci. Eng. 2024, 12, 545. [Google Scholar] [CrossRef]
- COMSOL. Acoustics Module User’s Guide. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.aco/html_AcousticsModuleManual.html (accessed on 12 November 2024).
- Tang, J.; Petrov, P.S.; Piao, S.; Kozitskiy, S.B. On the method of source images for the wedge problem solution in ocean acoustics: Some corrections and appendices. Acoust. Phys. 2018, 64, 225–236. [Google Scholar] [CrossRef]
- Zhostkov, R.A. Remote seismoacoustic probing of the bottom of a sea covered by ice. Bull. Russ. Acad. Sci. Phys. 2020, 84, 94–97. [Google Scholar] [CrossRef]
- Wen-Yu, L.; Chun-Mei, Y.; Ji-Xing, Q.; Zhang, R.H. Benchmark solutions for sound propagation in an ideal wedge. Chin. Phys. 2013, 22, 054301. [Google Scholar] [CrossRef]
- Bottero, A.; Cristini, P.; Komatitsch, D. On the Influence of Slopes, Source, Seabed and Water Column Properties on T Waves: Generation at Shore. Pure Appl. Geophys. 2020, 177, 5695–5711. [Google Scholar] [CrossRef]
- Deane, G.; Buckingham, M. An analysis of the three-dimensional sound field in a penetrable wedge with a stratified fluid or elastic basement. J. Acoust. Soc. Am. 1993, 93, 1319–1328. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M.; Lysanov, Y.P. Fundamentals of Ocean Acoustics; Springer: New York, NY, USA, 2003. [Google Scholar]
- Brekhovskikh, L.M.; Godin, O.A. Acoustics of Layered Media I: Plane and Quasi-Plane Waves; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Callies, J.; Wu, W.; Peng, S.; Zhan, Z. Vertical-slice ocean tomography with seismic waves. Geophys. Res. Letters. 2023, 50, e2023GL102881. [Google Scholar] [CrossRef]
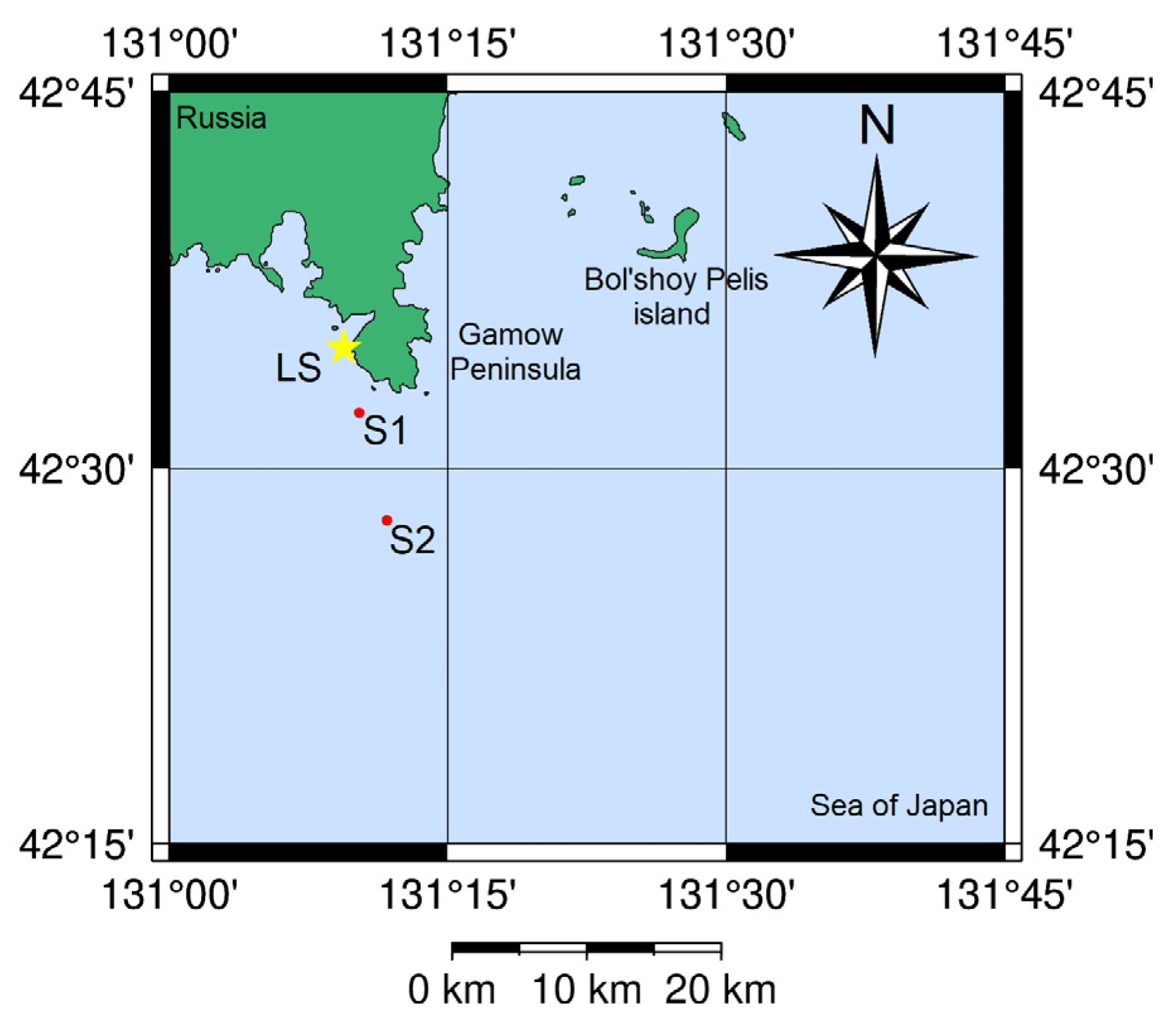
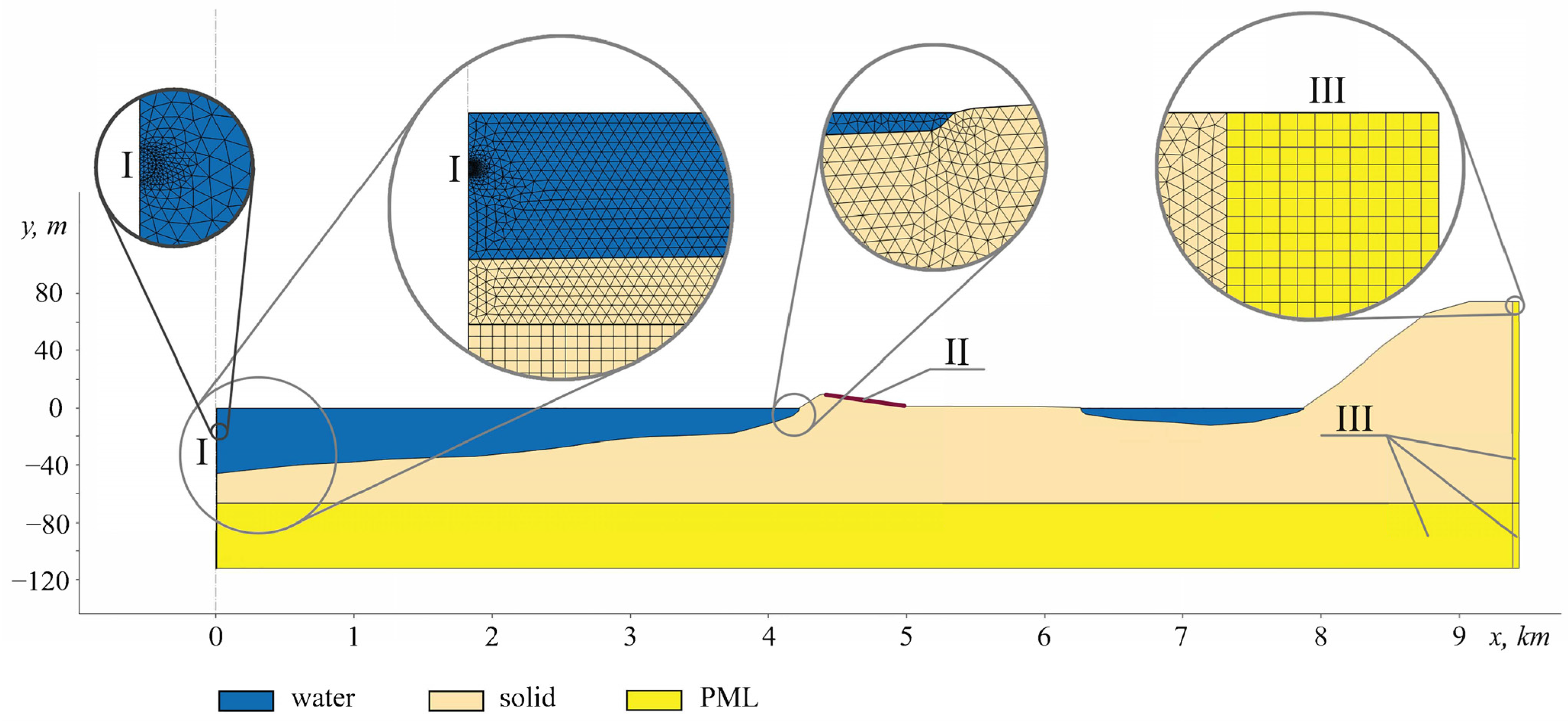
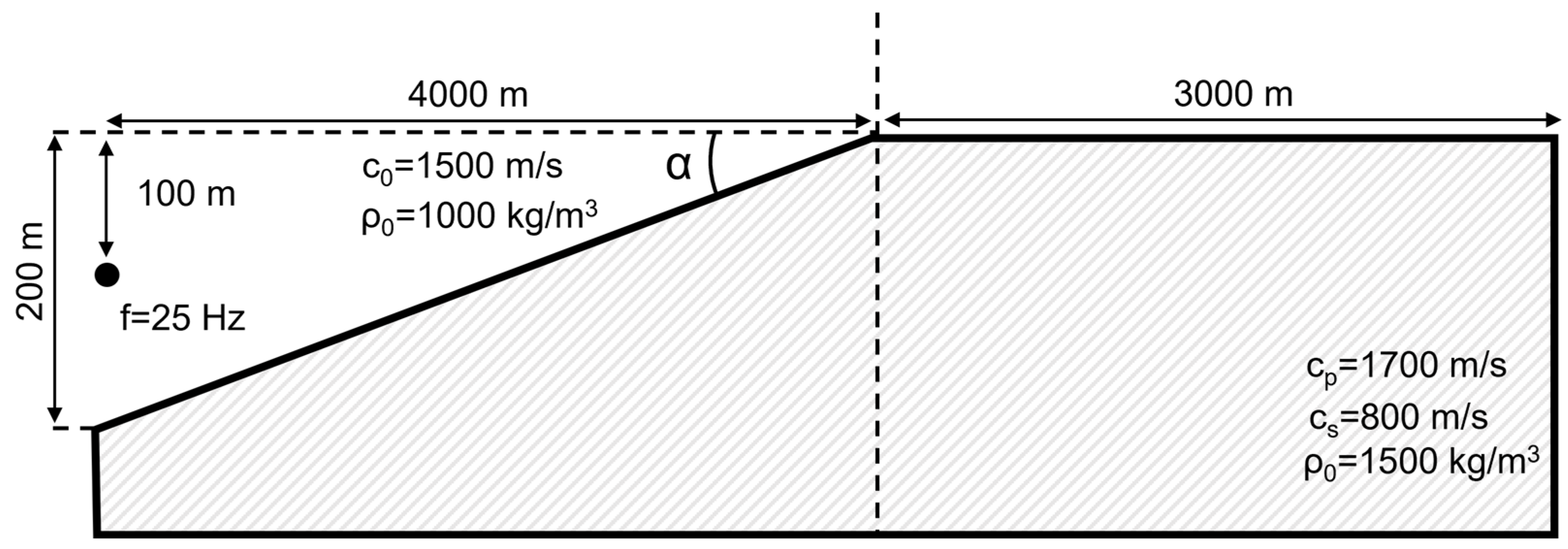
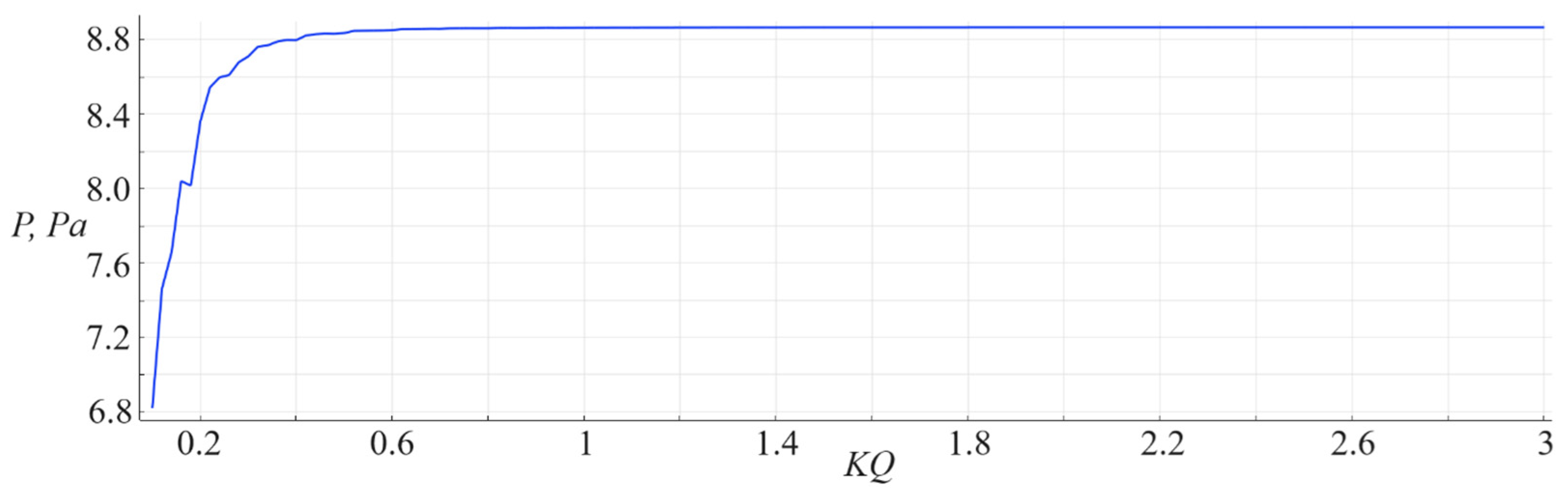
| Distance, m | GEBCO Depth (Measured), m | Measured Signal , nm | Estimated Amplitude , nm | |
|---|---|---|---|---|
| Point S1 | 4300 | 48 (52) | 2.5 | 2.6 ± 0.6 |
| Point S2 | 13,000 | 62 (74) | 0.9 | 0.9 ± 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolgikh, G.; Bolsunovskii, M.; Zharkov, D.; Zhostkov, R.; Presnov, D.; Razin, A.; Shurup, A. Numerical Simulation of Seismoacoustic Wave Transformation at Sea–Land Interface. J. Mar. Sci. Eng. 2024, 12, 2112. https://doi.org/10.3390/jmse12122112
Dolgikh G, Bolsunovskii M, Zharkov D, Zhostkov R, Presnov D, Razin A, Shurup A. Numerical Simulation of Seismoacoustic Wave Transformation at Sea–Land Interface. Journal of Marine Science and Engineering. 2024; 12(12):2112. https://doi.org/10.3390/jmse12122112
Chicago/Turabian StyleDolgikh, Grigory, Mikhail Bolsunovskii, Denis Zharkov, Ruslan Zhostkov, Dmitriy Presnov, Andrey Razin, and Andrey Shurup. 2024. "Numerical Simulation of Seismoacoustic Wave Transformation at Sea–Land Interface" Journal of Marine Science and Engineering 12, no. 12: 2112. https://doi.org/10.3390/jmse12122112
APA StyleDolgikh, G., Bolsunovskii, M., Zharkov, D., Zhostkov, R., Presnov, D., Razin, A., & Shurup, A. (2024). Numerical Simulation of Seismoacoustic Wave Transformation at Sea–Land Interface. Journal of Marine Science and Engineering, 12(12), 2112. https://doi.org/10.3390/jmse12122112







