Sensitivity Analysis of Underwater Structural-Acoustic Problems Based on Coupled Finite Element Method/Fast Multipole Boundary Element Method with Non-Uniform Rational B-Splines
Abstract
1. Introduction
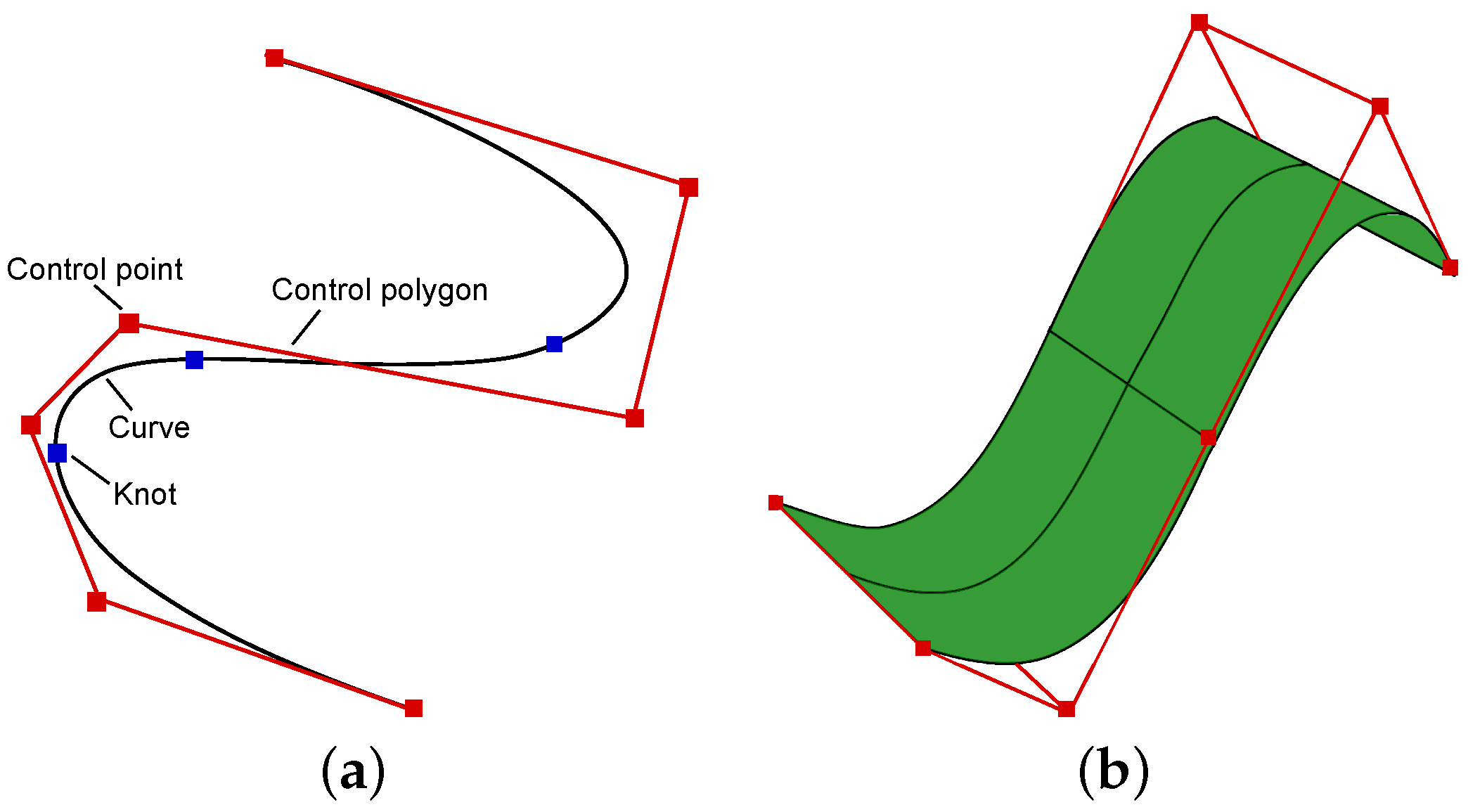
2. Non-Uniform Rational B-Splines (NURBS)
3. Structural-Acoustic Coupling
3.1. FEM Analysis
3.2. BEM Analysis
3.3. FEM–BEM Coupling Analysis
4. Sensitivity Analysis for Shape Design
5. Fast Multipole Boundary Element Method (FMBEM)
5.1. FMM Formulations for Acoustic State Analysis
5.2. FMM Formulas for Sensitivity Study of Acoustic Design
6. Numerical Examples
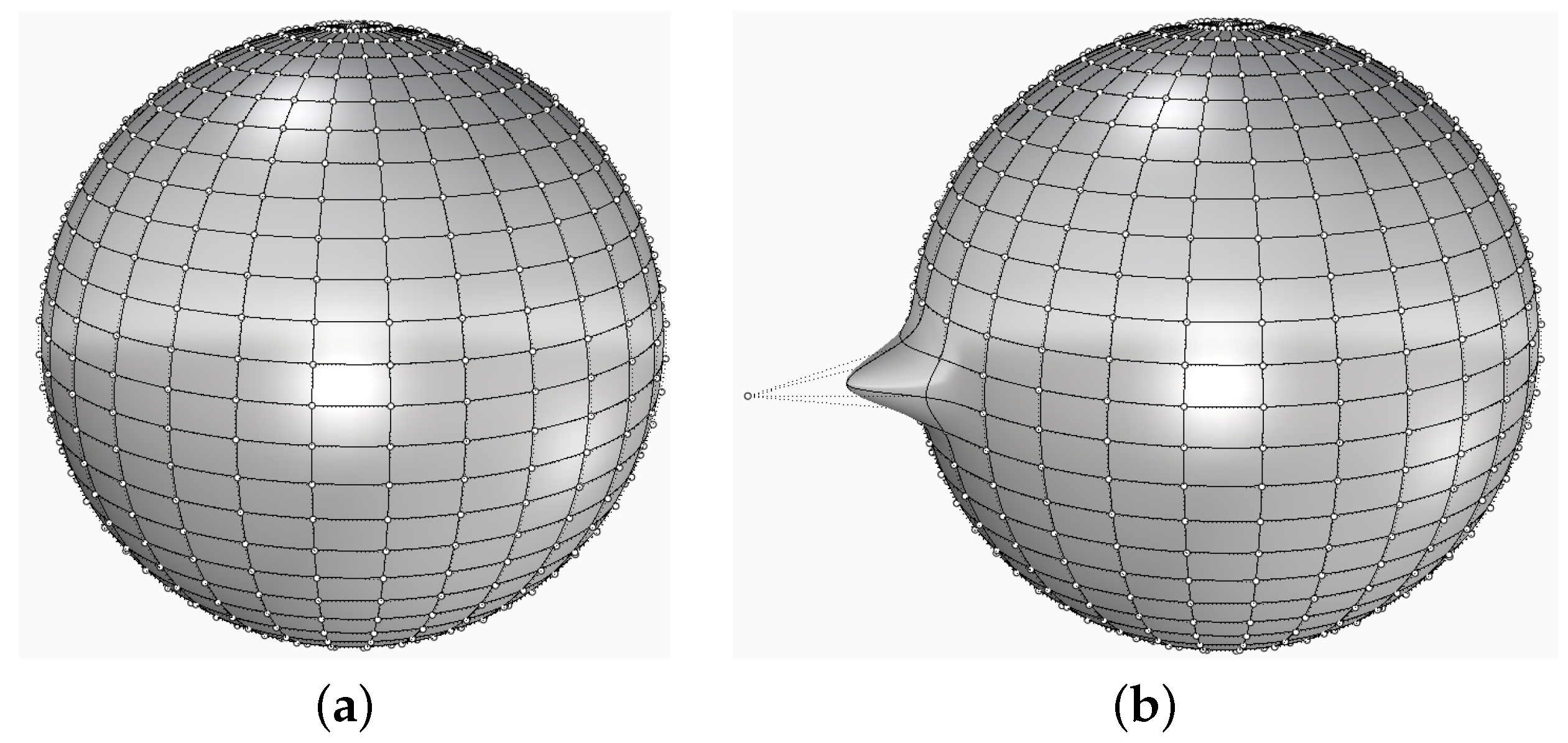
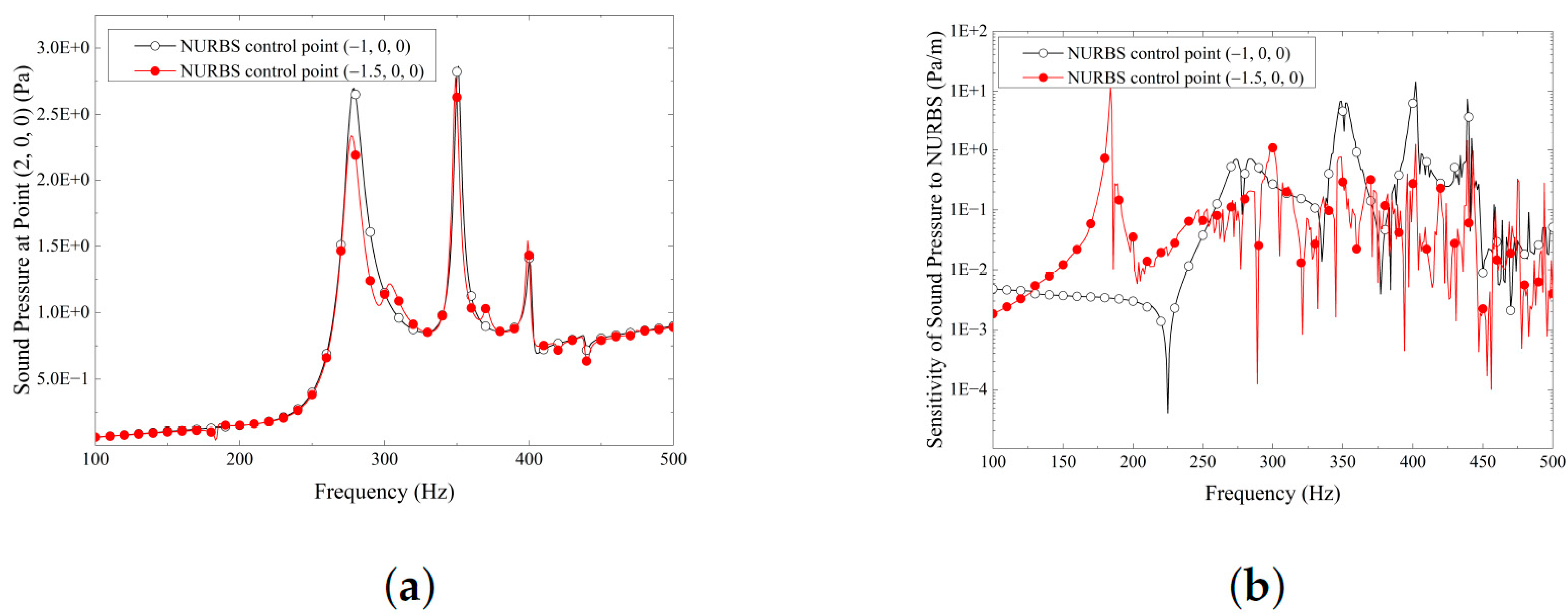
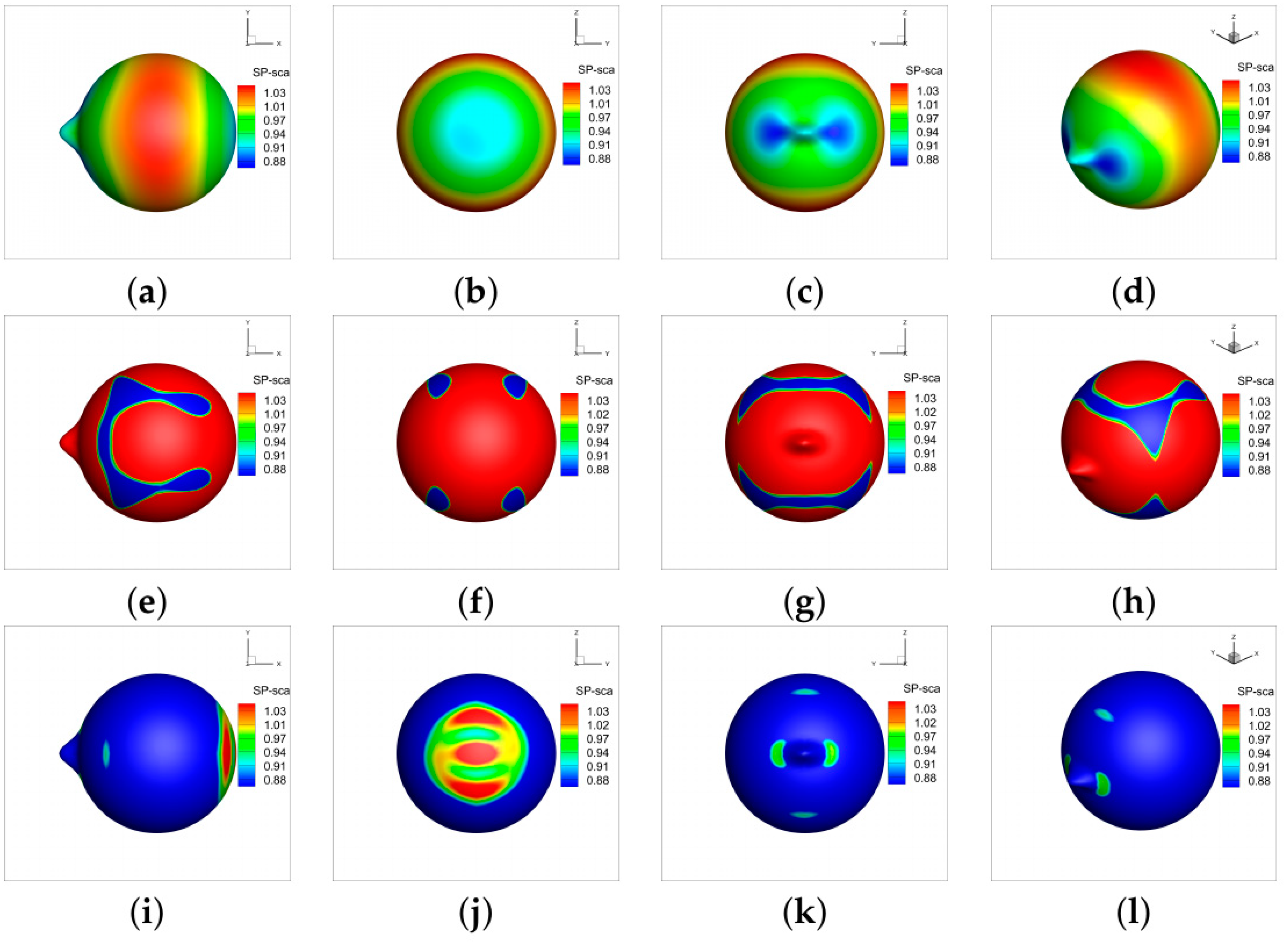
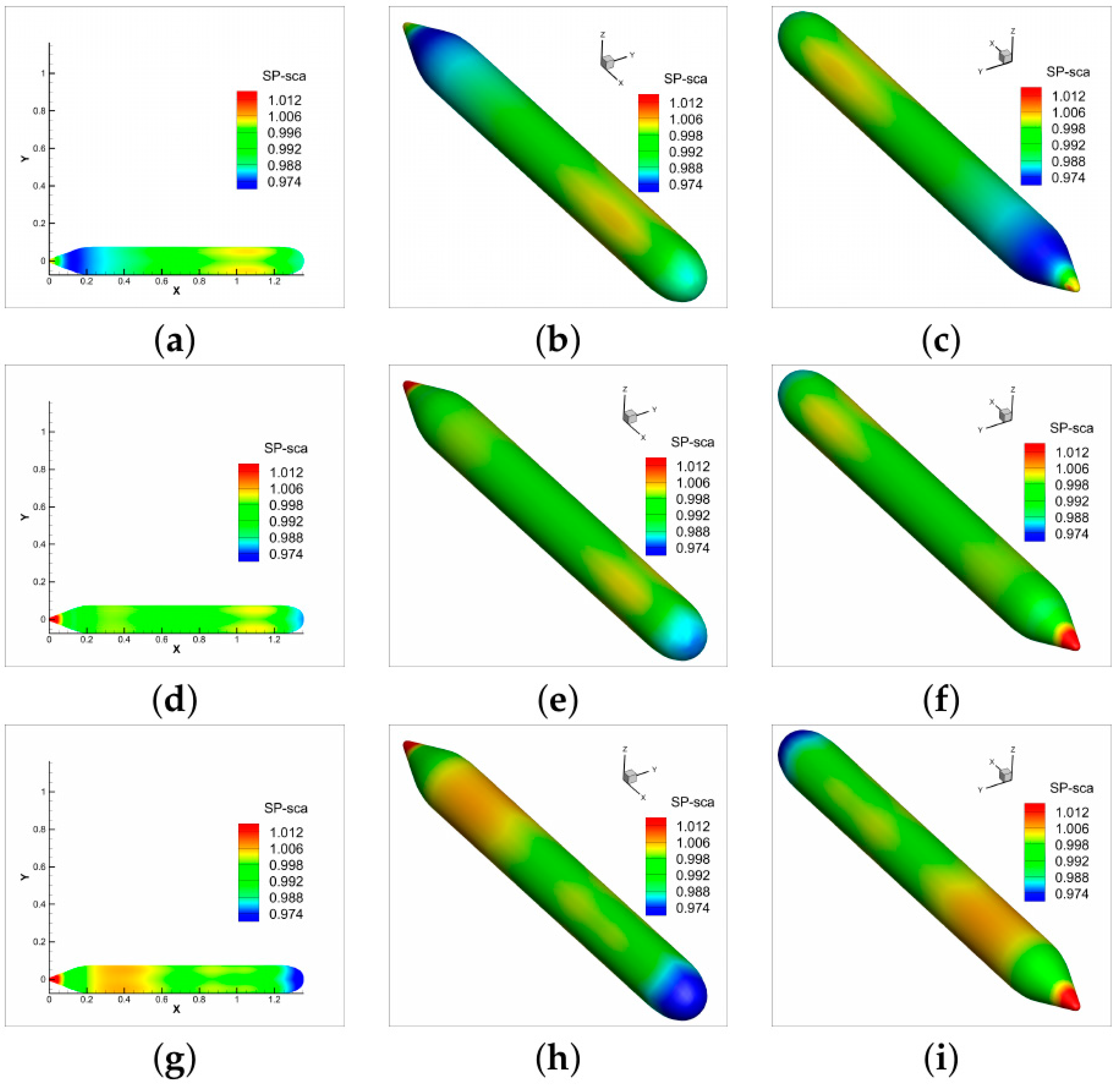
6.1. Spherical Models
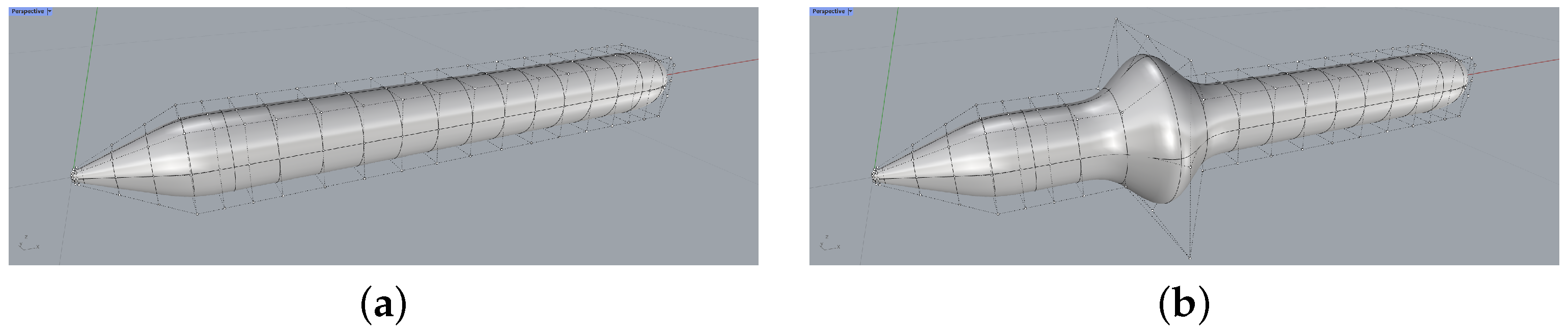
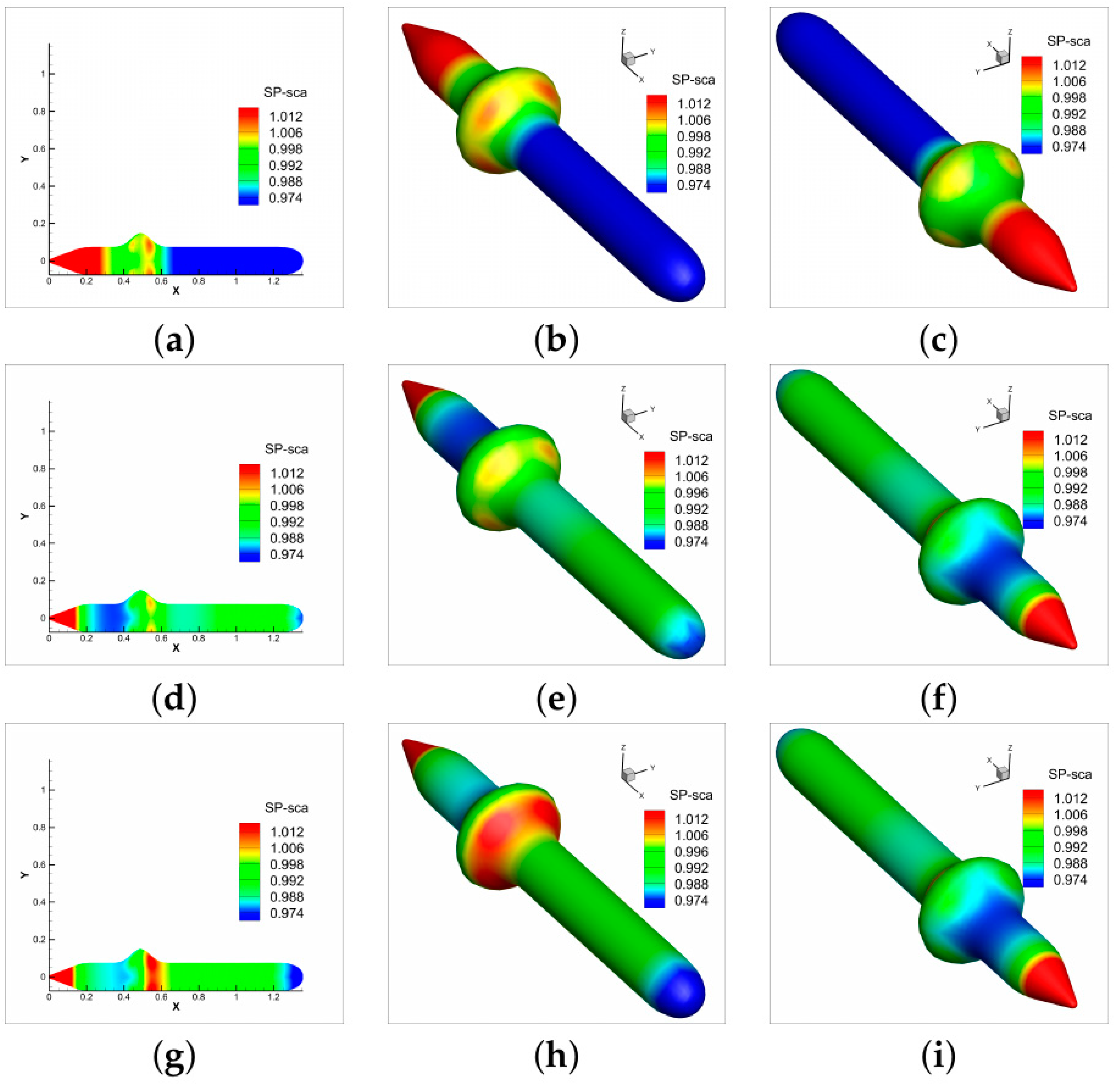
6.2. Submarine Model
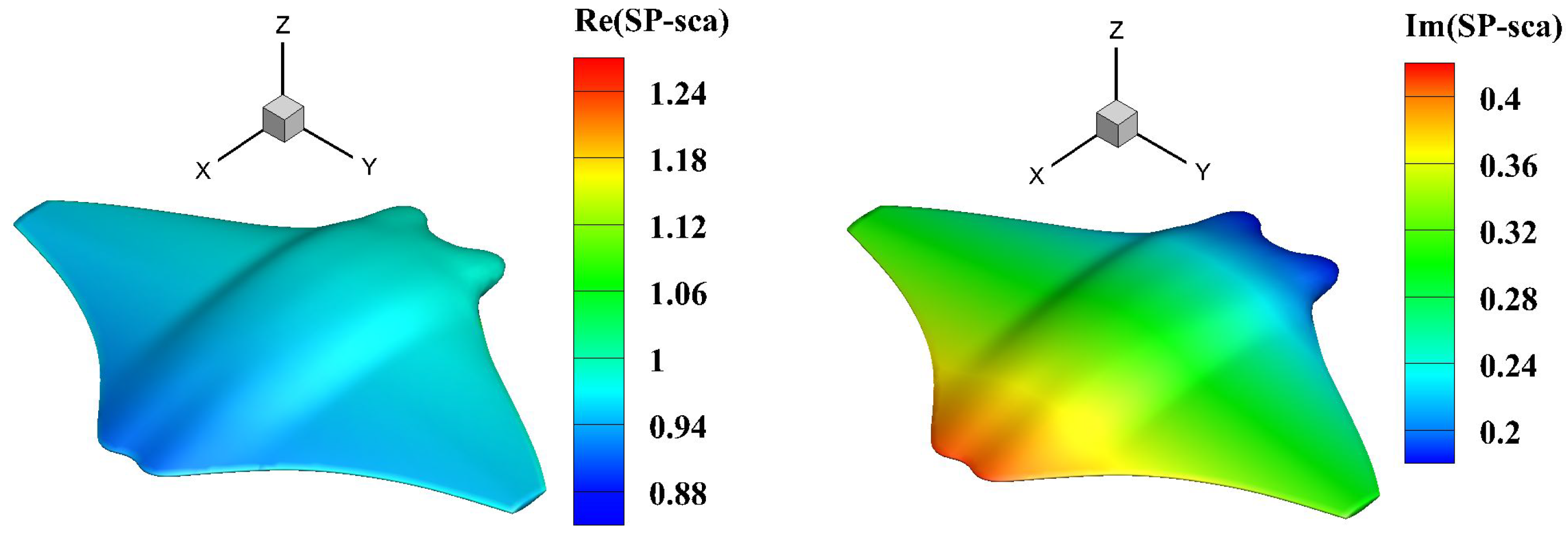
6.3. Fish Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Junger, M.C.; Feit, D. Sound, Structures, and Their Interaction; MIT Press: Cambridge, MA, USA, 1986; Volume 225. [Google Scholar]
- Sommerfeld, A. Partial Differential Equations in Physics; Academic Press: Cambridge, MA, USA, 1949; pp. v–vi. [Google Scholar] [CrossRef]
- Engleder, S.; Steinbach, O. Stabilized boundary element methods for exterior Helmholtz problems. Numer. Math. 2008, 110, 145–160. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Lian, H.; Atroshchenko, E.; Ding, C.; Bordas, S. Seamless integration of computer-aided geometric modeling and acoustic simulation: Isogeometric boundary element methods based on Catmull-Clark subdivision surfaces. Adv. Eng. Softw. 2020, 149, 102879. [Google Scholar] [CrossRef]
- Everstine, G.C.; Henderson, F.M. Coupled finite element/boundary element approach for fluid-structure interaction. J. Acoust. Soc. Am. 1990, 87, 1938–1947. [Google Scholar] [CrossRef]
- Fritze, D.; Marburg, S.; Hardtke, H.J. FEM-BEM-coupling and structural-acoustic sensitivity analysis for shell geometries. Comput. Struct. 2005, 83, 143–154. [Google Scholar] [CrossRef]
- Martinsson, P.; Rokhlin, V. A fast direct solver for boundary integral equations in two dimensions. J. Comput. Phys. 2005, 205, 1–23. [Google Scholar] [CrossRef]
- Martinsson, P.; Rokhlin, V. A fast direct solver for scattering problems involving elongated structures. J. Comput. Phys. 2007, 221, 288–302. [Google Scholar] [CrossRef]
- Bebendorf, M. Rjasanow, S. Adaptive Low-Rank Approximation of Collocation Matrices. Computing 2003, 70, 1–24. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, V. A fast algorithm for particle simulations. J. Comput. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Coifman, R.; Rokhlin, V.; Wandzura, S. The fast multipole method for the wave equation: A pedestrian prescription. IEEE Antennas Propag. Mag. 1993, 35, 7–12. [Google Scholar] [CrossRef]
- Rokhlin, V. Diagonal Forms of Translation Operators for the Helmholtz Equation in Three Dimensions. Appl. Comput. Harmon. Anal. 1993, 1, 82–93. [Google Scholar] [CrossRef]
- Chen, L.; Marburg, S.; Zhao, W.; Liu, C.; Chen, H. Implementation of isogeometric fast multipole boundary element methods for 2D half-space acoustic scattering problems with absorbing boundary condition. J. Theor. Comput. Acoust. 2019, 27, 1850024. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Liu, C.; Chen, H.; Marburg, S. Isogeometric Fast Multipole Boundary Element Method Based on Burton-Miller Formulation for 3D Acoustic Problems. Arch. Acoust. 2019, 44, 475–492. [Google Scholar] [CrossRef]
- Schneider, S. FE/FMBE coupling to model fluid-structure interaction. Int. J. Numer. Methods Eng. 2008, 76, 2137–2156. [Google Scholar] [CrossRef]
- Kim, N.H.; Dong, J. Shape sensitivity analysis of sequential structural-acoustic problems using FEM and BEM. J. Sound Vib. 2006, 290, 192–208. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, J.; Lian, H.; Yu, B.; Atroshchenko, E.; Li, P. A BEM broadband topology optimization strategy based on Taylor expansion and SOAR method-Application to 2D acoustic scattering problems. Int. J. Numer. Methods Eng. 2023, 124, 5151–5182. [Google Scholar] [CrossRef]
- Marburg, S. Developments in structural-acoustic optimization for passive noise control. Arch. Comput. Methods Eng. 2002, 9, 291–370. [Google Scholar] [CrossRef]
- Lamancusa, J. Numerical optimization techniques for structural-acoustic design of rectangular panels. Comput. Struct. 1993, 48, 661–675. [Google Scholar] [CrossRef]
- Hambric, S.A. Sensitivity Calculations for Broad-Band Acoustic Radiated Noise Design Optimization Problems. J. Vib. Acoust. 1996, 118, 529–532. [Google Scholar] [CrossRef]
- Marburg, S.; Hardtke, H.J. Shape optimization of a vehicle hat-shelf: Improving acoustic properties for different load cases by maximizing first eigenfrequency. Comput. Struct. 2001, 79, 1943–1957. [Google Scholar] [CrossRef]
- Choi, K.; Shim, I.; Wang, S. Design Sensitivity Analysis of Structure-Induced Noise and Vibration. J. Vib. Acoust. 1997, 119, 173–179. [Google Scholar] [CrossRef]
- Wang, S. Design Sensitivity Analysis of Noise, Vibration, and Harshness of Vehicle Body Structure. Mech. Struct. Mach. 1999, 27, 317–335. [Google Scholar] [CrossRef]
- Zheng, C.; Matsumoto, T.; Takahashi, T.; Chen, H. Explicit evaluation of hypersingular boundary integral equations for acoustic sensitivity analysis based on direct differentiation method. Eng. Anal. Bound. Elem. 2011, 35, 1225–1235. [Google Scholar] [CrossRef]
- Simpson, R.; Bordas, S.; Trevelyan, J.; Rabczuk, T. A two-dimensional Isogeometric Boundary Element Method for elastostatic analysis. Comput. Methods Appl. Mech. Eng. 2012, 209–212, 87–100. [Google Scholar] [CrossRef]
- Simpson, R.; Bordas, S.; Lian, H.; Trevelyan, J. An isogeometric boundary element method for elastostatic analysis: 2D implementation aspects. Comput. Struct. 2013, 118, 2–12. [Google Scholar] [CrossRef]
- Hughes, T.; Cottrell, J.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Chen, L.; Lu, C.; Lian, H.; Liu, Z.; Zhao, W.; Li, S.; Chen, H.; Bordas, S.P. Acoustic topology optimization of sound absorbing materials directly from subdivision surfaces with isogeometric boundary element methods. Comput. Methods Appl. Mech. Eng. 2020, 362, 112806. [Google Scholar] [CrossRef]
- Shen, X.; Du, C.; Jiang, S.; Sun, L.; Chen, L. Enhancing deep neural networks for multivariate uncertainty analysis of cracked structures by POD-RBF. Theor. Appl. Fract. Mech. 2023, 125, 103925. [Google Scholar] [CrossRef]
- Scott, M.; Simpson, R.; Evans, J.; Lipton, S.; Bordas, S.; Hughes, T.; Sederberg, T. Isogeometric boundary element analysis using unstructured T-splines. Comput. Methods Appl. Mech. Eng. 2013, 254, 197–221. [Google Scholar] [CrossRef]
- Takahashi, T.; Matsumoto, T. An application of fast multipole method to isogeometric boundary element method for Laplace equation in two dimensions. Eng. Anal. Bound. Elem. 2012, 36, 1766–1775. [Google Scholar] [CrossRef]
- Chen, L.; Cheng, R.; Li, S.; Lian, H.; Zheng, C.; Bordas, S. A sample-efficient deep learning method for multivariate uncertainty qualification of acoustic-vibration interaction problems. Comput. Methods Appl. Mech. Eng. 2022, 393, 114784. [Google Scholar] [CrossRef]
- Ginnis, A.; Kostas, K.; Politis, C.; Kaklis, P.; Belibassakis, K.; Gerostathis, T.; Scott, M.; Hughes, T. Isogeometric boundary-element analysis for the wave-resistance problem using T-splines. Comput. Methods Appl. Mech. Eng. 2014, 279, 425–439. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Xu, Y.; Li, S.; Liu, Z.; Atroshchenko, E.; Kerfriden, P. Generalized isogeometric boundary element method for uncertainty analysis of time-harmonic wave propagation in infinite domains. Appl. Math. Model. 2023, 114, 360–378. [Google Scholar] [CrossRef]
- Shen, X.; Du, C.; Jiang, S.; Zhang, P.; Chen, L. Multivariate uncertainty analysis of fracture problems through model order reduction accelerated SBFEM. Appl. Math. Model. 2024, 125, 218–240. [Google Scholar] [CrossRef]
- Simpson, R.; Liu, Z.; Vázquez, R.; Evans, J. An isogeometric boundary element method for electromagnetic scattering with compatible B-spline discretizations. J. Comput. Phys. 2018, 362, 264–289. [Google Scholar] [CrossRef]
- Xu, Y.; Li, H.; Chen, L.; Zhao, J.; Zhang, X. Monte Carlo Based Isogeometric Stochastic Finite Element Method for Uncertainty Quantization in Vibration Analysis of Piezoelectric Materials. Mathematics 2022, 10, 1840. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Lian, H.; Ma, Y.; Meng, Z.; Li, P.; Ding, C.; Bordas, S.P. Reduced order isogeometric boundary element methods for CAD-integrated shape optimization in electromagnetic scattering. Comput. Methods Appl. Mech. Eng. 2024, 419, 116654. [Google Scholar] [CrossRef]
- Chen, L.; Liu, C.; Zhao, W.; Liu, L. An isogeometric approach of two dimensional acoustic design sensitivity analysis and topology optimization analysis for absorbing material distribution. Comput. Methods Appl. Mech. Eng. 2018, 336, 507–532. [Google Scholar] [CrossRef]
- Xu, G.; Li, M.; Mourrain, B.; Rabczuk, T.; Xu, J.; Bordas, S.P. Constructing IGA-suitable planar parameterization from complex CAD boundary by domain partition and global/local optimization. Comput. Methods Appl. Mech. Eng. 2018, 328, 175–200. [Google Scholar] [CrossRef]
- Li, S.; Trevelyan, J.; Wu, Z.; Lian, H.; Wang, D.; Zhang, W. An adaptive SVD-Krylov reduced order model for surrogate based structural shape optimization through isogeometric boundary element method. Comput. Methods Appl. Mech. Eng. 2019, 349, 312–338. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Liu, Z.; Chen, H.; Atroshchenko, E.; Bordas, S. Structural shape optimization of three dimensional acoustic problems with isogeometric boundary element methods. Comput. Methods Appl. Mech. Eng. 2019, 355, 926–951. [Google Scholar] [CrossRef]
- Lian, H.; Chen, L.; Lin, X.; Zhao, W.; Bordas, S.P.A.; Zhou, M. Noise Pollution Reduction through a Novel Optimization Procedure in Passive Control Methods. Comput. Model. Eng. Sci. 2022, 131, 1–18. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Natarajan, S.; Zhao, W.; Chen, X.; Bordas, S. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput. Methods Appl. Mech. Eng. 2022, 395, 114997. [Google Scholar] [CrossRef]
- Chen, L.; Li, K.; Peng, X.; Lian, H.; Lin, X.; Fu, Z. Isogeometric Boundary Element Analysis for 2D Transient Heat Conduction Problem with Radial Integration Method. CMES-Comput. Model. Eng. Sci. 2021, 126, 125–146. [Google Scholar] [CrossRef]
- Chen, L.; Li, H.; Guo, Y.; Chen, P.; Atroshchenko, E.; Lian, H. Uncertainty quantification of mechanical property of piezoelectric materials based on isogeometric stochastic FEM with generalized n th-order perturbation. Eng. Comput. 2023, 1–21. [Google Scholar] [CrossRef]
- Rehman, F.U.; Huang, L.; Anderlini, E.; Thomas, G. Hydrodynamic Modelling for a Transportation System of Two Unmanned Underwater Vehicles: Semi-Empirical, Numerical and Experimental Analyses. J. Mar. Sci. Eng. 2021, 9, 500. [Google Scholar] [CrossRef]
- Burton, A.J.; Miller, G.F. The Application of Integral Equation Methods to the Numerical Solution of Some Exterior Boundary-Value Problems. Proc. R. Soc. Lond. 1971, 323, 201–210. [Google Scholar] [CrossRef]
- Ciskowski, R.D.; Brebbia, C.A. Boundary Element Methods in Acoustics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Marjan, A.; Huang, L. Topology optimisation of offshore wind turbine jacket foundation for fatigue life and mass reduction. Ocean. Eng. 2023, 289, 116228. [Google Scholar] [CrossRef]
- Huang, L.; Pena, B.; Liu, Y.; Anderlini, E. Machine learning in sustainable ship design and operation: A review. Ocean. Eng. 2022, 266, 112907. [Google Scholar] [CrossRef]
- Chen, L.; Lian, H.; Liu, Z.; Gong, Y.; Zheng, C.; Bordas, S. Bi-material topology optimization for fully coupled structural-acoustic systems with isogeometric FEM-BEM. Eng. Anal. Bound. Elem. 2022, 135, 182–195. [Google Scholar] [CrossRef]
- Zheng, C.; Matsumoto, T.; Takahashi, T.; Chen, H. A wideband fast multipole boundary element method for three dimensional acoustic shape sensitivity analysis based on direct differentiation method. Eng. Anal. Bound. Elem. 2012, 36, 361–371. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Zhou, Z.; Xu, Y.; Qu, Y. Sensitivity Analysis of Underwater Structural-Acoustic Problems Based on Coupled Finite Element Method/Fast Multipole Boundary Element Method with Non-Uniform Rational B-Splines. J. Mar. Sci. Eng. 2024, 12, 98. https://doi.org/10.3390/jmse12010098
Cao Y, Zhou Z, Xu Y, Qu Y. Sensitivity Analysis of Underwater Structural-Acoustic Problems Based on Coupled Finite Element Method/Fast Multipole Boundary Element Method with Non-Uniform Rational B-Splines. Journal of Marine Science and Engineering. 2024; 12(1):98. https://doi.org/10.3390/jmse12010098
Chicago/Turabian StyleCao, Yonghui, Zhongbin Zhou, Yanming Xu, and Yilin Qu. 2024. "Sensitivity Analysis of Underwater Structural-Acoustic Problems Based on Coupled Finite Element Method/Fast Multipole Boundary Element Method with Non-Uniform Rational B-Splines" Journal of Marine Science and Engineering 12, no. 1: 98. https://doi.org/10.3390/jmse12010098
APA StyleCao, Y., Zhou, Z., Xu, Y., & Qu, Y. (2024). Sensitivity Analysis of Underwater Structural-Acoustic Problems Based on Coupled Finite Element Method/Fast Multipole Boundary Element Method with Non-Uniform Rational B-Splines. Journal of Marine Science and Engineering, 12(1), 98. https://doi.org/10.3390/jmse12010098






