Secure Rate-Splitting Multiple Access for Maritime Cognitive Radio Network: Power Allocation and UAV’s Location Optimization
Abstract
1. Introduction
- We design a novel secure RSMA strategy for the maritime cognitive to support both primary and maritime UAV’s transmissions. In the proposed strategy, the secondary maritime UAV’s transmission can not only broadcast secondary information but also protect the primary transmission. Through the flexible allocation of the transmission resources, both users’ QoS can be provided.
- We formulate an optimization problem to maximize the UAV’s transmission rate under the RSMA decoding principle and primary information security requirements. To solve the above non-convex problem, we design a CPFS algorithm to allocate the transmit power and design the UAV’s location. In addition, the worst case is analyzed, which is considered as the lower-bound to the UAV’s transmission.
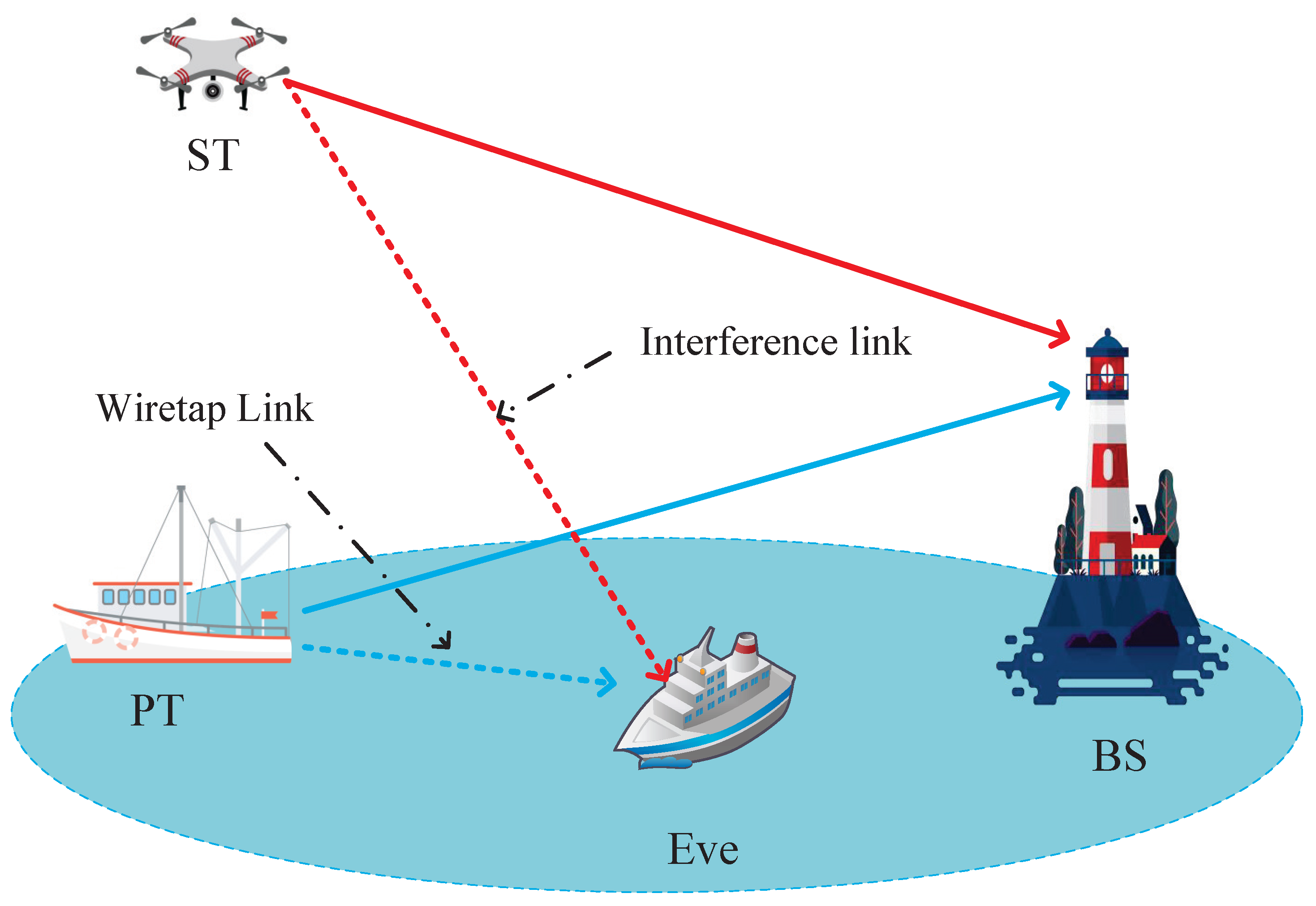
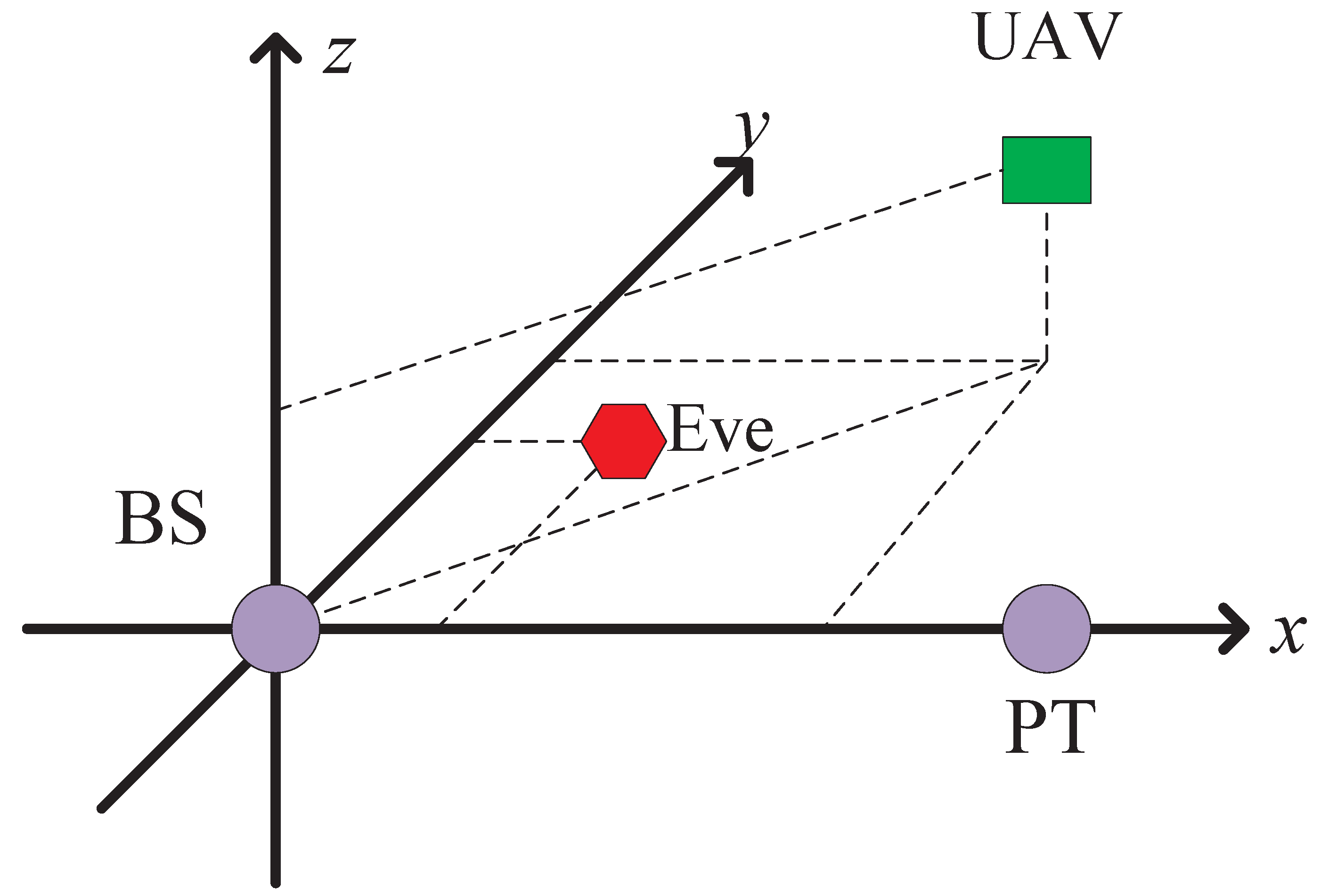
2. System Model and Problem Formulation
3. RSMA-Based Cognitive Maritime Transmission Strategy
3.1. Power Allocation
3.2. UAV’s Location Optimization
| Algorithm 1 The proposed CPFS algorithm. |
|
4. RSMA-Based Cognitive Maritime Transmission with Powerful Eve
4.1. Power Allocation
4.2. UAV’s Location Optimization
| Algorithm 2 The proposed iterative algorithm. |
|
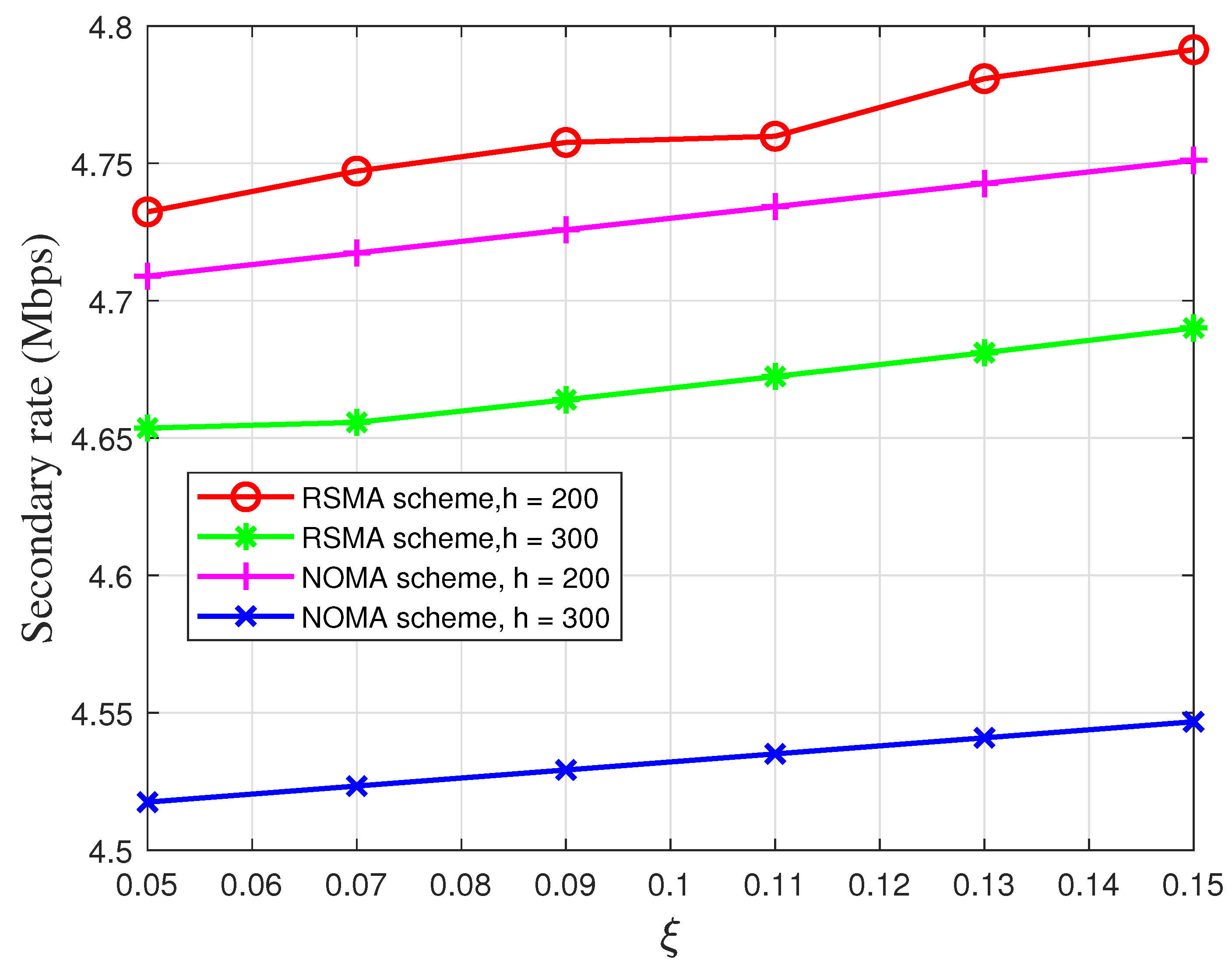
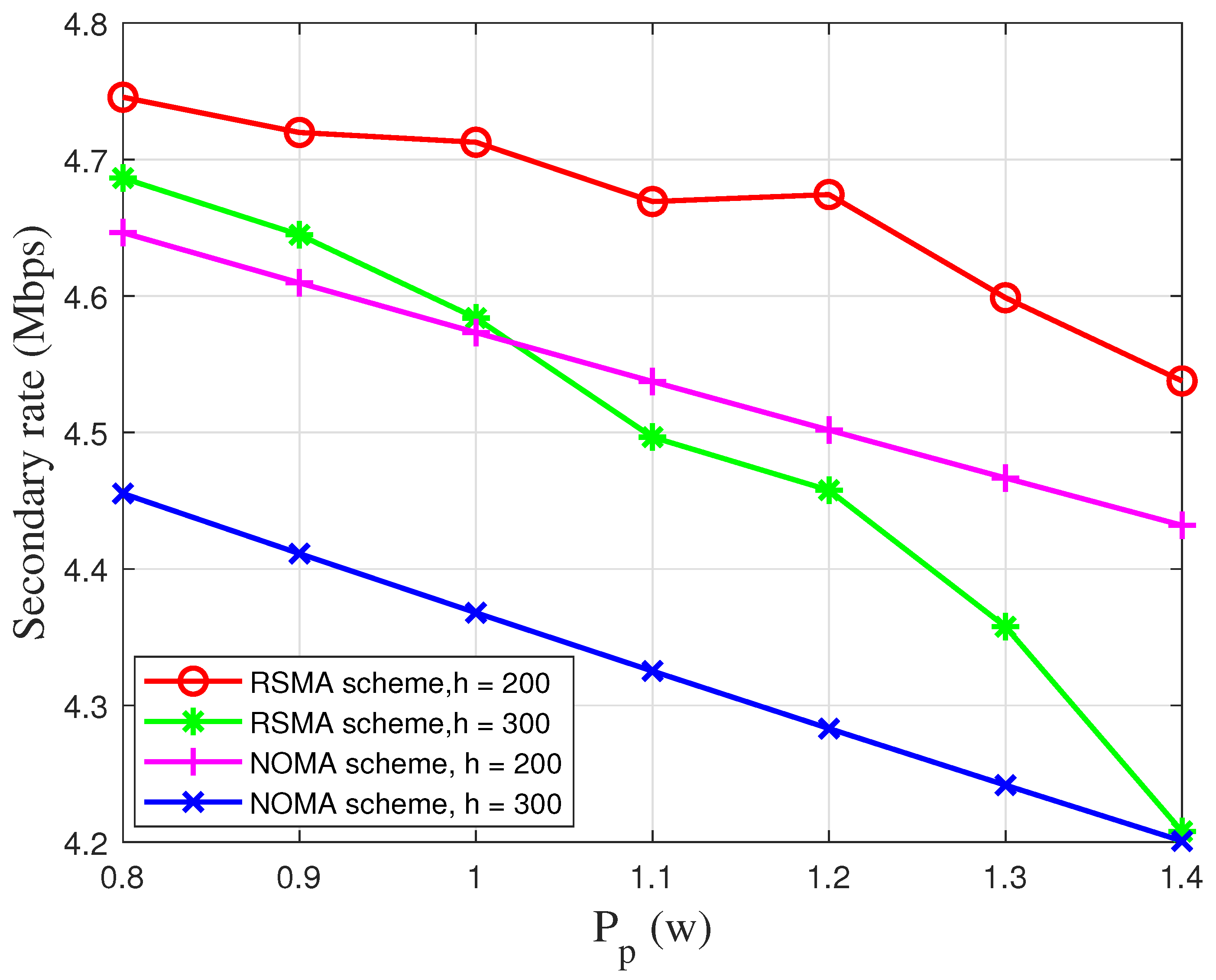
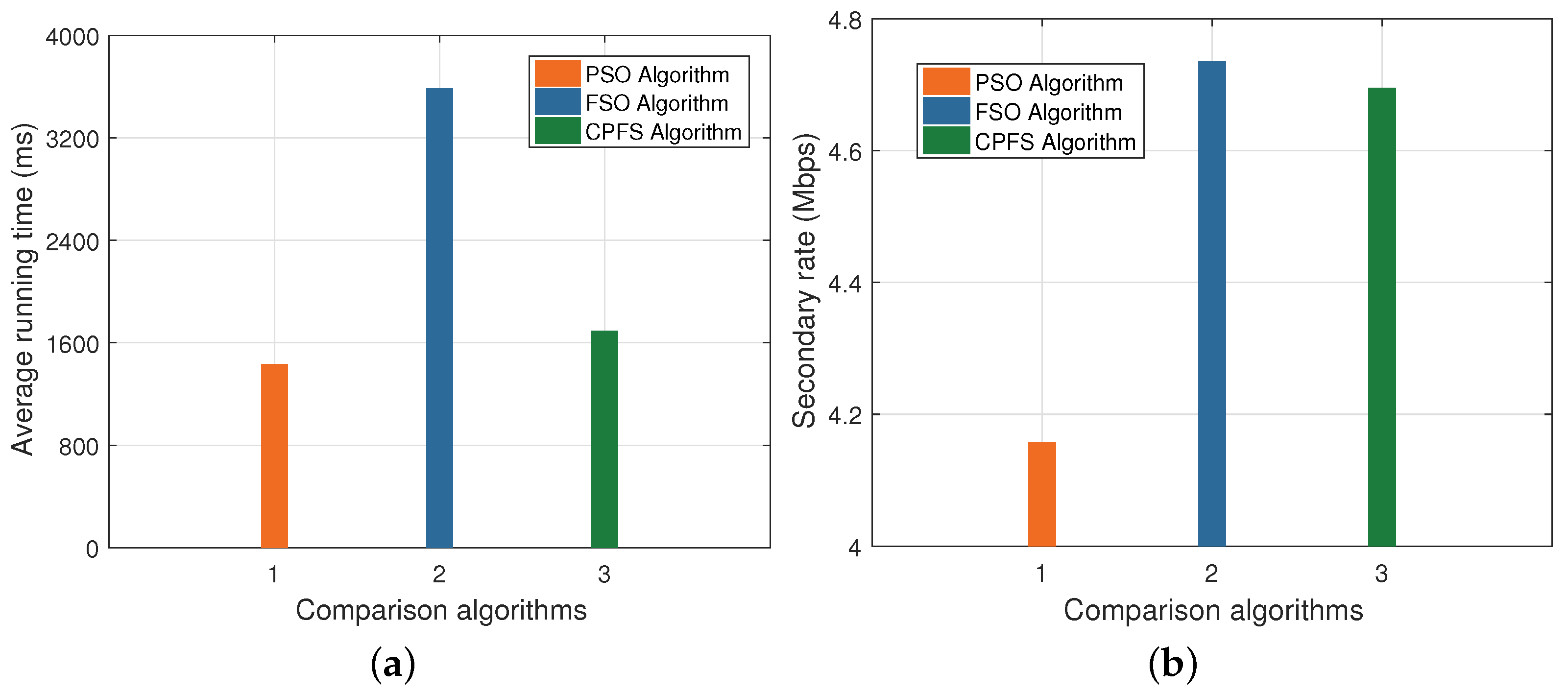
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arienzo, L. Green RF/FSO Communications in Cognitive Relay-Based Space Information Networks for Maritime Surveillance. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 1182–1193. [Google Scholar] [CrossRef]
- Wang, D.; He, T.; Zhou, F.; Cheng, J.; Zhang, R.; Wu, Q. Outage-driven link selection for secure buffer-aided networks. Sci. China Inf. Sci. 2022, 65, 182303. [Google Scholar] [CrossRef]
- Su, X.; Meng, L.; Huang, J. Intelligent Maritime Networking With Edge Services and Computing Capability. IEEE Trans. Veh. Technol. 2020, 69, 13606–13620. [Google Scholar] [CrossRef]
- Arguedas, V.F.; Pallotta, G.; Vespe, M. Maritime traffic networks: From historical positioning data to unsupervised maritime traffic monitoring. IEEE Trans. Intell. Transp. Syst. 2017, 19, 722–732. [Google Scholar] [CrossRef]
- Tang, R.; Feng, W.; Chen, Y.; Ge, N. NOMA-based UAV communications for maritime coverage enhancement. China Commun. 2021, 18, 230–243. [Google Scholar] [CrossRef]
- Xu, K.; Zhao, M.-M.; Cai, Y.; Hanzo, L. Low-Complexity Joint Power Allocation and Trajectory Design for UAV-Enabled Secure Communications with Power Splitting. IEEE Trans. Commun. 2021, 69, 1896–1911. [Google Scholar] [CrossRef]
- Wang, D.; Wu, M.; He, Y.; Pang, L.; Xu, Q.; Zhang, R. An HAP and UAVs collaboration framework for uplink secure rate maximization in NOMA-enabled IoT networks. Remote Sens. 2022, 14, 4501. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV Communications via Joint Trajectory and Power Control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.; Guo, S.; Yuan, D. Deployment and Association of Multiple UAVs in UAV-Assisted Cellular Networks With the Knowledge of Statistical User Position. IEEE Trans. Wirel. Commun. 2022, 21, 6553–6567. [Google Scholar] [CrossRef]
- Li, L.; Chang, T.-H.; Cai, S. UAV Positioning and Power Control for Two-Way Wireless Relaying. IEEE Trans. Wirel. Commun. 2020, 19, 1008–1024. [Google Scholar] [CrossRef]
- Jiang, M.; Li, Y.; Zhang, Q.; Qin, J. Joint Position and Time Allocation Optimization of UAV Enabled Time Allocation Optimization Networks. IEEE Trans. Commun. 2019, 67, 3806–3816. [Google Scholar] [CrossRef]
- Wang, J.-B.; Zeng, C.; Ding, C.; Zhang, H.; Lin, M.; Wang, J. Unmanned Surface Vessel Assisted Maritime Wireless Communication Toward 6G: Opportunities and Challenges. IEEE Wirel. Commun. 2022, 29, 72–79. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, J.-B.; Ding, C.; Zhang, H.; Lin, M.; Cheng, J. Joint Optimization of Trajectory and Communication Resource Allocation for Unmanned Surface Vehicle Enabled Maritime Wireless Networks. IEEE Trans. Commun. 2021, 69, 8100–8115. [Google Scholar] [CrossRef]
- Clerckx, B.; Mao, Y.; Jorswieck, E.A.; Yuan, J.; Love, D.J.; Erkip, E.; Niyato, D. A Primer on Rate-Splitting Multiple Access: Tutorial, Myths, and Frequently Asked Questions. IEEE J. Sel. Areas Commun. 2023, accepted.
- Xiao, Y.; Tegos, S.A.; Diamantoulakis, P.D.; Ma, Z.; Karagiannidis, G.K. On the Ergodic Rate of Cognitive Radio Inspired Uplink Multiple Access. IEEE Commun. Lett. 2023, 27, 95–99. [Google Scholar] [CrossRef]
- Gamal, S.; Rihan, M.; Hussin, S.; Zaghloul, A.; Salem, A.A. Multiple Access in Cognitive Radio Networks: From Orthogonal and Non-Orthogonal to Rate-Splitting. IEEE Access 2021, 9, 95569–95584. [Google Scholar] [CrossRef]
- Acosta, M.R.C.; Moreta, C.E.G.; Koo, I. Joint Power Allocation and Power Splitting for MISO-RSMA Cognitive Radio Systems With SWIPT and Information Decoder Users. IEEE Syst. J. 2021, 15, 5289–5300. [Google Scholar] [CrossRef]
- Dizdar, O.; Clerckx, B. Rate-Splitting Multiple Access for Communications and Jamming in Multi-Antenna Multi-Carrier Cognitive Radio Systems. IEEE Trans. Inf. Forensics Secur. 2022, 17, 628–643. [Google Scholar] [CrossRef]
- Li, X.; Fan, Y.; Yao, R.; Wang, P.; Qi, N.; Miridakis, N.I.; Tsiftsis, T.A. Rate-Splitting Multiple Access-Enabled Security Analysis in Cognitive Satellite Terrestrial Networks. IEEE Trans. Veh. Tech. 2022, 71, 11756–11771. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Champagne, B.; Zhu, W.-P.; Al-Dhahir, N. Secure and Energy Efficient Transmission for RSMA-Based Cognitive Satellite-Terrestrial Networks. IEEE Wirel. Commun. Lett. 2021, 10, 251–255. [Google Scholar] [CrossRef]
- Tong, Y.; Li, D.; Yang, Z.; Xiong, Z.; Zhao, N.; Li, Y. Outage Analysis of Rate Splitting Networks with an Untrusted User. IEEE Trans. Veh. Tech. 2023, 72, 2626–2631. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, Q.; Chen, W.; Ng, D.W.K. Rate-Splitting Multiple Access for Intelligent Reflecting Surface-Aided Secure Transmission. IEEE Commun. Lett. 2023, 27, 482–486. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.; Huang, F.; Zhang, R.; Gu, X.; Pan, J. A V2I and V2V collaboration framework to support emergency communications in ABS-aided Internet of Vehicles. IEEE Trans. Green Commun. Netw. 2023, to be published. [CrossRef]
- Zhang, W.; Zhang, W. An Efficient UAV Localization Technique Based on Particle Swarm Optimization. IEEE Trans. Veh. Technol. 2022, 71, 9544–9557. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, F.; Lin, W.; Ding, Z.; Al-Dhahir, N. Cooperative hybrid nonorthogonal multiple access-based mobile-edge computing in cognitive radio networks. IEEE Trans. Cognit. Commun. Netw. 2022, 8, 1104–1117. [Google Scholar] [CrossRef]
- Yu, Z.; Si, Z.; Li, X.; Wang, D.; Song, H. A Novel Hybrid Particle Swarm Optimization Algorithm for Path Planning of UAVs. IEEE Internet Things J. 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Khan, S.U.; Yang, S.; Wang, L.; Liu, L. A Modified Particle Swarm Optimization Algorithm for Global Op-timizations of Inverse Problems. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar]
- Nobar, S.K.; Ahmed, M.H.; Morgan, Y.; Mahmoud, S.A. Resource Allocation in Cognitive Radio-Enabled UAV Communication. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 296–310. [Google Scholar] [CrossRef]
- Lu, X.; Yang, W.; Yan, S.; Li, Z.; Ng, D.W.K. Covertness and Timeliness of Data Collection in UAV-Aided Wireless-Powered IoT. IEEE Internet Things J. 2021, 9, 12573–12587. [Google Scholar] [CrossRef]
- Hadzi-Velkov, Z.; Pejoski, S.; Zlatanov, N.; Schober, R. UAV-Assisted Wireless Powered Relay Networks With Cyclical NOMA-TDMA. IEEE Wirel. Commun. Lett. 2020, 9, 2088–2092. [Google Scholar] [CrossRef]
- He, Y.; Wang, D.; Huang, F.; Zhang, R.; Pan, J. Trajectory optimization and channel allocation for delay sensitive secure transmission in UAV-relayed VANETs. IEEE Trans. Veh. Technol. 2022, 71, 4512–4517. [Google Scholar] [CrossRef]
- Liu, A.; Lau, V.K.N. Optimization of Multi-UAV-Aided Wireless Networking Over a Ray-Tracing Channel Model. IEEE Trans. Wirel. Commun. 2019, 18, 4518–4530. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| UAV’s altitude, h | 200 m, 300 m |
| Maximum transmission power of UAV, | 2 Watt |
| Maximum transmission power of PT, | 2 Watt |
| Security outage threshold, | 0.09 |
| Secondary decoding threshold, | 1.5 Mbps |
| Secondary decoding threshold, | 2 Mbps |
| Noise power, | −174 dBm/Hz |
| Communication frequency | 5.9 GHz |
| Number of simulations runs | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, L.; Li, J.; He, Y.; Wang, W. Secure Rate-Splitting Multiple Access for Maritime Cognitive Radio Network: Power Allocation and UAV’s Location Optimization. J. Mar. Sci. Eng. 2023, 11, 1012. https://doi.org/10.3390/jmse11051012
Min L, Li J, He Y, Wang W. Secure Rate-Splitting Multiple Access for Maritime Cognitive Radio Network: Power Allocation and UAV’s Location Optimization. Journal of Marine Science and Engineering. 2023; 11(5):1012. https://doi.org/10.3390/jmse11051012
Chicago/Turabian StyleMin, Lingtong, Jiawei Li, Yixin He, and Weiguang Wang. 2023. "Secure Rate-Splitting Multiple Access for Maritime Cognitive Radio Network: Power Allocation and UAV’s Location Optimization" Journal of Marine Science and Engineering 11, no. 5: 1012. https://doi.org/10.3390/jmse11051012
APA StyleMin, L., Li, J., He, Y., & Wang, W. (2023). Secure Rate-Splitting Multiple Access for Maritime Cognitive Radio Network: Power Allocation and UAV’s Location Optimization. Journal of Marine Science and Engineering, 11(5), 1012. https://doi.org/10.3390/jmse11051012







