A Novel Region-Construction Method for Multi-USV Cooperative Target Allocation in Air–Ocean Integrated Environments

Abstract

The effective defense of sparsely populated border islands, surrounded by a multifaceted sea, against enemy infiltration poses a crucial problem in national defense. One possible solution is to deploy multiple unmanned surface vessels (USVs) to form an intelligent patrol and defense system. With the designated or daily patrols of USVs, we need to allocate target positions in real time to ensure their continuous operation. Currently, the state-of-art methods contain two major problems of target deadlock and local optimization, which limit the efficiency of reaching the target. To this end, we proposed a novel Region-Construction (RECO) method aimed at high-efficiency target allocation. Firstly, a dynamic calculation approach in K value for unsupervised clustering and time factor’s lead-in for Market-Based Mechanism (MBM) method was created to resolve potential target deadlock among USVs. Secondly, we proposed a novel construction strategy in a non-complete graph (NCG) consisting of neighborhood connection and pheromone extension to provide enough feasible nodes for solution searching. Finally, we introduced adjustment of search range and edge weights, and activated node interaction in traditional Ant Colony Optimization (ACO) algorithm in NCG to obtain the optimal combination of each USV’s target allocations. We established a simulation platform with an airborne managing base station and several USVs. The experimental results demonstrated that when the number of USVs was four, the average time for all USVs to reach the target in the RECO method reduced by 10.9% and 7.7% compared to the MBM and ACO methods, respectively. This reduction was 25% and 11.6% for 6 USVs, 25.7% and 21.8% for 8 USVs, 20% and 19% for 10 USVs. It reflects that the proposed RECO allocation method has shown improvements in terms of successfully-assigned USVs’ quantity and operational efficiency, compared to the state-of-art MBM and ACO algorithms.

1. Introduction

Defending border islands has always been a significant issue in the realm of national defense, complicated by environmental conditions that hinder the long-term stationing of military forces. Consequently, implementing an intelligent defense and patrol system comprising unmanned surface vessel (USV) swarms and airborne surveillance bases emerges as a feasible solution. When multiple USVs need to efficiently execute a specific system-level target, the first question is when to assign what target to which USV. The process of decomposing a system-level target into several sub-targets and then assigning them to each agent is called multi-agent target allocation. Its simulation scene with USV clusters is depicted in Figure 1. Each USV will spend a certain amount of resources and time to complete the target, and the cost of completing the target by the USVs is called the total cost of the USV system. The goal of multi-USV target allocation is to minimize the total cost of the entire USV system while completing all targets. This issue belongs to a typical NP-hard problem, and as the number of USVs and targets in the system grows, the number of possible target allocation solutions increases exponentially, posing a severe challenge to finding an optimal solution [1].

There are several methodologies employed in multi-agent target allocation. We can categorize them into four mainstream types:

(1)

Behavior-based method;

(2)

Greedy-based method;

(3)

Idle chain method;

(4)

Learning-based method.

Next, we will describe the existing research results and characteristics of the above four methods in paragraphs.

One approach to multi-agent target allocation is based on behaviors, which are patterns of responses to specific stimuli that are embedded in the agents [2]. When a behavior is activated, it motivates the agent to perform a specific action. A typical example of this approach is the behavior-based, fault-tolerant, distributed cooperative framework ALLIANCE proposed by Parker in 1995 [3]. A parameter learning framework, L-ALLIANCE, was later proposed based on ALLIANCE [4]. Another behavior-based approach is the Broadcast of Local Eligibility (BLE) method proposed by Werger [5], in which agents broadcast their eligibility for a target and prevent unqualified peers from participating. This method is easy to implement and particularly suitable for scenarios with weak communication capabilities and limited bandwidth. However, the efficiency of target allocation in this method is low, and some sensor elements are required. Additionally, Carrillo proposed a multi-agent meta-reasoning method that can select target allocation algorithms to use based on changes in communication quality levels [6]. Zhou focused on addressing the computational complexity of global search in multi-agent target allocation and the optimality of solutions in local search. They proposed the D-NSGA3 method, which combines multi-objective evolutionary algorithms with greedy algorithms to ensure search capability and solution diversity [7]. Karami achieved target decomposition and allocation by maximizing the composite utility function, with targets being executed by an integrated target and motion planner that is robust to unknown numbers of re-planning targets [8]. Aziz considered the natural computational problem of allocating agents to maximize the number of targets completed under a budget constraint. They provided a detailed approximation result, including general and important constraint settings, and complexity analysis of the polynomial-time algorithm [9]. Soleimanpour used Newton’s law of gravity to make the target point exert gravity on the agents and change their positions in the search space. They also designed a control parameter to achieve a clear balance between exploration and exploitation [10]. Zitouni formalized the target allocation problem in multi-agent systems from a set-theoretic perspective, which helps researchers understand the nature and time complexity of the problem and develop effective solutions. The allocation results are significantly influenced by the choice of allocation criteria [11].

Another approach to multi-agent target allocation is the greedy-based method. The characteristic of this approach is that it prioritizes the best choice in each step of execution, while ignoring the overall solution. Therefore, its direct drawback is the tendency to fall into local optima, with a representative method being auction-based strategies, which has its roots in the fundamental idea proposed in 1981 [12]. Researchers in robotics use auction-based coordination systems because of their robustness and effectiveness. Markets and prices allow modern economists to allocate resources among competitors [13]. Many real-world robot applications use auction-based methods, such as distributed mapping [14,15], secure sweeping [16], multi-robot path planning [17,18], and even collaborative timed targets within limited communication range. Alshaboti investigated the performance of two commonly-used approaches, auction-based and threshold-based, in multi-objective dynamic target allocation scenarios. They demonstrated that the auction-based method using a fuzzy inference system outperformed the adaptive threshold-based method in terms of load balancing, while the adaptive threshold-based method achieved better results in terms of travel distance [19]. The main advantage of auction-based methods is their simplicity and the fact that they allow for decentralized application on real robots. Each robot locally computes its own value and broadcasts it to other robots while accepting broadcasts from other robots. There is no central auctioneer in the system, so no single robot fails.

The Idle Chain Method (ICM) was first proposed by the sociologist White in 1970 [20] and was initially used to explore the evolution of biological tissue structures. Later, Chase identified it as a new mechanism for resource allocation among animals [21]. For MRS, when an idle robot appears in the group or an unassigned target appears in the environment, this robot or target must be reassigned. When this gap is filled, a new gap appears in the system, creating an idle chain that drives the entire system to achieve dynamic reallocation. Dahl used the ICM in dynamic multi-agent target allocation and combined it with distributed reinforcement learning to achieve optimal allocation of the entire system [22].

As MRS continues to evolve, research has increasingly focused on high dynamics and large-scale unknown environments. Therefore, algorithm designers cannot predict all possible states that agents may encounter and pre-design corresponding behaviors. Heuristic methods have been widely utilized in MRS target allocation, especially Ant Colony Optimization (ACO) algorithm. Qizilbash constructed a multi-robot planner for combined task allocation and path finding based on ACO for pick-up and drop-off tasks in industrial warehouse applications [23]. Yan proposed an improved ACO algorithm based on fuzzy logic and a dynamic pheromone volatilization rule is developed to solve the TSP-typed task assignment problem with specific and distinct starting and ending points [24]. Xue carried out an exact algorithm to minimize the max task time and reduce the total task time based on the Hungarian algorithm and ACO to enhance the system’s effectiveness and practicability [25]. Besides that, reinforcement learning algorithms, especially Q-learning, have been a novel method in MRS with unknown, dynamic, and large-scale environments due to their simplicity and excellent real-time performance. Kapetanakis developed two learning methods for multi-agent systems called multiple single-agent learning and social multi-agent learning, with the key difference being whether teammates’ knowledge is used in learning [26]. Kovac used reinforcement learning to solve a box-pushing problem in MRS [27]. Taylor proposed a method for transferring learned knowledge from one target to another with a different state space to reduce training time [28]. Chuang proposed a new method using Bayesian Networks to handle multi-agent target allocation problems and effectively solve search and rescue targets in centralized, decentralized, and distributed systems composed of multiple low-cost agents in dynamic environments [29].

However, a persistent challenge in multi-USV target allocation is that the problem belongs to the NP-hard class. The initial allocation of target points for each USV is entirely unrestricted, and the allocation schemes are flexible and diverse, necessitating intelligent dynamic allocation methods to rapidly identify suitable multi-USV target allocation strategies. In a single allocation cycle, two primary objectives must be achieved: (1) minimizing the total operational distance for all USVs, and (2) minimizing the variance in the operational distances of individual USVs. This is done to maximize the coverage of the collaborative defense system during each cycle and to minimize conflicts generated after the path planning. Given the nature of the problem being addressed, which involves multi-variable optimization, and considering the real-time requirements of multi-USV target allocation in specific environments such as island defense, among the existing four major classes of methods, the greedy-based approach is relatively more suitable for this study. However, since the objective is to achieve global optimization, traditional greedy algorithms, which primarily focus on achieving local optima at each step, need to be further improved to fulfill the intended goals of this study.

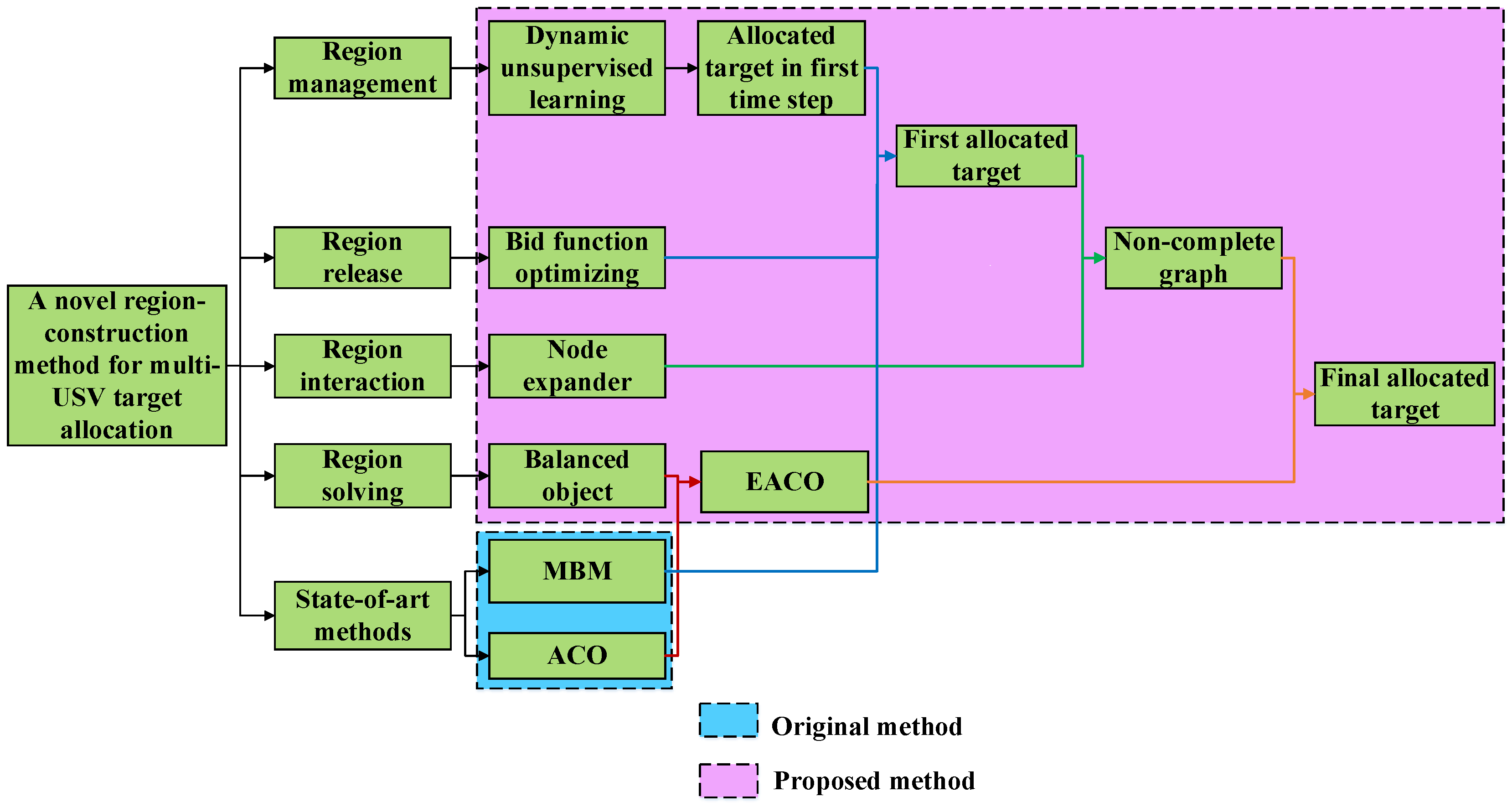
To address the above issues, this paper presented a multi-USV target allocation strategy based on Regional-Construction (RECO), aimed at improving the traditional Marked-Based Mechanism (MBM) method which belongs to greedy-based method. The strategy consists of four aspects: (1) utilizing dynamic unsupervised clustering algorithms to enable USVs to reach distant target points at the initial moment, achieving regional management and reducing potential target deadlock in the initial state; (2) optimizing the bidding function in MBM method by incorporating a target deadlock resolution time factor, facilitating regional release for idle USVs prone and decreasing potential target deadlock during operation; (3) connecting the target sequences generated by USVs under the optimized MBM method sequentially according to the nearest neighbor method, expanding the available target options, and forming a significantly reduced Multiple Traveling Salesman Problem (M-TSP) compared to the complete graph sequence; (4) employing an Extended Ant Colony Optimization (EACO) algorithm for solving the final target sequences of each USV, alleviating the immense algorithmic complexity of the NP-hard problem and establishing interactions between multiple USVs.

The structure of this paper follows a coherent outline. Firstly, it presents the overall idea and procedural framework, while highlighting the problem the paper aims to address. Subsequently, representative conventional methods for multi-USV target allocation are introduced, exposing their two specific limitations, thereby laying the groundwork for proposing improvement strategies. Next, a Region-Construction approach is proposed to tackle the identified limitations, encompassing four sub-solutions: region management, region release, region interaction, and region solving. Each sub-solution is described in a separate section, emphasizing their innovative processes and originality. Following this, a simulation platform is constructed to conduct experiments, including two categories of tests: one to evaluate the effectiveness of the proposed method in resolving the aforementioned limitations, and another to compare the specific performance of the proposed method with two traditional methods. Finally, a comprehensive analysis and summary are provided, discussing the proposed method and the experimental results.

The innovations and benefits of this paper can be summarized as follows:

(1)

In the context of greedy-based methods, which often focus on achieving optimal substructures without comprehensive discussions on global and categorical aspects, we introduce the concept of regional discourse to address the target allocation problem. We propose a comprehensive and systematic process of region evolution consisting of four interconnected modules. This approach allows the greedy algorithm to leverage its advantages while significantly reducing the likelihood of falling into local optima;

(2)

In clustering-based methods, the formation of clusters is typically based on static patterns, and feasible solutions between different clusters are considered independently. Consequently, when an agent completes its tasks within a cluster, it becomes challenging to account for the completion of tasks in other clusters. Moreover, when the performance of individual agents varies, it becomes difficult to timely adjust or release cluster-bound tasks, leading to complex deadlock scenarios. To address this, we introduce dynamic handling strategies in the processes of region formation and resolution. By considering dynamic factors such as the value of K and time, we resolve target deadlocks, enhancing the flexibility of clustering approaches and reducing the variance in performance parameters among different solution sequences, thereby improving the overall optimality of clustering methods;

(3)

In graph theory-based searching, solving the problem on a complete graph is more likely to yield global optimal solutions, but it comes at the cost of increased computational complexity. On the other hand, solving the problem on an incomplete graph is faster, but it may overlook optimal solutions in the solution space. To address this trade-off, we propose strategies of neighbor connection and information pheromone expansion in constructing incomplete graphs, incorporating the concept of interaction. This approach allows for both fast search capability and sufficient necessary node connections in the constructed incomplete graph, facilitating the search for optimal solutions.

To summarize, the primary issues addressed by the proposed approach are: (1) overcoming the target deadlock phenomenon in the initial state of USVs resulting from the traditional MBM’s selection of the optimal bid in each round; (2) overcoming the target deadlock phenomenon during the intermediate operation of USVs due to the single form of the bidding function in the traditional MBM; and (3) overcoming the locally optimal feasible solutions generated by the round-by-round bidding competition in the traditional MBM. By effectively addressing these three phenomena, our system enhances the operational efficiency of multi-USV collaborative systems under a single batch of target sequences through a more rational target allocation scheme.

2. Materials and Methods

2.1. General Idea of This Paper

An overall flow chart of this paper is shown in Figure 2, and the process of the proposed RECO method is shown in Figure 3. This paper studied and implemented a multi-USV target allocation method suitable for patrolling and defense near border islands. The market-based mechanism method based on bidding and auctioning principles serves as the foundation for this approach, which is improved by proposing a Region-Construction (RECO) method. The paper first introduced the traditional market-based mechanism method, then expounded on the proposed improvement method, which is divided into four components named region management, region release, region interaction and region solving, respectively. For the regional management module, a dynamic unsupervised clustering algorithm was employed to overcome potential target deadlock at the USVs’ initial positions; for the regional release module, an optimized bidding function incorporating a waiting time factor was utilized to address potential target deadlock in the middle positions of USVs; for the regional interaction module, a strategy for constructing an non-complete graph under the M-TSP problem was proposed; for the regional solving module, an Extended Ant Colony Optimization (EACO) algorithm was used to obtain the relative optimal solution, reducing the variance of execution times for each USV and overcoming potential local optimality in execution times. Relevant simulation experiments demonstrated that the adopted improvement method successfully increases the number of available USVs and target execution efficiency within a single batch of targets. Combined with an efficient information exchange system for multiple USVs, this paper provides a solution for efficient patrolling of targets by USVs in unmanned border defense scenarios.

2.2. Traditional Market-Based Machnisum Method for Multi-USV Target Allocation

2.2.1. Process Analysis

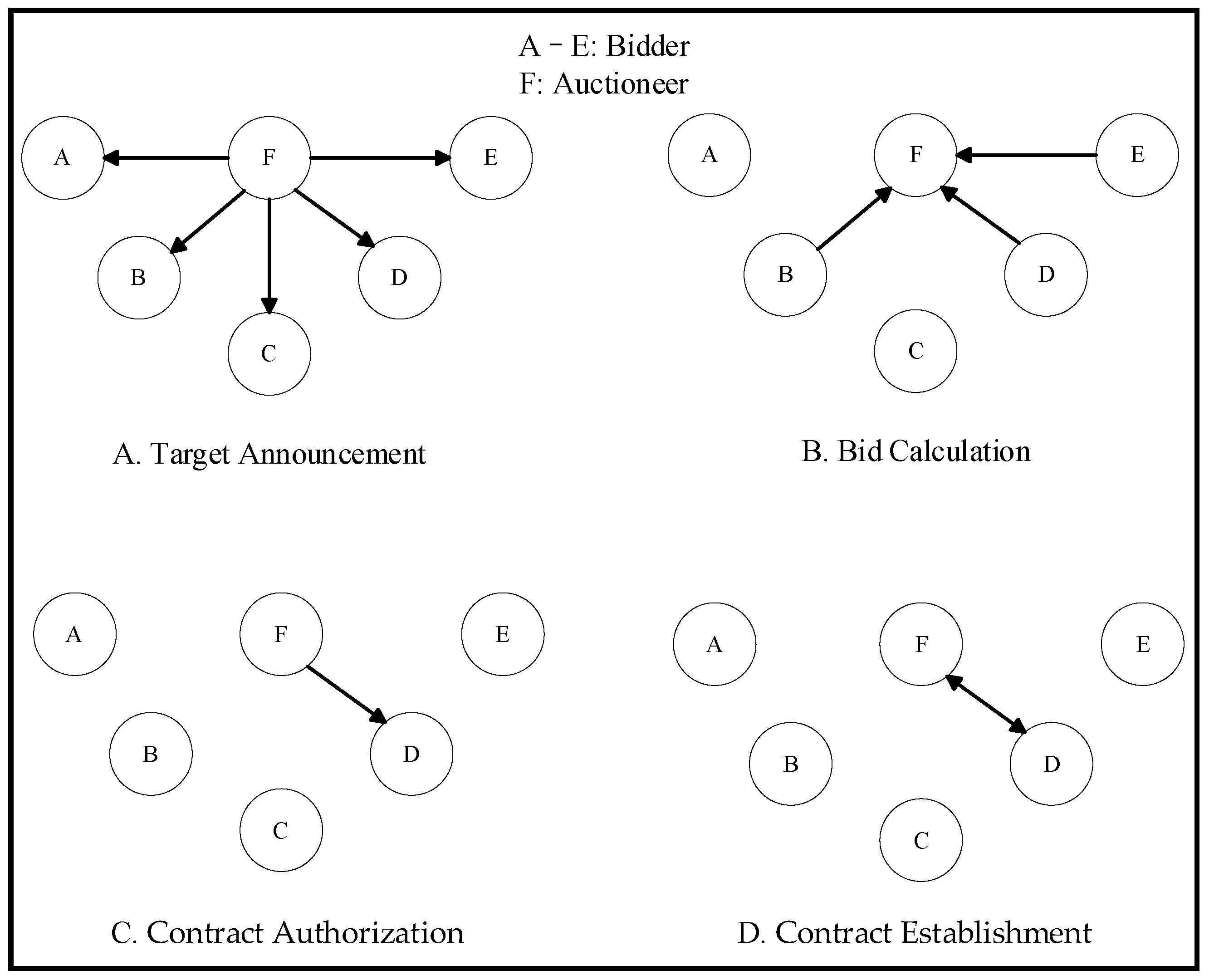
In the target allocation process for USVs, traditional Market-Based Mechanism (MBM) methods rely on bidding and auctioning based on the resources and time required for USVs to reach their assigned targets [30]. In large-scale environments, this allocation process primarily consists of four steps: target announcement, bid calculation, contract authorization, and contract establishment, as illustrated in Figure 4.

The following sections detail the specific workflow of multi-USV target allocation based on traditional MBM, including target announcement, bid calculation, contract authorization, and contract establishment.

Target Announcement: The “auctioneer” is the central computer in a multi-USV system that receives and records target information transmitted by individual USVs during the assignment process. If a USV discovers and reports an unassigned target, the auctioneer broadcasts the target information to all USVs. The broadcasted information includes target location and the deadline for bidding, among other details.

Bid Calculation: Upon receiving target information from the central computer, USVs first determine whether the target location is within their map. If the target point is in the map and the USV can plan a feasible route to the target location, it calculates the cost of the route in terms of resources and time consumption. This cost is then submitted as a “bid price” to the central computer via point-to-point communication, which primarily includes the USV’s information and the cost to reach the target point.

Contract Authorization: After broadcasting the target information, the central computer enters a waiting stage, recording bids from participating USVs. Once the bidding time expires, the central computer stops receiving bids and compares the submitted bid values, selecting the USV with the lowest cost as the winner of the auction and sending a request to establish a contract.

Contract Establishment: The winning USV and the central computer confirm the auction contract, and the USV adds the successfully bid target point to its subsequent execution sequence. It is important to note that during the contract establishment process, if a USV cannot plan a feasible route to the target point due to external environment changes, it needs to cancel the contract with the central computer. Upon receiving the contract cancellation request from the USV, the central computer stops contract establishment and rebroadcasts the information of the unassigned target point, seeking a suitable USV to perform the target.

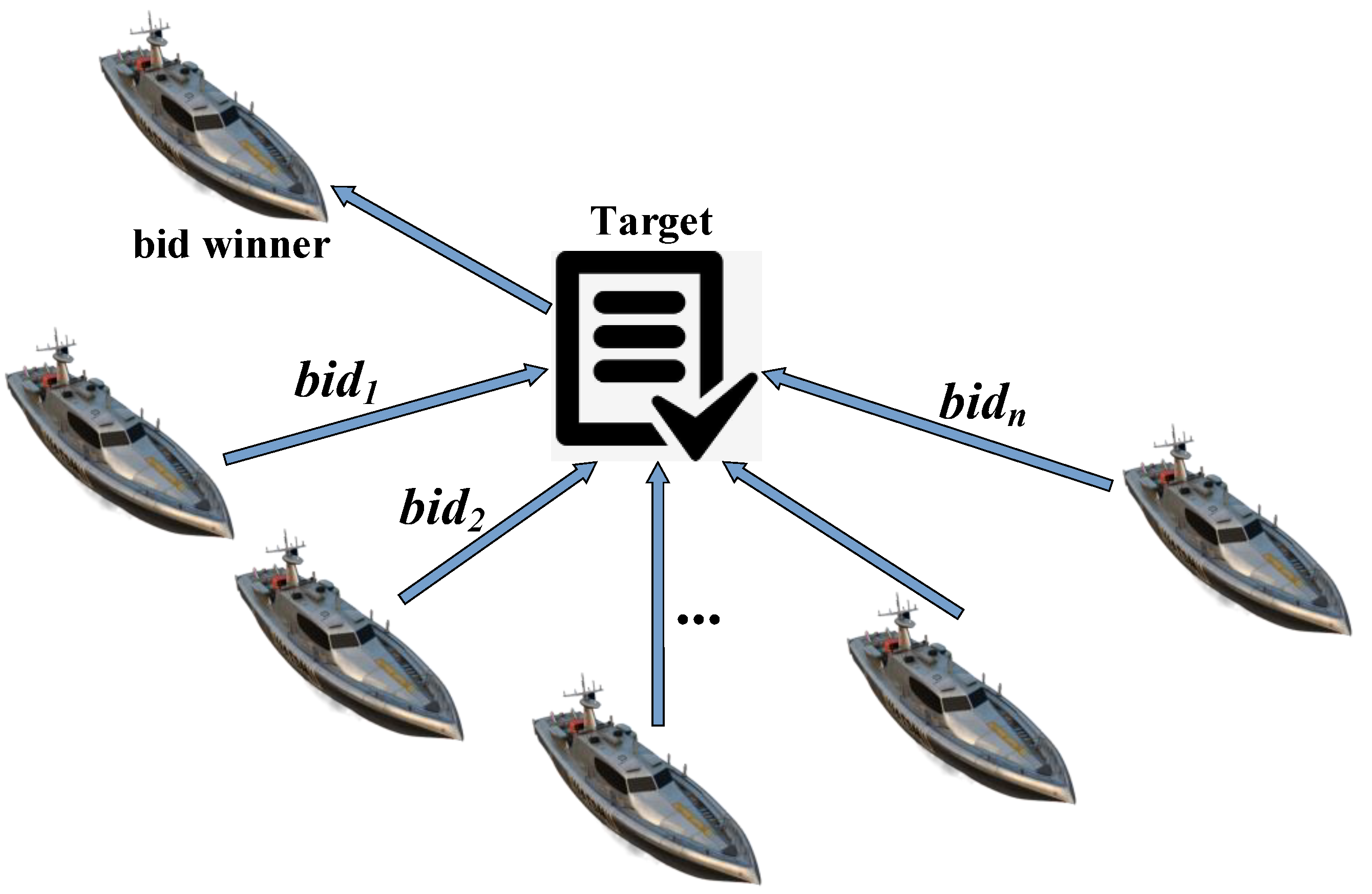
The operational principle of target allocation based on MBM for multi-USV collaborative systems is illustrated in Figure 5. For the same target point, all USVs submit bids, with the bid value of the nth USV denoted as $bi{d}_n$. The USV with the minimum bid value $\min bid=\min (bi{d}_1,bi{d}_2,\cdots ,bi{d}_n)$ is declared the winner and is assigned the target point.

2.2.2. Algorithm Description and Allocation Pattern Analysis

In a USV system, the information considered includes the positions of various target points, target locations, USV positions, and travel costs that reflect the relative relationships between target points. The goals that a multi-USV collaborative system aims to achieve is determined by the awarded target in a new auction round. In multi-USV systems, there are typically three system objectives:

(1)

MINISUM: Maximize the total travel cost for all USVs;

(2)

MINIMAX: Minimize the maximum travel cost among all USVs;

(3)

MINIAVE: Minimize the average travel cost for all USVs.

The travel cost for a single USV refers to the total distance traveled along its planned route, starting from its initial position and sequentially reaching each target point. As the cost of a single USV performing a target depends on the targets already completed, each USV must consider the targets assigned to it in previous rounds when a new auction begins. In traditional MBM target allocation strategies, the MINISUM system objective is typically employed to measure travel costs. 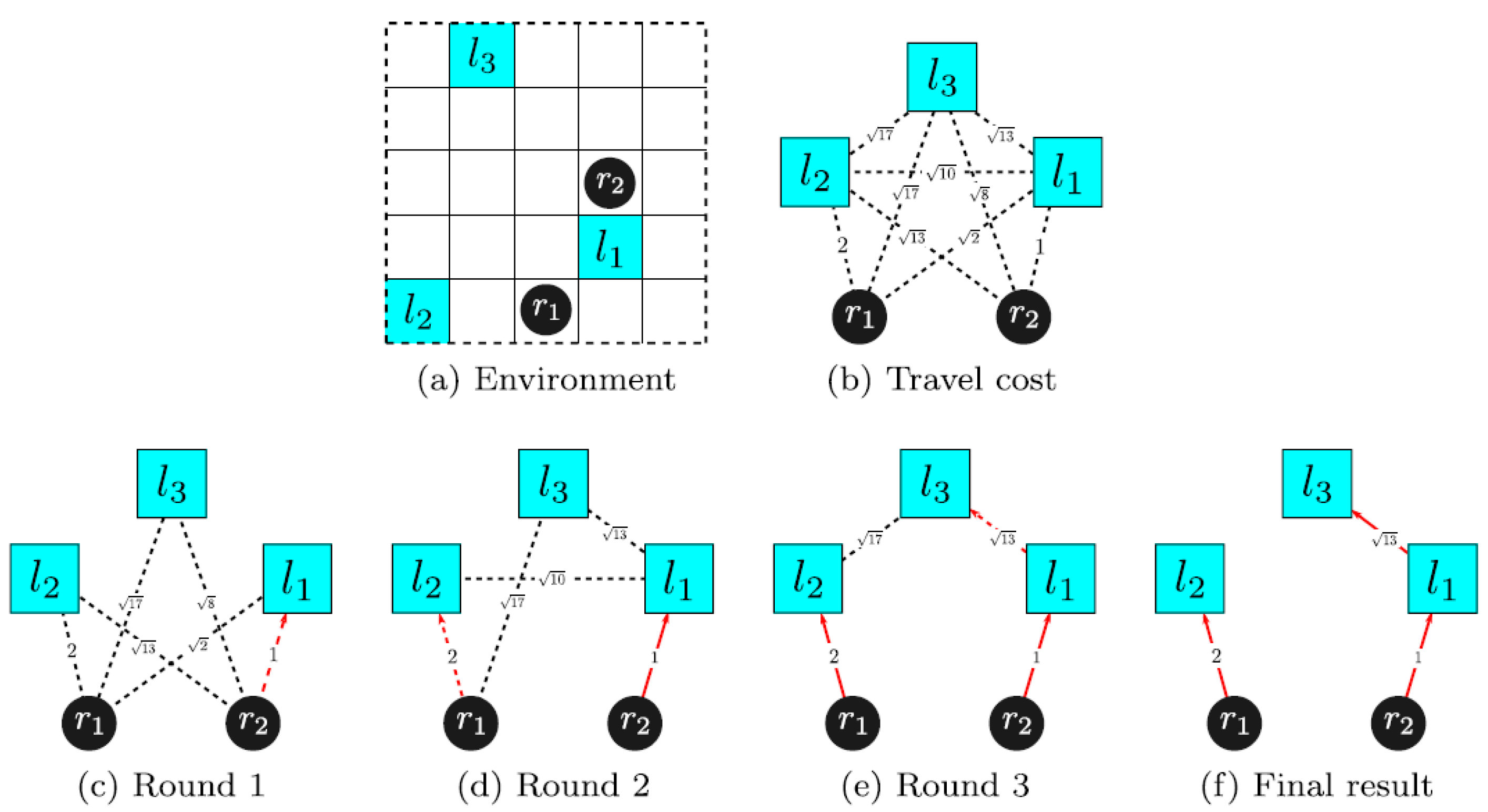Figure 6 demonstrates how the MINISUM objective is used for target awarding and allocation.

Figure 6a illustrates a local environment with three target points $\{l_1,l_2,l_3\}$ and two USVs $\{r_1,r_2\}$. The three target points will be allocated to the two USVs following the MINISUM rule. Each USV estimates its travel cost by calculating the distances to the target points. In the first round, USV $r_1$ offers the lowest travel cost of $\sqrt{2}$ for target point $l_1$, a travel cost of 2 for $l_2$, and a travel cost of $\sqrt{17}$ for $l_3$. Meanwhile, USV $r_2$ offers a lower travel cost of 1 for $l_1$ compared to $r_1$. Consequently, target point $l_1$ is successfully allocated to USV $r_2$.

In the second round, although $r_2$ has not moved to the target point execution area, the next bid value for the other targets depends on the already allocated target point $l_1$. The travel cost from $r_1$ to $l_2$ is 2, and from $r_1$ to $l_3$ is $\sqrt{17}$, resulting in a bid of 2 from $r_1$ for $l_2$. Additionally, $r_2$’s bid for $l_2$ is less than $\sqrt{10}$. Therefore, $r_1$ wins the second round of bidding and is assigned target point $l_2$. In the third round, only target point $l_3$ remains unassigned in this environment, and the bids from $r_1$ and $r_2$ for this target point are $\sqrt{17}$ and $\sqrt{13}$, respectively. As a result, $r_2$ secures the final target point, $l_3$, with a relatively lower bid. At this point, all target points in the environment have been successfully allocated. If $T^i$ represents the target point assigned in round $i$, then in this environment, $T^1=\left\{l_2\right\}$, $T^2=\{l_1,l_3\}$. According to the MINISUM objective, the cost estimate for USV $r_i$ with respect to target $l_j$ is obtained using Equation (1), where $last(T^i)$ represents the most recent target point $l$ assigned to USV $r_i$ and $U$ represents the current sequence of unassigned targets.

$$cost(i,j)=dis(last(T^i),l_j)\begin{array}{cc}& l_j\in U\end{array}$$

(1)

In summary, the pseudocode for multi-USV target allocation based on the traditional MBM (Algorithm 1) is shown in Algorithm 1. Algorithm 1 describes the entire process from bidding and reordering to execution. Firstly, each USV updates the entire environment by communicating with each other, gaining an understanding of the targets that have not yet been assigned. Then, each USV will bid for unallocated targets based on the MINISUM team objective, and the USV with the lowest cost will win the target, subsequently adjusting the execution order of the targets.

Algorithm 1: Traditional MBM method

Input: The target locations $L=\{l_1,l_2,\cdots ,l_m\}$ with targets $O=\{o_1,o_2,\cdots ,o_n\}$ 1 Initialize the environment 2 while there are still unreachable targets in the environment do 3  Update $U$: the set of currently unreachable targets 4  if $U\ne \varnothing$ then 5   for $l_j\in U$ do estimate $cost(i,j)=dis(last(T^i),l_j)$ 6   Bid for the $\overline{l}$ with the smallest travel cost 7   if $r_i=\arg \underset{r_i\in R}{\min }dis(last(T^i),\overline{l})$ then 8    Update $T^i=T^i\cup \left\{\overline{l}\right\}$ and $U=U\backslash \left\{\overline{l}\right\}$ 9    Reorder $T^i\to {\widehat{T}}^i$ 10   end 11  end 12  if ${\widehat{T}}^i\ne \varnothing$ then 13   Go to explore the first indexed location $l^{\ast }$ in ${\widehat{T}}^i$ 14   if USV $r_i$ visits the location then 15    Update ${\widehat{T}}^i\ne {\widehat{T}}^i\backslash \{l^{\ast }\}$ 16    if find a target o then update $U_D=U_D\cup loc(o)$ 17   end 18  end 19 end

2.2.3. Simulation Example and Disadvantage Analysis of Traditional Market-Based Mechanism Method

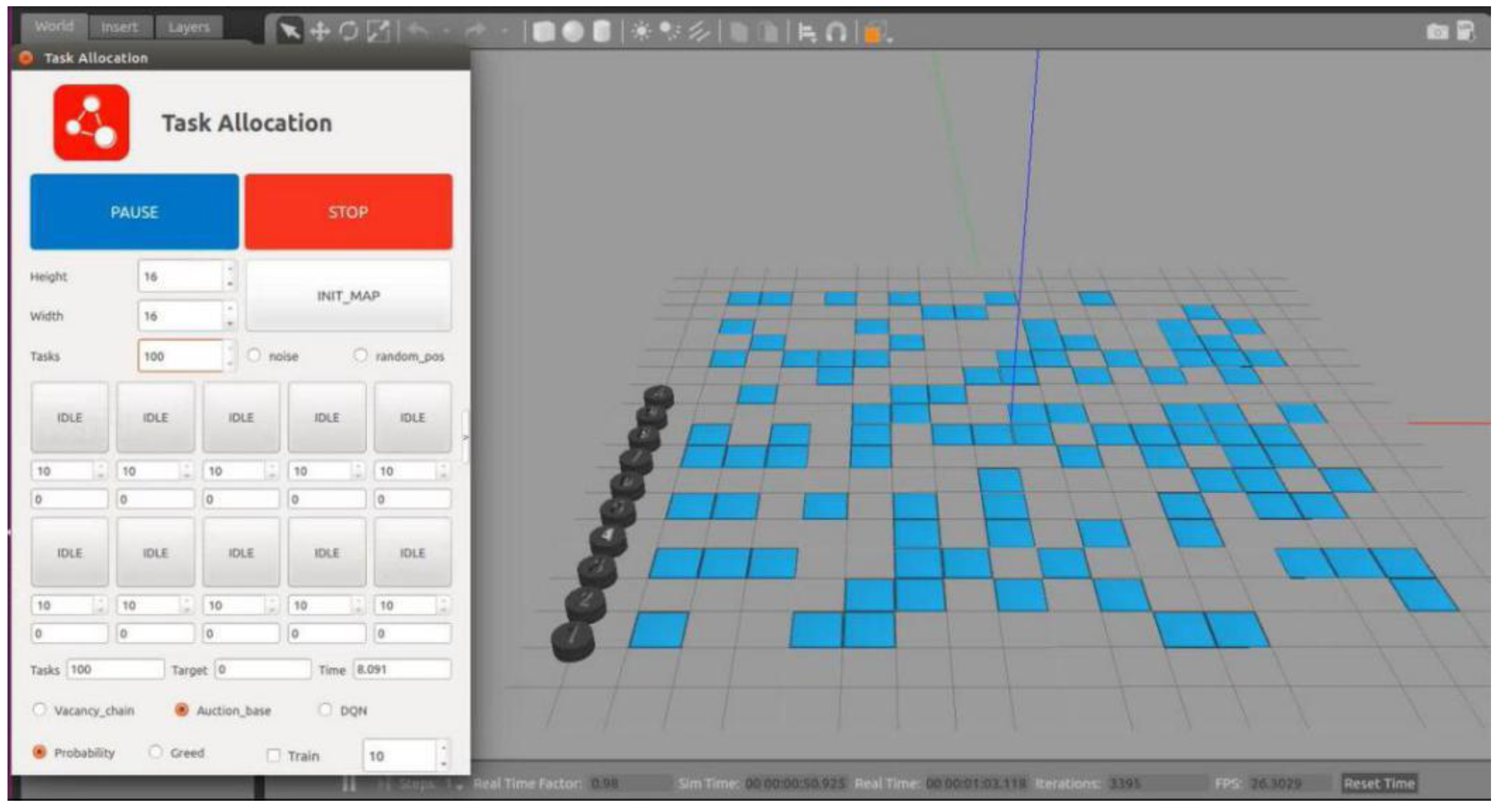
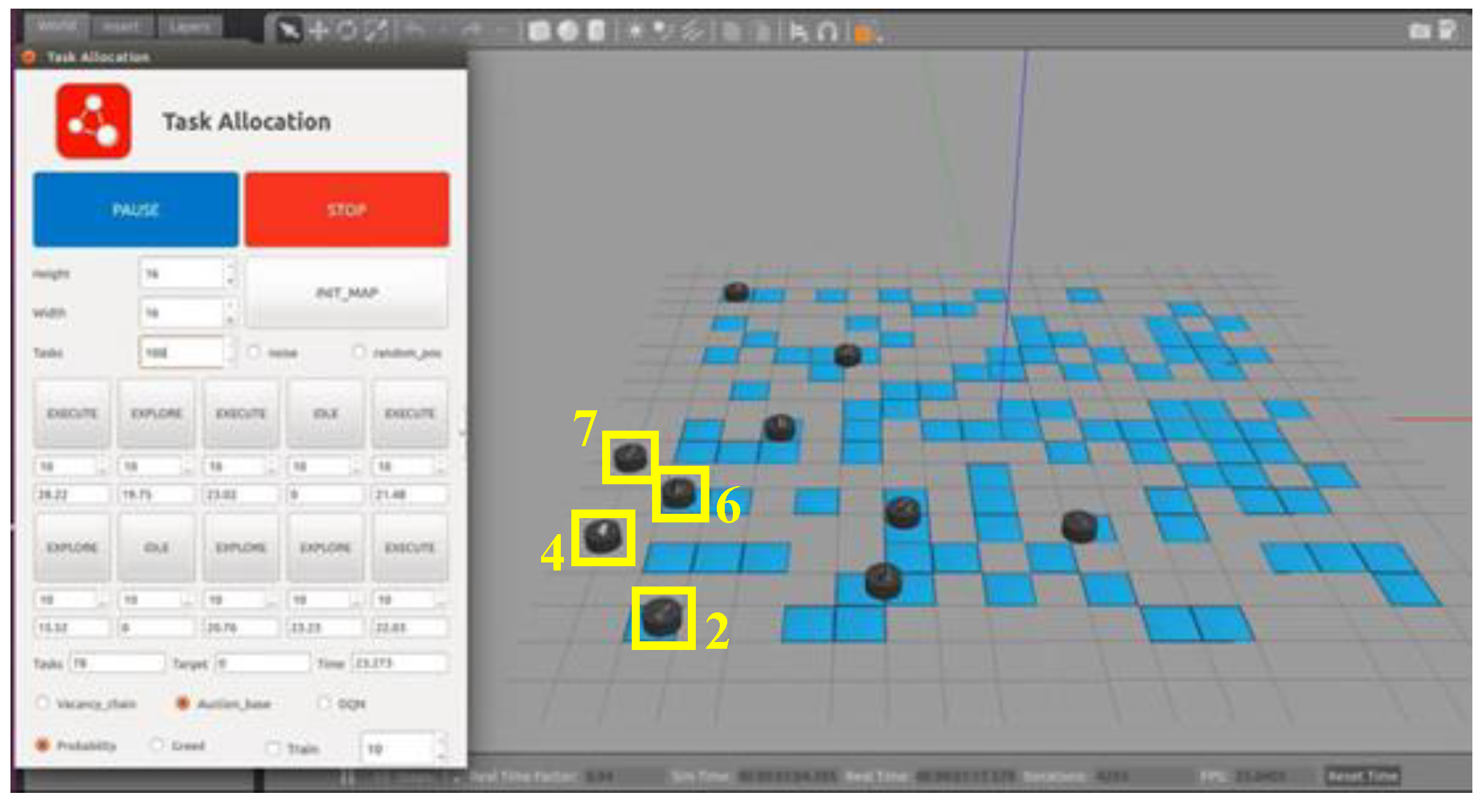
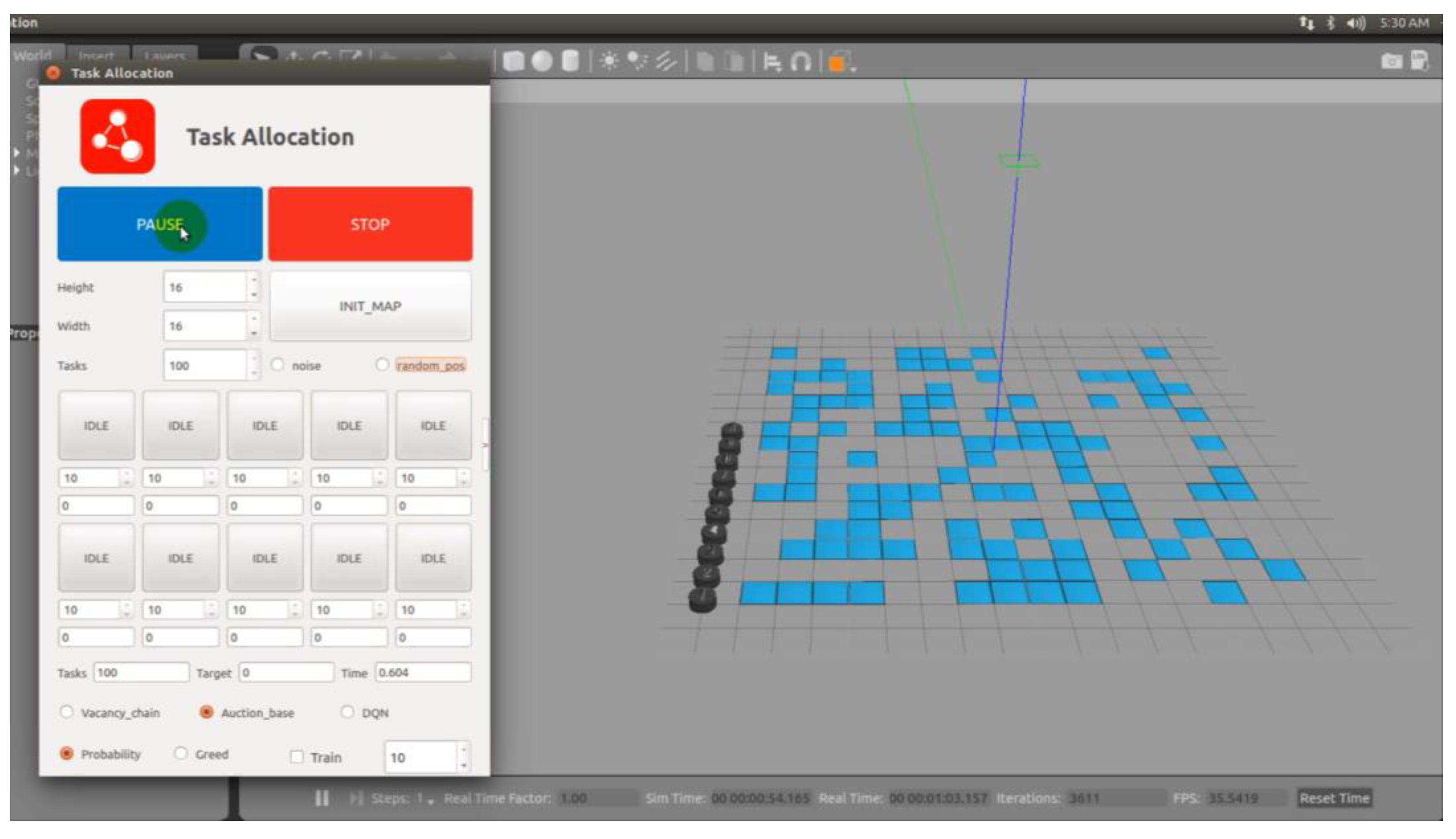
In Robot Operation System (ROS), the traditional MBM is applied to allocate targets for multiple USVs within the Gazebo platform. The simulation environment is shown in Figure 7.

The left side of Figure 7 displays the target allocation control terminal, which allows setting the number of participating USVs, the number of target points, and other relevant parameters. Upon initializing the map, the black discs on the right represent the mobile USVs in the simulation environment, while the blue regions represent the target points that the USVs need to reach and execute in an unknown environment.

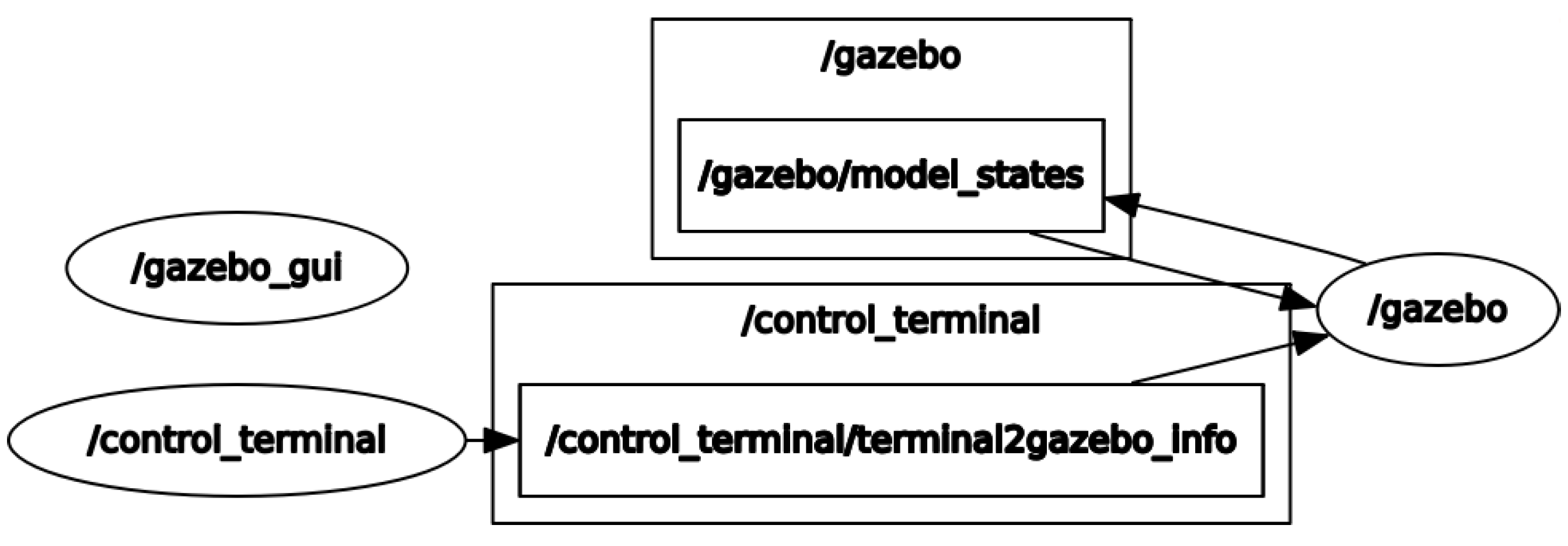
This target allocation system primarily includes five packages: allocation_common, allocation_gazebo, control_terminal, gazebo_description, and task_allocation. Task_allocation is the core of target allocation, while control_terminal is responsible for message publishing and updating the USV states within the Gazebo environment. Allocation_common, allocation_gazebo, and gazebo_description configure the relevant parameters and simulation environment for the target allocation process. The interaction of various nodes and topics after launching the system is shown in Figure 8.

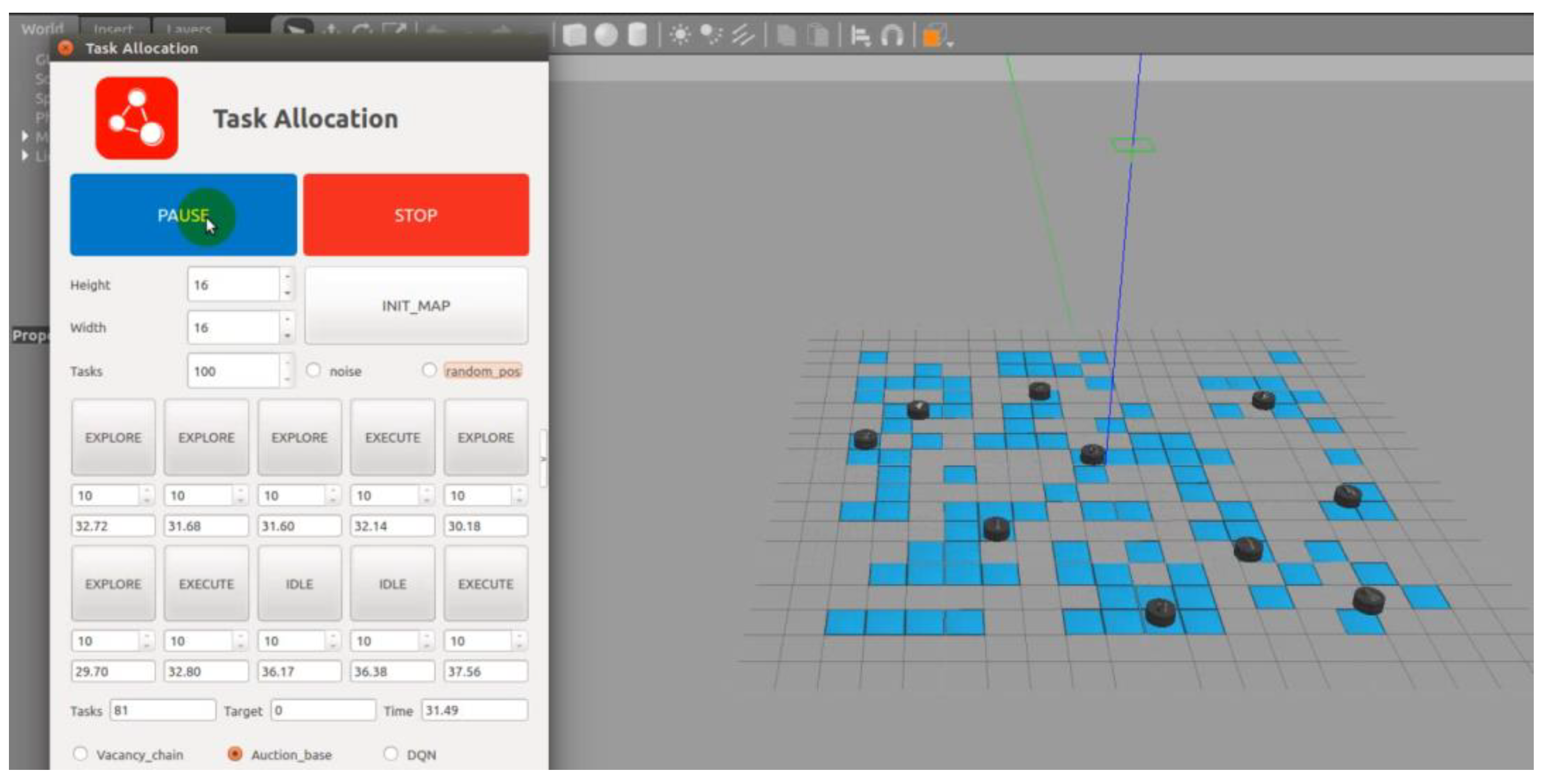
When applying the traditional MBM for target allocation, the distances between all unallocated target points in the scene and each USV are calculated first, identifying the nearest unallocated target point for each USV. Since multiple USVs may find the same nearest target point, the ownership of the target is determined by comparing bids, and the winning USV inserts the target into its target sequence. Once the target is assigned, the USV updates its expected position to the location of the allocated target point and searches for unallocated targets again, proceeding to the next round of bidding and competition.

During the process of target allocation for multiple USVs using the traditional MBM, three major issues were identified, as follows.

(1) Inconsistency in the completion time of target sequences for each USV

Using this algorithm for target allocation, the USVs start bidding for the next target point before reaching their first assigned target. Although this method quickly generates a target sequence for each USV and determines the ownership of all target points, the varying travel distances of each USV and the uneven computational capabilities of their operating nodes lead to a significant difference in the completion times of their respective target sequences. This increases system overhead and reduces overall efficiency. While the issue of node computational capabilities is difficult to improve due to the limitations of computer processing speed, the travel distances of each USV can be optimized, and the variance in execution time can be reduced through planning algorithms.

(2) USVs deadlocked at their initial positions by target allocation

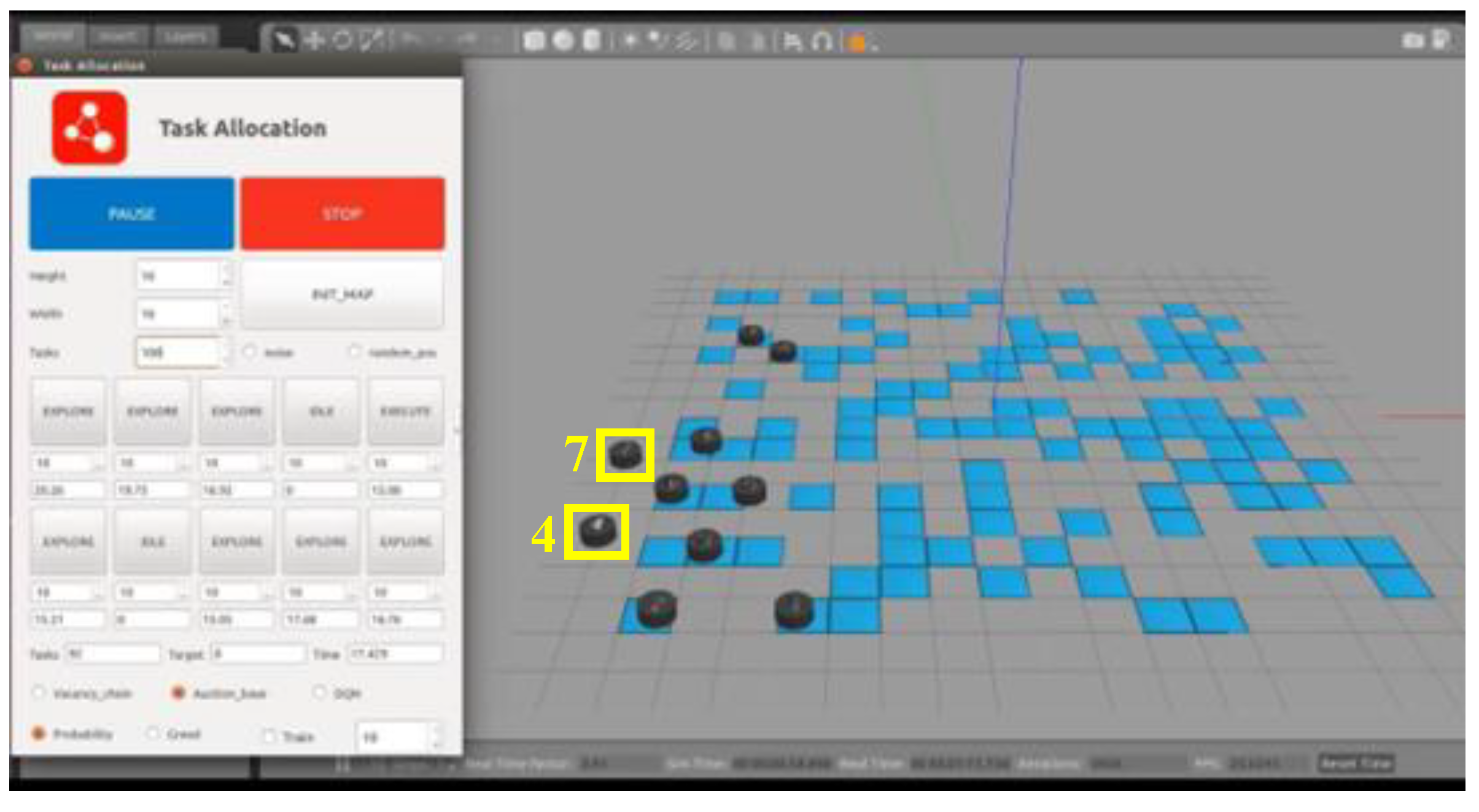
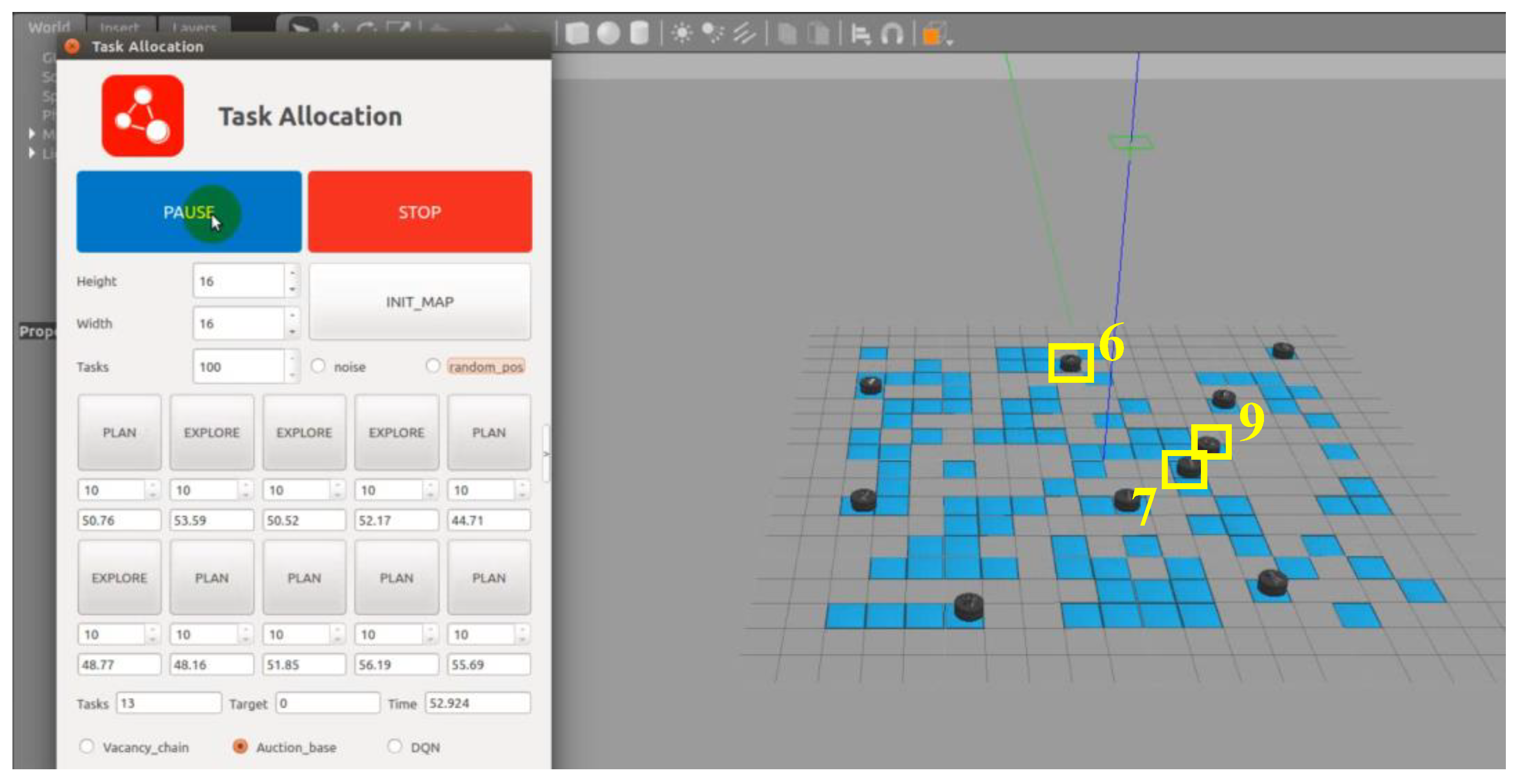
Furthermore, the traditional MBM typically employs distance-related bidding functions, causing some USVs to be deadlocked at their initial positions or during target execution, significantly reducing the efficiency of the multi-USV system. An example is shown in Figure 9. During the first round of the MBM, USVs 4 and 7 remain at their initial positions without winning any bids. Since the traditional bidding function is solely distance-dependent, the initial positions of these two USVs become locked. As they participate in bidding for unallocated targets in the system, their bid values continuously exceed those of other USVs due to the increasing distance from unexecuted target points. Consequently, they fail in each round of bidding, and no targets are successfully assigned to these USVs, even after all targets have been executed by other USVs. This situation is referred to as a USV being deadlocked at its initial position.

(3) USVs deadlocked by target allocation during operation

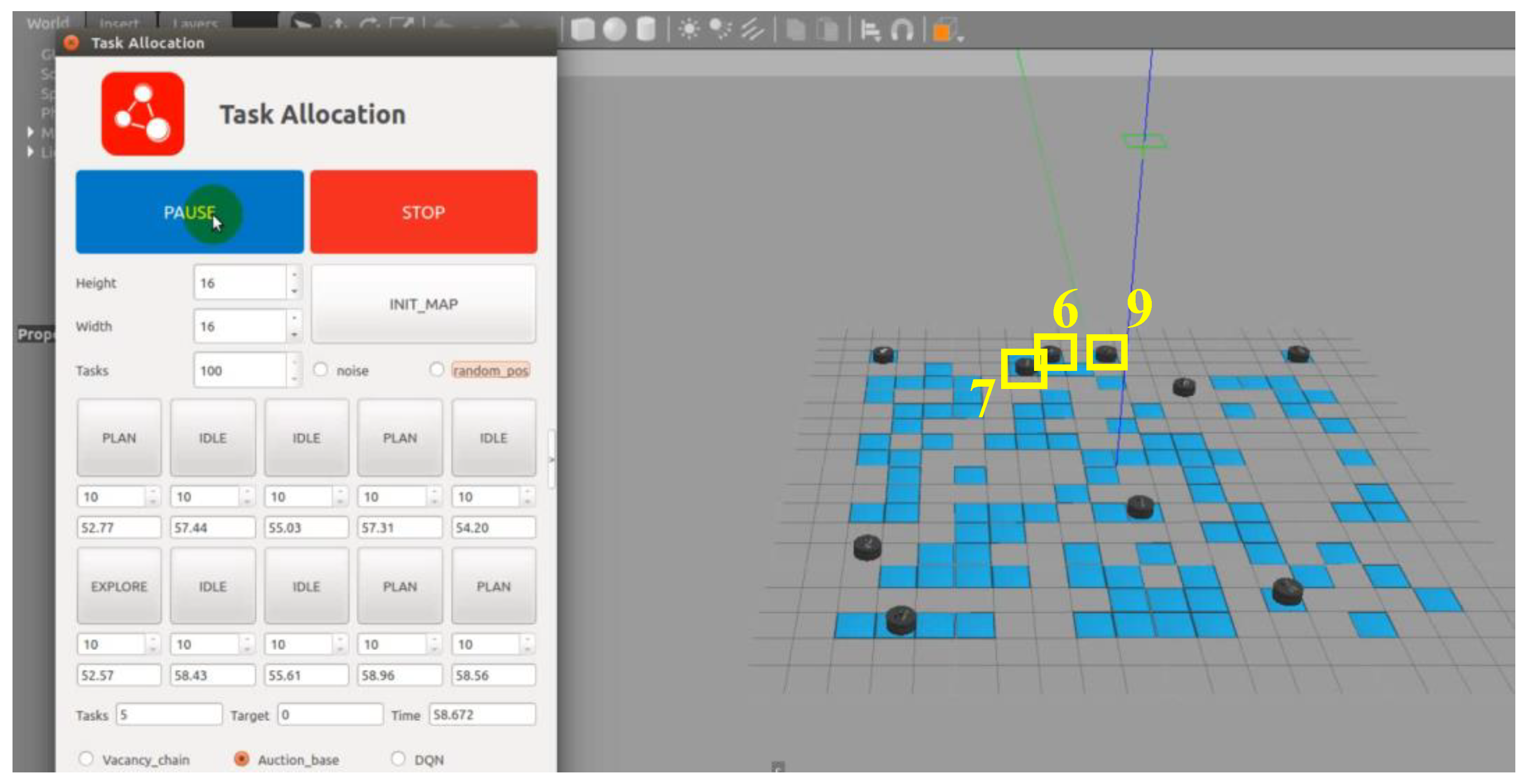
As shown in Figure 10, although USVs 2 and 6 are initially assigned targets, they become “stranded” at their target points and fail to win bids for unallocated targets on the right side as they reach their targets in a left-to-right manner and lose subsequent bidding rounds against other USVs. As illustrated in Figure 11, aside from USVs 4 and 7 being deadlocked at their initial positions, USVs 1, 2, 6, and 9 are deadlocked during target execution and cannot break free. Theoretically, the more USVs in a multi-USV system, the higher the system efficiency. Initially, the system has ten homogeneous USVs. However, as can be observed from the figure, only four USVs participate in target allocation towards the end, resulting in a system efficiency far below the expected level, with idle USVs never being assigned targets. Therefore, it is necessary to improve the original algorithm strategy to meet the efficiency requirements of multi-USV systems.

2.3. Dynamic Unsupervised Clustering for Region Management

In the initial stages of patrolling USVs, they typically present in single-file or closely arranged formations. Employing traditional MBM alone may result in USVs converging on nearby target areas during their first bidding process to complete patrol and defense targets. This approach neglects more distant target areas and consequently reduces efficiency. To address this issue, we propose incorporating dynamic unsupervised clustering algorithms into the initial phase of target assignment. This allows the vessels to promptly and smoothly reach more distant target locations from their starting positions, ensuring rapid coverage of target-related areas while preventing two scenarios: (1) the occurrence of target deadlock at the initial positions, which is the primary phenomenon aimed to circumvent; and (2) a tendency for closely located vessels to participate in bidding for mostly identical targets, resulting in local optima.

K-means clustering is one of the most representative algorithms in unsupervised clustering that employs the iterative approach. However, the traditional K-means clustering algorithm suffers from two major drawbacks, namely, the difficulty of determining the appropriate K value and the dependency for convergence on the initialization of cluster centers. To address these issues, we propose an improved dynamic unsupervised clustering algorithm, specifically designed for the initial step of multi-USV target allocation. The algorithm can be divided into four steps as follows:

Step 1:

The central base station receives initial GPS locations from all USVs. Establish a coordinate system with the target point in the lower-left corner as the origin, convert the absolute GPS positions of all USVs into relative coordinates through coordinate transformation, and take the coordinate positions of each target point as input. Determine the dynamic K-value based on the number of targets, the number of USVs, and target complexity. Employ heuristic initialization methods to select K initial target clustering centers.

Step 2:

For any given sample point, compute its distance to the K target clustering centers, incorporating target assignment status as weight. Assign the sample point to the target with the closest center for clustering. Iterate this process n times.

Step 3:

In each iteration, update the centroid of each target’s clustered points utilizing methods such as gradient descent.

Step 4:

After the first three steps, set a corresponding threshold for the K target clustering centers. If the position changes are minimal, it is assumed that a stable state has been achieved, and the iteration is terminated. Different colors can be assigned to distinguish between various clustering blocks and centers.

In comparison to the traditional K-means clustering algorithm, the main improvements of the proposed algorithm lie in three aspects. Firstly, a dynamic K value calculation approach is introduced, which correlates the number of clusters with the number of targets, USVs, and target complexity. Secondly, target allocation information is incorporated as weights when calculating the distance between sample points and cluster centers, optimizing the clustering process. Thirdly, the gradient descent method is employed to update the cluster centers, accelerating the convergence of the algorithm. These three improvements effectively overcome the two major issues of the K-means clustering method.

2.4. Optimization of Objective Function for Region Release

In response to the issue in the original algorithm where USVs with closer distances are unable to bid for corresponding target points due to varying node computational capabilities, an interval execution approach is employed. That is, a USV only begins bidding for the next target point after reaching its current target. In the original algorithm, each USV only bids for the target point closest to itself, while comparing its bid value with those of other USVs for the same target. The closer a USV is to the target point, the smaller its corresponding bid value. The USV with the smallest bid value successfully wins the bid. The bidding function is solely related to the distance between the target point and the USV.

However, since USVs always bid for the target points closest to them, when there is always a USV closer to the target point being bid on, the bidding USV may experience prolonged periods of unsuccessful bidding. This directly leads to multiple USVs being deadlocked during the entire target allocation process, particularly in non-random USV positioning scenarios, significantly reducing system efficiency. Consequently, a proposal is made to consider the time factor in the bidding function by incorporating the deadlock duration of USVs into the bidding function, as illustrated in Equation (2).

$$bid=distance-factor\ast wait\_time$$

(2)

The new bidding function considers not only the distance factor but also the USV deadlock time. The variable ‘$wait\_time$’ represents the time spent from the completion of the USV’s current objective until its participation in the next objective. The longer this time, the lower the bid value for the nearest target point, which gradually increases the likelihood of the USV being assigned to the objective, ultimately resolving the deadlock. The variable ‘$factor$’ represents the weight of the ‘$wait\_time$’ factor, allowing for its adjustment. If there is low tolerance for USV waiting time or a desire to increase the USV’s objective participation within the system, ‘$factor$’ can be increased. Conversely, if the focus is on optimizing the total path traveled by the USV during the entire objective allocation process, ‘$factor$’ can be appropriately reduced.

2.5. Non-Complete Graph Construction for Region Interaction

Among the two aforementioned improvement methods, the clustering algorithm addresses the target deadlock issue during the initial stage of the USVs, while the waiting time optimization bidding function method resolves the target deadlock issue during the operational phase of the USVs. Thus, both improvement algorithms primarily aim to overcome the target deadlock issue, which is easily generated in traditional MBM. However, the multi-USV cooperative target allocation system involves a single invocation of multiple USVs to perform a set of target sequences for continuous patrols. The total time it takes for the entire system to reach the targets depends on the USV with the longest completion time. Therefore, the main objective of this system is to minimize the variance in the total time required for each USV to complete its target sequences, overcoming the local optimum issue that traditional MBM tends to generate.

If only the two improvement methods mentioned above are adopted, the value $wait\_time$ still needs to reach a certain threshold before the USV can resolve the target deadlock. In other words, the total time for each USV to complete its targets is affected by the number of short-term deadlock occurrences, and it still cannot guarantee that the completion times of each USV will be consistent.

In summary, this study proposes a solution strategy for Multiple Traveling Salesman Problem (M-TSP) with non-complete graph (NCG) based on the Extended Ant Colony Optimization (EACO) algorithm, which aims to reduce the variance in the execution time of target sequences for each USV after improving the MBM, and to overcome the local optimum phenomenon inherent in the previous model.

In this improved system, the role of the improved MBM can be summarized as follows: it generates a set of pre-determined target allocation sequences for each USV to choose from and, based on this, partially extends M-TSP Complete Graph problem to M-TSP NCG problem, overcoming the high computational complexity brought about by the NP-hard problem, and significantly improving the system’s computational efficiency.

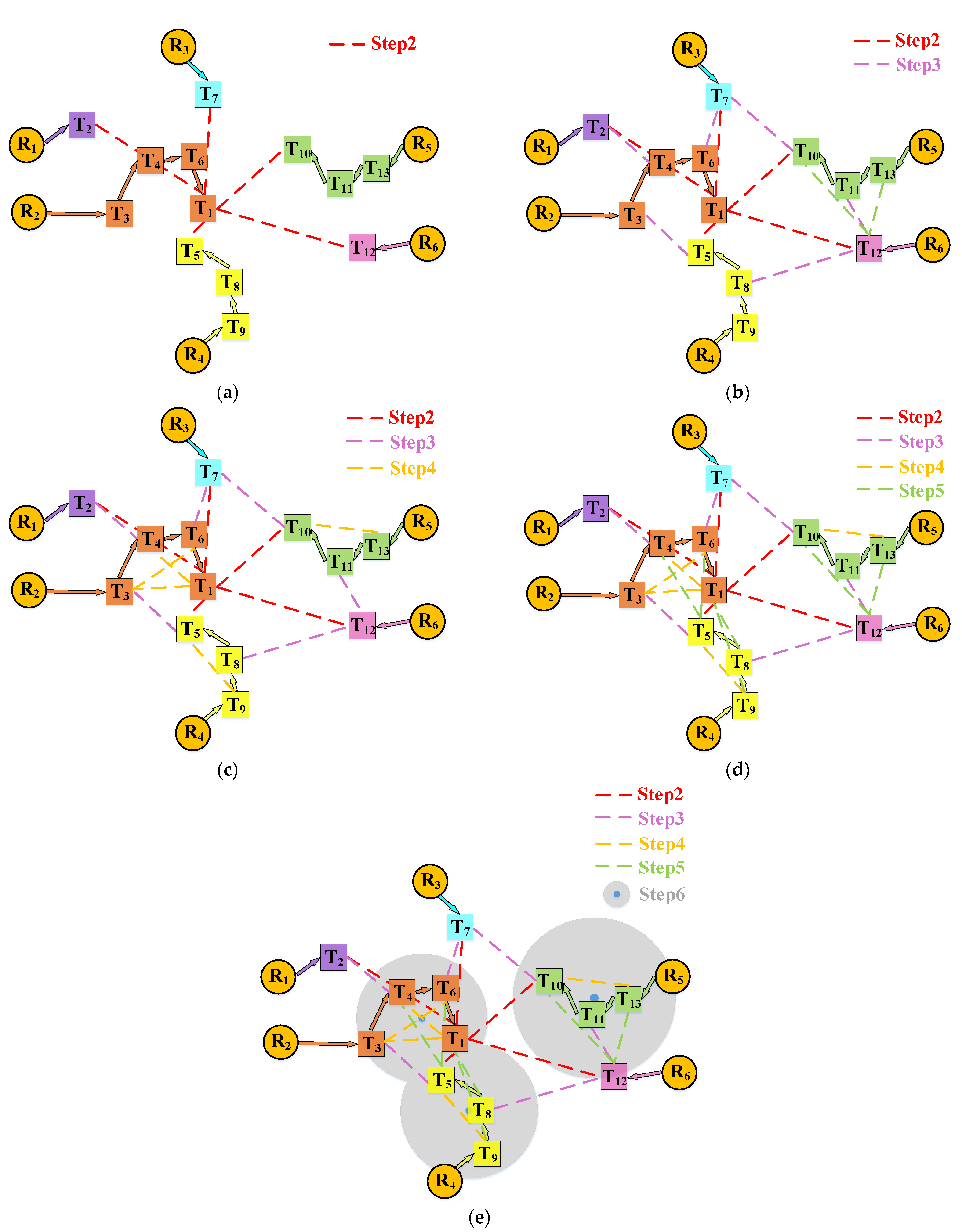
First, an appropriate M-TSP NCG must be constructed. If only the target sequences solved by the regional management and regional release optimization under the MBM are connected to the corresponding USVs, the optimal solution for the target sequences assigned to each USV after solving the graph theory model will likely be consistent with the solution obtained by the MBM. Therefore, in this NCG generated by USVs and target points, additional connection segments need to be added to generate a better feasible solution. This study proposes a construction strategy for solving the M-TSP NCG, and Figure 12 shows an example of the method. The specific method flow is as follows:

Step 1:

The target point with the farthest sum distance from all USVs is point 1.

Step 2:

For each USV’s target sequence assigned under MBM by the regional management and regional release, the Dijkstra algorithm is used to obtain the shortest distance from point 1 to the target point in each target sequence, and point 1 is connected to all obtained target points.

Step 3:

Assign the remaining target points with numbers starting from 2, from left to right. When the horizontal coordinates are the same, number from top to bottom. Connect the two closest target points in the target sequence with the longest total travel distance under the improved MBM for the USV and the target sequence with the shortest total travel distance for the USV. Similarly, connect the two closest target points in the target sequence with the second-longest total travel distance under the improved MBM for the USV and the target sequence with the second-shortest total travel distance for the USV.

Step 4:

Connect the adjacent target points in the target sequence assigned to the USV under the improved MBM for the connected target points mentioned above.

Step 5:

Each USV is assigned a target sequence in step 2, at this point forming a closed loop within the NCG.

Step 6:

For each such closed loop, an extended searching pheromone is constructed. This involves using the centroid of the loop’s configuration as the center to build a ring that extends outward until it reaches the first target node of another USV. This node is then connected to all nodes in the corresponding closed loop that have not yet been linked. The USVs exchange ROS topic of coordinate transformation among themselves, enabling them to be aware of each other’s relative distances and angles. Since the central base station sends coordinate information of the target point to the USVs at the first time, this collectively provides the conditions for the USVs to directly generate pheromones. The purpose of constructing this pheromone is to expand closed loops formed due to short distances between targets, thereby incorporating long-distance connections between target nodes into target sequences that only contain short-distance closed loops. As a result, target sequences with smaller variances are more likely to form between different USVs, thus overcoming local optimality.

2.6. Extended Ant Colony Optimization Searching for Region Solving

Once the NCG is constructed, graph search methods can be employed to solve the target allocation sequence. The optimization function aims to minimize both the total time for all USVs to complete their targets and the variance of operating time across all USVs. The Ant Colony Optimization (ACO) algorithm, as a heuristic algorithm, offers advantages in the rapid exploration of solution spaces in graph theory. When searching for the optimal solution in NCG using the ACO, the fixed connection rules of full connection no longer apply. The algorithm can thus increase the likelihood of finding the global optimal solution through a locally dynamic search.

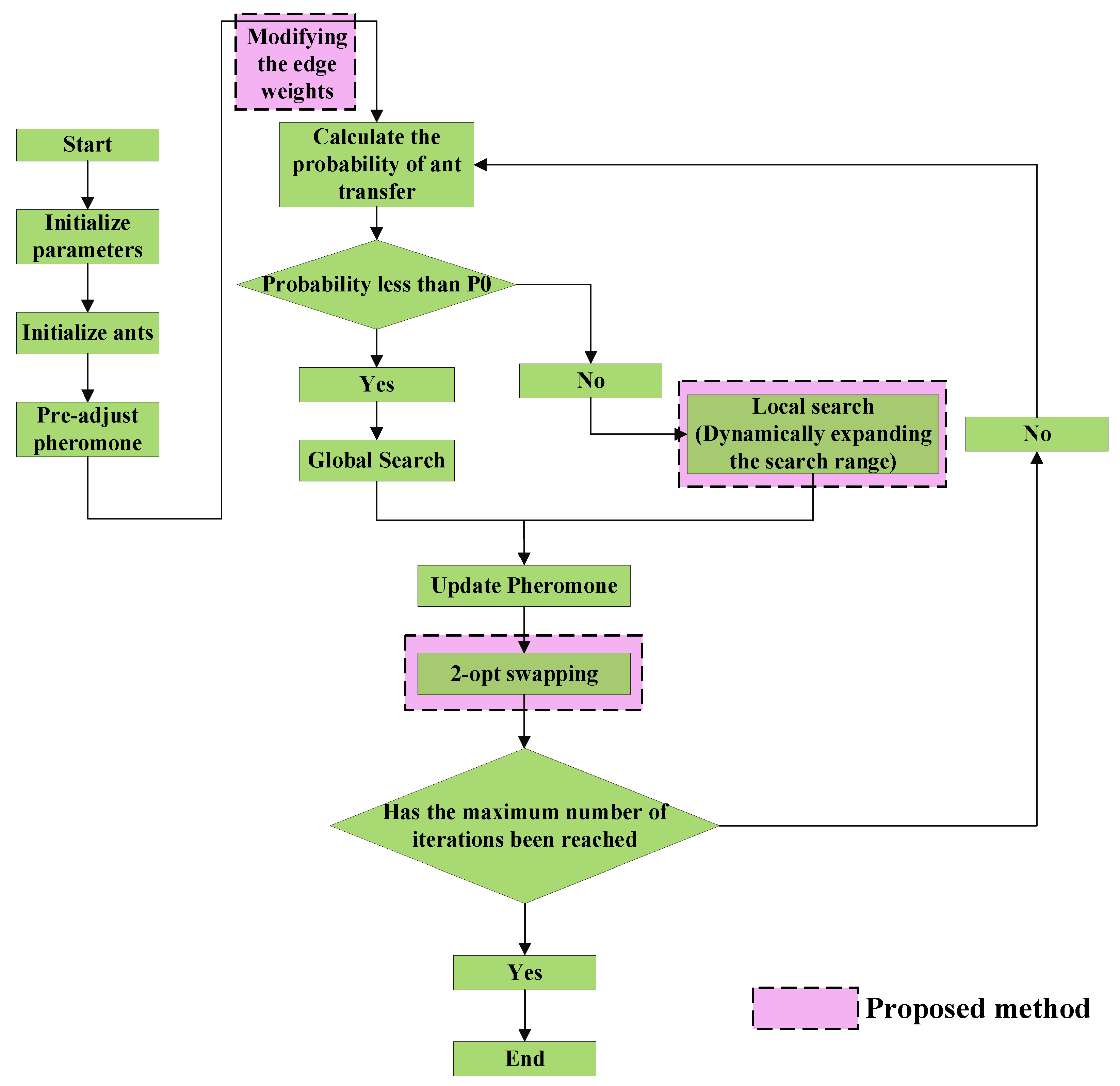
Therefore, we propose an Extended ACO (EACO) algorithm to handle M-TSP in an NCG, as depicted in Figure 13. The optimization work is primarily conducted from the following three perspectives:

(1)

Dynamically expanding the local search range: Utilizing a dynamic range expansion strategy to find the feasible solutions. The algorithm searches for feasible solutions in a gradually expanding range, and stops when a solution with a total cost less than the auction-based method is found.

(2)

Modifying the edge weights: The method modifies the edge weights in the graph based on the target list loop and the multiplier value. This allows the algorithm to find feasible solutions iteratively by increasing the search range for the solutions.

(3)

2-Opt swapping technique: The method incorporates the 2-opt swapping technique to improve the solutions iteratively. This allows the algorithm to find better solutions by swapping nodes and updating the paths to minimize the total cost.

2.7. Efficient Information Communication across Multiple Terminals

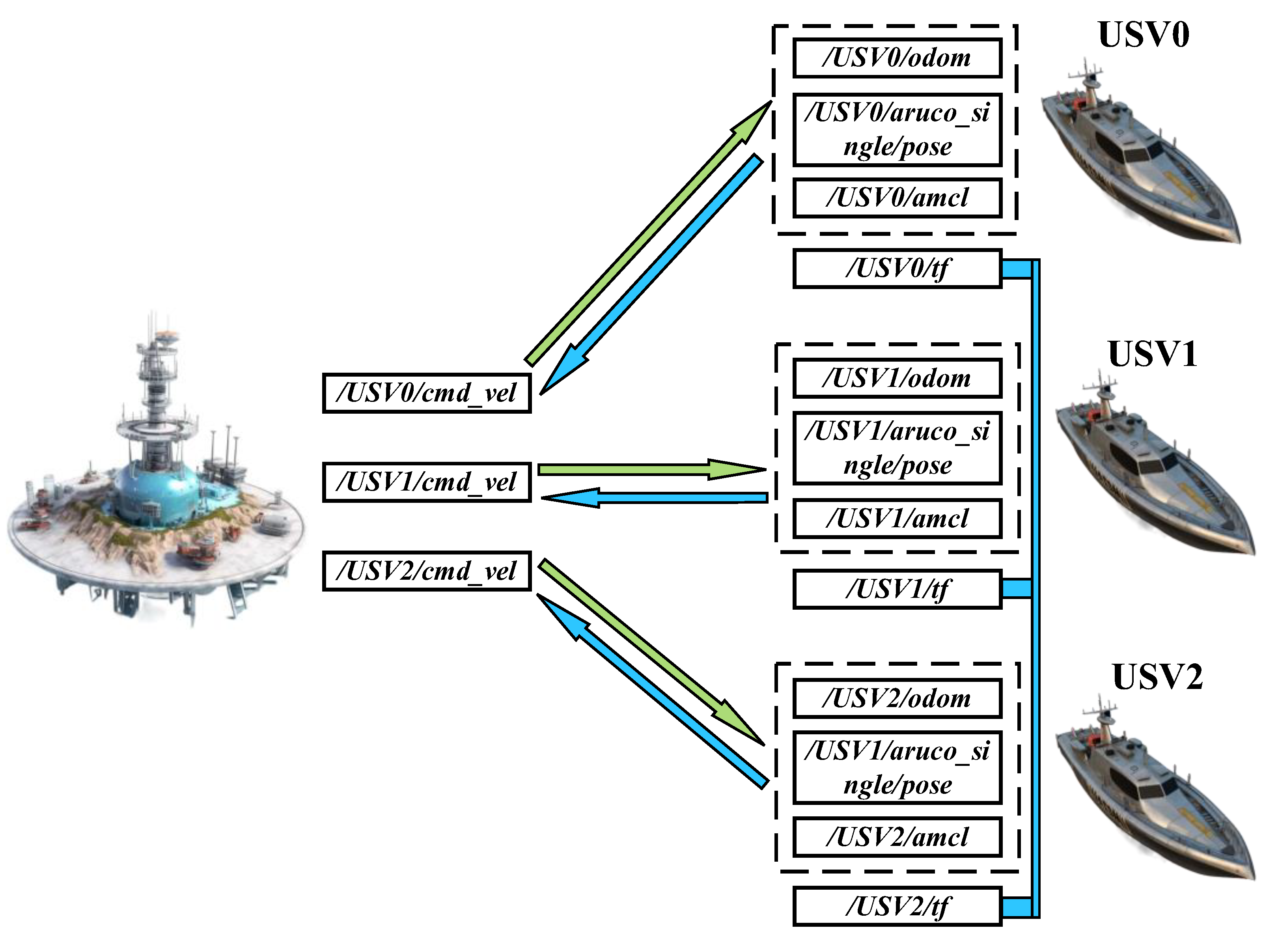
When deploying a multi-USV cooperative system on a physical platform, reliable real-time communication requires each USV entity to transmit its self-positioning, coordinate transformation, speed, and environmental map information, among others [31]. To facilitate this, we propose a mechanism for multiple-source data fusion in USV detection and perception data transmission to an airborne base station. Its structure is depicted in Figure 14. Firstly, callback functions are defined to receive odometry, probability positioning, and laser radar data, respectively. Then, these data are encapsulated and processed, generating a 4-byte ID and accompanying information length. Next, an effective network connection is established using the socket protocol mode, and coordinate transformation is performed on pose information. Finally, various data sources are integrated together to achieve pose information position transformation, and the accumulated string is sent through the odometry port with their respective IDs. This algorithm effectively achieves the fusion and transmission of multiple data sources.

The core of the proposed mechanism is an algorithm designed for transmitting data from USVs to an aerial base station, which includes/odom data detected by the odometer, /scan data detected by the LIDAR, and USV’s/pose data detected by AMCL probability localization. The algorithm consists of ten steps:

Step 1:

Define a callback function for the odometer to receive the linear and angular velocity information measured by each USV.

Step 2:

Define a callback function for AMCL to receive the pose information measured by each USV.

Step 3:

Define a callback function for the LIDAR to receive the scan information, including the start and end angles, increment angle, time interval, scan duration, minimum and maximum range, number of measurements per revolution, and intensity array.

Step 4:

Define a callback function for the pose to receive and display the pose information measured by each USV.

Step 5:

Package all the information detected by the odometer, LIDAR, and amcl for each unmanned ship, and pack each group of information into a 4-byte ID, along with the information length.

Step 6:

Receive the parameters of the odometer and scan ports, and establish an effective network connection in accordance with the socket protocol for smooth transmission.

Step 7:

Subscribe to the odometer, LIDAR, and AMCL callback functions in the form of topics, which reflect the odometer information, pose covariance matrix, and LIDAR scan information for each USV.

Step 8:

Initialize the data server node.

Step 9:

Perform coordinate transformation on the listened pose information.

Step 10:

Perform position transformation on the pose information measured by AMCL, and combine all the information detected by the odometer, LIDAR, and AMCL for each USV. Finally, accumulate the information into a string format, along with the corresponding ID, and send it through the odometer port.

In the operation of the information exchange and transmission mechanism involving two USVs, the topic and node interaction relationship between the USVs is illustrated in Figure 15. As shown in the figure, all server-side topic publishers have successfully sent the corresponding topics to each USV, and the velocity topics have been effectively published in the respective clients, thus confirming the correct functioning of the multi-USV information exchange and transmission mechanism. Moreover, there are 10 topics and nodes, respectively, and under the distributed node manager mechanism, the topics of different USVs are placed under distinct node managers. This indicates that the increase in topics and nodes when the number of USVs emerges does not excessively consume computational resources.

3. Results and Discussions

3.1. Target Deadlock Resolution Effect of Regional Management and Regional Release Methods

To verify the impact of the proposed regional setup improvement algorithm on the operational efficiency of multi-USV target allocation, we conducted an experimental comparative analysis with the traditional MBM. We assessed the efficiency improvements brought by the improved system by considering both the number of USVs deployed and the total execution time of the objectives.

First, we performed simulation experiments to evaluate the deadlock resolution effect of the MBM under regional management and deregulation methods. The simulation experiments were carried out on an Ubuntu 16.04 platform equipped with ROS and visualized using the Gazebo simulation environment. We compared the improved MBM based on regional management and deregulation with the traditional MBM, recording the time taken to complete objectives using the two algorithms and the number of USVs deployed at the start of the objectives. The deadlock situations during the entire target allocation process could be approximated using the initial deadlock situations. As non-random initial USV positions are more representative in scenarios such as island defense, and the USVs face more bidding phenomena, we did not randomize the USV initial positions in the simulation experiments. The USVs were distributed in vertical rows, as shown in Figure 16.

The improved MBM based on regional management and deregulation first utilized clustering to obtain the center points of each category, and then applied a bidding function incorporating a time factor to bid on the center points, determining the USVs’ arrival at center points with different category. As system latency may cause untimely information updates, multiple USVs may simultaneously bid on the same category center point, failing to disperse the USVs. Therefore, before each USV initializes its position, it checks whether the previous USV has successfully initialized its position and executes sequentially. Simulations showed that this strategy effectively resolved the aforementioned issues, with the initialization results of USVs’ position under clustering shown in Figure 17. From the figure, it is evident that during the initial target allocation, the USVs are already dispersed across the center points of various categories on the map. Consequently, the number of conflict avoidance occurrences between USVs during subsequent target allocations is significantly reduced, making the entire objective completion process smoother.

As shown in Figure 18 and Figure 19, after USV 6 reaches the target point, USVs 7 and 9 cannot successfully bid on their current target point positions using the distance-related bidding function in the original algorithm. By incorporating the time factor into the bidding function, both USVs successfully bid on two target points closer to USV 6, as they were deadlocked for a period before being assigned new objectives.

3.2. Local Optimal Resolution Effect of Region Interaction and Region Sloving Methods

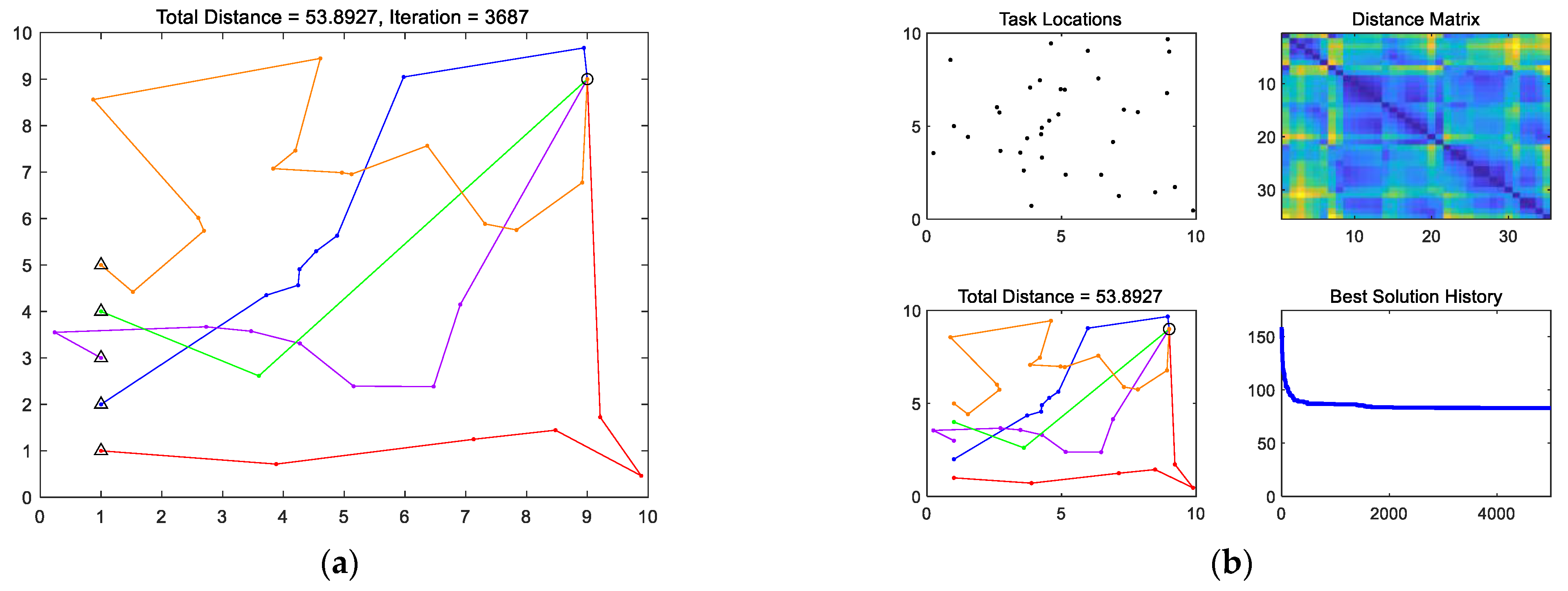
Upon completion of the MBM optimized by regional management and regional release, a set of feasible solutions are obtained. Based on the NCG connection criterion presented below, a NCG construction for M-TSP solution can be performed. After constructing this NCG, the M-TSP problem can be solved using the proposed EACO algorithm. Figure 20 displays the assignment of 33 target points to 5 USVs named R₀ to R₅ following the regional interaction method, where represents a USV.

Table 1. Number and coordinates of each target point.

Target Mark	Coordinate	Target Number	Coordinate	Target number	Coordinate
T1	(9.0,9.0)	T12	(3.9,0.7)	T23	(6.4,7.6)
T2	(0.3,3.6)	T13	(4.2,7.5)	T24	(6.5,2.4)
T3	(0.9,8.6)	T14	(4.2,4.6)	T25	(6.9,4.1)
T4	(1.5,4.4)	T15	(4.3,4.9)	T26	(7.1,1.2)
T5	(2.6,6.0)	T16	(4.3,3.3)	T27	(7.3,5.9)
T6	(2.7,5.7)	T17	(4.5,5.3)	T28	(7.8,5.8)
T7	(2.7,3.7)	T18	(4.9,5.6)	T29	(8.5,1.4)
T8	(3.5,3.6)	T19	(5.0,7.0)	T30	(8.9,9.7)
T9	(3.6,2.6)	T20	(5.1,7.0)	T31	(8.9,6.8)
T10	(3.7,4.3)	T21	(5.2,2.4)	T32	(9.2,1.7)
T11	(3.8,7.1)	T22	(6.0,9.0)	T33	(9.9,0.5)

presents the target point numbering and corresponding coordinate positions obtained according to the numbering rules proposed in Section 2.5.

The target point with the largest total distance from all USVs, labeled as T₁ with coordinates (9, 9), is represented by “○” symbol in the graph. During the solution process, the initial target point for each USV is T₁. After obtaining the initial target assignment sequence for each USV through the genetic algorithm, the USV with the largest distance between the penultimate target point in the sequence and the target point T₁ will be ultimately assigned to T₁. In this case, USV R_4′s penultimate assigned target point is T₉, which is the farthest from T₁, thus R₄ is eventually assigned to T₁. The final target sequences assigned to each USV and their respective total travel distances are shown in

Table 2. The target sequence and total operating distance assigned to each USV.

USV Mark	Real-Time Coordinate													Total Distance
	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t11	t12	t13
R1	S1			T12			T26		T29	T33	T32			10.6221
R2	S2			T10	T14	T15	T17	T18		T22				8.9669
R3	S3	T2		T7	T8	T16	T21		T24	T25				9.3039
R4	S4				T9							T1		11.3267
R5	S5	T4	T6	T5	T3	T13	T11	T19	T20	T23	T27	T28	T31	13.6731

. The table records the midway positions of each USV at a certain period, with t₁ to t₁₃ as the chronological evolution.

From the iterative curve of the best solution in Figure 20, it can be observed that the EACO method exhibits a rapid convergence of the optimal solution, indicating that the non-complete graph constructed in this study has a relatively low computational complexity. Regarding the travel distances of each USV, the maximum value is only 26.9% higher than the average value, while the minimum value is only 16.8% lower than the average value. This demonstrates that the proposed algorithm is less prone to falling into local optima. Overall, the experimental results demonstrate that this paper provides a comprehensive solution that considers both the computational efficiency of greedy-based methods and the avoidance of local optima.

3.3. Comparative Experiments

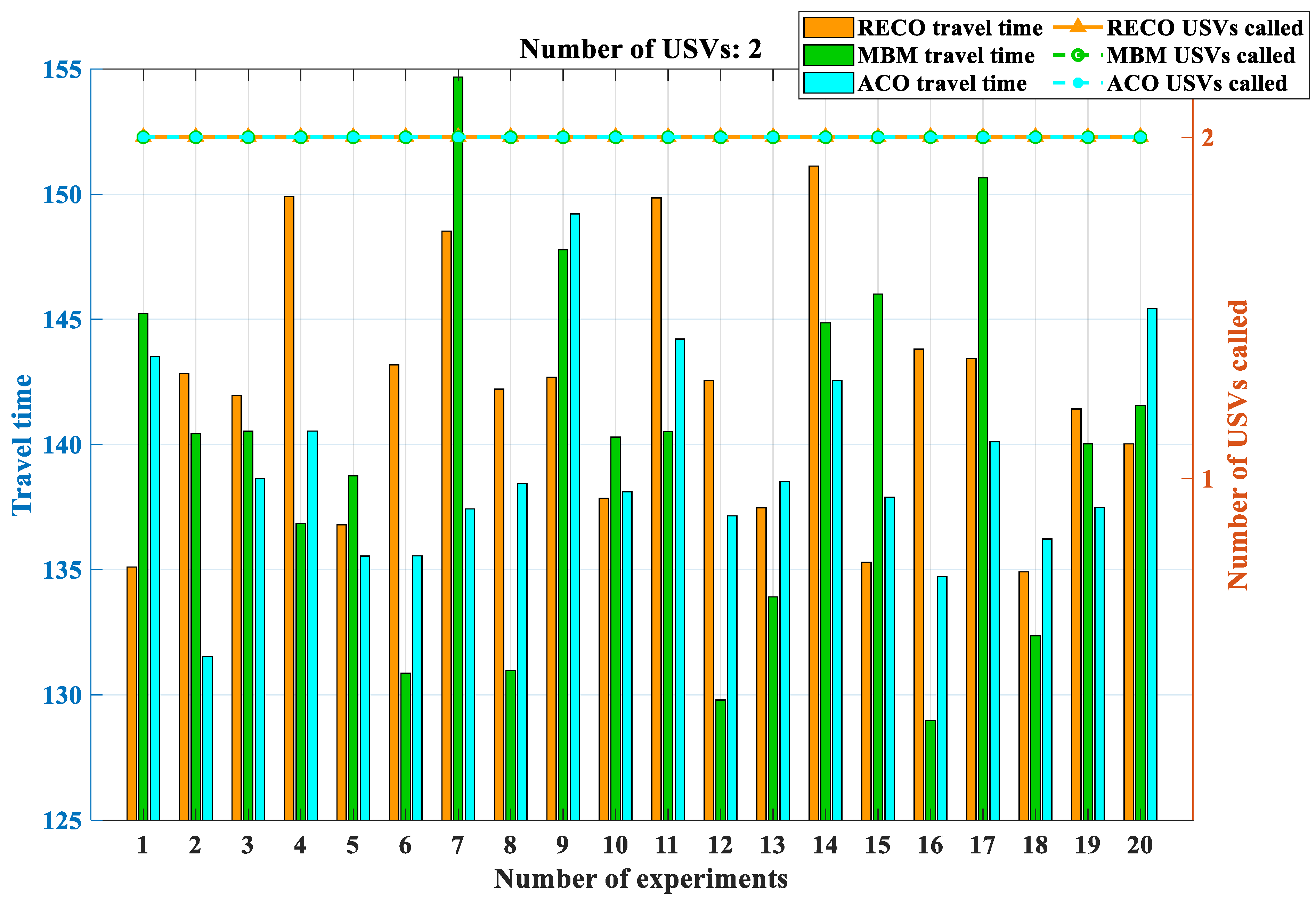
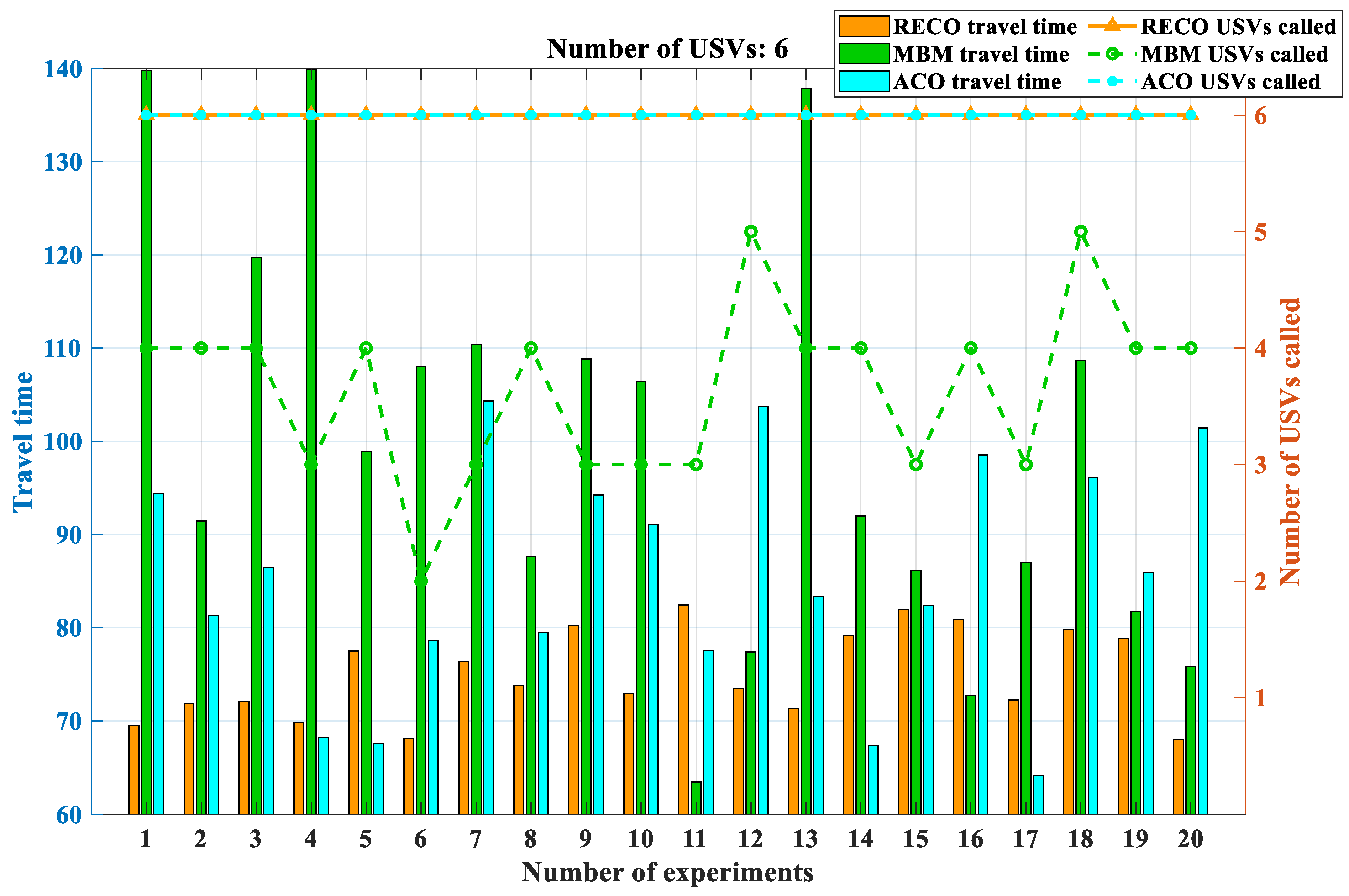
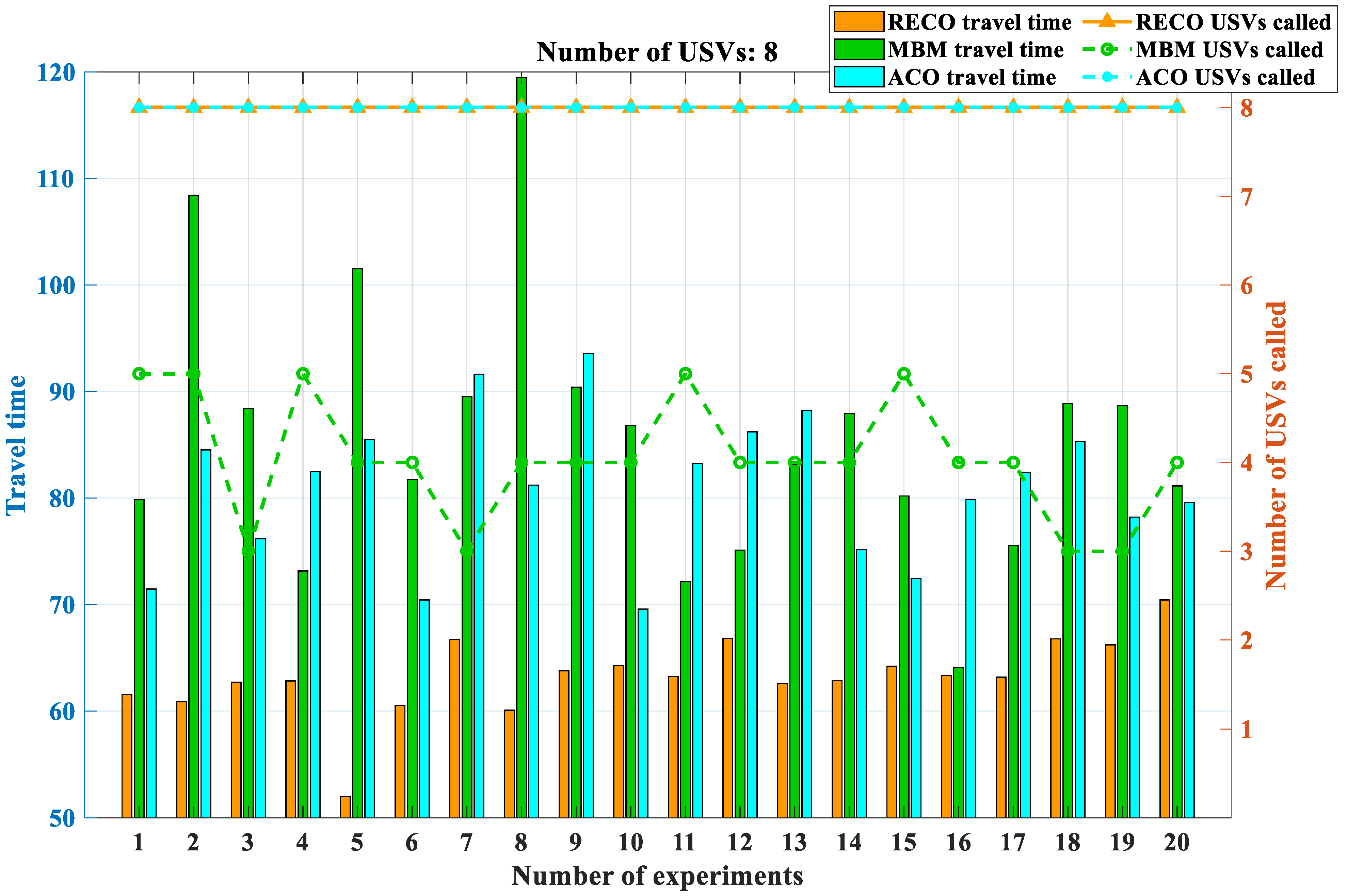
The experiments were divided into five groups with USV quantities of 2, 4, 6, 8, and 10, and each experiment had 100 target points with constant positions. To prevent accidental occurrences from affecting the simulation experiments, each experimental and control group was repeated 20 times. Due to the nature of tasks such as island defense, USVs are initially deployed within the same designated area, resulting in fixed initial positions for the USVs. However, when it comes to searching for target points, different combinations need to be explored. This serves two purposes: firstly, to assess the specific performance of the proposed method, and secondly, to guide the adaptation of USVs to various defense patterns, ultimately achieving complete coverage patrol of the island. In the context of region management, the distribution density of target points has a significant impact on the positioning of the clustered centroids. This, in turn, affects the magnitude of the bidding function during the clustering process, making the resolution of USV deadlock more or less challenging and further influencing the subsequent region release process. Therefore, we employ two different schemes for generating target points. One scheme generates target points in denser and distinct clusters, resulting in greater distances between the centroids of each cluster. The other scheme generates target points in a more scattered manner, making clustering more difficult and increasing the likelihood of centroids being close to each other. However, since USVs are unable to navigate into the central base station, both strategies adhere to the principle of having no target points within the central 2 × 2 grid region to simulate a realistic environment for island defense with a central base station. To evaluate these two schemes, we generate 10 sets of target sequences for each scheme, with variations in the distribution patterns of target points within each set. It is important to note that the number of USVs remains constant throughout these evaluations. The simulation results are shown in Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25.

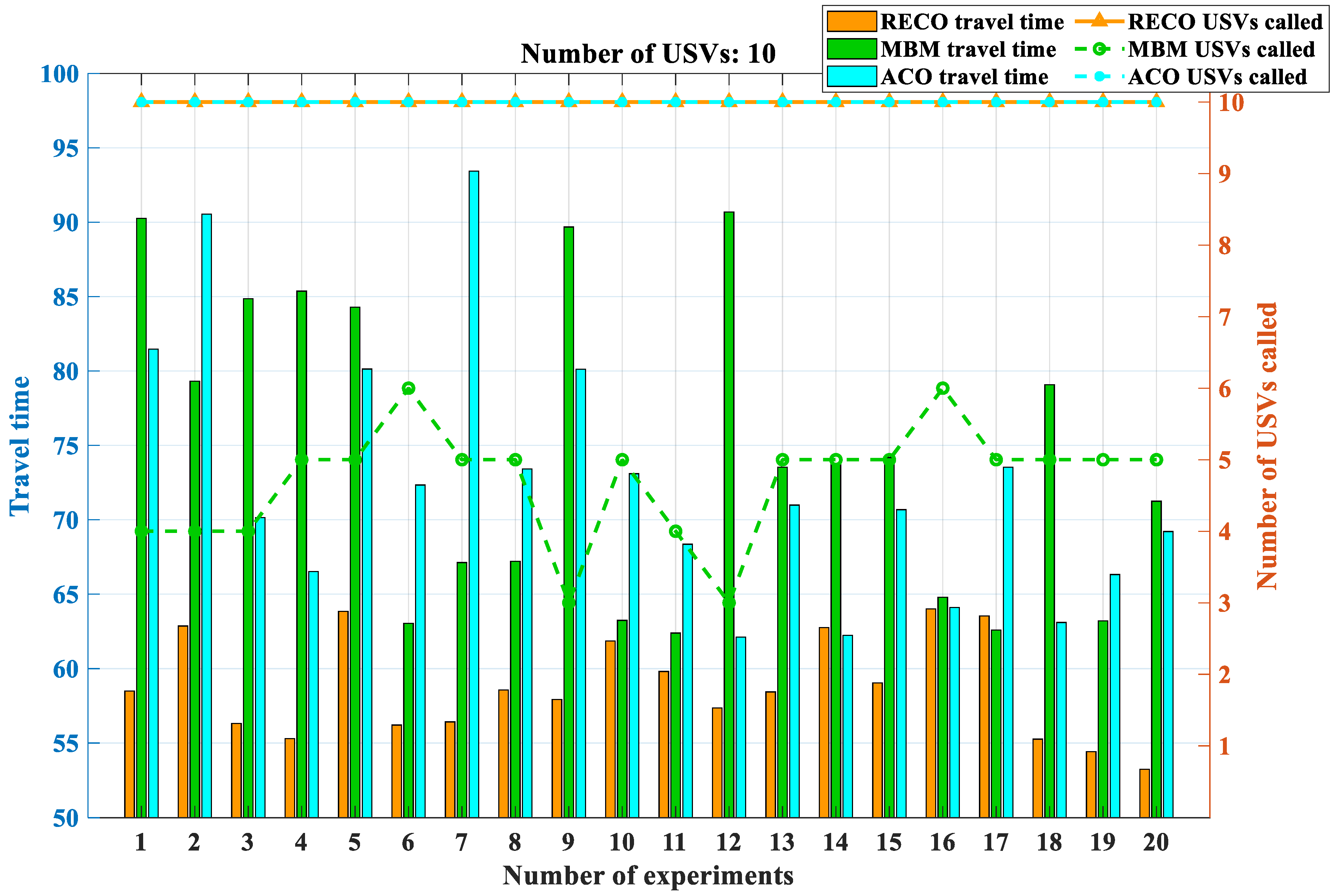
When the number of USVs is two, the comparison between the original algorithms and the proposed methods reveals a small difference in the time required to complete all objectives. At this stage, it is feasible to deploy all USVs at the beginning of the objectives, resulting in minimal deadlocks within the original algorithms. However, as the number of USVs increases, deadlocks begin to emerge within the original algorithms, hindering the completion of objectives.

In contrast, the EACO method exhibits a significant reduction in the time needed to accomplish the same set of objectives compared to the original algorithms. This notable decrease in execution time translates into a substantial increase in overall efficiency. As the number of USVs within the multi-USV system continues to increase, the system’s efficiency exhibits gradual improvement.

Furthermore, the RECO method displays a clear advantage over the MBM method in terms of the number of USVs deployed. The RECO method effectively avoids any unresolved deadlock situations during the deployment of USVs. This advantage not only contributes to enhanced efficiency but also ensures that all USVs can be effectively utilized for the assigned tasks without any disruptions caused by deadlocks.

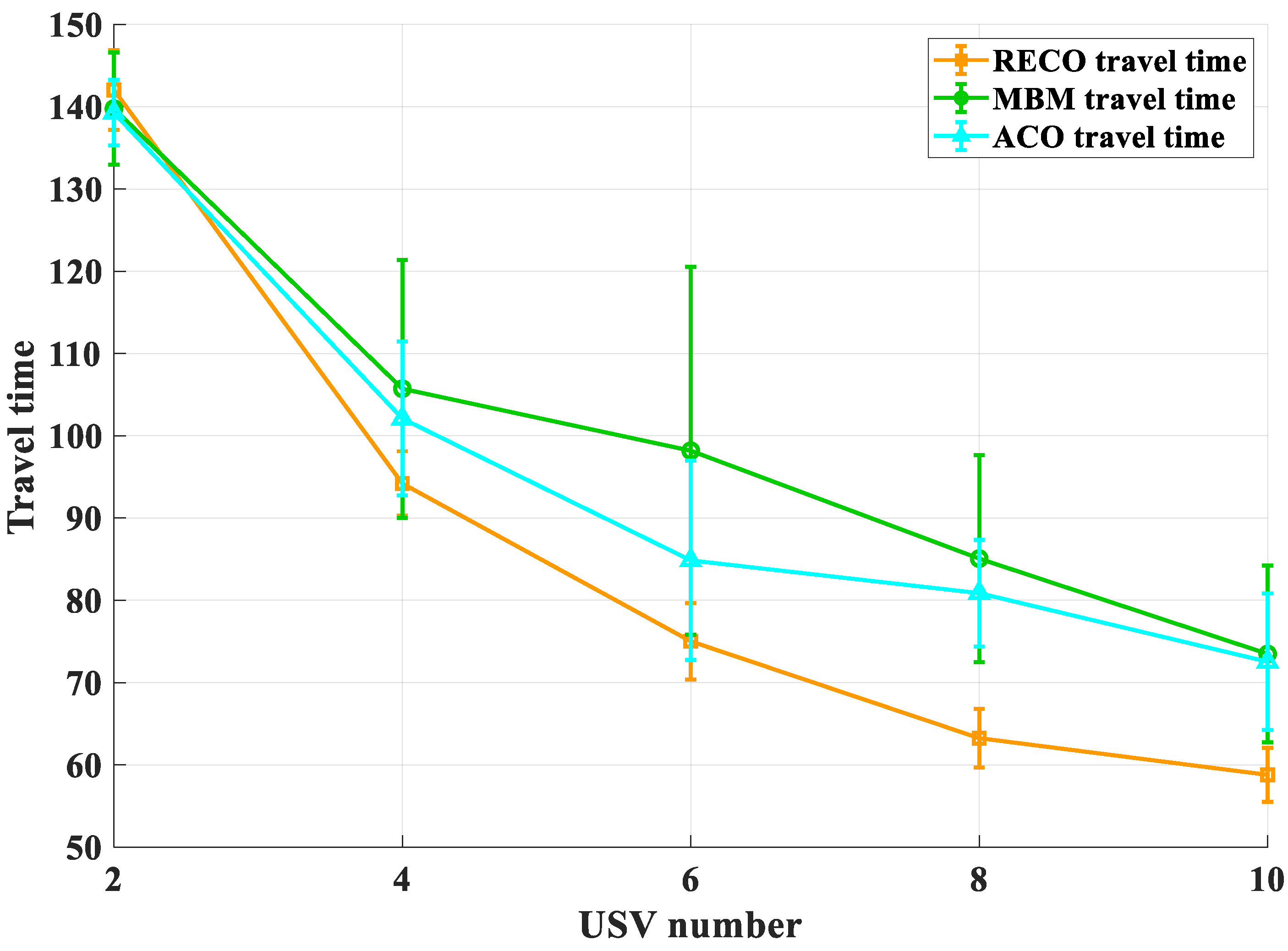
The analysis of the data presented in Figure 26, along with

Table 3. Comparison of average time (unit: s) with target arriving for different number of USVs.

USV Number	RECO Method	MBM Method	ACO Method
2	142.05	139.76	139.25
4	94.20	105.72	102.09
6	75.02	100.07	84.85
8	63.24	85.07	80.87
10	58.78	73.48	72.53

and

Table 4. Comparison of time variance (unit: s) with target arriving for different number of USVs.

USV Number	RECO Method	MBM Method	ACO Method
2	24.74	51.13	16.57
4	15.67	257.93	91.91
6	22.66	524.18	154.16
8	13.36	166.76	44.29
10	11.27	121.21	72.48

, provides valuable insights into the performance of different methods. Firstly, when the number of unmanned surface vessels (USVs) is relatively low, there appears to be no notable distinction in terms of algorithm execution time or the number of USVs initially deployed between the RECO, MBM, and ACO methods. This observation suggests that these methods perform similarly under such conditions.

However, as the number of USVs increases, an interesting trend emerges. The original methods, namely RECO, MBM, and ACO, exhibit a more pronounced issue known as USV deadlock. This phenomenon leads to a significant increase in execution time for achieving objectives compared to the EACO method. The EACO method, on the other hand, shows improved efficiency in handling larger numbers of USVs, likely due to its ability to mitigate the occurrence of USV deadlock.

An analysis of the variance in execution time provides additional insights. Both the MBM and ACO methods exhibit relatively high variance, indicating significant fluctuations in execution time across different instances or scenarios. In contrast, the RECO method demonstrates smoother variance compared to the original two methods. This smoother variance highlights the algorithmic stability of the EACO method, suggesting that it is less susceptible to being trapped in local optima.

These findings underscore the advantages of the EACO method in terms of scalability and stability. As the number of USVs increases, the EACO method shows improved performance, mitigating the issue of USV deadlock and achieving objectives more efficiently. The reduced variance in execution time further indicates the robustness of the EACO method, suggesting its ability to consistently produce effective solutions.

In summary, the proposed RECO mechanism method is significantly superior to the state-of-the-art MBM and ACO methods in the efficiency of target allocation; the more USVs there are in a multi-USV system, the more apparent this advantage becomes.

4. Conclusions

Defending border islands has always been a significant issue in the realm of national defense, complicated by environmental conditions that hinder the long-term stationing of military forces. Consequently, implementing an intelligent defense and patrol system comprising unmanned surface vessel (USV) swarms and airborne surveillance bases emerges as a feasible solution. For USVs, the establishment of new objectives in single-batch cycles guides the collaborative patrol and defense of the USV swarm. During this process, it becomes essential to assign corresponding targets to multiple USVs, a task falling within the ambit of multi-agent cooperative target allocation.

Market-Based Mechanism (MBM) and Ant Colony Optimization (ACO), as representatives of auction-based and learning-based methods, respectively, are widely applied in the field of multi-agent cooperative target allocation. However, both methods suffer from common issues such as target deadlock and local optimization, which become more pronounced with increasing USV numbers. Direct application of these methods, therefore, may not be suitable for the complex, large-scale, long-term defense target allocation of USVs. To this end, we propose a Region-Construction (RECO) method, with its region management and release modules overcoming target deadlock, and its region interaction and solution modules overcoming local optimization. With its efficiency advantages, this suite of methods offers the feasibility of extending to other application scenarios of multi-agent target allocation. Through the analysis and experiment of the proposed method, specific conclusions are as follows:

(1)

When applying the MBM for cooperative target allocation among multiple USVs, target deadlock may occur at the initial stage as not all USVs can win bids. This issue can be effectively resolved by utilizing unsupervised clustering algorithms, allowing each USV to enter different major regions at the initial step. Modifications consist of dynamic K value calculation, weight optimization, and the use of gradient descent, can be employed in classical clustering methods like K-Means to overcome the deficiencies, which contain two aspects: choosing difficulty in K values and the dependence of convergence on the initialization of cluster centers.

(2)

During cooperative target allocation of multiple USVs using the MBM, target deadlock may occur at the initial stage if the bid function considers limited factors. By optimizing the bid function and introducing a waiting time factor that reduces the bid function as waiting time increases, target deadlock during operation can be released using a dissolution concept.

(3)

In a fully connected graph, the number of connections increases exponentially with the rise in target nodes, leading to high computational complexity if the target sequence allocation scheme for USVs is directly searched through the complete graph. By generating an initial node connection scheme using the MBM and constructing a non-complete graph through neighborhood connection and pheromone extension, the complexity of graph resolution can be effectively reduced.

(4)

When searching for the optimal solution in non-complete graph using the ACO, the fixed connection rules of full connection no longer apply. The algorithm can thus increase the likelihood of finding the global optimal solution through a locally dynamic search. Efficient local dynamic search modes can be implemented through strategies like dynamically expanding the local search range, adjusting edge weights, and employing 2-opt local search.

In this study, comparative experiments (20 for each method with fixed USV number, totaling 300 trials) were conducted for the proposed RECO method, along with the MBM and ACO methods, with USV numbers set at 2, 4, 6, 8, and 10. The results showed that when the number of USVs was 4, the average time for all USVs to reach the target in the RECO method reduced by 10.9% and 7.7% compared to the MBM and ACO methods, respectively. This reduction was 25% and 11.6% for 6 USVs, 25.7% and 21.8% for 8 USVs, and 20% and 19% for 10 USVs. The results reflect that the proposed method exhibits outstanding performance and significantly improved operational efficiency with large-scale USVs, and indicate that the study offers a viable solution for large-scale USV patrol and defense issues.

We seek further summarization as the issues addressed in this paper are representative and emblematic of the challenging NP-hard problems that currently perplex researchers. Such problems often arise in scenarios involving a large number of agents, and researchers in these domains often grapple with the trade-off between seeking global optimal solutions and ensuring computational efficiency, as these two objectives tend to conflict with each other. Greedy algorithms have proven to be highly valuable in optimizing objectives, exhibiting remarkable computational efficiency, and are well-suited for timely defense strategies such as USV island patrol. However, due to their focus on single-step optimization strategies, these methods struggle to search for global optimal solutions. The approach discussed in this paper addresses this limitation by establishing regions and optimizing the objective function based on greedy algorithms. It appropriately expands the solution space, albeit within reasonable computational limits, by encompassing regions that are highly likely to generate subsets of optimal solutions. This original framework combines a set of initial solutions generated by greedy algorithms with a non-complete graph construction strategy that involves dynamic clustering, objective function optimization, neighbor connections, and pheromone extension. Finally, a heuristic algorithm is employed to solve the objective sequence within this non-complete graph. Thus, this paper presents a comprehensive solution that considers both the computational efficiency of greedy-based methods and the avoidance of local optima.

However, in our experimental results, we observed cases where the RECO method exhibited longer target arrival times compared to the MBM and ACO methods. This discrepancy is primarily attributed to the sensitivity of the RECO method to the distribution of target points, indicating the need for further improvement in algorithm stability. Therefore, in future research, we plan to introduce AI, such as imitation learning in reinforcement learning, to utilize the solutions generated by the RECO method as valuable experiences, guiding AI to learn the algorithmic patterns and enhance robustness.