Research on Position Sensorless Control of RDT Motor Based on Improved SMO with Continuous Hyperbolic Tangent Function and Improved Feedforward PLL
Abstract
1. Introduction
- (1)
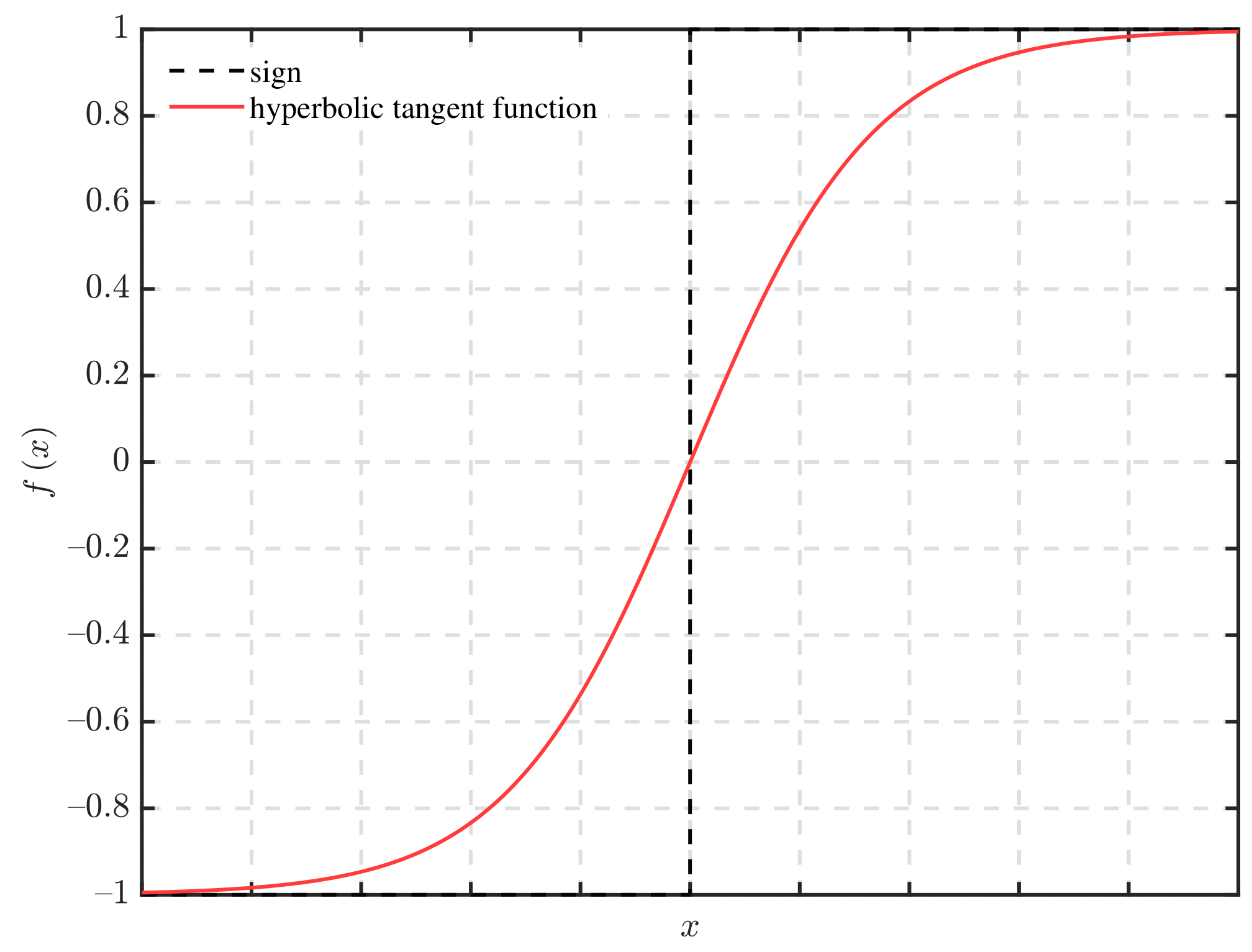
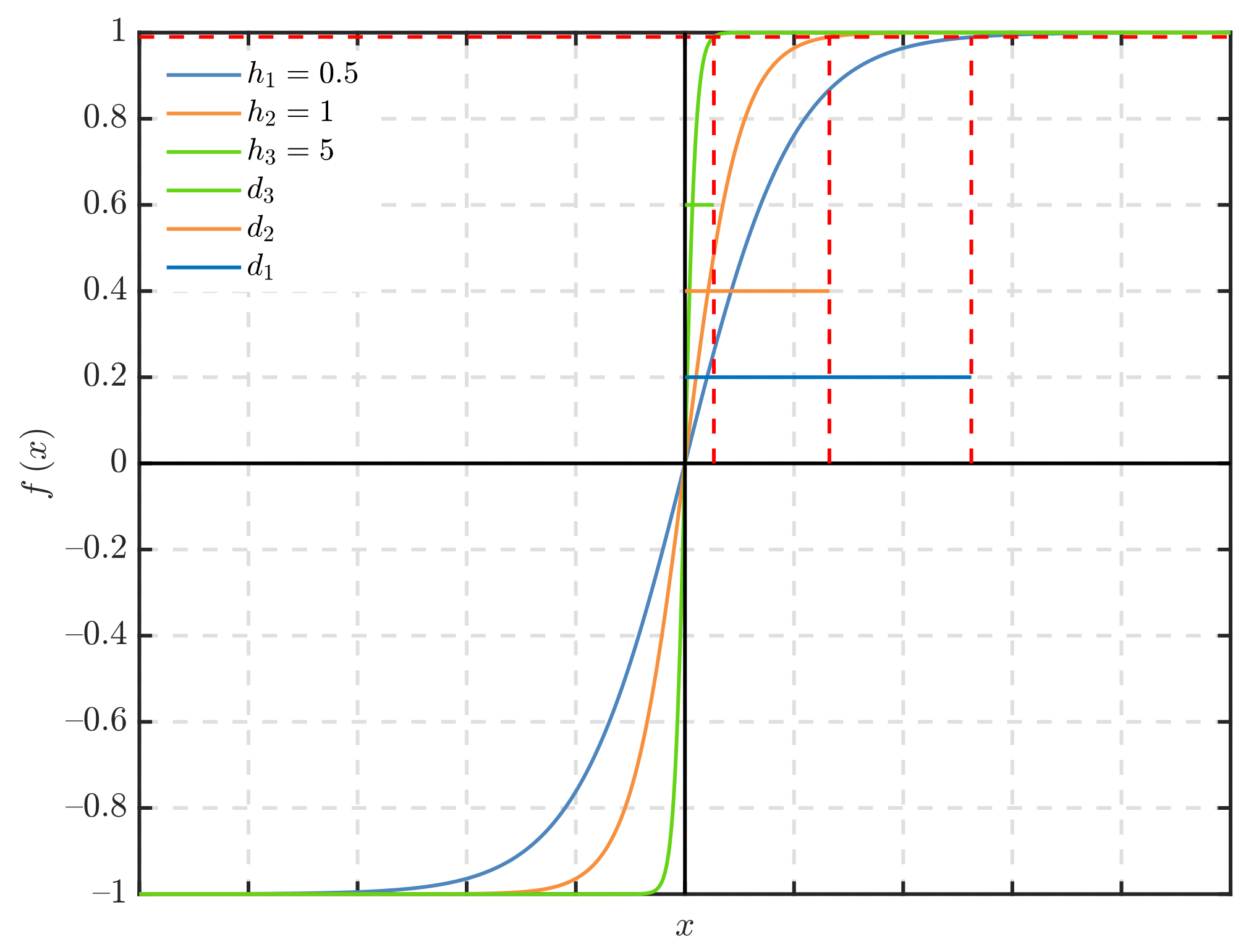
- This study addresses SMO chattering by replacing the sign function with a continuous hyperbolic tangent function and selecting an appropriate boundary layer width. An observer based on the back-EMF model is developed to eliminate the LPF, reduce phase delay, and enhance the back-EMF signal estimation precision;
- (2)
- Through optimization of the traditional PLL structure and the addition of feedforward compensation, this study has successfully realized position extraction during bi-directional rotation of the motor, while significantly improving the accuracy of position extraction during acceleration and deceleration.
2. PMSM Mathematical Model
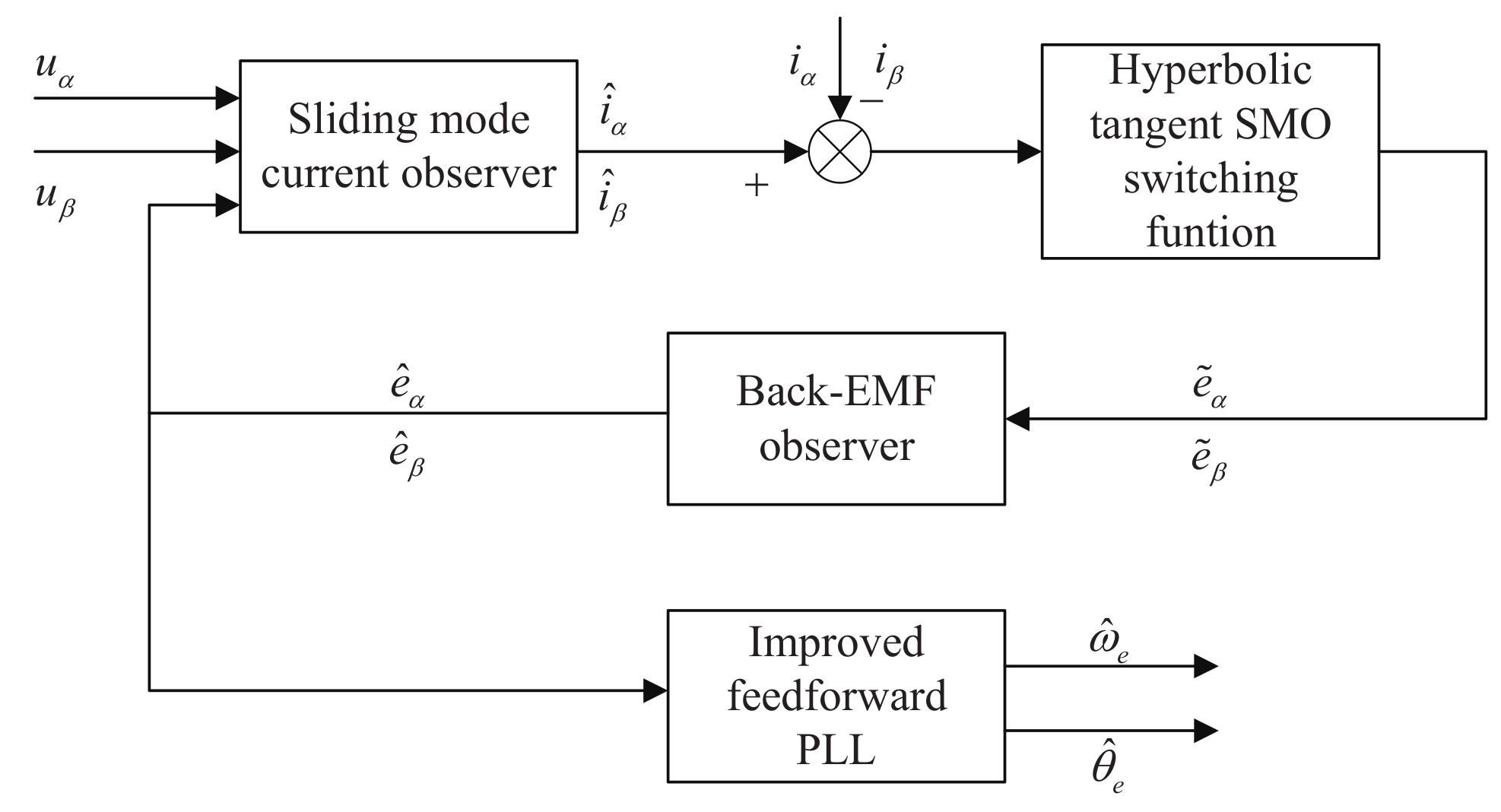
3. SMO Design for PMSM Rotor Position Estimation
4. Rotor Position and Speed Extraction
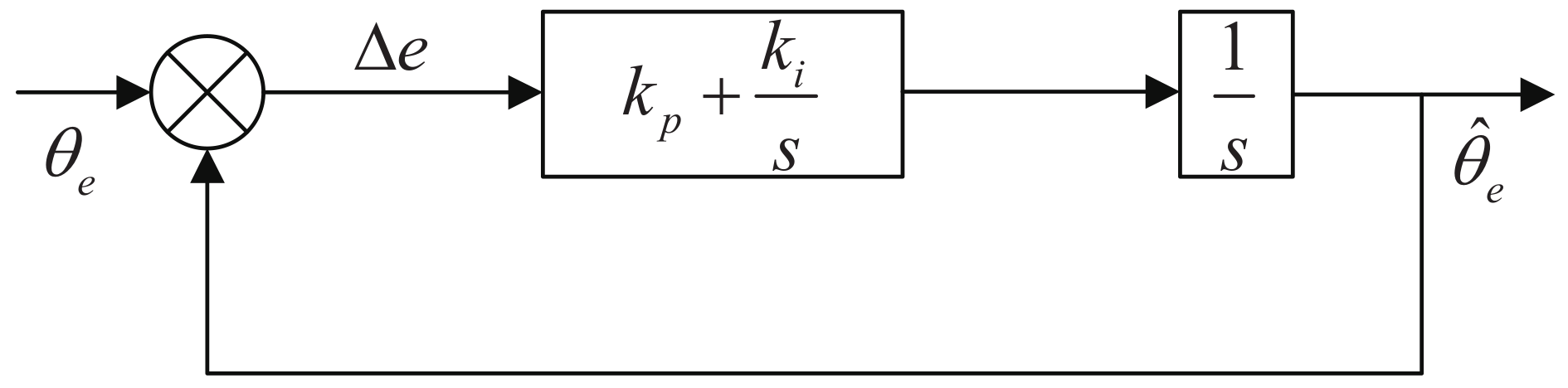
4.1. Traditional PLL Analysis
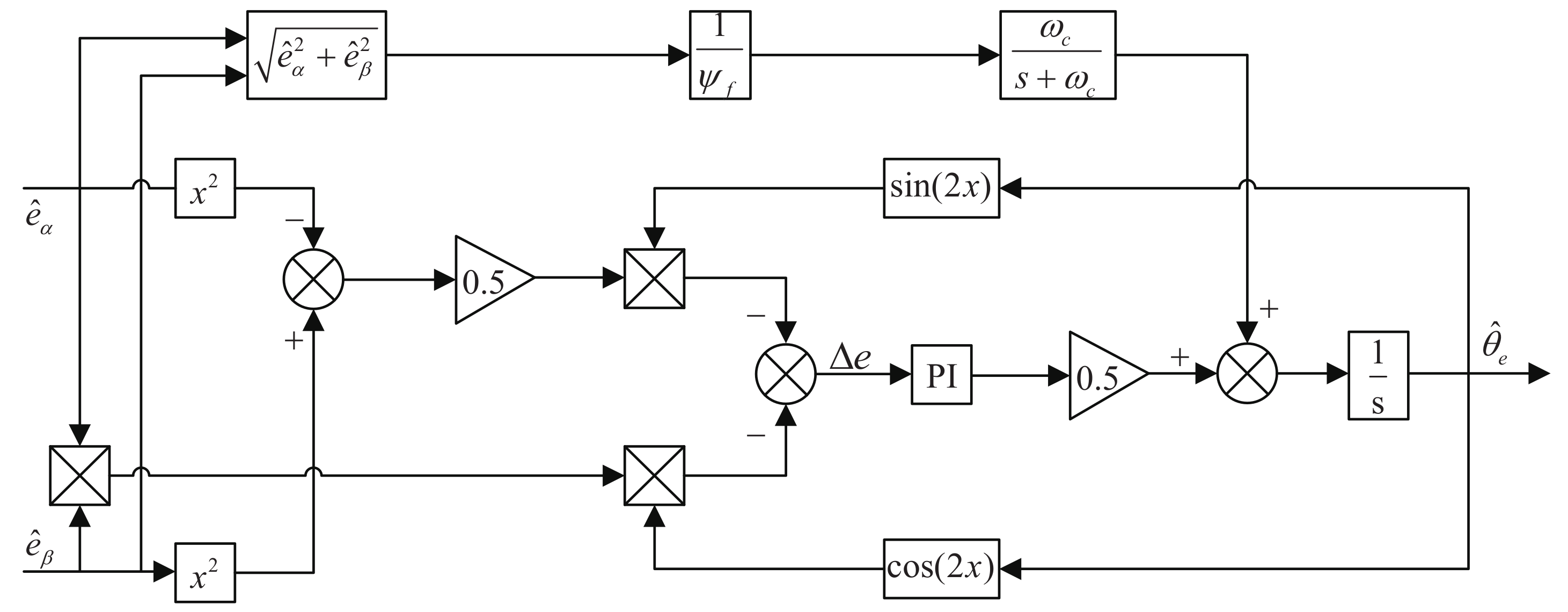
4.2. Improved PLL Analysis
- (1)
- Improve the inability of the conventional PLL to reliably extract position information during motor reversal;
- (2)
- During motor acceleration and deceleration, the conventional PLL’s error problem has been resolved.
5. Simulation Verification
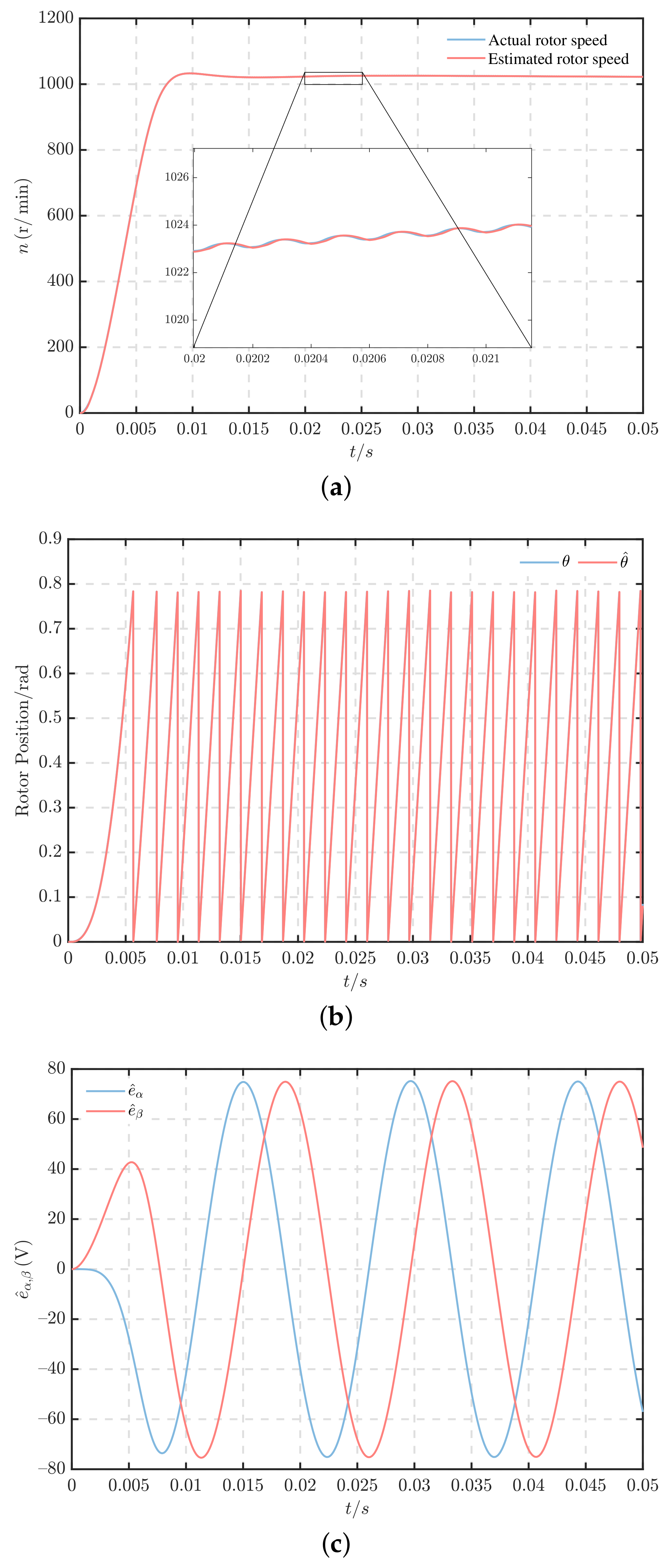
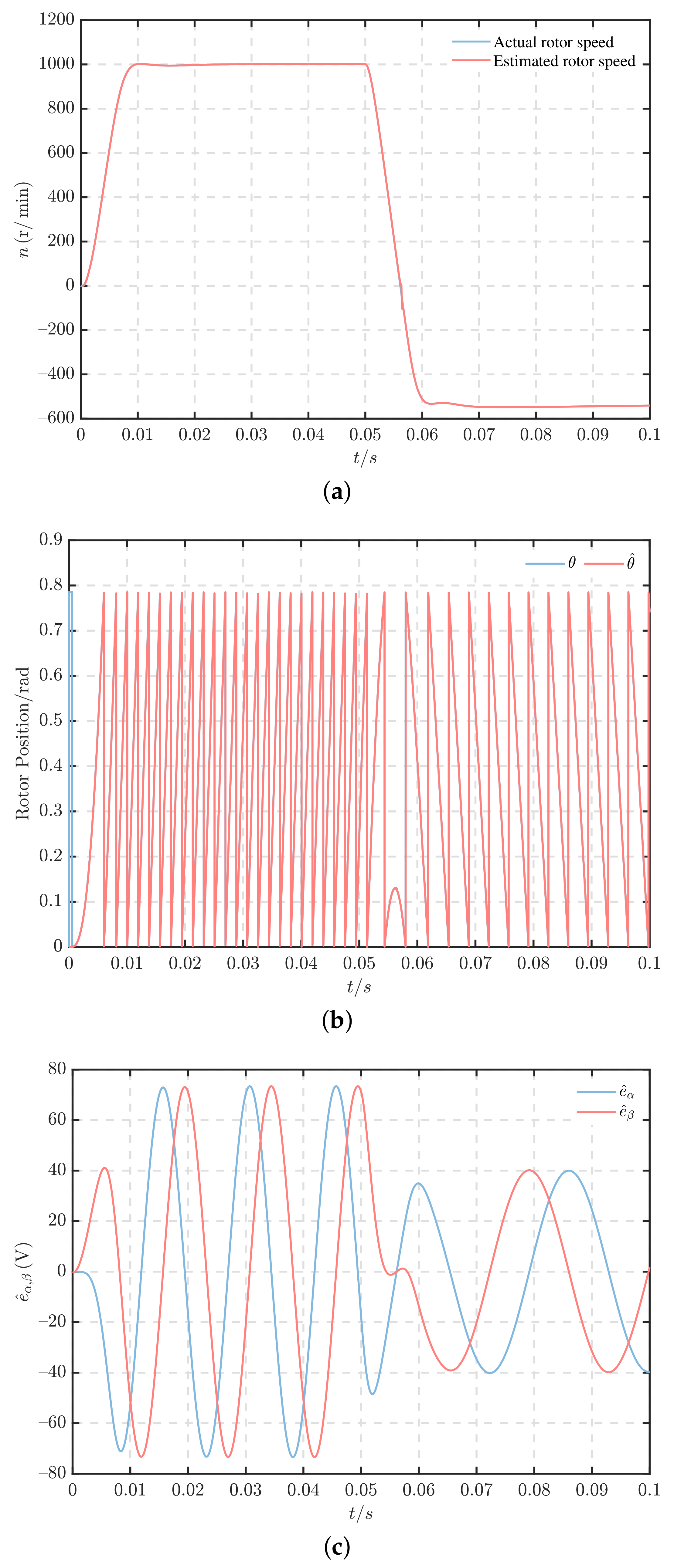
5.1. Steady-State Performance
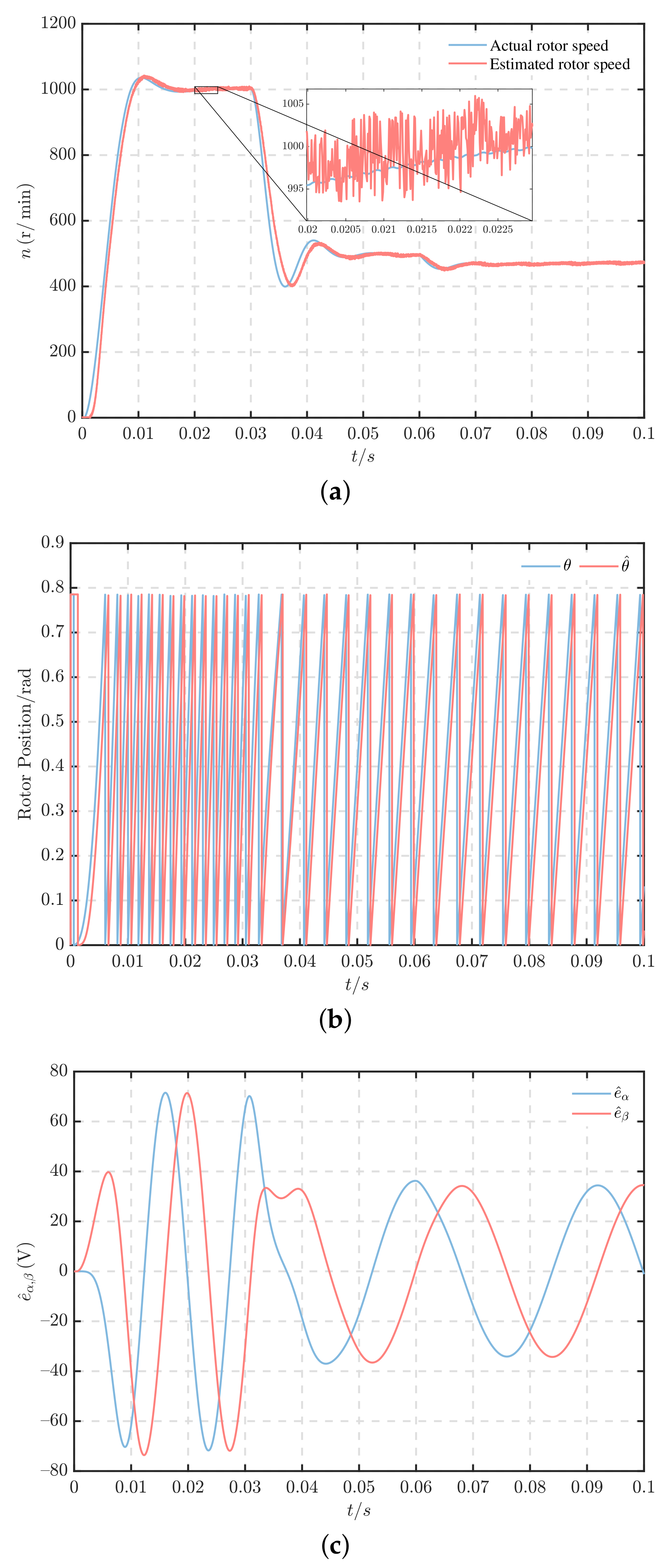
5.2. Dynamic Performance
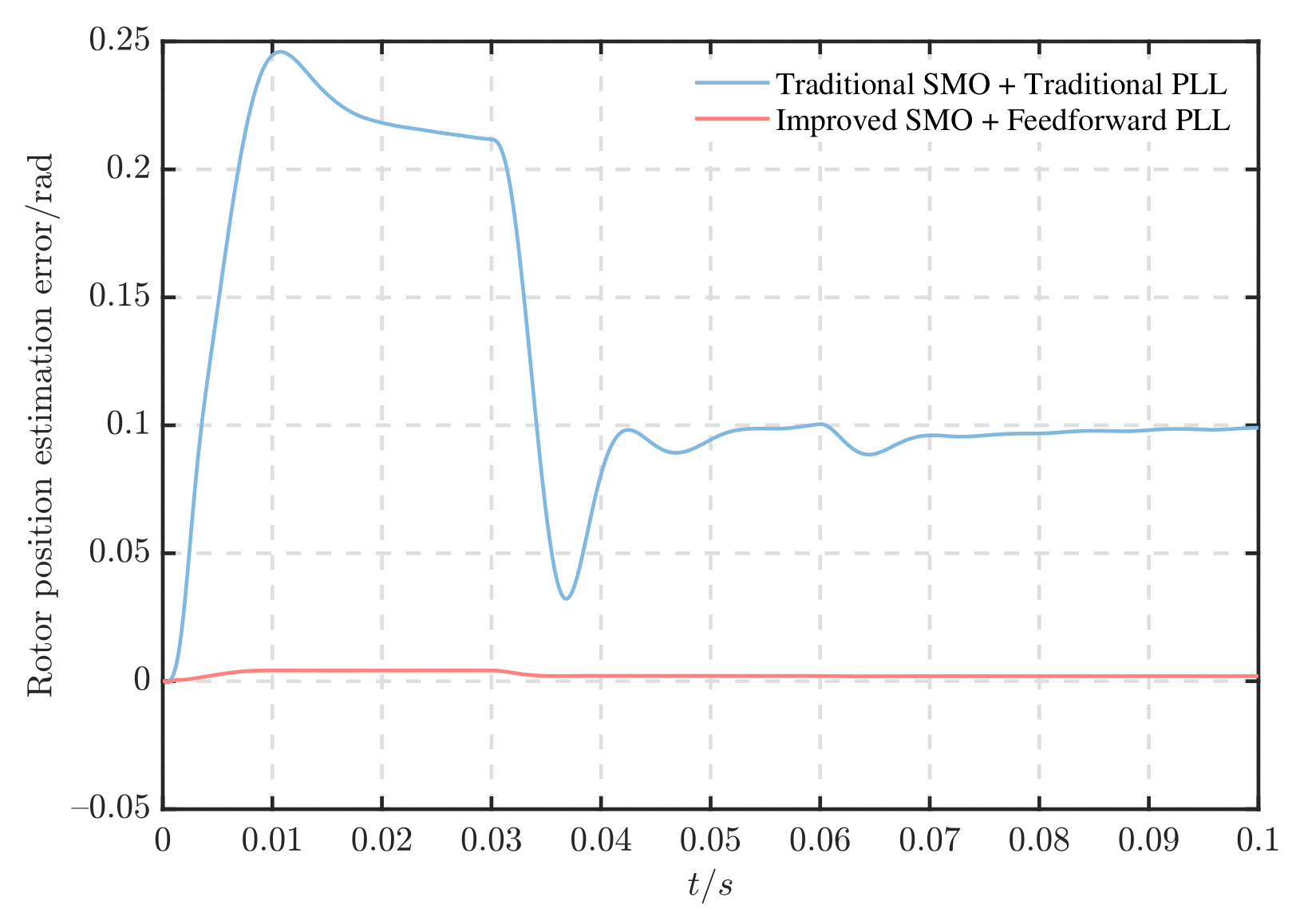
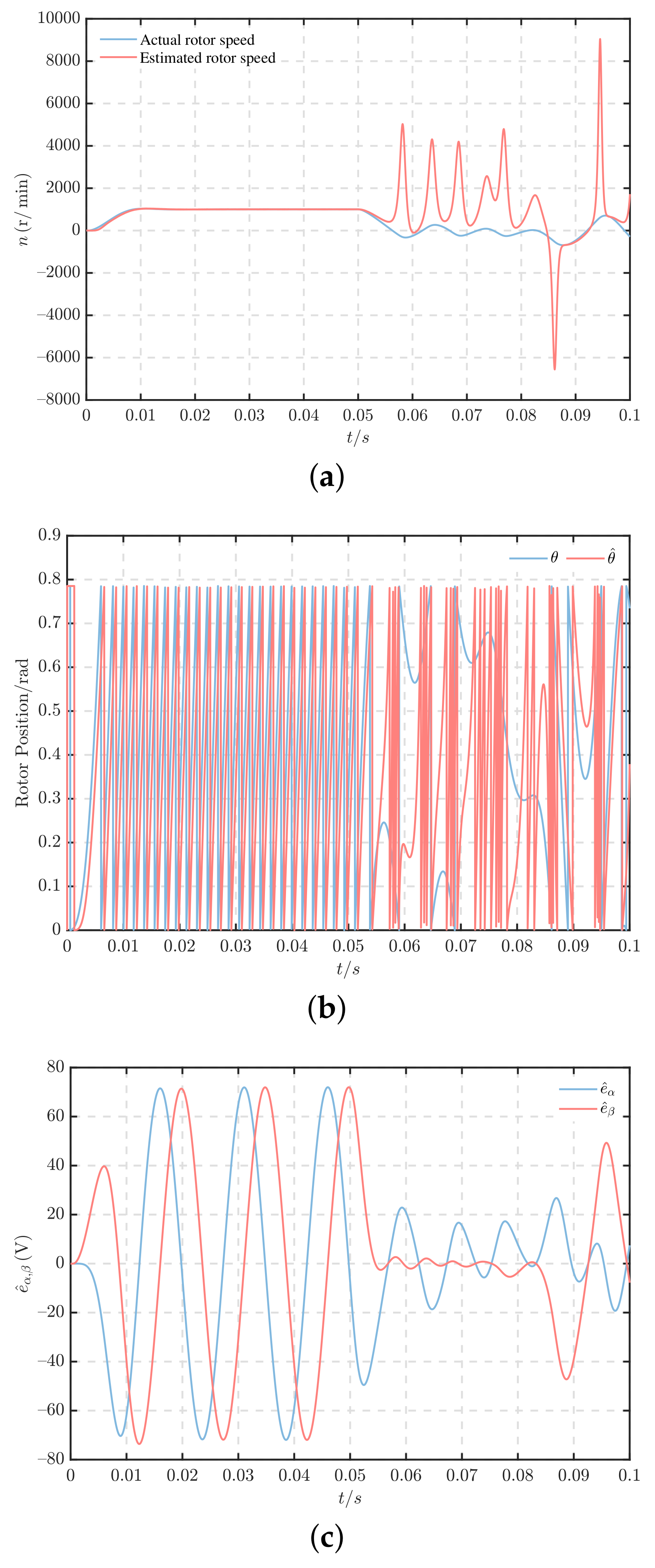
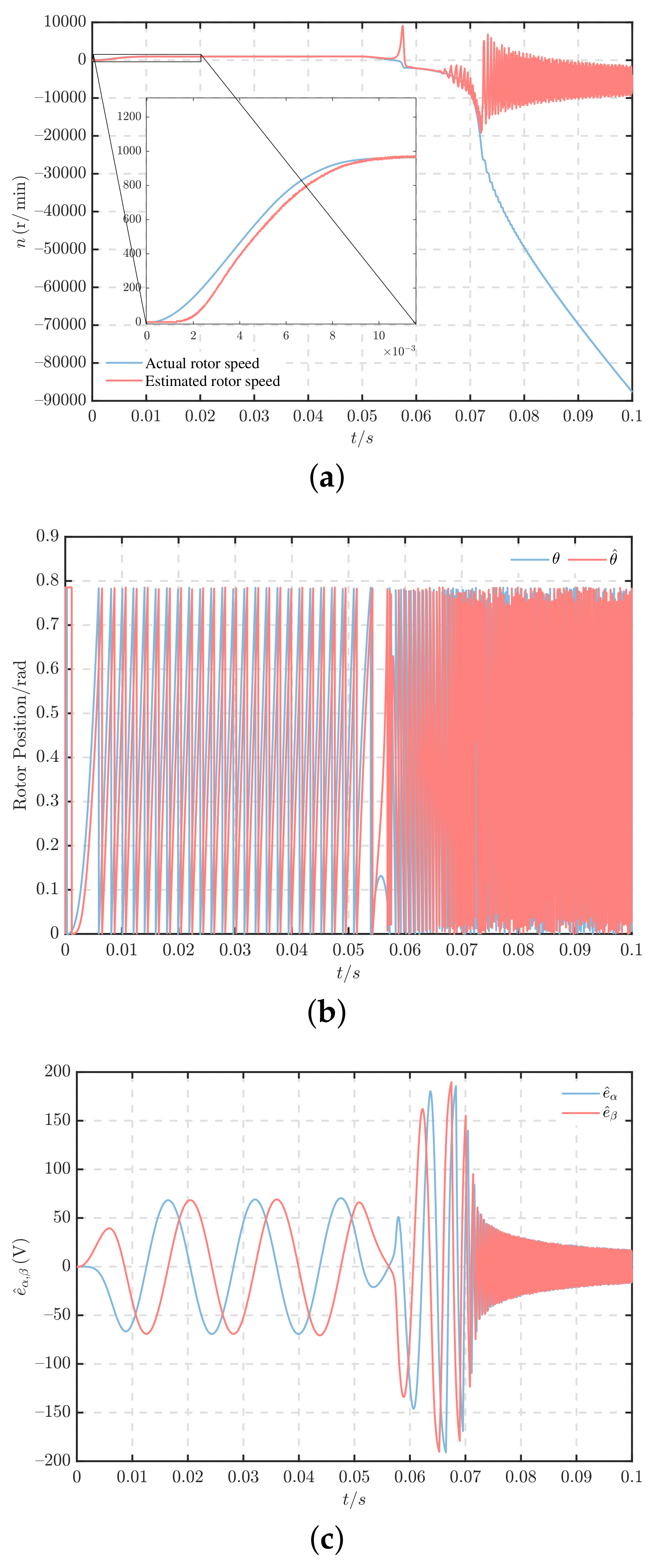
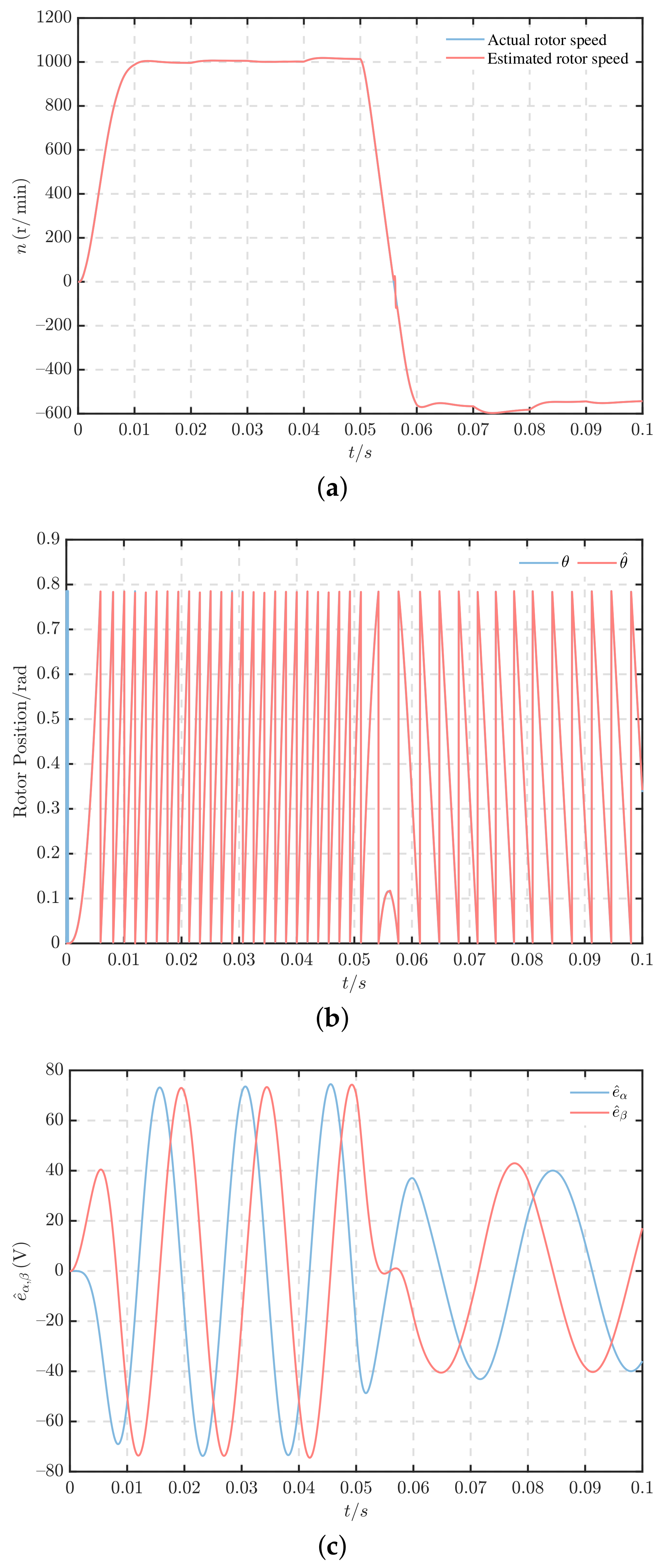
5.3. Forward and Reverse
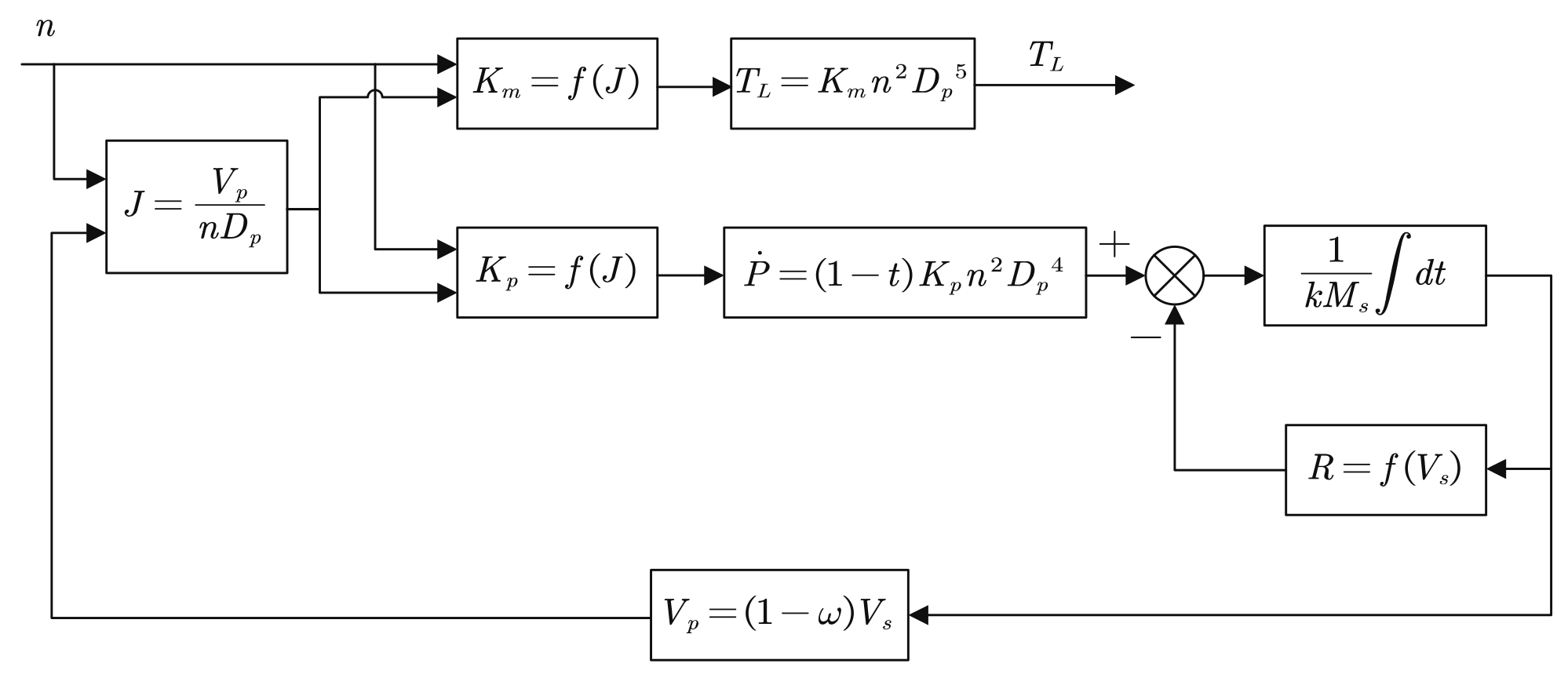
5.4. Performance under Ship Propeller Load
6. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bai, H.; Yu, B. Position estimation of fault-tolerant permanent magnet motor in electric power propulsion ship system. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 890–898. [Google Scholar] [CrossRef]
- Du, J.; Li, J.; Lewis, F.L. Distributed 3D Time-Varying Formation Control of Underactuated AUVs with Communication Delays Based on Data-Driven State Predictor. IEEE Trans. Ind. Inform. 2022, 1–9, early access. [Google Scholar] [CrossRef]
- Qin, J.; Du, J. Robust adaptive asymptotic trajectory tracking control for underactuated surface vessels subject to unknown dynamics and input saturation. J. Mar. Sci. Technol. 2022, 27, 307–319. [Google Scholar] [CrossRef]
- Qin, J.; Du, J.; Li, J. Adaptive finite-time trajectory tracking event-triggered control scheme for underactuated surface vessels subject to input saturation. IEEE Trans. Intell. Transp. Syst. 2023, 1–11, early access. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z.; Hua, Q.; Shang, W.; Luo, Q.; Yu, K. AI-Empowered Speed Extraction via Port-like Videos for Vehicular Trajectory Analysis. IEEE Trans. Intell. Transp. Syst. 2023, 1–12, early access. [Google Scholar] [CrossRef]
- Qin, J.; Du, J. Minimum-learning-parameter-based adaptive finite-time trajectory tracking event-triggered control for underactuated surface vessels with parametric uncertainties. Ocean Eng. 2023, 271, 113634. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Liu, W.; Wu, H.; Han, B.; Zhao, J. Quantifying Arctic oil spilling event risk by integrating analytic network process and fuzzy comprehensive evaluation model. Ocean Coast. Manag. 2022, 228, 106326. [Google Scholar] [CrossRef]
- Bai, H.; Yu, B.; Ouyang, W.; Yan, X.; Zhu, J. HF-based sensorless control of a FTPMM in ship shaftless rim-driven thruster system. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16867–16877. [Google Scholar] [CrossRef]
- Yan, X.; Liang, X.; Ouyang, W.; Liu, Z.; Liu, B.; Lan, J. A review of progress and applications of ship shaft-less rim-driven thrusters. Ocean Eng. 2017, 144, 142–156. [Google Scholar] [CrossRef]
- Sulligoi, G.; Vicenzutti, A.; Menis, R. All-electric ship design: From electrical propulsion to integrated electrical and electronic power systems. IEEE Trans. Transp. Electrif. 2016, 2, 507–521. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, W. An adaptive sliding-mode observer with a tangent function-based PLL structure for position sensorless PMSM drives. Int. J. Electr. Power Energy Syst. 2017, 88, 63–74. [Google Scholar] [CrossRef]
- Bai, H.; Zhu, J.; Qin, J.; Sun, J. Fault-tolerant control for a dual-winding fault-tolerant permanent magnet motor drive based on SVPWM. IET Power Electron. 2017, 10, 509–516. [Google Scholar] [CrossRef]
- Qiao, Z.W.; Shi, T.N.; Wang, Y.D.; Yan, Y.; Xia, C.L.; He, X.N. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor. IEEE Trans. Ind. Electron. 2013, 60, 710–719. [Google Scholar] [CrossRef]
- Yang, Z.; Yan, X.; Ouyang, W.; Bai, H. Sensor lessPMSM Control Algorithm for Rim-Driven Thruster Based on Improved PSO. In Proceedings of the 2021 6th International Conference on Transportation Information and Safety, Wuhan, China, 22–24 October 2021; pp. 285–292. [Google Scholar]
- Seo, D.; Bak, Y.; Lee, K. An Improved Rotating Restart Method for a Sensorless Permanent Magnet Synchronous Motor Drive System Using Repetitive Zero Voltage Vectors. IEEE Trans. Ind. Electron. 2020, 67, 3496–3504. [Google Scholar] [CrossRef]
- Wang, G.L.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives-A Review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Zhang, X.G.; Li, Z.X. Sliding-Mode Observer-Based Mechanical Parameter Estimation for Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2016, 31, 5732–5745. [Google Scholar] [CrossRef]
- Yang, H.; Yang, R.; Hu, W.; Huang, Z.M. FPGA-Based Sensorless Speed Control of PMSM Using Enhanced Performance Controller Based on the Reduced-Order EKF. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 289–301. [Google Scholar] [CrossRef]
- Abo-Khalil, A.G.; Eltamaly, A.M.; Alsaud, M.S.; Sayed, K.; Alghamdi, A.S. Sensorless control for PMSM using model reference adaptive system. Int. Trans. Electr. Energy Syst. 2021, 31, e12733. [Google Scholar] [CrossRef]
- Bernard, P.; Praly, L. Estimation of Position and Resistance of a Sensorless PMSM: A Nonlinear Luenberger Approach for a Nonobservable System. IEEE Trans. Autom. Control. 2021, 66, 481–496. [Google Scholar] [CrossRef]
- Wang, G.L.; Hao, X.F.; Zhao, N.N.; Zhang, G.Q.; Xu, D.G. Current Sensor Fault-Tolerant Control Strategy for Encoderless PMSM Drives Based on Single Sliding Mode Observer. IEEE Trans. Transp. Electrif. 2020, 6, 679–689. [Google Scholar] [CrossRef]
- Wu, L.G.; Liu, J.X.; Vazquez, S.; Mazumder, S.K. Sliding Mode Control in Power Converters and Drives: A Review. IEEE-CAA J. Autom. Sin. 2022, 9, 392–406. [Google Scholar] [CrossRef]
- Kang, W.X.; Li, H. Improved sliding mode observer based sensorless control for PMSM. IEICE Electron. Express 2017, 14, 20170934. [Google Scholar] [CrossRef]
- Wibowo, W.K.; Jeong, S.K. Improved estimation of rotor position for sensorless control of a PMSM based on a sliding mode observer. J. Cent. South Univ. 2016, 23, 1643–1656. [Google Scholar] [CrossRef]
- Ren, N.N.; Fan, L.; Zhang, Z. Sensorless PMSM Control with Sliding Mode Observer Based on Sigmoid Function. J. Electr. Eng. Technol. 2021, 16, 933–939. [Google Scholar] [CrossRef]
- Ye, S.C.; Yao, X.X. An Enhanced SMO-Based Permanent-Magnet Synchronous Machine Sensorless Drive Scheme with Current Measurement Error Compensation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4407–4419. [Google Scholar] [CrossRef]
- Yang, Z.B.; Ding, Q.F.; Sun, X.D.; Lu, C.L.; Zhu, H.M. Speed sensorless control of a bearingless induction motor based on sliding mode observer and phase-locked loop. ISA Trans. 2022, 123, 346–356. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.; Hu, Y.H.; Gao, J.Q.; Wang, Y.G.; Yan, L.M. An Improved Delay-Suppressed Sliding-Mode Observer for Sensorless Vector-Controlled PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5913–5923. [Google Scholar] [CrossRef]
- Song, X.D.; Fang, J.C.; Han, B.C.; Zheng, S.Q. Adaptive Compensation Method for High-Speed Surface PMSM Sensorless Drives of EMF-Based Position Estimation Error. IEEE Trans. Power Electron. 2016, 31, 1438–1449. [Google Scholar] [CrossRef]
- Peng, H.; Zhu, X.; Yang, L.; Zhang, G. Robust controller design for marine electric propulsion system over controller area network. Control Eng. Pract. 2020, 101, 104512. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| number of pole pairs p | 4 |
| stator resistance | 2.875 |
| stator inductor | 8.5 |
| rotational inertia J | 0.001 |
| permanent magnet flux | 0.175 |
| DC voltage | 311 |
| Parameter | Value |
|---|---|
| Propeller diameter /m | 0.1 |
| Hull mass /kg | 100 |
| Water attachment coefficient k | 1.1 |
| Wake coefficient | 0.12285 |
| Thrust derating coefficient t | 0.146 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, H.; Yu, B.; Gu, W. Research on Position Sensorless Control of RDT Motor Based on Improved SMO with Continuous Hyperbolic Tangent Function and Improved Feedforward PLL. J. Mar. Sci. Eng. 2023, 11, 642. https://doi.org/10.3390/jmse11030642
Bai H, Yu B, Gu W. Research on Position Sensorless Control of RDT Motor Based on Improved SMO with Continuous Hyperbolic Tangent Function and Improved Feedforward PLL. Journal of Marine Science and Engineering. 2023; 11(3):642. https://doi.org/10.3390/jmse11030642
Chicago/Turabian StyleBai, Hongfen, Bo Yu, and Wei Gu. 2023. "Research on Position Sensorless Control of RDT Motor Based on Improved SMO with Continuous Hyperbolic Tangent Function and Improved Feedforward PLL" Journal of Marine Science and Engineering 11, no. 3: 642. https://doi.org/10.3390/jmse11030642
APA StyleBai, H., Yu, B., & Gu, W. (2023). Research on Position Sensorless Control of RDT Motor Based on Improved SMO with Continuous Hyperbolic Tangent Function and Improved Feedforward PLL. Journal of Marine Science and Engineering, 11(3), 642. https://doi.org/10.3390/jmse11030642






