Abstract
This work is devoted to increasing the computational efficiency of numerical methods for the one-way Helmholtz Equation (higher-order parabolic equation) in a heterogeneous underwater environment. The finite-difference rational Padé approximation of the propagation operator is considered, whose artificial computational parameters are the grid cell sizes and reference sound speed. The relationship between the parameters of the propagation medium and the artificial computational parameters is established. An optimized method for automatic determination of the artificial computational parameters is proposed. The optimization method makes it possible to account for any propagation angle and arbitrary variations in refractive index. The numerical simulation results confirm the adequacy and efficiency of the proposed approach. Automating the selection process of the computational parameters makes it possible to eliminate human errors and avoid excessive consumption of computational resources.
1. Introduction
Sound propagation in the underwater marine environment is described by the wave equation. Given the variety of heterogeneities that occur under water, as well as large distances, numerical modeling of the wave propagation appears to be a rather sophisticated problem. For over 20 years, improving the efficiency of computer modeling methods has remained an urgent task [1]. One of the most widely used approaches for solving this problem is the parabolic equation method [2] and its wide-angle generalizations [3,4,5], also known as the one-way Helmholtz equation. Although the first publications on the application of the parabolic equation method in hydroacoustics appeared half a century ago [6,7], it is still actively undergoing development [8,9,10]. The advantage of the parabolic equation method is the possibility of taking into account both vertical and horizontal inhomogeneities of the medium. Backscattering can also be modeled [11,12]. There are modifications for elastic medium and essentially three-dimensional space [13]. It is worth mentioning the recently developed iterative method for solving the Helmholtz equation as a series of the parabolic equation solutions [14], and the practical applications of this method for the numerical solution of computational underwater acoustics problems [15].
Another widely used approach to computing the acoustic field is the method of normal modes [16]. Although this method was initially asymptotic and applicable only for a horizontally homogeneous medium, a number of modifications have allowed this method to be used in practical problems. In particular, the KRAKEN [17] software tool for predicting acoustic transmission-loss in the ocean was developed on its basis.
The available general-purpose methods, such as the finite element [18] or boundary element [19] method, are not practically applicable to the problem of the acoustic wave propagation in the ocean. This is due to the huge size of the computational domain compared to the wavelength, which makes computations too slow or even impossible. Nevertheless, their use is reasonable for verification and testing of faster models and software implementations.
The application of the parabolic equation method is not limited to computational hydroacoustics. The method was first introduced by Leontovich and Fock in 1946 [20] to solve the problem of radio wave propagation in an inhomogeneous troposphere. Since then, new modifications have constantly been developed to account for complex inhomogeneities [21], boundary conditions [22,23] and to increase computational efficiency. In addition to the radio frequency range, the method is also successfully used in the optical range for computing a beam trajectory under various conditions [24,25]. A large number of numerical methods have been developed for the Schrodinger Equation [26,27], which is an analog of the diffraction parabolic equation. Another analogue of the parabolic equation of the diffraction theory is the Black–Scholes model [28], which has had a huge impact on financial mathematics. Heat transfer equation is also a parabolic one and is solved by similar numerical methods [29]. The principle of mathematical model universality [30] allows applying the same numerical methods to solve problems of a different physical nature.
There are many practical problems in underwater acoustics where sound propagation modeling plays a key role. [31]. These include remote sensing of the movement of ships and marine life [32], as well as determination of their characteristics [33]. Computer modeling is used to characterize sea currents and the seabed [34], and for estimating the global noise level from shipping and its impact on the world’s oceans [35,36]. The OALIB web resource [37] contains a large number of computational hydroacoustics methods software implementations, experimental data and other useful materials on the specified topic.
Each computer simulation method contains a number of artificial computational parameters. Such parameters include the size of the computational grid cells, the order of approximation, various thresholds and many others. These parameters are usually selected manually by the user (expert). The human factor can lead to modeling errors due to incorrectly selected parameters. Even if the parameters are chosen correctly, the solution may be suboptimal in terms of computational efficiency. For example, the choice of an insufficiently dense computational grid leads to incorrect results, and an overly dense one leads to overspending of the computational resources and slow modeling. Oceanologists, hydroacoustics, sailors and other potential users of the simulation results most often are not specialists in the numerical methods. After all, the need for an expert reduces the level of automation. This circumstance is a significant disadvantage that hinders the wider use of complex mathematical methods in practice.
Previously [38], the problem of computational grid optimization was formulated as the minimization of the discrete dispersion relation error. However, this approach did not take into account variations in the refractive index, which are highly significant in underwater acoustics. It was shown in [39], that a significant increase in performance can be achieved on a non-uniform height grid, but a specific deterministic algorithm for its generation depending on the environment parameters was not presented. The purpose of the present work is to develop an algorithm for the automatic selection of the artificial computational parameters, namely the size of the computational grid cells and the reference sound speed. For this purpose, analytical accuracy estimates depending on the computational parameters and properties of the propagation medium were derived. The optimization problem was formulated on this basis.
The paper is organized as follows. The next two sections present the mathematical formulation of the acoustic wave propagation problem in an inhomogeneous marine environment and derive a method for solving it using the finite-difference Padé approximations. Algorithms for optimizing the computational grid and reference sound speed are introduced in Section 4. Section 5 is devoted to the analysis of the optimization algorithm results for the various environmental parameters. Section 6 presents a comparative analysis of the numerical simulations for several common propagation conditions.
2. Mathematical Problem Statement and Definitions
Acoustic pressure in two-dimensional media on a fixed frequency f satisfies the Helmholtz equation in the following form [16]
where
is the sound speed, is a reference sound speed, which in general can be chosen arbitrarily, is the density of the medium. Unknown function is a complex value and is defined on set .
The Dirichlet boundary condition is posed on the upper boundary between the sea and air
One can use a special non-local boundary condition to take into account the rough sea surface [40]. A transparent boundary condition [41] is set at the lower boundary of the computational domain.
The wave process is generated by the initial condition
with known function , which corresponds to the radiation source pattern.
A schematic description of the considered problem is depicted in Figure 1.
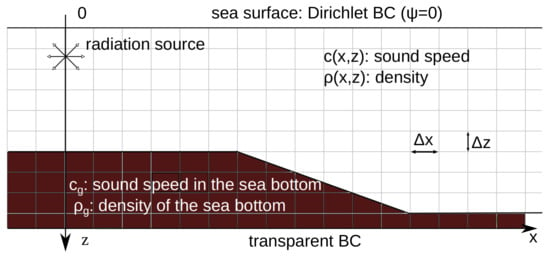
Figure 1.
A schematic description of the considered problem.
Using the change of variable [42]
we can omit the density function in operator D and rewrite Equation (1) in a more convenient form
Obviously, this replacement does not work in the case of density jumps, which usually occurs at the water–bottom boundary. In this case, it is recommended to divide the integration domain into separate parts, in which the density is continuous, and to stitch the boundaries using the boundary conditions [16]. In what follows, for simplicity, we assume that the density is constant throughout the underwater medium.
3. Finite-Difference Padé Approximation
In this section, we will show the derivation of a step-by-step solution to the Helmholtz equation. Special attention will be paid to the influence of input parameters on the solution. For a more detailed derivation and its theoretical aspects, we refer the reader to works [3,4,16,43,44].
We seek the numerical solution on a uniform computational grid with steps and .
Let us write down the expansion of the field into the plane waves in terms of the vertical wavenumber [45]
Variable is expressed via propagation angle as follows
To fulfill (3), it is sufficient to satisfy the following equation
Bearing in mind that in the case of uniform density
Equation (4) can be formally written as an expansion into waves propagating in the positive and negative directions along the x-axis
In what follows, we consider only waves propagating in the positive direction and, accordingly, discard the second term in (5). Then, the step-by-step solution is written as follows
Apply the rational Padé approximation [46,47] of order in the vicinity of point
where and are the Padé approximation coefficients,
Using the obtained rational approximation (8), the action of the propagation operator at each step in the variable x can be represented as a system of p one-dimensional differential equations [44]
where
System (9) is solved sequentially from top to bottom.
Operator (10) is approximated by the fourth-order Numerov method [48]
where
second difference operator is defined as follows
Thus, each line of system (9) can be solved by the tridiagonal matrix method in linear time.
Each step on requires p solutions of tridiagonal equations. Thus, the asymptotic complexity of the numerical scheme is expressed by the formula
4. Computational Parameters Optimization Algorithm
As can be seen from the previous section, there are the following artificial parameters of the numerical scheme: longitudinal grid step , transversal grid step and reference sound speed . It is common to select them manually based on semi-empirical considerations. In this section, we propose an algorithm for automatically determining them in an optimal way.
4.1. Computational Grid Optimization
Let us denote the minimum and maximum values of the sound speed in the desired medium as follows
Owing to (7), possible values of variable will belong to interval , where
where is the maximum propagation angle, which can be estimated from the geometry of the problem.
We first estimate the Numerov approximation error (11). To do this, we take a one-dimensional plane wave of the form
Now we can estimate the maximum error on the required range of the spectral variable
Keeping in mind that , it is reasonable to set .
Next, we estimate the approximation error of the propagation operator at each step along the x axis. Assume first, that there is no second derivative approximation error (). Then, the estimate reduces to the error between the original propagation operator (6) and its Padé approximation (8) on desired interval
To take into account the vertical discretization error (13), we need to keep in mind that each dot will be replaced by range . Then the error estimate at each step will be written as follows
Bearing in mind the asymptotic Formula (12), we obtain the following optimization problem. We are given the maximum distance from the source and the required accuracy at that distance. It is required to maximize the size of the computational grid cells
under condition
where is the number steps on x.
4.2. Reference Sound Speed Optimization
Let us now turn to the parameter and its optimal value determination. Figure 2 demonstrates the distribution of error when . It can be seen that the Padé approximation is local and the smallest error is observed at the point , increasing monotonically with distance from it in any direction. Recall that the value of can be chosen arbitrarily. It gives us the opportunity to choose values and in a way that interval most completely fell into the vicinity of the point with the best accuracy. Based on equality , we obtain the following optimal value.
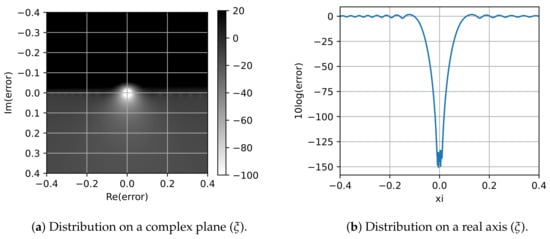
Figure 2.
Distribution of error when .
Note that the variations in sound speed and the required accuracy are known a priori, and the maximum propagation angle can be easily estimated from the geometry of the problem.
5. Optimization Results
This section presents the results of optimization for various propagation scenarios. In all subsequent examples in this section, the operation frequency is chosen equal to 500 Hz. Keeping in mind asymptotic Formula (12), the gain between methods is further calculated using the following formula
5.1. Influence of the Maximum Distance from the Source
First, consider the case of a homogeneous medium with constant sound speed m/s. The source frequency is 500 Hz. We will proceed from the maximum propagation angle . It is common in such case to set the value of also equal to 1500 m/s. However, Formula (15) gives optimal value of equal to m/s. Table 1 shows the optimal values of the computational grid cell sizes for various values of parameter and distance from the source . In all the examples, target accuracy is set to . It can be seen that the use of parameter calculated by Formula (15) allows us to use about four-times more sparse grid, which gives an approximate four-fold corresponding reduction in the propagation runtime. As expected, the location of segment in the middle of point gives more accurate approximation in (8). It is also clear from Table 1, that increasing the distance from the source leads to a decrease in the computational grid cell sizes.

Table 1.
Optimal values of the cell sizes, , , Hz, rational approximation order is .
5.2. Effect of the Maximum Propagation Angle
Next, let us look at how the maximum propagation angle affects the required density of the mesh. Table 2 shows the optimal values of the cell sizes for the various maximum propagation angles. It can be seen that with the increase in the propagation angle, the mesh density increases. It is important to note that for large propagation angles, it is impossible to obtain a mesh within the Padé approximation without the shift. Indeed, as can be seen from condition (14), as decreases, the required value of also decreases, which in turn requires a further decrease of . The proposed method of calculating the optimal allows one to overcome this limitation. It can be seen that this method allows taking into account the entire visible spectrum of propagation angles. At the same time, its gain increases with the increase in the maximum propagation angle.

Table 2.
Optimal values of the cell sizes, , 5000 m, Hz, rational approximation order is . “ - ” means that a reasonable grid could not be found.
5.3. Influence of the Approximation Order
Now let us consider how the order of approximation affects the computational grid and the performance of the numerical scheme. Table 3 shows the mesh sizes for several Padé approximation orders, second- and fourth-order approximations of the vertical operator (11). It is observable that the fourth-order Numerov scheme can significantly increase the performance of the whole scheme without increasing the computational costs. Bearing in mind that increasing the rational approximation order leads to an increase in computations at each step by x, Table 3, in addition to the mesh sizes, contains the value of asymptotic complexity (12), which is linearly related to the runtime of the propagation algorithm. The use of higher-order rational approximations also gives a significant increase in the performance of the numerical scheme. It is noteworthy that for the widely used Crank–Nicolson scheme, which corresponds to the approximation order [1/1], and propagation angle , it appears to be impossible to found a reasonable grid.

Table 3.
Optimal values of the cell sizes. , = 1000 m, , Hz, m/s. “ - ” means that a reasonable grid could not be found.
5.4. Effect of the Inhomogeneous Sound Velocity Profile
Finally, let us consider the optimization of the computational grid in a medium with an inhomogeneous refractive index. Suppose that the sound speed varies between 1500 and 1550 m/s. Table 4 shows the optimal values of the cell sizes for various distances from the source Comparing Table 1 and Table 4, it can be seen that the presence of inhomogeneities of the refractive index leads to a decrease in the required cell sizes. As before, shifting parameter gives an opportunity to increase the performance by about three times.

Table 4.
Optimal values of the cell sizes. , , Hz, rational approximation order is .
5.5. Specifics of the Optimization Algorithm Implementation
The computational grid optimization algorithm is implemented by simply iterating through various values of the computational grid cell sizes. This explains the fact that in the tables above, the optimal values are rounded. Given the small range of possible values, this simple approach turns out to be quite acceptable in terms of performance. In principle, it would be possible to implement minimization more efficiently. Bearing in mind the fact that the error monotonically increases with increasing grid step, it is possible to implement a binary-search-based algorithm. When the performance is critical, one can also use pre-tabulation of parameters for various input data.
Maximum propagation angle can be estimated by the following formula
where is the maximum angle of the antenna pattern, is the maximum slope angle between bottom and water. Both parameters are estimated directly from the direction of the source and the bottom relief.
6. Numerical Results
The solutions obtained by the wavenumber integration (WNI) method are used as a reference in all examples [16]. The WNI method is not an asymptotic one (unlike the normal mode method), and allows for a solution to be made on an arbitrary computational grid, which is convenient for point-by-point comparison. All the presented numerical examples are computed using an open source Python 3 software library [49] developed by the author.
6.1. Waveguide with a Perfectly Reflective Bottom
In the first example, we will consider the effect of the wave propagation angle on the accuracy of the numerical scheme. To do this, consider an extremely simple scenario: falling and multiple reflections of a directional beam. The acoustic field is generated by a narrow beam with a width of , directed at an angle of . The acoustic frequency of the source is 1000 Hz, the depth is 100 m. The sound speed is constant throughout the integration space and is equal to 1500 m/s. The Neumann condition is established on the lower boundary: . Figure 3 demonstrates the results of the numerical modeling using the Padé approximation method for two values of : 1500 m/s and 1591 m/s (corresponding to (15)). In both cases, the same grid was used: m, m, rational approximation order is equal to . The cell sizes was obtained for m/s and maximum propagation angle . Thus, the computational costs in both cases were identical. However, we see that the result obtained for the suboptimally selected = 1500 m/s differs from the expected one, namely, it fades rapidly as it moves away from the source.
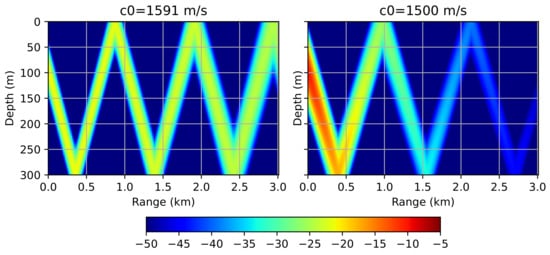
Figure 3.
Waveguide with a perfectly reflective bottom. Acoustic pressure distribution (), computed on a grid with cells m, m using optimal m/s (left) and suboptimal m/s (right).
Now let us compare the obtained results with the WNI method. Figure 4 shows a two-dimensional error distribution between the WNI method and the Padé method. In this example, different meshes were used: m, m for m/s and m, m for m/s. It can be seen that in both cases the results are barely distinguishable; however, the optimal choice of the parameter allows for the use a much more sparse grid.
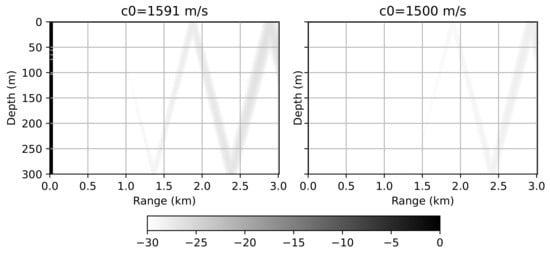
Figure 4.
Waveguide with a perfectly reflective bottom. Error distribution between the Padé approximation method and the WNI method (). m, m, m/s (left) and m, m, m/s (right).
6.2. Waveguide with an Inhomogeneous Refractive Index
In this example, we will add the inhomogeneity of the sound speed and show how it affects the accuracy and the required grid. We introduce the following linearly increasing vertical gradient of the sound speed: m/s and m/s. Figure 5 demonstrates the modeling results for the two various meshes. In the first case, maximum propagation angle and the sound speed variations in range m/s were accounted for during the optimization process. The corresponding computational parameters are 6 m, m, m/s. In the second case, the sound speed variations were ignored, leading to the following parameters: 20 m, m, m/s. It is clearly seen that ignoring the variation in refractive index leads to the fact that not the entire spectrum of waves is correctly taken into account.
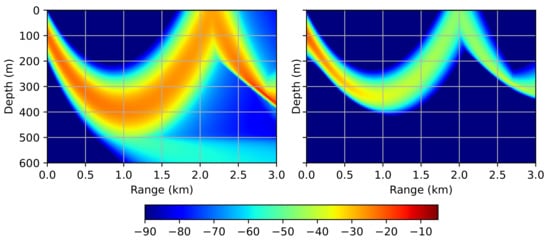
Figure 5.
Waveguide with an inhomogeneous refractive index. Acoustic pressure distribution (). 6 m, m, m/s (left) and 20 m, m, m/s (right).
Figure 6 depicts a two-dimensional error distribution between the WNI method and the Padé method. The results are presented for the two different values of . In both cases, variations of the refractive index were taken into account when optimizing the computational grid. As in the previous example, in both cases it is possible to achieve almost identical results, but the optimized value of allows to decimate the computational grid without reducing the solution accuracy.
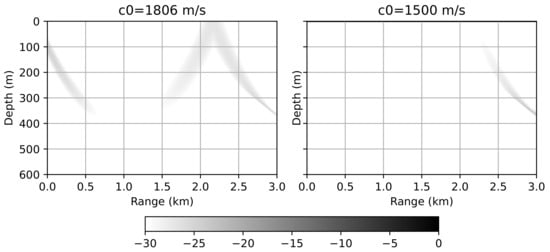
Figure 6.
Waveguide with an inhomogeneous refractive index. Error distribution between the Padé approximation method and the WNI method (). 6 m, m, m/s (left) and m, m, m/s (right).
6.3. Propagation in a Munk Profile
In the last example, we will demonstrate the propagation of acoustic waves in a deep-water Munk waveguide [16]. This is one of the most frequently encountered sound velocity profiles in the deep sea. Operational frequency f in this example is set to 50 Hz. Sound speed profile is depicted in Figure 7. Figure 8 demonstrates the result obtained by the proposed method and the error distribution. It is clearly seen that the error between the Padé and WNI solutions fits within the established acceptable range.
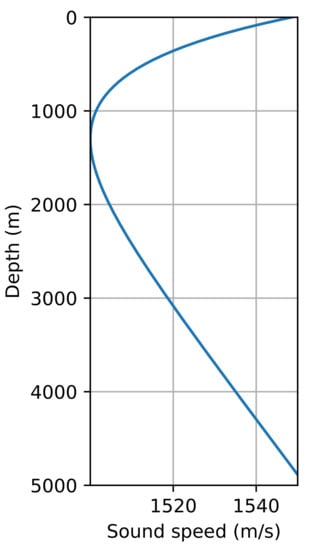
Figure 7.
The Munk profile.
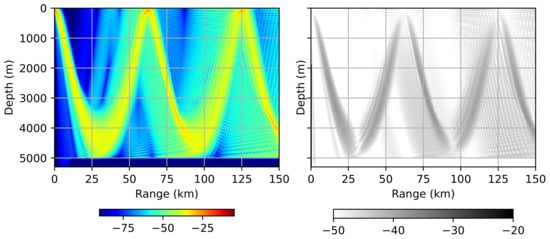
Figure 8.
Propagation in the Munk profile. Acoustic pressure distribution () (left) and error distribution () between the Padé and WNI solutions (right).
7. Conclusions
The proposed mesh optimization algorithm allows the parabolic equation method to be used as part of complex software systems without the need for manual intervention. Automatic selection of parameters prevents human errors and overconsumption of computing resources. Optimization of reference speed of sound allows performance to be enhanced by 3–20 times, while the greatest gain is achieved at large propagation angles. It is shown that the density of the computational mesh depends on a number of parameters: maximum angle of propagation, variation of the refractive index, required accuracy and maximum distance from the source. In general, it can be seen from the provided analysis that the complexity of the propagation medium, i.e., an increase in the mentioned parameters, leads to a thicker mesh. A dense grid is more difficult to select manually and requires more computational resources. Thus, the proposed method is most useful for complex propagation conditions.
The established optimization method does not introduce any new design changes to a well-researched and proven step-by-step numerical scheme. This means that all its properties, including stability, remain in force. In addition, the proposed method does not require any significant changes to the existing software implementations.
Expansion of the proposed method to the elastic equation is planned. Given the growing interest of the community in modeling in a substantially three-dimensional environment [1,13], the proposed method should also be extended to this case. Bearing in mind the previously mentioned principle of mathematical model universality, the proposed method can find applications in a number of other subject areas and mathematical models where parabolic equations are used.
Funding
This research was funded by the Russian Science Foundation grant number 21-71-00039.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Petrov, P.; Katsnelson, B.; Li, Z. Modeling Techniques for Underwater Acoustic Scattering and Propagation (Including 3D Effects). J. Mar. Sci. Eng. 2022, 10, 1192. [Google Scholar] [CrossRef]
- Collins, M.D.; Siegmann, W.L. Parabolic Wave Equations with Applications; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Fishman, L.; de Hoop, M.V.; Van Stralen, M.J.N. Exact constructions of square-root Helmholtz operator symbols: The focusing quadratic profile. J. Math. Phys. 2000, 41, 4881–4938. [Google Scholar] [CrossRef]
- Fishman, L.; McCoy, J.J. Derivation and application of extended parabolic wave theories. I. The factorized Helmholtz equation. J. Math. Phys. 1984, 25, 285–296. [Google Scholar] [CrossRef]
- Bamberger, A.; Engquist, B.; Halpern, L.; Joly, P. Higher order paraxial wave equation approximations in heterogeneous media. SIAM J. Appl. Math. 1988, 48, 129–154. [Google Scholar] [CrossRef]
- Hardin, R.H.; Tappert, F.D. Applications of the split-step Fourier method to the numerical solution of nonlinear and variable coefficient wave equations. SIAM Rev. 1973, 15, 4–23. [Google Scholar]
- Tappert, F.D. The parabolic approximation method. In Wave Propagation and Underwater Acoustics; Springer: Cham, Switzerland, 1977; pp. 224–287. [Google Scholar]
- Kozitskiy, S. Coupled-Mode Parabolic Equations for the Modeling of Sound Propagation in a Shallow-Water Waveguide with Weak Elastic Bottom. J. Mar. Sci. Eng. 2022, 10, 1355. [Google Scholar] [CrossRef]
- Chen, C.F. Reflection on Collins’ split-step Padé solution for the parabolic equation. J. Acoust. Soc. Am. 2022, 151, R3–R4. [Google Scholar] [CrossRef]
- Tu, H.; Wang, Y.; Ma, X.; Zhu, X. Applying the Chebyshev–Tau spectral method to solve the parabolic equation model of wide-angle rational approximation in ocean acoustics. J. Theor. Comput. Acoust. 2022, 30, 2150013. [Google Scholar] [CrossRef]
- Collins, M.D.; Evans, R.B. A two-way parabolic equation for acoustic backscattering in the ocean. J. Acoust. Soc. Am. 1992, 91, 1357–1368. [Google Scholar] [CrossRef]
- Mills, M.J.; Collins, M.D.; Lingevitch, J.F. Two-way parabolic equation techniques for diffraction and scattering problems. Wave Motion 2000, 31, 173–180. [Google Scholar] [CrossRef]
- Lin, Y.T.; Porter, M.B.; Sturm, F.; Isakson, M.J.; Chiu, C.S. Introduction to the special issue on three-dimensional underwater acoustics. J. Acoust. Soc. Am. 2019, 146, 1855–1857. [Google Scholar] [CrossRef]
- Petrov, P.S.; Ehrhardt, M.; Trofimov, M. On decomposition of the fundamental solution of the Helmholtz equation over solutions of iterative parabolic equations. Asymptot. Anal. 2022, 126, 215–228. [Google Scholar] [CrossRef]
- Petrov, P.S.; Ehrhardt, M.; Tyshchenko, A.G.; Petrov, P.N. Wide-angle mode parabolic equations for the modelling of horizontal refraction in underwater acoustics and their numerical solution on unbounded domains. J. Sound Vib. 2020, 484, 115526. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Porter, M.B. The KRAKEN Normal Mode Program; Technical Report; Naval Research Lab: Washington, DC, USA, 1992. [Google Scholar]
- Reddy, J.N. Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Kirkup, S.M. The Boundary Element Method in Acoustics; Integrated Sound Software; University of Central Lancashire: Preston, UK, 2007. [Google Scholar]
- Leontovich, M.A.; Fock, V.A. Solution of the problem of propagation of electromagnetic waves along the Earth’s surface by the method of parabolic equation. J. Phys. USSR 1946, 10, 13–23. [Google Scholar]
- Apaydin, G.; Ozgun, O.; Kuzuoglu, M.; Sevgi, L. A novel two-way finite-element parabolic equation groundwave propagation tool: Tests with canonical structures and calibration. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2887–2899. [Google Scholar] [CrossRef]
- Levy, M.F. Transparent boundary conditions for parabolic equation solutions of radiowave propagation problems. IEEE Trans. Antennas Propag. 1997, 45, 66–72. [Google Scholar] [CrossRef]
- Lytaev, M.S. Nonlocal Boundary Conditions for Split-Step Padé Approximations of the Helmholtz Equation with Modified Refractive Index. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1561–1565. [Google Scholar] [CrossRef]
- Bekker, E.V.; Sewell, P.; Benson, T.M.; Vukovic, A. Wide-angle alternating-direction implicit finite-difference beam propagation method. J. Light. Technol. 2009, 27, 2595–2604. [Google Scholar] [CrossRef]
- Hadley, G.R. Wide-angle beam propagation using Padé approximant operators. Opt. Lett. 1992, 17, 1426–1428. [Google Scholar] [CrossRef]
- Schwendt, M.; Pötz, W. Transparent boundary conditions for higher-order finite-difference schemes of the Schrödinger equation in (1 + 1) D. Comput. Phys. Commun. 2020, 250, 107048. [Google Scholar] [CrossRef]
- Zlotnik, A.; Romanova, A. On a Numerov–Crank–Nicolson–Strang scheme with discrete transparent boundary conditions for the Schrödinger equation on a semi-infinite strip. Appl. Numer. Math. 2015, 93, 279–294. [Google Scholar] [CrossRef]
- Wang, J.; Wen, S.; Yang, M.; Shao, W. Practical finite difference method for solving multi-dimensional black-Scholes model in fractal market. Chaos Solitons Fractals 2022, 157, 111895. [Google Scholar] [CrossRef]
- Savović, S.; Drljača, B.; Djordjevich, A. A comparative study of two different finite difference methods for solving advection–diffusion reaction equation for modeling exponential traveling wave in heat and mass transfer processes. In Ricerche di Matematica; Springer: Cham, Switzerland, 2021; pp. 1–8. [Google Scholar]
- Samarskii, A.A.; Mikhailov, A.P. Principles of Mathematical Modelling: Ideas, Methods, Examples; Taylor and Francis: New York, NY, USA, 2002. [Google Scholar]
- Etter, P.C. Underwater Acoustic Modeling and Simulation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Wang, D.; Huang, W.; Garcia, H.; Ratilal, P. Vocalization source level distributions and pulse compression gains of diverse baleen whale species in the Gulf of Maine. Remote Sens. 2016, 8, 881. [Google Scholar] [CrossRef]
- Dai, M.; Li, Y.; Ye, J.; Yang, K. Joint Tracking of Source and Environment Using Improved Particle Filtering in Shallow Water. J. Mar. Sci. Eng. 2021, 9, 1203. [Google Scholar] [CrossRef]
- Guarino, A.L.; Smith, K.B.; Godin, O.A. Bottom attenuation coefficient inversion based on the modal phase difference between pressure and vertical velocity from a single vector sensor. J. Theor. Comput. Acoust. 2022, 30, 2150008. [Google Scholar] [CrossRef]
- Erbe, C.; Marley, S.A.; Schoeman, R.P.; Smith, J.N.; Trigg, L.E.; Embling, C.B. The effects of ship noise on marine mammals a review. Front. Mar. Sci. 2019, 6, 606. [Google Scholar] [CrossRef]
- Manul’chev, D.; Tyshchenko, A.; Fershalov, M.; Petrov, P. Estimating Sound Exposure Levels Due to a Broadband Source over Large Areas of Shallow Sea. J. Mar. Sci. Eng. 2022, 10, 82. [Google Scholar] [CrossRef]
- Ocean Acoustics Library. 2023. Available online: https://oalib-acoustics.org/ (accessed on 23 January 2023).
- Lytaev, M.S. Automated Selection of the Computational Parameters for the Higher-Order Parabolic Equation Numerical Methods. Int. Conf. Comput. Sci. Appl. 2020, 12249, 296–311. [Google Scholar]
- Sanders, W.M.; Collins, M.D. Nonuniform depth grids in parabolic equation solutions. J. Acoust. Soc. Am. 2013, 133, 1953–1958. [Google Scholar] [CrossRef]
- Brooke, G.H.; Thomson, D.J. Non-local boundary conditions for high-order parabolic equation algorithms. Wave Motion 2000, 31, 117–129. [Google Scholar] [CrossRef]
- Arnold, A.; Ehrhardt, M. Discrete transparent boundary conditions for wide angle parabolic equations in underwater acoustics. J. Comput. Phys. 1998, 145, 611–638. [Google Scholar] [CrossRef]
- Yevick, D.; Thomson, D.J. A hybrid split-step/finite-difference PE algorithm for variable-density media. J. Acoust. Soc. Am. 1997, 101, 1328–1335. [Google Scholar] [CrossRef]
- Levy, M.F. Parabolic Equation Methods for Electromagnetic Wave Propagation; The Institution of Electrical Engineers: London, UK, 2000. [Google Scholar]
- Lytaev, M.S. Rational interpolation of the one-way Helmholtz propagator. J. Comput. Sci. 2022, 58, 101536. [Google Scholar] [CrossRef]
- Brekhovskikh, L.M. Waves in Layered Media; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Baker, G.A.; Graves-Morris, P. Padé Approximants; Cambridge University Press: Cambridge, UK, 1996; Volume 59. [Google Scholar]
- Collins, M.D. A split-step Padé solution for the parabolic equation method. J. Acoust. Soc. Am. 1993, 93, 1736–1742. [Google Scholar] [CrossRef]
- Lee, D.; Schultz, M.H. Numerical Ocean Acoustic Propagation in Three Dimensions; World Scientific: Singapore, 1995. [Google Scholar]
- Lytaev, M.S. PyWaveProp. Wave Propagation Library for Python 3. 2023. Saint Petersburg. Available online: https://github.com/mikelytaev/wave-propagation (accessed on 23 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).