4.2. Propeller Performance Improvement by Blade Tip Geometry Reformation
In this section, we present the results of the optimization studies for reference geometries 4381 and 4382. In both cases, the reference propeller is a five-bladed model with a diameter D = 0.305 m. The design advance coefficient, for which a maximization of efficiency is attempted via blade tip-rake reformation, is J = 0.889. During the optimization, the VLM viscous drag coefficient is set to zero, whereas the leading-edge suction force coefficient is kept the same as the reference propeller geometry. This decision is justified from the fact that changes in the rake distribution are expected to affect significantly the viscous pressure on the blades; thus, it is omitted during the first step in the optimization study. However, for the optimal geometry, additional simulations with CFD are used for viscous drag coefficient calibration. Regarding the control points defining the pitch and maximum camber distributions, for the 4381 propeller, all control points are considered active. For the case of the 4382 propeller, control points with radial positions r/R > 0.5 are considered active, as shown in
Figure 4. Only the active control points are to be multiplied with the proportional coefficient. It was found that for the skewed propeller, the pitch and maximum camber distributions with no alteration near the hub, yielded better performance, justifying the above decision.
The optimal propeller geometries where derived as the best candidates among (5) optimization studies performed for the same problem but starting with different initial reference geometries. The optimal design variable vectors for the examined propellers are summarized in
Table 5. Regarding the rake transition point (x
1), for both propellers the optimal value is close to 70% of tip radius R.
The optimal maximum rake (x
2) in both cases corresponds to a suction-side rake, as shown in
Figure 9 and
Figure 10 for the modified 4381 and 4382 propellers, respectively. Finally, the optimal pitch and maximum camber proportional coefficients are smaller than the corresponding value of the reference geometry. The geometric parameters for the reference and modified propellers are provided in
Appendix A. Regarding the CFD simulations for both the initial and modified geometries, we present below the selected plots. In
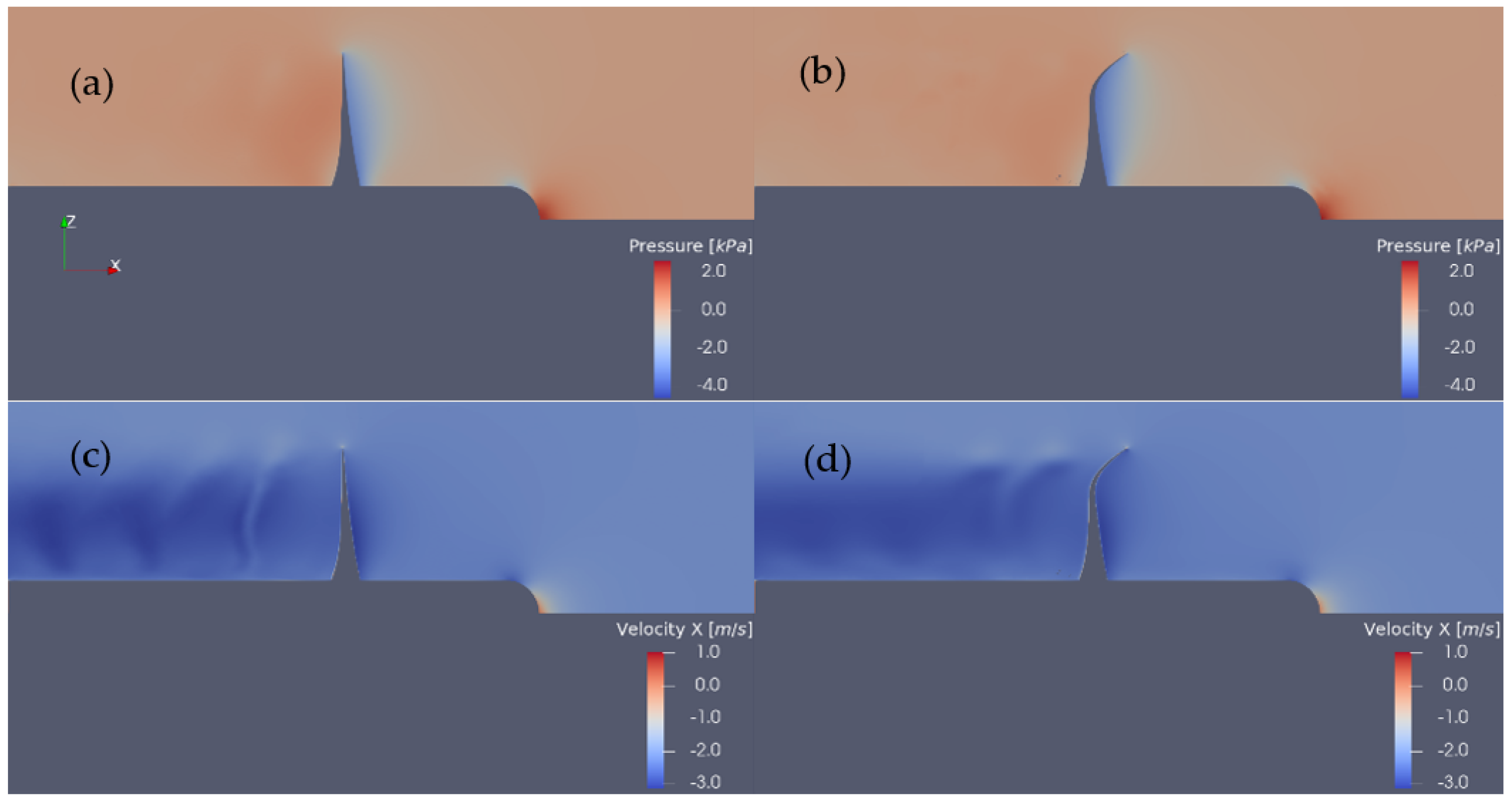
Figure 9, contour plots concerning calculated velocity and pressure fields are presented on the vertical xy plane for both the initial 4381 propeller geometry and the modified one.
Moreover, in
Figure 11, the corresponding comparison concerning the pressure contour on a cylindrical section at radius r/R = 0.95 is shown. In the contour of pressure (top subplots of
Figure 9), we observe the different configuration of the suction side between the original and the modified blade (left and right subplots, respectively). The effect of the blade tip-rake can also be seen in the structure of the wake, as observed by the increase in the axial x-component velocity in the bottom subplots.
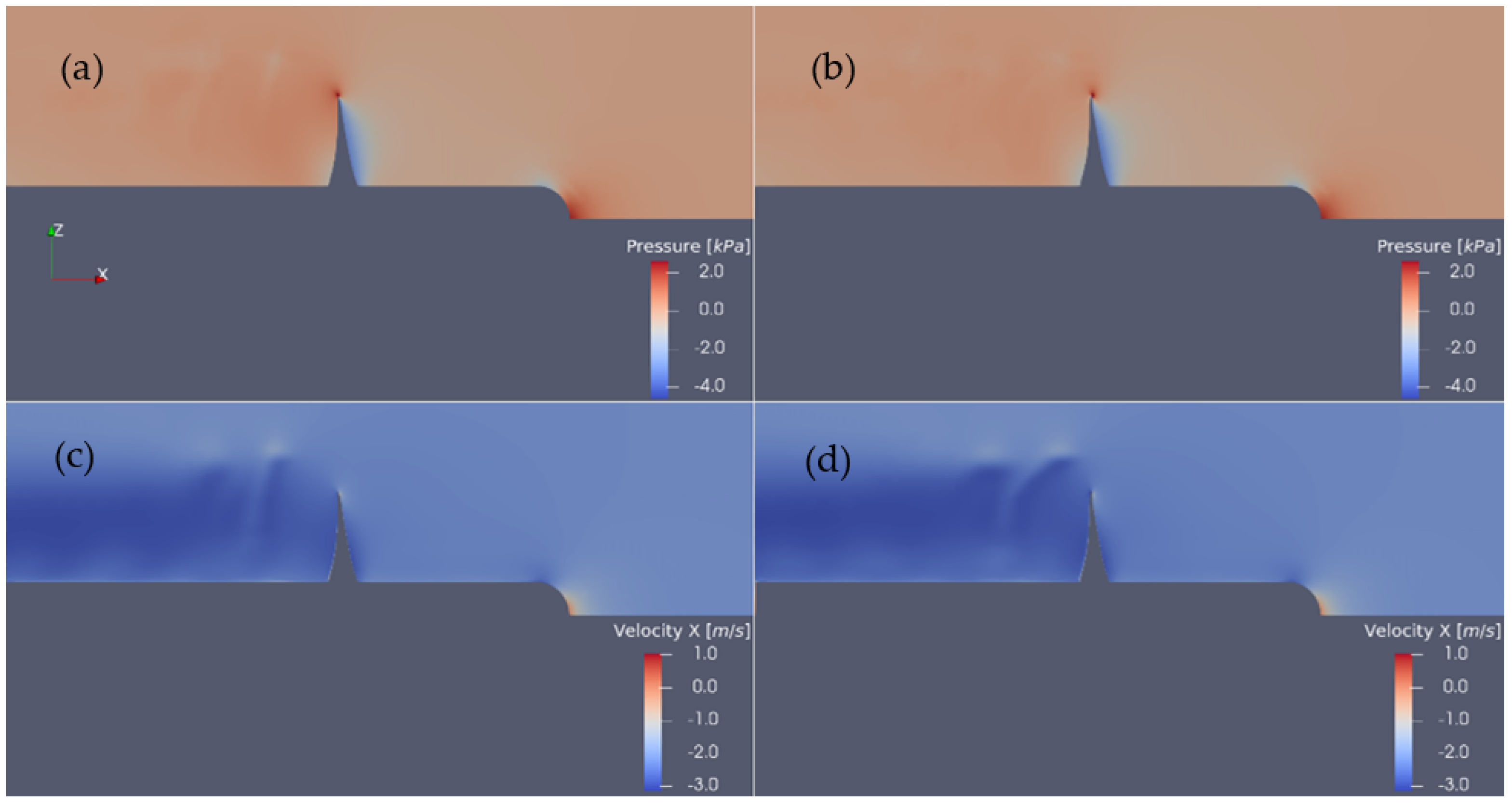
The corresponding plots concerning the initial 4382 skewed propeller geometry and the modified one are presented in
Figure 10 and
Figure 12. However, we notice that the differences concerning the added rake effect are not so obvious in the case of the skewed propeller 4382 in
Figure 10, since in this case, the skew-induced rake influences the geometric modification of tip geometry. The comparison of the pressure contour for the initial and the tip-rake-modified skewed propellers on the cylindrical cut at radius r/R = 0.95 is illustrated in
Figure 12. The difference concerning the locations of the hydrofoil is evident when comparing
Figure 11 and
Figure 12. A common observation from the results is that the modified part of the blade tip geometry increases the pressure at the stagnation point. This is justified since one of the parameters that is adjusted in the optimization process is the camber distribution along the radial increase.
More details concerning the velocity streamlines on the blade for the normal and skewed blade geometries are presented in
Figure 13 and
Figure 14, respectively, as obtained by the post-processing of the CFD results.
Furthermore, the pressure comparison between the original and the optimized propellers can be found in
Figure 15, where the pressure coefficient is plotted over a normalized chord parameterization for four different cylindrical sections, namely r/R = {0.3, 0.5, 0.7, 0.9}. The normalization of pressure is performed using
. By comparing the pressure coefficients, we can observe how the loading of the propeller changes in various radial positions. More specifically, at r/R = 0.3 and for both propellers, there is a difference in the pressure coefficient values at the TE indicating a global change in the flow field of the blade, which is also evident in
Figure 13 and
Figure 14. At r/R = 0.5, there is a drop at the pressure side which is mitigated by the higher velocities in the suction side. Lastly, at r/R = 0.7–0.9, it is clear that the decrease in the suction pressure contributes to a gain in the total sectional force and especially lift. In this setting, as suggested by
Figure 16, for the modified 4381, the total thrust will be reduced, whereas for the modified 4382 propeller, the thrust is expected to increase.
In addition,
Figure 16 contains the pressure coefficient envelope for the 4381 study case at radial position r = 0.7 R, as obtained using viscous-CFD and the calibrated VLM in terms of the reference and the modified geometries. The VLM runs for this case are based on a mesh of (11 × 6) and the coefficients are shown in
Table 6 that follows, which contains a summary of the VLM friction-drag and leading-edge suction force coefficients obtained as a best fit to the CFD data. Typically, VLM post-processing is focused on the average velocity and the pressure difference; however, this shows that in general, the VLM are capable of producing additional results concerning the pressure coefficient on the upper and lower sides that can further facilitate the design and optimization of propeller blades.
Next, in
Table 7, the relative changes between the reference and the modified propeller geometries in terms of the open water curve coefficients calculated using vortex-lattice and MaPFlow are presented. The ideal-flow model over predicts the gain in efficiency as expected. This over prediction, however, is expected to be less for the full-scale propeller geometry where Reynold’s number is significantly larger. The reduction in thrust is also more significant in CFD simulations, suggesting that careful examination of the modified propeller geometry needs to be performed before the optimal geometry is considered an alternative to the reference geometry for the design advance coefficient.
Generally, for the 4381-modified propeller geometry, a performance enhancement of 1.1% is accomplished based on the CFD results, indicating that the vortex-lattice can facilitate the optimization study of a propeller model in the preliminary phase. Similarly, for the case of the skewed propeller, an efficiency gain of 0.5% is predicted from the CFD results. In practical applications, the thrust coefficient needs to be kept very close to the design value. Particularly, the zero-skew 4381-modified geometry shows the 1.12% performance gain with a 4% and 5% decrease in the thrust and torque coefficient, respectively. Regarding the skewed propeller model, the modified 4382 shows a 0.5% efficiency gain based on viscous simulations which also corresponds to a 2.7% and 2.3% increase in the thrust and torque coefficients, respectively. It must be noted that contrary to the reduction in KT and KQ for 4382 obtained by using VLM, an increase in both coefficients is observed using CFD. This observation relies on the fact that VLM is calibrated using the experimental data of the original geometry.
The VLM results show similar trends with CFD in terms of efficiency gain, even though the ideal-flow model over predicts the efficiency gain and under predicts the reduction in thrust and torque. The overprediction of efficiency gain is expected, since ideal-flow models neglect viscous effects. It is evident from the findings that special attention needs to be paid to the optimization of skewed propellers since viscous effects are expected to be more significant. Especially for CFD, closer examination of the sectional thrust (normal in the propeller plane) and the circumferential force (tangent to the propeller plane) which affects torque can also be used to relate the final results with the details of the flow.
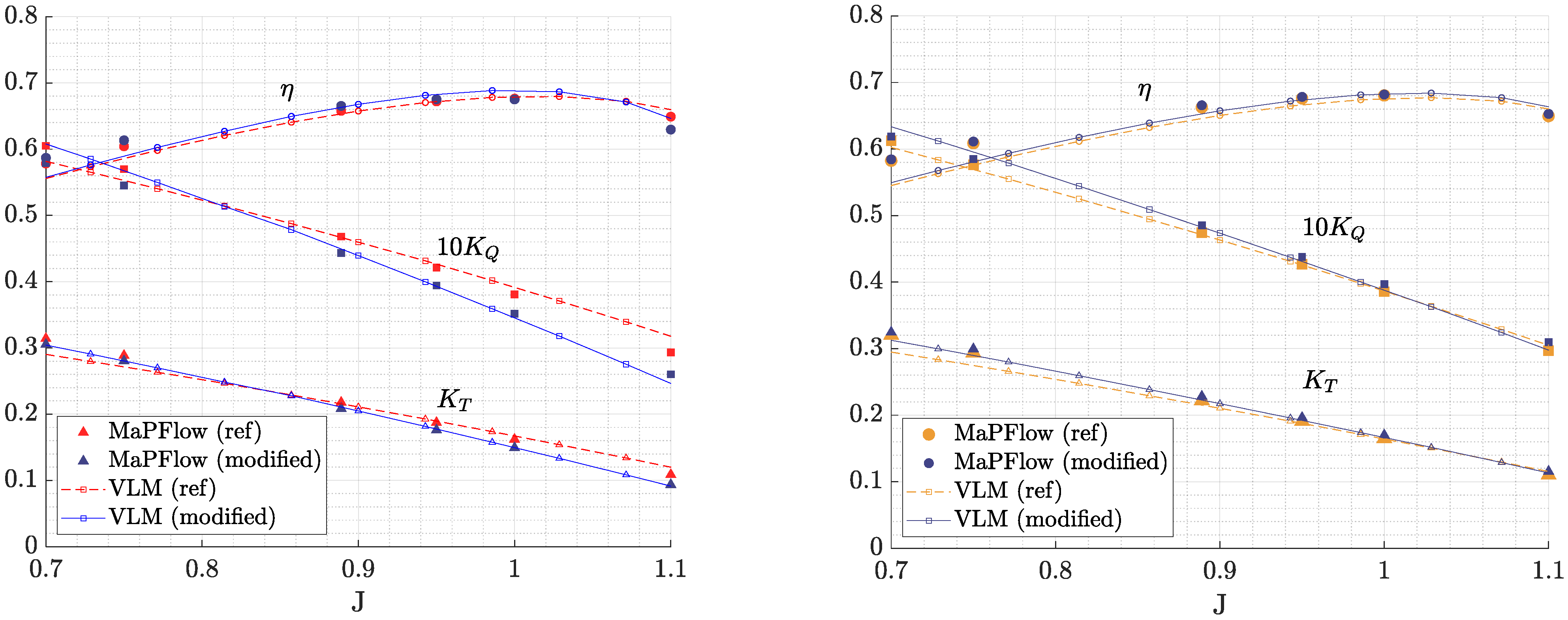
A comparison between the reference and the modified propeller open water curves obtained with the calibrated VLM and the viscous-CFD results is presented in
Figure 17. In
Figure 17, the MaPFlow results are included with symbols, i.e., triangles for the thrust coefficient, squares for the moment coefficient, and circles for the efficiency. The cost-effectiveness of the VLM allows for a denser grid for the open water curves and at a fraction of the computational cost required for the viscous-CFD.
It is important to note that the optimization studies conducted with the VLM, consider a zero friction-drag coefficient, with results provided in
Table 7. Moreover, if CFD-calibrated coefficients are to be used for open water curve prediction, as shown in
Figure 17 with the coefficients from
Table 6, then VLM shows similar trends with the viscous-CFD, as expected for design advance ratios near the design point J = 0.889. It is evident from
Figure 17 that for the case of the 4381 propeller, the proposed geometry modifications at advance coefficients between 0.8 and 1.0 lead to a thrust reduction, whereas for the 4382 case study at the same range of advance coefficients geometry modifications increase both thrust and the moment as predicted from CFD. This distinction, between the VLM settings during optimization and after calibration using CFD, is important for the present analysis.
However, at advance coefficients outside the range of J = {0.8–1.0} some numerical discrepancies are observed between the calibrated-VLM and the viscous-CFD predictions, which can be attributed to the limitations of the VLM in terms of predicting effects of large angles of attack and flow separation phenomena on open-water performance. This is evident for the efficiency predictions at advance coefficients greater than 1.0 for the study case of 4381 in
Figure 17 (left). Moreover, some discrepancies are also evident for the thrust coefficient predictions at advance ratios greater than 1.0 for the 4382 study case at
Figure 17 (right).
To sum up, the calibrated-VLM is capable of providing a good compromise between accuracy and computational cost in terms of open-water performance predictions at advance coefficients near the propeller design point.