Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption
Abstract
1. Introduction
2. Characteristics of the Bulk Carrier Used in the Numerical Model
3. Description of the Numerical Model
3.1. Propeller Optimization Model for the Operation Performance
3.2. Propeller Models with Different FCR
3.3. Propeller Performance Based on CFD Technique
3.3.1. Governor Equations
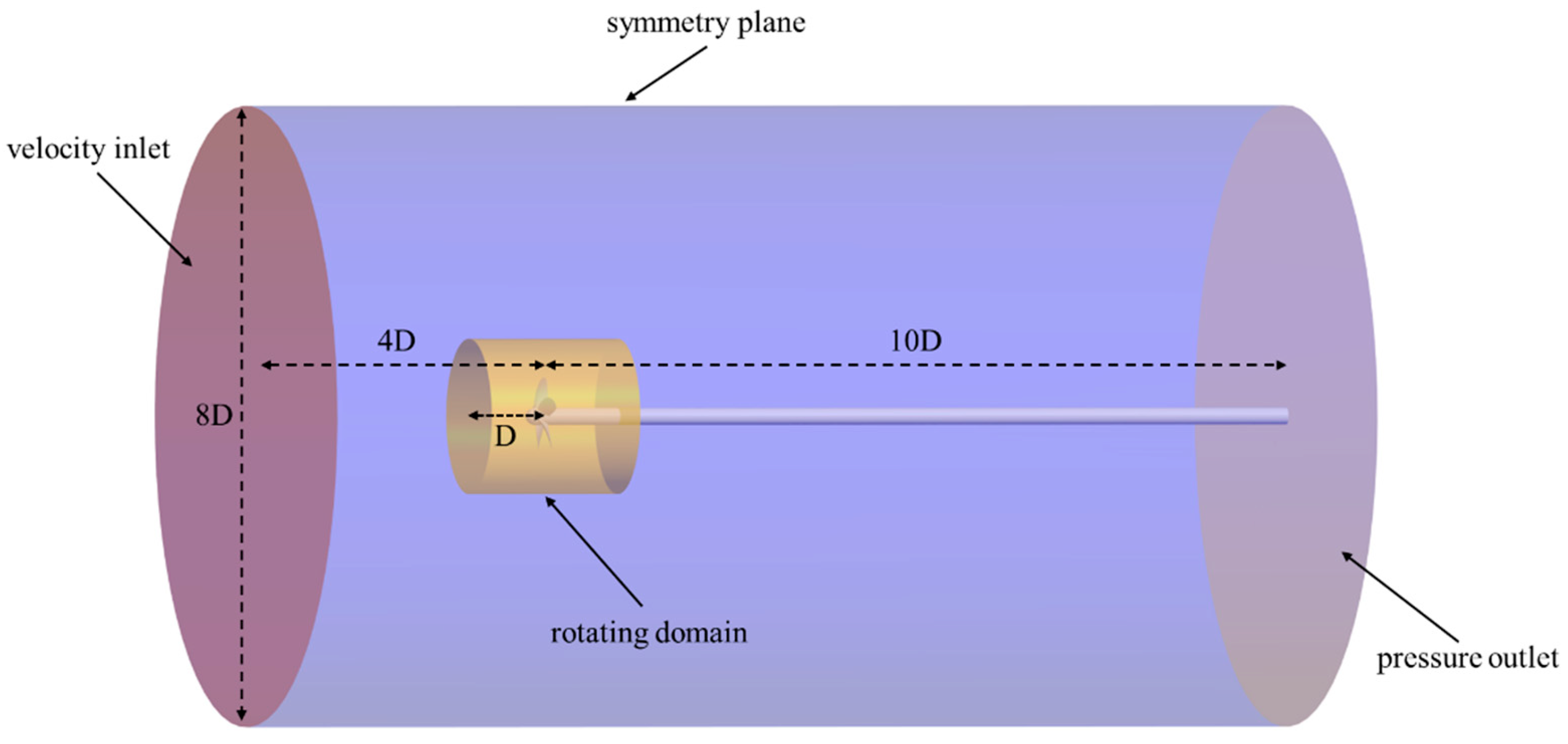
3.3.2. Computational Domain and Boundary Conditions
3.3.3. Mesh Generation
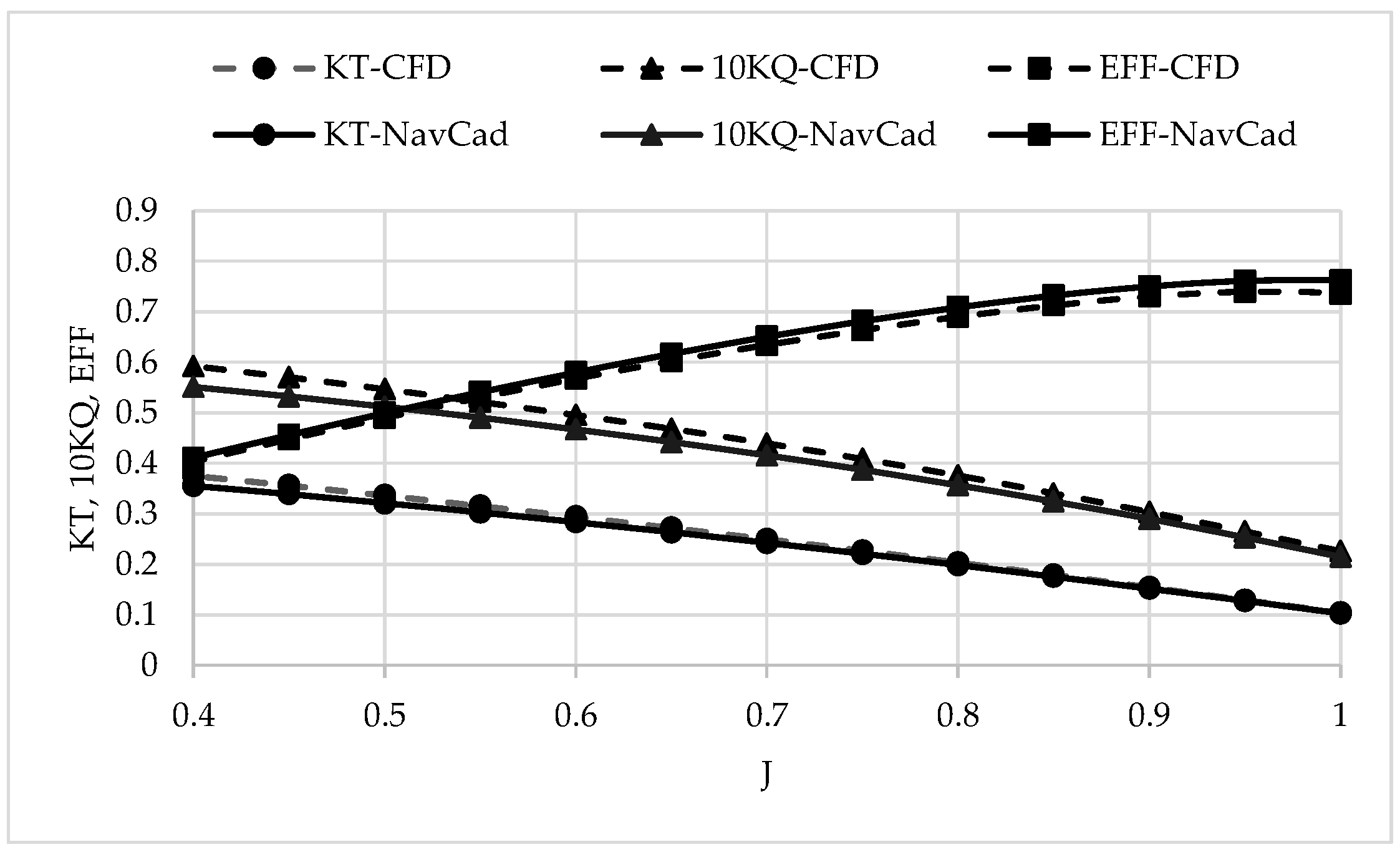
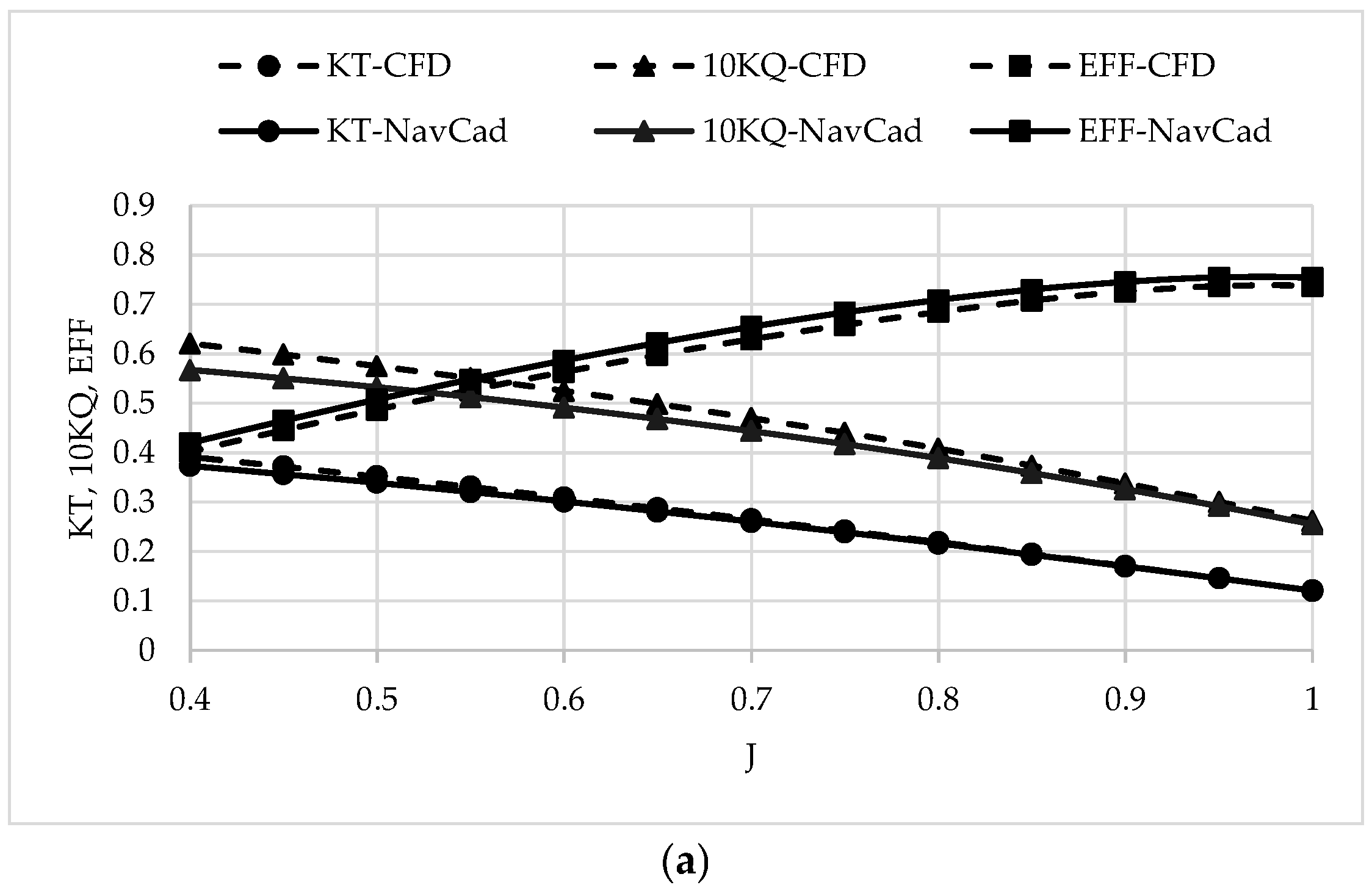
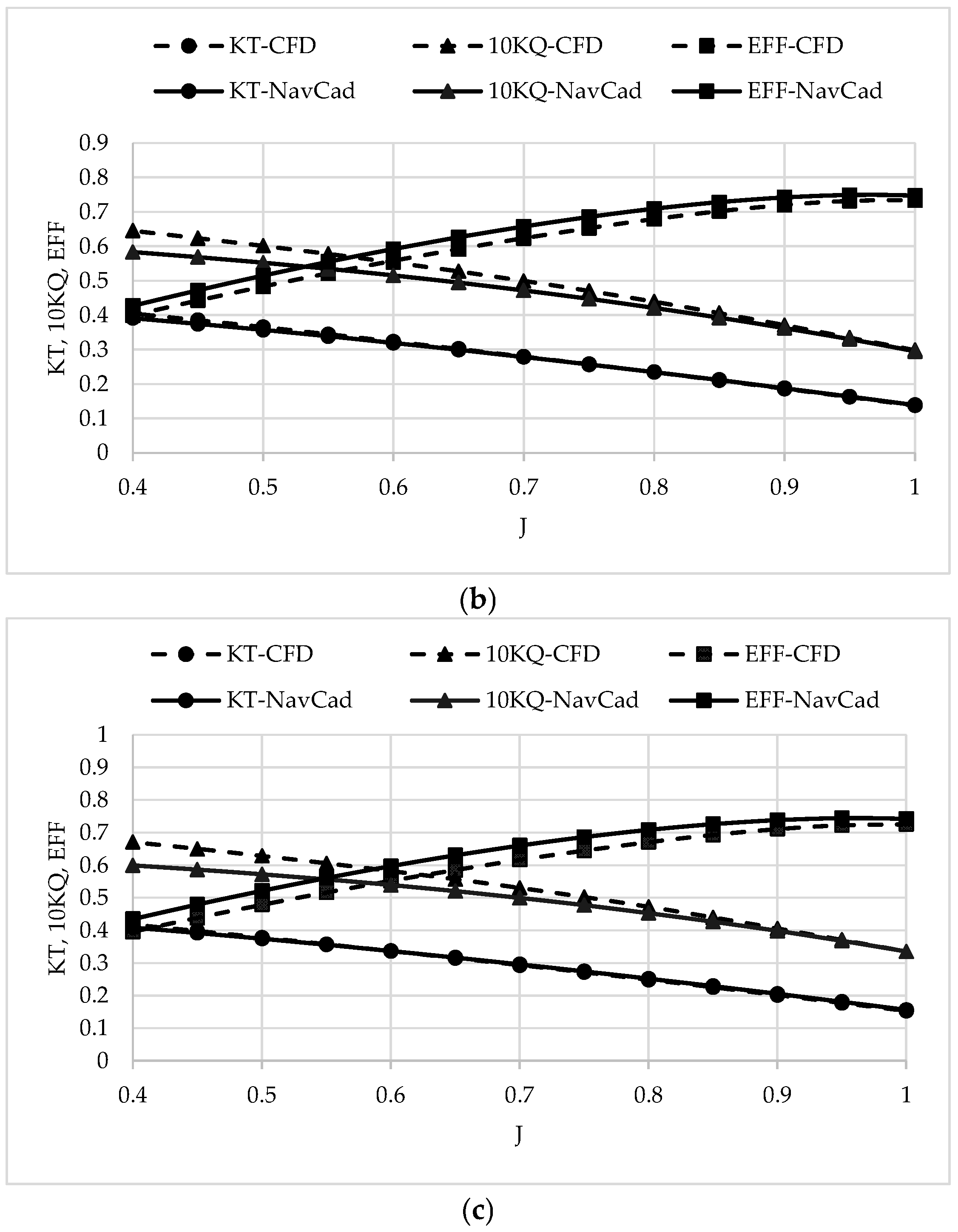
3.3.4. Validation of Propeller Performance Using CFD
3.3.5. Test Matrix of Different Camber Ratio Propellers
4. Results and Discussion
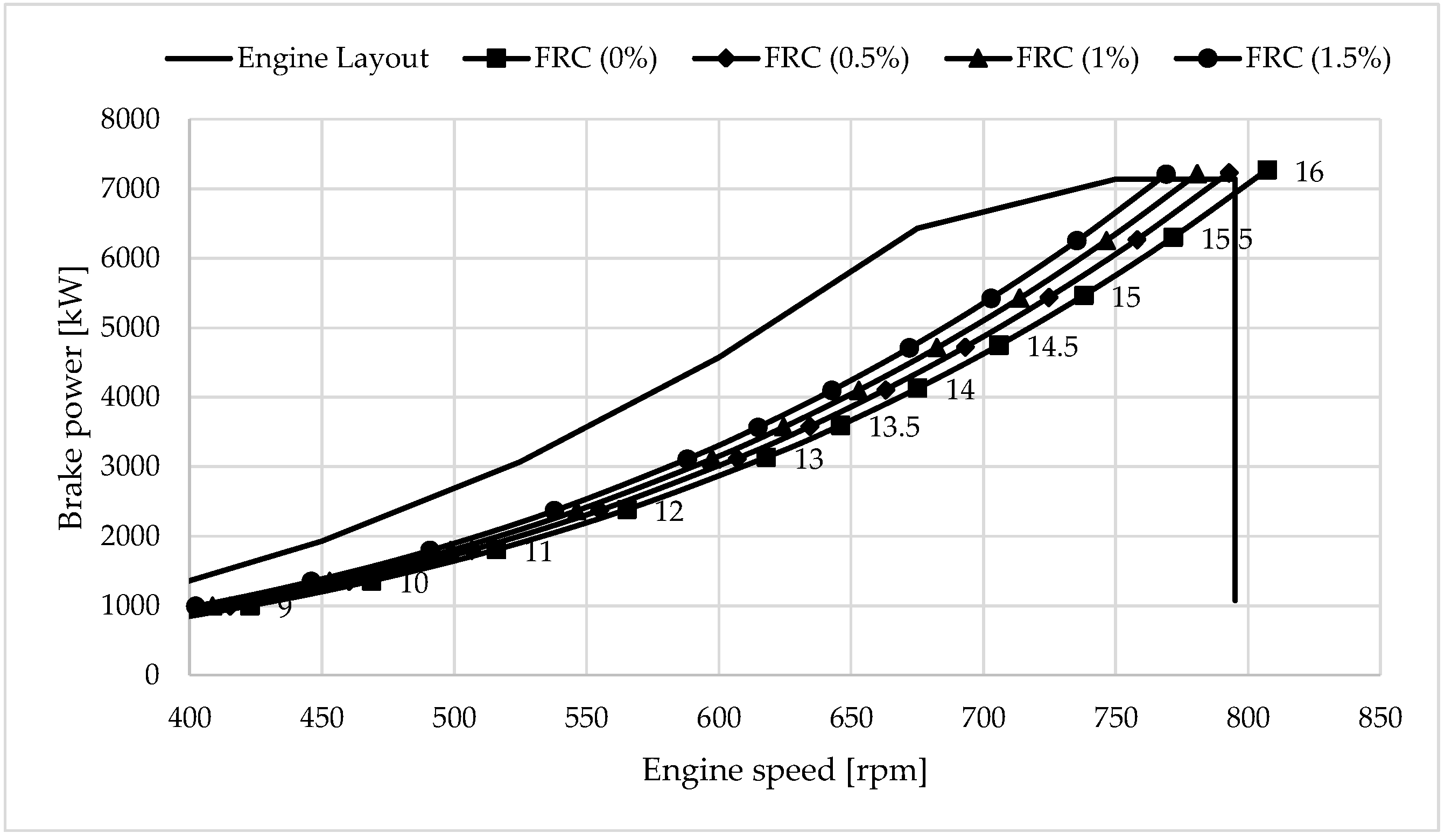
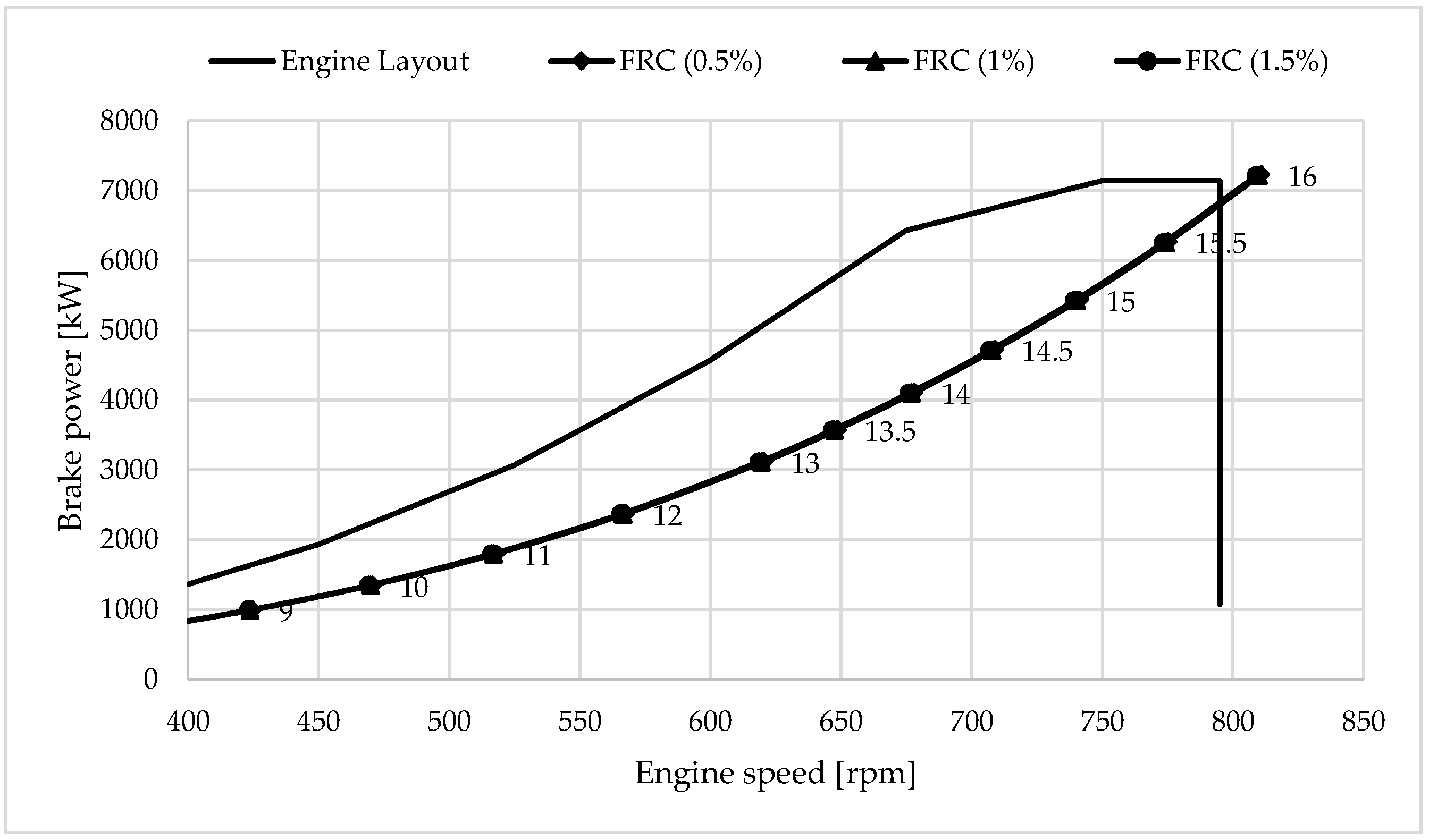
4.1. Effect of Optimizing the Propeller at the Minimum Fuel Consumption over the Maximum Propeller Efficiency
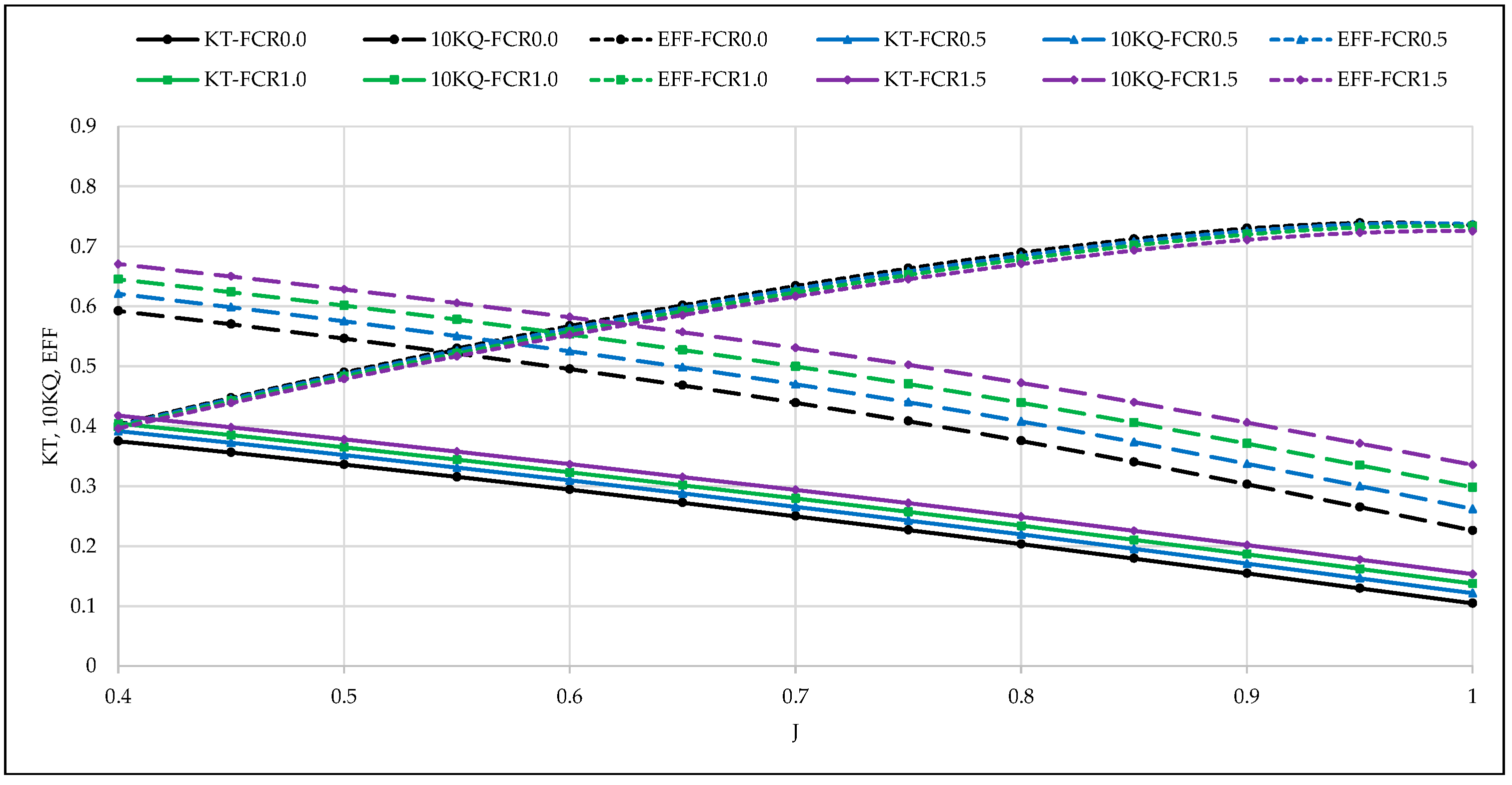
4.2. Effect of FCR on Propeller Performance
5. Conclusions
- The open-water curves from both CFD and NavCad models exhibit strong agreement across different propellers and FCR levels;
- Increasing the FCR level slightly enhances propeller efficiency by improving thrust and torque coefficients;
- Higher FCR levels contribute to fuel savings and lower exhaust emissions, achieving up to a 3% reduction compared to the reference propeller;
- Noise levels are reduced by approximately 5% compared to the baseline, which improves operational comfort and environmental compliance;
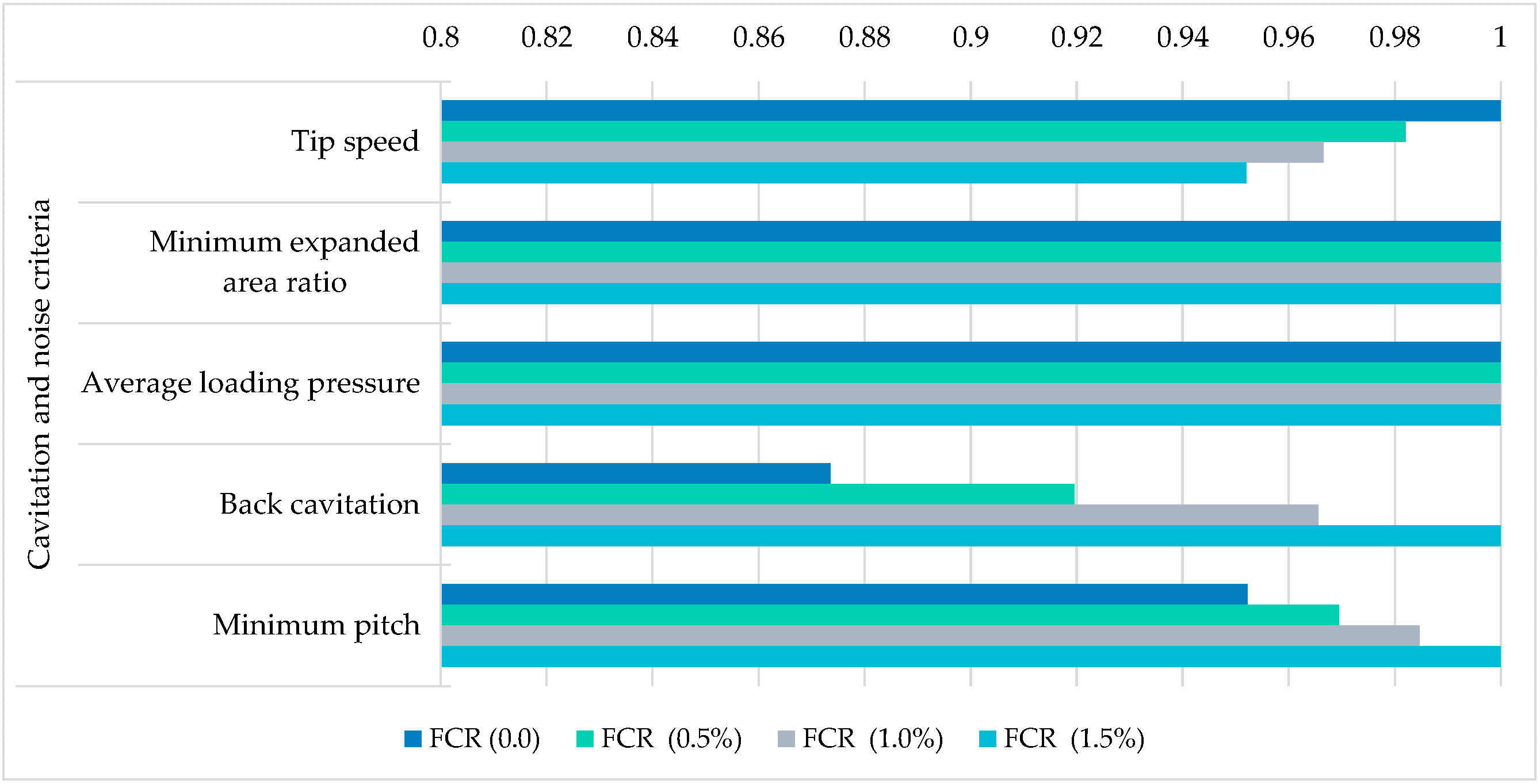
- There is no change in the cavitation criteria, such as the minimum expanded area ratio and average loading pressure. However, back cavitation and minimum pitch to avoid cavitation increase with higher FCR levels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D | Three dimensional |
| A | Matrix of linear inequality constraints |
| Aeq | Matrix of linear equality constraints |
| API | Application programming interface |
| b | Vector of linear inequality constraints |
| beq | Vector of linear equality constraints |
| BSFC | Brake-specific fuel consumption |
| c | Inequality constraints |
| ceq | Equality constraints |
| CFD | Computational fluid dynamics |
| CO2 | Carbon dioxide |
| CRP | Contra-rotating propeller |
| D | Propeller diameter |
| DES | Detached Eddy Simulation |
| DNS | Direct Numerical Simulation |
| EAR | Expanded blade area ratio |
| EARmin | Minimum expanded blade area ratio to avoid cavitation |
| ESD | Energy saving devices |
| f(x) | Optimization model objective |
| FC | Fuel consumption |
| FCR | Face camber ratio |
| g(x) | Penalty function |
| g | Acceleration |
| GA | Genetic algorithm |
| GBR | Gearbox ratio |
| i, j | Cartesian coordinates |
| IMO | International Maritime Organization |
| ITTC | International Towing Tank Conference |
| j | Number of constraints |
| J | Advance coefficient |
| k | turbulent kinetic energy |
| KQ | Torque coefficient |
| KT | Thrust coefficient |
| lb | Lower bounds |
| LES | Large Eddy Simulation |
| MARPOL | International Convention for the Prevention of Pollution from Ships |
| n | Propeller speed |
| NOx | Nitrogen oxides |
| p | Pressure |
| P/D | Pitch-to-diameter ratio |
| PB | Brake power |
| PSO | Particle swarm optimization |
| Q | Torque |
| R | Constant |
| RANS | Reynolds-Averaged Navier-Stokes |
| RBM | Rigid Body Motion |
| RT | Total resistance |
| SOx | Sulfur oxides |
| SST | Shear stress transport |
| t | TimeThrust deduction factor |
| T | Thrust |
| u | Velocity |
| ub | Upper bounds |
| v | Fluid kinematic viscosity |
| V | Incoming velocities |
| VA | Advance speed |
| Vs | Ship design speed |
| w | Wake fraction |
| x | Number of variables |
| y+ | Dimensionless wall distance |
| Z | Number of propeller blades |
| γ | Kinematic viscosityTurbulent viscosity |
| ηo | Open-water propeller efficiency |
| ρ | Density |
| ω | Specific dissipation rate |
Appendix A
| Solution Technique | Max Efficiency | Min Fuel Consumption | |||||
|---|---|---|---|---|---|---|---|
| Software | NavCad | CFD | |||||
| Parameters | No FCR | No FCR | No FCR | Light FCR | Medium FCR | Heavy FCR | |
| Propeller type | Wageningen B-Series | ||||||
| Ship Speed | Vs | 14.5 | 14.5 | 14.5 | 14.5 | 14.5 | 14.5 |
| FCR [%] | 0.0 | 0.0 | 0.0 | 0.5 | 1.0 | 1.5 | |
| Propeller characteristics | D [m] | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 |
| EAR [-] | 0.57 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | |
| P [m] | 4.92 | 6.58 | 6.58 | 6.58 | 6.58 | 6.58 | |
| N [RPM] | 91 | 75 | 74 | 73 | 72 | 71 | |
| Thrust [kN] | 576.5 | 576.5 | 576.5 | 576.5 | 576.5 | 576.5 | |
| Torque [kN.m] | 473.7 | 573.3 | 588.3 | 595.7 | 604.0 | 613.0 | |
| ηo [%] | 59.3 | 59.3 | 58.5 | 58.8 | 58.9 | 59.0 | |
| J [-] | 0.51 | 0.62 | 0.63 | 0.64 | 0.65 | 0.66 | |
| KT [-] | 0.19 | 0.28 | 0.28 | 0.29 | 0.30 | 0.31 | |
| KQ [-] | 0.02 | 0.05 | 0.05 | 0.05 | 0.05 | 0.06 | |
| w [-] | 0.38 | 0.38 | 0.38 | 0.38 | 0.38 | 0.38 | |
| t [-] | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 | |
| Cavitation and noise criteria | Tip Speed [m/s] | 28.6 | 23.6 | 23.3 | 22.9 | 22.6 | 22.2 |
| EARmin [-] | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | 0.47 | |
| Average loading pressure [kPa] | 35.5 | 43.6 | 43.4 | 43.4 | 43.4 | 43.4 | |
| Back Cavitation [%] | 2.0 | 7.4 | 7.6 | 8.0 | 8.4 | 8.7 | |
| Pitchmin [m] | 4110.6 | 4978.7 | 5039.1 | 5131.0 | 5211.5 | 5292.3 | |
| Gearbox characteristics | GBR [-] | 7.76 | 9.51 | 9.51 | 9.51 | 9.51 | 9.51 |
| Engine characteristics | Speed [RPM] | 706 | 714 | 706 | 693 | 682 | 672 |
| Speed percentage [%] * | 94.1 | 95.2 | 94.1 | 92.4 | 90.9 | 89.6 | |
| Brake Power [kW] | 4715 | 4682 | 4747 | 4720 | 4713 | 4710 | |
| Engine load percentage [%] ** | 66.0 | 65.6 | 66.50 | 66.12 | 66.01 | 65.97 | |
| BSFC [g/kW.h] | 191.0 | 192.0 | 191.5 | 189.6 | 188.3 | 187.0 | |
| Fuel consumption [kg/nm] | 62.17 | 61.95 | 62.69 | 61.74 | 61.19 | 60.74 | |
| Exhaust emissions | CO2 [kg/nm] | 197.1 | 196.3 | 198.7 | 195.7 | 194.0 | 192.5 |
| NOx [kg/nm] | 2.25 | 2.16 | 2.29 | 2.35 | 2.41 | 2.48 | |
| SOx [kg/nm] | 3.11 | 3.10 | 3.13 | 3.09 | 3.06 | 3.04 | |
References
- Tadros, M.; Ventura, M.; Guedes Soares, C. Review of current regulations, available technologies, and future trends in the green shipping industry. Ocean Eng. 2023, 280, 114670. [Google Scholar] [CrossRef]
- Bouman, E.A.; Lindstad, E.; Rialland, A.I.; Strømman, A.H. State-of-the-art technologies, measures, and potential for reducing GHG emissions from shipping—A review. Transp. Res. D Transp. Environ. 2017, 52, 408–421. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Tadros, M.; Ventura, M.; Guedes Soares, C. Decision support system for ship energy efficiency management based on an optimization model. Energy 2024, 292, 130318. [Google Scholar] [CrossRef]
- DNV. Maritime Forecast to 2050: Energy Transition Outlook 2020; DNV: Oslo, Norway, 2020. [Google Scholar]
- Vettor, R.; Guedes Soares, C. Development of a ship weather routing system. Ocean Eng. 2016, 123, 1–14. [Google Scholar] [CrossRef]
- Prpić-Oršić, J.; Vettor, R.; Faltinsen, O.M.; Guedes Soares, C. The influence of route choice and operating conditions on fuel consumption and CO2 emission of ships. J. Mar. Sci. Technol. 2016, 21, 434–457. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Khan, S.; Grudniewski, P.; Muhammad, Y.S.; Sobey, A.J. The benefits of co-evolutionary Genetic Algorithms in voyage optimisation. Ocean Eng. 2022, 245, 110261. [Google Scholar] [CrossRef]
- Taskar, B.; Sasmal, K.; Yiew, L.J. A case study for the assessment of fuel savings using speed optimization. Ocean Eng. 2023, 274, 113990. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I. The impact of biofouling on the propeller performance. Ocean Eng. 2021, 219, 108376. [Google Scholar] [CrossRef]
- Xing-Kaeding, Y.; Streckwall, H.; Gatchell, S. ESD design and analysis for a validation bulk carrier. Int. Shipbuild. Prog. 2017, 63, 137–168. [Google Scholar] [CrossRef]
- Tacar, Z.; Sasaki, N.; Atlar, M.; Korkut, E. An investigation into effects of Gate Rudder® system on ship performance as a novel energy-saving and manoeuvring device. Ocean Eng. 2020, 218, 108250. [Google Scholar] [CrossRef]
- Stark, C.; Xu, Y.; Zhang, M.; Yuan, Z.; Tao, L.; Shi, W. Study on Applicability of Energy-Saving Devices to Hydrogen Fuel Cell-Powered Ships. J. Mar. Sci. Eng. 2022, 10, 388. [Google Scholar] [CrossRef]
- Gaggero, S.; Martinelli, M. Pre-swirl fins design for improved propulsive performances: Application to fast twin-screw passenger ships. J. Ocean Eng. Mar. Energy 2023, 9, 69–91. [Google Scholar] [CrossRef]
- Mohd Noor, C.W.; Noor, M.M.; Mamat, R. Biodiesel as alternative fuel for marine diesel engine applications: A review. Renew Sust Energ Rev 2018, 94, 127–142. [Google Scholar] [CrossRef]
- Bicer, Y.; Dincer, I. Clean fuel options with hydrogen for sea transportation: A life cycle approach. Int. J. Hydrog. Energy 2018, 43, 1179–1193. [Google Scholar] [CrossRef]
- Hansson, J.; Månsson, S.; Brynolf, S.; Grahn, M. Alternative marine fuels: Prospects based on multi-criteria decision analysis involving Swedish stakeholders. Biomass Bioenergy 2019, 126, 159–173. [Google Scholar] [CrossRef]
- Islam Rony, Z.; Mofijur, M.; Hasan, M.M.; Rasul, M.G.; Jahirul, M.I.; Forruque Ahmed, S.; Kalam, M.A.; Anjum Badruddin, I.; Yunus Khan, T.M.; Show, P.-L. Alternative fuels to reduce greenhouse gas emissions from marine transport and promote UN sustainable development goals. Fuel 2023, 338, 127220. [Google Scholar] [CrossRef]
- Tadros, M.; Shi, W.; Xu, Y.; Song, Y. A unified cross-series marine propeller design method based on machine learning. Ocean Eng. 2024, 314, 119691. [Google Scholar] [CrossRef]
- Carlton, J. Marine Propellers and Propulsion, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- Markussen, P.A. On the Optimum Wageningen B-Series Propeller Problem with Cavitation-Limiting Restraint. J. Ship Res. 1979, 23, 108–114. [Google Scholar] [CrossRef]
- Hydrocomp. NavCad: Hydrodynamic and Propulsion System Simulation. HydroComp Inc. Available online: https://www.hydrocompinc.com/solutions/navcad/ (accessed on 15 April 2024).
- Nouri, N.M.; Mohammadi, S.; Zarezadeh, M. Optimization of a marine contra-rotating propellers set. Ocean Eng. 2018, 167, 397–404. [Google Scholar] [CrossRef]
- Gaggero, S.; Tani, G.; Villa, D.; Viviani, M.; Ausonio, P.; Travi, P.; Bizzarri, G.; Serra, F. Efficient and multi-objective cavitating propeller optimization: An application to a high-speed craft. Appl. Ocean Res. 2017, 64, 31–57. [Google Scholar] [CrossRef]
- Obwogi, E.O.; Shen, H.-l.; Su, Y.-m. The design and energy saving effect prediction of rudder-bulb-fin device based on CFD and model test. Appl. Ocean Res. 2021, 114, 102814. [Google Scholar] [CrossRef]
- Vlašić, D.; Degiuli, N.; Farkas, A.; Martić, I. The preliminary design of a screw propeller by means of computational fluid dynamics. Brodogradnja 2018, 69, 129–147. [Google Scholar] [CrossRef]
- Epps, B.P.; Kimball, R.W. OpenProp v3: Open-Source Software for the Design and Analysis of Marine Propellers and Horizontal-Axis Turbines. Available online: https://www.epps.com/openprop (accessed on 1 October 2016).
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Controllable pitch propeller optimization through meta-heuristic algorithm. Eng. Comput. 2021, 37, 2257–2271. [Google Scholar] [CrossRef]
- Anevlavi, D.; Zafeiris, S.; Papadakis, G.; Belibassakis, K. Efficiency Enhancement of Marine Propellers via Reformation of Blade Tip-Rake Distribution. J. Mar. Sci. Eng. 2023, 11, 2179. [Google Scholar] [CrossRef]
- Perić, M. Prediction of cavitation on ships. Brodogradnja 2022, 73, 39–58. [Google Scholar] [CrossRef]
- Gaafary, M.M.; El-Kilani, H.S.; Moustafa, M.M. Optimum design of B-series marine propellers. Alex. Eng. J. 2011, 50, 13–18. [Google Scholar] [CrossRef]
- Xie, G. Optimal Preliminary Propeller Design Based on Multi-objective Optimization Approach. Procedia Eng. 2011, 16, 278–283. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Design of Propeller Series Optimizing Fuel Consumption and Propeller Efficiency. J. Mar. Sci. Eng. 2021, 9, 1226. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Kumar Subramanian, R.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Bertetta, D.; Brizzolara, S.; Gaggero, S.; Viviani, M.; Savio, L. CPP propeller cavitation and noise optimization at different pitches with panel code and validation by cavitation tunnel measurements. Ocean Eng. 2012, 53, 177–195. [Google Scholar] [CrossRef]
- Aktas, B.; Atlar, M.; Turkmen, S.; Shi, W.; Sampson, R.; Korkut, E.; Fitzsimmons, P. Propeller cavitation noise investigations of a research vessel using medium size cavitation tunnel tests and full-scale trials. Ocean Eng. 2016, 120, 122–135. [Google Scholar] [CrossRef]
- MacPherson, D.M. Small Propeller Cup: A Proposed Geometry Standard and a New Performance Model. In Proceedings of the 8th Propeller and Shafting Symposium (SNAME), Virginia Beach, VA, USA, 23–24 September 1997. [Google Scholar]
- Samsul, M.B. Blade Cup Method for Cavitation Reduction in Marine Propellers. Pol. Marit. Res. 2021, 28, 54–62. [Google Scholar] [CrossRef]
- Mohammad Nouri, N.; Mohammadi, S. Numerical investigation of the effects of camber ratio on the hydrodynamic performance of a marine propeller. Ocean Eng. 2018, 148, 632–636. [Google Scholar] [CrossRef]
- Guan, G.; Zhang, X.; Wang, P.; Yang, Q. Multi-objective optimization design method of marine propeller based on fluid-structure interaction. Ocean Eng. 2022, 252, 111222. [Google Scholar] [CrossRef]
- MAN Diesel & Turbo. Four-Stroke Project Guides. MAN Diesel & Turbo. Available online: https://www.man-es.com/marine/products/planning-tools-and-downloads/project-guides/four-stroke (accessed on 22 July 2022).
- Tadros, M.; Vettor, R.; Ventura, M.; Guedes Soares, C. Effect of propeller cup on the reduction of fuel consumption in realistic weather conditions. J. Mar. Sci. Eng. 2022, 10, 1039. [Google Scholar] [CrossRef]
- The MathWorks Inc. Fmincon. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html (accessed on 2 June 2017).
- Michalewicz, Z.; Schoenauer, M. Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 1996, 4, 1–32. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, M. Fuel economy optimization of an Atkinson cycle engine using genetic algorithm. Appl. Energy 2013, 105, 335–348. [Google Scholar] [CrossRef]
- Byrd, R.H.; Mary, E.H.; Nocedal, J. An Interior Point Algorithm for Large-Scale Nonlinear Programming. SIAM J. Optimiz. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Optimization procedure to minimize fuel consumption of a four-stroke marine turbocharged diesel engine. Energy 2019, 168, 897–908. [Google Scholar] [CrossRef]
- Holtrop, J. A statistical re-analysis of resistance and propulsion data. Int. Shipbuild. Prog. 1984, 31, 272–276. [Google Scholar]
- Holtrop, J. A Statistical Resistance Prediction Method With a Speed Dependent Form Factor. In Proceedings of the Scientific and Methodological Seminar on Ship Hydrodynamics (SMSSH ’88), Varna, Bulgaria, 17–22 October 1988; Bulgarian Ship Hydrodynamics Centre: Varna, Bulgaria, 1988; pp. 1–7. [Google Scholar]
- Holtrop, J.; Mennen, G.G.J. An approximate power prediction method. Int. Shipbuild. Prog. 1982, 29, 166–170. [Google Scholar] [CrossRef]
- Kaplan, A. Progressive Pitch Distributions: (Part 2) Performance. HydroComp, Inc. Available online: https://www.hydrocompinc.com/wp-content/uploads/2020/02/NMPA-Newsletter-Part-2-HCI.pdf (accessed on 12 May 2024).
- Kuiper, G. Cavitation Inception on Ship Propeller Models. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 1981. [Google Scholar]
- Van Oossanen, P. Calculation of Performance and Cavitation Characteristics of Propellers Including Effects on Non-Uniform Flow and Viscosity. Ph.D. Thesis, Technical University Delft, Delft, The Netherlands, 1974. [Google Scholar]
- Hydrocomp. PropCad: Propeller Design for Manufacture. Available online: https://www.hydrocompinc.com/solutions/propcad/#:~:text=PropCad%20keeps%20your%20drawings%2C%20reports,blade%20shapes%20with%20progressive%20pitch (accessed on 8 July 2024).
- Siemens. Simcenter STAR-CCM+ Documentation (Version 2301); Siemens Digital Industries Software: Plano, TX, USA, 2023. [Google Scholar]
- Grlj, C.G.; Degiuli, N.; Farkas, A.; Martić, I. Numerical Study of Scale Effects on Open Water Propeller Performance. J. Mar. Sci. Eng. 2022, 10, 1132. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- ITTC. ITTC–Recommended Procedures and Guidelines: Practical Guidelines for Ship Self-Propulsion CFD. In Proceedings of the 30th International Towing Tank Conference, ITTC, Hobart, Australia, 17–22 September 2014. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill: New York, NY, USA, 1988; pp. 72–83. [Google Scholar]
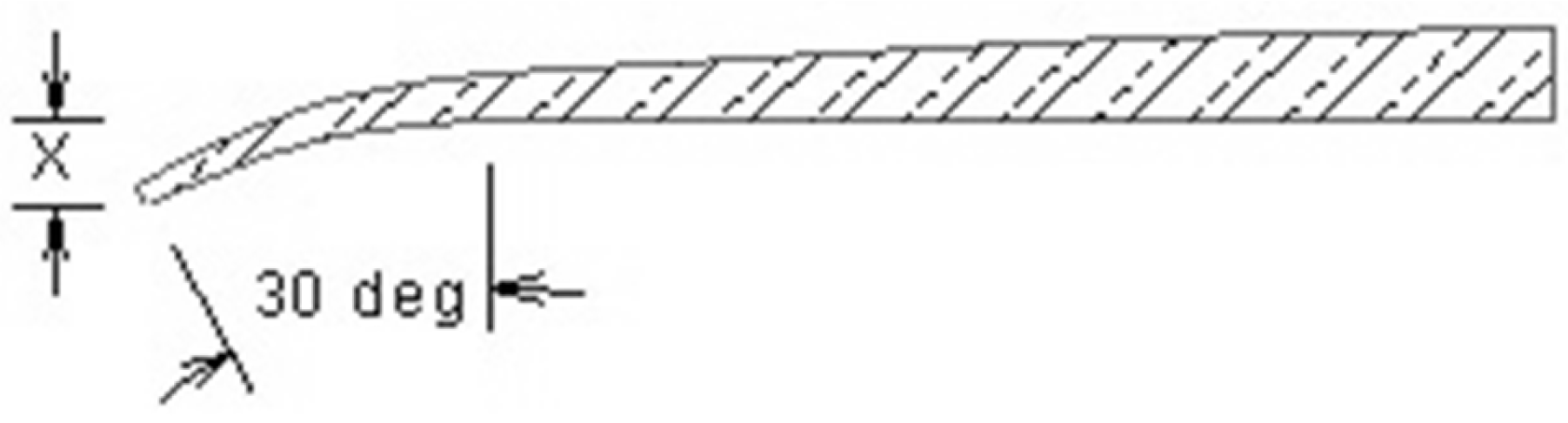

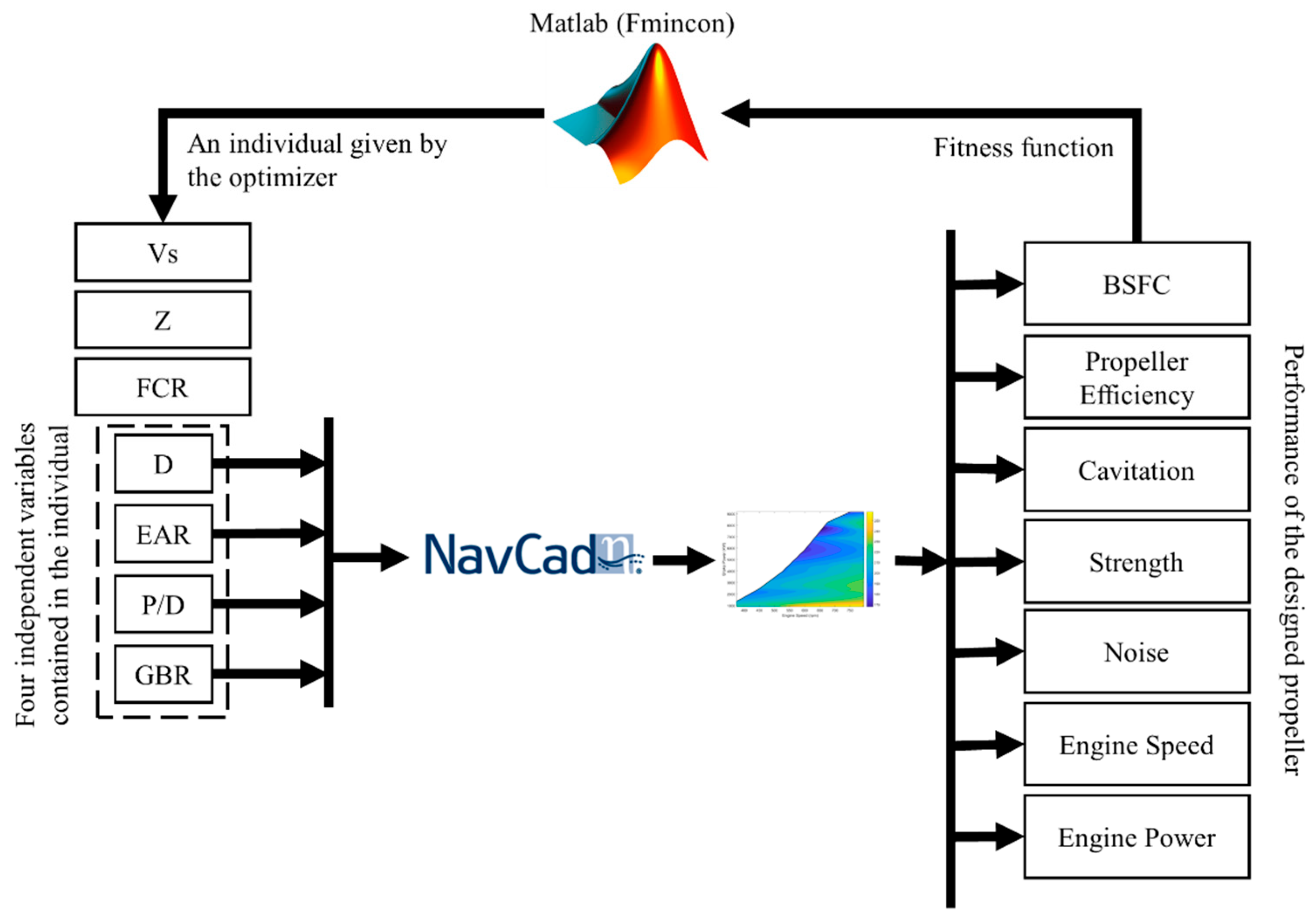

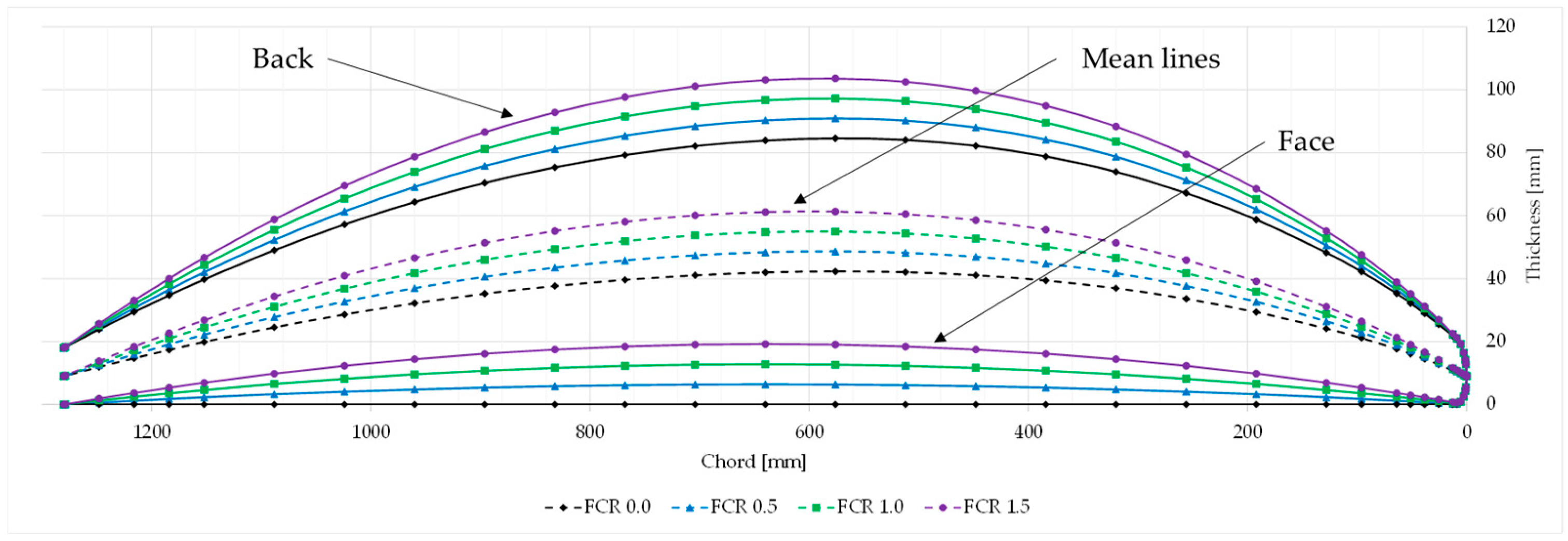




| Item | Unit | Value |
|---|---|---|
| Length waterline | m | 154.00 |
| Breadth | m | 23.11 |
| Draft | m | 10.00 |
| Displacement | tonne | 27,690 |
| Service speed | knot | 14.5 |
| Maximum speed | knot | 16.0 |
| Rated power | kW | 7140 |
| Item | Unit | Value |
|---|---|---|
| Engine builder | - | MAN Energy Solutions |
| Brand name | - | MAN |
| Bore | mm | 320 |
| Stroke | mm | 440 |
| Displacement | Liter | 4954 |
| Number of cylinders | - | 14 |
| Rated speed | rpm | 750 |
| Rated power | kW | 7140 |
| Item | Unit | Value |
|---|---|---|
| Number of propellers | - | 1 |
| Propeller series | B-series | |
| Type of propeller | - | FPP |
| Diameter | mm | 6000 |
| Expanded blade area ratio | - | 0.57 |
| Pitch-to-diameter ratio | - | 0.82 |
| J [-] | V [m/s] | |
|---|---|---|
| FCR 0% | 0.4–1 | 3–7.5 |
| FCR 0.5% | 0.4–1 | 3–7.5 |
| FCR 1.0% | 0.4–1 | 3–7.5 |
| FCR 1.5% | 0.4–1 | 3–7.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tadros, M.; Sun, Z.; Shi, W. Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption. J. Mar. Sci. Eng. 2024, 12, 2225. https://doi.org/10.3390/jmse12122225
Tadros M, Sun Z, Shi W. Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption. Journal of Marine Science and Engineering. 2024; 12(12):2225. https://doi.org/10.3390/jmse12122225
Chicago/Turabian StyleTadros, Mina, Zehao Sun, and Weichao Shi. 2024. "Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption" Journal of Marine Science and Engineering 12, no. 12: 2225. https://doi.org/10.3390/jmse12122225
APA StyleTadros, M., Sun, Z., & Shi, W. (2024). Effect of Propeller Face Camber Ratio on the Reduction of Fuel Consumption. Journal of Marine Science and Engineering, 12(12), 2225. https://doi.org/10.3390/jmse12122225








