Enhanced Ant Colony Algorithm for Discrete Dynamic Berth Allocation in a Case Container Terminal
Abstract
:1. Introduction
2. Literature Review
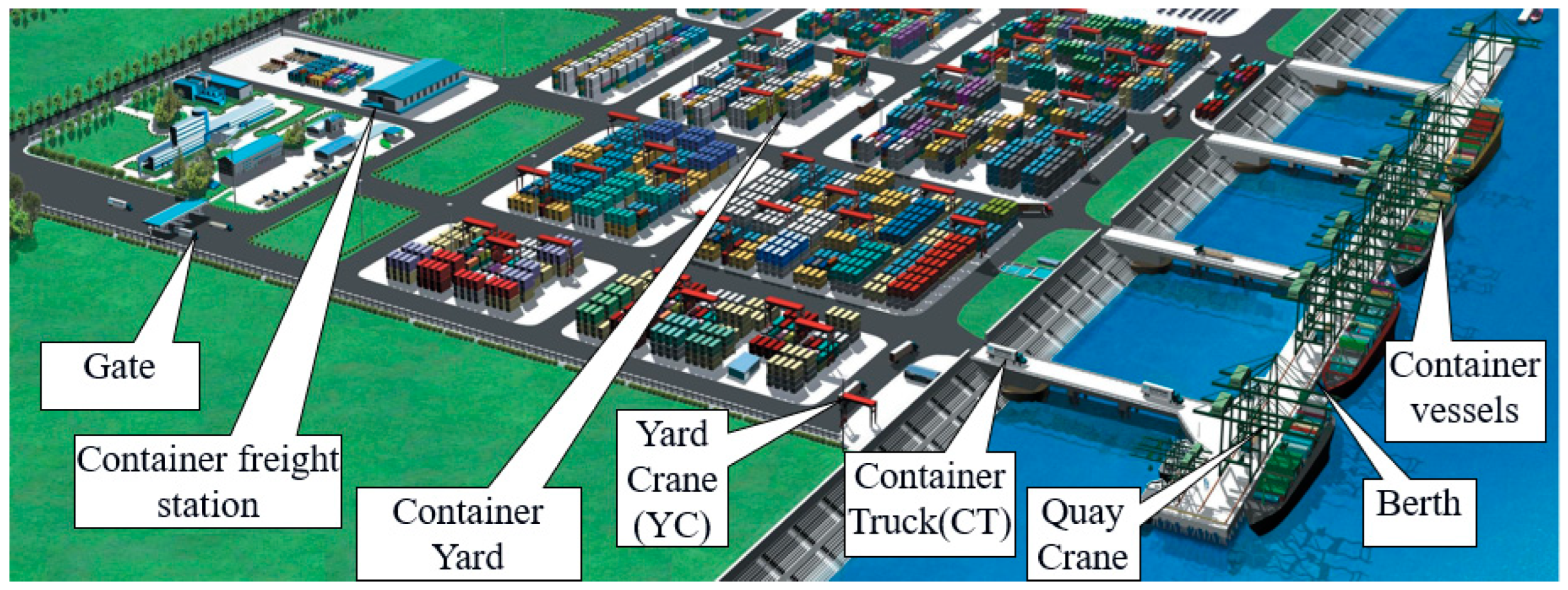
3. Problem Statement and Model Formulation
- (a)
- It is known beforehand and regarded as immutable, i.e., it is fixed.
- (b)
- It depends on where the vessels berthed.
- (c)
- It depends on the quantity of cranes serving the vessels.
- (d)
- The working schedule of the cranes is highly relied on.
- (e)
- All the mentioned conditions (b–c) need to be handled at the same time.
3.1. Notation
| Notation |
| Sets |
| B: Set of berths, B = {1, 2, …, nb}; |
| C: Set of QCs, C = {1, 2, …, nc}; |
| J: Set of incoming vessels during a planning period, J = {1, 2, ..., n}; |
| Model-Related Notations |
| n: Number of incoming vessels within a planning period, positive integer; |
| nb: Number of available berths in a port; |
| nc: Number of quay cranes; |
| njcap: Container capacity of vessel j; |
| njl: Number of containers to be loaded/unloaded on vessel j; |
| Oi: An ordered subset of vessels to be loaded/unloaded at berth i; |
| tijb: Moment of vessel j starting to berth at berth i; |
| tjw: Arrival moment of vessel j to the waiting area, tjw ≥ 0; |
| Tjb: Time duration of a vessel to berth and leave, assumed to be fixed and the same for different vessels, Tjb > 0; |
| tijfl: The finishing moment of loading/unloading vessel j at berth i, tijfl = tijl + Tijl; |
| tijl: The beginning moment of loading and unloading vessel j at berth i; |
| Tijl: Duration of loading and unloading vessel j at berth i; a function of njl, njcap, and njc; |
| PACO-Related Notations |
| dij’: Time distance between vessels j and j′; |
| e(j,j′): Edge connecting i and j; |
| tk(i): The length of time during which the kth ant starts from berth i to the end through all sections of the path; |
| Q: Constant, the amount of information released by an ant after the complete path search is complete; |
| Lk: The path length through which the kth ant passes; |
| nant: Quantity of ants in a colony; |
| ncon: Quantity of iterations of convergence; |
| nmaxitr: Maximum allowable number of iterations; |
| nitr: Current number of iterations; |
| nk(s): Notation of the number of nodes passed by the current ant k in the step s; |
| pjj’k(oi): Probability of ants k choosing vessel j’ from vessel j as the next candidate within the ordered subset of berth i; |
| α: Adjustable parameters controlling the relative impact of pheromone trajectories ; |
| β: Adjustable parameters controlling the relative impact of heuristic desirability; |
| ρ: Constant, a coefficient of evaporation; 0 < ρ < 1(1 − ρ) expresses pheromone decay during t and t + 1; |
| : The intensity of the trail on edge (j,j′) at time t; |
| : A heuristic measure of the desirability of adding edge (j,j′) to the solution being built; |
| : A total incremental quantity of the pheromones laid by all ants on edge (j,j ″); |
| : An incremental quantity of pheromones laid by the kth ant on edge (j,j′) during time t and time t + 1, which is a function of the length Lk of tour Tk(t): |
| Variables |
| njc: Decision variable; number of quay cranes assigned to the vessel j; |
| xijo: Binary decision variable, with a value of one when vessel j at berth i is served at service time t and a value of 0 otherwise; |
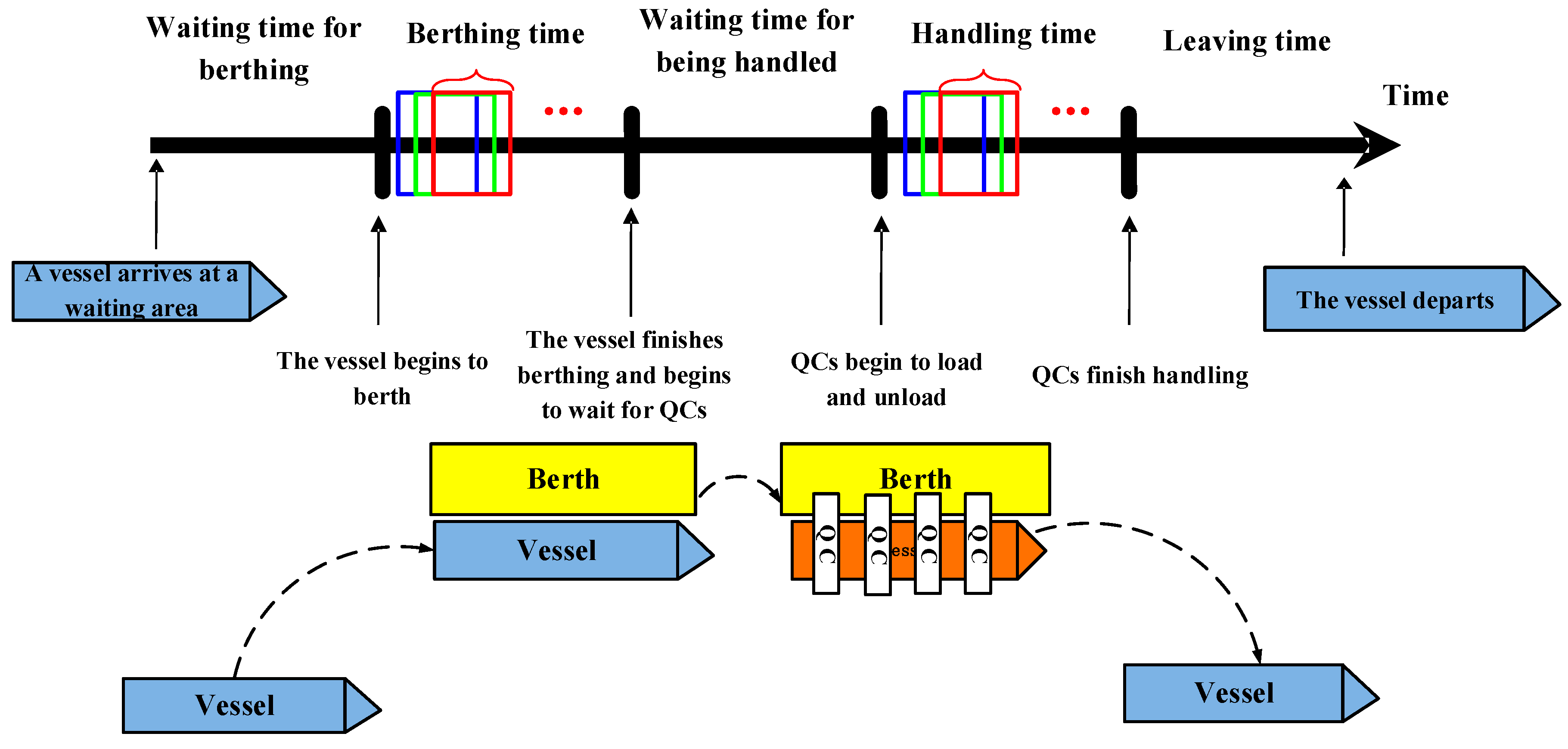
3.2. Single-Berth Model
3.3. Multi-Berth Model
- The vessels arrival time is random;
- The vessel loading and unloading times are derived from the number of containers, the quantity of QCs, the productivity of QCs, and other related factors;
- The mooring space must conform to the real conditions of the vessel (depth and length of water) of the constraints;
- The vessels moving from one berth to another will not be considered, where each vessel has only one berth opportunity;
- The number of assigned QCs does not exceed the number of QCs allowed to work simultaneously;
- When a large quantity of Quay Cranes (QCs) operates on a single vessel simultaneously, they can influence each other, potentially affecting the overall utilization rate of QC s. In cases where more than two terminal container cranes are operating simultaneously, one of them operates at a reduced capacity, typically around 90%.
4. Solution Algorithm
4.1. The Basic Principle of the Ant Colony Algorithm
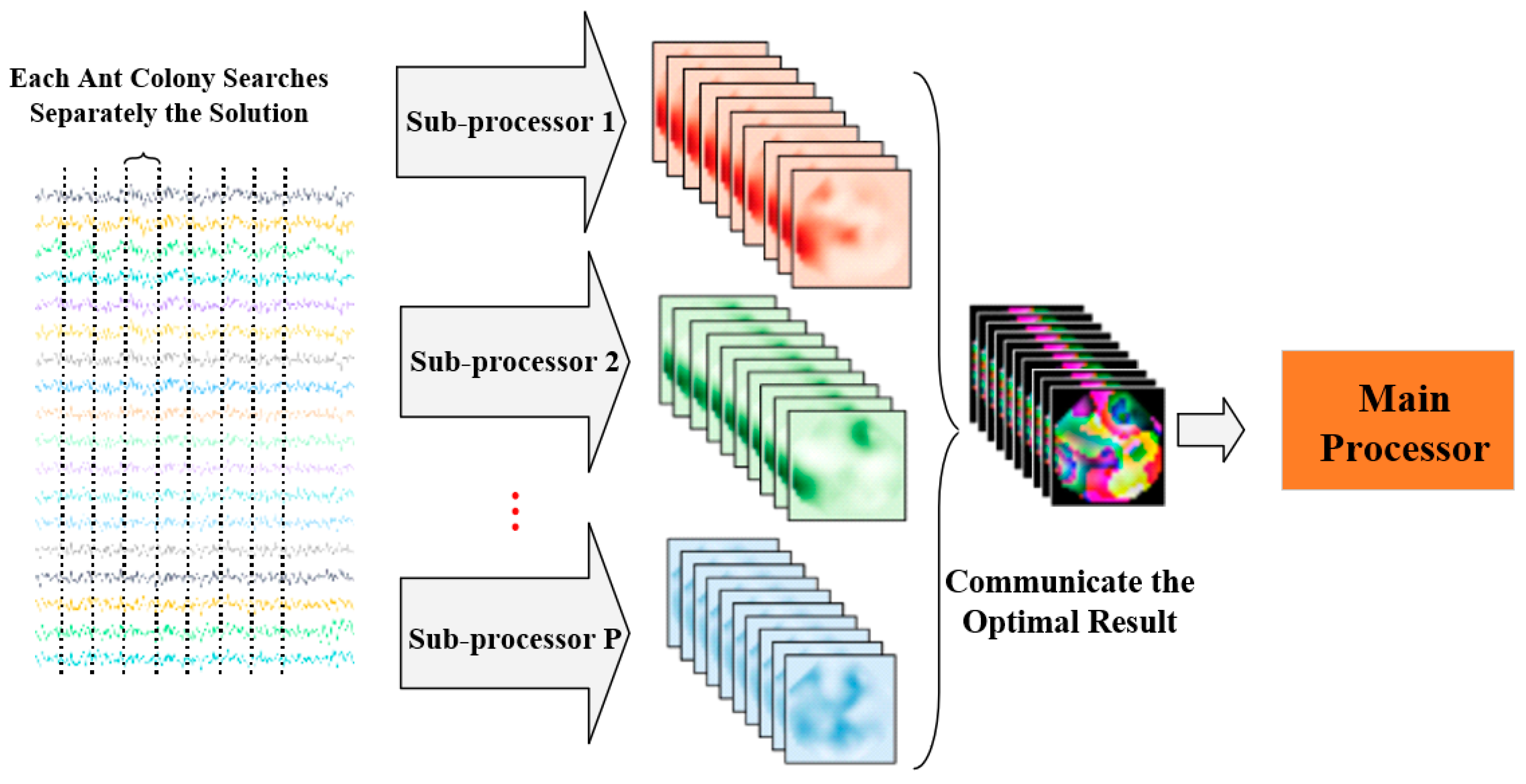
4.2. The Basic Principle of the Parallel Ant Colony Algorithm
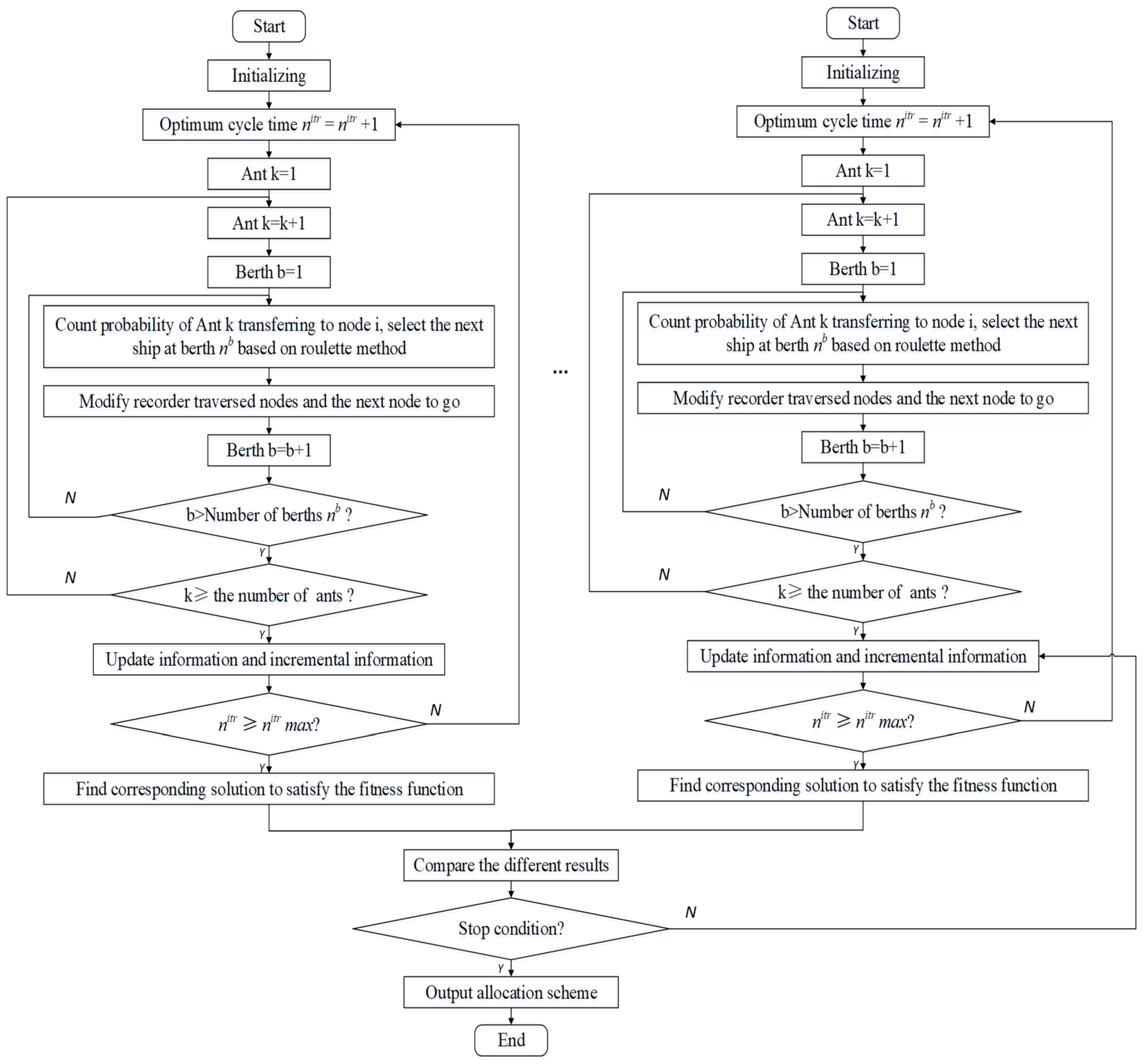
4.3. PACO for BAP
- (1)
- According to the concentration of hormones on the path, the ant selects the next path with the corresponding probability.
- (2)
- The ant no longer chooses nodes for the next path, which have been passed in this cycle, by using a data structure (tabu matrix) to control.
- (3)
- After completing a cycle, the ant releases pheromones in corresponding concentrations according to the length of the path and updates the pheromone concentration of the traversed path. In the initial stage, m ants are randomly placed on nodes with an equal amount of information on each path.
4.3.1. Solution Encoding
4.3.2. PACO for the Berth Allocation Problem
- (1)
- Individual ants select elements (container vessel) j to go according to the probability calculated through the state transition probability formula (3), where j ∈ tabu k, cjj′ is a time equal to vessel j’s time of completion minus vessel j’s arrival time, and lk is the path of all nodes the ant has walked, namely, the total time of all vessels staying in the port.
- (2)
- Modify the tabu search list pointer that is for ant j to move to the new element (container vessel) after choosing, and put the element (container vessel) into the individual ant’s tabu search list.
- (3)
- If the elements (container vessels) in Set C have not been traversed, which means k < m, then k = k + 1; otherwise, continue.
5. Numerical Experiments
5.1. Determination of Parameter Values
5.2. Results of Single-Berth Allocation
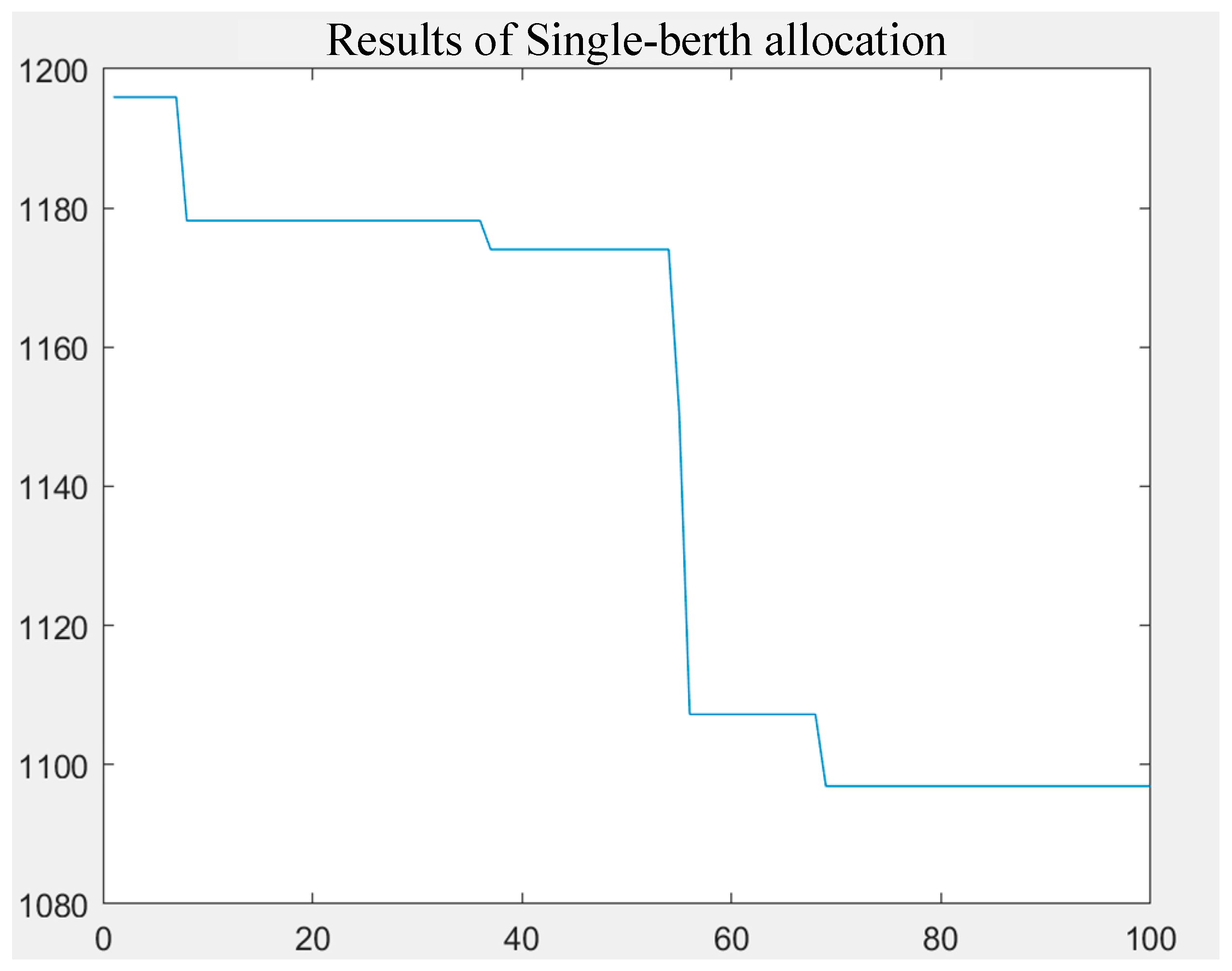
5.2.1. Based on ACO
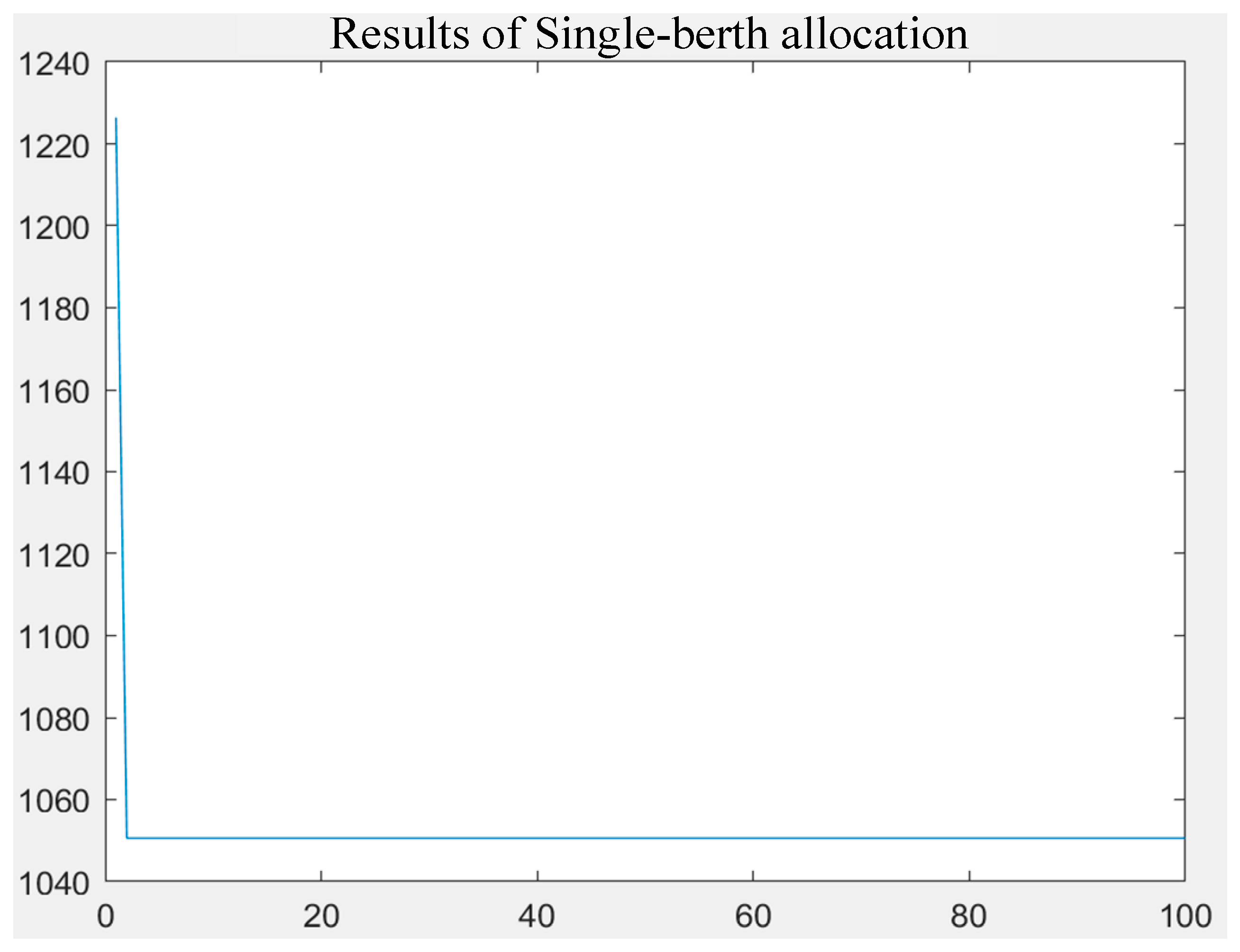
5.2.2. Based on PACO
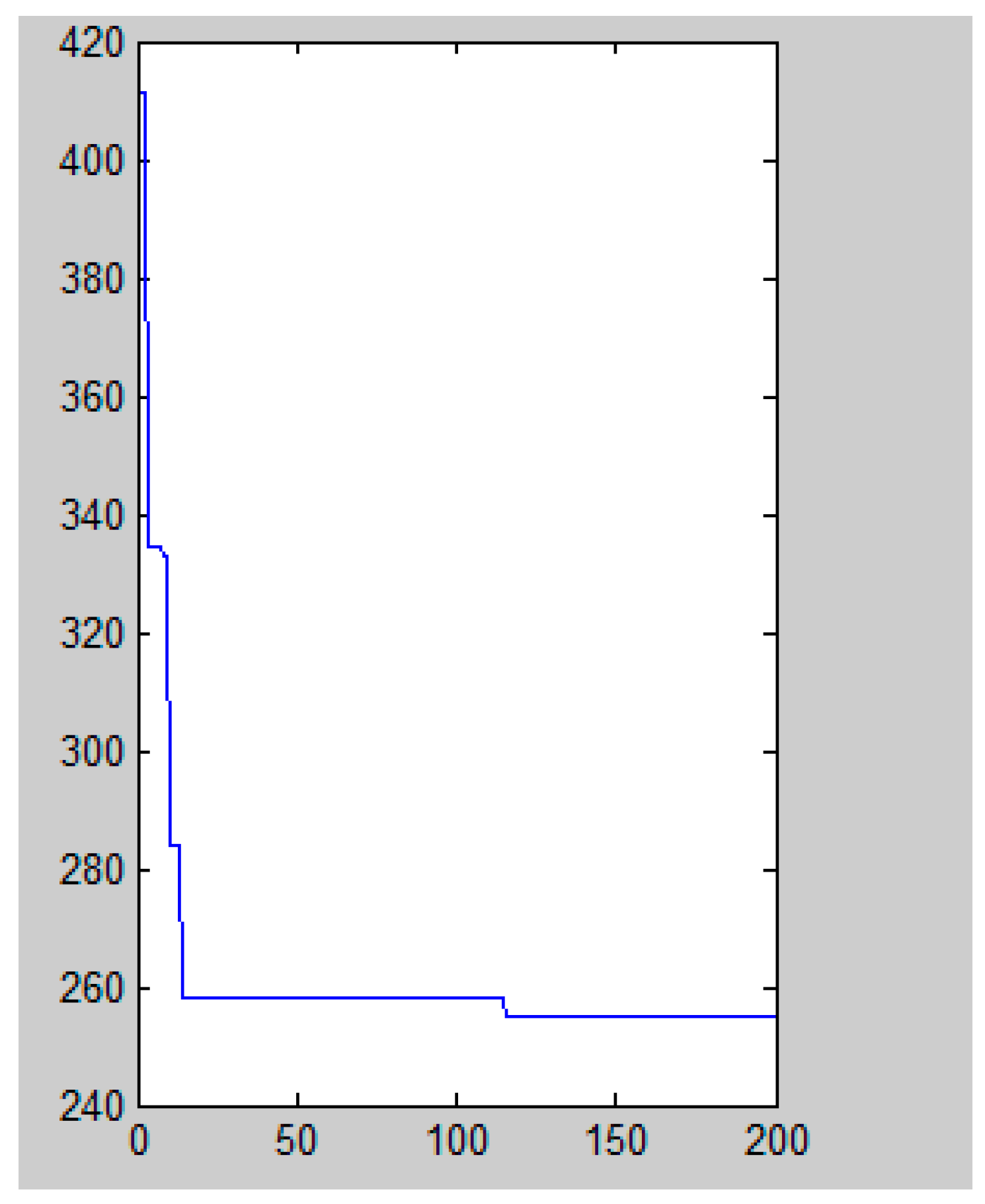
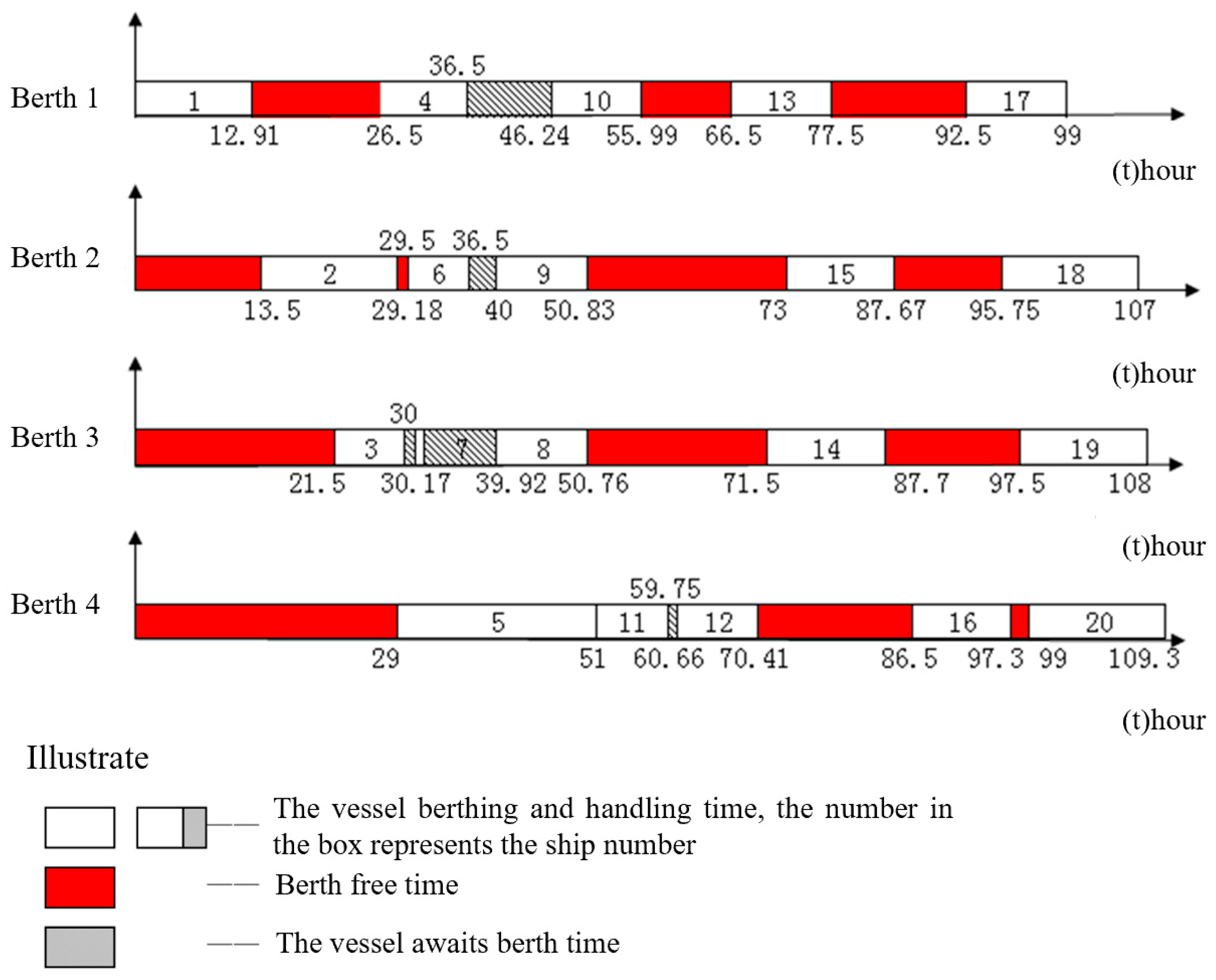
5.3. Results of Multi-Berth Allocation
5.3.1. Based on ACO
5.3.2. Based on PACO
5.4. Sensitivity Analysis
5.5. Benchmarking Analysis with Other Algorithms
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, B.; Hua, G. Optimizing berth operation system in container terminal by simulation. In Proceedings of the IEEE International Conference on Logistics, 2017, Sydney, NSW, Australia, 24–27 July 2016. [Google Scholar]
- Yu, M.; Wang, S.; Cai, Y. A dispatching method for trucks at container terminal by using fuzzy-cnp concept. In Proceedings of the 2010 International Conference on Logistics Engineering and Intelligent Transportation Systems, Wuhan, China, 26–28 November 2010; pp. 1–4. [Google Scholar]
- Roy, D.; de Koster, R. Stochastic modeling of unloading and loading operations at a container terminal using automated lifting vehicles. Eur. J. Oper. Res. 2018, 266, 895–910. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A follow-up survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2015, 244, 675–689. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Frojan, P.; Francisco, C.J.; Alvarez, V.R.; Koulouris, G.; Manuel, T.J. The continuous berth allocation problem in a container terminal with multiple quays. Expert Syst. Appl. Int. J. 2015, 42, 7356–7366. [Google Scholar] [CrossRef]
- Jakub, W.; Maciej, D. Selecting algorithms for large berth allocation problems. Eur. J. Oper. Res. 2020, 283, 844–862. [Google Scholar]
- Lin, S.W.; Ting, C.J. Solving the dynamic berth allocation problem by simulated annealing. Eng. Optim. 2014, 46, 308–327. [Google Scholar] [CrossRef]
- Mauri, G.R.; Lorena LA, N.; Lorena LA, N.; Laporte, G. An adaptive large neighborhood search for the discrete and continuous berth allocation problem. Comput. Oper. Res. 2016, 70, 140–154. [Google Scholar] [CrossRef]
- Rodriguez-Molins, M.; Salido, M.A.; Barber, F. Robust scheduling for berth allocation and quay crane assignment problem. Math. Probl. Eng. 2014, 2014, 834927. [Google Scholar] [CrossRef]
- Ćustić, A.; Sokol, V.; Punnen, A.P.; Bhattacharya, B. The bilinear assignment problem: Complexity and polynomially solvable special cases. Math. Program. 2017, 166, 185–205. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, C.; Zhang, Z. Solving NP-Hard Problems with Physarum-Based Ant Colony System. Trans. Comput. Biol. Bioinform. 2017, 14, 108–120. [Google Scholar] [CrossRef]
- Issam, E.H.; Azza, L.; Yassine, T. A multi-objective model for discrete and dynamic Berth Allocation Problem. In Proceedings of the 2nd International Conference on Big Data, Cloud, and Applications, Tetouan, Morocco, 29–30 March 2017. [Google Scholar]
- Hsu, H.P. A HPSO for solving dynamic and discrete berth allocation problem and dynamic quay crane assignment problem simultaneously. Swarm Evol. Comput. 2016, 271, 156–168. [Google Scholar] [CrossRef]
- Hu, Z.H. Multi-objective genetic algorithm for berth allocation problem considering daytime preference. Comput. Ind. Eng. 2015, 89, 2–14. [Google Scholar] [CrossRef]
- Lin, S.W.; Ying, K.C.; Wan, S.Y. Minimizing the total service time of discrete dynamic berth allocation problem by an iterated greedy heuristic. Sci. World J. 2014, 2014, 218925. [Google Scholar] [CrossRef]
- Türkoğulları, Y.B.; Taşkın, Z.C.; Aras, N.; Altınel, İ.K. Optimal berth allocation, time-variant quay crane assignment and scheduling with crane setups in container terminals. Eur. J. Oper. Res. 2016, 2016, 985–1001. [Google Scholar] [CrossRef]
- Simrin, A.; Diabat, A. The dynamic berth allocation problem. RAIRO—Oper. Res. 2015, 49, 473–494. [Google Scholar] [CrossRef]
- Kovac, N.; Davidovic, T.; Stanimirovic, Z. Evolutionary algorithm for the minimum cost hybrid berth allocation problem. In Proceedings of the International Conference on Information, Intelligence, Systems and Applications, Corfu, Greece, 6–8 July 2015; pp. 1–6. [Google Scholar]
- Kordić, S.; Davidović, T.; Kovač, N.; Dragović, B. Combinatorial approach to exactly solving discrete and hybrid berth allocation problem. Appl. Math. Model. 2016, 40, 8952–8973. [Google Scholar] [CrossRef]
- Budipriyanto, A.; Wirjodirdjo, B.; Pujawan, I.N.; Gurning, S. A simulation study of collaborative approach to berth allocation problem under uncertainty. Asian J. Shipp. Logist. 2017, 33, 127–139. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Miao, L. A bi-objective robust model for berth allocation scheduling under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2017, 106, 294–319. [Google Scholar] [CrossRef]
- Eisen, H.E.; Van der Lei, J.E.; Zuidema, J.; Koch, T.; Dugundji, E.R. An Evaluation of First-Come, First-Served Scheduling in a Geometrically-Constrained Wet Bulk Terminal. Front. Future Transp. 2021, 23, 709822. [Google Scholar] [CrossRef]
- Bai, Y.; Lv, Y.; Zhang, J. Smart mobile robot fleet management based on hierarchical multi-agent deep Q network towards intelligent manufacturing. Eng. Appl. Artif. Intel. 2023, 124, 106534. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhi, Y.; Yang, X.F. Multi-agent and ant colony optimization for ship integrated power system network reconfiguration. J. Syst. Eng. Electron. 2022, 2, 489–496. [Google Scholar] [CrossRef]
- Randall, M.; Lewis, A. A Parallel Implementation of Ant Colony Optimization. J. Parallel Distrib. Comput. 2015, 62, 1421–1432. [Google Scholar] [CrossRef]
- Yu, M.; He, Z.; Li, D.; Yin, L. Research on multi-AGV path planning in automated container terminal. In Proceedings of the 2019 5th International Conference on Transportation Information and Safety (ICTIS), Liverpool, UK, 14–17 July 2019. [Google Scholar]
- Yu, M.; Wang, S. The Application Research of Container Berth Allocation Based on Ant Colony Algorithms. In Proceedings of the ICTIS 2011 Wuhan China: Multimodal Approach to Sustained Transportation System Development: Information, Technology, Implementation, Wuhan, China, 30 June–2 July 2011; pp. 1755–1761. [Google Scholar]
- Li, H.T.; Zhen, N.M.; Peng, T.S. Dynamic Ant Colony Genetic Algorithm Based on TSP. Mach. Des. Manuf. 2019, 12, 147–149. [Google Scholar]
- Zhang, X.J.; Wang, K.; Cao, M.Y. Coordinated Optimization of Berth Assignment and Box Allocation in Simulation Environment. Mod. Manuf. Eng. 2022, 3, 13–18. [Google Scholar]
- Niu, M.; Wang, Z.Y.; Li, Y.J. Considering the integration optimization of berth allocation and ship scheduling using priority. High-Tech Commun. 2020, 30, 972–981. [Google Scholar]
- Zhang, M.; Jiang, Z.; Wang, L.; Yao, Y. Research on Parallel Ant Colony Algorithm for 3D Terrain Path Planning. In Asian Simulation Conference; Springer: Singapore, 2017; pp. 74–82. [Google Scholar]
- Xu, D.; Li, C.L.; Leung JY, T. Berth allocation with time-dependent physical limitations on vessels. Eur. J. Oper. Res. 2012, 216, 47–56. [Google Scholar] [CrossRef]
- Dorigo, M.; Di Caro, G.; Gambardella, L.M. Ant algorithms for discrete optimization. Artif. Life 1999, 5, 137–172. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2019; pp. 311–351. [Google Scholar]
- Geza, K.; Balazs, L.; Janos, J. Parallel Ant Colony Algorithm for Shortest Path Problem. Period. Polytech. Civ. Eng. 2019, 63, 243–254. [Google Scholar]
- Chen, X.; Dai, Y. Research on an Improved Ant Colony Algorithm Fusion with Genetic Algorithm for Route Planning. In Proceedings of the IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020. [Google Scholar]
- Huang, W.; Huang, M.; Wang, H.; Software, S.O.; University, J.N. Application research of ant colony algorithm based on association rules in cross-selling. Comput. Digit. Eng. 2014. [CrossRef]
- Chowdhury, S.; Marufuzzaman, M.; Tunc, H.; Bian, L.; Bullington, W. A modified Ant Colony Optimization algorithm to solve a dynamic traveling salesman problem: A case study with drones for wildlife surveillance. J. Comput. Des. Eng. 2019, 6, 368–386. [Google Scholar] [CrossRef]
- Guo, W.; Ji, M.; Zhu, H. Collaborative Optimization of Berth Allocation and Yard Storage in Container Terminals. Traffic Transp. Eng. 2019, 7, 56–70. [Google Scholar]
- Ge, Y.; Wang, A. Spatial scheduling strategy for irregular curved blocks based on the modified genetic ant colony algorithm (MGACA) in shipbuilding. Int. J. Prod. Res. 2018, 56, 3099–3115. [Google Scholar] [CrossRef]


| No. of Vessels | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Inter-arrival time (h) | 0.0 | 13.5 | 8.0 | 5.0 | 2.5 | 0.5 | 0.5 | 1.5 | 5.0 | 0.0 |
| Loading/unloading time (h) | 12.9 | 11.7 | 8.7 | 19. 7 | 22.0 | 11. 5 | 9.8 | 10.8 | 10.8 | 9.8 |
| No. of Vessels | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Inter-arrival time (h) | 14.0 | 8.8 | 7.3 | 5.0 | 1.5 | 13.5 | 6.0 | 3.25 | 1.8 | 1.5 |
| Loading/unloading time (h) | 9.7 | 9.8 | 11.0 | 12. 5 | 14.7 | 10.7 | 6. 8 | 11.3 | 10.0 | 10.3 |
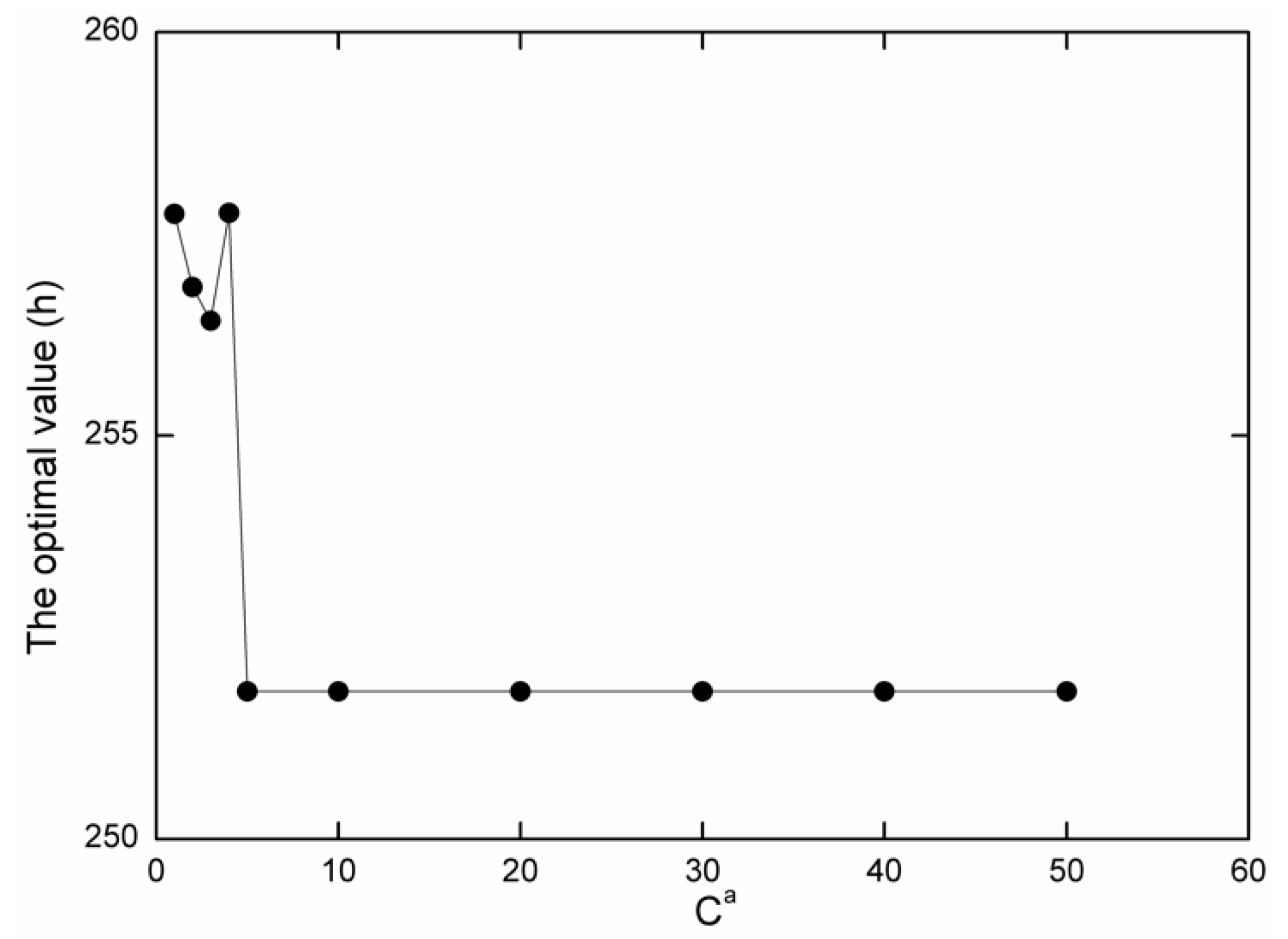
| Ca | The Optimal Value (the Total Residence Time of All Vessels in the Port) | Started Convergence Algebra |
|---|---|---|
| 1 | 257.75 | 7 |
| 2 | 256.84 | 5 |
| 3 | 256.42 | 5 |
| 4 | 257.76 | 1 |
| 5 | 251.83 | 5 |
| 10 | 251.83 | 3 |
| 20 | 251.83 | 2 |
| 30 | 251.83 | 2 |
| 40 | 251.83 | 1 |
| 50 | 251.83 | 1 |
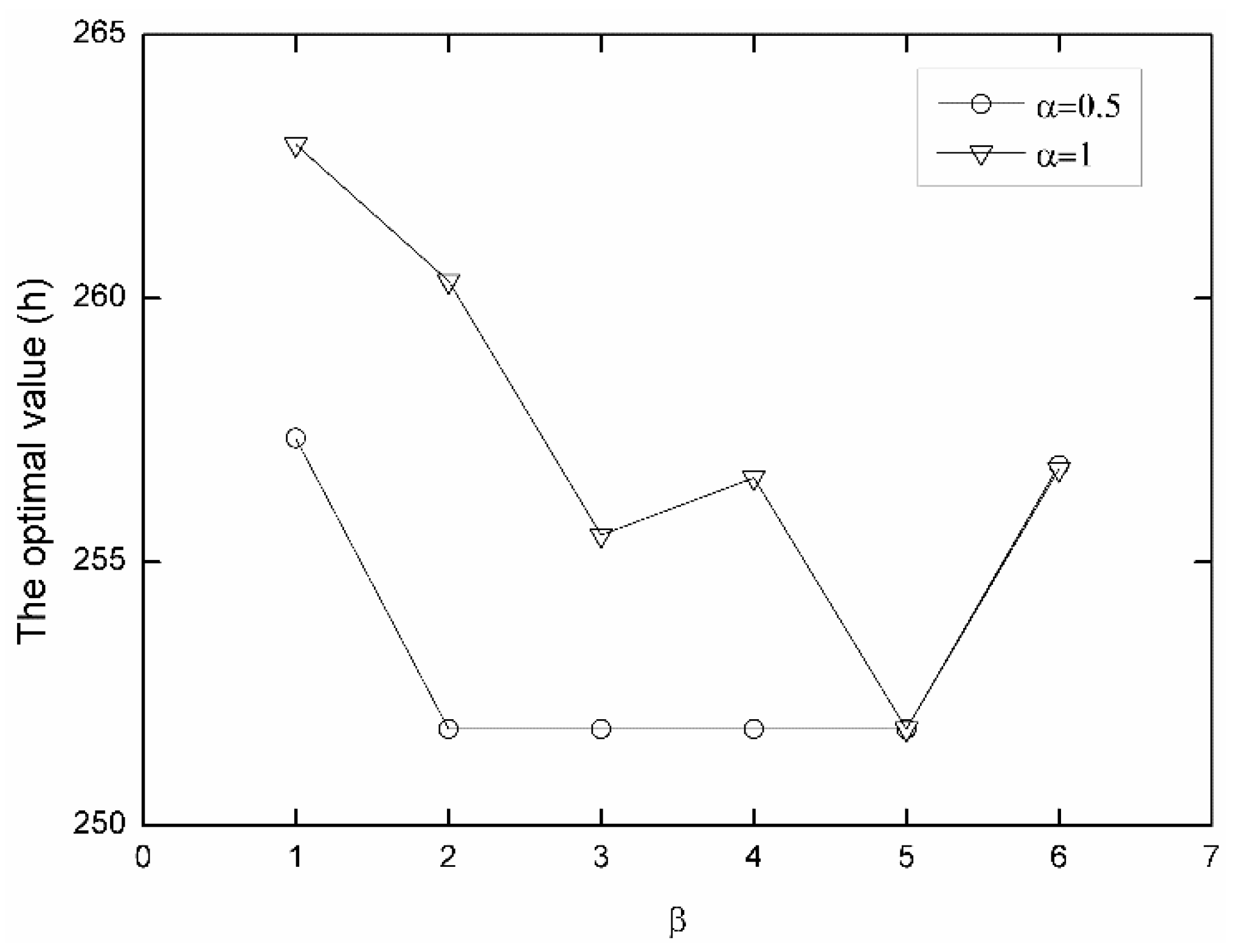
| α | β | The Optimal Value (the Total Residence Time of All Vessels in the Port) | Started Convergence Algebra |
|---|---|---|---|
| 0.5 | 1 | 257.35 | 53 |
| 0.5 | 2 | 251.83 | 15 |
| 0.5 | 3 | 251.83 | 21 |
| 0.5 | 4 | 251.83 | 3 |
| 0.5 | 5 | 251.83 | 3 |
| 0.5 | 6 | 256.84 | 6 |
| 1 | 1 | 262.92 | 22 |
| 1 | 2 | 260.33 | 21 |
| 1 | 3 | 255.51 | 6 |
| 1 | 4 | 256.60 | 5 |
| 1 | 5 | 251.83 | 3 |
| 1 | 6 | 256.76 | 2 |
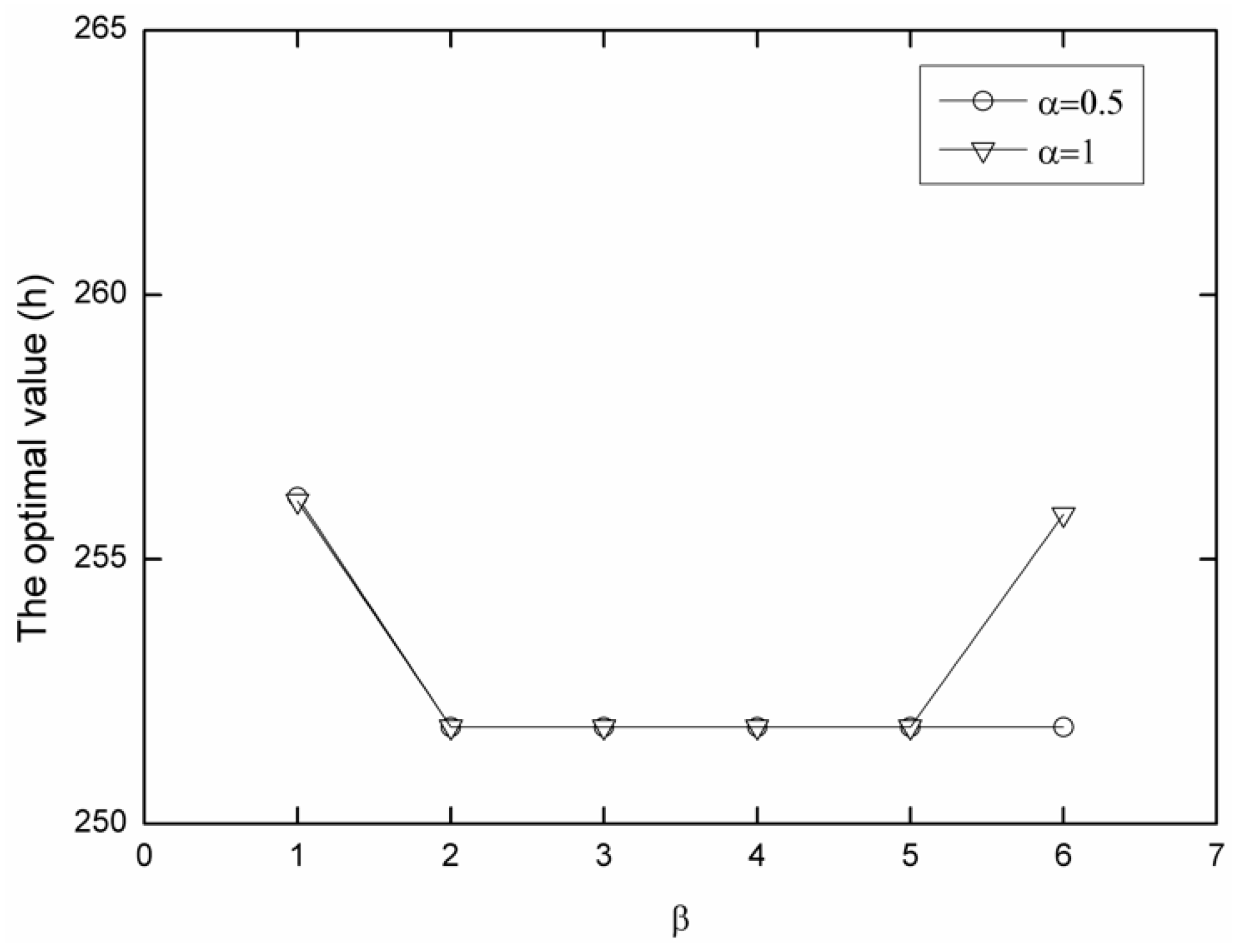
| α | β | The Optimal Value (the Total Residence Time of All Vessels in the Port) | Started Convergence Algebra |
|---|---|---|---|
| 0.5 | 1 | 256.18 | 29 |
| 0.5 | 2 | 251.83 | 22 |
| 0.5 | 3 | 251.83 | 8 |
| 0.5 | 4 | 251.83 | 2 |
| 0.5 | 5 | 251.83 | 2 |
| 0.5 | 6 | 251.83 | 17 |
| 1 | 1 | 256.10 | 14 |
| 1 | 2 | 251.83 | 6 |
| 1 | 3 | 251.83 | 5 |
| 1 | 4 | 251.83 | 2 |
| 1 | 5 | 251.83 | 2 |
| 1 | 6 | 255.85 | 2 |
| Actual | GA | PSO | ACO | PACO | |
|---|---|---|---|---|---|
| The total port time for the 20 vessels in the case (h) | 304.4 | 254.17 | 257.25 | 257.2 | 251.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Lv, Y.; Wang, Y.; Ji, X. Enhanced Ant Colony Algorithm for Discrete Dynamic Berth Allocation in a Case Container Terminal. J. Mar. Sci. Eng. 2023, 11, 1931. https://doi.org/10.3390/jmse11101931
Yu M, Lv Y, Wang Y, Ji X. Enhanced Ant Colony Algorithm for Discrete Dynamic Berth Allocation in a Case Container Terminal. Journal of Marine Science and Engineering. 2023; 11(10):1931. https://doi.org/10.3390/jmse11101931
Chicago/Turabian StyleYu, Meng, Yaqiong Lv, Yuhang Wang, and Xiaojing Ji. 2023. "Enhanced Ant Colony Algorithm for Discrete Dynamic Berth Allocation in a Case Container Terminal" Journal of Marine Science and Engineering 11, no. 10: 1931. https://doi.org/10.3390/jmse11101931
APA StyleYu, M., Lv, Y., Wang, Y., & Ji, X. (2023). Enhanced Ant Colony Algorithm for Discrete Dynamic Berth Allocation in a Case Container Terminal. Journal of Marine Science and Engineering, 11(10), 1931. https://doi.org/10.3390/jmse11101931







