Three-Dimensional Trajectory Tracking for a Heterogeneous XAUV via Finite-Time Robust Nonlinear Control and Optimal Rudder Allocation

Abstract

This paper proposes a novel three-dimensional trajectory tracking control methodology for a heterogeneous X-rudder autonomous underwater vehicle (XAUV) that can achieve finite-time convergence, complex actuator dynamics handling, and energy-efficient optimized rudder allocation. Under a compound robust control scheme, the trajectory tracking problem is decomposed into three sub-problems: kinematics control, dynamics control, and rudder allocation. For kinematics control, a novel finite-time line-of-sight (FTLOS) guidance law is proposed, which can achieve faster position and orientation tracking when compared with classical LOS guidance, and is rarely studied in the existing finite time control methods. In the dynamics control loop, global finite-time terminal sliding mode control (FTTSMC) laws are provided to solve the heading control, pitching control, and surge velocity tracking control problems, where finite-time convergence is achieved in both the approaching stage and sliding mode holding stage. The multi-source uncertainties with unknown upper bounds in both kinematics and dynamics loops are well treated by finite-time extended disturbance observers (FTEDOs), thus ensuring the system robustness. Moreover, the influence of complex actuator dynamics is fully considered by employing a RBFNN compensator to deal with the propeller saturation and proposing an energy-efficient optimal rudder allocator to tackle the multi-objective and multi-constraint heterogeneous X-rudder angle assignment problem. Finally, simulation verifications are carried out for two different scenarios, where Case 1 focuses on the adaptability of the algorithm to different conditions and Case 2 focuses on the superiority of the algorithm over three other commonly used algorithms. The comparative simulation results show that the proposed controller has good adaptability to different initial and disturbance conditions, and performs better than three other classical controllers, especially in convergence speed, tracking accuracy, stability, and energy consumption.

1. Introduction

In the past few years, XAUVs have received significant attention owing to its great advantages in maneuverability, controllability, rudder efficiency, and anti-sinking ability in jamming situations [1,2]. However, compared with conventional cross rudder AUVs, the control problem of XAUVs is more complicated due to the heterogeneous rudder layout.

Trajectory tracking is a key control problem for AUVs to accomplish complex underwater tasks. Although trajectory tracking of conventional AUVs has been extensively studied, related research has been rarely reported for XAUVs, and most of the existing XAUV research focuses on 2D decoupled control [3,4]. From this standpoint, three-dimensional trajectory tracking of a heterogeneous XAUV will be addressed in this paper.

In most of the existing literature, the trajectory tracking problem has been divided into two parts: kinematics control and dynamics control. For kinematic control, line-of-sight (LOS) guidance law is considered to be an effective method [5]. Moreover, to further improve the application range and guidance performance, a variety of improved LOS guidance laws have been studied, such as the fuzzy optimization algorithm-based adaptive line-of-sight (ALOS) guidance law [6], the RBFNN-based ILOS guidance law [7], etc. For dynamics control with actuator dynamics and unknown disturbances, a series of robust control methods have been studied, including but not limited to, decoupled nonlinear PID (NLPID) control [8], sliding mode control [9,10], fuzzy control [11,12], neural network control [13,14], model predictive control [15,16], data-driven control [17], etc.

Note that most of the aforementioned trajectory tracking studies can only guarantee asymptotic stability without considering the convergence time. However, finite-time tracking is more preferable for AUVs in real scenarios, since finite-time tracking can provide faster response, higher tracking precision, and better disturbance-rejection ability than the asymptotic control approach [18,19]. In recent years, some methods have been proposed for finite-time control. In [20], a novel fuzzy finite-time command filtered backstepping approach was proposed to tackle the finite-time tracking control problem for a class of nonlinear systems with input saturation. In [21], a novel nonsingular finite-time backstepping controller was constructed for marine vessel to achieve trajectory tracking with unknown external disturbances. However, most of the current studies on the finite-time control of AUVs only focus on the finite-time convergence of the control part, whereas the finite-time of guidance law has been ignored.

Another technical challenge for trajectory tracking is the unknown uncertainties caused by system parameter perturbations or external disturbances, which could severely degrade the closed-loop system performance. To obtain strong disturbance rejection ability, disturbance observers and neural network compensators are the most commonly used methods [22]. In [23], a nonsingular fast terminal sliding mode controller was constructed based on a fast finite-time state observer, which was designed to estimate the lumped uncertainties and disturbances. In [24], a multi-layer neural network and adaptive robust control techniques were combined to compensate for unknown dynamics of systems including nonlinear damping terms, unknown parameters, and environmental disturbances due to waves, wind, and ocean currents. In [25], a local recurrent neural network and an adaptive observer were designed to achieve unknown nonlinear function approximation and state estimation. In [26], an extended state observer (ESO) and projection neural networks were utilized to estimate the compound uncertainties induced by internal model uncertainties and external disturbances, based on which the output-feedback path-following controller was implemented for AUVs. However, most of the disturbance observation studies have paid more attention to the unknown disturbances contained in the dynamics and kinematics models while ignoring the ocean environment-induced perturbations of attack angle and drift angle.

Complex actuator dynamics are also key factors to be considered in completing the trajectory tracking mission, since actuator dynamics such as input saturation, dead zone, and time delay may have great influences on the control performance [27,28]. In recent years, many efforts have been made to solve this problem. In [29], the problem of non-symmetric dead-zones with unknown parameters was considered as a combination of linear input and bounded disturbances, and was finally estimated and compensated by RESO. Both actuator dynamics and system uncertainties were considered in [30] for the heading tracking of an AUV, and a high-order adaptive fuzzy sliding mode control law was designed to guarantee the asymptotic stability. In [31], to solve the unknown bound of actuator saturation, a novel saturated kinetic control law was proposed based on the indirect adaptive fuzzy method. In [32], to estimate the unknown parameter of input saturation and the unknown upper bound of uncertainties, adaptation laws were proposed. In [33], novel auxiliary systems were embedded in an adaptive fuzzy sliding mode controller to tackle the input saturation problem and achieve diving control. However, most of the existing research on the complex actuator dynamics is oriented towards cross-rudder AUVs, and usually only the characteristics of the propeller are considered. Compared with cross rudder AUVs, the XAUV studied in this paper not only faces the constraints of the propeller, but also confronts the problems caused by heterogeneous rudder surface layout, so it is more complex.

In order to make the control strategy more practical, this paper will focus on proposing a three-dimensional tracking control algorithm with finite time convergence, as well as solving the multi-source unknown uncertainties and complex actuator dynamics problems encountered by AUVs in actual scenarios. Besides, the X-rudder studied in this paper has a heterogeneous control surface, which is more difficult to control than the conventional cross rudder. Based on the above-mentioned contents, this paper will strive to provide useful references for the research of similar underwater vehicles. To the best of the authors’ knowledge, the main contributions are summarized as follows:

(1)

The finite-time convergence strategy is deeply integrated with the whole controller design process. The novel FTLOS guidance law and finite-time feedback kinematics control law is designed for the kinematics control loop. Improved global finite-time terminal sliding mode control (FTTSMC) laws are proposed for heading control, pitching control, and surge velocity tracking control in the dynamics control loop, where finite time convergence is considered in both the approaching stage and sliding mode holding stage. The FTEDOs are designed to tackle the multi-source unknown uncertainties existing in both the kinematics and dynamics loops. Compared with the existing literature on finite-time control [20,21], this paper not only focuses on the finite convergence of dynamics control, but also proposes a new finite-time convergence guidance algorithm that is easy to implement, making the finite-time control method more comprehensive and effective.

(2)

The influences of actuator dynamics are fully considered, including not only the propeller input saturation problem, but also the complex dynamics mechanism and various constraints of the heterogeneous X-rudder. To deal with the propeller input saturation problem, an adaptive RBFNN compensator is integrated into the surge velocity tracking control law, while for X-rudder dynamics and constraints, a multi-objective optimal rudder allocator is proposed that can realize the rudder angle allocation and energy consumption optimization at the same time, as well as meet the saturation constraints of rudder angle and rudder steering velocity. Compared with the general literatures on actuator characteristics, the research in this paper is more comprehensive.

(3)

Multi-source disturbances are considered in both the kinematics model and dynamics model. In particular, $\dot{\alpha }$ and $\dot{\beta }$ are treated as unknown uncertainties, rather than directly obtained by differential calculation, taking into account the noise problem in the measurement process, which makes the controller design more practical. For the multi-source unknown disturbances, FTEDOs are designed to realize fast and accurate disturbance estimation based on motion state, which greatly improves the robustness of the system. Compared with the conventional disturbance observer, this method can realize the estimation of both the disturbance and its derivative, and shows finite time convergence.

The remainder of this paper is organized as follows. Section 2 presents the XAUV model and three-dimensional trajectory tracking problem. Section 3 proposes the compound finite-time robust control scheme and presents the detailed deriving process of the kinematics controller, dynamics controller, and optimal rudder allocator. Section 4 validates the proposed control algorithm through comparative simulation cases. Section 5 demonstrates the conclusions and suggests future works.

2. XAUV Modeling and Problem Formulation

2.1. Preliminaries and Nomenclatures

Lemma 1.

([34]) The radial basis function neural network (RBFNN) system can be employed to approximate the unknown smooth function f(x) in the following way

$$f(x)={\widehat{W}}^T\varphi (x,\xi )+\epsilon (x)$$

(1)

where $x$ denotes a general state scalar, ${\widehat{W}}^T$ is the weight matrix which connects the hidden layer to the output layer, $\varphi (x,\xi )$ is the radial basis function, $\epsilon (x)$ is the approximation error that satisfies $\left|\epsilon (x)\right|\le \overline{\epsilon }$ with $\overline{\epsilon }>0$.

The ideal weight$W^{\ast T}$is defined as

$$W^{\ast T}=\arg \underset{{\widehat{W}}^T,\widehat{\xi }\in R}{\min }\left\{\sup \left|f(x)-{\widehat{W}}^T\varphi (x,\xi )\right|\right\}$$

(2)

Lemma 2.

([35]) The equilibrium point $x=0$ is globally finite-time stable if there exists a Lyapunov function satisfying:

$$\dot{V}(x)+{\lambda }_{1}V(x)+{\lambda }_2{V}^k(x)\le 0$$

(3)

where ${\lambda }_1>0$, ${\lambda }_2>0$, $0<k<1$. The settling time can be given by:

$$t\le \frac{1}{{\lambda }_1(1-k)}\ln \frac{{\lambda }_1{V}^{1-k}(x_0)+{\lambda }_2}{{\lambda }_2}$$

(4)

where $V(x_0)$ is the initial value of $V(x)$.

Lemma 3.

([36]) For the scalars $x_i(i=1,2,\dots ,n)$, the following inequality holds:

$${\left({\displaystyle \sum _{i=1}^n\left|x_i\right|}\right)}^p\le {\displaystyle \sum _{i=1}^n{\left|x_i\right|}^p}\le n^{1-p}{\left({\displaystyle \sum _{i=1}^n\left|x_i\right|}\right)}^p$$

(5)

where $0\le p\le 1$is a constant.

Notation: The symbols $sign(x)$, $sat(x)$, and $si{g}^r(x)$ are utilized in this paper and are defined as follows:

$$\left\{\begin{array}{l}sign(x)=\left\{\begin{array}{cc}1,& x\ge 0\\ -1,& x<0\end{array}\right.\hfill \\ sat(x)=\left\{\begin{array}{ll}{x}_{\max },\hfill & x\ge x_{\max }\hfill \\ \begin{array}{l}x,\\ -x_{\max }\end{array}\hfill & \begin{array}{l}-x_{\max }<x<x_{\max }\\ x<-x_{\max }\end{array}\hfill \end{array}\right.\hfill \\ si{g}^r(x)={\left|x\right|}^{r}sign(x)\hfill \end{array}\right.$$

(6)

Nomenclature: The main nomenclature utilized in this paper is listed in Table 1.

Table 1. The main nomenclature in this paper.

Nomenclature	Definition
XAUV	X-rudder autonomous underwater vehicle
FTLOS	Finite-time line-of-sight
FTEDO	Finite-time extended disturbance observer
FTTSMC	Finite-time terminal sliding mode control
DOF	Degree of freedom
RBFNN	Radial basis function neural network
SQP	Sequential quadratic programming
{I}	Inertial reference frame
{B}	Body-fixed frame
{F}	Frenet–Serret frame
$\mathit{\eta }={(x,y,z,\theta ,\psi )}^T$	The position and orientation variables in {I}
$\mathit{\nu }={(u,v,w,q,r)}^T$	The linear and angular velocities in {B}
${(x_d,y_d,z_d,{\theta }_d,{\psi }_d)}^T$	Desired position and orientation variables in {I}
${(x_e,y_e,z_e,{\theta }_e,{\psi }_e)}^T$	The tracking error vectors in {F}
$X_T$	The propeller thrust
${({\tau }_v,{\tau }_w,{\tau }_q,{\tau }_r)}^T$	The X-rudder forces and torques
${({\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4)}^T$	The X-rudder angles
${({\theta }_{FTLOS},{\psi }_{FTLOS})}^T$	The proposed FTLOS guidance laws
${(u_d,q_d,r_d)}^T$	The kinematics control laws
${\left[{\tau }_{rd},{\tau }_{qd}\right]}^T$	The desired rudder torques generated by dynamics control

2.2. XAUV Modeling

Compared with conventional cross-rudder AUVs, the XAUV studied here adopts a heterogeneous X-type stern rudder arrangement. The vehicle is assumed to be neutrally buoyant and the hydrodynamic restoring force is large enough in the roll direction. Therefore, five DOF mathematical models are considered in this paper.

The kinematic model of the XAUV takes the following form:

$$\left\{\begin{array}{c}\dot{x}=u\cos (\theta )\cos (\psi )-v\sin (\psi )+w\sin (\theta )\cos (\psi )\hfill \\ \dot{y}=u\cos (\theta )\sin (\psi )+v\cos (\psi )+w\sin (\theta )\sin (\psi )\hfill \\ \dot{z}=-u\sin (\theta )+w\cos (\theta )\hfill \\ \dot{\theta }=q\hfill \\ \dot{\psi }=r/\cos (\theta )\hfill \end{array}\right.$$

(7)

where ${(x,y,z,\theta ,\psi )}^T$ denote the position and orientation variables of the XAUV in the earth-fixed inertial frame; ${(u,v,w,q,r)}^T$ denote the linear and angular velocities of the XAUV in the body-fixed frame.

The dynamics model of the XAUV can be described as follows:

$$\begin{array}{ll}\left(m-X_{\dot{u}}\right)\dot{u}\hfill & =X_{u\left|u\right|}u\left|u\right|+\left(X_{wq}-m\right)wq+X_{qq}{q}^2+X_{rr}rr\hfill \\ \hfill & +\left(X_{vr}+m\right)vr+X_T+d_u\hfill \\ \left(m-Y_{\dot{v}}\right)\dot{v}\hfill & = Y_{v\left|v\right|}v\left|v\right|+Y_{r\left|r\right|}r\left|r\right|+\left(Y_{ur}-m\right)ur\hfill \\ \hfill & +Y_{uv}uv+{\tau }_v+d_v\hfill \\ \left(m-Z_{\dot{w}}\right)\dot{w}\hfill & =Z_{w\left|w\right|}w\left|w\right|+Z_{q\left|q\right|}q\left|q\right|+\left(Z_{uq}+m\right)uq+Z_{uw}uw\hfill \\ \hfill & +{\tau }_w+d_w\hfill \\ \left(I_{yy}-M_{\dot{q}}\right)\dot{q}\hfill & =M_{w\left|w\right|}w\left|w\right| +M_{q\left|q\right|}q\left|q\right|+M_{uq}uq\hfill \\ \hfill & +M_{uw}uw+{\tau }_q+d_q\hfill \\ (I_{zz}-N_{\dot{r}})\dot{r}\hfill & =N_{v\left|v\right|}v\left|v\right|+N_{r\left|r\right|}r\left|r\right|+N_{ur}ur+N_{uv}uv\hfill \\ \hfill & + {\tau }_r+d_r\hfill \end{array}$$

(8)

where $m$ is the vehicle mass; $I_{yy}$ and $I_{zz}$ denote moments of inertia; $R_{\ast }$ ($R=X,Y,Z,M,N$) are the hydrodynamics coefficients; $d_{\ast }$ is the unknown oceanic disturbance induced forces and moments; $X_T$ is the propeller thrust; ${\tau }_v$, ${\tau }_w$, ${\tau }_q$, and ${\tau }_r$ are the control forces and torques generated by the X-rudder.

To facilitate controller design, the dynamics model of X-rudder AUVs can be rewritten as

$$\left\{\begin{array}{l}\dot{u}=f_u+g_u{X}_T+D_u\\ \dot{v}=f_v+g_v{\tau }_v+D_v\\ \dot{w}=f_w+g_w{\tau }_w+D_w\\ \dot{q}=f_q+g_q{\tau }_q+D_q\\ \dot{r}=f_r+g_r{\tau }_r+D_r\end{array}\right.$$

(9)

where $D_{\ast }$ denotes a lumped unknown disturbance with unknown upper bounds; $f_{\ast }$ and $g_{\ast }$ are known functions, which can be easily deduced from Equation (8).

The X-rudder forces and torques in Equation (9) can be further expressed as

$$\left\{\begin{array}{l}{\tau }_v=Y_{uu{\delta }_1}{u}^2{\delta }_1+Y_{uu{\delta }_2}{u}^2{\delta }_2+Y_{uu{\delta }_3}{u}^2{\delta }_3+Y_{uu{\delta }_4}{u}^2{\delta }_4\\ {\tau }_w=Z_{uu\delta 1}{u}^2{\delta }_1+Z_{uu\delta 2}{u}^2{\delta }_2+Z_{uu\delta 3}{u}^2{\delta }_3+Z_{uu\delta 4}{u}^2{\delta }_4\\ {\tau }_q=M_{uu\delta 1}{u}^2{\delta }_1+M_{uu\delta 2}{u}^2{\delta }_2+M_{uu\delta 3}{u}^2{\delta }_3+M_{uu\delta 4}{u}^2{\delta }_4\\ {\tau }_r=N_{uu{\delta }_1}{u}^2{\delta }_1+N_{uu{\delta }_2}{u}^2{\delta }_2+N_{uu{\delta }_3}{u}^2{\delta }_3+N_{uu{\delta }_4}{u}^2{\delta }_4\end{array}\right.$$

(10)

where $Y_{\ast }$, $Z_{\ast }$, $M_{\ast }$, and $N_{\ast }$ are the rudder coefficients; ${\delta }_1$, ${\delta }_2$, ${\delta }_3$, and ${\delta }_4$ are the four rudder angles of the X-rudder AUV.

2.3. Problem Formulation

As depicted in Figure 1, the XAUV is required to track the desired trajectory in three-dimensional space. {I} and {B} are the inertial reference frame and body-fixed frame, respectively. P is a moving point on the desired trajectory associated with the Frenet–Serret frame $\left\{F\right\}$.

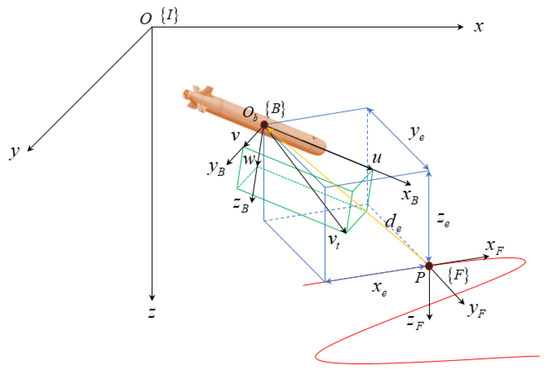
Figure 1. Trajectory tracking in three-dimensional space.

Define the actual position vectors of the XAUV as ${(x,y,z)}^T$; define also the position vectors of moving point P as ${(x_d,y_d,z_d)}^T$. The position tracking error vectors in $\left\{I\right\}$ can be calculated by

$$\left\{\begin{array}{c}{x}_e^I=x-x_d\\ y_e^I=y-y_d\\ z_e^I=z-z_d\end{array}\right.$$

(11)

Similarly, the orientation tracking error vector can be calculated by

$$\left\{\begin{array}{c}{\theta }_e={\theta }_b-{\theta }_d\\ {\psi }_e={\psi }_b-{\psi }_d\end{array}\right.$$

(12)

where ${\theta }_b=\theta +\alpha$, $\alpha =\arctan \left(-w/u\right)$, ${\psi }_b=\psi +\beta$, $\beta =\arctan \left(v/\sqrt{u^2+w^2}\right)$, ${\theta }_d=\arctan \left(\frac{-{\dot{z}}_d}{\sqrt{{\dot{x}}_d^2+{\dot{y}}_d^2}}\right)$ and ${\psi }_d=\arctan ({\dot{y}}_d/{\dot{x}}_d)$.

Furthermore, the trajectory-tracking errors can be expressed in $\left\{F\right\}$ as

$$\left[\begin{array}{l}{x}_e\\ y_e\\ z_e\end{array}\right]=\left[\begin{array}{ccc}\cos {\psi }_d& -\sin {\psi }_d& 0\\ \sin {\psi }_d& \cos {\psi }_d& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}\cos {\theta }_d& 0& \sin {\theta }_d\\ 0& 1& 0\\ -\sin {\theta }_d& 0& \cos {\theta }_d\end{array}\right]\left[\begin{array}{l}{x}_e^I\\ y_e^I\\ z_e^I\end{array}\right]$$

(13)

Differentiating Equations (12) and (13) yields

$$\left\{\begin{array}{c}{\dot{x}}_e=\cos \left({\psi }_e\right)\cos \left({\theta }_e\right)v_t-U_p\left(1-c_{s1}{y}_e+c_{s2}{z}_e\right)\hfill \\ {\dot{y}}_e=\sin \left({\psi }_e\right)\cos \left({\theta }_e\right)v_t-c_{s1}{x}_e{U}_p\hfill \\ {\dot{z}}_e=-\sin \left({\theta }_e\right)v_t+c_{s2}{x}_e{U}_p\hfill \\ {\dot{\theta }}_e=q+\dot{\alpha }-c_{s2}{U}_p\hfill \\ {\dot{\psi }}_e=r/\cos \left(\theta \right)+\dot{\beta }-c_{s1}{U}_p\hfill \end{array}\right.$$

(14)

where $U_p=\sqrt{{\dot{x}}_d^2+{\dot{y}}_d^2+{\dot{z}}_d^2}$ is the resultant velocity of point $P$; $c_{s1}$ and $c_{s2}$ are the curvature and torsion of $P$, respectively; $c_{s1}={\dot{\psi }}_d/U_p$, $c_{s2}={\dot{\theta }}_d/U_p$, $v_t=\sqrt{u^2+v^2+w^2}$ denotes the resultant velocity of the XAUV.

Remark 1.

Using the general way, the $\dot{\alpha }$and$\dot{\beta }$can be derived by$\dot{\alpha }=(u\dot{w}-w\dot{u})/(u^2+w^2)$and $\dot{\beta }=(\dot{v}\sqrt{u^2+w^2}-v\frac{u\dot{u}+w\dot{w}}{\sqrt{u^2+w^2}})/v_t^2$, where $\dot{u}$,$\dot{v}$, and $\dot{w}$are unknown. Although a simple way to obtain the accelerations would be by differentiation of measured velocities, the approach is not practical, since velocity measurement are commonly corrupted by noise. To address this problem, $\dot{\alpha }$and $\dot{\beta }$are treated as uncertainties in this paper.

Therefore, according to Remark 1, the tracking error dynamics model Equation (14) can be rewritten as:

$$\left\{\begin{array}{c}{\dot{x}}_e=\cos \left({\psi }_e\right)\cos \left({\theta }_e\right)v_t-U_p\left(1-c_{s1}{y}_e+c_{s2}{z}_e\right)\hfill \\ {\dot{y}}_e=\sin \left({\psi }_e\right)\cos \left({\theta }_e\right)v_t-c_{s1}{x}_e{U}_p\hfill \\ {\dot{z}}_e=-\sin \left({\theta }_e\right)v_t+c_{s2}{x}_e{U}_p\hfill \\ {\dot{\theta }}_e=q+D_{\alpha }-c_{s2}{U}_p\hfill \\ {\dot{\psi }}_e=r/\cos \left(\theta \right)+D_{\beta }-c_{s1}{U}_p\hfill \end{array}\right.$$

(15)

where $D_{\alpha }=\dot{\alpha }$ and $D_{\beta }=\dot{\beta }$ denote unknown uncertainties.

The total control objective of three-dimensional trajectory tracking is to derive a control law such that the tracking error vectors can converge to zero.

To achieve this control objective, three sub-problems should be addressed:

Sub-problem 1.

Given a desired trajectory and the trajectory tracking error model Equation (15), derive effective virtual control laws${\left[u_d,q_d,r_d\right]}^T$, so that all the trajectory tracking error vectors${\left[x_e,y_e,z_e,{\theta }_e,{\psi }_e\right]}^T$can converge to 0 in finite time.

Sub-problem 2.

Given the desired virtual control laws${\left[u_d,q_d,r_d\right]}^T$and the dynamics model Equation (9), derive an effective robust nonlinear control law${\left[X_T,{\tau }_{qd},{\tau }_{rd}\right]}^T$so that the tracking errors $u-u_d$,$q-q_d$, and$r-r_d$can converge to 0 in finite-time.

Sub-problem 3.

Given the desired virtual rudder torque control laws ${\left[{\tau }_{qd},{\tau }_{rd}\right]}^T$and the dynamics model Equation (10), derive an optimal rudder allocation law to generate the control input ${\left[{\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4\right]}^T$so that the accurate rudder angle allocation and energy consumption optimization can be achieved at the same time, despite the saturation constraints of rudder angle and rudder steering velocity.

2.4. Assumptions

Assumption 1.

The uncertainties $D_i(i=u,v,w,q,r,\alpha ,\beta )$are bounded and second-order differentiable.

Assumption 2.

Like other marine vehicles, the XAUV also faces the input saturation problem, which means the propeller thrust and rudder angles here should be bounded, viz.$\left|X_T\right|\le {\overline{X}}_T$and $\left|{\delta }_i\right|\le \overline{\delta },(i=1,2,3,4)$, where ${\overline{X}}_T$ and $\overline{\delta }$ are known positive constants. Besides, the rudder steering velocity should also be bounded, viz.$\left|d{\delta }_i/dt\right|\le {\overline{\delta }}^{\prime },(i=1,2,3,4)$, where ${\overline{\delta }}^{\prime }$ is a known positive constant.

Assumption 3.

The vehicle is assumed to be neutrally buoyant and the hydrodynamic restoring force is large enough in the roll direction.

3. Control Methodology

To achieve three-dimensional trajectory tracking of XAUVs with multiple unknown uncertainties and complex actuator dynamics, a compound robust control law is proposed based on finite-time kinematics control, finite-time dynamics control, and optimal rudder allocation, as shown in Figure 2. Firstly, the FTEDO method is introduced in Section 3.1 to deal with the multi-source unknown uncertainties. Secondly, the FTLOS guidance-based finite-time kinematics control method is proposed in Section 3.2. Then, the global finite-time terminal sliding mode control method is designed for dynamics control in Section 3.3. Finally, the optimal rudder allocation method is employed in Section 3.4 to tackle the multi-objective and multi-constraint heterogeneous X-rudder angle assignment problem.

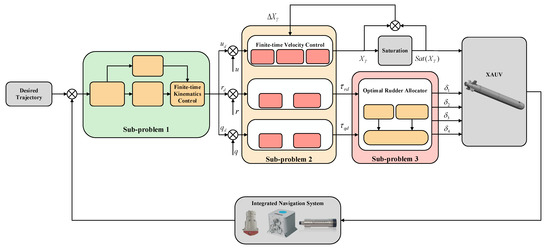
Figure 2. The proposed control structure.

3.1. Finite-Time Extended Disturbance Observer

Unknown external disturbances bring uncertainties to the mathematical model, which could severely degrade the closed-loop system performance or even cause system instability. To achieve robust dynamics control, fast and accurate disturbance estimation is critical. To address this problem, a second-order FTEDO is constructed here to estimate the unknown lumped uncertainties in both the kinematics and dynamics models. Compared with the general disturbance observer, this method can achieve faster convergence in finite time.

In order to facilitate the controller design process in the following sections, the unknown uncertainties ${\left[D_{\alpha },D_{\beta },D_u,D_q,D_r\right]}^T$ should be estimated.

Rewrite the model with uncertainty in the following general form:

$$\dot{X}=F_x+B{U}_x+D$$

(16)

where $X$ is the state variable, $F_x$ and $B$ are known functions, $U_x$ is the control input, and $D$ is the unknown uncertainty which needs to be estimated.

To estimate the unknown uncertainties, the second order FTEDO is designed as follows [37]:

$$\left\{\begin{array}{c}{\dot{Z}}_0=F_x+B{U}_x+P_0\hfill \\ P_0=-{\lambda }_{0}si{g}^{\frac{2}{3}}(Z_0-X)+Z_1\hfill \\ {\dot{Z}}_1=P_1=-{\lambda }_{1}si{g}^{\frac{1}{2}}(Z_1-P_0)+Z_2\hfill \\ {\dot{Z}}_2=-{\lambda }_2\mathrm{sgn}(Z_2-P_1)\hfill \\ Z_1=\widehat{D};Z_2=\widehat{\dot{D}}\hfill \end{array}\right.$$

(17)

where ${\lambda }_i(i=0,1,2)$ are positive observer gains;$Z_i(i=0,1,2)$ and $P_i(i=0,1)$ are auxiliary variables. The detailed expressions of FTEDOs for ${\left[D_{\alpha },D_{\beta },D_u,D_q,D_r\right]}^T$ are listed in Table A1 of the Appendix A.

Define the estimation errors as:

$$\left\{\begin{array}{c}{\Phi }_0=Z_0-X\\ {\Phi }_1=Z_1-D\\ {\Phi }_2=Z_2-\dot{D}\end{array}\right.$$

(18)

Then, the estimation error dynamics can be obtained as:

$$\left\{\begin{array}{c}{\dot{\Phi }}_0=-{\lambda }_{0}si{g}^{\frac{2}{3}}({\Phi }_0)+{\Phi }_1\hfill \\ {\dot{\Phi }}_1=-{\lambda }_{1}si{g}^{\frac{1}{2}}({\Phi }_1-{\dot{\Phi }}_0)+{\Phi }_2\hfill \\ {\dot{\Phi }}_2=-{\lambda }_2\mathrm{sgn}({\Phi }_2-{\dot{\Phi }}_1)-\ddot{D}\hfill \end{array}\right.$$

(19)

Remark 2.Utilizing the proposed FTEDO, the estimation errors${\Phi }_i(i=0,1,2)$can be stabilized to zero in finite time, which means there exists a time constant$t_r$such that${\Phi }_i=0(i=0,1,2)$holds for$t\ge t_r$ [38].

3.2. Finite-Time Kinematics Control

To solve the kinematics control sub-problem, the following finite-time control law is proposed:

$$\left\{\begin{array}{l}{u}_d=\left[-k_1{x}_e+U_p-k_{2}si{g}^{r_1}(x_e)\right]\frac{\cos \beta \cos \alpha }{\cos {\psi }_e\cos {\theta }_e}\\ q_d=-{\widehat{D}}_{\alpha }+c_{s2}{U}_p+{\dot{\theta }}_{FTLOS}-k_3\left({\theta }_e-{\theta }_{FTLOS}\right)-k_{4}si{g}^{r_2}({\theta }_e-{\theta }_{FTLOS})+z_e{v}_t\frac{\sin {\theta }_e-\sin {\theta }_{FTLOS}}{{\theta }_e-{\theta }_{FTLOS}}\\ r_d=\cos \theta \left[-{\widehat{D}}_{\beta }+c_{s1}{U}_p+{\dot{\psi }}_{FTLOS}-k_5\left({\psi }_e-{\psi }_{FTLOS}\right)-k_{6}si{g}^{r_3}\left({\psi }_e-{\psi }_{FTLOS}\right)-y_e{v}_t\cos {\theta }_e\frac{\sin {\psi }_e-\sin {\psi }_{FTLOS}}{{\psi }_e-{\psi }_{FTLOS}}\right]\end{array}\right.$$

(20)

where $k_i>0 (i=1,2,3,4,5,6)$; $0<r_i<1 (i=1,2,3)$.

Note that the control law Equation (20) does not have a non-singular problem, since

$$\underset{a\to b}{\lim }\frac{\sin a-\sin b}{a-b}\stackrel{\nabla =a-b}{\to }\underset{\nabla \to 0}{\lim }\frac{\sin a-\sin \left(a-\nabla \right)}{\nabla }=\cos a$$

(21)

The symbols ${\widehat{D}}_{\alpha }$ and ${\widehat{D}}_{\beta }$ in Equation (20) are the estimations of $D_{\alpha }$ and $D_{\beta }$, which can be calculated by the FTEDOs in Equation (17), as shown in Table A1 of the Appendix A.

${\theta }_{FTLOS}$ and ${\psi }_{FTLOS}$ are the proposed FTLOS guidance laws:

$$\left\{\begin{array}{c}{\theta }_{FTLOS}=\arctan \left[(z_e+si{g}^{r_4}(z_e))/{\Delta }_z\right]\hfill \\ {\psi }_{FTLOS}=-\arctan \left[(y_e+si{g}^{r_5}(y_e))/{\Delta }_y\right]\end{array}\right.$$

(22)

where $0<r_4<1$, $0<r_5<1$; ${\Delta }_y>0$, ${\Delta }_z>0$. Compared with the conventional LOS guidance law, the FTLOS law can achieve faster convergence.

Proposition 1.

Utilizing the proposed kinematics control law Equation (20), the FTEDOs in Equation (17), and the FTLOS guidance law Equation (22), the kinematics error variables${\left[x_e,y_e,z_e,{\theta }_e-{\theta }_{FTLOS},{\psi }_e-{\psi }_{FTLOS}\right]}^T$can converge to zero in finite time.

Proof. 

To prove the stability and finite-time convergence of the kinematics control algorithm, position and orientation tracking errors ${\left[x_e,y_e,z_e,{\theta }_e-{\theta }_{FTLOS},{\psi }_e-{\psi }_{FTLOS}\right]}^T$ are considered in the following Lyapunov function:

$$V_1=\frac{1}{2}{x}_e^2+\frac{1}{2}{y}_e^2+\frac{1}{2}{z}_e^2+\frac{1}{2}{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2+\frac{1}{2}{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2$$

(23)

Based on Equation (15), the derivative of Equation (23) is given by:

$$\begin{array}{cc}\hfill {\dot{V}}_1& =x_e{\dot{x}}_e+y_e{\dot{y}}_e+z_e{\dot{z}}_e+\left({\theta }_e-{\theta }_{FTLOS}\right)\left({\dot{\theta }}_e-{\dot{\theta }}_{FTLOS}\right)+\left({\psi }_e-{\psi }_{FTLOS}\right)\left({\dot{\psi }}_e-{\dot{\psi }}_{FTLOS}\right)\hfill \\ & =x_e\frac{u\cos \left({\psi }_e\right)\cos \left({\theta }_e\right)}{\cos \alpha \cos \beta }-U_p{x}_e+y_e\sin \left({\psi }_e\right)\cos \left({\theta }_e\right)v_t-z_e\sin \left({\theta }_e\right)v_t\hfill \\ & +\left({\theta }_e-{\theta }_{FTLOS}\right)\left(q+D_{\alpha }-c_{s2}{U}_p-{\dot{\theta }}_{FTLOS}\right)+\left({\psi }_e-{\psi }_{FTLOS}\right)\left[r/\cos \left(\theta \right)+D_{\beta }-c_{s1}{U}_p-{\dot{\psi }}_{FTLOS}\right]\hfill \end{array}$$

(24)

Substituting the kinematics control law into Equation (24) yields:

$$\begin{array}{cc}\hfill {\dot{V}}_1& =-k_1{x}_e^2-k_2{\left|x_e\right|}^{r_1+1}-k_3{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2-k_4{\left|{\theta }_e-{\theta }_{FTLOS}\right|}^{r_2+1}\hfill \\ & -k_5{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2-k_6{\left|{\psi }_e-{\psi }_{FTLOS}\right|}^{r_3+1}+\left({\theta }_e-{\theta }_{FTLOS}\right){\tilde{D}}_{\alpha }\hfill \\ & +\left({\psi }_e-{\psi }_{FTLOS}\right){\tilde{D}}_{\beta }-z_e{v}_t\sin {\theta }_{FTLOS}+y_e{v}_t\cos {\theta }_e\sin {\psi }_{FTLOS}\hfill \end{array}$$

(25)

Based on Equation (22), one can obtain

$$\left\{\begin{array}{c}\sin {\theta }_{FTLOS}=\frac{z_e+si{g}^{r_4}(z_e)}{\sqrt{{(z_e+si{g}^{r_4}(z_e))}^2+{\Delta }_z^2}}\hfill \\ \sin {\psi }_{FTLOS}=-\frac{y_e+si{g}^{r_5}(y_e)}{\sqrt{{(y_e+si{g}^{r_5}(y_e))}^2+{\Delta }_y^2}}\end{array}\right.$$

(26)

Using Young’s inequality, there exists

$$\left\{\begin{array}{c}\left({\theta }_e-{\theta }_{FTLOS}\right){\tilde{D}}_{\alpha }\le \frac{1}{2{\xi }_1}{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2+\frac{{\xi }_1}{2}{\tilde{D}}_{\alpha }^2\hfill \\ \left({\psi }_e-{\psi }_{FTLOS}\right){\tilde{D}}_{\beta }\le \frac{1}{2{\xi }_2}{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2+\frac{{\xi }_2}{2}{\tilde{D}}_{\beta }^2\end{array}\right.$$

(27)

where ${\xi }_1>0$, ${\xi }_2>0$.

Substituting Equations (26) and (27) into Equation (25), the derivative of $V_1$ can be further derived as

$$\begin{array}{l}{\dot{V}}_1\le -k_1{x}_e^2-k_2{\left|x_e\right|}^{r_1+1}-(k_3-\frac{1}{2{\xi }_1}){\left({\theta }_e-{\theta }_{FTLOS}\right)}^2-k_4{\left|{\theta }_e-{\theta }_{FTLOS}\right|}^{r_2+1}\\ -(k_5-\frac{1}{2{\xi }_2}){\left({\psi }_e-{\psi }_{FTLOS}\right)}^2-k_6{\left|{\psi }_e-{\psi }_{FTLOS}\right|}^{r_3+1}-z_e{v}_t\frac{z_e+si{g}^{r_4}(z_e)}{\sqrt{{(z_e+si{g}^{r_4}(z_e))}^2+{\Delta }_z^2}}\\ -y_e{v}_t\cos {\theta }_e\frac{y_e+si{g}^{r_5}(y_e)}{\sqrt{{(y_e+si{g}^{r_5}(y_e))}^2+{\Delta }_y^2}}+\frac{{\xi }_1}{2}{\tilde{D}}_{\alpha }^2+\frac{{\xi }_2}{2}{\tilde{D}}_{\beta }^2\\ =-k_1{x}_e^2-k_2{\left|x_e\right|}^{r_1+1}-(k_3-\frac{1}{2{\xi }_1}){\left({\theta }_e-{\theta }_{FTLOS}\right)}^2-k_4{\left|{\theta }_e-{\theta }_{FTLOS}\right|}^{r_2+1}\\ -(k_5-\frac{1}{2{\xi }_2}){\left({\psi }_e-{\psi }_{FTLOS}\right)}^2-k_6{\left|{\psi }_e-{\psi }_{FTLOS}\right|}^{r_3+1}\\ -{\Gamma }_1{z}_e^2-{\Gamma }_1{\left|z_e\right|}^{r_4+1}-{\Gamma }_2{y}_e^2-{\Gamma }_2{\left|y_e\right|}^{r_5+1}+\frac{{\xi }_1}{2}{\tilde{D}}_{\alpha }^2+\frac{{\xi }_2}{2}{\tilde{D}}_{\beta }^2\end{array}$$

(28)

where ${\Gamma }_1=\frac{v_t}{\sqrt{{(z_e+si{g}^{r_4}(z_e))}^2+{\Delta }_z^2}}>0$, ${\Gamma }_2=\frac{v_t\cos {\theta }_e}{\sqrt{{(y_e+si{g}^{r_5}(y_e))}^2+{\Delta }_y^2}}>0$.

Considering the fact that ${\tilde{D}}_{\alpha }$ and ${\tilde{D}}_{\beta }$ can converge to zero after $t_r$ (Remark 2) and recalling Lemma 3, one can obtain:

$$\begin{gathered} {\dot{V}}_1\le -\min \left\{k_1,{\Gamma }_1,{\Gamma }_2,(k_3-\frac{1}{2{\xi }_1}),(k_5-\frac{1}{2{\xi }_2})\right\}\cdot \left[x_e^2+y_e^2+z_e^2+{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2+{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2\right] \\ -\min \left\{k_2,{\Gamma }_2,{\Gamma }_1,k_4,k_6\right\}\cdot \left[{(x_e^2)}^{\frac{r_1+1}{2}}+{(y_e^2)}^{\frac{r_5+1}{2}}+{(z_e^2)}^{\frac{r_4+1}{2}}+{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2{}^{\times \frac{r_2+1}{2}}+{\left({\psi }_e-{\psi }_{FTLOS}\right)}^{2\times }{}^{\frac{r_3+1}{2}}\right] \\ \le -\min \left\{k_1,{\Gamma }_1,{\Gamma }_2,(k_3-\frac{1}{2{\xi }_1}),(k_5-\frac{1}{2{\xi }_2})\right\}\cdot \left[x_e^2+y_e^2+z_e^2+{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2+{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2\right] \\ -\min \left\{k_2,{\Gamma }_2,{\Gamma }_1,k_4,k_6\right\}\cdot {(x_e^2+y_e^2+z_e^2+{\left({\psi }_e-{\psi }_{FTLOS}\right)}^2+{\left({\theta }_e-{\theta }_{FTLOS}\right)}^2)}^{\frac{r_x+1}{2}} \\ =-2\min \left\{k_1,{\Gamma }_1,{\Gamma }_2,(k_3-\frac{1}{2{\xi }_1}),(k_5-\frac{1}{2{\xi }_2})\right\}\cdot V_1-2^{\frac{r_x+1}{2}}\min \left\{k_2,{\Gamma }_2,{\Gamma }_1,k_4,k_6\right\}\cdot V_1^{\frac{r_{{}_x}+1}{2}} \\ =-{\Gamma }_3{V}_1-{\Gamma }_4{V}_1^{\frac{r_x+1}{2}} \end{gathered}$$

(29)

where ${\Gamma }_3=2\min \left\{k_1,{\Gamma }_1,{\Gamma }_2,(k_3-\frac{1}{2{\xi }_1}),(k_5-\frac{1}{2{\xi }_2})\right\}$, ${\Gamma }_4=2^{\frac{r_x+1}{2}}\min \left\{k_2,{\Gamma }_2,{\Gamma }_1,k_4,k_6\right\}$,$r_x=\min \left\{r_1,r_2,r_3,r_4,r_5\right\}$.

According to Lemma 2, it can be concluded that the kinematics error variables ${\left[x_e,y_e,z_e,{\theta }_e-{\theta }_{FTLOS},{\psi }_e-{\psi }_{FTLOS}\right]}^T$ can converge to zero in finite time $t\le t_r+\frac{1}{{\Gamma }_3(1-\frac{r_x+1}{2})}\ln \frac{{\Gamma }_3{V}_1^{1-\frac{r_x+1}{2}}(0)+{\Gamma }_4}{{\Gamma }_4}$.

□

3.3. Finite-Time Dynamics Control

To solve the sub-problem of dynamics control, finite-time heading control, pitching control, and surge velocity tracking control are carried out.

3.3.1. Finite-Time Heading Control

To solve the heading control problem, a FTTSMC law is proposed. The detailed design process can be implemented as follows.

Define the heading angular velocity error as

$$z_r=r-r_d$$

(30)

Furthermore, define a terminal sliding mode surface as follows:

$$s_r=z_r+c_1{\displaystyle {\int }_0^t{z}_{r}dt}+c_2{\displaystyle {\int }_0^{t}si{g}^{r_6}(z_r)dt}$$

(31)

where $c_1>0$, $c_2>0$, $0<r_6<1$.

Differentiating Equation (31) yields:

$$\begin{array}{cc}\hfill {\dot{s}}_r& ={\dot{z}}_r+c_1{z}_r+c_{2}si{g}^{r_6}(z_r)\hfill \\ & =f_r+g_r{\tau }_r+D_r-{\dot{r}}_d+c_1{z}_r+c_{2}si{g}^{r_6}(z_r)\hfill \end{array}$$

(32)

To eliminate the heading angular velocity error to zero in finite time, the desired torque control law is proposed as:

$${\tau }_{rd}=\frac{1}{g_r}\left[-f_r-{\widehat{D}}_r+{\dot{r}}_d-c_1{z}_r-c_{2}si{g}^{r_6}(z_r)-k_7{s}_r-k_{8}si{g}^{r_7}(s_r)\right]$$

(33)

where $k_7>0$, $k_8>0$; $0<r_7<1$; ${\widehat{D}}_r$ is the estimation of $D_r$, which can be calculated by Equation (17), as shown in the Table A1 of the Appendix A.

Proposition 2.

Utilizing the proposed control law${\tau }_{rd}$, the heading angular velocity error$z_r$can converge to zero in finite time.

Proof. 

To prove the stability and finite-time convergence of heading control, the analysis process is divided into two parts: The first part is to prove that the proposed heading control law can approach the sliding mode in finite time. The second part is to prove that the heading tracking error can converge to 0 in finite time once the sliding mode is entered.

To prove the first part, the following Lyapunov candidate is considered:

$$V_2=\frac{1}{2}{s}_r^2$$

(34)

Differentiating Equation (34) yields:

$$\begin{array}{cc}\hfill {\dot{V}}_2& =s_r{\dot{s}}_r\hfill \\ & =s_r\left[f_r+g_r{\tau }_r+D_r-{\dot{r}}_d+c_1{z}_r+c_{2}si{g}^{r_6}(z_r)\right]\hfill \end{array}$$

(35)

Substituting Equation (33) into Equation (35), one can obtain:

$$\begin{array}{cc}\hfill {\dot{V}}_2& =s_r\left[-k_7{s}_r-k_{8}si{g}^{r_7}(s_r)+{\tilde{D}}_r\right]\hfill \\ & =-k_7{s}_r^2-k_8{\left|s_r\right|}^{r_7+1}+s_r{\tilde{D}}_r\hfill \\ & \le -k_7{s}_r^2-k_8{\left|s_r\right|}^{r_7+1}+\frac{1}{2{\sigma }_1}{s}_r^2+\frac{{\sigma }_1}{2}{\tilde{D}}_r^2\hfill \\ & =-(k_7-\frac{1}{2{\sigma }_1})s_r^2-k_8{\left|s_r\right|}^{r_7+1}+\frac{{\sigma }_1}{2}{\tilde{D}}_r^2\hfill \\ & =-2(k_7-\frac{1}{2{\sigma }_1})V_2-2^{\frac{r_7+1}{2}}{k}_8{V}_2^{\frac{r_7+1}{2}}+\frac{{\sigma }_1}{2}{\tilde{D}}_r^2\hfill \end{array}$$

(36)

where ${\sigma }_1$ is a user-defined positive constant such that $k_7-\frac{1}{2{\sigma }_1}>0$.

Note that the estimation error ${\tilde{D}}_r$ will converge to zero in finite time $t_r$. Consequently, Equation (36) can be further derived as:

$$\begin{array}{cc}\hfill {\dot{V}}_2& =-2(k_7-\frac{1}{2{\sigma }_1})V_2-2^{\frac{r_7+1}{2}}{k}_8{V}_2^{\frac{r_7+1}{2}}\hfill \\ & =-{\Gamma }_5{V}_2-{\Gamma }_6{V}_2^{\frac{r_7+1}{2}}\hfill \end{array}$$

(37)

where ${\Gamma }_5=2(k_7-\frac{1}{2{\sigma }_1})$; ${\Gamma }_6=2^{\frac{r_7+1}{2}}{k}_8$.

According to Lemma 2, it can be concluded that utilizing the control law ${\tau }_{rd}$, the sliding mode surface $s_r$ can converge to zero in finite time $t\le t_r+\frac{1}{{\Gamma }_5(1-\frac{r_7+1}{2})}\ln \frac{{\Gamma }_5{V}_2^{1-\frac{r_7+1}{2}}(0)+{\Gamma }_6}{{\Gamma }_6}$.

Furthermore, it can be proven that once $s_r$ converges to zero, the heading angular velocity error $z_r$ can converge to zero in finite time.

When $s_r=0$, one can obtain:

$${\dot{z}}_r=-c_1{z}_r-c_{2}si{g}^{r_6}(z_r)$$

(38)

Consider the following Lyapunov candidate for the sliding mode holding stage:

$$V_3=\frac{1}{2}{z}_r^2$$

(39)

Differentiating Equation (39) yields:

$$\begin{array}{cc}\hfill {\dot{V}}_3& =z_r{\dot{z}}_r\hfill \\ & =-c_1{z}_r^2-c_2{\left|z_r\right|}^{r_6+1}\hfill \\ & =-2c_1{V}_3-2^{\frac{r_6+1}{2}}{c}_2{V}_3^{\frac{r_6+1}{2}}\hfill \\ & =-{\Gamma }_7{V}_3-{\Gamma }_8{V}_3^{\frac{r_6+1}{2}}\hfill \end{array}$$

(40)

where ${\Gamma }_7=2c_1$, ${\Gamma }_8=2^{\frac{r_6+1}{2}}{c}_2$.

Recalling Lemma 2, it can be concluded that utilizing the control law ${\tau }_{rd}$, $z_r$ can converge to zero in finite time $t\le t_r+\frac{1}{{\Gamma }_5(1-\frac{r_7+1}{2})}\ln \frac{{\Gamma }_5{V}_2^{1-\frac{r_7+1}{2}}(0)+{\Gamma }_6}{{\Gamma }_6}+\frac{1}{{\Gamma }_7(1-\frac{r_6+1}{2})}\ln \frac{{\Gamma }_7{V}_3^{1-\frac{r_6+1}{2}}(0)+{\Gamma }_8}{{\Gamma }_8}$.

Therefore, Proposition 2 can be proven.

□

3.3.2. Finite-Time Pitching Control

Similar to heading control, the FTTSMC law is proposed for pitching control.

Define the pitching angular velocity error and sliding mode surface as

$$\left\{\begin{array}{c}{z}_q=q-q_d\hfill \\ s_q=z_q+c_3{\displaystyle {\int }_0^t{z}_{q}dt}+c_4{\displaystyle {\int }_0^{t}si{g}^{r_8}(z_q)dt}\end{array}\right.$$

(41)

where $c_3>0$; $c_4>0$; $0<r_8<1$.

Differentiating Equation (41) yields:

$$\begin{array}{cc}\hfill {\dot{s}}_q& ={\dot{z}}_q+c_3{z}_q+c_{4}si{g}^{r_8}(z_q)\hfill \\ & =f_q+g_q{\tau }_q+D_q-{\dot{q}}_d+c_3{z}_q+c_{4}si{g}^{r_8}(z_q)\hfill \end{array}$$

(42)

To eliminate the pitching angular velocity error to zero in finite time, the desired torque control law is proposed as:

$${\tau }_{qd}=\frac{1}{g_q}\left[-f_q-{\widehat{D}}_q+{\dot{q}}_d-c_3{z}_q-c_{4}si{g}^{r_8}(z_q)-k_9{s}_q-k_{10}si{g}^{r_9}(s_q)\right]$$

(43)

where $k_9>0$, $k_{10}>0$; $0<r_9<1$; ${\widehat{D}}_q$ is the estimation of $D_q$, which can be calculated by Equation (17), as shown in Table A1 of the Appendix.

Remark 3.

Utilizing the same method as Section 3.3.1, it can be proven that the proposed FTTSMC law Equation (43) and FTEDO Equation (17) can achieve finite-time pitching control successfully.

3.3.3. Finite-Time Velocity Tracking Control

The objective of surge control is to derive an effective control law to generate the control input $X_T$ so that the surge velocity error $u-u_d$ can converge to zero in finite time.

Considering the influence of actuator saturation, the surge velocity tracking model is rewritten as follows.

$$\begin{array}{cc}\hfill \dot{u}& =f_u+g_{u}sat(X_T)+D_u\hfill \\ & =f_u+g_u(X_T+\Delta X_T)+D_u\hfill \end{array}$$

(44)

where $\Delta X_T=sat(X_T)-X_T$.

Define the surge velocity tracking error and sliding mode surface as

$$\left\{\begin{array}{c}{z}_u=u-u_d\hfill \\ s_u=z_u+c_5{\displaystyle {\int }_0^t{z}_{u}dt}+c_6{\displaystyle {\int }_0^{t}si{g}^{r_{10}}(z_u)dt}\end{array}\right.$$

(45)

where $c_5>0$, $c_6>0$; $0<r_{10}<1$.

Differentiating Equation (45) yields

$${\dot{s}}_u=f_u+g_u(X_T+\Delta X_T)+D_u-{\dot{u}}_d+c_5{z}_u+c_{6}si{g}^{r_{10}}(z_u)$$

(46)

To achieve effective surge tracking control despite the unknown uncertainty and input saturation problem, the surge controller is designed as

$$X_T=\frac{1}{g_u}\left[-f_u-{\widehat{D}}_u+{\dot{u}}_d-c_5{z}_u-c_{6}si{g}^{r_{10}}(z_u)-k_{11}{s}_u-k_{12}si{g}^{r_{11}}(s_u)\right]-\Delta {\widehat{X}}_T$$

(47)

where $k_{11}>0$, $k_{12}>0$; $0<r_{11}<1$; ${\widehat{D}}_u$ is the FTEDO utilized to estimate $D_u$, which can be calculated by Equation (17), as shown in Table A1 of the Appendix A. $\Delta {\widehat{X}}_T$ is the RBFNN compensator utilized to estimate $\Delta X_T$.

The RBFNN compensator $\Delta {\widehat{X}}_T$ is designed as

$$\Delta {\widehat{X}}_T={\widehat{W}}_u^T{\varphi }_u$$

(48)

where ${\widehat{W}}_u^T$ denotes the estimate weight matrix; ${\varphi }_u$ represents the Gaussian basis function, $0<{\varphi }_u<1$.

The parameter updating law of ${\widehat{W}}_u^T$ is designed as follows.

$${\dot{\widehat{W}}}_u^T=k_{13}{s}_u{g}_u{\varphi }_u-k_{14}\Delta {\tilde{X}}_T$$

(49)

where $k_{13}>0$, $k_{14}>0$, $\Delta {\tilde{X}}_T$ represents the estimation error of the RBFNN.

Remark 4.

Utilizing the same method as Section 3.3.1, it can be proven that the proposed FTTSMC law Equation (47), FTEDO Equation (17), and RBFNN Equations (48) and (49) can achieve finite-time surge velocity tracking control successfully.

3.4. Optimal Rudder Allocation

For conventional cross-rudder AUVs, there exists a clear relationship between rudder angle and rudder torque, but this is not applicable for XAUVs. Due to the special layout of the X-rudder, solving the rudder angles ${\left[{\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4\right]}^T$ from the desired rudder torques ${\left[{\tau }_{rd},{\tau }_{qd}\right]}^T$ is a complex MIMO (multi input–multi output) problem; the solution is not unique. The commonly used pseudo inverse method can calculate the rudder angles, but unfortunately, it cannot tackle the problem of rudder angle and speed constraints. To solve this complex problem, the nonlinear sequential quadratic programming (SQP) algorithm is utilized in this paper. The cost function $J$ is defined as:

$$\left\{\begin{array}{c}\min J=\underset{\begin{array}{l}Yawing torque \\ allocation error\end{array}}{\underbrace{\xi {({\tau }_r-{\tau }_{rd})}^2}}+\underset{\begin{array}{l}Pitching torque \\ allocation error\end{array}}{\underbrace{\xi {({\tau }_q-{\tau }_{qd})}^2}}+\underset{Control effect}{\underbrace{(1-\xi ){\delta }^T\delta }}\\ s·t· 0\le \xi \le 1\hfill \\ \begin{array}{l}\hspace{1em}{\tau }_r=N_{uu{\delta }_1}{u}^2{\delta }_1+N_{uu{\delta }_2}{u}^2{\delta }_2+N_{uu{\delta }_3}{u}^2{\delta }_3+N_{uu{\delta }_4}{u}^2{\delta }_4\hfill \\ \hspace{1em}{\tau }_q=M_{uu{\delta }_1}{u}^2{\delta }_1+M_{uu{\delta }_2}{u}^2{\delta }_2+M_{uu{\delta }_3}{u}^2{\delta }_3+M_{uu{\delta }_4}{u}^2{\delta }_4\hfill \\ \hspace{1em}\delta ={\left[{\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4\right]}^T\hfill \\ \hspace{1em}\left|\delta \right|\le \overline{\delta }\hfill \\ \hspace{1em}\left|d\delta /dt\right|\le {\overline{\delta }}^{\prime }\end{array}\end{array}\right.$$

(50)

where $\xi$ is the weight coefficient utilized to balance the optimization objectives; $\overline{\delta }$ denotes the saturation constraint value of rudder angle; ${\overline{\delta }}^{\prime }$ denotes the saturation constraint value of rudder steering velocity.

Moreover, since the value of weight coefficient $\xi$ will directly affect the optimization objective, the following adaptive scheme is utilized to adjust the parameter:

$$\xi ={\xi }_{\min }+({\xi }_{\max }-{\xi }_{\min })(1-e^{-{\varpi }_r\sqrt{x_e^2+y_e^2+z_e^2}})$$

(51)

where ${\xi }_{\min }>0$, ${\xi }_{\max }>0$, ${\varpi }_r>0$.

Remark 5.

Utilizing the proposed cost function Equation (50) and parameter updating law Equation (51), the global optimal rudder allocation can be achieved; that is, when the tracking error is large, the torque allocation error is considered more in the optimization objective, while when the tracking error is small, more attention will be paid to energy consumption problem.

4. Simulation

In this section, comparative simulations are carried out utilizing MATLAB tools to verify the effectiveness and robustness of the proposed control method. The simulation preparation is introduced in Section 4.1 and the simulation results are demonstrated in Section 4.2 and Section 4.3.

4.1. Simulation Preparation

The main parameters of the XAUV model utilized in the simulation are demonstrated in Table 2. To give readers a better understanding of the proposed method, the detailed implementation process of the three-dimensional tracking control algorithm is shown in Table 3, which is realized using programming language S function in the simulation, and can be expended to other languages as needed in future use.

Table 2. The main parameters of the XAUV model.

$X_{\dot{u}}=-0.93 \mathrm{kg}$	$Z_{w\left|w\right|}= -131 \mathrm{k}\mathrm{g}/\mathrm{m}$	$N_{r\left|r\right|}=-94 \mathrm{k}\mathrm{g}·{\mathrm{m}}^2/\mathrm{r}\mathrm{a}{\mathrm{d}}^2$	$M_{uu{\delta }_2}=2.1744 \mathrm{kg}/\mathrm{rad}$
$X_{u\left|u\right|}=-1.62 \mathrm{k}\mathrm{g}/\mathrm{m}$	$Z_{q\left|q\right|}=-0.632 \mathrm{k}g\mathrm{.}\mathrm{m}/\mathrm{r}\mathrm{a}{\mathrm{d}}^2$	$N_{ur}=-2 \mathrm{k}\mathrm{g}·\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}$	$M_{uu{\delta }_3}=-2.1744 \mathrm{kg}/\mathrm{rad}$
$X_{wq}=-35.5 \mathrm{k}\mathrm{g}/\mathrm{r}\mathrm{a}\mathrm{d}$	$Z_{uq}=-5.22 \mathrm{k}\mathrm{g}/\mathrm{r}\mathrm{a}\mathrm{d}$	$N_{uv}=-24 \mathrm{kg}$	$M_{uu{\delta }_4}=2.1744 \mathrm{kg}/\mathrm{rad}$
$X_{qq}=-1.93 \mathrm{k}\mathrm{g}·\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}$	$Z_{uw}=-28.6 \mathrm{k}\mathrm{g}/\mathrm{m}$	$Y_{uu{\delta }_1}=-3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$N_{uu{\delta }_1}=2.1744 \mathrm{kg}/\mathrm{rad}$
$X_{rr}=-1.93 \mathrm{k}\mathrm{g}·\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}$	$I_{yy}=3.45 \mathrm{kg}\cdot {\mathrm{m}}^2$	$Y_{uu{\delta }_2}=3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$N_{uu{\delta }_2}=2.1744 \mathrm{kg}/\mathrm{rad}$
$X_{vr}=35.5 \mathrm{k}\mathrm{g}/\mathrm{r}\mathrm{a}\mathrm{d}$	$M_{\dot{q}}= -4.88 \mathrm{kg}\cdot {\mathrm{m}}^2/\mathrm{rad}$	$Y_{uu{\delta }_3}=-3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$N_{uu{\delta }_3}=2.1744 \mathrm{kg}/\mathrm{rad}$
$Y_{\dot{v}}=-35.5 \mathrm{kg}$	$M_{w\left|w\right|}= 3.18 \mathrm{kg}$	$Y_{uu{\delta }_4}=3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$N_{uu{\delta }_4}=2.1744 \mathrm{kg}/\mathrm{rad}$
$Y_{v\left|v\right|}=-1310 \mathrm{k}\mathrm{g}/\mathrm{m}$	$M_{q\left|q\right|}=-188 \mathrm{k}\mathrm{g}·{\mathrm{m}}^2/\mathrm{r}\mathrm{a}{\mathrm{d}}^2$	$Z_{uu{\delta }_1}=3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$m=30.48 \mathrm{kg}$
$Y_{r\left|r\right|}=0.632 \mathrm{k}\mathrm{g}·\mathrm{m}/\mathrm{r}\mathrm{a}{\mathrm{d}}^2$	$M_{uq}=-2 \mathrm{k}\mathrm{g}·\mathrm{m}/\mathrm{r}\mathrm{a}\mathrm{d}$	$Z_{uu{\delta }_2}=-3.4083\mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	${\overline{X}}_T=6.48 \mathrm{N}$
$Y_{ur}=5.22 \mathrm{k}\mathrm{g}/\mathrm{r}\mathrm{a}\mathrm{d}$	$M_{uw}=24 \mathrm{kg}$	$Z_{uu{\delta }_3}=3.4083 \mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	$\overline{\delta }={35}^{\circ }$
$Y_{uv}=-28.6 \mathrm{k}\mathrm{g}/\mathrm{m}$	$I_{zz}=3.45 \mathrm{kg}\cdot {\mathrm{m}}^2$	$Z_{uu{\delta }_4}=-3.4083\mathrm{kg}/(\mathrm{m}\cdot \mathrm{rad})$	${\overline{\delta }}^{\prime }={10}^{\circ }/\mathrm{s}$
$Z_{\dot{w}}= -35.5 \mathrm{kg}$	$N_{v\left|v\right|}= -3.18 \mathrm{kg}$	$M_{uu{\delta }_1}=-2.1744 \mathrm{kg}/\mathrm{rad}$	$N_{\dot{r}}= -4.88\mathrm{kg}$

Table 3. Implementation of three-dimensional tracking control algorithm.

Algorithm: Three-dimensional trajectory tracking

Given control parameters

Procedure:

Input:  Collect the data ${(x,y,z,\theta ,\psi )}^T$$\mathrm{and} {(u,v,w,q,r)}^T$ from the integrated navigation system;  Calculate the reference trajectory ${(x_d,y_d,z_d,{\theta }_d,{\psi }_d)}^T$.

Finite-time kinematics control law:  (1) $\mathrm{Calculate} {\widehat{D}}_{\alpha }$$\mathrm{and} {\widehat{D}}_{\beta }$ according to Equation (15);  (2) $\mathrm{Derive} \mathrm{tracking} \mathrm{error} {(x_e,y_e,z_e,{\theta }_e,{\psi }_e)}^T$ according to Equation (13);  (3) $\mathrm{Calculate} \mathrm{FTLOS} \mathrm{guidance} \mathrm{law} {({\theta }_{FTLOS},{\psi }_{FTLOS})}^T$ according to Equation (20);  (4) $\mathrm{Calculate} \mathrm{the} \mathrm{Finite}-\mathrm{time} \mathrm{kinematics} \mathrm{control} \mathrm{law} {(u_d,q_d,r_d)}^T$ according to Equation (18).

Finite-time dynamics control law:   Heading control law:   (1) $\mathrm{Calculate} \mathrm{the} \mathrm{tracking} \mathrm{error} z_r$ according to Equation (28);   (2) $\mathrm{Calculate} \mathrm{the} \mathrm{terminal} \mathrm{sliding} \mathrm{mode} \mathrm{surface} s_r$ utilizing Equation (29);   (3) $\mathrm{Calculate} {\widehat{D}}_r$ according to Equation (15);   (4) $\mathrm{Calculate} \mathrm{the} \mathrm{desired} \mathrm{torque} {\tau }_{rd}$ utilizing the finite-time control law Equation (31).   Pitching control law:   (1) $\mathrm{Calculate} \mathrm{the} \mathrm{tracking} \mathrm{error} z_q$ according to Equation (39);   (2) $\mathrm{Calculate} \mathrm{the} \mathrm{terminal} \mathrm{sliding} \mathrm{mode} \mathrm{surface} s_q$ utilizing Equation (39);   (3) $\mathrm{Calculate} {\widehat{D}}_q$ according to Equation (15);   (4) $\mathrm{Calculate} \mathrm{the} \mathrm{desired} \mathrm{torque} {\tau }_{qd}$ utilizing the finite-time control law Equation (41).   Velocity tracking control law:   (1) $\mathrm{Calculate} \mathrm{the} \mathrm{tracking} \mathrm{error} z_u$ according to Equation (43);   (2) $\mathrm{Calculate} \mathrm{the} \mathrm{terminal} \mathrm{sliding} \mathrm{mode} \mathrm{surface} s_u$ utilizing Equation (43);   (3) $\mathrm{Calculate} {\widehat{D}}_q$ according to Equation (15);   (4) $\mathrm{Update} \mathrm{the} \mathrm{weight} \mathrm{coefficient} {\widehat{W}}_u^T$ according to Equation (47);   (5) $\mathrm{Calculate} \mathrm{the} \mathrm{RBFNN} \mathrm{compensator} \Delta {\widehat{X}}_T$ utilizing Equation (46);   (6) $\mathrm{Calculate} \mathrm{the} \mathrm{propeller} \mathrm{control} \mathrm{input} X_T$ utilizing the finite-time control law Equation (45).

Optimal rudder allocation:   (1) $\mathrm{Update}$ according to Equation (49);   (2) $\mathrm{Calculate} \mathrm{the} \mathrm{rudder} \mathrm{angles} {({\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4)}^T$ utilizing Equation (48).

The X-rudder equations Equation (10) update (For simulation)  Dynamics equations Equation (9) update (For simulation)  Kinematics equations Equation (7) update (For simulation)

End procedure

Repeat procedure

In the following sections, comparative analyses are carried out based on the simulation results for two different scenarios. Case 1 mainly focuses on the adaptability of the algorithm to different initial conditions and different unknown disturbances, where a straight line with fixed depth and fixed heading is selected as the reference trajectory. Case 2 mainly focuses on the superiority of the proposed algorithm over other algorithms, where a complex three-dimensional curve is selected as the reference trajectory, and three other commonly used algorithms in existing literatures are applied for comparison purpose.

When selecting parameters of the proposed control algorithm, the following steps are recommended:

• According to the parameter range mentioned above, prepare a group of basic parameters and make the system converge through debugging. In the process of adjustment, adjust the conventional parameters first and then the exponential parameters;
• On the basis of system convergence, the kinematic control parameters are adjusted to improve the convergence speed;
• Further adjust the dynamic control parameters to optimize the tracking control accuracy and convergence speed;
• Adjust the parameters of rudder allocation to optimize the energy consumption.

The main parameters of the proposed controller utilized in the simulation are shown in Table 4.

Table 4. The main parameters of the proposed controller.

$k_1=0.05$	$k_2=0.105$	$k_3=0.1225$	$k_4=0.0228$	$k_5=0.0168$	$k_6=0.031$	$k_7=0.01$
$k_8=4.5$	$k_9=0.01$	$k_{10}=4.5$	$k_{11}=0.01$	$k_{12}=4.5$	$k_{13}=0.5$	$k_{14}=1.2$
$c_1=0.01$	$c_2=0.008$	$c_3=0.01$	$c_4=0.008$	$c_5=0.01$	$c_6=0.5$	$r_1=0.95$
$r_2=0.95$	$r_3=0.95$	$r_4=0.98$	$r_5=0.98$	$r_6=0.95$	$r_7=0.95$	$r_8=0.98$
$r_9=0.98$	$r_{10}=0.98$	$r_{11}=0.98$	${\Delta }_y=9.702$	${\Delta }_z=5.267$

4.2. Case 1

To test the effectiveness of the proposed controller, straight line tracking is carried out in Case 1, where the desired trajectory is parameterized by ${\left[x_d,y_d,z_d\right]}^T={\left[1.2t\mathrm{m},10\mathrm{m},20\mathrm{m}\right]}^T$. Furthermore, in order to verify the adaptability of the control algorithm, four subcases are implemented with different initial conditions and different unknown disturbances.

The initial conditions of the four subcases are as follows: (1) Subcase 1.1: ${\left[x_0,y_0,z_0\right]}^T={\left[5\mathrm{m},16\mathrm{m},24\mathrm{m}\right]}^T$; (2) Subcase 1.2: ${\left[x_0,y_0,z_0\right]}^T={\left[5\mathrm{m},14\mathrm{m},15\mathrm{m}\right]}^T$; (3) Subcase 1.3: ${\left[x_0,y_0,z_0\right]}^T={\left[5\mathrm{m},5\mathrm{m},26\mathrm{m}\right]}^T$; (4) Subcase 1.4: ${\left[x_0,y_0,z_0\right]}^T={\left[5\mathrm{m},3\mathrm{m},15\mathrm{m}\right]}^T$.

Moreover, different disturbances are set in the simulation of the four subcases. The first two subcases are set with time-varying disturbances, whereas the latter two subcases are set with time-varying and segmented disturbances. The detailed disturbance settings of Case 1 are shown in Table 5.

Table 5. Disturbance settings of the four subcases in case 1.

Subcases	Disturbance Settings
Subcase 1.1	$\left\{\begin{array}{c}{D}_u=31.41\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})\\ D_v=32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})\\ D_w=32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})\\ D_q=8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})\\ D_r=8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})\end{array}\right.$
Subcase 1.2	$\left\{\begin{array}{c}{D}_u=47.12\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})\\ D_v=49.49\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})\\ D_w=49.49\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})\\ D_q=12.50\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})\\ D_r=12.50\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})\end{array}\right.$
Subcase 1.3	$\left\{\begin{array}{c}{D}_u=\left\{\begin{array}{cc}31.41\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})& 0<t\le 75\\ 15.71\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})& 75<t\le 150\end{array}\right.\\ D_v=\{\begin{array}{cc}32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})& 0<t\le 75\\ 16.50\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})& 75<t\le 150\end{array}\\ D_w=\{\begin{array}{cc}32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})& 0<t\le 75\\ 16.50\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})& 75<t\le 150\end{array}\\ D_q=\left\{\begin{array}{cc}8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})& 0<t\le 75\\ 4.17\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})& 75<t\le 150\end{array}\right.\\ D_r=\left\{\begin{array}{cc}8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})& 0<t\le 75\\ 4.17\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})& 75<t\le 150\end{array}\right.\end{array}\right.$
Subcase 1.4	$\left\{\begin{array}{c}{D}_u=\left\{\begin{array}{cc}31.41\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})& 0<t\le 50\\ \begin{array}{l}15.71\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})\\ 23.56\times \left[0.01+0.1\sin (0.3t)\right]/(m-X_{\dot{u}})\end{array}& \begin{array}{l}50<t\le 100\\ 100<t\le 150\end{array}\end{array}\right.\\ D_v=\left\{\begin{array}{cc}32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})& 0<t\le 50\\ \begin{array}{l}16.50\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})\\ 24.74\times \left[0.01+0.01\sin (0.3t)\right]/(m-Y_{\dot{v}})\end{array}& \begin{array}{l}50<t\le 100\\ 100<t\le 150\end{array}\end{array}\right.\\ D_w=\left\{\begin{array}{cc}32.99\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})& 0<t\le 50\\ \begin{array}{l}16.50\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})\\ 24.74\times \left[0.01+0.01\sin (0.3t)\right]/(m-Z_{\dot{w}})\end{array}& \begin{array}{l}50<t\le 100\\ 100<t\le 150\end{array}\end{array}\right.\\ D_q=\left\{\begin{array}{cc}8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})& 0<t\le 50\\ \begin{array}{l}4.17\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})\\ 6.25\times \left[0.01+0.1\cos (0.3t)\right]/(I_{yy}-M_{\dot{q}})\end{array}& \begin{array}{l}50<t\le 100\\ 100<t\le 150\end{array}\end{array}\right.\\ D_r=\left\{\begin{array}{cc}8.33\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})& 0<t\le 50\\ \begin{array}{l}4.17\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})\\ 6.25\times \left[0.01+0.1\cos (0.3t)\right]/(I_{zz}-N_{\dot{r}})\end{array}& \begin{array}{l}50<t\le 100\\ 100<t\le 150\end{array}\end{array}\right.\end{array}\right.$

The 3D trajectory tracking performances of the four subcases are shown in Figure 3, which clearly shows that the proposed controller can regulate the XAUV to the desired trajectory no matter what the initial position of the vehicle is. In order to show the tracking performance more clearly, the tracking errors are demonstrated in Figure 4, which shows that the tracking accuracy of the controller is very high. To conduct more quantitative analysis with simulation data, the tracking error data analysis of the steady-state stage is carried out for the four subcases. Mean absolute error ($MAE(\ast )$) and variance ($VAR(\ast )$) are selected as the data evaluation criteria, since these two indexes reflect the most concerned tracking accuracy and tracking stability, respectively. The detailed data analysis results are shown in Table 6. It is not difficult to see that the tracking error value and fluctuation under the four subcases are kept at a very low level, and the tracking effect of Subcase 1.3 is the best.

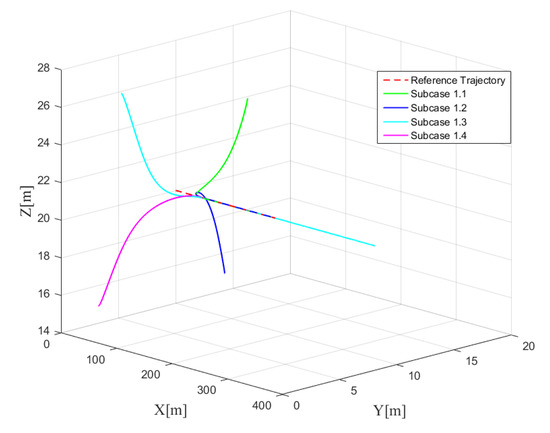
Figure 3. 3D trajectory tracking performance of Case 1.

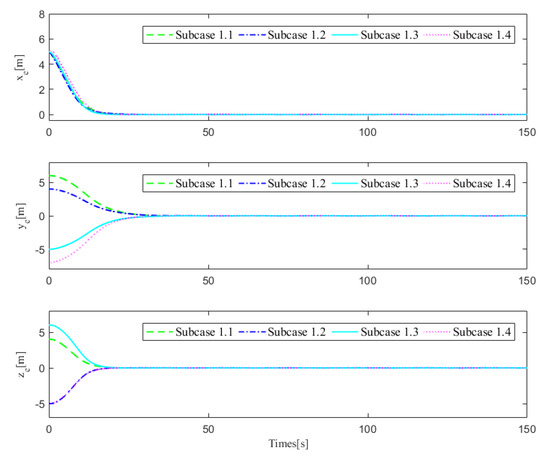
Figure 4. Tracking errors of Case 1.

Table 6. Data analysis of steady-state for Case 1 (from 40 s to 150 s).

	Subcase 1.1	Subcase 1.2	Subcase 1.3	Subcase 1.4
$MAE(x_e)$	0.0018	0.0025	0.0012	0.2502
$VAR(x_e)$	$3.7462\times {10}^{-6}$	$7.6557\times {10}^{-6}$	$1.9200\times {10}^{-6}$	$6.2452\times {10}^{-5}$
$MAE(y_e)$	0.0212	0.0492	0.0061	0.0086
$VAR(y_e)$	0.0001	0.0003	$3.9061\times {10}^{-5}$	$7.6014\times {10}^{-5}$
$MAE(z_e)$	0.0085	0.0195	0.0070	0.0064
$VAR(z_e)$	$3.1243\times {10}^{-5}$	$8.5429\times {10}^{-5}$	$1.9558\times {10}^{-5}$	$1.5026\times {10}^{-5}$

Furthermore, to better verify the anti-disturbance ability of proposed controller, the disturbance estimation performances of the four subcases are shown in Figure 5 and Figure 6. The results indicate that the FTEDO proposed in this paper can achieve fast and accurate unknown disturbance estimation, so as to improve the robustness of the controller. Another key part of the proposed controller that needs to be verified is the handling of input saturation problem. As shown in Figure 7 and Figure 8, with the help of the RBFNN compensator and optimal rudder allocator, the propeller force and rudder angles can be well limited to the specified ranges.

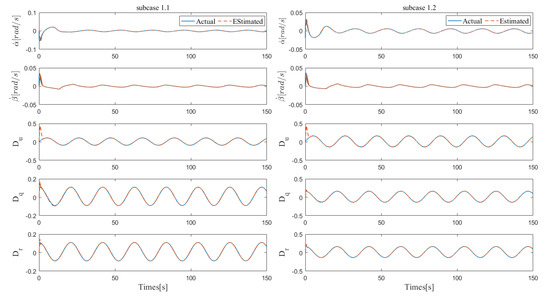
Figure 5. Disturbance estimations of subcases 1.1 and 1.2.

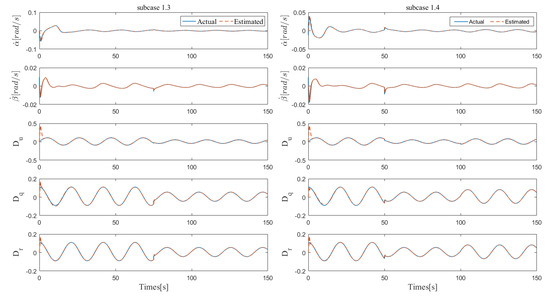
Figure 6. Disturbance estimations of subcases 1.3 and 1.4.

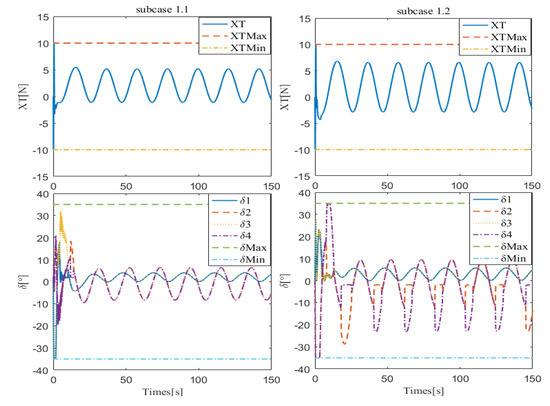
Figure 7. Control inputs of subcases 1.1 and 1.2.

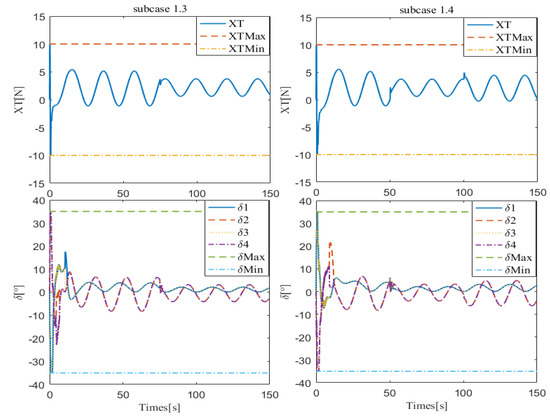
Figure 8. Control inputs of subcases 1.3 and 1.4.

From the above simulation results, it can be concluded that the proposed controller can achieve high precision 3D trajectory tracking despite different initial conditions, different unknown disturbances, and complex actuator dynamics.

4.3. Case 2

To further prove the superiority of the proposed control algorithm, comparative simulations are carried out in Case 2. Specifically, three other commonly used algorithms in existing literatures are applied for comparison purpose. The specific definitions of the control methods utilized in Case 2 are shown in Table 7.

Table 7. Different control methods utilized for comparison in Case 2.

Name	Method
Proposed method	The control method proposed in Section 3
Method 1	LOS + ISMC [39]: (1) Kinematics control: LOS guidance law; (2) Dynamics control: integral terminal sliding mode controller; (3) Rudder allocation: pseudo inverse method.
Method 2	LOS + FPID [40]: (1) Kinematics control: LOS guidance law; (2) Dynamics control: Fuzzy PID method; (3) Rudder allocation: pseudo inverse method.
Method 3	LOS + Backstepping [41]: (1) Kinematics control: LOS guidance law; (2) Dynamics control: Backstepping method; (3) Rudder allocation: pseudo inverse method.

Compared with Case 1, the desired trajectory and unknown disturbances set in Case 2 are more complex. Specifically, a complex 3D curve is set as the desired trajectory, which is parameterized by:

$$\begin{array}{l}{x}_d=1.5t\\ y_d=20\sin (0.023562t)\\ z_d=10+9t/120\end{array}$$

(52)

The disturbances added to Case 2 are both time-varying and state-depended, as shown below:

$$\left\{\begin{array}{l}{D}_u=31.41\times \left[0.01\sin (0.3t)+0.01\cos (0.2t)+0.01u^2+0.01\right]/(m-X_{\dot{u}})\\ D_v=13.20\times \left[0.01\sin (0.3t)+0.01\cos (0.2t)+0.01v^2-0.01\right]/(m-Y_{\dot{v}})\\ D_w=16.49\times \left[0.01\sin (0.3t)+0.01\cos (0.2t)+0.01w^2-0.01\right]/(m-Z_{\dot{w}})\\ D_q=8.33\times \left[0.01\cos (0.3t)+0.01\sin (0.2t)+0.01r^2+0.01\right]/(I_{yy}-M_{\dot{q}})\\ D_r=8.33\times \left[0.01\cos (0.3t)+0.01\sin (0.2t)+0.01r^2+0.01\right]/(I_{zz}-N_{\dot{r}})\end{array}\right.$$

(53)

The initial position and posture vectors of Case 2 are selected as $\eta =[1.4\mathrm{m},10\mathrm{m},10\mathrm{m},0\mathrm{rad},0\mathrm{rad}]$ and the initial velocity vectors are given by $\nu =\left[1\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s},0\mathrm{m}/\mathrm{s},0\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s},0\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}\right]$. The comparisons of 3D trajectory tracking performances are shown in Figure 9 and the 2D profiles are shown in Figure 10. From the 3D figure, it seems that all three methods can achieve good trajectory tracking; however from the 2D profiles, it can be seen that the tracking performances of the three methods are different. To better analyze the tracking performances, the transitions of tracking errors are illustrated in Figure 11, which clearly shows that the proposed controller performs best with almost no overshoot and chattering, while the other two controllers show overshoot and steady-state chattering, more or less. To conduct more quantitative analysis with simulation data, the tracking error data analysis in the steady-state stage is carried out for the four methods. Similar to Case 1, mean absolute error ($MAE(\ast )$) and variance ($VAR(\ast )$) are calculated, with detailed data analysis results shown in Table 8. From the perspective of tracking error, the proposed method and Method 1 perform better, while Method 2 and Method 3 perform slightly worse. By comparing the variance of tracking errors, it can be easily found that the tracking stability of the proposed method is the best. Therefore, based on the above analysis, it can be concluded that the proposed method performs best in tracking accuracy and stability. Next, the advantages of the proposed controller are verified one by one through comparative simulations. Compared with the general sliding mode controller, the biggest advantage of the controller proposed in this paper is the improvement of the sliding mode surface and the finite-time convergence. In order to demonstrate this advantage, the sliding mode surfaces of proposed controller and Method 1 are specially shown in Figure 12. It is easily seen that the controller proposed in this paper can achieve the fast convergence of the sliding mode surface almost instantaneously and in the steady-state stage, the sliding mode surface basically has no chattering, while the conventional sliding mode controller has a longer convergence time and poor steady-state performance. Therefore, it can be proven that the finite-time convergence method proposed in this paper has obvious advantages.

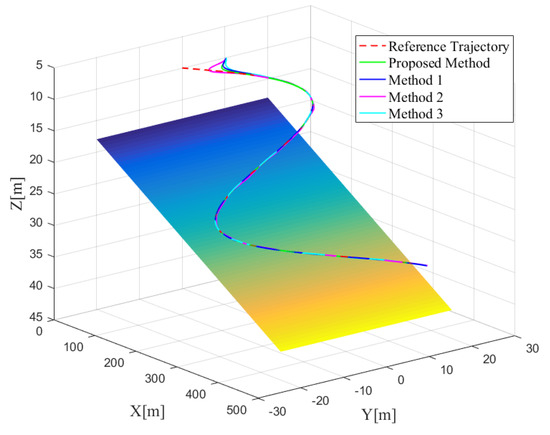
Figure 9. 3D trajectory tracking comparison of Case 2.

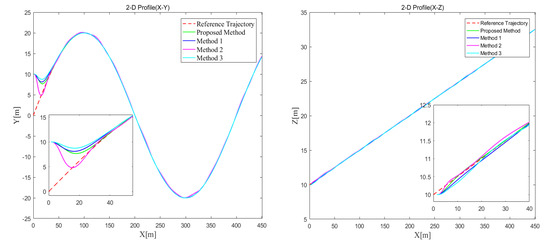
Figure 10. 2D profile comparison of Case 2.

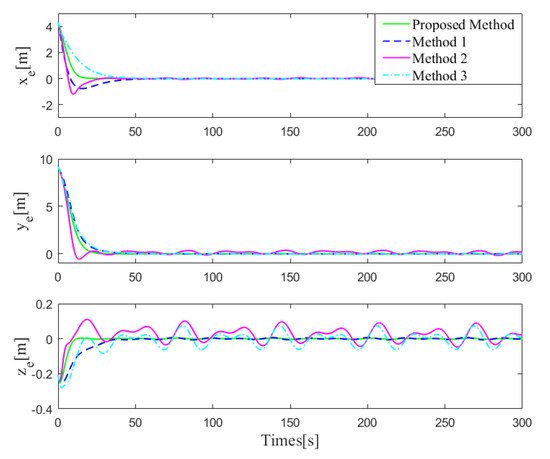
Figure 11. The tracking error comparison.

Table 8. Data analysis of steady-state for Case 2 (from 50 s to 300 s).

	Proposed	Method 1	Method 2	Method 3
$MAE(x_e)$	0.0017	0.0021	0.2725	0.0020
$VAR(x_e)$	$7.1582\times {10}^{-6}$	$3.9549\times {10}^{-5}$	0.0010	$2.6512\times {10}^{-5}$
$MAE(y_e)$	0.0034	0.0035	0.1655	0.0254
$VAR(y_e)$	$1.0279\times {10}^{-5}$	$3.1699\times {10}^{-5}$	0.0168	0.0009
$MAE(z_e)$	0.0014	0.0031	0.0379	0.0316
$VAR(z_e)$	$7.9887\times {10}^{-7}$	$1.3651\times {10}^{-5}$	0.0014	0.0014

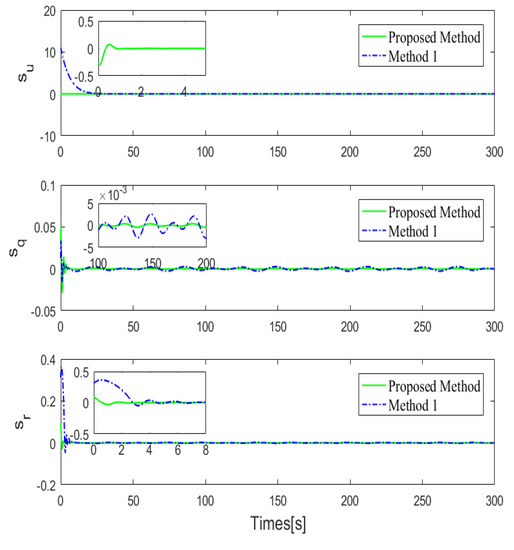
Figure 12. The comparison of sliding mode surface.

Compared with the general controller, another advantage of the proposed controller is the fast disturbance-handling ability. As shown in Figure 13, for multiple complex unknown disturbances contained in the model, the FTEDOs can quickly realize high-precision disturbance estimation. In particular, the fast and high-precision estimation of $D_{\alpha }$ and $D_{\beta }$ makes the controller more practical.

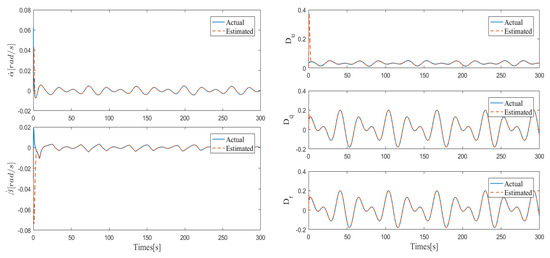
Figure 13. The unknown cuncertainties estimation of Case 2.

In addition, the proposed control algorithm has great advantages in dealing with the complex dynamics of the actuators, which can be proven by Figure 14 and Figure 15. It is easily seen from Figure 14 that with the help of the RBFNN compensator and optimal rudder allocator, the input saturation problem of propeller and X-rudder has been properly solved. More importantly, it can be seen from Figure 15 that the optimal rudder allocator designed in this paper has obvious advantages in energy consumption when compared with three other control methods.

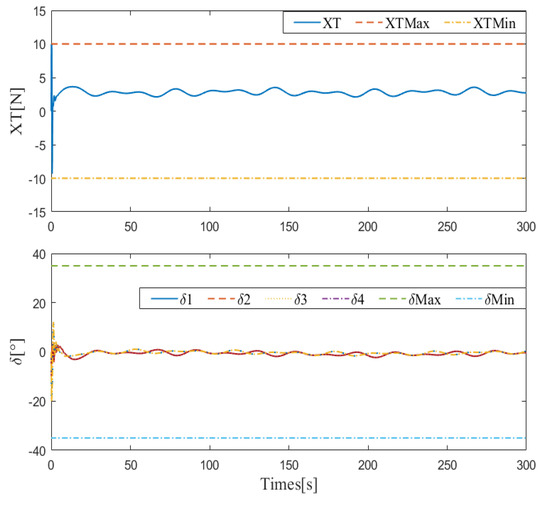
Figure 14. The control inputs of proposed method.

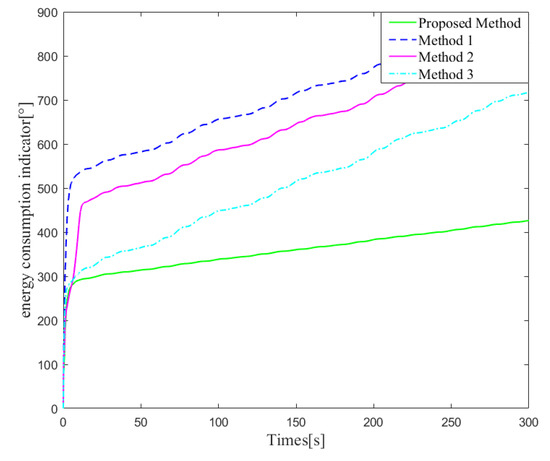
Figure 15. The energy consumption comparsion.

Based on the aforementioned analyses, it is easy to draw the following conclusions. The controller proposed in this paper can effectively solve the multi-source unknown disturbances and complex actuator problems and realize the finite time three-dimensional trajectory tracking control, and shows obvious advantages in tracking rate, stability, and energy consumption.

5. Conclusions and Future Works

In this paper, the problem of three-dimensional trajectory tracking is addressed for a heterogeneous XAUV subject to multi-source uncertainties and complex actuator dynamics. A novel compound control method is developed to improve the system performances, which consists of a kinematics loop, a dynamics loop, and rudder allocation. Compared with the general finite-time tracking control algorithm, the proposed controller focuses not only on finite-time dynamics control, but also on the finite time convergence of kinematic guidance, where a novel FTLOS guidance law and a finite-time feedback control law are designed in the kinematics loop to ensure the fast position and orientation tracking. In the dynamics loop, global FTTSMC laws are provided to solve the heading control, pitching control, and surge velocity tracking control problems, which concern not only the fast convergence in the approaching stage, but also the fast convergence in the sliding mode stage. To improve the system robustness, FTEDOs are designed to ensure fast unknown uncertainties estimation. Besides, the influences of the complex propeller and X-rudder dynamics are fully considered and tackled by the RBFNN compensator and the energy-efficient optimal rudder allocator. Finally, comparative simulation cases of two different scenarios are carried out: Case 1 proves that the proposed control method has good adaptability to different initial conditions and different unknown disturbances; Case 2 shows that compared with three other commonly used control methods [39,40,41], the proposed method has obvious advantages in convergence speed, tracking accuracy, stability, and energy consumption. Compared with the existing literature on XAUV control [3,4,42], this paper extends the research to the three-dimensional and introduces the idea of finite time convergence control with more constraints considered, thus making it more practical.

Although the superiority of the proposed algorithm has been proven by the above simulation results, the actual underwater experiment is not ready at present due to the limitations of time, equipment, and test conditions, which will be addressed in our future works.