Sparse Polynomial Chaos Expansion for Uncertainty Quantification of Composite Cylindrical Shell with Geometrical and Material Uncertainty
Abstract
:1. Introduction
2. Finite Element Method
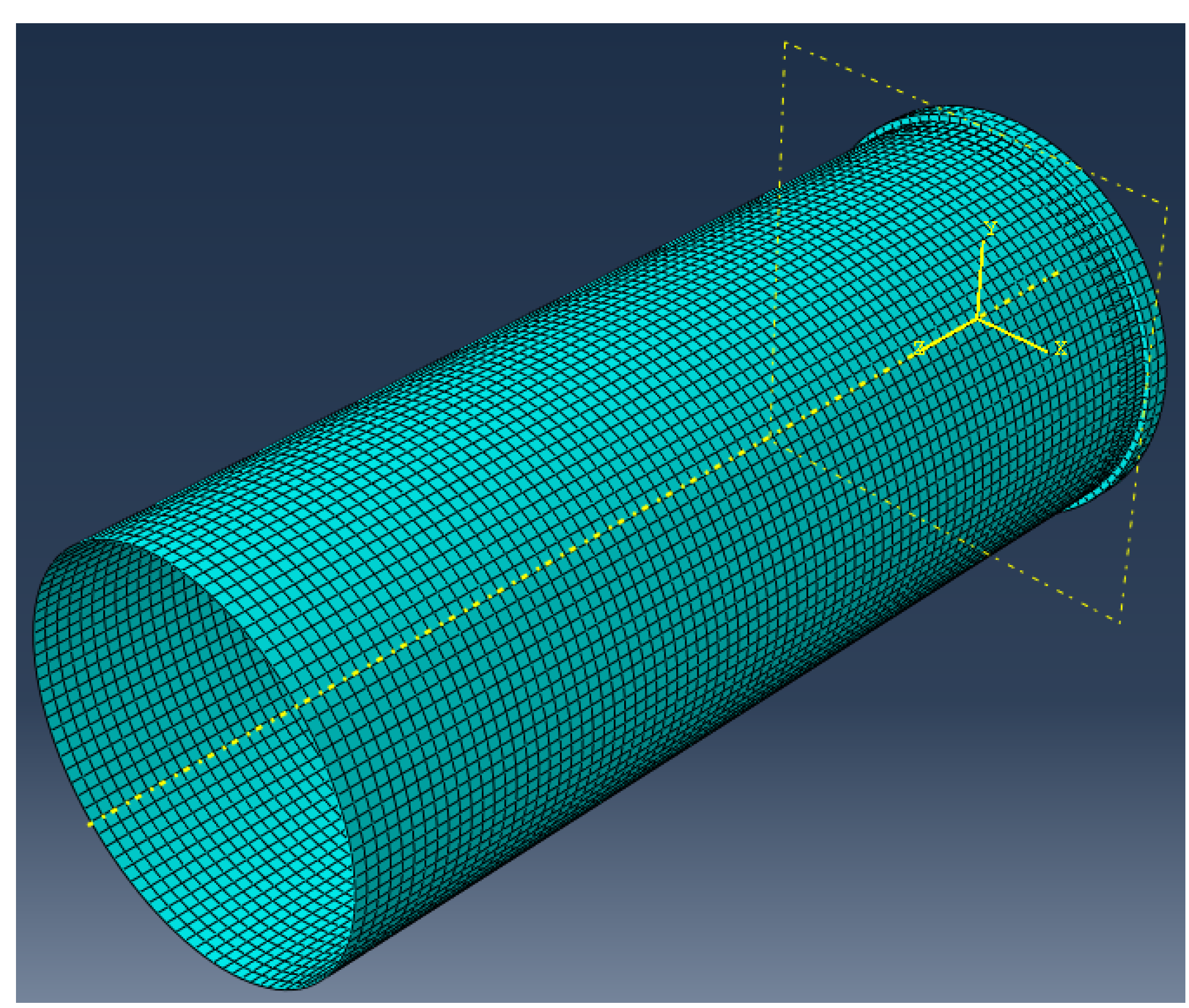
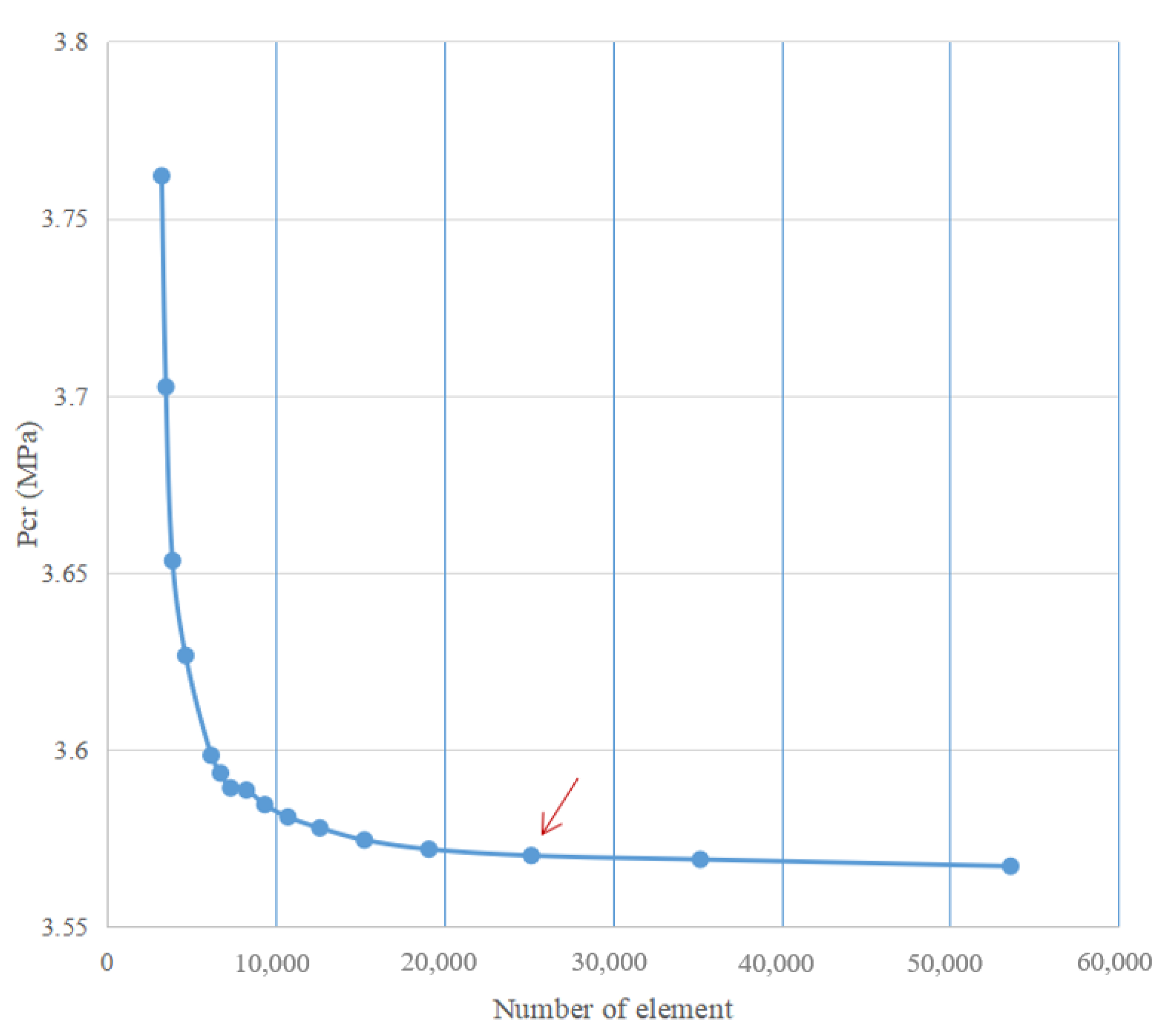
2.1. Finite Element Modeling
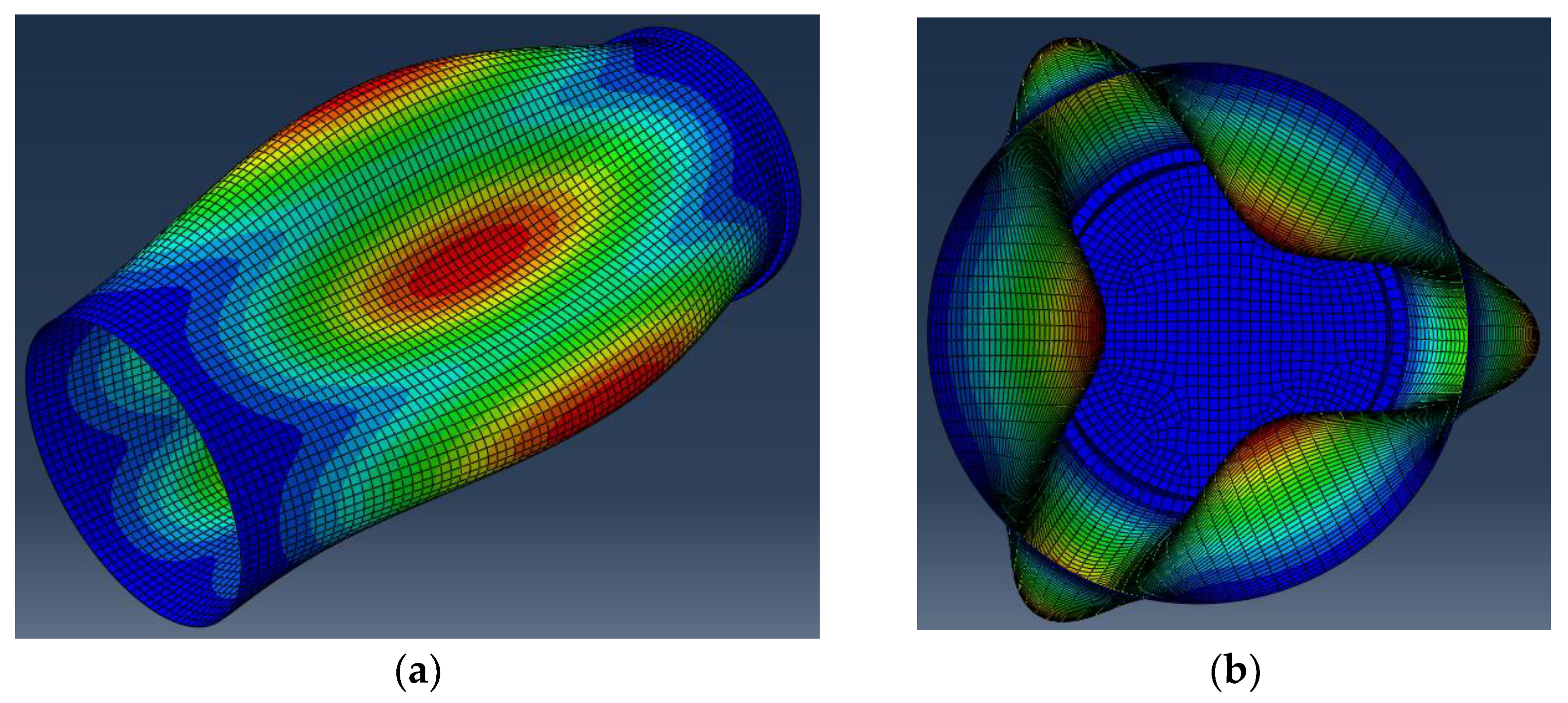
2.2. Finite Element Analysis Results
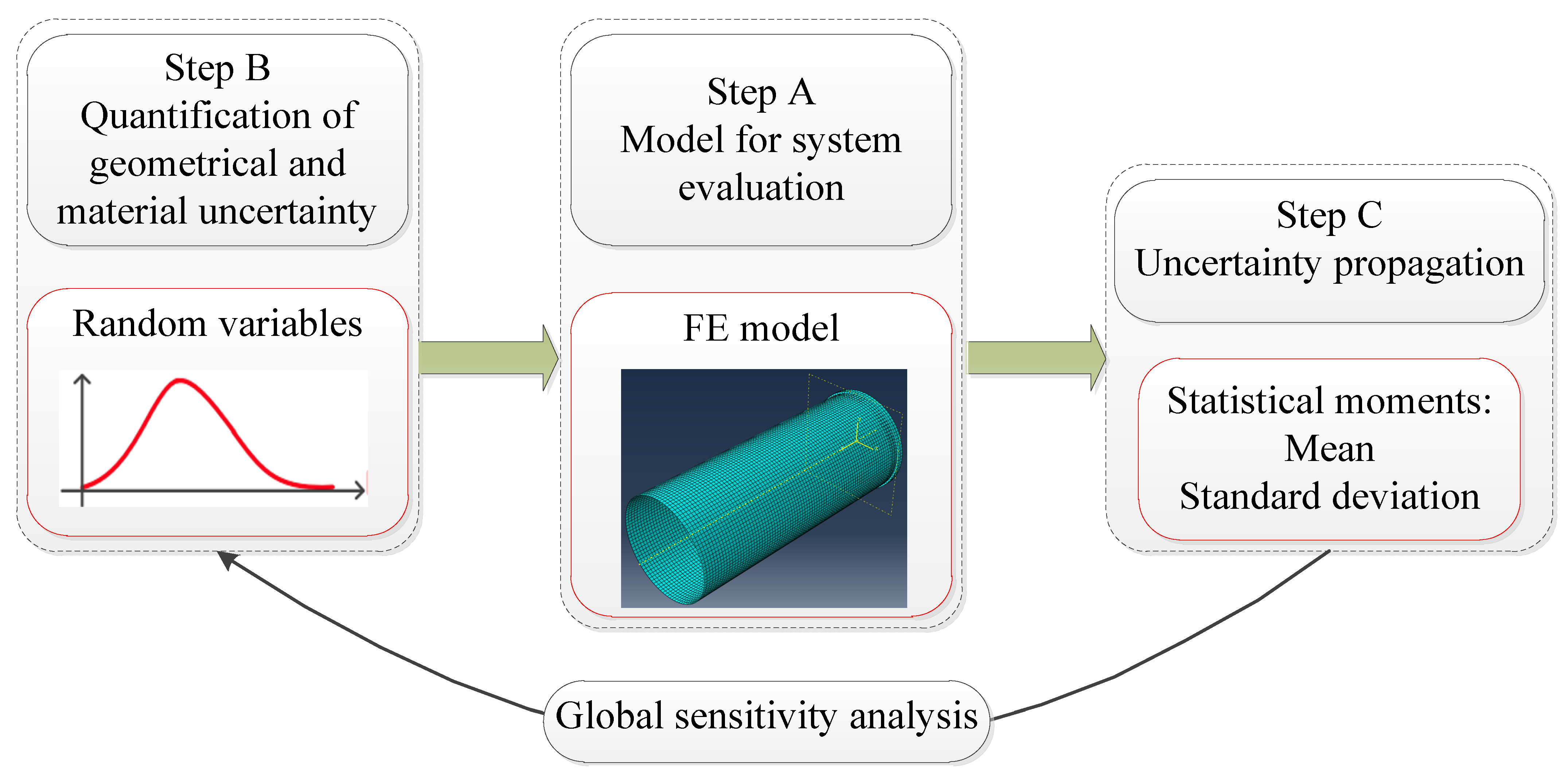
3. Sparse Polynomial Chaos Expansion
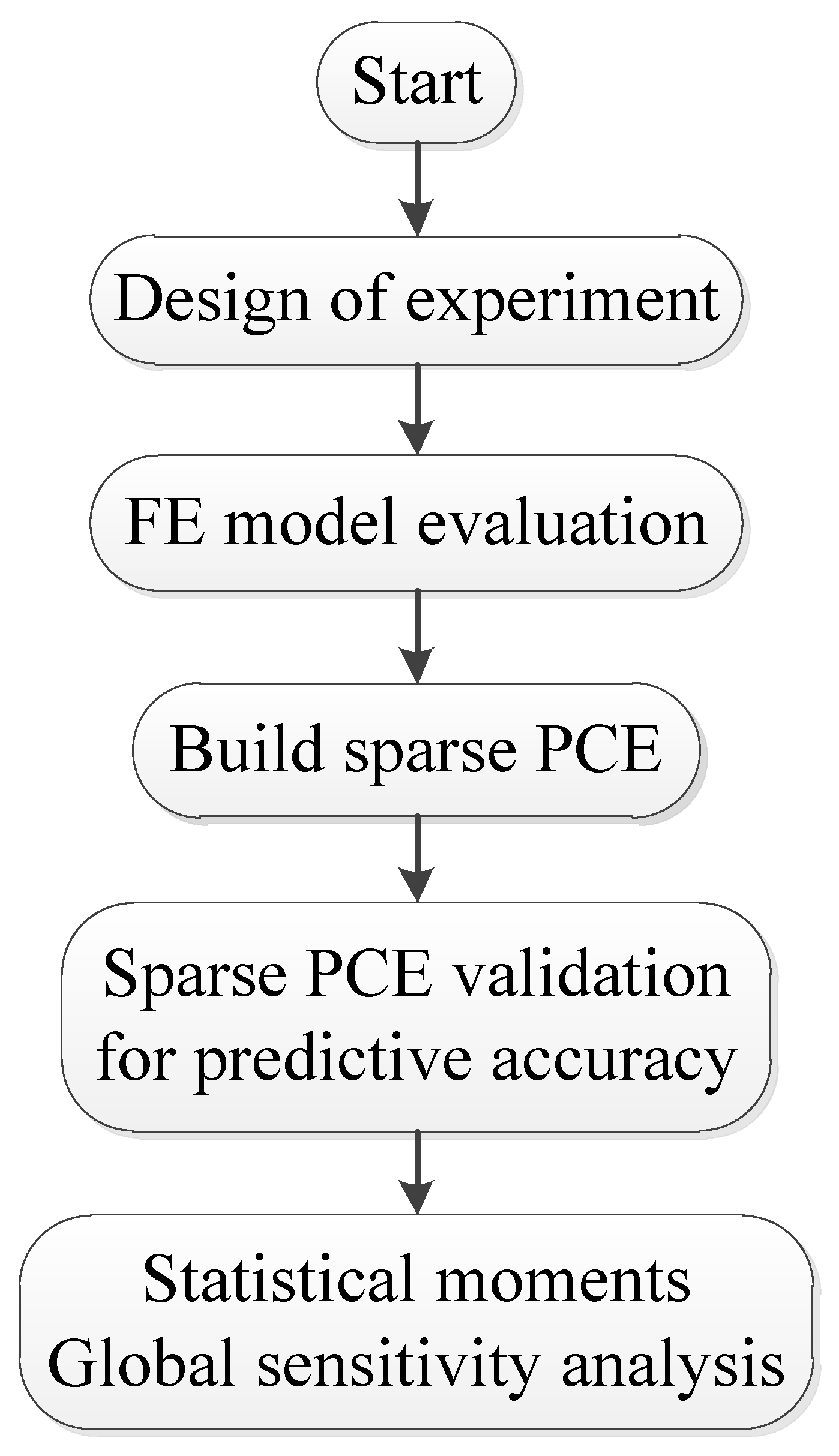
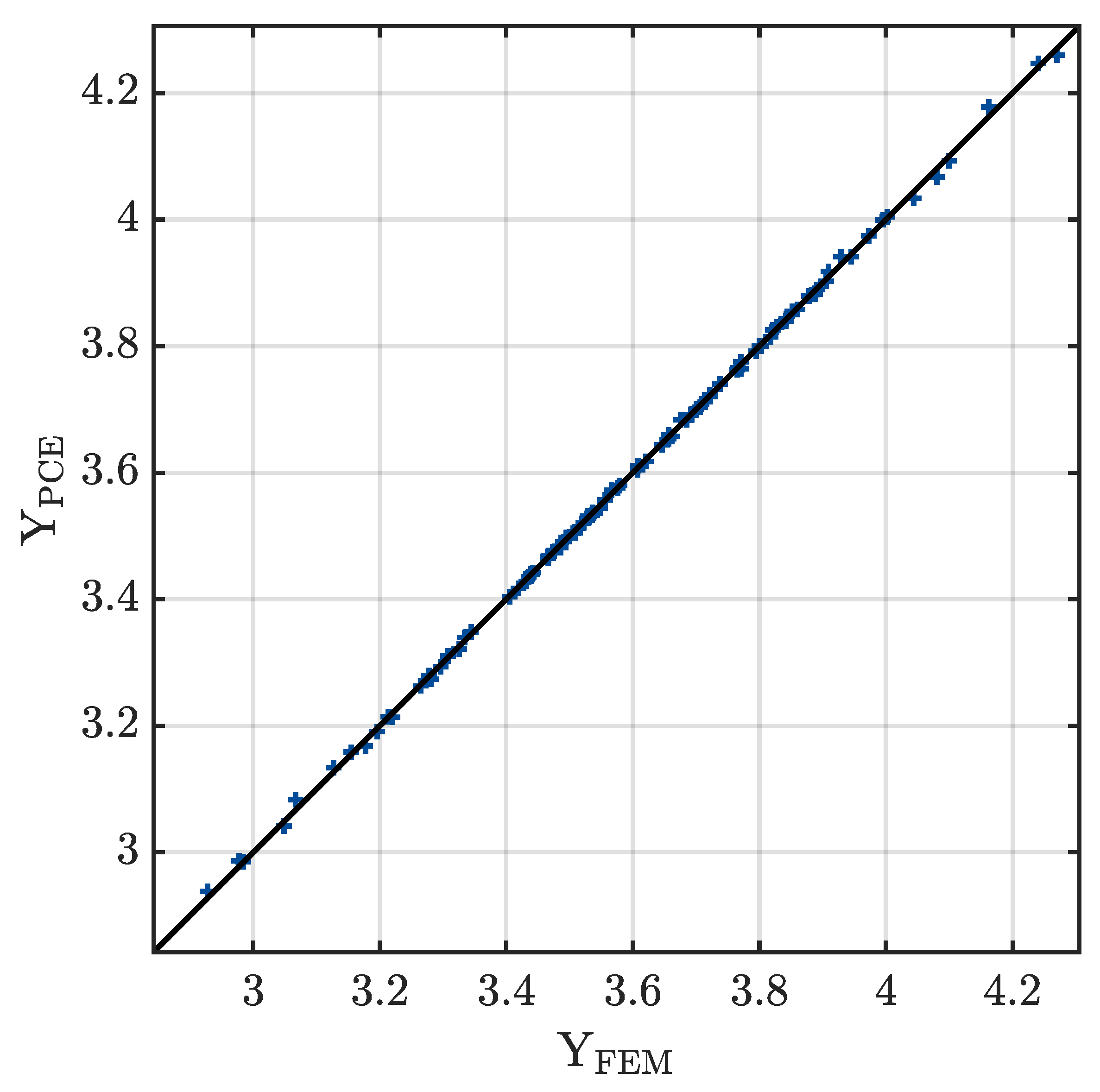
3.1. Modeling and Validation
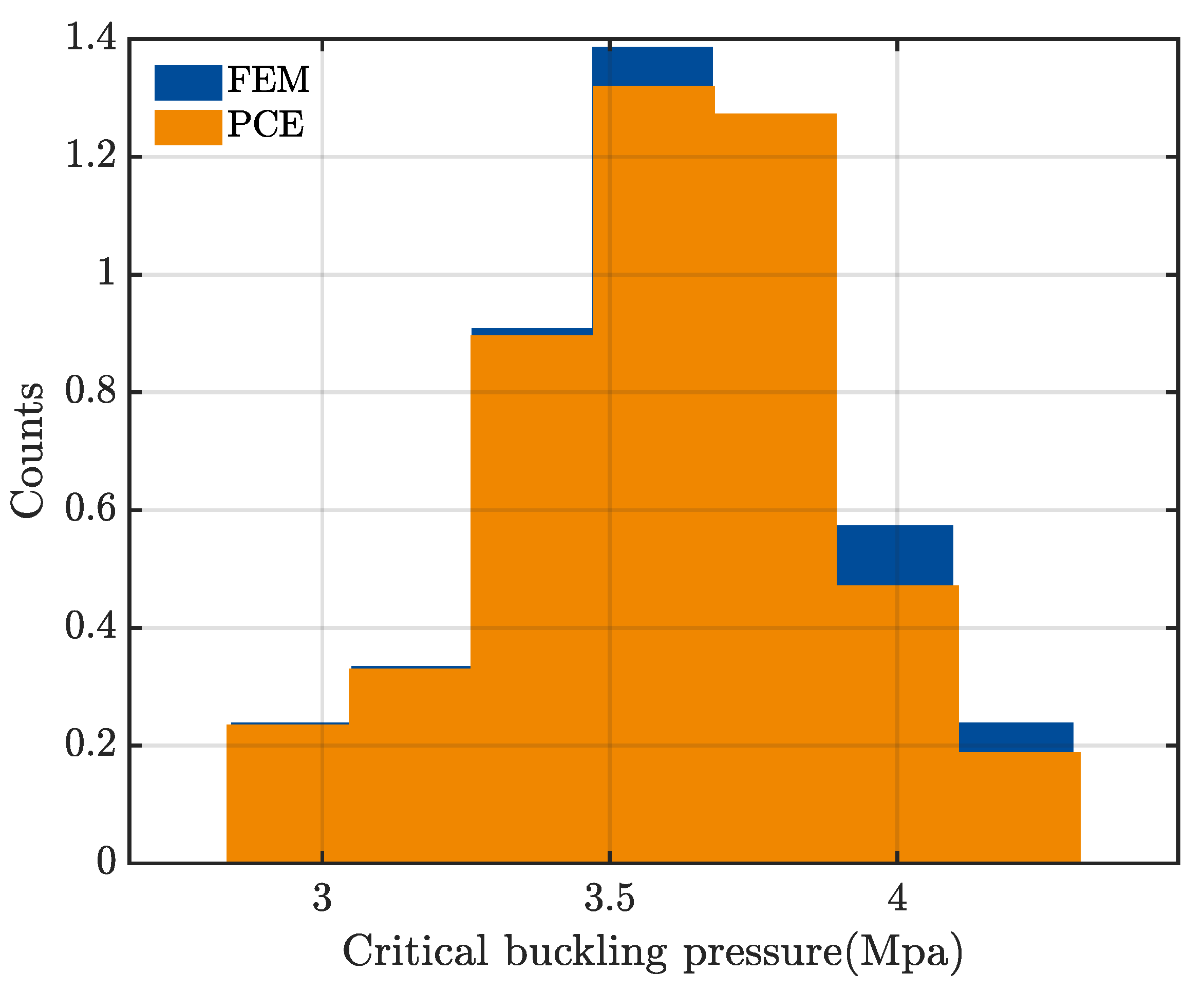
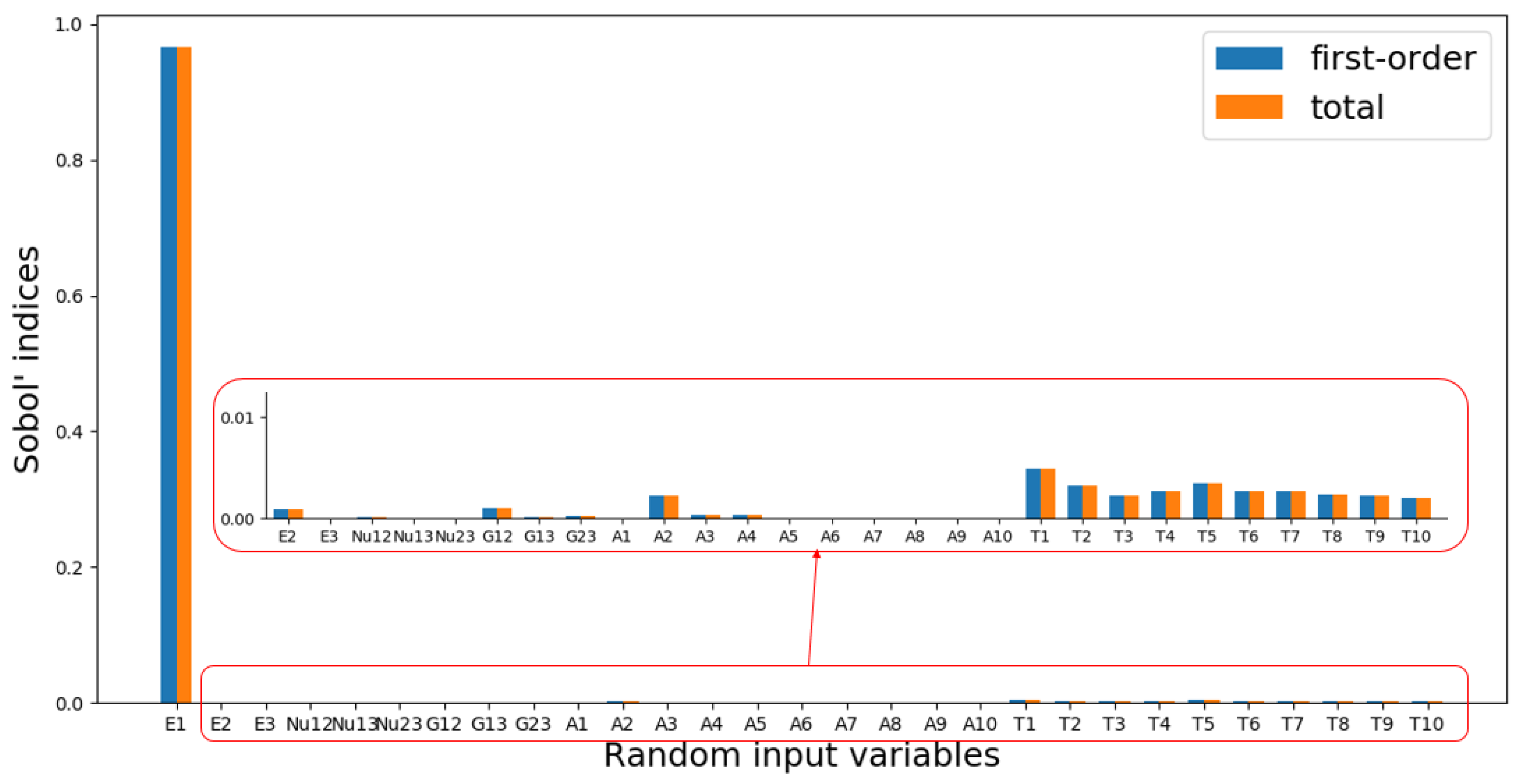
3.2. Uncertainty Quantification
4. Conclusions
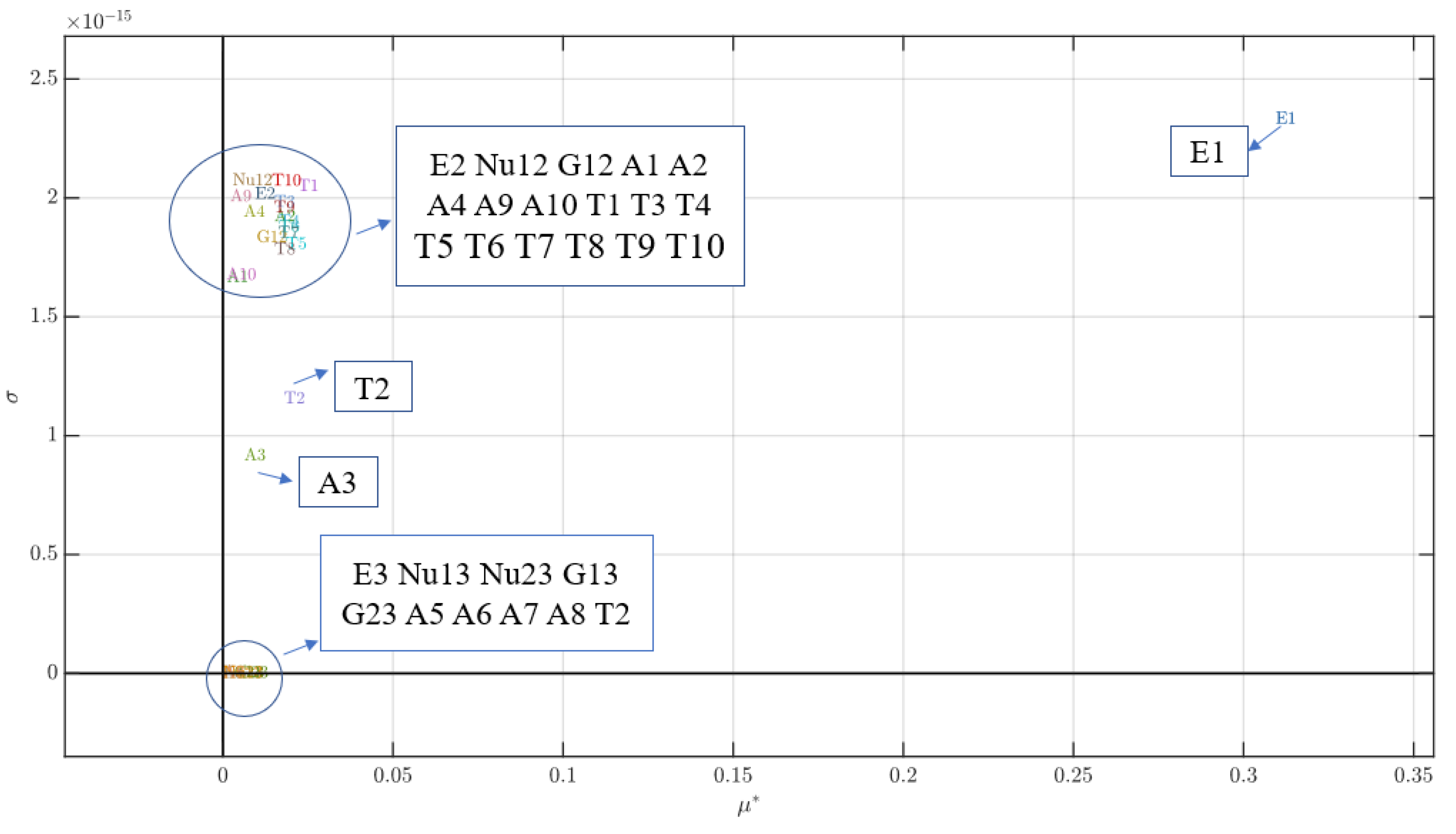
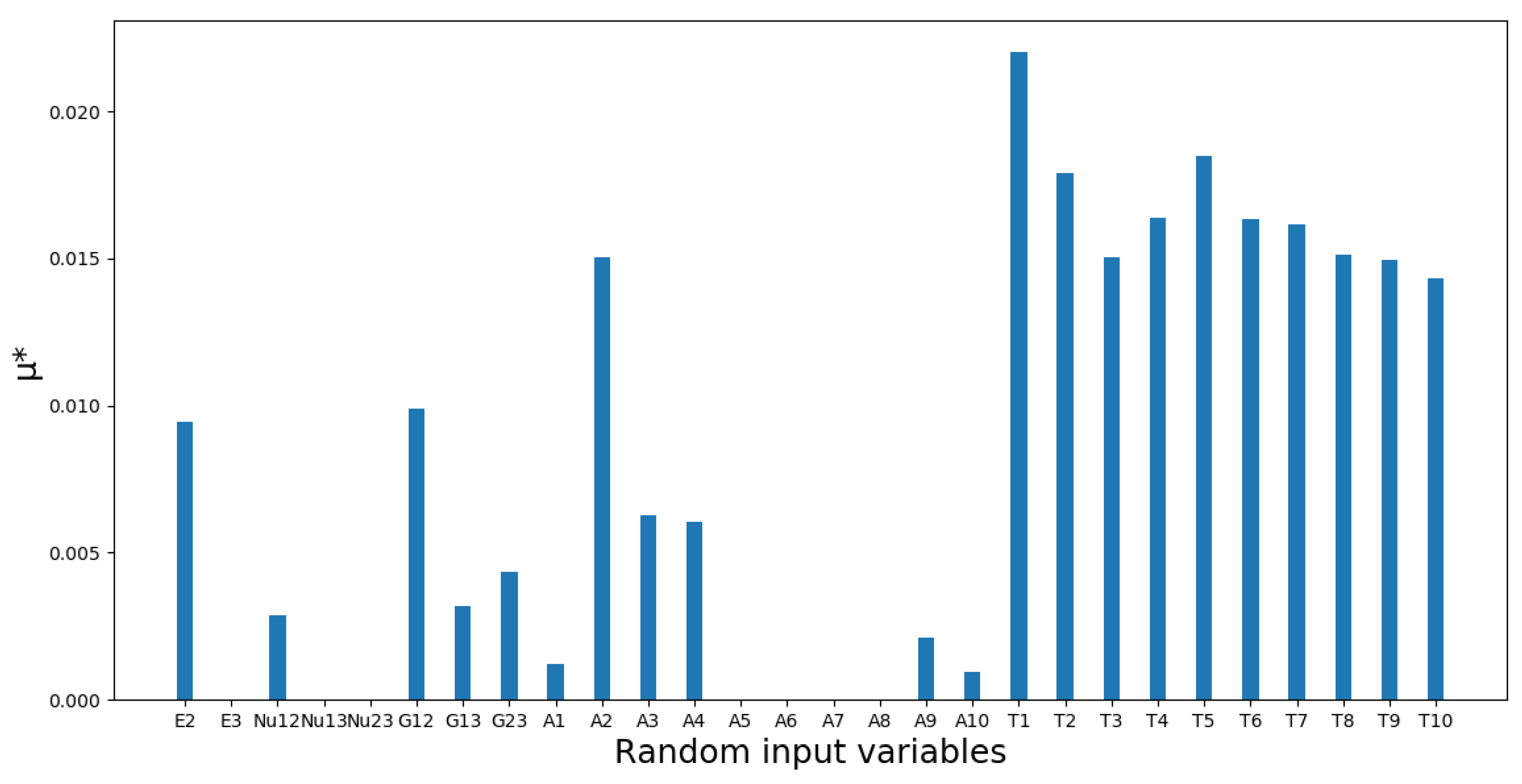
- The uncertainty of the longitudinal modulus of composite materials has a significant influence on the critical buckling pressure of composite cylindrical shells, whereas the uncertainties with respect to the transverse modulus, shear modulus, and Poisson’s ratio have a weak influence. When the coefficient of variation of ply thickness and orientation angle does not surpass 2%, the uncertainties regarding ply thickness and orientation angle have a weak influence on the critical buckling pressure.
- E2, G12, A2, T1, T2, T3, T4, T5, T6, T7, T8, T9, T10 are the most influential random variables on variations in critical buckling pressure other than E1.
- Sparse PCE is effective for the 29-dimensional problem with a limited design sample consisting of 350 samples (about 12 times the dimensionality), and normalization did not need to be performed for input variables ranging from 0.421 to 121 in this study, indicating the robustness of sparse PCE.
- The critical buckling pressure obtained using FEM and sparse PCE indicates good matches.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ross, C.T.F. A conceptual design of an underwater vehicle. Ocean Eng. 2006, 33, 2087–2104. [Google Scholar] [CrossRef]
- Smith, C.S. Design of submersible pressure hulls in composite materials. Mar. Struct. 1991, 4, 141–182. [Google Scholar] [CrossRef]
- Graham, D. Composite pressure hulls for deep ocean submersibles. Compos. Struct. 1995, 32, 331–343. [Google Scholar] [CrossRef]
- Carvelli, V.; Panzeri, N.; Poggi, C. Buckling strength of GFRP under-water vehicles. Compos. Part B Eng. 2001, 32, 89–101. [Google Scholar] [CrossRef]
- Davies, P.; Choqueuse, D.; Bigourdan, B.; Chauchot, P. Composite Cylinders for Deep Sea Applications: An Overview. J. Press. Vessel. Technol.-Trans. Asme 2016, 138, 060904. [Google Scholar] [CrossRef]
- Sobhani, E.; Moradi-Dastjerdi, R.; Behdinan, K.; Masoodi, A.R.; Ahmadi-Pari, A.R. Multifunctional trace of various reinforcements on vibrations of three-phase nanocomposite combined hemispherical-cylindrical shells. Compos. Struct. 2022, 279, 114798. [Google Scholar] [CrossRef]
- Błachut, J. Experimental Perspective on the Buckling of Pressure Vessel Components. Appl. Mech. Rev. 2014, 66, 010803. [Google Scholar] [CrossRef]
- Krikanov, A.A. Composite pressure vessels with higher stiffness. Compos. Struct. 2000, 48, 119–127. [Google Scholar] [CrossRef]
- Lopatin, A.V.; Morozov, E.V. Buckling of composite cylindrical shells with rigid end disks under hydrostatic pressure. Compos. Struct. 2017, 173, 136–143. [Google Scholar] [CrossRef]
- Nguyen, H.L.T.; Elishakoff, I.; Nguyen, V.T. Buckling under the external pressure of cylindrical shells with variable thickness. Int. J. Solids Struct. 2009, 46, 4163–4168. [Google Scholar] [CrossRef] [Green Version]
- Wei, R.; Pan, G.; Jiang, J.; Shen, K. Influence of ply angle and length on buckling behavior of composite shells under hydrostatic pressure. J. Reinf. Plast. Compos. 2019, 38, 478–491. [Google Scholar] [CrossRef]
- Rasheed, H.A.; Yousif, O.H. Stability of Anisotropic Laminated Rings and Long Cylinders Subjected to External Hydrostatic Pressure. J. Aerosp. Eng. 2005, 18, 129–138. [Google Scholar] [CrossRef]
- Geier, B.; Meyer-Piening, H.-R.; Zimmermann, R. On the influence of laminate stacking on buckling of composite cylindrical shells subjected to axial compression. Compos. Struct. 2002, 55, 467–474. [Google Scholar] [CrossRef]
- Hernández-Moreno, H.; Douchin, B.; Collombet, F.; Choqueuse, D.; Davies, P. Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure. Compos. Sci. Technol. 2008, 68, 1015–1024. [Google Scholar] [CrossRef] [Green Version]
- Chun, S.K.; Guang, P. Optimizing the buckling strength of filament winding composite cylinders under hydrostatic pressure. J. Reinf. Plast. Compos. 2018, 37, 892–904. [Google Scholar] [CrossRef]
- Shen, K.-C.; Pan, G. Buckling and strain response of filament winding composite cylindrical shell subjected to hydrostatic pressure: Numerical solution and experiment. Compos. Struct. 2021, 276, 114534. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Shell instability analysis by using mixed interpolation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 419. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Analyzing FG shells with large deformations and finite rotations. World J. Eng. 2019, 16, 636–647. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Hygro-thermo-elastic nonlinear analysis of functionally graded porous composite thin and moderately thick shallow panels. Mech. Adv. Mater. Struct. 2022, 29, 594–612. [Google Scholar] [CrossRef]
- Błachut, J. Buckling of composite domes with localised imperfections and subjected to external pressure. Compos. Struct. 2016, 153, 746–754. [Google Scholar] [CrossRef]
- Castro, S.G.P.; Mittelstedt, C.; Monteiro, F.A.C.; Degenhardt, R.; Ziegmann, G. Evaluation of non-linear buckling loads of geometrically imperfect composite cylinders and cones with the Ritz method. Compos. Struct. 2015, 122, 284–299. [Google Scholar] [CrossRef]
- Schillo, C.; Rostermundt, D.; Krause, D. Experimental and numerical study on the influence of imperfections on the buckling load of unstiffened CFRP shells. Compos. Struct. 2015, 131, 128–138. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, G. Collapse of thick-walled subsea pipelines with imperfections subjected to external pressure. Ocean Eng. 2020, 213, 107705. [Google Scholar] [CrossRef]
- Teixeira, A.P.; Palencia, O.G.; Soares, C.G. Reliability Analysis of Pipelines With Local Corrosion Defects Under External Pressure. J. Offshore Mech. Arct. Eng.-Trans. Asme 2019, 141. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Liu, Z.; Tian, X.; Ji, R.; Li, H. Reliability-based load and resistance factor design of composite pressure vessel under external hydrostatic pressure. Compos. Struct. 2011, 93, 2844–2852. [Google Scholar] [CrossRef]
- Cai, B.; Liu, Y.; Liu, Z.; Tian, X.; Ji, R.; Zhang, Y. Probabilistic analysis of composite pressure vessel for subsea blowout preventers. Eng. Fail. Anal. 2012, 19, 97–108. [Google Scholar] [CrossRef]
- Hai-Bang, L.; Desceliers, C.; Lu Minh, L.; Tien-Thinh, L.; Binh Thai, P.; Long, N.-N.; Van Thuan, D.; Minh, L. Quantification of Uncertainties on the Critical Buckling Load of Columns under Axial Compression with Uncertain Random Materials. Materials 2019, 12, 1828. [Google Scholar] [CrossRef] [Green Version]
- Gerhardt, E.; Marczak, R.J.; Amico, S.C. Numerical-experimental structural instability analysis of composite tubes considering manufacturing parameters and imperfections. Polym. Compos. 2021, 42, 1530–1542. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Qian, S.-Y.; Wang, N.-W.; Xiong, W.; Wu, W.-Q. A review on stochastic multiscale analysis for FRP composite structures. Compos. Struct. 2022, 284, 115132. [Google Scholar] [CrossRef]
- Solazzi, L.; Vaccari, M. Reliability design of a pressure vessel made of composite materials. Compos. Struct. 2022, 279, 114726. [Google Scholar] [CrossRef]
- Rafiee, R.; Torabi, M.A. Stochastic prediction of burst pressure in composite pressure vessels. Compos. Struct. 2018, 185, 573–583. [Google Scholar] [CrossRef]
- Hocine, A.; Maizia, A.; Ghouaoula, A.; Dehmous, H. Reliability Prediction of Composite Tubular Structure under Mechanical Loading by Finite Element Method. J. Fail. Anal. Prev. 2018, 18, 1439–1446. [Google Scholar] [CrossRef]
- Balokas, G.; Kriegesmann, B.; Rolfes, R. Data-driven inverse uncertainty quantification in the transverse tensile response of carbon fiber reinforced composites. Compos. Sci. Technol. 2021, 211, 108845. [Google Scholar] [CrossRef]
- Kalfountzos, C.D.; Bikakis, G.S.E.; Theotokoglou, E.E. Deterministic and probabilistic buckling response of fiber–metal laminate panels under uniaxial compression. Aircr. Eng. Aerosp. Technol. 2021, 94, 745–759. [Google Scholar] [CrossRef]
- Yetgin, A.; Özaslan, E.; Acar, B. Probabilistic Burst Strength Evaluation of a Filament Wound Composite Pressure Vessel. In Proceedings of the Pressure Vessels and Piping Conference, Virtual, Online, 3 August 2020. [Google Scholar] [CrossRef]
- Moon, C.-J.; Kim, I.-H.; Choi, B.-H.; Kweon, J.-H.; Choi, J.-H. Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications. Compos. Struct. 2010, 92, 2241–2251. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Efficient computation of global sensitivity indices using sparse polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2010, 95, 1216–1229. [Google Scholar] [CrossRef]
- Konakli, K.; Sudret, B. Polynomial meta-models with canonical low-rank approximations: Numerical insights and comparison to sparse polynomial chaos expansions. J. Comput. Phys. 2016, 321, 1144–1169. [Google Scholar] [CrossRef] [Green Version]
- Fajraoui, N.; Marelli, S.; Sudret, B. Sequential Design of Experiment for Sparse Polynomial Chaos Expansions. SIAM/ASA J. Uncertain. Quantif. 2017, 5, 1085–1109. [Google Scholar] [CrossRef]
- Sudret, B. Uncertainty Propagation and Sensitivity Analysis in Mechanical Models–Contributions to Structural Reliability and Stochastic Spectral Methods. Ph.D. Thesis, Université Blaise Pascal, Clermont-Ferrand, France, 2007. [Google Scholar]
| Symbol | Unit | Mean | Coefficient of Variation | Distribution |
|---|---|---|---|---|
| E1 | GPa | 121 | 10% | Normal |
| E2 | GPa | 8.6 | 6% | Normal |
| E3 | GPa | 8.6 | 6% | Normal |
| Nu12 | - | 0.253 | 8% | Normal |
| Nu13 | - | 0.253 | 8% | Normal |
| Nu23 | - | 0.421 | 8% | Normal |
| G12 | GPa | 3.35 | 8% | Normal |
| G13 | GPa | 3.35 | 8% | Normal |
| G23 | GPa | 2.68 | 8% | Normal |
| Property | Symbol | Unit | Mean | Coefficient of Variation | Distribution |
|---|---|---|---|---|---|
| Ply thickness | Ti (i = 1, 2, …, 10) | mm | 0.3 | 2% | Normal |
| Orientation angle | Ai (i = 1, 2, …, 10) | degree | θ | 2% | Normal |
| Sparse PCE Result | Value |
|---|---|
| Number of input variables | 29 |
| Maximal degree | 1 |
| Size of full basis | 30 |
| Size of sparse basis | 23 |
| Full model evaluations | 350 |
| Leave-one-out error | 2.9839 × 10−4 |
| Validation error | 2.8282 × 10−4 |
| Mean value | 3.5777 |
| Standard deviation | 0.3149 |
| Coefficient of variation | 8.801% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Zhang, X.; Shen, K.; Pan, G. Sparse Polynomial Chaos Expansion for Uncertainty Quantification of Composite Cylindrical Shell with Geometrical and Material Uncertainty. J. Mar. Sci. Eng. 2022, 10, 670. https://doi.org/10.3390/jmse10050670
Chen M, Zhang X, Shen K, Pan G. Sparse Polynomial Chaos Expansion for Uncertainty Quantification of Composite Cylindrical Shell with Geometrical and Material Uncertainty. Journal of Marine Science and Engineering. 2022; 10(5):670. https://doi.org/10.3390/jmse10050670
Chicago/Turabian StyleChen, Ming, Xinhu Zhang, Kechun Shen, and Guang Pan. 2022. "Sparse Polynomial Chaos Expansion for Uncertainty Quantification of Composite Cylindrical Shell with Geometrical and Material Uncertainty" Journal of Marine Science and Engineering 10, no. 5: 670. https://doi.org/10.3390/jmse10050670
APA StyleChen, M., Zhang, X., Shen, K., & Pan, G. (2022). Sparse Polynomial Chaos Expansion for Uncertainty Quantification of Composite Cylindrical Shell with Geometrical and Material Uncertainty. Journal of Marine Science and Engineering, 10(5), 670. https://doi.org/10.3390/jmse10050670







