Research on the Depth Control Strategy of an Underwater Profiler Driven by a Mixture of Ocean Thermal Energy and Electric Energy
Abstract
:1. Introduction
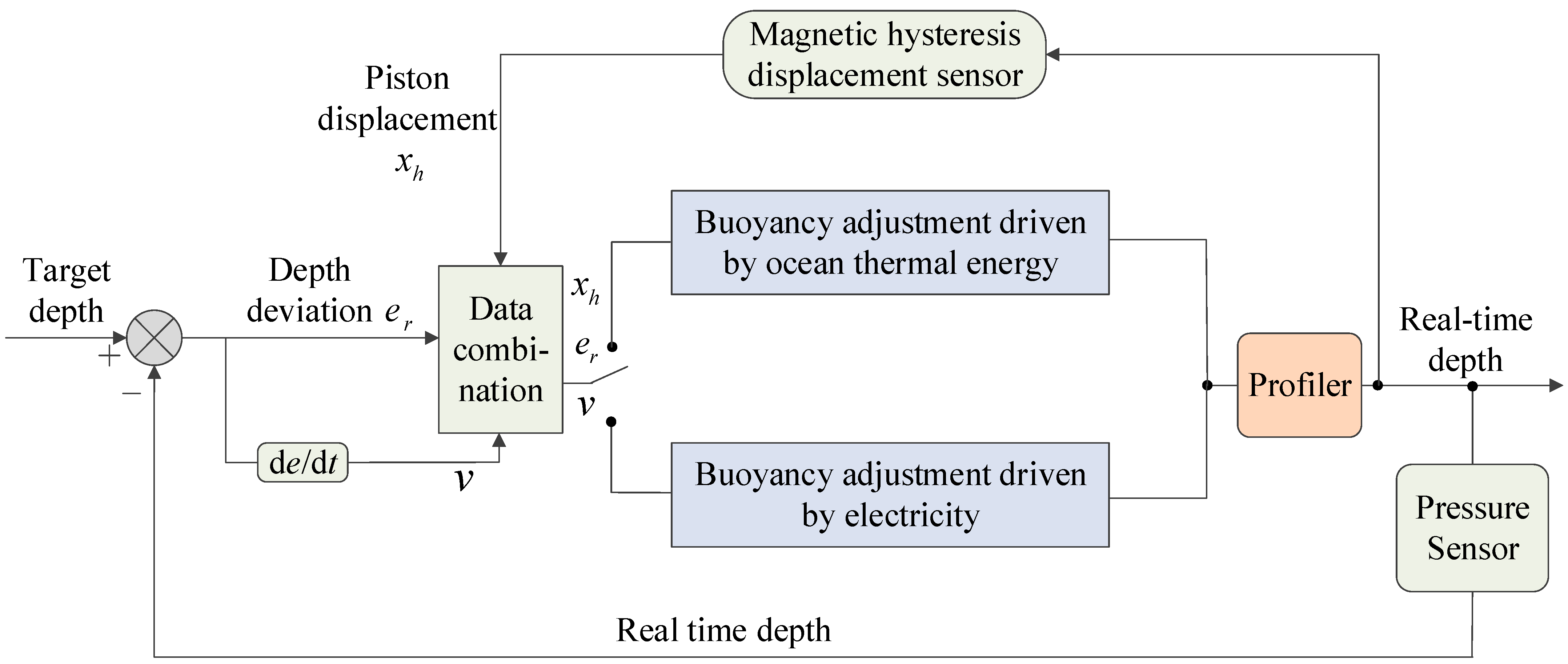
2. Buoyancy Regulation System
3. Depth Control Strategy of Profiler
3.1. Depth Control Algorithm That Profiler Driven by Ocean Thermal Energy
3.2. Depth Control Algorithm That Profiler Driven by Electric Energy
- (1)
- Sliding mode control method
- (2)
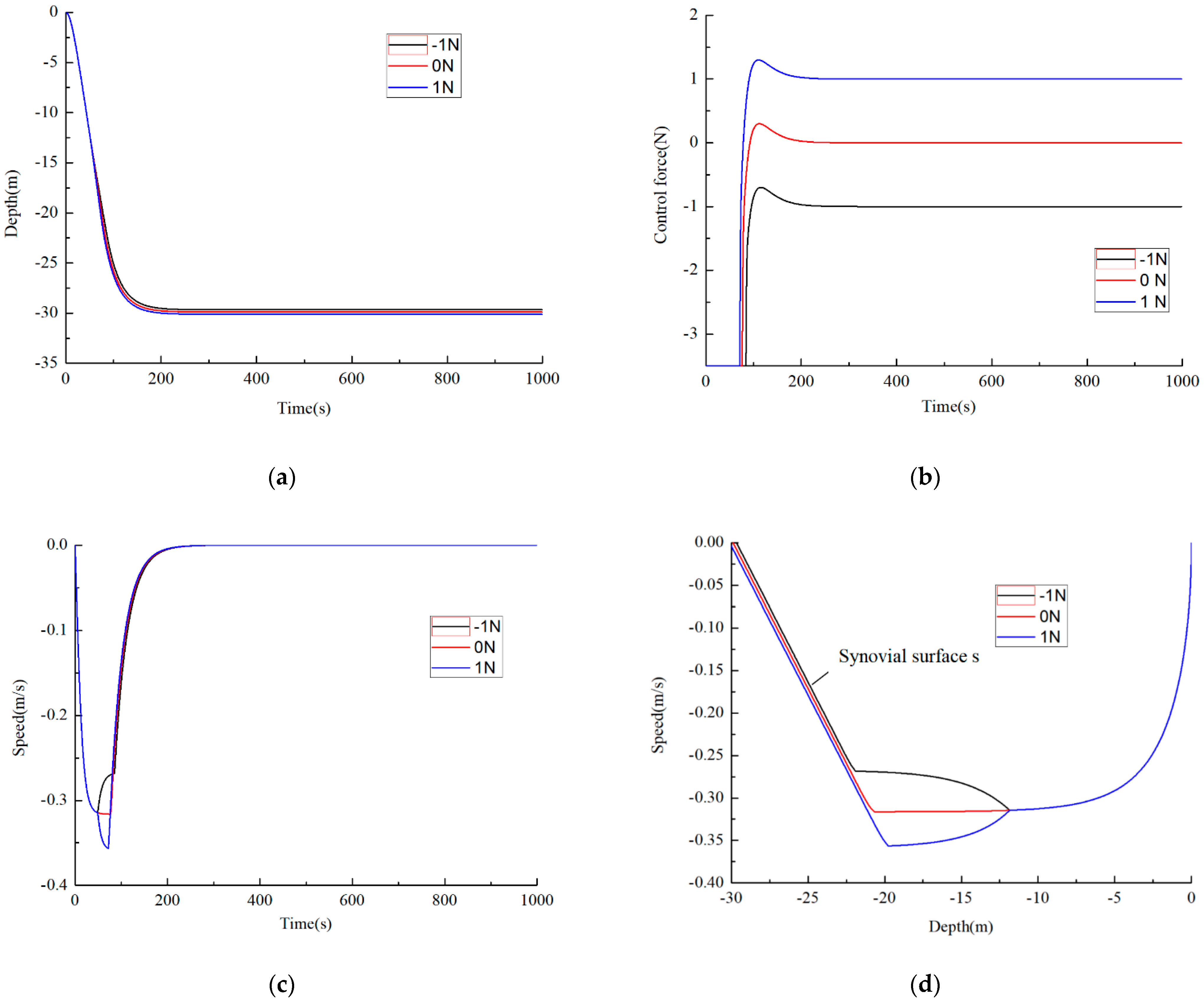
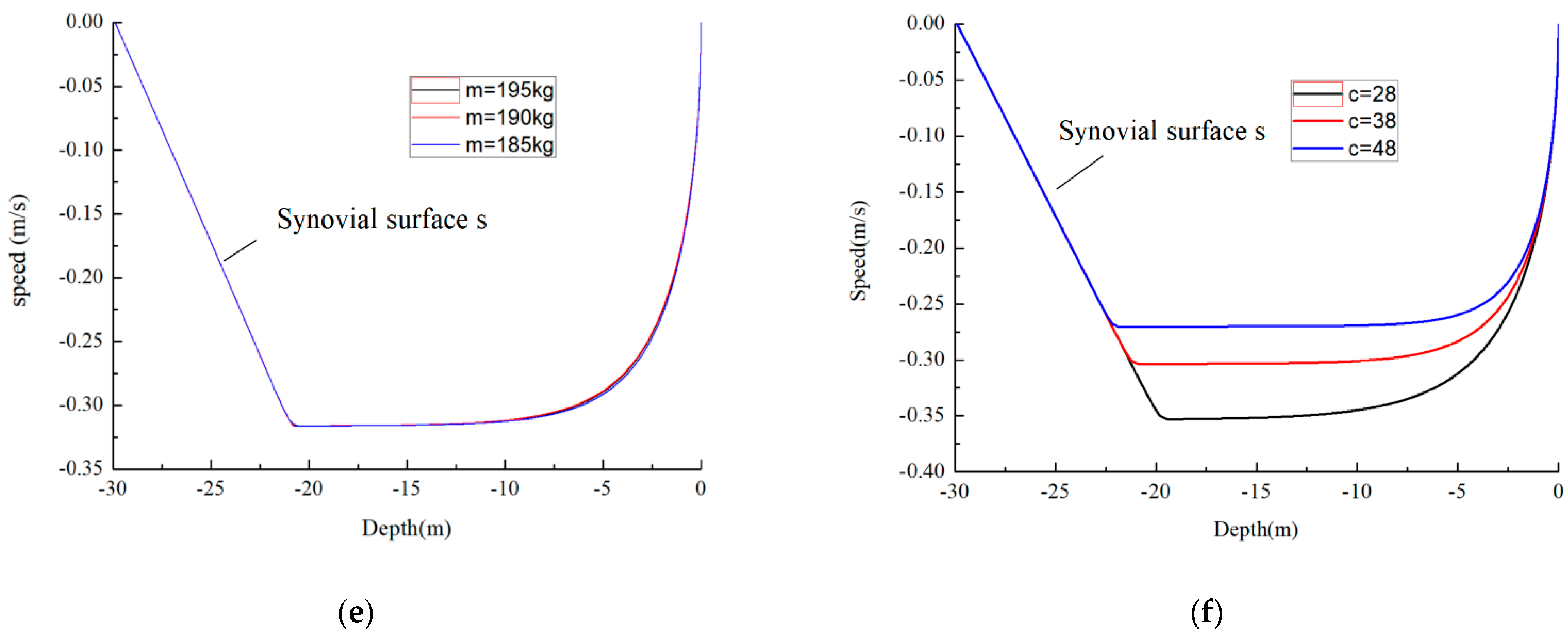
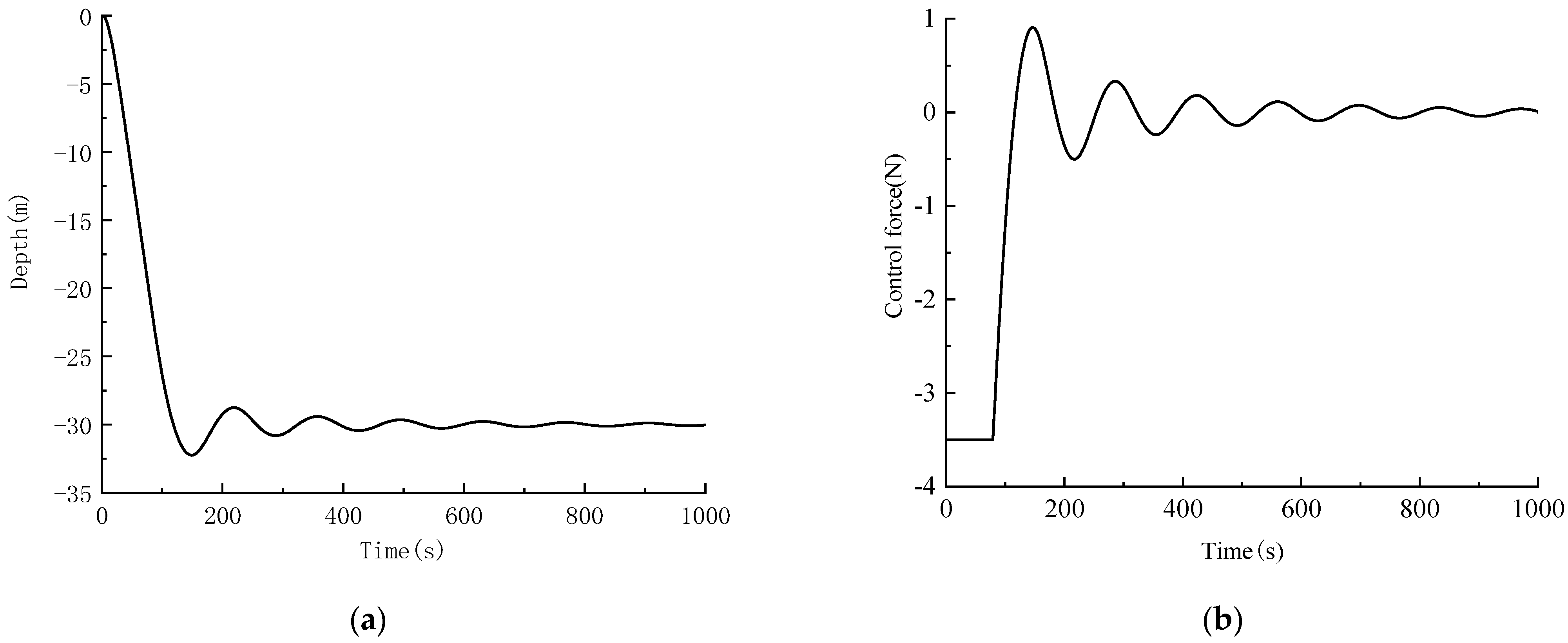
- Simulation analysis of the sliding mode control
3.3. Depth Control Algorithm That Profiler Driven by Electric Energy and Ocean Thermal Energy
4. Experimental Results
- (1)
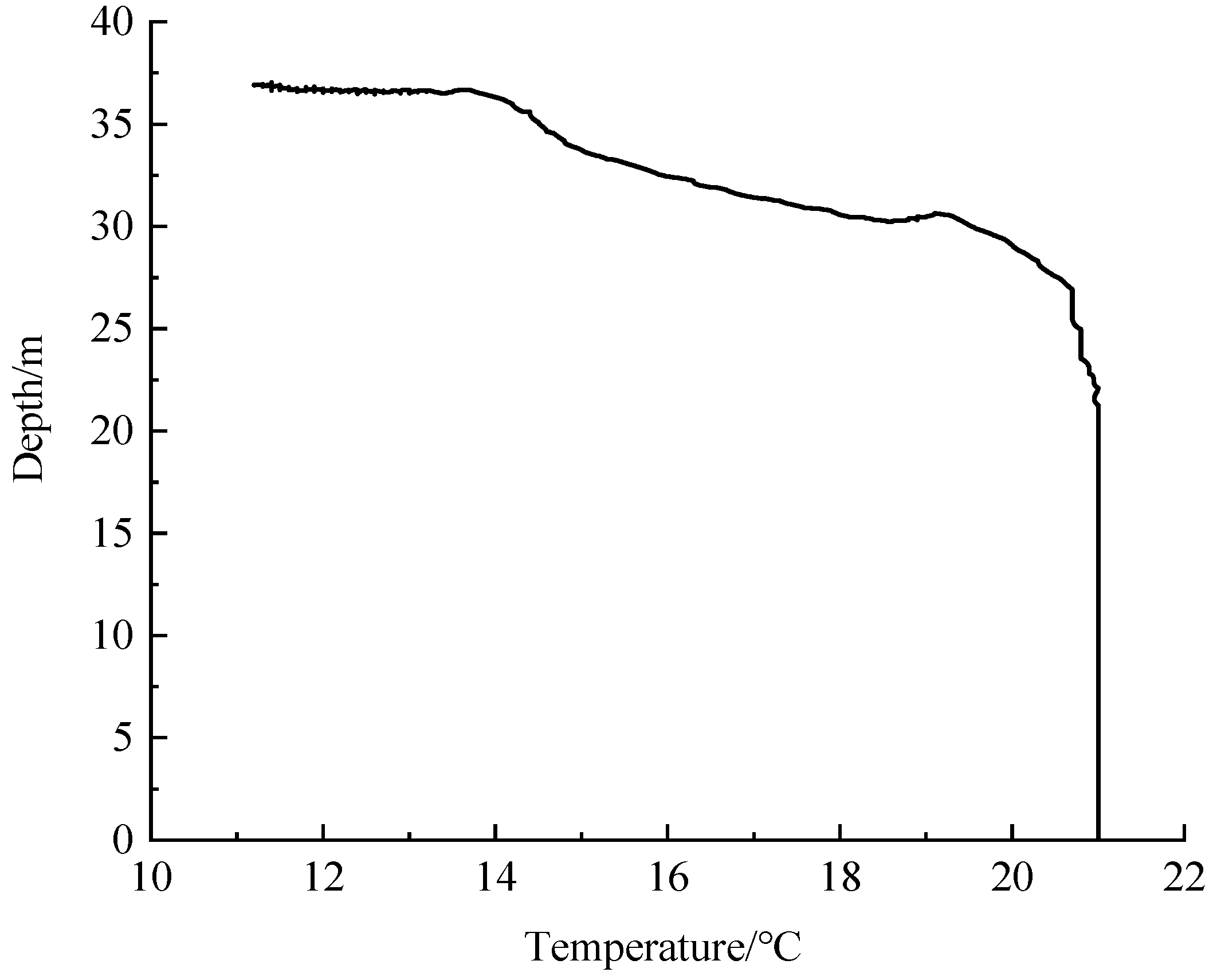
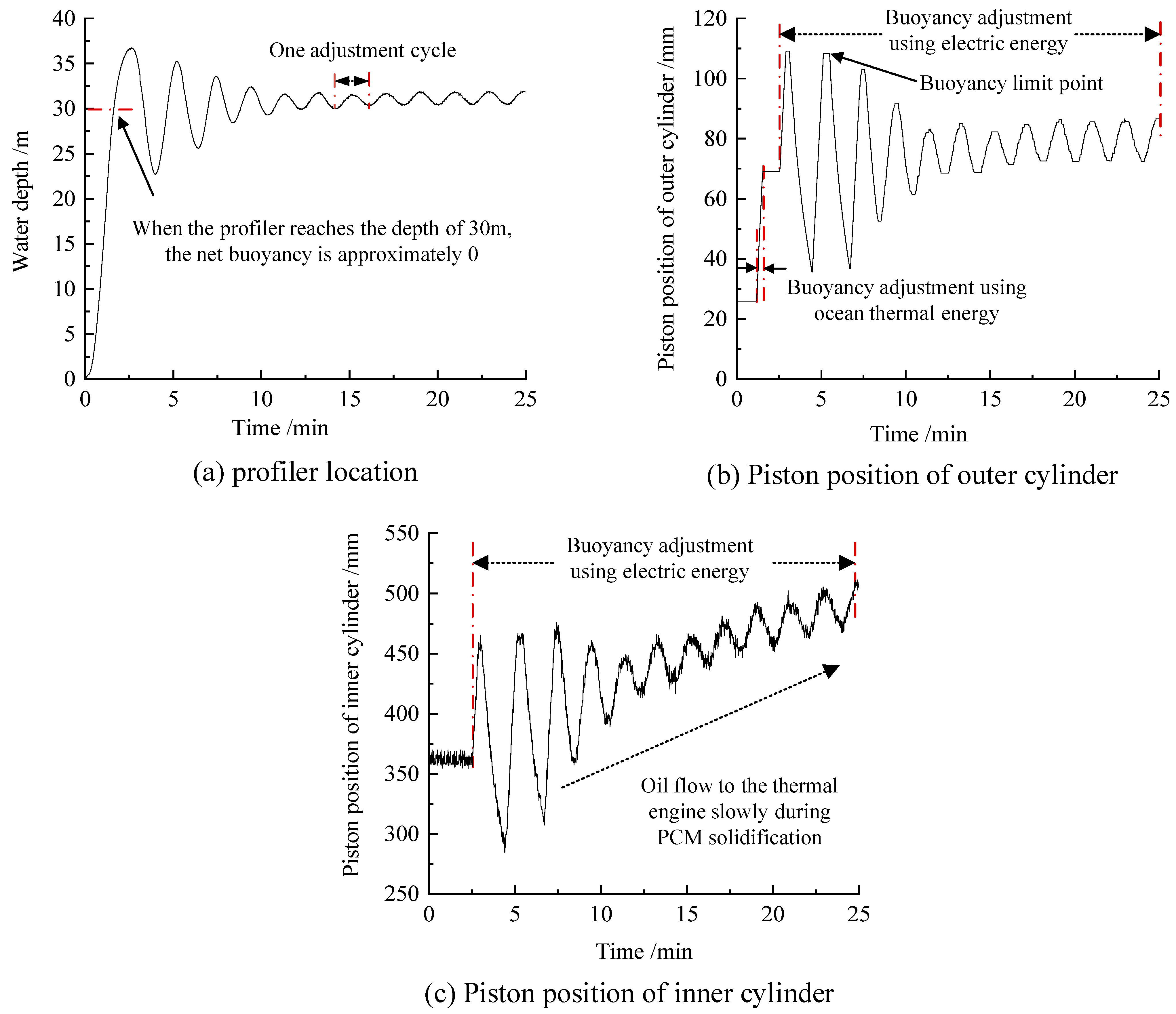
- Fixed-depth-control test in the lake
- (2)
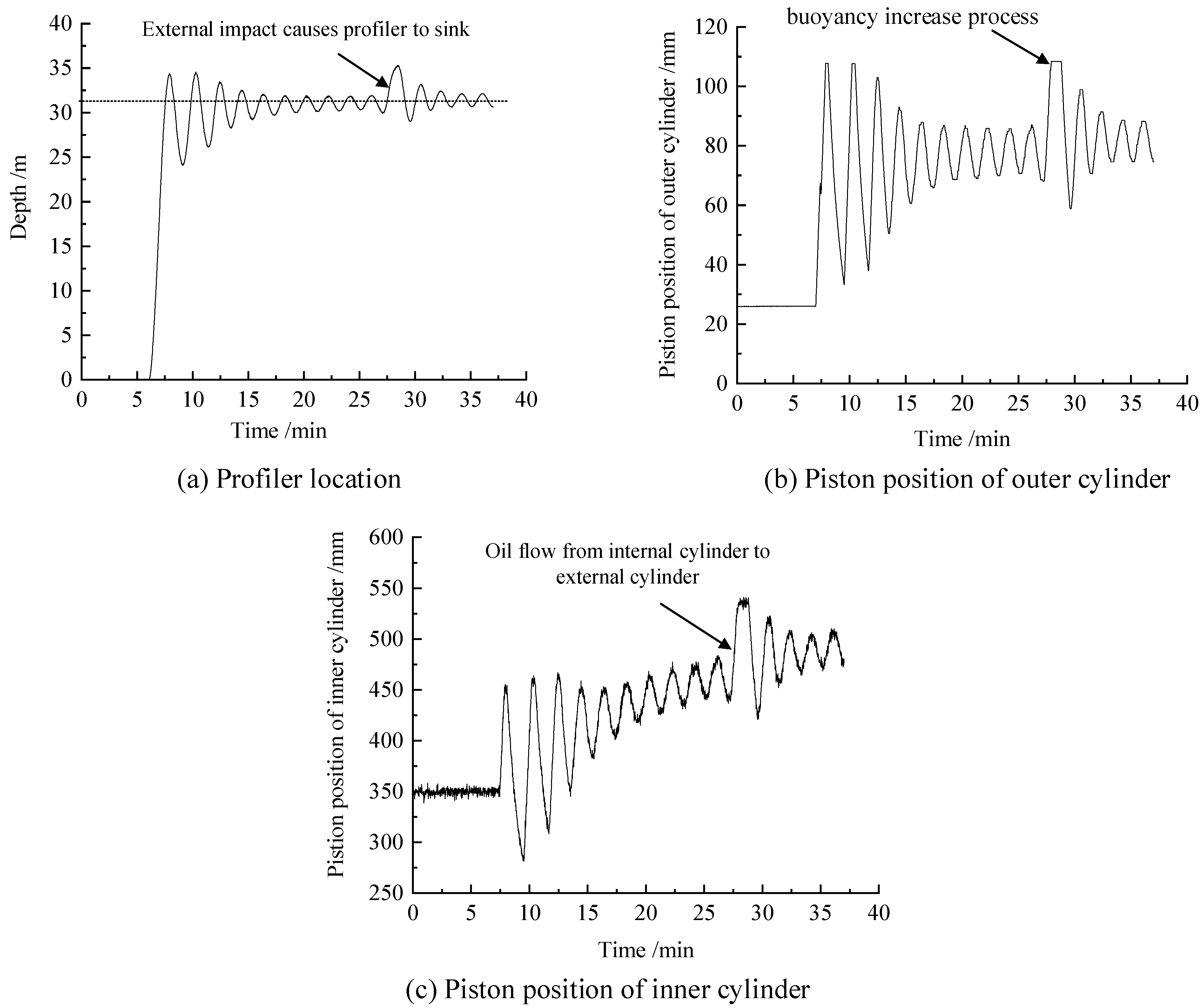
- Fixed-depth-control disturbance experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, H.; Choi, J.Y.; Park, J.; Ruda, M.; Prasad, R.; Chao, Y.; Choi, S. Towards the optimal operation of a thermal-recharging float in the ocean. Ocean. Eng. 2018, 156, 381–395. [Google Scholar] [CrossRef]
- Wang, Z.; Carriveau, R.; Ting, D.S.-K.; Xiong, W.; Wang, Z. A review of marine renewable energy storage. Int. J. Energy Res. 2019, 43, 6108–6150. [Google Scholar] [CrossRef]
- Khan, N.; Kalair, A.; Abas, N.; Haider, A. Review of ocean tidal, wave and thermal energy technologies. Renew. Sustain. Energy Rev. 2017, 72, 590–604. [Google Scholar] [CrossRef]
- Tian, B.; Yu, J. Current status and prospects of marine renewable energy applied in ocean robots. Int. J. Energy Res. 2019, 43, 2016–2031. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y.; Wang, S. Ocean thermal energy application technologies for unmanned underwater vehicles: A comprehensive review. Appl. Energy 2020, 278, 115752. [Google Scholar] [CrossRef]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Zhang, H.W.; Wang, Y.H.; Shu, H.C.; Wu, Y.Q.; Liu, D. Application and Improvement of the Interlayer Thermal Engine Powered by Ocean Thermal Energy in an Underwater Glider [C]. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–4. [Google Scholar]
- Chao, Y. Autonomous Underwater Vehicles and Sensors Powered by Ocean Thermal Energy; IEEE: Piscataway Township, NJ, USA, 2016. [Google Scholar]
- Haldeman, C.D.; Schofield, O.; Webb, D.C.; Valdez, T.I.; Jones, J.A. Implementation of Energy Harvesting System for Powering Thermal Gliders for Long Duration Ocean Research; IEEE: Piscataway Township, NJ, USA, 2015. [Google Scholar]
- Wang, G.; Yang, Y.; Wang, S.; Zhang, H.; Wang, Y. Efficiency analysis and experimental validation of the ocean thermal energy conversion with phase change material for underwater vehicle. Appl. Energy 2019, 248, 475–488. [Google Scholar] [CrossRef]
- Xia, Q.; Chen, Y.; Yang, C.; Zhang, T.; Zang, Y. A new model of phase change process for thermal energy storage. Int. J. Energy Res. 2018, 42, 3877–3887. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y.; Wang, S.; Yang, Y. Ocean thermal energy harvesting with phase change material for underwater glider. Appl. Energy 2016, 178, 557–566. [Google Scholar] [CrossRef]
- Wang, G.; Yang, Y.; Wang, S.; Zhang, H.; Wang, Y. Modification of the phase change transfer model for underwater vehicles: A molecular dynamics approach. Int. J. Energy Res. 2020, 44, 11323–11344. [Google Scholar] [CrossRef]
- Xia, Q.; Chen, Y.; Yang, C.; Chen, B.; Muhammad, G.; Ma, X. Maximum efficiency point tracking for an ocean thermal energy harvesting system. Int. J. Energy Res. 2020, 44, 2693–2703. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Ma, Z.; Wang, S. A thermal engine for underwater glider driven by ocean thermal energy. Appl. Therm. Eng. Des. Processes Equip. Econ. 2016, 99, 455–464. [Google Scholar] [CrossRef]
- Kim, H.S.; Shin, Y.K. Expanded adaptive fuzzy sliding mode controller using expert knowledge and fuzzy basis function expansion for UFV depth control. Ocean. Eng. 2007, 34, 1080–1088. [Google Scholar] [CrossRef]
- Park, J.Y.; Kim, N.; Yoon, H.K.; Cho, H. Adaptive depth controller design for a submerged body moving near free surface. Appl. Ocean. Res. 2016, 58, 83–94. [Google Scholar] [CrossRef]
- Makavita, C.D.; Jayasinghe, S.G.; Nguyen, H.D.; Ranmuthugala, D. Experimental Study of a Command Governor Adaptive Depth Controller for an Unmanned Underwater Vehicle. Appl. Ocean. Res. 2019, 86, 61–72. [Google Scholar] [CrossRef]
- Qiao, L.; Ruan, S.; Zhang, G.; Zhang, W. Robust H2 Optimal Depth Control of an Autonomous Underwater Vehicle with Output Disturbances and Time Delay. Ocean. Eng. 2018, 165, 399–409. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, K.; Xu, H.; Feng, X. Experimentally Verified Depth Control of an Unmanned Semi-submersible Vehicle. IEEE Access 2019, 7, 94254–94262. [Google Scholar] [CrossRef]
- Tiwari, B.K.; Sharma, R. Design and Analysis of a Variable Buoyancy System for Efficient Hovering Control of Underwater Vehicles with State Feedback Controller. J. Mar. Sci. Eng. 2020, 8, 263. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Wei, Z.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Adaptive robust sliding mode control of autonomous underwater glider with input constraints for persistent virtual mooring. Appl. Ocean. Res. 2020, 95, 102027. [Google Scholar] [CrossRef]
- Mu, W.; Zou, Z.; Liu, G.; Yang, Y.; Shi, L. Depth Control Method of Profiling Float Based on an Improved Double PD Controller. IEEE Access 2019, 7, 43258–43268. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, Q.; Li, H.; Yang, S.; Li, X. Depth Control for a Deep-Sea Self-Holding Intelligent Buoy Under Ocean Current Disturbances Based on Finite-Time Boundedness Method. IEEE Access 2019, 7, 114670–114684. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Choi, H.S.; Jin, H.S.; Han-Sol, J.; Huang, J.; Lee, J.H. Robust Adaptive Depth Control of Hybrid Underwater Glider in Vertical Plane. Adv. Technol. Innov. 2020, 5, 135–146. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Wang, Y.; Zhang, H.; Zhang, L. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and seawater density variation. Ocean. Eng. 2017, 143, 66–78. [Google Scholar] [CrossRef]
- Zhou, H.; Fu, J.; Liu, C.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Dynamic modeling and endurance enhancement analysis of deep-sea gliders with a hybrid buoyancy regulating system. Ocean. Eng. 2020, 217, 108146. [Google Scholar] [CrossRef]




| Parameter Name | Value/Introduction |
|---|---|
| Length | 2.6 m |
| Diameter | 0.4 m |
| Weight | 185 kg |
| Operating depth range | 200 m |
| Buoy-driven mode | Ocean thermal energy and electricity |
| Sensor | Pressure sensors, six-axis attitude sensors, thermometers, depth sensors, displacement sensors |
| Maximum buoyancy regulation force | 8 N |
| Functional | Autonomous profile movement, fixed deep suspension |
| Typical speed | 0.35 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Q.; Chen, B.; Sun, X.; Yang, C.; Zhang, S.; Chen, Y. Research on the Depth Control Strategy of an Underwater Profiler Driven by a Mixture of Ocean Thermal Energy and Electric Energy. J. Mar. Sci. Eng. 2022, 10, 640. https://doi.org/10.3390/jmse10050640
Xia Q, Chen B, Sun X, Yang C, Zhang S, Chen Y. Research on the Depth Control Strategy of an Underwater Profiler Driven by a Mixture of Ocean Thermal Energy and Electric Energy. Journal of Marine Science and Engineering. 2022; 10(5):640. https://doi.org/10.3390/jmse10050640
Chicago/Turabian StyleXia, Qingchao, Bingzhe Chen, Xiaotong Sun, Canjun Yang, Sheng Zhang, and Yanhu Chen. 2022. "Research on the Depth Control Strategy of an Underwater Profiler Driven by a Mixture of Ocean Thermal Energy and Electric Energy" Journal of Marine Science and Engineering 10, no. 5: 640. https://doi.org/10.3390/jmse10050640
APA StyleXia, Q., Chen, B., Sun, X., Yang, C., Zhang, S., & Chen, Y. (2022). Research on the Depth Control Strategy of an Underwater Profiler Driven by a Mixture of Ocean Thermal Energy and Electric Energy. Journal of Marine Science and Engineering, 10(5), 640. https://doi.org/10.3390/jmse10050640







