Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties in the Vertical Plane
Abstract
:1. Introduction
- (1)
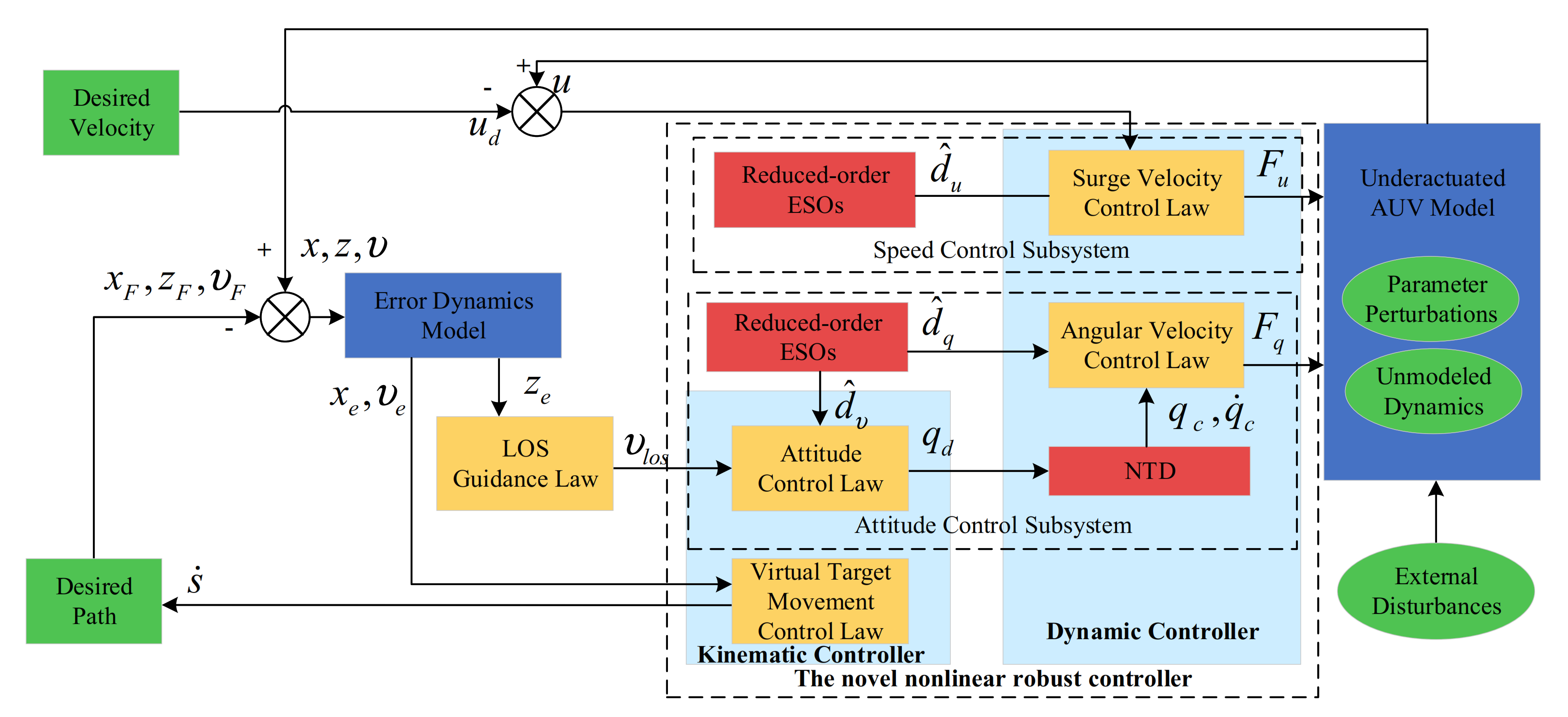
- To relax the requirement of having an accurate estimation of the model parameters, and reduce dependence on the precise mathematical model, the unknown time-varying attack angular velocity in the dynamic model of the path-following error is treated as kinematic uncertainty, while the linear superposition of the external environment disturbances, the perturbations in the internal model parameters, and other unmodeled dynamics in the dynamic model is treated as the lumped dynamic uncertainties. Four reduced-order ESOs are introduced for an accurate estimation of the kinematic and dynamic uncertainties. Compared with previous studies [36,37], which are based on the assumption that the attack angle was neglected or regarded as constant, the unknown time-varying attack angle is considered in this paper, which is suitable for a challenging marine environment.
- (2)
- To eliminate the effect of input saturation and handle the “explosion of complexity” associated with a traditional backstepping method, an NTD is utilized to track the virtual control signal and its derivative. Compared with the traditional dynamic surface control method presented in [18,38], the NTD is a time-optimal solution that provides the fastest tracking of the input signal [29].
- (3)
- Based on the constructed reduced-order ESOs and NTD, an augmented back-stepping controller is constructed to enhance the robustness against the external environment disturbances, the perturbations in the internal model parameters, and other unmodeled dynamics. Compared with the previous study [39] on vertical path-following control of underactuated AUVs, the proposed controller is simplified and is more suitable for underactuated AUVs cruising in complex marine environment. Then, the nominal working condition without disturbances, the working condition with multiple uncertainties, and the conditions which better replicate the actual environment are introduced to further evaluate the effectiveness, superiority, and robustness of the mentioned controller.
2. Underactuated AUV Model and Problem Formulation
2.1. The Underactuated AUV Model
2.2. Path-Following Error Dynamics
2.3. Problem Formulation
3. Path-Following Controller Design
3.1. Design of Reduced-Order ESOs
3.2. The LOS Guidance Law Design
3.3. The Kinematic Controller Design
3.3.1. The Virtual Target Movement Control Law Design
3.3.2. Attitude Control Law Design
3.4. Dynamic Controller Design
3.4.1. Angular Velocity Control Law Design
3.4.2. Surge Velocity Control Law Design
4. Stability Analysis of the Closed-Loop System
- (1)
- The tracking errors, , andultimately converge to an arbitrarily narrow bound around zero.
- (2)
- The heave velocity which is not controlled directly is uniformly ultimate bounded.
5. Numerical Simulation and Comparative Analysis
5.1. Comparative Analysis of the Path-Following Performance in the Nominal Working Condition without Disturbances
| Initial conditions of the underactuated AUV | |
| Controller parameters |
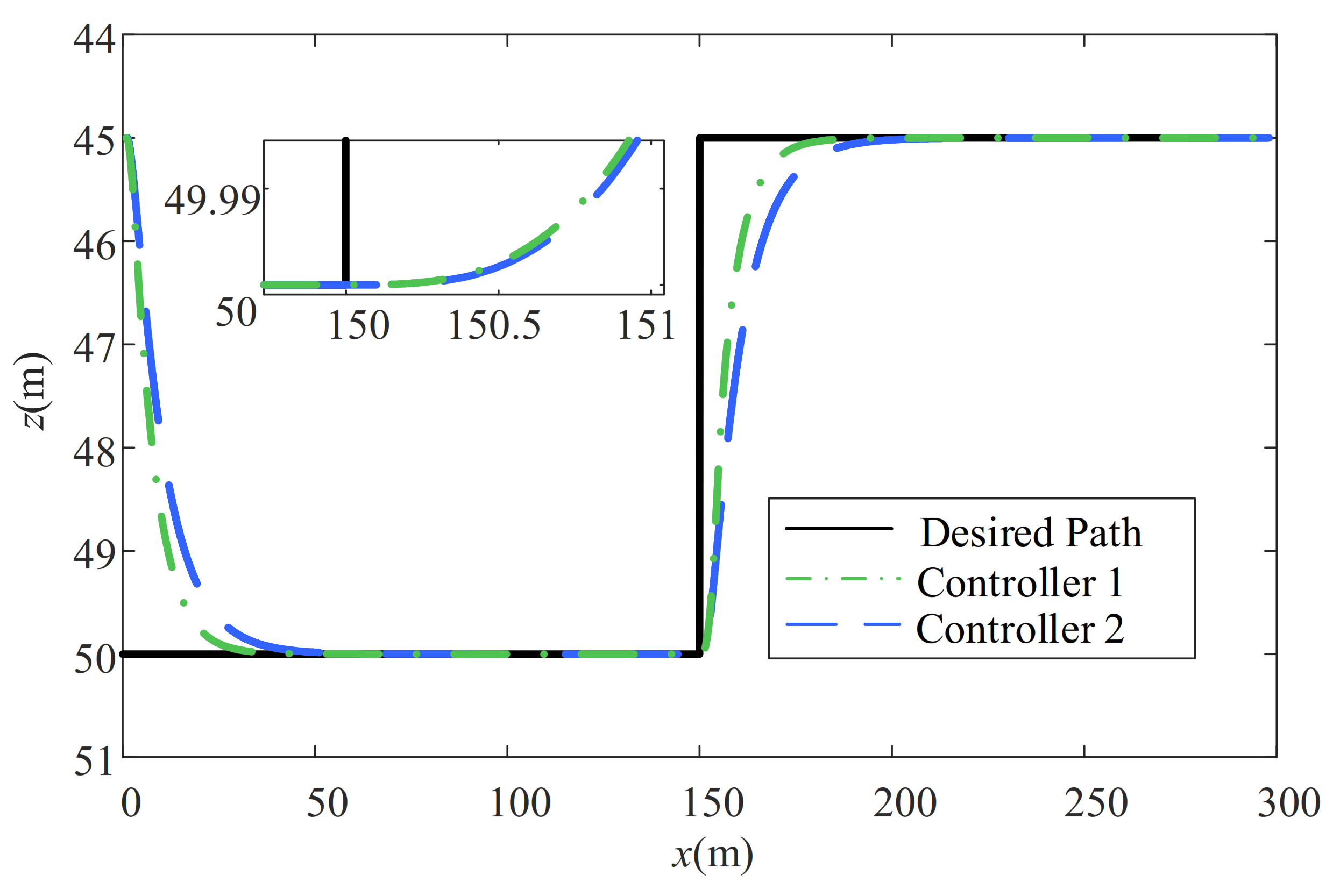
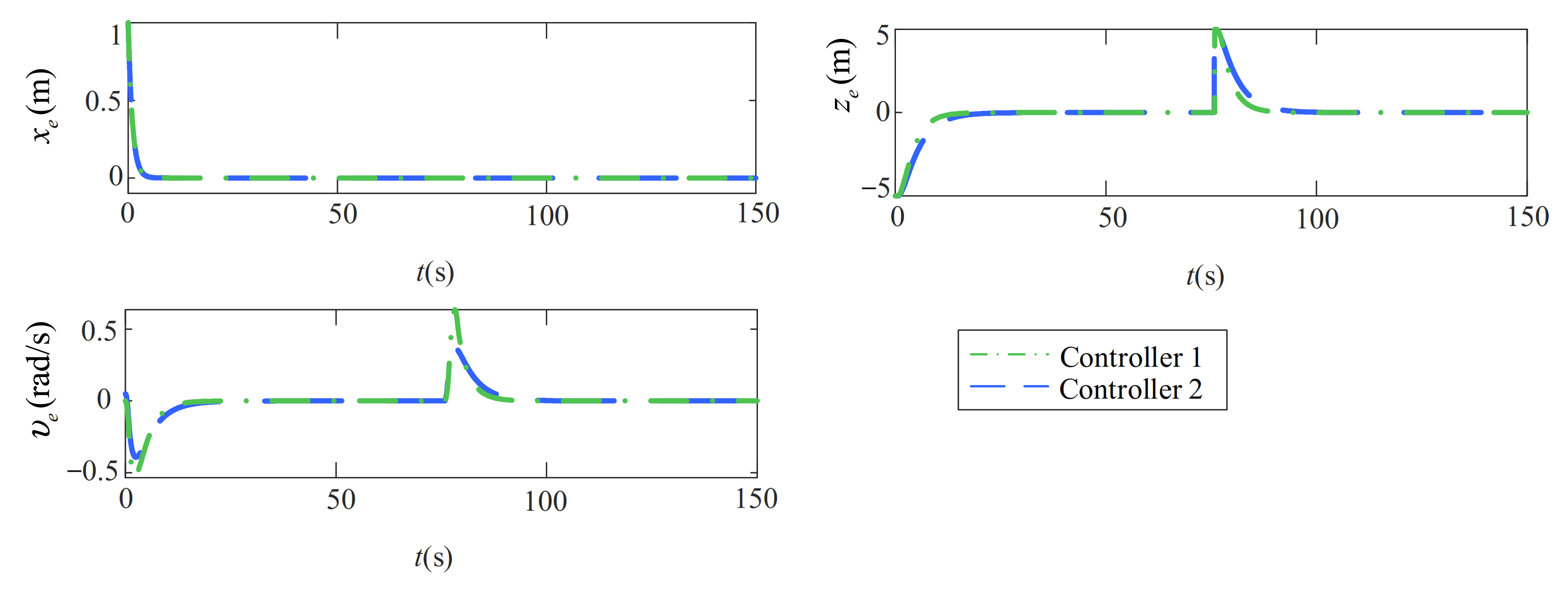
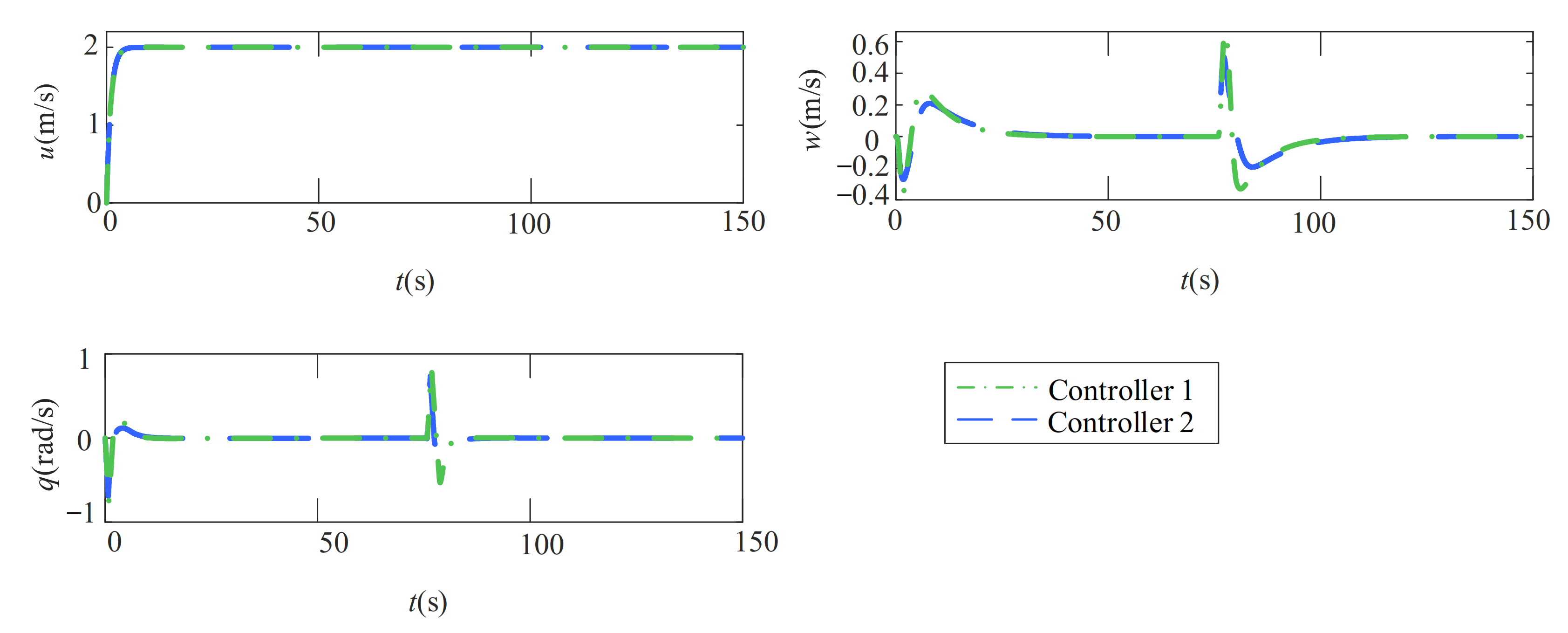
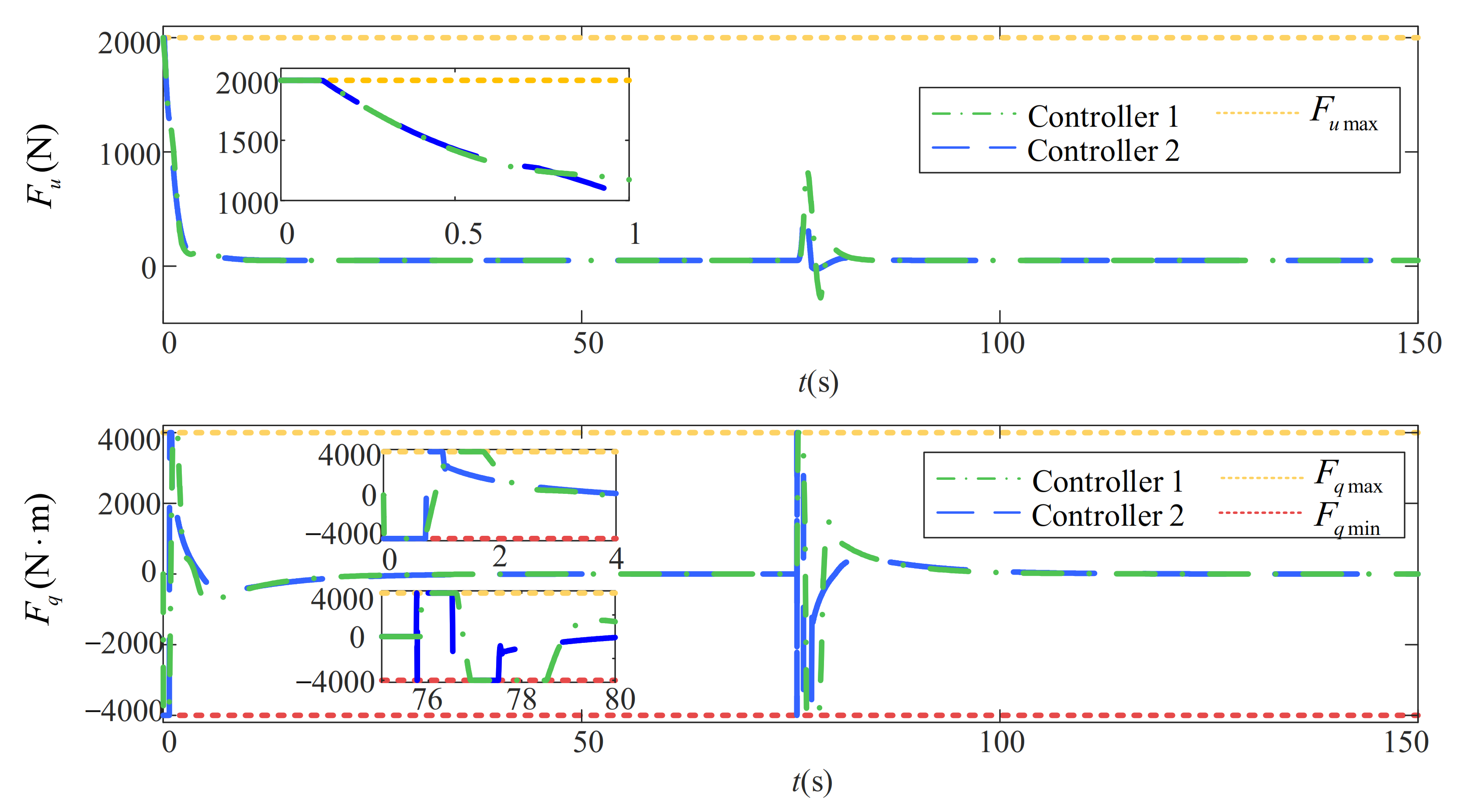

5.2. Comparative Analysis of the Path-Following Performance under Multiple Uncertainties
| Initial position and posture of the underactuated AUV | |
| Controller parameters |


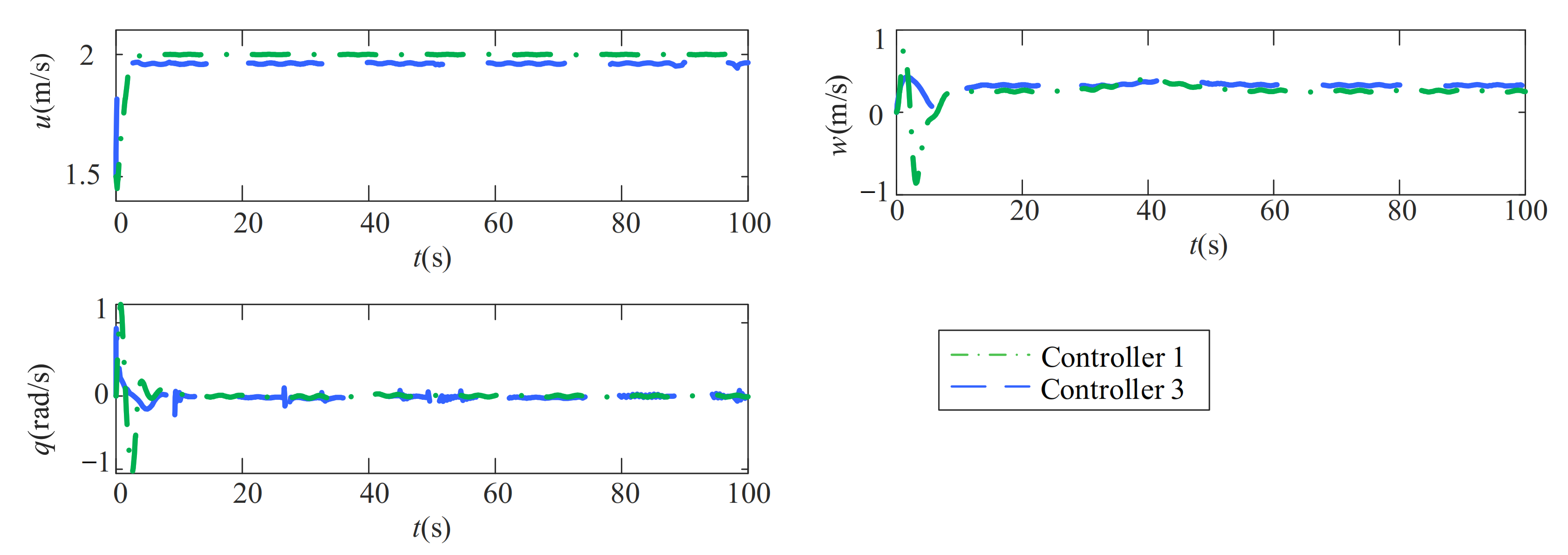
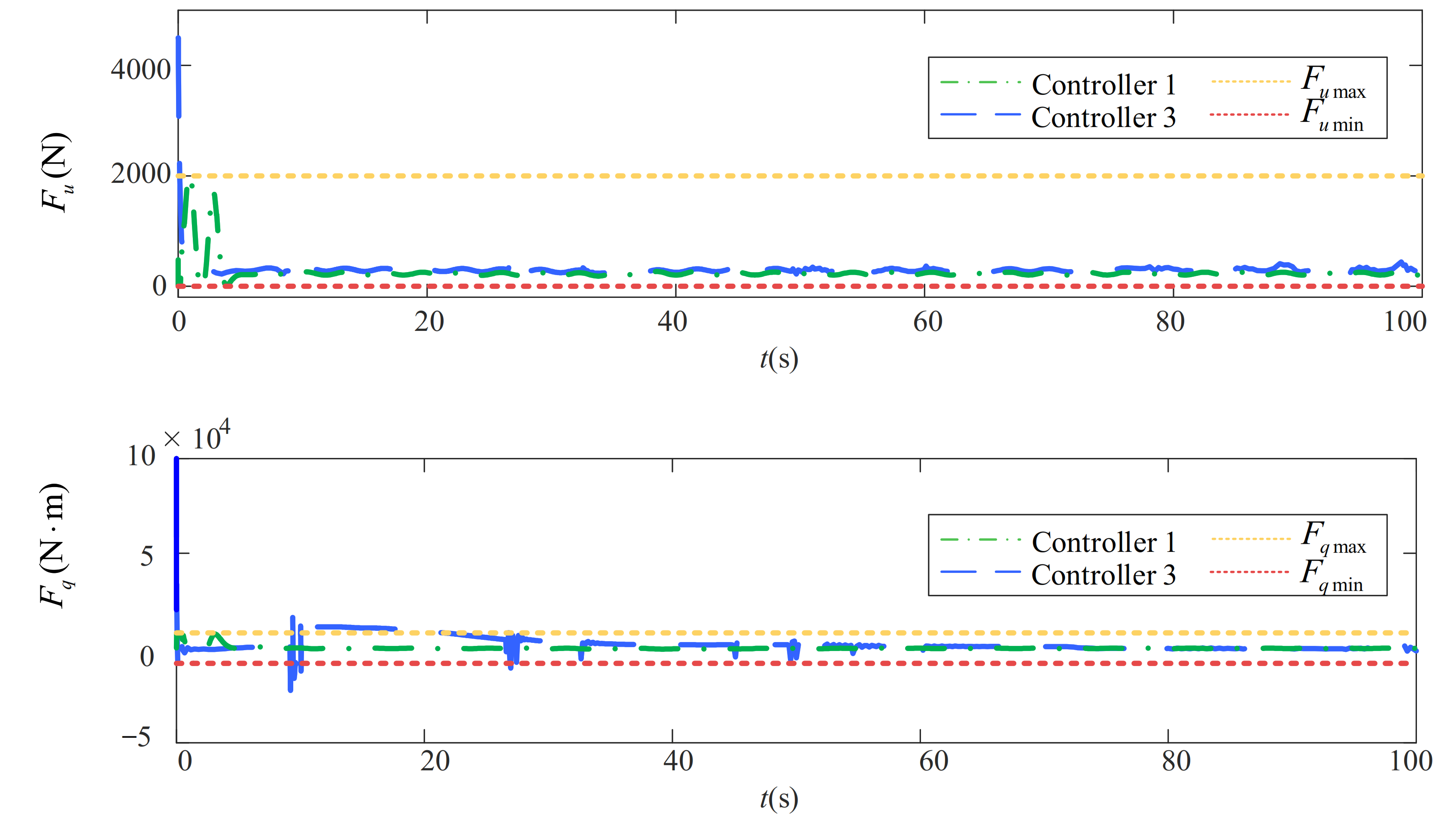
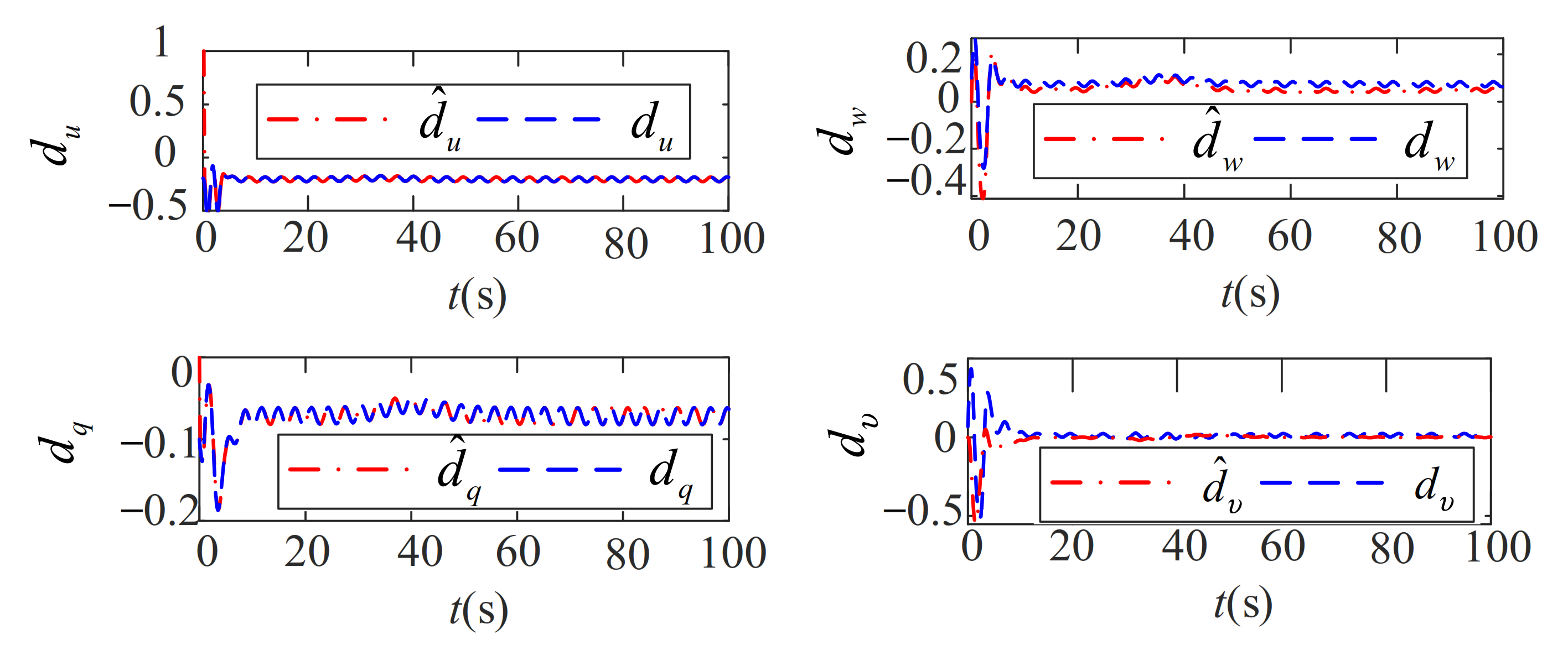
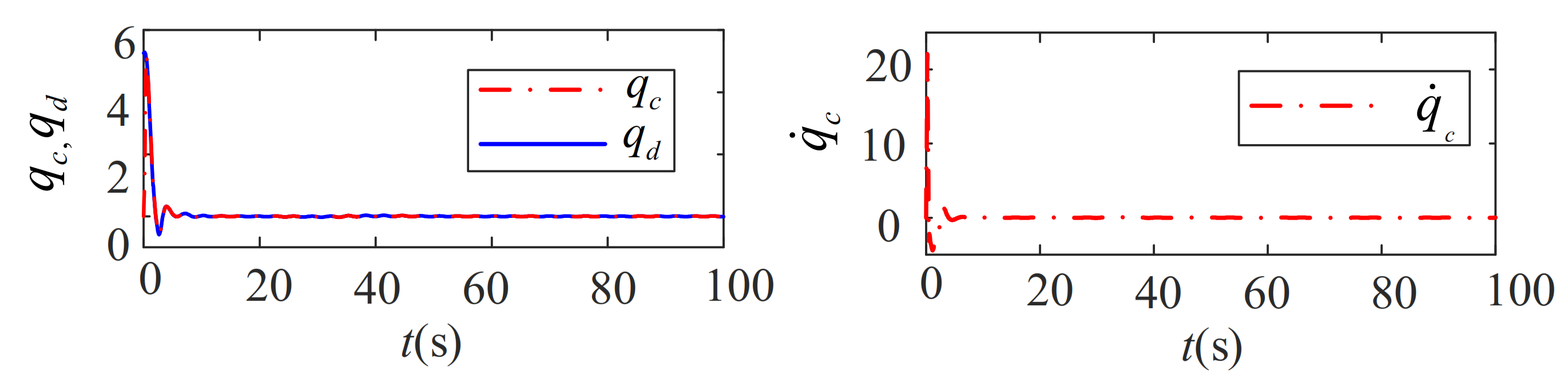
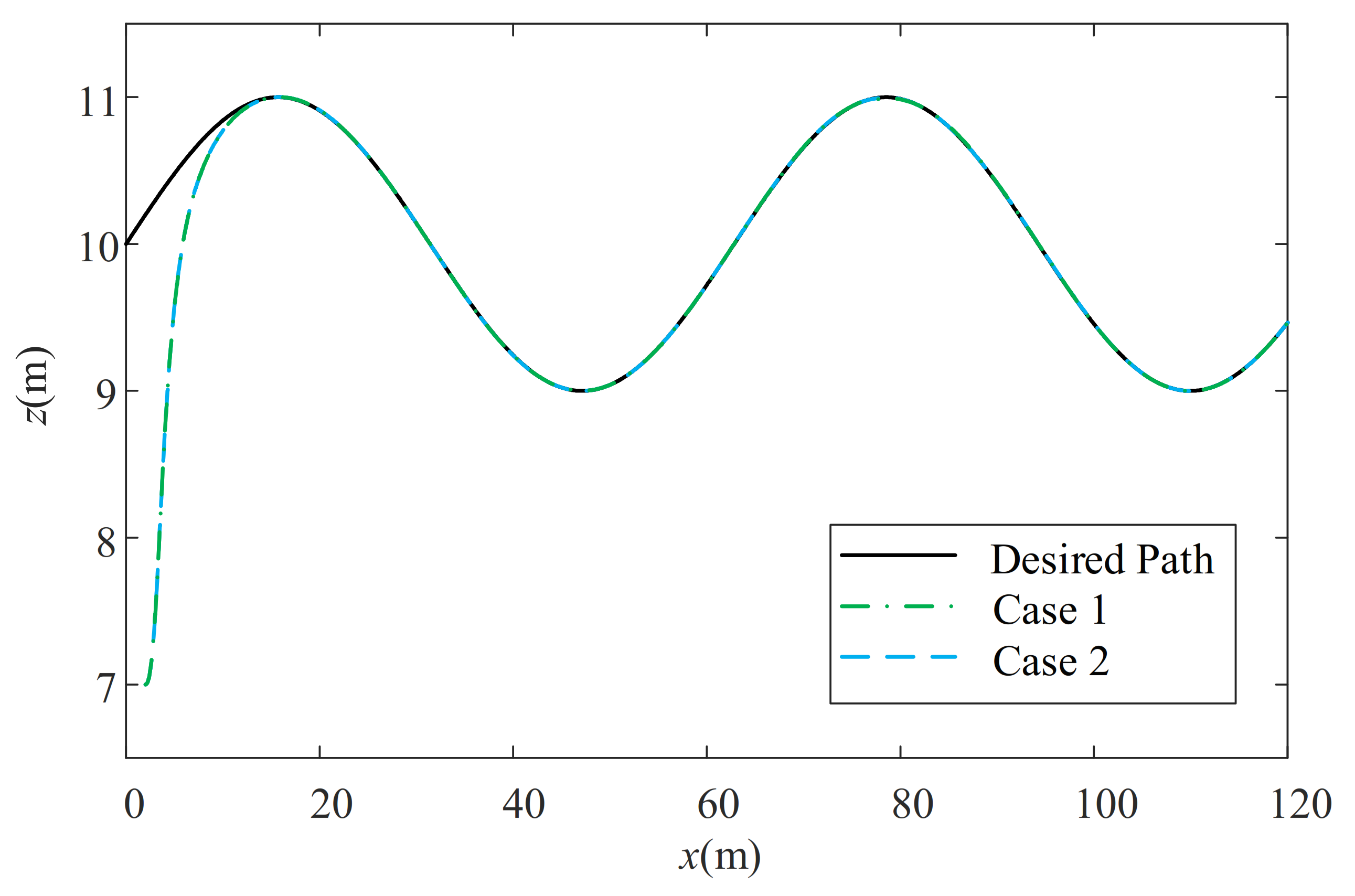
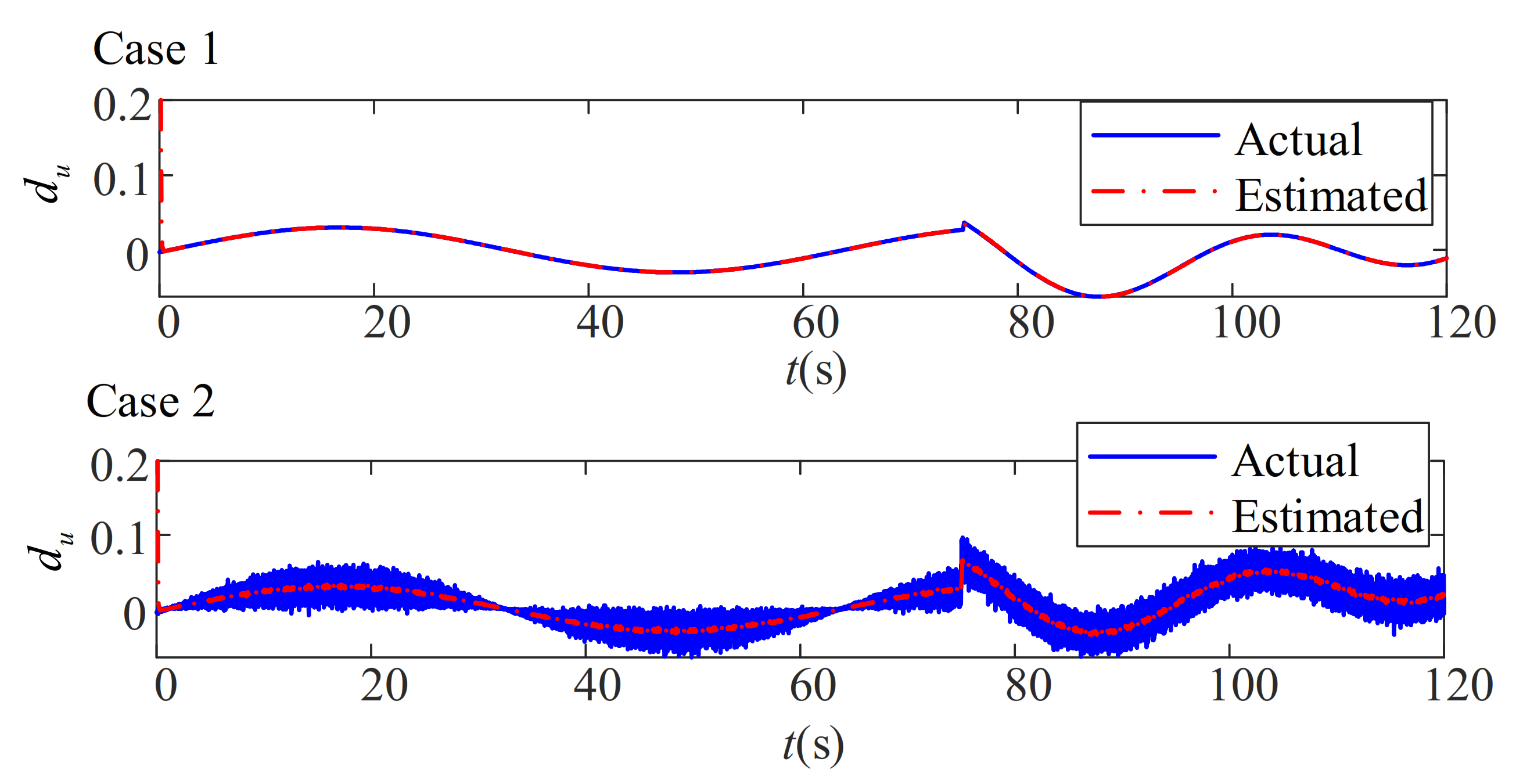
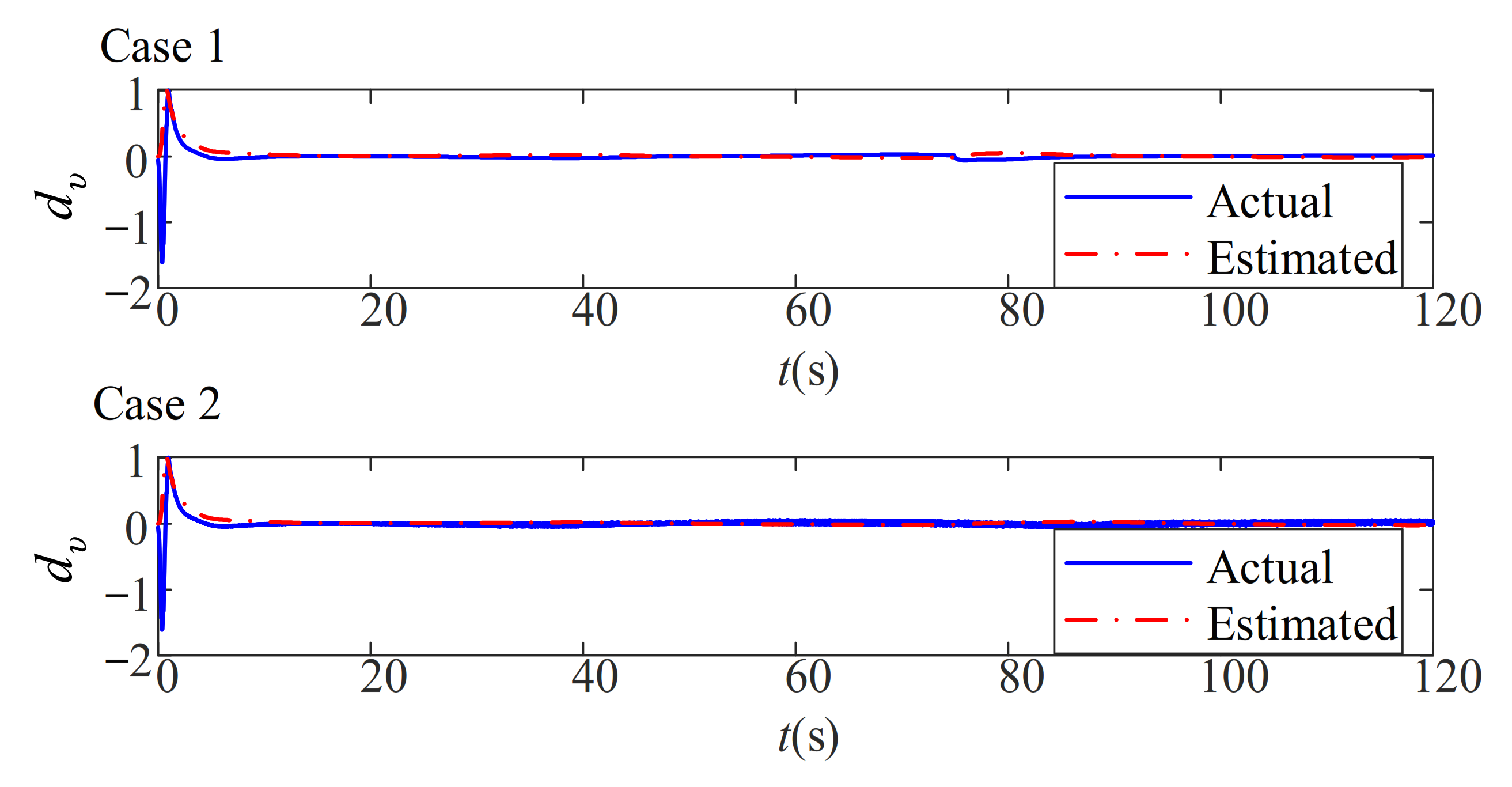
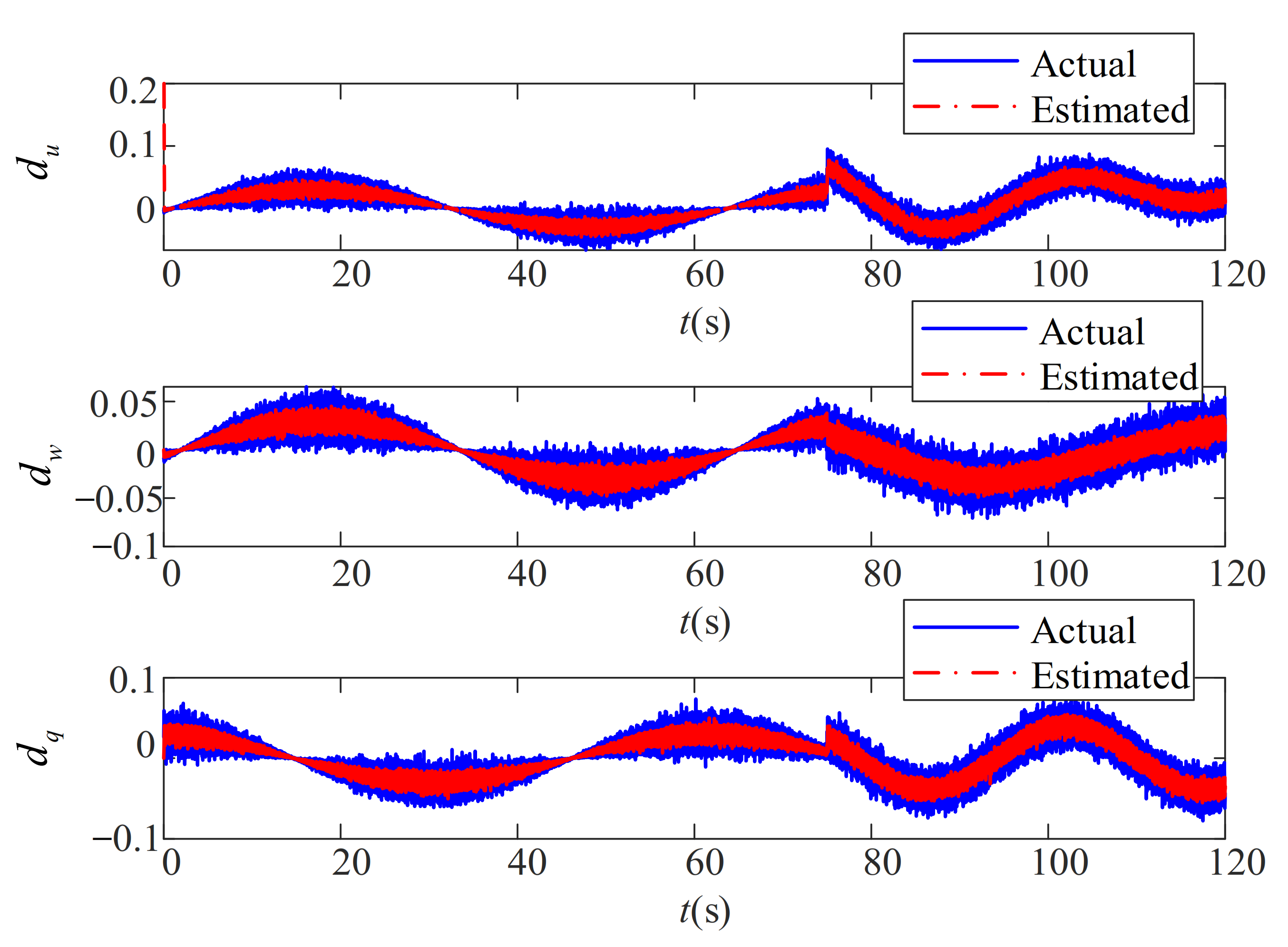
5.3. Robustness Analysis for the Path-Following Performance in the Conditions Which Better Replicate the Actual Environment
- Case 1:
- Case 2:
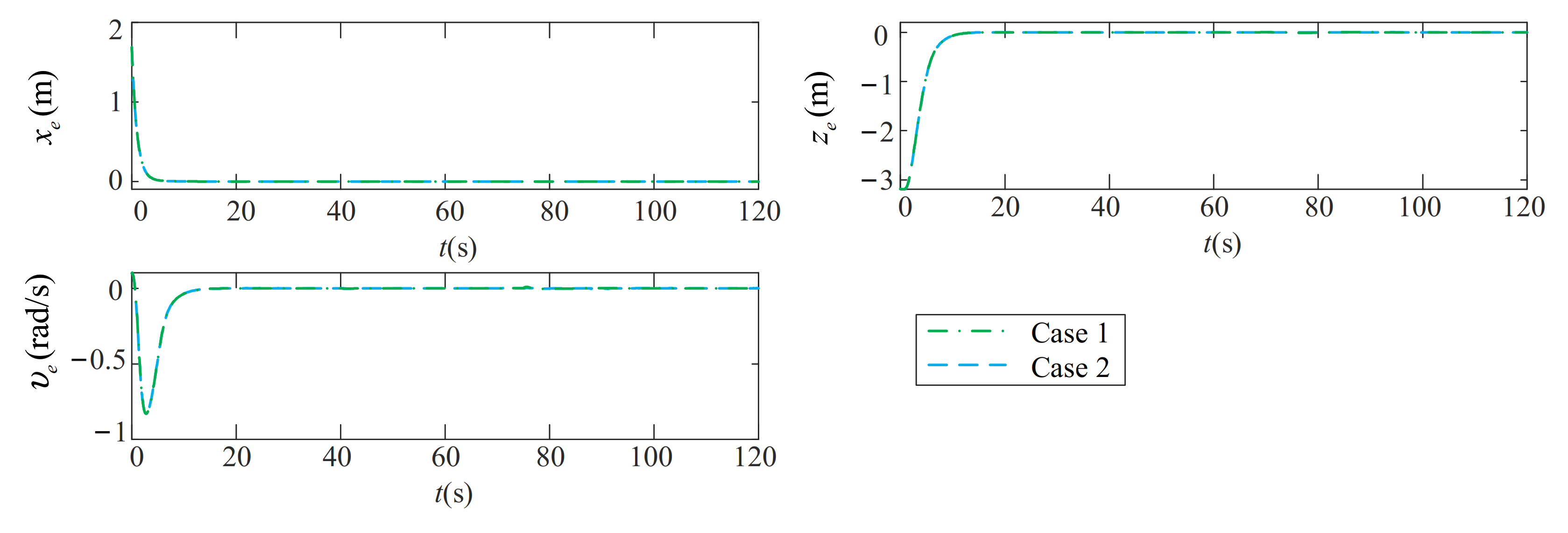
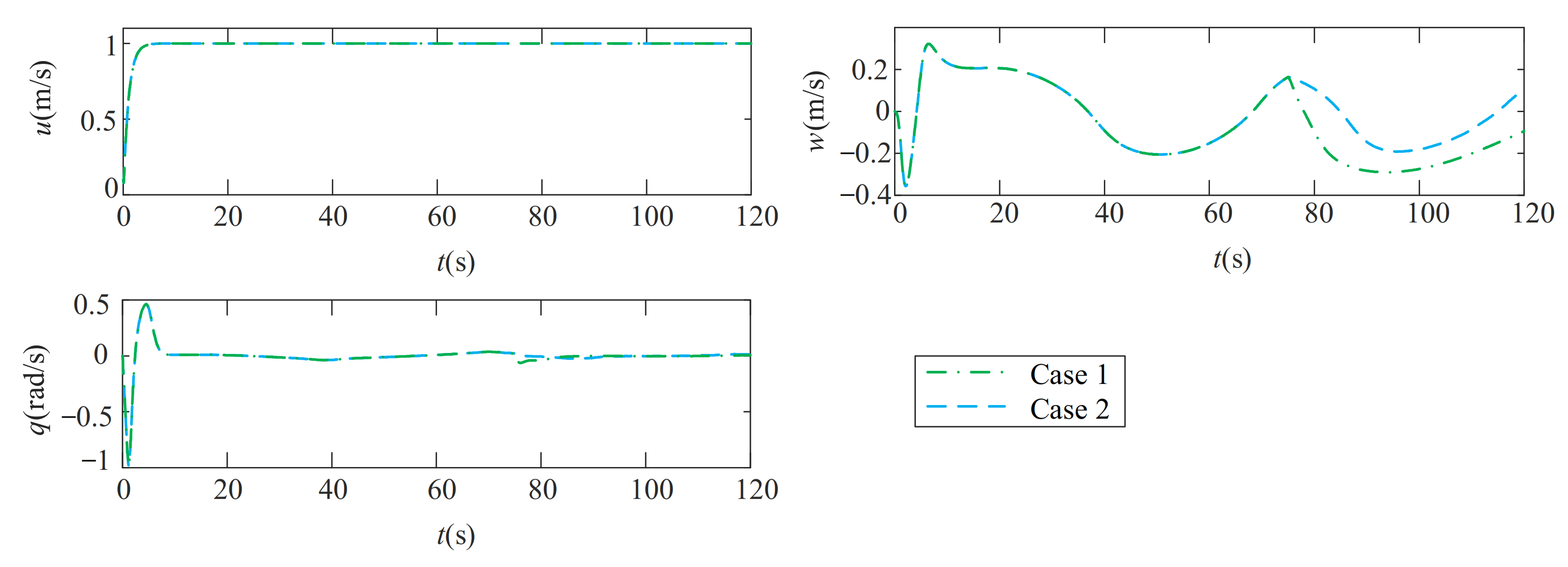
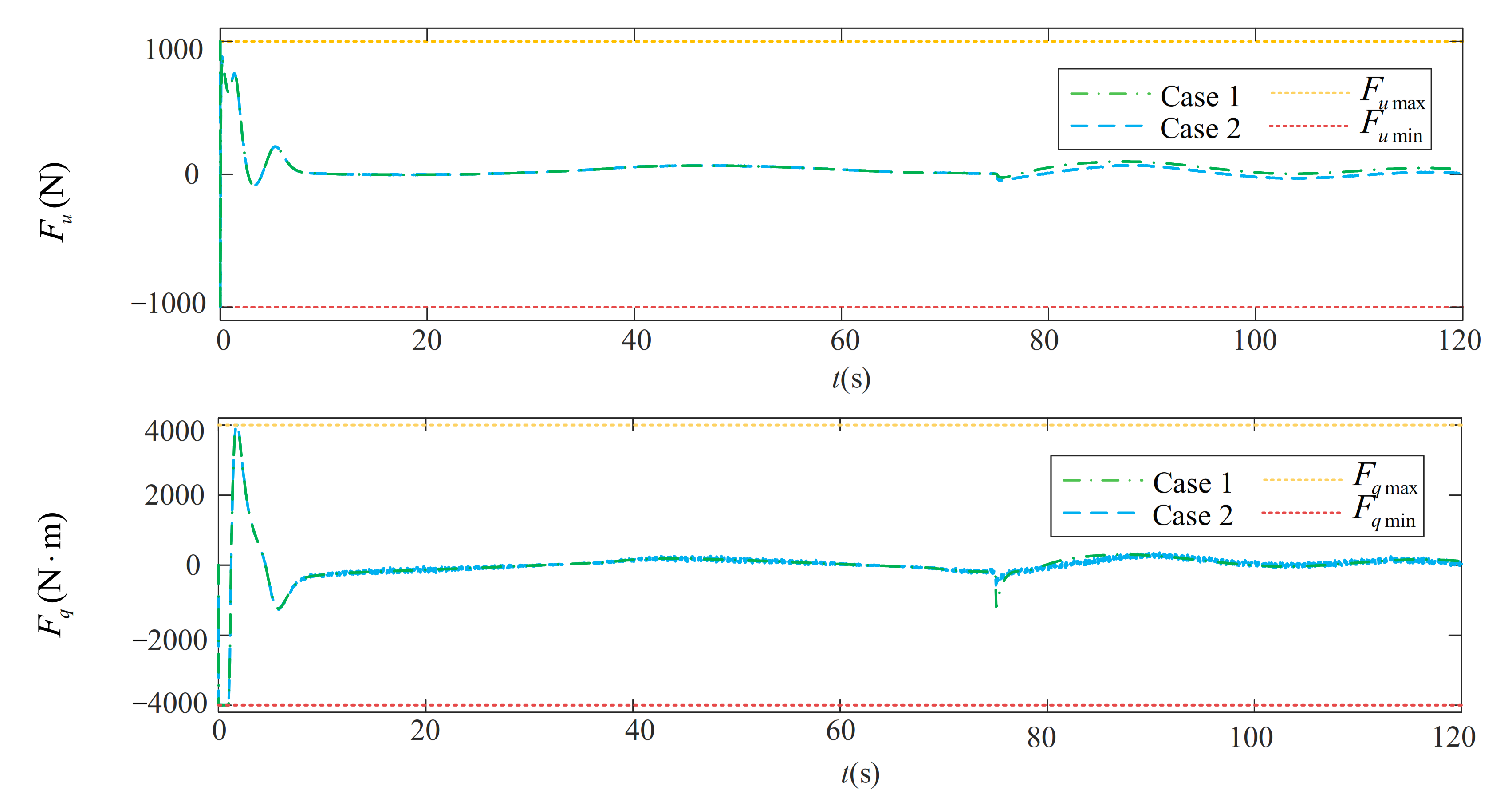


6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiang, X.; Yu, C.; Zhang, Q. Robust fuzzy 3D path following for autonomous underwater vehicle subject to uncertainties. Comput. Oper. Res. 2017, 84, 165–177. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Wang, J. Constrained control of autonomous underwater vehicles based on command optimization and disturbance estimation. IEEE Trans. Ind. Electron. 2018, 66, 3627–3635. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.; Liu, K. Globally stable adaptive dynamic surface control for cooperative path following of multiple underactuated autonomous underwater vehicles. Asian J. Control 2018, 20, 1204–1220. [Google Scholar] [CrossRef]
- Duan, K.; Fong, S.; Chen, C.P. Multilayer neural networks-based control of underwater vehicles with uncertain dynamics and disturbances. Nonlinear Dyn. 2020, 100, 3555–3573. [Google Scholar] [CrossRef]
- Fan, S.; Chan, K.; Chin, C. Motion Analysis of an Autonomous Underwater Vehicle Tethered with an Optical Fiber for Real-Time Surveillance. IEEE J. Ocean. Eng. 2020, 46, 434–446. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X.; Lapierre, L.; Zhang, Q. Nonlinear guidance and fuzzy control for three-dimensional path following of an underactuated autonomous underwater vehicle. Ocean Eng. 2017, 146, 457–467. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Shi, Y.; Buckham, B. Path-following control of an AUV: A multiobjective model predictive control approach. IEEE Trans. Control Syst. Technol. 2018, 27, 1334–1342. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zheng, Z.; Sun, L.; Xie, L. Error-constrained LOS path following of a surface vessel with actuator saturation and faults. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1794–1805. [Google Scholar] [CrossRef]
- Wichlund, K.; Sordalen, O.; Egeland, O. Control properties of underactuated vehicles. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 2009–2014. [Google Scholar]
- Xiang, X.; Yu, C.; Zhang, Q.; Xu, G. Path-following control of an auv: Fully actuated versus under-actuated configuration. Mar. Technol. Soc. J. 2016, 50, 34–47. [Google Scholar] [CrossRef]
- He, S.; Dai, S.-L.; Luo, F. Asymptotic trajectory tracking control with guaranteed transient behavior for MSV with uncertain dynamics and external disturbances. IEEE Trans. Ind. Electron. 2018, 66, 3712–3720. [Google Scholar] [CrossRef]
- Cho, G.R.; Li, J.H.; Park, D.; Jung, J.H. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation. Ocean Eng. 2020, 201, 107131. [Google Scholar] [CrossRef]
- Xia, G.; Xia, X.; Sun, X. Formation control with collision avoidance for underactuated surface vehicles. Asian J. Control 2021. [Google Scholar] [CrossRef]
- Yan, S. Sliding mode tracking control of autonomous underwater vehicles with the effect of quantization. Ocean Eng. 2018, 151, 322–328. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, M.; Xu, J. Robust adaptive sliding mode control of underactuated autonomous underwater vehicles with uncertain dynamics. Ocean Eng. 2019, 173, 802–809. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X.; Zuo, M.; Xu, G. Robust variable-depth path following of an under-actuated autonomous underwater vehicle with uncertainties. Ind. J. Geo-Mar. Sci. 2017, 46, 2543–2551. [Google Scholar]
- Seok Park, B. Neural network-based tracking control of underactuated autonomous underwater vehicles with model uncertainties. J. Dyn. Syst. Meas. Control 2015, 137, 184–204. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, M.; Xu, J. Global adaptive neural network control of underactuated autonomous underwater vehicles with parametric modeling uncertainty. Asian J. Control 2019, 21, 1342–1354. [Google Scholar] [CrossRef]
- Liang, X.; Qu, X.; Hou, Y.; Li, Y.; Zhang, R. Finite-time unknown observer based coordinated path-following control of unmanned underwater vehicles. J. Frankl. Inst. 2021, 358, 2703–2721. [Google Scholar] [CrossRef]
- Kim, E.; Fan, S.; Bose, N.; Nguyen, H. Current Estimation and Path Following for an Autonomous Underwater Vehicle (AUV) by Using a High-gain Observer Based on an AUV Dynamic Model. Int. J. Control Autom. Syst. 2020, 19, 478–490. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Luo, M.; Yang, C. MPC-based 3-D trajectory tracking for an autonomous underwater vehicle with constraints in complex ocean environments. Ocean Eng. 2019, 189, 106309. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castañeda, H. Guidance and Control Based on Adaptive Sliding Mode Strategy for a USV Subject to Uncertainties. IEEE J. Ocean. Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Lapierre, L.; Zhang, Q.; Li, W. Approach-angle-based three-dimensional indirect adaptive fuzzy path following of under-actuated AUV with input saturation. Appl. Ocean Res. 2021, 107, 102486. [Google Scholar] [CrossRef]
- Aguiar, A.P.; Hespanha, J.P. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty. IEEE Trans. Autom. Control 2007, 52, 1362–1379. [Google Scholar] [CrossRef] [Green Version]
- Lapierre, L.; Jouvencel, B. Robust nonlinear path-following control of an AUV. IEEE J. Ocean. Eng. 2008, 33, 89–102. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J.; Jiang, Z.-P. Robust and adaptive path following for underactuated autonomous underwater vehicles. Ocean Eng. 2004, 31, 1967–1997. [Google Scholar] [CrossRef]
- Liao, Y.-l.; Wan, L.; Zhuang, J.-Y. Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel. Procedia Eng. 2011, 15, 256–263. [Google Scholar] [CrossRef] [Green Version]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Dan, W.; Peng, Z. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles with Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, J.; Han, Q.-L. Path-following control of autonomous underwater vehicles subject to velocity and input constraints via neurodynamic optimization. IEEE Trans. Ind. Electron. 2018, 66, 8724–8732. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, S.; Miao, J. DO-LPV-based robust 3D path following control of underactuated autonomous underwater vehicle with multiple uncertainties. ISA Trans. 2020, 101, 189–203. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, G.C.; Cao, J.; Pang, S.; Sun, Y.S. Underactuated AUV Nonlinear Finite-Time Tracking Control Based on Command Filter and Disturbance Observer. Sensors 2019, 19, 4987. [Google Scholar] [CrossRef] [Green Version]
- Subudhi, B.; Mukherjee, K.; Ghosh, S. A static output feedback control design for path following of autonomous underwater vehicle in vertical plane. Ocean Eng. 2013, 63, 72–76. [Google Scholar] [CrossRef]
- Mahapata, S.; Subudhi, B. Design of a steering control law for an autonomous underwater vehicle using nonlinear H∞ state feedback technique. Nonlinear Dyn. 2017, 90, 837–854. [Google Scholar] [CrossRef]
- Guo, C.; Han, Y.; Yu, H.; Qin, J. Spatial path-following control of underactuated auv with multiple uncertainties and input saturation. IEEE Access 2019, 7, 98014–98022. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X. Vertical plane path following control of an under-actuated autonomous underwater vehicle. In Proceedings of the 2016 IEEE International Conference on Underwater System Technology: Theory and Applications (USYS), Penang, Malaysia, 13–14 December 2016. [Google Scholar]
- Miao, J.; Wang, S.; Zhao, Z.; Li, Y.; Tomovic, M.M. Spatial curvilinear path following control of underactuated AUV with multiple uncertainties. ISA Trans. 2017, 67, 107–130. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Wang, W.; Xu, G.; Xiang, X.; Li, Y. Optimal robust trajectory tracking control of a X-rudder AUV with velocity sensor failures and uncertainties. Ocean Eng. 2020, 198, 106949. [Google Scholar] [CrossRef]
- Xingling, S.; Honglun, W. Back-stepping active disturbance rejection control design for integrated missile guidance and control system via reduced-order ESO. ISA Trans. 2015, 57, 10–22. [Google Scholar] [CrossRef]
- Shao, X.; Wang, H. Active disturbance rejection based trajectory linearization control for hypersonic reentry vehicle with bounded uncertainties. ISA Trans. 2015, 54, 27–38. [Google Scholar] [CrossRef]
- Lapierre, L.; Soetanto, D. Nonlinear path-following control of an AUV. Ocean Eng. 2007, 34, 1734–1744. [Google Scholar] [CrossRef]
- Arnold, V. Mathematical Method of Classic Mechanics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3. [Google Scholar]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles: Design for Underactuated and Nonlinear Marine Systems; Springer Science & Business Media: Boston, MA, USA, 2009. [Google Scholar]
- McEwen, R.; Streitlien, K. Modeling and control of a variable-length auv. In Proceedings of the 12th International Symposium on Unmanned Untethered Submersible Technology, Durham, NH, USA, 27 August 2001. [Google Scholar]
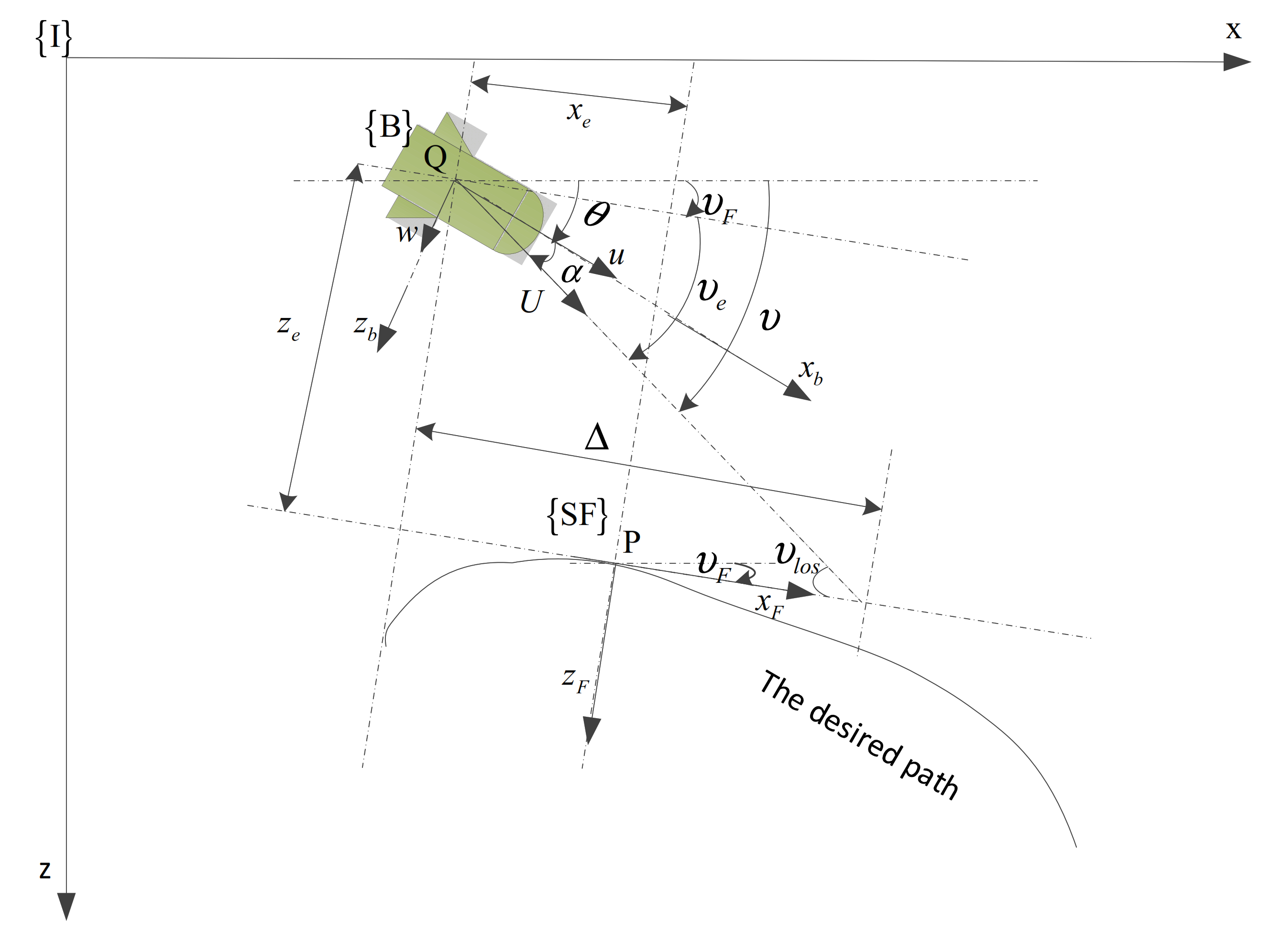
| Earth-fixed frame | |
| Body-fixed frame | |
| Serret-Frenet frame | |
| Inertial position and orientation vectors of AUV | |
| Body-fixed velocity vector | |
| Path following error vector | |
| Position and elevation angle vector of virtual target P | |
| Attack angle of AUV | |
| Course angle of AUV | |
| Total speed of AUV | |
| Look-ahead distance | |
| Line-of-sight (LOS) angle |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, J.; Deng, K.; Zhang, W.; Gong, X.; Lyu, J.; Ren, L. Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties in the Vertical Plane. J. Mar. Sci. Eng. 2022, 10, 238. https://doi.org/10.3390/jmse10020238
Miao J, Deng K, Zhang W, Gong X, Lyu J, Ren L. Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties in the Vertical Plane. Journal of Marine Science and Engineering. 2022; 10(2):238. https://doi.org/10.3390/jmse10020238
Chicago/Turabian StyleMiao, Jianming, Kankan Deng, Wenrui Zhang, Xi Gong, Jifang Lyu, and Lei Ren. 2022. "Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties in the Vertical Plane" Journal of Marine Science and Engineering 10, no. 2: 238. https://doi.org/10.3390/jmse10020238
APA StyleMiao, J., Deng, K., Zhang, W., Gong, X., Lyu, J., & Ren, L. (2022). Robust Path-Following Control of Underactuated AUVs with Multiple Uncertainties in the Vertical Plane. Journal of Marine Science and Engineering, 10(2), 238. https://doi.org/10.3390/jmse10020238





