Digital Filter Design for Force Signals from Eulerian–Lagrangian Analyses of Wave Impact on Bridges
Abstract
1. Introduction
2. Numerical Model
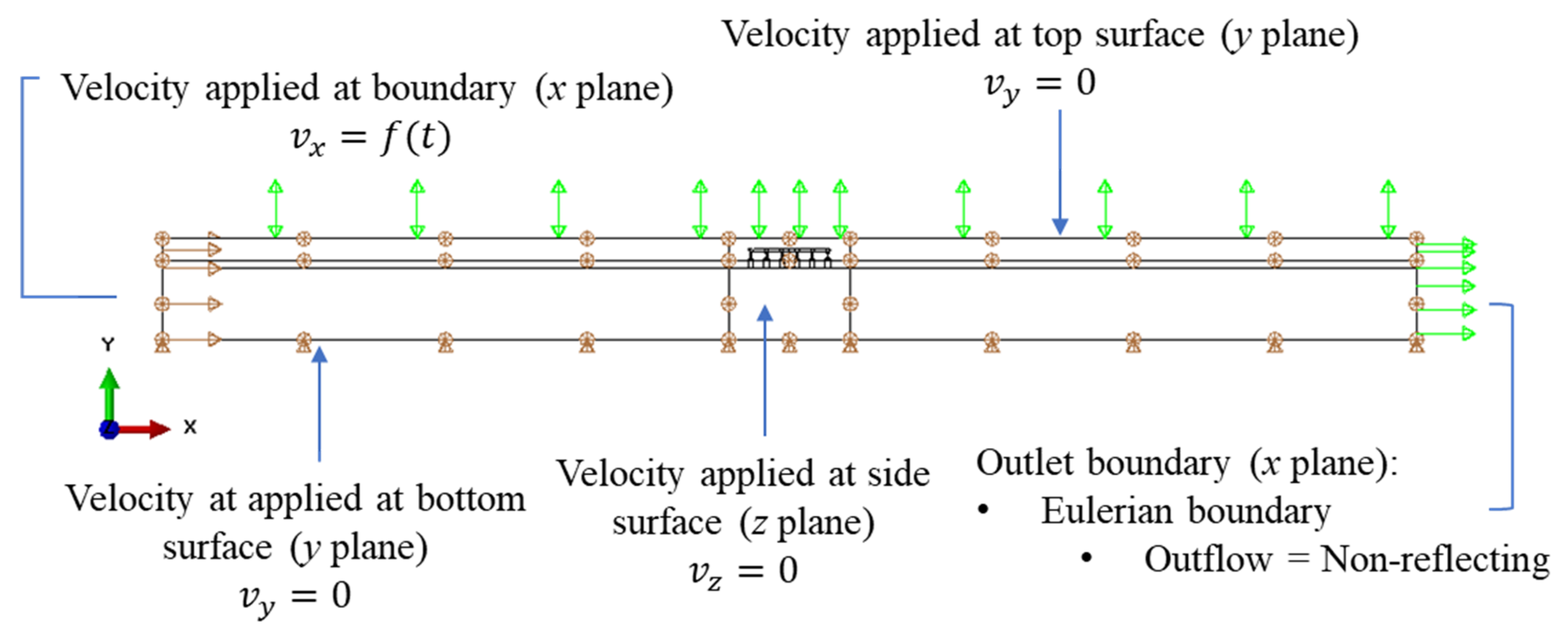
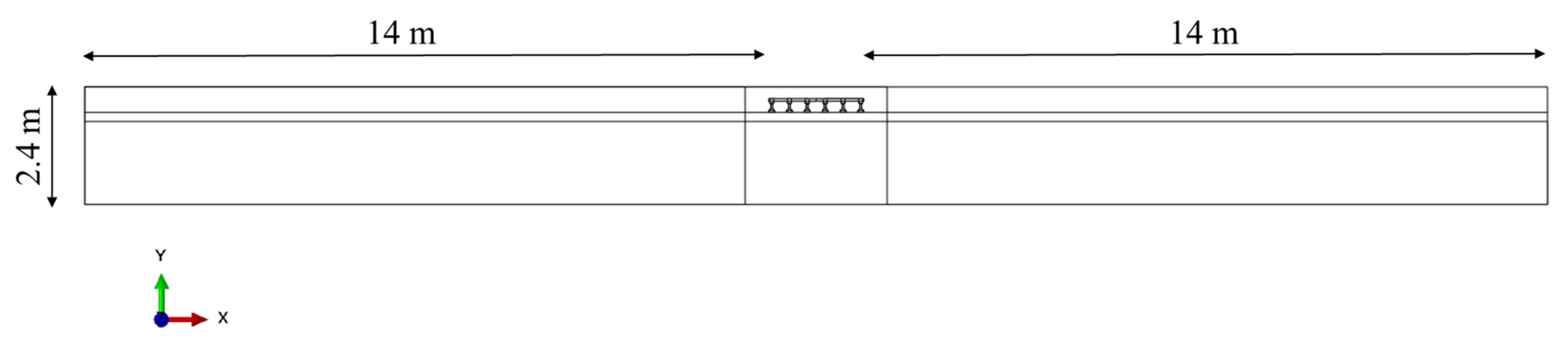
2.1. Wave Flume
2.2. Surface Contact Interaction Definition
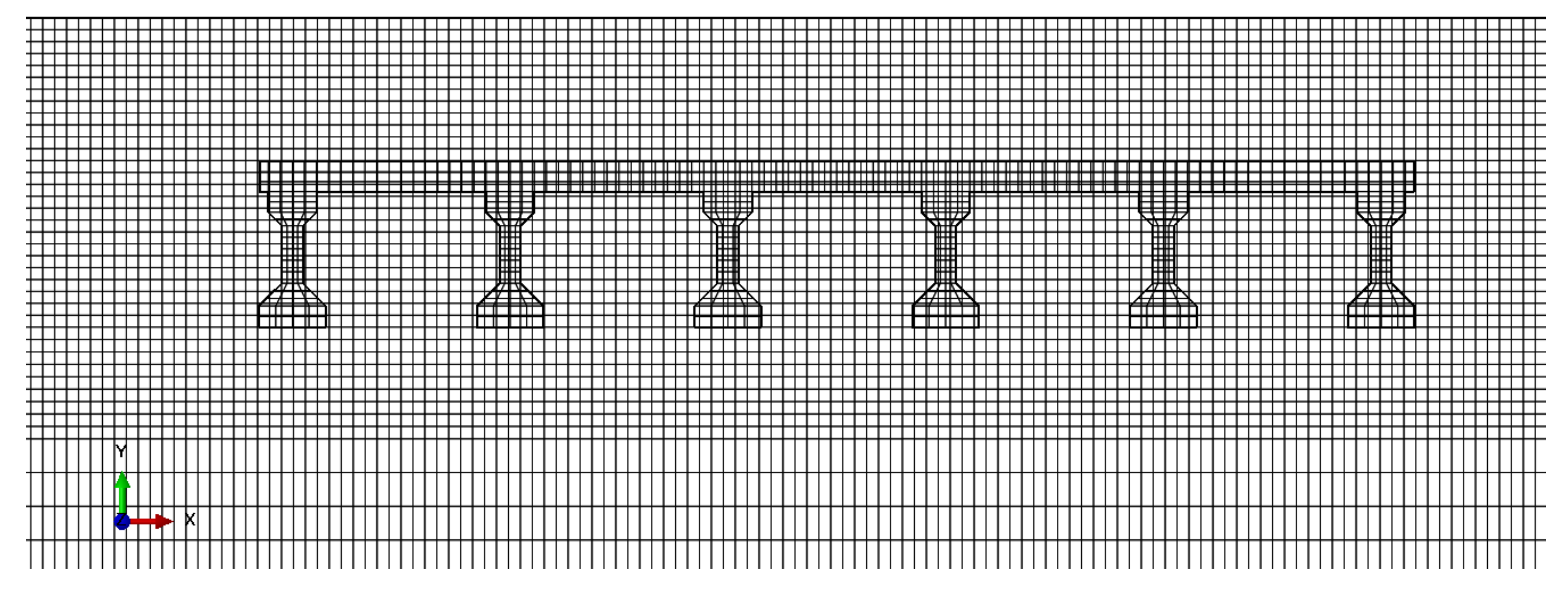
2.3. Meshing
2.4. Hourglass Control Parameters in Eulerian and Lagrangian Mesh
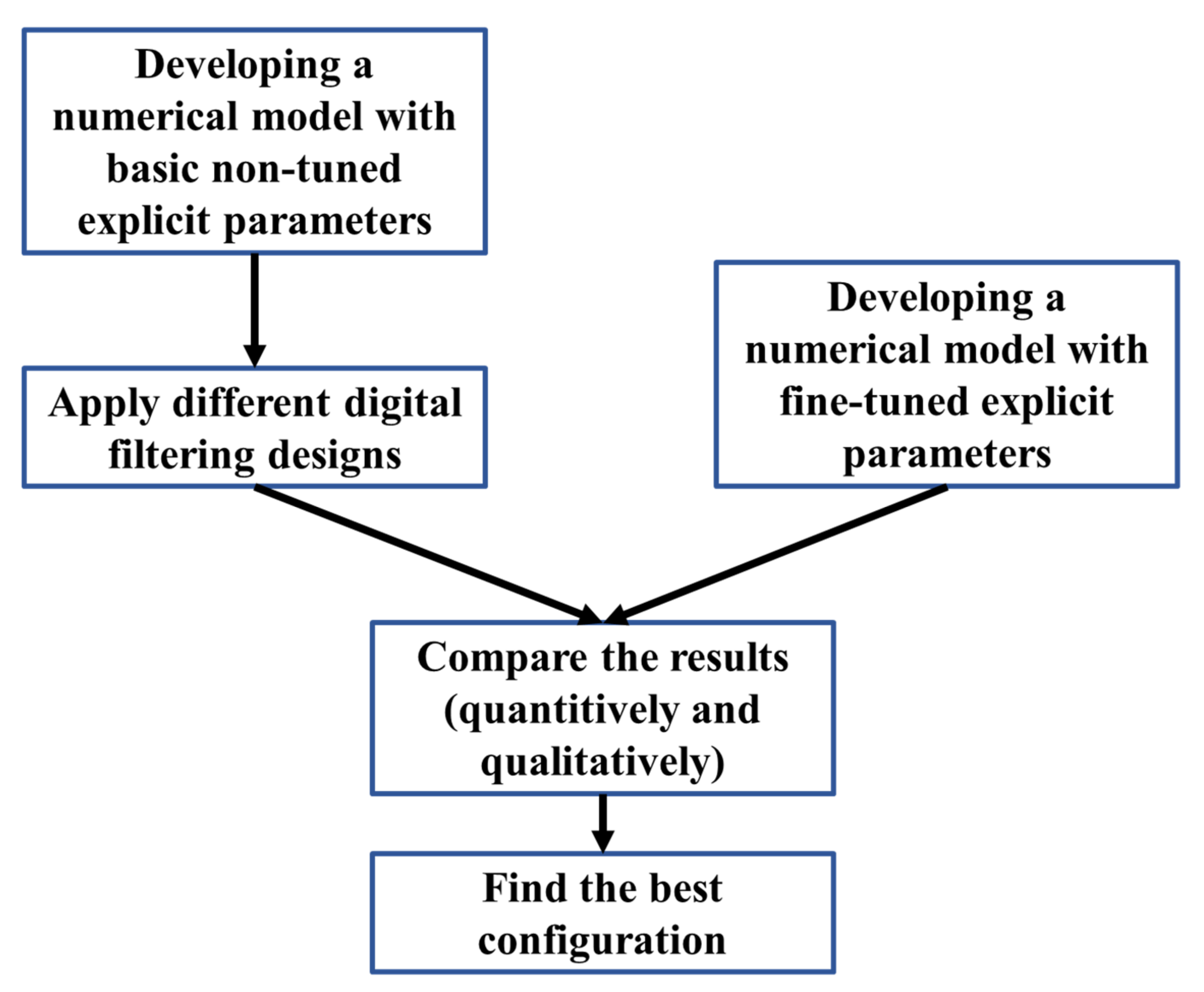
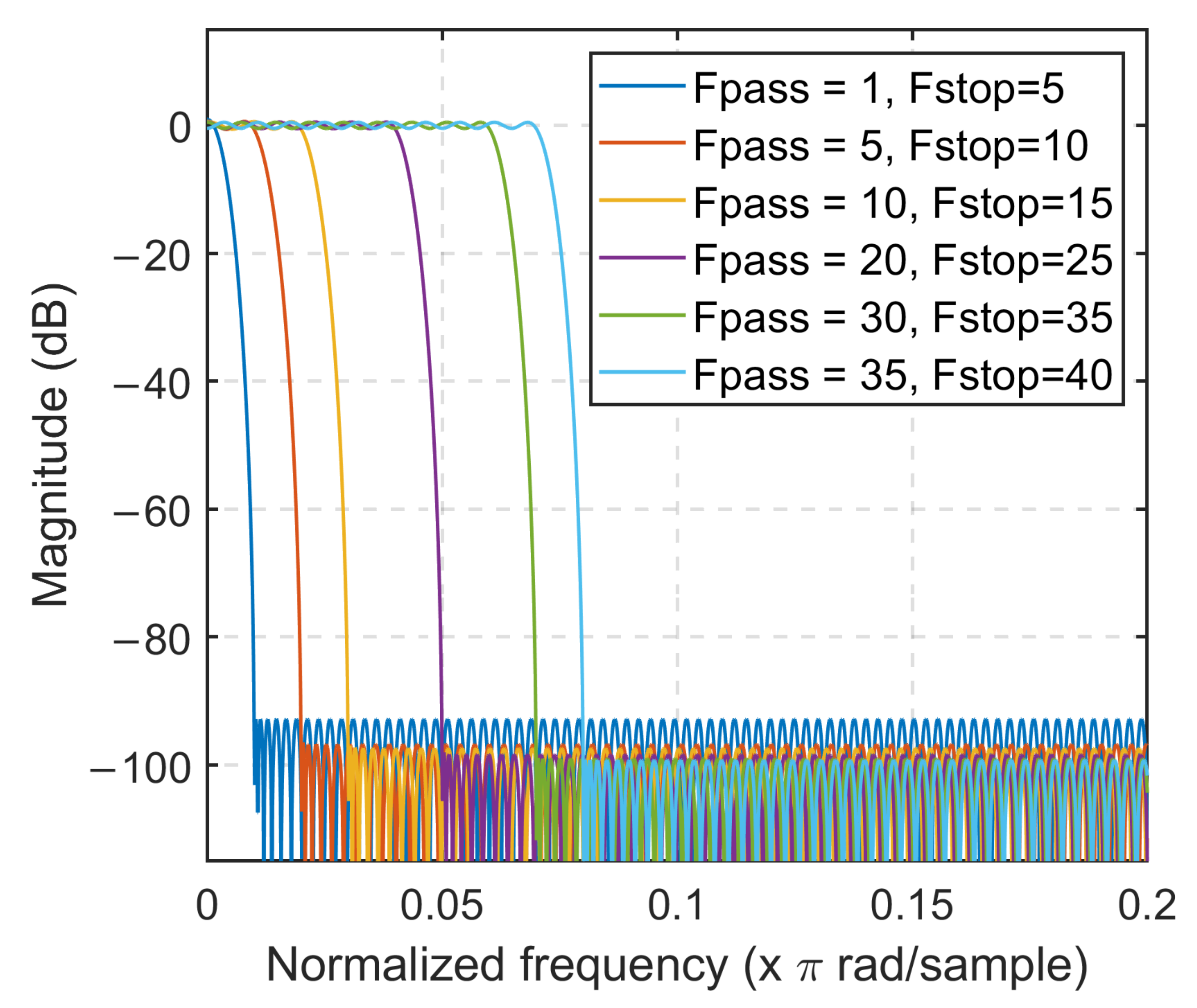
3. Parametric Study
4. Performance Metrics
4.1. Frequency Domain Error (FDE) Index
4.2. Maximum Force Error
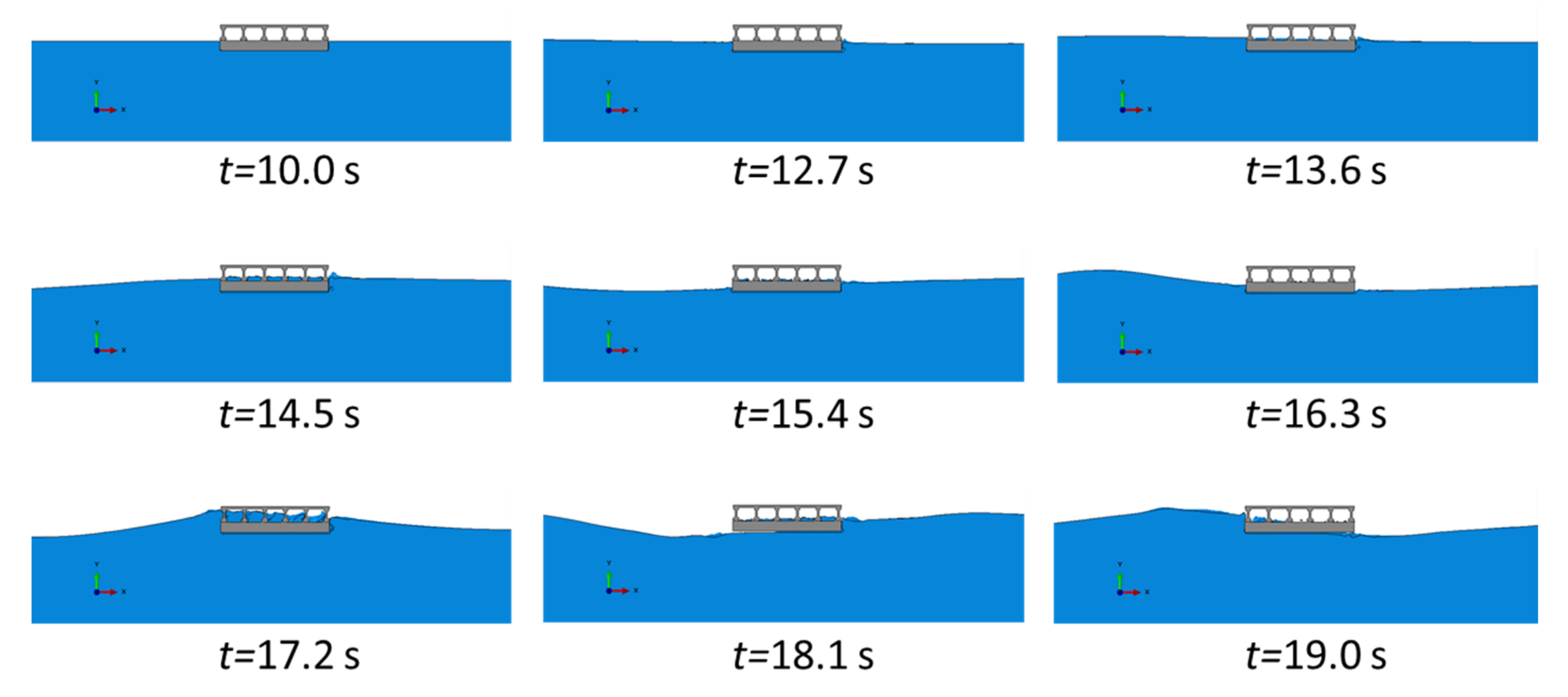
5. Results
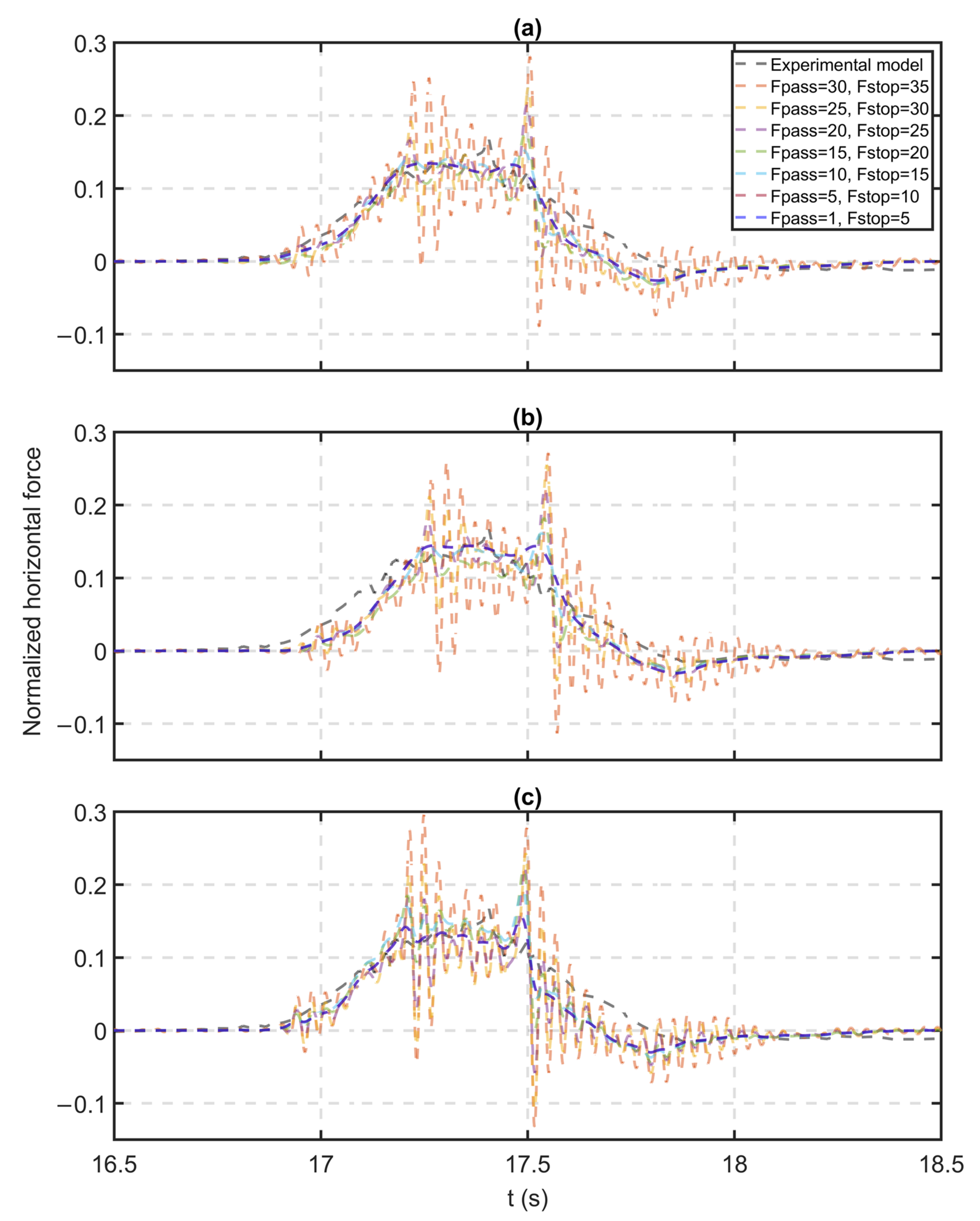
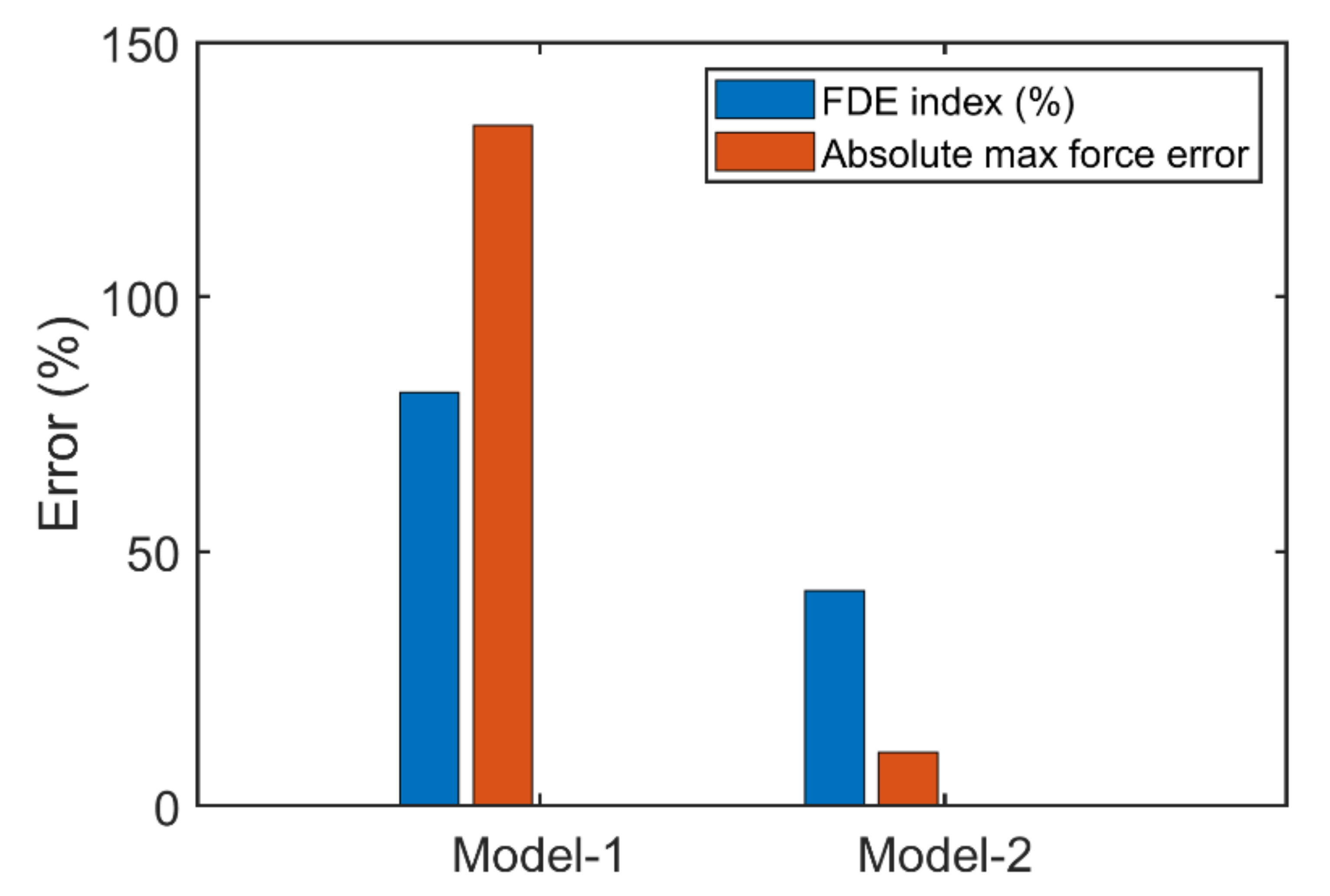
5.1. Model 1
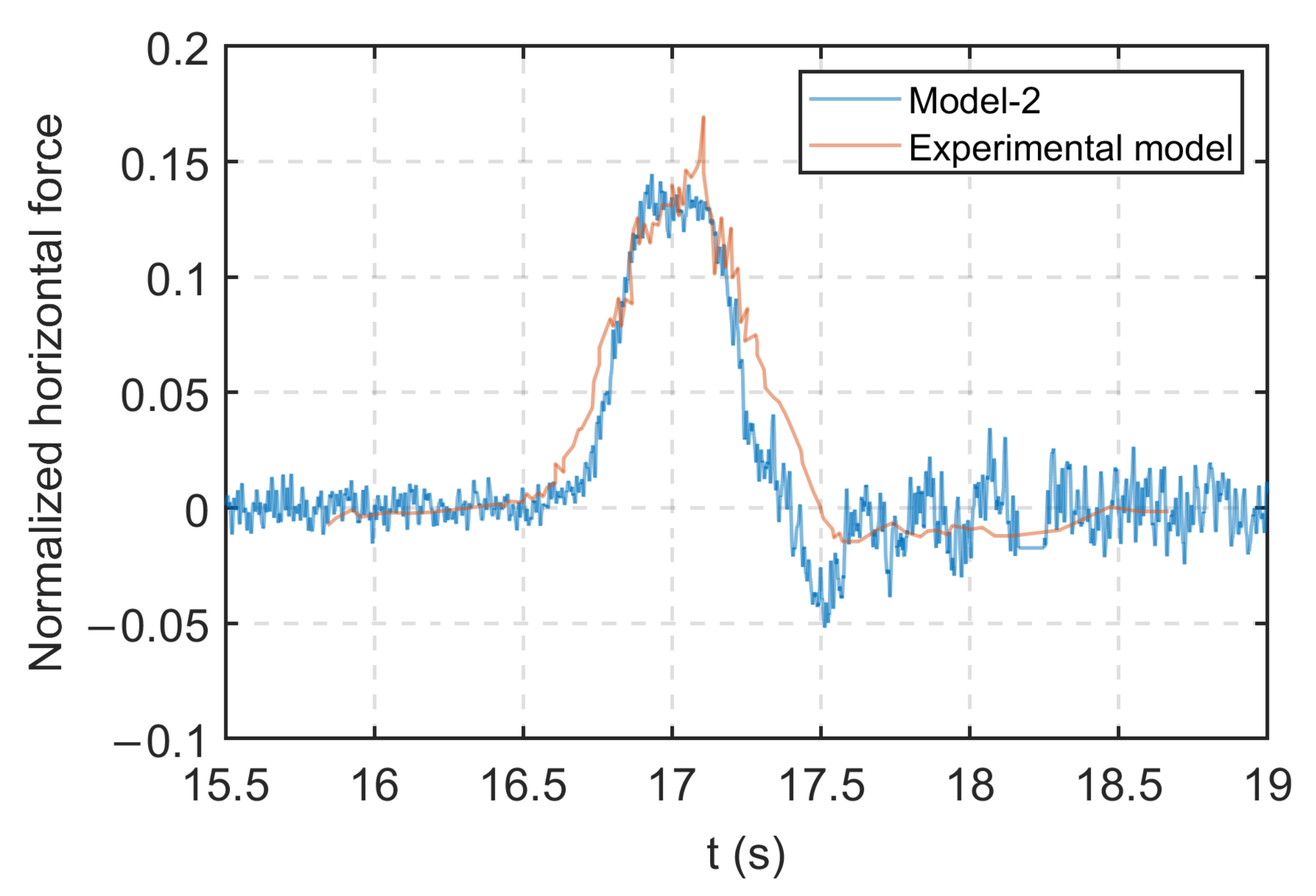
5.2. Model 2
6. Conclusions
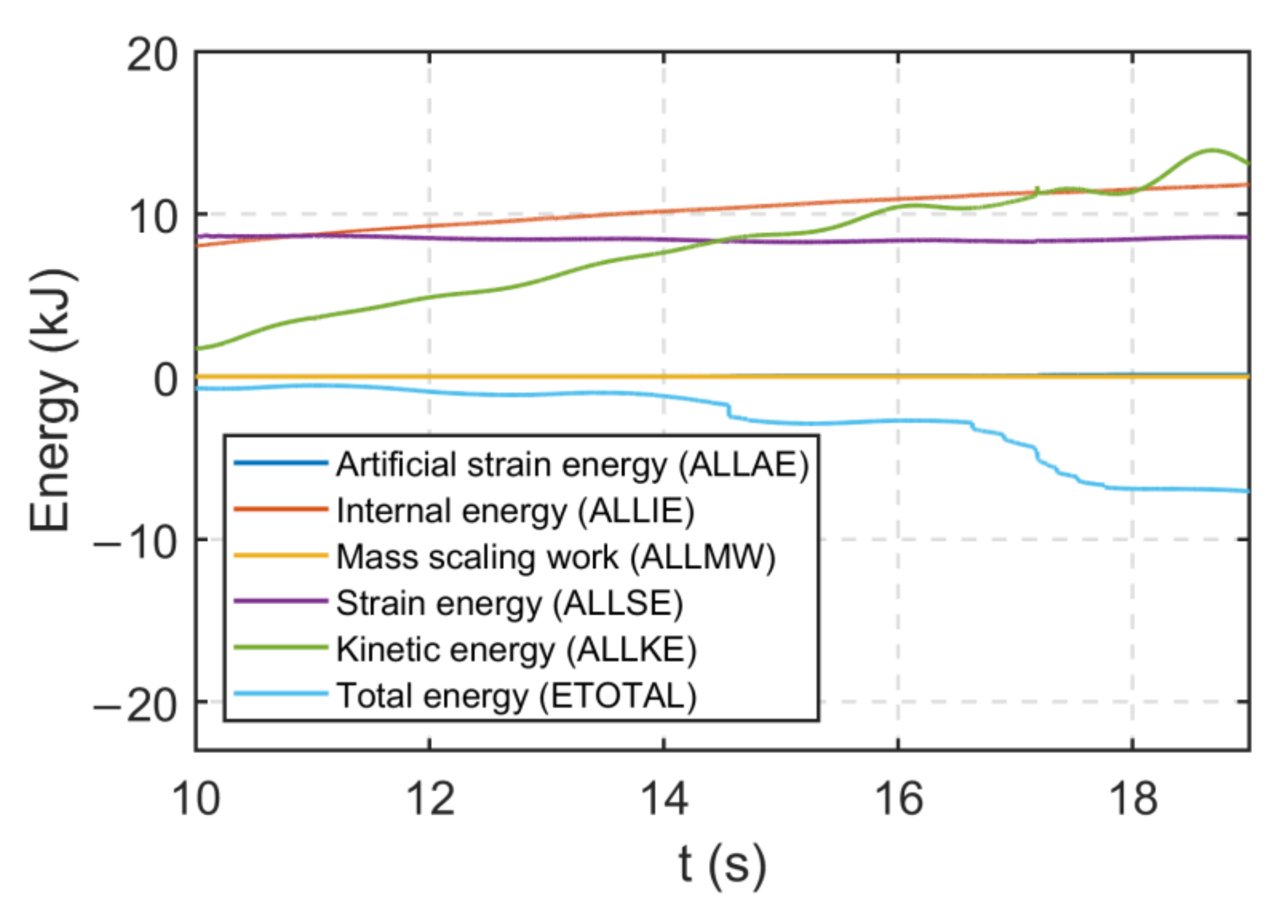
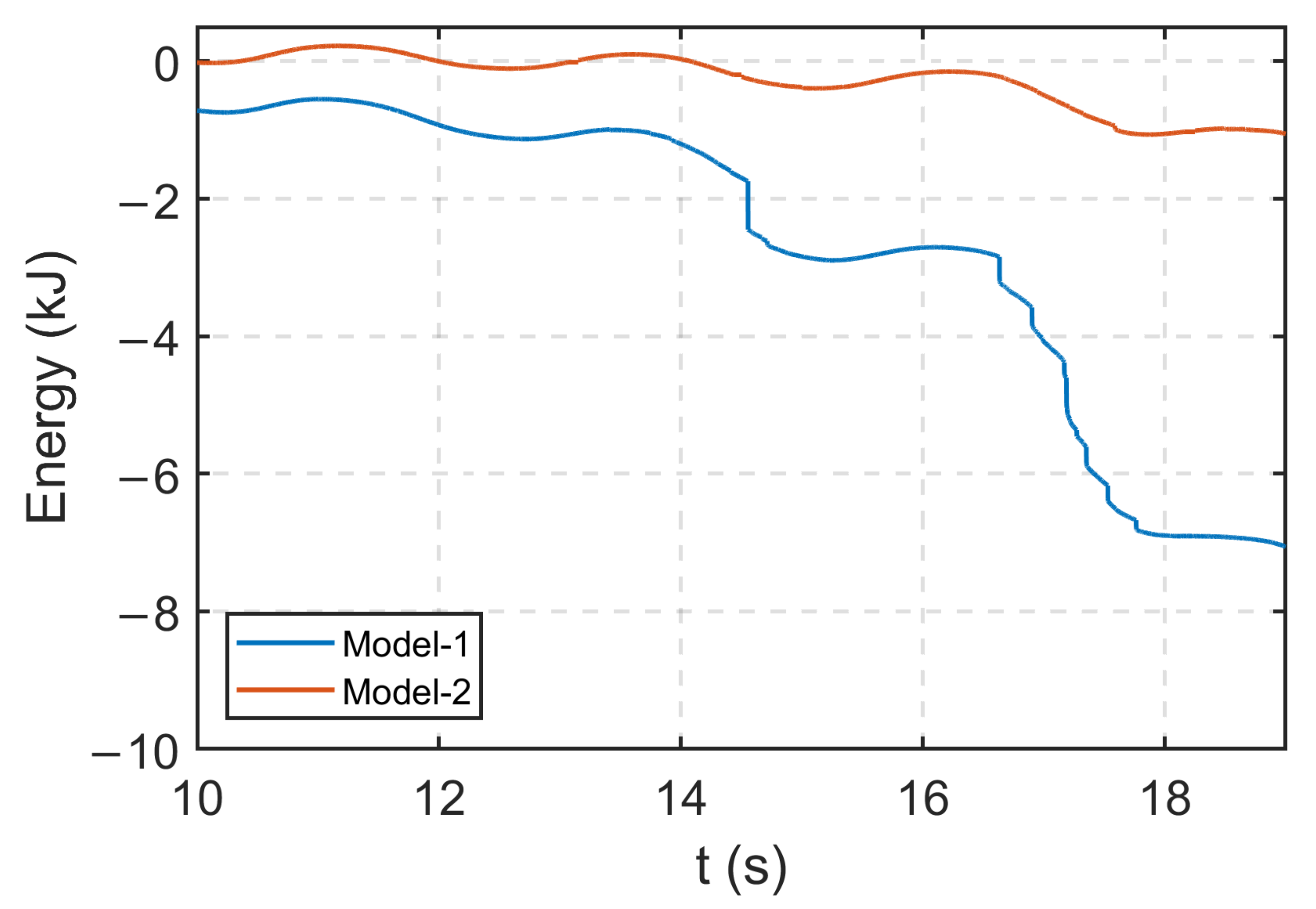
- The energy balance shown in Figure 13 indicates that the numerical artifacts were likely the result of Eulerian–Lagrangian surface interactions when waves impacted the bridge superstructure. It was observed that numerical artifacts in the unfiltered signals were significantly reduced after optimizing the modeling parameters defining the contact interaction between the Eulerian and Lagrangian elements.
- A poor choice of modeling parameters in CEL models was shown to lead to unwanted force signal oscillations and an increase in total energy. This deficiency can be addressed by either optimizing the modeling parameters of the FE model or filtering the force signal.
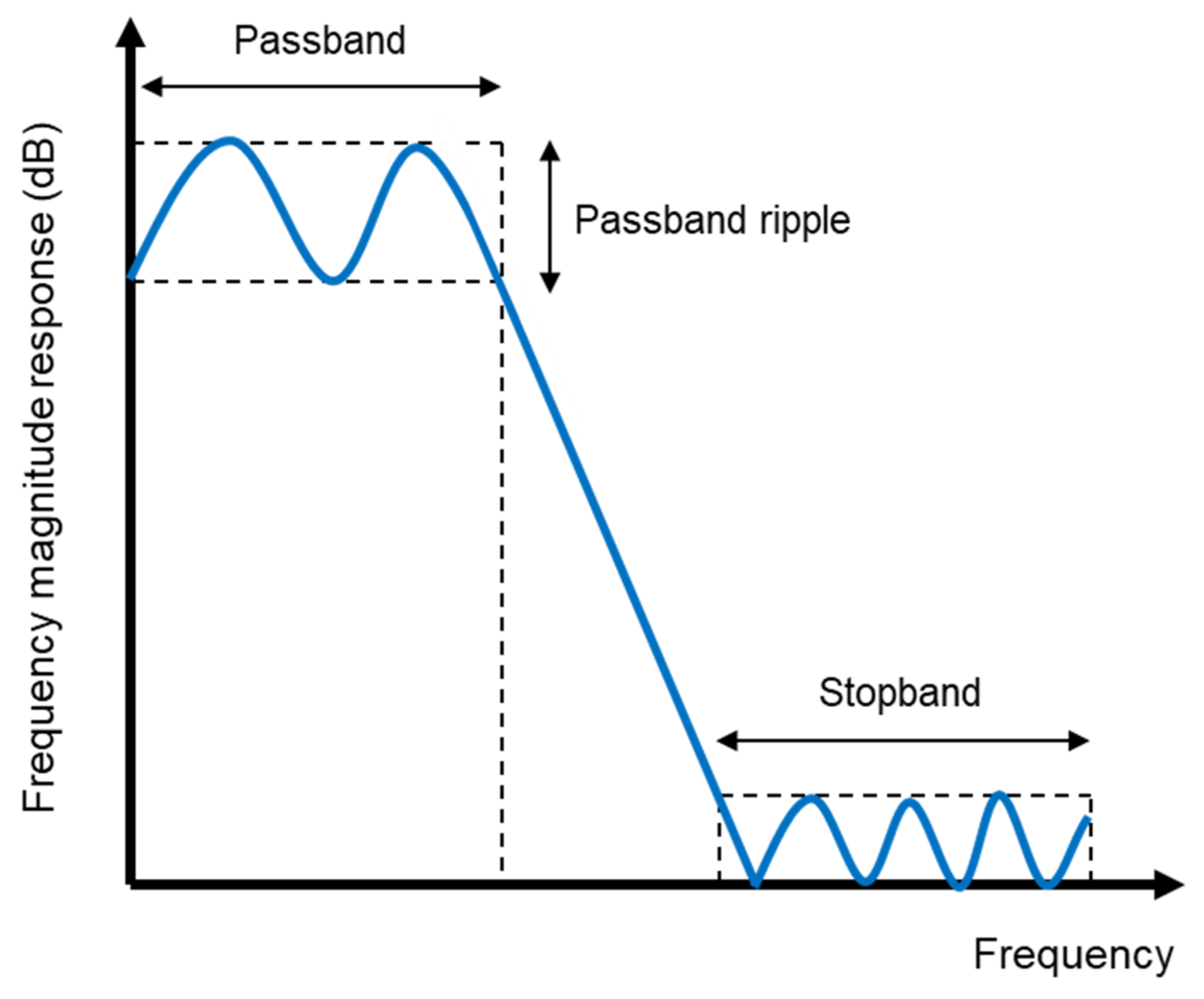
- Although a clear relationship was observed between the FDE index of filtered force signals and passband ripple magnitude, no discernible trend was observed in the relationship between maximum force error and passband ripple magnitude.
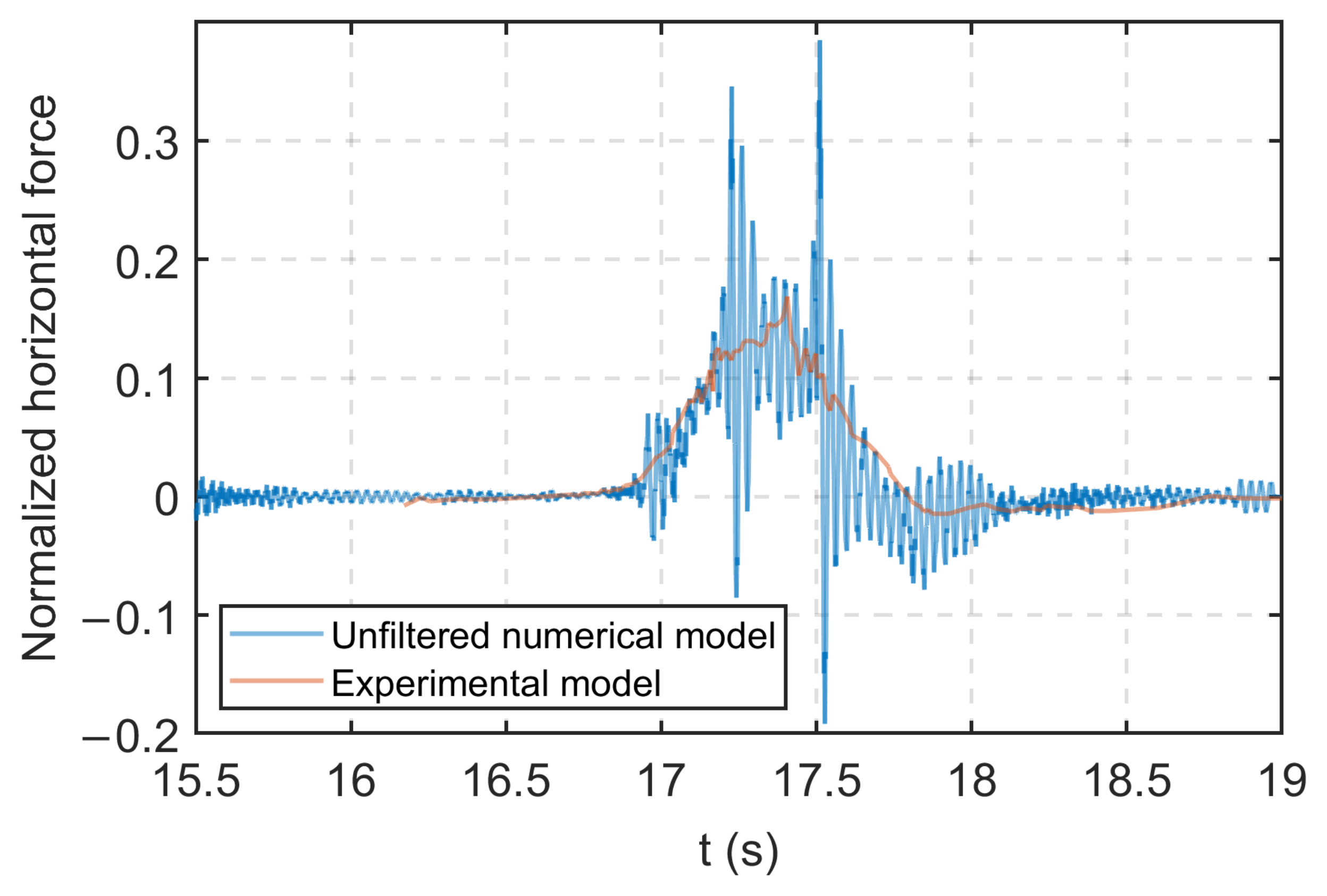
- Filter configurations that provided the lowest FDE index error did not provide the lowest maximum force error.
- Applying a filter to the force signal from model 1 with a passband frequency equal to the fundamental frequency of the superstructure produced a FDE index similar to that of the unfiltered signal calculated with optimized model 2, although the maximum force error of the model 1-filtered signal was significantly higher than the maximum error of the unfiltered signal from model 2.
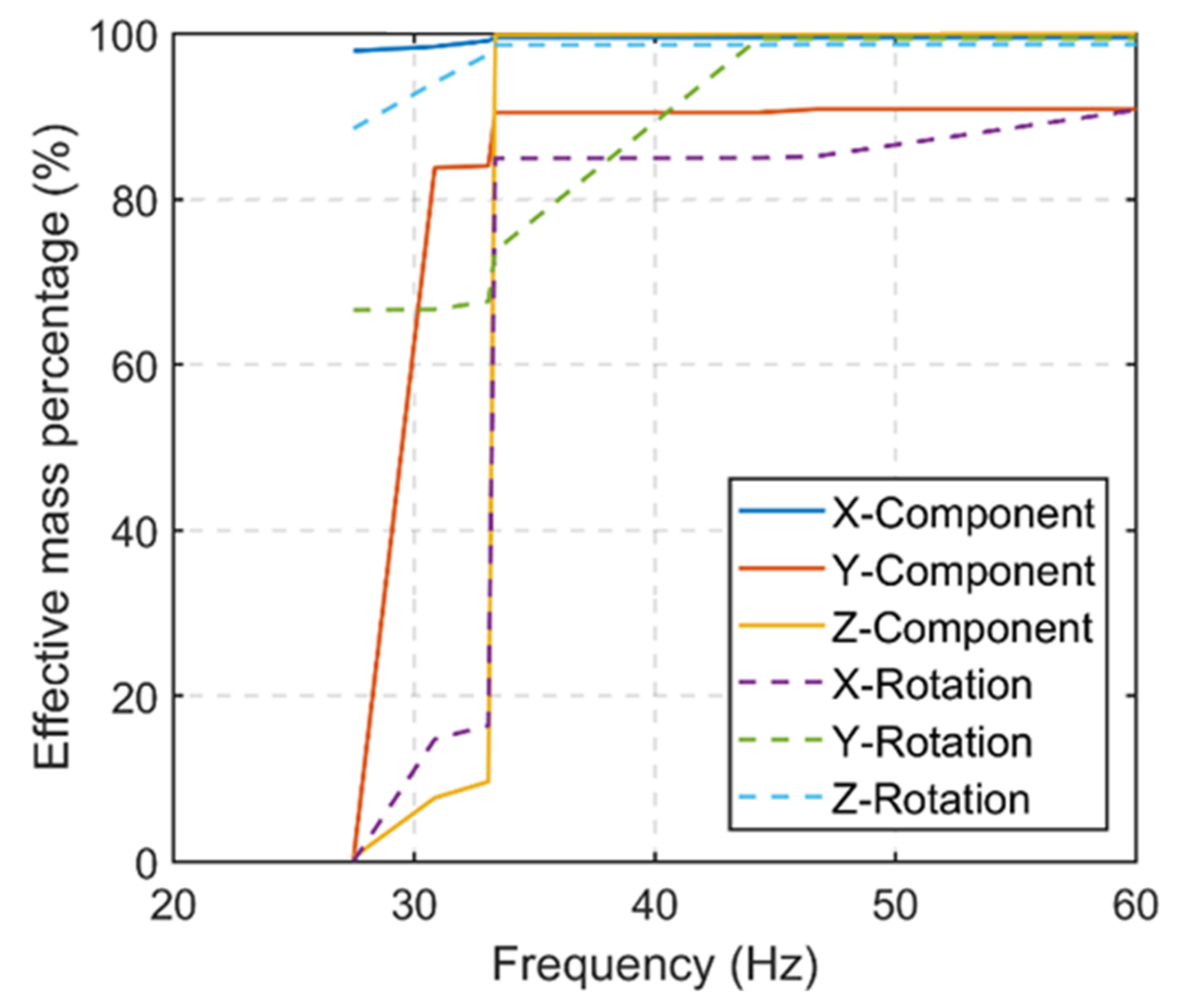
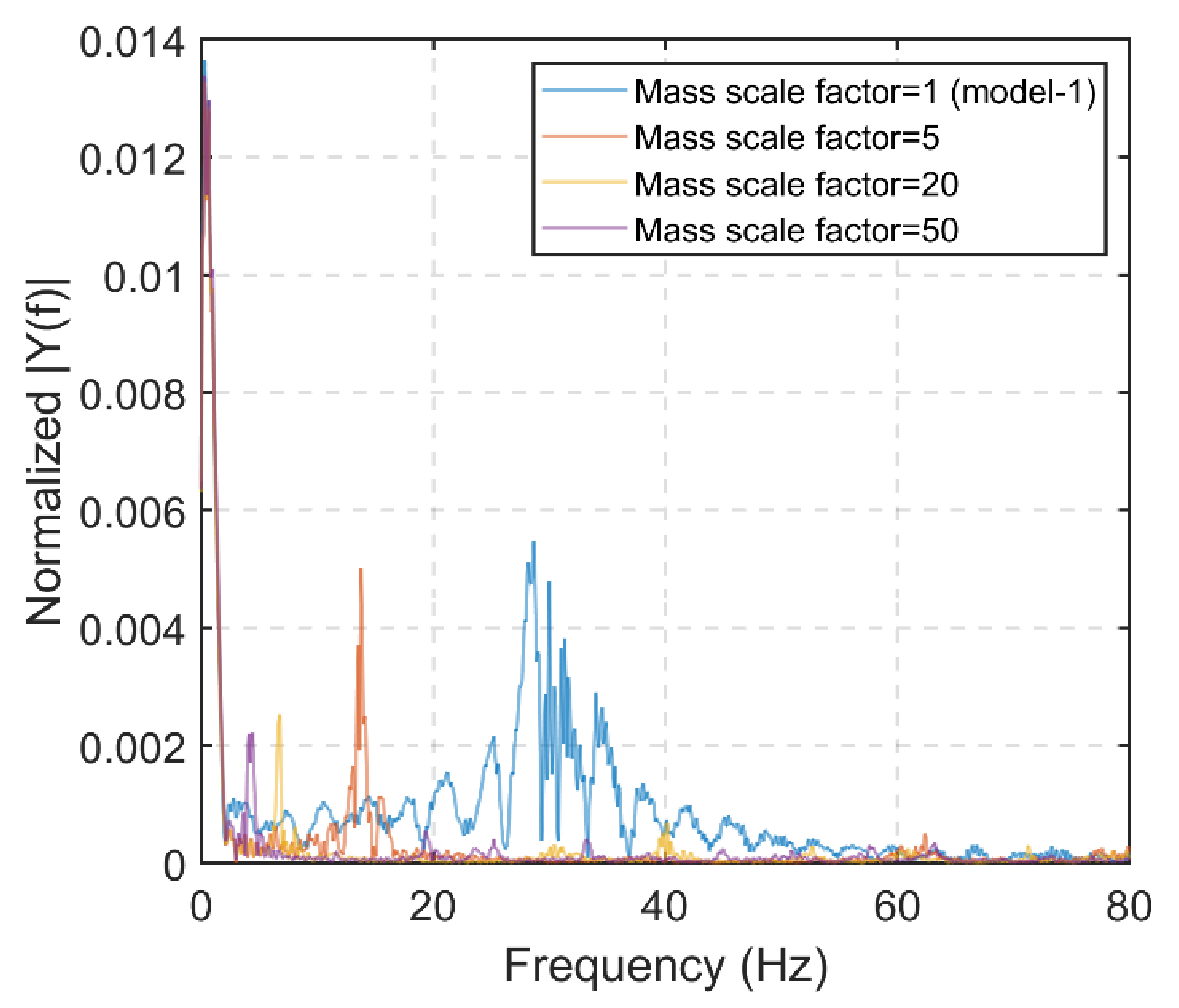
- Filter configurations with stopband and passband frequencies (1 to 20 Hz) lower than the fundamental frequency of the superstructure, approximately 27 Hz based on the FFT of the calculated force signal (Figure 14), produced the lowest FDE index and maximum force errors.
- The optimized parameters used in model 2 (Table 4) were shown to be effective in reducing force signal artifacts and are recommended for future studies analyzing wave–superstructure interactions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Nickas, W.N.; Renna, R.; Sheppard, N.; Mertz, D.R. Hurricane-Based Wave Attacks; Florida Department of Transportation: Tallahassee, FL, USA, 2005.
- Huang, B.; Zhu, B.; Cui, S.; Duan, L.; Zhang, J. Experimental and Numerical Modelling of Wave Forces on Coastal Bridge Superstructures with Box Girders, Part I: Regular Waves. Ocean Eng. 2018, 149, 53–77. [Google Scholar] [CrossRef]
- Zhu, D.; Dong, Y. Experimental and 3D Numerical Investigation of Solitary Wave Forces on Coastal Bridges. Ocean Eng. 2020, 209, 107499. [Google Scholar] [CrossRef]
- Marin, J.; Sheppard, D.M. Storm Surge and Wave Loading on Bridge Superstructures. In Proceedings of the Structures Congress 2009: Don’t Mess with Structural Engineers: Expanding Our Role, Austin, TX, USA, 30 April–2 May 2009; pp. 1–10. [Google Scholar]
- Kerenyi, K.; Sofu, T.; Guo, J. Hydrodynamic Forces on Inundated Bridge Decks; U.S. Department of Transportation: Mclean, VA, USA, 2009.
- Lau, T.L.; Ohmachi, T.; Inoue, S.; Lukkunaprasit, P. Experimental and Numerical Modeling of Tsunami Force on Bridge Decks; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Bozorgnia, M. Computational Fluid Dynamic Analysis of Highway Bridge Superstructures Exposed to Hurricane Waves; University of Southern California: Los Angeles, CA, USA, 2012; ISBN 1267892595. [Google Scholar]
- Bradner, C.; Schumacher, T.; Cox, D.; Higgins, C. Experimental Setup for a Large-Scale Bridge Superstructure Model Subjected to Waves. J. Waterw. Port Coast. Ocean. Eng. 2011, 137, 3–11. [Google Scholar] [CrossRef]
- Yim, S.C.; Azadbakht, M. Tsunami Forces on Selected California Coastal Bridges; California Department of Transportation: Sacramento, CA, USA, 2013.
- Lee, K.; Jeong, S. Large Deformation FE Analysis of a Debris Flow with Entrainment of the Soil Layer. Comput. Geotech. 2018, 96, 258–268. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, C.; Tian, H.; Sun, Y.; Zhang, S. Mechanical Behaviors of Pipeline Inspection Gauge (Pig) in Launching Process Based on Coupled Eulerian-Lagrangian (CEL) Method. Int. J. Press. Vessel. Pip. 2022, 197, 104622. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, K. Analysis of the Impact Force of Debris Flows on a Check Dam by Using a Coupled Eulerian-Lagrangian (CEL) Method. Comput. Geotech. 2019, 116, 103214. [Google Scholar] [CrossRef]
- Liu, C.; Huang, Z. A Mixed Eulerian-Lagrangian Simulation of Nonlinear Wave Interaction with a Fluid-Filled Membrane Breakwater. Ocean Eng. 2019, 178, 423–434. [Google Scholar] [CrossRef]
- Liu, S.; Tang, X.; Li, J. A Decoupled Arbitrary Lagrangian-Eulerian Method for Large Deformation Analysis of Saturated Sand. Soils Found. 2022, 62, 101110. [Google Scholar] [CrossRef]
- Gargari, S.F.; Kolahdoozan, M.; Afshar, M.H.; Dabiri, S. An Eulerian–Lagrangian Mixed Discrete Least Squares Meshfree Method for Incompressible Multiphase Flow Problems. Appl. Math. Model. 2019, 76, 193–224. [Google Scholar] [CrossRef]
- Majlesi, A.; Amori, D.; Montoya, A.; Du, A.; Matamoros, A.; Shahriar, A.; Nasouri, R. Eulerian-Lagrangian Simulation of Wave Impact on Coastal Bridges. In Bridge Safety, Maintenance, Management, Life-Cycle, Resilience and Sustainability; CRC Press: Boca Raton, FL, USA, 2022; pp. 117–125. ISBN 1003322646. [Google Scholar]
- Nasouri, R.; Shahriar, A.; Majlesi, A.; Matamoros, A.; Montoya, A.; Testik, F.Y. Hydrodynamic Demands on Coastal Bridges Due to Wave Impact. In Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations; CRC Press: Boca Raton, FL, USA, 2021; pp. 1241–1248. ISBN 0429279116. [Google Scholar]
- Xiang, T.; Istrati, D. Assessment of Extreme Wave Impact on Coastal Decks with Different Geometries via the Arbitrary Lagrangian-Eulerian Method. J. Mar. Sci. Eng. 2021, 9, 1342. [Google Scholar] [CrossRef]
- Do, T.Q.; van de Lindt, J.W.; Cox, D.T. Performance-Based Design Methodology for Inundated Elevated Coastal Structures Subjected to Wave Load. Eng. Struct. 2016, 117, 250–262. [Google Scholar] [CrossRef]
- Montoya, A.; Matamoros, A.; Testik, F.; Nasouri, R.; Shahriar, A.; Majlesi, A. Structural Vulnerability of Coastal Bridges under Extreme Hurricane Conditions; Transportation Consortium of South-Central States: Baton Rouge, LA, USA, 2019.
- Majlesi, A.; Nasouri, R.; Shahriar, A.; Montoya, A.; Matamoros, A. Structural Vulnerability of Coastal Bridges under a Variety of Hydrodynamic Conditions. In Tran-SET 2020; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 120–125. [Google Scholar]
- Xiang, T.; Istrati, D.; Yim, S.C.; Buckle, I.G.; Lomonaco, P. Tsunami Loads on a Representative Coastal Bridge Deck: Experimental Study and Validation of Design Equations. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 4020022. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, J.; Hong, R.; Guo, A.; Li, H. Experimental Investigation of Focused Wave Action on Coastal Bridges with Box Girder. Coast. Eng. 2021, 165, 103857. [Google Scholar] [CrossRef]
- Istrati, D.; Buckle, I.; Lomonaco, P.; Yim, S. Deciphering the Tsunami Wave Impact and Associated Connection Forces in Open-Girder Coastal Bridges. J. Mar. Sci. Eng. 2018, 6, 148. [Google Scholar] [CrossRef]
- Xu, G.; Chen, Q.; Zhu, L.; Chakrabarti, A. Characteristics of the Wave Loads on Coastal Low-Lying Twin-Deck Bridges. J. Perform. Constr. Facil. 2018, 32, 4017132. [Google Scholar] [CrossRef]
- Yim, S.C.; Olsen, M.J.; Cheung, K.F.; Azadbakht, M. Tsunami Modeling, Fluid Load Simulation, and Validation Using Geospatial Field Data. J. Struct. Eng. 2014, 140, A4014012. [Google Scholar] [CrossRef]
- Azadbakht, M.; Yim, S.C. Bridge Superstructure Design for Tsunamis: A State-of-the-Art Methodology for Tsunami Modeling, Load Simulation, and Structural Response Assessment. In Proceedings of the Structures Congress 2015, Oregon, Portland, 23–25 April 2015; pp. 345–354. [Google Scholar]
- Azadbakht, M.; Yim, S.C. Effect of Trapped Air on Wave Forces on Coastal Bridge Superstructures. J. Ocean Eng. Mar. Energy 2016, 2, 139–158. [Google Scholar] [CrossRef]
- Azadbakht, M.; Yim, S.C. Simulation and Estimation of Tsunami Loads on Bridge Superstructures. J. Waterw. Port Coast. Ocean Eng. 2015, 141, 4014031. [Google Scholar] [CrossRef]
- Majlesi, A.; Nasouri, R.; Shahriar, A.; Amori, D.; Montoya, A.; Du, A.; Matamoros, A. Explicit Finite Element Analysis of Coastal Bridges under Extreme Hurricane Waves. In Tran-SET 2021; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 324–331. [Google Scholar]
- Ataei, N.; Padgett, J.E. Influential Fluid–Structure Interaction Modelling Parameters on the Response of Bridges Vulnerable to Coastal Storms. Struct. Infrastruct. Eng. 2015, 11, 321–333. [Google Scholar] [CrossRef]
- Majlesi, A.; Asadi-Ghoozhdi, H.; Bamshad, O.; Attarnejad, R.; Masoodi, A.R.; Ghassemieh, M. On the Seismic Evaluation of Steel Frames Laterally Braced with Perforated Steel Plate Shear Walls Considering Semi-Rigid Connections. Buildings 2022, 12, 1427. [Google Scholar] [CrossRef]
- Schumacher, T.; Hameed, A.W.; Higgins, C.; Erickson, B. Characterization of Hydrodynamic Properties from Free Vibration Tests of a Large-Scale Bridge Model. J. Fluids Struct. 2021, 106, 103368. [Google Scholar] [CrossRef]
- Douglass, S.; Chen, Q.; Olsen, J. Wave Forces on Bridge Decks; Final Report; U.S. Department of Transportation and Federal Highway Administration Office of Bridge Technology: Washington, DC, USA, 2006.
- Cuomo, G.; Tirindelli, M.; Allsop, W. Wave-in-Deck Loads on Exposed Jetties. Coast. Eng. 2007, 54, 657–679. [Google Scholar] [CrossRef]
- Bradner, C.; Schumacher, T.; Cox, D.; Higgins, C. Large–Scale Laboratory Observations of Wave Forces on a Highway Bridge Superstructure; Transportation Research and Education Center: Portland, OR, USA, 2011. [Google Scholar]
- Simulia, A.V. 6.13 Documentation; Dassault Systemes: Velizy-Villacoublay, France, 2013. [Google Scholar]
- Shahriar, A.; Majlesi, A.; Nasouri, R.; Montoya, A.; Matamoros, A.; Testik, F. Generation of Periodic Wave Using Lagrange-Plus Remap Finite Element Method for Evaluating the Vulnerability of Coastal Bridges to Extreme Weather Events. In Tran-SET 2020; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 133–140. [Google Scholar]
- Dean, R.G. Water Wave Mechanics for Engineers and Scientists. Adv. Ser. Ocean Eng. 1984, 2, 353. [Google Scholar]
- Lamb, H. Hydrodynamics; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Madsen, O.S. On the Generation of Long Waves. J. Geophys. Res. 1971, 76, 8672–8683. [Google Scholar] [CrossRef]
- Qiu, G.; Henke, S.; Grabe, J. Application of a Coupled Eulerian–Lagrangian Approach on Geomechanical Problems Involving Large Deformations. Comput. Geotech. 2011, 38, 30–39. [Google Scholar] [CrossRef]
- Benson, D.J. Computational Methods in Lagrangian and Eulerian Hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Benson, D.J.; Okazawa, S. Contact in a Multi-Material Eulerian Finite Element Formulation. Comput. Methods Appl. Mech. Eng. 2004, 193, 4277–4298. [Google Scholar] [CrossRef]
- Abaqus, V. 6.14 Documentation; Dassault Systemes Simulia Corporation: Providence, RI, USA, 2014; p. 651. [Google Scholar]
- Olovsson, L.; Simonsson, K.; Unosson, M. Selective Mass Scaling for Explicit Finite Element Analyses. Int. J. Numer. Methods Eng. 2005, 63, 1436–1445. [Google Scholar] [CrossRef]
- Dragovich, J.J.; Lepage, A. FDE Index for Goodness-of-fit between Measured and Calculated Response Signals. Earthq. Eng. Struct. Dyn. 2009, 38, 1751–1758. [Google Scholar] [CrossRef]

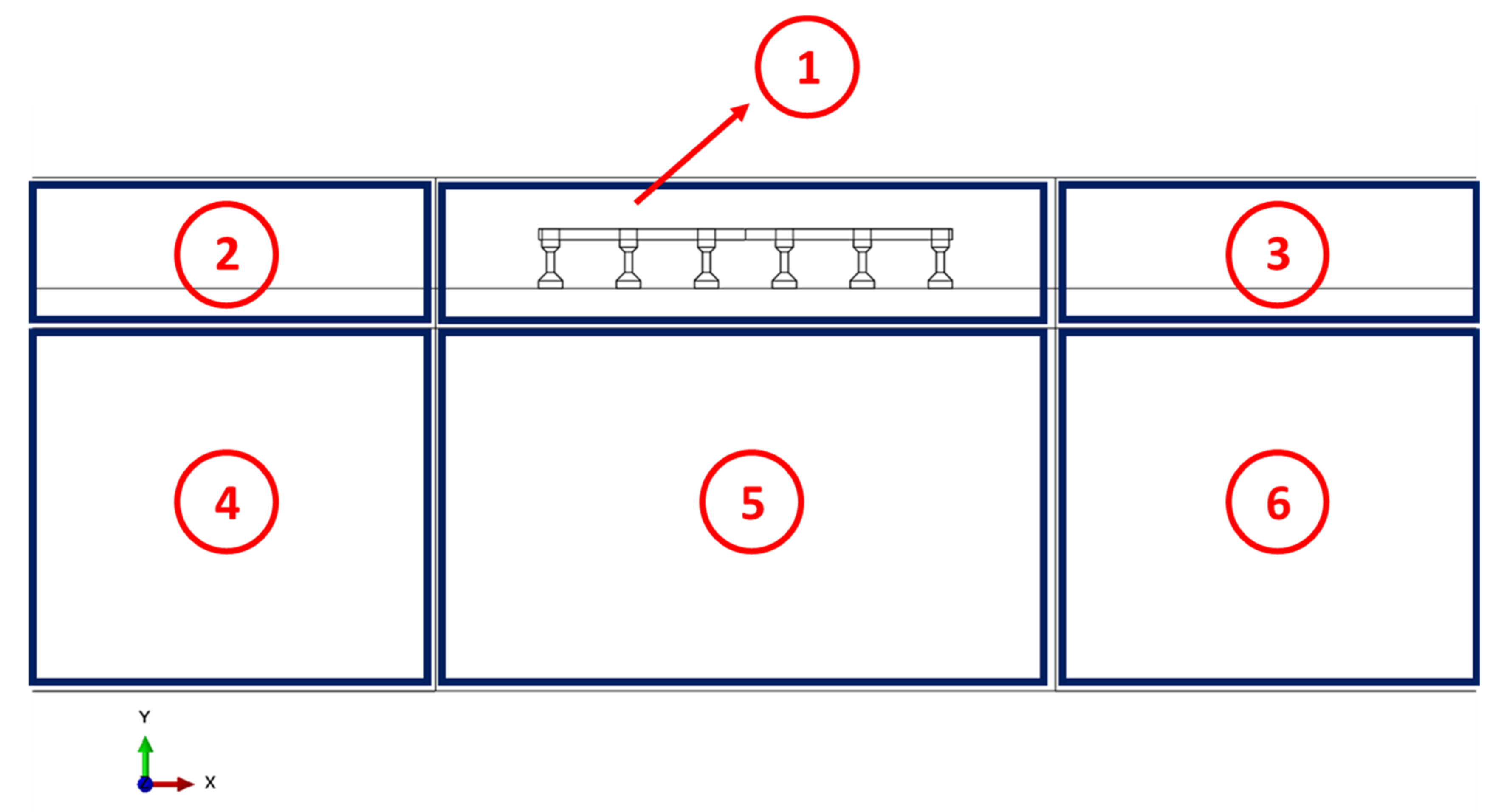
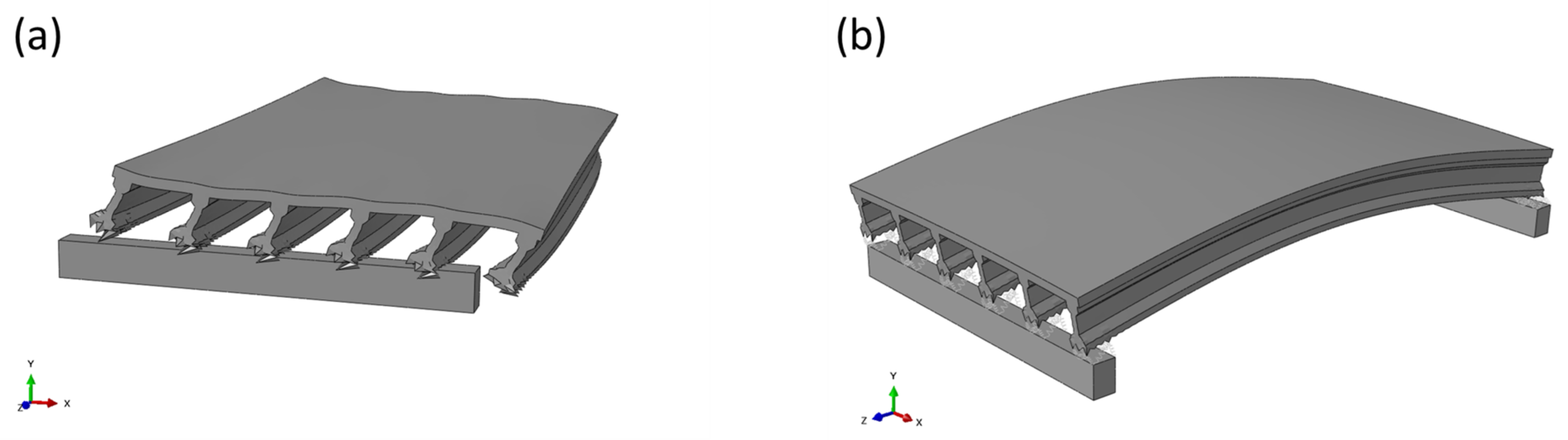

| Parameters | Model (1:5) | Prototype (1:1) |
|---|---|---|
| Span length, S | 3.45 m | 17.27 m |
| Width, H | 1.94 m | 9.70 m |
| Girder height | 0.23 m | 1.14 m |
| Girder Spacing (CL to CL) | 0.37 m | 1.83 m |
| Deck thickness | 0.05 m | 0.25 m |
| Overall height | 0.28 m | 1.40 m |
| Span weight | 19.0 kN | 2375 kN |
| Span mass | 1.94 t | 242 t |
| Parameters | Magnitude |
|---|---|
| Initial water depth, h | 1.9 m |
| Wave height, H | 0.5 m |
| Wave period, T | 2.5 s |
| Domain Length, L | 30 m |
| Mesh Size (cm) | |||||||
|---|---|---|---|---|---|---|---|
| Region 1 | Regions 2 and 3 | Regions 4 and 6 | Region 5 | ||||
| Δx | Δy | Δx | Δy | Δx | Δy | Δx | Δy |
| 2.0 | 2.0 | 11.2 | 2.0 | 11.2 | 5.6 | 2.0 | 5.6 |
| Model | Mass Scale Factor | Damping (%) | Eulerian Domain | Lagrangian Domain | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hourglass Control | α | s | b1 | b2 | Hourglass Control | α | s | b1 | b2 | |||
| 1 | 1 | 0.0 | Default | DV a | DV a | 0.06 | 1.2 | Default | DV a | DV a | 0.06 | 1.2 |
| 2 | 50 | 4.0 | Combined b | 0.25 | 1 | 0.06 | 1.2 | Combined b | 0.25 | 1 | 0.06 | 1.2 |
| Model | 1 | 2 |
|---|---|---|
| Computational time (days) | 15 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majlesi, A.; Shahriar, A.; Nasouri, R.; Khodadadi Koodiani, H.; Montoya, A.; Du, A.; Matamoros, A. Digital Filter Design for Force Signals from Eulerian–Lagrangian Analyses of Wave Impact on Bridges. J. Mar. Sci. Eng. 2022, 10, 1751. https://doi.org/10.3390/jmse10111751
Majlesi A, Shahriar A, Nasouri R, Khodadadi Koodiani H, Montoya A, Du A, Matamoros A. Digital Filter Design for Force Signals from Eulerian–Lagrangian Analyses of Wave Impact on Bridges. Journal of Marine Science and Engineering. 2022; 10(11):1751. https://doi.org/10.3390/jmse10111751
Chicago/Turabian StyleMajlesi, Arsalan, Adnan Shahriar, Reza Nasouri, Hamid Khodadadi Koodiani, Arturo Montoya, Ao Du, and Adolfo Matamoros. 2022. "Digital Filter Design for Force Signals from Eulerian–Lagrangian Analyses of Wave Impact on Bridges" Journal of Marine Science and Engineering 10, no. 11: 1751. https://doi.org/10.3390/jmse10111751
APA StyleMajlesi, A., Shahriar, A., Nasouri, R., Khodadadi Koodiani, H., Montoya, A., Du, A., & Matamoros, A. (2022). Digital Filter Design for Force Signals from Eulerian–Lagrangian Analyses of Wave Impact on Bridges. Journal of Marine Science and Engineering, 10(11), 1751. https://doi.org/10.3390/jmse10111751






