The design of low-speed submersible vessels typically does not consider hydrodynamic resistance as one of the important design constraints. For this reason, these vessels often have intricate geometries, often unfavourable from the hydrodynamic resistance point of view. Furthermore, the geometry of various types of submarines is highly varying, depending on the purpose of the vessel and size. Thus, typical methods of approximating its hydrodynamic resistance are not available since there is little data on similar vessels, and since the geometry is not comparable to other shapes found in the field of naval architecture, such as ships or submarines. Calculating the resistance of these objects requires model-scale experiments or numerical simulations. These results are being published more frequently, increasing the overall level of knowledge on the topic.
The topic has attracted a number of researchers who have published their findings of specific projects or purely scientific investigations. Huifeng et al. [
1] conducted CFD simulations of a towed manned submersible, calculating the resistance coefficient to be 0.82. Jiang et al. [
2] presented a CFD study of the hydrodynamic resistance of an autonomous remotely operated submersible for forward motion and descent. Wei et al. [
3] used the response surface method to optimise the hydrodynamic resistance of a submersible, where they varied the length of the stern, length of the bow, and aspect ratio of the rudder, among others. Kotb et al. [
4] conducted an investigation on the drag of an 18 m long tourist submersible, separately calculating the hydrodynamic resistance for various parts of the submersible’s geometry. Phillips et al. [
5] used CFD to investigate and compare hydrodynamic resistance of three different types of submersible hull design. Additionally, they studied the effect of a submersible’s bow shape on overall resistance, finding that an elliptical bow with a higher length-to-diameter ratio reduces resistance. Khan et al. [
6] showed a study of how different pressure body shapes influence hydrodynamic resistance. They tested four different geometries, and concluded that a conic shape is most favourable. Karim et al. [
7] studied the performance of the k-
SST turbulence model for estimating submersible resistance in a 2D CFD investigation, also comparing different grids. Chen et al. [
8] studied the effect of sailing depth on the resistance coefficients of the SUBOFF using a RANS approach.
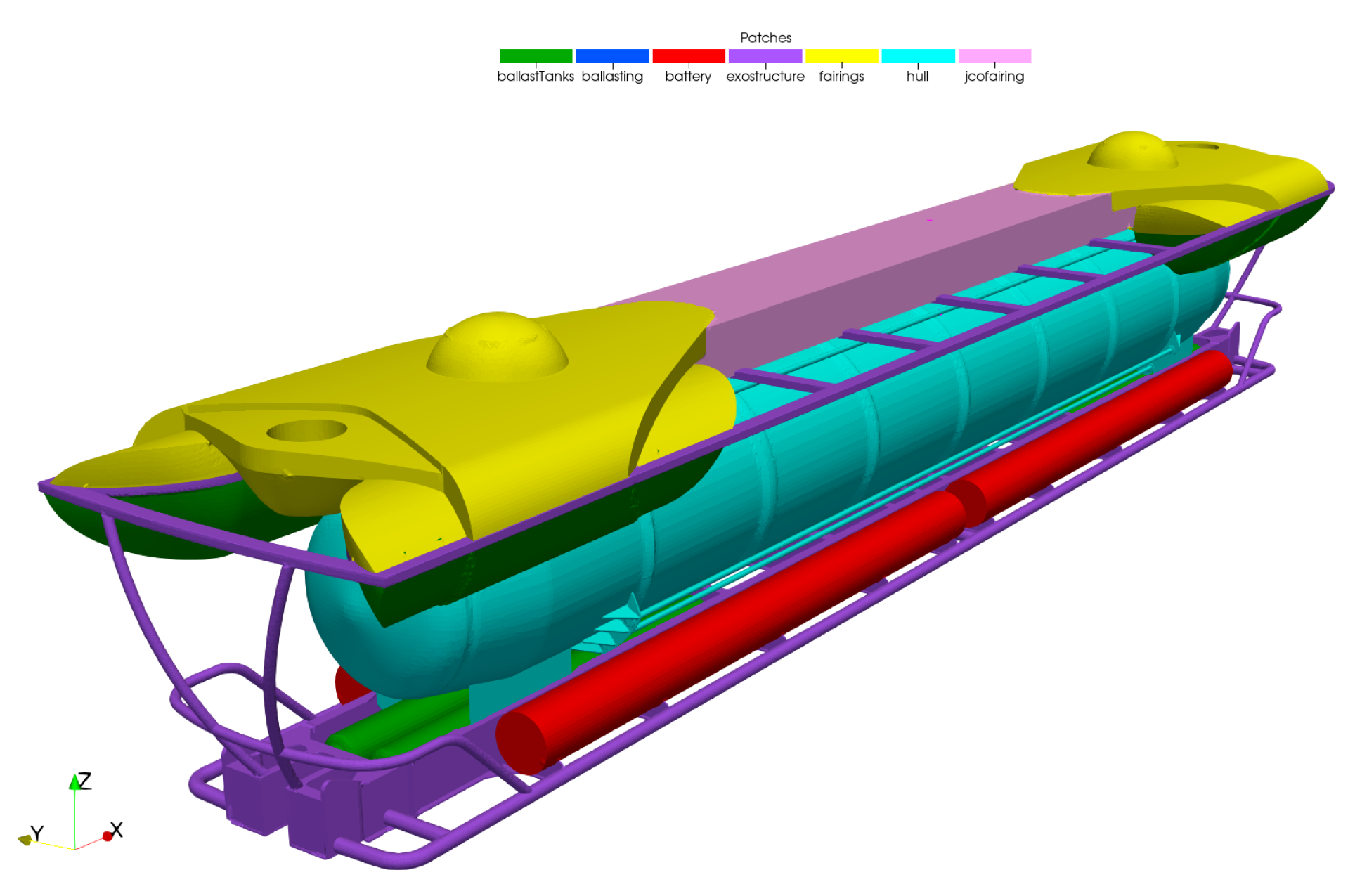
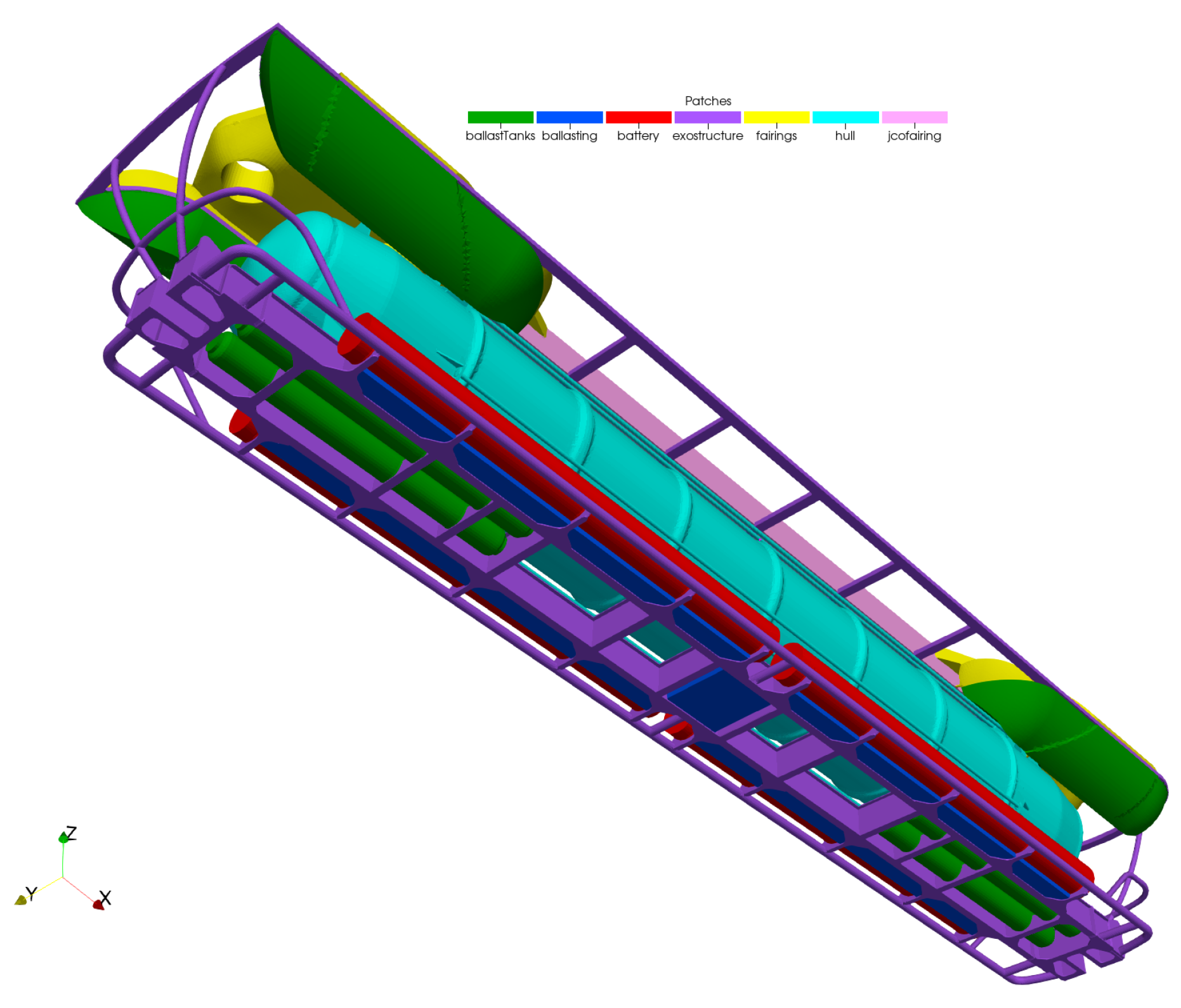
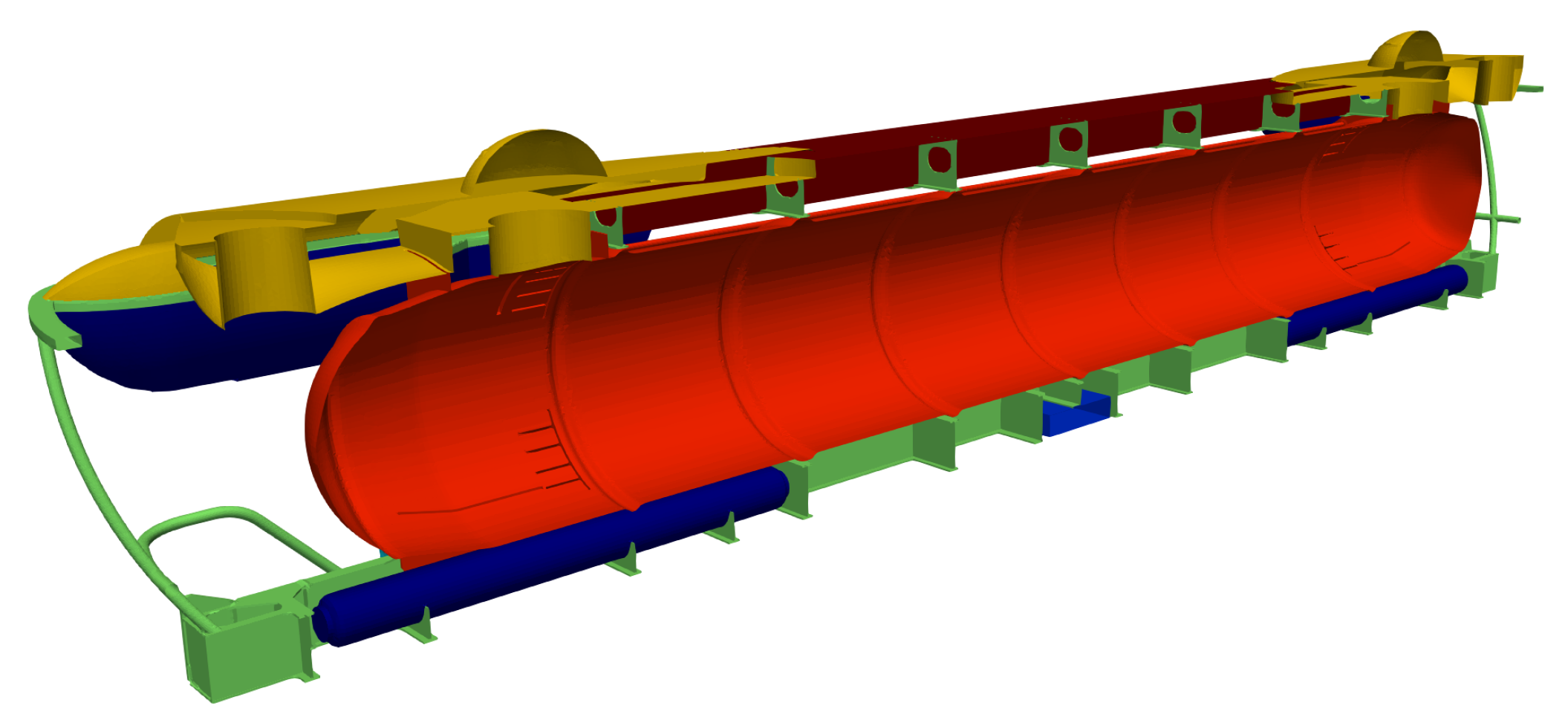
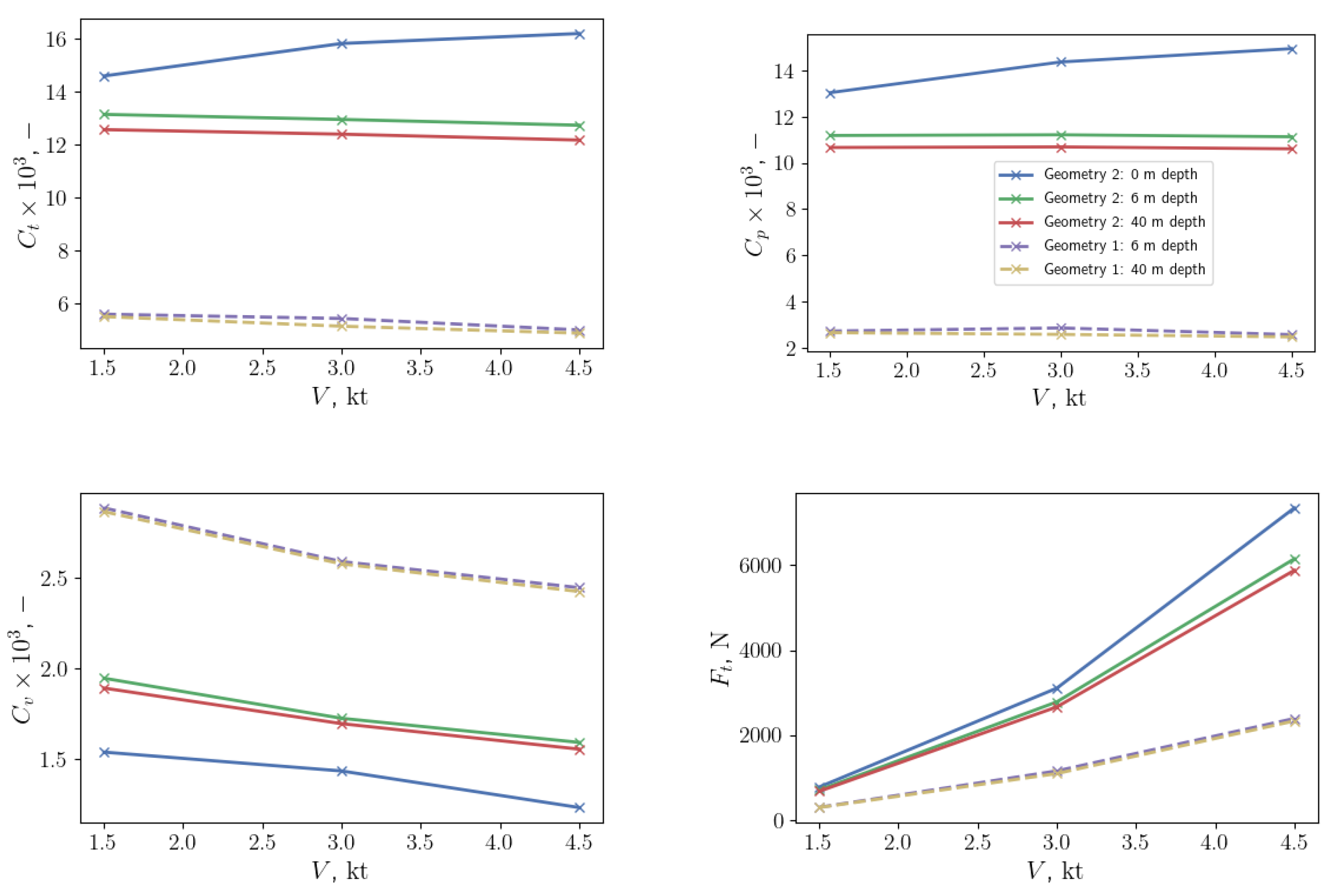
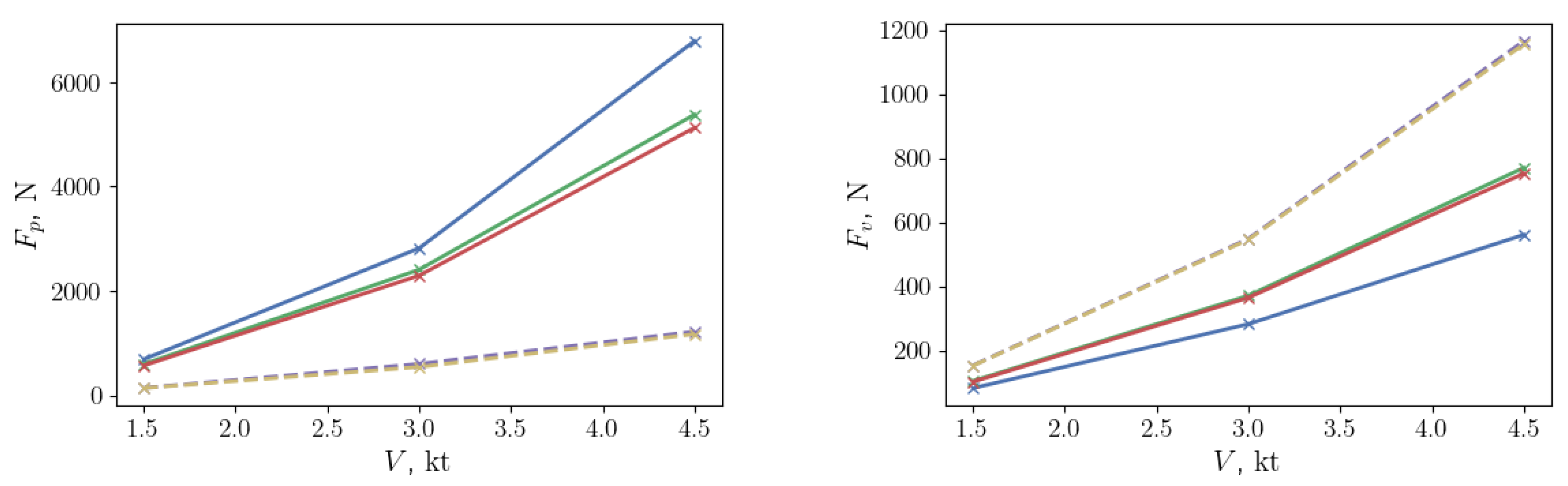
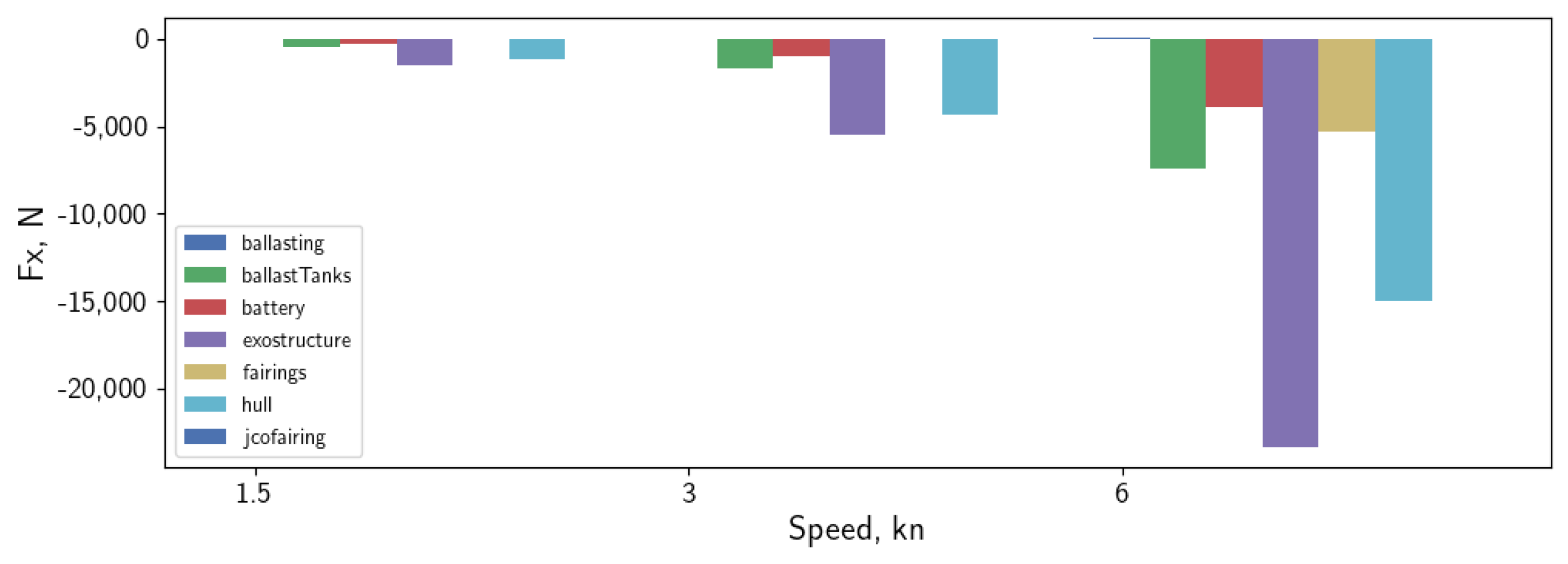
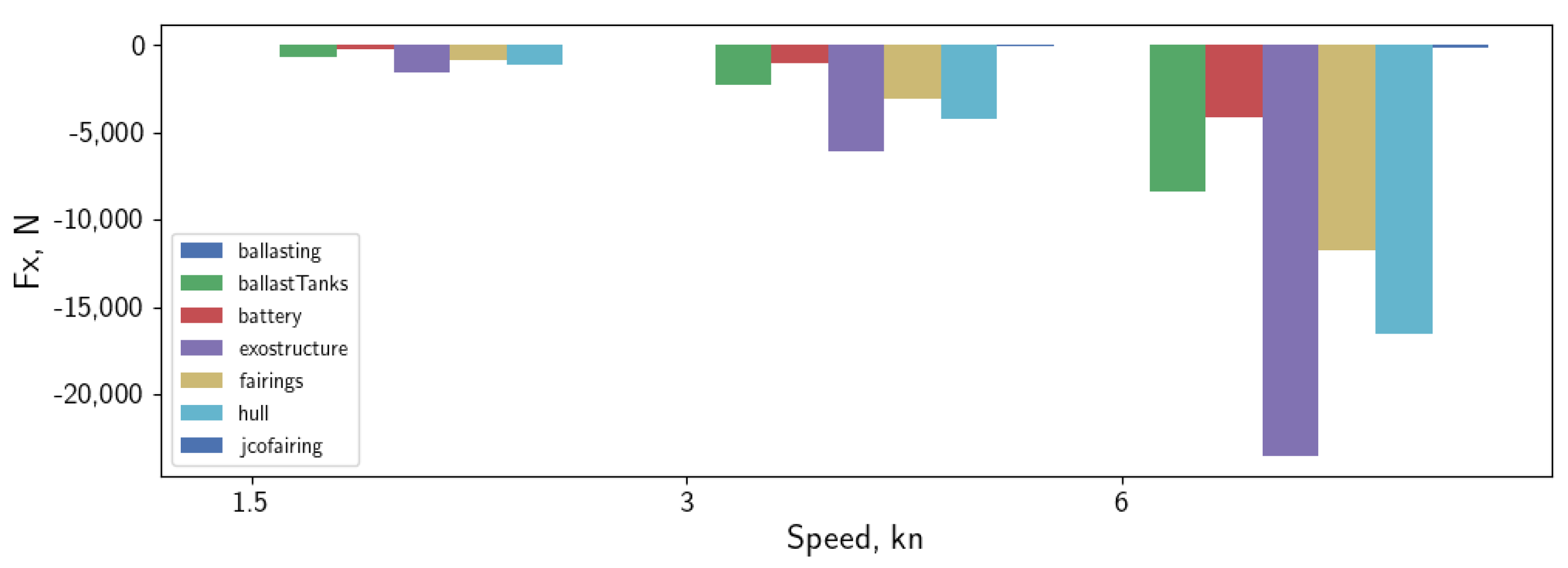
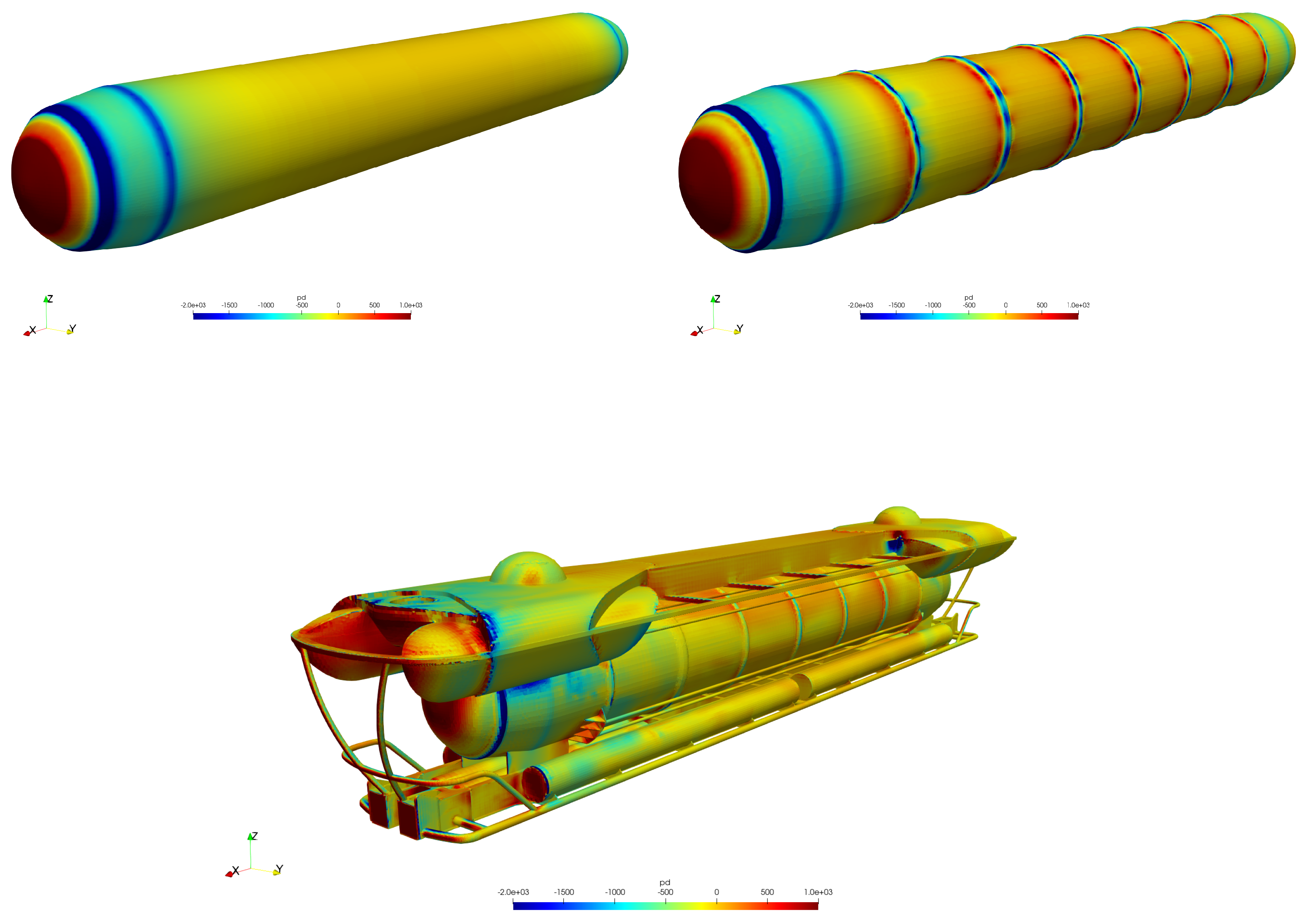
In this paper, an investigation of hydrodynamic resistance is conducted for a 25 m tourist submarine designed for depths up to 40 m and speeds up to 3 knots. More details about the structural design of this innovative underwater vehicle can be found in [
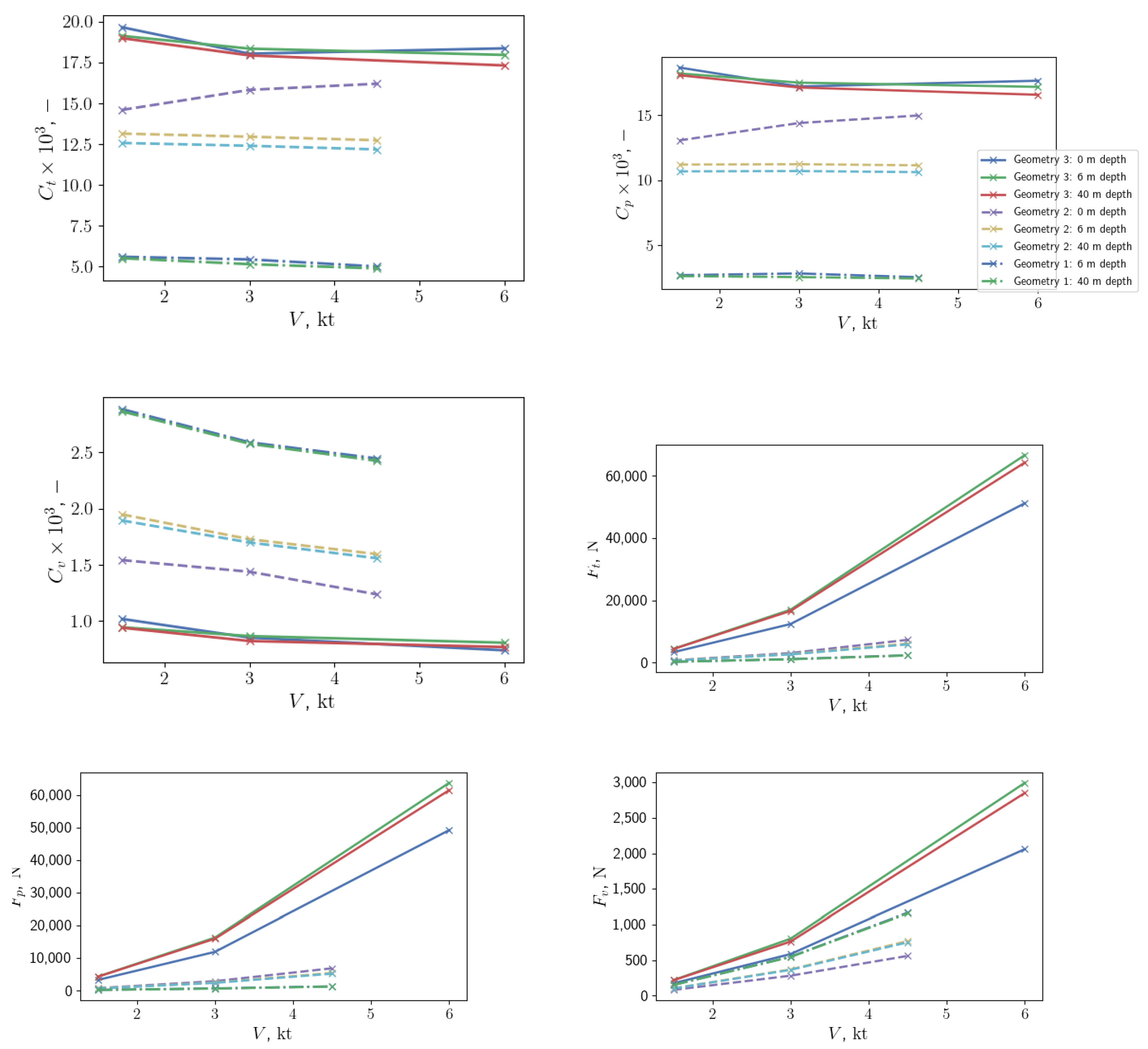
9]. The main purpose of the study is to evaluate the total hydrodynamic resistance of the submarine and its contribution to the resistance of different hull elements. Additionally, the influence of structural elements orthogonally exposed to the flow to the overall resistance is studied. The effect of the free surface on the resistance is considered and analysed. The main goal of the present study is to gain a better understanding of how structural element placement (relative to flow) influences the resistance of the submarine, and how the total resistance behaves compared to conventional submarines. Three different geometry configurations are considered with different amounts of geometrical elements present outside the cylindrical pressure hull: smooth cylindrical pressure hull, pressure hull with orthogonal ring protrusions, and finally, the full geometry of the submarine, including the pressure hull with rings and other external elements. Resistance coefficients for different geometries are compared and discussed. Simulations are carried out at two different depths and at the free surface to study the influence of resistance of the free surface on different geometries.
The paper is organised as follows.
Section 2 presents the numerical analysis of the submarine; laying out flow equations and the numerical modelling approaches, describing the submarine that is the subject of the study, describing simulated conditions are shown in detail, describing the numerical simulation set up, and showing the numerical results. Section three contains a discussion of the obtained results, while section four gives a short conclusion of the work.