Numerical Model of Constrained Wave Energy Hyperbaric Converter under Full-Scale Sea Wave Conditions
Abstract
1. Introduction
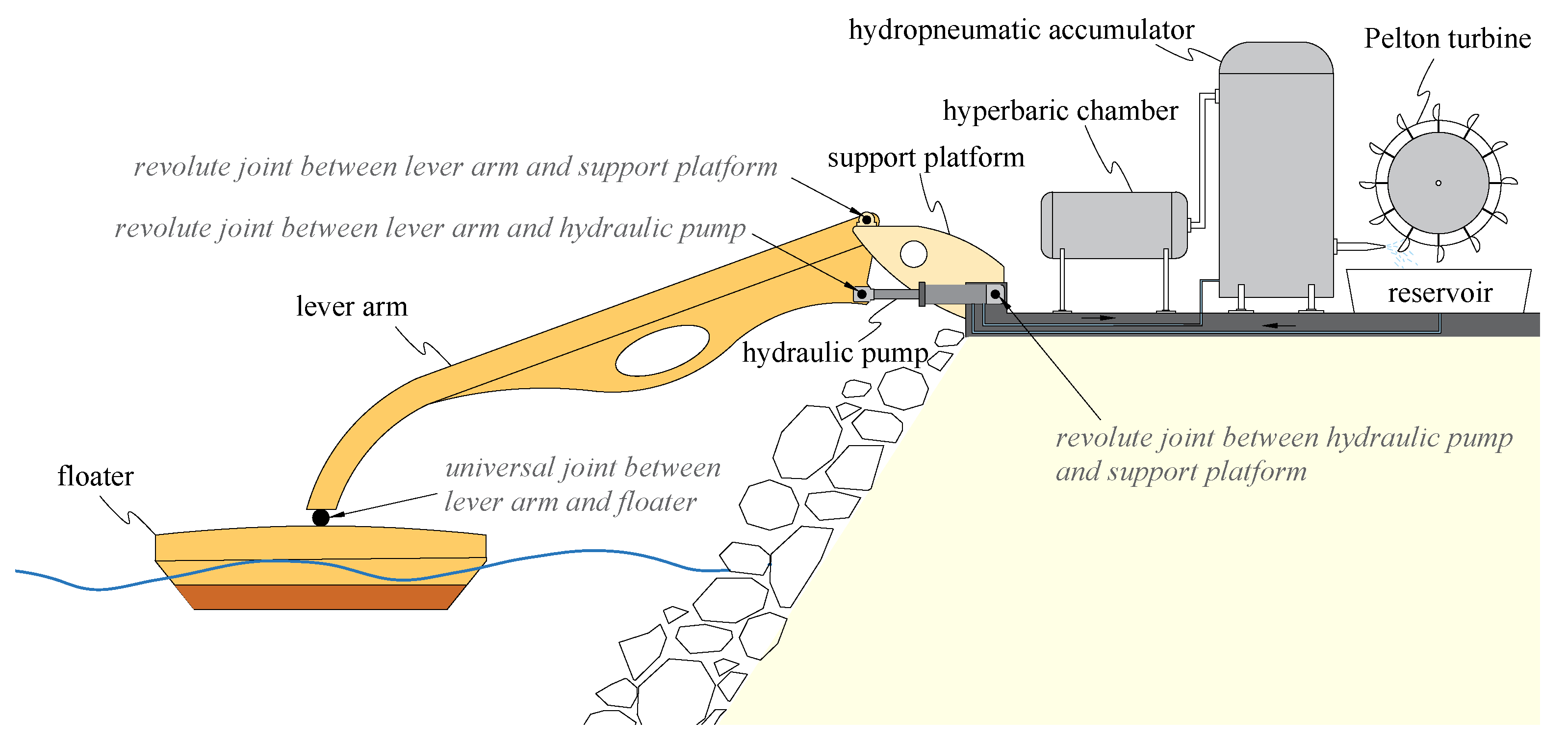
2. Numerical Model
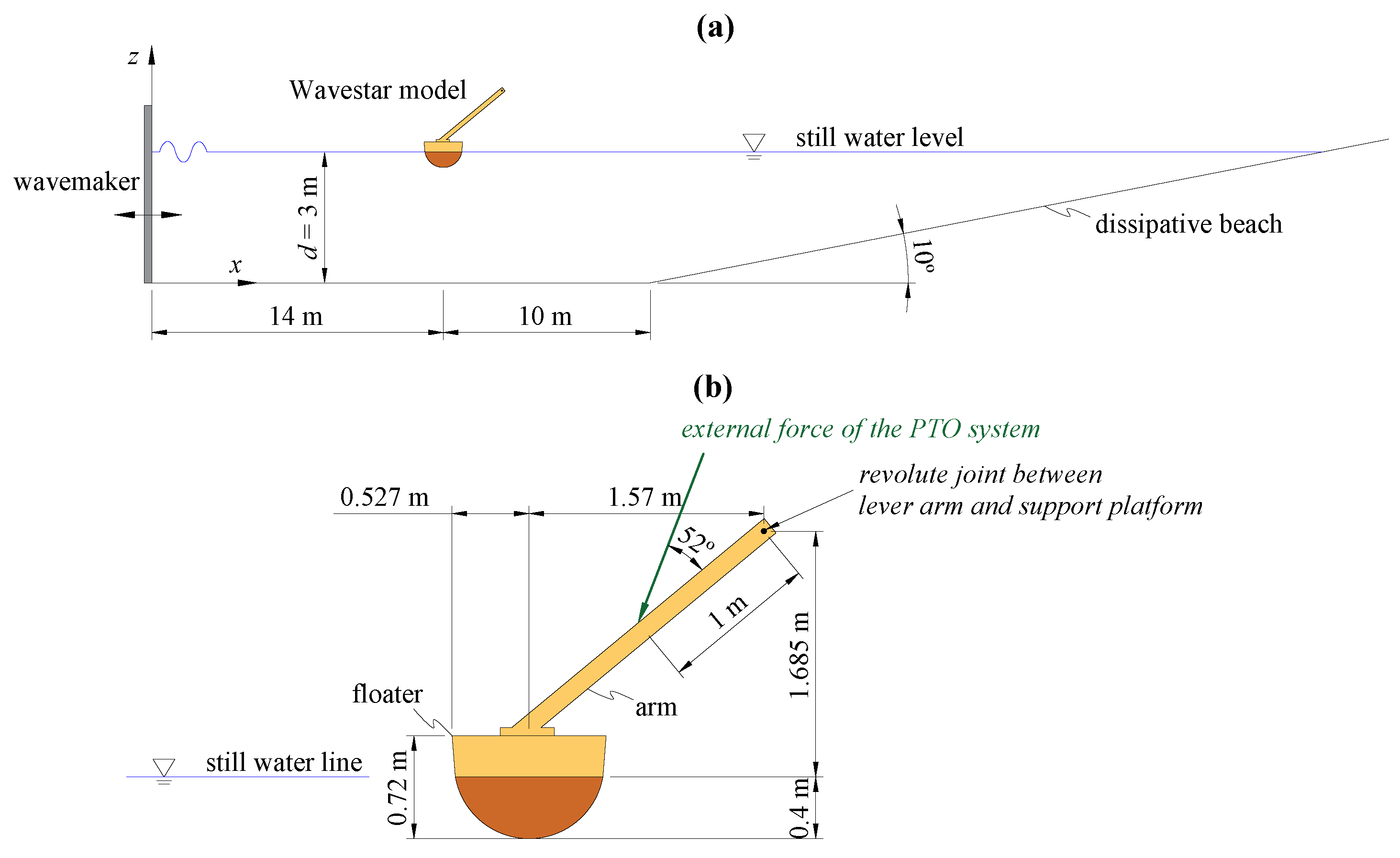
3. Numerical Model Validation
4. Results and Discussion
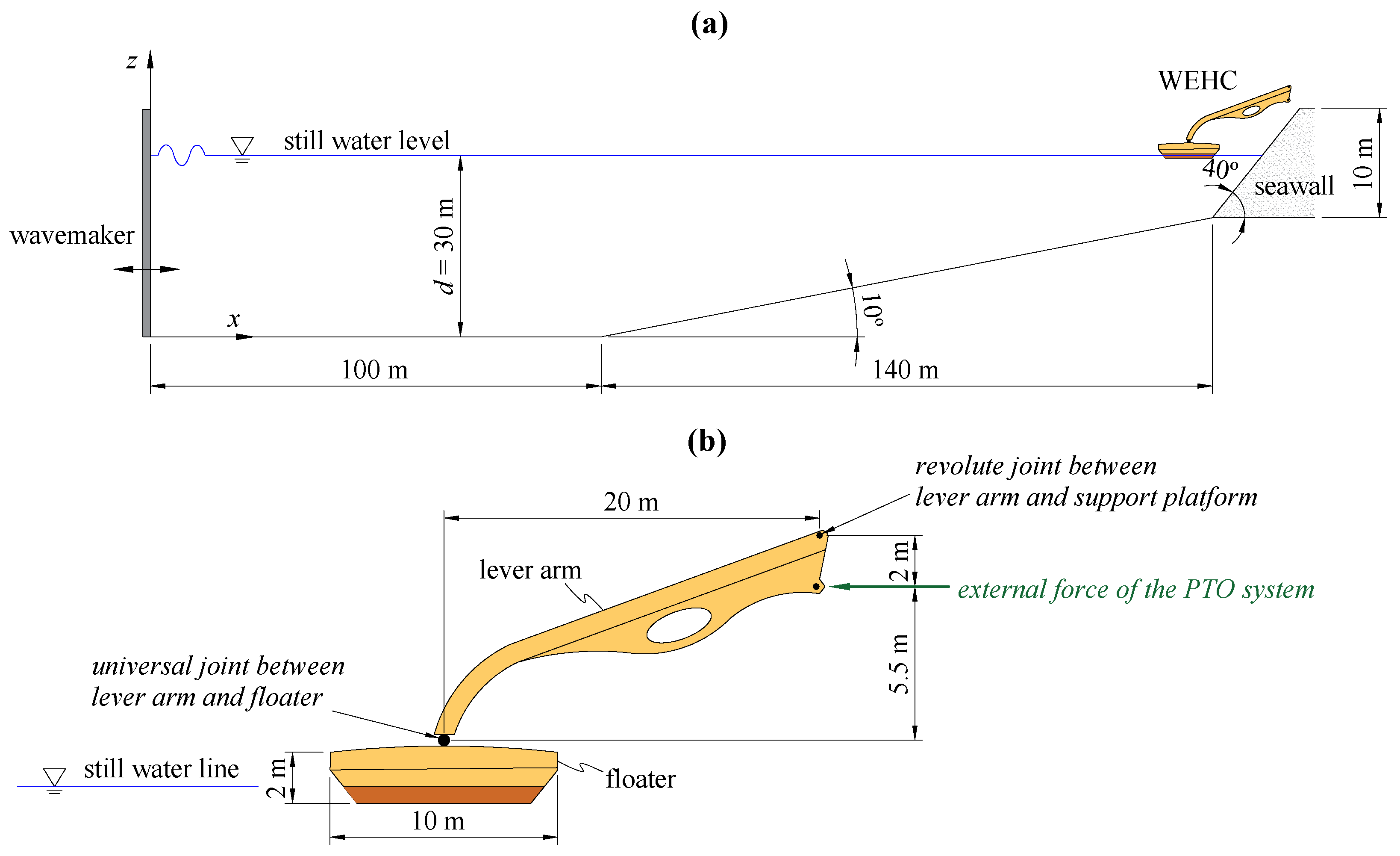
4.1. Simulation Set-Up
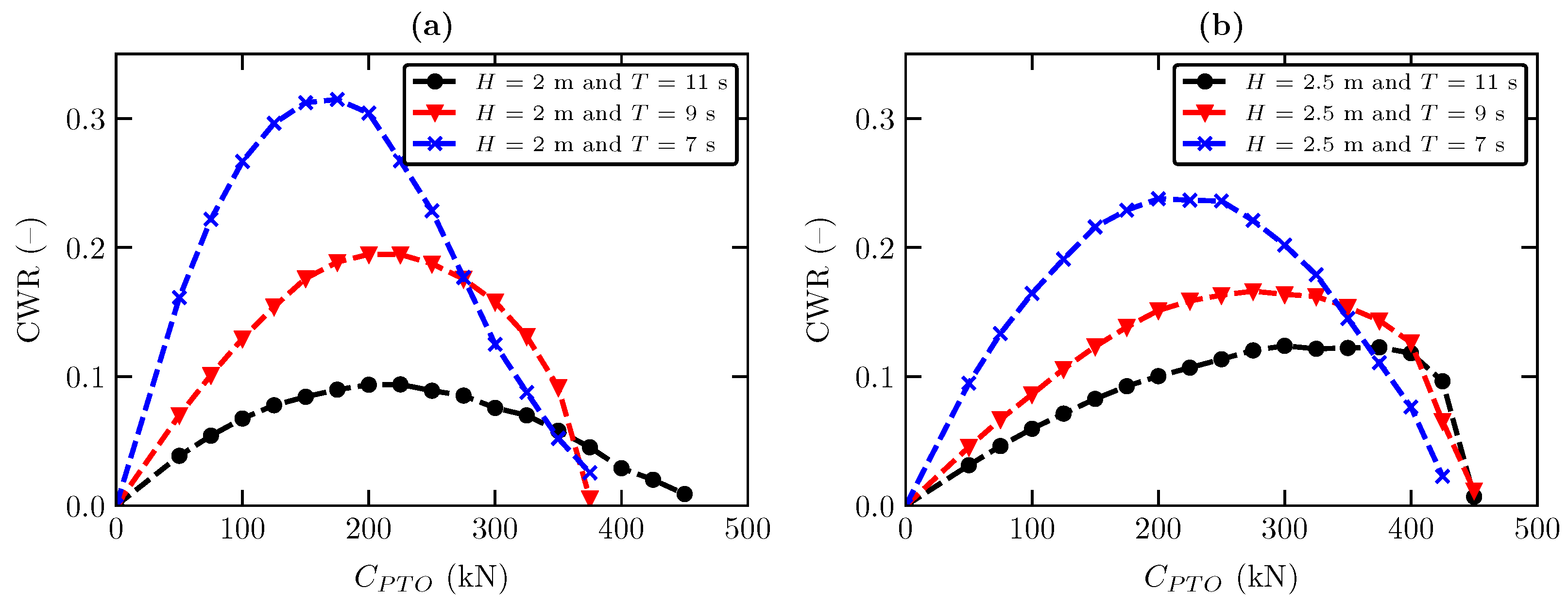
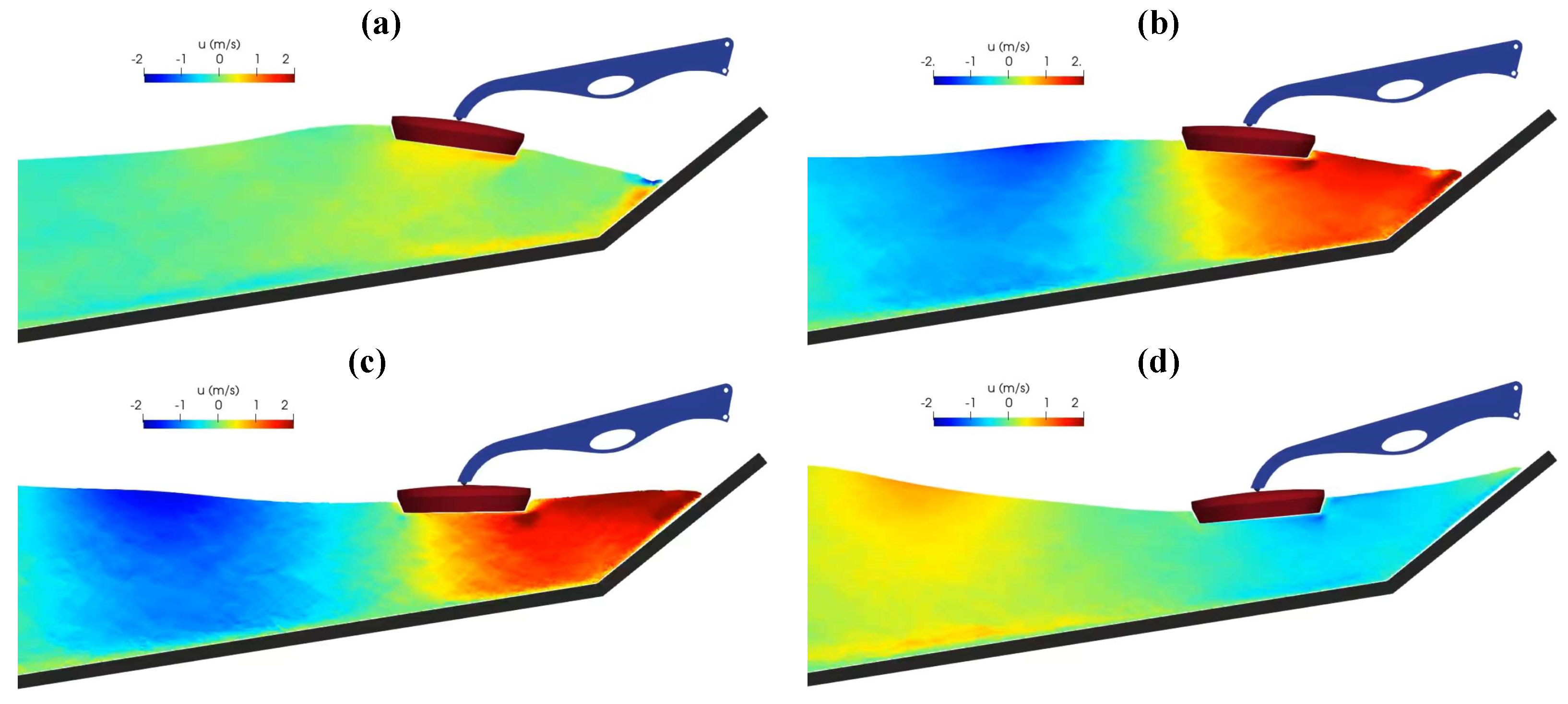
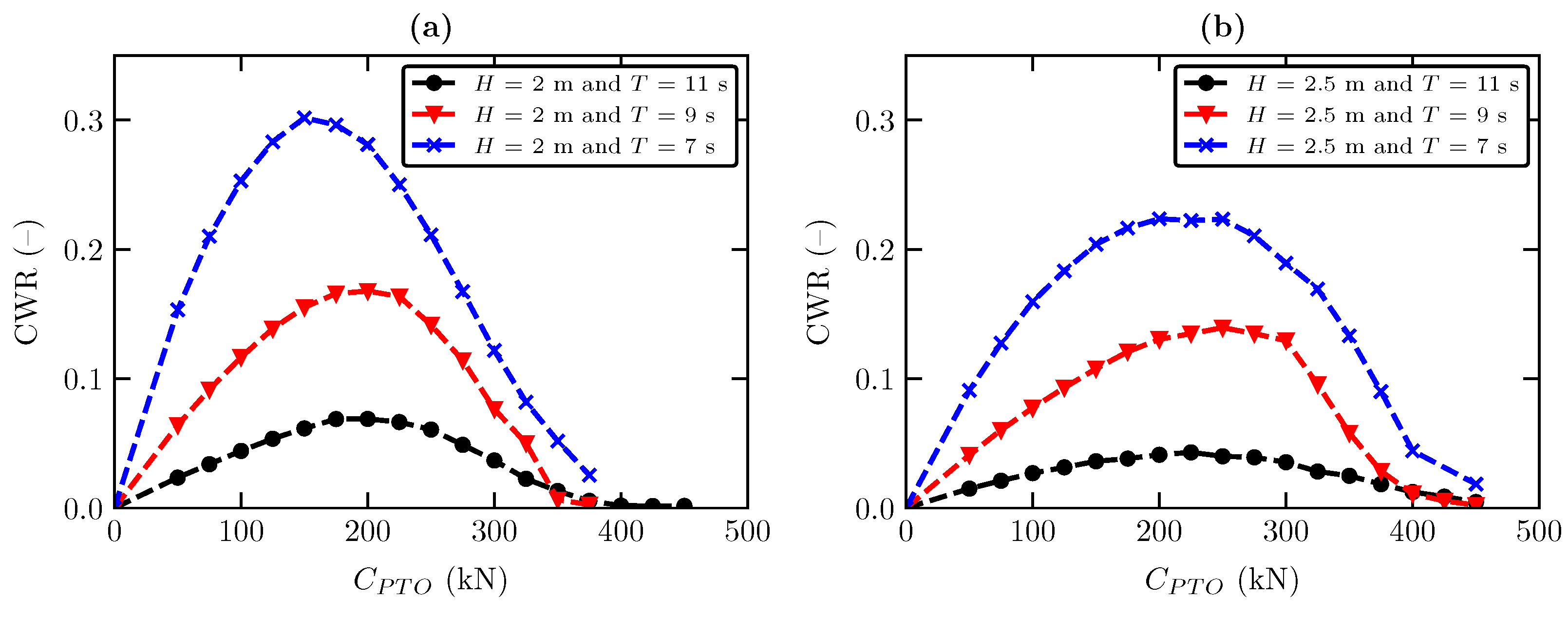
4.2. Power Absorption under Regular Sea State
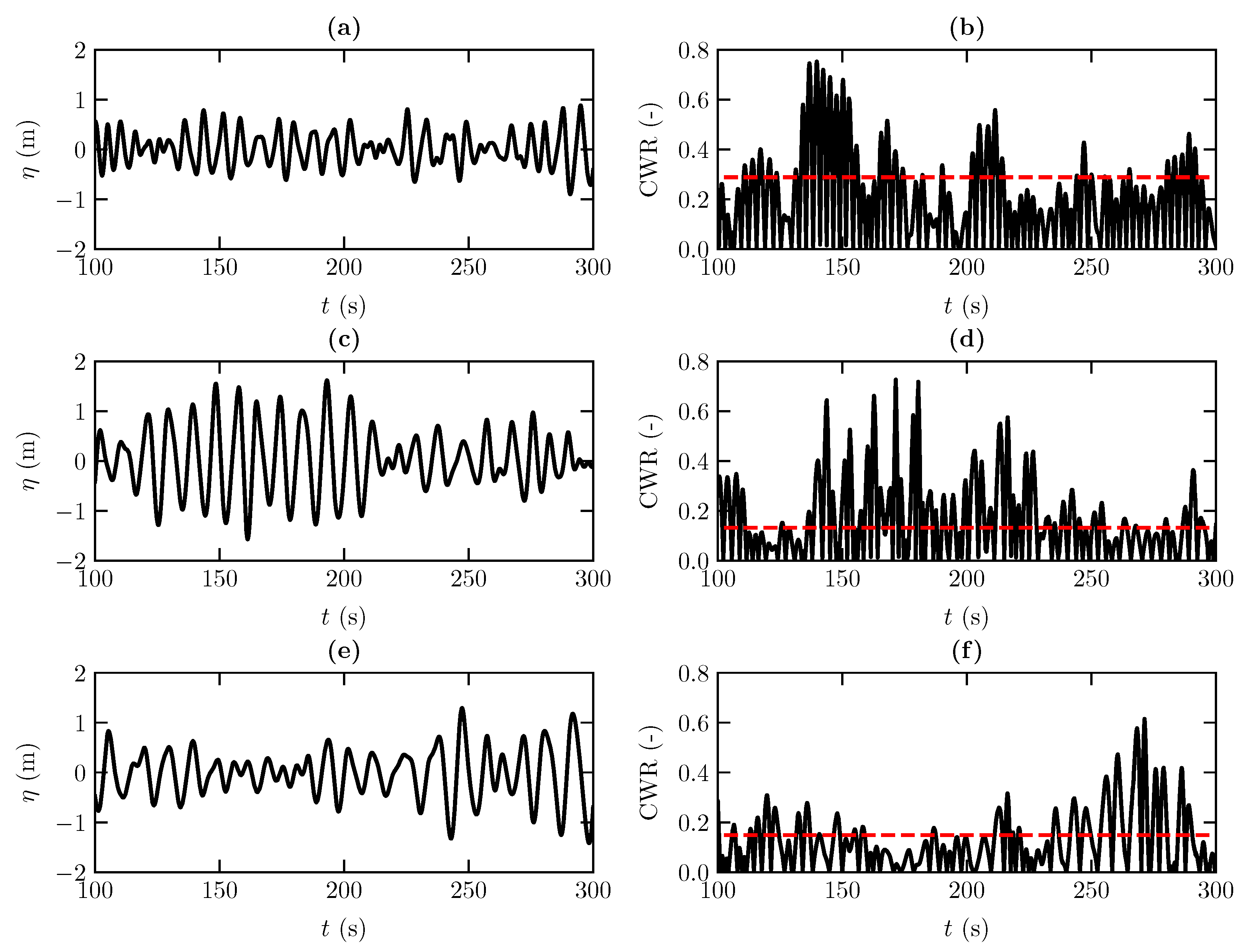
4.3. Power Absorption under Irregular Sea State
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Estefen, S.F.; da Costa, P.R.; Ricarte, E.; Pinheiro, M.M. Wave Energy Hyperbaric Device for Electricity Production. In Proceedings of the Volume 5: Ocean Space Utilization, Polar and Arctic Sciences and Technology, The Robert Dean Symposium on Coastal and Ocean Engineering, Special Symposium on Offshore Renewable Energy, San Diego, CA, USA, 10–15 June 2007. [Google Scholar] [CrossRef]
- Estefen, S.F.; Esperanca, P.d.T.T.; Ricarte, E.; da Costa, P.R.; Pinheiro, M.M.; Clemente, C.H.P.; Franco, D.; Melo, E.; de Souza, J.A. Experimental and Numerical Studies of the Wave Energy Hyberbaric Device for Electricity Production. In Proceedings of the Volume 6: Nick Newman Symposium on Marine Hydrodynamics, Yoshida and Maeda Special Symposium on Ocean Space Utilization, Special Symposium on Offshore Renewable Energy, Estoril, Portugal, 15–20 June 2008. [Google Scholar] [CrossRef]
- Garcia-Rosa, P.B.; Cunha, J.P.V.S.; Lizarralde, F.; Estefen, S.F.; Costa, P.R. Efficiency optimization in a wave energy hyperbaric converter. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009. [Google Scholar] [CrossRef]
- Martínez, M.; Molina, M.; Machado, I.; Mercado, P.; Watanabe, E. Modelling and simulation of wave energy hyperbaric converter (WEHC) for applications in distributed generation. Int. J. Hydrogen Energy 2012, 37, 14945–14950. [Google Scholar] [CrossRef]
- Machado, I.R.; Watanabe, E.H.; Garcia-Rosa, P.B. Modeling and analysis of a sea wave energy converter. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, Brazil, 29 November–2 December 2015. [Google Scholar] [CrossRef]
- Michele, S.; Sammarco, P.; d’Errico, M. Weakly nonlinear theory for oscillating wave surge converters in a channel. J. Fluid Mech. 2017, 834, 55–91. [Google Scholar] [CrossRef]
- Michele, S.; Renzi, E. A second-order theory for an array of curved wave energy converters in open sea. J. Fluids Struct. 2019, 88, 315–330. [Google Scholar] [CrossRef]
- Penalba, M.; Davidson, J.; Windt, C.; Ringwood, J.V. A high-fidelity wave-to-wire simulation platform for wave energy converters: Coupled numerical wave tank and power take-off models. Appl. Energy 2018, 226, 655–669. [Google Scholar] [CrossRef]
- Kleefsman, K.; Fekken, G.; Veldman, A.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid based simulation method for wave impact problems. J. Comput. Phys. 2005, 206, 363–393. [Google Scholar] [CrossRef]
- Agamloh, E.B.; Wallace, A.K.; von Jouanne, A. Application of fluid–structure interaction simulation of an ocean wave energy extraction device. Renew. Energy 2008, 33, 748–757. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Causon, D.M.; Mingham, C.G.; Qian, L. Numerical simulation of floating bodies in extreme free surface waves. Nat. Hazards Earth Syst. Sci. 2011, 11, 519–527. [Google Scholar] [CrossRef]
- Qian, L.; Causon, D.; Mingham, C.; Ingram, D. A free-surface capturing method for two fluid flows with moving bodies. Proc. R. Soc. Math. Phys. Eng. Sci. 2005, 462, 21–42. [Google Scholar] [CrossRef]
- Bangun, E.P.; Utsunomiya, T. Evaluation of Viscous Forces Acting on A Moving Body by Navier-Stokes Solver. In Proceedings of the OCEANS 2008—MTS/IEEE Kobe Techno-Ocean, Kobe, Japan, 8–11 April 2008. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.; Greaves, D.; Reeve, D.; Hunt-Raby, A.; Graham, D.; James, P.; Lv, X. A Level Set Immersed Boundary Method for Water Entry and Exit. Commun. Comput. Phys. 2010, 8, 265–288. [Google Scholar] [CrossRef]
- Ransley, E.; Greaves, D.; Raby, A.; Simmonds, D.; Jakobsen, M.; Kramer, M. RANS-VOF modelling of the Wavestar point absorber. Renew. Energy 2017, 109, 49–65. [Google Scholar] [CrossRef]
- Shabana, A.A. Dynamics of Multibody Systems; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Mazhar, H.; Heyn, T.; Pazouki, A.; Melanz, D.; Seidl, A.; Bartholomew, A.; Tasora, A.; Negrut, D. CHRONO: A parallel multi-physics library for rigid-body, flexible-body, and fluid dynamics. Mech. Sci. 2013, 4, 49–64. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Taylor, M.; Sugiyama, H.; Negrut, D. Chrono: An Open Source Multi-physics Dynamics Engine. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.; Tagliafierro, B.; Altomare, C.; Domínguez, J.M.; Gómez-Gesteira, M.; Viccione, G. Efficiency and survivability analysis of a point-absorber wave energy converter using DualSPHysics. Renew. Energy 2020, 162, 1763–1776. [Google Scholar] [CrossRef]
- Ropero-Giralda, P.; Crespo, A.J.C.; Coe, R.G.; Tagliafierro, B.; Domínguez, J.M.; Bacelli, G.; Gómez-Gesteira, M. Modelling a Heaving Point-Absorber with a Closed-Loop Control System Using the DualSPHysics Code. Energies 2021, 14, 760. [Google Scholar] [CrossRef]
- Tagliafierro, B.; Martínez-Estévez, I.; Domínguez, J.M.; Crespo, A.J.; Göteman, M.; Engström, J.; Gómez-Gesteira, M. A numerical study of a taut-moored point-absorber wave energy converter with a linear power take-off system under extreme wave conditions. Appl. Energy 2022, 311, 118629. [Google Scholar] [CrossRef]
- Monaghan, J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Brito, M.; García-Feal, O.; Domínguez, J.M.; Crespo, A.J.C.; Canelas, R.B.; Ferreira, R.M.L.; Neves, M.G. Coupling between DualSPHysics and Chrono-Engine: Towards large scale HPC multiphysics simulations. In Proceedings of the 11th SPHERIC International Workshop, Munich, Germany, 14–16 June 2016. [Google Scholar]
- Canelas, R.; Brito, M.; Feal, O.; Domínguez, J.; Crespo, A. Extending DualSPHysics with a Differential Variational Inequality: Modeling fluid-mechanism interaction. Appl. Ocean. Res. 2018, 76, 88–97. [Google Scholar] [CrossRef]
- Brito, M.; Canelas, R.; García-Feal, O.; Domínguez, J.; Crespo, A.; Ferreira, R.; Neves, M.; Teixeira, L. A numerical tool for modelling oscillating wave surge converter with nonlinear mechanical constraints. Renew. Energy 2020, 146, 2024–2043. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From fluid dynamics to multiphysics problems. Comput. Part. Mech. 2022, 9, 867–895. [Google Scholar] [CrossRef]
- Tasora, A.; Anitescu, M. A matrix-free cone complementarity approach for solving large-scale, nonsmooth, rigid body dynamics. Comput. Methods Appl. Mech. Eng. 2011, 200, 439–453. [Google Scholar] [CrossRef]
- Zheng, X.; Chen, G.; Cao, W.; Xu, H.; Zhao, R.; Xu, Q.; Kramer, M.; Touzé, D.L.; Borthwick, A.G.; Li, Y. On the energy conversion characteristics of a top-mounted pitching absorber by using smoothed particle hydrodynamics. Energy Convers. Manag. 2021, 250, 114893. [Google Scholar] [CrossRef]
- Crespo, A.; Domínguez, J.; Rogers, B.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Fourtakas, G.; Dominguez, J.M.; Vacondio, R.; Rogers, B.D. Local uniform stencil (LUST) boundary condition for arbitrary 3-D boundaries in parallel smoothed particle hydrodynamics (SPH) models. Comput. Fluids 2019, 190, 346–361. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Mazhar, H.; Heyn, T.; Negrut, D.; Tasora, A. Using Nesterov’s Method to Accelerate Multibody Dynamics with Friction and Contact. ACM Trans. Graph. 2015, 34, 32:1–32:14. [Google Scholar] [CrossRef]
- Stewart, D.E. Rigid-Body Dynamics with Friction and Impact. SIAM Rev. 2000, 42, 3–39. [Google Scholar] [CrossRef]
- Anitescu, M.; Hart, G.D. A constraint-stabilized time-stepping approach for rigid multibody dynamics with joints, contact and friction. Int. J. Numer. Methods Eng. 2004, 60, 2335–2371. [Google Scholar] [CrossRef]
- Anitescu, M. Optimization-based simulation of nonsmooth rigid multibody dynamics. Math. Program. 2006, 105, 113–143. [Google Scholar] [CrossRef]
- Canelas, R.B.; Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M.; Ferreira, R.M. A Smooth Particle Hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 2015, 78, 581–593. [Google Scholar] [CrossRef]
- English, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C.; Stansby, P.K.; Lind, S.J.; Chiapponi, L.; Gómez-Gesteira, M. Modified dynamic boundary conditions (mDBC) for general-purpose smoothed particle hydrodynamics (SPH): Application to tank sloshing, dam break and fish pass problems. Comput. Part. Mech. 2022, 9, 911–925. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary Conditions Generated by Dynamic Particles in SPH Methods. Comput. Mater. Contin. 2007, 5, 173–184. [Google Scholar]
- Leimkuhler, B.J.; Reich, S.; Skeel, R.D. Integration Methods for Molecular Dynamics. In Mathematical Approaches to Biomolecular Structure and Dynamics; Mesirov, J.P., Schulten, K., Sumners, D.W., Eds.; Springer: New York, NY, USA, 1996; pp. 161–185. [Google Scholar] [CrossRef]
- Monaghan, J.J.; Kos, A. Solitary Waves on a Cretan Beach. J. Waterw. Port Coastal Ocean. Eng. 1999, 125, 145–155. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ransley, E.J.; Greaves, D.; Jakobsen, M.; Kramer, M.; Ringwood, J.V. Validation of a CFD-based numerical wave tank model for the power production assessment of the wavestar ocean wave energy converter. Renew. Energy 2020, 146, 2499–2516. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.; Crespo, A.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-crested wave generation and absorption for SPH-based DualSPHysics model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Pontes, M.T.; Aguiar, R.; Pires, H.O. A Nearshore Wave Energy Atlas for Portugal. J. Offshore Mech. Arct. Eng. 2003, 127, 249–255. [Google Scholar] [CrossRef]
- Zhang, F.; Crespo, A.; Altomare, C.; Domínguez, J.; Marzeddu, A.; ping Shang, S.; Gómez-Gesteira, M. DualSPHysics: A numerical tool to simulate real breakwaters. J. Hydrodyn. 2018, 30, 95–105. [Google Scholar] [CrossRef]
- Hasselmann, K.F.; Barnett, T.P.; Bouws, E.; Carlson, H.C.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deut. Hydrogr. Z. 1973, 8, 1–95. [Google Scholar]







| Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|
| H (m) | 0.1 | 0.15 | 0.25 | 0.25 |
| T (s) | 1.4 | 1.4 | 1.4 | 2.8 |
| (-) | 0.103 | 0.154 | 0.257 | 0.07 |
| Test 1 | Test 2 | Test 3 | Test 4 | |
|---|---|---|---|---|
| z (m) | 10% | 8% | 7% | 9% |
| (m/s) | 11% | 6% | 5% | 13% |
| State 1 | State 2 | State 3 | State 4 | State 5 | State 6 | |
|---|---|---|---|---|---|---|
| H (m) | 2 | 2 | 2 | 2.5 | 2.5 | 2.5 |
| T (s) | 7 | 9 | 11 | 7 | 9 | 11 |
| (-) | 0.083 | 0.054 | 0.040 | 0.104 | 0.067 | 0.050 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brito, M.; Bernardo, F.; Neves, M.G.; Neves, D.R.C.B.; Crespo, A.J.C.; Domínguez, J.M. Numerical Model of Constrained Wave Energy Hyperbaric Converter under Full-Scale Sea Wave Conditions. J. Mar. Sci. Eng. 2022, 10, 1489. https://doi.org/10.3390/jmse10101489
Brito M, Bernardo F, Neves MG, Neves DRCB, Crespo AJC, Domínguez JM. Numerical Model of Constrained Wave Energy Hyperbaric Converter under Full-Scale Sea Wave Conditions. Journal of Marine Science and Engineering. 2022; 10(10):1489. https://doi.org/10.3390/jmse10101489
Chicago/Turabian StyleBrito, Moisés, Francisco Bernardo, Maria G. Neves, Diogo R. C. B. Neves, Alejandro J. C. Crespo, and José M. Domínguez. 2022. "Numerical Model of Constrained Wave Energy Hyperbaric Converter under Full-Scale Sea Wave Conditions" Journal of Marine Science and Engineering 10, no. 10: 1489. https://doi.org/10.3390/jmse10101489
APA StyleBrito, M., Bernardo, F., Neves, M. G., Neves, D. R. C. B., Crespo, A. J. C., & Domínguez, J. M. (2022). Numerical Model of Constrained Wave Energy Hyperbaric Converter under Full-Scale Sea Wave Conditions. Journal of Marine Science and Engineering, 10(10), 1489. https://doi.org/10.3390/jmse10101489








