2.1. FSI Analysis for Soil Penetration
To numerically simulate the phenomenon of an anchor pile penetrating into the burial soil of subsea HVDC cable, FSI analysis based on the CEL technique was applied in the present study. The CEL technique utilizing the merits of both the Lagrangian and the Eulerian theory is usefully applied in the FSI simulation. In the FSI simulation using the CEL technique, the Eulerian domain is tracked as it flows through the fluid mesh by calculating its Eulerian volume fraction (EVF). Each Eulerian element is specified as a percentage representing the portion of the element filled with a fluid material. If the Eulerian element is fully filled with the fluid material, its EVF becomes 1.0, while if there is no fluid material in the Eulerian element, its EVF becomes 0.0. Contact between Eulerian domains and Lagrangian domains is realized via a general contact algorithm based on penalty contact theory. The penalty contact theory has better convergence of numerical solutions than the kinematic contact theory. In the penalty contact theory, some pseudo seeds are generated on the edges and faces of Lagrangian domains, while anchor points are generated on the surface of Eulerian domains. The penalty contact theory approximates hard pressure–overclosure behavior. The penalty contact theory allows small penetration of the Eulerian domain into the Lagrangian domain. The Lagrange element is able to move through the Eulerian domain without resistance until the fluid element’s EVF is greater than 0.0. The CEL technique generally adopts the explicit time integration scheme. In the explicit time integration scheme, a central difference method is used to solve the differential equations of the non-linear system. The next time step solution of the differential equations can be obtained directly from the solution of the previous time step, such that no iteration is required. Difficult contact problems can be also easily solved utilizing the explicit time integration scheme.
The FSI analysis method numerically simulates the phenomenon of the interaction between a fluid and a structure by coupling the Eulerian technique that embodies a fluid region by the Finite Volume Method (FVM) and the Lagrangian technique that defines a structural region by the Finite Element Method (FEM) [
15,
16,
17,
18,
19]. For the numerical simulation of soil penetration using the FSI analysis, the MSC.Nastran SOL700 module [
15], which is a general-purpose nonlinear finite element analysis code based on the explicit time integration method, was used in the present study. In the FSI analysis, the contact surfaces of fluid–structure elements are connected and behave in a fluid–structure coupled algorithm. When the structural elements of the Lagrangian model on the contact surface interact with the boundary conditions of displacement and velocity on the fluid surface elements of the Eulerian fluid model, the fluid reaction force is transmitted to the elements of the Lagrangian model by the fluid–structure coupling algorithm. As shown in
Figure 1, while the deformation or motion of the structure, which is the Lagrangian elements, has an effect on the boundary of the fluid region, which is the Eulerian elements, the pressure generated in the fluid region acts as an external load of the structure. To reflect the interaction between the fluid and structure media, the common boundary surface where the two media are in contact with each other is set as the coupling surface, through which the two media exchange the interaction behaviors.
In the numerical simulation of the present study, the anchor pile, the structural region, was embodied as the Lagrangian element, and the air domain and soil belonging to the fluid region were applied as the Eulerian elements.
2.2. Numerical Simulation Model of Anchor Pile
It is reported that the largest number of subsea HVDC cables have been embedded in the southwest sea located between the Jeonnam coast and Jeju Island of Korea [
3,
17,
18]. As for the specification of the anchor pile used for the numerical simulation in the present study, the 0.8 ton class anchor pile reported to be mainly used in the aquaculture farms of the southwest sea were considered [
2]. A three-dimensional design model of the 0.8 ton class anchor pile’s structural shape was generated by measuring the dimension of an actual product. The numerical simulation model generated based on the three-dimensional design model and the actual configuration are shown in
Figure 2. As shown in
Figure 2, the Lagrangian finite element model of the anchor pile was organized by mixing the 3-node and 4-node shell elements and generated using 1085 nodes and 843 elements.
To reflect the material properties of the anchor pile, which is made of a general steel, the property values of 7850 kg/m3, 210 Gpa, and 0.3 were applied as the density, modulus of elasticity, and the Poisson’s ratio, respectively. In addition, the weight of the generated finite element model was arranged to be same as that of the actual anchor pile.
2.3. Numerical Simulation Model of Soil Penetration
The soil penetration numerical simulation model was configured in the same way as the conditions of the field verification test that was conducted to verify the safe depth of burial soil against the drop impact of the anchor pile. The configuration of the soil penetration numerical simulation model is shown in
Figure 3.
As shown in
Figure 3, in the soil penetration numerical simulation model, the air layer region of the atmosphere, and the ground region were modeled as Eulerian elements, and the anchor pile, modeled as a Lagrangian element, was placed at the same drop height as that of the field verification test. The drop height was determined to be 13.5 m, taking into account the water depth of the sea area where the frequency of actual subsea HVDC cable damage accidents was reported to be high and the drop speed in seawater [
2]. The drop speed was set as the drop speed in seawater, taking into account the drag coefficient for the shape of the anchor pile and estimated from the following formula [
3]:
where
and
are the densities of the anchor pile and seawater, respectively,
is the volume of the anchor pile,
is the acceleration of gravity,
is the drag coefficient,
is the projected area of the anchor pile, and
is the drop motion speed of the anchor pile. The values of 0.133 m
3, 0.028 m
2, and 0.82 were applied, respectively [
3], to the volume of the anchor pile, projected area, and the drag coefficient, and the drop speed was calculated to be 11.98 m/s by applying Equation (1). As represented in Equation (1), for the same falling object, the drop speed is affected by the fluid density in the target drop domain. That is, as the fluid density increases, the drop speed decreases.
As for the size ratio of the horizontal space and the fluid–structure elements of the numerical analysis model, the width and length of the horizontal space were set to be 3.0 m based on the existing research results [
17] on the accuracy and calculation time of the FSI analysis, and the element size of the Eulerian model was densely organized at the rate of 25% compared to the element size of the Lagrangian model. The Eulerian model of the air layer region was made up of 532,800 nodes and 288,000 elements by applying an 8-node solid element as the element form, and 1.184 kg/m
3, 1.05 N/m
2, and 101,325 Pa were applied as the density, bulk modulus, and atmospheric pressure, respectively. As for the soil burial depth of the numerical simulation model, 3.0 m was applied, which is the general construction burial depth [
2] of the subsea HVDC cables actually installed in the southwest sea of Korea, and three types of soil—a clay layer, sand layer, and a clay–sand mixed layer—were considered, which are the representative types of the soil under which subsea HVDC cables are embedded. The clay–sand mixed layer was made up of 1.0 m clay layer at the top and 2.0 m sand layer immediately beneath it. In addition, the total soil depth was modeled as 5.0 m, commonly taking into account 2.0 m-deep general soil below the burial soil to reflect the conditions of the field verification test. The Eulerian model of the seabed region was made up of 197,334 nodes and 106,667 elements by applying an 8-node solid element as the element form.
As for the material model of the seabed, the Mohr-Coulomb yield model [
16] was considered. The material property values of the seabed required for the numerical simulation were estimated referring to the existing research results, and the detailed property values were put in order and are shown in
Table 1 [
20,
21,
22,
23,
24].
The interaction between the Eulerian region (air layer and soil) and the Lagrangian region (anchor pile) was taken into account by setting the common boundary surface of the anchor pile where the Eulerian regions and the Lagrangian region are in contact with each other as the interaction surface. As for the Equation of State (EOS) required to numerically embody the material behavior of the Eulerian region in the FSI analysis, the following linear polynomial EOS was applied [
25]:
where
is the pressure,
,
is the reference density,
is the whole material density,
are Eulerian fluid constants, and
is the specific internal energy per unit mass.
2.4. Numerical Simulation Results for Soil Penetration of Anchor Pile
In order to review the feasibility of the numerical simulation method used in this study in advance, the FSI analysis method applied in this study was similarly simulated and compared with the study results of the underwater drop test of the bearing steel sphere [
26].
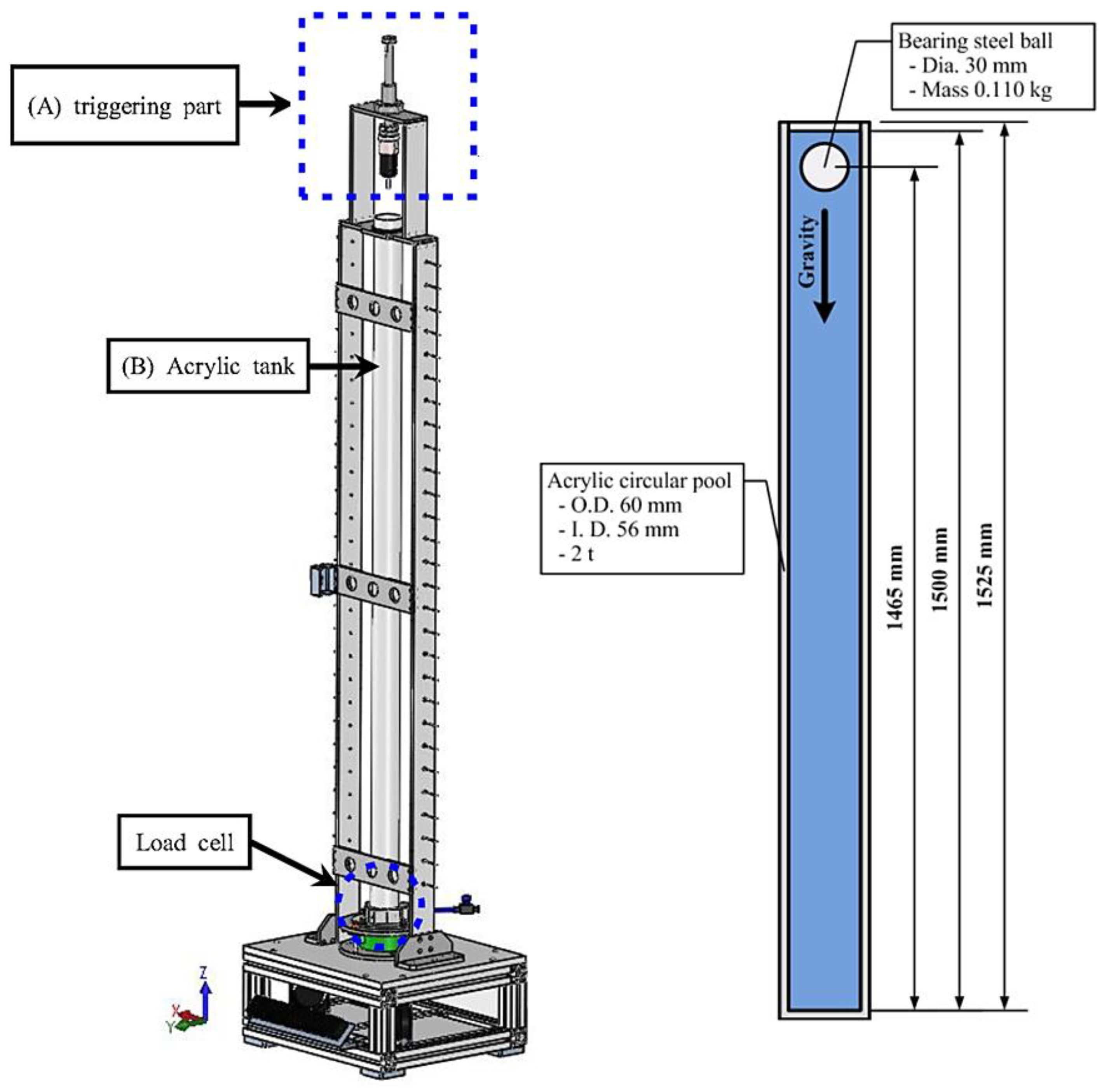
Figure 4 shows the configuration and detailed dimensions of the testing device for the underwater drop test of the bearing steel sphere.
As shown in
Figure 4, in the underwater drop test of the bearing steel sphere, with a diameter of 30 mm and mass of 0.11 kg, comprised the sphere being freely dropped into a tank with the water level of 1500 mm. Then, the change in position of the sphere was measured at the direction of gravity for the one second. In order to compare the accuracy of the FSI analysis based on the CEL method applied in this study with the existing test research results, a numerical simulation model was generated as shown in
Figure 5. As shown in
Figure 5, the 8-node solid Lagrangian element was used for the bearing steel sphere, and it was composed of 124 nodes and 24 elements. The Euler grid of fluid in the water tank used a hexahedron element and was composed of 77,959 nodes and 42,140 elements. The density and bulk modulus of elasticity for the fluid were applied as 1000 kg/m
3 and 2.1 GPa, respectively. In order to reflect the interaction of the fluid–structure model, the surface of the bearing steel sphere, which is the common boundary domain where the two models are in contact, was set as the coupling surface. The grid size of the Eulerian model was applied densely by the rate of 25% compared to the element size of the Lagrangian model, the same as the soil penetration numerical simulation model in
Section 2.3.
Figure 6 shows the representative results of the underwater drop movement distance of the sphere according to the fall time of the bearing steel sphere calculated from the FSI analysis.
As shown in
Figure 6, the underwater drop movement distance of the bearing steel sphere varied with time variation due to the loss of kinetic energy caused to the interaction with the fluid.
Figure 7 graphically represents the FSI simulation results of the underwater drop movement distance of the bearing steel sphere, comparing previous research results [
26], the actual test, the computational fluid dynamics (CFD) analysis, and the theoretical solution.
As shown in
Figure 7, both the FSI analysis results and the CFD analysis results, excluding the results of the theoretical solution, represented almost complete solution convergence and also had high agreement with the actual test results. Through a comparative review of the bearing steel sphere, it was verified that significant results can be derived from the FSI analysis based on the CEL method used in this study as applied to the underwater fall simulation. Such simulation is similar to the soil penetration simulation of anchor piles to determine the burial depth that can ensure the safety of subsea HVDC cables. The verified numerical modeling and simulation methods were applied to the simulation-based case studies for the anchor pile penetration to various types of soil in which the subsea HVDC cables are to be embedded.
The penetration characteristics resulting from the drop impact of the anchor pile were evaluated for each case where the seabed soil was a clay layer, sand layer, or clay–sand mixed layer, using the numerical model represented in
Figure 3.
Figure 8 shows the numerical simulation results of the anchor pile’s final penetration into each type of soil.
As shown in
Figure 8, the maximum penetration depths of the anchor pile were calculated to be 3.85 m, 2.07 m, and 2.82 m, respectively, in the case of the clay layer, sand layer, and clay–sand mixed layer. The relative maximum penetration in the clay layer was found to be larger than that of the sand layer and the clay–sand mixed layer by 86% and 37% or more, respectively. The difference of penetration depth can be considered to be caused by the material properties of the soil. In particular, the internal friction angle is the angle between a horizontal plane and a straight line with respect to the normal and shear stresses acting on the soil particles, and is a soil property that represents the shear resistance characteristic. As represented in the material properties of soil in
Table 1, the internal friction angle of the sand layer was much larger than that of the clay layer, and it can be seen that the relatively small penetration depth in the sand layer was affected by the internal friction angle.
The subsea HVDC cables in the southwest sea of Korea are generally installed at a burial depth of 3.0 m [
2,
4]. However, the numerical simulation results showed that, although subsea HVDC cables can be safely protected from the penetration of an anchor pile by the burial method itself alone in the sand layer and clay–sand mixed layer, an additional protective facility for subsea HVDC cables is required to be constructed in the case of the clay layer.
The variance of the anchor pile drop speed and the variance of the soil penetration in clay layer, sand layer, and clay–sand mixed layer are shown in
Figure 9 and
Figure 10, respectively.
The variance of drop speed and the variance of the soil penetration shown in
Figure 9 and
Figure 10, respectively, were measured in reference to the node at the extreme end of the anchor pile model. As shown in
Figure 9, while the drop speed of the anchor pile rapidly decreased from the point in time when the soil penetration started in the case of the sand layer, the clay layer showed a characteristic where the drop speed decreased, after the maximum drop speed was constantly maintained, down to the soil penetration depth of about 2.0 m. In addition, the clay–sand mixed layer showed an intermediate type of drop speed behavior between the clay layer and the sand layer. As shown in
Figure 10, the soil penetration of the anchor pile was maintained at the maximum penetration depth of 3.85 m at the point in time of 1.7 s after the drop of the anchor pile in the clay layer; it was maintained at the maximum penetration depth of 2.07 m at the point in time of 1.5 s after the drop of the anchor pile in the case of the sand layer; and it was maintained at the maximum penetration depth of 2.82 m at the point in time of 1.6 s after the drop of the anchor pile in the case of the clay–sand mixed layer. The convergence tolerance of the numerical simulation was considered as both displacement and energy convergence tolerances, and their values were set to 0.001, a default value recommended in the MSC.Nastran SOL700 module [
15]. From the penetration depth variation of
Figure 10, it was confirmed that the numerical solutions were converged.
Considering the decreasing drop speed characteristic of the anchor pile and the results of the maximum soil penetration time, the soil burial safety of the sand layer was superior to that of the clay layer and the clay–sand mixed layer.