Experimental Study of the Effect of Backfill Conditions on Soil Responses around a Pipeline under Wave–Current Load

Abstract

Waves and currents coexist widely in the ocean, and the interaction of waves and currents plays an important role in the instability of submarine pipelines. So far, most studies have concentrated on discussing the dynamic reaction within the seabed around a pipeline under pure wave action, monotypic sediment, and an exposed or fully buried condition. In this study, the effect of current characteristics (e.g., current velocity and propagation direction) and backfilling conditions (e.g., backfill depth and sand property) on the dynamic response around the submarine pipeline is investigated by conducting laboratory experiments. Pipeline was buried in the excavated trench using three types of sand with the median size of 0.150 mm, 0.300 mm and 0.045 mm, respectively. Five relative backfilled depths, with the ratios of backfill depth over the pipeline diameter being 0, 1/2, 1, 3/2 and 2, were tested. The excess pore pressure was measured simultaneously by using the pore pressure sensors installed around the pipeline surface and beneath the pipeline. Results show that both the pore pressure amplitude and its descent rate gradually decrease with an increasing backfill depth, which decreases the soil liquefaction potential. Under the co-current actions, the decrease rate of the pore pressure along the vertical direction increases with an increasing current velocity. However, the increased current velocity leads to a decrease of the attenuation rate under the counter-current actions compared with the pure wave actions, and the counter-current effect on the pore pressure within the seabed is greater than the co-current. The results indicate that the dynamic response around the pipeline in coarse sand is close to that without the backfill scenario, even if the backfill depth reaches up to two times that of the pipeline diameter. It is found that the larger the median particle size of backfill sand, the smaller the impact on pore pressure within the seabed beneath the pipeline.

1. Introduction

Pipelines are widely used in coastal and ocean engineering, and usually installed in trenches for safety and stability, while sand is often used as the backfill material in practice. The backfill depth has a great influence on the in-situ stability of the pipeline. In general, thick backfill depth can protect the pipeline better, but it significantly increases the cost. Though thin backfill depth is economical, the pipeline may be unstable in this scenario. Therefore, how to backfill a trench under wave and current load to appropriately and economically protect the pipeline needs to be investigated.

In the past decades, extensive studies have been conducted to investigate effective stress and distribution of excess pore pressure around the pipeline within the seabed induced by wave loading. Cheng et al. [1] studied the wave-induced seepage force on soil responses around a rigid and deformable pipeline using the boundary element method. They found that the uplift seepage force could reach up to 60% of the drainage weight if the pipeline was close to the seabed surface. McDougal et al. [2] proposed an analytical model to calculate the wave-induced pore pressure and pressure force around the buried pipeline. Magda [3,4,5] studied the saturation effect on the dynamic responses within the seabed around the submarine pipelines using the finite element method. He developed an empirical formula for computing the lifting force of the buried pipelines under different saturation conditions. Note that all the above studies assumed the pipeline was rigid and fixed, and only wave-induced pore pressure and uplift force were considered for evaluating pipeline safety. Yang et al. [6] (2014) conducted laboratory experiments to investigate the protection of the unidirectional flow generated-induced scour around the pipe by placing a rubber plate beneath the pipe. They found that when the length of the rubber plate reached a critical value, there was no scour taking place around the pipe. Using laboratory experiments, Sun et al. [7] investigated the wave-induced soil response around a partially buried pipeline in a trench. Gao et al. [8] investigated the wave-induced pore pressure around a buried or partially buried pipeline in a silty bed. They found that the residual pore pressure dominated the soil liquefaction in their study. Recently, Zhai et al. [9] carried out experiments and performed a numerical simulation to investigate the wave-induced pore pressure around twin pipelines. They found that the distance between two pipes had a great effect on the pore pressure and effective stress around the pipelines.

However, the other dynamic responses such as effective stress, pipeline deformation and uplift force, are also crucial to the stability of the pipelines [10]. For example, shear failure could happen near the pipeline due to effective stress. Jeng and Cheng [11] studied wave-induced soil responses around the pipeline, including effective stress and soil displacement, by using a finite element model. They found that the potential shear failure around the pipelines could be evaluated through the Mohr–Coulomb yield criterion. A two-dimensional finite element numerical model was established by Jeng [12] to calculate the wave-induced soil dynamics around an elastic pipeline. The results presented were that when the depth function of shear modulus remained unchanged, the permeability effect on the wave-induced pore pressure along the pipeline surface, within a coarse sand seabed, was greater than that within a fine sand seabed. Seabed response induced by cnoidal wave was modeled by Zhou et al. [13] with the finite element method. They found that the difference between the maximum pore pressure and vertical effective stress, caused by the cnoidal wave and Stokes wave, could be up to 60–70%. Gao et al. [14] considered the influence of overburden geometry and the property of backfill material on the pipeline surface and the stress inside the pipeline caused by waves, as well as the nonlinear effect of waves. Zhai et al. [15] analyzed the relationship of the seepage action around the pipeline, wave parameters and the pipeline size. The stronger wave action, the larger seabed permeability and pipeline diameter, and the smaller flow gap ratio would lead to the movement of soil particles. Under wave actions, the seepage changes periodically along the seabed surface. The horizontal seepage discontinuity exists at the bottom of the pipeline where the flow rate is 0.

Lin et al. [16] studied the stability of pipelines laid in trenches under wave load using the finite element method. They found that half-buried or even fully buried pipelines cannot plenarily decrease the excess pore pressure. However, when the thickness of the overlying soil layer was more than 1.375 times of the pipeline diameter, the backfill sand could effectively protect the pipelines from liquefaction. Based on the generalized Biot model, Luan et al. [17] evaluated the momentary liquefaction potential around a buried pipeline by the finite element method. A two-dimensional coupling model was developed by Duan [18] to study the liquefaction potential around partially buried pipelines in the trench of a non-cohesive seabed. Biot’s consolidation equation and the Reynolds-Averaged Navier–Stokes (RANS) equation were adopted to govern the dynamic response within the seabed, as well as the wave motion. Similarly, a three-dimensional hybrid model, combining the RANS equation with Biot’s consolidation equation, was established by Li et al. [19]. The numerical simulation showed that the liquefaction depth increases with the decreasing saturation degree and wave height. Under the anisotropic seabed condition, there is a nonlinear relationship between the maximum liquefaction depth and the seabed permeability. Wang et al. [20] applied a meshfree model to assess the relationship of wave parameters, soil characteristics and the liquefaction depth. Under the same wave action, the excess pore pressure is relatively great within the seabed with low saturation and permeability. The liquefaction depth around the pipeline increases with the increases of wave height and wave period. It was also found that the probability of liquefaction instability decreases with the increase of backfill depth. Apart from regular waves, Lin and Wang [21] established a two-dimensional numerical model to study the pore pressure and seepage force around the pipeline under the solitary wave action. The pore pressure gradient within the dense seabed soils is smaller when compared with the loose seabed. The larger permeability coefficient corresponds to the smaller Young’s modulus, and the more significant the vertical force on the pipeline. With the increase of the permeability coefficient and wave amplitude, the downward vertical force apparently increases, while the upward force decreases slightly. The vertical force is an order of magnitude greater than the horizontal force.

All these studies mentioned above were carried out for investigating the wave–seabed–pipeline interaction. However, as one of the most important marine environmental loads, the current effect on the dynamic response within the seabed around the pipeline cannot be ignored [22]. Mostafa [23] modified a coupled BEM–FEM to simulate the interaction among nonlinear-wave, current and pipelines. The model explained the sand beneath the pipeline could be washed away due to the large pressure gradient induced by the gap of seabed and pipelines. Compared with different buried depths of pipelines built above the flat seabed, more and more studies have been conducted about trench backfilling. Zhou et al. [24] studied the wave–current-induced responses within the seabed soil around the pipeline under different soil characteristics and embedment conditions. Half-buried pipeline showed the resistance to soil liquefaction in the fine sand seabed. Under the same pipeline–seabed configuration, the comparison of the liquefaction depth and scour depth beneath the pipeline showed that the occurrence of liquefaction was accompanied by larger scour depth. Ye et al. [25] investigated the soil responses within the poro-elastic seabed under the wave–current interaction. They found that the following current led to a higher possibility of seabed instability. Foo et al. [26] considered the effect of the current on wave–seabed–pipeline interaction. They found that the increase of current velocity would lead to the increase of the pore pressure amplitude. The looser seabed soil and the lower relative density caused the higher residual pore pressure, but it had little effect on the oscillating pore pressure. Hu et al. [27] used an ionic soil stabilizer (ISS) to solidify the soil and to improve the pipeline stability in combined waves and current. However, it tends to cause liquefaction as the seabed soil becomes dense. Recently, Gao et al. [28] performed a numerical simulation to investigate the combined wave–current- induced pore pressure around the twin pipelines. They found that when the forward current velocity exceeds a threshold, the residual pore pressure and liquefaction depth increases with the increase of the current velocity.

The afore-discussed previous studies focused on exploring the dynamic response around the pipeline under the fixed buried condition and wave actions in a homogeneous seabed. Recent studies have taken the co-existence of currents and waves into account. However, most of the researches adopted numerical simulation and analytical solutions to reflect the wave–current–seabed–pipeline interaction, where assumptions and simplifications are usually made in order to run the numerical calculation or obtain analytical solutions. In this regard, an experimental model can better represent the dynamic characteristics of the seabed under combined wave–current conditions, which motivates this study. In this study, we investigate the dynamic response of backfill depths, backfill materials and current properties on the seabed soil around the pipeline, under different wave–current conditions, which is significant for pipeline stability.

2. Experimental Setup

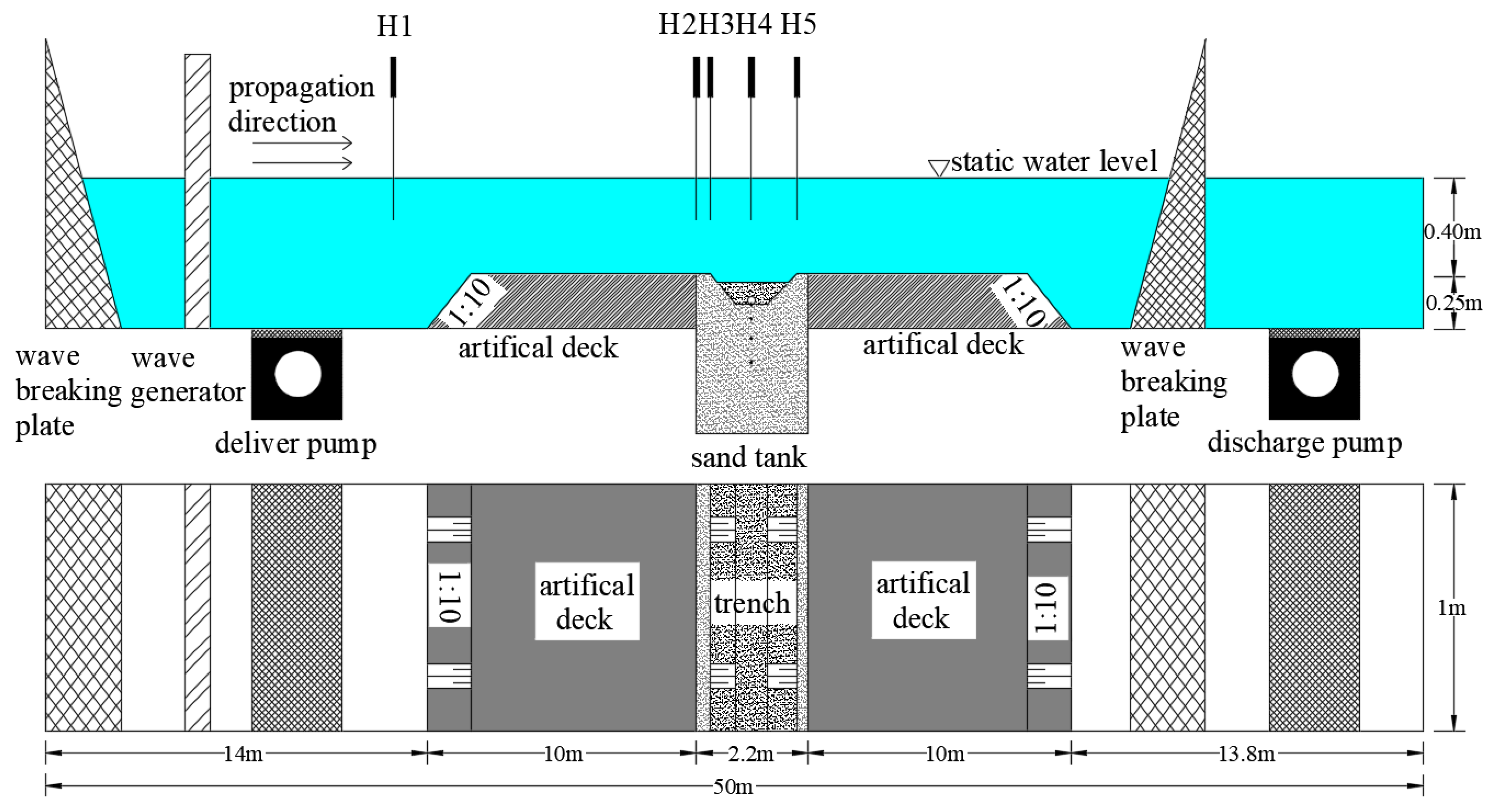
Figure 1 shows the experimental wave flume, which was 50 m long, 1 m wide and 1.3 m high. The upstream end of the wave flume was equipped with a hydraulic piston-type wave-maker. The ranges of wave period and wave height were 0.5~5 s and 2~40 cm, respectively. The deviation between the maximum wave height and the average wave height were within 3%, and the deviation between the maximum wave period and the average wave period were within 2%. The downstream end had a sponge-type wave absorber to dissipate the energy of the incident wave and reduce the wave reflection effect. The bidirectional flow generation system was composed of the pumps, the flow pipe, the valve and the control system. The maximum discharge of the flow generation system was 2000 m³/h and the maximum operating frequency was 50 Hz with the accuracy of 3%.

A sand tank was located in the middle of the wave flume; the tank was 2.2 m long, 0.75 m wide and 0.33 m deep. The top of the sand tank was raised by 0.25 m through constructing a plywood floor on both sides. Two plywood ramps, with a gradient of 1:10, were built at the end of the floors to ensure a smooth transition of waves before entering the measurement section.

The sand tank was filled with uniform quartz sand to model the sandy seabed. To prepare the highly saturated soil sample, the sand was slowly poured into the sediment basin and stirred with water. The soil sample was then gradually introduced into the sand tank until the soil surface was level with the rigid surface. The soil was consolidated for 72 h under the water column with 0.4 m depth so that the settlement of the soil surface was negligible. The pipeline was installed in the trench after the soil consolidation and wave flume was filled with water to the designed depth. The basic physical parameters of the backfill soils are summarized in

Table 1. Basic parameters of the fine sandy soil.

Soil Parameter	Symbol	Fine Sand	Medium Sand	Silt
Median particle size	${\mathrm{d}}_{50}$(mm)	0.15	0.30	0.045
Relative weight of soil	${\mathrm{s}=\mathsf{\gamma }}_{\mathrm{s}}/\mathsf{\gamma }$	2.68	2.67	2.61
Permeability Coefficient	$K$ (cm/s)	3.57 × 10−3	2.68 × 10−2	3.20 × 10−7
Maximum Void Ratio	${\mathrm{e}}_{\max }$	0.871	0.920	0.950
Minimum Void Ratio	${\mathrm{e}}_{\min }$	0.411	0.514	0.523
Measured Void Ratio	e	0.584	0.694	0.624
Natural Gravity	${\mathsf{\gamma }}_{\mathrm{t}}$ (kN/m3)	16.90	17.2	16.17
Effective Gravity	${\mathsf{\gamma }}^{\prime }$ (kN/m3)	10.34	9.819	11.05
Porosity	$\mathrm{n}=\mathrm{e}/(1+\mathrm{e})$	0.369	0.410	0.384
Relative Compactness	${\mathrm{D}}_{\mathrm{r}}=\frac{{\mathrm{e}}_{\max }-\mathrm{e}}{{\mathrm{e}}_{\max }{-\mathrm{e}}_{\min }}$	0.624	0.557	0.763

.

In the experiment, wave height of 0.08 m, wave period of 1.2 s and water depth of 0.4 m were set as scenario T0. In scenario T0, fine sand with a median particle diameter of 0.15 mm was chosen as the seabed soil. The pipeline was made of acrylic with a smooth surface and its diameter D was 8 cm, the trench depth was 16 cm and the backfill depth was $e$, as shown in Figure 2. Current velocity of 0.1 m/s, 0.2 m/s and 0.3 m/s, both the co-current actions (scenario A1–A3) and counter-current actions (scenario A4–A6), were investigated in this study. As shown in Figure 2, the pore pressure around the pipeline was collected by four pore pressure gauges, denoted as P1, P2, P3 and P4, respectively. The pore pressure gauges beneath the pipeline with distances of 3 cm, 8 cm and 18 cm, corresponding to P5, P6 and P7, respectively, were used to measure pore pressure. The maximum range of the pore pressure gauge was 30 kPa with an accuracy of 0.1%. The free surface elevation and the vertical velocity were measured by wave height gauges and acoustic doppler velocity profilers (ADVP), respectively. The wave height measurement system consisted of the wave height gauge, the data acquisition toolbox and the analysis software. The measuring range of the wave height gauge was 50 cm, the measurement accuracy was 0.001 mm, and the sampling frequency was 400 Hz. The profile resolution of ADVP was 1 mm with the sampling frequency of 100 Hz, the flow velocity range was 0–3 m/s and the accuracy was 1 mm/s.

After opening the wave-making system with the wave reaching a steady state, the flow generation system was started. By reading the ADVP data, pore pressure could be collected when the wave–current action was stable.

3. Dynamic Response around the Pipeline with Different Backfill Depth

3.1. Dynamic Response around the Pipeline

Figure 3 shows the time histories of the excess pore pressure around the pipeline with different relative backfill depths under scenario T0. The pore pressure amplitude was calculated from the averaged value over 10 wave cycles in the stable section. The dimensionless pore pressure $\left|p\right|/p_0$ was adopted to represent the relative change of dynamic response within the seabed after adding the flow action, where $\left|p\right|$ is the pore pressure amplitude at the measuring point, $p_0$ is the pore pressure amplitude of the seabed surface under the pure wave action. As shown in Figure 3, the pore pressure amplitudes along the pipeline surface were broadly similar when the relative backfill depth was 0. However, the dimensionless pore pressure amplitude was 0.897 at the top of the pipeline and 0.960 at the bottom, which shows an increase of 7.02%. The reason could be that there was a certain gap between the pipeline and seabed. The water particle movement beneath the pipeline bottom turned out to be intense. Because the flow was blocked by the structure, the pipeline–seabed interface was prone to scour and overhang. P1 was located at the incoming side of the pipeline, which was subjected to water flow force directly, so its pore pressure amplitude was the largest along the pipeline.

It can be seen from Figure 3b that when the backfill depth was D/2, the dimensionless pore pressure amplitude at the top of the pipeline was 0.856. Due to the pore pressure gauge P4 being buried in the seabed, it decreased to 0.456 at the pipeline bottom, which decreased by 46.76%. When the backfill depth increased to D, the pore pressure amplitude was 0.866 at P2, but it significantly decreased to 0.302 at P4. Figure 3b,d indicates that the pore pressure amplitude at P2 decreased to 0.738 because all the gauges were completely buried in the soil, and it decreased to 0.254 at P4 when the backfill depth was 3D/2. It shows that the pore pressure at P2 further decreased to 0.519 when the trench was fully covered up, and it decreased to 0.224 at P4. Due to the interstitial flow force between the pipeline and seabed, the pore pressure amplitude at the pipeline bottom could be larger than that at the top without backfill. Once the pipeline was buried in the soil, the pore pressure amplitude at the pipeline bottom became the smallest along the pipeline circumference, while it reached the largest at the top point. With an increasing backfill depth, the pore pressure amplitude around the pipeline gradually decreased.

To investigate the current effect on dynamic response within the seabed, the excess pore pressures around the pipeline were further studied under different wave–current conditions, as well as the backfill depths. Figure 4 and Figure A1 show that the variation trend of the pore pressure amplitude around the pipeline under the wave action was similar to those with the combined wave and current (co- and counter-current) loadings. In general, the co-current increased the pore pressure, while the counter-current decreased the pore pressure for all backfill depths. The increase/decrease of the pore pressure increased with the increase of the current velocity (absolute velocity for counter-current). Figure 4 also shows that the impact of the current on the pore pressure was reduced when the backfill depth increased. This may be ascribed to the fact that the pore pressure attenuation greatly increases vertically downward. Analysis of Figure 4 and Figure A1 also indicates that the impact of the counter-current on the pore pressure was much stronger than that acted on by the co-current for otherwise identical conditions. In addition, the pore pressure gradually decreased in growth rate under the co-current actions when the backfill depth increased; while the pore pressure decreased in descent rate under the counter-current actions.

Figure 5 and Figure A2 show the effect of backfill depth on the pore pressure amplitude around the pipeline under different current conditions. It indicates that as the top point was located at the upper layer of the seabed, the effect of the wave–current interaction was more significant than the other measuring points. Additionally, the amplitude attenuation from the top to the bottom of the pipeline was strongly affected by the current velocity and propagation direction, which is consistent with the above analysis of a single measuring point.

In general, the co-current increases the range of the pore pressure amplitude (from the top to the bottom of the pipeline), while the counter-current decreases the range of the pore pressure amplitude for all backfill depths. The increase/decrease of the range of the pore pressure amplitude increases with the increase of the current velocity (absolute velocity for counter-current). It indicates that the ocean current with roughly the same wave propagation direction always generates excessive pore pressure within the seabed, which will pose a threat to the safety and stability of pipelines in the actual marine environment.

It is seen from each subfigure in Figure 5 and Figure A2, the range of pore pressure amplitude decreases when the backfill depth increases. This is because the relative position of the top point to the bottom point remains unchanged; the increase of the backfill depth leads to an increasing relative buried depth of the pipeline and a decreasing attenuation gradient of the pore pressure. Figure 5 and Figure A2 also indicate that the impact of the co-current on the distribution range of the pore pressure amplitude is slightly stronger than that acted on by the counter-current for otherwise identical conditions.

3.2. Dynamic Response Beneath the Pipeline

The pore pressure beneath the pipeline is the most important for the stability of the pipeline. Therefore, the influence of current conditions on the variation of pore pressure beneath the pipeline is discussed in detail under different backfill depths. Figure 6 and Figure A3 shows that the variation trend of pore pressure amplitude beneath the pipeline under wave action was similar to those with combined wave and current (co- and counter-currents) loadings. Compared with the pore pressure amplitude at P5 under the pure wave action, it increased by 4.86%, 10.22% and 13.04% with the co-current velocity of 0.1 m/s, 0.2 m/s and 0.3 m/s, respectively, and decreased by 5.76%, 17.27% and 27.45%, respectively, under the same counter-current actions when the relative backfill depth was 1/2. It increased by 1.21%, 2.88% and 3.28%, respectively, under the co-current actions and decreased by 4.23%, 14.08% and 23.94% under the counter-current actions with the relative backfill depth of 2. The results show that the variation of the dimensionless pore pressure amplitude increases with an increasing current velocity under both the co-current and counter-current actions. The increase/decrease of the pore pressure amplitude decreases gradually with the increase of the backfill depth under the co-current/counter-current actions. This is because the relative position of the measuring point increases with the increase of the backfill depth, and the attenuation gradient of the pore pressure amplitude decreases with the increase of the seabed depth. The effect of the counter-current on the pore pressure amplitude is significantly stronger than that of the co-current.

Within the range of 3 cm to 8 cm beneath the pipeline, the amplitude attenuation of the pore pressure was 0.264 under the pure wave action without backfill. The attenuation values were 0.265, 0.274 and 0.282, respectively, with the co-current velocity of 0.1 m/s, 0.2 m/s and 0.3 m/s and 0.234, 0.224 and 0.196 under the counter-current action. When the relative backfill depth increased to 2, the amplitude attenuation was 0.076 under the pure wave action, and it reduced to 0.075, 0.073 and 0.072 under the co-current actions, and 0.073, 0.065 and 0.060 under the counter-current actions.

It shows that the attenuation rate of the pore pressure amplitude along the vertical direction increases with the increase of the co-current velocity, and decreases under the counter-current actions. In general, the attenuation rate of the pore pressure amplitude decreases with the increase of the backfill depth under the co-current/counter-current actions. Figure A3b and Figure 6c show that when the relative backfill depths reach 3/2 and 2, the vertical distribution of the pore pressure, under the co-current actions, is almost parallel to that under the pure wave action. It indicates that the influence of the current velocity on the amplitude attenuation gradually weakens as the backfill depth increases.

Figure 7 and Figure A4 show the attenuation of the pore pressure amplitude beneath the pipeline under different backfill depths. It can be seen from Figure 7a that when the relative backfill depth is 1/2, the decrease of each measuring point (P4, P5, P6 and P7) beneath the pipeline is 52%, 45%, 39% and 36%, respectively, under the pure wave action. It indicates that the backfill sand with a certain depth was a great improvement on pipeline stability. As the pipeline backfills from the bare state to the completely buried state, the dimensionless pore pressure amplitudes at the bottom of the pipeline decrease by 0.504, 0.154, 0.054 and 0.024 at the adjacent backfill depths. It can be seen that the effect on the reduction of the pore pressure amplitude was gradually weakened with the increase of the backfill depth. Especially when the relative backfill depths reach 3/2 and 2, the dimensionless pore pressure amplitudes of P6 and P7 (the dimensionless depths of 0.414 and 0.586) are almost the same, presenting an approximate vertical state in the figure. It indicates that the variation of the pore pressure amplitude is mainly concentrated in the shallow seabed layer. The influence of the backfill depth on the pore pressure amplitude decreases gradually with an increasing backfill depth. When the pipeline is not completely buried (the relative backfill depth is less than 1), the backfill depth has a great influence on the pore pressure amplitude in the shallow seabed layer beneath the pipeline, and the influence gradually weakens with the increase of the seabed depth and the backfill depth.

Under the pure wave action, the amplitude attenuation of the pore pressure is 0.318 from P4 to P5 without backfill. The attenuation values reduce to 0.106, 0.065, 0.065 and 0.045 at the relative backfill depths from 1/2 to 2 with the step of 1/2. With the co-current velocity of 0.3 m/s, the attenuation values are 0.301, 0.104, 0.700, 0.071 and 0.056 when the relative backfill depth increases from 0 to 2 with the step of 1/2, and 0.253, 0.063, 0.045, 0.055 and 0.050 under the counter-current actions. Figure 7 and Figure A4 show that with the increase of the co-current velocity, the gap between the distribution curve of the pore pressure amplitude at adjacent backfill depth basically remains unchanged. However, it decreases with the increase of the counter-current velocity. It indicates that the amplitude attenuations beneath the pipeline are essentially coincident with the increase of the co-current velocity. However, it gradually decreases with the increase of the counter-current velocity. It can be seen that the distribution range of the pore pressure amplitude beneath the pipeline is larger under the co-current actions, which requires higher standards for pipeline stability design.

4. Dynamic Response around the Pipeline with Different Backfill Sands

4.1. Effect of Backfill Sand

To compare the excess pore pressure around the pipeline under different backfill conditions, silt (${\mathrm{d}}_{50}$ = 0.045 mm), fine sand (${\mathrm{d}}_{50}$ = 0.150 mm) and medium sand (${\mathrm{d}}_{50}$ = 0.300 mm) were used as the backfill materials. Figure 8 and Figure A5 show the pore pressure amplitude around the pipeline with different backfill materials under scenario T0. When the trench was backfilled with medium sand, the dimensionless pore pressure amplitudes at the pipeline bottom were 0.960 and 0.846, respectively, when the relative backfill depth increased from 0 to 1/2, with the attenuation value of 11.81%. However, the attenuation value was 53.11% when backfilled with fine sand. The attenuation gradient of the pore pressure amplitude decreased with the increases of the permeability coefficient and the porosity. Analysis above indicates that the attenuation rate of the pore pressure is obviously smaller in the medium sand seabed than that in the fine sand seabed.

With the increase of the backfill depth, the pore pressure amplitude along the circumference of the pipeline did not decrease significantly in the medium sand seabed. When the relative backfill depth increased from 1/2 to 2 with the step of 1/2, the attenuation rates at the pipeline bottom were 1.19%, 1.95% and 1.22%, respectively. When the pipeline was completely buried (e/D = 1), the pore pressure amplitude along the circumference of the pipeline showed little change. The reason is that medium sand with large particle gaps has a large permeability coefficient; with the increase of backfill depth, its effect on the attenuation rate of the pore pressure amplitude gradually decreases.

As shown in Figure A5a, the backfilled medium sand changes the pore pressure distribution beneath the pipeline within a pipeline diameter range. The dimensionless pore pressure amplitudes of P4 and P5 are smaller than that without backfill. However, under all backfill depths, the amplitude of P6 is slightly larger than that without backfill, which means the attenuation degree is less than that without backfill within the range of P5 to P6. As the variation of pore pressure amplitude in the upper backfill layer is quite small under the relatively large permeability coefficient, the attenuation degree almost remains unchanged under different backfill depths.

As shown in Figure A5b, when the trench was backfilled with silt, the pore pressure amplitudes at the horizontal axis (P1, P3) and the top point of the pipeline (P2) were both smaller than that of the fine sand seabed due to the effect of low permeability coefficient. When the relative backfill depths were 1/2 and 1, the pore pressure amplitude at the bottom of the pipeline was greater than that of the fine sand seabed. The reason could be that the wave-induced pore pressure was transferred through various channels around the pipeline, such as propagating directly from the shallow layer to the deep layer, or along the circumference to the pipeline bottom. The main seepage channel could be the smooth pipeline circumference in the silt seabed, resulting in less pore pressure attenuation. When the relative backfill depths increased to 3/2 and 2, there was little difference of the dimensionless pore pressure amplitude along the pipeline circumference, as well as beneath the pipeline, which was caused by the low permeability and the relatively large backfill depth.

It can be seen from Figure A5a that the dimensionless pore pressure around the pipeline had a slight decrease, so that it was difficult to ensure stability in the medium sand seabed. Compared to the dynamic response within the fine sand seabed, the pore pressure around the pipeline had a smaller amplitude when backfilled with silt. However, the dimensionless pore pressure amplitude beneath the pipeline was greater than that under the fine sand cases, which could affect the pipeline’s stability.

4.2. Effect of Current Velocity and Direction

To investigate the current effect on dynamic response within different backfill materials, the excess pore pressures around the pipeline were further studied under different wave–current conditions when the backfill depth equaled the pipeline diameter. As shown in Figure 9, compared with the pure wave action, the dimensionless pore pressure amplitudes at the pipeline bottom increased by 4.21%, 8.47% and 10.57%, respectively, in the fine sand seabed, under the co-current actions (scenario A1–A3), and decreased by 6.67%, 16.67% and 27.50%, respectively, under the counter-current actions (scenario A4–A6). The dimensionless pore pressure amplitudes increased by 4.09%, 8.33% and 11.23% and decreased by 5.72%, 13.25% and 22.29% in the medium sand seabed, under the co-current/counter-current actions. The values increased by 3.64%, 5.86% and 8.94% and decreased by 2.48%, 10.40% and 18.81% in the silt seabed, under the co-current/counter-current actions. For all backfill materials, the dimensionless pore pressure amplitude increased/decreased with the increase of the current velocity (absolute velocity for counter-current). The effect of the counter-current on pore pressure amplitude was significantly stronger than that of the co-current.

Analysis of measurements at P1 and P3, as shown in Figure 9 and Figure A6, indicates that the current effect on the wave-back side is basically the same as that on the wave-approach side under different backfill materials. Under the co-current actions, the maximum increases were 4.96% and 5.87% at the wave-approach and wave-back sides within the silt seabed when compared with scenario T0. The current effect on the pipeline circumference within the fine sand seabed were relatively small, as well as on the top and bottom points of the pipeline within the silt seabed. Compared with the pure wave action, the maximum increase of the dimensionless pore pressure amplitude was about 10% in the co-current conditions, and the maximum decrease was about 20% in the counter-current conditions.

It is seen from Figure 9 and Figure A6 that when comparing with the pure wave action, the dimensionless pore pressure amplitudes at P5 increased by 3.90%, 9.90% and 11.32% within the fine sand seabed under the co-current actions (scenario A1–A3), and decreased by 7.45%, 18.07% and 30.34% under the counter-current actions (scenario A4–A6). The dimensionless pore pressure amplitudes increased by 3.75%, 9.04% and 11.34% and decreased by 6.66%, 14.25% and 25.01% within the medium sand seabed, under the co-current/counter-current actions. The amplitude values increased by 3.42%, 7.87% and 8.82% and decreased by 4.42%, 10.61% and 21.21% within the silt seabed. Figure 9 and Figure A6 also show that a similar variation pattern can be found at 8 cm and 18 cm beneath the pipeline (the relative depths of −0.414 and −0.586). Variation of the dimensionless pore pressure amplitude increased with the increase of the current velocity. At the same current velocity, the counter-current effect on the pore pressure amplitude was greater than the co-current actions, and the response of the silt seabed to the current was less than that of the fine sand seabed. Analysis of Figure 9 and Figure A6 also indicates that within the thickness of one pipeline diameter beneath the pipeline, the influence of fine sand on the variation of the pore pressure amplitude decreased with the increase of the median diameter of backfill materials under the co-current actions; however, it increased at the depth beyond one pipeline diameter. Under the counter-current actions, the variation of the dimensionless pore pressure amplitude decreased with the increase of the median diameter of backfill materials.

5. Conclusions

In this study, the variation of the pore pressure around the pipeline under the wave-current interaction was explored by physical model tests. The influence of the backfill depth, the properties of backfill sands and current parameters on the dynamic response within the seabed were investigated.

With the increase of the backfill depth, the dimensionless pore pressure amplitude within the seabed gradually decreases, and it also decreases at adjacent backfill depths under all wave–current actions. This means the backfilling effect gradually weakens. Under the pure wave action, the dimensionless pore pressure amplitude beneath the pipeline decreases by more than 40% when the backfill depth increases from 0 to half of the pipeline diameter. When the relative backfill depth increases to 3/2 and 2, the pore pressure amplitude has almost no attenuation beyond one pipeline diameter beneath the pipeline.

With the increase of the backfill depth, the amplification/reduction of the pore pressure amplitude decreases under the co-current/counter-current actions, which means the current effect on the dynamic response within the seabed decreases. The reduction of the pore pressure amplitude at the adjacent backfill depth increases/decreases with the increase of the co-current/counter-current velocity. Similarly, the amplitude attenuation of the pore pressure increases with the increase of the co-current velocity along the depth direction, and vice versa.

When the trench was backfilled with medium sand, the pore pressure amplitude around the pipeline showed little difference from that without backfill, even when the relative backfill depth reached 2. This indicates that medium sand is not suitable to be used as backfill material for pipeline protection. The attenuation gradient of the pore pressure amplitude in silt seabed, within the range of half pipeline diameter beneath the pipeline, was greater than that in the fine sand seabed when the pipeline was half or completely buried.

The pore pressure amplitudes at the wave-approach and wave-back sides increased slightly within the silty seabed under co-current actions. However, there was little difference of the response degree on the current within the fine and medium sand seabed. The maximum increase was about 10% in the co-current actions, and the maximum decrease was about 20% in the counter-current actions along the pipeline surface when compared to the pure wave action. Beneath the pipeline, the response of silt and fine sand on the current was basically the same, and it was smaller than that of medium sand under the co-current actions. The decrease of the dimensionless pore pressure within the fine sand was greater than that of the other backfill materials under the counter-current actions.