Acquisition of Sorption and Drying Data with Embedded Devices: Improving Standard Models for High Oleic Sunflower Seeds by Continuous Measurements in Dynamic Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Moisture Content Determination
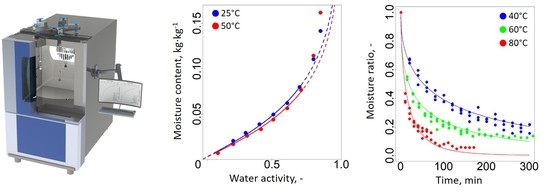
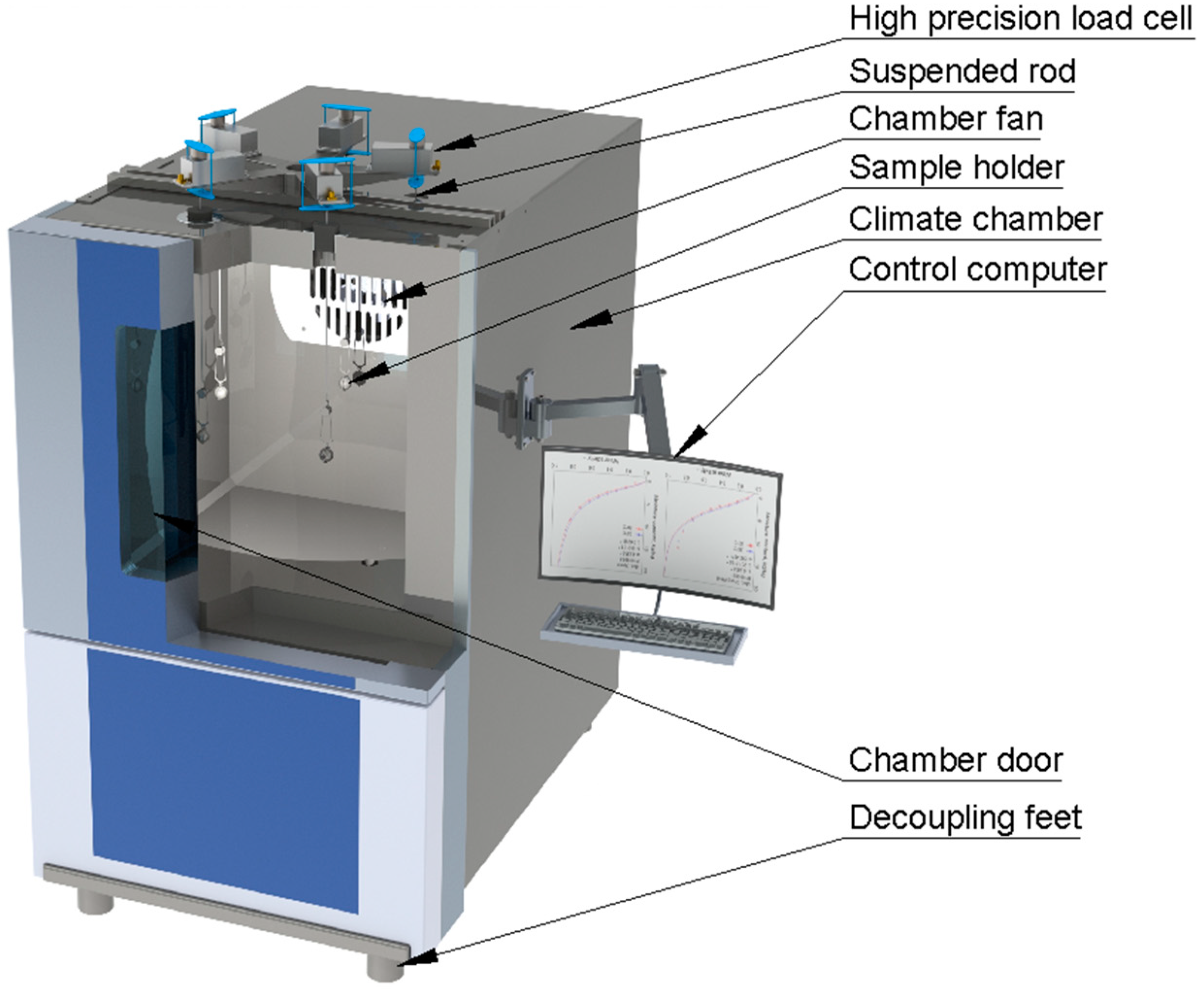
2.3. Determination of Dynamic Vapor Sorption Isotherms
2.4. Sorption Isotherm Models
2.5. Thin-Layer Drying Experiments
2.6. Empirical Drying Model
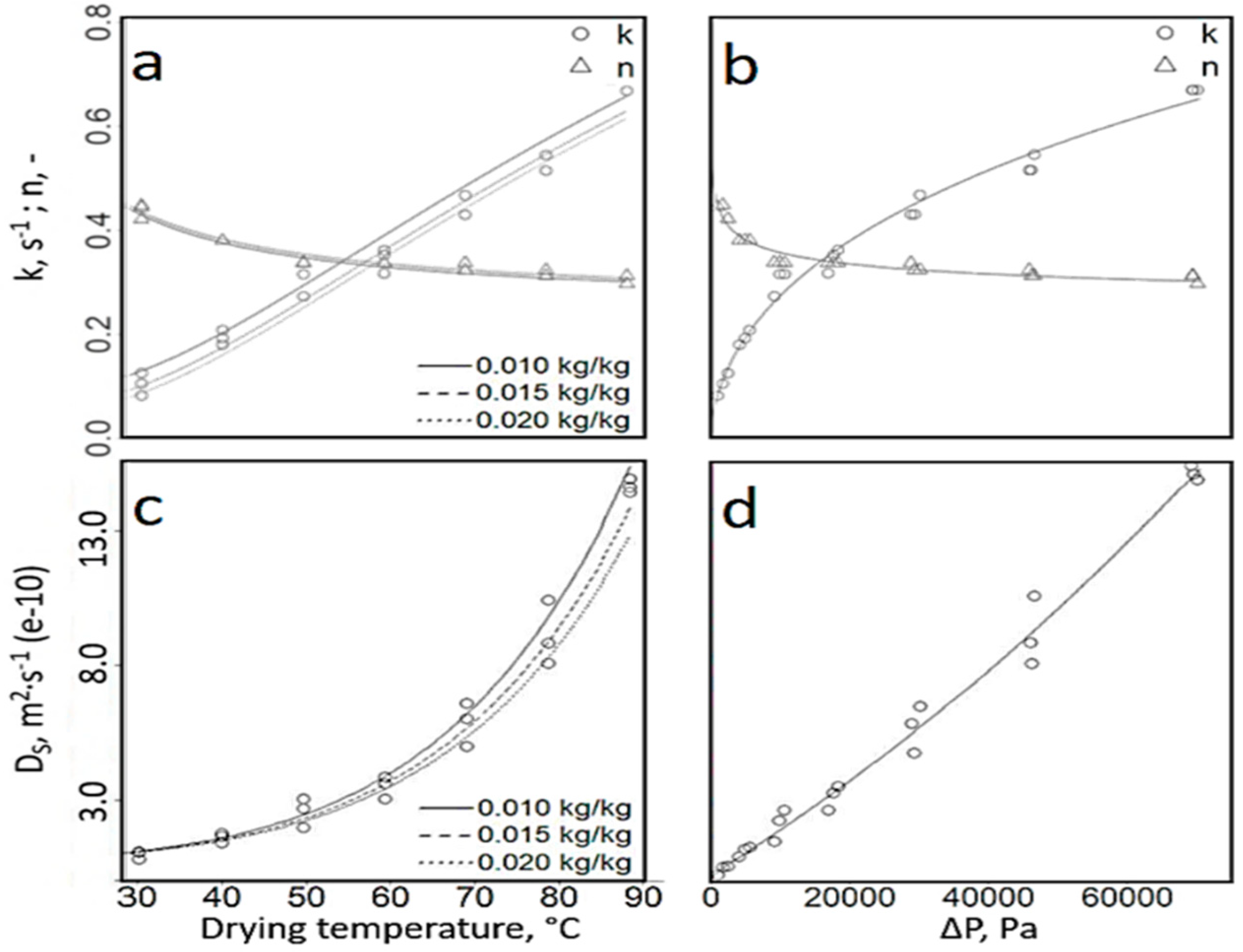
2.7. Analytical Estimation of Diffusion Coefficients
2.8. Statistical Analysis
3. Results and Discussion
3.1. Analysis of Moisture Sorption Models
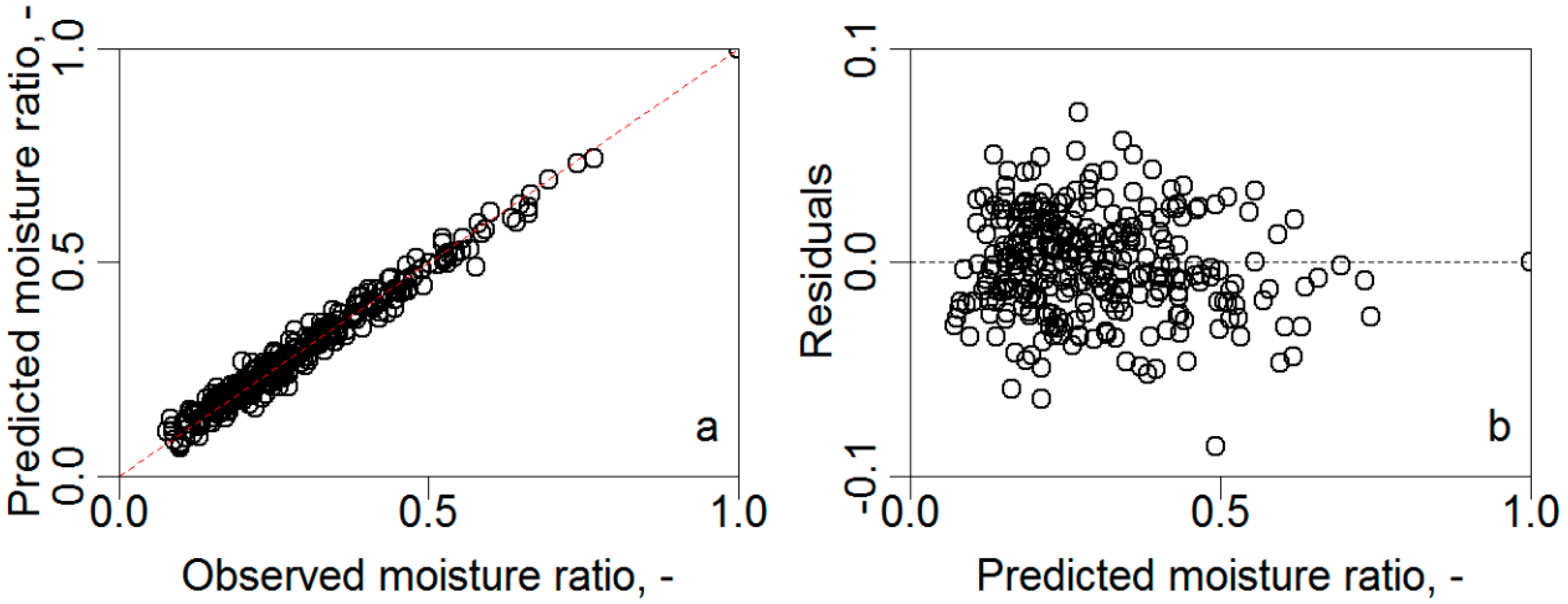
3.2. Modelling of Thin-Layer Drying Behavior
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| aw | water activity |
| MC | moisture content |
| MCe | equilibrium moisture content |
| MCt | moisture content at time t |
| DVS | dynamic vapour sorption apparatus |
| kg | kilogram |
| g | gram |
| mg | milligram |
| m | meter |
| mm | millimeter |
| rh | relative humidity, % |
| min | minutes |
| Pvs | water vapor partial pressure, Pa |
| Psat | saturation vapor pressure, Pa |
| T | temperature, °C |
| a, b, c, d, e, f, g | model constants |
| G.A.B. | Guggenheim, Anderson, DeBoer |
| x | absolute humidity, kg water per kg of dry air |
| s | second |
| MR | moisture ratio |
| t | time |
| k | rate constant, min−1 |
| n | dimensionless coefficient of page equation |
| P | pressure, Pa |
| D | moisture diffusivity, m2∙s−1 |
| av | kernel’s surface specific area in m2∙m−3 |
| ANOVA | analysis of variance |
| MAPE | mean absolute perecentage error |
| R2 | coefficient of determination |
| p | probability level at which significance is assumed |
References
- Robertson, J.A.; Chapman, G.W.; Wilson, R.L. Effect of moisture content of oil type sunflower seed on fungal growth and seed quality during storage. J. Am. Oil Chem. Soc. 1984, 61, 768–771. [Google Scholar] [CrossRef]
- Mazza, G.; Jayas, D.S.S. Equilibrium moisture characteristics of sunflower seeds, hulls, and kernels. Trans. ASAE 1991, 34, 534–538. [Google Scholar] [CrossRef]
- Giner, S.A.; Gely, M.C. Sorptional parameters of sunflower seeds of use in drying and storage stability studies. Biosyst. Eng. 2005, 92, 217–227. [Google Scholar] [CrossRef]
- Maciel, G.; De la Torre, D.; Izquierdo, N.; Cendoya, G.; Bartosik, R. Effect of oil content of sunflower seeds on the equilibrium moisture relationship and the safe storage condition. Agric. Eng. Int. 2015, 17, 248–258. [Google Scholar]
- Mujumdar, A.S.; Beke, J. Grain drying: Basic principles. In Handbook of Postharvest Technology: Cereals, Fruits, Vegetables, Tea, and Spices; Chakraverty, A., Mujumdar, A.S., Raghavan, G.S.V., Ramaswamy, H.S., Eds.; Marcel Dekker: New York, NY, USA, 2003; pp. 119–138. [Google Scholar]
- Guillard, V.; Bourlieu, C.; Gontard, N. Theoretical background. In Food Structure and Moisture Transfer; Springer: New York, NY, USA, 2013; pp. 3–33. [Google Scholar]
- Argyropoulos, D.; Alex, R.; Kohler, R.; Müller, J. Moisture sorption isotherms and isosteric heat of sorption of leaves and stems of lemon balm (Melissa officinalis L.) established by dynamic vapor sorption. LWT-Food Sci. Technol. 2012, 47, 324–331. [Google Scholar] [CrossRef]
- Argyropoulos, D.; Müller, J. Effect of convective-, vacuum- and freeze drying on sorption behaviour and bioactive compounds of lemon balm (Melissa officinalis L.). J. Appl. Res. Med. Aromat. Plants 2014, 1, 59–69. [Google Scholar] [CrossRef]
- Arslan, N.; Toğrul, H. Moisture sorption isotherms for crushed chillies. Biosyst. Eng. 2005, 90, 47–61. [Google Scholar] [CrossRef]
- Stubberud, L.; Arwidsson, H.G.; Graffner, C. Water-solid interactions: I. A technique for studying moisture sorption/desorption. Int. J. Pharm. 1995, 114, 55–64. [Google Scholar] [CrossRef]
- Hill, C.A.S.; Norton, A.J.; Newman, G. The water vapour sorption properties of Sitka spruce determined using a dynamic vapour sorption apparatus. Wood Sci. Technol. 2010, 44, 497–514. [Google Scholar] [CrossRef]
- Kachrimanis, K.; Noisternig, M.F.; Griesser, U.J.; Malamataris, S. Dynamic moisture sorption and desorption of standard and silicified microcrystalline cellulose. Eur. J. Pharm. Biopharm. 2006, 64, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Kohler, R.; Dück, R.; Ausperger, B.; Alex, R. A numeric model for the kinetics of water vapor sorption on cellulosic reinforcement fibers. Compos. Interfaces 2003, 10, 255–276. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, L.; Han, Z.; Xie, B.; Wu, S. The effects of leaching methods on the combustion characteristics of rice straw. Biomass Bioenergy 2013, 49, 22–27. [Google Scholar] [CrossRef]
- Vollenbroek, J.; Hebbink, G.A.; Ziffels, S.; Steckel, H. Determination of low levels of amorphous content in inhalation grade lactose by moisture sorption isotherms. Int. J. Pharm. 2010, 395, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Hill, C.A.S.; Jalaludin, Z.; Curling, S.F.; Anandjiwala, R.D.; Norton, A.J.; Newman, G. The dynamic water vapour sorption behaviour of natural fibres and kinetic analysis using the parallel exponential kinetics model. J. Mater. Sci. 2011, 46, 479–489. [Google Scholar] [CrossRef]
- Nurhadi, B.; Roos, Y.H. Dynamic water sorption for the study of amorphous content of vacuum-dried honey powder. Powder Technol. 2016, 301, 981–988. [Google Scholar] [CrossRef]
- Santalla, E.M.; Mascheroni, R.H. Equilibrium moisture characteristics of high oleic sunflower seeds and kernels. Dry. Technol. 2003, 21, 147–163. [Google Scholar] [CrossRef]
- Santalla, E.M.; Mascheroni, R.H. Moisture diffusivity in high oleic sunflower seeds and kernels. Int. J. Food Prop. 2010, 13, 464–474. [Google Scholar] [CrossRef]
- Henderson, S.M.; Pabis, S. Grain drying theory IV, The effect of airflow rate on the drying index. J. Agric. Eng. Res. 1962, 7, 85–89. [Google Scholar]
- Hutchinson, D.; Otten, L. Thin-layer air drying of soybeans and white beans. Int. J. Food Sci. Technol. 1983, 18, 507–522. [Google Scholar] [CrossRef]
- Munder, S.; Argyropoulos, D.; Müller, J. Class-based physical properties of air-classified sunflower seeds and kernels. Biosyst. Eng. 2017, 164, 124–134. [Google Scholar] [CrossRef]
- ISO 665:2000 Oilseeds—Determination of Moisture and Volatile Matter Content; International Organization for Standardization (ISO): Geneva, Switzerland, 2000.
- Al-Muhtaseb, A.H.; McMinn, W.A.M.; Magee, T.R.A. Moisture sorption isotherm characteristics of food products: A review. Food Bioprod. Process. 2002, 80, 118–128. [Google Scholar] [CrossRef]
- Argyropoulos, D.; Heindl, A.; Müller, J. Assessment of convection, hot-air combined with microwave-vacuum and freeze-drying methods for mushrooms with regard to product quality. Int. J. Food Sci. Technol. 2011, 46, 333–342. [Google Scholar] [CrossRef]
- Shahari, N.A. Mathematical Modelling of Drying Food Products: Application to Tropical Fruits. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2012. [Google Scholar]
- Udomkun, P.; Argyropoulos, D.; Nagle, M.; Mahayothee, B.; Janjai, S.; Müller, J. Single layer drying kinetics of papaya amidst vertical and horizontal airflow. LWT-Food Sci. Technol. 2015, 64, 67–73. [Google Scholar] [CrossRef]
- Becker, H.A. A study of diffusion in solids of arbitrary shape, with application to the drying of the wheat kernel. J. Appl. Polym. Sci. 1959, 1, 212–226. [Google Scholar] [CrossRef]
- Giner, S.A.; Mascheroni, R.H. PH—Postharvest technology. J. Agric. Eng. Res. 2001, 80, 351–364. [Google Scholar] [CrossRef]
- Sun, D.W.; Woods, J.L. Low temperature moisture transfer characteristics of wheat in thin layers. Trans. ASAE 1994, 37, 1919–1926. [Google Scholar] [CrossRef]
- Giner, S.A.; Mascheroni, R.H. PH—Postharvest technology. Biosyst. Eng. 2002, 81, 85–97. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing 2015. Available online: https://www.r-project.org (accessed on 17 September 2015).
- Grothendieck, G. nls2: Non-Linear Regression with Brute Force 2013. Available online: https://cran.r-project.org/web/packages/nls2/nls2.pdf (accessed on 17 September 2015).
- Djendoubi Mrad, N.; Bonazzi, C.; Boudhrioua, N.; Kechaou, N.; Courtois, F. Influence of sugar composition on water sorption isotherms and on glass transition in apricots. J. Food Eng. 2012, 111, 403–411. [Google Scholar] [CrossRef]
- Saravacos, G.D.; Tsiourvas, D.A.; Tsami, E. Effect of temperature on the water adsorption isotherms of sultana raisins. Dry. Technol. 1986, 4, 633–649. [Google Scholar] [CrossRef]
- Ling, M. Manometrische Bestimmung der NO2-Sorptionsisothermen von Superberliner Blau—Derivaten und Charakterisierung der inneren Oberflächen mittels der BET—Methode. Ph.D. Thesis, Universität Hamburg, Hamburg, Germany, 2001. [Google Scholar]
- Simha, H.V.V.; Pushpadass, H.A.; Franklin, M.E.E.; Kumar, P.A.; Manimala, K. Soft computing modelling of moisture sorption isotherms of milk-foxtail millet powder and determination of thermodynamic properties. J. Food Sci. Technol. 2016, 53, 2705–2714. [Google Scholar] [CrossRef] [Green Version]
- Mathlouthi, M.; Rogé, B. Water vapour sorption isotherms and the caking of food powders. Food Chem. 2003, 82, 61–71. [Google Scholar] [CrossRef]
- Brunauer, S. The Adsorption Of Gases And Vapors Vol I; Oxford University Press: London, UK, 1943. [Google Scholar]
- Pixton, S.W.; Warburton, S. Moisture content relative humidity equilibrium, at different temperatures, of some oilseeds of economic importance. J. Stored Prod. Res. 1971, 7, 261–269. [Google Scholar] [CrossRef]
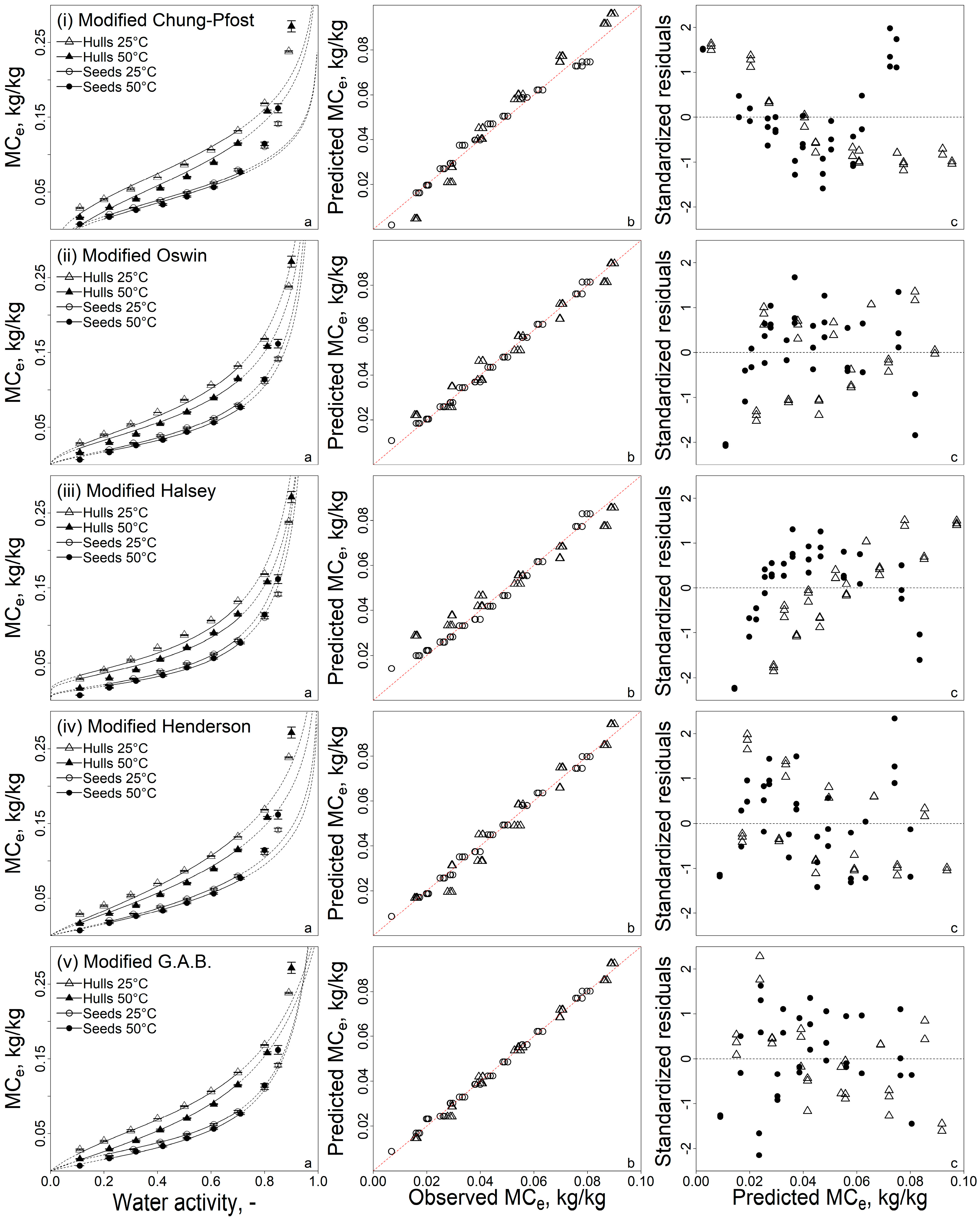
| Model | Original Plant Material | Validity (aW) |
|---|---|---|
| Modified Chung-Pfost | ||
| Maize and maize components | 0.1–0.9 | |
| Modified Oswin | ||
| Various | 0.3–0.5 | |
| Modified Halsey | ||
| Maize, wheat flour, laurel, nutmeg | 0.1–0.8 | |
| Modified Henderson | ||
| Maize | - | |
| Modified G.A.B. | ||
| Various | <0.94 |
| Equation | a | b | c | R2 | MAPE, % | ||||
|---|---|---|---|---|---|---|---|---|---|
| (i) Mod. Chung-Pfost | Seeds | 28.181 | *** | 208.987 | *** | 611.811 | *** | 0.988 | 7.900 |
| (ii) Mod. Oswin | 0.048 | *** | −1.58 · 10−4 | *** | 1.607 | *** | 0.992 | 8.131 | |
| (iii) Mod. Halsey | −3.895 | *** | −4.60 · 10−3 | *** | 1.159 | *** | 0.978 | 13.884 | |
| (iv) Mod. Henderson | 0.102 | *** | 207.939 | *** | 1.145 | *** | 0.995 | 5.408 | |
| (v) Mod. G.A.B. | 2.88 · 10−2 | *** | 0.919 | *** | 167.831 | *** | 0.994 | 5.923 | |
| (i) Mod. Chung-Pfost | Hulls | 17.761 | *** | 47.204 | *** | 240.673 | *** | 0.985 | 9.173 |
| (ii) Mod. Oswin | 9.94 · 10−2 | *** | −0.001 | *** | 1.776 | *** | 0.992 | 6.618 | |
| (iii) Mod. Halsey | −3.255 | *** | −9.87 · 10−3 | *** | 1.245 | *** | 0.982 | 9.964 | |
| (iv) Mod. Henderson | 0.208 | *** | 54.690 | *** | 1.299 | *** | 0.991 | 6.112 | |
| (v) Mod. G.A.B. | 0.070 | *** | 0.775 | *** | 122.616 | *** | 0.997 | 3.207 |
| x | T, °C | D (m2∙s−1)∙10−10 | R2 | MAPE, % | |
|---|---|---|---|---|---|
| 0.010 kg·kg−1 | 30 | 0.643 | *** | 0.979 | 4.088 |
| 40 | 1.317 | *** | 0.985 | 6.935 | |
| 50 | 2.620 | *** | 0.991 | 6.217 | |
| 60 | 3.467 | *** | 0.970 | 10.903 | |
| 70 | 6.277 | *** | 0.989 | 7.547 | |
| 80 | 10.190 | *** | 0.996 | 5.059 | |
| 90 | 14.800 | *** | 0.995 | 7.399 | |
| 0.015 kg·kg−1 | 30 | 0.593 | *** | 0.984 | 4.303 |
| 40 | 1.231 | *** | 0.987 | 5.591 | |
| 50 | 2.258 | *** | 0.974 | 11.780 | |
| 60 | 3.222 | *** | 0.979 | 11.238 | |
| 70 | 4.627 | *** | 0.969 | 11.187 | |
| 80 | 7.796 | *** | 0.990 | 7.829 | |
| 90 | 14.310 | ** | 0.997 | 5.611 | |
| 0.020 kg·kg−1 | 30 | 0.342 | *** | 0.979 | 3.556 |
| 40 | 0.978 | *** | 0.980 | 5.790 | |
| 50 | 1.529 | *** | 0.954 | 10.944 | |
| 60 | 2.634 | *** | 0.988 | 5.715 | |
| 70 | 5.696 | *** | 0.982 | 9.844 | |
| 80 | 8.559 | *** | 0.993 | 5.203 | |
| 90 | 14.490 | ** | 0.999 | 2.152 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munder, S.; Argyropoulos, D.; Müller, J. Acquisition of Sorption and Drying Data with Embedded Devices: Improving Standard Models for High Oleic Sunflower Seeds by Continuous Measurements in Dynamic Systems. Agriculture 2019, 9, 1. https://doi.org/10.3390/agriculture9010001
Munder S, Argyropoulos D, Müller J. Acquisition of Sorption and Drying Data with Embedded Devices: Improving Standard Models for High Oleic Sunflower Seeds by Continuous Measurements in Dynamic Systems. Agriculture. 2019; 9(1):1. https://doi.org/10.3390/agriculture9010001
Chicago/Turabian StyleMunder, Simon, Dimitrios Argyropoulos, and Joachim Müller. 2019. "Acquisition of Sorption and Drying Data with Embedded Devices: Improving Standard Models for High Oleic Sunflower Seeds by Continuous Measurements in Dynamic Systems" Agriculture 9, no. 1: 1. https://doi.org/10.3390/agriculture9010001
APA StyleMunder, S., Argyropoulos, D., & Müller, J. (2019). Acquisition of Sorption and Drying Data with Embedded Devices: Improving Standard Models for High Oleic Sunflower Seeds by Continuous Measurements in Dynamic Systems. Agriculture, 9(1), 1. https://doi.org/10.3390/agriculture9010001