Pressure Drop Across Animal Occupied Zone of Dairy Barns Under Multiple Scenarios ^†

Abstract

In naturally ventilated dairy barns, many questions regarding airflow, indoor air quality, and emissions are still unanswered, often resulting in inaccurate environmental control of the housing. Particularly, limited understanding of the implications of the constantly changing outdoor weather conditions in interaction with the building design and the role of the characteristics of the animals’ movement inside the building enhances uncertainties in the estimation of airflows within and across the barns. Computational fluid dynamics (CFD) have been used in the past to better understand the dynamics of barn climate, but the models are typically too slow to be used for real-time prediction and control. We investigated the effect of animal characteristics (i.e., animal location, orientation, body posture, and dimensions) on the pressure drop in the animal occupied zone considering inlet wind speed from 0.1 m s⁻¹ to 5 m s⁻¹ and wind direction of 0° and 90° in a CFD model. The cow position in general had little impact on the pressure drop at low wind speeds, but became relevant at higher wind speeds. Cows distributed in a more organized alignment showed less airflow resistance, and, therefore, a lower pressure drop and higher air velocities. Moreover, the cow breed affected the pressure drop, with higher withers resulting in a higher pressure drop and air resistance. In contrast, the effects of cow lying–standing ratio on the pressure drop and airflow resistance coefficients were negligible for both investigated wind directions. Our study aims to provide guidance for optimizing parametrizations of the animal occupied zone in order to enhance the speed of simulations without significant loss in model accuracy. In addition, the conclusions drawn from our study may support the adaption of building design and herd management to improve the effectiveness of ventilation concepts of naturally ventilated dairy barns.

1. Introduction

Understanding the airflow patterns inside livestock buildings is one of the key issues to evaluate animals and farm workers health, as well as environmental impact. With the air, excess heat and humidity, as well as pollutants like ammonia, odors, and dust, are carried away [1]. Adequate air exchange ensures a comfortable indoor climate (temperature, humidity, gas concentrations) and helps to control emissions to the environment. Hence, a detailed understanding of air motion (i.e., air velocities, flow directions, and turbulence) is necessary to meet livestock needs and environmental regulations [2]. In naturally ventilated livestock buildings, however, airflow is complex and highly variable as it is driven by the interaction of wind and thermal forces. Moving livestock, itself acting as flow obstacle, renders the situation even more complex [3,4]. Simulating animals in realistic or simplified geometries using computational fluid dynamics (CFD) is computationally challenging for real-time or quasi-real-time applications, especially for large-sized commercial livestock houses (often more than one thousand square meters of floor space) housing large numbers of animals inside (often several hundreds or thousands of animals) or for the parametric studies with numerous simulation cases. As a result, porous media modeling of animals has emerged as a feasible alternative.

Obtaining high-resolution airflow data through direct measurements and predicting airflow patterns in real livestock houses is very challenging. In the case of naturally ventilated buildings, hundreds of square meters of “window” area and fluctuating boundary conditions (e.g., highly variable wind velocity) render it particularly challenging to capture representative flow rates, leading to errors of up to 100% in some cases [1]. Purely experimental approaches need long monitoring periods covering multiple seasons to capture a statistically significant dataset with measurements under comparable boundary conditions [5]. At the same time, they usually struggle to provide the flow field information in sufficient resolution [2]. As a result, field measurements of ventilation rates and interior airflow often suffer from low spatial resolution and high uncertainty.

Therefore, in recent decades, CFD has become a support tool to complement barn airflow measurements as it can resolve the interior airflows of livestock buildings with theoretically unlimited spatial resolution [2,6,7]. By using CFD, researchers can virtually observe air speed and circulation in every corner of the building, under various ventilation scenarios, which is invaluable for diagnosing ventilation effectiveness and improving barn designs.

While CFD offers, in principle, high resolution, modeling a large barn in full geometric detail poses serious challenges. Ideally, the CFD model includes every interior object (animals, pens, equipment, etc.) explicitly in the geometry. However, meshing dozens of objects with realistic shapes would result in an extremely large number of computational cells. As a result, comprehensive CFD simulations with fully detailed animal geometry can suffer from convergence problems in the solver and often become too slow or even infeasible to run for many practical purposes [7,8].

The setup of comprehensive parameter studies or quasi-real-time simulations, thus, requires an efficient parametrization of areas that are characterized by complex geometries. One way to tackle this problem is by using a sub-grid-scale modeling approach for the animals and other interior obstacles. In this direction, even when using steady-state approaches such as Reynolds-averaged Navier–Stokes (RANS), it is common to parametrize small-scale flow obstacles as porous zones, for example, using the Darcy law [9]. Porous media modeling has been used to model partitions or slatted floors or the animals themselves as flow obstacles within the animal occupied zones (AOZ) [10,11,12]. In this approach, the cumulative effect of the interior or animals on the airflow (drag and turbulence) is represented by porous media parameters (such as pressure resistance coefficients). It has been found that, compared to 3D modeled geometries of 22 dairy cows, a porous media model can save around 90% computational time based on 15 CPUs for steady-state simulations while still capturing the bulk effect of the obstacles on airflow, representing a good compromise between accuracy and simulation efficiency [13].

Despite the fact that the actual values of the resistance can depend considerably on the object distribution and the incident angle of the flow, many authors have considered the porous medium as isotropic in the three main directions [12,14]. Recent studies showed that this simplification of isotropic zones with a fixed resistance coefficient can lead to larger inaccuracy when calculating local air exchange of the AOZ under turbulent flow conditions [13]. Implementing the direction-dependent coefficients improves the porous model’s predictions compared to a fully resolved geometry model [7].

To build a reliable sub-grid (porous) model of a larger group of animals, it is crucial to understand how various configuration parameters of the animal group affect the overall pressure drop across the zone. Different configurations can include the number of animals (which determines the porosity or solid volume fraction of the zone), the spacing and arrangement of animals (which relates to the tortuosity of the porous zone and the airflow paths through it), and the orientation of animals relative to the wind (i.e., the individual blocking potential). Each of these factors can alter the pressure drop.

Bustos-Vanegas et al. [3] simulated the airflow around lying and standing cows and showed that the viscous resistance was significant only in the case of a standing configuration or under cross-flow conditions. The largest influence of the wind angle was observed for the cows in standing position where inertial force decreased by about half when the direction changes from cross-flow to transvers flow. Further Hartje [7] found for a single cow model that the pressure drop was highest when a cow was lying down broadside to the flow and lowest when the cow was standing facing the flow head-on. In general, a larger frontal area exposed to the airflow (such as a cow’s side profile vs. front profile) creates a greater resistance and pressure drop [7]. In the case of pigs, for example, Wu et al. [15] showed that the two main factors determining the air resistance of a group were the stocking density of the animals and their live weight (size). Stocking density is directly related to porosity (how much open space is left between animals), and live weight correlates with the body size (surface area) of the animals. A denser packing of animals or larger-bodied animals both increase the flow. Similarly, if animals are arranged in a line vs. scattered, or if there are gaps between them, the ease with which air can percolate through (or around) the group will change. The porous media resistance parameters must be tuned to capture the dominant influences of group configuration on airflow [3,13,16]. Such findings reaffirm that multiple configuration parameters—not just the number of animals, but also their spatial distribution and size—significantly affect the pressure drop through an animal occupied zone.

When parameterizing animal groups as obstacles, another practical consideration is that the configuration is not static. Animal distribution inside the AOZ varies depending on the activities of the animals, related for example to the time of the day. So far in CFD modeling, it is often neglected that in real barns animals move around, change posture, and grow over time, while any fixed obstacle representation approximates only a transient situation. As animals move or adopt different postures, the porous medium’s tortuosity changes. As animals grow (or different breeds with larger/smaller bodies are considered), the blockage effect increases or decreases, modifying the effective porosity of the zone. In consequence, it is crucial to understand the range of possible resistance values to use porous media models with high accuracy compared to fully resolved geometries. Ultimately, to simulate robust ventilation or to predict emissions accurately, we need to account for how much the pressure drop can fluctuate as the animal layout evolves.

With our study we aim to quantify the sensitivity of airflow resistance to the arrangement and attributes of the animals acting as obstacles. Our primary objective is to evaluate the extent to which pressure drop through an AOZ differs under various animal configurations, and to estimate and quantify the impact on the flow pattern downstream. By that, we aim to evaluate whether a single porous media approximation is sufficient or if multiple sets of parameters (or adaptive parameters) are needed to cover the spectrum of real-world configurations.

The following two key hypotheses determine our investigation:

• Tortuosity Hypothesis: Given the number of animals in the group (which corresponds to the porosity of the medium) as constant, the spatial alignment of animals in the group (which contributes to the tortuosity and the effective flow path lengths through the group) has a significant influence on the pressure drop across the group and on the flow pattern downwind of the group.
• Size/Posture Effects Hypothesis: The physical size and shape of the obstacles—related to animal body size, breed, or posture (standing vs. lying)—have a significant impact on the pressure drop and the downstream airflow pattern. Larger or more aerodynamically “wide” animals block more air, causing higher pressure losses, while smaller or narrow-profile animals allow easier flow. For example, a group of heavy-breed cows (or cows lying on their side exposing a broad area) is expected to create a stronger wake and disturbance in the airflow than a group of lighter or narrower animals (or cows facing head-on), all else being equal.

By testing these hypotheses, our study will determine to what extent animal count vs. arrangement vs. size each contribute to airflow resistance. If the range of variability is small, one parameter set may suffice, but if it is large, the model may need to incorporate configuration-specific adjustments. Answering this question will ultimately lead to more robust, accurate, and efficient CFD predictions of barn climate and emissions when using porous modeling approaches.

2. Materials and Methods

This study is based on a CFD model introduced by Doumbia et al. [13] which was based on a preceding study of Bustos-Vanegas et al. [3]. It uses simplified cow geometries composed of cylindrical objects. The simplification of cylindrical cow geometries builds on a previous study by Mondaca and Choi [17], who showed that this approximation very well reproduces the flow patterns generated by detailed polygon cow models. At the same time, less meshing effort is required, which leads to a substantial reduction of preparation and computation time.

Lying and standing cows were distributed randomly within the AOZ. While in the original study only three angle positions of cows were implemented (15°, 30°, and 90°), in the present study, different sets of angle positions were permitted (any angle randomly chosen between 0° and 90°). In addition, in the original study [13], the AOZ had the dimension of L_AOZ = 10.8 m, W_AOZ = 4.9 m, and H_AOZ = 1.6 m, consisting of 22 cows with a density of 2.4 m² cow⁻¹, following the same dimension as one of the AOZs in the prototype dairy barn in Dummerstorf [18]. However, in order to allow cows more freedom in a random distribution within the AOZ and to more generalize the dimensions of the AOZ, in the present study, the AOZ was enlarged to accommodate 33 cows and had the width of the AOZ being half of the length of the AOZ, while keeping the cow density the same as in the original study, i.e., L_AOZ = 17.1 m, W_AOZ = 8.55 m, and H_AOZ = 1.6 m.

2.1. Numerical Model

As this study focused on investigating the effects of animal configurations on the pressure drop variations to provide information on a better characterization of porous media model of the AOZ, all CFD simulations were carried out based on an individual AOZ consisting of 33 cows with a density of 2.4 m² cow⁻¹ without considering the entire housing system. The configurations of the AOZ varied for different scenarios, which are described in detail in Section 2.3.

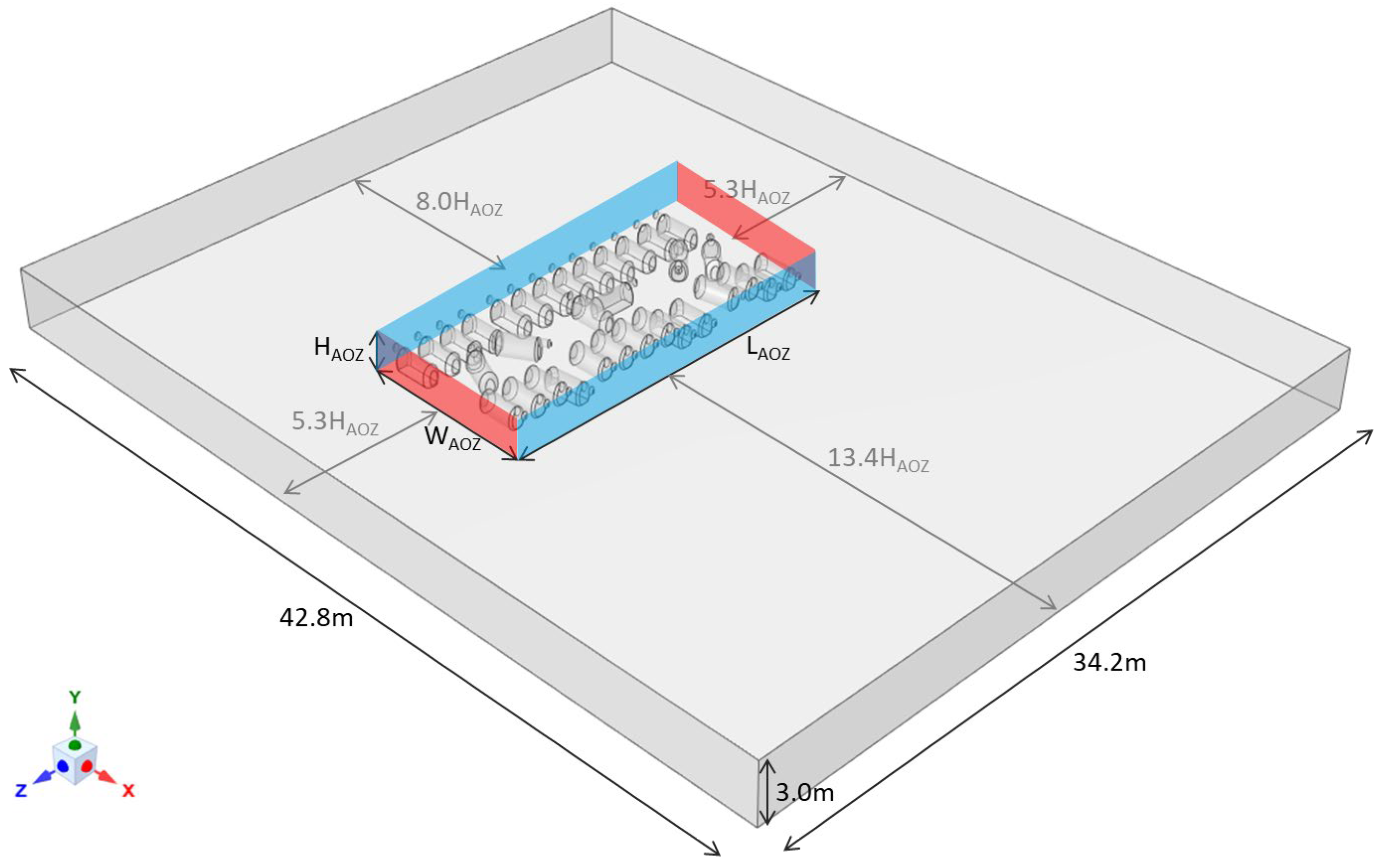
As shown in Figure 1, the dimensions of the computational domain were length × width × height = 42.8 m × 34.2 m × 3.0 m, following the guidelines in the literature [19], in which the front and lateral boundaries were greater than 5 H_AOZ away from the AOZ, and the downstream boundary were greater than 10 H_AOZ away from the AOZ. Instead of using the recommended value of 5 H_AOZ, the top boundary was shortened to 1.9 H_AOZ (i.e., 3 m) based on a preceding study that simulated the computational domain as a virtual wind tunnel with the height of 3 m [3].

For each AOZ configuration, two wind directions of 0° and 90° and nine velocity magnitudes of 0.1, 0.2, 0.5, 0.8, 1.2, 2, 3, 4, and 5 m s⁻¹ were simulated. The front boundary was set to velocity inlet with constant velocity value in each case. The k and ω values were used for representing the turbulence. The downstream boundary was set to pressure outlet with zero static pressure. For the top, bottom, and lateral boundaries and the cows, a no-slip wall boundary was used. This study focused on the wind-driven ventilation conditions when the temperature difference between indoor and outdoor is small and therefore thermal buoyancy is neglectable.

As this study is based on our previous study [13] using the same geometric models of the cows with the same cow density, the same meshing strategy was deemed valid and, thus, was adopted in this paper. Thus, the mesh convergence study was not repeated. In the final mesh used in this study, the minimum surface size was defined as 0.005 m on the ground surface, and 0.0005 m on the cows applying a mesh inflation with a maximum of 10 layers and a mesh growth rate of 1.2, in order to obtain a wall y+ smaller than one. The cell size around the AOZ and in the remaining domain were set to 0.4 m and 0.8 m, respectively. These resulted in a total cell number of 7,581,938 for the baseline case. Further details about the meshing and results of the mesh convergence study can be found in [13].

The simulation setup was validated by comparing with the data from on-farm measurements of air velocities at nine locations at 3 m high inside the prototype dairy barn in Dummerstorf, which was not reachable by cows to prevent cows from damaging the sensors. For the validation case in the preceding study [13] and the baseline case in the present paper, the dairy cow geometric models, cow density, AOZ height, and meshing strategies of the AOZ, as well as the turbulence model and numeric scheme, were kept the same. The results showed that the simulated and measured air velocity had the same direction except at one measurement location and had an RMSE of 0.04 m s⁻¹, indicating that the CFD model using 3D simplified cow geometries was considered valid for simulations. More details about the model validation can be found in the publication [13]. The CFD validation procedure was not repeated in this study.

All simulations were run in steady state (time independent) and adiabatic (no heat transfer) mode using the software ANSYS (version 2022 R1) with the Reynolds-averaged Navier–Stokes (RANS) equations. The k-omega SST model was chosen as the turbulence model. The pressure velocity coupling scheme was set to couple to reach better convergence. The spatial discretization schemes were kept standard, which means second-order upwind for the momentum, turbulent kinetic energy, and the specific dissipation rate, and second-order for the pressure. As suggested by the Fluent user guide, convergence was considered as being achieved when the residuals were below 10⁻³ overall.

2.2. Pressure Drop of the AOZ

In classical porous media modeling, building on the theory of Henry Darcy, a momentum source term S_i is added to the governing equations of fluid flow:

$$S_i={\displaystyle \frac{\mathsf{\Delta }Pi}{\mathsf{\Delta }xi}}=\left(\mu \times D_{ij}+0.5\times {\rho \times F}_{ij}\times \left|u\right|\right)u_i$$

with $D_{ij}=\left[\begin{array}{ccc}{D}_{x_1}& 0& 0\\ 0& D_{x_2}& 0\\ 0& 0& D_{x_3}\end{array}\right]$ and $F_{ij}=\left[\begin{array}{ccc}{F}_{x_1}& 0& 0\\ 0& F_{x_2}& 0\\ 0& 0& F_{x_3}\end{array}\right]$.

Here, (∆Pi)/(∆xi) (Pa m⁻¹) is the pressure drop per length unit in the direction x_i of the Cartesian coordinate, μ (Pa s) is the air dynamic viscosity, D_ij (m⁻²) is the viscous resistance, F_ij (m⁻¹) is the inertial resistance, ρ (kg m⁻³) is the air density, and u_i (m s⁻¹) is the velocity component. The first term, which is linear in the velocity, is characterized by the permeability of the porous medium, while the second term, which is quadratic in the velocity, reflects turbulence effects.

In the present study, we modeled the obstacles in different AOZ configurations explicitly and evaluated the pressure drop in order to evaluate effects of obstacle size and position on the resistance parameters that can be further used in porous modeling. The airflow was introduced in the two main Cartesian directions. The corresponding pressure drop, ΔP_x and ΔP_z, was evaluated by calculating the pressure difference between the planes upstream and downstream of the AOZ.

2.3. AOZ Variations

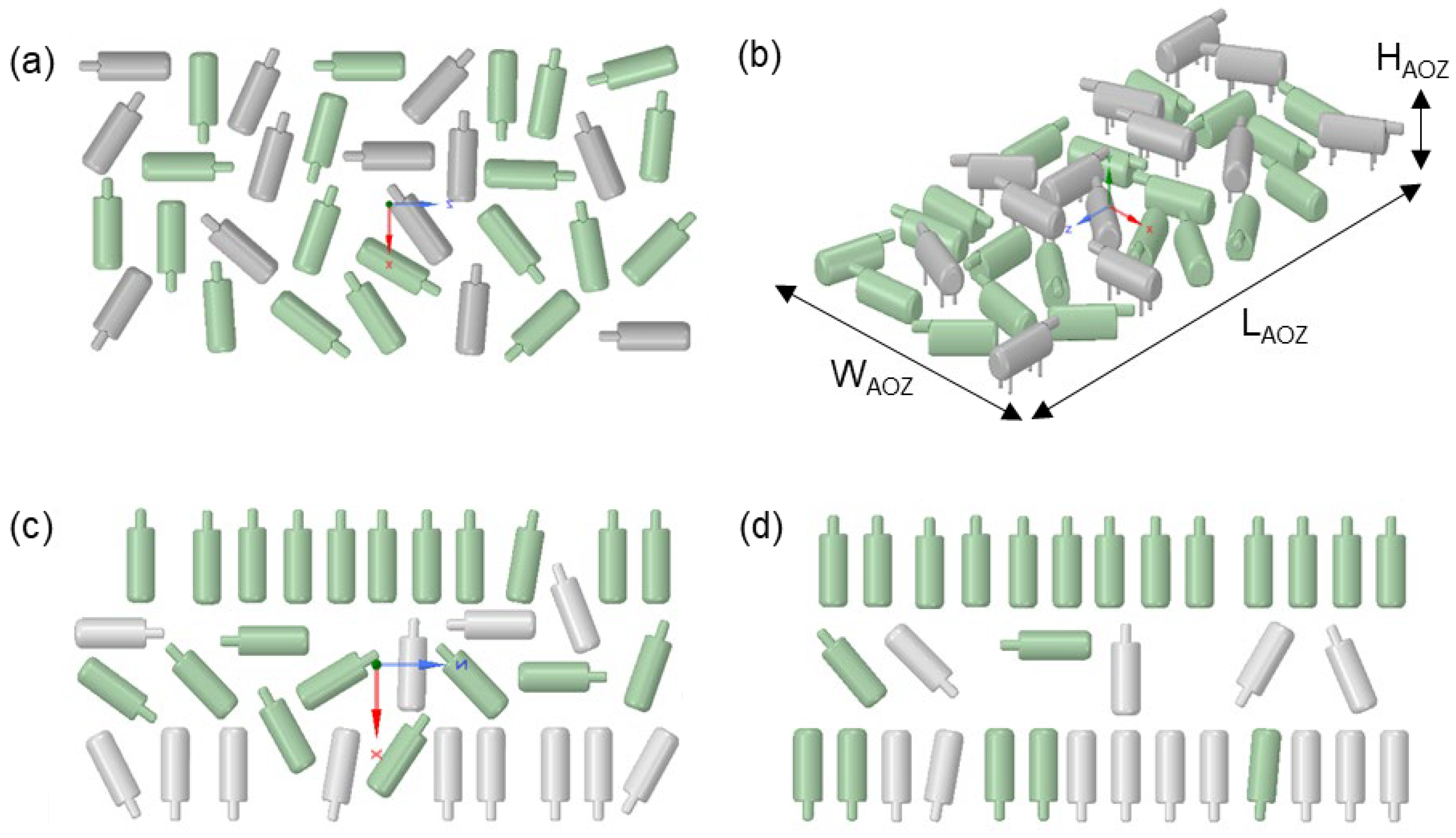
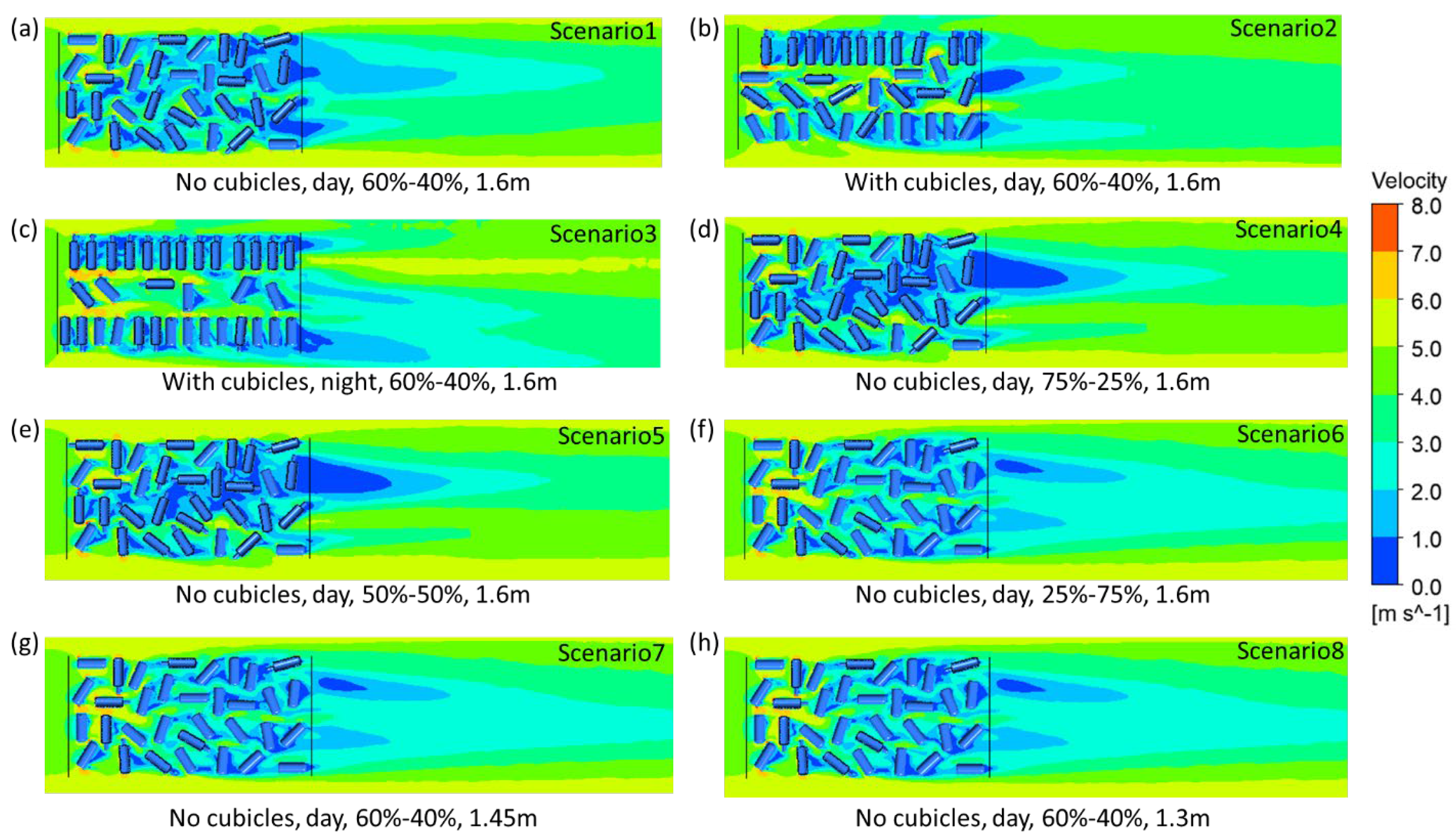
The AOZ models (dimensions L_AOZ = 17.1 m, W_AOZ = L_AOZ/2, H_AOZ are varied upon different scenarios) are shown in Figure 2. Three parameters of the configurations of the AOZ (cow positioning, lying–standing ratio, and cow breed) were investigated. Different sets of these parameter values resulted in a total of eight scenarios. As a baseline we considered a ratio of 60% in lying (in green) and 40% in standing (in gray) positions, as cows typically spend more than half the day lying per day [20]. No cubicles, AOZ height of 1.6 m, and two wind directions were also considered in the baseline case.

Table 1. Designed simulation scenarios.

Scenario No.	Cubicles	Day or Night	Lying–Standing Ratio	AOZ Height (m)	Wind Speed (m s−1)	Wind Direction (°)
1 (baseline)	No	Day	60–40%	1.6	0.1 to 5	0, 90
2	Yes	Day	60–40%	1.6	0.1 to 5	0, 90
3	Yes	Night	60–40%	1.6	0.1 to 5	0, 90
4	No	Day	75–25%	1.6	0.1 to 5	0, 90
5	No	Day	50–50%	1.6	0.1 to 5	0, 90
6	No	Day	25–75%	1.6	0.1 to 5	0, 90
7	No	Day	60–40%	1.45	0.1 to 5	0, 90
8	No	Day	60–40%	1.3	0.1 to 5	0, 90

shows a summary of all designed scenarios.

2.3.1. Cow Position

The three AOZ configurations reflect typical spatial distribution characteristics of cows in loose housing without cubicles versus cubicle housing, where in the latter case we distinguish cow positioning during the day and at night (cf. Scenarios 1–3 in Table 1).

In loose housing, the animals are allowed to move freely and have free access to all functional areas throughout the entire building; thus, they are also free to lie in the cubicles as they please or throughout the entire lying area in barns with unstructured free lying areas. In housing systems without cubicles, this implies a variety of possible angles between the main airflow direction and the animals in lying and standing position, which is reflected in the configuration “no cubicles” (Scenario 1). The “with cubicles” configuration (Scenarios 2 and 3) is where cubicles and beds have been installed inside the AOZ in order to create places to rest. In those systems, part of the variety in angles is lost as the animals are triggered to align parallel to each other in the cubicle. In the alley between the cubicles, the full range of angles may occur. The “with cubicles at night” configuration (Scenario 3) corresponds to a situation in cubicle housing with less activity, where cows lie inside the beds or are about to lie down there. Only a few animals are found in the alleys.

The porosity of the AOZ is the same in all three configurations; however, the tortuosity must be expected to differ which will affect the pressure drop. The tortuosity measures the effective length of the transport route through a porous medium and depends on the average angle between the main flow direction and the pores, while the porosity is defined by the animal density, which is constant throughout the scenarios.

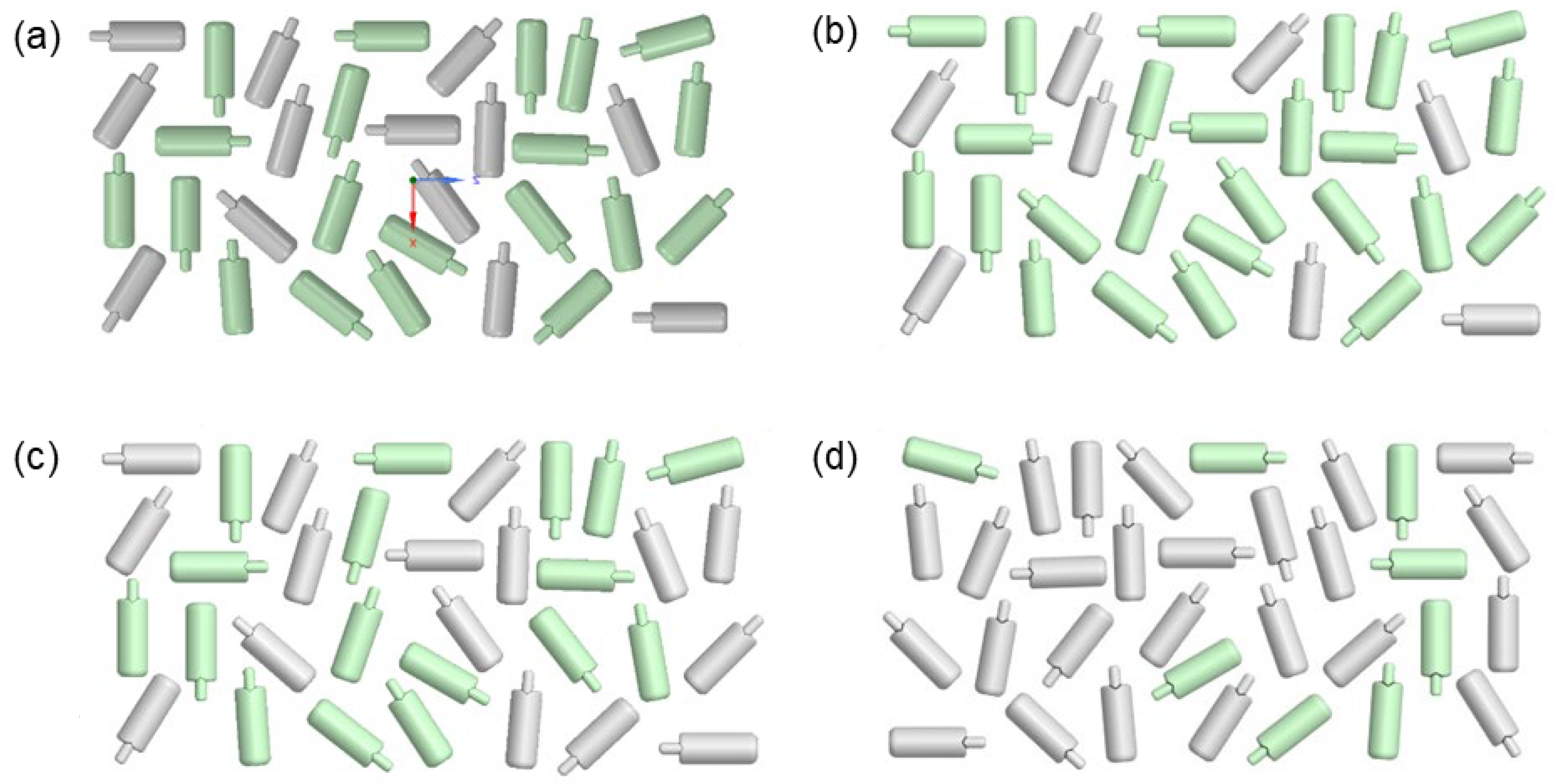
2.3.2. Cow Lying–Standing Ratio

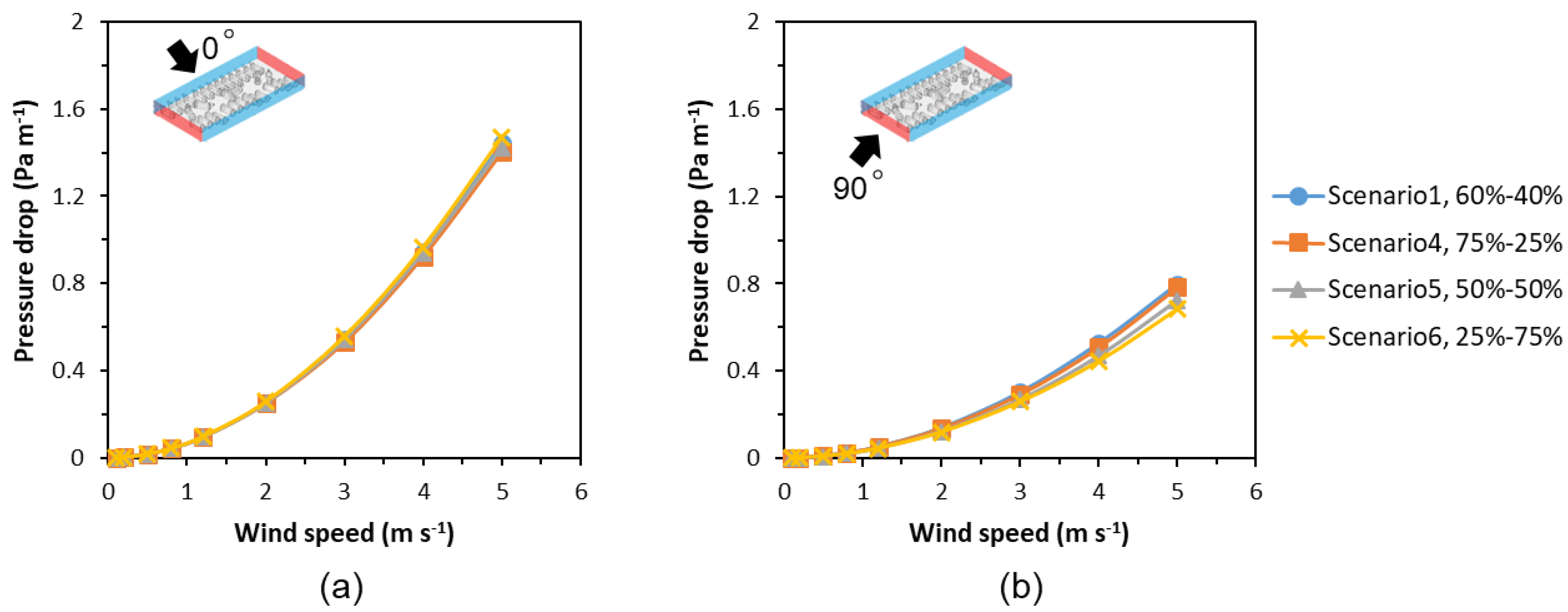
The original AOZ is composed of 60% lying cows and 40% standing cows. The reasoning behind this was that cows spend, under thermo-neutral conditions, 10 to 14 h per day lying [21]. However, the activity and location of cows differs during the day and in reaction to microclimatic conditions. Taking this variability into account, three additional lying–standing ratios for the AOZ configuration without cubicles were explored (cf. Scenario 4–6 in Table 1). Those are 75% lying–25% standing, 50% lying–50% standing, and 25% lying–75% standing (where the latter may occur under very hot conditions) (Figure 3).

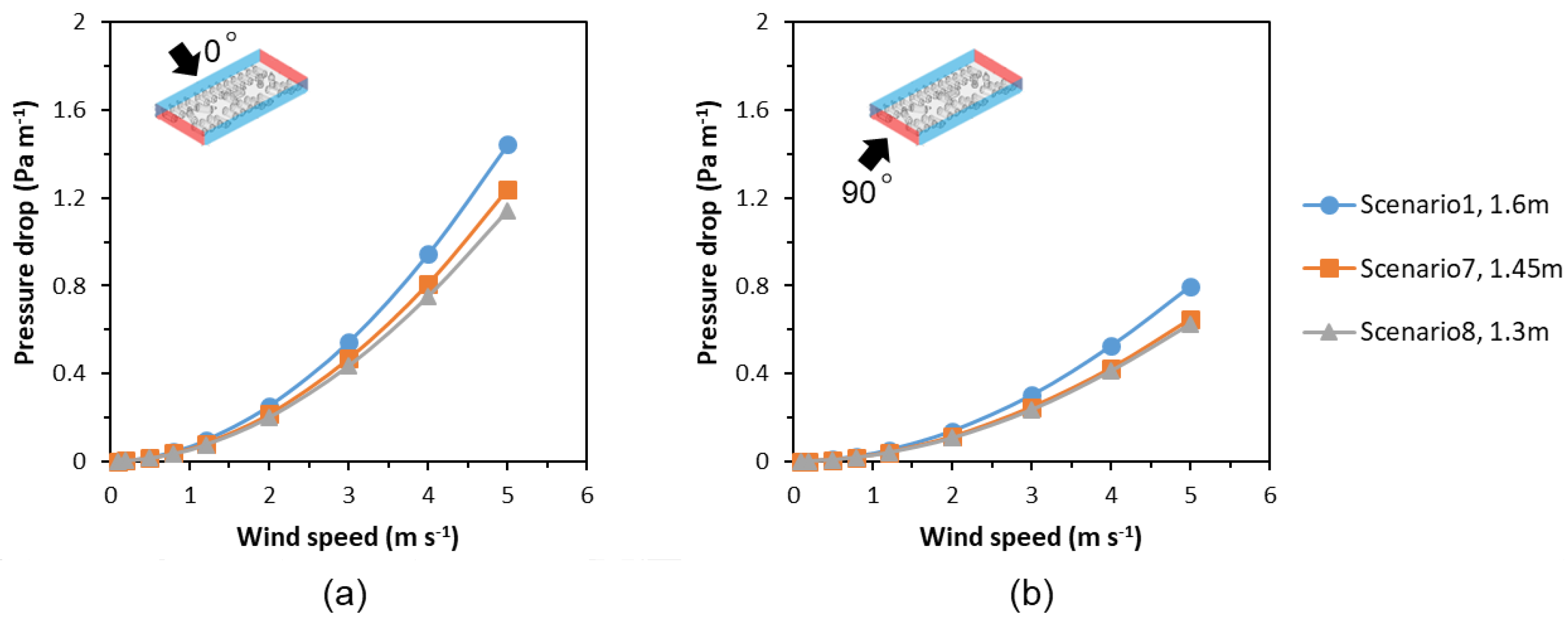
2.3.3. Cow Breed

The cow breed chosen for the original AOZ was Holstein Friesian (H_AOZ = 1.6 m), which is the widely used breed for dairy farming. However, there are other breeds that differ considerably in size and, thus, must be expected to affect pressure drop in a different way. In the present study we considered two additional breeds, the red Holstein (height H′_AOZ = 1.45 m) and jersey (H″_AOZ = 1.3 m) cattle (cf. Scenarios 7 and 8 in Table 1). Those breeds were chosen because of their popularity around the world. Holstein breeds are globally the most important dairy cattle breed due to their high milk yields. The Red Holstein is, after the Holstein Friesian, particularly popular. The Jersey cattle breed is famous for its good feed efficiency and the high quality of the milk. The different body heights of these breeds result in a low-rise upper ceiling of the AOZ, which is about 90% of H_AOZ for Red Holstein and about 80% of H_AOZ for Jersey. Effects of each of these heights were simulated for the baseline scenario without cubicles.

3. Results and Discussion

3.1. Effects of Cow Position

The comparisons of pressure drop per unit length for scenarios with different cow positions are shown in Figure 4 (the exact pressure drop values can be found in Supplementary Materials). It was found that the pressure drop increased with the increasing wind speed for all scenarios and both wind directions. The variation in the pressure drop in relation to the wind speed showed a similar trend to the literature [3,21] but higher values. For example, the pressure drop at 0.5 m s⁻¹ wind speed and 0° wind direction was 0.018 Pa m⁻¹ for Scenario 1, which was higher than the values determined by Bustos-Vanegas et al. [3], with 0.013 Pa m⁻¹, and by Wu et al. [21], with 0.009 Pa m⁻¹. The higher pressure drop was mainly caused by the higher cow density of 2.4 m² cow⁻¹ compared to the literature, with 2.85 m² cow⁻¹ [3] and 12 m² cow⁻¹ [21], which caused larger blocking effects of the animals to the airflows.

At 0° wind direction, the pressure drop of Scenario 1 was close to Scenario 2 at low wind speed and was slightly higher than Scenario 2 when the wind speed was greater than 4 m s⁻¹, but was much higher than Scenario 3, with the highest difference being of 0.269 Pa m⁻¹ at 5 m s⁻¹ wind speed (Figure 4a). This was because during the night, more cows were aligned, with two rows of cubicles. This yields lower flow resistance between cows in a row. In consequence, the effective path lengths for the passing wind were shorter; therefore, lower pressure drop occurred when the flow went across the AOZ.

When considering the AOZ as a porous medium, changing the position of animals and the direction of inflows does not change the porosity. Ergun [16] has successfully related the pressure drop across a porous medium with spherical elements to the porosity of the porous medium. However, in our case, the porosity was constant among different AOZ configurations, indicating that the porosity was not the reason causing differences in the pressure drop. The other possible reason would be the tortuosity of the AOZ, which measures the distortion of the flow path through the region compared to a straight flow path. For the scenarios with cubicles, especially the night case, i.e., Scenario 3, cows were in a more organized alignment than the random distribution. Therefore, the tortuosity of the AOZ in Scenario 3 would be lower than Scenario 1, which explains the reason for the lower pressure drop that occurred in Scenario 3 (Figure 4).

The observed differences in airflow resistance are consistent with the observations in the airflow patterns, as shown in Figure 5c, in which higher air velocity was observed at the downwind of the AOZ compared with daytime cases (Figure 5a,b) (the exact air velocity values and the coordinates can be found in Supplementary Materials).

At 90° wind direction, the pressure drop was much lower than that at 0° wind direction, which might be related to the smaller airflow blocking area and was reflected by the lower viscous and inertial resistance for each case (

Table 2. Summary of viscous resistance D and inertial resistance F.

Scenario No.	Wind Direction 0°		Wind Direction 90°
	D (m−2)	F (m−1)	D (m−2)	F (m−1)
1	943.19	0.09	507.45	0.05
2	1075.57	0.09	341.97	0.05
3	976.28	0.07	336.46	0.05
4	1036.96	0.09	386.10	0.05
5	1070.05	0.09	259.24	0.05
6	998.35	0.09	430.23	0.04
7	744.62	0.08	441.26	0.04
8	805.30	0.07	330.94	0.04

). Bustos-Vanegas et al. [3] also observed the dependence of inertial resistance on inflow direction for different AOZ configurations. There was only a slight difference with relative deviation of 6% in pressure drop at wind speed of 5 m s⁻¹ between the case during the night (Scenario 3) and the cases during the day (Scenarios 1 and 2), while the inertial resistance remained the same at 0.05 m⁻¹ for the three cases. This could be reflected by the slightly higher air velocities downstream of the AOZ for Scenario 3 compared with Scenarios 1 and 2, as shown in Figure 6. Even though the difference in pressure drop among three scenarios was small, the viscous resistance in Scenario 1 was around 33% higher than Scenarios 2 and 3. This is in line with expectations, as the resistance in the case without cubicles (i.e., cows were distributed with arbitrary angles) should be larger than with cubicles where the wind was channeled through the alley.

3.2. Effects of Cow Lying–Standing Ratio

Figure 7 compares the pressure drop per unit length for the cases with different cow lying–standing ratios at two wind directions. In contrast to the cow position, the cow lying–standing ratio had negligible effects on the pressure drop at 0° wind direction with an average deviation of 1.9% and a maximum deviation of 6.3%. Slight differences in the airflow pattern downstream of AOZ were found, i.e., three weak regions were observed for Scenarios 1 and 4 (Figure 5a,d), and two weak regions were observed for Scenarios 5 and 6 (Figure 5e,f). The inertial resistance remained the same, with the value of 0.09 m⁻¹ for all four scenarios.

At 90° wind direction, the pressure drops were lower than the scenarios at 0° wind direction. The differences in pressure drop among different scenarios became apparent at higher wind speeds, with Scenario 6 showing the lowest values and a relative deviation of 14.6% from Scenario 1 at 5 m s⁻¹ wind speed. This was probably due to a larger air penetration ratio when there were more standing cows, which reduced the resistance of cows to the airflows, and this was reflected by the lower inertial resistance of 0.04 m⁻¹ (Table 2) and higher air velocities downstream of the AOZ (Figure 6f) for Scenario 6. This is consistent with the findings of Bustos-Vanegas et al. [3] that the inertial resistance was double resting cows > resting cows > standing cows at 90° wind directions.

While the spatial arrangement of the animals may have significant impact on the pressure drop, it can be concluded that pure modifications in the lying–standing ratio of cows are, in general, negligible at cross-ventilation conditions (i.e., 0° wind direction) when estimating the pressure drop along the animal occupied zone. Although those modifications in body posture may occur frequently as a consequence of animal activity patterns (related, for example, to daily rhythm of feeding and rumination or as a reaction to adaptation to microclimatic conditions), a ratio of 50:50 can be assumed without introducing significant uncertainty in the pressure drop estimation.

3.3. Effects of Cow Breed

The differences in cow breed are mainly reflected in the different heights of the AOZ in this study. It can be seen in Figure 8 that the higher the AOZ, the higher the pressure drop per unit length. The biggest difference was found between Scenario 1 and Scenario 8 at 5 m s⁻¹ wind speed with the values of 0.203 Pa m⁻¹ and 0.299 Pa m⁻¹ at 0° and 90° wind direction, respectively. The inertial resistance decreased linearly by about 0.01 m⁻¹ per 0.15 m reduction of animal height for 0° wind direction, while the similar inertial resistance of 0.04–0.05 m⁻¹ (Table 2) was observed for all three AOZ heights when the wind approached with an angle of 90°.

Moreover, at 90° wind direction, small differences in the pressure drop between Scenario 7 and Scenario 8 were observed with an average relative difference of 5.3%. The same airflow pattern (Figure 6g,h) was observed between two scenarios.

It has to be noted that the present study only focuses on the wind-driven ventilation conditions at the two most practically relevant wind directions (0° and 90°), which represent cross-ventilation and longitudinal ventilation scenarios encountered in naturally ventilated dairy barns. Therefore, the pressure drop variations in relation to cow configurations are primarily applicable to the conditions similar to the investigated configurations. To capture the practical situation in dairy barns, buoyancy effects and a broader range of wind directions from 0° to 360° with denser directional intervals should be considered.

4. Conclusions

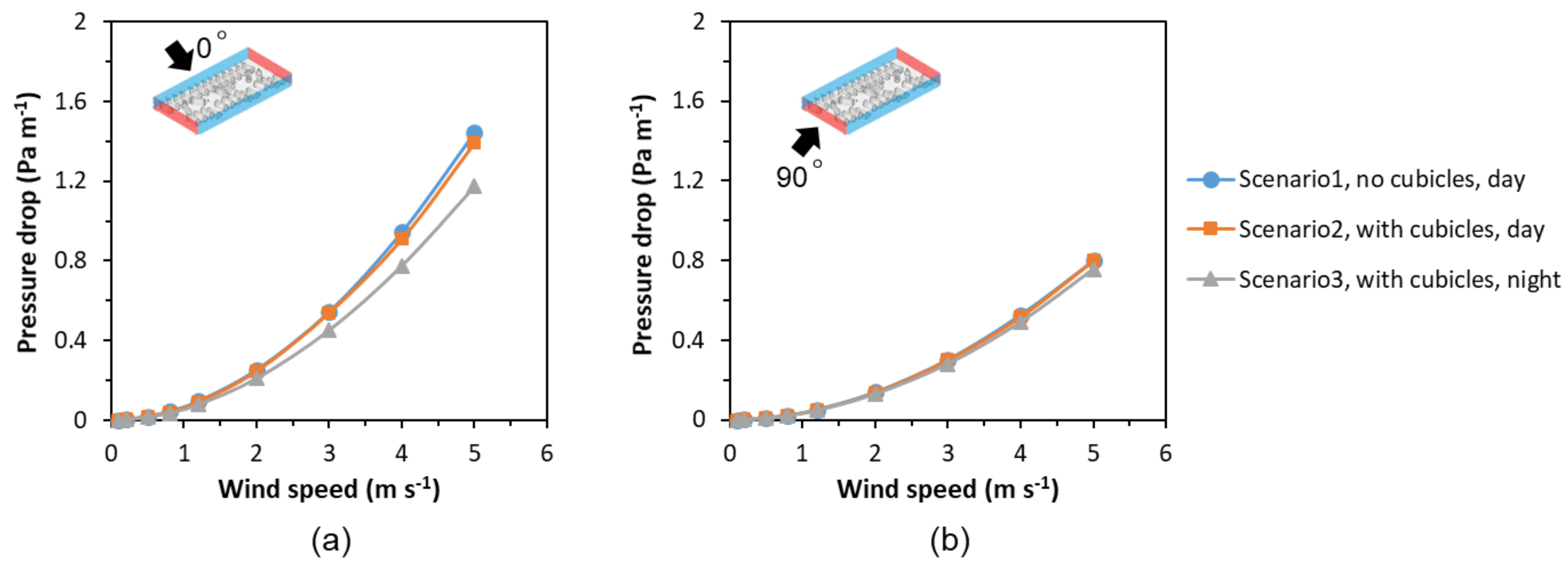
The range of variability in pressure drop per unit length associated with AOZ configurations, including cow spatial arrangement, cow lying–standing ratio, and cow breed at two wind directions, was studied. The following conclusions were drawn.

The pressure drop increased with the increasing wind speed for all scenarios. At 0° wind direction, higher pressure drop values were obtained than at 90° wind direction, reflected by higher viscous and inertial resistance. The cow position, in general, had little impact on the pressure drop at low wind speeds, while showing differences among different scenarios when the wind speed was over 2 m s⁻¹, with the highest difference of 0.269 Pa m⁻¹ between Scenario 1 and Scenario 3 at 5 m s⁻¹ wind speed and 0° wind direction.

Cows distributed in a more organized alignment, i.e., in Scenario 3, showed less airflow resistance, and, therefore, a lower pressure drop and higher air velocities across the AOZ, which can be explained by shorter effective path lengths in such alignments. Those results confirm our tortuosity hypothesis.

We further found that the cow breed affected the pressure drop, with higher AOZ showing higher pressure drop and air resistance. In contrast, it was found that the effects of cow lying–standing ratio on the pressure drop and airflow resistance coefficients were negligible, with a maximum deviation of 6.3% at 0° wind direction. This is likely related to the fact that the overall blocking potential is similar in both cases and the distribution of lying and standing cows affects the air resistance (e.g., if standing and lying cows alternate, the effective path length for the flow increases, while a row of only standing or only lying cows may be associated with similar path lengths). In consequence, the initial size–posture hypothesis could be only partly confirmed in this study.

Representing the AOZ with the porous medium and using the resistance coefficient derived by this study supports the setup of more accurate CFD models. However, our study primarily supports the importance of tortuosity, while the porosity effects were not investigated. In order to understand the influence of the effective path length through the AOZ in different scenarios in more detail, future investigations are needed to calculate the tortuosity of each AOZ configuration and to explore the sensitivity of the resistance coefficients to the deviations in cow orientation and spacing. Moreover, the present study only considered wind-driven ventilation conditions at two main wind directions, which limits the applicability of the obtained flow resistance only to the situations similar to the investigated scenarios. Future studies that consider the buoyancy effects and a broader range of wind directions will be conducted. Meanwhile, the directional anisotropy of viscous resistance and inertial resistance will be explored in future work. By that, it will become feasible to determine more accurate resistance coefficients for different configurations without the need to explicitly simulate distinct AOZ configurations.