Next Article in Journal
Assessment of Heavy Metal Soil Contamination and Remediation Strategies in Eastern Slovakia: A Case Study from Dargov
Previous Article in Journal
Field Performance and Wear Behavior of Atmospheric Plasma Spraying (APS) Coated Discs Used in Agricultural Disc Harrows
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agriculture
Volume 16
Issue 1
10.3390/agriculture16010115
agriculture-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Effect of Cutting Technique on the Degree of Damage to Fruit Tree Shoots

by
Tomasz Nowakowski
1,
Karol Tucki
2,* and
Łukasz Gruz
2
1
Department of Biosystems Engineering, Institute of Mechanical Engineering, Warsaw University of Life Sciences, Nowoursynowska Street 164, 02-787 Warsaw, Poland
2
Department of Production Engineering, Institute of Mechanical Engineering, Warsaw University of Life Sciences, Nowoursynowska Street 164, 02-787 Warsaw, Poland
*
Author to whom correspondence should be addressed.
Agriculture 2026, 16(1), 115; https://doi.org/10.3390/agriculture16010115 (registering DOI)
Submission received: 2 December 2025 / Revised: 30 December 2025 / Accepted: 31 December 2025 / Published: 2 January 2026
(This article belongs to the Section Agricultural Technology)
Browse Figures
Versions Notes

Abstract

The aim of the study was to assess the effect of various fruit tree shoot cutting techniques and variable wood moisture content on the formation of damage on the cut surface, using fractal dimension analysis. The experiments were conducted on shoots of two cultivars of apple and pear trees, at four levels of moisture content and using three cutting units: a chainsaw, a circular saw, and bypass loppers. The obtained cross-sectional images were digitally processed, and the degree of damage was evaluated using the fractal dimension. Analysis of variance demonstrated a significant effect of shoot moisture content, plant species, and cutting tool type on the fractal dimension value, which represents the complexity of the cut edge. The best cutting quality was observed for shoots with the highest moisture content and those cut with a pair of loppers and a circular saw, whereas the greatest damage was caused by the chainsaw. Apple cultivars exhibited the lowest susceptibility to damage, while pear cultivars showed the highest. These findings confirm the crucial role of both cutting technique selection and material moisture in determining cutting quality, and the applied fractal analysis proved to be a useful tool for the objective assessment of damage. The obtained results contribute to the optimisation of tool selection and to the design of orchard machinery, especially in relation to the development of mechanical pruning systems.

1. Introduction

One of the major challenges currently facing modern agriculture is the need to reduce the use of chemical plant protection products and to gradually withdraw many active substances that have been widely applied in crop protection in recent decades [1,2,3]. This trend has accelerated the development of biological plant protection products and alternative orchard management practices, including mechanical operations supporting tree maintenance [4,5,6].
Modern orchards are increasingly equipped with advanced irrigation and fertilisation systems that improve resource efficiency and production stability [7,8]. Chemical thinning is now less frequently applied and, when required, is often replaced by manual thinning. Orchard maintenance operations are performed using modern machinery, and tree pruning is increasingly carried out using mechanical systems [9,10].
One of the fundamental practices in orchards is the pruning of fruit tree shoots. The timing, technique, and intensity of pruning are of key importance for physiological processes occurring within the plant. When executed correctly and at the appropriate time, pruning affects both tree growth and fruiting performance. It plays a crucial role in stimulating fruit development and improving yield through its influence on photosynthetic efficiency and nutrient transport within branches [11]. Pruning is used to shape the tree crown and to maintain its appropriate size and density. Vigorously growing fruit trees require pruning that limits both crown height and spread. This reduces the tendency of trees to produce excessive numbers of small fruits. At the same time, a reduced crown size enables the remaining fruits to reach the size characteristic of a given cultivar [12,13].
Numerous guidelines exist for selecting the most suitable pruning system to meet specific requirements. This decision is largely individual and depends, among other factors, on orchard size, the modernity of plantings, and the tree training system, in which specially selected and properly trained cultivars may be subjected to mechanical pruning, as well as on logistical aspects, since orchards located at a considerable distance from the farm may render machine operation economically unprofitable. Mechanical pruning represents a potential alternative to manual pruning, as it reduces both the time required for pruning and associated costs while maintaining or even increasing efficiency [14,15]. The precision of shoot pruning may be revolutionised by currently developed decision support systems based on local point clouds and neural networks [16,17]. The most commonly applied cutting units in mechanical pruning are cutter booms equipped with circular saws, shearing units, or sickle bar blades.
Both the local and global markets offer a wide range of devices and tools for pruning and orchard maintenance, as well as for the care of other crops. The growing demand for pruning machinery results from several factors, including increasing labour costs and related maintenance expenses (legal requirements, health insurance, registration, and accommodation), as well as a shortage of qualified workers. Mechanical pruning alone is often insufficient and must be followed by manual pruning. Pruning costs depend on numerous factors and, due to their labour- and time-intensive nature, usually account for 10–15% [18,19]. According to Niederholzer [20], in plum production, these costs may reach up to 25% of total expenditures. Studies indicate that combining mechanical and manual pruning improves yield performance, while the overall cost remains comparable to that of traditional pruning [21].
Long-term experimental results and orchard practice show that mechanical pruning is feasible for certain species, such as citrus trees and olives, which do not require selective interior pruning [22,23,24]. Therefore, mechanical pruning is widely applied, for instance, in Italy, mainly in the management of citrus orchards. Comparative studies of manual and mechanical pruning were conducted using a sickle bar equipped with five cutting blades for the ‘Fortune’ mandarin cultivar. Two levels of mechanical pruning intensity were applied. No differences were observed in terms of yield or fruit quality. In all pruning treatments, fruit size reached the highest grade. It was observed, however, that the exclusive use of mechanical pruning over a three-year period resulted in a 22% reduction in yield relative to manual pruning. Mechanical pruning shortened the time required for pruning by 13% relative to manual pruning [25,26].
Studies on mechanical pruning using a cutter boom equipped with circular saws for the ‘Clemenules’ mandarin cultivar were conducted by Fonte [27]. Twelve pruning variants were applied, including separate mechanical and manual treatments as well as alternating systems. It was found that alternating mechanical pruning in one year with manual pruning in the following year was a more effective solution than the exclusive application of mechanical pruning or annual mechanical pruning combined with manual inspection. The fruit yield achieved using this approach was higher and comparable to that obtained with the manual pruning strategy.
Four-year studies using mechanical pruning at varying intensity levels, as well as integrated mechanical and manual pruning of ‘Fino 95’ lemon trees, demonstrated advantages over conventional manual pruning practices. Continuous mechanical pruning proved to be the fastest, most cost-effective, and most productive method, but it significantly altered crown shape by increasing shoot density in the inner part of the tree. The introduction of mechanical pruning systems into orchard management strategies reduces costs without decreasing yield [28].
The application of mechanical pruning using a cutter boom equipped with shearing units in a 12-year-old spindle-trained ‘Pinova’ apple orchard resulted in changes in crown structure. Such crowns exhibited poorer light penetration in the central and apical parts, required more intensive fruit thinning, and showed a tendency to produce small-sized fruits [29]. Nevertheless, it is already evident that the use of mechanical pruning in apple orchards enables time savings compared with manual pruning [30]. The use of a cutter boom equipped with circular saws for pruning plum shoots resulted in a tendency toward the formation of a fruiting wall. Moreover, mechanical pruning must be combined with manual pruning, which is essential for regulating the upper parts of the crown as well as growth within the inter-row space [31]. It is important to note that the timing of mechanical pruning, its intensity, and the type of cutting unit applied are of key importance [32,33,34,35].
Studies on manual and mechanical pruning indicate that fully mechanised pruning systems can be managed without compromising fruit yield and quality [36].
However, the risk of wound formation on trees during mechanical pruning remains a significant concern. Such wounds promote the spread of viral and fungal infections. Infection-related issues are also reported in the harvesting of energy crops, where reducing damage to the stump caused by cutting units ensures proper shoot regrowth in the following agrotechnical season [37].
The surface formed after cutting is very difficult to assess. However, the acquired data prove useful for drawing conclusions about the applied cutting system and its impact on the plant. Therefore, methods based on computer image analysis are increasingly used for the examination and qualitative assessment of biological structures [38,39,40]. It is also widely used in the investigation of branched structures such as blood vessels and neurons [41,42]. Numerous mathematical methods are available for calculating the fractal dimension; in the present study, the box-counting method was employed.
Despite the wide application of mechanical pruning systems and the growing number of studies addressing their agronomic and economic effects, the quality of cut surfaces and the extent of cutting-induced damage are still most often assessed qualitatively or based on visual inspection. Quantitative, objective methods enabling a direct comparison of different cutting units, plant species, and material conditions remain limited, particularly in relation to fruit tree pruning.
The aim of the study was to assess the effect of different fruit tree shoot cutting techniques and variable shoot moisture content on the resulting damage using a method based on fractal dimension measurement.
The manuscript presents results obtained for two apple cultivars (‘Ligol’, ‘Gloster’) and two pear cultivars (‘Conference’, ‘Hortensia’).

2. Materials and Methods

2.1. Study Material

The study was conducted on two apple cultivars (‘Ligol’, ‘Gloster’) and two pear cultivars (‘Conference’, ‘Hortensia’). Shoots used for the experiments were collected from two orchard farms. Apple shoots of the cultivars ‘Ligol’ and ‘Gloster’ were obtained in Branków (Warka Commune, Grójec District, Mazowieckie Province, Poland), whereas pear shoots of the cultivars ‘Conference’ and ‘Hortensia’ were collected in Ostrowiec (Chynów Commune, Grójec District, Mazowieckie Province, Poland).
Shoot samples were taken from the following trees
  • a 12-year-old ‘Ligol’ apple tree grafted on the ‘P60’ rootstock, planted at 1.2 m within rows and 3.5 m between rows (Figure 1a);
  • a 12-year-old ‘Gloster’ apple tree grafted on the ‘M9’ rootstock, planted at 1.2 m within rows and 3.5 m between rows (Figure 1b);
  • a 12-year-old ‘Conference’ pear tree grafted on the ‘Caucasian pear’ rootstock, planted at 2.0 m within rows and 3.8 m between rows (Figure 1c);
  • a 12-year-old ‘Hortensia’ pear tree grafted on the ‘Caucasian pear’ rootstock, planted at 2.0 m within rows and 3.8 m between rows (Figure 1d).
All samples were cut at the same time under similar weather conditions and then transported to the laboratory. Characterisation was performed for the collected shoot samples. The measurements were carried out using a digital calliper, type MAUa-E24F, with a range of 0–150 mm and an accuracy of 0.01 mm, as well as a 3 m tape measure with an accuracy of 1 mm. The results are summarised in Table 1.
Four levels of moisture content of fruit tree shoots were evaluated. The average moisture content of the fresh sample was determined using the oven-drying method in accordance with ASABE Standard S358 [43]. The samples were dried in an SLW 115 TOP (POL-EKO, Wodzisław Śląski, Poland) laboratory drying oven at a temperature of 103 ± 0.4 °C for 24 h. They were weighed on a WLC 0.6/A1 (RADWAG, Radom, Poland) electronic balance with an accuracy of 0.01 g.
Before measuring moisture content, the laboratory dryer was turned on and the drying temperature and duration were programmed. The samples were placed in the dryer once the set temperature was reached. Randomly selected shoots from the same plant were chopped using a manual pruner and placed on steel trays. Then, 30 g samples were weighed (three samples per plant) and placed in the SLW 115 TOP laboratory dryer. After drying was completed, the samples were removed from the dryer and weighed again.
The moisture content was calculated using the following formula:
M C = m w − m s m w × 100 %
where MC is the moisture content of the fresh sample, %; mw is the weight of the fresh sample, g; ms is the weight of the sample after drying, g.
The apple cultivar ‘Ligol’, bred in 1972 in Poland, shows moderate vigour and early fruiting but requires intensive pruning and fruit thinning due to heavy cropping and alternate bearing [44,45,46,47].
The apple cultivar ‘Gloster’, a German variety bred in 1951, forms an erect crown, enters fruiting early, and requires careful pruning; it shows moderate frost resistance but is susceptible to apple scab [48,49,50,51].
The pear cultivar ‘Conference’, bred in the United Kingdom in 1884, exhibits moderate vigour, good resistance to diseases and adverse weather conditions, and is self-fertile [52,53,54,55].
The pear cultivar ‘Hortensia’, a hybrid bred in Dresden-Pillnitz, shows low susceptibility to scab but sensitivity to fire blight and requires slightly acidic soils (pH 6.2–6.7) [56,57].

2.2. Test Stand

To assess the effect of the applied cutting technique on the degree of damage to fruit tree shoots, three devices equipped with different cutting units were used. The first cutting unit analysed was a chainsaw mounted on a battery-powered electric saw, Husqvarna model 436Li (Figure 2a). The maximum cutting speed was 15 m·s−1. The saw was fitted with a 12-inch guide bar and a chain with a 3/8-inch pitch (Figure 2b) [58].
In the study, a chain with a 3/8-inch pitch and a length of 30 cm, consisting of 45 drive links and 22 Chamfer Chisel cutting teeth, was used. The thickness of the drive links was 1.1 mm. The chain body (drive links, tie straps, and rivets) as well as the cutting teeth were made of structural alloy steel. In addition, the cutting teeth themselves were thermally hardened by quenching.
The factory-installed chain for the Husqvarna 436Li battery-powered chainsaw is typically a model with a 3/8-inch pitch, a 1.1 mm drive link thickness, and various bar lengths (e.g., 30 cm, 35 cm), with the corresponding number of drive links (e.g., 45, 52) and cutting teeth (e.g., 22, 26). It is a Chamfer Chisel–type chain, designed for smaller chainsaws and characterized by low vibration, such as the Husqvarna H38 model (Table 2).
The second cutting unit was a circular saw of the METABO KS 216 M Lasercut (Metabowerke GmbH, Nürtingen, Germany) (Figure 2c). The saw was mains-powered and featured a rated power of 1.1 kW [68]. The rotational speed under load was 3450 rev·min−1. The saw was equipped with a 216 mm diameter blade with 40 carbide-tipped teeth, each with a width of 2.4 mm (Figure 2d).
The METABO circular saw (Metabowerke GmbH, Nürtingen, Germany) was equipped with a 216 mm diameter blade, featuring 40 WZ-type teeth (alternating bevel), with a negative rake angle of 5°. The blade body thickness was 1.8 mm, with teeth tipped with sintered carbides, each 2.4 mm wide (Figure 2d). The teeth were made of HW/CT material, a cemented carbide composed of tungsten carbide (WC) and titanium carbide (TiC) as the hard phase, bonded with cobalt (Co) (see Table 3 for detailed specifications and literature references).
The third cutting unit used in the study was the cutting blade of a pair of bypass loppers, Fiskars model L28 Hook type S (Figure 2e,f). The maximum shoot diameter enabling efficient cutting was up to 40 mm [76].
The two-handed bypass lopper had handles made of aluminum, to which hardened steel blades were attached. Additionally, the blades were coated with a non-stick PTFE (polytetrafluoroethylene) layer, which minimizes friction and ensures a clean cut.
The blade of the Fiskars L28 SingleStep (Fiskars, Espoo, Finland) bypass lopper was made of hardened steel. The blades are also coated with a non-stick PTFE (polytetrafluoroethylene) layer, which reduces friction and ensures a clean cut, facilitating both operation and maintenance of the tool.

2.3. Methodology

The acquired image of the cut shoot was analysed using the fractal dimension. Fractal dimension analysis has been applied to the estimation of complex, irregular shapes. Its effectiveness has been confirmed in medical applications, including the analysis of positron emission tomography images, radiographic images, computed tomography scans, and magnetic resonance images.
The assessment of damage generated during shoot cutting, based on fractal dimension measurement, required a series of photographs of the cut shoots to be acquired [77]. Shoots were randomly selected from the prepared apple and pear samples. Each shoot was then mounted sequentially in a vice, where the cutting procedure was performed. Each sample was photographed in a top-down orientation using a Sony α500 camera (Sony, Tokyo, Japan) (12 MP, CMOS sensor 24.4 × 15.6 mm). The camera was mounted on a tripod, and photographs were taken from a distance of 20 cm from the lens (Figure 3a). The object being photographed was illuminated with two white light lamps (4000 K). Images were saved in JPEG format with a resolution of 4592 × 3056 pixels/inch.
For each moisture level, 10 images were acquired for each of the four shoot types (apple cultivars ‘Ligol’ and ‘Gloster’, and pear cultivars ‘Conference’ and ‘Hortensia’) and for each of the three cutting units (chainsaw—PL, circular saw—PT, bypass loppers—SN). In total, 120 images were collected within each moisture series. The acquired images served as input files for further graphic processing using Adobe Photoshop CS6 (version 13.0; Adobe, San Jose, CA, USA).
The obtained images were initially cropped and cleaned using the “Eraser” function in Adobe Photoshop with the options “Smooth,” “Contiguous,” and “Tolerance” set to 32%, and “Opacity” set to 100%, leaving only the shoot with visible damage while preserving the original resolution (Figure 3b). Color information was then removed, resulting in a black-and-white image (Figure 3c). The prepared images were subsequently imported into ImageJ 1.54 g. The shoot outline was extracted using the “Find Edges” function, which allowed the determination of the fractal dimension using the box-counting method (Figure 3d).
In this method, the image is covered with a grid of square cells with increasing sizes ranging: 2, 3, 4, 6, 8, 12, 16, 32 to 64 pixels, required to cover the binary image. The software then counts the number of grid cells covering the object and generates a double logarithmic plot [78,79,80]. The fractal dimension (D) is defined as the absolute value of the slope of the resulting linear function [81,82,83]. All prepared cross-sections of fruit tree shoots were subjected to this analysis. An example logarithmic plot of the fractal dimension D obtained for a ‘Ligol’ apple shoot cut with a chainsaw at moisture level MC2 is shown in Figure 4.
The experimental results were evaluated using analysis of variance (ANOVA). Homogeneous groups of the fractal dimension (D) were identified and classified using Duncan’s multiple range test. The analysis was carried out using the STATISTICA software package, version 13.3. Detailed results of the analysis are provided in the Supplementary Materials.
Before performing the analysis of variance, the assumption of normality of the fractal dimension (D) was verified for each group defined by moisture content (MC) × cutting unit (Z) × tree type (T). The statistical analyses were conducted using the STATISTICA software package, version 13.3. A total of 48 normality plots were generated, and the Shapiro–Wilk test was applied. For all 48 groups, the assumption of normality of the fractal dimension (D) was satisfied, as the obtained p-values exceeded the significance level of 0.05 (p > 0.05).
The analysis followed a full factorial design with moisture content, cutting unit type, and tree cultivar included as factors, along with their interactions.
Homogeneity of variances was subsequently verified using Levene’s test. As the data met the assumptions of normality and homoscedasticity, a parametric analysis of variance (ANOVA) was applied to evaluate the effects of moisture content (MC), cutting unit (Z), tree type (T), and their interactions on the fractal dimension (D).

3. Results

The highest moisture content was obtained for samples collected directly after harvest. The subsequent three moisture levels resulted from natural drying of the shoots. The samples were stored in a closed room on openwork platforms. During the experiment, the room conditions were as follows: temperature ranged from 19 to 20 °C and relative humidity from 54 to 61%. Both moisture content measurements and fractal dimension measurements were always performed at the same time for all types of shoots. Shoots for moisture content determination were collected randomly. In this way, four moisture content levels were obtained, for which further analyses were conducted (Figure 5). It can be observed that the highest moisture content was recorded for the pear cultivars ‘Hortensja’ and ‘Conference’, followed by the apple cultivars ‘Ligol’ and ‘Gloster’. The mean values for each level were as follows: MC1 = 49.50%, MC2 = 37.42%, MC3 = 27.54%, and MC4 = 22.10%.
Shoots used for cutting tests and moisture content determination were randomly selected at each moisture level in order to minimize potential systematic bias associated with drying duration and the sequence of tool application.
Examples of cut surfaces of the ‘Gloster’ apple shoots obtained for the investigated cutting units are shown in Figure 6. When cutting with bypass loppers, visible crushing of the shoot epidermis can be observed on one side of the cut surface. Local cracks and tears are visible to the naked eye on this side (Figure 6c). The contour outline shows an irregular shape of the cut plane formed during cutting. The fractal dimension (D) value is 1.154 (Figure 6d). The next sample analysed was obtained using a circular saw. The internal part of the shoot was cut smoothly, without tearing. However, the outer surface exhibited damage in the form of fine splinters—wood fragments resembling “hairs”—whose number gradually increases toward the region of the cracked epidermis (Figure 6c). The shoot contour prepared for fractal analysis reveals surface irregularities along half of the shoot perimeter on the side of the partially detached epidermis, and the corresponding fractal dimension (D) equals 1.189 (Figure 6d). Cutting performed with the electric chainsaw resulted in the most severe damage. Extensive tearing of the shoot tissue was evident. A portion of the shoot was forcibly torn out, leaving strongly frayed internal and external elements that were not fully cut but rather ruptured (Figure 6e). The image prepared for fractal dimension (D) calculation illustrates the extent of perimeter damage, and the resulting fractal dimension (D) equals 1.221 (Figure 6d). These results indicate that higher fractal dimension (D) values correspond to greater complexity of the image, as well as increased damage and reduced cutting quality caused by the applied cutting unit. Considering variables such as tree species and cutting unit type, it may be inferred that both the fruit tree cultivar and the cutting tool affect the value of the fractal dimension.
These qualitative differences in cut surface morphology were consistently reflected in the corresponding fractal dimension values, with higher D values indicating increased surface irregularity and damage severity.
The obtained results demonstrate that the intensity of damage varies depending on the applied cutting unit and the fruit tree species (Table 4).
For instance, at the first moisture level (MC1), the mean fractal dimension (D) for ‘Gloster’ apple shoots cut with a chainsaw (PL) was 1.160, whereas for the same shoots cut with a circular saw (PT), the value decreased by 0.008 to D = 1.152. In contrast, for ‘Gloster’ shoots cut with bypass loppers at the first moisture level (MC1), the mean fractal dimension (D) was the lowest among the analysed cases and equalled 1.144. For apple cultivars, shoot moisture content was found to affect the degree of cross-sectional damage. In the case of ‘Ligol’ apple shoots cut with a chainsaw (PL), the fractal dimension increased from 1.160 at the first moisture level (MC1) to 1.176 at the fourth moisture level (MC4). The lowest level of damage was produced by the bypass loppers (S), as the fractal dimension (D) at the first moisture level (MC1) ranged from 1.141 to 1.155, regardless of the species and cultivar of the tested fruit tree shoots. The greatest surface damage was caused by the chainsaw (PL), for which the fractal dimension (D) at the first moisture level (MC1) ranged from 1.160 to 1.166.
To determine whether the fractal dimension (D) obtained in the study, which characterises the extent of shoot damage, differs significantly with respect to moisture content (MC1, MC2, MC3, MC4), cutting unit (PL—chainsaw, PT—circular saw, S—bypass loppers), and the four shoot types (apple cultivars ‘Ligol’ and ‘Gloster’, and pear cultivars ‘Conference’ and ‘Hortensia’), an analysis of variance (ANOVA) was performed (Table 5). The analysis included both two-factor and three-factor interactions among the investigated parameters. The results revealed that all main factors, as well as the interactions between moisture content (MC) and tree species (T), and between moisture content (MC) and cutting unit (Z), had a significant effect on the fractal dimension (D).
Since the analysis of variance of the obtained fractal dimension (D) results revealed significant differences with respect to moisture content, cutting unit, and the four types of fruit tree shoots, Duncan’s multiple range test was performed.
This test enables the identification of group means that differ significantly from one another and classifies them into homogeneous subsets based on their similarity. To enhance the readability of the results listed in Table 6, the values were arranged in non-decreasing order. Based on this analysis, it was found that shoots of the investigated fruit trees at the highest moisture content (MC1 = 49.50%) exhibited the lowest degree of damage, regardless of the cutting unit used (Figure 7). In contrast, variations in moisture content within the range from 37.42% to 22.10% did not result in significant differences in the fractal dimension (D). A detailed evaluation of fractal dimension (D) values in relation to fruit tree species demonstrated that the lowest values occurred for ‘Ligol’ apple shoots (D = 1.155), while the highest values were recorded for shoots of the ‘Conference’ pear cultivar (D = 1.161) (Figure 8). The remaining shoots, namely those of the ‘Gloster’ apple and the ‘Hortensia’ pear, exhibited a wide dispersion of fractal dimension (D) values, spanning both homogeneous groups. A similar range of damage, expressed by comparable fractal dimension (D) values, was observed for the bypass loppers (S) and the circular saw (PT), which formed a single homogeneous group (Figure 9). The chainsaw produced the highest fractal dimension value, reaching D = 1.175.
The research primarily focused on assessing the impact of cutting units on pear and apple cultivars using fractal dimension analysis. Trees at the same developmental stage were used in the experiments. The collected shoot samples were comparable in diameter, with a standard deviation not exceeding 1.48 mm. Every effort was made to maintain highly comparable experimental conditions in order to obtain reliable results.
It is agreed that the growth intensity of apple cultivars grafted onto P60 and M9 rootstocks is extremely important and determines tree vigour. However, based on a detailed analysis of the distribution of fractal dimension (D) values into homogeneous groups according to tree type (T) (Table 6), which grouped the apple cultivars into a single homogeneous group, it was concluded that the type of rootstock did not significantly affect the final results.

4. Analysis and Discussion

The application of shoot pruning techniques that reduce the risk of wounding is intended to limit the risk of wood decay and the occurrence of fungi and other pathogens [84,85]. Studies on cutting quality assessment conducted by Nowakowski and Nowakowski [86] for ‘Idared’ apple, ‘Węgierka Dąbrowicka’ plum, ‘Groniasta z Ujfehertoi’ sour cherry, and ‘Conference’ pear, using fractal dimension analysis, confirm that plant species significantly affect the degree of shoot damage.
The applied cutting unit was also identified as a significant factor. The anvil loppers caused the least damage, followed by the bypass loppers, the circular saw, and the chainsaw. These findings contribute to the evaluation of the applied cutting units and expand practical knowledge, as international literature offers limited information on the impact of pruning tools on trees [87].
Considering all investigated moisture levels, the chainsaw was identified as the cutting tool that caused the most severe damage to shoots among the three tested cutting units. Numerous surface irregularities, frayed edges, and detached shoot fragments were observed in the samples. Cutting with the circular saw was carried out without major complications. In most cases, the cuts were of acceptable quality. No significant chipping of wood fragments from the samples was observed. However, small hair-like splinters were present along the cut perimeter.
These observations can be further interpreted in terms of the distinct mechanical principles governing the cutting process. Bypass loppers and circular saws primarily operate through a shear-dominated mechanism, which results in cleaner separation of plant tissues and reduced surface irregularity. In contrast, chainsaws generate a combination of cutting and tearing forces, leading to extensive tissue disruption and increased complexity of the cut surface. From a biological standpoint, higher surface irregularity may adversely affect wound healing by enlarging the exposed tissue area and facilitating pathogen penetration. Smoother cut surfaces are generally associated with faster callus formation and reduced susceptibility to fungal and bacterial infections. The results further demonstrate that higher shoot moisture content significantly reduces cutting-induced damage, regardless of the cutting unit used, likely due to increased tissue elasticity that limits crack propagation during cutting. Although the numerical differences in fractal dimension values appear modest, they consistently correspond to visible qualitative differences in surface morphology. Such differences may be agronomically relevant, as even minor increases in surface complexity can influence wound sealing efficiency and long-term tree health under orchard conditions. Therefore, the application of fractal dimension analysis provides a robust quantitative framework for evaluating cutting quality and supports more informed selection of pruning tools in orchard management.
The bypass loppers performed properly. Cracking of the outer shoot tissues occurred, although the overall cut surface remained smooth. In some samples, partial separation of wood layers was observed. It is essential that the cutting unit severs the shoots without crushing or tearing them and without damaging the bark. The aim is to obtain a smooth and compact cut surface, which minimises the area available for the penetration of pathogenic microorganisms into plant tissues.
The application of fractal analysis for the evaluation of different cutting techniques across various tree species under varying shoot moisture conditions enabled the detection of subtle differences in the images of shoot edges. However, further research on image analysis methods for cut shoots is still required. Reliance on a single parameter to evaluate the cutting process cannot adequately capture the complexity of such a multifaceted process.
An example of a complementary metric is the Surface Smoothness Index (SSI), defined as the ratio of smooth, undamaged areas of the cut surface to the total surface area. The closer the SSI value is to unity, the lower the degree of shoot damage. Additional parameters may include the Area Deformation Coefficient (ADC), defined as the ratio of the cross-sectional area of the uncut branch to the cross-sectional area of the cut surface, and the Perimeter Deformation Coefficient (PDC), defined as the ratio of the perimeter of the cut surface to the perimeter of the uncut branch [88].
At this stage of the study, the research focused on the application of a method based on fractal dimension measurements to assess the extent of damage to fruit tree shoots as a function of the applied cutting technique. Given the promising results obtained, the next stage of the research will involve investigations aimed at correlating these findings with direct wound healing processes, including wound severity, susceptibility to infection, callus formation, and their effects on tree productivity.
Although fractal dimension analysis proved to be a sensitive tool for assessing cutting-induced damage, it should be noted that the complexity of wound formation may require the use of additional complementary parameters for a comprehensive evaluation.

5. Conclusions

Owing to continuous technological progress, there is increasing access to a wide range of machines and tools for cutting vegetation. The trend toward replacing traditional manual tools with modern mechanical orchard pruning machines is driven by labour cost reduction, improved operational efficiency, the introduction of high-yield orchard cultivars adapted to mechanised treatments, and the maintenance of satisfactory cutting quality.
Based on the conducted experiment investigating the effect of cutting technique on the degree of damage to fruit tree shoots using selected apple and pear cultivars and different manual cutting tools, it may be concluded that cutting quality varies depending on both the fruit tree species and the applied cutting unit. The apple cultivars ‘Ligol’ and ‘Gloster’ were the least susceptible to damage during cutting. They were followed by the pear cultivars ‘Hortensia’ and ‘Conference’. The applied cutting units also generated different levels of damage. The obtained results indicate that the selection of cultivars for orchard planting is important when mechanical crown training systems are intended to be used. The bypass loppers and the circular saw proved to be the least destructive cutting units, while the chainsaw was the most damaging. Consequently, the chainsaw should mainly be applied for tree-clearing operations, where cutting quality is of minor importance. Quantitative and qualitative analyses of cutting units are essential for the design of orchard machinery and contribute to the further development of such solutions. It was also demonstrated that the moisture content of fruit tree shoots significantly affects cutting quality, with the strongest effect observed at high moisture levels.
It should be noted that among the tested apple (‘Ligol’, ‘Gloster’) and pear (‘Hortensia’, ‘Conference’) cultivars, pear shoots exhibited greater susceptibility to damage, irrespective of the cutting unit used. Therefore, for pears, the most recommended cutting tool is the bypass lopper, whereas for mechanical cutting, the circular saw is preferred.
From a practical perspective, bypass loppers and circular saws produced the least surface damage and are recommended for pruning fruit tree shoots, particularly at higher moisture levels. Chainsaws should be used primarily for clearing operations where cutting quality is of secondary importance. Careful selection of cutting tools is especially important for pear trees, which showed higher susceptibility to cutting-induced damage.
The proposed approach may support decision-making in orchard management by facilitating the selection of pruning tools that minimize shoot damage.
In addition, the results confirm that fractal dimension analysis constitutes a sensitive and objective quantitative tool for assessing cutting-induced damage to fruit tree shoots. Its application enables the comparison of different cutting techniques, tools, and plant species under controlled conditions, complementing traditional qualitative evaluations. The proposed methodology may therefore support both the optimization of orchard pruning practices and the further development of mechanized pruning systems aimed at improving cutting quality while maintaining operational efficiency.
Nevertheless, further studies integrating fractal dimension analysis with direct biological indicators of wound healing and long-term tree performance are recommended to fully validate the practical relevance of the proposed approach.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agriculture16010115/s1, Figure S1. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8654, p = 0.0883). Figure S2. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8886, p = 0.1637). Figure S3. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9255, p = 0.4053). Figure S4. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9479, p = 0.6439). Figure S5. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9906, p = 0.9975). Figure S6. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9095, p = 0.2773). Figure S7. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8889, p = 0.1647). Figure S8. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8478, p = 0.0547). Figure S9. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8597, p = 0.0757). Figure S10. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9173, p = 0.3349). Figure S11. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9409, p = 0.5634). Figure S12. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9767, p = 0.9449). Figure S13. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9588, p = 0.7726). Figure S14. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8813, p = 0.1349). Figure S15. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8811, p = 0.1344). Figure S16. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9761, p = 0.9407). Figure S17. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9649, p = 0.8394). Figure S18. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9581, p = 0.7636). Figure S19. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8470, p = 0.0535). Figure S20. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9446, p = 0.6047). Figure S21. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9764, p = 0.9429). Figure S22. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8852, p = 0.1498). Figure S23. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9613, p = 0.8011). Figure S24. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8758, p = 0.1167). Figure S25. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9314, p = 0.4619). Figure S26. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9122, p = 0.2967). Figure S27. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9697, p = 0.8884). Figure S28. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9541, p = 0.7174). Figure S29. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9400, p = 0.5529). Figure S30. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8767, p = 0.1195). Figure S31. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9382, p = 0.5335). Figure S32. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9098, p = 0.2794). Figure S33. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8515, p = 0.0605). Figure S34. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9102, p = 0.2826). Figure S35. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8458, p = 0.0518). Figure S36. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9214, p = 0.3684). Figure S37. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8623, p = 0.0812). Figure S38. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9566, p = 0.7462). Figure S39. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9480, p = 0.6454). Figure S40. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9125, p = 0.2989). Figure S41. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9133, p = 0.3041). Figure S42. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9147, p = 0.3150). Figure S43. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9776, p = 0.9512). Figure S44. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9507, p = 0.6762). Figure S45. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.8657, p = 0.0890). Figure S46. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9433, p = 0.5900). Figure S47. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9195, p = 0.3530). Figure S48. Normal Q–Q plot of fractal dimension (D) values used for assessing data normality with the Shapiro–Wilk test (W = 0.9651, p = 0.8420).

Author Contributions

Conceptualization, K.T., Ł.G. and T.N.; methodology, K.T., Ł.G. and T.N.; software, K.T., Ł.G. and T.N.; validation, K.T.; formal analysis, K.T. and T.N.; investigation, K.T., Ł.G. and T.N.; data curation, K.T., Ł.G. and T.N.; writing—original draft preparation, K.T. and T.N.; writing—review and editing, K.T. and T.N.; visualization, K.T. and T.N.; supervision, K.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Barda, M.S.; Karamaouna, F.; Kati, V.; Stathakis, T.I.; Economou, L.P.; Perdikis, D.C. Flowering Plant Patches to Support the Conservation of Natural Enemies of Pests in Apple Orchards. Agric. Ecosyst. Environ. 2025, 381, 109405. [Google Scholar] [CrossRef]
  2. Berk, P.; Hocevar, M.; Stajnko, D.; Belsak, A. Development of Alternative Plant Protection Product Application Techniques in Orchards, Based on Measurement Sensing Systems: A Review. Comput. Electron. Agric. 2016, 124, 273–288. [Google Scholar] [CrossRef]
  3. Baima, L.; Nari, L.; Nari, D.; Bossolasco, A.; Blanc, S.; Brun, F. Sustainability Analysis of Apple Orchards: Integrating Environmental and Economic Perspectives. Heliyon 2024, 10, e38397. [Google Scholar] [CrossRef]
  4. Hua, W.; Zhang, Z.; Zhang, W.; Liu, X.; Hu, C.; He, Y.; Mhamed, M.; Li, X.; Dong, H.; Saha, C.K.; et al. Key Technologies in Apple Harvesting Robot for Standardized Orchards: A Comprehensive Review of Innovations, Challenges, and Future Directions. Comput. Electron. Agric. 2025, 235, 110343. [Google Scholar] [CrossRef]
  5. Jamshidi, B.; Khabbaz Jolfaee, H.; Mohammadpour, K.; Seilsepour, M.; Dehghanisanij, H.; Hajnajari, H.; Farazmand, H.; Atri, A. Internet of Things-Based Smart System for Apple Orchards Monitoring and Management. Smart Agric. Technol. 2025, 10, 100715. [Google Scholar] [CrossRef]
  6. Pawikhum, K.; Yang, Y.; He, L.; Heinemann, P. Development of a Machine Vision System for Apple Bud Thinning in Precision Crop Load Management. Comput. Electron. Agric. 2025, 236, 110479. [Google Scholar] [CrossRef]
  7. Alcaide Zaragoza, C.; González Perea, R.; Fernández García, I.; Camacho Poyato, E.; Rodríguez Díaz, J.A. Open Source Application for Optimum Irrigation and Fertilization Using Reclaimed Water in Olive Orchards. Comput. Electron. Agric. 2020, 173, 105407. [Google Scholar] [CrossRef]
  8. Kanaga Priya, P.; Reethika, A.; Vijaykumar, G.; James Deva Koresh, H. Robotics-Assisted Precision and Sustainable Irrigation, Harvesting, and Fertilizing Processes. In Hyperautomation in Precision Agriculture; Singh, S., Sood, V., Srivastav, A.L., Ampatzidis, Y., Eds.; Academic Press: Cambridge, MA, USA, 2025; pp. 217–226. [Google Scholar] [CrossRef]
  9. Sun, G.; Hu, T.; Liu, X.; Peng, Y.; Leng, X.; Li, Y.; Yang, Q. Optimizing Irrigation and Fertilization at Various Growth Stages to Improve Mango Yield, Fruit Quality and Water-Fertilizer Use Efficiency in Xerothermic Regions. Agric. Water Manag. 2022, 260, 107296. [Google Scholar] [CrossRef]
  10. Sharma, K.; Sharma, J.C.; Sharma, S.; Sharma, N.; Sharma, R.; Ananthakrishnan, S.; Hashem, A.; Almutairi, K.F.; Abd_Allah, E.F. Optimizing Leaf Nutrient Status, Growth, and Yield Parameters in High-Density Apple Orchards (cv. Super Chief) via Integrated Drip Irrigation and Fertigation Techniques. Heliyon 2024, 10, e36136. [Google Scholar] [CrossRef]
  11. Chen, Y.; Zheng, X.; Ju, C.; Bao, F. A Support Vector Model of Pruning Trees Evaluation Based on OTSU Algorithm. arXiv 2022, arXiv:2207.03638. [Google Scholar]
  12. Mika, A. Cięcie Drzew i Krzewów Owocowych (Cutting Fruit Trees and Shrubs); Wydawnictwo PWRiL: Warszawa, Poland, 2020; p. 224. [Google Scholar]
  13. Pieniążek, S. Sadownictwo (Fruit-Growing); Wydawnictwo PWRiL: Warszawa, Poland, 2000; p. 680. [Google Scholar]
  14. Allegro, G.; Martelli, R.; Valentini, G.; Pastore, C.; Mazzoleni, R.; Pezzi, F.; Filippetti, I. Effects of Mechanical Winter Pruning on Vine Performances and Management Costs in a Trebbiano Romagnolo Vineyard: A Five-Year Study. Horticulturae 2023, 9, 21. [Google Scholar] [CrossRef]
  15. Chueca, P.; Mateu, G.; Garcerá, C.; Fonte, A.; Ortiz, C.; Torregrosa, A. Yield and Economic Results of Different Mechanical Pruning Strategies on “Navel Foyos” Oranges in the Mediterranean Area. Agriculture 2021, 11, 82. [Google Scholar] [CrossRef]
  16. Xinxing, L.; Buwen, L.; Hui, L. Pruning decision system for apple tree based on local point cloud and BP neural network. Trans. Chin. Soc. Agric. Eng. 2021, 37, 170–176. [Google Scholar] [CrossRef]
  17. Koszela, K. Computer Image Analysis and Artificial Neural Networks in the Qualitative Assessment of Agricultural Products. Agric. Eng. 2015, 3, 15–22. [Google Scholar] [CrossRef]
  18. Mateu, G.; Caballero, P.; Torregrosa, A.; Segura, B.; Juste, F.; Chueca, P. Análisis de la influencia de las operaciones de cultivo sobre los costes de producción en la citricultura de la Comunidad Valenciana. Levante Agrícola Rev. Int. Cítricos 2018, 440, 60–64. [Google Scholar]
  19. Nunez, J.A.G. The Effects of Mechanical Pruning on Yield, Fruit Quality and Vegetative Growth in Apple and Sweet Cherry. Ph.D. Thesis, Washington State University, Pullman, WA, USA, 2016; p. 193. [Google Scholar]
  20. Niederholzer, F.; Jarvis-Shean, K.; Lightle, D.; Milliron, L.; Stewart, D.; Summer, D.A. Sample Costs to Establish an Orchard and Produce Prunes; University of California Cooperative Extension (UCCE), UC Agriculture and Natural Resources (UC ANR), UC Davis: Sacramento Valley, CA, USA, 2018; p. 23. [Google Scholar]
  21. Martí, B.; González, E. The influence of mechanical pruning in cost reduction, production of fruit, and biomass waste in citrus orchards. Appl. Eng. Agric. 2010, 26, 531–540. [Google Scholar] [CrossRef]
  22. Dias, A.; Falcão, J.; Pinheiro, A.; Peça, J. Effect of Mechanical Pruning on Olive Yield in a High-Density Olive Orchard: An Account of 14 Years. Agronomy 2022, 12, 1105. [Google Scholar] [CrossRef]
  23. Jiménez-Brenes, F.M.; López-Granados, F.; de Castro, A.I.; Torres-Sánchez, J.; Serrano, N.; Peña, J.M. Quantifying pruning impacts on olive tree architecture and annual canopy growth by using UAV-based 3D modelling. Plant Methods 2017, 13, 55. [Google Scholar] [CrossRef]
  24. Farinelli, D.; Onorati, L.; Ruffolo, M.; Tombesi, A. Mechanical Pruning of Adult Olive Trees and Influence on Yield and on Efficiency of Mechanical Harvesting. Acta Hortic. 2011, 924, 203–209. [Google Scholar] [CrossRef]
  25. Intrigliolo, F.; Roccuzzo, G. Modern Trends of Citrus Pruning in Italy. Adv. Hortic. Sci. 2013, 25, 187–192. [Google Scholar] [CrossRef]
  26. Martin-Gorriz, B.; Porras Castillo, I.; Torregrosa, A. Effect of mechanical pruning on the yield and quality of ‘Fortune’ mandarins. Span. J. Agric. Res. 2014, 12, 952–959. [Google Scholar] [CrossRef]
  27. Fonte, A.; Torregrosa, A.; Garcerá, C.; Mateu, G.; Chueca, P. Mechanical Pruning of ‘Clemenules’ Mandarins in Spain: Yield Effects and Economic Analysis. Agronomy 2022, 12, 761. [Google Scholar] [CrossRef]
  28. Martin-Gorriz, B.; Martínez-Barba, C.; Torregrosa, A. Lemon trees response to different long-term mechanical and manual pruning practices. Sci. Hortic. 2021, 275, 109700. [Google Scholar] [CrossRef]
  29. Mika, A.; Buler, Z.; Treder, W. Mechanical pruning of apple trees as an alternative to manual pruning. Acta Sci. Pol. Hortorum Cultus 2016, 15, 113–121. [Google Scholar]
  30. Zimmer, J.; Schwender, C. Mechanical pruning in organic apple production—Especially with regard to pathogens and pests. In Proceedings of the Ecofruit: 17th International Conference on Organic Fruit-Growing, Hohenheim, Germany, 15–17 February 2016; pp. 224–227. [Google Scholar]
  31. Miljan, C.; Cvijanović, J.S. Mechanical plum pruning. J. Agric. Food Environ. Sci. 2022, 76, 28–34. [Google Scholar] [CrossRef]
  32. Pekitkan, F.G. Mechanical properties of Okuzgozu (Vitis vinifera L. cv.) grapevine canes. J. King Saud Univ. Sci. 2024, 36, 103034. [Google Scholar] [CrossRef]
  33. Carvalho, L.R.; Nuñes, P.R.; Santos, S.L.; Teixeira, L.J.; Araújo, A.R.; Cavalcante, L.I.H. Impact of First Mechanical Fructification Pruning on Mango Orchards. Int. J. Fruit Sci. 2021, 21, 1059–1072. [Google Scholar] [CrossRef]
  34. Pekitkan, F.G.; Eliçin, A.K.; Sessiz, A. Bazı yerli tip üzüm (Vitis vinifera L.) çeşitlerinin budama sürgünlerinin kesme özelliklerinin belirlenmesi. ÇOMÜ Ziraat Fak. Derg. 2020, 8, 33–40. [Google Scholar] [CrossRef]
  35. Rosecrance, R.; Milliron, L.; Niederholzer, F. Mechanical pruning of ‘Improved French’ prune trees. Acta Hortic. 2021, 1322, 253–258. [Google Scholar] [CrossRef]
  36. Barcia, F.; Prieto, J.; Trentacoste, E.R. Effects of Mechanical Box Pruning Intensity on Bud Development, Vegetative Growth, and Yield Components on cv. Cabernet-Sauvignon in Mendoza, Argentina. OENO One 2023, 57, 153–163. [Google Scholar] [CrossRef]
  37. Nowakowski, T.; Tucki, K. Impact of blade geometric parameters on the specific cutting energy of willow (Salix viminalis) stems. Appl. Sci. 2025, 15, 696. [Google Scholar] [CrossRef]
  38. Wąsik, R.; Michalec, K. Image analysis in wood testing—Selected examples. Agric. Eng. 2016, 20, 183–195. [Google Scholar] [CrossRef]
  39. Chaber, R.; Łasecki, M.; Kuczyński, K.; Cebryk, R.; Kwaśnicka, J.; Olchowy, C.; Łach, K.; Pogodajny, Z.; Koptiuk, O.; Olchowy, A.; et al. Hounsfield Units and Fractal Dimension (Test HUFRA) for Determining PET Positive/Negative Lymph Nodes in Pediatric Hodgkin’s Lymphoma Patients. PLoS ONE 2020, 15, e0229859. [Google Scholar] [CrossRef]
  40. Irie, M.S.; Rabelo, G.D.; Spin-Neto, R.; Dechichi, P.; Borges, J.S.; Soares, P.B.F. Use of Micro-Computed Tomography for Bone Evaluation in Dentistry. Braz. Dent. J. 2018, 29, 227–232. [Google Scholar] [CrossRef]
  41. Losa, G.A. The Living Realm Depicted by the Fractal Geometry. Fractal Geom. Nonlinear Anal. Med. Biol. 2015, 1, 11–15. [Google Scholar] [CrossRef]
  42. Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; John Wiley & Sons: Chichester, UK, 2003; p. 337. [Google Scholar]
  43. ASABE Standards 2011; Moisture Measurement—Forages ASABE S358.2 (R2008). American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2011; pp. 780–781.
  44. Kruczyńska, D. Nowe Odmiany Jabłoni; Hortpress: Warszawa, Poland, 2008; pp. 110–180. ISBN 978-83-8921-149-1. [Google Scholar]
  45. Ugolik, M. Odmiany Jabłoni; Plantpress: Kraków, Poland, 1996; pp. 44–86. ISBN 83-85982-11-6. [Google Scholar]
  46. Kurek, E.; Ozimek, E.; Sobiczewski, P.; Słomka, A.; Jaroszuk-Ściseł, J. Effect of Pseudomonas luteola on mobilization of phosphorus and growth of young apple trees (Ligol)—Pot experiment. Sci. Hortic. 2013, 164, 270–276. [Google Scholar] [CrossRef]
  47. Samuolienė, G.; Viškelienė, A.; Sirtautas, R.; Kviklys, D. Relationships between apple tree rootstock, crop-load, plant nutritional status and yield. Sci. Hortic. 2016, 211, 167–173. [Google Scholar] [CrossRef]
  48. Markuszewski, B.; Kopytowski, J. Effects of some soil cultivation methods on the growth and yielding of apple trees grafted on semi-dwarf rootstocks and ‘Antonowka’ seedling with B 9 interstock. Zesz. Nauk. Inst. Sadow. I Kwiaciarstwa 2008, 16, 21–34. [Google Scholar]
  49. Klimek, K.E.; Kapłan, M.; Najda, A.B. Effect of growth regulators on quality of apple tree maidens. Acta Agrophys. 2018, 25, 277–288. [Google Scholar] [CrossRef]
  50. Kapłan, M.; Klimek, K.E.; Buczyński, K. Analysis of the Impact of Treatments Stimulating Branching on the Quality of Maiden Apple Trees. Agriculture 2024, 14, 1757. [Google Scholar] [CrossRef]
  51. Hodun, G. Evaluation of the Occurrence of Old Trees and Variety Identification in the Mountain Area and the Izer Mountains. 2018. Available online: http://2018.lgdpartnerstwoizerskie.pl/wp-content/uploads/2021/10/Studium-o-odmianach_CALOSC.pdf (accessed on 28 November 2025).
  52. Łysiak, G. Uprawa i Odmiany Gruszy; Hortpress: Warszawa, Poland, 2006; p. 156. ISBN 83-89211-18-1. [Google Scholar]
  53. Terzoudis, K.; Kusma, R.; Hertog, M.L.A.T.M.; Nicolaï, B.M. Metabolic adaptation of ‘Conference’ pear to postharvest hypoxia: The impact of harvest time and hypoxic pre-treatments. Postharvest Biol. Technol. 2022, 189, 111937. [Google Scholar] [CrossRef]
  54. Janssens, P.; Diels, J.; Vanderborght, J.; Elsen, F.; Elsen, A.; Deckers, T.; Vandendriessche, H. Numerical calculation of soil water potential in an irrigated ‘Conference’ pear orchard. Agric. Water Manag. 2015, 148, 113–122. [Google Scholar] [CrossRef]
  55. Guerra, M.; Marcelo, V.; Casquero, P.A. Postharvest quality enhancement in high-russet ‘Conference’ pears: The role of organic farming and edible coatings. Postharvest Biol. Technol. 2025, 229, 113680. [Google Scholar] [CrossRef]
  56. Nadulski, R.; Wróblewska-Barwińska, K.; Strzałkowska, K. Experimental characteristic of textural properties of the selected varieties of pears. Agric. Eng. 2012, 16, 165–173. [Google Scholar]
  57. Kolniak-Ostek, J. Identification and quantification of polyphenolic compounds in ten pear cultivars by UPLC-PDA-Q/TOF-MS. J. Food Compos. Anal. 2016, 49, 65–77. [Google Scholar] [CrossRef]
  58. Parts, Instructions, and Technical Support for 436Li. Available online: https://www.husqvarna.com/pl/wsparcie/436li/ (accessed on 20 November 2025).
  59. Nevrkla, P.; Staněk, L.; Neruda, J. Analysis of Selected Functional Parameters of Saw Chains. J. For. Sci. 2025, 71, 72–85. [Google Scholar] [CrossRef]
  60. Poje, A.; Mihelič, M. Influence of Chain Sharpness, Tension Adjustment and Type of Electric Chainsaw on Energy Consumption and Cross-Cutting Time. Forests 2020, 11, 1017. [Google Scholar] [CrossRef]
  61. Pandur, Z.; Bačić, M.; Šušnjar, M.; Landekić, M.; Šporčić, M.; Jambreković, B.; Lepoglavec, K. Energy Consumption and Cutting Performance of Battery-Powered Chainsaws. Forests 2023, 14, 1329. [Google Scholar] [CrossRef]
  62. Dado, M.; Kučera, M.; Salva, J.; Hnilica, R.; Hýrošová, T. Influence of Saw Chain Type and Wood Species on the Mass Concentration of Airborne Wood Dust during Cross-Cutting. Forests 2022, 13, 2009. [Google Scholar] [CrossRef]
  63. Kaliniewicz, Z.; Maleszewski, Ł.; Krzysiak, Z. Influence of Saw Chain Type and Wood Species on the Kickback Angle of a Chainsaw. Tech. Sci. 2018, 21, 323–334. [Google Scholar] [CrossRef]
  64. Bauske, E.; Fuder, J.; Rains, G. Chainsaw Chains and Bars. CAES Field Report 2025. Available online: https://fieldreport.caes.uga.edu/wp-content/uploads/2025/08/C-1208_4.pdf (accessed on 23 December 2025).
  65. Maciak, A.; Kubuśka, M. The Influence of Initial Tension on Blunting of Chainsaw Blades and Cutting Efficiency. For. Res. Pap. 2018, 79, 261–268. [Google Scholar] [CrossRef]
  66. Robb, W.; Nevrkla, P. Assessment of Portable Chainsaw Chains. Arboric. J. 2020, 42, 228–236. [Google Scholar] [CrossRef]
  67. Maciak, A.; Kubuśka, M.; Moskalik, T. Instantaneous Cutting Force Variability in Chainsaws. Forests 2018, 9, 660. [Google Scholar] [CrossRef]
  68. KS 216 M. Available online: https://www.metabo.com/com/en/tools/sawing/mitre-saws/ks-216-m-mitre-saw/610216000 (accessed on 20 November 2025).
  69. Metabo GmbH. KS 216 M Lasercut Operating Instructions and Technical Data. Available online: https://manuals.plus/metabo/ks-216-m-lasercut-crosscut-saw-manual (accessed on 23 December 2025).
  70. Metabo GmbH. Metabo Service Portal—KS 216 M Lasercut Manual Search. Available online: https://www.metabo-service.com/en/manual/19216190 (accessed on 23 December 2025).
  71. Frezwid. Types of Blades: HM, HW—Cemented Carbide, What Is It? Available online: https://frezwid.com.pl/poradnik/rodzaje-ostrzy/hm-hw-widia-weglik-spiekany-co-to-takiego (accessed on 23 December 2025).
  72. ISprzet. Cemented Carbide—Properties and Applications. Available online: https://www.isprzet.pl/pl/blog/weglik-spiekany.html (accessed on 23 December 2025).
  73. Orłowski, K.; Ochrymiuk, T. Dynamics of cutting power during sawing with circular saw blades as an effect of wood properties changes in the cross section. Ann. Wars. Univ. Life Sci.—SGGW For. Wood Technol. 2013, 83, 322–328. [Google Scholar]
  74. Gołombek, K.; Dobrzański, L.A. Hard and Wear Resistance Coatings for Cutting Tools. J. Achiev. Mater. Manuf. Eng. 2007, 24, 24221. Available online: http://jamme.acmsse.h2.pl/papers_vol24_2/24221.pdf (accessed on 23 December 2025).
  75. ASM International. ASM Handbook: Properties and Selection of Carbides; ASM International: Materials Park, OH, USA, 2021. [Google Scholar]
  76. Fiskars L28 Hook typ S. Available online: https://www.fiskars.com/en-gb/gardening/products/loppers (accessed on 20 November 2025).
  77. Nowakowski, T.; Dąbrowska, M.; Sypuła, M.; Strużyk, A. A method for evaluating the size of damages to fruit trees during pruning using different devices. Sci. Hortic. 2018, 242, 30–35. [Google Scholar] [CrossRef]
  78. Trafalski, M.; Kozakiewicz, M.; Jurczyszyn, K. Application of fractal dimension and texture analysis to evaluate the effectiveness of treatment of a venous lake in the oral mucosa using a 980 nm diode laser: A preliminary study. Materials 2021, 14, 4140. [Google Scholar] [CrossRef]
  79. Gawlik, J.; Magdziarczyk, J.; Wojnar, L. Analiza Fraktalna Struktury Geometrycznej Powierzchni. In Innowacje w Zarządzaniu i Inżynierii Produkcji; Konferencja: Zakopane, Poland, 2011; pp. 382–396. [Google Scholar]
  80. Scholz, C.H.; Mandelbrot, B.B. Fractals in Geophysics; Springer: New York, NY, USA, 1989; p. 313. [Google Scholar]
  81. Wang, R.; Singh, A.K.; Kolan, S.R.; Tsotsas, E. Fractal analysis of aggregates: Correlation between the 2D and 3D box-counting fractal dimension and power law fractal dimension. Chaos Solitons Fractals 2022, 160, 112246. [Google Scholar] [CrossRef]
  82. Losa, G.A.; Ristanović, D.U.; Ristanović, D.E.; Zaletel, I.; Beltraminelli, S. From Fractal Geometry to Fractal Analysis. Appl. Math. 2016, 7, 346–354. [Google Scholar] [CrossRef]
  83. Di Ieva, A.; Grizzi, F.; Jelinek, H.; Pellionisz, A.J.; Losa, G.A. Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 2013, 19, 403–417. [Google Scholar] [CrossRef]
  84. Zhang, L.; Koc, A.B.; Wang, X.N.; Jiang, Y.X. A review of pruning fruit trees. IOP Conf. Ser. Earth Environ. Sci. 2018, 153, 062029. [Google Scholar] [CrossRef]
  85. Badrulhisham, N.; Othman, N. Knowledge in Tree Pruning for Sustainable Practices in Urban Setting: Improving Our Quality of Life. Procedia—Soc. Behav. Sci. 2017, 234, 210–217. [Google Scholar] [CrossRef]
  86. Nowakowski, T.; Nowakowski, M. Assessment of tree sprouts pruning with various types of cutting units. Agric. Eng. 2018, 22, 95–103. [Google Scholar] [CrossRef]
  87. Marchi, E.; Neri, F.; Fioravanti, M.; Picchio, R.; Goli, G.; Di Giulio, G. Effects of Cutting Patterns of Shears on Occlusion Processes in Pruning. Croat. J. For. Eng. 2013, 34, 295–304. [Google Scholar]
  88. Safvati, M.; Minaei, S.; Mahdavian, A. Comparative analysis of fractal dimension and novel geometric indices for assessing branch cutting quality. Measurement 2025, 248, 116941. [Google Scholar] [CrossRef]
Agriculture 16 00115 g001
Figure 1. Fruit tree shoots: (a) apple cultivar ‘Ligol’; (b) apple cultivar ‘Gloster’; (c) pear cultivar ‘Conference’; (d) pear cultivar ‘Hortensia’.
Figure 1. Fruit tree shoots: (a) apple cultivar ‘Ligol’; (b) apple cultivar ‘Gloster’; (c) pear cultivar ‘Conference’; (d) pear cultivar ‘Hortensia’.
Agriculture 16 00115 g001
Agriculture 16 00115 g002
Figure 2. Cutting units: (a) Husqvarna 436Li electric chainsaw; (b) chainsaw guide bar; (c) METABO KS 216 M Lasercut circular saw; (d) saw blade; (e) Fiskars L28 bypass loppers; (f) cutting blade of the loppers.
Figure 2. Cutting units: (a) Husqvarna 436Li electric chainsaw; (b) chainsaw guide bar; (c) METABO KS 216 M Lasercut circular saw; (d) saw blade; (e) Fiskars L28 bypass loppers; (f) cutting blade of the loppers.
Agriculture 16 00115 g002
Agriculture 16 00115 g003
Figure 3. Stages of image preparation for analysis (‘Ligol’ apple, moisture level MC2, chainsaw): (a) image of the cut shoot; (b) surface of the shoot cross-section after background removal; (c) cross-section after removal of colour information; (d) cross-section after contour extraction.
Figure 3. Stages of image preparation for analysis (‘Ligol’ apple, moisture level MC2, chainsaw): (a) image of the cut shoot; (b) surface of the shoot cross-section after background removal; (c) cross-section after removal of colour information; (d) cross-section after contour extraction.
Agriculture 16 00115 g003
Agriculture 16 00115 g004
Figure 4. Determination of the fractal dimension using the box-counting method for the shoot of the apple cultivar ‘Ligol’, cut with a chainsaw (moisture content—MC2): D—fractal dimension; N—number of grid cells covering the shoot edge; r—grid cell side length.
Figure 4. Determination of the fractal dimension using the box-counting method for the shoot of the apple cultivar ‘Ligol’, cut with a chainsaw (moisture content—MC2): D—fractal dimension; N—number of grid cells covering the shoot edge; r—grid cell side length.
Agriculture 16 00115 g004
Agriculture 16 00115 g005
Figure 5. Moisture content values obtained for shoots of the apple cultivars ‘Ligol’ and ‘Gloster’ and the pear cultivars ‘Conference’ and ‘Hortensia’.
Figure 5. Moisture content values obtained for shoots of the apple cultivars ‘Ligol’ and ‘Gloster’ and the pear cultivars ‘Conference’ and ‘Hortensia’.
Agriculture 16 00115 g005
Agriculture 16 00115 g006
Figure 6. Example cross-section of a ‘Gloster’ apple shoot sample: (a) cut with bypass loppers; (b) contour outlined for analysis; (c) cut with a circular saw; (d) contour outlined for analysis; (e) cut with an electric chainsaw; (f) contour outlined for analysis.
Figure 6. Example cross-section of a ‘Gloster’ apple shoot sample: (a) cut with bypass loppers; (b) contour outlined for analysis; (c) cut with a circular saw; (d) contour outlined for analysis; (e) cut with an electric chainsaw; (f) contour outlined for analysis.
Agriculture 16 00115 g006
Agriculture 16 00115 g007
Figure 7. Variations in fractal dimension (D) as a function of shoot moisture content (MC) for different cutting units (Z).
Figure 7. Variations in fractal dimension (D) as a function of shoot moisture content (MC) for different cutting units (Z).
Agriculture 16 00115 g007
Agriculture 16 00115 g008
Figure 8. Variations in fractal dimension (D) as a function of tree type (T) at different shoot moisture levels (MC).
Figure 8. Variations in fractal dimension (D) as a function of tree type (T) at different shoot moisture levels (MC).
Agriculture 16 00115 g008
Agriculture 16 00115 g009
Figure 9. Variations in fractal dimension (D) as a function of cutting unit type (Z) for different fruit tree shoot types (T).
Figure 9. Variations in fractal dimension (D) as a function of cutting unit type (Z) for different fruit tree shoot types (T).
Agriculture 16 00115 g009
Table 1. Parameters of the fruit tree shoots analysed in the study.
Table 1. Parameters of the fruit tree shoots analysed in the study.
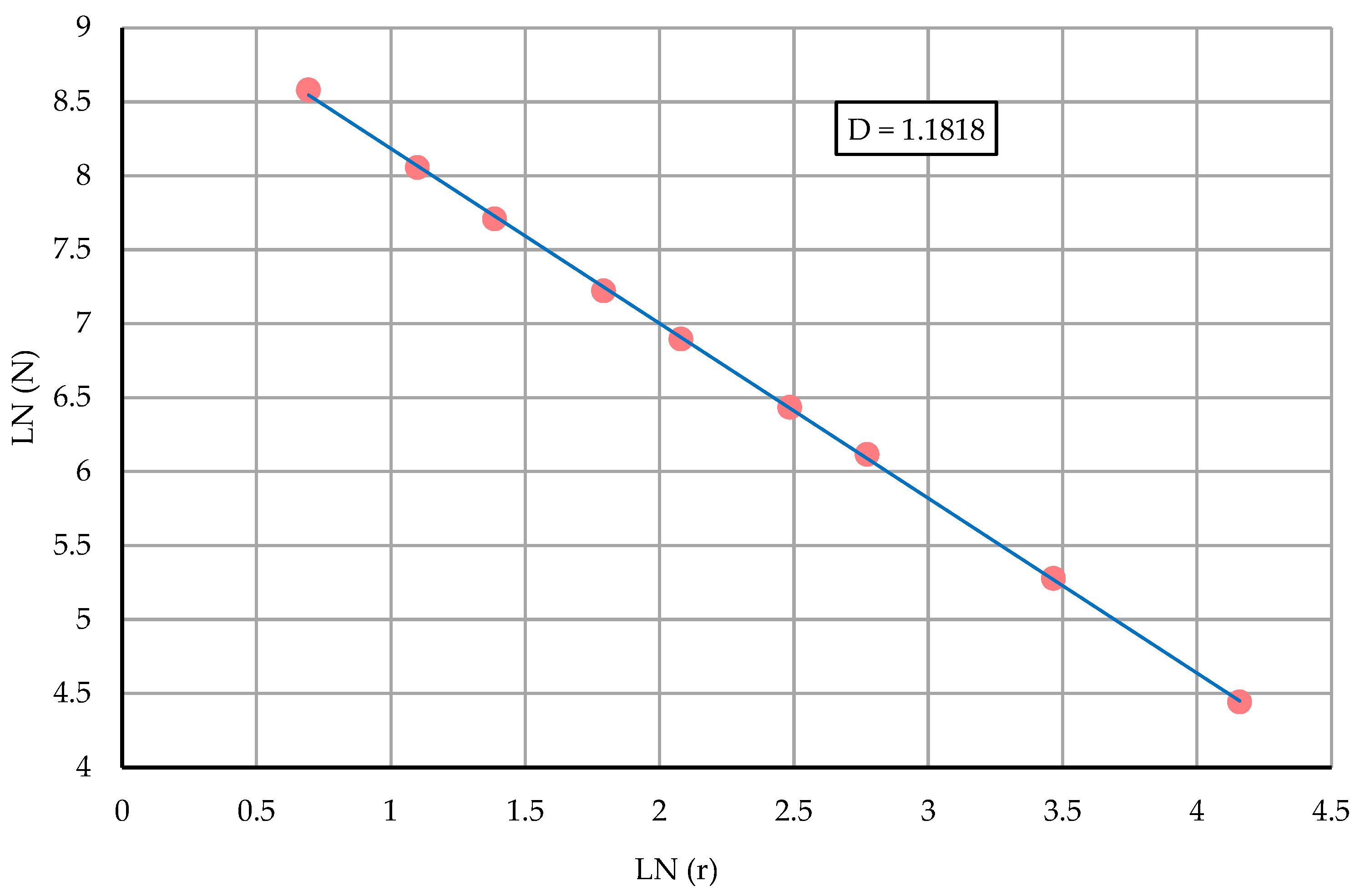
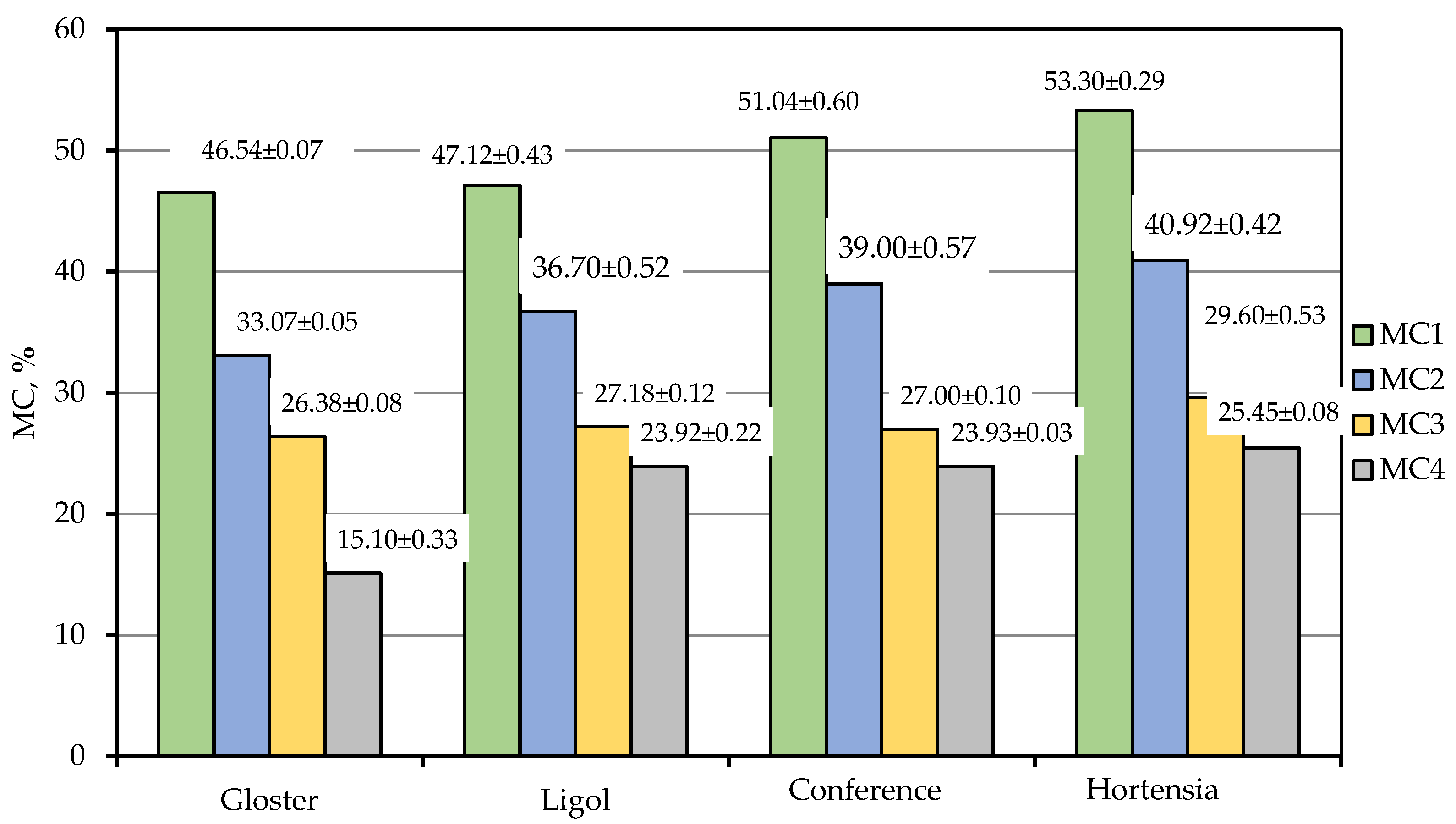
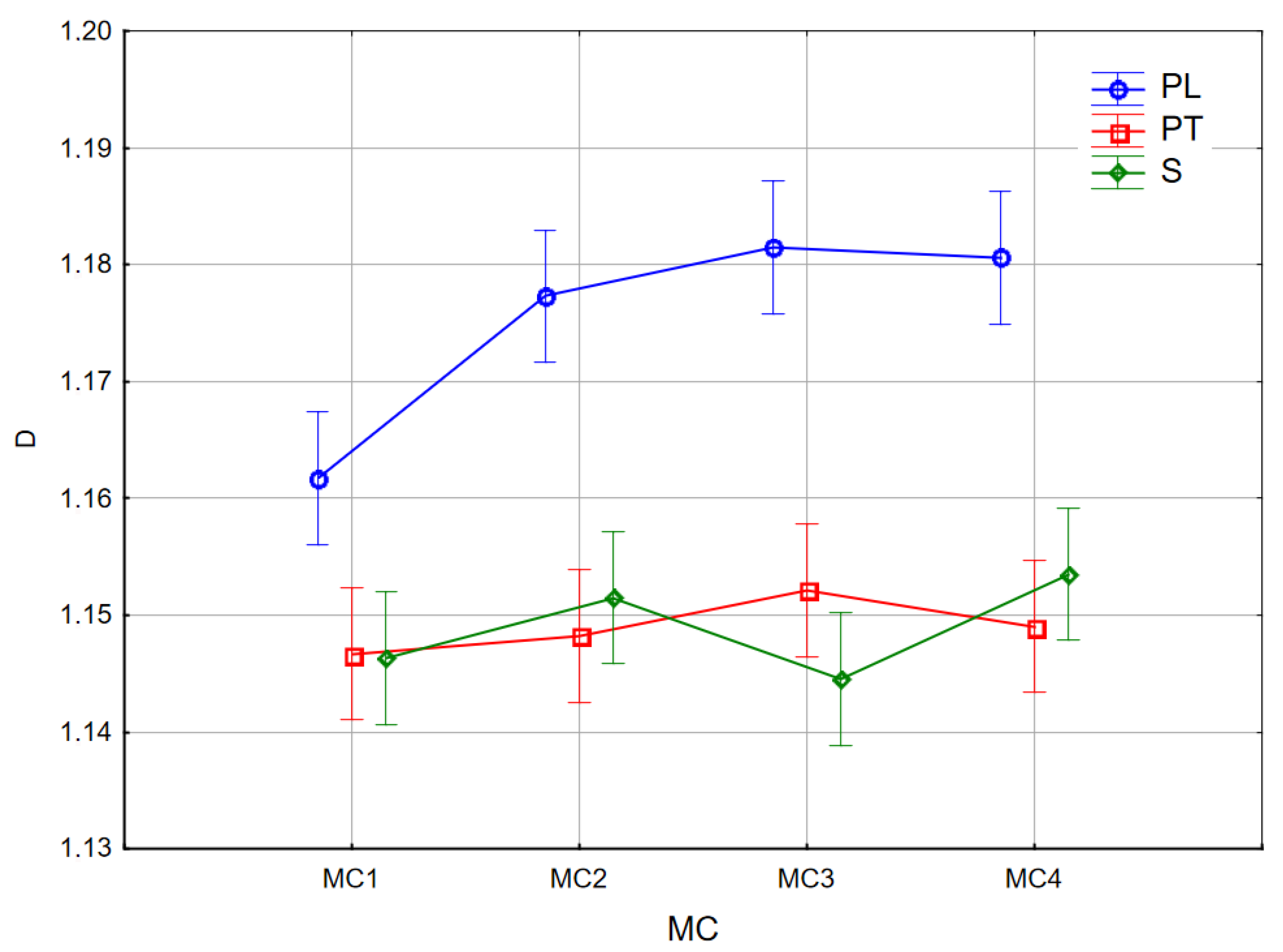
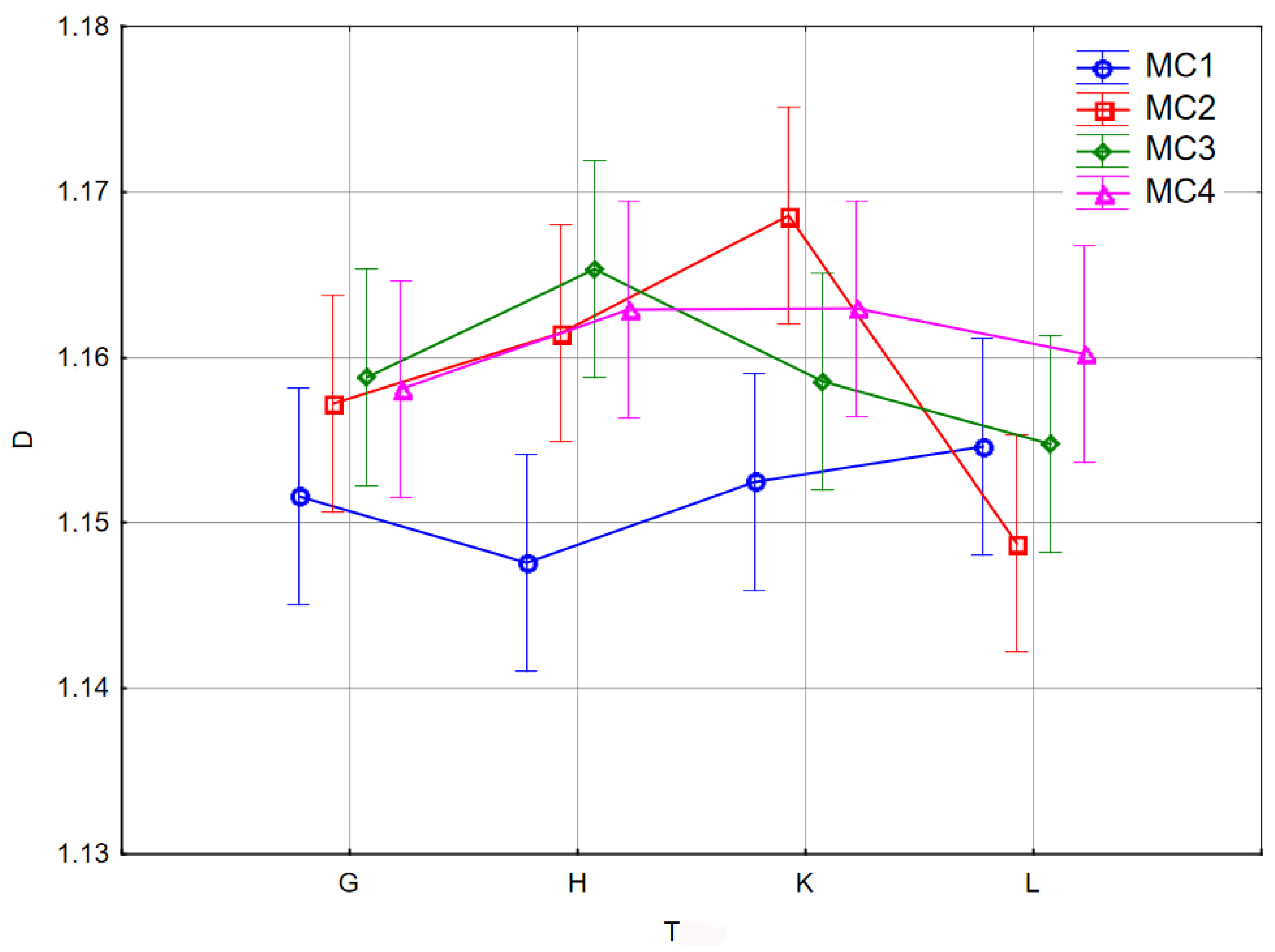
CultivarUnitMeanMin *Max *MedianStandard DeviationCV *
HortensiaLengthcm39.218.064.037.513.233.6
Diametermm9.336.9912.519.161.4815.88
ConferenceLengthcm31.519.047.032.07.223.0
Diametermm8.166.7610.227.990.8410.25
LigolLengthcm42.326.056.043.08.319.6
Diametermm9.947.9113.469.781.3613.67
GlosterLengthcm39.320.063.039.513.434.0
Diametermm9.287.5812.638.991.2213.14
* Min—Minimum value; Max—Maximum value; CV—Coefficient of variation.
Table 2. Specification of the cutting chain used in the Husqvarna 436Li chainsaw.
Table 2. Specification of the cutting chain used in the Husqvarna 436Li chainsaw.
CategoryParameterValue/DescriptionTechnical Significance and Literature Background
Chain geometryPitch3/8″The pitch determines the spacing of the cutting teeth and the dynamic load characteristics during cutting. Chains with a 3/8″ mini pitch are commonly used in electric and battery-powered chainsaws due to their lower torque demand and reduced vibration levels [59,60].
Guide bar groove width (gauge)1.1 mmA smaller drive link thickness results in a narrower kerf, reducing cutting resistance and energy demand, which is particularly important for battery-powered devices [61].
Cutter profile typeChamfer ChiselThe semi-chisel (chamfered) profile represents a compromise between cutting aggressiveness and edge durability. Literature indicates that chamfer chisel cutters exhibit higher resistance to dulling and lower kickback risk compared to full chisel profiles [62,63].
Vibration and kickback reductionYes (low-kickback design)The use of ramped depth gauges and PIXEL-type geometry reduces kickback risk and vibration transmitted to the operator, improving ergonomics and occupational safety [64].
Geometrical variantsGuide bar length/number of drive links25 cm/40 drive linksShorter guide bars provide higher cutting precision and lower moment of inertia, which is advantageous in tree maintenance operations and cutting small-diameter shoots [65].
30 cm/45 drive linksThe most commonly used configuration in compact chainsaws, offering a balance between cutting reach and operational stability [60].
35 cm/52 drive linksProvides greater cutting depth, but at the cost of increased dynamic and energy loads [61].
Material constructionChain bodyStructural alloy steelThe drive links, tie straps, and rivets are manufactured from alloy steel with enhanced fatigue strength and abrasion resistance. Studies indicate that the material properties of the chain body significantly affect fatigue life and overall durability [66].
Cutting teeth—materialAlloy steelThe cutting teeth are made from the same base alloy steel as the chain body but are subjected to additional processing. Material homogeneity reduces the risk of cracking at the tooth–link interface [67].
Cutting teeth—treatmentHeat hardening/surface hardeningThermal hardening increases the hardness of the cutting edge, improves wear resistance, and extends the service life between sharpening cycles. Literature confirms that this process significantly affects cutting efficiency and energy consumption [63,66].
Table 3. Technical specification of the METABO circular saw blade HW/CT 216 × 2.4 × 30 Z40 WZ.
Table 3. Technical specification of the METABO circular saw blade HW/CT 216 × 2.4 × 30 Z40 WZ.
CategoryParameterValue/DescriptionTechnical Significance and Literature Background
Basic dimensionsDiameter × cutting width × bore216 × 2.4 × 30 mmStandard dimensions for 216 mm circular saw blades; determines cutting depth, compatibility with various saw models, and kerf width. Suitable for compact and stationary circular saws [69,70].
Number of teethTeeth count40Number of teeth affects cutting speed, smoothness, and material removal rate. Higher tooth count generally produces smoother cuts, but may increase cutting resistance [70,71].
Tooth shapeWZ (alternating bevel)Alternating bevel geometry (left/right) with 5° negative rake angleProvides balanced cutting action, reduced vibration, and safer operation. WZ teeth are common for cross-cutting wood [71,72].
Blade body thicknessThickness1.8 mmDetermines rigidity and stability during cutting. Thicker body reduces vibration but slightly increases kerf and energy demand [72].
Rake angleCutting edge angle−5° (negative)Negative rake improves control, reduces tear-out in cross-cutting, and lowers feed force, enhancing safety and surface finish [72,73].
MaterialTeeth and bodyHW/CT cemented carbide (WC + TiC bonded with Co)HW/CT is a very hard and wear-resistant material. Tungsten carbide (WC) and titanium carbide (TiC) form the hard phase, while cobalt (Co) acts as a metallic binder, providing toughness. Material selection directly affects tool life and cutting efficiency [74,75].
Compatible saw modelsApplicationsKS 216 M Lasercut, KGS 216 M, KGSV 216 M, KGSV 72 Xact, KGSV 72 Xact SYMBlade dimensions and arbor design compatible with multiple 216 mm Metabo saw models, ensuring interchangeability and operational flexibility [69,70].
Table 4. Calculated values of the fractal dimension.
Table 4. Calculated values of the fractal dimension.
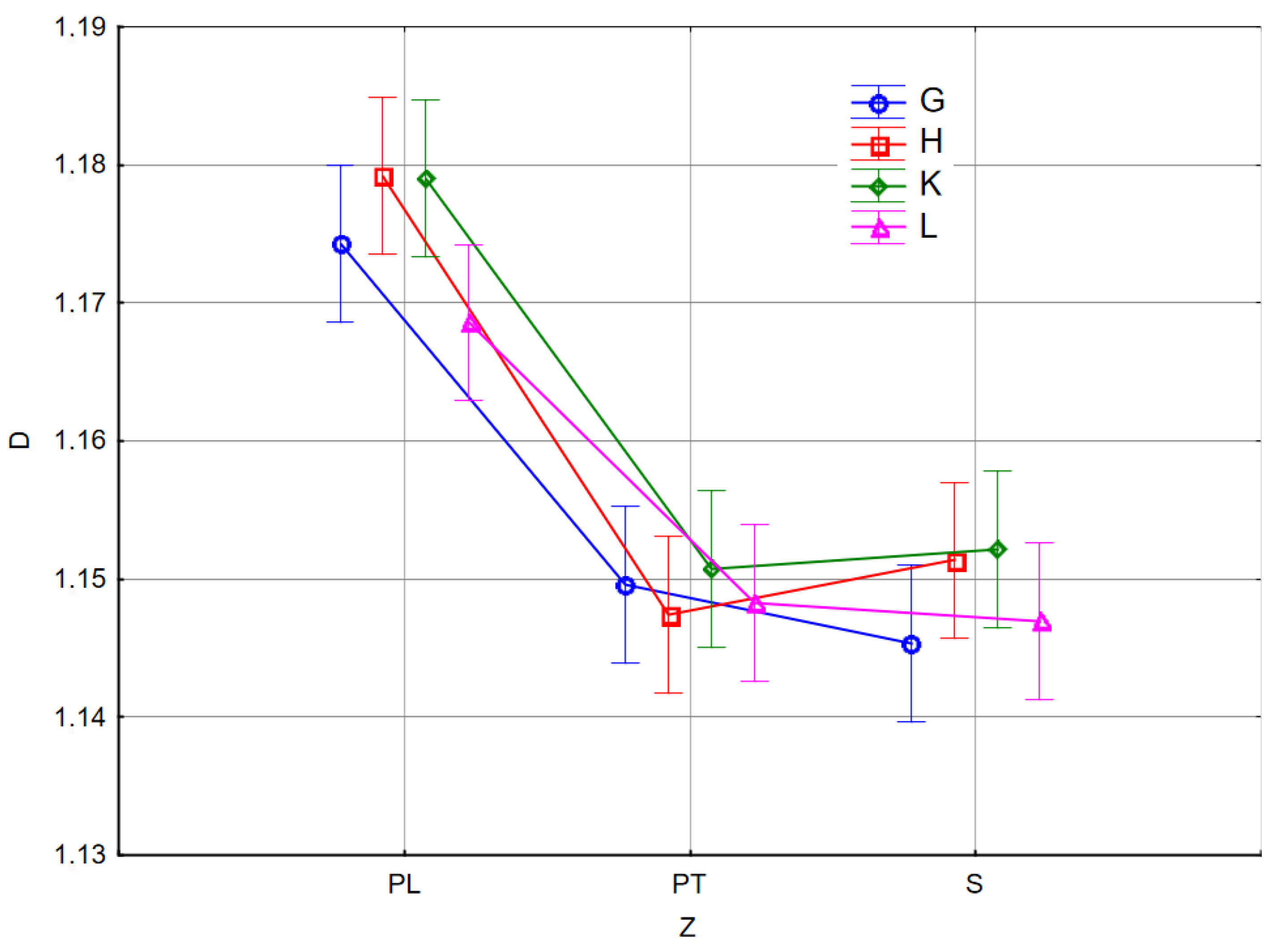
MCCutting UnitsTreeMeanMedianMinMaxStandard
Deviation		CV
MC1PLG1.1601.1461.1321.2150.0292.527
H1.1661.1641.1331.1960.0171.418
K1.1611.1571.1361.1830.0181.538
L1.1601.1561.1331.1900.0211.805
PTG1.1521.1411.1191.2110.0312.683
H1.1361.1361.1191.1550.0100.917
K1.1501.1431.1331.2030.0201.748
L1.1491.1521.1221.1880.0211.821
SG1.1441.1431.1311.1550.0080.728
H1.1411.1421.1291.1600.0090.785
K1.1471.1451.1161.2040.0242.058
L1.1551.1571.1321.1750.0131.113
MC2PLG1.1681.1691.1471.1940.0161.335
H1.1801.1831.1491.2080.0191.573
K1.1961.1891.1621.2710.0332.718
L1.1661.1721.1411.1880.0171.492
PTG1.1551.1511.1321.1910.0201.763
H1.1491.1481.1231.1780.0161.362
K1.1501.1501.1251.1730.0121.073
L1.1401.1401.1141.1610.0151.359
SG1.1501.1461.1311.1770.0171.442
H1.1561.1601.1251.1800.0171.488
K1.1601.1591.1251.1970.0191.662
L1.1411.1371.1271.1590.0121.075
MC3PLG1.1881.1851.1661.2270.0191.596
H1.1841.1821.1501.2250.0211.734
K1.1811.1861.1581.2040.0161.338
L1.1731.1731.1361.2120.0191.636
PTG1.1491.1471.1311.1720.0121.010
H1.1581.1571.1271.2010.0242.073
K1.1501.1541.1131.1700.0161.405
L1.1521.1501.1401.1820.0121.080
SG1.1391.1431.1111.1720.0181.608
H1.1551.1511.1341.2060.0211.792
K1.1451.1391.1191.1780.0181.583
L1.1391.1391.1181.1690.0151.287
MC4PLG1.1821.1891.1501.2100.0211.776
H1.1871.1901.1581.2340.0211.784
K1.1781.1781.1491.2100.0181.544
L1.1761.1751.1371.2090.0252.100
PTG1.1431.1461.1041.1790.0201.737
H1.1471.1481.1291.1680.0131.131
K1.1541.1551.1281.1710.0131.107
L1.1521.1501.1351.1720.0131.092
SG1.1491.1521.1221.1660.0131.154
H1.1541.1541.1371.1650.0100.860
K1.1571.1581.1441.1840.0110.985
L1.1531.1531.1261.1790.0151.321
MC1, MC2, MC3, MC4—moisture content levels; PL—chainsaw; PT—circular saw; S—bypass loppers; G—‘Gloster’; H—‘Hortensia’; K—‘Conference’; L—‘Ligol’.
Table 5. Analysis of main factors and interactions affecting the fractal dimension (D).
Table 5. Analysis of main factors and interactions affecting the fractal dimension (D).
FactorSum of SquareDegree
of Freedom		Mean SquareFemp;
F-Ratio		p-Value
Main factors
MC: Moisture Content0.006430.002160.0003
T: Tree0.002730.000930.0440
Z: Cutting Unit0.073820.03691110.0000
Interactions
MC × T0.006590.000720.0233
MC × Z0.006660.001130.0035
T × Z0.001960.000310.4651
MC × T × Z0.0059180.000310.4685
Error0.14354320.0003--
Table 6. Classification of fractal dimension (D) values into homogeneous groups based on moisture content (MC), cutting unit (Z), and tree type (T).
Table 6. Classification of fractal dimension (D) values into homogeneous groups based on moisture content (MC), cutting unit (Z), and tree type (T).
Moisture Content MC, %Sample SizeMean, %Homogeneous Groups
Group IGroup II
49.501201.152 ± 0.021 ×
37.421201.159 ± 0.023×
27.541201.159 ± 0.024×
22.101201.161 ± 0.022×
Tree TSample SizeMean, %Homogeneous Groups
Group IGroup II
L1201.155 ± 0.019×
G1201.156 ± 0.024××
H1201.159 ± 0.023××
K1201.161 ± 0.024 ×
Cutting Unit ZSample SizeMean, %Homogeneous Groups
Group IGroup II
S1601.149 ± 0.016×
PT1601.149 ± 0.017×
PL1601.175 ± 0.022 ×
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Nowakowski, T.; Tucki, K.; Gruz, Ł. The Effect of Cutting Technique on the Degree of Damage to Fruit Tree Shoots. Agriculture 2026, 16, 115. https://doi.org/10.3390/agriculture16010115

AMA Style

Nowakowski T, Tucki K, Gruz Ł. The Effect of Cutting Technique on the Degree of Damage to Fruit Tree Shoots. Agriculture. 2026; 16(1):115. https://doi.org/10.3390/agriculture16010115

Chicago/Turabian Style

Nowakowski, Tomasz, Karol Tucki, and Łukasz Gruz. 2026. "The Effect of Cutting Technique on the Degree of Damage to Fruit Tree Shoots" Agriculture 16, no. 1: 115. https://doi.org/10.3390/agriculture16010115

APA Style

Nowakowski, T., Tucki, K., & Gruz, Ł. (2026). The Effect of Cutting Technique on the Degree of Damage to Fruit Tree Shoots. Agriculture, 16(1), 115. https://doi.org/10.3390/agriculture16010115

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop