Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice
Abstract
:1. Introduction
2. Materials and Methods
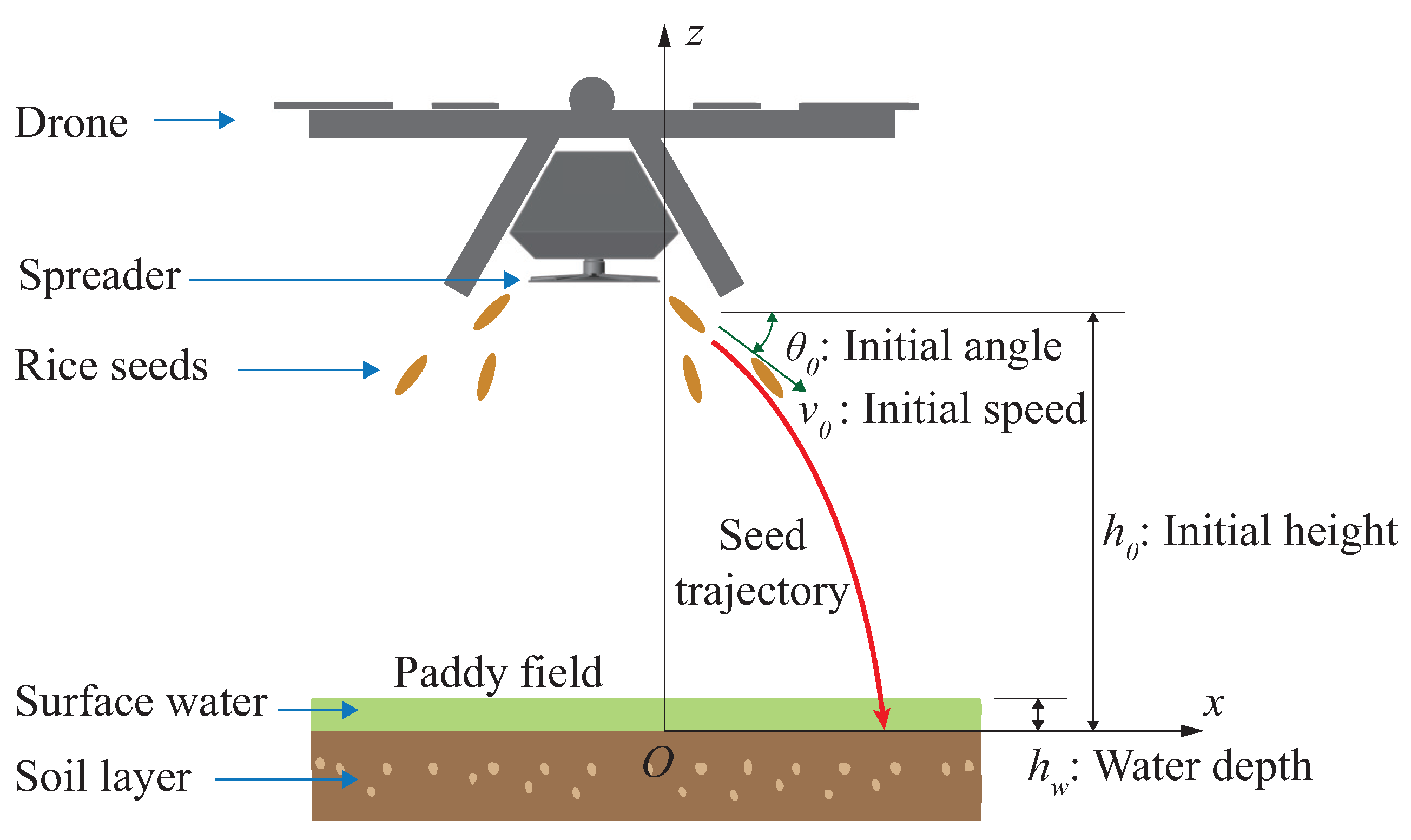
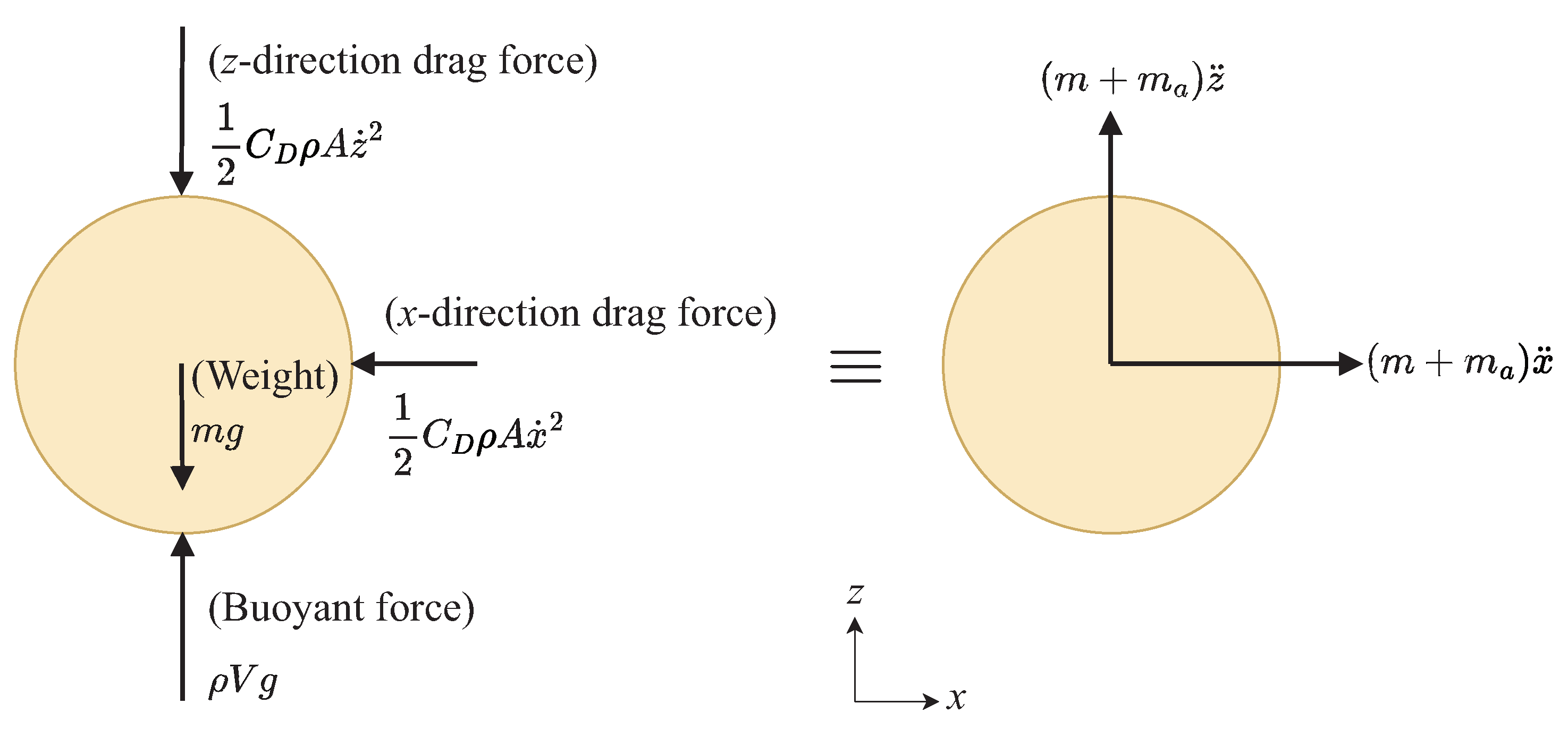
2.1. Dynamics of Rice Seed Flight
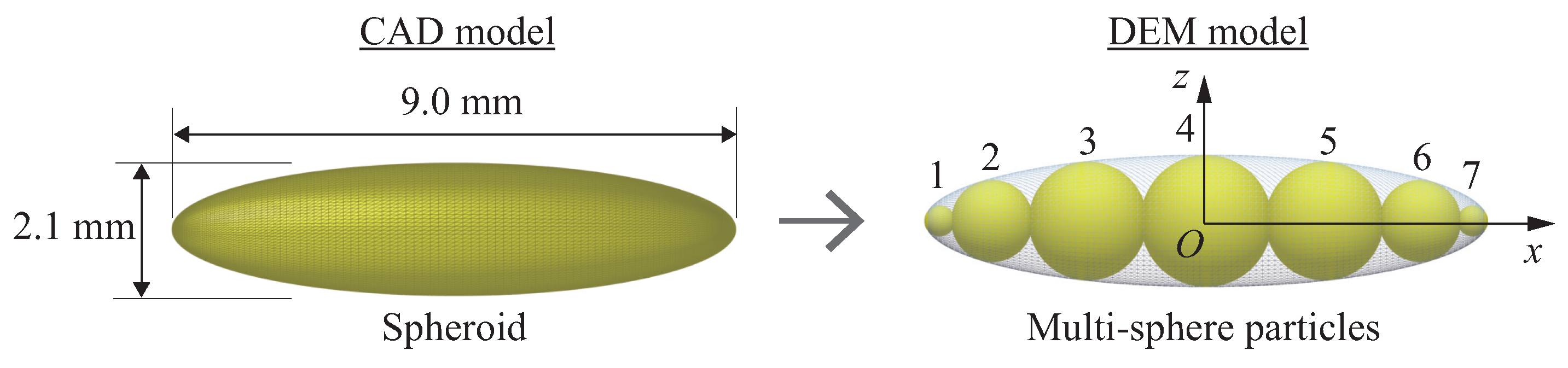
2.2. Contact Model and Parameters
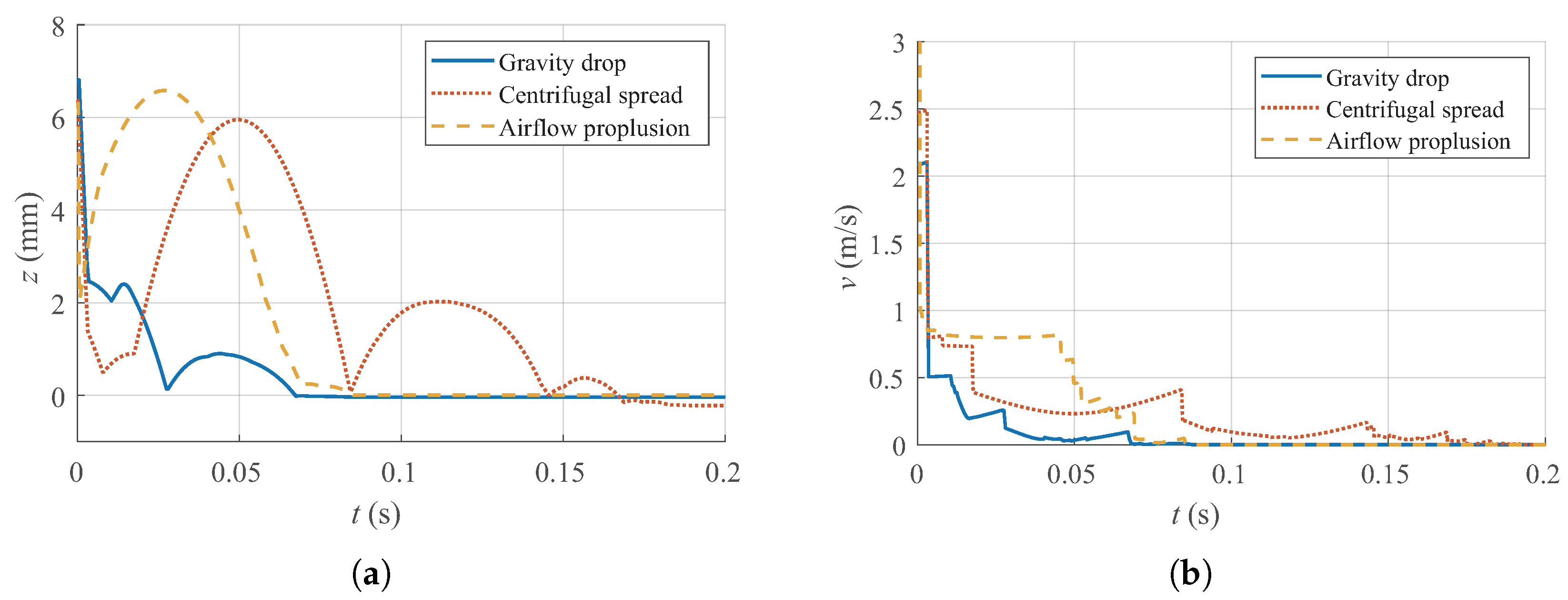
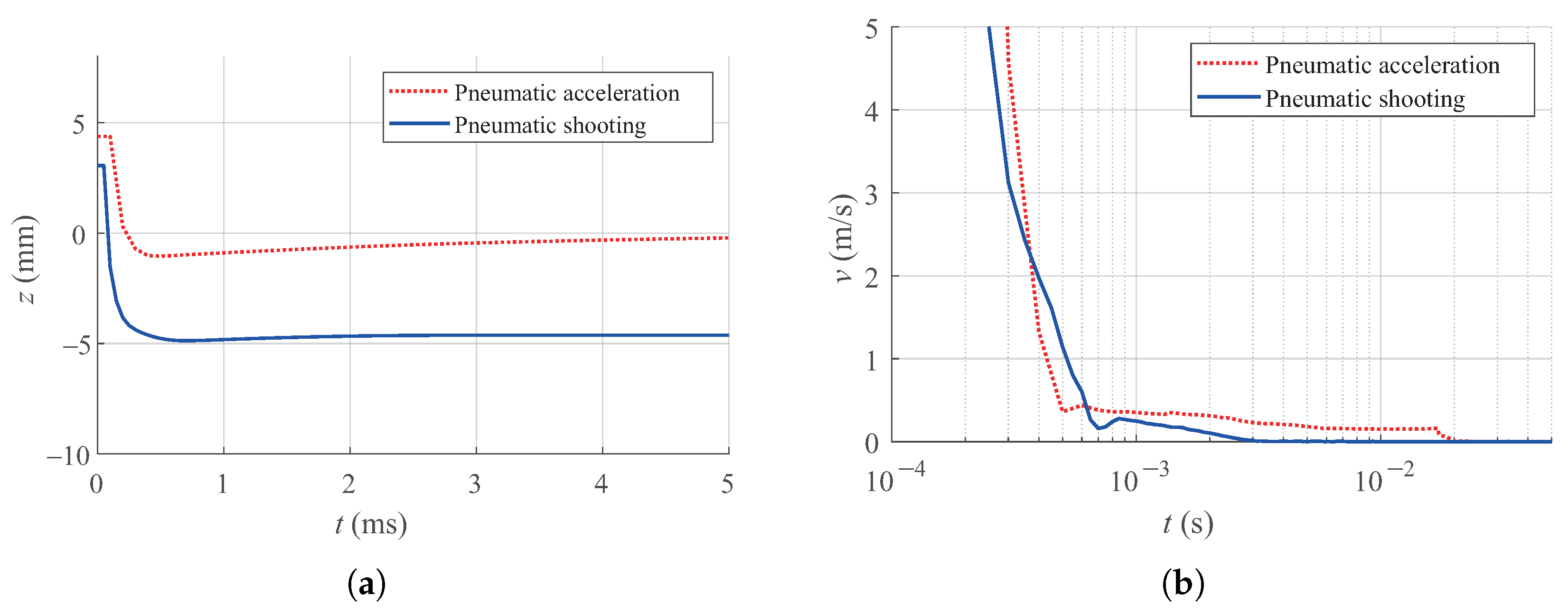
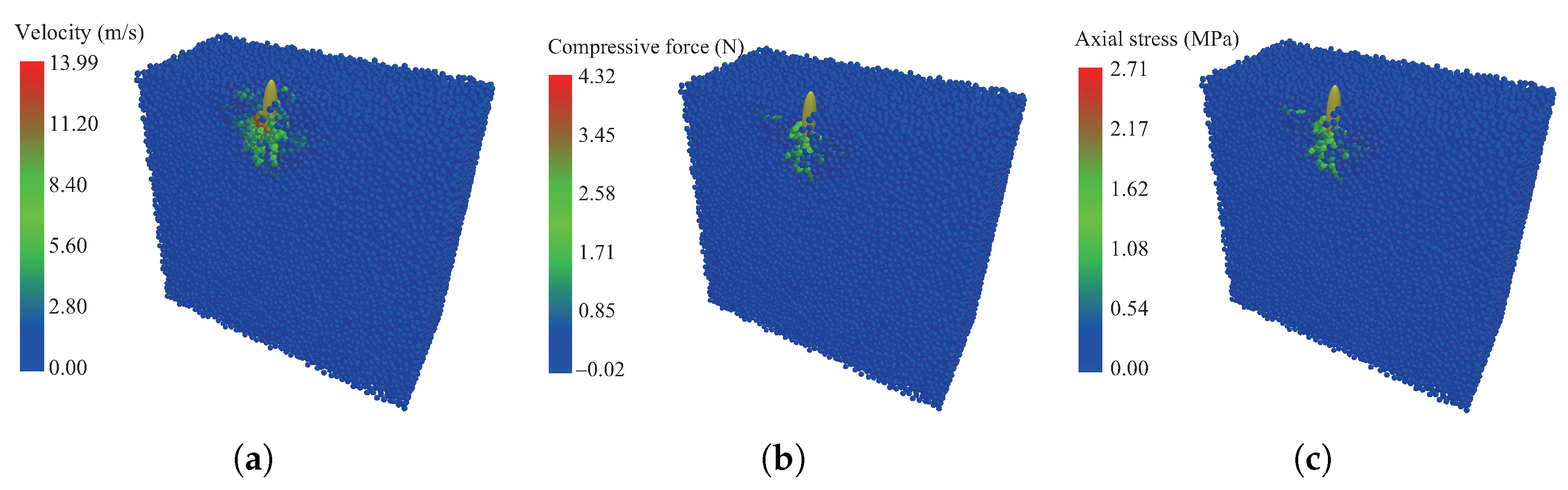
3. DEM Simulation Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seck, P.A.; Diagne, A.; Mohanty, S.; Wopereis, M.C.S. Crops That Feed the World 7: Rice. Food Secur. 2012, 4, 7–24. [Google Scholar] [CrossRef]
- Wu, H.; Jin, R.; Liu, A.; Jiang, S.; Chai, L. Savings and Losses of Scarce Virtual Water in the International Trade of Wheat, Maize, and Rice. Int. J. Environ. Res. Public Health 2022, 19, 4119. [Google Scholar] [CrossRef]
- Neupane, D.; Adhikari, P.; Bhattarai, D.; Rana, B.; Ahmed, Z.; Sharma, U.; Adhikari, D. Does Climate Change Affect the Yield of the Top Three Cereals and Food Security in the World? Earth 2022, 3, 45–71. [Google Scholar] [CrossRef]
- Samal, P.; Babu, S.C.; Mondal, B.; Mishra, S.N. The Global Rice Agriculture towards 2050: An Inter-Continental Perspective. Outlook Agric. 2022, 51, 164–172. [Google Scholar] [CrossRef]
- Mohidem, N.A.; Hashim, N.; Shamsudin, R.; Che Man, H. Rice for Food Security: Revisiting Its Production, Diversity, Rice Milling Process and Nutrient Content. Agriculture 2022, 12, 741. [Google Scholar] [CrossRef]
- Zhao, W.; Chou, J.; Li, J.; Xu, Y.; Li, Y.; Hao, Y. Impacts of Extreme Climate Events on Future Rice Yields in Global Major Rice-Producing Regions. Int. J. Environ. Res. Public Health 2022, 19, 4437. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.S.; Nagarjuna, D.; Murthy, K.R. Productivity and Profitability in Dry Direct Sown Rice through Mechanization. Int. J. Chem. Stud. 2021, 9, 17–20. [Google Scholar] [CrossRef]
- Bautista, A.P.; Mataia, A.; Austria, C.; Tiongco, M.; Laborte, A. Adoption and Performance of Direct-seeded Rice (DSR) Technology in the Philippines. Philipp. J. Sci. 2023, 152, 459–484. [Google Scholar] [CrossRef]
- Saha, R.; Patra, P.S.; Ahmed, A.S. Impact of Mechanical Transplanting on Rice Productivity and Profitability- Review. Int. J. Econ. Plants 2021, 8, 226–230. [Google Scholar] [CrossRef]
- Hossen, M.A.; Shahriyar, M.M.; Islam, S.; Paul, H.; Rahman, M.M. Rice Transplanting Mechanization in Bangladesh: Way to Make It Sustainable. Agric. Sci. 2022, 13, 130–149. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Nauman, M.H.; Ghafoor, A.; Farooque, A.A.; Haydar, Z.; Ashraf, M.U.; Awais, M. Direct Seeding of Basmati Rice through Improved Drills: Potential and Constraints in Pakistani Farm Settings. Appl. Eng. Agric. 2021, 37, 53–63. [Google Scholar] [CrossRef]
- Qi, P.; Wang, Z.; Wang, C.; Xu, L.; Jia, X.; Zhang, Y.; Wang, S.; Han, L.; Li, T.; Chen, B.; et al. Development of Multifunctional Unmanned Aerial Vehicles versus Ground Seeding and Outplanting: What Is More Effective for Improving the Growth and Quality of Rice Culture? Front. Plant Sci. 2022, 13, 953753. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhu, Y.; Zhang, X.; Liao, Q.; Fu, H.; Cheng, Q.; Chen, Z.; Sun, Y.; Ma, J.; Zhang, J.; et al. Unmanned Aerial Vehicle Direct Seeding or Integrated Mechanical Transplanting, Which Will Be the next Step for Mechanized Rice Production in China? —A Comparison Based on Energy Use Efficiency and Economic Benefits. Energy 2023, 273, 127223. [Google Scholar] [CrossRef]
- Liu, W.; Zou, S.; Xu, X.; Gu, Q.; He, W.; Huang, J.; Huang, J.; Lyu, Z.; Lin, J.; Zhou, Z.; et al. Development of UAV-based Shot Seeding Device for Rice Planting. Int. J. Agric. Biol. Eng. 2022, 15, 1–7. [Google Scholar] [CrossRef]
- Lysych, M.; Bukhtoyarov, L.; Druchinin, D. Design and Research Sowing Devices for Aerial Sowing of Forest Seeds with UAVs. Inventions 2021, 6, 83. [Google Scholar] [CrossRef]
- Kawamura, K.; Asai, H.; Yasuda, T.; Khanthavong, P.; Soisouvanh, P.; Phongchanmixay, S. Field Phenotyping of Plant Height in an Upland Rice Field in Laos Using Low-Cost Small Unmanned Aerial Vehicles (UAVs). Plant Prod. Sci. 2020, 23, 452–465. [Google Scholar] [CrossRef]
- Zuo, Q.; Kuai, J.; Zhao, L.; Hu, Z.; Wu, J.; Zhou, G. The Effect of Sowing Depth and Soil Compaction on the Growth and Yield of Rapeseed in Rice Straw Returning Field. Field Crop. Res. 2017, 203. [Google Scholar] [CrossRef]
- Yang, W.; Xu, D.; Li, S.; Tang, X.; Pan, S.; Chen, X.; Mo, Z. Emergence and Seedling Establishment of Rice Varieties at Different Sowing Depths. J. Plant Growth Regul. 2022, 41, 1672–1686. [Google Scholar] [CrossRef]
- Zhang, S.; Tekeste, M.Z.; Li, Y.; Gaul, A.; Zhu, D.; Liao, J. Scaled-up Rice Grain Modelling for DEM Calibration and the Validation of Hopper Flow. Biosyst. Eng. 2020, 194, 196–212. [Google Scholar] [CrossRef]
- Bagheri, G.; Bonadonna, C. On the Drag of Freely Falling Non-Spherical Particles. Powder Technol. 2016, 301, 526–544. [Google Scholar] [CrossRef]
- Sanjeevi, S.K.P.; Padding, J.T. On the Orientational Dependence of Drag Experienced by Spheroids. J. Fluid Mech. 2017, 820, R1. [Google Scholar] [CrossRef]
- Ouchene, R. Numerical Simulation and Modeling of the Hydrodynamic Forces and Torque Acting on Individual Oblate Spheroids. Phys. Fluids 2020, 32, 073303. [Google Scholar] [CrossRef]
- Goossens, W.R. Review of the Empirical Correlations for the Drag Coefficient of Rigid Spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- Falkovich, G. Fluid Mechanics: A Short Course for Physicists; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Son, K.J. A Discrete Element Model for the Influence of Surfactants on Sedimentation Characteristics of Magnetorheological Fluids. Korea-Aust. Rheol. J. 2018, 30, 29–39. [Google Scholar] [CrossRef]
- Douglas, J.F.; Gasiorek, J.M.; Swaffield, J.A.; Jack, L.B. Fluid Mechanics, 5th ed.; Pearson: London, UK, 2005. [Google Scholar]
- Xie, Y.; Hong, Y.; Zhang, X.; Ren, J. Analysis of Mud Splashing Pattern of Paddy Field Blade Using Computational Fluid Dynamics. Comput. Electron. Agric. 2020, 176, 105639. [Google Scholar] [CrossRef]
- Wu, Z.; Li, M.; Lei, X.; Wu, Z.; Jiang, C.; Zhou, L.; Ma, R.; Chen, Y. Simulation and Parameter Optimisation of a Centrifugal Rice Seeding Spreader for a UAV. Biosyst. Eng. 2020, 192, 275–293. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, Z.; Xu, X.; Gu, Q.; Zou, S.; He, W.; Luo, X.; Huang, J.; Lin, J.; Jiang, R. Evaluation Method of Rowing Performance and Its Optimization for UAV-based Shot Seeding Device on Rice Sowing. Comput. Electron. Agric. 2023, 207, 107718. [Google Scholar] [CrossRef]
- Zhijun, W.; Yu, C.; Shengcai, S.; Hao, D.; Xiaobing, L.; Lijia, X. Design and Experimental Analysis of Drone Rice Direct Seeding Device. J. Eng. Sci. Technol. Rev. 2023, 16, 132–139. [Google Scholar] [CrossRef]
- Mohan, M.; Richardson, G.; Gopan, G.; Aghai, M.M.; Bajaj, S.; Galgamuwa, G.A.P.; Vastaranta, M.; Arachchige, P.S.P.; Amorós, L.; Corte, A.P.D.; et al. UAV-Supported Forest Regeneration: Current Trends, Challenges and Implications. Remote Sens. 2021, 13, 2596. [Google Scholar] [CrossRef]
- Anbumozhi, V.; Yamaji, E.; Tabuchi, T. Rice Crop Growth and Yield as Influenced by Changes in Ponding Water Depth, Water Regime and Fertigation Level. Agric. Water Manag. 1998, 37, 241–253. [Google Scholar] [CrossRef]
- Sudhir-Yadav; Gill, G.; Humphreys, E.; Kukal, S.; Walia, U. Effect of Water Management on Dry Seeded and Puddled Transplanted Rice. Part 1: Crop Performance. Field Crop. Res. 2011, 120, 112–122. [Google Scholar] [CrossRef]
- Bogacki, P.; Shampine, L.F. A 3(2) Pair of Runge - Kutta Formulas. Appl. Math. Lett. 1989, 2, 321–325. [Google Scholar] [CrossRef]
- Son, K.J. Mathematical Modeling of Collisional Heat Generation and Convective Heat Transfer Problem for Single Spherical Body in Oscillating Boundaries. Mathematics 2023, 11, 4637. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, T.; Wang, X.; Hu, L.; Wang, S.; Luo, X.; Ji, J. Determination of Discrete Element Modelling Parameters of a Paddy Soil with a High Moisture Content (>40%). Agriculture 2022, 12, 2000. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, J.; Chen, X.; Yu, J.; Liu, M.; Zhang, Q. Parameter Calibration of Soil in the Poyang Lake Region Based on Discrete Element Method. Am. J. Biochem. Biotechnol. 2020, 16, 538–548. [Google Scholar] [CrossRef]
- Tienan, Z.; Zhou, H.; Ji, J.; Sun, F.; Qin, Z. Parameter Calibration of the Discrete Element Simulation Model for Soaking Paddy Loam Soil Based on the Slump Test. PLoS ONE 2023, 18, e0285428. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Shi, M.; Yu, C.; Yu, Z.; Kuang, F.; Xiong, W.; Xue, K. Tool-Straw-Paddy Soil Coupling Model of Mechanical Rotary-Tillage Process Based on DEM-FEM. Comput. Electron. Agric. 2023, 215, 108410. [Google Scholar] [CrossRef]
- Zou, L.; Yan, D.; Niu, Z.; Yuan, J.; Cheng, H.; Zheng, H. Parametric Analysis and Numerical Optimisation of Spinach Root Vibration Shovel Cutting Using Discrete Element Method. Comput. Electron. Agric. 2023, 212, 108138. [Google Scholar] [CrossRef]
- Son, K.J. A Numerical Study of the Influence of Rheology of Cohesive Particles on Blade Free Planetary Mixing. Korea-Aust. Rheol. J. 2018, 30, 199–209. [Google Scholar] [CrossRef]
- Wilkinson, S.; Turnbull, S.; Yan, Z.; Stitt, E.; Marigo, M. A Parametric Evaluation of Powder Flowability Using a Freeman Rheometer through Statistical and Sensitivity Analysis: A Discrete Element Method (DEM) Study. Comput. Chem. Eng. 2017, 97, 161–174. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Mehrotra, A.; Muzzio, F.J.; Tomassone, M.S. Cohesive Effects in Powder Mixing in a Tumbling Blender. Powder Technol. 2006, 165, 105–114. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Simsek, E.; Rickelt, S.; Wirtz, S.; Scherer, V. Review and Extension of Normal Force Models for the Discrete Element Method. Powder Technol. 2007, 171, 157–173. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Wirtz, S.; Scherer, V. A Study on Tangential Force Laws Applicable to the Discrete Element Method (DEM) for Materials with Viscoelastic or Plastic Behavior. Chem. Eng. Sci. 2008, 63, 1523–1541. [Google Scholar] [CrossRef]
- Marshall, J.S.; Li, S. Adhesive Particle Flow; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Bortolotti, C.T.; Santos, K.G.; Francisquetti, M.C.C.; Duarte, C.R.; Barrozo, M.A.S. Hydrodynamic Study of a Mixture of West Indian Cherry Residue and Soybean Grains in a Spouted Bed. Can. J. Chem. Eng. 2013, 91, 1871–1880. [Google Scholar] [CrossRef]
- Hui, C.Y.; Lin, Y.Y.; Baney, J.M.; Jagota, A. The Accuracy of the Geometric Assumptions in the JKR (JohnsonKendallRoberts) Theory of Adhesion. J. Adhes. Sci. Technol. 2000, 14, 1297–1319. [Google Scholar] [CrossRef]
- Feng, Y.; Han, K.; Owen, D.; Loughran, J. On Upscaling of Discrete Element Models: Similarity Principles. Eng. Comput. 2009, 26, 599–609. [Google Scholar] [CrossRef]
- Feng, Y.T.; Owen, D.R.J. Discrete Element Modelling of Large Scale Particle Systems—I: Exact Scaling Laws. Comput. Part. Mech. 2014, 1, 159–168. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-Dimensional Discrete Element Modelling of Tillage: Determination of a Suitable Contact Model and Parameters for a Cohesionless Soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Ahmad, F.; Qiu, B.; Ding, Q.; Ding, W.; Khan, Z.M.; Shoaib, M.; Chandio, F.A.; Rahim, A.; Khaliq, A. Discrete Element Method Simulation of Disc Type Furrow Openers in Paddy Soil. Int. J. Agric. Biol. Eng. 2020, 13, 103–110. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Huang, Y.; Ji, J. An Efficient Method for Determining DEM Parameters of a Loose Cohesive Soil Modelled Using Hysteretic Spring and Linear Cohesion Contact Models. Biosyst. Eng. 2022, 215, 283–294. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, C.; Quan, W.; Xie, S.; Shi, F.; Ma, Z.; Wu, M. Calibration Parameter of Soil Discrete Element Based on Area Difference Method. Agriculture 2023, 13, 648. [Google Scholar] [CrossRef]
- Kim, Y.S.; Siddique, M.A.A.; Kim, W.S.; Kim, Y.J.; Lee, S.D.; Lee, D.K.; Hwang, S.J.; Nam, J.S.; Park, S.U.; Lim, R.G. DEM Simulation for Draft Force Prediction of Moldboard Plow According to the Tillage Depth in Cohesive Soil. Comput. Electron. Agric. 2021, 189, 106368. [Google Scholar] [CrossRef]








| Fluid | Density | Viscosity |
|---|---|---|
| Air | 1.225 | |
| Paddy water | 1090 |
| Sowing Type | Launch Speed 1 (m/s) | Launch Angle 1 |
|---|---|---|
| Gravitational drop | 2 | 0 |
| Centrifugal spreading | 2.79 | 18.9 |
| Airflow propulsion | 18.11 | 83.7 |
| Pneumatic discharge | 75.03 | 88.5 |
| Pneumatic shooting | 225 | 89.5 |
| Sowing Type | Terminal Speed (m/s) | Terminal Angle |
|---|---|---|
| Gravitational drop | 2.08 | 49.1 |
| Centrifugal spreading | 2.47 | 42.3 |
| Airflow propulsion | 14.48 | 83.7 |
| Pneumatic discharge | 57.29 | 88.5 |
| Pneumatic shooting | 144.64 | 89.5 |
| ID | x-Position (mm) | Radius (mm) |
|---|---|---|
| 1 | 0.245 | |
| 2 | 0.654 | |
| 3 | 0.947 | |
| 4 | 0.00 | 1.050 |
| 5 | 1.89 | 0.947 |
| 6 | 3.42 | 0.654 |
| 7 | 4.26 | 0.245 |
| Property | Rice | Soil |
|---|---|---|
| Mass density () | 1250 | 2527 |
| Shear modulus (MPa) | 237.5 | 68.5 |
| Poisson’s ratio | 0.275 | 0.314 |
| Parameter | Rice–Soil | Soil–Soil |
|---|---|---|
| Coefficient of restitution | 0.55 | 0.3 |
| Coefficient of sliding friction | 0.2 | 0.36 |
| Coefficient of rolling friction | 0.08 | 0.18 |
| Surface energy () | 0.75 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, K.J. Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice. Agriculture 2025, 15, 422. https://doi.org/10.3390/agriculture15040422
Son KJ. Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice. Agriculture. 2025; 15(4):422. https://doi.org/10.3390/agriculture15040422
Chicago/Turabian StyleSon, Kwon Joong. 2025. "Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice" Agriculture 15, no. 4: 422. https://doi.org/10.3390/agriculture15040422
APA StyleSon, K. J. (2025). Discrete Element Method Analysis of Soil Penetration Depth Affected by Spreading Speed in Drone-Seeded Rice. Agriculture, 15(4), 422. https://doi.org/10.3390/agriculture15040422






