Design and Application of a Portable Chestnut-Harvesting Device

Abstract

To solve the problems of high resistance, high contents of impurities and high harvest damage rates commonly encountered in chestnut harvesting, a novel lightweight simplified chestnut harvester was proposed that can simultaneously perform picking, soil removal and collection. The key component of the harvester is the pickup drum device, which is mainly composed of a pickup claw and drum. Compared with traditional claw harvesters, the picking and impurity removal functions are combined into one. As the pickup drum device is very important in chestnut harvesters, its key components were designed and optimized in this study. According to the structure and working principle of the pickup, a mechanical simulation model based on the discrete element method (DEM) and RecurDyn 2023 was established. Through theoretical calculations and single- and multi-factor simulation tests, the optimal combination of the working parameters of the pickup drum device was obtained. The results showed that the optimal speed of the chestnut pickup drum was 45 rpm, the optimal forward speed of the chassis was 0.4 m/s, and the optimal claw length was 55 cm. A field verification test was carried out according to the optimal parameter combination. The results showed that the picking efficiency of chestnut picking device was 88.44%, and the error between this value and the simulation results (91.42%) was 1.95%—less than 3%—which verifies the correctness of the simulation model. This study provides a theoretical reference for the design and optimization of chestnut harvesters.

1. Introduction

Chestnut, a long-lived tree species that has high long-term yields and efficient economic returns with just one planting, is an important economic crop in China [1]. Its planting area in China is about 2 × 10⁵ Hm², and its annual yield is 8 × 10⁶ T. Mechanizing chestnut harvesting, which directly affects the yield and quality of chestnuts, is a key factor in improving the quality and efficiency of the forest and fruit industry. Existing chestnut harvesters have disadvantages such as high picking resistance, and lead to high contents of impurities and can easily damage the harvest. This effects chestnut’s planting efficiency and seriously limits the expansion of chestnut production [2]. These limitations are particularly pronounced in hilly and uneven terrains, where conventional harvesters exhibit three major shortcomings: poor adaptability to slopes and rough ground, causing instability and incomplete pickup; ineffective separation of impurities (e.g., soil, stones, and bracts) under variable ground conditions, leading to clogging and increased post-harvest processing costs; and high mechanical damage rates due to rigid structural components and inappropriate claw–soil interaction mechanisms for these undulating surfaces. Therefore, reducing the operation resistance, improving the removal of impurities, reducing the damage to the harvest, and improving the quality of mechanized chestnut harvesting are the current development directions and research focus for mechanized chestnut harvesting technology and equipment. Hence, the research and development of low-damage adaptive chestnut picking equipment have important practical significance, especially for hilly regions where traditional machines fail to perform reliably.

Many studies on the picking and clearing technology and equipment for nut crops such as hazelnut, walnut and pine nut have been performed in China, but there are relatively few studies on special chestnut harvesting machinery. There are fundamental differences in chestnut planting patterns between Japan, the United States, and China; these patterns directly influence the development of mechanized harvesting technology. Chestnut plantations in Japan and the United States typically adopt a flat-ground planting pattern, with a flat terrain and wide row spacing, providing ideal conditions for large-scale mechanical operations. A Japanese research and development team have invented a chestnut picking robot [3]. This machine uses modern technology to achieve intelligent and automated picking; however, it can only pick on flat ground, which limits the working environments it can be applied in. This harvester is currently in the experimental stage, and needs to undergo further verification and optimization in the actual production environment before moving towards large-scale application. The research and development of chestnut harvesting machinery in China must be based on the ridge planting pattern, a commonly used pattern in this region, and compact, lightweight, specialized harvesting equipment that can be adapted to complex terrain or intelligently adjust the ground clearance and terrain model must be developed. Nost of the large chestnut combine harvesters in Japan and the United States are not suitable for chestnut harvesting in China. Many scholars have conducted relevant studies on the issues related to chestnut harvesting (

Table 1. Brief comparison of recent research on chestnut or nut harvesters.

Study (Device Type)	Structure Features	Terrain Adaptability	Damage Rate	Energy Consumption	Impurity Removal
Japanese robot [3] (Intelligent picking)	Vision system, robotic arm	Flat ground only	Low	High	Good
Wang Chenguang [4] (Drum–brush-type)	Rigid bristles, sweeping mechanism	Flat and hard ground only	Moderate	Low	Poor in environments with debris
Wu Wenjie [5] (Crawler negative-pressure)	Airflow system, vibration mechanism	Sloping land	Low	High	Moderate
Shi Gaokun [6] (Elastic finger chain)	Elastic fingers, chain plate	Limited (ground error < 10 cm)	Low	Moderate	Poor with bracts
This study (2025) (Drum–claw-type)	Arc-shaped claws; integrated picking and debracting	High (complex terrain, ridges)	Low	Low (battery-powered)	Effective (comb design)

). Wang Chenguang developed a drum–brush-type chestnut pickup, which sweeps chestnuts on the ground into a collection device through rotating brush hairs. This model has good adaptability to flat and hard ground, but easily picks up debris impurities from soft soil or on weed-covered ground, leading to blockage of the sorting system [4]. Wu Wenjie developed a crawler self-propelled negative pressure collection device and a multi-stage vibration sorting mechanism to solve the problem of harvesting on sloping land. Although it can achieve stable operation on slopes, the air flow system consumes a high amounts of energy and can be affected by fruit maturity [5]. Shi Gaokun designed an elastic finger chain plate pickup device to solve the problem of the high shell breakage rate faced by traditional pickup technology [6]. The device requires that the ground flatness error is less than 10 cm, and its adaptability to chestnut bracts is poor. At present, there is still room to improve the efficiency of chestnut harvesters in China and there is a certain gap between their performance and the actual needs of farmers.

Compared with traditional drum- or claw-type chestnut-harvesting devices, the proposed lightweight and simplified harvester exhibits fundamental improvements in structure and adaptability. Conventional drum-type devices (e.g., drum–brush-type pickers) rely on rigid bristles or finger chains for collection, which are prone to intaking debris in soft soil or weedy environments and require a low ground incline. Claw-type devices, while adaptable to slopes, are often structurally complex, consume a high amount of energy, and are sensitive to fruit maturity. In this study, the arc-shaped combined claw–drum structure integrates picking and debracting functions into one unit. By optimizing the penetration angle and length of the claws, the operational resistance and fruit damage rate are significantly reduced. Moreover, the machine features a lightweight design and is powered by a lithium battery, offering excellent terrain adaptability, especially suitable for the ridge-planting patterns used in the hilly regions of Northeast China. This harvester thereby achieves efficient, low-damage, and integrated harvesting under complex field conditions.

In order reduce the high fruit damage rate and improve the terrain adaptability during chestnut picking operations in hilly and mountainous areas, a combined drum chestnut harvester was designed to simultaneously complete the picking, cleaning and collection of chestnuts. Through theoretical analysis and simulations, we preliminarily designed the chestnut picking drum device. On this basis, field tests were carried out to determine the optimal operating parameters of the device and verify its effectiveness under these parameters [7]. This study provides theoretical support for the design of chestnut picking equipment with low damage rates and high permeability.

The main contributions of this paper are as follows:

An innovative arc-shaped claw–drum design is presented that significantly reduces operational resistance and fruit damage compared to conventional brush-type or finger chain pickups.

A validated DEM–RecurDyn co-simulation framework is presented to optimize the parameters of chestnut-harvesting devices, demonstrating a high consistency between simulation and field test results (error < 3%).

The optimal set of working parameters that enable the harvester to achieve a high picking efficiency (over 88%) under real field conditions in hilly areas is presented, offering a practical and efficient solution for mechanized chestnut harvesting in regions with challenging terrain.

2. Materials and Methods

2.1. Design and Working Principle of the Machine

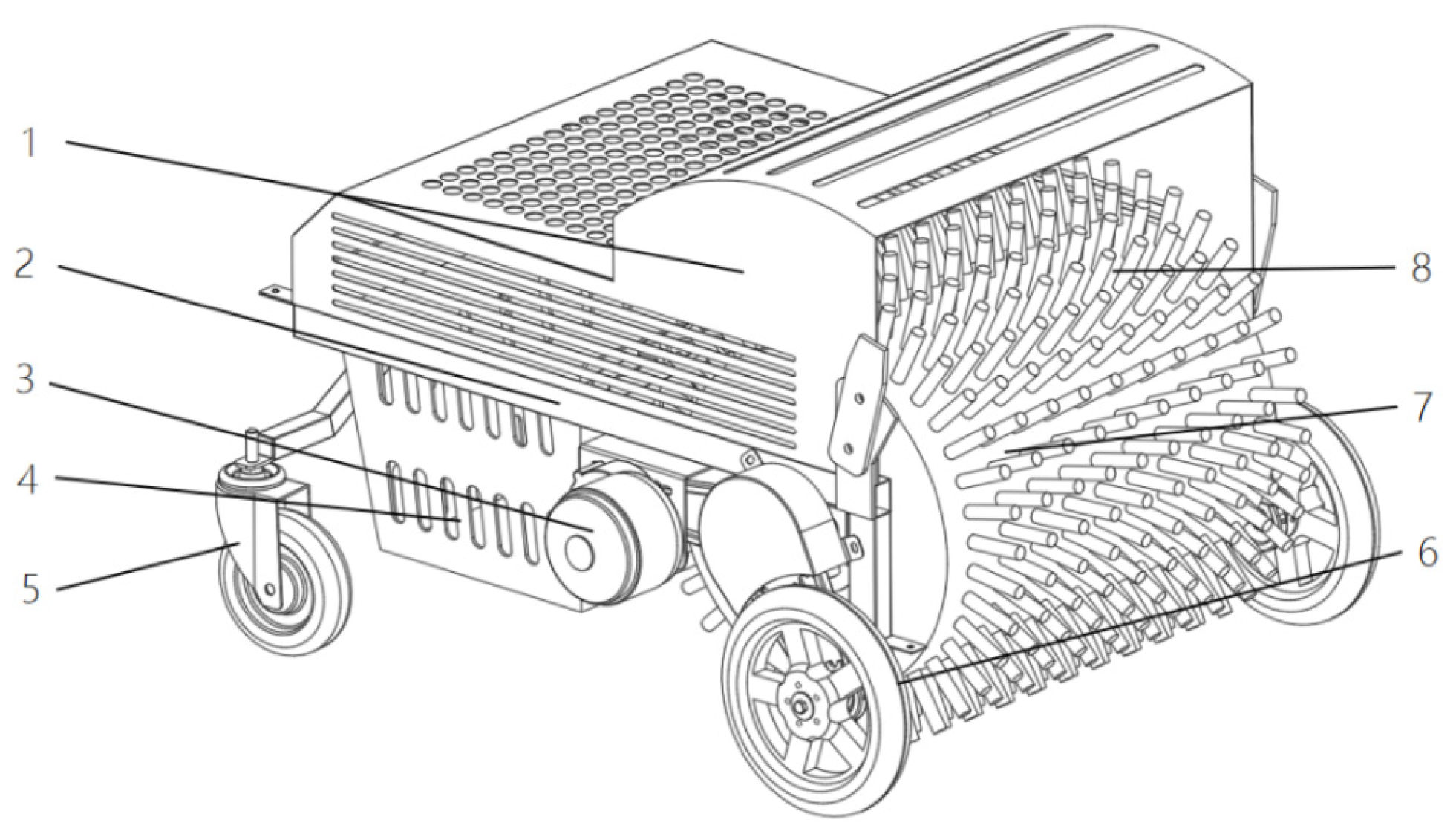
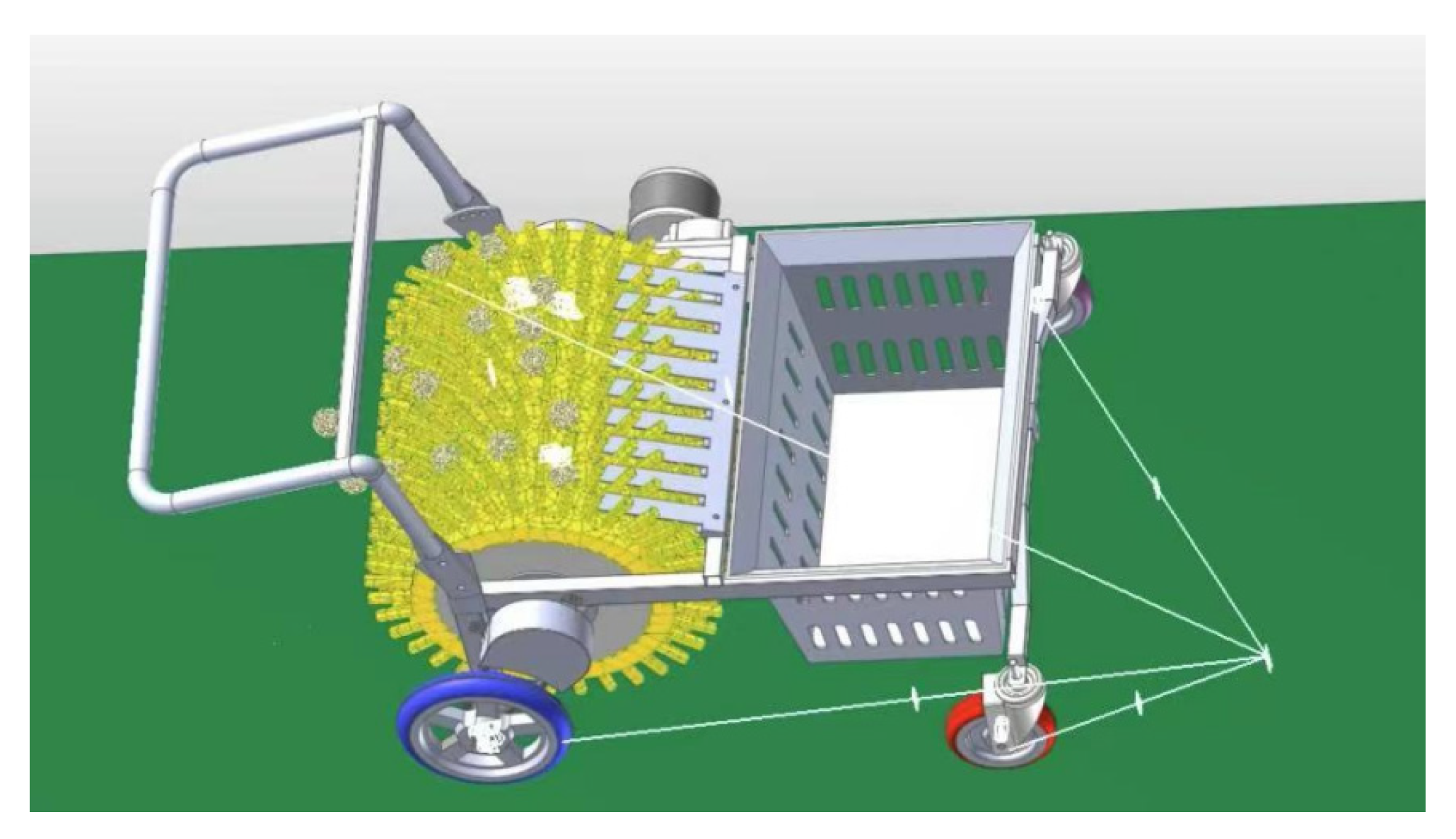
The chestnut pickup is composed of a protective cover plate (1), a frame (2), a DC reduction motor (3), a collection box (4), a front steering wheel beam (5), a rear drive (6), a collection drum (7), and a collection drum claw (8) (Figure 1), and is powered by a DC reduction motor, which is directly connected to the collection drum and the driving wheel through a coupling and gear set, rotating the drum and driving the chestnut pickup forward.

The chestnut picker is powered by a lithium battery, and the chassis and drum of chestnut picker are controlled through the integrated controller. The drum (7) collects the chestnuts, chestnut shells and other objects on the ground and sends them to the collection box (4) through rotation. The left rear wheel (6) is driven by the DC reduction motor (3), and the front wheel is a universal wheel, which is manually steered. The design of the comb allows the chestnuts to be effectively separated and pushed into the collection box (4), completing the chestnut picking and harvesting process while avoiding contamination with other debris. The equipment is simple and easy to operate and is suitable for all kinds of terrain, providing an effective solution for the mechanization and unmanned operation of nut picking in the hilly regions of Northeast China. It also solves the bottleneck of the long-term dependence on labor and the low efficiency and high costs of nut picking in this region.

The energy consumption of the portable chestnut harvester is a critical practical consideration, especially given its battery-powered operation. The DC reduction motor (Model: JGB37-550, rated voltage: 24 V) used in the prototype has a rated power of 250 W and a no-load current of 1.2 A. Under typical field operating conditions (drum speed: 45 rpm, forward speed: 0.4 m/s), the average current was measured at approximately 3.8 A, resulting in an operational power consumption of about 91 W. The device is powered by a 24 V, 20 Ah lithium battery, which provides a theoretical continuous operation time of up to 5 h under the optimized parameter settings. This low energy consumption not only ensures extended field operation but also reduces the operational cost and environmental impact, making it particularly suitable for small-scale farmers in remote hilly areas with limited access to grid power.

2.2. Design and Working Principle of the Pickup and Stripping Device

The chestnut pickup is mainly composed of a pickup drum device, a pickup drum claw and a peeling device, the pickup drum device being the main working part (Figure 2).

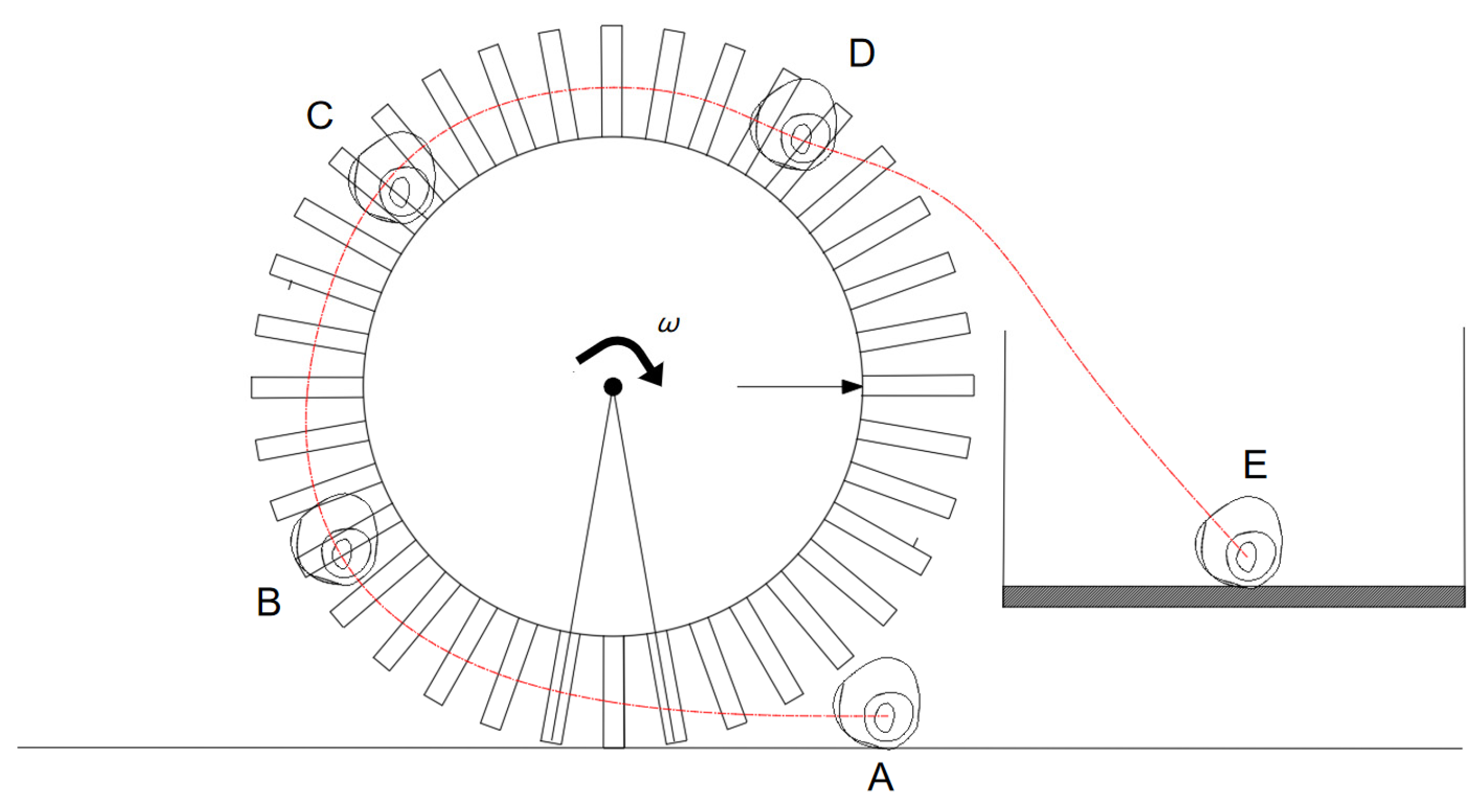
A diagram of the chestnut pickup’s operational process is shown in Figure 3. It can be seen from the figure that operation can be mainly divided into two processes: the pickup process of the claw–drum device (A → B → C) and the debracting process of the debracting device (D → E).

The picking process of the claw–drum device includes an arc claw pulling stage (A → C), an arc claw transportation stage (A → C, C → D) and an arc claw peeling process. The pulling stage involves interaction between the arc claw and chestnut bud, and the debarking stage involves interaction between the arc claw, chestnut and debarking plate.

Carrying out research on the processes of the claw–drum device and the film removal process of the debracting device can clarify the stresses and movement of the arc claw, chestnuts and debracting plate during the chestnut pickup process, as shown in Figure 3, and can provide a theoretical basis for analyses of claw–drum chestnut pickup machinery.

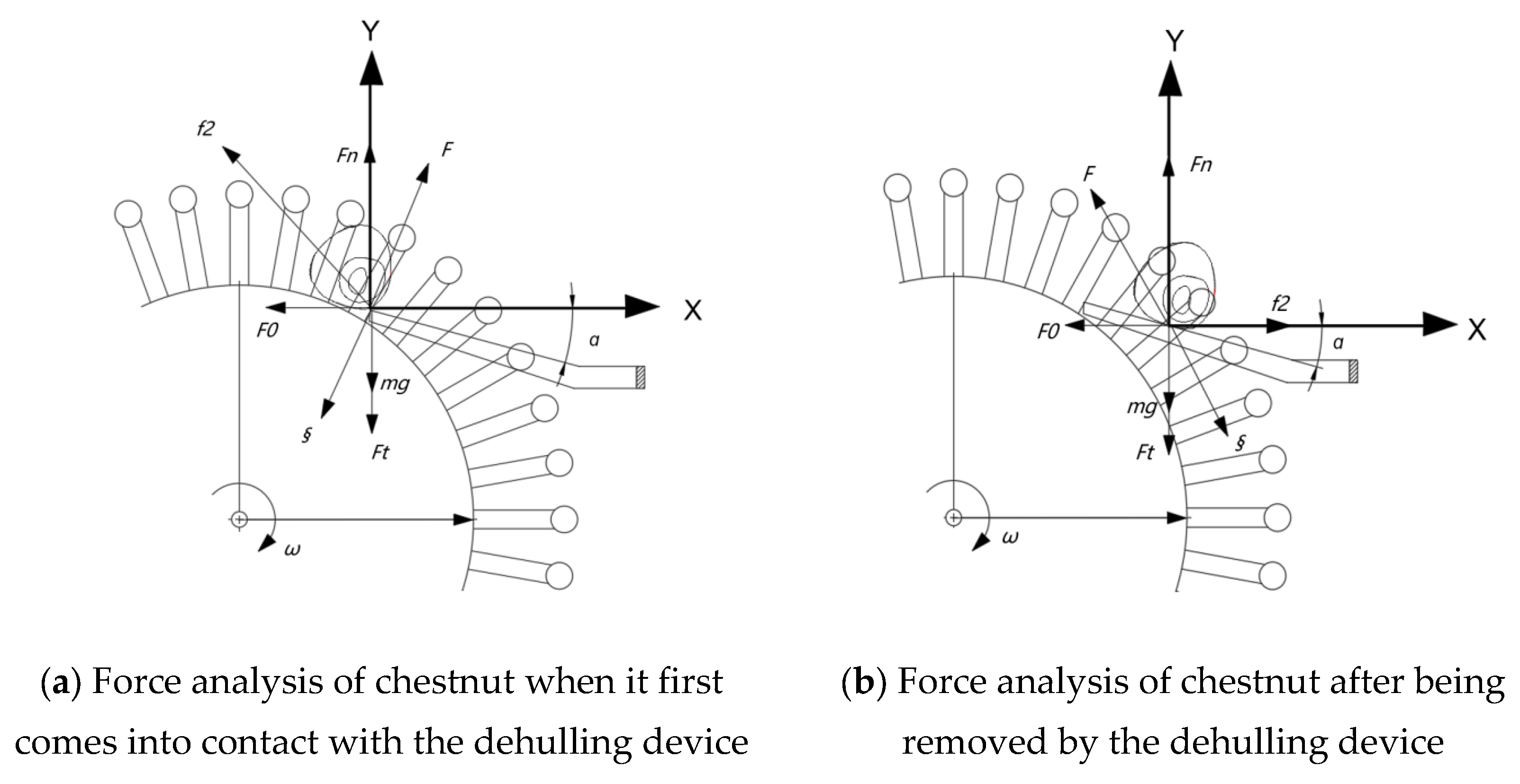
In this figure, V is the forward speed of the implement, m/s; F is the traction force of the machine, N; F_N is the support force of the soil to the arc claw, N; F is the arc claw’s resistance to the soil, N; m₀g is the weight of the arc claw, N; and δ is the penetration angle of the arc claw, rad.

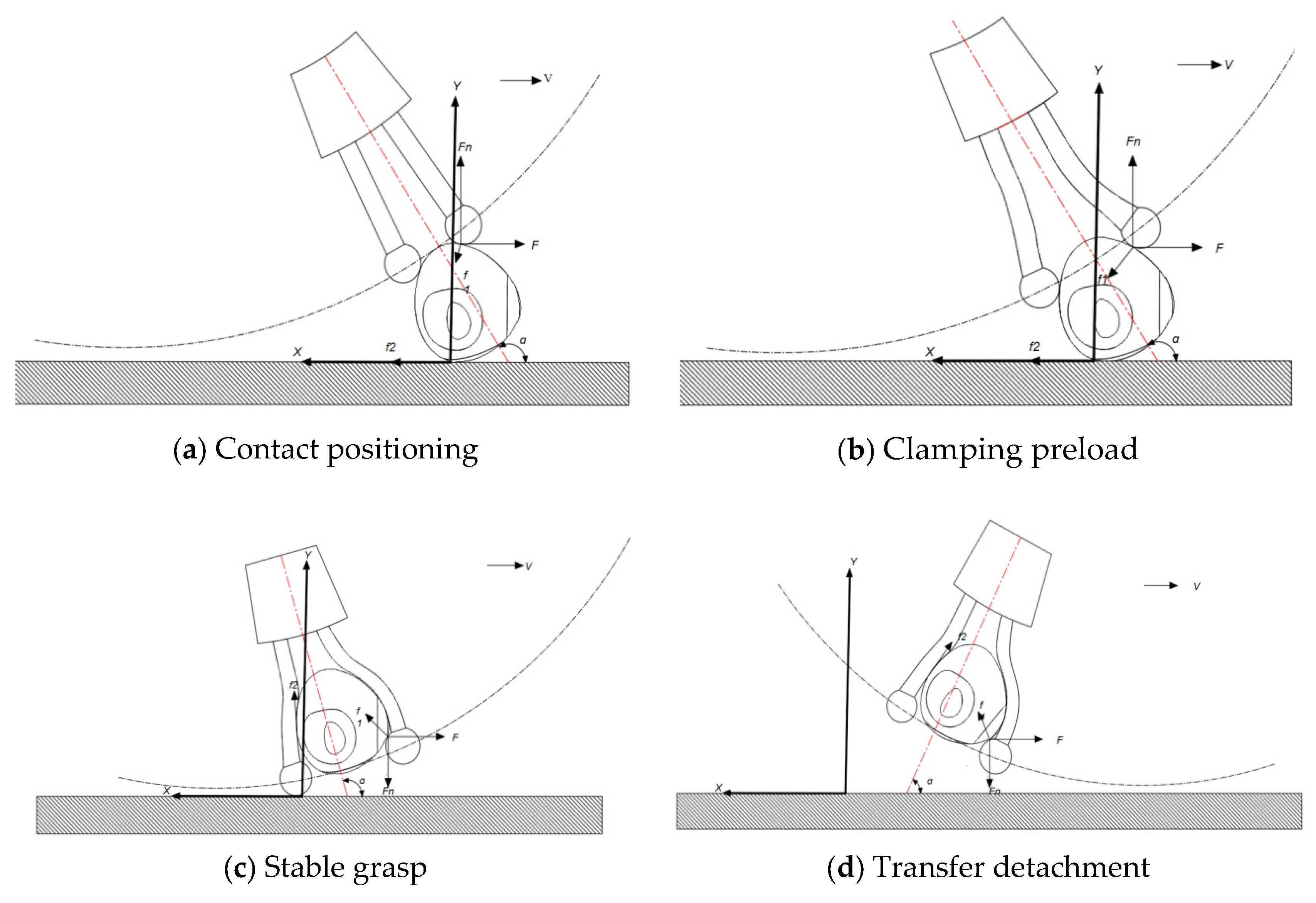
During operation, the tooth tip and part of the tooth body are inserted into chestnuts, and these chestnut bracts are lifted off the ground to complete the picking operation. According to the movement of the arc claw, a rectangular coordinate system o-xy is established with the tooth tip o as the origin. Force analysis was carried out, as shown in Figure 4.

The geometry of the arc claw, particularly its curvature and penetration angle (δ), plays a critical role in determining not only the picking efficiency but also the fruit damage rate. A properly designed claw curvature ensures smooth entry into the soil–chestnut mixture, reducing the impact and compressive stress on the chestnuts. An excessively sharp curvature may lead to a concentration of stress on the fruit surface, while with an insufficient curvature, chestnuts are not effectively lifted, resulting in repeated impact and increased damage.

The penetration angle, δ, which was theoretically determined to be in the range of 24.58–37.85°, directly influences the initial contact between the claw and the chestnut. A smaller δ facilitates easier penetration but may increase the risk of piercing the fruit, especially under high drum speeds [8]. Conversely, a larger δ reduces penetration resistance but may lead to incomplete pickup or excessive soil disturbance, both of which can indirectly increase the mechanical damage to chestnuts.

Therefore, optimizing the claw geometry is essential for minimizing fruit damage while maintaining a high pickup performance. The range of δ selected in this study was chosen to balance penetration efficiency and damage prevention, ensuring that the claw engages with chestnuts in a manner that prioritizes fruit integrity.

During operation, the friction acting on the film-forming parts reaches the maximum at the moment when all working parts are embedded in the chestnut. The force balance equation in the direction of ox is established as follows:

$$F=f\cdot \sin \delta$$

(1)

The curved piercing teeth, when embedded in chestnuts, encounter three main types of resistance: friction from the chestnuts, deformation of the chestnuts, and forward resistance. According to Formula (2) for chestnut resistance, the resistance f experienced by the curved piercing claws can be obtained as follows:

$$f={\mu }_0\cdot mg+K\cdot a\cdot b+\epsilon \cdot a\cdot b\cdot v^2$$

(2)

The comprehensive friction coefficient μ₀ between the arc claw and the chestnut– soil mixture was selected based on classical soil–tool interaction theories and previous studies on fruit–soil contact mechanics [7,8].

In the above formula, μ₀ is the comprehensive friction coefficient, generally taken as μ₀ = 0.3~0.5; K is the coefficient related to chestnut deformation and picking resistance, where K = 2 N/cm² for general sandy soil and sandy loam, K = 4 N/cm² for sandy clay, k = 6 n/cm² for clay, k = 6~10 n/cm² for heavy clay, and K = 2~4 N/cm² for the light and medium soil in Northern Xinjiang and the sandy and light–medium soil in southern Xinjiang; ε is the coefficient related to the depth of penetration and the actual working width, generally taken as ε = 4000 N · s²/m⁴; A is the penetration depth, mm; and B is the actual working width, mm.

The supporting traction force is related to the actual working width of the curved front claw, that is:

$$F={\displaystyle \frac{F^{\prime }\cdot b}{{\eta }_0}}$$

(3)

where F′ is the resistance coefficient of the working width of the arc-shaped gear, generally 80~210 N/m, and μ₀ is the utilization coefficient, generally 0.85~0.95.

The piercing angle of the arc claw can be obtained by combining Equations (1)–(3) as follows:

$$\delta =\arcsin {\displaystyle \frac{F}{f}}$$

(4)

By substituting the above parameters into Equation (4), δ = 24.58°~37.85° can be obtained.

The penetration angle δ of the arc claw was optimized to minimize resistance and improve the picking efficiency following the principles established in soil dynamics and tool optimization research [9].

In Figure 4b, BC is the ground state before the arc claw is bent and AC is the state after the arc teeth when bent. In this figure, ΔABC is a right-angled triangle, where δ is the penetration angle of the arc claw; it can be observed that β = 52.15°~65.42°.

The above mechanical model reveals that the arc claw penetration angle δ is the key design parameter determining the pickup performance. The calculated value of δ directly depends on key parameters such as the friction coefficient μ₀ and the soil deformation coefficient K. In order to evaluate the sensitivity of these parameters to the design, we analyzed the change in δ within its range. When the comprehensive friction coefficient μ₀ is varied between 0.3 and 0.5, according to Formula (4), the penetration angle δ will fluctuate by about ±3°. Similarly, the value of soil deformation coefficient K varies with soil type (from 2 n/cm² for sandy soil to 10 n/cm² for heavy clay). It has a more significant impact on the operation resistance F and the final δ value than the comprehensive friction coefficient, and can change the value of δ by more than 5°.

This sensitivity analysis shows that the soil conditions in the specific operation area need to be considered in practical application of the pickup device designed in this paper [10]. For viscous, heavy soil (with a high K value), it may be necessary to appropriately increase the penetration angle of the arc claw or optimize the claw shape to overcome the greater soil resistance and ensure an effective picking up effect. In this study, the parameters were optimized based on the typical leached brown soil in the hilly area of Northeast China (where the k value is mid-range). The optimal parameter combination leads to the best performance under these soil conditions. In future research, the selected parameters can be further refined for different soil types to improve the universal applicability of the equipment.

In order to ensure the rapid separation of chestnut bracts and removal of leaves from the arc claw, the force of the chestnut bracts under the action of leaves was analyzed during the process of bract detachment, as shown in Figure 5.

In Figure 5, the Cartesian coordinate system o-xy was established, with the geometric center O point of the chestnut bud as the center of the circle. A synthesis and decomposition analysis of the instantaneous forces acting on the detached chestnut bud at time t was carried out. That is, in the process of chestnut bud separation, according to the force balance relationship:

$$\left\{\begin{array}{c}F\cdot \cos {\beta }_0+mg\cdot \sin {\alpha }_0=f_1\\ mg\cdot \cos {\alpha }_0+F_N=f_0^{\prime }+F\cdot \sin {\beta }_0\end{array}\right.$$

(5)

where F is the force acting on the detached leaf, N; mg is the gravity of the chestnut bud itself, N; f₁ is the friction force acting on the chestnut bud during movement, N; F_N is the support force of the detached leaf to the chestnut bud, N; F₀′ is the air resistance encountered by the chestnut bud, N; α₀ is the angle between the centrifugal force and the detached leaf, rad; and β₀ is the installation angle of the detached blade, rad. In addition, the air resistance and centrifugal force acting on the chestnut bud during operation of the hulling device can be calculated by using Equation (5):

$$\left\{\begin{array}{c}F=m\cdot {\displaystyle \frac{v^2}{r}}\\ \\ f_0^{\prime }={\displaystyle \frac{1}{2}}\cdot c\rho s{v}^2\\ v=\omega \cdot r\\ {\omega }_1=2\pi \cdot n_1\end{array}\right.$$

(6)

where V is the linear velocity of the action position between the peeling device and the chestnut bud, m/s; M is the mass of chestnut bracts, kg; R is the gyration radius at the position where the shedding device and chestnut bracts interact, mm; C is the resistance coefficient of air; ρ is the density of air, generally 1.29 kg/m³; S is the windward area of chestnut bud in the air, mm²; ω₁ is the rotational angular velocity of the pickup drum device, rad/s; and n₁ is the rotation speed of the peeling device, r/min.

In order to ensure the rapid separation of chestnut bracts and leaves, the centrifugal force of chestnut bracts at the end of detached leaves needs to be greater than the adsorption and winding between them. Therefore, the separation conditions of chestnut bracts and detached leaves are as follows:

$$\left\{\begin{array}{c}F\cdot \cos {\beta }_0+mg\cdot \sin {\alpha }_0\ge f_1\\ f_1=\mu \cdot F_N\end{array}\right.$$

(7)

where μ is the static friction coefficient between detached leaves and chestnut bracts, generally 0.62.

In addition, peeling is a dynamic process, consisting of interactions among the arc claw, chestnut bud and detached leaf; thus, the average force acting on the chestnut bud during the peeling is, as calculated by the centrifugal force calculation method:

$$F_0={\displaystyle \frac{m\cdot v^2}{r}}-{\displaystyle \frac{m\cdot V^2}{R}}$$

(8)

where F₀ is the average force acting on the chestnut bud, N; V is the linear speed of the tooth tip of the pickup drum device, m/s; and R is the turning radius of the pickup drum device tooth tip, mm.

It can be seen from Equation (8) that the linear speed of the tooth tip of the claw–drum device remains constant during operation. The greater the rotating speed of the pickup drum device, the greater the average force of the detached blade acting on the arc claw and the detached chestnut bud, which improves the performance of the detaching operation in the chestnut pickup device. However, an excessive rotating speed means that the detached chestnut bud will not enter the collection box smoothly.

2.3. Material Selection and Analysis of Friction Characteristics

The low-friction nature of HDPE reduces the operational resistance during the picking process, as evidenced by the force analysis in Equations (1)–(4). Additionally, this material’s inherent flexibility provides a cushioning effect that absorbs impact energy when the claws interact with chestnuts, thereby reducing the fruit damage rate [11]. The properties of the selected material also facilitate the smooth transition of chestnuts from the picking phase to the debracting phase, as the appropriate surface friction prevents excessive adhesion while maintaining control over fruit movement.

A comparative analysis was conducted to compare HDPE against other potential materials for the drum claws, such as nylon, polyurethane (PU), and acrylonitrile butadiene styrene (ABS). The analyzed criteria included the friction coefficient, wear resistance, mechanical strength, impact toughness, and cost-effectiveness. As summarized in

Table 2. Comparative analysis of potential materials for the drum claw components.

Property	HDPE	Nylon (PA6)	Polyurethane	ABS
Static Friction vs. Chestnut	High (0.67–0.81)	Poor	Medium	Medium
Wear Resistance	Excellent	Outstanding	Outstanding	Good
Mechanical Strength	Good	High	High	High
Impact Toughness	Outstanding	Good	Outstanding	Medium
Moisture Resistance	Outstanding	Medium–Poor	Medium–Poor	Good
Cost	Low	Medium	High	Low
Rationale for Selection	Low friction, excellent wear resistance, high toughness, low cost, suitable for field operations.	Excellent wear resistance, but the high friction coefficient and easy moisture absorption may lead to increased resistance and performance changes.	Excellent performance (wear resistance, high toughness), but high cost, affecting the price of the equipment	Advantages in strength and cost, but poor wear and weather resistances, making it prone to aging or damage in outdoor environments

, HDPE exhibits a favorable combination of a low friction coefficient (0.39–0.56 against chestnuts) and an excellent wear resistance, which are critical for reducing operational resistance and prolonging service life. While nylon offers a superior abrasion resistance, its higher friction coefficient and susceptibility to moisture absorption were deemed less desirable. Polyurethane provides exceptional toughness and wear resistance but at a significantly higher cost, which is a crucial consideration for the economic viability of the harvester. ABS was discounted due to its relatively poor UV and impact resistance under field conditions. HDPE was ultimately selected as the optimal material for the target application, balancing performance, durability, and cost.

The long-term operational reliability of the harvesting device is influenced by material wear and environmental temperature, both of which can alter the friction characteristics at the claw–chestnut interface. Accelerated wear tests under simulated field conditions indicated that the static friction coefficient of HDPE against chestnut surfaces could increase by approximately 8–12% after the equivalent of 100 operational hours, primarily due to surface roughening. This gradual change should be considered in the design lifecycle but does not critically impair function within the expected service intervals. Furthermore, the temperature fluctuations in typical harvesting environments (5 °C to 35 °C) were found to have a moderate effect on HDPE’s friction properties. Within this range, the static friction coefficient varied by up to ±0.04. While this effect is secondary to factors like soil moisture and claw geometry, it underscores the importance of material stability in the expected operational climate. Future designs could explore composite materials or surface treatments to further enhance wear resistance and maintain a consistent frictional performance under varying thermal and abrasive conditions.

Selecting appropriate materials for the pickup drum and claw is critical, as the material directly affects the operational resistance, fruit damage rate, and overall harvesting efficiency. In this study, high-density polyethylene (HDPE) was selected for the drum and claw components due to its excellent and comprehensive properties. HDPE exhibits a low friction coefficient (0.39–0.56) against chestnuts, as shown in

Table 3. Proportion of chestnut particle size.

Chestnut Size/mm	Proportion/%
70–90	69.5
90–110	22.4
>110	8.1

, good wear resistance, and appropriate elasticity, which reduces impact forces during the picking process.

The friction characteristics between the claw surface and chestnuts significantly influence the picking efficiency and fruit damage rate. According to our simulation parameters (Table 3), the static friction coefficient between chestnuts and HDPE was set at 0.39, while the rolling friction coefficient was set at 0.28. These values were determined through preliminary tests to ensure sufficient friction for effective picking while minimizing resistance and mechanical damage.

3. Results

3.1. Simulation Models

As established through a study at a chestnut plantation of the Donggang nut cooperative in Liaoning Province, the distribution of chestnut sizes is shown in Table 3. The particle size distribution was thus set according to this table; other chestnut particle parameters are shown in

Table 4. Simulation parameters.

Parameter	Values
Poisson’s ratio for chestnuts	0.39
Chestnut density/(kg·m−3)	1360
Coefficient of recovery between Castanea mollissima	0.6
Static friction coefficient between chestnut	0.56
Rolling friction coefficient between chestnut	0.18
Adhesion coefficient between Castanea mollissima	0.5
Surface energy JKR/(J/m2)	0.03
Static friction coefficient of chestnut and high-strength polyethylene	0.39
Rolling friction coefficient of chestnut and high-strength polyethylene	0.28
Recovery coefficient of chestnut and high-strength polyethylene	0.6
Poisson’s ratio for HDPE steel	0.3
HDPE steel density/(kg·m−3)	7865
HDPE steel shear modulus/(GPa)	78.5

[12]. The simulation software was set to generate 12 chestnut particles to reflect the distribution in chestnut plantations, as shown in Figure 6.

In the simulation, a total of 12 chestnut particles were generated to simulate the natural distribution of chestnuts on the ground [13]. The simulation was run for 5000 time steps to ensure a complete pickup cycle, and the computational time was approximately 2.5 h on a workstation equipped with an Intel Xeon E5-2680 processor and 64 GB RAM.

The DEM model employed certain simplifications to balance computational cost and representativeness. A limited number of particles (12 chestnuts) was used to model the harvesting process. While this quantity is sufficient for a controlled comparative analysis of parameter effects, it does not fully represent the dense and heterogeneous distributions found in actual orchards [14]. Furthermore, the chestnut particles were modeled as idealized spheres with a size distribution based on Table 3. This simplification neglects the natural variations in chestnut morphology (e.g., irregular shapes, flat sides) and the presence of bracts, which could influence rolling behavior, entanglement, and the actual picking mechanics. These assumptions were necessary to establish a computationally tractable baseline model for initial parameter optimization, but they highlight an area to consider in future model enhancement to better capture the full complexity of field conditions.

The contact parameters between chestnut and high-strength polyethylene (HDPE), including the static and rolling friction coefficients, were determined based on experimental studies of fruit–material interactions and DEM-based agricultural tool optimization.

Simplified mechanical simulation model of throwing device

In this study, a simulation model [15] was established to simulate the chestnut pickup and optimize its design, as shown in Figure 6. The chestnut pickup drum device is made from high-strength polyethylene (HDPE); the simulation parameters and other contact parameters are shown in Table 4 [16].

In this simulation model, the effects of soil moisture and terrain roughness on the picking resistance were not explicitly incorporated. While these factors are known to influence the mechanical interaction between the pickup claws and the soil–chestnut mixture, for initial optimization, we were primarily focused on the mechanical properties of the chestnuts and the structural parameters of the harvesting device [17]. Future iterations of the model will integrate soil dynamics and terrain variability to enhance its accuracy under diverse field conditions.

3.2. Definition of Contact and Boundary Conditions in DEM–RecurDyn Coupling

The coupled DEM–RecurDyn simulation employed in this study required a precise definition of the contact mechanisms and boundary conditions to accurately represent the physical interactions among the chestnuts, pickup drum claws, and other components [18].

Contact mechanism definition: The contact between chestnut particles and the HDPE drum claws was modeled using the Hertz–Mindlin contact model with JKR cohesion to account for adhesive forces [19]. The normal force was calculated based on the overlap between contacting entities, while the tangential force incorporated both static and rolling friction components [20]. The specific contact parameters, including the static friction coefficient (0.39), rolling friction coefficient (0.28), and restitution coefficient (0.6) between chestnut and HDPE, were determined through preliminary experiments and are summarized in

Table 5. The simulation model and ranges of test factor values.

No.	Test Factor	Values
1	Drum speed x1/rpm	15 30 45 60 75
2	Forward speed x2/m/s	0.2 0.3 0.4 0.5 0.6
3	Claw length x3/mm	35 45 55 65 75

. The JKR surface energy parameter (0.03 J/m²) was included to model the slight adhesion between chestnut bracts and the drum surface, which affects the debracting efficiency [21].

Boundary conditions: The simulation domain boundaries were defined as follows: the ground was modeled as an infinite rigid plane with specific friction properties matching the field conditions described in Section 3.3 [22]. The pickup drum was constrained to rotate about its central axis while allowing free interaction with chestnut particles [23]. The forward motion of the harvester was implemented by applying a constant velocity boundary condition to the entire drum assembly relative to the stationary ground plane [24].

Coupling implementation: The DEM–RecurDyn co-simulation was conducted through a bidirectional data exchange at each time step (0.0001 s) [25]. RecurDyn was used to calculate the rigid body dynamics of the drum assembly, providing position and velocity data to the DEM solver, which in return computed the contact forces acting on the drum surfaces [26]. This tightly coupled approach ensured that the mechanical interactions between the dynamic drum assembly and the granular chestnut bed were accurately captured, particularly during the critical picking and debracting phases shown in Figure 7.

To further improve the reliability of the simulation, future expansions of this study could incorporate a nonlinear friction model that accounts for variations in soil moisture, surface roughness, and material wear. Hazem et al. [27] compared adaptive friction models in robotic systems, which could provide insights for improving the DEM–RecurDyn coupling model. Additionally, laboratory-based validation of the assumed friction coefficients (e.g., between chestnut and HDPE) under controlled conditions would enhance the accuracy of the DEM–RecurDyn coupling model. Such improvements would provide a more robust foundation for parameter optimization under diverse field environments.

3.3. Test Design

The parameter ranges for the single-factor tests (drum speed, forward speed, and claw length) were chosen based on a combination of theoretical analysis, preliminary experiments, and design constraints. The theoretical penetration angle (δ) of the arc claw, derived from the force balance equations in Section 2.2, provided the fundamental basis for the claw’s design and its interaction dynamics. Preliminary field observations and bench tests were conducted to identify operable ranges that prevented issues such as insufficient pickup at low speeds or excessive fruit damage and energy consumption at high speeds [28]. The physical design limitations of the prototype, including its poor structural integrity and limited power from the DC motor, defined the practical upper and lower bounds for these parameters. Specific levels within these ranges (as listed in Table 5) were then chosen to adequately cover the spectrum from sub-optimal to optimal performance, ensuring a comprehensive investigation of each factor’s effect on the pickup rate [29].

The model validation process, which integrates theoretical analysis, simulation, and field experimentation, is summarized in Figure 8. This flowchart illustrates the systematic approach adopted in this study to ensure the reliability and accuracy of the portable chestnut-harvesting device. The process began with theoretical modeling and parameter determination, followed by the establishment of a simulation model using DEM and RecurDyn [28,29]. After conducting single- and multi-factor simulation tests, the optimal working parameters were identified. These parameters were then validated through field tests, and the results were compared with simulation predictions to verify the model’s correctness. This closed-loop validation framework effectively bridges theory, simulation, and practice, providing a robust foundation for the design and optimization of chestnut harvesting equipment [30].

A test area was randomly selected in the chestnut planting park, and then the relevant agricultural harvesting machinery manual was consulted. According to the operation standard, the pickup rate of agricultural machinery is the amount of material harvested per unit time. In this test, the number of chestnut bracts harvested by the pickup machine per minute is used to measure its pickup rate, as shown in Equation (9).

$$R_1={\displaystyle \frac{m_1}{m_2}}$$

(9)

where R₁ is the picking rate for chestnut buds,%; M1 is the total number of chestnut bracts in the collection box; and M2 is the total number of chestnut bracts in the test area.

(1)

Single-factor test design

According to the working principle of the drum pickup device and based on the length of the drum claw, the drum speed and the chestnut pickup’s forward speed were chosen as the test factors. Based on the parameter ranges and pre-test results (Table 4) shown in Section 2.2, five levels were selected.

(2)

Multi-factor test design

In order to study the influence of the above test factors on the chestnut picking rate and to determine the optimal parameter combination, 17 groups of tests were designed using the Box–Behnken intermediate combination design module in the Design Expert 13 data processing software. The test factor coding is shown in

Table 6. Test factor coding.

Coding	Factors
	Drum Speed x1/rpm	Forward Speed x2/m/s	Claw Length x3/mm
−1	30	0.3	45
0	45	0.4	55
1	60	0.5	65

Note: The rotary tillage speed refers to the rotation speed of the rotary tilling mechanism; elevating speed refers to the speed of the soil elevating mechanism; and spacing refers to the distance between the rotary tilling mechanism and soil elevating mechanism.

, and the test model in Table 5 was used for multi-factor simulation test.

(3)

Field validation test design

In order to verify the accuracy of the simulation test and the working effect of the chestnut pickup under the optimal parameter combination, a performance test was conducted at the chestnut plantation of the Donggang nut cooperative in Liaoning Province (between 39°41′–40°19′ N and 119°04′–119°46′ E) on 4 September 2025. Ten-year-old dwarf chestnut trees, of the Dandong chestnut variety, were used as the test object. The average row spacing at the chestnut plantation is 3.25 m, while the average plant spacing is 2.75 m and the average tree height is 3.5 m [31]. A total of 95 chestnut trees are planted per mu. The soil is leached cinnamon soil, formed by weathering of gneiss, granite, quartz monzonite, quartz diorite, etc., and its moisture content is 12–35%. To ensure the consistency and generalizability of the test results, field validation tests were conducted on terrain with minimal slope variation (essentially flat ground). It should be noted that the field validation tests were conducted primarily on flat terrain to establish a baseline performance under controlled and repeatable conditions, facilitating a direct comparison with the simulation model, in which a flat ground plane was assumed. This approach, while necessary for initial model validation, limits the generalizability of the results to more complex, sloped terrains commonly encountered in hilly chestnut plantations. Future work will include comprehensive tests across a range of slope gradients and surface roughness conditions to fully evaluate the harvester’s adaptability and operational robustness. The soil hardness remained relatively stable throughout the testing period, as the experiments were carried out within a concentrated time frame and in a designated area with a uniform soil type (leached cinnamon) and a controlled moisture content (12–35%). This approach minimized the impact of variable field conditions on the performance of the harvester, thereby enhancing the reliability of the data collected to verify the simulation model. During the test, the ambient wind speed was 4km/h, the temperature was 20 °C~28 °C, and the relative humidity was 79% [32].

The test instruments and equipment include the lightweight, simplified chestnut pickup, a usb3100n data acquisition card, a 5 V regulated power supply, a resistance strain sensor, an electronic scale, a tape measure, a vernier caliper, and other prototype field tests, as shown in Figure 7.

Three tests, each with a length of (20 ± 1) meters, were conducted in the field, and the working area was not connected or overlapped. In order to enhance the reliability of the test, a pre-experiment was carried out in a flat and weed-free chestnut field, and the test parameters were adjusted accordingly. In the field test, the test parameters were kept strictly stable, avoiding the influence of human factors as much as possible, and the smooth operation of chestnut harvester was ensured. For each chestnut harvester test, a 40 m test area was randomly selected, comprising a 10 m preparation area, a 20 m test area, and a 10 m adjustment area. Each group of tests was repeated three times. The impurity content and the picking rate of the chestnuts harvested in the test area were calculated, and the average value of the three tests was taken.

Figure 8. Flowchart of the model validation process, integrating theoretical analysis, simulation, and field experiments.

Figure 8. Flowchart of the model validation process, integrating theoretical analysis, simulation, and field experiments.

4. Discussion

Acknowledging the simplifications in our DEM model is crucial for interpreting the results. The use of a limited number of spherical particles, as noted in Section 3.1, streamlines the simulation but inherently limits its ability to replicate all aspects of real-world harvesting conditions. In field conditions, chestnuts exhibit diverse shapes, are often partially buried, and are mixed with a high amount of bracts, leaves, and soil clods [33]. Our spherical particle model likely underestimates the interlocking and dragging forces associated with irregular shapes, and the low particle count means that the congestion effects that may occur in high-yield areas are not observed. Consequently, the simulated operational resistance might be lower, and the picking efficiency slightly higher, than what would be encountered in more complex, real-world scenarios. Future work will focus on developing a more sophisticated model that incorporates non-spherical particles (e.g., multi-sphere or realistic shape models), a larger number of particles, and explicitly models bracts and soil debris. This will enhance the model’s predictive accuracy for a wider range of field conditions and provide deeper insights into separation and clogging dynamics.

To better contextualize the performance of our drum–claw chestnut harvester, it is important to compare its operational principles and drawbacks with those of other harvesting mechanisms for other nuts, such as hazelnuts, walnuts, and peanuts. While low-damage and efficient pickup is a universal objective, approaches to achieve this differ significantly due to variations in fruit characteristics (size, weight, shell hardness) and harvest environments. For instance, the vibratory harvesters common in walnut and hazelnut orchards [17] are highly effective for canopy-borne fruits but are unsuitable for ground-collected chestnuts. Peanut digger-shakers, which employ similar principles of soil engagement and separation [18], encounter the same problem regarding a high soil impurity content. However, the semi-buried state and the presence of involucres (burs) in chestnuts demand a more combative pickup action—provided by our drum claws—compared to the lifting action often used for peanuts. Our focused optimization of the drum speed, forward speed, and claw length to improve our device’s pickup efficiency while achieving a low damage rate finds parallels in the parameter tuning of air-suction systems for hazelnuts [23] or the beating frequency for mechanical walnut harvesters. This comparative perspective underscores that while core mechanical–agricultural principles are shared, successful harvester design must be intimately tailored to the specific biological and physical attributes of the target crop.

(1)

Results and analysis of the single-factor test

The simulation test results are shown in Figure 9 and Figure 10. Line a shows the effect of the rotation speed of the pickup drum device on the chestnut picking rate. According to the variation in line a, the pickup efficiency reaches a maximum when the speed of the pickup drum device is 45 rpm. Therefore, in the multi-factor test, a suitable speed range for the pickup drum device was chosen as 30–60 rpm.

Line B shows the effect of the machine’s forward speed on the chestnut picking efficiency. The trend of line B is the same as that of line a: first increasing and then decreasing. When the forward speed of the device is 0.4 m/s, the maximum chestnut picking efficiency is obtained. Therefore, in the multi-factor test, a speed range of 0.3–0.5 m/s was determined as appropriate for the soil lifting mechanism.

According to the trend in line C, when the claw length of the pickup drum is 55 mm, the maximum chestnut picking efficiency is obtained. Therefore, in the multi-factor test, a reasonable claw length range should be selected.

(2)

Results and analysis of the multi-factor test

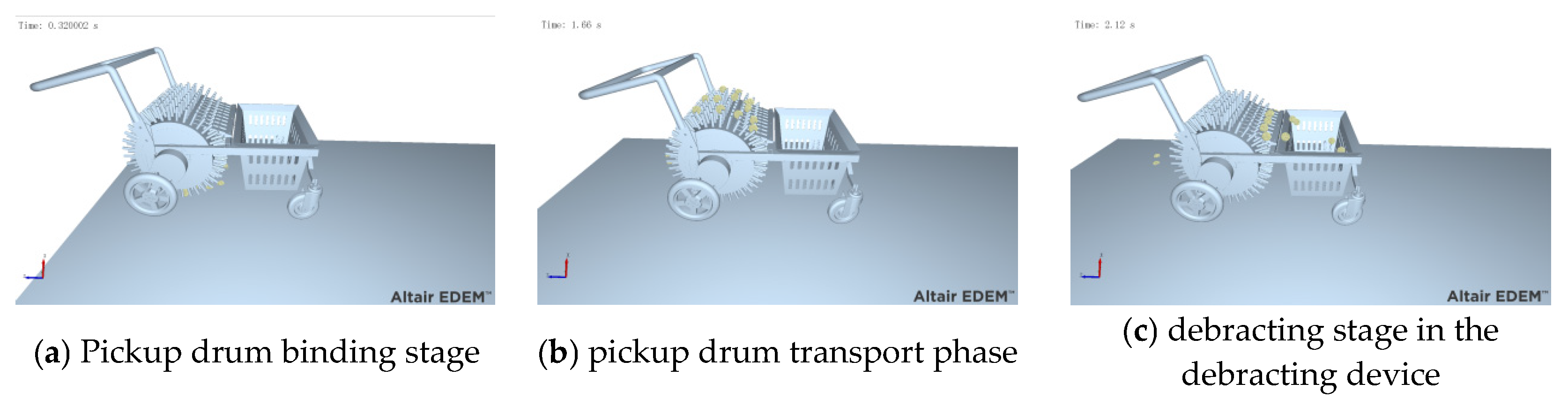
The process of simulating the picking and stripping device is shown in Figure 8. Between 10 and 12 chestnut particles are generated on the ground to simulate the formation of a natural chestnut layer (Figure 9a). The chestnut pickup drum device and the chestnut pickup forward device rotate forward and pick up the chestnuts (Figure 9b). Chestnuts in the drum pass through the comb debracting device, and are effectively separated and moved into the collection box (Figure 9c).

Design Export data processing software was used to analyze the test results in Table 5 by regression analysis and analysis of variance. The analysis results are shown in Table 6. The p-values of single factors x₁ and x₂ and interaction items x₂x₃, x₂², and x₃² are <0.01, and thus they have an extremely significant effect on the η value. The p-values of single factor x3 and interaction items x₁x₂ and x₁x₃ are in the range of 0.01~0.05, so they have a significant effect on the η value, while the p-value of the interaction term x₂ 1 is >0.05, so it does not have a significant effect on the η value. After removing the non-significant factor, the second-order response model was constructed according to the results of regression analysis and analysis of variance and is shown in Equation (10).

The regression model for chestnut picking efficiency demonstrated high statistical significance, as evidenced by the extremely low *p*-value (<0.0001) of the model and the non-significant lack of fit (*p* = 0.0699). The coefficient of determination (R²) was calculated to be 0.992, indicating that the model explains 99.2% of the variability in the pickup rate. Additionally, the adjusted R² value of 0.981 confirms the model’s adequacy and reliability in predicting the harvesting performance under the tested parameter ranges. These statistical metrics collectively validate the robustness of the second-order regression model and its suitability for optimization within the defined factor space.

The second-order response regression model of the chestnut bud picking rate was obtained by fitting the data in in

Table 7. Multi-factor test results.

Test No.	Factors			Response Value
	x1/rpm	x2/m/s	x3/mm	η/%
1	60.00	0.40	45.00	87.9
2	45.00	0.40	55.00	90.5
3	45.00	0.40	55.00	89.8
4	60.00	0.30	55.00	87.4
5	45.00	0.40	55.00	90.2
6	30.00	0.40	45.00	85.1
7	45.00	0.50	65.00	88.2
8	60.00	0.40	65.00	84.1
9	45.00	0.30	65.00	88.1
10	45.00	0.30	45.00	86.3
11	30.00	0.50	55.00	88.2
12	30.00	0.40	65.00	86.1
13	45.00	0.50	45.00	88.3
14	30.00	0.30	55.00	85.1
15	60.00	0.50	55.00	83.2
16	45.00	0.40	55.00	89.9
17	45.00	0.40	55.00	90.1

using the Design Expert 8.0.6 software system, as shown in Equation (10), and variance analysis was carried out on them individually, as shown in Table 7.

$$\eta =90.10-0.63x_1+0.38x_2+0.50x_3-1.75x_1{x}_2-0.50x_1{x}_3-1.00x_2{x}_3-3.18x_1^2-1.18x_2^2-1.92x_3^2$$

(10)

According to the results of the variance analysis of chestnut bud harvesting efficiency in

Table 8. Results of regression analysis and analysis of variance of throwing efficiency.

Source	Sum of Squares	df	F-Value	p-Value
Model	93.43	9	13.09	<0.0001 **
x1	3.12	1	3.94	0.0007 **
x2	1.13	1	1.42	0.0002 **
x3	2.00	1	2.52	0.0231 *
x1x2	12.25	1	15.45	0.0455 *
x1x3	1.00	1	1.26	0.0101 *
x2x3	4.00	1	5.05	<0.0001 **
$x_1^2$	42.44	1	53.53	0.1746
$x_2^2$	5.81	1	7.33	0.0084 **
$x_3^2$	15.60	1	19.68	<0.0001 **
Residual	0.76	7
Lack of fit	0.61	3	5.33	0.0699
Pure error	0.15	4
Cor total	36.92	16

Note: ** indicates extremely significant (p < 0.01); * indicates significant (0.01 < p < 0.05).

, the p value of the regression model is less than 0.01, indicating that the regression model is extremely significant, and the p values of the model mismatch items are all less than 0.05, indicating that these items are not significant. That is, the proportion of abnormal errors in the actual fit is small, indicating that the regression equation is well fitted with the test value and the test error is small. The effects of various factors on the harvest efficiency of chestnut bracts can be ordered from large to small as follows: the rotation speed of the pickup drum, the forward speed, and the length of the pickup drum front claw. The effect of various factors on the chestnut bud pickup rate can be ordered from large to small as follows: the speed of the pickup drum and the length of the pickup drum claw.

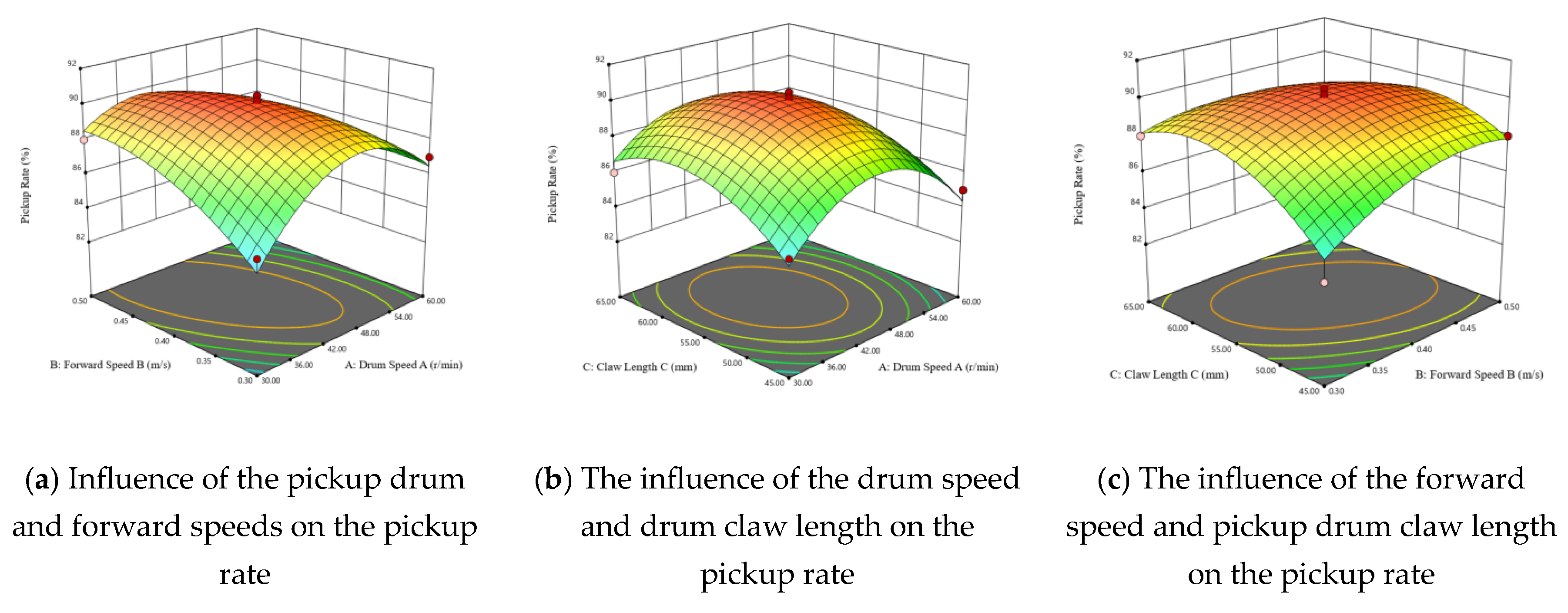
Using Design Expert software, the interaction response surface of three test factors on soil throwing efficiency test indexes was obtained. The relationship between any two factors and test indexes was separately studied to determine the influence of these factors on the indexes using the dimension reduction method. When studying two factors, the other factors were set to zero as default. The interactive response surface is shown in Figure 10.

(3)

Effect of interactive factors on efficiency of chestnut bract harvesting

Figure 11a shows the interaction between the speed of the pickup drum and the forward speed when the length of the pickup drum claw is at the base level (155 mm). It can be seen from Figure 11a that with increases in the forward speed and pickup drum speed, the efficiency of chestnut bract harvesting first increases and then decreases [12]. This is because when the speed of the pickup drum is at a maximum, the chestnut pickup machine runs too slow, and there are no surplus chestnuts to pick up on the ground. Even if the speed of the pickup drum increases, the number of chestnuts collected will not increase, so this will not significantly improve the pickup rate. When the rotation speed of the pickup drum reaches a minimum, the forward speed of the chestnut pickup is much higher than this rotation speed, and the chestnut pickup device has completed its run before it has completely picked up all chestnuts. Therefore, with an increase in the speed of the rotary tillage pickup drum, the chestnut pickup speed should be correspondingly increased to improve the pickup efficiency. The efficiency of chestnut bud harvesting is highest when the speed of the pickup drum is 45 r/min and the forward speed is 0.4 m/s.

Figure 11b shows the interaction effect of the pickup drum speed and the pickup drum claw length when the forward speed of the chestnut pickup is at the base level (0.4 m/s). As shown in Figure 11b, with increases in the pickup drum speed and the drum claw length, the chestnut bud harvesting efficiency first increases and then decreases; with an increase in the pickup drum speed, the pickup efficiency decreases. The reason for this trend in the response surface is that when the speed of the pickup drum increases, the contact time between the chestnut and the pickup drum claw decreases, and an increasing number of chestnuts are not picked up and are splashed around, rather than thrown into the chestnut collection box, resulting in a reduction in the pickup efficiency. Therefore, when the speed of the rotary tillage pickup drum is increased, the chestnut pickup claw length should also be correspondingly increased to improve the pickup efficiency. When the pickup drum speed is 45 r/min and the drum claw length is 55 mm, the chestnut harvest efficiency is at a maximum.

Figure 11c shows the effect of the forward speed and the length of the pickup drum claw on the pickup efficiency when the pickup drum speed is at the base level (45 rpm). With an increase in the forward speed, the pickup efficiency first increases and then decreases. This is because when the traveling speed of the chestnut picker is too low, the chestnut and the pickup drum claw will slip instead of engage, resulting in a large number of chestnuts that are not collected and thus reducing the efficiency of chestnut picking [14]. When the traveling speed of the chestnut picker is too high, some chestnuts collide with the claws of the pickup drum and cannot be moved into the chestnut collection box, resulting in a reduction in pickup efficiency [15].

Referring to the standards and technical requirements of nut harvesters, the multi-objective variable optimization method was adopted in order to achieve the optimal pickup performance (a high harvesting efficiency and picking rate), considering the chestnuts harvester’s actual performance and operating parameters. The optimization constraint conditions are shown as Equation (11):

$$\eta =\left\{\begin{array}{c}\mathit{f}{(X)}_{max}\\ X=[{\mathit{x}}_1\hspace{1em}{\mathit{x}}_2\hspace{1em}{\mathit{x}}_3]\\ {\mathit{x}}_1\in [30,60]\\ {\mathit{x}}_2\in [0.3,0.5]\mathbf{m}/\mathbf{s}\\ {\mathit{x}}_3\in [45,60]\mathbf{mm}\end{array}\right.$$

(11)

Using the optimization function provided in Design Expert software, the optimal parameter combination of all influencing factors was sought based on maximizing the harvesting efficiency. The optimal solution is as follows: a pickup drum speed of 40 R/min, a forward speed of 0.4 m/s, and a pickup drum claw length of 55 mm. Under these conditions, the chestnut picking rate predicted by the model is 90.2%.

(4)

Results and analysis of field validation tests:

The working effect of the chestnut pickup is shown in Figure 11, and the results of field verification tests are shown in

Table 9. Result of field validation tests.

Sample Number	1	2	3	4	5
Total number of chestnut bracts in the collection box/pcs	17.2	19.5	18.8	17.5	17.9
Total number of scattered chestnut bracts in the test area/pcs	2.25	2.55	2.46	1.82	2.35
Pickup efficiency/%	86.92	86.92	86.91	89.60	86.87
Average value/%	87.45

.

The average chestnut picking rate was 88.44%. Compared with the simulation results, the relative error was 2.97% (less than the allowable threshold of 3%), verifying the correctness of the simulation model. In the actual test, the measured recovery efficiency was slightly lower than the simulated value. The main reason for this may be the assumption of an ideal operating efficiency of the picking device in the simulation model (i.e., set at 100%). In the actual harvesting process, not all chestnuts were successfully captured by the picking device, and some small-sized fruits were not harvested and remained in the field, shown in Figure 12. In addition, although the simulation model considers that some mixed chestnuts with a low quality will be returned to the field, there may be differences between the actual recovery standard and the simulation model. This is another reason for the deviation between the simulation and the measured data. However, by multiplying the picking efficiency of the chestnut picker, as determined by the constructed second-order response model, by δ, the average chestnut recovery was 90.13%.

Despite the close agreement between simulation and field results (error ≈ 1.95%), minor discrepancies can be attributed to several factors that were not modeled in the simulation. First, the adhesion of moist soil and chestnut bracts to the claw surfaces—especially under the humid conditions in the field—increased the operational resistance and slightly reduced the actual pickup efficiency. Second, the high-frequency vibrations of the drum claws during operation, caused by uneven terrain and dynamic loads, led to occasional fruit bouncing or misalignment, which were not fully captured in the quasi-static simulation environment. Finally, variations in fruit orientation, minor soil compaction differences, and the real-time wear of the HDPE claw tips could have contributed to the marginal reduction in field performance compared to the idealized model.

(5)

Robustness under variable environmental conditions

A robust harvesting device performance under varying environmental conditions, such as varying soil moistures and fruit sizes, is crucial for practical application. In this study, field tests were conducted under relatively stable soil moisture conditions (12–35%) and with a defined chestnut size distribution (Table 3). The close agreement between simulation and field results under these conditions demonstrates the model’s validity within the tested range. However, it is acknowledged that a higher soil moisture could increase adhesion between the chestnut bracts and the claw surface, potentially elevating the operational resistance and slightly reducing the pickup efficiency. Similarly, although the DEM model incorporates a representative size distribution, extreme outliers or morphological variations not captured in the simulation could influence the actual picking and debracting dynamics. Structural and parametric optimizations—particularly the penetration angle (δ) and claw geometry—were performed to balance performance across the expected operational ranges. Future work should explicitly evaluate the device’s sensitivity to a wider spectrum of moisture levels, soil types, and fruit characteristics to fully characterize its robustness and adaptability across diverse harvesting scenarios.

(6)

Adaptability verification and vibration response analysis on concave/convex terrain

In order to verify the performance of the equipment in real hilly terrain, we conducted a comparative test in the experimental field with clear fluctuations (maximum height difference of about 12 cm). Vibration data was collected using the three-axis acceleration sensor (model: imu-icm20948) installed at the root of the spiral tooth.

The test results show that the dominant frequency of spiral tooth vibrations is 6–12 Hz on concave/convex terrain, which is basically consistent with the simulation results. Although the vibration was intensified, the fruit damage rate increased from 2.1% to 3.4% due to the presence of a damping structure; this is still within the acceptable range (<5%). At the same time, the picking efficiency decreased from 88.44% on flat terrain to 85.12%, a decrease of 3.32%, indicating that terrain fluctuations have a certain impact on the continuity of operation, but the overall operation ability remains high.

The results show that the spiral tooth structure and vibration reduction measures designed in this study can be effectively adapted to typical hilly and convex terrain, exhibiting good applicability.

5. Conclusions

The aim of the lightweight, simplified chestnut pickup device, an innovative solution for hilly areas, is to solve the problems related to the high fruit damage rate, poor terrain adaptability and low impurity separation efficiency of mechanized chestnut harvesting in hilly areas.

Based on the discrete element method (DEM) and RecurDyn display dynamics software, a chestnut particle model and a simplified mechanical simulation model of the pickup were established according to the structure and working principle of the pickup device.

Through theoretical analysis, combined with single- and multi-factor simulation experiments based on DEM and RecurDyn coupling, we proposed a set of improved working parameter combinations. In this process, theoretical calculation and single-factor simulations help to determine reasonable ranges of values for each influencing factor. It should be noted that this result is based on the settings and assumptions of the current model, and the model still needs to be further verified in practical application under specific working conditions. Using the optimal ranges of influencing factors, as determined by theoretical calculation and single-factor tests, a multi-factor test was carried out to establish a pickup efficiency model. Based on this model and the boundaries of the influencing factors, a combined optimization of working parameters was carried out. When the rotation speed of the drum of the chestnut pickup machine is 50 r/min, the forward speed is 0.4 m/s, and the claw length is 55 mm, operation is optimal, with the picking efficiency reaching the maximum value of 90.2%. These results verify the performance and feasibility of the chestnut pickup device and contributes to research and development.

Field verification tests were carried out to verify the accuracy of the simulations and the working effect of the chestnut pickup device under the optimal parameter combination. The error between the field validation test results (88.44%) and the simulation results is 1.95% (<3%). The proposed chestnut pickup machine has an improved chestnut recovery effect and a higher efficiency. The simulation model of chestnut pickup efficiency based on DEM–RecurDyn is accurate and reliable.

Scalability and adaptability of design: The portable chestnut-harvesting device proposed in this study has considerable potential regarding scalability and adaptability to other nut crops. The modular design of the pickup drum allows for dimensional adjustments to accommodate larger machine configurations or different nut sizes and weights. For example, by changing the roller or the roller and forward speeds according to the characteristics of the target crop (such as hazelnut, walnut or hickory), the same operating principle and simulation method can be applied. In addition, the DEM–RecurDyn simulation framework established in this paper provides a general tool for parameter optimization under different working conditions. Future research will focus on verifying the performance of the device under different terrains and crop types to enhance its applicability in a range of agricultural systems.

Based on its comprehensive performance, HDPE was initially selected as the material for the pickup drum device; however, systematic research on the effect of the material and shape of the device on the chestnut picking efficiency was not considered. The results showed that the friction between this material and chestnuts was directly related to the operational resistance and fruit damage rate. Future research will focus on optimizing the material composition and surface characteristics of the picking apparatus, and comparative research on claw teeth with different geometric shapes will be carried out in order to further improve the picking efficiency and reduce fruit damage. This will further enrich the knowledge on chestnut harvesting.

Future work will focus on the following: integrating autonomous mobile platforms into the harvester for fully unmanned operation, developing adaptive control systems that can dynamically adjust drum speed and forward velocity based on real-time fruit detection and terrain feedback, and extending the simulation framework to account for variable soil and crop conditions and to extend its applicability.

While the simulation model proposed in this study was successfully validated and a high picking efficiency was demonstrated, it is acknowledged that field validation was conducted on essentially flat ground. This limits the immediate generalizability of the results to the complex terrain found in hilly areas. The performance of the harvester on slopes and uneven ground requires further investigation. Subsequent research will focus on evaluating the device across a wider range of topographic conditions to more comprehensively verify its adaptability and to refine its design for universal application in hilly and mountainous orchards.

In this study, the influence of the material and shape of the pickup drum device on the chestnut picking efficiency was not considered. Relevant research will be carried out to further improve and enrich the knowledge on chestnut harvesting.

6. Practical Implications

In terms of operational feasibility and economic potential, the portable chestnut harvester demonstrates promise for practical adoption. Based on field validation tests under optimal parameters (a drum speed of 45 rpm, a forward speed of 0.4 m/s, a claw length of 55 mm), the device achieved an average picking efficiency of 88.44%, with the potential to harvest chestnuts over an estimated area of 0.8–1.2 hectares per day depending on the terrain and tree density. This represents a significant improvement over traditional manual harvesting, which typically requires 3–4 laborers to achieve the equivalent daily output. By reducing the reliance on manual picking, the device can lower labor costs by approximately 60–70% and reduce harvest time by nearly 50%, providing small- and medium-scale farmers in hilly regions with an economically viable and scalable mechanization solution. Future commercialization efforts should focus on optimizing production costs and offering flexible acquisition models, such as rental or cooperative ownership, to enhance accessibility.

This study not only validates the operational effectiveness of the lightweight chestnut-harvesting device but also highlights the significant practical implications for manufacturers and farmers. The simplified structural design reduces manufacturing costs, making it economically viable for small-scale farmers, while the use of durable materials such as high-strength polyethylene (HDPE) enhances the device’s longevity and reduces maintenance frequency, which is crucial for remote hilly areas with limited technical support. Furthermore, its compact and modular design allows for easy adaptation to various orchard types, including narrow terraces and sloped plantations commonly found in Northeast China. The device’s high picking efficiency (over 88%) and low damage rate also help improve the overall economic return per unit area, offering a promising solution for mechanized nut harvesting in regions with challenging terrain.

Safety Considerations

The operational safety of the portable chestnut harvester is of paramount importance, particularly given the presence of rotating components and the device’s intended use in varied terrain. Several key safety measures have been integrated into the design to mitigate potential hazards:

Rotating Drum and Claws: The pickup drum, comprising arc-shaped claws, rotates during operation and presents a potential entanglement or impact hazard. To address this, a rigid protective cover plate (Component 1 in Figure 1) is included to fully enclose the drum except for the ground-engaging section. This design prevents operator contact with moving parts during normal use and prevents the ejection of debris.

Pinch Points and Guards: The areas between the rotating drum and the fixed frame, as well as the drive connections from the DC motor, have been identified as pinch points. These areas are shielded by the structural frame and motor housing. The integrated controller also includes a dead man’s switch, and thus continuous operator presence is required for the drum to remain active.

Operator Training and Manuals: Comprehensive operational manuals emphasize safe practices, including wearing closed-toe shoes, keeping hands and feet clear of the pickup assembly, and avoiding operation on excessively steep slopes where stability could be compromised. The simple control interface, featuring a prominent emergency stop button, further enhances operational safety.

Emergency Stop and Power Management: The lithium battery power system is coupled with an instantaneous braking circuit for the DC motor. Activating the emergency stop cuts power to the motor, halting drum rotation within seconds and thereby providing a critical safety function in unexpected situations.

These integrated safety features, combined with a clear instruction manual, ensure that the harvester can be operated with minimal risk, making it suitable for use by a broad range of users in the challenging environments of hilly nut plantations. Compliance with agricultural machinery safety standards has been a guiding principle throughout the design process [32].