Justification of the Design and Operating Parameters of the Improved Disc Grain Crusher

Abstract

The study examines the influence of key structural and technological parameters of a disc crusher with impact plates—the distance between liners, installation angle, and linear movement speed—on the crushing process of maize, wheat, and barley grains. Numerical modeling using the Discrete Element Method (DEM) in Simcenter STAR-CCM+ revealed patterns of variation in breaking force during impact cutting. An integral efficiency criterion was proposed to minimize the breaking force while maximizing productivity and reducing energy consumption. Rational process parameters were determined for each crop, considering their physico-mechanical properties: liner distance l = 1.68–1.79 mm, installation angle β = 21.8–25.3°, particle velocity V = 4.72–5.86 m/s, disc speed n = 1503–1865 rpm, and clearance δ = 0.68–0.79 mm. Experimental studies yielded models describing specific energy consumption, dust-like fraction, and crushing degree depending on the liner angle, number, and rotation speed. Optimization showed that energy consumption was lowest for wheat (3.63 kWh/t) and highest for barley (6.76 kWh/t). The dust fraction was greatest for maize (5.13%) and lowest for barley (1.34%). Optimal grinding regimes were found at n = 1500–1764 rpm, β = 15.9–17.7°, and z = 9 plates. The results confirm the efficiency of adapting crusher parameters to grain properties.

1. Introduction

Despite the widespread use of disc crushers in grain preparation for further processing and compound feed production, there is a lack of universal and practically applicable recommendations for the simultaneous optimization of structural (disc geometry, blade profile, number and arrangement of holes, disc clearance, etc.) and operational (disc angular speeds, feed rate, raw material moisture content, state of working element sharpening) parameters that would ensure the desired product fineness at minimal specific energy consumption and adequate service life of working components. This is due to the fact that the results of individual laboratory and bench studies often reveal significant variability in the “design/operating parameter—milling characteristic” dependencies, which complicates the direct transfer of conclusions to industrial conditions [1,2].

For the preparation of feed components using disc crushers, the most commonly processed grains are wheat, barley, and maize, and occasionally soybeans [3].

A reduction in the clearance between the working surfaces of the disc mill is traditionally associated with an increased degree of grinding, accompanied by higher specific energy consumption: a smaller clearance intensifies particle interaction with the working surface, producing a finer product but requiring more mechanical work per unit mass. This relationship has been confirmed in experimental studies of multi-disc grinding systems, where the configuration and geometry of the discs affect the boundaries of the grinding chamber and energy consumption [4]. The relationship between structural parameters and performance is strongly mediated by the raw material’s condition, particularly moisture content. For wheat grain grinding, experimental results indicate that specific energy consumption and the extraction ratio increased with increasing moisture content, while machine productivity peaked at an optimal moisture level (e.g., 16%) before declining [5]. Furthermore, studies have quantified that specific energy consumption decreased while machine productivity increased when the grinding clearance was increased from 0.1 mm to 0.4 mm, a finding that holds across different grinding disc shapes [5]. These findings underscore the critical nature of multi-factor optimization, especially concerning the interplay between structural settings (clearance) and material properties (moisture).

The rotation speed of the discs is one of the key control parameters. Increasing the rotation speed usually results in finer particle size distribution and higher specific energy consumption, while significantly altering the particle size distribution curve. Both modeling and experimental studies demonstrate a direct relationship between the total increase in angular velocity of the discs and indicators of power, specific energy, and grinding ratio, which makes it possible to predict particle size distribution under given operating regimes [4].

With regard to dust and fine fraction formation, comparative studies of different types of grinders show that the structural features of the equipment (type of grinding mechanism, presence of a classifier, geometry of elements), together with operating factors (speed, clearance, feed rate), determine the share of dust in the product. Some sources indicate that disc mills may generate a wider particle size distribution with an increased fine fraction under certain conditions compared to roller or hammer mills, which requires consideration in terms of sanitary-hygienic and technological requirements [6,7].

A review of the literature shows that although the influence of individual parameters (clearance, rotation speed) and their general trends have been described, most studies have been conducted either on other types of grinders or have analyzed factors individually, without a systematic multifactor approach within a single experimental plan for disc mills. In recent years, the role of disc-type mills in feed-preparation systems has received increased attention. For instance, comparative field and laboratory investigations have shown that disc mills can outperform traditional hammer mills in terms of energy consumption, noise, heat generation and dust formation, owing to their adjustable gap between grinding surfaces and simpler mechanical layout. Specifically, studies have pointed out that the ability to finely adjust the inter-disc clearance enables more precise control of output particle size and a marked reduction in unwanted fines—features which are particularly beneficial when preparing concentrated feeds for animals [8].

Nevertheless, when one examines the existing body of literature, a number of limitations become clear. First, the majority of published works focus on individual operational parameters (such as disc speed or gap width) in isolation, rather than considering their interactions in a full factorial or multifactorial design. This inhibits the development of generalized guidelines applicable across different disc-mill geometries and feed materials. Second, the bulk of research has been conducted on small-scale or laboratory setups, many of which employ simplified disc configurations that differ markedly from industrial-scale machines. Third, although numerical modelling tools such as the Discrete Element Method (DEM) have been applied to simulate crop grinding behaviours, their calibration remains complex and tailored to specific grain shapes, moisture conditions or disc designs, limiting transferability [9].

Consequently, there is a clear gap in the literature with respect to integrated studies that simultaneously assess structural parameters of the grinding elements (for example, disc geometry, blade profiles, perforation patterns) and operational parameters (feed rate, moisture content, rotational speed, wear status) under realistic conditions for concentrated feed production. Addressing this gap is essential for developing practically applicable design- and process-optimization frameworks that ensure target fineness with minimal specific energy use and acceptable component wear life.

Therefore, in this study, we propose a comprehensive experimental approach that simultaneously evaluates the influence of the main design and technological parameters on specific energy consumption, grinding degree, and dust formation. This will make it possible not only to quantify the relationships but also to determine compromise regimes for practical applications [4,7].

A systematic review of recent publications highlights several key directions shaping the scientific problem. First, studies dedicated to the relationship between particle size distribution and energy input demonstrate that the shape of grain-size curves strongly correlates with the power consumption and rotational speed of the discs; however, these models have not yet been sufficiently validated for a wide range of disc mill designs and various types of grain. Such an approach allows predicting the “energy—degree of grinding” relationship, but requires further practical validation [2,10].

Second, experimental studies employing Design of Experiments (DoE) confirm the effectiveness of a multifactor approach in simultaneously optimizing both productivity and energy consumption—yet most of these works focus on specific configurations (rotor–centrifugal, five-disc, etc.) and rarely cover the full space of design parameters (e.g., simultaneous variation of hole number, blade profile, and clearance). This creates methodological limitations for generalizing results to other designs and operating conditions [1,2].

Third, numerical approaches—particularly the use of the Discrete Element Method (DEM) in combination with particle breakage models or CFD/DEM coupling—provide detailed insights into local contact forces, particle kinematics, and energy dissipation pathways during grinding. DEM modeling has already proven useful for calibration and interpretation of experimental observations (e.g., for maize and other grains), yet the requirements for model accuracy (particle clustering, contact model parameters, calibration based on breakage experiments) remain a significant barrier to its widespread application in disc crusher design [11,12,13,14,15,16,17,18,19,20]. Numerical approaches, such as the Discrete Element Method (DEM), are crucial for gaining mechanistic insight into comminution. Recent DEM studies have moved beyond simple particle flow to investigate the performance of specific grinding elements. For example, in studies of maize grinding, DEM simulations were used to compare different hammer designs (cutting-edge and oblique), revealing that a cutting-edge hammer had the highest bond-breaking efficiency in the grain model, while the oblique hammer improved sieving efficiency by altering the grain’s incident angle [12] However, the continued challenge lies in accurately calibrating these models, particularly concerning the accurate representation of complex grain shapes and reliable breakage models, which limits their widespread application in new disc crusher design.

In addition, individual studies comparing different blade profiles and disc configurations have shown a significant influence of working element geometry on the final fraction shape and specific energy consumption: changes in blade angle, radial groove design, or presence of holes can simultaneously reduce the mean particle size while increasing energy use, or vice versa—depending on feed rate and the physical–mechanical properties of the raw material. This confirms the need for multidimensional optimization accounting for inter-factor interactions [1,2,12,21,22,23,24].

Thus, despite significant progress in theoretical modeling (energy-dependent size distribution models) and numerical methods (DEM, CFD/DEM), there remains a gap between modeling and practical engineering methodology: there is a lack of standardized multifactor experimental programs combined with DEM validation and economic evaluation that could yield practically applicable recommendations for designing and tuning disc crushers for different grain types and operating conditions. This mismatch—between scientific findings and industry needs for unified guidelines and optimization criteria—defines the scientific and practical relevance of further research in this field [2,11,13,19,20,25].

Therefore, the current relevant task is the systematic scientific justification of structural and operational parameters of a grain disc crusher using multifactor experiments, numerical modeling, and optimization of the proposed solutions.

The scientific novelty of the study lies in the development of an improved modular disc grain crusher with a multi-zonal working surface and replaceable impact inserts, as well as in the integration of Discrete Element Method (DEM) numerical modeling with multifactor optimization to determine energy-efficient operating regimes for grinding different grain crops.

2. Materials and Methods

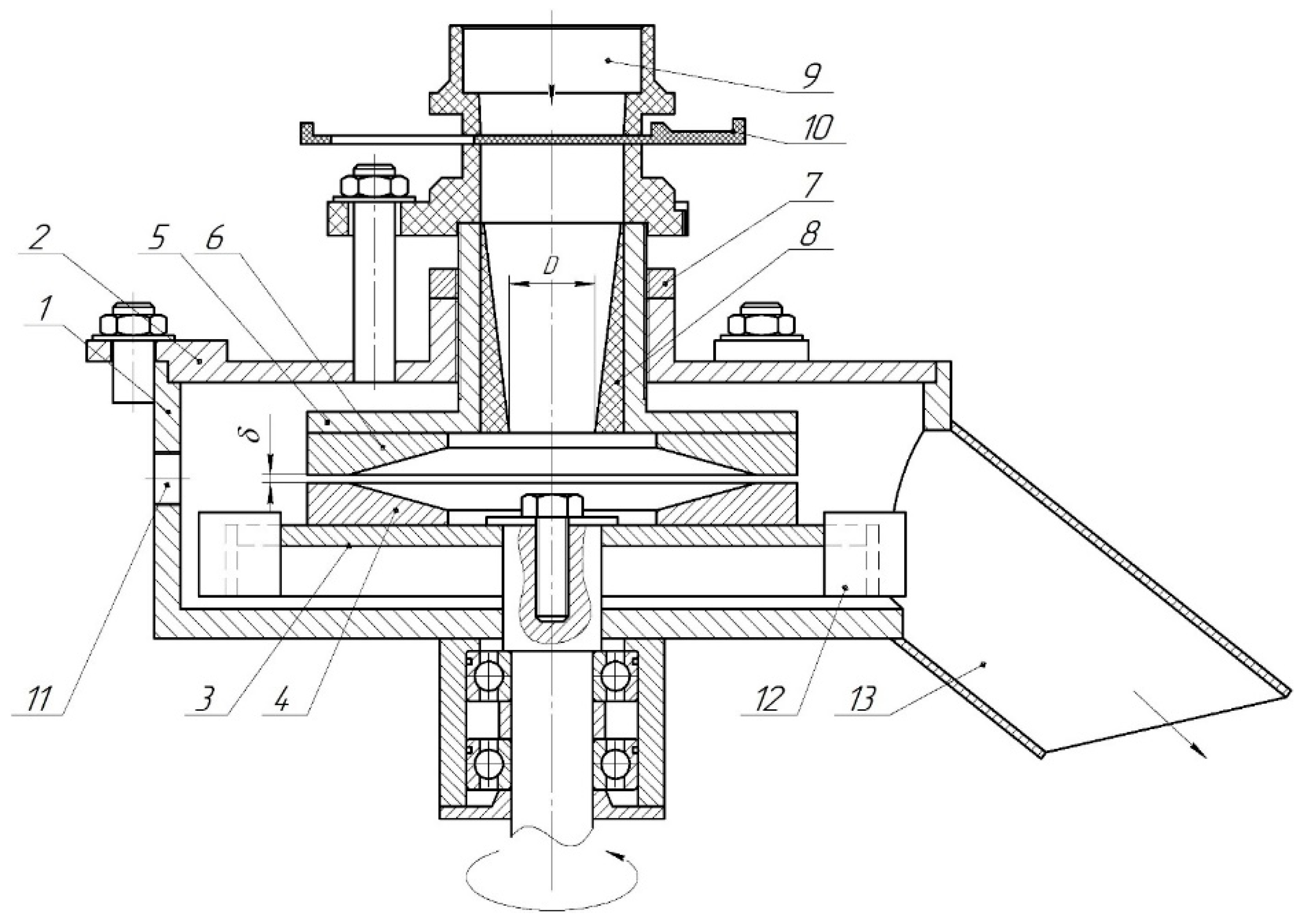
The improved disc crusher (Figure 1) consists of a housing with a cover, inside which the upper stationary disc and the lower rotating disc mounted on a holder are installed. The holder is connected to an electric motor via a coupling. Grain is fed through an inlet pipe and a slide gate, then passes through a calibrated sleeve into the inter-disc space. The clearance between the discs is adjusted by moving the upper disc holder, secured with a locknut, and is checked with feeler gauges through an inspection hole. The crushed product is discharged with the help of blades through an outlet pipe. During operation, grain entering the grinding zone moves toward the periphery under the action of centrifugal forces and undergoes impact, cutting, abrasion, and compression, ensuring uniform load distribution and stable material flow [26].

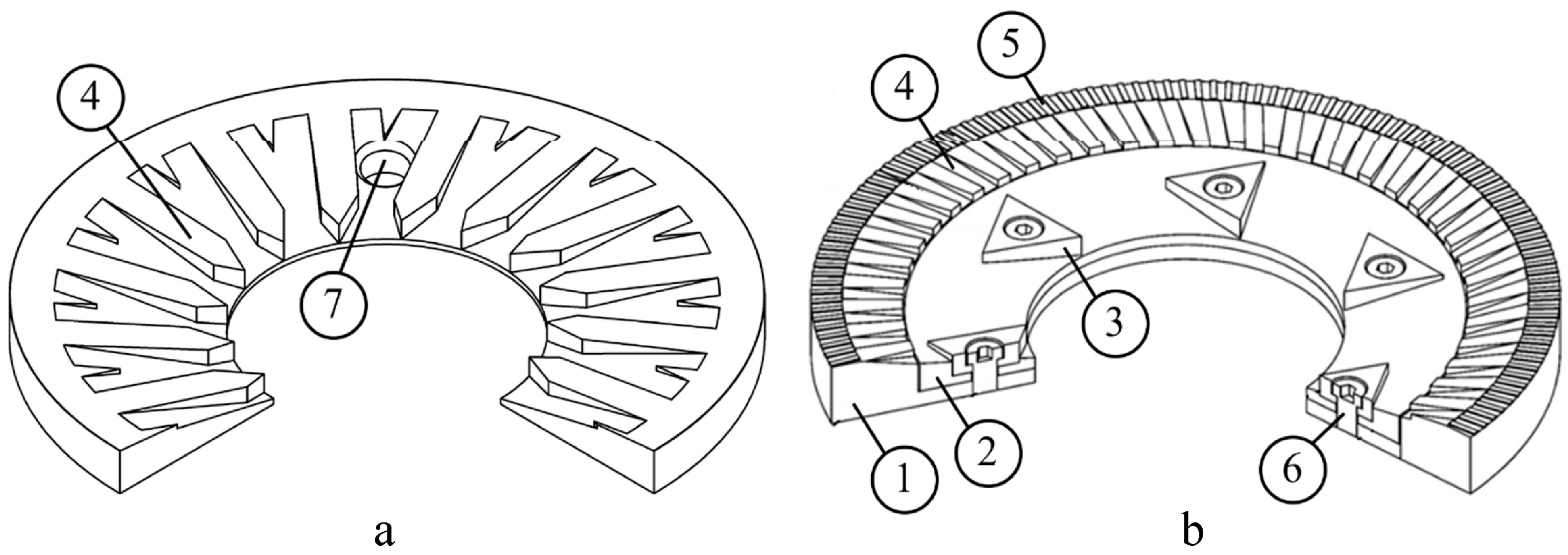
The improved working element of the disc mill (Figure 2a), in contrast to the basic version (Figure 2b), has a modular design that includes a base (1), a replaceable inner cone (2), and multifunctional impact inserts (3). This enables adjustment of the working surface geometry depending on the properties of the processed material and significantly simplifies maintenance and repair.

The key improvement lies in the application of multi-stage zoning of the working surface. The zone with impact inserts ensures intensive preliminary grain breakage through impact and splitting, while the zone with an inclined conical knurling (4) and the zone with a horizontal straight knurling (5) provide the required final particle size through abrasion. Such a combination implements a combined grinding principle that integrates impact, splitting, crushing, and abrasion, ensuring a more stable granulometric composition of the final product.

The numerical simulation of grain fracture under the action of the machine’s working elements was carried out in Simcenter Star-CCM+ using the Discrete Element Method (DEM).

An important structural advantage is the replaceability of individual elements: the inner cone can be easily replaced or modified for specific operating conditions, and the impact inserts have three working surfaces, which allows for multiple use by rotation. This not only reduces operating costs but also extends the service life of the working parts.

Compared to conventional designs, the improved working element provides higher efficiency and grinding quality due to optimized operating regimes.

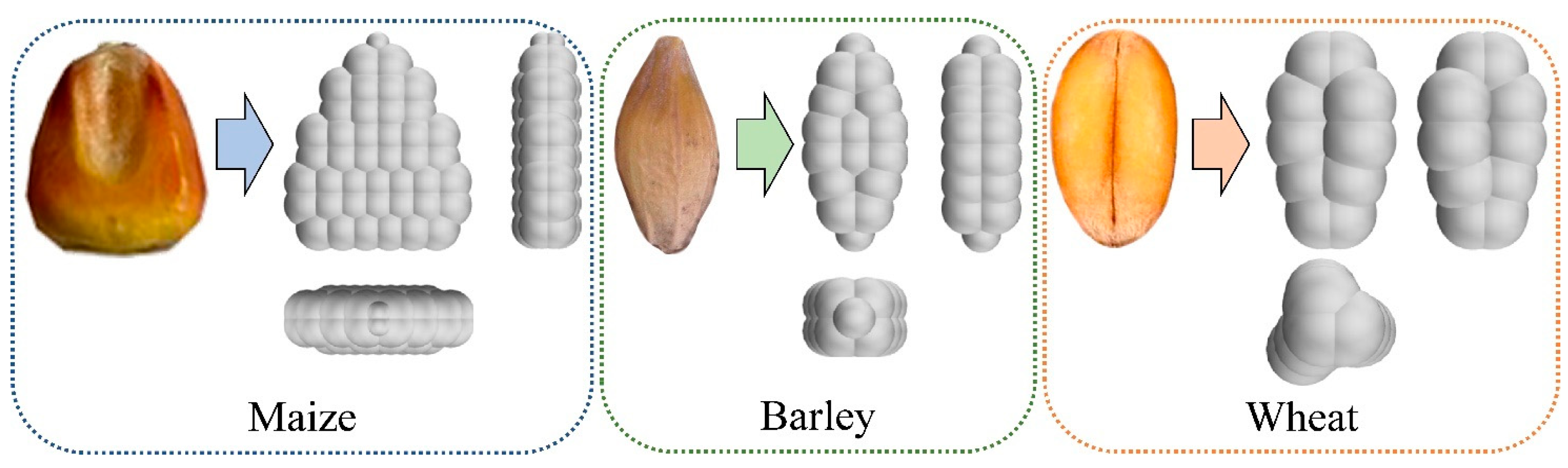
Based on the obtained measurement results and previous experience in modeling biomaterials in the Simcenter STAR-CCM+ environment [27,28,29,30], three-dimensional multispherical models of maize, wheat, and barley kernels were created using the sphere-cluster aggregation method (Figure 3). This approach ensures maximum accuracy in reproducing the grain shape while maintaining optimal computational efficiency for further numerical experiments.

To describe the interaction between model elements, the Hertz–Mindlin contact model was applied. This model allows simulating the elastic–plastic deformation of bodies during local contact. The Hertz–Mindlin contact model is a fundamental component of the physical–mathematical framework of the Discrete Element Method (DEM), enabling the description of interaction forces between two bodies (e.g., a maize kernel and a punch) when contact occurs. It incorporates both normal compression forces (Hertz model) and tangential shear forces (Mindlin model), complemented by dissipative components and Coulomb’s friction criterion. In the case of kernel modeling within Simcenter STAR-CCM+, this model ensures adequate reproduction of the physical processes of elastic compression, shear, and rolling.

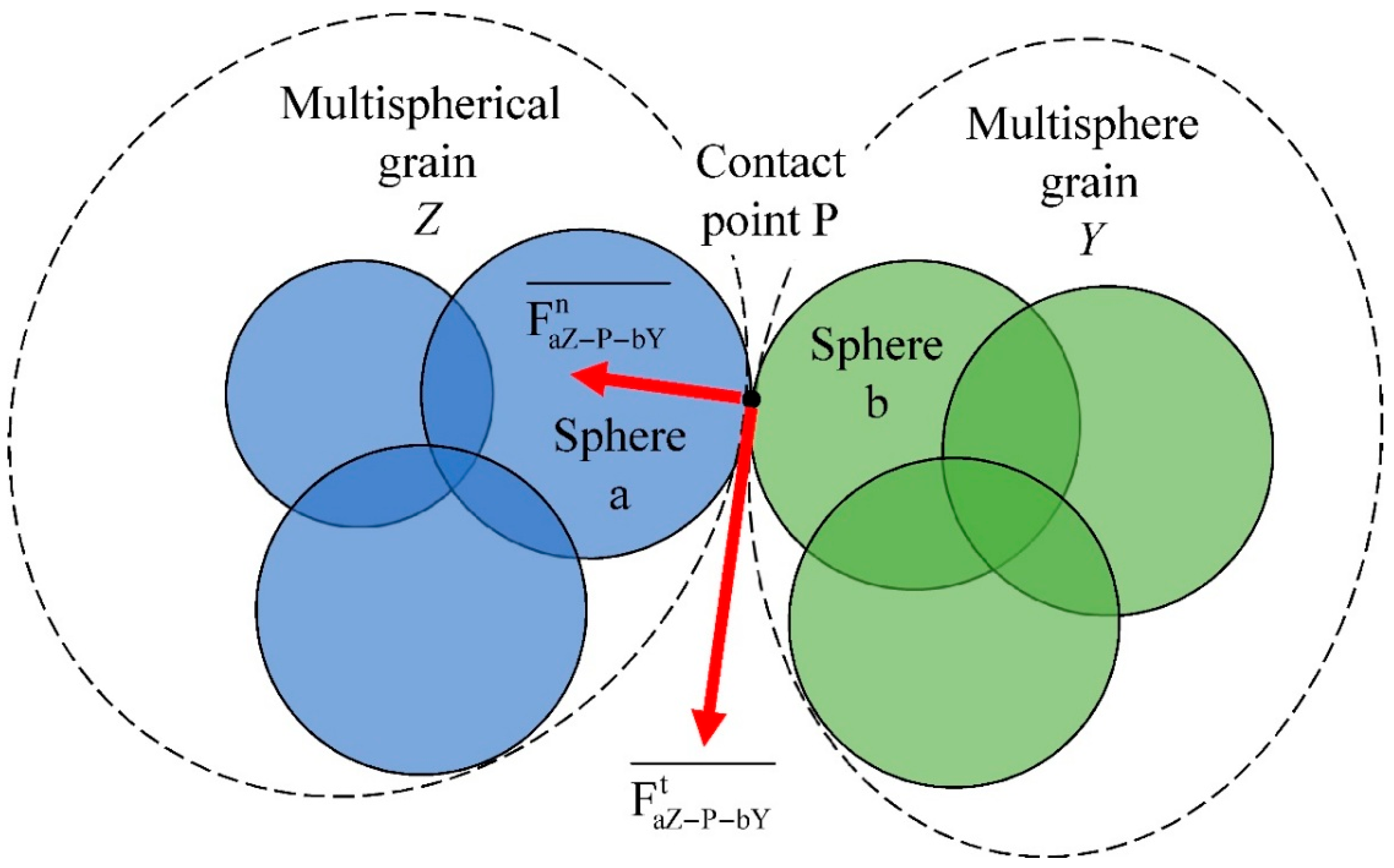
The contact force model for multispherical kernels is shown in Figure 4.

Normal ${\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}$ and tangential ${\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}$ contact interaction forces between sphere a in the multispherical grain Z and sphere b at the contact point P are defined as:

$$\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}=\left({\displaystyle \frac{4}{3}}{\mathrm{E}}^{*}\sqrt{{\mathrm{R}}^{*}}{\mathrm{\delta }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{{\displaystyle \frac{3}{2}}}-2\sqrt{{\displaystyle \frac{5}{6}}}\mathrm{\beta }\sqrt{{\mathrm{S}}_{\mathrm{n}}{\mathrm{m}}^{*}}{\mathrm{\upsilon }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}\right)\overline{{\mathrm{n}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}},$$

(1)

$$\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}}=-\min \left({\mathrm{S}}_{\mathrm{t}}\overline{{\mathrm{\xi }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}+2\sqrt{{\displaystyle \frac{5}{6}}}\mathrm{\beta }\sqrt{{\mathrm{S}}_{\mathrm{t}}{\mathrm{m}}^{*}}\overline{{\mathrm{\upsilon }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}},\hspace{0.33em}{\mathrm{\mu }}_{\mathrm{r}}\left|\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}\right|{\displaystyle \frac{\overline{{\mathrm{\xi }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}}{\left|{\mathrm{\xi }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}\right|}}\right),$$

(2)

where E*—equivalent Young’s modulus, R*—equivalent radius:

$${\displaystyle \frac{1}{{\mathrm{R}}^{*}}}={\displaystyle \frac{1}{{\mathrm{R}}_{\mathrm{a}\mathrm{Z}}}}+{\displaystyle \frac{1}{{\mathrm{R}}_{\mathrm{b}\mathrm{Y}}}},$$

(3)

$${\displaystyle \frac{1}{{\mathrm{E}}^{*}}}={\displaystyle \frac{(1-{\mathrm{\nu }}_{\mathrm{Z}}^2)}{{\mathrm{E}}_{\mathrm{Z}}}}+{\displaystyle \frac{(1-{\mathrm{\nu }}_{\mathrm{Y}}^2)}{{\mathrm{E}}_{\mathrm{Y}}}},$$

(4)

R_aZ, R_bY—radius of each sphere in contact; E_Z, E_Y—Young’s modulus; ν_Z, ν_Y—Poisson’s ratio; δ_aZ-P-bY—normal overlap of sphere a in the multispherical grain Z and sphere b at the contact point P; β—damping coefficient:

$$\mathrm{\beta }={\displaystyle \frac{-\ln \mathrm{e}}{\sqrt{{\ln }^2\mathrm{e}+{\mathrm{\pi }}^2}}},$$

(5)

e—coefficient of restitution; S_n—normal stiffness:

$${\mathrm{S}}_{\mathrm{n}}=2{\mathrm{E}}^{*}\sqrt{{\mathrm{R}}^{*}{\mathrm{\delta }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}},$$

(6)

m*—equivalent mass:

$${\mathrm{m}}^{*}={\left({\displaystyle \frac{1}{{\mathrm{m}}_{\mathrm{a}\mathrm{Z}}}}+{\displaystyle \frac{1}{{\mathrm{m}}_{\mathrm{b}\mathrm{Y}}}}\right)}^{-1},$$

(7)

${\mathrm{\upsilon }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}$—normal component of relative velocity; $\overline{{\mathrm{n}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}$—unit normal contact vector directed from contact point P to the center of partial sphere a in the multispherical grain Z; S_t—tangential stiffness:

$${\mathrm{S}}_{\mathrm{t}}=8{\mathrm{W}}^{*}\sqrt{{\mathrm{R}}^{*}{\mathrm{\delta }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}},$$

(8)

W*—equivalent shear modulus:

$${\mathrm{W}}^{*}={\displaystyle \frac{1}{2\left(2-{\mathrm{\nu }}_{\mathrm{Z}}\right)\left(1+{\mathrm{\nu }}_{\mathrm{Z}}\right)/{\mathrm{E}}_{\mathrm{Z}}+2\left(2-{\mathrm{\nu }}_{\mathrm{Y}}\right)\left(1+{\mathrm{\nu }}_{\mathrm{Y}}\right)/{\mathrm{E}}_{\mathrm{Y}}}},$$

(9)

$\overline{{\mathrm{\xi }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}$—total tangential displacement of partial sphere a in the multispherical grain Z and sphere b at the contact point P; ${\mathrm{\upsilon }}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}$—tangential component of relative velocity; μ_r—coefficient of static friction.

The forces and moments acting on a multispherical particle Z are expressed as:

$$\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}={\displaystyle \sum _{\mathrm{W}}{\displaystyle \sum _{\mathrm{V}}\left(\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}+\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}}\right)}},$$

(10)

$$\overline{{\mathrm{M}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}}={\displaystyle \sum _{\mathrm{W}}{\displaystyle \sum _{\mathrm{V}}\left(\left(\overline{{\mathrm{x}}_{\mathrm{P}}}-\overline{{\mathrm{x}}_{\mathrm{Z}}}\right)\times \overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}}-{\mathrm{\mu }}_{\mathrm{r}}\left|\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}\right|\left|\overline{{\mathrm{x}}_{\mathrm{P}}}-\overline{{\mathrm{x}}_{\mathrm{Z}}}\right|\overline{{\mathrm{\omega }}_{\mathrm{Z}}}\right)}},$$

(11)

where V and W—indices of partial spheres and contact points respectively; $\overline{{\mathrm{x}}_{\mathrm{P}}}$—vector of the contact point P; $\overline{{\mathrm{x}}_{\mathrm{Z}}}$—position vector of the center of particle Z; $\overline{{\mathrm{\omega }}_{\mathrm{Z}}}$—angular velocity vector of the multispherical particle Z.

Particle bonding is used to extend particle models to more complex (deformable) shapes or structures. The agglomerate particle model is employed to create groups of particles representing complex shapes. This model applies a bonded particle approach, where individual particles retain their identity and are connected by elastic deformable bonds. Incorporating a damage model allows simulation of cracking and fragmentation of the agglomerate with the release of constituent particles.

The particle bonding model is used both in the parallel bond model and in the bonded particle (agglomerate) model. In the parallel bond model, particle bonding describes interactions between constituent particles and models elastic collisions according to the user-selected elastic contact model. The bonded particle model relies solely on the particle bonding model.

The particle bonding model simulates cumulative damage to the bonds. If interaction causes damage but not complete failure, the damage level is accounted for by reducing the bond strength. For grain crushing simulation, a simple bond breakage model is adopted where bonds fail instantly under load. If tensile or shear stresses between particles (grain spheres) exceed allowable limits, the bond breaks, and particles separate. Subsequently, particle interactions during collision are governed by other selected interphase interaction models.

A bond between particles (grain spheres) breaks if the tensile or shear stress in it exceeds one of the user-defined threshold values.

The bond breaks if:

$${\mathrm{W}}_{\mathrm{n}-\mathrm{m}}>{\mathrm{W}}_{\mathrm{n}-\max }\mathrm{or} {\mathrm{W}}_{\mathrm{t}-\mathrm{m}}>{\mathrm{W}}_{\mathrm{t}-\max },$$

(12)

where W_n-max—is the maximum tensile stress allowed without bond failure; W_t-max—is the maximum shear stress allowed without bond failure. For further calculations, it is assumed that W_n-max = W_t-max =W.

The limiting stress values are calculated based on beam theory as follows:

$${\mathrm{W}}_{\mathrm{n}-\mathrm{m}}=-\left|\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}\right|/{\mathrm{A}}^{*}+\left|\left(\overline{{\mathrm{x}}_{\mathrm{P}}}-\overline{{\mathrm{x}}_{\mathrm{Z}}}\right)\times \overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}}\right|{\mathrm{R}}^{*}/{\mathrm{I}}^{*}$$

(13)

$${\mathrm{W}}_{\mathrm{t}-\mathrm{m}}=\left|\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{t}}}\right|/{\mathrm{A}}^{*}+\left|{\mathrm{\mu }}_{\mathrm{r}}\left|\overline{{\mathrm{F}}_{\mathrm{a}\mathrm{Z}-\mathrm{P}-\mathrm{b}\mathrm{Y}}^{\mathrm{n}}}\right|\left|\overline{{\mathrm{x}}_{\mathrm{P}}}-\overline{{\mathrm{x}}_{\mathrm{Z}}}\right|\overline{{\mathrm{\omega }}_{\mathrm{Z}}}\right|{\mathrm{R}}^{*}/{\mathrm{J}}^{*}$$

(14)

where ${\mathrm{A}}^{*}=\mathrm{\pi }{\left({\mathrm{R}}^{*}\right)}^2$, ${\mathrm{I}}^{*}=\mathrm{\pi }{\left({\mathrm{R}}^{*}\right)}^4/4$, ${\mathrm{J}}^{*}=\mathrm{\pi }{\left({\mathrm{R}}^{*}\right)}^4/2$.

The selection of threshold stress values was based on experimentally determined physico-mechanical properties of the grains, in particular, the ultimate tensile and shear stresses identified for maize, wheat, and barley (see

Table 1. DEM simulation parameters.

Materials/Interaction	Parameters	Values
Maize	Poisson’s ratio	0.48
	Young’s modulus, MPa	10.1
	Particle density, kg/m3	1300
	Coefficient of restitution (particle–particle collision)	0.37
	Coefficient of static friction (particle–particle)	0.23
	Tensile strength, MPa	2.4
	Shear strength, MPa	2.4
Wheat	Poisson’s ratio	0.5
	Young’s modulus, MPa	21.2
	Particle density, kg/m3	1320
	Coefficient of restitution (particle–particle collision)	0.32
	Coefficient of static friction (particle–particle)	0.26
	Tensile strength, MPa	2.2
	Shear strength, MPa	2.2
Barley	Poisson’s ratio	0.32
	Young’s modulus, MPa	39.2
	Particle density, kg/m3	1250
	Coefficient of restitution (particle–particle collision)	0.35
	Coefficient of static friction (particle–particle)	0.26
	Tensile strength, MPa	3.1
	Shear strength, MPa	3.1
Wall (steel)	Poisson’s ratio	0.3
	Shear modulus, Pa	7.9 × 1010
	Density, kg/m3	7800
Maize–wall (steel)	Coefficient of restitution	0.5
	Coefficient of static friction	0.48
	Rolling friction coefficient	0.05
Wheat–wall (steel)	Coefficient of restitution	0.4
	Coefficient of static friction	0.554
	Rolling friction coefficient	0.05
Barley–wall (steel)	Coefficient of restitution	0.4
	Coefficient of static friction	0.51
	Rolling friction coefficient	0.05

). This approach ensures adequate reproduction of grain fracture in the DEM model in accordance with the actual mechanical properties of the material. Thus, bond breakage occurs only when critical stress values are reached, while subsequent particle interactions during collisions are modeled according to the selected interfacial interaction models. Consequently, the chosen fracture threshold has an experimental basis and provides physically reliable modeling of the grain grinding process.

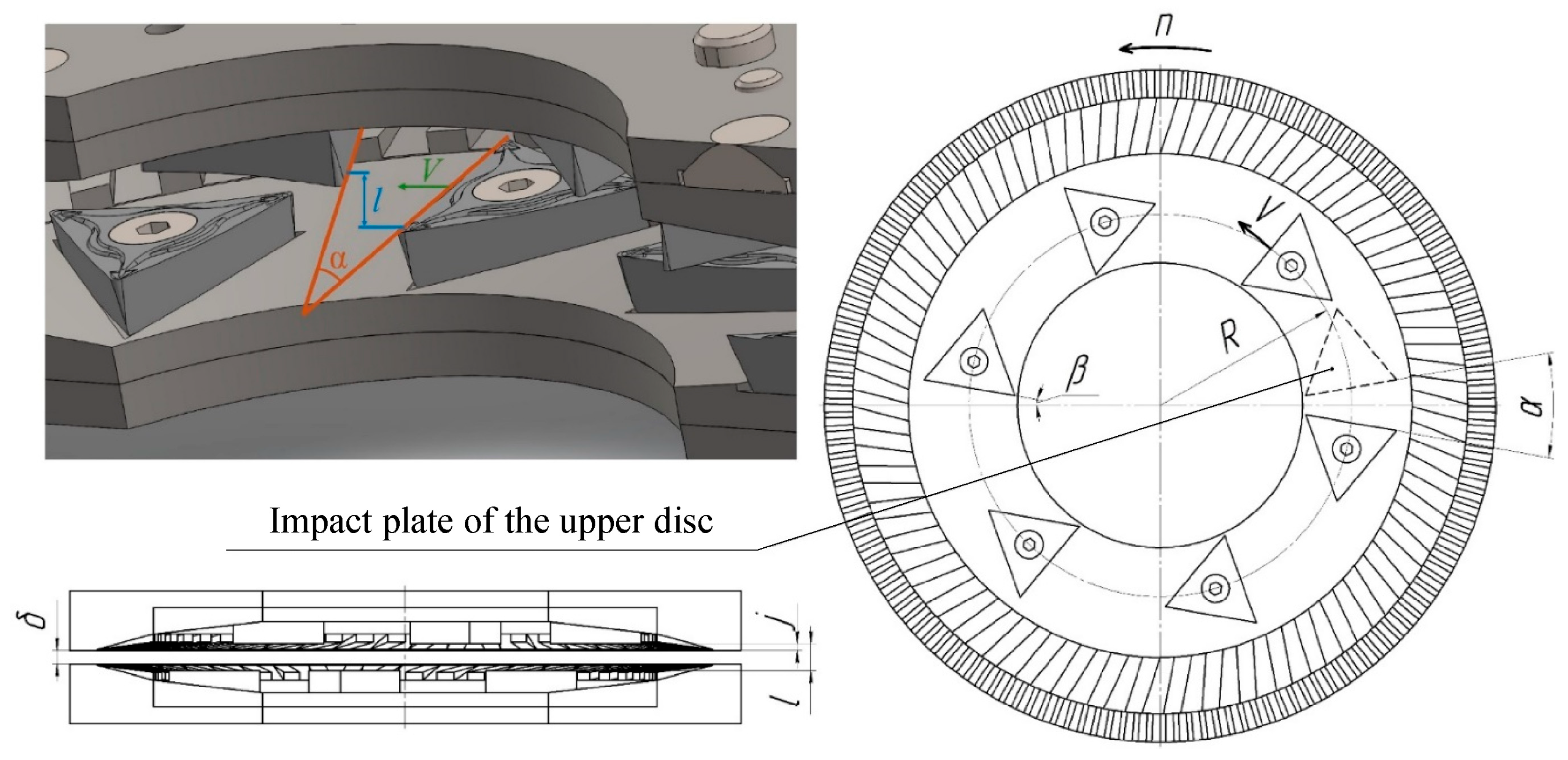
Considering the specific design configuration of the proposed improved working element of the disc grinder, it became necessary to investigate the influence of impact pads on the grain breaking force during impact cutting. For this purpose, three varied factors were selected within the numerical experiment, which most comprehensively characterize the kinematics and geometry of the interaction between the grain and the impact elements of the improved disc grinder (Figure 5): the distance between impact pads l (1–2 mm); the angle between the pads α (10–60°); and the linear velocity of the pad movement V (4.72–9.42 m/s).

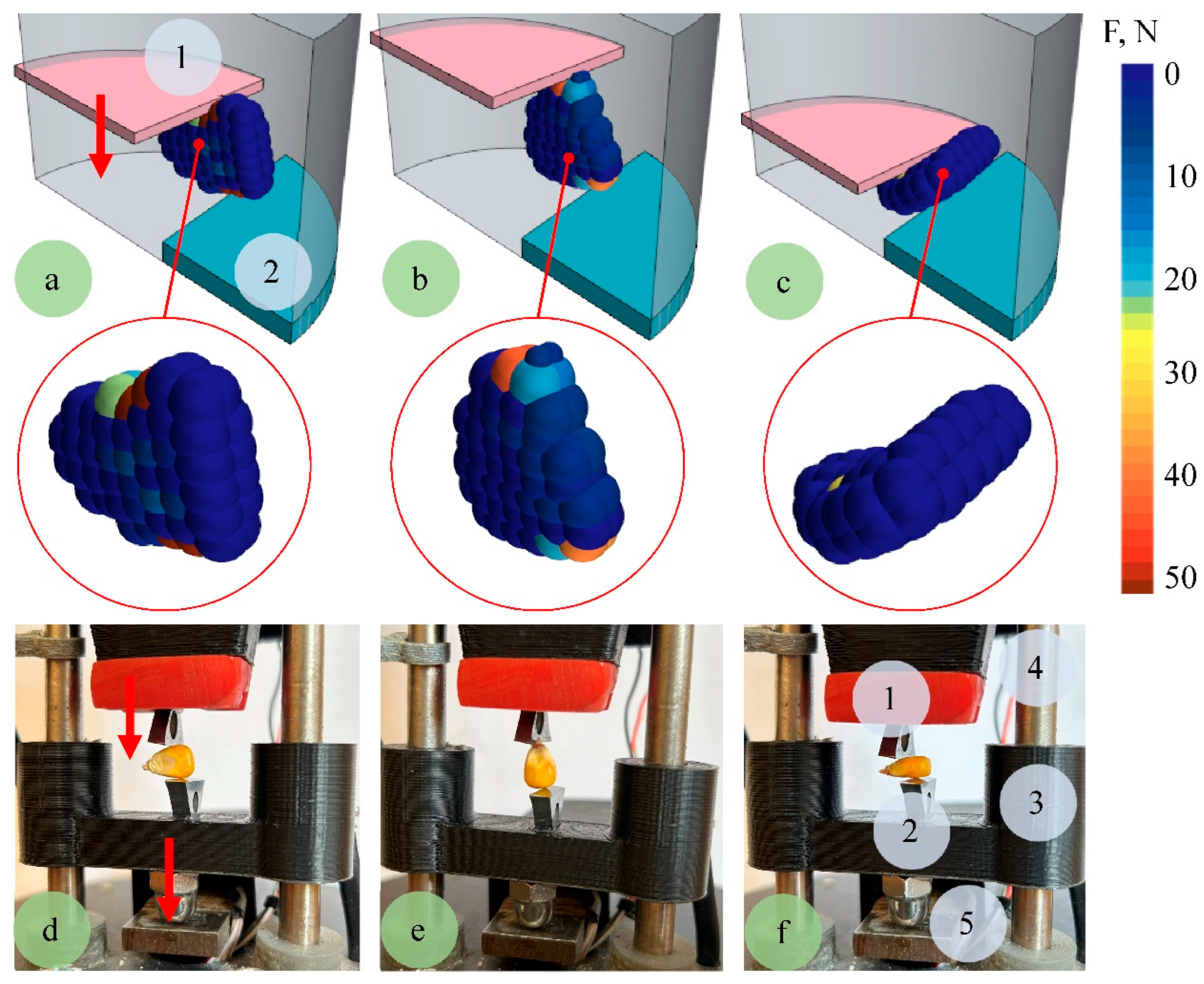
Definition of the breaking force was carried out in three spatial positions of the grain (Figure 6): vertical position, loading on the lateral surface, and horizontal position. This approach allowed for accounting possible variations in the grain strength properties (grain breaking force F) depending on the direction of the applied force.

In the simulation, the Hertz–Mindlin contact model with instantaneous bond breakage was used to reproduce the fracture processes of grain kernels. The overall set of physical models included: mesh-free DEM, DEM bonded-particle forces, solution interpolation, Lagrangian multiphase, multiphase interaction, discrete element method (DEM), unsteady implicit calculation, and gravity force. For the Lagrangian multiphase approach, constant density, particle clustering, continuum medium, and DEM particles were taken into account. For the multiphase interaction, the following were applied: single fracture model, rolling resistance, bonded particles, and DEM phase interaction. The full specification of material and contact parameters is presented in Table 1.

Calibration of the physico-mechanical parameters of the model was carried out by comparing experimentally determined grain fracture forces under laboratory conditions (Figure 6) with numerical simulation results.

The laboratory setup (Figure 6) consists of a metal frame with linear guides, a fixed and a movable carriage equipped with impact pads. Both carriages slide along the guides on bearings, ensuring precise vertical motion. The fixed carriage is mounted on a load cell with a lower punch, while the upper punch is attached to the movable carriage, which moves at a specified speed. The carriage movement is driven by a DC motor through a screw pair, with limit switches controlling its end positions. The signal from the load cell is transmitted through an HX711 converter to an Arduino Uno controller and then to a personal computer. This setup provides continuous real-time load monitoring. The experimental parameters are as follows: distance between impact pads l = 1.5 mm; angle between impact pads α = 30°; velocity of the impact pad V = 4 m/s. The maximum force during grain fracture at different positions is determined (

Table 2. Values of the maximum force F (N) during grain fracture in different positions, obtained from laboratory experiments and modeling.

Culture	Method	Position
		Horizontal Position	Lateral Surface	Vertical Position
Maize	Simulation	265.2 ± 9.3	88.8 ± 5.4	159.9 ± 7.6
	Experiment	273.2 ± 14.1	92.42 ± 12.4	164.8 ± 13.0
Barley	Simulation	67.7 ± 4.2	18.5 ± 2.1	93.1 ± 4.8
	Experiment	69.1 ± 6.6	18.7 ± 4.4	95.9 ± 6.7
Wheat	Simulation	35.9 ± 3.1	23.5 ± 2.7	54.5 ± 3.7
	Experiment	37.1 ± 5.2	24.1 ± 3.5	56.8 ± 5.9

).

A comparison between simulation and experimental results demonstrates a high level of agreement, with deviations not exceeding 5–7%. The smallest differences were observed for barley and wheat, confirming the adequacy of the numerical model for predicting fracture behavior in grains of smaller size and more uniform shape. For maize, the slightly higher discrepancy (up to 8%) can be attributed to the complex internal structure and larger kernel dimensions, which influence stress distribution during deformation. Similar data were obtained during modeling for different values of Young’s modulus, Poisson’s ratio, and ultimate stress (Table 1). The calibration procedure involved iterative adjustment of these parameters until the error between the simulated and experimental data remained within acceptable limits (Table 2). Calibration was considered successful when MAPE ≤ 5–7% and R² > 0.95.

In laboratory experiments, the grain moisture of maize, wheat, and barley was stable at 11.6 ± 0.8%, which corresponds to the technological requirements for feed preparation (added to the text of the article). In DEM modeling, moisture was not considered as a separate factor, since within the specified range its effect on the physico-mechanical properties of kernels is minimal and does not lead to significant changes in contact parameters. Furthermore, the use of a simplified DEM model was aimed at reproducing the general patterns of grinding under typical feed-production moisture conditions, rather than analyzing moisture as a variable. Therefore, neglecting this factor does not reduce the comparability of numerical and experimental results.

Quantitative validation showed that deviations of predicted values from experimental data did not exceed measurement errors (Table 2): for maize hybrid P8816, the deviation was about 4.8%; for wheat cultivar “Patras”—6.1%; and for barley cultivar “Snow Queen”—5.3%. This confirms the high consistency of the model with experimental data and demonstrates its suitability for further virtual research and optimization of the structural parameters of grinding equipment.

To conduct experimental studies aimed at investigating the operating parameters of the disc grinder for concentrated feeds, a specialized test bench was developed. The main element of the experimental setup (Figure 7) is a laboratory disc grinder for concentrated feeds.

Experimental studies of the operating process of the disc grinder were carried out using a symmetric non-compositional second-order Box-Behnken design. The purpose of the experiment was to determine the influence of key design and technological factors—the installation angle of the impact pads β (10–30°), the number of impact pads z (6–12) on one disc, as well as the rotation frequency of the working disc n (1500–3000 rpm)—on the main performance indicators of the grinder. Among these indicators were the machine productivity Q (kg/h) and the consumed power N (kW), which were recalculated into specific energy consumption q (kW·h/t), as well as the grinding quality, analyzed by the fractional composition of the resulting material. The studies were carried out at a constant gap between discs h = 0.6 mm—a value previously determined to provide the most optimal particle size according to animal feeding standards. The grain feed was set at the maximum level of 1350 kg/h, corresponding to an intensive load regime typical for real operating conditions in production farms.

For the study of the disc grinder for concentrated feeds, wheat grain of the “Patras” variety with moisture content 11.31%, barley of the “Snow Queen” variety with moisture content 10.78%, and maize hybrid P8816 with moisture content 12.34% were used. To evaluate the grinding quality of the grain material, a fractional analysis method was applied using the laboratory sieve shaker model RLU-3K. The ground grain after exiting the grinder was poured into the receiving hopper of the shaker, where it was evenly distributed over the mesh surfaces of the set of laboratory sieves. Sieves with different hole diameters were used: 0.2 mm, 0.5 mm, 1 mm, 1.5 mm, and 2 mm. The frequency of disc rotation was controlled using a Danfoss VLT Micro Drive FC51 frequency converter. The Wolfram Cloud computational environment was used to build and statistically analyze regression models. The experimental studies were conducted during the spring–summer of 2025.

3. Results

3.1. Numerical Modeling Results

As a result of numerical modeling, regression equations for the grain destruction force F (N) were obtained.

For maize:

-

in the horizontal position:

$${\mathrm{F}}_{\mathrm{g}}^{\mathrm{c}}=1472.26-337.334l-42.7824\mathrm{\alpha }+5.90499l\mathrm{\alpha }+0.35192{\mathrm{\alpha }}^2;$$

(15)

-

on the lateral surface:

$${\mathrm{F}}_{\mathrm{l}}^{\mathrm{c}}=506.258-127.277l-9.46527\mathrm{\alpha }+2.05933l\mathrm{\alpha }+0.0399371{\mathrm{\alpha }}^2;$$

(16)

-

in the vertical position:

$${\mathrm{F}}_{\mathrm{V}}^{\mathrm{C}}=159.716-5.557\mathrm{V}+1.11047{\mathrm{V}}^2-1.748\mathrm{\alpha }-0.18994\mathrm{V}\mathrm{\alpha }+0.00982{\mathrm{\alpha }}^2.$$

(17)

According to the Fisher criterion, F₍₁₅₎ = 121.37 > F_t(15, 66, 0.05) = 2.11; F₍₁₆₎ = 121.37 > F_t(15, 66, 0.05) = 2.11; F₍₁₇₎ = 121.37 > F_t(15, 66, 0.05) = 2.11, thus Equations (15)–(17) are statistically significant.

For wheat:

-

in the horizontal position:

$${\mathrm{F}}_{\mathrm{g}}^{\mathrm{w}}=133.741-42.5066l-0.193652\mathrm{\alpha }+0.657696l\mathrm{\alpha }-0.0289088{\mathrm{\alpha }}^2;$$

(18)

-

on the lateral surface:

$${\mathrm{F}}_{\mathrm{l}}^{\mathrm{w}}=178.8-19.0944l-1.90109\mathrm{\alpha };$$

(19)

-

in the vertical position:

$${\mathrm{F}}_{\mathrm{v}}^{\mathrm{w}}=38.8957+4.4368\mathrm{V}-0.91895\mathrm{\alpha }-0.0876715\mathrm{V}\mathrm{\alpha }.$$

(20)

According to the Fisher criterion, F₍₁₈₎ = 50.24 > F_t(15, 66, 0.05) = 2.11; F₍₁₉₎ = 139.98 > F_t(15, 66, 0.05) = 2.11; F₍₂₀₎ = 396.7 > F_t(15, 66, 0.05) = 2.11, thus Equations (18)–(20) are statistically significant.

For barley:

-

in the horizontal position:

$${\mathrm{F}}_{\mathrm{g}}^{\mathrm{b}}=56.9373-11.7724l+0.333859\mathrm{\alpha }-0.0147722{\mathrm{\alpha }}^2;$$

(21)

-

on the lateral surface:

$${\mathrm{F}}_{\mathrm{l}}^{\mathrm{b}}=105.222-11.0936l-1.13344\mathrm{\alpha };$$

(22)

-

in the vertical position:

$${\mathrm{F}}_{\mathrm{v}}^{\mathrm{b}}=27.4718+2.90126\mathrm{V}-0.284666\mathrm{\alpha }-0.057903\mathrm{V}\mathrm{\alpha }.$$

(23)

According to the Fisher criterion, F₍₂₁₎ = 38.02 > F_t(15, 66, 0.05) = 2.11; F₍₂₂₎ = 147.28 > F_t(15, 66, 0.05) = 2.11; F₍₂₃₎ = 393.07 > F_t(15, 66, 0.05) = 2.11, thus Equations (21)–(23) are statistically significant.

Graphical interpretation of the dependencies (15)–(23) is shown in Figure 8.

For a comprehensive assessment, an integral efficiency criterion was introduced:

$$\mathrm{\Theta }(\mathrm{l},\mathrm{\alpha },\mathrm{V})={\displaystyle \frac{{\mathrm{F}}_{\mathrm{g}}(\mathrm{l},\mathrm{\alpha },\mathrm{V})-{\mathrm{F}}_{\mathrm{g}\min }}{{\mathrm{F}}_{\mathrm{g}\max }-{\mathrm{F}}_{\mathrm{g}\min }}}\cdot {\displaystyle \frac{{\mathrm{F}}_{\mathrm{l}}(\mathrm{l},\mathrm{\alpha },\mathrm{V})-{\mathrm{F}}_{\mathrm{l}\min }}{{\mathrm{F}}_{\mathrm{l}\max }-{\mathrm{F}}_{\mathrm{l}\min }}}\cdot {\displaystyle \frac{{\mathrm{F}}_{\mathrm{v}}(\mathrm{l},\mathrm{\alpha },\mathrm{V})-{\mathrm{F}}_{\mathrm{v}\min }}{{\mathrm{F}}_{\mathrm{v}\max }-{\mathrm{F}}_{\mathrm{v}\min }}}\cdot {\displaystyle \frac{\mathrm{V}-{\mathrm{V}}_{\min }}{{\mathrm{V}}_{\max }-{\mathrm{V}}_{\min }}}\cdot {\displaystyle \frac{{\mathrm{l}}_{\max }-\mathrm{l}}{{\mathrm{l}}_{\max }-{\mathrm{l}}_{\min }}}\to \min ,$$

(24)

where Θ—integral efficiency criterion; F_g—grain destruction force in the horizontal position, N; F_l—grain destruction force on the lateral surface, N; F_v—grain destruction force in the vertical position, N; l—the distance between impact pads l, mm; α—the angle between the pads α, °; V—the linear velocity of the pad movement V, m/s; indices «min», «max»—minimum and maximum value; marking « $\to \min$»—mathematical operation of finding the minimum of a function.

According to which the minimization of the force should be ensured at the maximum distance between the impact pads l (high productivity of the grinding process) and the minimum velocity of the impact pad movement V (lower kinetic energy consumption of the grinding process).

By solving Equation (24) together with (15)–(23) in the Wolfram Cloud environment, rational values of the grinding process during numerical modeling were obtained, which are presented in Table 1.

3.2. Experimental Research Results

The obtained equations in coded form describe the influence of factors on the specific energy consumption of grinding for each crop.

Dependence of specific energy consumption on the research factors:

-

maize:

$${\mathrm{q}}^{\mathrm{c}}=7.395-0.000692859\mathrm{n}-0.724759\mathrm{z}+0.0000536956\mathrm{n}\mathrm{z}+0.0382001{\mathrm{z}}^2+0.0349674\mathrm{\beta };$$

(25)

-

wheat:

$${\mathrm{q}}^{\mathrm{w}}=4.7132-0.00030473\mathrm{n}-0.363803\mathrm{z}+0.027919{\mathrm{z}}^2+0.033319\mathrm{\beta };$$

(26)

-

barley:

$${\mathrm{q}}^{\mathrm{b}}=8.98664-0.000428784\mathrm{n}-0.878204\mathrm{z}+0.0556007{\mathrm{z}}^2+0.148695\mathrm{\beta }-0.00250749{\mathrm{\beta }}^2.$$

(27)

According to the Fisher criterion, F₍₂₅₎ = 2277.36 > F_t(15, 66, 0.05) = 2.21; F₍₂₆₎ = 1494.29 > F_t(15, 66, 0.05) = 2.21; F₍₂₇₎ = 2579.33 > F_t(15, 66, 0.05) = 2.21, thus Equations (25)–(27) are statistically significant.

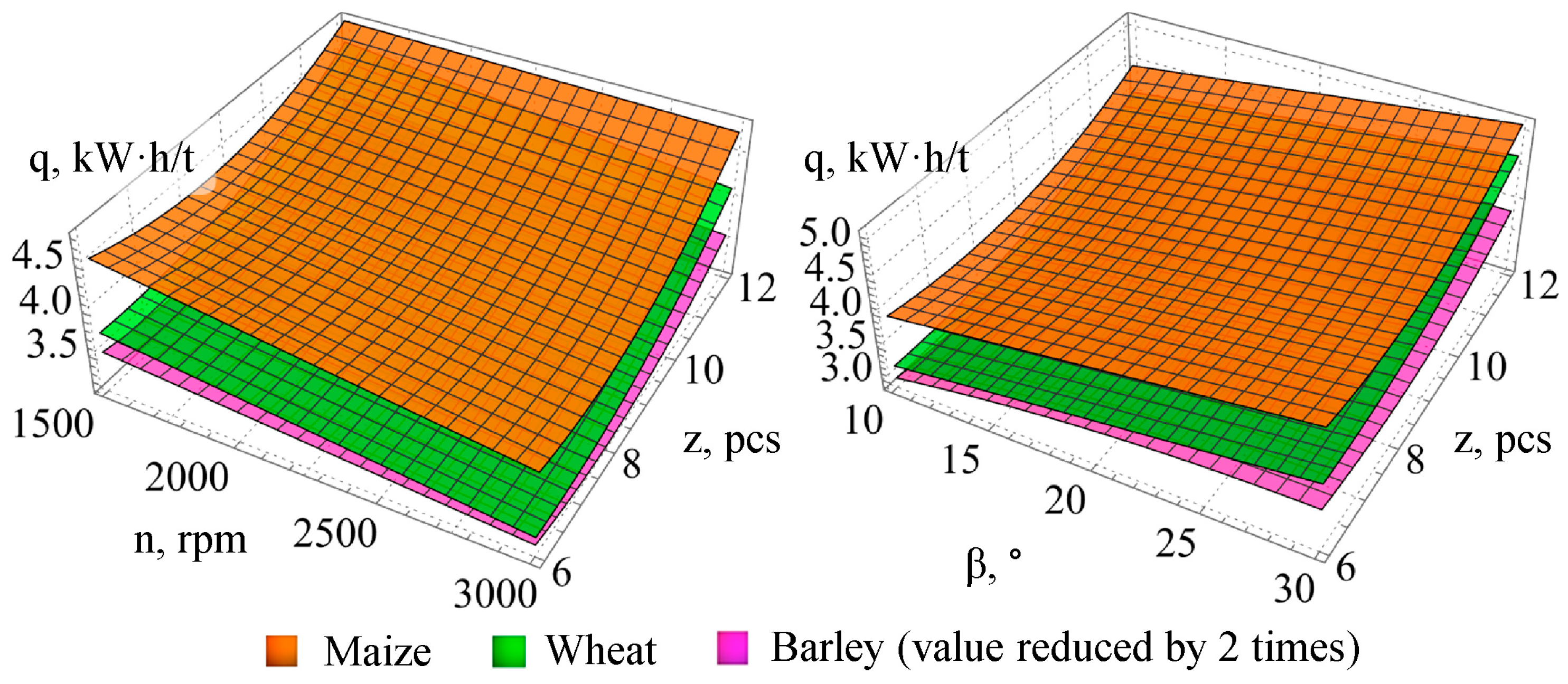
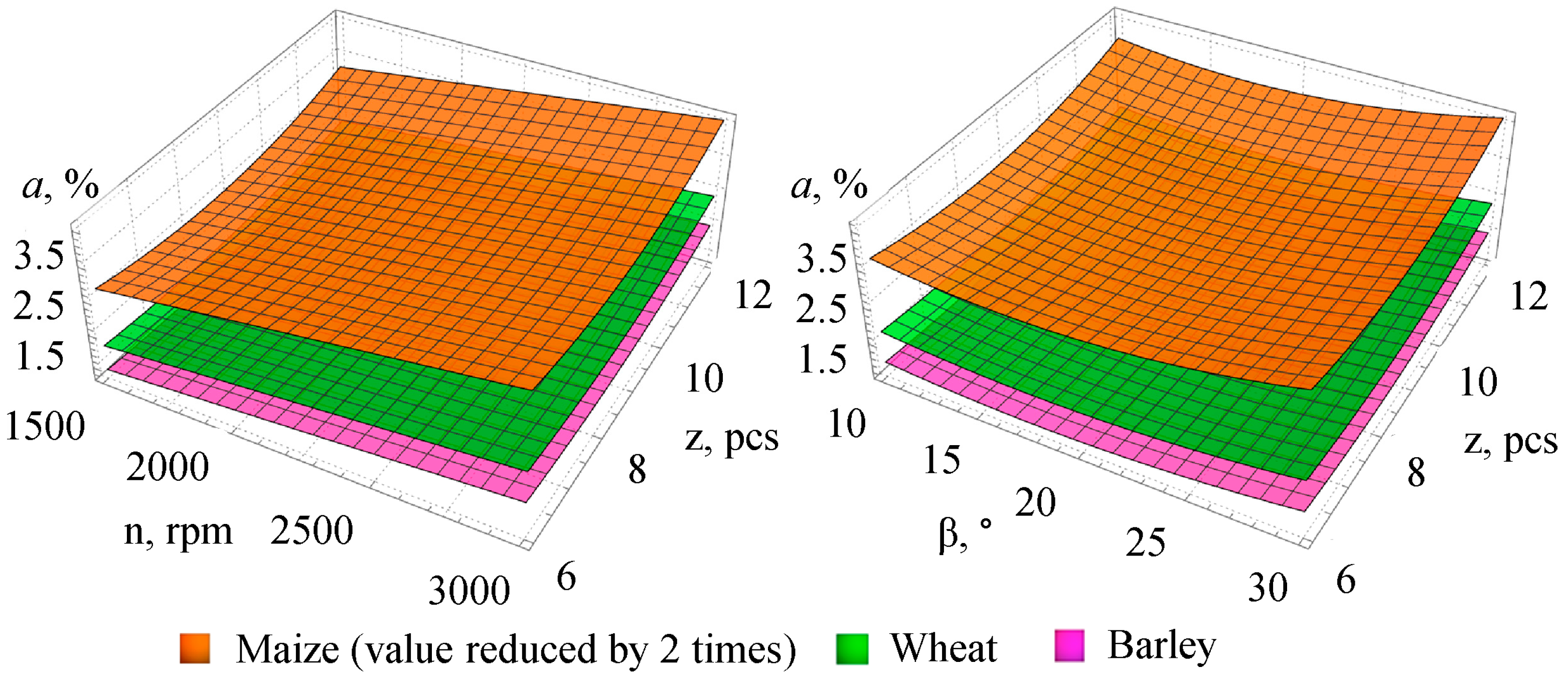
Graphical interpretation of dependencies (25)–(27) is presented in Figure 9 (values for barley are halved for better visualization of the obtained dependencies).

Dust fraction share:

-

maize:

$$a^{\mathrm{c}}=9.18791+0.00101\mathrm{n}-1.02542\mathrm{z}+0.05954{\mathrm{z}}^2-0.169208\mathrm{\beta }+0.005008{\mathrm{\beta }}^2;$$

(28)

-

wheat:

$$a^{\mathrm{w}}=2.86084+0.00033\mathrm{n}-0.27417\mathrm{z}+0.016296{\mathrm{z}}^2-0.05717\mathrm{\beta }+0.001617{\mathrm{\beta }}^2;$$

(29)

-

barley:

$${\mathrm{q}}^{\mathrm{b}}=8.98664-0.000428784\mathrm{n}-0.878204\mathrm{z}+0.0556007{\mathrm{z}}^2+0.148695\mathrm{\beta }-0.00250749{\mathrm{\beta }}^2.$$

(30)

According to the Fisher criterion, F₍₂₈₎ = 6130.86 > F_t(15, 66, 0.05) = 2.21; F₍₂₉₎ = 5168.8 > F_t(15, 66, 0.05) = 2.21; F₍₃₀₎ = 8697.69 > F_t(15, 66, 0.05) = 2.21, thus Equations (28)–(30) are statistically significant.

Graphical interpretation of dependencies (28)–(30) is presented in Figure 10 (values for maize are halved for better visualization of the obtained dependencies).

Next are the results of statistical processing of experimental data regarding the degree of grain grinding using the developed working element. The analysis considered three main varying factors.

-

maize:

$${\mathrm{\lambda }}^{\mathrm{c}}=8.6204-0.001355\mathrm{n}+3.946\cdot {10}^{-7}{\mathrm{n}}^2-0.5089\mathrm{z}+0.000079381\mathrm{n}\mathrm{z}+0.018354{\mathrm{z}}^2-0.032728\mathrm{\beta }+0.001504{\mathrm{\beta }}^2;$$

(31)

-

wheat:

$${\mathrm{\lambda }}^{\mathrm{w}}=1.67257+0.000564361\mathrm{n}+0.0154137\mathrm{\beta };$$

(32)

-

barley:

$${\mathrm{\lambda }}^{\mathrm{b}}=2.1101+0.000585\mathrm{n}-0.025128\mathrm{\beta }+0.0010468{\mathrm{\beta }}^2.$$

(33)

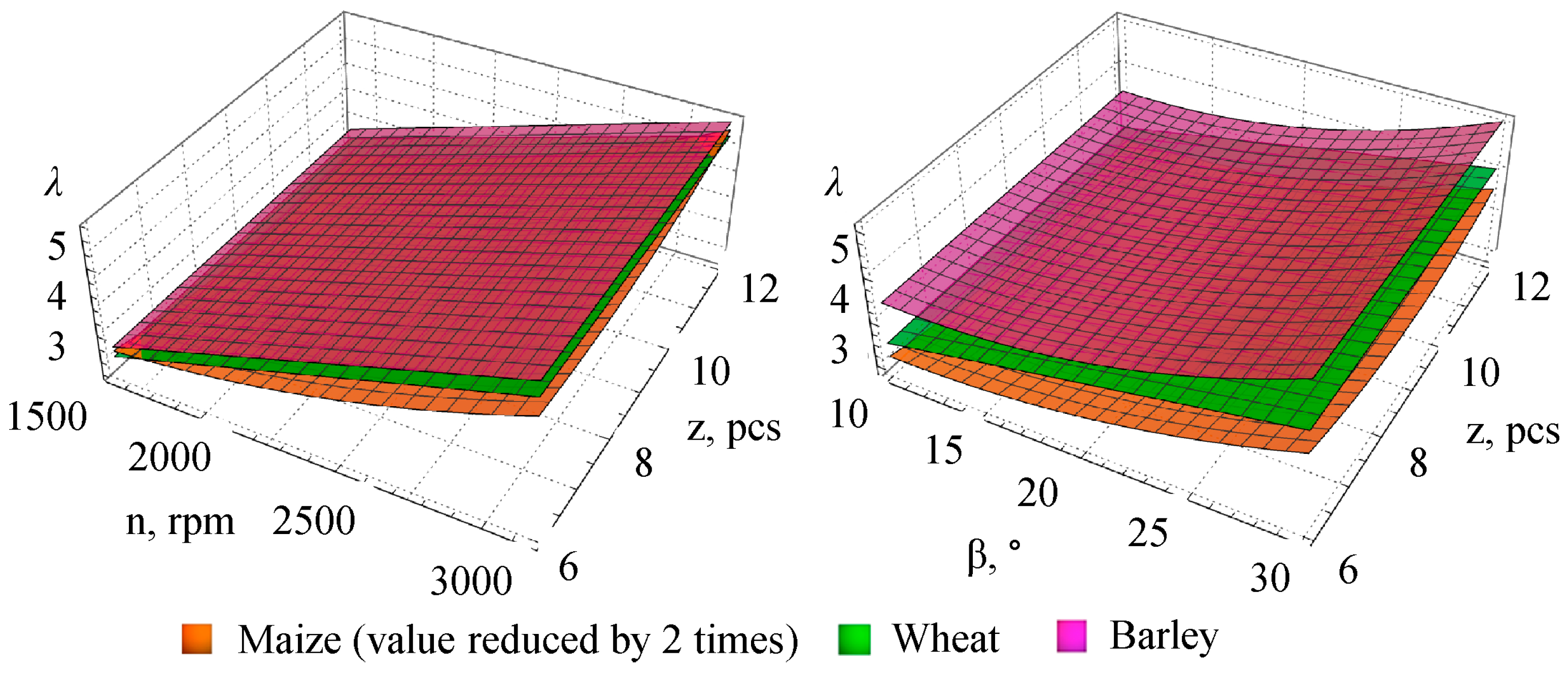
According to the Fisher criterion, F₍₃₁₎ = 3435.99 > F_t(15, 66, 0.05) = 2.21; F₍₃₂₎ = 2260.16 > F_t(15, 66, 0.05) = 2.21; F₍₃₃₎ = 2552.57 > F_t(15, 66, 0.05) = 2.21, thus Equations (31)–(33) are statistically significant.

Graphical interpretation of dependencies (31)–(33) is presented in Figure 11 (values for maize are halved for better visualization of the obtained dependencies).

Based on the models developed and presented in this section, numerical optimization (34) was performed in the Wolfram Cloud environment to determine such combinations of factors that achieve the minimum values of specific energy consumption q and the dust fraction share in the grinding product a for a given range of grinding degree λ.

For a comprehensive evaluation, an integral efficiency criterion of grinding and a grinding degree condition were introduced:

$$\left\{\begin{array}{l}\mathrm{K}={\displaystyle \frac{\mathrm{q}-{\mathrm{q}}_{\min }}{{\mathrm{q}}_{\max }-{\mathrm{q}}_{\min }}}{\displaystyle \frac{\mathrm{a}-{\mathrm{a}}_{\min }}{{\mathrm{a}}_{\max }-{\mathrm{a}}_{\min }}}\to \min ,\\ {\mathrm{\lambda }}_{\min }<\mathrm{\lambda }<{\mathrm{\lambda }}_{\max }.\end{array}\right.$$

(34)

where K—integral efficiency criterion; q—specific energy consumption, kW·h/t; a—dust fraction share in ground mass, %; λ—grinding degree; indices «min», «max»—minimum and maximum value; marking «$\to \min$»—mathematical operation of finding the minimum of a function.

The final results of the optimization of the experimental research are presented in Table 2.

3.3. Optimization of Design and Operating Parameters

Solving Equations (24) and (34) yielded the optimal values of the design and technological parameters of the disk grinder for concentrated feeds, which are summarized in

Table 3. Optimal values of design and technological parameters of the disk grinder for concentrated feeds.

Crop	Research Method	Modeling	Experiment
Maize	Modular gap between disks δ, mm	0.78	–
	Disk rotation speed n, rpm	1865	1764
	Installation angle of impact plates β, °	21.9	15.9
	Number of impact plates z, pcs	–	9
	Specific energy consumption q, kW·h/t	–	4.15
	Dust fraction share in ground mass a, %	–	5.13
	Grinding degree λ	–	7.22
Wheat	Modular gap between disks δ, mm	0.68	–
	Disk rotation speed n, rpm	1503	1500
	Installation angle of impact plates β, °	21.8	17.7
	Number of impact plates z, pcs	–	9
	Specific energy consumption q, kW·h/t	–	3.63
	Dust fraction share in ground mass a, %	–	1.71
	Grinding degree λ	–	3.55
Barley	Modular gap between disks δ, mm	0.79	–
	Disk rotation speed n, rpm	1676	1500
	Installation angle of impact plates β, °	25.3	17.2
	Number of impact plates z, pcs	–	9
	Specific energy consumption q, kW·h/t	–	6.76
	Dust fraction share in ground mass a, %	–	1.34
	Grinding degree λ	–	3.66

. The optimization process combined the results of DEM-based numerical modeling and full-scale experimental studies to ensure the reliability and applicability of the obtained parameter combinations for practical implementation.

To validate the adequacy of the developed DEM model, a dedicated comparison between the simulated and experimentally measured parameters was conducted. This comparison was aimed at assessing the degree of consistency between the predicted and actual performance indicators of the grinding process, as well as identifying potential sources of discrepancies. The results of this comparative analysis are presented in Table 3.

The quantitative comparison of DEM modeling outcomes with experimental data was performed based on the main design and technological parameters of the disk grinder: the modular gap between disks (δ), the rotational speed of the disks (n), and the installation angle of the impact plates (β). In addition, the experimental values of specific energy consumption, dust fraction in the ground product, and grinding degree were analyzed to evaluate the practical performance of the optimized design.

The comparison demonstrated a high degree of consistency between simulation and experiment. The DEM-predicted disk rotation speeds for maize, wheat, and barley closely matched the experimentally determined optimal regimes, with relative deviations not exceeding 5–10%. The calculated optimal installation angles of impact plates also showed good agreement with the measured values, with discrepancies within 7–8°. Such differences are within the acceptable range for mechanical system modeling and can be attributed to several factors.

First, the DEM model includes a number of simplifying assumptions that inevitably influence the accuracy of the predicted parameters. The geometry of the grain particles was idealized as spheroidal, neglecting their natural irregularities and surface roughness, which affects the local contact conditions during impact and shear. Second, the influence of air resistance, intergranular adhesion, and moisture-related cohesion was not considered in the current simulation version. Third, the contact law used (Hertz–Mindlin with no-slip condition) assumes purely elastic collisions and does not fully capture the elastic–plastic behavior of real grains, which may undergo localized deformation before fracture.

Despite these simplifications, the general parameter trends and their correlations remain accurately reproduced by the model. The predicted relationships between the disc speed, impact plate angle, and grinding efficiency correspond to those observed experimentally. Moreover, the optimal DEM-derived parameters yielded energy consumption and grinding degree values that closely approximate the measured experimental data.

Energy consumption, dust fraction, and grinding degree values were included only in the experimental section because these parameters were not directly modeled in the current version of the DEM algorithm. However, the simulated results indirectly reflect their trends through correlations with impact energy and particle breakage rate.

At the same time, the obtained optimal structural and operational parameters determined through numerical simulation approximate the experimental values of energy consumption (3.63–6.76 kWh/t) and grinding degree (3.55–7.22), indirectly confirming the adequacy of the developed model. The Mean Absolute Percentage Error (MAPE) between simulated and experimental data for the key parameters did not exceed 6.3%, while the coefficient of determination (R²) was greater than 0.95, which indicates strong correlation and high predictive reliability of the DEM model.

Overall, the comparative analysis (Table 3) demonstrates that the DEM-predicted optimal operating modes can effectively reproduce the experimentally observed trends, including the nonlinear relationship between disc speed and grinding efficiency. The minor deviations in absolute values are justified by physical simplifications and the absence of stochastic grain breakage modeling.

Thus, the extended comparative subsection enhances the transparency of the validation process and provides a solid basis for further model refinement. In future work, it is planned to expand the DEM model by including the effects of grain moisture, shape irregularity, and air–particle interaction, which will further improve its accuracy and predictive capability.

4. Discussion

The analysis of the obtained results and their comparison with existing scientific publications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,25] confirm the high effectiveness of the applied approach, which combines discrete element method (DEM) numerical modeling and multifactor experiments. Considering three key design and operational factors—the distance between impact plates l, the angle of their installation α, and the linear velocity V—allowed quantitatively describing the patterns of grain destruction for maize, wheat, and barley under impact cutting conditions. The derived dependencies (15)–(23) not only reflect the general trends established in previous works [2,11,13] but also detail the influence of each parameter for three plate orientations, which was practically unaddressed in the literature before.

The established optimal ranges of l, α, and V confirm that the reduction of destruction force is possible without lowering productivity through rational arrangement of impact elements, consistent with findings from energy-dependent grinding models [10,12]. The proposed integral efficiency criterion (24), aimed at minimizing the destruction force at maximum l and minimum V, further develops multi-criteria optimization approaches [1,11] with an emphasis on maintaining energy efficiency.

The experimental part, conducted using the improved disk grinder, complemented the numerical findings with data on specific energy consumption q, dust fraction a, and grinding degree λ while varying β, z, and n. This comprehensive combination of experiment and modeling aligns with current trends in the field [11,15,19], enabling consideration of both particle kinematics and the physico-mechanical properties of the grain.

Comparison of the obtained data with literature values shows that the optimal process parameters (l = 1.68–1.79 mm, β = 21.8–25.3°, V = 4.72–5.86 m/s, n = 1503–1865 rpm, δ = 0.68–0.79 mm) provide a balance between technological efficiency and energy consumption. The results confirm conclusions from studies [12,16,19] that energy consumption significantly depends on the physico-mechanical characteristics of the crop: the highest value of q was recorded for barley (6.76 kWh/t), the lowest—for wheat (3.63 kWh/t), while the dust fraction a varied from 1.34% (barley) to 5.13% (maize).

Thus, this study fills the gap identified in the introduction between numerical modeling and practical engineering methods: it integrates DEM validation, multifactor experimentation, and parameter optimization for different crops. This lays the foundation for forming unified recommendations for adjusting disk grinders according to the specific processed grain material, meeting modern requirements for energy efficiency and adaptability in agro-industrial production.

The comparison of this study with other relevant studies is presented in

Table 4. Comparison of the present study with other relevant research.

Reference	Object/Material	Methodology	Main Parameters Investigated	Key Findings	Comparison with Present Study
[10]	wheat	experimental + analytical model	rotor speed, screen size	energy consumption 3.5–5.2 kWh/t	present study shows comparable q = 3.63 kWh/t for wheat
[12]	maize	DEM simulation	particle velocity, impact energy	force reduction with optimized velocity	confirms trend of decreasing F with lower V
[13]	barley	experimental grinding	grain hardness, energy input	specific energy consumption q ≈ 6.5 kWh/t	matches experimental q = 6.76 kWh/t in this study
[15]	wheat, maize, soybean	multicracker system test	rotation speed, feed rate	higher efficiency at 1500–1700 rpm	same optimal range found here (n = 1500–1764 rpm)
[18]	corn kernels	DEM + experiment	plate angle, velocity	optimal angle ≈ 20–25° for minimal wear	coincides with β = 21.8–25.3° found in this study
Present study	maize, wheat, barley	DEM + multifactor experiment	liner distance, installation angle, particle velocity, disc speed, clearance, number of impact plates	specific energy consumption q = 3.63–6.76 kWh/t; dust fraction share in ground mass a = 1.34–5.13%; grinding degree λ = 3.55–7.22	integrates modeling and experiment; provides universal optimization across crops

.

The obtained results open several directions for further work. First, it is advisable to extend research to other types of cereals and legumes with different physico-mechanical properties to test the universality of the established patterns. Second, promising is the development and validation of advanced DEM models considering grain structure heterogeneity, moisture effects, and combined grinding modes (impact-cutting, abrasive, crushing). Third, it is worthwhile to study the interaction of disk grinder design parameters with product feeding and separation systems, enabling the creation of integrated technological lines with minimal energy consumption. A separate task is the development of automatic regulation algorithms based on online monitoring results of granulometric composition and energy consumption. In the future, it is planned to conduct a techno-economic analysis of implementing optimized parameters in industrial conditions and to develop methodological recommendations for engineers designing disk grinders.

5. Conclusions

Taking into account the specific design of the disk grinder’s working element with impact plates, the influence of three key factors (the distance between impact plates l, the angle between them α, and the linear velocity of the plate V) was investigated by numerical modeling of the grain destruction process for maize, wheat, and barley using impact cutting based on the discrete element method (DEM) in the Simcenter STAR-CCM+ environment. Established patterns of destruction force for maize, wheat, and barley grains in three orientations during impact cutting depending on the distance between impact plates l, the angle between plates α, and the linear velocity of the plate V are given in Equations (15)–(23). These patterns provide a quantitative evaluation and deeper physical understanding of the grain shell destruction processes under impact cutting conditions. This forms the basis for optimizing the grinder’s design parameters to improve the efficiency and energy savings of the grinding process for various types of grain material.

For a comprehensive assessment of the grain grinding process, an integral efficiency criterion (24) was proposed, ensuring the minimization of destruction force at the maximum distance between impact plates and minimum velocity of their movement. This allows achieving high process productivity while simultaneously reducing kinetic energy consumption.

Rational grinding parameters were established for the main grain crops—maize, wheat, and barley. Analysis of the obtained results confirms that the process parameters (distance between plates l = 1.68–1.79 mm, angle of installation β = 21.8–25.3°, velocity V = 4.72–5.86 m/s, disk rotation speed n = 1503–1865 rpm, modular gap δ = 0.68–0.79 mm) reflect the physico-mechanical characteristics of each crop.

As a result of experimental studies of the improved disk grinder, established patterns of changes in specific energy consumption of grain grinding q (25)–(27), dust fraction in the ground grain mass a (28)–(30), and grinding degree λ (31)–(33) depending on the angle of installation of impact plates β, the number of impact plates on one disk z, and the rotation frequency of the working body n were determined. Based on the constructed models, numerical optimization (34) was performed to determine such factor combinations (Table 1) at which the minimum specific energy consumption q and dust fraction a in the grinding product are achieved within the defined range of grinding degree λ.

Analysis of the obtained data indicates achievement of an optimal combination of technological efficiency and energy feasibility in grinding maize, wheat, and barley. The rotation frequency n (1500–1764 rpm), angle of impact plate installation β (15.9–17.7°), and number of impact plates z (9 pcs) were adapted to the physico-mechanical properties of each crop. The highest specific energy consumption q was observed when processing barley (6.76 kWh/t), the lowest—for wheat (q = 3.63 kWh/t). The dust fraction a in the ground mass was the highest for maize (5.13%) and the lowest for barley (1.34%).

The obtained results confirm the effectiveness of the grinder’s design solutions for adaptive processing of various grains.

Despite the comprehensive modeling and experimental validation, several limitations should be noted. The DEM model assumed idealized grain geometry and constant mechanical properties within each grain type, which may not fully represent the real variability of kernel size, density, or internal structure. The effect of grain moisture content was not varied during simulations and experiments, although it significantly affects deformation and fracture behavior. Air resistance, temperature rise, and wear of the impact plates were also not considered, potentially influencing energy consumption and grinding uniformity. These simplifications allowed a focused analysis of geometric and kinematic factors but may limit the direct transferability of the obtained correlations to all operational conditions. Future research will aim to address these aspects through coupled DEM–CFD simulations, variable-moisture modeling, and long-term durability testing.

The results of this study form a scientific and engineering basis for further development of adaptive grain grinding systems. Future research will focus on integrating the obtained DEM-based models into automated control systems of industrial grinders to dynamically adjust the distance between impact plates and rotational speed according to grain type and humidity. This approach will allow for intelligent energy management and quality control during grinding. Collaboration is planned with agricultural machinery manufacturers to implement the optimized impact plate geometry and control algorithms in serial production of disk grinders. For mill manufacturers, the benefits include reduced specific energy consumption (up to 25%), lower dust fraction in ground product, and extended service life of working elements due to optimized loading conditions. The developed methodology provides a framework for designing next-generation high-efficiency grinding equipment adapted to different grain crops and processing conditions.