Study on Shutdown Process of Agricultural Irrigation Pump Device
Abstract
1. Introduction
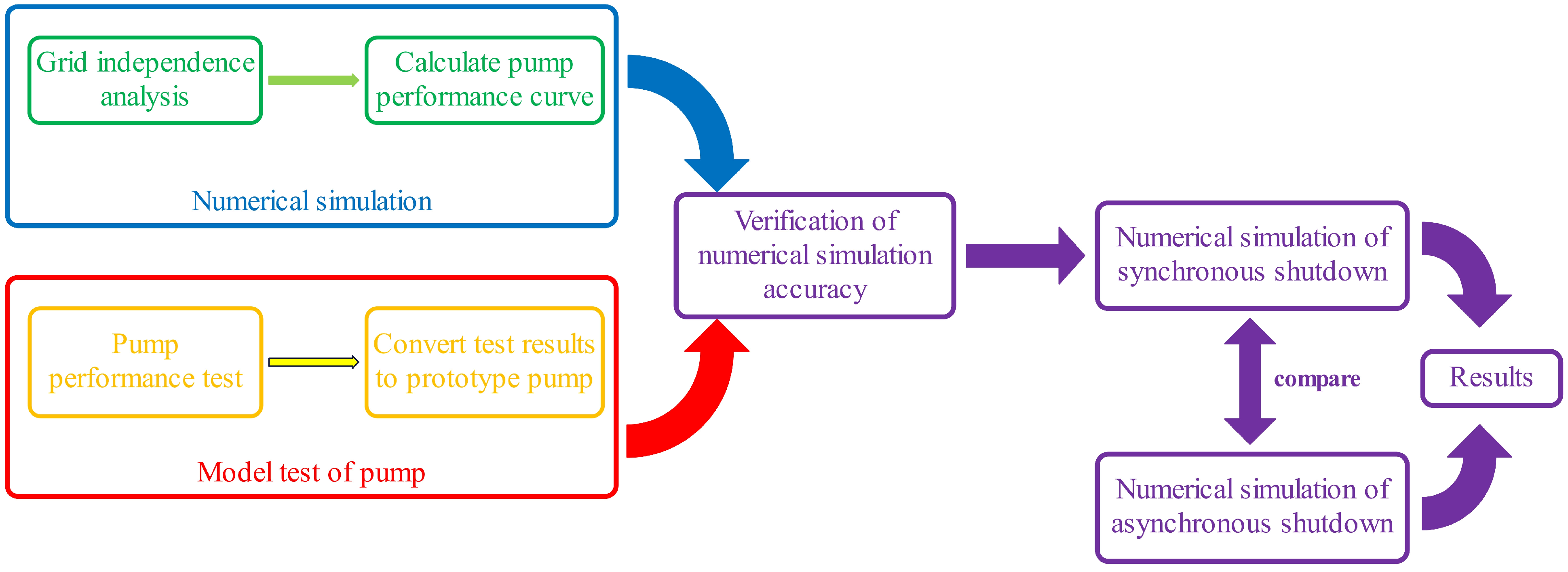
2. Materials and Methods
2.1. Governing Equation
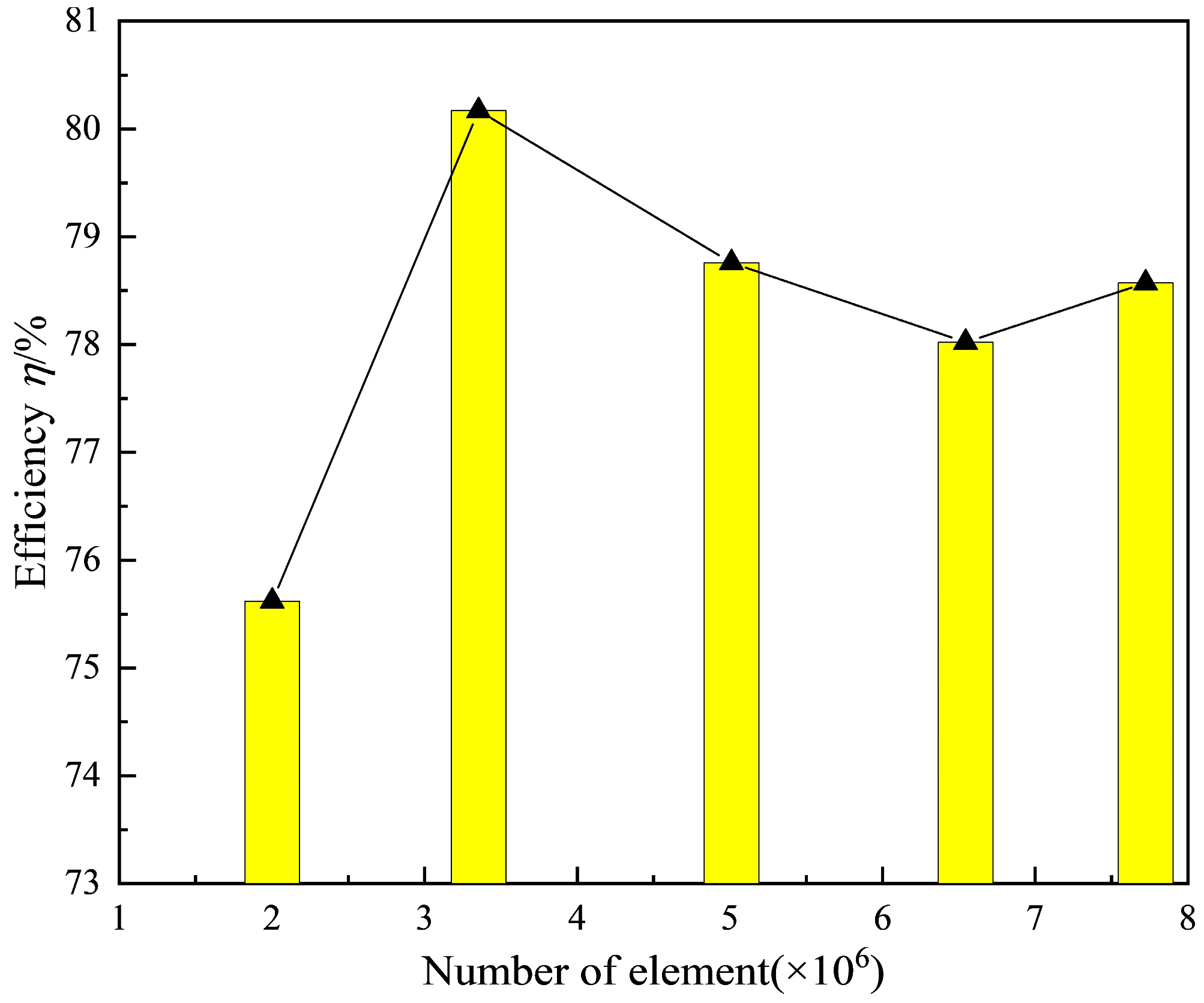
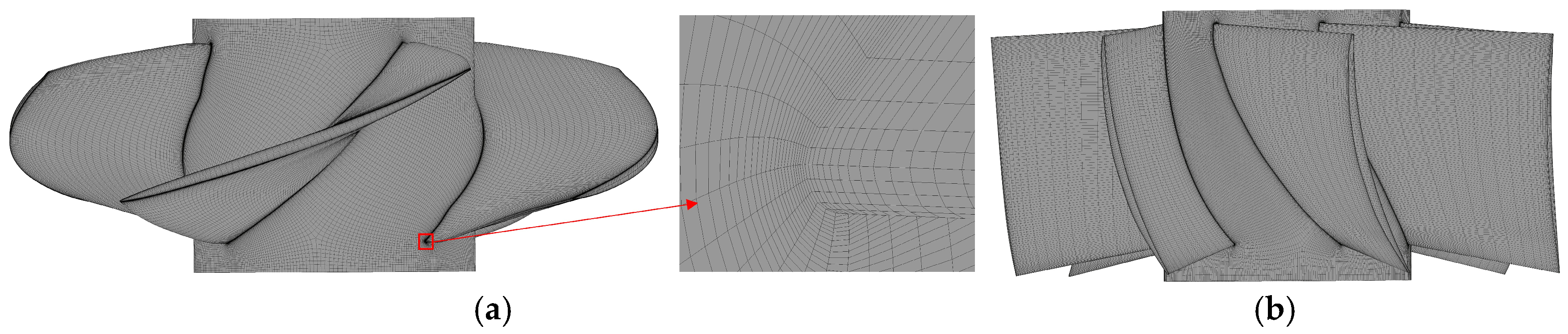
2.2. Three-Dimensional Model and Grid Division
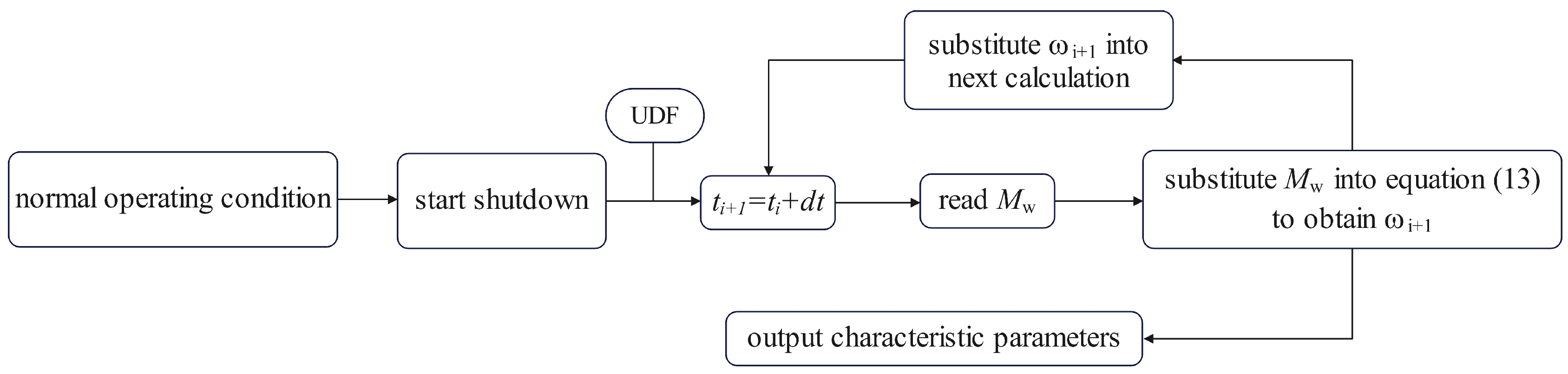
2.3. Calculation Method of Pump Shutdown Process
2.4. Boundary Conditions and Calculation Settings
2.5. Model Test
2.5.1. Test Equipment
2.5.2. Experimental Result Conversion Method
2.5.3. Verification of Numerical Simulation Accuracy
3. Results and Discussion
3.1. Analysis of the Transition Process of Pump Device Synchronous Shutdown
3.1.1. Analysis of the External Characteristics of Pump Device Synchronous Shutdown Process
3.1.2. Evolution of the Internal State of Pump Device
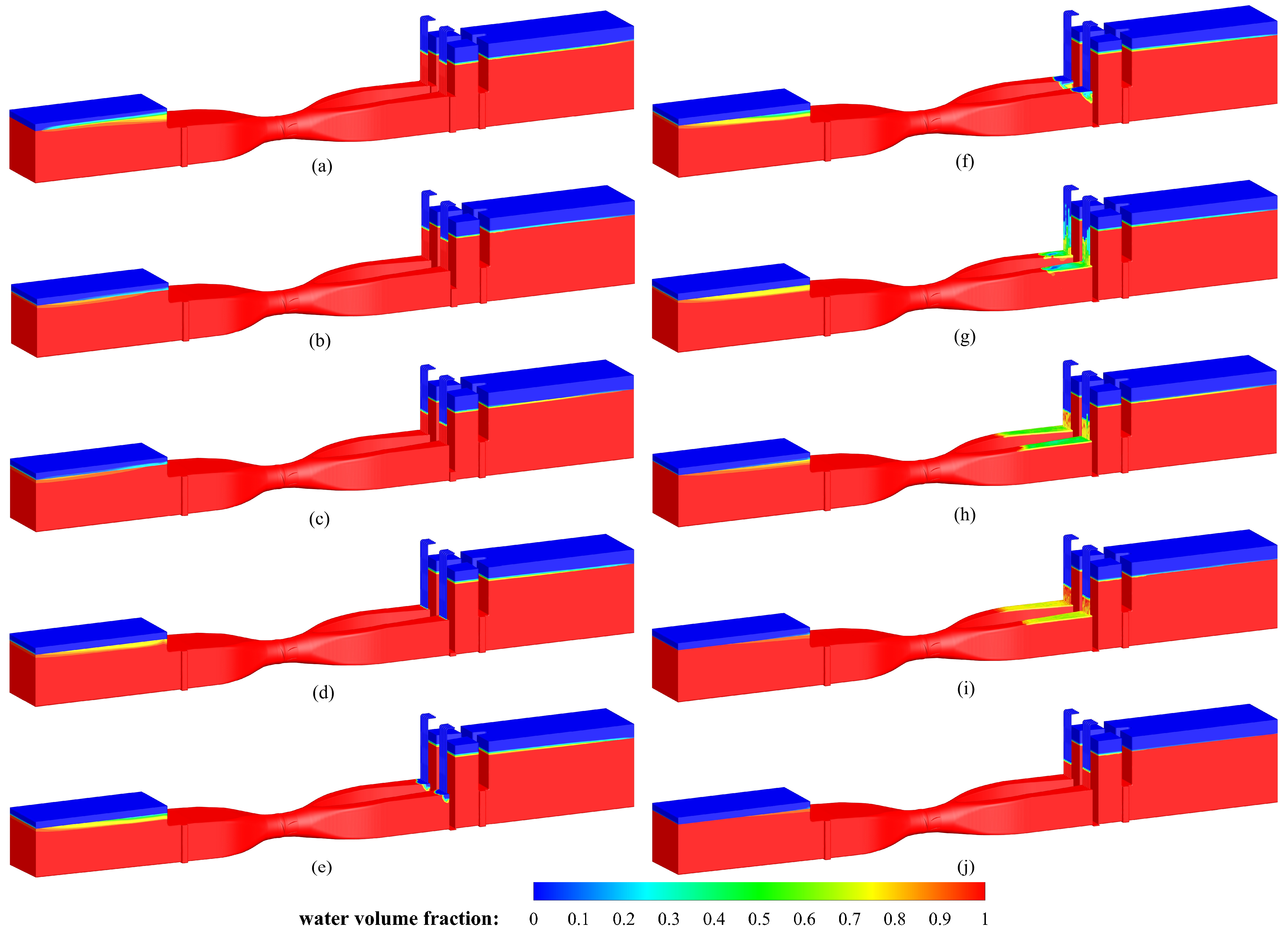
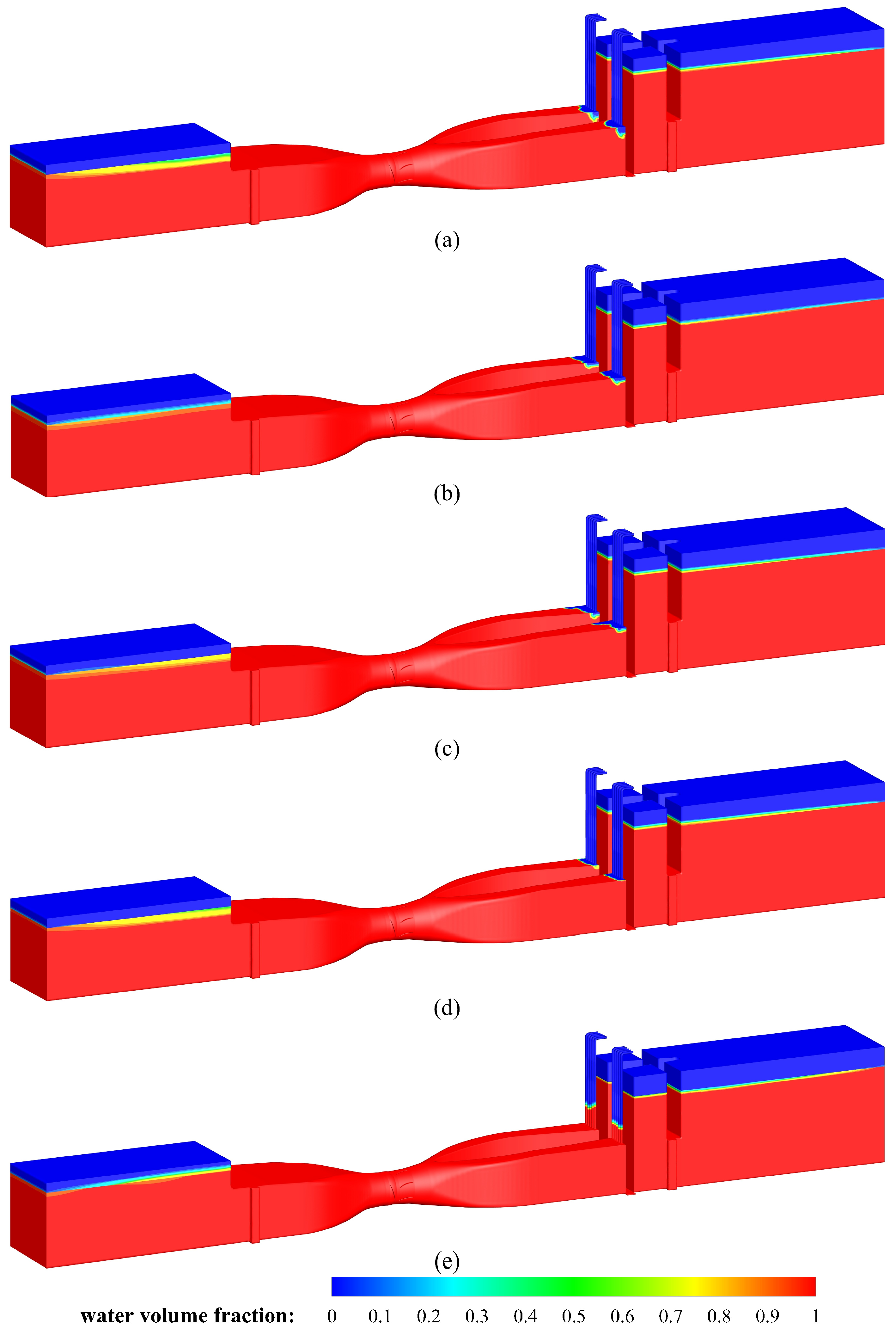
3.1.3. Evolution of Air–Water Two-Phase Inside Pump Device
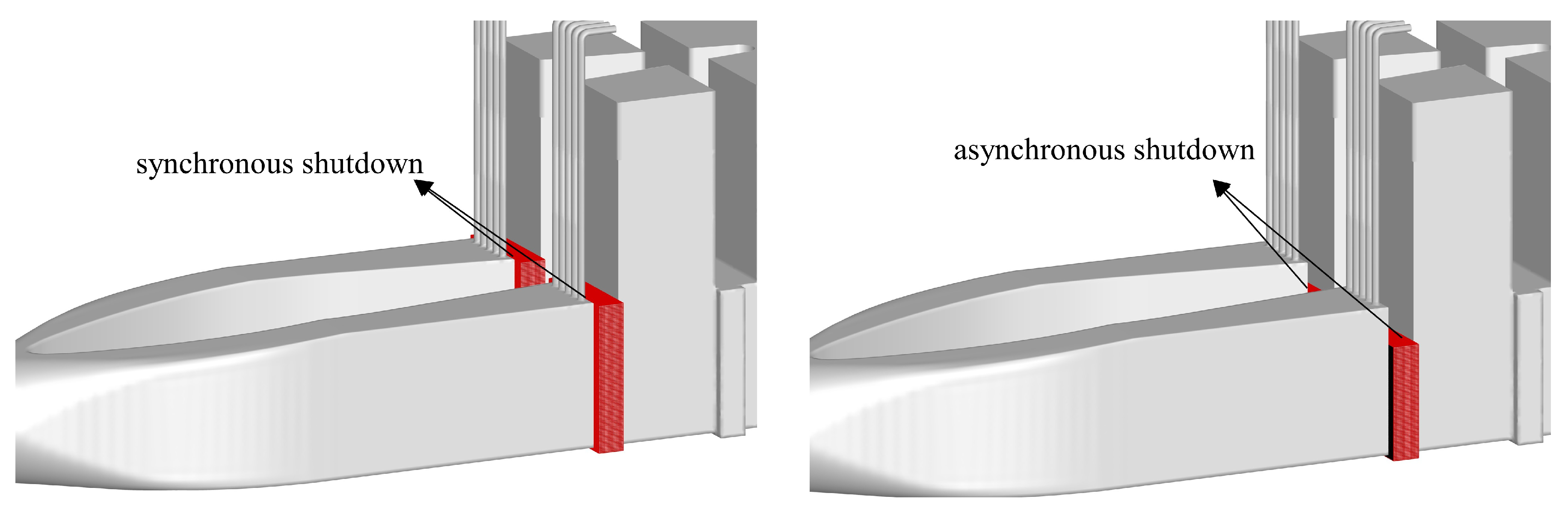
3.2. Comparison and Analysis of Synchronous and Asynchronous Shutdown Process
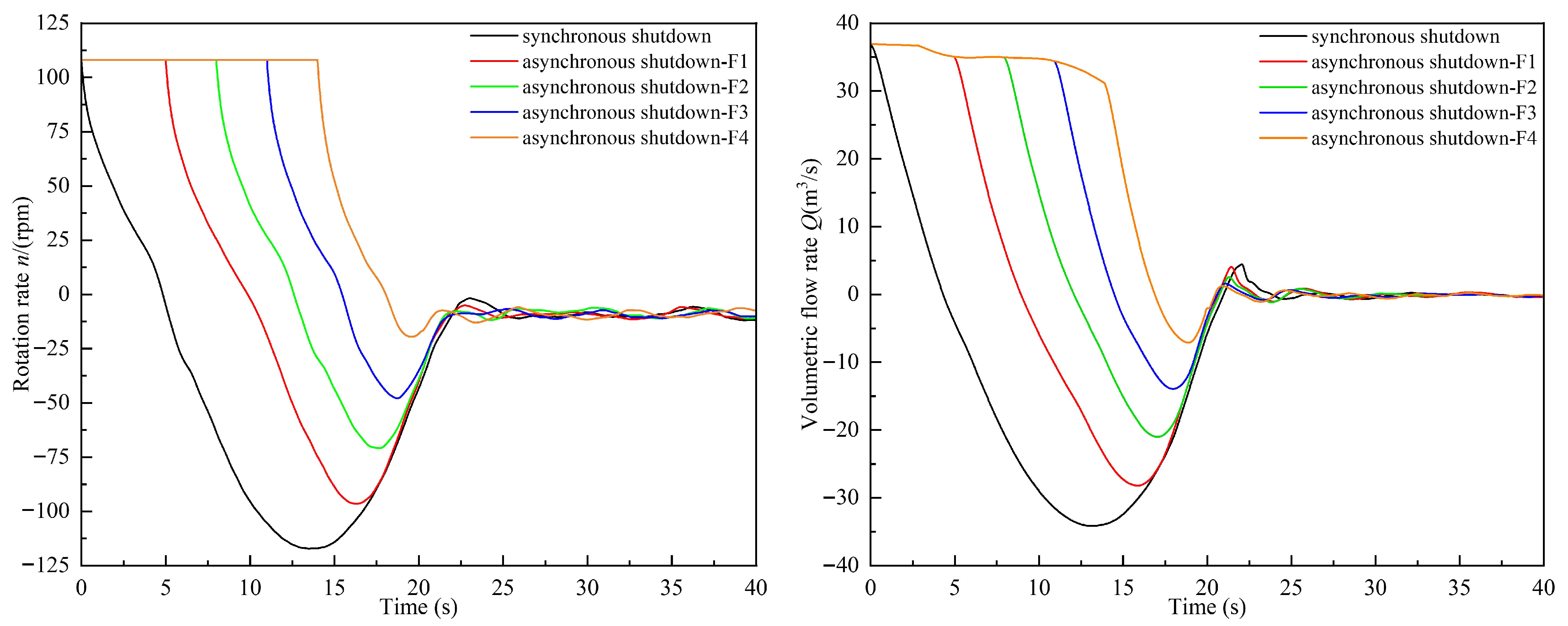
3.2.1. Comparison of External Characteristics of Synchronous and Asynchronous Shutdown
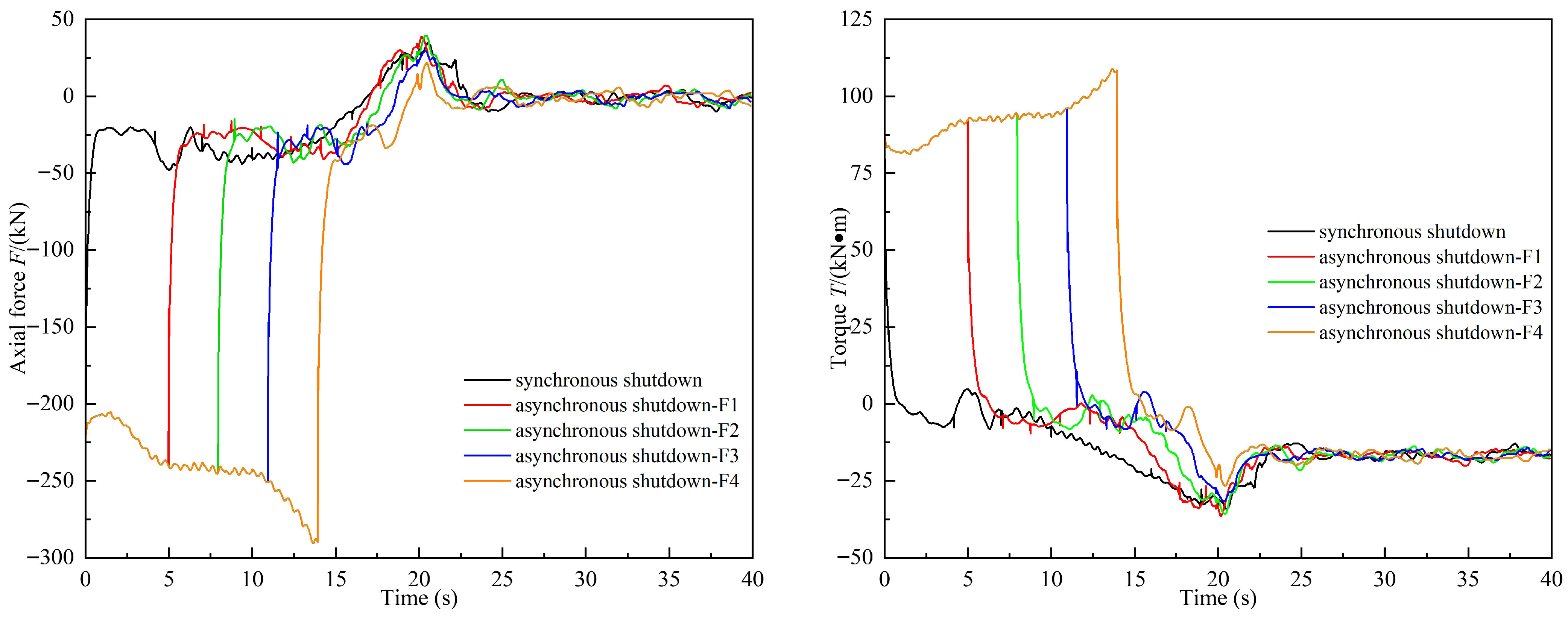
3.2.2. Comparison of Internal Characteristics During Shutdown Process of Different Schemes
4. Conclusions
- (1)
- During the synchronous shutdown, as the rapid gate gradually closes, the water flow rate beneath the rapid gate increases, resulting in a corresponding growth of the vortex zone on its inner side. When the rapid gate is 90% closed, negative pressure zones develop in the outlet passage. A portion of the air drawn into the outlet passage subsequently forms an air–water mixture near the top of the passage. Complete expulsion of this entrapped air requires approximately 40 min.
- (2)
- Compared with the synchronous shutdown, the asynchronous shutdown method effectively reduces both the reverse rotation rate and the reverse volumetric flow rate of the pump during the shutdown process. It also significantly diminishes the low-pressure zone at the top of the outlet passage and the vortex zone on the inner side of the gate. Although the torque and axial force of the pump increase during shutdown, these do not cause damage to the unit. Therefore, asynchronous shutdown is a safer and more reliable operational strategy.
- (3)
- During the shutdown process, when the rapid gate is completely closed, the water flow and pump do not stop immediately, and the two are still in reverse motion. A negative pressure condition develops in the outlet passage, which briefly draws in reverse flow. In this study, the adverse effects of water hammer are mitigated by air drawn into the outlet passage through the air vents. The introduced air alleviates the negative pressure and helps maintain flow continuity. Under the influence of inertia and air vents, the water flow appears in a short period of reciprocating motion after the gate closure, while the rotation rate of the pump impeller gradually decays to 0 rpm.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VOF | Volume of Fluid |
| UDF | User-Defined Function |
References
- Yan, D.F. Pumping Station Engineering; China Water Power Press: Beijing, China, 2005. [Google Scholar]
- Zhang, R.; Tan, S.Y.; Ding, X.J. Flow loss characteristics of a shaft tubular pump based on entropy production theory. Adv. Sci. Technol. Water Resour. 2022, 42, 6–12. [Google Scholar] [CrossRef]
- Yuan, R.; Jin, H.Y.; Xu, X.D. Physical model experimental analysis of bi-directional Shaft tubular pump device. Fluid Mach. 2020, 48, 7–13. [Google Scholar] [CrossRef]
- Fang, G.C.; Yang, J.F.; Kan, K.; Duan, H.L.; Guo, H.J. Hydraulic stability and dynamic stress analysis of large vertical shaft tubular pump under multiple working conditions. J. Yangtze River 2021, 52, 317–321. [Google Scholar] [CrossRef]
- Ji, D.; Lu, W.; Xu, B.; Xu, L.; Jiang, T. Study on the Energy Loss Characteristics of Shaft Tubular Pump Device under Stall Conditions Based on the Entropy Production Method. J. Mar. Sci. Eng. 2023, 11, 1521. [Google Scholar] [CrossRef]
- GB 50265-2022; Pumping Station Design Standards. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Planning Press: Shanghai, China, 2022.
- García-Chica, A.; Rodriguez-Perez, A.M.; Caparros-Mancera, J.J.; Rodríguez-Gonzalez, C.A.; Chica, R.M. Integrated photovoltaic system for rainwater collection and sustainable irrigation. Irrig. Sci. 2025, 1–11. [Google Scholar] [CrossRef]
- Li, H.; Yao, G.L. Research development of the Transition Process of Pumping Station System Shutdown. Jilin Water Conserv. 2021, 1, 32–35. [Google Scholar] [CrossRef]
- Chen, S.S.; Zhou, Z.F.; He, Z.N.; Ge, Q.; Yan, D.F. Transient process of tubular pumping station with quick-stop gate breaking flow while pump is off. J. Hohai Univ. Nat. Sci. 2008, 36, 179–184. [Google Scholar]
- Chen, S.S.; Yan, D.F.; Jiang, L.J.; Lu, W.G.; Wang, L.S. Numerical Calculation of Hydraulic Transients for a Low-head Pumping station during Its Suspending Period. J. Trans. Chin. Soc. Agric. Mach. 2004, 35, 58–60+71. [Google Scholar]
- Zhou, D.Q.; Zhang, R.T.; Qu, B.; Wang, X.S.; Yan, Y.F. Research on hydraulic transient of vertical axial-flow pumping station at power failure. J. Hohai Univ. Nat. Sci. 2006, 3, 272–275. [Google Scholar]
- Song, J. Numerical Simulation of Dynamic Behavior with Rapid-Drop Gate in Vertical Axial Pumping Station During Its Suspending Period. Ph.D. Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar]
- Hu, C.Y.; Zhang, X.W.; Tang, F.P.; Xu, X.D.; Huang, C.B.; Jing, L. Influence of Overflow Hole Diameter on Transition Process of Axial Flow Pump System. J. Trans. Chin. Soc. Agric. Mach. 2023, 54, 181–191. [Google Scholar] [CrossRef]
- Xu, W.J.; Xu, G.; Qian, C.; Ding, J.L.; Sun, Y.H.; Zhang, F.X.; Yang, F. Numerical calcu-lation and analysis of transition process of large shaft tubular pumping station. Water Resour. Power 2025, 43, 120–123+184. [Google Scholar] [CrossRef]
- Ding, C. Simulink Simulation of Low-Lift Pump Installation during Pump Stop. Guangdong Water Resour. Hydropower 2020, 9, 33–37. [Google Scholar]
- Xia, H.P. Study on Transition Process of Starting and Stopping of Vertical Shaft Crossflow Pump System. Ph.D. Thesis, Yangzhou University, Yangzhou, China, 2019. [Google Scholar]
- Jiao, H.F. Study on the Characteristics of the Start-up and Shutdown Transition Process of the Bi-Directional Full-Flow Pump. Ph.D. Thesis, Yangzhou University, Yangzhou, China, 2024. [Google Scholar]
- Jiao, H.F.; Chen, Z.G.; Wang, W.; Chen, S.S. Hydraulic Characteristics of Motor-pump during Shutdown Transition Process. Trans. Chin. Soc. Agric. Mach. 2023, 54, 236–245. [Google Scholar] [CrossRef]
- Li, Y.Y.; Guo, P.P.; Cao, M.J.; Sun, L.G. Investigation into the Energy Loss Mechanism of Pump Turbine During the Runaway Process Based on Entropy Production Theory. J. Phys. Conf. Ser. 2024, 2854, 012047. [Google Scholar] [CrossRef]
- Man, Z.; Xu, Z.; Gui, Z.H.; Han, W.F.; Zhao, Y.F.; Zhang, F.; Xu, L.C.; Zheng, Y.; Kan, K. Research on the performance of pump-turbine during the transition process from pump mode to turbine mode. Front. Energy Res. 2024, 12, 1421865. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Z.; Zheng, Y. Study on shutdown transition process of large low head pumping station. J. Water Conserv. Constr. Manag. 2020, 40, 73–79. [Google Scholar] [CrossRef]
- Luo, W.; Chen, J. The simple algorithm of stop-pump water hammer. J. Drain. Irrig. Mach. Eng. 2005, 2, 16–19. [Google Scholar]
- Fan, X.J.; Song, B.B.; Xia, Y.B. Analysis of Water Hammer Protection in High Lift Water Pump System. Yellow River 2022, 44, 136–139+144. [Google Scholar] [CrossRef]
- Yang, J.J.; Gao, X.L. Study on transition process calculation and water hammer protection measures of pumping station. Shaanxi Water Resour. 2024, 11, 101–105. [Google Scholar] [CrossRef]
- Zhong, G.C.; Shao, C.L. Numerical simulation of gas-liquid twp-phase flow in pump during transition process of cutting off gas. Light Ind. Mach. 2021, 39, 30–36+42. [Google Scholar] [CrossRef]
- Kan, K.; Chen, H.; Zheng, Y.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2020, 164, 109–121. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Li, Z.H.; Liao, W.L.; Luo, X.Q. Numerical investigation of free surface effect on performance of bulb turbine. J. Hydroelectr. Eng. 2018, 37, 8–14. [Google Scholar] [CrossRef]
- Zhang, F.L. Protection of water hammer in pumping station by air vents. Shandong Water Resour. 2011, 3, 16+18. [Google Scholar] [CrossRef]
- Liu, Z.R. Calculation of water hammer and protective measures for stopping pump. Gansu Shuili Shuidian Jishu 2004, 3, 235–236+238. [Google Scholar]
- Hua, Y. Analysis of Unsteady Flow in Hydraulic Turbine with Dynamic Mesh Technology. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2009. [Google Scholar]
- Kan, K.; Zheng, Y.; Chen, H.X.; Zhou, D.Q.; Dai, J.; Binama, M.; Yu, A. Numerical simulation of transient flow in a shaft extension tubular pump unit during runaway process caused by power failure. Renew. Energy 2020, 154, 1153–1164. [Google Scholar] [CrossRef]
- Ge, X.F.; Zhang, J.; Zhang, J.; Liu, D.M.; Zheng, Y.; Chen, H.X. Review of Research on the Three-Dimensional Transition Process of Large-Scale Low-Lift Pump. Energies 2022, 15, 8338. [Google Scholar] [CrossRef]
- Zhang, X.W.; Tang, F.P.; Liu, C.; Shi, L.J.; Liu, H.Y.; Sun, Z.Z.; Hu, W.Z. Numerical Simulation of Transient Characteristics of Start-Up Transition Process of Large Vertical Siphon Axial Flow Pump station. Front. Energy Res. 2021, 9, 706975. [Google Scholar] [CrossRef]
- Ahn, S.H.; Xiao, Y.; Wang, Z.; Zhou, X.; Luo, Y. Numerical prediction on the effect of free surface vortex on intake flow characteristics for tidal power station. Renew. Energy 2017, 101, 617–628. [Google Scholar] [CrossRef]


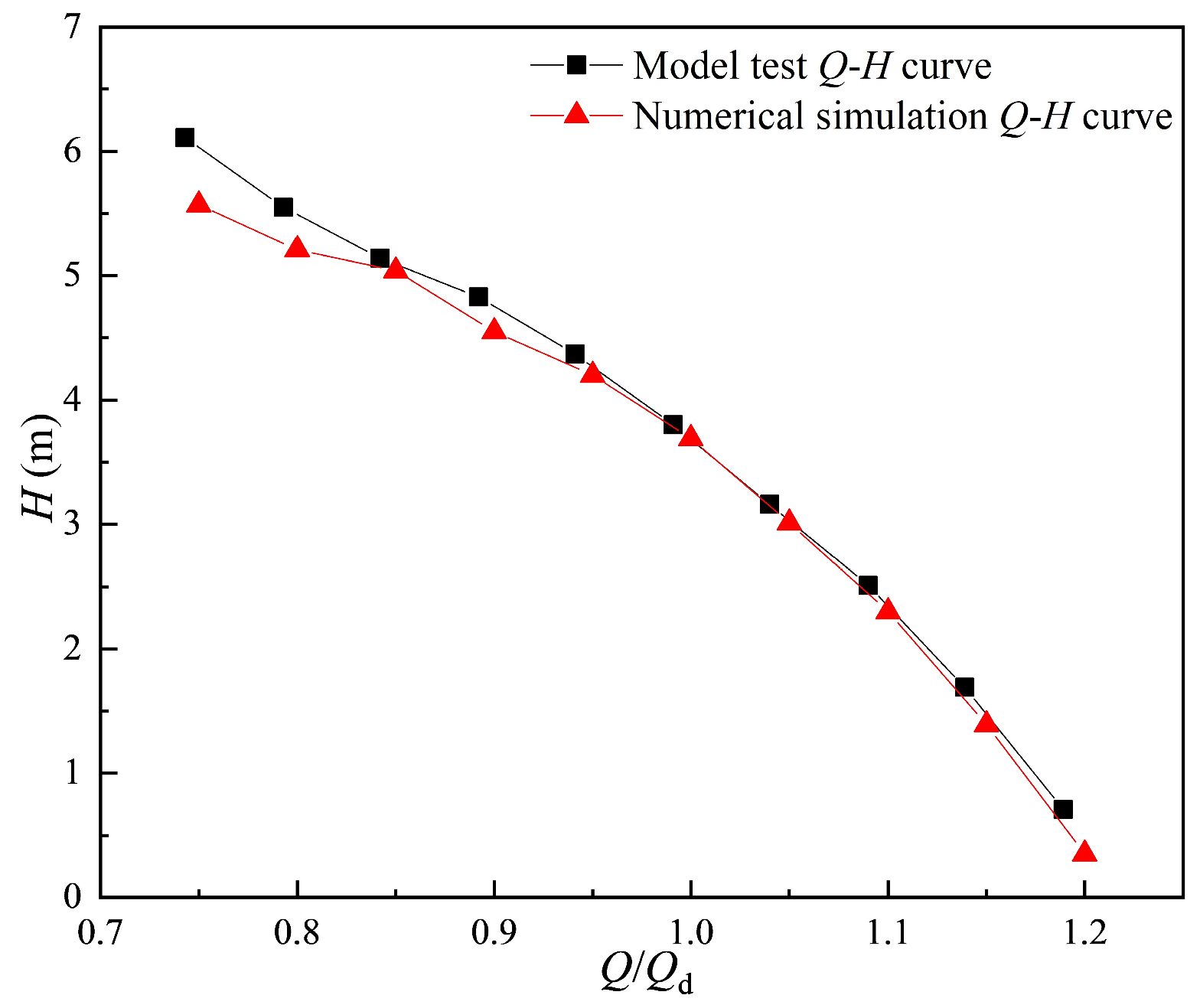

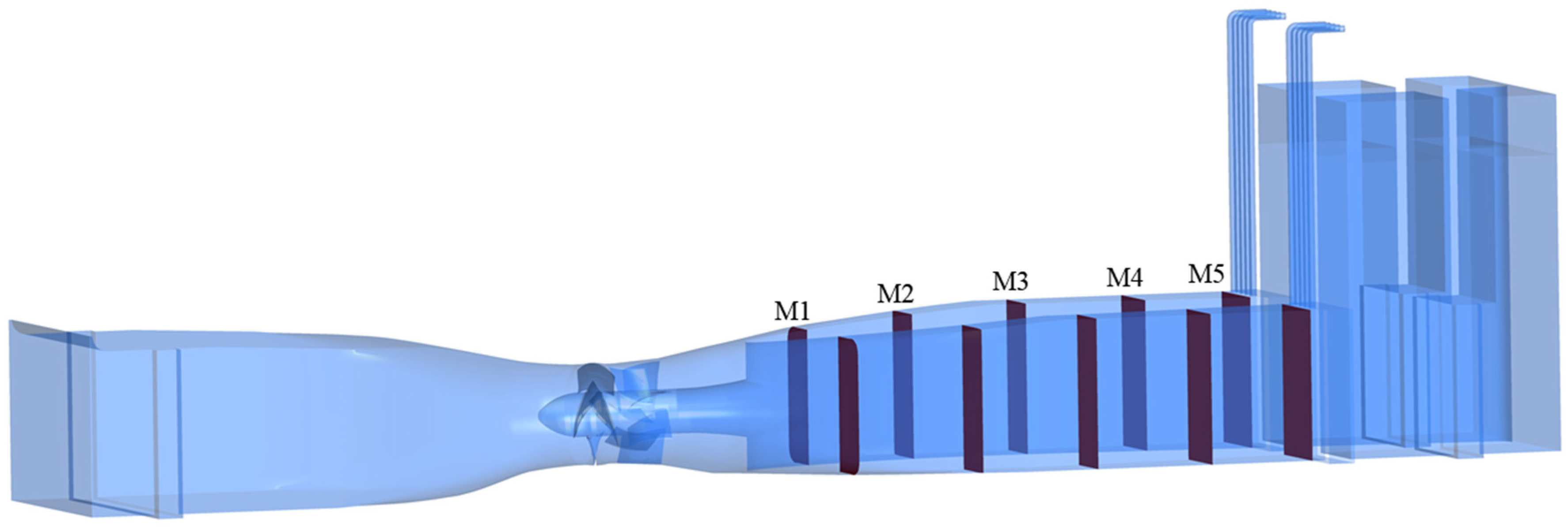
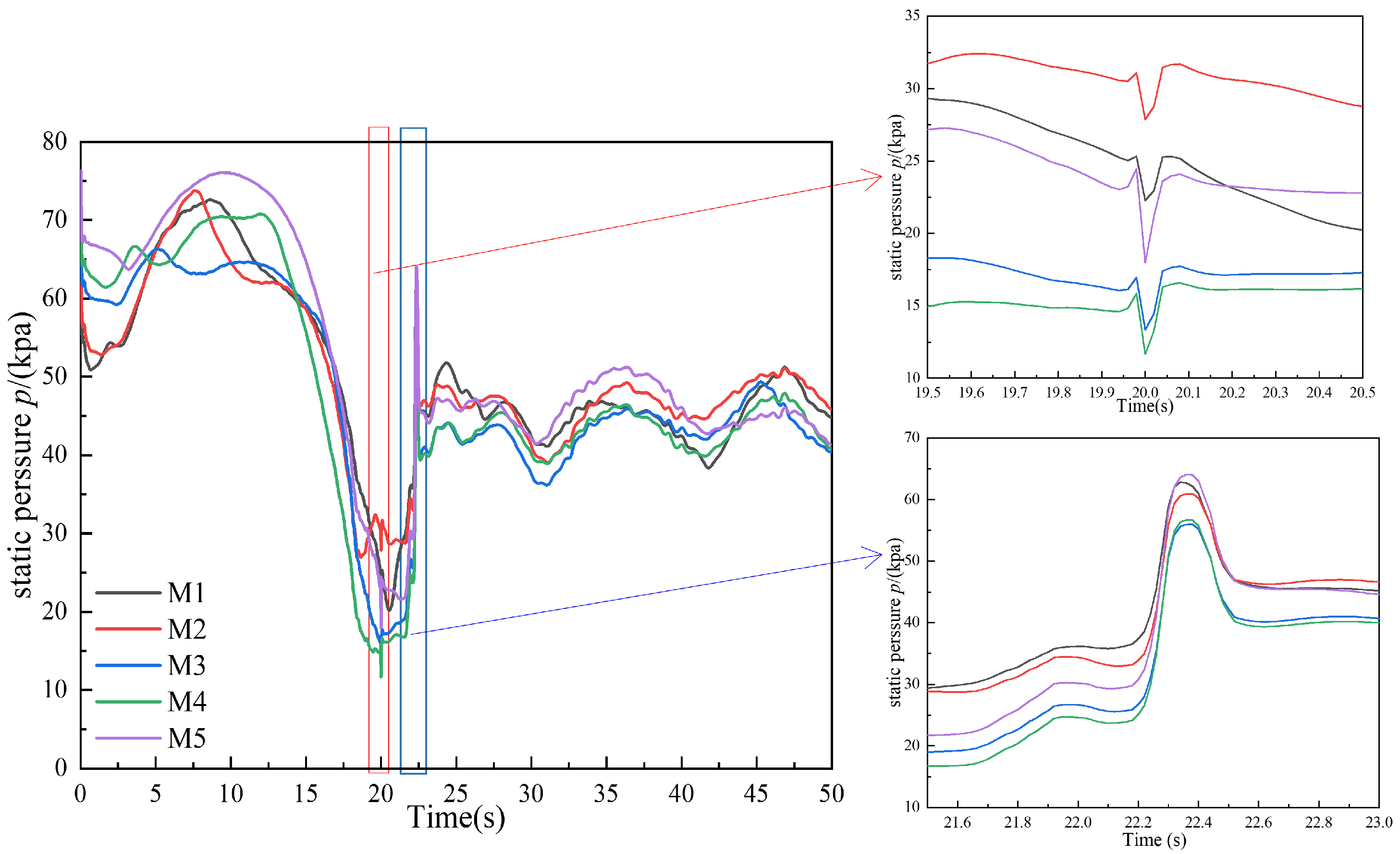

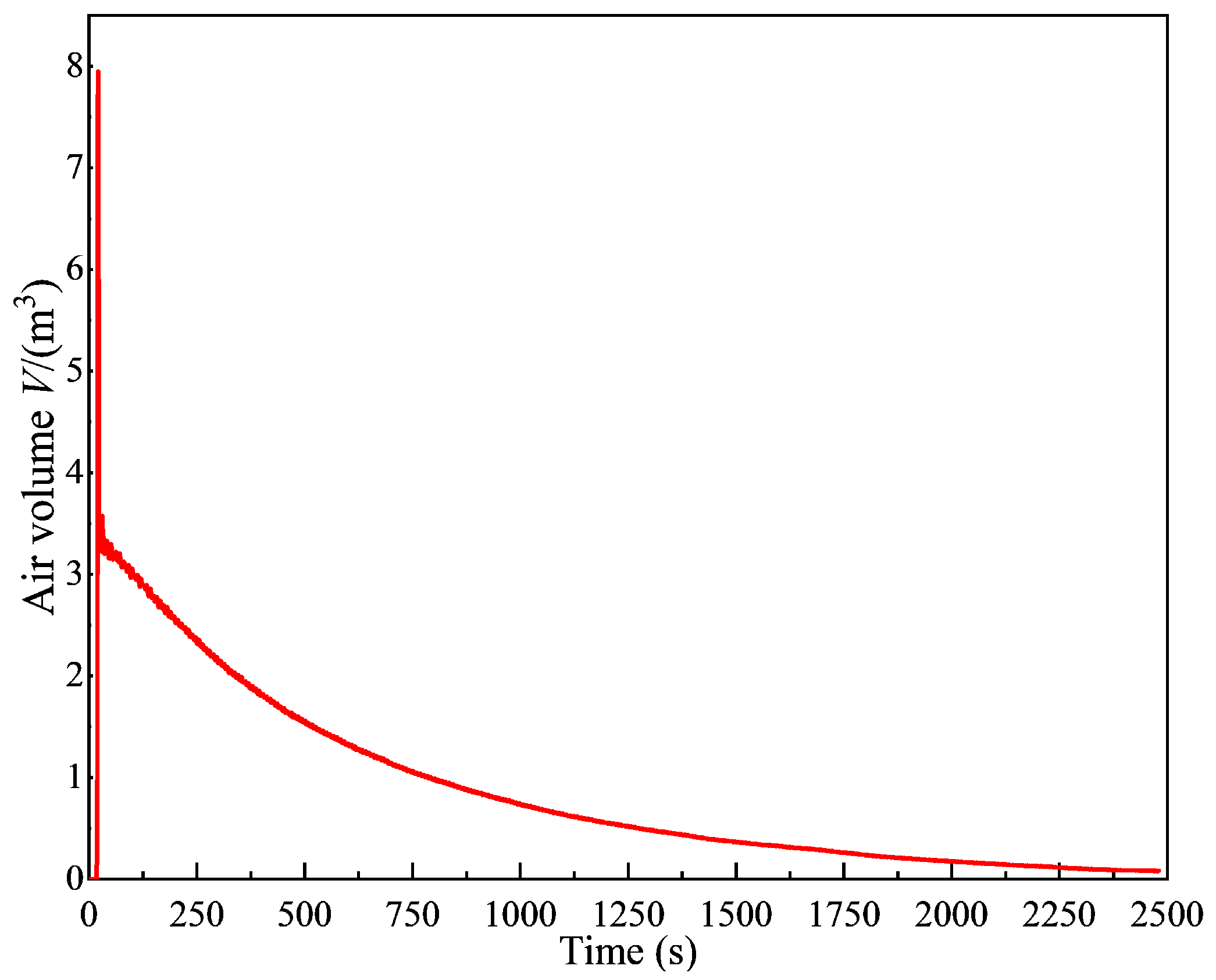





| Measuring Parameters | Test Instrument | Instrument Model | Measuring Error |
|---|---|---|---|
| Head | Differential pressure transmitter | LDG-500s | ±0.1% |
| Flow rate | Electromagnetic flowmeter | V15712-HD1A1D7D | ±0.2% |
| Torque and rotation speed | Torque and speed sensor | JCZL2-500 | ±0.1% |
| Scheme | Opening Degrees |
|---|---|
| synchronous shutdown | 100% |
| asynchronous shutdown-F1 | 75% |
| asynchronous shutdown-F2 | 60% |
| asynchronous shutdown-F3 | 45% |
| asynchronous shutdown-F4 | 30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Lu, W.; Xu, L.; Duan, H.; Zhu, B. Study on Shutdown Process of Agricultural Irrigation Pump Device. Agriculture 2025, 15, 2241. https://doi.org/10.3390/agriculture15212241
Cao W, Lu W, Xu L, Duan H, Zhu B. Study on Shutdown Process of Agricultural Irrigation Pump Device. Agriculture. 2025; 15(21):2241. https://doi.org/10.3390/agriculture15212241
Chicago/Turabian StyleCao, Weiwei, Weigang Lu, Lei Xu, Hongfei Duan, and Bo Zhu. 2025. "Study on Shutdown Process of Agricultural Irrigation Pump Device" Agriculture 15, no. 21: 2241. https://doi.org/10.3390/agriculture15212241
APA StyleCao, W., Lu, W., Xu, L., Duan, H., & Zhu, B. (2025). Study on Shutdown Process of Agricultural Irrigation Pump Device. Agriculture, 15(21), 2241. https://doi.org/10.3390/agriculture15212241




