Influence of Air Layer Characteristics on the Heat Transfer Performance of Photovoltaic Dairy Barn Roofs

Abstract

To enhance energy utilization efficiency, dairy farmers have increasingly adopted photovoltaic (PV) panels on barn roofs. However, there is currently a general separation between the barn construction and the additional aspects of the PV system. It is unclear to dairy farmers whether rooftop PV panels will have an impact on the dairy barn, particularly on the thermal environment. This study investigated the influence of air layer properties, specifically thickness and ventilation conditions, on the thermal performance of PV dairy barn roofs. Utilizing the harmonic analysis method, the study quantified its dynamic thermal properties. The results demonstrated that increasing the air layer thickness in ventilated roofs decreases heat flux and improves thermal resistance (1.67–2.15 times higher than non-PV roofs). In contrast, sealed air layers exhibit consistently high thermal resistance (up to 3.33 times higher). Optimizing ventilated air layer thickness (0.20–0.30 m) effectively minimizes heat ingress and prevents PV efficiency degradation. These results provide valuable insights for optimizing the design of energy-efficient PV dairy barns, enhancing thermal comfort, and contributing to low-carbon energy solutions in livestock facilities.

1. Introduction

Livestock systems contribute to 6.2 Gt CO₂ equivalent emissions, constituting approximately 12 percent of all anthropogenic greenhouse gas (GHG) emissions [1]. Given this substantial contribution, integrating photovoltaic (PV) systems into dairy barns offers a promising approach to mitigate emissions while enhancing energy efficiency and thermal comfort for livestock. PV technology offers a sustainable solution to the growing global demand for clean energy. China is actively promoting a development model that integrates distributed PV systems into dairy operations [2]. As PV technology becomes more prevalent in agriculture, research has increasingly focused on PV barns. It is not clear to dairy farmers whether rooftop PV panels will have an impact on the dairy barn, particularly how roof configurations affect their internal thermal environments [3]. Building-attached photovoltaic (BAPV) systems create an insulating air layer between the panels and the roof, which primarily affects heat transfer through conduction, convection, and radiation, thereby influencing the overall thermal performance of the roof.

Studies on heat transfer through air layers in indoor environments have extensively examined the thermal behavior of these systems. Installing PV systems on existing building roofs can limit energy infiltration into interiors, thereby reducing heat gain and improving the thermal insulation performance of building envelopes [4]. The study of air layer characteristics in building envelopes holds significant theoretical and practical value. Research shows that air layers effectively regulate thermal environments: airflow removes heat and reduces roof surface temperature [5], with tilt angle and ventilation design critically affecting convective heat transfer efficiency [6]. Numerical simulations demonstrate that optimized air layer structures can reduce roof heat transfer by up to 30% [7] while providing dual functions of thermal insulation and heat dissipation [8]. These characteristics not only enhance building energy efficiency (reducing cooling loads by 15–40%) but also synergize with photovoltaic systems, proving crucial for achieving carbon-neutral buildings. Within agricultural applications, Tikul et al. optimized roof geometries and materials for tropical beef cattle barns [9]. Pan et al. performed comparative numerical simulations of thermal environments in farm buildings with diverse roof designs [10]. These studies collectively emphasize the need for further research on the thermal performance of PV dairy barn roofs.

Existing research primarily focuses on civil buildings, and studies on livestock housing are relatively scarce. Analysis of existing models indicates that livestock housing roofs often feature greater length and material diversity compared to conventional structures [11]. These characteristics significantly impact both fluid dynamics within air layers and roof heat transfer mechanisms. The elongated roof profile directly impacts boundary layer development, airflow velocity distribution, and thermal uniformity along the air channel. Current methodologies predominantly rely on computational fluid dynamics (CFD) simulations [12]. However, some studies use oversimplified approaches to calculate convective heat transfer coefficients [13,14]. Moreover, certain methodologies fail to adequately address the unique environmental and operational conditions of air layers in dairy barn roofs [15]. In parallel, China has prioritized the development of PV dairy farming systems in recent years. This initiative has sparked practical inquiries from agricultural stakeholders regarding the potential of PV systems to enhance thermal insulation performance in barn roof design. However, the specific impact of air layer characteristics on the thermal performance of PV dairy barn roofs remains underexplored, particularly in the context of varying air layer thickness. While prior studies have examined PV roofs in civil structures, critical knowledge gaps persist for livestock-specific applications—particularly regarding how extreme roof lengths impact air layer dynamics, and how material limitations constrain thermal regulation. Addressing these gaps is crucial for optimizing barn design, enhancing energy efficiency, and reducing carbon emissions in dairy farming operations.

For periodic temperature fluctuations in multilayer structures with complex boundary conditions, the harmonic analysis method is particularly suitable due to its ability to efficiently evaluate dynamic thermal performance while maintaining computational efficiency [16]. Compared to traditional steady-state analysis methods, harmonic analysis effectively captures transient heat transfer characteristics, making it especially applicable to non-steady-state thermal environment studies in agricultural buildings influenced by diurnal and seasonal cycles. Building on this, the study progresses through a structured framework: (1) Integrate summer field test data with harmonic analysis to systematically investigate the thermodynamic characteristics of air layers in PV dairy barn roofs. (2) Develop a mathematical model to quantify the impact of key parameters (e.g., air layer thickness and ventilation conditions) on roof heat transfer performance. (3) Validate equivalent thermal resistance properties under different air layer configurations (ventilated vs. sealed) to clarify heat flux attenuation and time lag effects. (4) Propose optimization criteria based on dynamic thermal performance to guide the selection of air layer thickness in PV barn roof design. The findings aim to enhance energy efficiency and support carbon neutrality goals in livestock facilities through technical innovation and theoretical advancements.

2. Materials and Methods

2.1. Overview of the Test Barn

The experimental site was an open dairy barn located on a cattle farm in Dongying City, Shandong Province, China (37°29′29″ N, 118°17′56″ E), as shown in Figure 1. Dongying has a temperate monsoon continental climate with hot and rainy summers and high humidity. The barn housed 920 cows and utilized mixed ventilation. The barn measured 32 m in span, 372 m in length, and 4.5 m in eave height. The roof had a slope angle θ of 17.17°, oriented 46.24° northwest in a gable direction, and was constructed with a single-layer color steel plate without insulation. The building structure employed the portal frame structure, with color steel panels made of hot-dip galvanized steel sheets—both representing the standard structural form and materials for modern dairy barns. A total of 1152 PV modules (total capacity: 299.52 kW) were installed on the south-facing roof of the western section, while the eastern section’s south-facing roof and both sections’ north-facing roofs remained unmodified. The PV panels covered the roof area of 1886 m². For clarity, all subsequent references to “roof” in this study specifically refer to the south-facing roof. A ventilated air layer was established between the PV panels and the roof, with a length l of 12.12 m, an inlet-outlet height differential h of 3.75 m, and a thickness δ_a of 0.12 m. The PV mounting structure was universal.

2.2. Thermal Environment Testing of the Test Barn

This study monitored indoor and outdoor barn environments for dry-bulb temperature, relative humidity, wind speed, and solar radiation intensity. Data were collected from 5 June to 17 September 2023. The east area of the barn (unmodified roof configuration) was the control group, while the west area (PV-equipped roof configuration) was the test group. To confirm independence between roof sections, the same parameters were measured in another identical barn. The Scheirer-Ray-Hare test for nonparametric two-way ANOVA analysis. The data was used for subsequent calculations.

Dry-bulb temperature and relative humidity were continuously monitored using a UT330-USB datalogger (Uni-Trend Technology (China) Co., Ltd., Dongguan, China; accuracy: ±0.5 °C for dry-bulb temperature and ±3% for relative humidity; interval: 1 h), positioned 2.0 m above ground level. Wind speed was measured with a Kestrel 5500 weather meter (Nielsen-Kellerman Co., Ltd., Boothwyn, US; accuracy: ±0.1 m·s⁻¹; interval: 1 h), installed at 1.5 m height. Solar radiation intensity was recorded using a TES-1333R solar power meter (TES Electrical Electronic Co., Ltd., Taibei, China; accuracy: ±10 W·m⁻²; interval: 1 min), mounted at 1.5 m elevation.

2.3. PV Roof Design

Three conditions were established to evaluate the thermal performance of the roof under distinct design scenarios:

Condition A: A monolithic single-layer color steel plate roof (no additional modifications), as depicted in Figure 2a.

Condition B: A composite roof combining a single-layer color steel plate with PV panels, creating a ventilated air layer (open) at varying air layer thicknesses, as depicted in Figure 2b.

Condition C: A composite roof integrating a single-layer color steel plate with PV panels, forming a sealed air layer (enclosed) at varying air layer thicknesses, as depicted in Figure 2c.

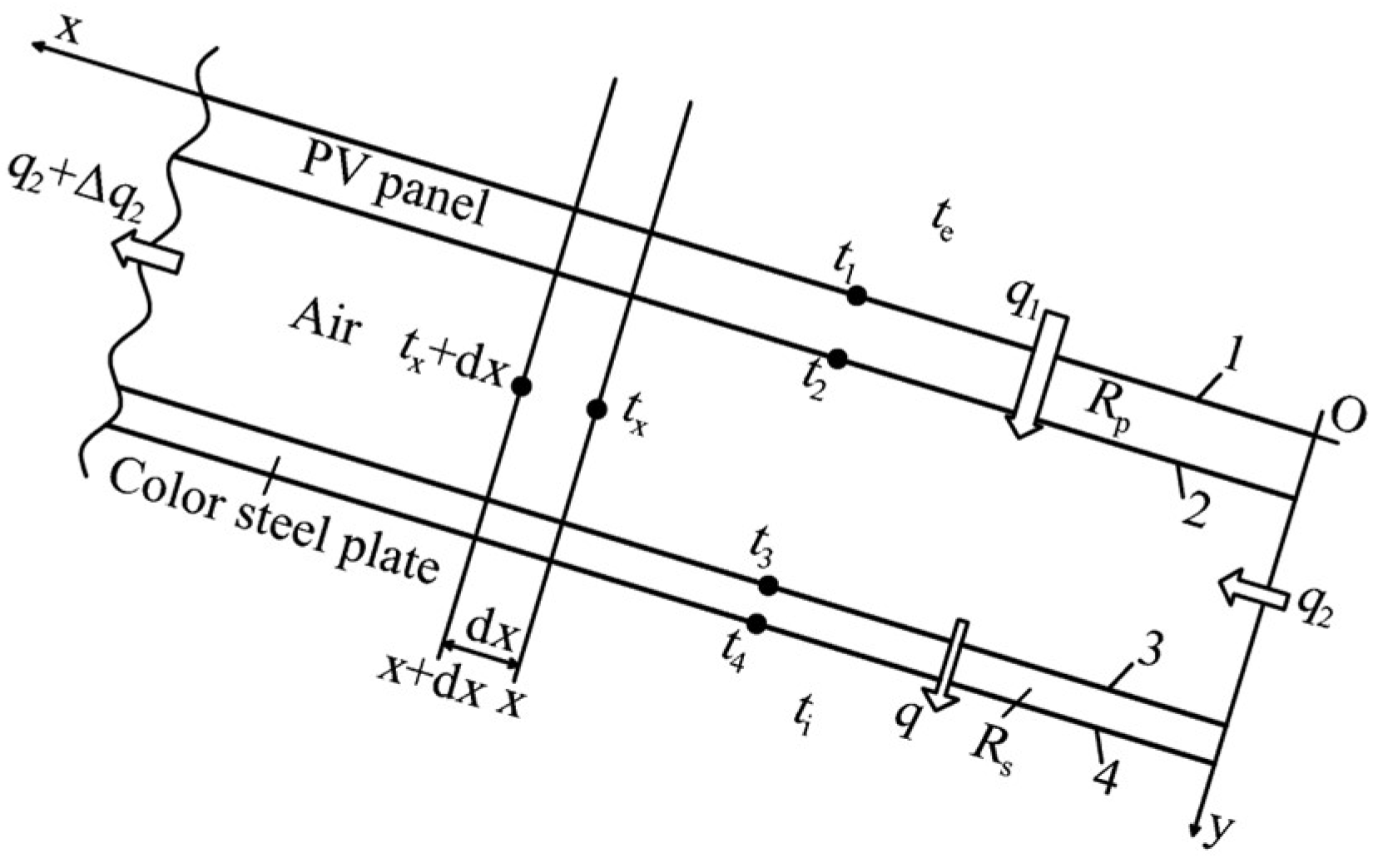
2.4. Heat Transfer Modeling

2.4.1. Thermal Performance Indicators for Roofs

This study employed the harmonic analysis method to evaluate the thermal performance of the PV dairy barn roofs. The data on which the calculations were based is the aforementioned thermal environment test data. The outdoor air temperature t_e (°C) was modeled as a periodic harmonic fluctuation around its mean value t_e0 (°C) with an amplitude of A_te and a period of T (h). The temperature at time Z (h) is defined as:

$$\begin{array}{c}\begin{array}{c}{t}_{\mathrm{e}}=\end{array}{t}_{\mathrm{e}0}+A_{t_e}\cos \left(2\mathsf{\pi }Z/T\right).\end{array}$$

(1)

Thermal performance indicators, including thermal resistance R (m²·K·W⁻¹), heat storage coefficient S (W·m⁻²·K⁻¹), thermal inertness index D (dimensionless), and outdoor sol-air temperature t_se (°C), were derived from the Thermal Design Code for Civil Buildings (GB 50176-2016) [17]. The thermophysical properties of air were obtained from standard tables [16] using linear interpolation. The amplitude A_tse (°C) and peak time Z_tse (h) of the integrated outdoor temperature were calculated based on these parameters. The characteristic number correlation equation for the mean convective heat transfer coefficients of the inner and outer surfaces of the barn roof is expressed as [18]:

$$\begin{array}{c}\begin{array}{c}Nu=\end{array}0.037\left(R{e}^{0.8}-23,500\right)P{r}^{1/3} (0.6<Pr<60),\end{array}$$

(2)

where Nu is the Nusselt number (dimensionless). Re is the Reynolds number (dimensionless). Pr is the Prandtl number (dimensionless). The calculated h_e and h_i represent the convective heat transfer coefficients for the outer and inner surfaces, respectively, in units of W·m⁻²·K⁻¹.

For varying operational conditions, the surface heat storage coefficient Y (W·m⁻²·K⁻¹) and the damping factor ν (dimensionless) were derived using the generalized equation for any layer n and its preceding layer n − 1:

$$\begin{array}{c}\begin{array}{c}{Y}_n=\end{array}{\displaystyle \frac{S_n\sqrt{i}\tanh R_n{S}_n\sqrt{i}+Y_{n-1}}{1+Y_{n-1}/S_n\sqrt{i}\cdot \tanh R_n{S}_n\sqrt{i}}},\end{array}$$

(3)

$$\begin{array}{c}\begin{array}{c}{\nu }_n=\end{array}{e}^{R_n{S}_n\sqrt{i}{\displaystyle \frac{S_n\sqrt{i}+Y_{n-1}}{S_n\sqrt{i}+Y_n}}},\end{array}$$

(4)

where i is the imaginary unit. R_n (m²·K·W⁻¹) and S_n (W·m⁻²·K⁻¹) are thermal resistance and coefficient of heat accumulation of the nth layer, respectively, n = 1, 2, 3, …

The total delay time ∑ε (h) is determined by Equation (5):

$$\begin{array}{c}\begin{array}{c}\sum \epsilon =\end{array}\left({\tan }^{-1}{\displaystyle \frac{1}{1+\sqrt{2}{h}_{\mathrm{e}}/Y_1}}-{\tan }^{-1}{\displaystyle \frac{1}{1+\sqrt{2}{Y}_{\mathrm{r}}/h_{\mathrm{i}}}}\right)\times {\displaystyle \frac{T}{360}}+{\displaystyle \frac{T}{2\mathsf{\pi }\sqrt{2}}}\sum R_n{S}_n,\end{array}$$

(5)

where Y_r is the heat storage coefficient of the inner surface of the envelope when the fluctuation is reversed, in units of W·m⁻²·K⁻¹.

2.4.2. Calculations for Different Conditions

1.

Condition A:

The mean heat flux q₀ (W·m⁻²) entering the barn through the roof was calculated using the fundamental law of thermal conductivity [16]. The amplitude A_q (W·m⁻²) and peak time Z_q (h) of the heat flux were derived from Equations (6) and (7), respectively:

$$\begin{array}{c}\begin{array}{c}{A}_q=\end{array}{A}_{t_{\mathrm{se}}}{h}_{\mathrm{i}}/\nu ,\end{array}$$

(6)

$$\begin{array}{c}\begin{array}{c}{Z}_q=Z_{t_{\mathrm{se}}}+\end{array}\sum \epsilon .\end{array}$$

(7)

2.

Condition B:

A ventilated air layer structure is established between the color steel plate and the PV panel, as depicted in Figure 3. The thermal resistances of the PV panel and the color steel plate are R_p and R_s, respectively, both in units of m²·K·W⁻¹. A structural unit dx at position x is analyzed, where t_x (°C) represents the air temperature of the air layer at x. The heat flux entering the air layer through the PV panels is q₁, the heat flux of the air flowing into the air layer is q₂, the heat flux of the air flowing out of the air layer is q₂ + Δq₂, and the heat flux entering the barn through the color steel plate is q, all in units of W·m⁻². The temperatures t₁, t₂, t₃, and t₄ correspond to the temperatures of walls 1, 2, 3, and 4, respectively, all in units of °C. The thermal conditions were analyzed based on the study of Bagusowski [19].

The wind speed u_a (m·s⁻¹) in the ventilated air layer and the integrated temperature of the air layer at x, t_sx (°C) were calculated using Equations (8)–(10):

$$\begin{array}{c}\begin{array}{c}{u}_{\mathrm{a}}=\end{array}\sqrt{0.08h\left(t_{\mathrm{s}x}-t_{\mathrm{e}}\right)/\xi },\end{array}$$

(8)

$$\begin{array}{c}\begin{array}{c}{t}_{\mathrm{s}x}=\end{array}{\displaystyle \frac{h_{\mathrm{r}}{t}_2+h_{\mathrm{c}}{t}_x}{h_{\mathrm{r}}+h_{\mathrm{c}}}},\end{array}$$

(9)

$$\begin{array}{c}\begin{array}{c}{h}_{\mathrm{r}}=\end{array}{C}_0{\epsilon }_{\mathrm{s}}b\phi ,\end{array}$$

(10)

where ξ is the total local resistance factor (dimensionless). h_r is the radiative heat transfer coefficient of the air layer surfaces (W·m⁻²·K⁻¹). h_c is the convective heat transfer coefficient of the air layer surface (W·m⁻²·K⁻¹). C₀ is the blackbody radiative coefficient (5.67 W·m⁻²·K⁻⁴). ε_s is the relative radiation coefficient (dimensionless). b is the temperature difference correction factor (K³). φ is the view factor (dimensionless). For the characteristic number correlation equation of h_c, the modified Gnilinski formula [20] was used:

$$\begin{array}{c}\begin{array}{c}Nu=\end{array}{\displaystyle \frac{\left(f/8\right)\left(Re-1000\right)Pr}{1+12.7\sqrt{f/8}\left(P{r}^{2/3}-1\right)}}\left[1+{\left(2{\delta }_{\mathrm{a}}/l\right)}^{2/3}\right]c_{\mathrm{t}}\epsilon (0.5\le Pr\le 2000,3000\le Re\le 5\times {10}^6),\end{array}$$

(11)

where $f={\left(1.82\lg Re-1.64\right)}^{-2}$. f is the Darcy friction factor for turbulent flow in the tube (dimensionless). c_t is the temperature correction factor (dimensionless). ε is the correction factor (dimensionless), which depends on the body size l/δ_a (dimensionless) of the ventilated air layer, as shown in

Table 1. Correction coefficient (ε) varies with body size (l/δ_a) of ventilated air layer.

Index	Value
l/δa	20	30	40	60	80	≥100
ε	1.28	1.18	1.13	1.05	1.02	1.00

, and is calculated by linear interpolation:

The heat balance equations for the roof structural unit dx have the following form, from which the mean air temperature t_a0 in the air layer can be calculated. Subsequently, the mean heat flux q₀ entering the barn through the roof can be determined:

$$\left\{\begin{array}{l}{h}_{\mathrm{e}}\left(t_{\mathrm{se}}-t_1\right)+\left(t_2-t_1\right)/R_{\mathrm{p}}=0\\ \left(t_{\mathrm{se}}-t_1\right)/\left(1/h_{\mathrm{e}}+R_{\mathrm{p}}\right)+h_{\mathrm{c}}\left(t_x-t_2\right)+h_r\left(t_3-t_2\right)=0\\ h_{\mathrm{c}}\left(t_x-t_2\right)\mathrm{d}x+h_{\mathrm{c}}\left(t_x-t_3\right)\mathrm{d}x-Gc\mathrm{d}{t}_x=0\\ h_r\left(t_2-t_3\right)+h_{\mathrm{c}}\left(t_x-t_3\right)+\left(t_{\mathrm{i}}-t_3\right)/\left(1/h_{\mathrm{i}}+R_{\mathrm{c}}\right)=0\\ \left(t_3-t_4\right)/R_{\mathrm{s}}+h_{\mathrm{i}}\left(t_{\mathrm{i}}-t_4\right)=0,\end{array}\right.$$

(12)

where $\begin{array}{c}\begin{array}{c}G=v_{\mathrm{a}}{\delta }_{\mathrm{a}}\end{array}{\rho }_{\mathrm{a}}\end{array}$, G is the volume of air passing through the air layer when the width of the air layer is 1 m (kg·s⁻¹). ρ_a is the air density (kg·m⁻³).

The air temperature differential equation for the air temperature wave in the air layer unit dx has the following form, from which the amplitude A_ta of the air temperature in the air layer, the peak time Z_ta of the air temperature in the air layer, and the amplitude A_q of the heat flux entering the barn through the roof can be calculated:

$$\begin{array}{c}\begin{array}{c}{h}_{\mathrm{c}}\left({\dot{t}}_{\mathrm{se}}/{\dot{\nu }}_1\mathrm{d}x+{\dot{t}}_1/{\dot{\nu }}_3\mathrm{d}x\right)-Gc\mathrm{d}{\dot{t}}_x-\sum \dot{B}\mathrm{d}x{\dot{t}}_x=\end{array}0.\end{array}$$

(13)

The boundary conditions have the following form: when $x=0$, ${\dot{t}}_x={\dot{t}}_{\mathrm{o}}$. Where ∑$\dot{B}$ is the total heat absorption coefficient of both surfaces inside the air layer (W·m⁻²·K⁻¹). The values of $\dot{t}$, $\dot{\nu }$, $\dot{B}$, and $\dot{Y}$ are quantities with corresponding amplitudes over time.

The peak time Z_q of the heat flux entering the barn through the roof is calculated using Equation (14):

$$\begin{array}{c}\begin{array}{c}{Z}_q=Z_{t_{\mathrm{a}}}+\end{array}\sum \epsilon .\end{array}$$

(14)

3.

Condition C:

The roof was constructed with a single-layer color steel plate overlapped with PV panels, forming a sealed air layer. A sealed air layer structure was established between the color steel plate and the PV panel. For the characteristic correlation equation of h_c for the sealed air layer, the correlation equation was corrected based on Hollands’s study [21]:

$$\begin{array}{c}\begin{array}{c}Nu=1+1.44\left[1-1708/\left(Ra\cos \theta \right)\right]\left[1-1708{\left(\sin 1.8\theta \right)}^{1.6}/\left(Ra\cos \theta \right)\right]+\left[{\left(Ra\cos \theta /5830\right)}^{1/3}-1\right]\end{array},\end{array}$$

(15)

where Ra is the Rayleigh number (dimensionless).

The radiative heat transfer coefficient h_r between the surfaces on both sides of the air layer was calculated using the same method as described in Equation (10). The mean air temperature t_a0, its amplitude A_ta, and peak time Z_ta of the sealed air layer were calculated using the same approach as in Condition B. These values were then used to determine the mean heat flux q₀ entering the barn through the roof, its amplitude A_q, and peak time Z_q.

2.5. Correlation Equation Validation Methodology

For the modified characteristic number correlation equation, the thermal boundary layer thickness of the air layer was used for validation. The equation for the thermal boundary layer thickness is referenced in [22]:

$${\delta }_{\mathrm{t}}=0.376xR{e}^{-1/5},$$

(16)

where δ_t is the thermal boundary layer thickness.

When δ_a exceeds a critical value, the correlation equation for the mean convective heat transfer coefficient of the ventilated air layer should be approximated as the correlation equation for the longitudinal flow over a flat plate, calculated according to the method described in [14]:

$$Nu=0.037R{e}^{4/5}P{r}^{1/3}(0.6<Pr<60).$$

(17)

3. Results and Discussion

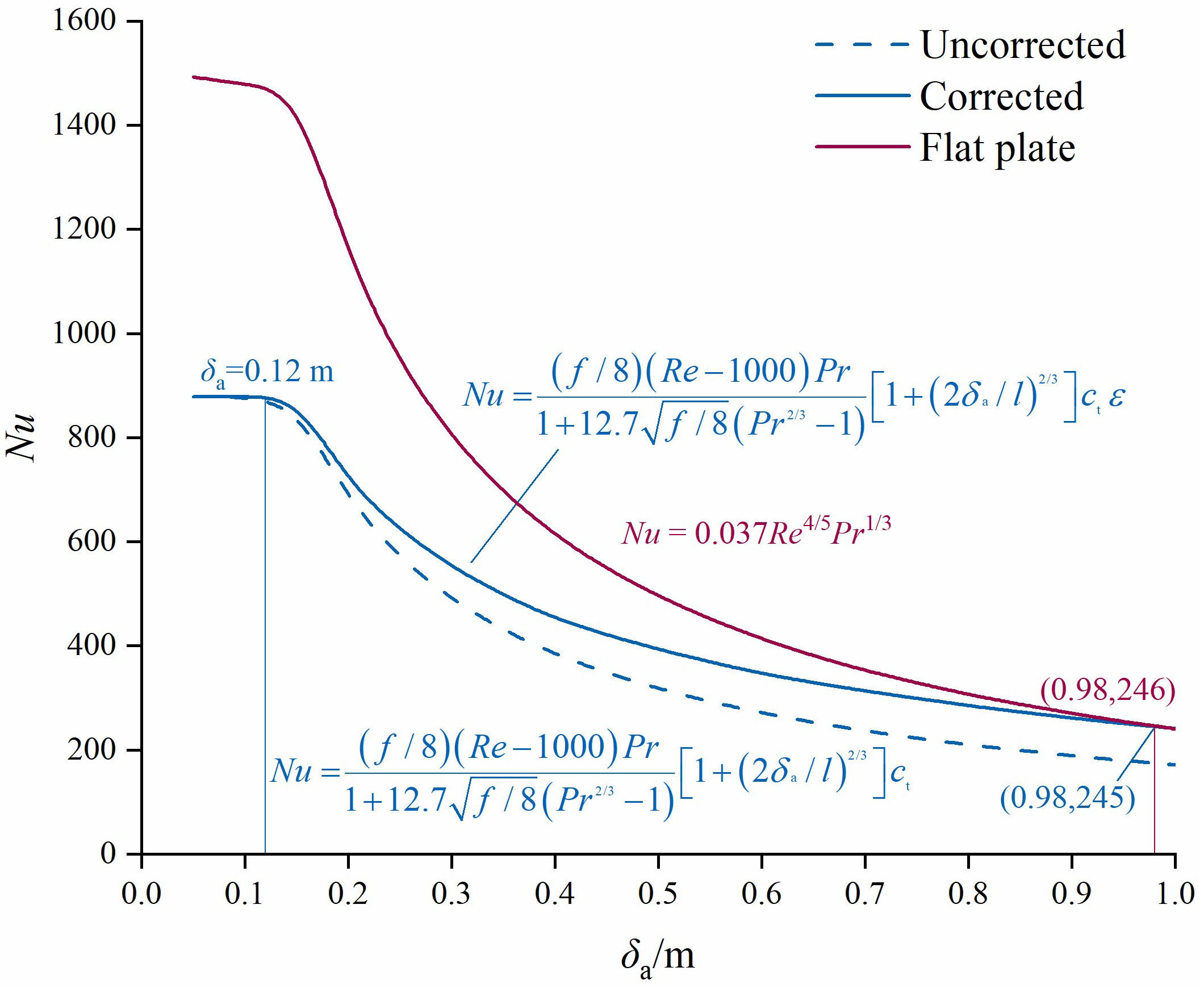
3.1. Corrections to Relevant Calculation Formulas for PV Dairy Barns

For the characteristic number correlation of the mean convective heat transfer coefficient in the ventilated air layer, the Gnielinski formula was referenced. The Gnielinski formula is currently the most accurate correlation available for turbulent forced convective heat transfer in pipes [16]. However, the model for turbulent convective heat transfer in pipes was not entirely identical to that in ventilated air layers. Therefore, the Gnielinski formula was not entirely applicable to the calculation of turbulent convective heat transfer in ventilated air layers, particularly when the body size of the ventilated air layer (l/δ_a) is less than 40, where significant errors occur. As shown in Figure 4, when l/δ_a was less than 40, the error exceeded 13%. Corrections were necessary. Bagusrovsky’s study on ventilated air layers proposed correction coefficients in Table 1 [19]. However, the characteristic number correlation equation he proposed was applied to steady-state convective heat transfer, while his proposed characteristic number correlation equation for unsteady-state turbulent heat transfer was relatively concise but rough, considering only the air layer thickness and airflow velocity. This did not apply to this study. Therefore, this study applied the correction coefficients to the Gnielinski formula. The boundary layer approximation method was widely used to solve natural convection in air layers under various boundary conditions [23]. The boundary layer developed along the airflow direction, with the maximum thickness occurring at the end [24]. The results are shown in Figure 4. When the air layer thickness reached the critical value equal to the air boundary layer thickness (δ_a = 0.98 m), the characteristic number correlation equation using the Gnielinski formula should be approximately equal to the characteristic number correlation equation for external flow over a flat plate. Contrary to intuitive expectations, Nu did not change linearly with δ_a. When δ_a > 0.3 m, the growth rate of Nu decreased by 63% due to boundary layer detachment. This non-linear relationship was critical for optimizing δ_a beyond empirical ranges.

3.2. Setting of Air Layer Thickness

The PV modules installed on the barn roof created an air layer between the PV panels and the roof. Currently, there are no mandatory regulations in China, nor any other country, regarding the setting of this gap. A larger gap required higher PV mounting, more steel materials, and higher costs. Therefore, engineering practices tend to favor lower PV mounting brackets. For the lower limit, China’s standard GB/T 51368 recommends a ventilation gap of more than 0.1 m [25]. The primary purpose of this recommendation is to reduce the temperature rise on the backside of the PV modules by enhancing roof ventilation and ensuring installation and maintenance space for the modules. For the upper limit, Michael et al. [24] set an air layer spacing of 0.01–0.5 m in their study, while Naghavi et al. [26] set a range of 0–0.3 m. Additionally, it has been reported that in France, solar panels mounted on roofs should not exceed 0.3 m above the roof height, and in Germany, they generally should not exceed 0.3–0.5 m above the roof height [27]. Therefore, in this study, the results for gradient thicknesses in the range of 0.05–0.50 m were calculated, and the range of 0.10–0.30 m was considered acceptable for engineering practice. Subsequent discussions are based on this range.

3.3. Thermal Environment Test Data

The harmonic analysis method demonstrates particular efficacy for PV roof thermal assessment in agricultural buildings due to its computational efficiency in resolving periodic heat transfer. Harmonic analysis captures transient dynamics critical for livestock thermal comfort. Despite methodological concerns regarding zonal interference, statistical verification confirmed negligible orientation bias (p = 0.29 for dry-bulb temperature; p = 0.44 for relative humidity). The key parameters derived from the experimental results are summarized in

Table 2. Thermal environment test results of the test barn.

Environmental Parameter	Value	Unit
Mean value of outdoor air velocity	0.9	m·s−1
Mean value of outdoor temperature	29.4	°C
Amplitude of outdoor temperature	5.8	°C
Peak time of outdoor temperature	14.0	h
Mean value of solar radiation intensity outdoors	184	W·m−2
Amplitude of solar radiation intensity outdoors	232	W·m−2
Peak time of solar radiation intensity outdoors	12.0	h
Mean value of indoor temperature	28.0	°C
Amplitude of indoor temperature	3.0	°C
Peak time of indoor temperature	14.0	h

. Notably, solar radiation intensity and associated values were converted to represent the radiation projected onto the barn’s south-facing roof.

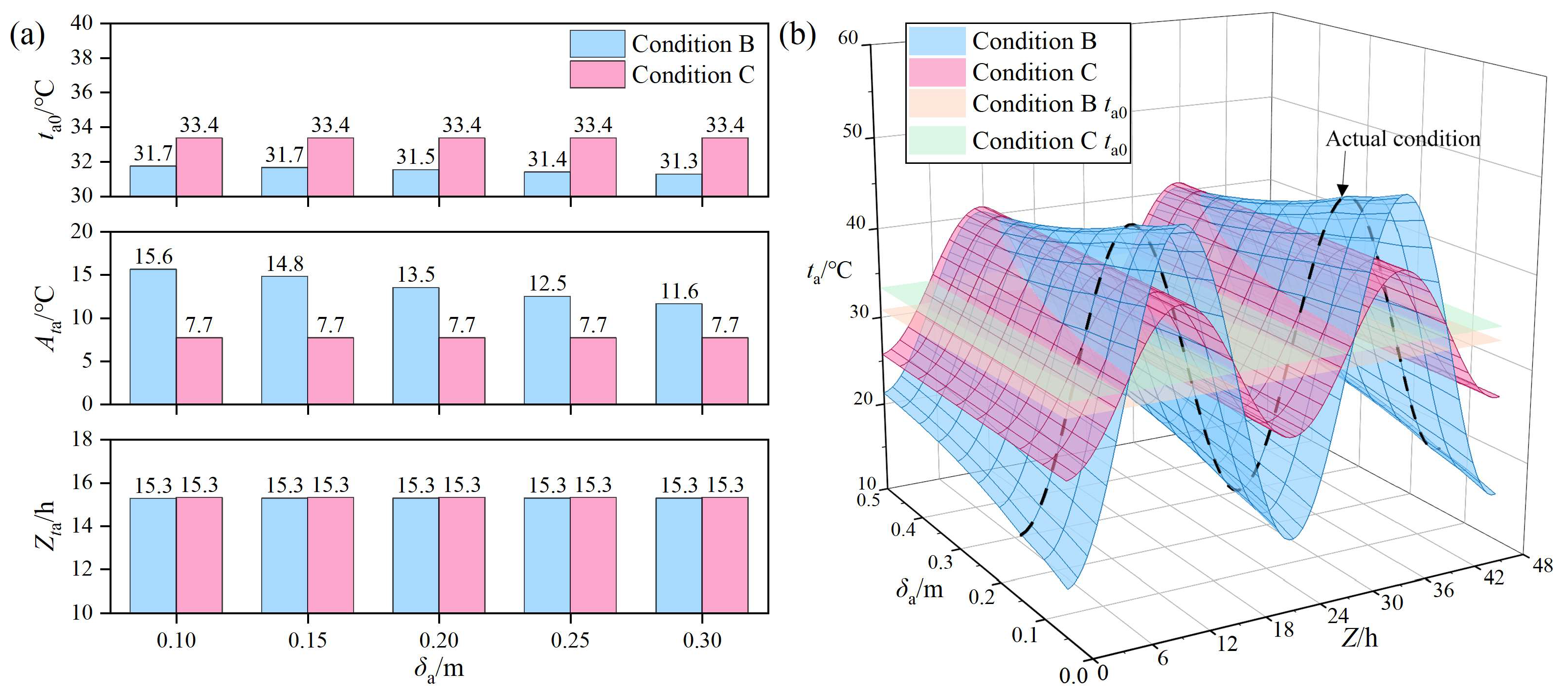
3.4. Variation in Air Layer Temperature with Air Layer Thickness

The results of the tests on the thermal environment inside and outside the barn were presented in the attached file. The results of calculating t_a, q, and R_eq based on the calculation method in Section 2.4 were presented in Section 3.3, Section 3.4, and Section 3.5, respectively. The harmonic images of the air layer temperature t_a as a function of air layer thickness δ_a are shown in Figure 5, based on the mean air temperature t_a0, amplitude A_ta, and peak time Z_ta of the air layer for Condition B and Condition C.

In ventilated air layers (Condition B), when δ_a = 0.12 m (the actual condition of the test barn), the mean air temperature of the air layer t_a0 was 31.7 °C, the amplitude of the air temperature of the air layer A_ta was 14.8 °C, and the peak time of the air temperature Z_ta was 15.3 h. As δ_a increased, t_a0 and A_ta decreased, while Z_ta remained almost unchanged. At δ_a = 0.05 m, t_a0 and A_ta reached their maximum values. At δ_a = 0.10 m, t_a0 = 31.7 °C and A_ta = 15.6 °C. At δ_a = 0.30 m, t_a0 = 31.3 °C and A_ta = 11.6 °C. At δ_a = 0.05 m, t_a0 and A_ta reached their minimum values. The rate of change of t_a0 increased with the increasing δ_a from 0.05 m to 0.50 m, peaking at 2.7 °C·m⁻¹ at δ_a = 0.20 m, and then decreased as δ_a continued to increase. For the ventilated air layer, the thermal characteristics of the air entering the layer were initially consistent with those of the outdoor air. As the air flows through the layer, it is heated by the heat passing through the PV panels, resulting in a higher outlet temperature compared to the inlet temperature. In this study, as the air layer thickness δ_a increases, the temperature difference between the outlet and inlet of the air layer decreases gradually. With increasing air inflow, the heat storage capacity of the air within the layer strengthens, the convective heat transfer effect diminishes, and the thermal characteristics of the air layer become more stable, exhibiting higher uniformity along the direction of the air layer.

For sealed air layers (Condition C), the rates of change of t_a0, A_ta, and Z_ta were very minimal and almost unaffected by increases in δ_a. Within the studied range, t_a0 = 33.4 °C, A_ta = 7.7 °C, and Z_ta = 15.3 h. The t_a0 for Condition C was significantly higher than that for Condition B, while A_ta was significantly lower. There was no significant difference in Z_ta between Conditions B and C. For the sealed air layer, heat transfer was primarily through radiation and remains nearly constant regardless of increases in δ_a. This results in minimal changes in the thermal state of the air layer within the studied range. Unlike the ventilated air layer, the air in the sealed air layer was enclosed and stable, rarely carrying heat away through convective heat transfer or outflowing air [28]. It was continuously heated by the heat passing through the PV panels, leading to a higher t_a0 and lower A_ta, as expected. Z_ta showed no significant difference between the sealed and ventilated air layers. This was because the effect on the overall system peak times was mainly due to the larger heat storage coefficient of the PV panels. The higher t_a0 results in the PV panels being exposed to higher temperatures, which is detrimental to their power generation efficiency. Higher ambient temperature and solar irradiance caused increased cell temperatures [29]. An increase in temperature would directly lead to efficiency degradation [30].

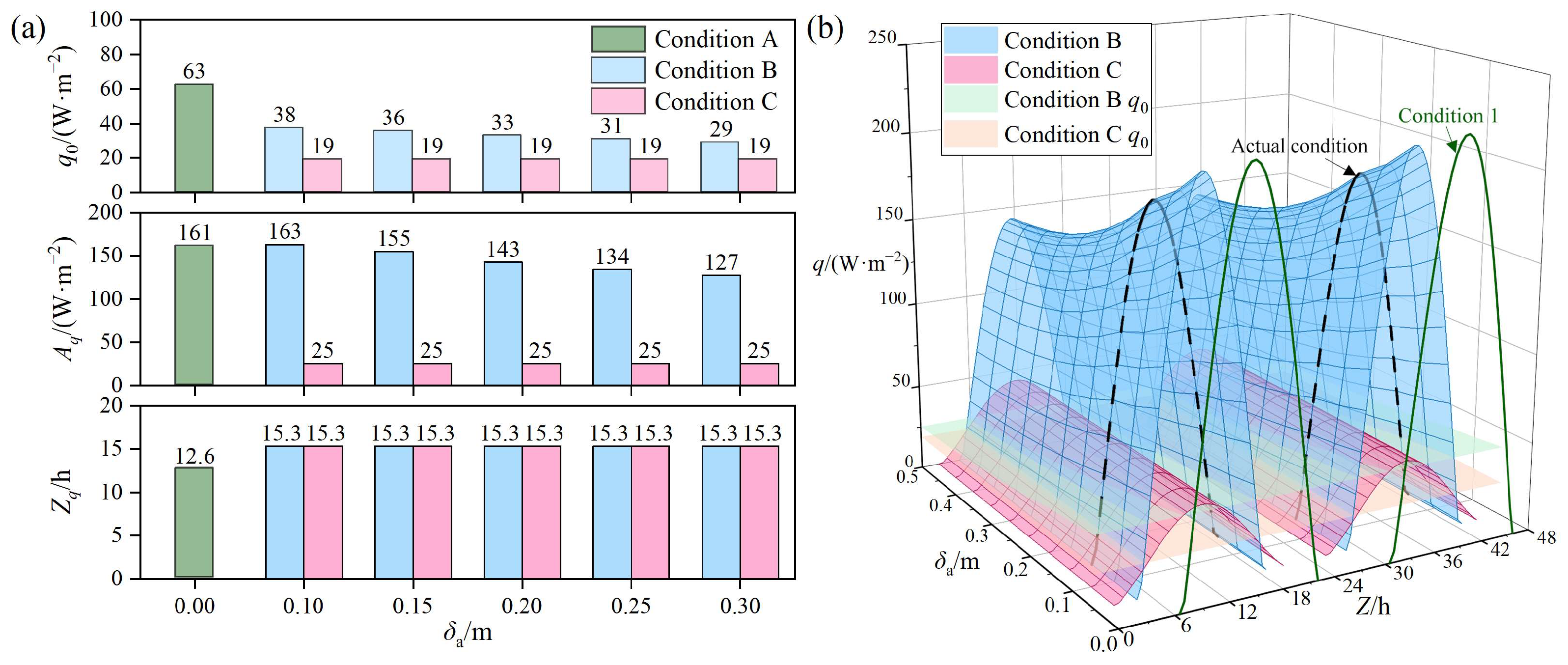
3.5. Variation in Heat Entering the Barn Through the Roof with Air Layer Thickness

The harmonic image of the heat flux q entering the barn through the roof as a function of air layer thickness δ_a is shown in Figure 6, based on the mean heat flux q₀, amplitude A_q, and peak time Z_q under the three conditions.

Under the baseline configuration (Condition A), the mean heat flux q₀ was 63 W·m⁻², the amplitude A_q was 161 W·m⁻², and the peak time Z_q was 12.6 h.

In ventilated air layers (Condition B), when δ_a = 0.12 m (the actual condition of the test barn), the mean heat flux q₀ was 36 W·m⁻², the amplitude A_q was 155 W·m⁻², and the peak time Z_q was 15.3 h. As δ_a increased, q₀ and A_q decreased, while Z_q remained nearly constant. At δ_a = 0.10 m, q₀ = 38 W·m⁻² and A_q = 163 W·m⁻². At δ_a = 0.30 m, q₀ = 29 W·m⁻² and A_q = 127 W·m⁻². At δ_a = 0.50 m, q₀ and A_q reached their minimum values. Compared to Condition A, the mean heat flux q₀ entering the barn through the roof in Condition B was significantly lower. For example, at δ_a = 0.10 m, q₀ in Condition B was only 60% of that in Condition A, and at δ_a = 0.30 m, it was only 47% of that in Condition A. The amplitude A_q of heat flux entering the barn through the roof in Condition B was slightly larger at the initial value of δ_a = 0.05 m. As δ_a increased to 0.10 m, A_q in Condition B reached the same level as in Condition A. At δ_a = 0.30 m, A_q was only 79% of that in Condition A, and at δ_a = 0.50 m, it reached its minimum value. The peak time Z_q of the heat flux entering the barn through the roof in Condition B was delayed by 2.7 h overall compared to Condition A. For the ventilated air layer, within the studied range, as the air layer thickness δ_a increased, convective heat transfer weakened, and heat transfer efficiency decreased, leading to a reduction in both q₀ and A_q. Compared to Condition A, q₀ in Condition B was significantly lower. The significant effect of a portion of the heat originally passing through the PV panels, heating the air in the air layer, and flowing out with the airflow was notable. In contrast, the heat transfer resistance of the PV panels themselves was minimal and insufficient to significantly affect the amount of heat passing through them. The addition of the ventilated air layer increased the system’s volatility, resulting in A_q in Condition B being slightly larger than in Condition A when the air layer thickness was small. As the air layer thickness increases, the thermal characteristics of the air layer become more stable, and A_q became significantly lower than in Condition A. The results of this study were consistent with those of Wang et al. [31], Li et al. [14], and Ma et al. [32], and the conclusions obtained were in agreement.

In sealed air layers (Condition C), the rates of change of q₀, A_q, and Z_q were minimal and almost unaffected by increases in δ_a. Within the studied range, q₀ = 19 W·m⁻², A_q = 25 W·m⁻², and Z_q = 15.3 h. Compared to Conditions 1 and 2, the mean heat flux q₀ and its amplitude A_q entering the barn through the roof in Condition C were significantly lower. For example, q₀ in Condition C was only 30% of that in Condition A, 50% of that in Condition B at δ_a = 0.10 m, and 65% of that in Condition B at δ_a = 0.30 m. Similarly, A_q in Condition C was only 15% of that in Condition A, 15% of that in Condition B at δ_a = 0.10 m, and 19% of that in Condition B at δ_a = 0.30 m. At δ_a = 0.50 m, A_q in Condition B reached its minimum value, but A_q in Condition C remained significantly lower, at approximately 21% of that in Condition B. The peak time Z_q of the heat flux entering the barn through the roof in Condition C was delayed by 2.7 h overall compared to Condition A, which was approximately equal to that in Condition B. For the sealed air layer, both convective and radiative heat transfer remained nearly constant with increasing δ_a within the studied range, resulting in the stability of q₀ and A_q. Compared to Condition B, q₀ and A_q in Condition C were significantly lower. This stability was attributed to the enclosed nature of the air layer in Condition C, where both convective and radiative heat transfer remained almost unchanged. In contrast, in Condition B, the air in the air layer could flow freely, allowing for more effective heat removal through thermal and wind pressure. In this study, convective heat transfer played a minor role, while radiative heat transfer dominated, consistent with the findings of Bruno et al. [29].

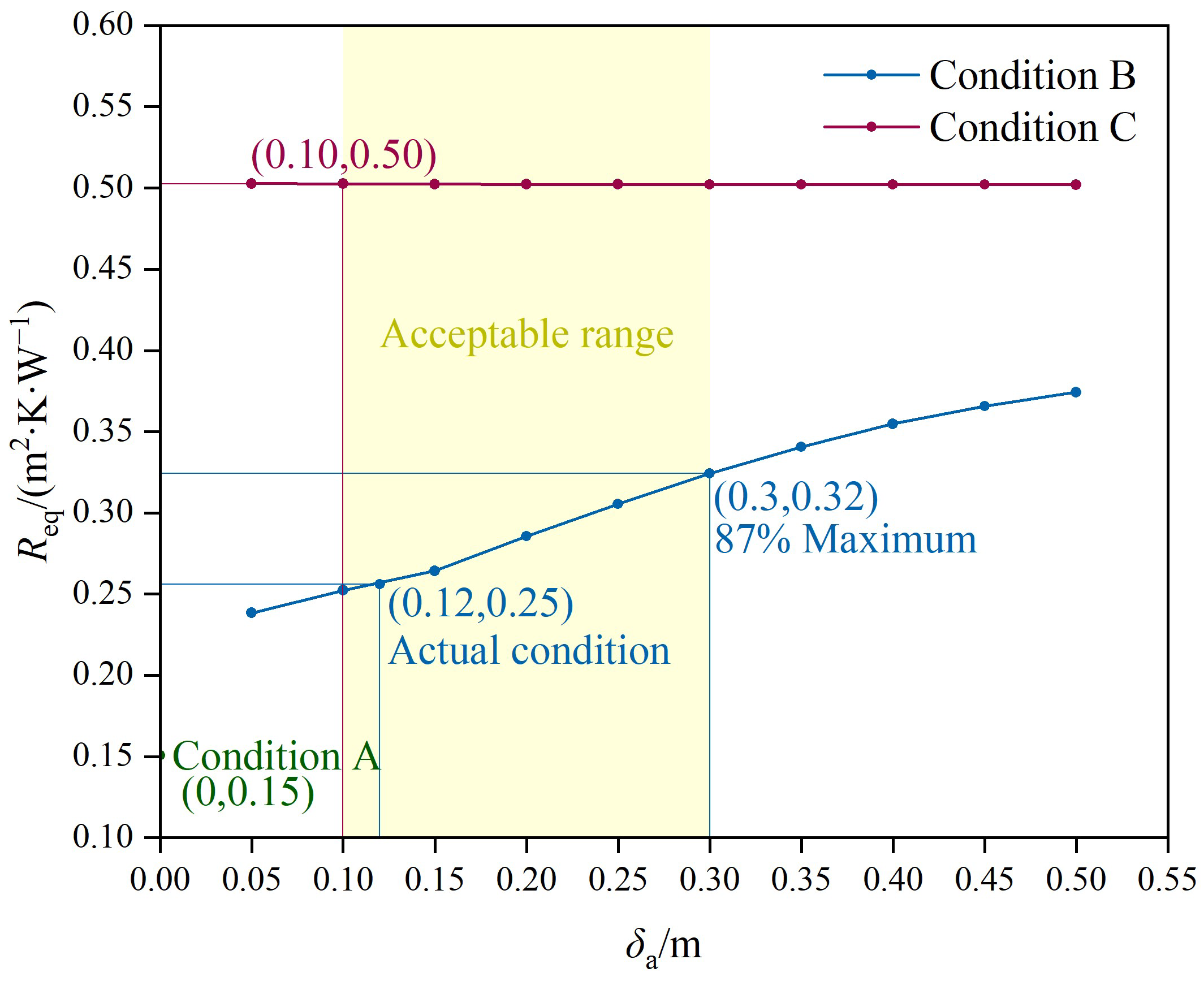
3.6. Variation in Roof Equivalent Thermal Resistance with Air Layer Thickness

The variation in the equivalent thermal resistance of the roof R_eq with air layer thickness δ_a for the three conditions is shown in Figure 7, based on the mean heat flux q₀ entering the barn through the roof.

The baseline roof (Condition A) showed that the equivalent thermal resistance R_eq was 0.15 m²·K·W⁻¹.

With ventilated air layers (Condition B), when δ_a = 0.12 m (the actual condition of the test barn), the equivalent thermal resistance R_eq was 0.26 m²·K·W⁻¹. In Condition B, R_eq increased with increasing δ_a. At δ_a = 0.10 m, R_eq = 0.25 m²·K·W⁻¹. At δ_a = 0.30 m, R_eq reached 87% of its maximum value, with R_eq = 0.32 m²·K·W⁻¹. The maximum was achieved at δ_a = 0.50 m. Compared to Condition A, the equivalent thermal resistance R_eq of the roof in Condition B was significantly higher. For example, at δ_a = 0.10 m, R_eq in Condition B was 1.67 times that of Condition A, and at δ_a = 0.30 m, it was 2.15 times that of Condition A. For the ventilated air layer, the equivalent thermal resistance R_eq increased with increasing air layer thickness δ_a. Although the heat transfer mechanism in ventilated air layers was complex and could not be easily calculated using a simple one-dimensional steady-state heat transfer model, the overall effect could still be understood through the concept of equivalent thermal resistance. Thermal resistance characterized the degree to which the structure obstructs heat transfer. R_eq increased significantly with increasing δ_a, reaching 87% of its maximum value at δ_a = 0.30 m. Compared to Condition A, R_eq in Condition B was significantly higher, as the air layer reduces heat transfer and removes part of the heat through airflow.

In sealed configurations (Condition C), the rate of change of R_eq was minimal and almost unaffected by increases in δ_a. The Building components and building elements—Thermal resistance and thermal transmittance—Calculation method (ISO 6946:2007) proposes that the thermal resistance of the air layer no longer changes when the thickness exceeds 0.025 m [33], while the value in the Thermal Design Code for Civil Buildings (GB 50176-2016) is 0.02 m [17]. Zhang and Yang showed that when the thickness exceeded 0.02 m, the heat transfer was slightly influenced by the thickness [34]. The range of this study started from 0.05 m, so it was reasonable that R_eq was almost constant. Within the studied range, R_eq remained approximately 0.50 m²·K·W⁻¹ as δ_a varies. Compared to both Condition A and Condition B, the equivalent thermal resistance R_eq of the roof in Condition C was significantly higher. For example, R_eq in Condition C was 3.33 times that of Condition A, 1.99 times that of Condition B at δ_a = 0.10 m, and approximately 1.55 times that of Condition B at δ_a = 0.30 m. For the sealed air layer, R_eq remained nearly constant as δ_a increased. This was primarily due to the dominant role of radiative heat transfer, which depended more on the radiative properties of the air layer surfaces than on the air layer thickness itself. Compared to Condition B, R_eq in Condition C was significantly higher. While the ventilated air layer also provided some thermal insulation, the enhanced convective heat transfer due to airflow results in a less significant increase in thermal resistance compared to the sealed air layer. The heat transfer in the sealed air layer had been numerically investigated by Boukendil et al. [35] and Nath et al. [36], who determined the heat transfer coefficient and thermal resistance of the air layer. Zhang et al. [37] studied the effects of boundary conditions, thermophysical properties of materials, and wall configurations on the heat transfer conditions of cavity walls through numerical simulations. They then conducted a comprehensive analysis of the heat transfer of the insulating air layer in the building envelope [28]. These studies suggested that the optimal thickness of the air layer varies significantly across different studies, and the specific thermal resistance of the air layer thickness was strongly influenced by different working conditions. In this study, the suitable range of air layer thickness had reached a stable range compared to the results of previous studies, which was consistent with the trend observed in those studies.

The scenario described in this study, where δ_a = 0.12 m, was a common practical engineering application. It was easily achievable when attaching PV panels to the roof of a dairy barn, with existing regulations for PV panel mounting brackets. In this case, R_eq was 1.75 times that of the roof without PV panels. If the PV panel mounting bracket was raised to 0.30 m, R_eq could be increased to 2.15 times that of the roof without PV panels. If the gap between the PV panels and the color steel plate was fully sealed, R_eq could be increased to 3.33 times that of the roof without PV panels. Taking all factors into account, a ventilated air layer of 0.2–0.3 m thickness was considered preferable in this study. It minimized as much heat as possible entering the barn and avoided excessive air layer temperatures that would cause the efficiency of the PV panels to decrease. The optimized δ_a (0.2–0.3 m) corresponds to the transition zone of Nu variation (Figure 4), balancing heat dissipation and structural cost—a finding unobtainable without the modified model.

Parametric verification confirmed the robustness of optimal air layer configurations across common dairy barn structural parameters in China. For roof slopes ranging from 1:3 to 1:5, the R_eq variation remained within 4% compared to the baseline slope of 17.17° in this study. Similarly, for barn spans between 28 m and 32 m –representative of modern facilities—R_eq showed almost no fluctuation when maintaining identical δ_a and ventilation conditions. However, climatic adaptability remained critical. While the computational methodology (harmonic analysis in Section 2.4) maintained universal applicability, external environmental parameters necessitate region-specific validation. This demonstrated that while structural parameter variations yielded negligible impact, the proposed optimization framework required climatic calibration through localized input data rather than algorithmic changes.

3.7. Prospects

In practical applications, the long-term performance of PV dairy barn roofs, including durability and maintenance requirements, needs further validation to ensure the stability and reliability of their thermal performance. Further refining the model by constructing a two-dimensional framework. Combining engineering costs, a comprehensive cost–benefit analysis should be conducted to determine the optimal balance point of different air layer thicknesses in terms of economic benefits. Future work should also focus on estimating the energy consumption within the barn to further optimize the design of PV dairy barn roofs and improve energy efficiency, thereby enhancing the thermal comfort of livestock and contributing to the overall sustainability of dairy farming operations.

4. Conclusions

This study investigated the impact of air layer thickness on the thermal performance of PV dairy barn roofs through theoretical calculations. The key findings are summarized as follows:

• Convective heat transfer correlation: A characteristic number correlation equation for convective heat transfer in ventilated air layers was developed. The correlation aligns closely with the characteristic number for external flow over a flat plate when the air layer thickness exceeds a critical value. The modified characteristic number equations are more applicable to PV roof structures of agricultural or industrial buildings.
• Harmonic analysis of heat flux: Harmonic analysis revealed that for ventilated air layers, increasing the air layer thickness reduces the mean heat flux and its amplitude entering the barn through the roof, with minimal changes to the peak time. In contrast, for sealed air layers, the mean heat flux, amplitude, and peak time remain relatively stable regardless of changes in air layer thickness.
• Thermal resistance evaluation: The thermal resistance of the roof with a PV system was evaluated. Compared to a roof without a PV system, the thermal resistance of the roof with a ventilated air layer structure increases by 1.67–2.15 times, with further increases observed as air layer thickness grows. For a roof with a sealed air layer structure, the thermal resistance is 3.33 times higher, with little variation observed with increasing air layer thickness.

These findings provide valuable insights for optimizing the design of energy-efficient PV dairy barn roofs, enhancing thermal comfort, and contributing to low-carbon energy solutions in livestock facilities.