Crushing Modeling and Crushing Characterization of Silage Caragana korshinskii Kom.
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Materials
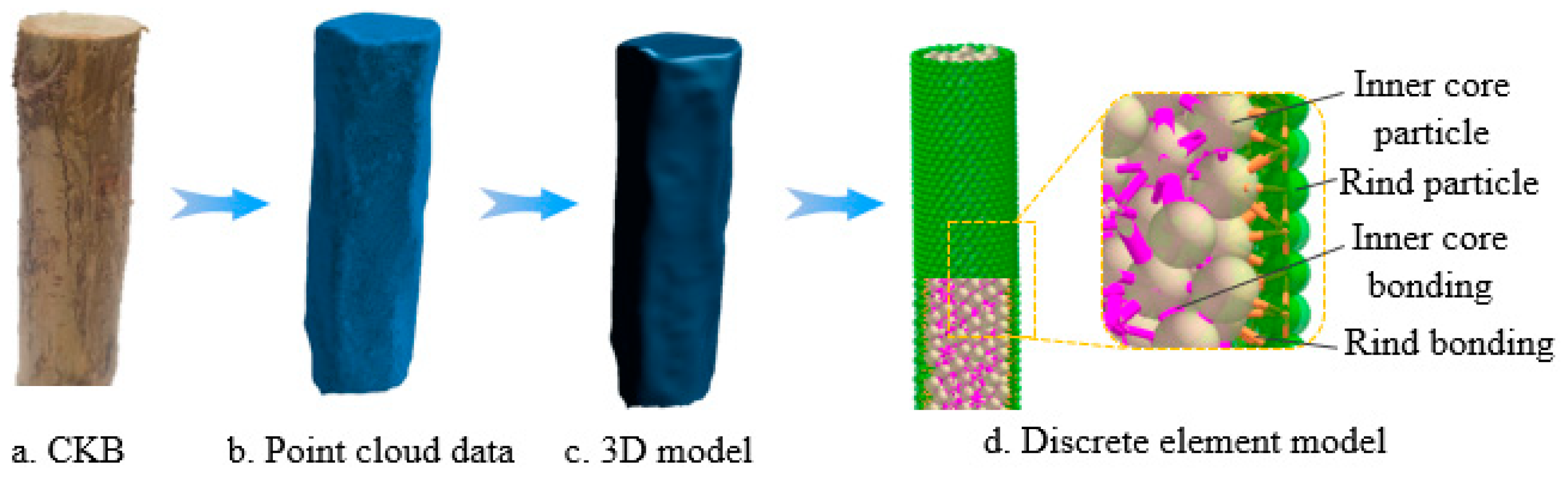
2.2. Model Construction Based on Reverse Engineering
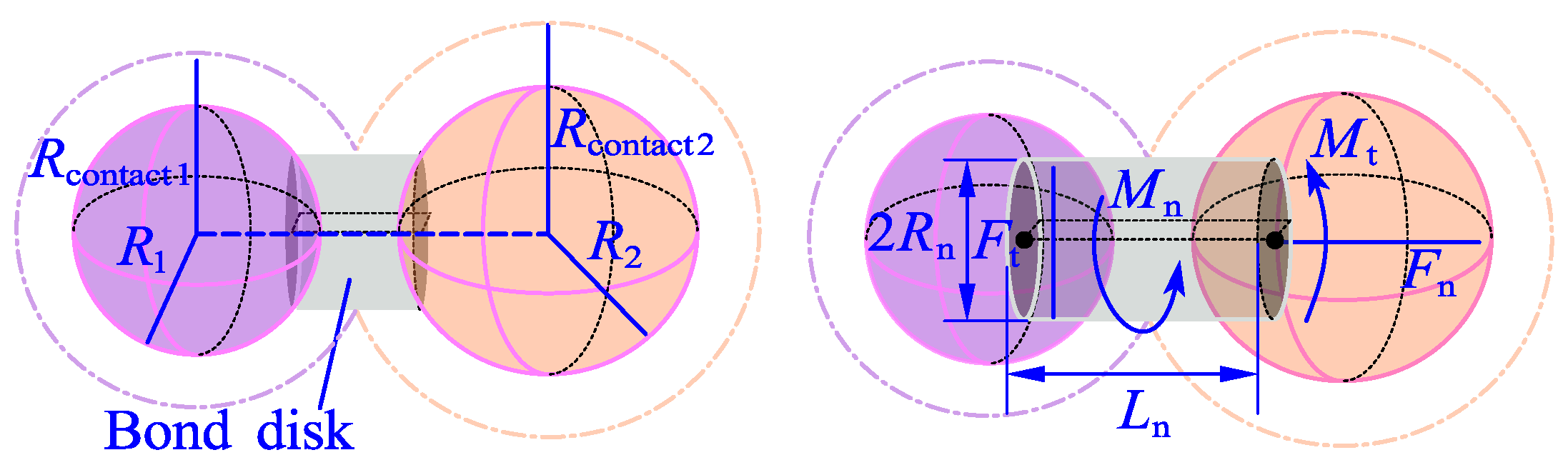
2.3. Bonding Model Destruction Criteria
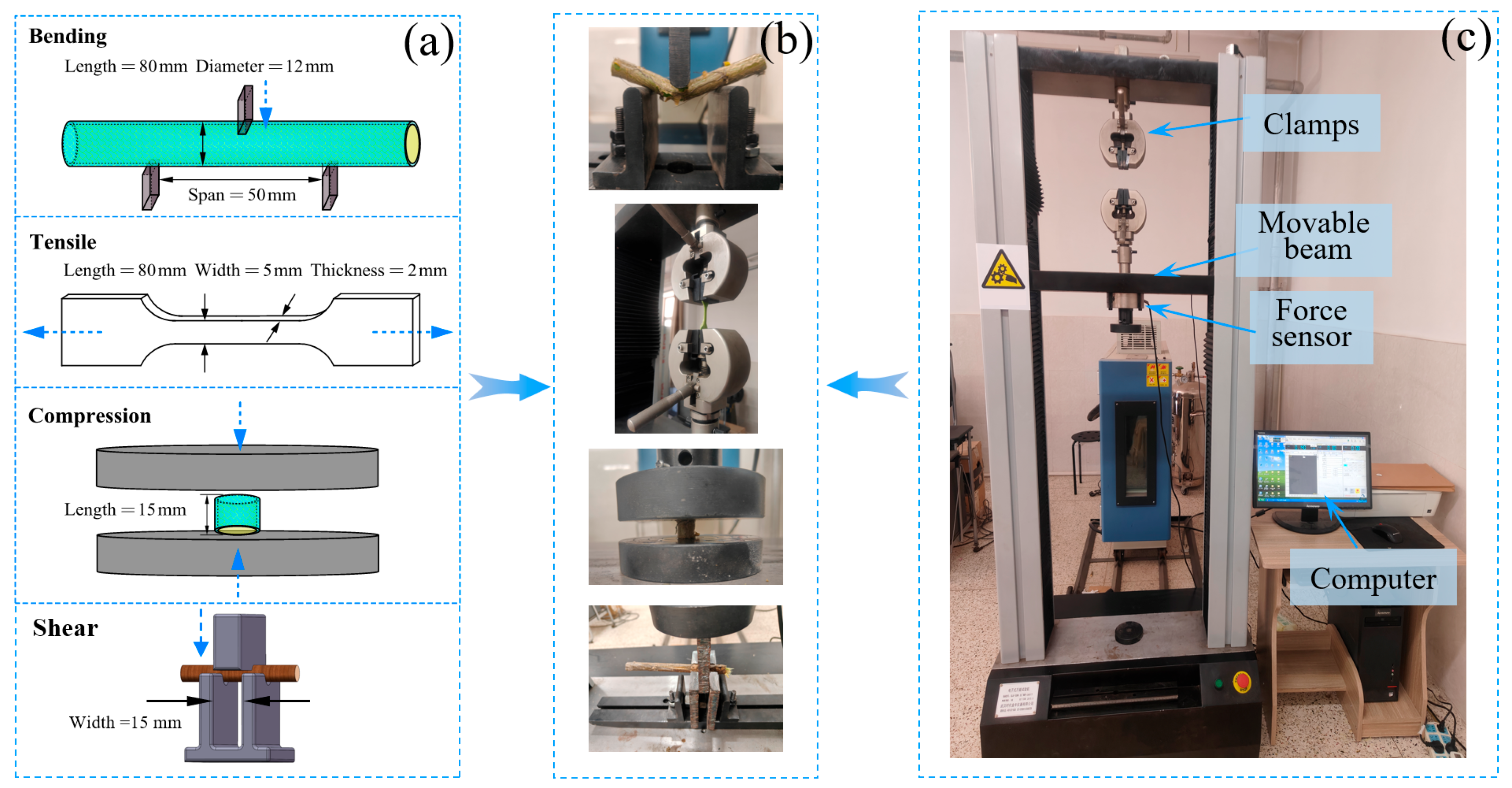
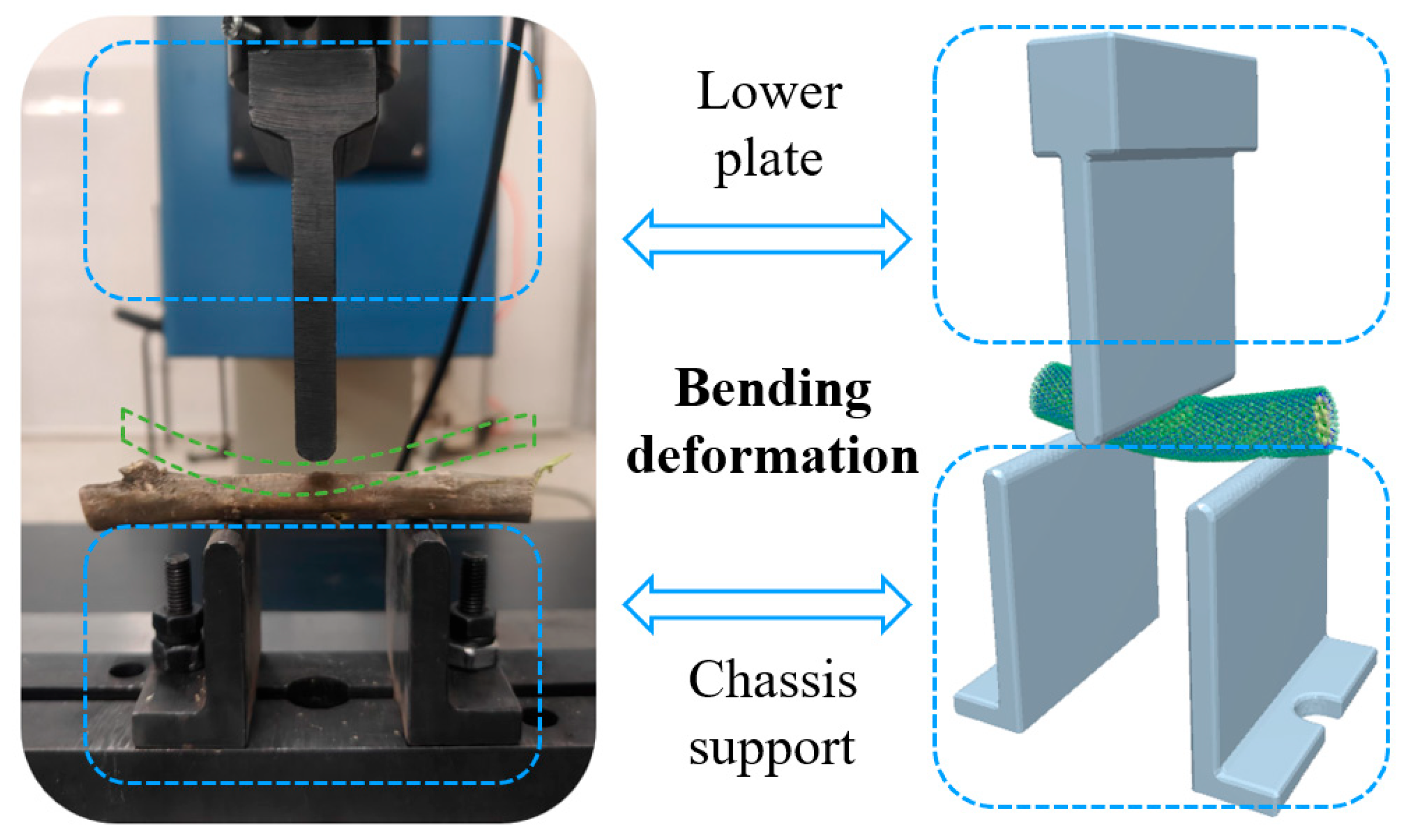
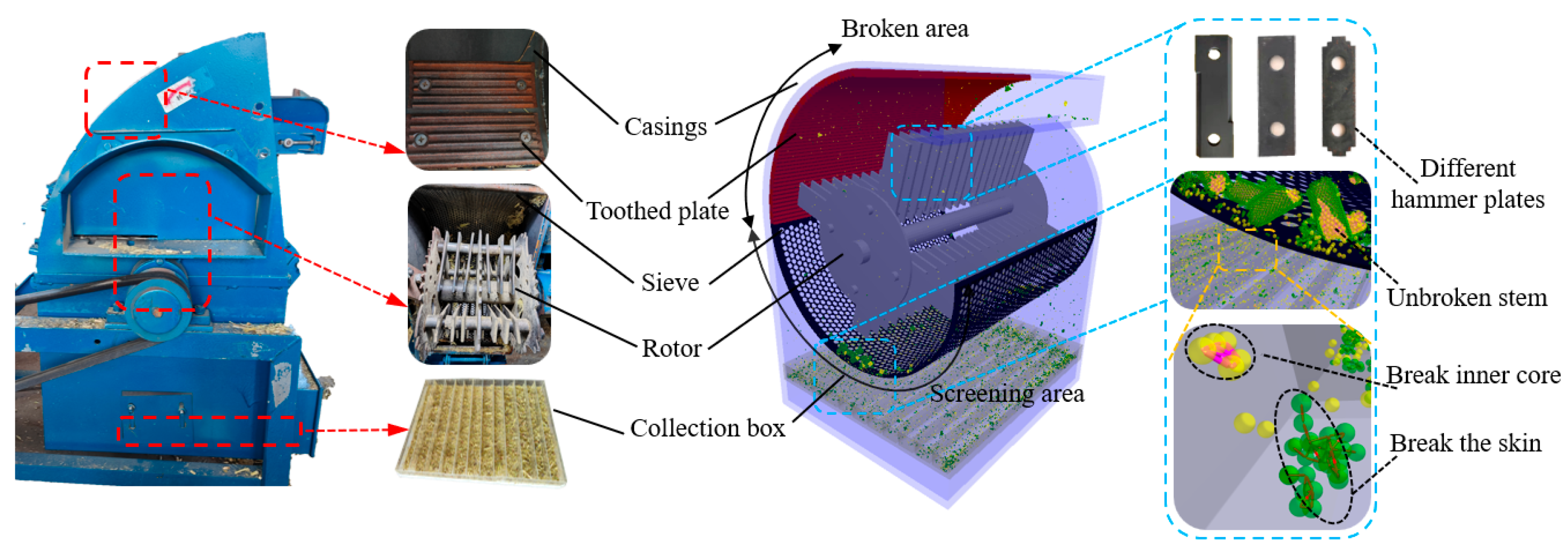
2.4. Mechanical Characteristic Parameter Test
2.5. Calibration Process for Bonding Parameters
2.5.1. Plackett–Burman Test
2.5.2. Steepest Climb Test
2.5.3. Box–Behnken Experimental Design
2.6. Test Validation
3. Results and Discussion
3.1. Physical Test Analysis
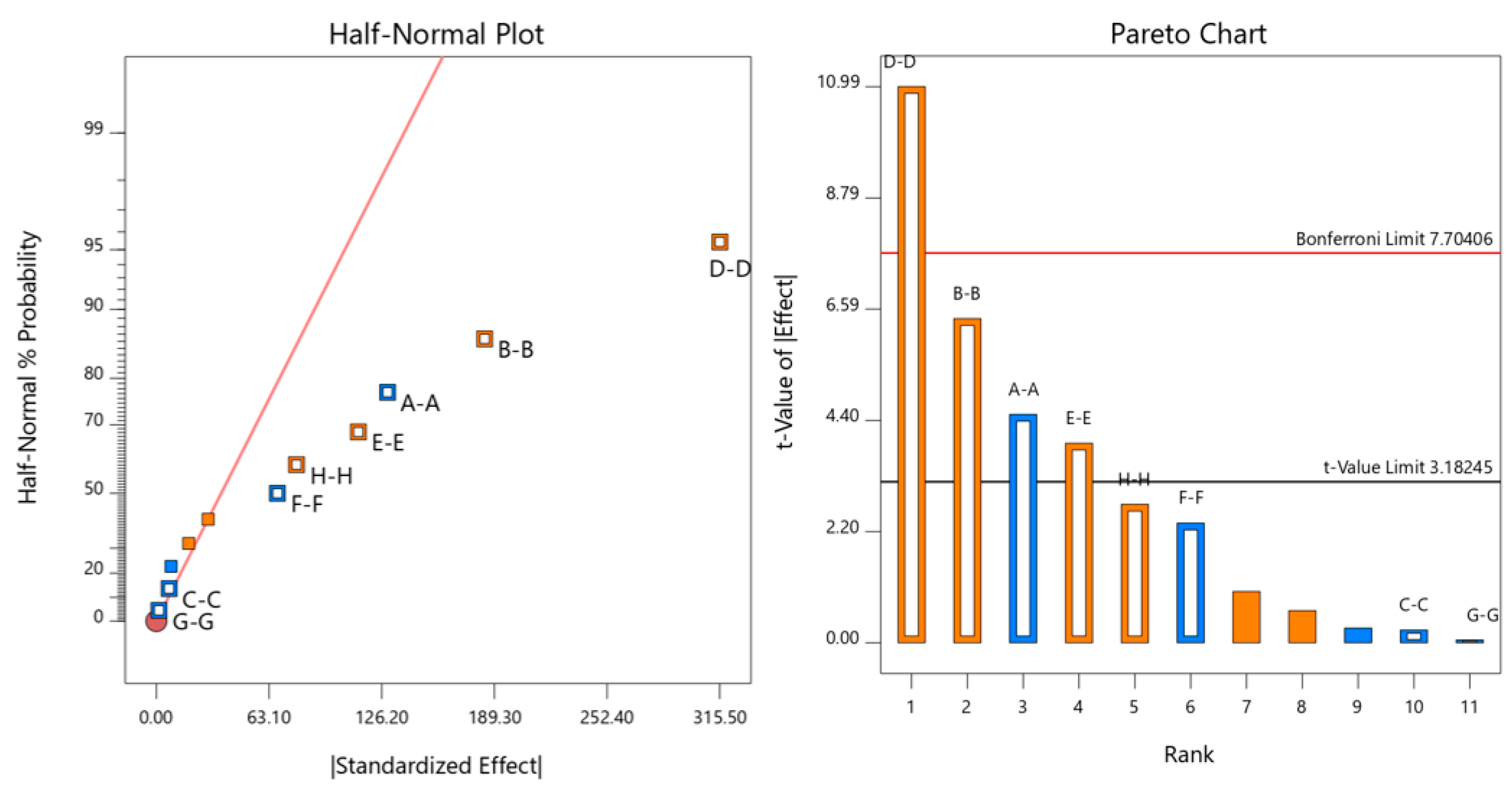
3.2. PB Test Analysis
3.3. Analysis of the Steepest Climb Test
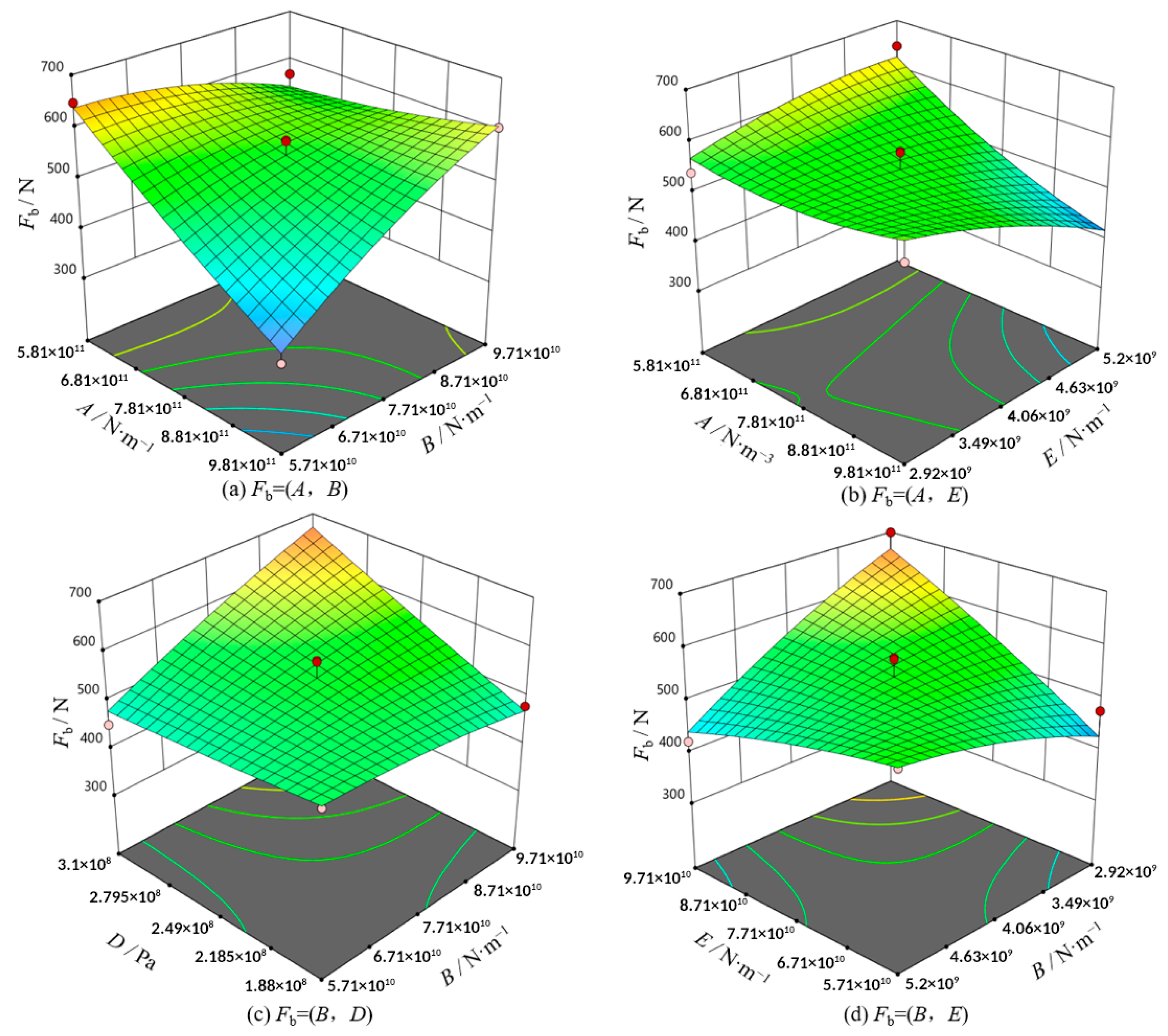
3.4. Analysis of the Box–Behnken Test Results
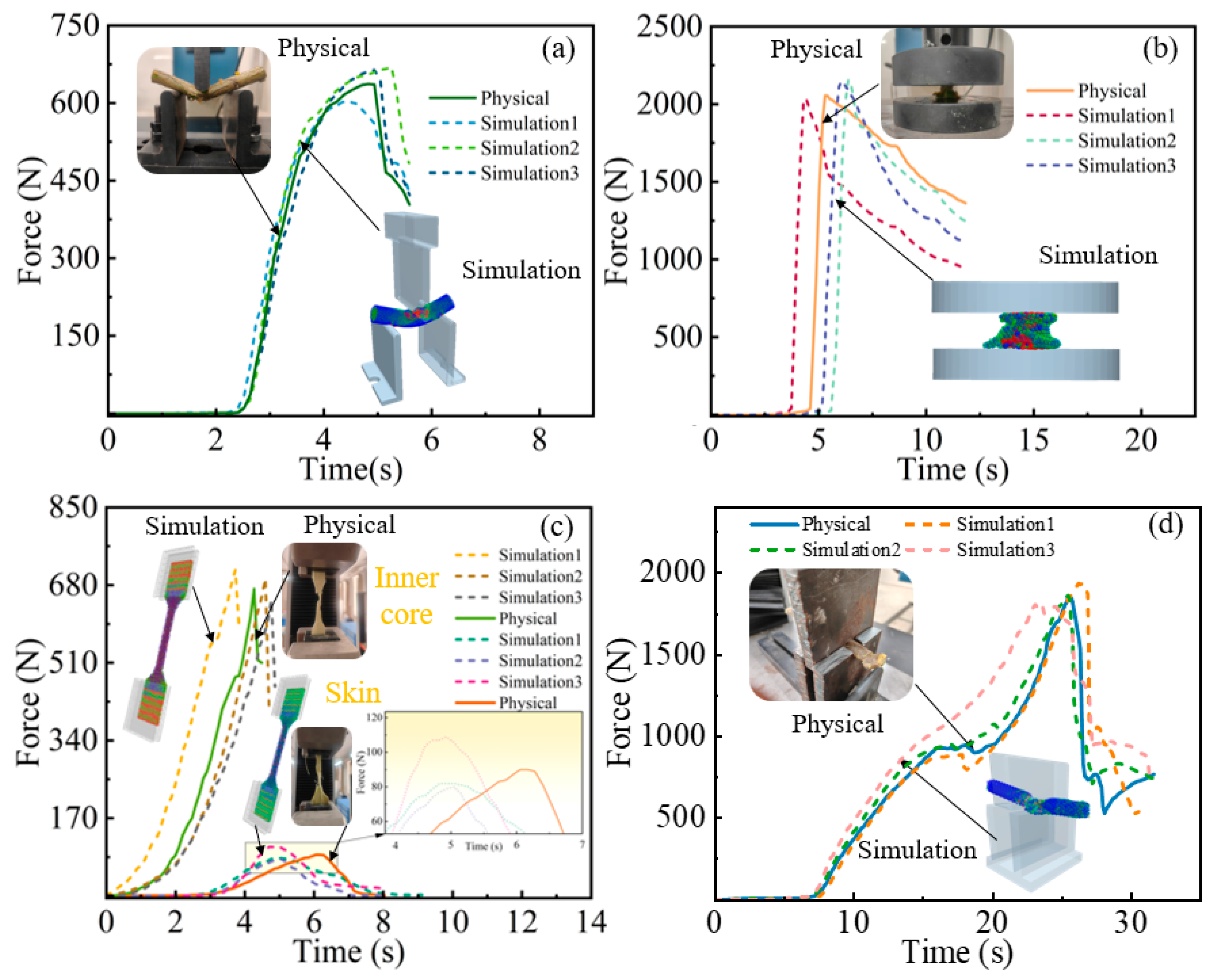
3.5. Determination of Optimal Parameter Combinations and Model Validation Tests
3.6. Simulation Verification and Performance Analysis
3.6.1. Crushing Simulation and Actual Test Verification
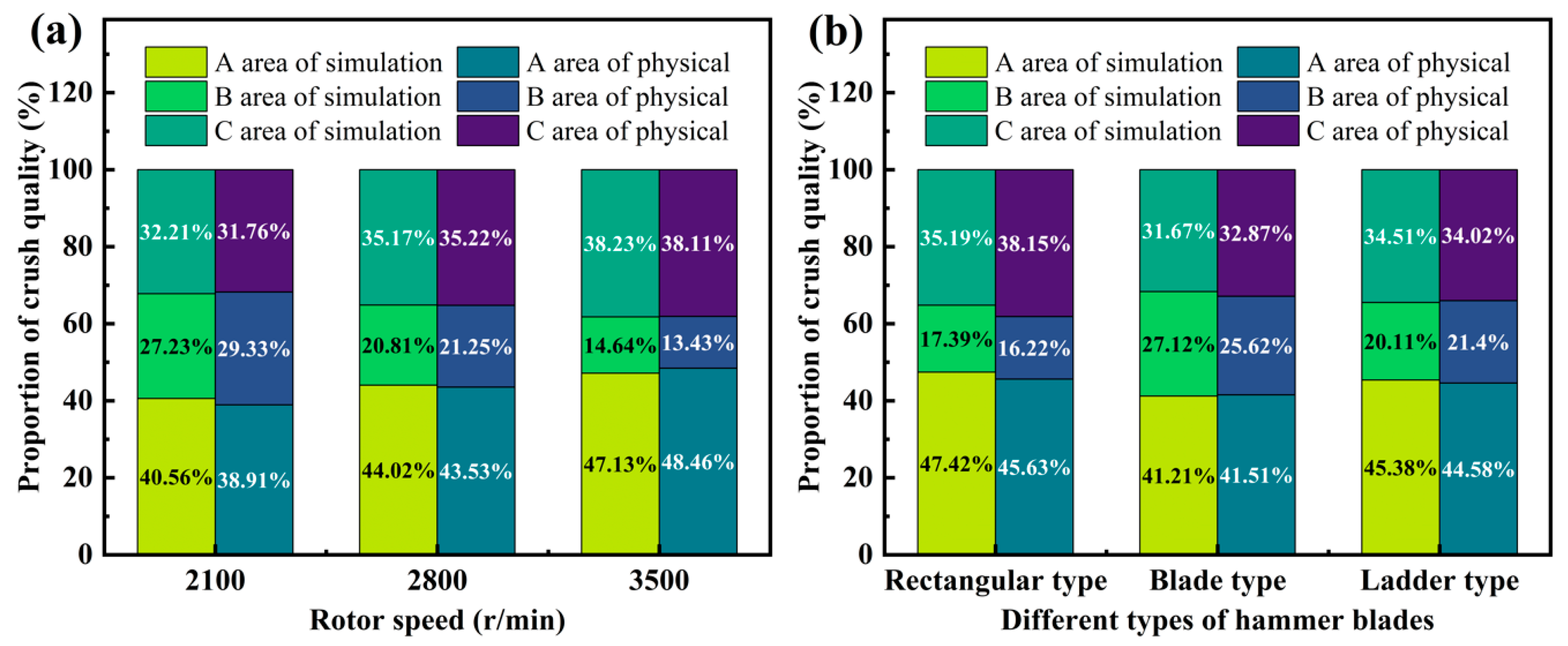
3.6.2. Analysis of the Radial Mass Distribution of Crushed Material
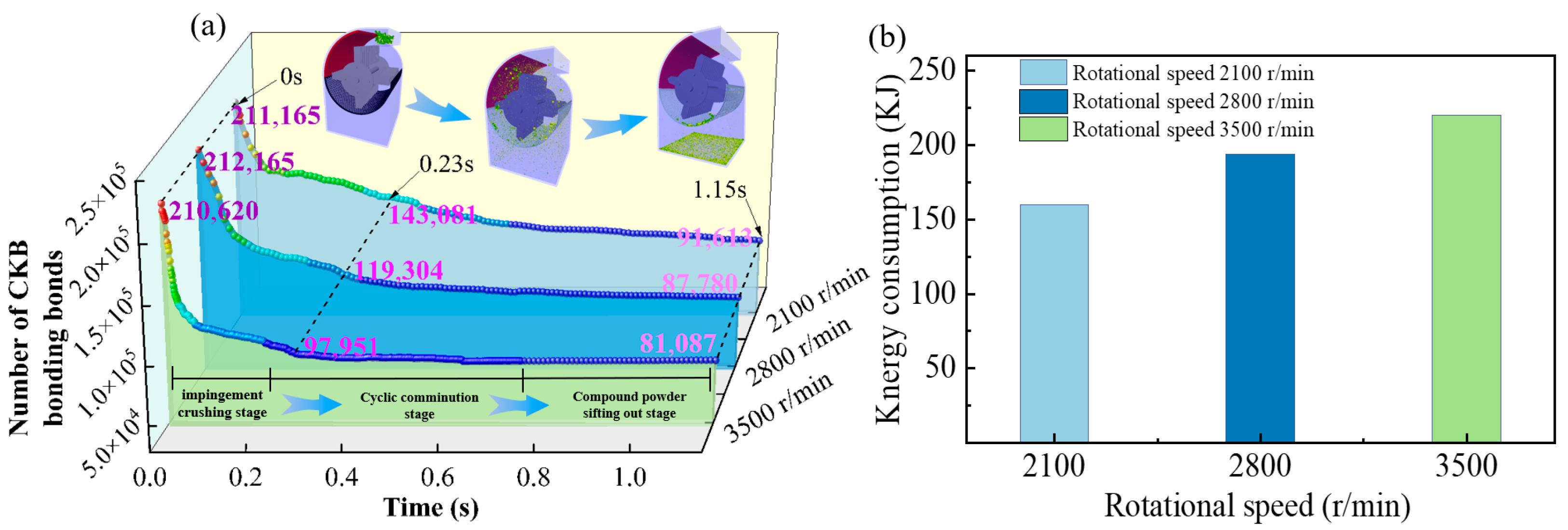
3.6.3. Effect of Different Rotational Speeds on Crushing Rate
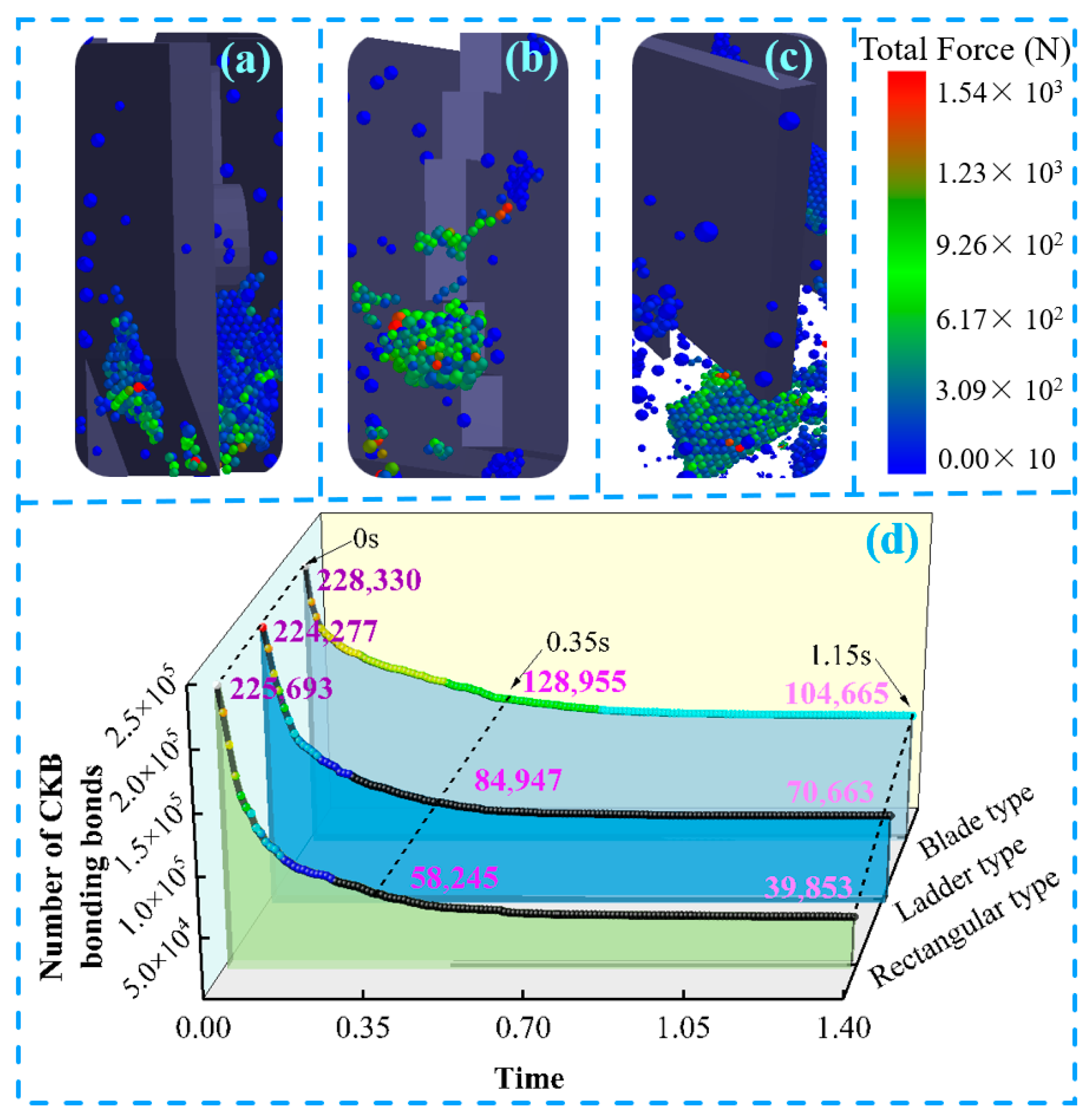
3.6.4. Effect of Different Hammer Blades on Crushing Rate
4. Conclusions
- This study focuses on the key issues in the crushing process of Caragana korshinskii Kom. during silage processing. A layered aggregate model of the epidermis–core structure was constructed using the discrete element method (DEM), and the Hertz–Mindlin with Bonding contact model was employed to characterize its heterogeneous mechanical properties. Reverse engineering and a multi-particle-size filling strategy were combined to effectively improve the modeling accuracy. Based on the simulation model, the effects of different hammer types and rotational speeds on crushing performance were analyzed. The specific research results are as follows:
- The Box–Behnken test was used to establish the second-order regression equation between the bending damage force and the significance parameter, and the measured bending damage force was used as the optimized solution objective to obtain the best combination of simulation parameters, i.e., the inner core normal stiffness (A) is 7.37 × 1011 N·m−1, the inner core shear stiffness (B) is 9.46 × 1010 N·m−1, the inner core shear stress (D) is 2.52 × 108 Pa, and the skin normal stiffness (E) is 4.01 × 109 N·m−1. The relative error between the simulated and measured bending damage force under the optimal parameter combination is 5.6%, and the errors of both tensile and compression tests are less than 9%, which verifies the accuracy of the model.
- The rotational speed is positively correlated to the crushing efficiency, and the bond decay rate is the highest at 3500 rpm (ΔN/Δt = 1.25 × 105 s−1). The relative error of the crushing rate between the simulation and the bench test has an average value of 6.18%, and the material distribution pattern is consistent, which verifies the feasibility of the discrete element model in the optimal design of the CKB crushing device, and it can effectively guide the research and development of the crushing equipment with low consumption and high efficiency.
- The total amount of bonding bonds under the action of rectangular hammers (58,245) is 26.5% and 28.9% lower than that of stepped (79,432) and edged (81,905) hammers, which is more effective in destroying the viscoelastic bonding energy through the composite stress mode. The mass distribution of the crushed material shows a significant radial gradient of tooth plate impact zone > separation end zone > hammer’s initial crushing zone, which provides a key design parameter for the optimization of the annular flow layer structure of the crushing equipment.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Yu, Z.; Zhu, Q.; Zhou, X.; Peng, C. Assessment of Biomass Utilization Potential of Caragana Korshinskii and Its Effect on Carbon Sequestration on the Northern Shaanxi Loess Plateau, China. Land Degrad. Dev. 2020, 31, 53–64. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L.; Knighton, J.; Evaristo, J.; Wassen, M. Contrasting Adaptive Strategies by Caragana Korshinskii and Salix Psammophila in a Semiarid Revegetated Ecosystem. Agric. For. Meteorol. 2021, 300, 108323. [Google Scholar] [CrossRef]
- Kratky, L.; Jirout, T. Modelling of Particle Size Characteristics and Specific Energy Demand for Mechanical Size Reduction of Wheat Straw by Knife Mill. Biosyst. Eng. 2020, 197, 32–44. [Google Scholar] [CrossRef]
- Wang, X.; Tian, H.; Xiao, Z.; Zhao, K.; Li, D.; Wang, D. Numerical Simulation and Experimental Study of Corn Straw Grinding Process Based on Computational Fluid Dynamics–Discrete Element Method. Agriculture 2024, 14, 325. [Google Scholar] [CrossRef]
- Yang, X.; Sun, X.; Li, B.; Liu, Y.; Wang, S.; Gao, X.; Dong, Y. Design and Experimental Study of a Cleaning Device for Edible Sunflower Harvesting. Agriculture 2024, 14, 1344. [Google Scholar] [CrossRef]
- Lei, X.; Hu, H.; Wu, W.; Liu, H.; Liu, L.; Yang, W.; Zhou, Z.; Ren, W. Seed Motion Characteristics and Seeding Performance of a Centralised Seed Metering System for Rapeseed Investigated by DEM Simulation and Bench Testing. Biosyst. Eng. 2021, 203, 22–33. [Google Scholar] [CrossRef]
- Wu, J.; Tang, Q.; Mu, S.; Yang, X.; Jiang, L.; Hu, Z. Design and Test of Self-Leveling System for Cleaning Screen of Grain Combine Harvester. Agriculture 2023, 13, 377. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, M.; Xie, J.; Cao, S.; Wu, A.; Wang, Z. Discrete Element Modeling and Physical Experiment Research on the Biomechanical Properties of Cotton Stalk. Comput. Electron. Agric. 2023, 204, 107502. [Google Scholar] [CrossRef]
- Jiang, P.; Li, Y.; Li, J.; Meng, H.; Peng, X.; Zhang, B.; He, J.; Kan, Z. Experimental Research on the Bending and Fracture Characteristics of Cotton Stalk. Trans. Asabe 2021, 64, 1771–1779. [Google Scholar] [CrossRef]
- Liu, W.; Su, Q.; Fang, M.; Zhang, J.; Zhang, W.; Yu, Z. Parameters Calibration of Discrete Element Model for Corn Straw Cutting Based on Hertz-Mindlin with Bonding. Appl. Sci. 2023, 13, 1156. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Dong, Y.; Huang, M.; Zhang, T.; Cheng, J. Development of a Variable-Diameter Threshing Drum for Rice Combine Harvester Using MBD-DEM Coupling Simulation. Comput. Electron. Agric. 2022, 196, 106859. [Google Scholar] [CrossRef]
- Ma, Z.; Traore, S.N.; Zhu, Y.; Li, Y.; Xu, L.; Lu, E.; Li, Y. DEM Simulations and Experiments Investigating of Grain Tank Discharge of a Rice Combine Harvester. Comput. Electron. Agric. 2022, 198, 107060. [Google Scholar] [CrossRef]
- Chen, X.; Bai, J.; Wang, X.; Fang, W.; Hong, T.; Zang, N.; Fang, L.; Wang, G. Calibration and Testing of Discrete Elemental Simulation Parameters for Pod Pepper Seeds. Agriculture 2024, 14, 831. [Google Scholar] [CrossRef]
- Schramm, M.; Tekeste, M.Z. Wheat Straw Direct Shear Simulation Using Discrete Element Method of Fibrous Bonded Model. Biosyst. Eng. 2022, 213, 1–12. [Google Scholar] [CrossRef]
- Li, S.; Huan, X.; Wang, T.; Hui, Y.; You, Y.; Wang, D. Biomechanical Properties and Discrete Element Modeling of PSR Stalks during Silage Harvest. Comput. Electron. Agric. 2024, 217, 108644. [Google Scholar] [CrossRef]
- Hu, Y.; Xiang, W.; Duan, Y.; Yan, B.; Ma, L.; Liu, J.; Lyu, J. Calibration of Ramie Stalk Contact Parameters Based on the Discrete Element Method. Agriculture 2023, 13, 1070. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, X.; Wu, S.; Chen, C.; Wang, J.; Yuan, S.; Chen, B.; Li, P.; Xu, R. Numerical Simulation of Particle Motion at Cucumber Straw Grinding Process Based on EDEM. Int. J. Agric. Biol. Eng. 2020, 13, 227–235. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, H.; Hua, J. DEM Simulation of Energy Transitions in a Hammer Mill: Effect of Impeller Configurations, Agitation Speed, and Fill Level. Powder Technol. 2021, 394, 1077–1093. [Google Scholar] [CrossRef]
- Shi, Y.; Xin, S.; Wang, X.; Hu, Z.; Newman, D.; Ding, W. Numerical Simulation and Field Tests of Minimum-Tillage Planter with Straw Smashing and Strip Laying Based on EDEM Software. Comput. Electron. Agric. 2019, 166, 105021. [Google Scholar] [CrossRef]
- Wei, X.; Lei, P.; Pin, J.; De, M. Discrete Element Model Building and Optimization of Double-layer Bonding of Rape Shoots Stems at Harvest Stage. Trans. Chin. Soc. Agric. Mach. 2023, 54, 112–120. (In Chinese) [Google Scholar]
- Peng, C.; Chen, J.; He, X.; Sun, S.; Yin, Y.; Chen, Z. Discrete Element Modeling and Verification of the Simulation Parameters for Chopped Hybrid Broussonetia Papyrifera Stems. Int. J. Agric. Biol. Eng. 2024, 17, 23–32. [Google Scholar] [CrossRef]
- Wang, S.; Yu, Z.; Aorigele; Zhang, W. Study on the Modeling Method of Sunflower Seed Particles Based on the Discrete Element Method. Comput. Electron. Agric. 2022, 198, 107012. [Google Scholar] [CrossRef]
- Shu, Z.; Gong, S.; Yun, S. Simulation optimization and experiment of separation device for ramie stalks based on discrete element method. J. Chin. Agric. Mech. 2017, 38, 60–67. [Google Scholar]
- Yu, L.; Feng, Z.; Song, X.F.; Wang, F.; Zhang, F.Y.; Li, X.Z.; Cao, X.Q. Study on mechanical properties for corn straw of double-layer bonding model based on discrete element method. J. Northeast Agric. Univ. 2022, 53, 45–54. [Google Scholar]
- Su, Y.; Xu, Y.; Cui, T.; Gao, X.; Xia, G.; Li, Y.; Qiao, M. Determination and Interpretation of Bonded-Particle Model Parameters for Simulation of Maize Kernels. Biosyst. Eng. 2021, 210, 193–205. [Google Scholar] [CrossRef]
- Ren, J.; Wu, T.; Mo, W.; Li, K.; Hu, P.; Xu, F.; Liu, Q. Discrete Element Simulation Modeling Method and Parameters Calibration of Sugarcane Leaves. Agronomy 2022, 12, 1796. [Google Scholar] [CrossRef]
- Yi, L.; Zai, W.; Qing, L.; Xing, W.; Yu, Z. Calibration of Discrete Element Model Parameters of Forage Rape Stalk at Early Pod Stage. Trans. Chin. Soc. Agric. Mach. 2020, 51, 236–243. (In Chinese) [Google Scholar]
- Kun, W.; Yue, S. Research Progress Analysis of Crop Stalk Cutting Theory and Method. Trans. Chin. Soc. Agric. Mach. 2020, 53, 1–20. (In Chinese) [Google Scholar]
- Su, Q.; Ma, X.; Liu, W.; Zhang, J.; Yu, Z.; Liu, Z. Elastoplastic fracture behavior of Caragana korshinskii Kom. branches: A discrete element model for biomechanical insights into shrub resource utilization. Front. Plant Sci. 2025, 16, 1590054. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Bai, J.; Fang, W.; Hong, T.; Zang, N.; Wang, G. Virtual Parameter Calibration of Pod Pepper Seeds Based on Discrete Element Simulation. Heliyon 2024, 10, 31686. [Google Scholar] [CrossRef]
- Guo, J.; Karkee, M.; Yang, Z.; Fu, H.; Li, J.; Jiang, Y.; Jiang, T.; Liu, E.; Duan, J. Discrete Element Modeling and Physical Experiment Research on the Biomechanical Properties of Banana Bunch Stalk for Postharvest Machine Development. Comput. Electron. Agric. 2021, 188, 106308. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, P.; Zhang, H.; Tan, C.; Wan, W. Calibration of Simulation Parameters of Xinjiang Cotton Straw Based on Discrete Element Method. Trans. Chin. Soc. Agric. Mach. 2024, 55, 76–84. [Google Scholar]
- Leblicq, T.; Smeets, B.; Vanmaercke, S.; Ramon, H.; Saeys, W. A Discrete Element Approach for Modelling Bendable Crop Stems. Comput. Electron. Agric. 2016, 124, 141–149. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Chen, J. Modeling of Flexible Wheat Straw by Discrete Element Method and Its Parameters Calibration. Int. J. Agric. Biol. Eng. 2018, 11, 42–46. [Google Scholar] [CrossRef]
- Kovács, Á.; Kerényi, G. Physical Characteristics and Mechanical Behaviour of Maize Stalks for Machine Development. Int. Agrophys. 2019, 33, 427–436. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Lee, S.-D.; Baek, S.-M.; Baek, S.-Y.; Jeon, H.-H.; Lee, J.-H.; Siddique, M.A.A.; Kim, Y.-J.; Kim, W.-S.; Sim, T.; et al. Development of DEM-MBD Coupling Model for Draft Force Prediction of Agricultural Tractor with Plowing Depth. Comput. Electron. Agric. 2022, 202, 107405. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J. Modeling Flexible Wheat Straw by DEM and its Parameter Calibration. Int. J. Agric. Biol. Eng. 2018, 11, 42–46. [Google Scholar]




| Parameters | Means | Code | |
|---|---|---|---|
| −1 | 1 | ||
| A | Inner core–inner core normal stiffness/(N·m−1) | 1.8 × 1011 | 9.81 × 1011 |
| B | Inner core–inner core shear stiffness/(N·m−1) | 1.7 × 1010 | 9.71 × 1010 |
| C | Inner core–inner core normal stress/Pa | 5.5 × 107 | 1.3 × 108 |
| D | Inner core–inner core shear stress/Pa | 6.5 × 107 | 3.1 × 108 |
| E | Skin–skin normal stiffness/(N·m−1) | 6.4 × 108 | 5.2 × 109 |
| F | Skin–skin shear stiffness/(N·m−1) | 6.8 × 107 | 5.9 × 108 |
| G | Skin–skin normal stress/Pa | 5.4 × 106 | 2.8 × 107 |
| H | Skin–skin shear stress/Pa | 5.4 × 105 | 2.8 × 106 |
| No. | A | B | C | D | E | F | G | H | Fb/N |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 565 |
| 2 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 990 |
| 3 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 502 |
| 4 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 307 |
| 5 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 480 |
| 6 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 690 |
| 7 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 314 |
| 8 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | −1 | 507 |
| 9 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 338 |
| 10 | 1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 308 |
| 11 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 378 |
| 12 | −1 | −1 | 1 | 1 | −1 | −1 | −1 | 1 | 818 |
| Code | A | B | D | E |
|---|---|---|---|---|
| −1 | 5.81 × 1011 | 5.71 × 1010 | 1.88 × 108 | 2.92 × 109 |
| 0 | 7.81 × 1011 | 7.71 × 1010 | 2.49 × 108 | 4.06 × 109 |
| 1 | 9.81 × 1011 | 9.71 × 1010 | 3.10 × 108 | 5.20 × 109 |
| No. | A | B | D | E | Fb/N |
|---|---|---|---|---|---|
| 1 | 0 | 0 | −1 | 1 | 405 |
| 2 | 1 | 0 | −1 | 1 | 373.8 |
| 3 | 1 | 0 | −1 | 0 | 519.4 |
| 4 | −1 | −1 | 0 | 0 | 647.6 |
| 5 | 0 | 0 | 1 | 1 | 581 |
| 6 | −1 | 0 | 1 | 0 | 646 |
| 7 | 0 | 1 | 1 | 0 | 657 |
| 8 | −1 | 1 | 0 | 0 | 569.8 |
| 9 | 0 | 0 | −1 | −1 | 515.2 |
| 10 | 0 | −1 | 0 | −1 | 475.8 |
| 11 | 0 | −1 | 0 | 1 | 536.8 |
| 12 | 1 | 0 | 1 | 0 | 585 |
| 13 | 0 | 0 | 0 | 0 | 481.5 |
| 14 | −1 | 0 | 0 | −1 | 540 |
| 15 | 0 | 1 | −1 | 0 | 481.1 |
| 16 | 0 | 0 | 0 | 0 | 576.8 |
| 17 | 1 | 1 | 0 | 0 | 606.3 |
| 18 | 0 | −1 | 1 | 0 | 451.7 |
| 19 | 0 | 0 | 0 | 0 | 579.7 |
| 20 | 1 | −1 | 0 | 0 | 380.1 |
| 21 | 1 | 0 | 0 | −1 | 549.3 |
| 22 | 0 | 1 | 0 | 1 | 421.9 |
| 23 | 0 | 1 | 0 | −1 | 699.6 |
| 24 | 0 | −1 | −1 | 0 | 516.3 |
| 25 | −1 | 0 | 0 | 1 | 647 |
| 26 | 0 | 0 | 1 | −1 | 585.6 |
| 27 | −1 | 0 | −1 | 0 | 578.4 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 5.212 × 105 | 8 | 65,148.42 | 26.35 | 0.0106 * | significant |
| A-A | 50,310.75 | 1 | 50,310.75 | 20.35 | 0.0204 * | |
| B-B | 1.014 × 105 | 1 | 1.014 × 105 | 41.00 | 0.0077 ** | |
| C-C | 154.08 | 1 | 154.08 | 0.0623 | 0.8190 | |
| D-D | 2.986 × 105 | 1 | 2.986 × 105 | 120.78 | 0.0016 ** | |
| E-E | 38,420.08 | 1 | 38,420.08 | 15.54 | 0.0291 * | |
| F-F | 13,804.08 | 1 | 13,804.08 | 5.58 | 0.0991 | |
| G-G | 6.75 | 1 | 6.75 | 0.0027 | 0.9616 | |
| H-H | 18,486.75 | 1 | 18,486.75 | 7.48 | 0.0717 | |
| Residual | 7417.58 | 3 | 2472.53 | |||
| Cor Total | 5.286 × 105 | 11 |
| No. | X1 | X2 | X4 | X5 | Fb/N |
|---|---|---|---|---|---|
| 1 | 1.80 × 1011 | 1.70 × 1010 | 6.50 × 107 | 6.40 × 108 | 431 |
| 2 | 3.80 × 1011 | 3.70 × 1010 | 1.26 × 108 | 1.78 × 109 | 742 |
| 3 | 5.81 × 1011 | 5.71 × 1010 | 1.88 × 108 | 2.92 × 109 | 680 |
| 4 | 7.81 × 1011 | 7.71 × 1010 | 2.49 × 108 | 4.06 × 109 | 649 |
| 5 | 9.81 × 1011 | 9.71 × 1010 | 3.10 × 108 | 5.20 × 109 | 589 |
| Source of Variation | Mean Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1.765 × 105 | 14 | 12,607.60 | 6.38 | 0.0013 ** |
| A | 32,434.36 | 1 | 32,434.36 | 16.41 | 0.0016 ** |
| B | 18,205.23 | 1 | 18,205.23 | 9.21 | 0.0104 * |
| D | 18,714.18 | 1 | 18,714.18 | 9.47 | 0.0096 ** |
| E | 1442.41 | 1 | 1442.41 | 0.7298 | 0.4097 |
| AB | 29,584.00 | 1 | 29,584.00 | 14.97 | 0.0022 ** |
| AD | 161.22 | 1 | 161.22 | 0.0816 | 0.7800 |
| AE | 15,473.99 | 1 | 15,473.99 | 7.83 | 0.0161 * |
| BD | 25,680.06 | 1 | 25,680.06 | 12.99 | 0.0036 ** |
| BE | 16,731.42 | 1 | 16,731.42 | 8.47 | 0.0131 * |
| DE | 396.11 | 1 | 396.11 | 0.2004 | 0.6624 |
| A2 | 490.69 | 1 | 490.69 | 0.2483 | 0.6273 |
| B2 | 2590.18 | 1 | 2590.18 | 1.31 | 0.2746 |
| D2 | 0.9122 | 1 | 0.9122 | 0.0005 | 0.9832 |
| E2 | 249.68 | 1 | 249.68 | 0.1263 | 0.7284 |
| Residual | 23,716.85 | 12 | 1976.40 | ||
| Lack of Fit | 17,472.27 | 10 | 1747.23 | 0.5596 | 0.7830 |
| Pure Error | 6244.58 | 2 | 3122.29 | ||
| Cor Total | 2.002 × 105 | 26 |
| No. | Relative Error of Bending Destructive Force/% | Relative Error of Axial Compression Force/% | Relative Error of Shear Force | Relative Error of Tensile Breaking Force/% | |
|---|---|---|---|---|---|
| Inner Core | Skin | ||||
| 1 | 5.0% | 4.5% | 6.1% | 6.3% | 8.5% |
| 2 | 4.0% | 4.0% | 5.2% | 3.4% | 8.9% |
| 3 | 5.6% | 2.1% | 3.8% | 3.6% | 9.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Yu, Z.; Aorigele; Su, Q.; Ma, X.; Liu, Z. Crushing Modeling and Crushing Characterization of Silage Caragana korshinskii Kom. Agriculture 2025, 15, 1449. https://doi.org/10.3390/agriculture15131449
Liu W, Yu Z, Aorigele, Su Q, Ma X, Liu Z. Crushing Modeling and Crushing Characterization of Silage Caragana korshinskii Kom. Agriculture. 2025; 15(13):1449. https://doi.org/10.3390/agriculture15131449
Chicago/Turabian StyleLiu, Wenhang, Zhihong Yu, Aorigele, Qiang Su, Xuejie Ma, and Zhixing Liu. 2025. "Crushing Modeling and Crushing Characterization of Silage Caragana korshinskii Kom." Agriculture 15, no. 13: 1449. https://doi.org/10.3390/agriculture15131449
APA StyleLiu, W., Yu, Z., Aorigele, Su, Q., Ma, X., & Liu, Z. (2025). Crushing Modeling and Crushing Characterization of Silage Caragana korshinskii Kom. Agriculture, 15(13), 1449. https://doi.org/10.3390/agriculture15131449








