Evaluation of a Pre-Cut Sugarcane Planter for Seeding Performance

Abstract

To investigate the relationship between the seeding performance of a novel pre-cut sugarcane planter designed by South China Agricultural University and operational settings, field seeding tests was conducted with the following protocol: First, the John Deere M1654 tractor’s forward velocity was calibrated, and the planter’s safe loading capacity was determined. Subsequently, eight experimental treatments (A–H) were designed to quantify the relationships between the three performance indicators: seeding density N, the seeding efficiency E and seeding uniformity (coefficient of variation, CV), and three key operational parameters: forward speed of planter v, the discharging sprocket rotational speed n, and the hopper outlet size w. Mathematical models (R20.979) between three key operational parameters with two performance indicators (N, E) was developed through analysis of variance (ANOVA) and regression analysis. The seeding rate per meter was confirmed to follow a Poisson distribution based on Kolmogorov–Smirnov (K–S) tests. When the CV was below 40%, the mean relative error remained within 3%. These findings provide a theoretical foundation for seeding performance prediction under field conditions.

1. Introduction

Sugarcane is a tropical and subtropical crop that serves as a raw material for sugar production. It can also be converted into ethanol as an energy substitute. Global sugarcane production reached 1869 × 10⁶ tons in 2020. Brazil, India and China stand out as the three leading countries in terms of sugarcane production, collectively contributing to 40%, 20%, and 10%, respectively [1]. With the rise in labor costs, there has been a gradual shift from traditional planting to mechanized planting. Sugarcane planters are mainly divided into whole-rode type and billets type.

Pre-cut sugarcane planters currently represent the main development direction. The seeding meter device is the core part of the planter. There are different types of seeding meter devices, such as chain conveyors [2,3], ribbon conveyors [4], fluted-wheels [5,6], etc. To achieve large-scale planting and good seeding uniformity, planters usually use multi-class seed metering device, which are typically a combination of various mechanical structures, such as chain conveyors, ribbon conveyors, fluted wheels, etc. These planters are characterized by their bulky, heavy, and complex structure. These planters are usually pulled directly by a tractor with a ground wheel for support rather than being attached with a three-point linkage, which results in a large turning radius [7,8,9]. Southern China’s sugarcane growing regions are scattered, rough, and small in area, a large turning radius will lead to wasted planting area [10]. In recent decades, as modern agriculture has advanced toward refined planting operations, many researchers have started to focus on precision seeders [11]. Su W, et al. [12] and Ma L, et al. [13] designed double-bud sugarcane seed metering devices. However, their seeding efficiency is low and their seed capacity is small. Currently, many field tests of seed metering devices use the evaluation indexes of multiple -seeds and missing seeds to assess performance. However, the assessment of seed metering device performance lacks comprehensiveness and depth.

To address the problem described above, a new sugarcane planter was designed by South China Agricultural University [14]. In this paper, this planter and its seed metering device structure and feature are first briefly described. Then, the relationships among the gear position, engine speed, and the change in the vehicle speed of the John Deere M1645 tractor, which suspends the planter, and the change in the centroid of the planter with cane seed quantity are studied. Eight field tests were carried out on the planter, and ANOVA and linear regression analysis were performed to examine the factors of the planter’s forward speed, the discharging sprocket rotational speed, and the outlet size of the hopper on the indicators of the average seeding rate per meter and the seeding efficiency of the planter. Finally, the distribution of cane seeds per meter was analyzed using the Kolmogorov–Smirnov test.

2. Materials and Methods

2.1. Machine Description and Seeding Operation

This new sugarcane planter designed by South China Agricultural University (SCAU, Guangzhou, Guangdong, China) mainly includes fertilizers, a furrow opener, a ground-wheel control system, a seed metering device, and a soil cover device as shown in Figure 1. Its technical index parameters are shown in

Table 1. Specifications of the sugarcane planter [15].

General	Parameter
Number of rows	Two
Type of seeding	Pre-cut seed with two buds
Seeding space (m)	1–1.4
Depth of furrow opener (mm)	250–350
Thickness of covering soil (mm)	80–150
Capacity of fertilizer (L)	341
Matched power (HP)	≥180
Overall weight (t)	About 1.5
Volume of hopper (m3)	3.246
Size of planter (mm)	3800 × 1900 × 2900 (Length × Width × Height)

.

The fertilizer discharge device is a rotary scraper fertilizer, featuring a non-clogging structure that ensures optimal performance when applying various fertilizers such as organic, inorganic, and compound fertilizers with excellent adaptability. The furrow opener is the shoe type, the angle between the shoe surface and the main beam is 120°, and the buried angle is 30°, which is acute. This design ensures that the whole ditching part can be sunk into finished cane land to disturb a large amount of soil, and open a wide ditch suitable for planting. Ground-wheel control system is made up of a ground wheel and a speed-dependent seeding control system. The internal gear sensor of the ground wheel detects the planter forward speed and transmits the speed signal to the speed-dependent seeding control system. After the control system processes the calculations, transmits a signal to adjust the discharging sprocket’s rotational speed. The seed metering device is made up of seeding cleats, middle cleats, a W-channel, a hopper, a pressure-limiting plate, and an amount-limiting device, among other components. Sugarcane seeds fall into the W-channel from the outlet of hopper and are carried by the seeding cleats out of the seed metering device. The amount-limiting device is positioned at the exit of the tunnel. The film- covering device consists primarily of a frame, an M-shaped soil- covering plate, a film mounting base, a soil- raising disc, and a suppression wheel. The operational process is as follows: once the sugarcane seed falls into the planting ditch, the M-shaped soil- covering plate gathers the soil from both sides of the ditch toward its center. This forms a turtleback shape for the soil layer above the cane seed. This shape offers certain advantages for enhancing the seeds’ drought resistance. The thickness of this turtleback-shaped soil layer depends on the height of the M-shaped soil cover plate. The planter can be coupled to the tractor via a hydraulic hitch system, which significantly reduces the turning radius during planting operations compared to conventional direct-towing methods.

The seed metering device is mainly composed of a hopper, a pressure-limiting plate, a W-channel, middle cleats, seeding cleats, and an amount-limiting device. The hopper is used to hold cane seeds, and the pressure-limiting plate at the bottom of the hopper controls the outlet size of the hopper (w) as shown in Figure 2a,b. The size of the hopper outlet (w) determines the rate of cane seed outflow and the jamming of cane seeds.

The cane seeds free fall from the hopper and flow through the W-channel, and then they are transported by the seeding cleats inside the channel. The cane seeds accumulating in the W-channel will move along the channel approaching to the direction of velocity due to the spatial constrain of the channel itself and the law of elongated cylindrical particles tends to be in the direction of motion [16]. The middle cleats can increase the disturbance of the cane seeds in the channel and prevent the cane seeds from avoiding interaction with the seeding cleats. The cane seeds are driven by the seeding cleats, which are transported from the bottom of the channel to the channel outlet. The seeding cleats and the middle cleats are simultaneously driven by the discharging sprocket. The amount-limiting plate is installed at the channel outlet, which can prevent too many cane seeds from being discharged at one time, increasing the seeding uniformity of the planter, as shown in Figure 3.

2.2. Evaluation Index

Seeding uniformity and density is key factor in crop growth [17]. Different regions have different requirements for seeding planters. By studying the seeding performance of sugarcane planters, planters can achieve different planting goals. The indices of seeding performance include the seeding density, seeding uniformity, and seeding efficiency.

The planting density of sugarcane planters is defined as the average seeding rate per meter N (seed/m). According to the machine structure of the planter itself, the theoretical value is calculated as follows:

$$N=0.067{\displaystyle \frac{qn}{v}}$$

(1)

where n is the discharging sprocket rotational speed, r/min; q is the average value of discharging per cleat, seed/cleat; v is the forward speed of the planter, km/h.

Seeding efficiency affects planting efficiency. Without considering the time required for filling the hopper and turning, in this study, the expression the seeding efficiency E (seed/s) is as follows:

$$E=1.11Nv$$

(2)

where N is the theoretical seeding density, seed; v is the forward speed of the planter, km/h.

The coefficient of variation ($CV$) describes the dispersion of a variable. Therefore, the coefficient of variation of seeding reflects the seeding uniformity. The practical coefficient of variation (${CV}_p$) for the planter is calculated as follows:

$${CV}_p={\displaystyle \frac{s_n}{{\overline{N}}_n}}\times 100\%$$

(3)

where $s_n$ is the standard deviation of the sample data, and ${\overline{N}}_n$ is the average value of the sample data, seed/m.

2.3. Probability Distribution and Kolmogorov–Smirnov Test

If the sample distribution of seeds per meter conforms to a theoretical probability distribution where the mean and standard deviation exhibit a specific functional relationship, the seeding uniformity of the seed metering device can be estimated based on the seeding density. To this end, this study performs a goodness-of-fit test between the data distribution of seeds per meter and a specified theoretical distribution. The Kolmogorov–Smirnov (K–S) test, a non-parametric method [18] that does not require prior assumptions about the data distribution [19], is employed.

The K–S test proceeds as follows [20]:

1.

Put forward the Hypothesis H_0-1:

Hypothesis H_0-1.

The cumulative distribution function of the sample data is equal to the cumulative distribution function of the theoretical distribution.

2.

Calculate the absolute differences between the cumulative distribution function of the sample data and that of the theoretical distribution. Take the maximum difference as the test statistic $D_s$, as shown in Equation (4).

$$D_s=\underset{x}{\max }\left|F_s\left(x\right)-F\left(x\right)\right|$$

(4)

where $D_s$ is the test statistic of the K–S test, $F_s\left(x\right)$ is the cumulative distribution function of sample data, $F\left(x\right)$ is the cumulative distribution function of the theoretical distribution, and s is the sample size.

3.

Determine the critical value $D_{s,\alpha }$ based on the sample size s and the significance level α.

4.

If $D_s$ < $D_{s,\alpha }$, accept the null Hypothesis H_0-1, indicating that the sample data conform to the theoretical distribution; otherwise, reject the null Hypothesis H_0-1.

After processing and analyzing the pre-experiment data, this study used the Poisson distribution to fit the distribution of the sample data of the seeding rate, and then used the K–S test method to examine the goodness of fit between the distribution of the sample data and the Poisson distribution. The Poisson distribution is suitable for describing the number of random events occurring within a unit of time (or space). Its cumulative distribution function is expressed as follows:

$$F\left(x;\lambda \right)=P(X\le x)=\sum _{i=0}^x{\displaystyle \frac{{\lambda }^i{e}^{-\lambda }}{i!}}$$

(5)

where x = 0, 1, 2…, denotes the number of event occurrences, λ > 0 represents the average number of events in the Poisson distribution and e is the base of the natural logarithm approximately equal to 2.718 [21].

To examine whether the sample data of the seeds per meter conformed to the Poisson distribution, the following null Hypothesis H_0-2 was proposed:

Hypothesis H_0-2.

The sample data of seeds per meter from different experimental groups, respectively, follow Poisson distributions with different parameters λ. The significance level was set at α = 0.05.

In the K–S test, the p-value is defined as the probability of observing the current D-value under the condition that the null Hypothesis H_0-2 holds. When the H value is 1, it indicates that the corresponding p ≤ α, and the null Hypothesis H_0-2 is rejected. When the H value is 0, it means that the corresponding p ≥ α, and the null Hypothesis H_0-2 is accepted [22]. That is to say, the hypothesis that the sample data of seeds per meter from different experimental groups, respectively, follow Poisson distributions with different parameters λ is valid.

2.4. Experimental Establishment

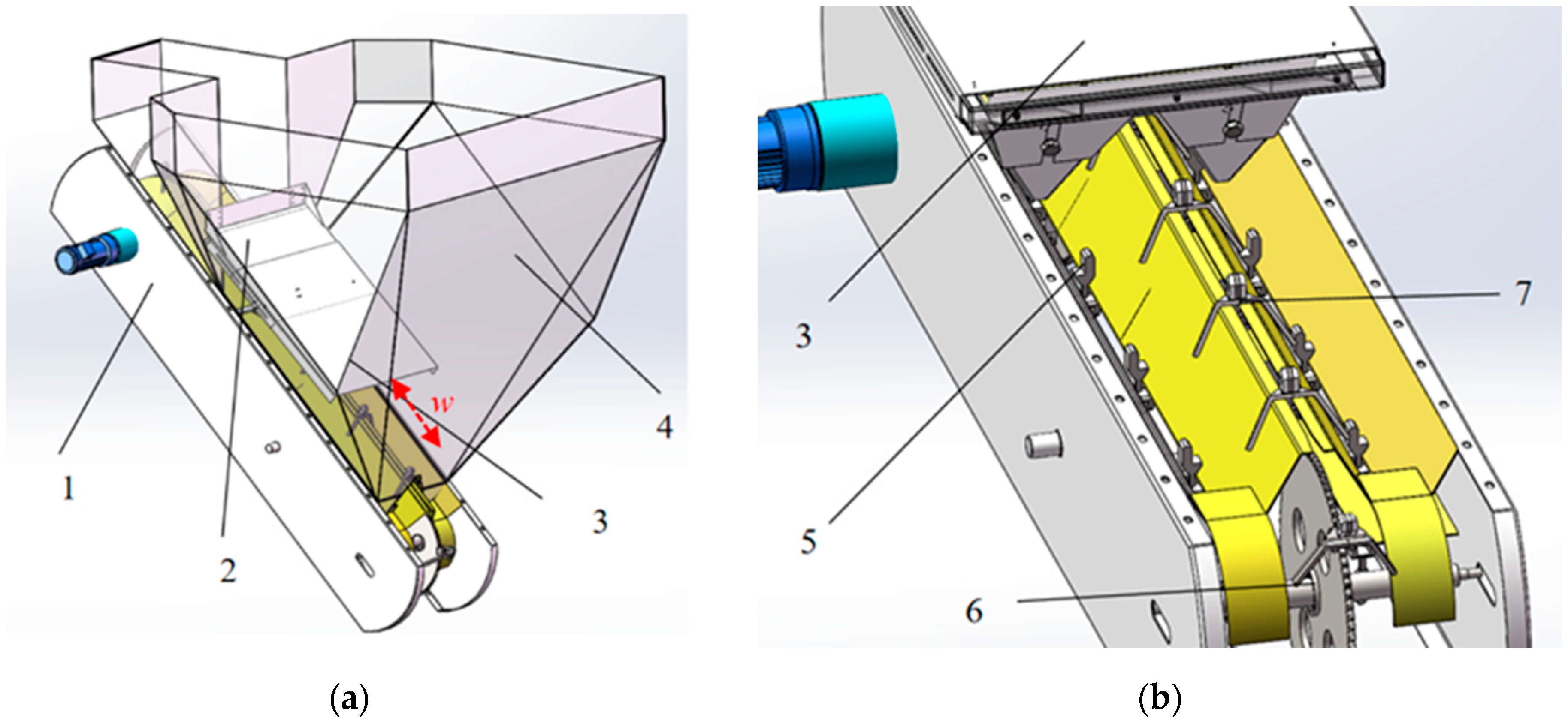
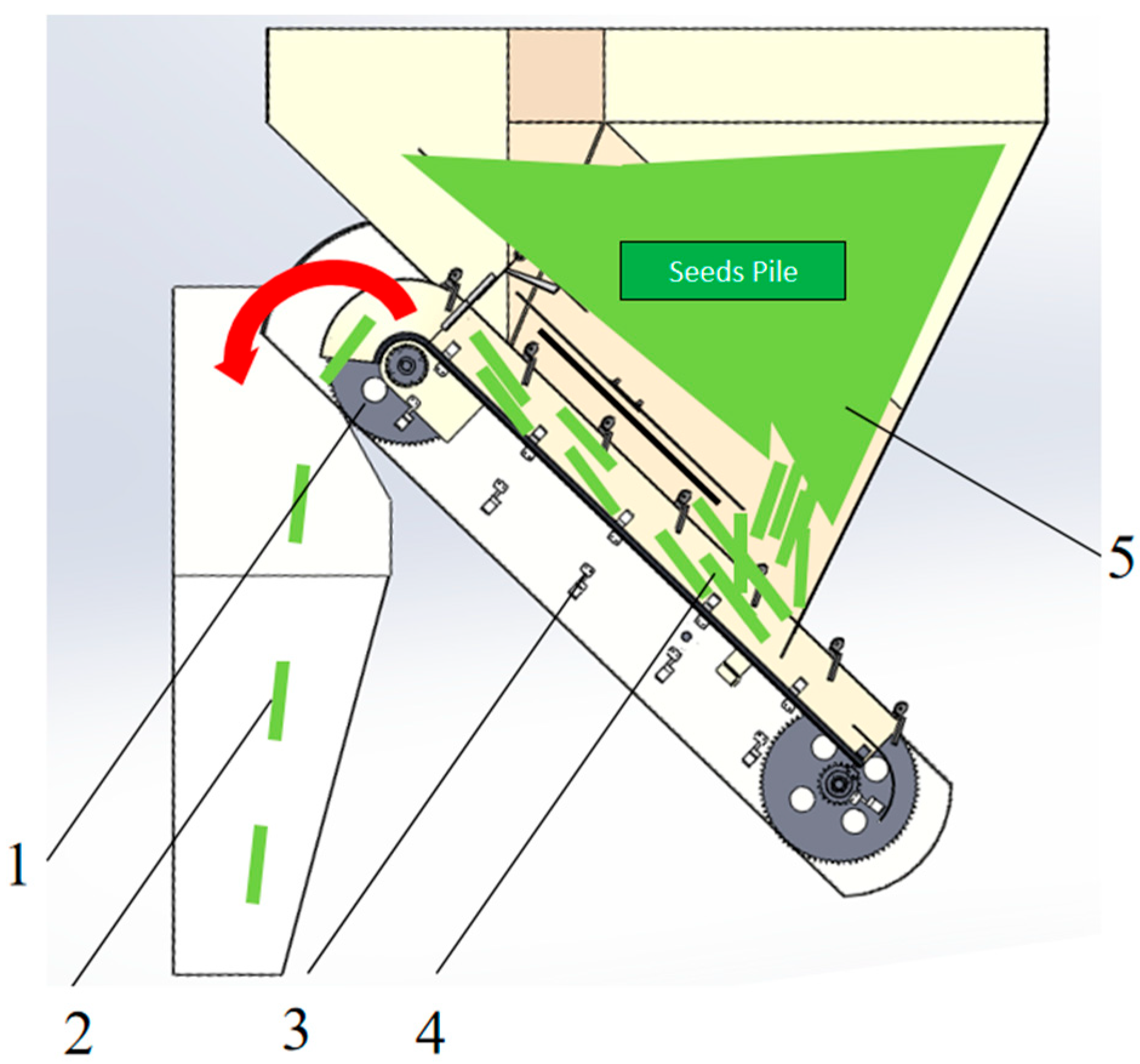
2.4.1. Experiment Design

In this study, three indexes were used for evaluating the performance of seeding: seeding density, seeding uniformity, and seeding efficiency. To verify the effects of the forward speed, discharging sprocket rotational speed, and the outlet size of the hopper on the index of seeding performance, a field test was conducted as shown in Figure 4.

Three different forward speeds v were used in this experiment: 4, 3, and 2 km/h. Two different hopper outlet sizes (w), 400 and 520 mm, were used to ensure that the hopper did not jam. Three different discharging sprocket rotational speeds n were used in this experiment: 120, 80, and 40 r/min.

The experiment followed a completely randomized design (CRD) with a fractional factorial design (FFD) approach. Only 8 key treatments were performed. This reduced the number of tests while still capturing the main effects and potential interactions, saving time and sources. The selected treatments are listed in

Table 2. Completely randomized experiment.

Treatment	Forward Speed v (km/h)	Discharging Sprocket Rotational Speed (r/min)	Hopper Outlet Size (mm)
A	4	80	400
B	3	80	400
C	2	80	400
D	3	120	520
E	2	80	520
F	4	120	520
G	3	80	520
H	2	40	520

.

This experiment was conducted at the testing base of Guangken Agricultural Machinery Service Co., Ltd., Zhanjiang City, Guangdong Province, China, on 11 March 2023. To reduce experimental error, the operating region was divided into the start region, test region, and termination region, as shown in Figure 5. The distances of the start, test, and termination regions were 15 m, 50 m, and 15 m, respectively. The number of seeds per meter was recorded in the test region. The planter was mounted on John Deere M1654 tractor and operated during field work. The type of sugarcane used was Guitang 91, grown in Zhanjiang city, Guangdong province. The average length and diameter of the seeds were 250 mm and 30 mm, respectively. In the test region, the seeding rate per meter was manually recorded for a two-row planter, generating 100 data points for treatments A to H. With 3 experimental replications, the total dataset included 300 data points.

The average seeding rate per meter was calculated from each treatment’s data. Using Equations (1) and (2), the average discharge amount per seeding cleat q and seeding efficiency E for each group were then determined. One-way analysis of variance (ANOVA) [23] was performed on q and E to investigate the influence of vehicle speed v, discharging sprocket rotational speed n, and hopper outlet size w on these parameters. Linear regression analysis was employed to establish mathematical relationships among the given operating parameters, the planter’s inherent structure, the average seeding rate per meter, and the seeding efficiency. When the distribution of the seeding rate sample data follows a Poisson distribution, the seeding uniformity can be reflected by the average seeding rate per meter. Therefore, the seeding performance of the planter can be directly predicted using its operating parameters and structural characteristics.

2.4.2. Speed Test of John Deere M1654 Tractor

The tractor M1654 used in the experiment lacked a real-time speed display and was equipped only with an engine speed gauge, which presents challenges when conducting speed-related tests. Therefore, this section analyzes the relationships among the vehicle speed, gear position, and engine speed of the John Deere M1654 tractor.

Within the tractor’s powertrain, speed transmission begins with the transfer of power from the engine to the main clutch, proceeds through the gearbox, reaches the main reducer, and is finally delivered to the drive wheels via the transfer case [24].

In the transmission system of the M1654 tractor, gear A1 and gear B4 adopt a geometric transmission design. According to reference [25], under the conditions of a constant engine speed, by measuring the vehicle speeds corresponding to any two gears (ignoring actual slippage factors), the common ratio of the transmission system can be calculated.

When operating in the B3 gear at an engine speed of 1500 RPM, the travel time of the John Deere M1654 tractor over a 50-m distance was measured manually. Under these conditions, the tractor’s speed was measured to be 5.1 km/h. Similarly, when the John Deere M1654 tractor was operated at 1500 RPM in the A2 gear, it traveled at a speed of 2.0 km/h. So, the drive train ratio for the M1654 tractor was calculated as 1.207. Based on this common ratio, the theoretical vehicle speed of any gear at a specified engine speed can be calculated using Equation (6):

$$v_z=8.93\times {10}^{-4}\times {1.207}^z{n}_z$$

(6)

where: z is the number of gears; $n_z$ is the engine speed, r/min; $v_z$ is the corresponding tractor speed at engine speed $n_z$ for gear z, km/h.

Therefore, when the vehicle speed is set at 3.0 km/h, the corresponding gear and speed would be A3 and 900, respectively; similarly, when the vehicle speed is set at 4.0 km/h, the gear and speed would be B3 and 1200. The study also compiled a selection of tractor models whose first 8 gears within satisfy the requirement for equal ratios. Please refer to

Table 3. Tractor models in which the first eight gear ratios within 200 HP are in an equal series.

Brand	Tractor	Gear
John Deere (John Deere, Moline, IL, USA)	940 and 1140	1 to 8
	6M series 1654, 6J series 1854	A1 to B4
CASE (CASE, Racine, WI, USA)	Farmall series 65A, 75A, 85A, 95A, 105A and 115A	2 to 8
	MXM series 120, 130, 140, and 155	A1 to A6
Landini Atlantis (Landini, Fabbrico, Italy)	70, 75, 80, 85 and 95	2 to 8
	105, 115, 130, 145 and 165	3 to 8
McCOR-MICK (McCormick, Basildon, UK)	XTX series 185	1–1 to 1–8

.

2.4.3. Centroid Analysis

The centroid of the planter, filled with different cane seed amounts, was measured to assess how many seeds the M1654 tractor mount can support. During operation, the total weight of the planter consists primarily of two components: the weight of the unloaded planter and the mass of the loaded seeds.

Firstly, the weight and centroid position of the unloaded planter were measured using the weighbridge, and then the centroid position of the planter with different cane seeds weights was measured using computer technology. When the planter is stationary on the ground, it is supported by the front furrow opener (P1) and two rear legs (P2 and P3). In this study, a weighbridge (range of 0–3 tons, accuracy to 0.5 kg) was used to measure the force on the three points of the unloaded planter, as shown in Figure 6. The weights of the three points $\mathrm{P}1$, $\mathrm{P}2$, and $\mathrm{P}3$ were 756 kg, 414 kg, and 535 kg, respectively. Therefore, the mass $M$ of the unloaded planter was calculated to be 1705 kg, and the horizontal distance $X_0$ from the center of planter C_P to the suspension point A_t was 1010 mm.

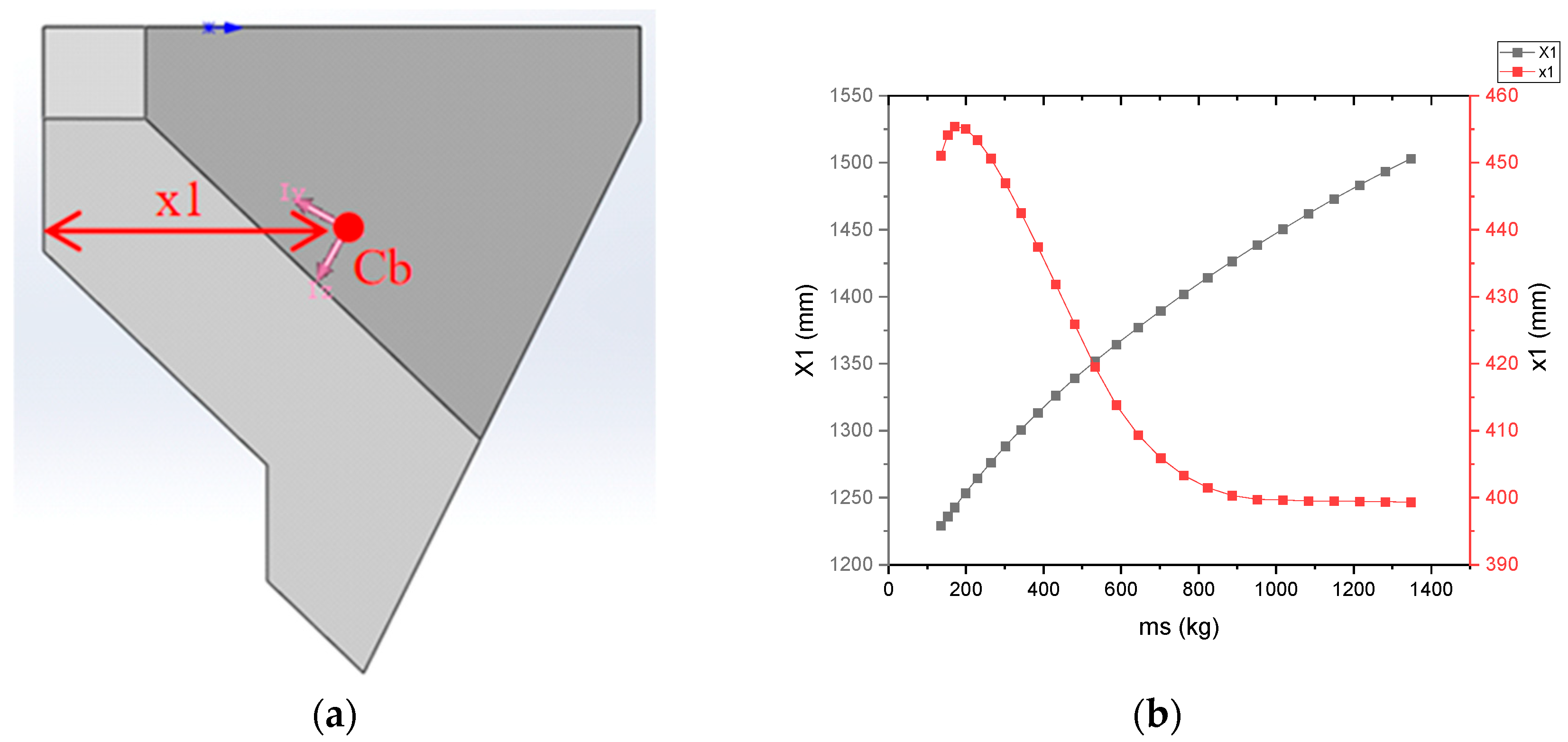
Then, using the software Solidworks (v2016), the material density of the cane seed pile model was set to 415 kg/m³. By modeling the cane seed pile with different cane seed quantities, the curve showing the change in the centroid position of the cane seed pile with mass was obtained, as shown in Figure 7a,b. The horizontal distance between the center of the mass and the suspension point was 350 mm, and the distance $X_h$ between the front end of the bucket and the suspension point was equal to 1566.49 mm. Using the centroid formula Equation (7) of the assembly, the change curve of the position of the planter’s centroid under different cane seed quantities was calculated, as shown in Figure 7b. When the planter is loaded with different masses of seeds, the formula for calculating its centroid position is given by Equation (7):

$$X_1={\displaystyle \frac{{\left(x_1+X_h\right)m}_1+X_0{m}_0}{m_1+m_0}}$$

(7)

where $X_1$ is the distance from the centroid to the suspension point after the planter is loaded with seeds, m; $X_0$ is the distance from the centroid to the suspension point when the planter is not loaded, m; $x_1$ is the distance from the centroid to the front end, m; $X_h$ is the distance between the front end of the hopper and the suspension point, m; $m_1$ is the mass of the loaded seeds, kg; $m_0$ is the self-weight of the unloaded planter, kg.

As the mass of seed pile increased from 200 kg to 800 kg, the distance of the centroid of the seed pile on the x–axis $x_1$ decreased rapidly, while $X_1$ gradually increased. When the mass of seed pile was more than 800 kg, $x_1$ remained almost constant, while $X_1$ continued to increase. The variation range of $x1$ was within 60 mm, and the variation range of $X_1$ was within 270 mm. The M1654 tractor has a hydraulic lifting capacity of up to 4000 kg at the 610 mm suspension point [26]. Therefore, based on the data in Figure 7b, the safe loading capacity of the planter was calculated as 360 kg. Under the assumptions of ignoring ground wheel support and uniform mass distribution of seeds within the hopper, the John Deere M1604 tractor can safely suspend the planter for field operations when the loading mass of seeds is less than 360 kg.

2.5. Statistical Analysis

All treatment datasets were imported into the statistical analysis software SPSS (v2017). Within SPSS, a series of analytical operations were carried out, including generating the seeding frequency table, performing the K–S test, conducting one-way analysis of variance, and executing regression analysis.

3. Results

3.1. Analysis of Experimental Data Results

As shown in Figure 8, the field test results were analyzed by counting the number of seeds per meter. After processing the experimental data, the mean and standard deviation were presented in

Table 4. The experimental values of the treatments.

Treatment	Mean (Seeds)	Std. Deviation	Discharging Rate per Cleat $\mathit{q}$ (Seeds)
A	3.25	1.538	2.46
B	3.95	1.751	2.24
C	7.11	2.823	2.69
D	9.32	3.362	3.53
E	7.86	3.294	3.5
F	7.11	2.651	3.5
G	6.03	2.498	3.43
H	5.79	2.754	4.08

. Using Equation (1), the average discharge per seed metering cleat was calculated and is also listed in Table 4.

3.2. Evaluation of Seeding Density

According to Equation (1), under the given n and v, the average seeding rate per meter N is determined by q. To explore the factors that affect q, one-way ANOVA was carried out on v, n, and w, respectively. The significance of each factor was measured through the F and t-tests, as listed in

Table 5. The analysis of variance for factors.

Source of Variance	F-Value	p-Value
Speed	0.291	0.759
Rotation	10.825	0.087
Hopper outlet size	38.272	0.001 *

Note: * Significant impact within a 99% confidence interval.

.

As seen in Table 5, the outlet size of the hopper had a very significant effect on the discharging rate per cleat. Speed and rotation had an insignificant impact on the discharging rate per cleat. When the outlet sizes of the hopper were 400 mm and 520 mm, the average values of q were 2.55 and 3.61. Assuming that the relationship between $q$ and $w$ is linear, Equation (1) can be written as Equation (8), where $\mathrm{k}$ is the proportionality coefficient.

$$N=k{\displaystyle \frac{wn}{v}}$$

(8)

Denoting $X$ as $w\times n/v$, a scatter plot was generated, and linear regression analysis was conducted, excluding a constant between $X$ and the mean $N$, as shown in Figure 9. The slope of the curve is 4.46 × 10⁻⁴ and R-squared is equal to 0.9959.

Therefore, the mathematical model of seeding is written as Equation (9).

$$N=4.46\times {10}^{-4}·{\displaystyle \frac{wn}{v}}$$

(9)

Therefore, the seeding density of the sugarcane planter can be directly calculated using the rotational speed of the discharging sprocket n, the forward speed of the planter v, and the outlet size of the hopper w.

3.3. Evaluation of Effect on Seeding Efficiency

ANOVA was used to test the significant difference in seeding efficiency at different v, w, and n values, as shown in

Table 6. ANOVA was used to test significant differences in seeding efficiency at different v, w, and n values.

Variance Source	F-Value	p-Value
Speed $v$	0.106	0.9
Rotation $n$	5.116	0.019 *
Hopper outlet size $w$	9.538	0.007 *

Note: * Significant impact within 95% confidence interval.

. The results show that the discharging sprocket rotational speed n and the hopper outlet size w had a significant effect on the seeding efficiency.

Linear regression analysis was conducted, taking q and n as independent variables and E as a dependent variable, as shown in Table 6. Therefore, the mathematical linear regression model of seeding efficiency in relation to the outlet size of the hopper and the discharging sprocket rotational speed is established as Equation (10). The model has an R-squared value of 0.979, so the fit is favorable.

$$E=0.241n+0.056w-27.17$$

(10)

Therefore, the seeding efficiency of the sugarcane planter can be directly estimated using the given rotational speed of the seeding sprocket wheel n and the outlet size of the hopper w.

3.4. Evaluation of Seeding Uniformity

To reduce the influence of random errors and improve the reliability of the experiment, the data from three replicate trials in each group were aggregated and processed. This was carried out to analyze the degree of fit between the distribution of seeding quantity per meter and the Poisson distribution. The frequency distribution of seeding of treatment A–H are shown in Figure 10. The frequency distributions of seeding show higher frequencies in the middle and lower frequencies on the sides, forming an approximately bell-shape curve. Skewness and Kurtosis are shown in

Table 7. The p-values of the K–S tests and parameter $\mathsf{\lambda }$ of the treatments.

Treatment	Skewness	Kurtosis	p-Value	$\mathsf{\lambda }$
A	0.151	0.052	0.093	3.25
B	0.623	0.673	0.241	3.95
C	0.579	0.416	0.958	7.11
D	0.478	0.399	0.950	9.32
E	0.738	0.514	0.435	7.86
F	0.476	0.567	0.999	7.11
G	0.452	0.267	1.000	6.03
H	0.331	−0.047	0.535	5.79

. The skewness is all greater than 0, which indicates that the seeding distribution is not symmetric about the mean and majority of the data distribution will be on the left side of the mean. The skewness values were all greater than 0 except for treatment H, which indicates that this seeding distribution was lighter-tailed with a steeper top curve [27].

The datasets of all treatments were fitted by Poisson distributions, with $\mathsf{\lambda }$ equal to N, using maximum likelihood estimation. The values of $\mathsf{\lambda }$ and the results of the K–S test (under confidence degree $\mathsf{\alpha }=0.05$) are shown in Table 7. All the p-values of K–S tests were larger than $\mathsf{\alpha }=0.05$, so the Poisson distributions fit the datasets of all treatments well [28].

As shown in Table 7, the mean and standard deviation of a Poisson distribution are both equal to the parameter $\mathsf{\lambda },$ which is equal to the mean $N$. Therefore, the theoretical variable coefficient ${CV}_t$ can be written as Equation (11) based on Equation (9).

$${CV}_t=47.35\sqrt{{\displaystyle \frac{v}{nw}}}$$

(11)

The practical variable coefficient ${CV}_p$ can be calculated as the mean divided by the std. deviation of sample data. The ${\mathsf{\epsilon }}_{\mathrm{a}}$ between ${CV}_p$ and ${CV}_t$ was 0.94–6.18%. When ${CV}_t$ was below 40%, the ${\mathsf{\epsilon }}_a$ was less than 3%, as shown in

Table 8. Theoretical variable coefficient ${\mathrm{C}\mathrm{V}}_{\mathrm{t}}$, the practical variable coefficient ${\mathrm{C}\mathrm{V}}_{\mathrm{p}}$ and the absolute error ${\mathsf{\epsilon }}_{\mathrm{a}}$ (%) between ${\mathrm{C}\mathrm{V}}_{\mathrm{t}}$ and ${\mathrm{C}\mathrm{V}}_{\mathrm{p}}$.

Treatment	${\mathit{C}\mathit{V}}_{\mathit{t}}$ (%)	${\mathit{C}\mathit{V}}_{\mathit{p}}$ (%)	Absolute Error ${\mathit{\epsilon }}_{\mathit{a}}$ (%)
A	52.94	46.76	6.18
B	45.85	42.72	3.13
C	37.43	35.28	2.15
D	32.83	35.44	2.61
E	35.10	36.37	1.27
F	37.91	37.53	0.38
G	40.21	37.61	2.60
H	46.43	47.37	0.94

.

Therefore, when the rotational speed of the seeding sprocket wheel n, the forward speed of the planter v, and the outlet size of hopper w of the planter are known, if the calculated theoretical coefficient of variation ${CV}_t$ is less than 40%, it is approximately equal to the actual coefficient of variation ${CV}_p$, with an error of less than 3%. This can relatively accurately reflect the seeding uniformity of the planter.

4. Discussion

This study conducted a comprehensive evaluation of a novel pre-cut sugarcane planter designed by South China Agricultural University. This sugarcane planter represents a breakthrough improvement over current domestic designs [23,29], which are constrained by low efficiency and a limited capacity. Compared to international counterparts (e.g., Gessner’s single-row planter [30] or Ury’s Manufacturing triple-row planter [31]), this tractor-mounted system achieved a 40% reduction in the turning radius and a superior hopper capacity, making it ideally suited for small-plot cultivation in southern China’s hilly regions—a practical solution to China’s challenges of high production costs and low mechanization rates in sugarcane farming.

Currently, many scholars analyze the probability of multiple seeding (exceeding a specific seed count) or missed seeding (falling below a specific count) within a unit distance under different working conditions through experiments. However, such an approach is limited because it only provides insights into seeding performance within specific numerical ranges. By conducting large-scale seeding experiments to analyze the probability distribution of seeds per meter, we can comprehensively understand the occurrence probability of each seeding quantity within a unit of distance. Coupled with the regression relationship between operational parameters of planter and seeding density, these findings allow for direct prediction of the occurrence probability for any seeding quantity range under arbitrary operational parameters. Furthermore, these findings can also be used to assess the planter’s performance for different regional planting requirements by adjusting the operational parameters of the planter.

The following limitations in this study require further investigation: (1) potential unexamined parameter interactions due to the completely randomized partial factorial design; (2) centroid shift phenomena during uneven seed accumulation and seeding uniformity under varying load conditions; (3) comprehensive economic evaluation (e.g., per-mu operational costs) through large-scale field trials.

5. Conclusions

A new type of pre-cut sugarcane planter designed by South China Agricultural University was used in field seeding experiments. Before the experiment, the vehicle speed of the John Deere M1654 tractor and the safe loading capacity of the planter were analyzed. Then, the distribution of the seeding rate per meter and the seeding performance of the planter at different forward speeds, discharging sprocket rotational speeds, and hopper outlet sizes were investigated through field experiments. The obtained conclusions were as follows:

• The outlet size of the hopper has a very significant effect on the discharging rate per cleat. When the outlet sizes of the hopper are 400 mm and 520 mm, the average values of q are 2.55 and 3.61. The mathematical model of the average seeding rate per meter of the planter in relation to the speed of the vehicle, the discharging sprocket rotational speed, and the outlet size of hopper is $N=4.46\times {10}^{-4}·{\displaystyle \frac{wn}{v}}$ (R² = 0.9959).
• Seeding efficiency is significantly affected by the discharging sprocket rotational speed and the outlet size of the hopper. The mathematical regression model is $E=0.241n+0.056w-27.17$ (R² = 0.979).
• The seeding rate per meter of the planter follows the Poisson distribution, and the Poisson distribution parameter $\mathsf{\lambda }$ is equal to the average seeding rate per meter. Its theoretical coefficient of variation is ${CV}_t=47.35\sqrt{{\displaystyle \frac{\mathrm{v}}{\mathrm{n}\mathrm{w}}}}$. When the theoretical coefficient of variation is less than 40%, the absolute error between the actual and theoretical coefficient of variation is less than 3%.