Abstract
The large-span insulated plastic greenhouse is a highly promising horticultural facility. The design parameters and configuration of structural components significantly impact their safety and load-bearing performance. However, current research in this field remains insufficient. In this study, the deformation, stress distribution, and stability of large-span insulated plastic greenhouses with different structural configurations were investigated using the finite element method. Subsequently, the ultimate bearing capacity of large-span insulated plastic greenhouses with varying ridge heights was examined. The research indicated that the greenhouse with a plane truss and double-layer tie rod exhibited the smallest deformation and stress in its members, as well as the highest ultimate load-bearing capacity. The analysis revealed that the installation of double-layer tie rods not only enhanced the collaborative effect of arch frames within the structural calculation unit but also reduced displacement along the Z direction, effectively mitigated the effect, reduced out-of-plane bending stress, and improved the ultimate load-bearing capacity. Ridge height affected the load-bearing capacity of the greenhouse structure. However, a higher ridge height did not necessarily result in a stronger ultimate load-bearing capacity. The greenhouse structure with a ridge height of 5 m demonstrated the maximum ultimate load-bearing capacity, capable of bearing 1.98 times the initial load. This study provides theoretical support for the configuration of structural components of large-span insulated plastic greenhouses and offers a scientific basis for the optimal design of ridge height.
1. Introduction
Facility horticulture is an important component of modern agriculture and plays a significant role in ensuring agricultural product supply [1,2]. As of recent data, the total area of facility horticulture in China reaches approximately 3.7 million hectares, accounting for nearly 80% of the global facility horticulture area [3]. After an extended period of development, agricultural facilities have established structural types that are suitable for the local climate in various production regions [4,5]. The structural safety of greenhouses is a prerequisite for ensuring normal production. However, plastic greenhouses are often designed with a low safety margin [6]. Many researchers have investigated the stability of greenhouse structures under various load conditions using experimental and numerical methods. For example, the study by Castellano et al. [7] carried out a full-scale load test of a double sloping roof greenhouse and a pitched roof greenhouse structure, focusing on the influence of wind and snow loads on their bearing capacity. Briassoulis et al. [8] developed a three-dimensional structural model of a large multi-span circular greenhouse, as well as a two-positioned frame model, utilizing linear, geometric, and material nonlinear analysis methods to investigate the greenhouse’s failure modes under wind and snow loads. Additionally, Wang et al. [9,10] used ANSYS software to analyze the static and dynamic responses and failure mechanisms of the single-tube and truss-type structures of a prefabricated ground-mounted solar greenhouse. These studies provide valuable references for the stability of greenhouse structures under various loads.
The large-span insulated plastic greenhouse is characterized by its large span and spacious interior, which enhances land utilization efficiency and ensures environmental stability [11,12], demonstrating significant application potential [13,14]. It has gained widespread recognition in the Yellow-Huai River Basin region of China. Compared with the conventional plastic greenhouses, the large-span insulated plastic greenhouse has a larger span and more complex structure, thus demanding higher standards for structural safety [15]. Several studies have been conducted on the static and dynamic load-bearing mechanisms of large-span insulated plastic greenhouses. Ren et al. [16] performed a structural analysis on a large-span plastic greenhouse that combines flat truss arches and spatial truss arches, analyzing the structural behavior under stress, deformation, and instability. The results indicate that structural safety was primarily governed by the strength and stiffness of the components. Wang et al. [17] examined the load-bearing characteristics and dynamic behavior of large-span plastic greenhouses with single-tube structures using static analysis and time history methods. The research found that such structures are more sensitive to non-uniformly distributed snow loads, with the time history analysis revealing a significant increase in maximum displacement and bending stress. However, these studies typically treat the configuration of the tie rod and ridge height as constant factors. The significance of tie rod configuration and ridge height for greenhouse load-bearing performance and structural stability has been overlooked. Thus, further research is needed on the load-bearing characteristics of the frame structures of large-span insulated plastic greenhouses.
In this research, three structures for a large-span insulated plastic greenhouse were designed. Finite element models of the 3-D frame structure were developed using ANSYS Workbench 2022. Three greenhouse structures were calculated under seven load actions, in accordance with the relevant design codes. The stress and deformation characteristics were analyzed. The most unfavorable load combination was identified. Then, under the most unfavorable load action, the instability mechanisms and ultimate bearing capacities of the three structures under double nonlinear conditions were further investigated. The load-bearing capacities of the three structures were evaluated, and the superior structure was chosen. Based on the chosen structure, 3-D models of large-span insulated plastic greenhouse structures with varying ridge heights were established. The ultimate bearing capacities were analyzed under the most unfavorable load combination. The research results can clearly determine the impact of tie rod configuration and ridge height on the load-bearing capacity of large-span insulated plastic greenhouses.
2. Materials and Methods
2.1. Greenhouse Structure
The greenhouse is located in Jiaozuo (113.2° E, 35.2° N), Henan, China, with a north–south orientation. It features an oval roof shape, a span of 20 m, a ridge height of 5.5 m, and a length of 80 m. The structure comprises the following components: arch frame, tie rod, central column, side column, cross beam, and diagonal brace. The spacing between the arch frames is 1 m. Central columns, inclined supports, and side columns are set every 4 m to form a bay. The upper parts of these central columns are linked by a cross beam along the length of the greenhouse, providing support to the arches. The side columns are positioned 5 m away from the central columns and are connected to the lower edges of the arches. Independent foundations are provided under the central and side columns, and strip foundations are placed under the arches. All components are connected by special metal connectors. Since the greenhouse structure is generated by repeating the components within each bay along the length, due to the repetitive modular design, only one structural bay was modeled for computational efficiency. Figure 1 displays actual photographs and a schematic diagram of the greenhouse structure.
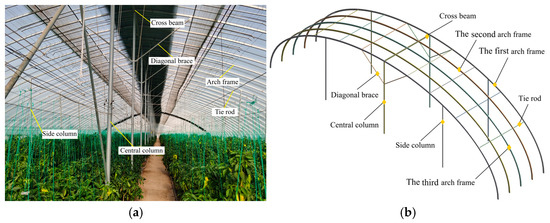
Figure 1.
The structure of the large-span insulated plastic greenhouse: (a) is the photo of the greenhouse structure; (b) is the schematic diagram of the greenhouse structure.
2.2. Experimental Design
The load-bearing capacity of large-span insulated plastic greenhouses is governed by their structural configuration. To study the effect of arch types and tie rods on the load-bearing mechanism of large-span insulated plastic greenhouses, this research focuses on two common arch frame types: rectangular tube and plane truss. The plane truss has strong structural rigidity and stability, and high space utilization. Rectangular tube is the cross-section type with the best bearing performance of the single tube structure. It is easy to install and has high assembly efficiency, which meets the requirements of the development of a light and simplified greenhouse structure. The tie rod configuration also affects the overall performance and stability of the greenhouse structure. The tie rod configurations adopt 2 schemes: single layer and double layer. Preliminary test results show that whether the tie rods are connected to the upper chord of the truss or the lower chord, the deformation, stress distribution, and load-bearing capacity of the structures are similar. Therefore, this research designed three greenhouse structures: a rectangular tube with a single-layer tie rod, a plane truss with a single-layer tie rod, and a plane truss with a double-layer tie rod. For convenience, the following are abbreviated as Type-A, Type-B, and Type-C. The schematic diagram of the 3 greenhouse structures is shown in Figure 2. The specifications and dimensions of the structural components are listed in Table 1. The 3 greenhouse structures have similar steel consumption. The steel usage for one calculation unit of Type-A, Type-B, and Type-C is 709.1, 700.9, and 748.2 kg.
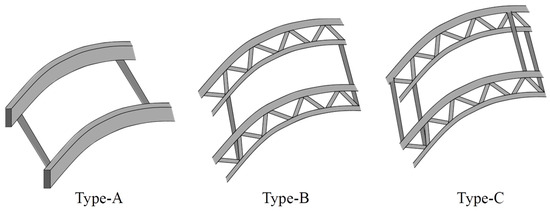
Figure 2.
Schematic diagram of 3 greenhouse structures.

Table 1.
Specifications of components with 3 greenhouse structures.
The Type-A structure uses 40 × 95 × 2 mm rectangular steel tubes for the arch frame, equipped with 8 tie rods connected to the lower edge of the arch frame. The arch frames of Type-B and Type-C structures are both made up of plane trusses with the same material specifications. The upper chord is made of 32 × 2 mm circular steel tubes, while the lower chord and web members use 25 × 2 mm circular steel tubes. The Type-B structure is equipped with 8 tie rods connected to the lower chord of the truss. The Type-C structure is equipped with 16 tie rods, arranged in 2 layers with 8 rods per layer, connected to the upper and lower chords of the truss, respectively. The layout positions and dimensions of the tie rods, central column, side column, cross beam, and diagonal brace are consistent. The tie rods use 32 × 2 mm circular steel tubes, the central columns use 76 × 2 mm circular steel tubes, the side columns use 60 × 2 mm circular steel tubes, the cross beam uses 50 × 70 × 2 mm rectangular steel tube, and the diagonal braces use 50 × 2 mm circular steel tubes.
Then, 3-D models of greenhouse structures with different ridge heights (3, 4, 5, 6, 7, and 8 m) were established based on the selected structures, to investigate the effect of ridge height on the ultimate bearing capacity of large-span insulated plastic greenhouses.
2.3. Load and Loading Method
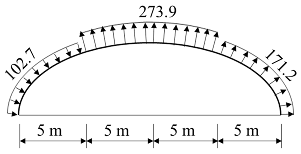
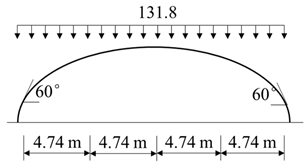
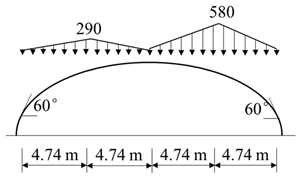
The study focuses particularly on constant load, wind load, uniform snow load, and non-uniform snow load. The load values in this study were determined according to the current greenhouse structural design load code of GB/T 51183-2016 [18]. The constant load of the large-span insulated plastic greenhouse mainly calculates the self-weight of the frame, and the variable loads calculate the snow load and wind load. To account for the influence of wind-induced snow drift, two cases of snow load distribution were considered: uniform and non-uniform. The standard values and loading forms of snow load and wind load for each part of the greenhouse surface are shown in Table 2.

Table 2.
Load values and loading methods for a large-span insulated plastic greenhouse.
2.4. Load Effect Combination
According to GB/T 51183-2016, the structure of the large-span insulated plastic greenhouse was evaluated based on the ultimate limit state of bearing capacity. During the operation of greenhouses, various loads do not occur simultaneously. Therefore, the combination of load effects must be applied. The partial factors and combination factors are shown in Table 3, totaling seven load combinations. The calculation method for the load effect design value under different load combinations is shown in Equation (1).

Table 3.
Partial factors and combination coefficients for 7 load combinations.
In Equation (1), is the load effect of constant loads, is the load effect of the first variable load, and is the load effect of the remaining variable loads. is the partial factor for constant loads, which is taken as 1.0. is the partial factor for the first variable load, while and are the partial factors and combination factors for the remaining variable loads. The partial factors and combination coefficients are shown in Table 3.
2.5. Modeling Method
2.5.1. Geometric Model
The structural performance was studied using ANSYS Workbench 2020. The greenhouse structure is built by repetitively using the structural members within each bay as the fundamental building blocks. To improve computational efficiency, a single structural bay was modeled and analyzed. Although the arch frame has curvature, it can actually be approximated as being composed of a series of short straight members [19]. Initially, point generation commands were utilized to create joints for the members. These nodes were then connected to form the structure members of the arch frame. By applying an offset command along the z-axis, the complete arch structure was modeled. Subsequently, the nodes were used to add tie rods, central columns, side columns, cross beam, and diagonal brace, thus completing the finite element model of the calculation unit. All components were considered as a part, with common finite element nodes among the structural members, which streamlined the calculation process. The lower parts of the arch frame, central columns, and side columns were welded to the foundation through embedded steel plates. These connections were modeled as fixed constraints due to their high rigidity, which effectively restricts translational motion and rotation. Fixed constraints were adopted as an idealized boundary condition to reduce model complexity.
2.5.2. Materials and Element Types
The structure of the greenhouse is made of galvanized steel pipes. According to the steel structure design standard GB 50017-2017 [20], the steel grade is Q235. The constitutive model of the steel material used the bilinear isotropic hardening model, with an elastic modulus of 200 GPa, a Poisson’s ratio of 0.3, a yield strength of 235 MPa, and a tangent modulus of 0 Pa. Consequently, the design value of structural resistance was taken as the yield strength. The frame mainly consists of slender rods, and the element type was the default beam188. This element is based on the Timoshenko beam theory, which calculates the change in rotational inertia caused by the bending and shear deformations of the beam under load. It is capable of adapting to both linear and nonlinear analysis.
2.5.3. Load Effect Calculation
Constant loads were automatically calculated by the software. Snow load is a vertical downward surface load, and wind load is a perpendicular force to the shed surface. The load transfer process of the covering material was simplified by applying snow and wind loads as “line pressure” on the arch frames. By considering large deformation, the effect of deformation on structural stiffness was incorporated. The load effect of the greenhouse structure (the deformation and stress distribution of the members) under constant load, uniform snow load, non-uniform snow load, and wind load was calculated separately. Then, the load effects under 7 load combinations were calculated according to Equation (1).
2.5.4. Double Nonlinear Buckling Analysis
Considering both material and geometric double nonlinear, buckling analysis of the structure was conducted to calculate the ultimate bearing capacity of the structure. The basic equation of nonlinear buckling analysis is as shown in Equation (2).
where is the displacement-dependent nonlinear stiffness matrix, is the displacement vector, is the load vector.
The structural members of the large-span insulated plastic greenhouse function as a cohesive unit to collectively withstand external loads. Under different load conditions, the structure deformation varies significantly, thereby affecting the structural stiffness matrix. In the analysis of double nonlinear buckling, the effect of these deformations on the stiffness matrix must be considered to accurately assess the structure’s ultimate load-bearing capacity. Therefore, in this study, the constant loads were first applied and kept constant, then variable loads were applied, and the loading form was kept unchanged. The double nonlinear buckling analysis was performed by gradually applying N times the variable load to calculate the ultimate load-bearing capacity. The steps of the double nonlinear buckling analysis are as follows. Two load steps were set up. First, only the constant load was applied in the first step. Then, 4 times the non-uniform snow load was applied in the second step. 200 load increment steps were established to simulate the process of gradual, incremental loading. The full Newton-Raphson method was used to solve, iteratively calculating the stress values of the structure under each load increment until structure failure. Finally, the load-displacement curve and load-stress relations were output. The ultimate load was determined based on the criterion that the maximum stress in the structure exceeds the material’s yield strength. For convenience, the ultimate load was expressed as a multiple of the initial load.
Following the above modeling approach, finite element models of greenhouses with different ridge heights were developed. After the permanent load was applied, the “Line pressure” command was used to gradually apply 4 times the uneven snow load. As specified in the load code, when there is an insulation quilt on the roof, the snow distribution coefficient for non-uniform snow loads is taken as 2. Therefore, the peak values of the initial snow load were identical for different ridge heights. In this study, the ultimate bearing capacities of large-span insulated plastic greenhouses with different ridges were compared under similar load conditions.
3. Results
3.1. Deformation Analysis
As a light steel structure, the total and directional deformation of the greenhouse may cause additional stress, reduce bearing capacity, and consequently affect the safety of the overall structure. To evaluate the stiffness of the three greenhouse structures and clarify their deformation characteristics, Table 4 shows the maximum deformation values in the X, Y, Z directions and the total deformation for all three structures under seven load combinations. It can be seen from Table 4 that when the wind load and snow load acted separately, the deformation direction of the greenhouse structures exhibited the opposite trend. Under combined loading, mutual cancelation occurred, leading to smaller deformations compared to single-load scenarios. The largest deformations occurred under Load action 3, followed by Load action 1, while simultaneous wind and snow loads resulted in relatively small overall deformations.

Table 4.
Maximum deformations of the 3 large-span insulated plastic greenhouses structures under 7 load combinations (mm).
It was evident that under load condition 3, the total deformation of the three structures was 53.8, 23.4, and 18.3 mm, respectively. The allowable deformation for long-span steel structures is 1/250th of the span length, equating to 80 mm. All structures satisfied this criterion under all seven load combinations. The Type-C structure has the smallest deformation components and total deformation values in the X, Y, and Z directions. Under seven load conditions, the total deformation amounts are 13.0, 10.4, 18.3, 8.5, 5.8, 4.4, and 10.6 mm, while the deformation components in the Z direction are 4.5, 4.2, 4.8, 2.3, 1.9, 1.0, and 1.5 mm. The Type-B structure exhibits the second smallest deformation. The total deformation under seven working conditions is 16.4, 12.5, 23.4, 11.1, 6.8, 5.6, and 13.5 mm, and the deformation components in the Z direction are 5.6, 5.2, 6.1, 3.0, 2.3, 1.1, and 2.0 mm. The Type-A structure has the largest deformation. Overall, the deformation of the plane truss frame is significantly lower than that of the rectangular tube frame. Compared to Type-B, the Type-C structure exhibits even less deformation, indicating that the addition of upper tie rods can reduce the total deformation and deformation components in the X, Y, and Z directions of the structure.
3.2. Stress Analysis
In the study of greenhouse structures, stress analysis serves not only as a crucial indicator for ensuring structural safety but also optimizes the arrangement of steel structural components through stress distribution analysis, providing robust data support for further structural design optimization. This study examined direct stress, in-plane bending stress, and out-of-plane bending stress to comprehensively characterize arch frame component stresses.
3.2.1. Stress of the Third Arch Frame
Figure 3, Figure 4 and Figure 5 show the stress distribution of the third arch frame under 7 load conditions for 3 structures. Similarly to the deformation analysis, when the wind load and snow load acted, respectively, the stress in the members showed the opposite trend. Therefore, when the two were combined, they would offset each other, and the stress of the member under the two variable load combinations was less than that under a single load. Therefore, under Load action 3, the member stresses were the largest, Load action 1 was the next, and when the wind load and snow load acted at the same time, the member stresses were relatively small.
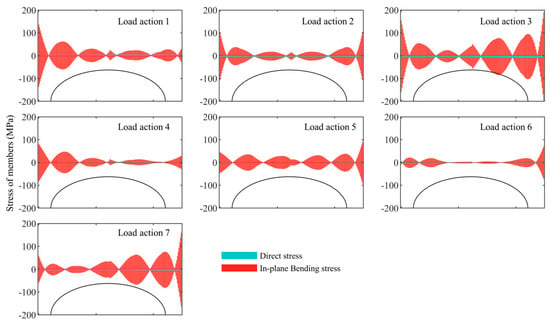
Figure 3.
Stress distribution in the third arch frame of the Type-A structure under 7 load conditions.
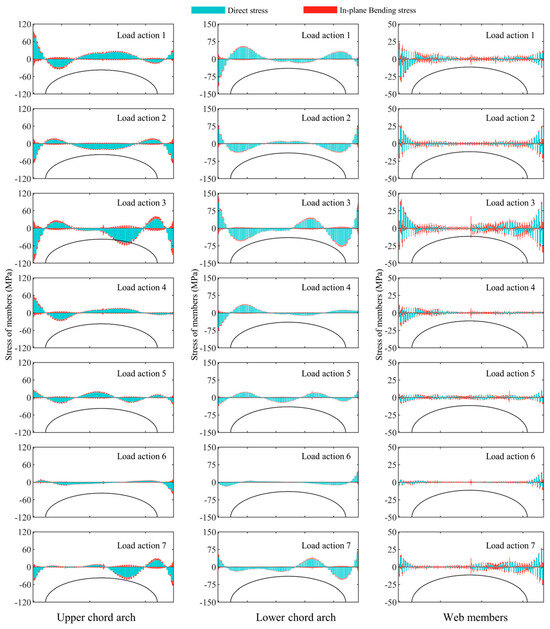
Figure 4.
Stress distribution in the third arch frame of the Type-B structure under 7 load conditions.
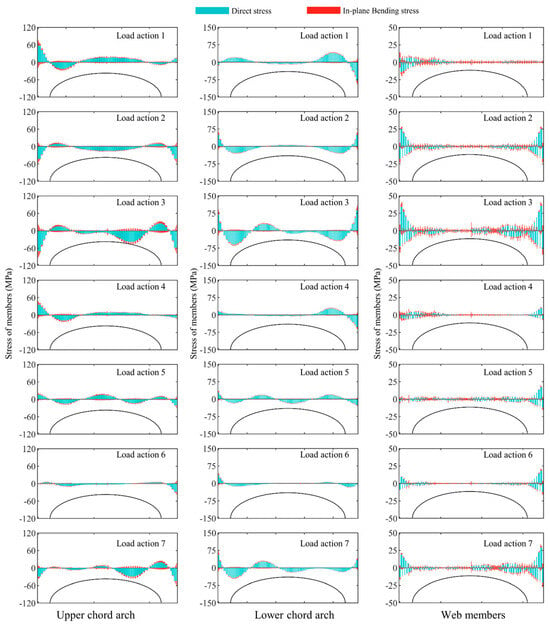
Figure 5.
Stress distribution in the third arch frame of the Type-C structure under 7 load conditions.
It can be observed that the Type-A structure mainly experienced in-plane bending stress, with a relatively small direct stress ranging from −7.9 to 4.0 MPa, while the out-of-plane bending stress was 0 MPa. The stress on the structural supports was the highest. For Type-B and Type-C structures, direct stress was mainly distributed on the components, with in-plane bending stress present but small, ranging from 0.7 to 25.6 MPa, while out-of-plane bending stress was 0 MPa. The stress at the lower chord support of the truss reached its maximum.
And the maximum combined stress of the Type-A structure was −196.6 MPa, with an average value of 45.9 MPa. For the Type-B structure, the maximum combined stress in the upper chord, lower chord, and web members was −113.1, 136.4, and 41.4 MPa, with corresponding average values of 22.3, 30.8, and 6.5 MPa. The maximum direct stress in members was 32.7 MPa, 110.9 MPa, and 33.9 MPa, with averages of 22.7 MPa, 31.6 MPa, and 5.4 MPa. For the Type-C structure, the maximum combined stress in the upper chord, lower chord, and web members was −91.5, 108.5, and 41.1 MPa, with average values of 17.4, 23.7, and 6.1 MPa. The maximum direct stress in members was 25.3, 87.4, and 35.5 MPa, with averages of 18.0, 24.3, and 5.2 MPa.
3.2.2. Stress of the Second Arch Frame
Figure 6, Figure 7 and Figure 8 show the stress distribution of the second arch under seven load conditions for three structures. It was observed that the stress distribution in the second arch of the three structures was similar to that of the third one, but all experienced out-of-plane bending stress. The stress in the second arch was less than that in the third arch. Under Load action 3, the maximum combined stress in the Type-A structure was −189.6 MPa, with an average value of 35.8 MPa. The maximum out-of-plane bending stress on the arch frame was 22.0 MPa, with an average value of 5.3 MPa.
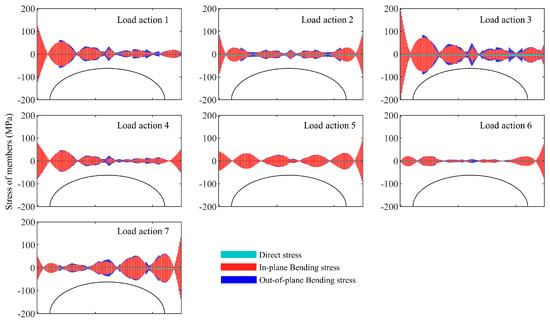
Figure 6.
Stress distribution in the second arch frame of the Type-A structure under 7 load conditions.
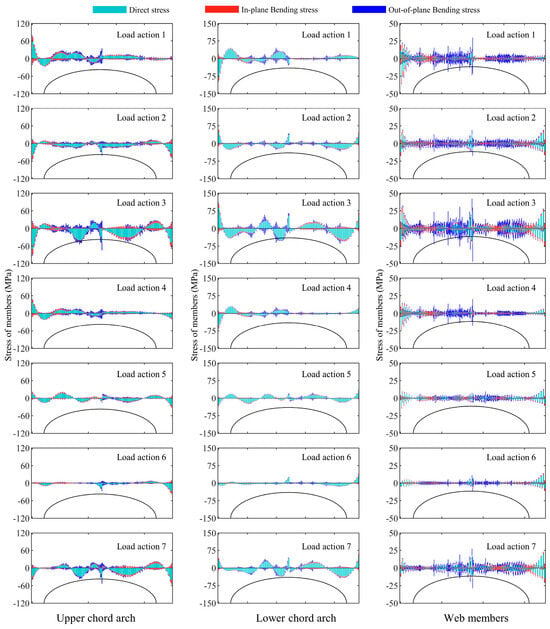
Figure 7.
Stress distribution in the second arch frame of the Type-B structure under 7 load conditions.
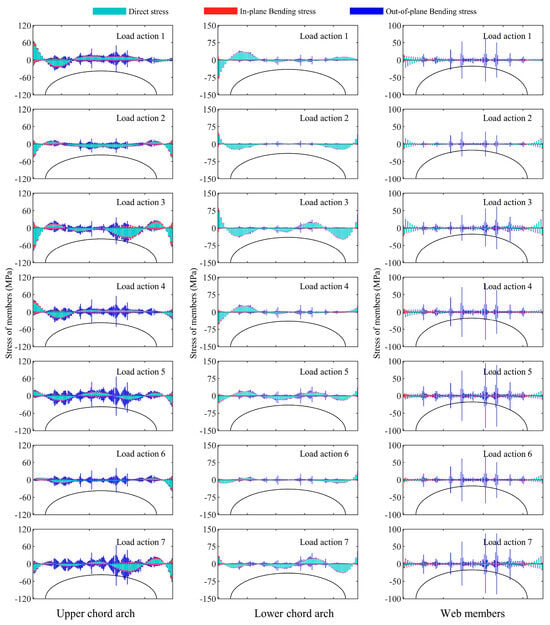
Figure 8.
Stress distribution in the second arch frame of the Type-C structure under 7 load conditions.
In the Type-B structure, the maximum combined stress in the upper chord, lower chord, and web members was −94.8, 110.3, and 42.4 MPa, with average values of 20.1, 24.9, and 7.8 MPa. The maximum direct stress in the members was 19.0, 87.4, and 23.9 MPa, with average values of 16.9, 23.3, and 5.0 MPa. The maximum out-of-plane bending stress in the members was 22.4, 28.8, and 25.6 MPa, with average values of 3.6, 4.2, and 4.2 MPa. The out-of-plane bending stress mainly existed in the connection area of the tie rod, with 0 MPa near the support. Similarly, in the Type-C structure, the maximum combined stress in the upper chord, lower chord, and web members was −78.6, 87.2, and 61.5 MPa, with average values of 15.4, 20.2, and 5.8 MPa. The maximum direct stress for the members was 18.6, 69.6, and 23.3 MPa, with average values of 13.9, 19.2, and 3.6 MPa. The maximum out-of-plane bending stresses were 22.4, 28.8, and 25.6 MPa, with average values of 4.3, 1.8, and 3.1 MPa.
3.2.3. Stress of the First Arch Frame
Figure 9, Figure 10 and Figure 11 show the stress distribution of the first arch under seven load conditions for three structures. It was observed that the distribution of stress in the first arch was similar to that of the second one, but the stress values were much smaller than those of the second arch frame. Under Load action 3, the maximum combined stress in the arch frame of the Type-A structure was −105.5 MPa, and the average value was 27.5 MPa. In the Type-B structure, the maximum combined stress in the upper chord, lower chord, and web members was −38.7, −45.2, and 44.3 MPa, with average values of 7.7, 9.4, and 6.4 MPa. The maximum direct stress in the members was 23.2, 26.2, and 9.3 MPa, with average values of 5.3, 6.9, and 2.4 MPa. The maximum out-of-plane bending stress in the members was 20.0, 27.3, and 33.3 MPa, with average values of 3.4, 4.4, and 5.3 MPa. Similarly, in the Type-C structure, the maximum combined stress in the upper chord, lower chord, and web members was 36.9, 31.1, and 49.6 MPa, with average values of 7.9, 7.8, and 4.8 MPa. The maximum direct stress in the members was 27.2, 23.6, and 12.3 MPa, with average values of 5.6, 7.3, and 2.9 MPa. The maximum out-of-plane bending stresses were 21.5, 12.1, and 45.2 MPa, with average values of 4.8, 1.7, and 3.0 MPa.
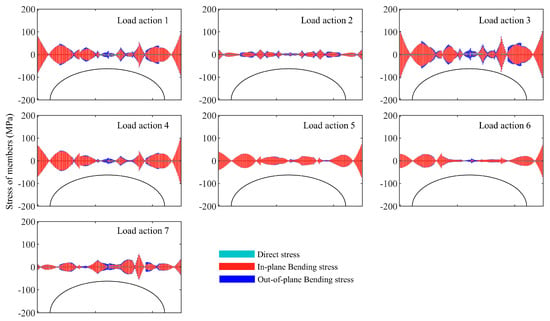
Figure 9.
Stress distribution in the first arch frame of the Type-A structure under 7 load conditions.
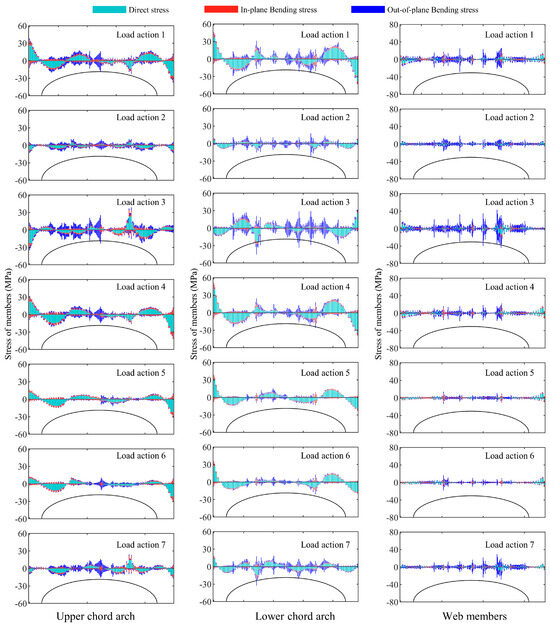
Figure 10.
Stress distribution in the first arch frame of the Type-B structure under 7 load conditions.
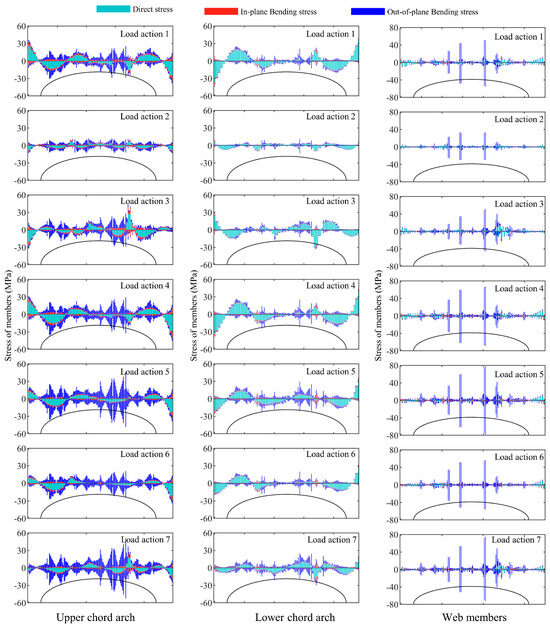
Figure 11.
Stress distribution in the first arch frame of the Type-C structure under 7 load conditions.
Upon analyzing the three sets of data, the differences in stress distribution among the three arch frames were manifested as follows. The stress was greatest in the third arch frame and smallest in the first one. Under Load action 3, the Type-C structure showed a decrease in the average combined stress in the third arch by 22.1%, 22.9%, and 5.8% compared to the Type-B structure. Similarly, the average combined stress in the second arch decreased by 23.7%, 18.8%, and 24.8%, respectively. In the first arch, the upper chord experienced a slight increase of 1.6% in combined stress, while the stress of the lower chord and web decreased by 17.3% and 25.4%, respectively. Compared to the Type-B structure, the average direct stress in the third arch of the Type-C structure was lower by 20.6%, 23.1%, and 4.8%. The second arch showed an average reduction of 17.8%, 17.7%, and 29.5% in the direct stress of its three members. While the first arch’s upper chord experienced an average increase of 7.1%, 6.2%, and 18.2%. Regarding out-of-plane bending stress, the Type-C structure exhibited an average increase of 19.3% in the top chord of the second arch frame compared to the Type-B structure, while the bottom chord and web members decreased by 56.8% and 26.2%. In the first arch frame, the out-of-plane bending stress in the upper chord increased by an average of 30.0%, while the lower chord and web members decreased by 60.5% and 43.2%.
In summary, compared with the Type-B structure, the combined stress of most components in the Type-C structure was generally reduced, except for a slight increase in the upper chord of the first arch frame. The direct stress of the second and third arches significantly decreased, while the first arch increased. The out-of-plane bending stress of the upper chord slightly increased, but the stress values of the lower chord and web members decreased significantly.
3.3. Ultimate Bearing Capacity Analysis
3.3.1. Load-Displacement and Load-Stress Relations of 3 Greenhouse Structures
To obtain an accurate critical buckling load, a double nonlinear stability analysis was performed. The load-displacement and load-stress relationships throughout the process were tracked, as shown in Figure 12. To more intuitively represent the ultimate load, the horizontal axis indicates the multiple of the initial load. It was observed that as the load increases, the stress of the three greenhouse structures before yielding were straight-line segments in equal proportion, indicating an elastic stress state. After yielding, the stress on the structures exhibited fluctuations but did not immediately fail, demonstrating a clear yielding phenomenon. After undergoing a relatively long plastic deformation process, the stress value on the structure gradually increased amid fluctuations until reaching its ultimate bearing capacity, indicating that the structure exhibited typical ductile failure. The Type-A structure was the first to yield, at a load equal to 1.0 times the initial load. When the load reached 1.82 times the initial load, the Type-B structure began to yield. Meanwhile, Type-C sustained a load at 1.86 times the initial capacity, indicating just a minor increase compared to Type-B. But it still exhibited a significant post-yielding increase. It could be concluded that Type-C has the highest ultimate bearing capacity, followed by Type-B, while Type-A has the lowest ultimate bearing capacity.
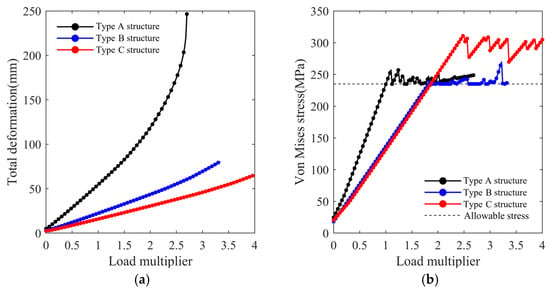
Figure 12.
(a) Load–displacement for three greenhouse structures; (b) Load–stress relationships for three greenhouse structures.
3.3.2. Failure Mechanisms of Three Structures
To thoroughly investigate the failure mechanisms of three structures, Figure 13 illustrates the evolution of Von-Mises equivalent stress in the members of three structures at yielding and ultimate states. For the Type-A structure, the outer side of the arch at the support location first entered the yielding state. The Type-B structure yielded first at the arch support location, specifically on the inner side of the lower chord. In contrast, the Type-C structure first yielded at the tie rod where the second arch connects, while the remaining portion of the structure remained in an elastic state. As the load continues to increase until reaching the ultimate state, the Type-B structure exhibits yielding at multiple locations, including both end supports, the lower chord near the supports, and the middle section of the crossbeam. For the Type-C structure, yielding points primarily appeared on the tie rods and corresponding web members on the side where snow accumulates, while other positions of the arch remain in the elastic state.
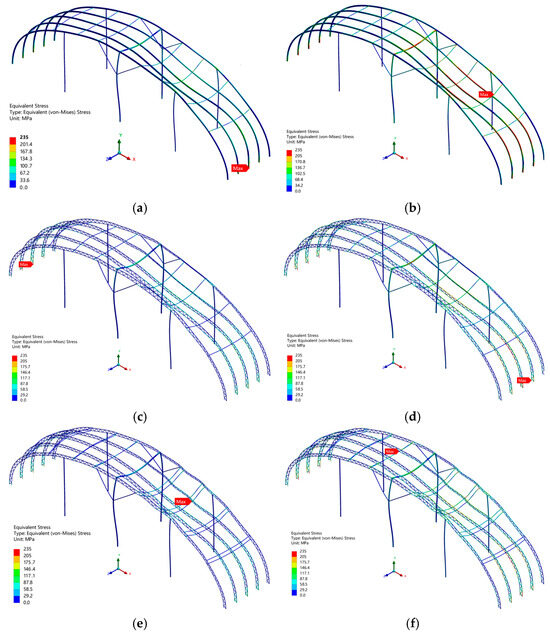
Figure 13.
Stress distribution in 3 greenhouse structures at yield and failure states. (a,b) are the Type-A structure at yield and failure states, (c,d) are the Type-B structure at yield and failure states, (e,f) are the Type-C structure at yield and failure states.
In summary, the three greenhouse structures have experienced strength failure. The weaknesses of the Type-B structure and Type-A structure were mainly concentrated in the support area of the arch frame, while for the Type-C structure, its weak points were primarily manifested in the tie rods and the web members connected to them. Under the ultimate state, the stress at the arch frame supports in the Type-C structure remained within the elastic range, approaching the yield limit but without yielding. It can be inferred that the stiffness of the tie rods was enhanced by increasing the size of the upper tie rods, thereby altering the load-bearing mode of the structure and improving the overall load-bearing capacity.
3.4. Ultimate Bearing Capacity of Large-Span Insulated Plastic Greenhouses with Different Ridge Heights
Ridge height is a key design parameter for large-span insulated plastic greenhouses. Analyzing the impact of ridge height on its load-bearing capacity can provide theoretical guidance for the design of large-span insulated plastic greenhouses. Figure 14 shows the load–displacement and load-stress relations of large-span insulated plastic greenhouses with different ridge heights. It can be observed from the figure that as the load increases, the deformation and stress curves of greenhouse structures with different ridge heights exhibit similar development trends. When the ridge height increased from 3 m to 8 m, the ultimate loads of the greenhouses were 1.58 times, 1.82 times, 1.98 times, 1.88 times, 1.9 times, and 1.84 times, respectively. Under the 1.98 times initial load (the ultimate load of the large-span insulated plastic greenhouse with a 5 m ridge height), the total deformations of these greenhouses were 37.1 mm, 33.5 mm, 33.3 mm, 34.2 mm, 34.8 mm, and 35.9 mm, respectively. It can be concluded that the ridge height has a significant impact on the ultimate load of the greenhouse structure. However, it was not the case that the greater the ridge height is, the stronger the ultimate bearing capacity of the greenhouse framework would be. The greenhouse structure with a ridge height of 5 m can bear the maximum load and exhibits minimal deformation.
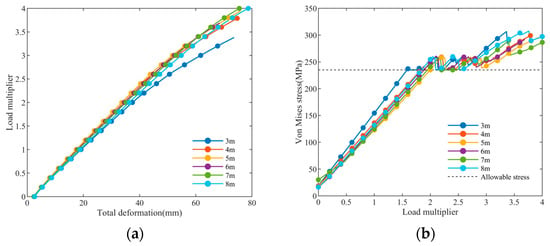
Figure 14.
(a) Load–displacement of large-span insulated plastic greenhouses with different ridge heights; (b) Load–stress relationships of large-span insulated plastic greenhouses with different ridge heights.
4. Discussion
This study established 3D finite element models of three types of large-span insulated plastic greenhouses to analyze their deformation characteristics, stress distribution, and stability under seven load conditions. The ultimate bearing capacity of a large-span insulated plastic greenhouse with different ridge heights was mainly explored. The results showed that the double-layer tie rod and plane truss structure had the minimum deformation, the minimum stress, and the highest ultimate bearing capacity. The ridge height had a significant effect on the bearing capacity of the greenhouse structure. The research provided theoretical support for the configuration of structural components of a thermal insulation plastic greenhouse and offered a scientific basis for the optimal design of ridge height.
It was found that the most unfavorable load action for the structures was constant load and non-uniform snow load. Similar research conclusions have also been obtained in Ren et al. and Wang et al.’s research and structural analysis of solar greenhouse [9,21].
In a calculation unit, the load-bearing components of the large-span insulated plastic greenhouse include arch frame, tie rod, central column, side column, cross beam, and diagonal brace. The arch frame serves as the primary load-bearing component, while the main function of the tie rods is to connect five arch frames along their length. The first and fifth arch frames are equipped with central columns, side columns, and diagonal braces as vertical support components, exhibiting greater stiffness than the other arch frames and thus classified as main arch frames. In contrast, the second, third, and fourth arch frames are categorized as secondary arch frames. The structure exhibits symmetry. By analyzing the stress in the first, second, and third arch frames, the stress of the entire computational unit can be evaluated. This study found that although each arch frame bears the same external load, among the three structures, the first arch frame consistently showed the smallest stress, while the third arch frame exhibited the largest. For the Type-C structure, the combined stress was generally lower than that of the Type-B structure, except for a slight increase in the upper chord of the first arch frame. Notably, compared to the Type-B structure, the direct stress in the secondary arch frames (second and third arch frames) of the Type-C structure was significantly lower, while the direct stress in the first arch frame increased. This indicates a redistribution of stress in the Type-C structure following the installation of double-layer tie rods. It can be inferred that due to the lower stiffness of the tie rods in the Type-B structure, they cannot effectively transmit deformation and internal forces, resulting in relatively independent operation of each arch frame within the structural unit and a lower synergistic effect. In contrast, the Type-C structure enhanced the stiffness of horizontal members by increasing the number of tie rods and optimizing their layout. This allowed the load effects on the second and third arch frames to be more effectively transmitted to the main arch frames via the tie rods, enabling shared external load-bearing and reducing the overall stress levels and deformation of the greenhouse structure. Wang et al. [10] examined the impact of tie rods on the stability of planar trusses within solar greenhouses and arrived at conclusions akin to those presented in this paper. However, they did not explore the effects of tie rods on stress redistribution between arches and out-of-plane bending stress.
Under the most unfavorable load combination, the Z direction displacement of the Type-C structure decreased by 1.3 mm compared to the Type-B structure, while the total displacement decreased by 5.1 mm. In the Type-C structure, the out-of-plane bending stress of the upper chord in the second arch frame increased by an average of 19.3%, while the lower chord and web members decreased by an average of 56.8% and 26.2%, respectively. In the first arch frame, the upper chord increased by an average of 30.0%, while the lower chord and web members decreased by an average of 60.5% and 43.2%. Although the out-of-plane bending stress of the upper chord increased, this stress in the lower chord and web members significantly decreased, leading to an overall reduction in out-of-plane stress across the entire arch frame. Under the most unfavorable load combination, the analysis of nonlinear instability mechanisms and ultimate bearing capacities for three structures revealed that the Type-C structure exhibits the highest ultimate bearing capacity. This suggests that the installation of double-layer tie rods in the Type-C structure enhanced horizontal stiffness and support, reducing displacement in the Z-axis direction, effectively mitigating the effect, decreasing out-of-plane bending stress, and ultimately improving the structure’s ultimate bearing capacity.
Ridge height is a key design parameter for large-span insulated plastic greenhouses. There have been many studies on the influence of greenhouse ridge height on lighting environment and ventilation rate [22,23,24]. However, it is often treated as a fixed geometric parameter in most greenhouse structural studies when analyzing structural safety. Shi et al. [25] discovered through full-scale model loading tests that ridge height had the greatest impact on the bearing capacity of truss-arch plastic greenhouse structures. This study found that the ridge height had a significant impact on the ultimate bearing capacity of large-span insulated plastic greenhouse structures. Moreover, the results showed that with the increase in ridge height, the ultimate bearing capacity of long-span insulated plastic greenhouse increased first and then decreased. When the ridge height was 5 m, the long-span insulated plastic greenhouse achieved a balance between stiffness and geometry, and its ultimate bearing capacity reached the maximum. Similarly, Hu et al. [26] discovered that the ridge height influences the in-plane buckling and postbuckling behavior of parabolic arches significantly in their study on the in-plane nonlinear elastic stability of parabolic steel arches. When studying the in-plane nonlinear elastic stability of concrete-filled steel tube truss arch, Liu et al. [27], Hu et al. [28], and Guo et al. [29] also found that the ridge height of arches has a significant influence on the stability capacity. The stability capacity reduces as the rise-to-span ratio declines. Our finding provides theoretical support for determining the ridge height of large-span insulated plastic greenhouses from a structural bearing capacity perspective.
Based on GB/T 51183-2016 load code for agricultural greenhouse structures, the load return period of large-span insulated plastic greenhouse is relaxed to 20 years. The basic wind pressure and basic snow pressure were 410 and 290 N/m2, respectively, which were suitable for the climatic conditions in most areas of the Huang Huai River Basin. The arch structure employed the commonly used planar truss and rectangular tubes in greenhouses. The research conclusions apply to the design requirements of a large-span thermal insulation plastic greenhouse in this area. In the follow-up work, we will be committed to exploring the applicability of these conclusions in different climatic regions. Considering the climatic conditions of the construction site for large-span insulated plastic greenhouses, including strong winds and rainstorms, we will analyze their impact on the structural stability of the greenhouse and develop a more comprehensive and universally applicable design guideline.
This study focused on the mechanical properties of large-span insulated plastic greenhouses with various structures under permanent, wind, and snow loads. During the research process, crop loads were not considered, nor were the potential impacts of different greenhouse crops, thermal effects, or dynamic wind loads on the research outcomes discussed. Future research should build upon the current findings and further examine the influence of crop load on greenhouse structures.
This study primarily relies on numerical simulation research. Experimental verification faces significant technical difficulties. On the one hand, experimental verification requires the construction of full-scale specimens and relies on special facilities such as wind tunnels and loading systems, which are subject to equipment scale and test costs [30,31]. In engineering practice, scaled models are often used for approximate simulation. On the other hand, the actual engineering is a multi-directional coupling load, and the experimental loading system is difficult to achieve accurate reproduction, resulting in systematic deviation between the experimental data and the actual engineering response. Although numerical simulation has significant advantages in modeling complex boundary conditions such as material nonlinearity and contact friction, the establishment of a highly reliable calculation model still needs to be verified by a professional mechanical experiment platform. The construction of a three-level verification system, including numerical simulation, scale experiment, and full-scale monitoring, can improve the engineering applicability of the calculation model, which should be the subject of future research.
5. Conclusions
The ridge height and structural components configuration affect the bearing performance of a large-span insulated plastic greenhouse. In this study, the structural features of large-span insulated plastic greenhouses with different structural configurations have been explored through deformation, stress, and stability analyses using with finite element method. Then, the ultimate bearing capacity of large-span insulated plastic greenhouses with different ridge heights was investigated. The results of the study are given below:
- (1)
- The most dangerous load combination for the large-span insulated plastic greenhouse structure is the combination of constant loads and non-uniform snow loads.
- (2)
- As the load-bearing system of a thermal insulation plastic greenhouse, the structure composed of double-layer tie rods and plane truss shows the minimum deformation and stress, and has higher bearing capacity.
- (3)
- Ridge height affects the load-bearing capacity of the large-span insulated plastic greenhouse structure, but it is not that the greater the ridge height, the stronger the ultimate bearing capacity of the greenhouse structure. The greenhouse structure with a ridge height of 5 m achieves the maximum ultimate load-bearing capacity, capable of withstanding 1.98 times the initial load.
- (4)
- The installation of double-layer tie rods enables stress redistribution in the arch frame on one hand, which better facilitates the collaborative action among arch frames in the structure calculation unit. On the other hand, it enhances the horizontal stiffness, reduces structural displacement along the Z direction, effectively mitigates the effect, and decreases the out-of-plane bending stress of the structure. Consequently, the ultimate bearing capacity of the structure is improved.
This study reveals the load-bearing characteristics of different types of large-span insulated plastic greenhouse structures, clarifying the influence of ridge height on the ultimate load-bearing capacity of large-span insulated plastic greenhouses. These results can also serve as a reference for engineers in the design and construction of these types of greenhouses.
Author Contributions
All authors contributed to the study conception and design. Conceptualization, F.P. and Y.L.; methodology, T.Z.; software, X.D.; validation, X.D.; formal analysis, H.D. and N.D.; investigation, X.D. and Y.Q.; resources, T.Z.; data curation, Z.G.; writing—original draft preparation, X.D.; writing—review and editing, Y.L. and Z.G.; visualization, X.D. and N.D.; supervision, F.P. and Z.G.; project administration, Y.L.; funding acquisition, X.D. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific and Technological Project in Henan Province, grant number 232102110293, and the Teaching and Practice Project of Henan Agricultural University, grant number 2023XJGLX014.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets used and/or analyzed during the present study are available from the corresponding author on reasonable request.
Acknowledgments
The authors express their sincere gratitude to Henan Yuyi Seed Technology Development Co., Ltd., for the support throughout the progress of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gorjian, S.; Ebadi, H.; Najafi, G.; Chandel, S.S.; Yildizhan, H. Recent advances in net-zero energy greenhouses and adapted thermal energy storage systems. Sustain. Energy Technol. Assess. 2021, 43, 100940. [Google Scholar] [CrossRef]
- Cao, K.; Xu, H.; Zhang, R.; Xu, D.; Bao, E. Renewable and sustainable strategies for improving the thermal environment of chinese solar greenhouses. Energy Build. 2019, 202, 109414. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, J.; Zhang, W.; Zhou, W.; Wang, J. Characteristics of soil salinity in representative plastic shed vegetable production areas in shandong province, China. Eurasian Soil Sci. 2023, 56, 488–501. [Google Scholar] [CrossRef]
- Iribarne, L.; Torres, J.A.; Pena, A. Using computer modeling techniques to design tunnel greenhouse structures. Comput. Ind. 2007, 58, 403–415. [Google Scholar] [CrossRef]
- Elsner, B.V.; Briassoulis, D.; Waaijenberg, D.; Mistriotis, A.; Zabeltitz, C.V.; Gratraud, J. Review of structural and functional characteristics of greenhouses in european union countries, Part II: Typical designs. J. Agric. Eng. Res. 2000, 75, 111–126. [Google Scholar] [CrossRef]
- Ha, T.; Kim, J.; Cho, B.; Kim, D.; Kim, H. Finite element model updating of multi-span greenhouses based on ambient vibration measurements. Biosyst. Eng. 2017, 161, 145–156. [Google Scholar] [CrossRef]
- Castellano, S.; Scarascia Mugnozza, G.; Vox, G. Collapse full scale test on a pitched roof greenhouse structure. Colt. Protette 2006, 35, 55–61. [Google Scholar]
- Briassoulis, D.; Dougka, G.; Dimakogianni, D.; Vayas, I. Analysis of the collapse of a greenhouse with vaulted roof. Biosyst. Eng. 2016, 151, 495–509. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, Y.; Bai, Y.; Wang, T. Numerical study on static properties and failure mechanisms of landing assembled chinese solar greenhouses. Comput. Electron. Agric. 2021, 188, 106347. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Jiang, Y.; Bai, Y.; Wang, T. Stability analysis of landing assembled Chinese solar greenhouses with discrete lateral braces under snow loads. Biosyst. Eng. 2023, 233, 168–180. [Google Scholar] [CrossRef]
- Li, H.; Zong, C.; Lu, J.; Zhao, S.; Yang, D.; Song, W. Experimental study on spatiotemporal variation patterns of thermal environment in the large-span insulated greenhouse. Appl. Therm. Eng. 2025, 264, 125530. [Google Scholar] [CrossRef]
- Ma, Y.; Li, X.; Fu, Z.; Zhang, L. Structural design and thermal performance simulation of shade roof of double-slope greenhouse for mushroom-vegetable cultivation. Int. J. Agric. Biol. Eng. 2019, 12, 126–133. [Google Scholar] [CrossRef]
- Ministry of Agriculture and Rural Affairs of the People’s Republic of China (MOA). Guidelines on Accelerating the Mechanization Development of Facility-Based Crop Cultivation; Ministry of Agriculture and Rural Affairs of the People’s Republic of China (MOA): Beijing, China, 2020. [Google Scholar]
- Wang, C.; Liu, K.; Ma, H.; Li, T.; Wang, S.; Zhang, D.; Wei, M. Solar radiation model and optimization of asymmetric large-span externally insulated plastic greenhouses. PLoS ONE 2025, 20, 0309734. [Google Scholar] [CrossRef]
- Xu, Y.; Lyu, X.; Song, H.; Lin, B.; Wei, M.; Yin, Y.; Wang, S. Large-span m-shaped greenhouse with superior wind resistance and ventilation performance. J. Wind. Eng. Ind. Aerodyn. 2023, 238, 105410. [Google Scholar] [CrossRef]
- Ren, J.; Wang, J.; Guo, S.; Li, X.; Zheng, K.; Zhao, Z. Finite element analysis of the static properties and stability of a large-span plastic greenhouse. Comput. Electron. Agric. 2019, 165, 104957. [Google Scholar] [CrossRef]
- Wang, C.; Xu, Z.; Jiang, Y.; Wang, T. Numerical analysis of static and dynamic characteristics of large-span pipe-framed plastic greenhouses. Biosyst. Eng. 2023, 232, 67–80. [Google Scholar] [CrossRef]
- GB/T 51183-2016; Code for the Design Load of Horticultural Greenhouse Structures. China Planning Press: Beijing, China, 2016.
- He, Y.; Wang, J.; Zhou, X.; Zhang, X. Stability of a pretensioned latticed three-dimensional arch structure with cross cable-strut arrangement. J. Constr. Steel Res. 2018, 147, 43–52. [Google Scholar] [CrossRef]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Li, M.; Wei, X.; Zhao, Q.; Wang, L. Numerical Simulation of Structural Performance in a Single-Tube Frame for 12 m-Span Chinese Solar Greenhouses Subjected to Snow Loads. Agronomy 2024, 14, 1122. [Google Scholar] [CrossRef]
- Mu, Z.; Bo, Y.; Xu, J.; Song, K.; Song, K.; Dong, B.; Wang, J.; Shu, S.; Wang, Y.; Guo, S. Development and application of greenhouse light environment simulation technology based on light path tracing. Comput. Electron. Agric. 2024, 218, 108652. [Google Scholar] [CrossRef]
- Abid, H.; Ketata, A.; Lajnef, M.; Chiboub, H.; Driss, Z. Impact of greenhouse roof height on microclimate and agricultural practices: CFD and experimental investigations. J. Therm. Anal. Calorim. 2024, 149, 5483–5495. [Google Scholar] [CrossRef]
- Xu, D.; Henke, M.; Li, Y.; Zhang, Y.; Liu, A.; Liu, X.; Li, T. Optimal design of light microclimate and planting strategy for chinese solar greenhouses using 3D light environment simulations. Energy 2024, 302, 131805. [Google Scholar] [CrossRef]
- Shi, Y.; Xie, H.; Zheng, X.; Chen, B. Experimental on mechanical performance of Truss Arch plastic greenhouse skeleton subjected vertical load. J. Agric. Mech. Res. 2024, 46, 154–160, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Hu, C.; Pi, Y.; Gao, W.; Li, L. In-plane non-linear elastic stability of parabolic arches with different rise-to-span ratios. Thin-Walled Struct. 2018, 129, 74–84. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Q.; Wang, Y.; Zhang, S. In-Plane Stability of Concrete-Filled Steel Tubular Parabolic Truss Arches. Int. J. Steel Struct. 2018, 18, 1306–1317. [Google Scholar] [CrossRef]
- Hu, Q.; Liu, C.; Yuan, C.; Wang, Y.; Zhang, S. Experimental Investigation into In-plane Stability of Concrete-Filled Steel Tubular Parabolic Arches Under Five-Point Concentrated Loads. Int. J. Steel Struct. 2020, 20, 2038–2050. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, H.; Pi, Y. In-plane failure mechanisms and strength design of circular steel planar tubular Vierendeel truss arches. Eng. Struct. 2017, 151, 488–502. [Google Scholar] [CrossRef]
- Peña, A.; Valera, D.L.; Pérez, F.; Ayuso, J.; Pérez, J. Behavior of greenhouse foundations subjected to uplift loads. Am. Soc. Agric. Eng. 2004, 47, 1651–1657. [Google Scholar] [CrossRef]
- Ming, G.; Youqin, H. Equivalent static wind loads for stability design of large span roof structures. Wind. Struct. 2015, 20, 95–115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).