Study on Outdoor Spectral Inversion of Winter Jujube Based on BPDF Models
Abstract
1. Introduction
2. Experimental Section
2.1. Samples and Instruments
2.2. Spectral Acquisition Method
2.3. Outdoor Spectral Inversion Method
2.3.1. Fresnel’s Law of Reflection
2.3.2. Nadal–Breon Model
2.3.3. Litvinov Model
2.3.4. Maignan Model
2.3.5. Xie–Cheng Model
2.3.6. Corrected Outdoor Spectra Method
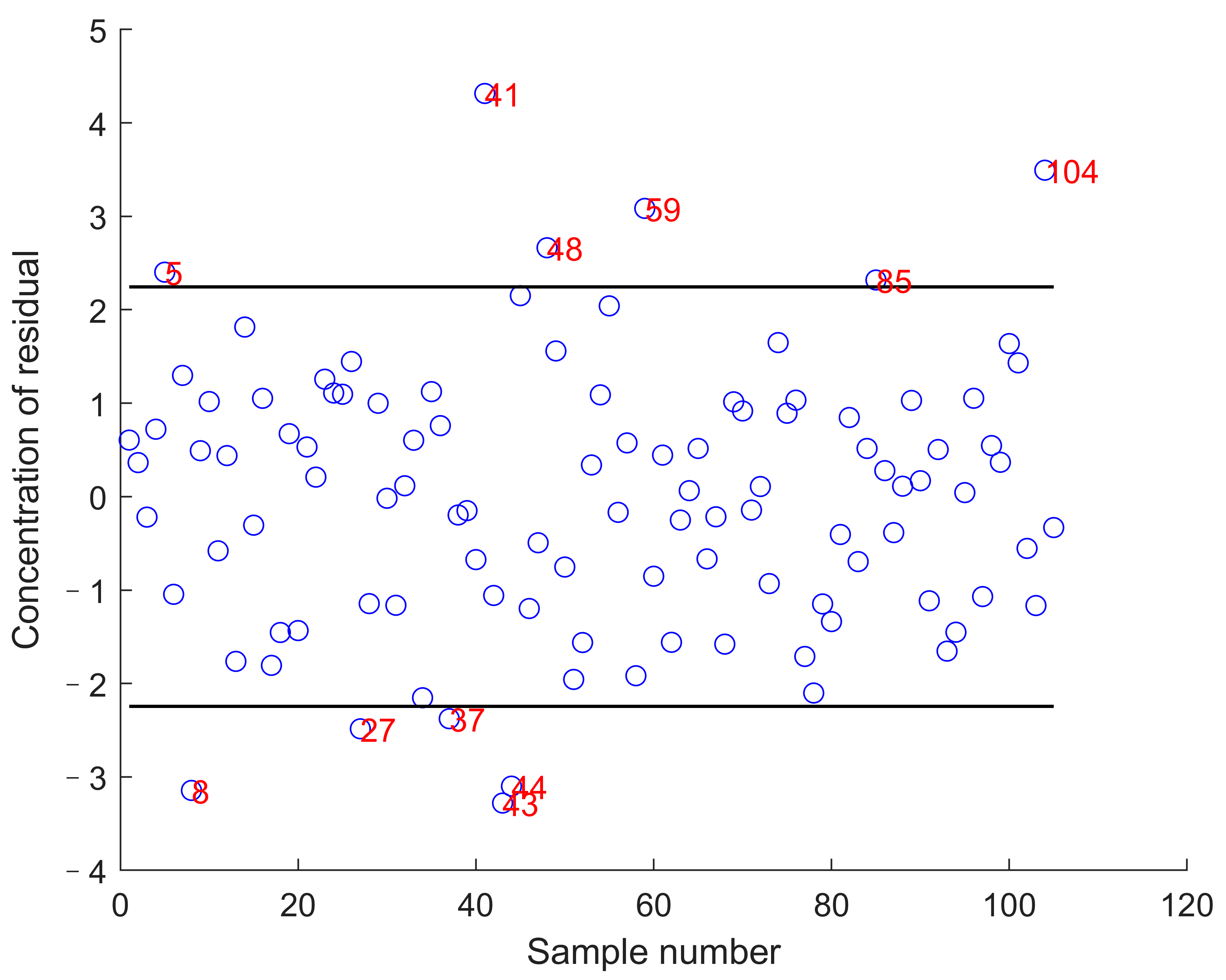
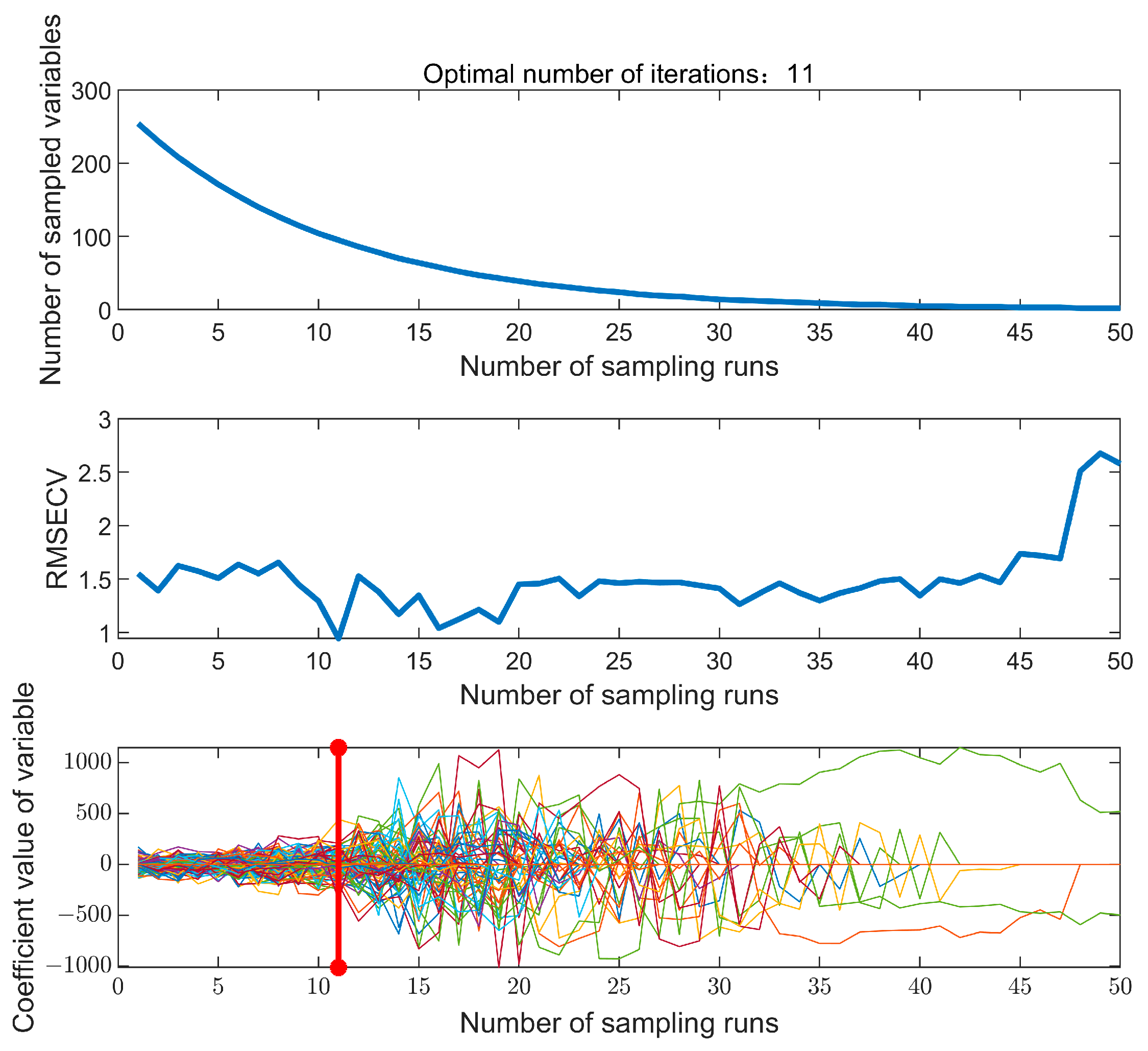
2.4. Spectral Data Processing
3. Results and Discussion
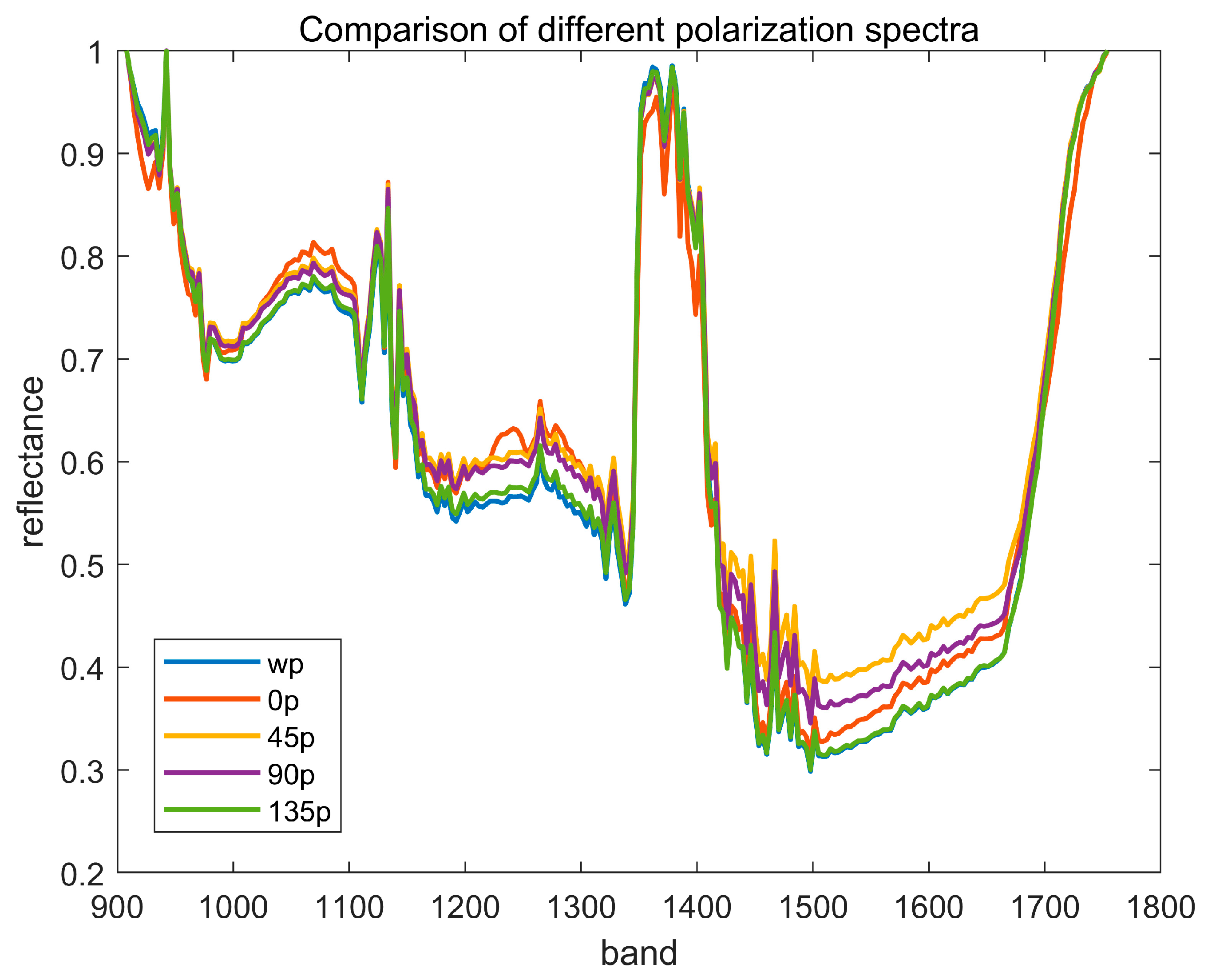
3.1. Outdoor Spectra of Winter Jujube in Different Polarization Directions
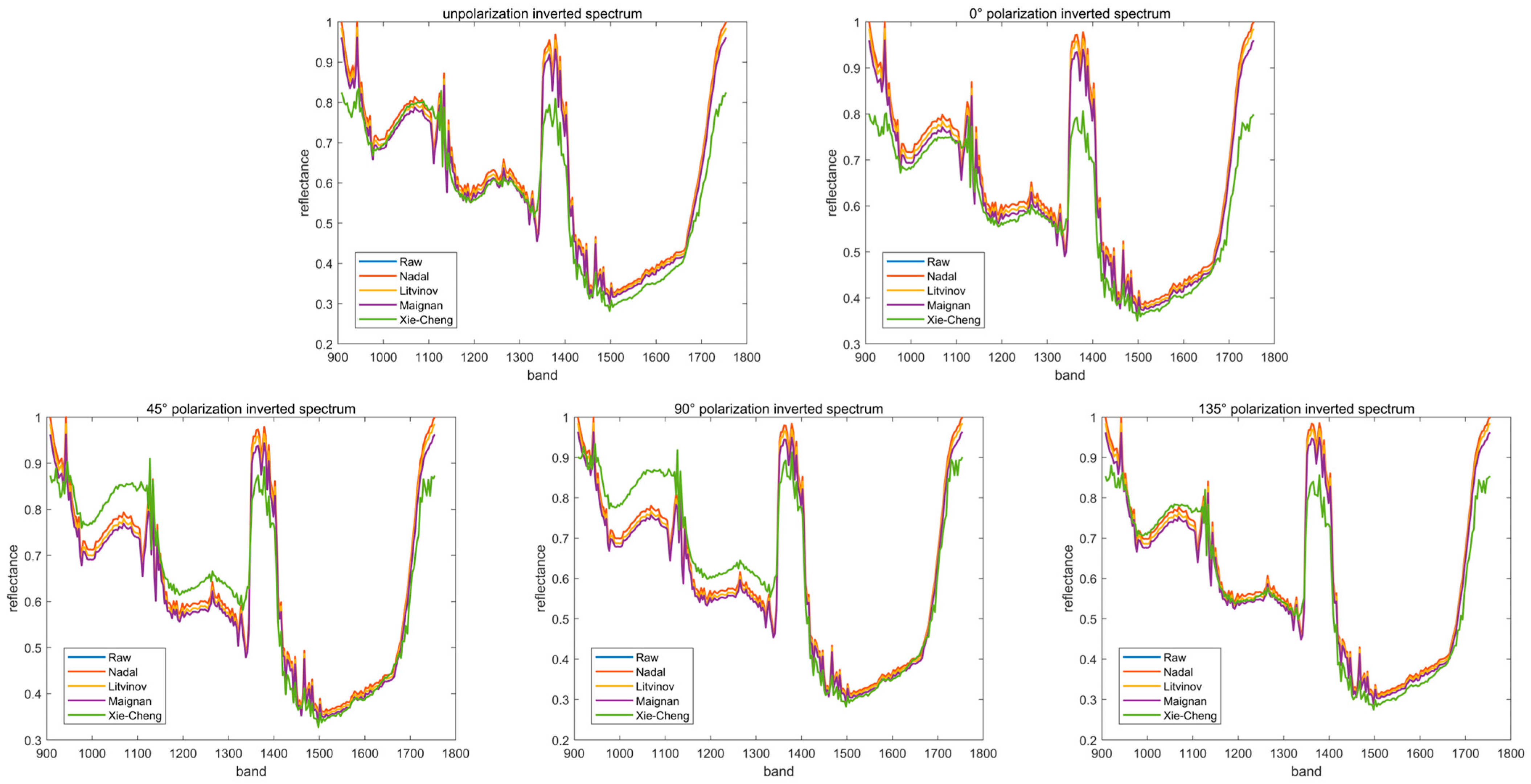
3.2. Outdoor Spectral Inversion
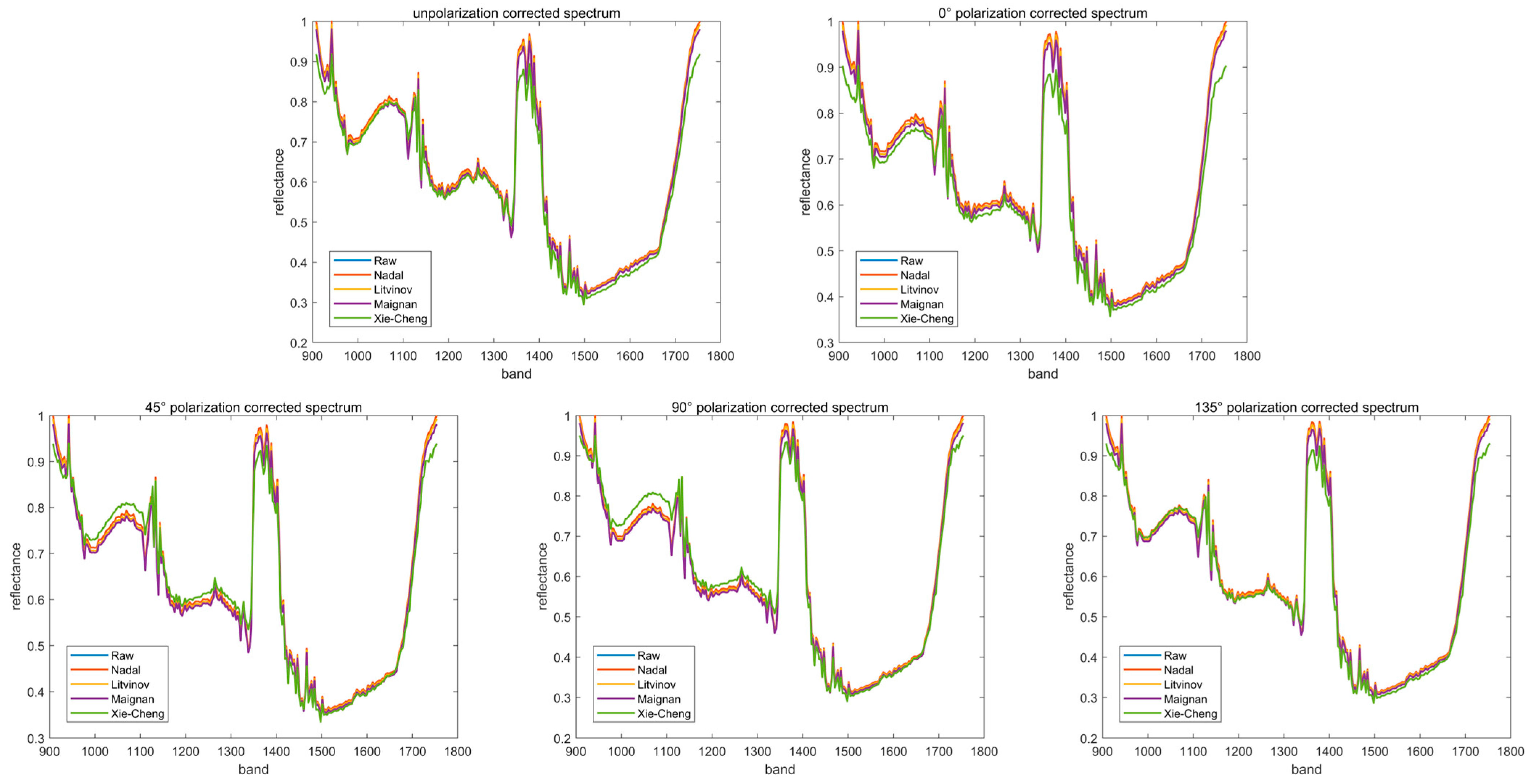
3.3. Correction of Outdoor Spectra and Its Feasibility Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, H.J.; Jin, X.W.; Zhang, Y.C.; Song, F.Y.; Shen, C.J. Current situation of winter jujube industry and research progress of preservation technology. Anhui Agric. Sci. 2023, 51, 1–4+8. [Google Scholar]
- Hou, F. Development status and countermeasures of Zhanhua winter jujube industry. Mod. Rural Sci. Technol. 2024, 5, 1–3. [Google Scholar]
- Xiong, C.H.; She, Y.X.; Jiao, X.; Shao, Y.; Jia, L.; Wang, M.; Xiao, M.; Wang, J. Application of hyperspectral imaging technology in nondestructive testing of agricultural products. Grain Oil Food Sci. Technol. 2023, 31, 109–122. [Google Scholar]
- Zou, Y.; Zhang, L.; Zhang, J.; Li, B.; Lv, X. Developmental Trends in the Application and Measurement of the Bidirectional Reflection Distribution Function. Sensors 2022, 22, 1739. [Google Scholar] [CrossRef]
- Lai, Q.; Liu, B.; Zhao, J.; Zhao, Z.; Tan, J. BRDF characteristics of different textured fabrics in visible and near-infrared band. Opt. Express 2020, 28, 3561–3575. [Google Scholar] [CrossRef] [PubMed]
- Shang, K.; Yan, L.; Zhang, F.Z.; Chu, J.; Yang, B.; Liu, S.; Tansey, K.; Jia, X.; Dubovik, O.; Zhang, Z.; et al. From BRDF to BPDF: A preliminary study on the evolution of remote sensing inversion base model. Chin. Sci. Inf. Sci. 2024, 54, 2001–2020. [Google Scholar]
- Xie, D.; Gu, X.; Cheng, T.; Yu, T.; Li, Z.; Chen, X.; Chen, H.; Guo, J. Initial research on the polarized reflectance of typical urban surface types measured by the Directional Polarimetric Camera. Sci. China (Earth Sci.) 2011, 54, 1199–1205. [Google Scholar] [CrossRef]
- Ti, R.F.; Fan, Y.Z.; Huang, H.L.; Liu, X.; Sun, X.; Hong, J.; Liu, S. Comparative analysis of surface BPDF model based on Gaofen-5 DPC and AERONET site data. J. Opt. 2022, 42, 146–154. [Google Scholar]
- Zhang, Z.H.; Yan, L.; Liu, S.Y.; Fu, Y.; Jiang, K.; Yang, B.; Liu, S.; Zhang, F. Inversion of leaf nitrogen content based on polarized reflectance model and random forest regression. Spectrosc. Spectr. Anal. 2021, 41, 2911–2917. [Google Scholar]
- Song, Z. H; Han, Y; Wei, C.Y; Chen, X; Gu, Q.Y; Liu, Z.P; Liu, S.S. Comparison of polarization spectral characteristics between oil-contaminated agricultural soils and wetland soils. Spectrosc. Spectr. Anal. 2022, 42, 2603–2609. [Google Scholar]
- Xu, J. Y; Huang, X; Luo, H.P; Liu, J.X; Suo, Y.T. Research on the effect of orientation and quality on the spatial characteristics of southern border fruit spectra and the inversion method. Spectrosc. Spectr. Anal. 2022, 42, 910–918. [Google Scholar]
- Gao, F.; Xu, J.Y.; Luo, H.P. Spatial characterization of spectral inversion and feasibility study of outdoor spectral correction. Spectrosc. Spectr. Anal. 2024, 44, 336–346. [Google Scholar]
- GB/T 5009.3-2016; National Standard for Food Safety Determination of Moisture in Food. China Standard Press: Beijing, China, 2016.
- Lei, D.T.; Luo, H. P; Gao, F; Di, Y.B. Quality detection of southern Xinjiang winter jujube based on polarization hyperspectral imaging. Food Res. Dev. 2025, 46, 172–177. [Google Scholar]
- Liu, J.X.; Liu, G.F.; Chen, D.L. Fresnel’s formula to discuss the change of amplitude of light waves upon reflection and refraction. Phys. Bull. 2021, 7, 23–26. [Google Scholar]
- Nadal, F.; Bréon, F.M. Parameterization of surface polarized reflectance derived from POLDER spaceborne measurements. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1709–1718. [Google Scholar] [CrossRef]
- Litvinov, P.; Hasekamp, O.; Cairns, B. Models for surface reflection of radiance and polarized radiance: Comparison with airborne multi-angle photopolarimetric measurements and implications for modeling top-of-atmosphere measurements. Remote Sens. Environ. 2010, 115, 781–792. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.; Fédèle, E.; Bouvier, M. Polarized reflectances of natural surfaces: Spaceborne measurements and analytical modeling. Remote Sens. Environ. 2009, 113, 2642–2650. [Google Scholar] [CrossRef]
- Xie, D.; Cheng, T.; Wu, Y.; Fu, H.; Zhong, R.; Yu, J. Polarized reflectances of urban areas: Analysis and models. Remote Sens. Environ. 2017, 19, 29–37. [Google Scholar] [CrossRef]
- Yang, B.; Zhao, H.; Chen, W. Semi-empirical models for polarized reflectance of land surfaces: Intercomparison using spaceborne POLDER measurements. J. Quant. Spectrosc. Radiat. Transf. 2017, 20, 13–20. [Google Scholar] [CrossRef]
- Cheng, J.H.; Chen, Z.G.; Zhang, Q.H. Comparative study of different wavelength selection methods in soil organic matter content detection. China Agric. Sci. Technol. Bull. 2020, 22, 162–170. [Google Scholar]
- Di, Y.B.; Luo, H.P.; Liu, H.Y.; Liu, H.; Kang, L.; Tong, Y. Quantitative Detection of Water Content of Winter Jujubes Based on Spectral Morphological Features. Agriculture 2025, 15, 482. [Google Scholar] [CrossRef]

| Index | Sample Set | Data Range | Average Value | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|
| Moisture | calibration set | 60.94–75.34 | 67.17 | 3.29 | 4.91 |
| prediction set | 63.15–71.84 | 67.08 | 2.49 | 3.71 | |
| SSC | calibration set | 23.9–38.6 | 31.38 | 3.16 | 10.09 |
| prediction set | 26.7–37.1 | 31.43 | 2.64 | 8.40 |
| Model | Parameter |
|---|---|
| Nadal–Breon | ρ = 5.16 β = 6 |
| Litvinov | α = 3.456 σ2 = 0.281 kr = 0.6 |
| Maignan | α = 7.235 |
| Xie–Cheng | A = 0.999 kr = 0.53 |
| Polarization | Model | R | RMSEP | Difference Rate/% |
|---|---|---|---|---|
| None | Nadal–Breon | 0.9981 | 0.0060 | 3.67 |
| Litvinov | 0.9980 | 0.0682 | 10.28 | |
| Maignan | 0.9966 | 0.0976 | 15.35 | |
| Xie–Cheng | 0.9742 | 0.1963 | 19.03 | |
| 0° | Nadal–Breon | 0.9978 | 0.0244 | 3.76 |
| Litvinov | 0.9976 | 0.0720 | 10.59 | |
| Maignan | 0.9954 | 0.1009 | 14.19 | |
| Xie–Cheng | 0.9746 | 0.2159 | 21.43 | |
| 45° | Nadal–Breon | 0.9982 | 0.0246 | 4.00 |
| Litvinov | 0.9979 | 0.0719 | 10.89 | |
| Maignan | 0.9942 | 0.0970 | 14.05 | |
| Xie–Cheng | 0.9586 | 0.1708 | 22.56 | |
| 90° | Nadal–Breon | 0.9982 | 0.0212 | 3.53 |
| Litvinov | 0.9980 | 0.0669 | 10.18 | |
| Maignan | 0.9977 | 0.0942 | 14.18 | |
| Xie–Cheng | 0.9643 | 0.1584 | 22.44 | |
| 135° | Nadal–Breon | 0.9985 | 0.0205 | 3.40 |
| Litvinov | 0.9983 | 0.0657 | 9.95 | |
| Maignan | 0.9965 | 0.0963 | 14.45 | |
| Xie–Cheng | 0.9781 | 0.1857 | 18.79 |
| Index | Spectra | Number of Principal Factors | Calibration Set | Prediction Set | |||
|---|---|---|---|---|---|---|---|
| Rc | RMSEC | Rp | RMSEP | RPIQ | |||
| Moisture | Raw | 10 | 0.9741 | 0.7778 | 0.6756 | 1.5091 | 2.0304 |
| Nadal–Breon | 10 | 0.9749 | 0.7609 | 0.7954 | 1.3169 | 2.1191 | |
| Litvinov | 11 | 0.9766 | 0.7328 | 0.8829 | 1.0637 | 2.5476 | |
| Maignan | 13 | 0.9739 | 0.7987 | 0.2636 | 2.2276 | 1.3474 | |
| Xie–Cheng | 11 | 0.9822 | 0.6382 | 0.7631 | 1.6651 | 1.4939 | |
| SSC | Raw | 16 | 0.9678 | 0.7801 | 0.5913 | 1.9331 | 1.9657 |
| Nadal–Breon | 8 | 0.8938 | 1.3727 | 0.5575 | 1.9035 | 1.7337 | |
| Litvinov | 18 | 0.9842 | 0.5329 | 0.8092 | 1.9323 | 1.5525 | |
| Maignan | 14 | 0.9784 | 0.6859 | 0.8712 | 1.3391 | 2.4084 | |
| Xie–Cheng | 11 | 0.9494 | 0.9569 | 0.6208 | 1.9377 | 1.7676 | |
| Index | Spectra | Number of Principal Factors | Calibration Set | Prediction Set | |||
|---|---|---|---|---|---|---|---|
| Rc | RMSEC | Rp | RMSEP | RPIQ | |||
| Moisture | Raw | 16 | 0.9839 | 0.5814 | 0.8000 | 1.5473 | 2.0174 |
| Nadal–Breon | 16 | 0.9876 | 0.5275 | 0.7595 | 1.9508 | 1.5719 | |
| Litvinov | 15 | 0.9840 | 0.5889 | 0.7345 | 1.8108 | 1.5888 | |
| Maignan | 16 | 0.9821 | 0.6008 | 0.7283 | 1.9425 | 1.6674 | |
| Xie–Cheng | 10 | 0.9569 | 0.9135 | 0.7144 | 1.7583 | 1.7440 | |
| SSC | Raw | 12 | 0.9611 | 0.8010 | 0.7484 | 2.1058 | 1.4365 |
| Nadal–Breon | 9 | 0.9244 | 1.0781 | 0.5308 | 2.1730 | 1.6222 | |
| Litvinov | 8 | 0.8869 | 1.3379 | 0.7490 | 1.6462 | 2.1110 | |
| Maignan | 12 | 0.9577 | 0.8285 | 0.6408 | 2.5428 | 1.2880 | |
| Xie–Cheng | 12 | 0.9540 | 0.8946 | 0.6390 | 1.7657 | 1.9539 | |
| Index | Spectra | Number of Principal Factors | Calibration Set | Prediction Set | |||
|---|---|---|---|---|---|---|---|
| Rc | RMSEC | Rp | RMSEP | RPIQ | |||
| Moisture | Raw | 12 | 0.9819 | 0.5862 | 0.7881 | 1.4949 | 1.8142 |
| Nadal–Breon | 9 | 0.9615 | 0.8523 | 0.7688 | 1.3956 | 1.9666 | |
| Litvinov | 12 | 0.9850 | 0.5664 | 0.8632 | 1.1617 | 2.3308 | |
| Maignan | 10 | 0.9770 | 0.7098 | 0.6839 | 1.6441 | 1.4817 | |
| Xie–Cheng | 12 | 0.9726 | 0.7512 | 0.8928 | 1.0755 | 2.2370 | |
| SSC | Raw | 19 | 0.9878 | 0.4688 | 0.6086 | 2.5941 | 1.1950 |
| Nadal–Breon | 11 | 0.9615 | 0.8210 | 0.6402 | 2.2459 | 1.0686 | |
| Litvinov | 11 | 0.9478 | 0.9190 | 0.6732 | 1.8209 | 1.8947 | |
| Maignan | 10 | 0.9523 | 0.8852 | 0.6174 | 2.0163 | 1.3763 | |
| Xie–Cheng | 23 | 0.9908 | 0.3894 | 0.6343 | 2.3762 | 1.4624 | |
| Index | Spectra | Number of Principal Factors | Calibration Set | Prediction Set | |||
|---|---|---|---|---|---|---|---|
| Rc | RMSEC | Rp | RMSEP | RPIQ | |||
| Moisture | Raw | 9 | 0.9650 | 0.8423 | 0.7736 | 1.3308 | 1.8890 |
| Nadal–Breon | 9 | 0.9679 | 0.8335 | 0.7774 | 1.3100 | 1.9993 | |
| Litvinov | 9 | 0.9634 | 0.8917 | 0.8316 | 1.0573 | 2.3654 | |
| Maignan | 9 | 0.9740 | 0.7524 | 0.7865 | 0.7524 | 2.3058 | |
| Xie–Cheng | 9 | 0.9710 | 0.7680 | 0.8077 | 1.3763 | 2.1423 | |
| SSC | Raw | 8 | 0.9346 | 1.0648 | 0.6060 | 2.1415 | 1.5410 |
| Nadal–Breon | 8 | 0.9297 | 1.0974 | 0.7518 | 1.6543 | 1.5263 | |
| Litvinov | 13 | 0.9646 | 0.8235 | 0.6937 | 2.0529 | 1.8024 | |
| Maignan | 7 | 0.9004 | 1.3360 | 0.6684 | 1.7891 | 1.7327 | |
| Xie–Cheng | 12 | 0.9557 | 0.8648 | 0.8211 | 1.5528 | 2.6403 | |
| Index | Spectra | Number of Principal Factors | Calibration Set | Prediction Set | |||
|---|---|---|---|---|---|---|---|
| Rc | RMSEC | Rp | RMSEP | RPIQ | |||
| Moisture | Raw | 14 | 0.9760 | 0.6420 | 0.6825 | 1.8778 | 2.2579 |
| Nadal–Breon | 15 | 0.9861 | 0.5176 | 0.6942 | 1.6665 | 2.0107 | |
| Litvinov | 13 | 0.9780 | 0.7221 | 0.5146 | 2.1742 | 1.4398 | |
| Maignan | 13 | 0.9714 | 0.8038 | 0.6567 | 1.9051 | 2.0054 | |
| Xie–Cheng | 16 | 0.9882 | 0.4797 | 0.6576 | 2.0364 | 1.9603 | |
| SSC | Raw | 10 | 0.9496 | 0.9443 | 0.5891 | 2.1134 | 1.8454 |
| Nadal–Breon | 12 | 0.9590 | 0.8635 | 0.6984 | 1.5201 | 2.2367 | |
| Litvinov | 14 | 0.9773 | 0.6565 | 0.8808 | 1.4623 | 2.9235 | |
| Maignan | 12 | 0.9574 | 0.9111 | 0.7371 | 1.5499 | 2.1937 | |
| Xie–Cheng | 14 | 0.9775 | 0.6279 | 0.6244 | 2.1811 | 1.5130 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, Y.; Yu, J.; Luo, H.; Liu, H.; Kang, L.; Tong, Y. Study on Outdoor Spectral Inversion of Winter Jujube Based on BPDF Models. Agriculture 2025, 15, 1334. https://doi.org/10.3390/agriculture15131334
Di Y, Yu J, Luo H, Liu H, Kang L, Tong Y. Study on Outdoor Spectral Inversion of Winter Jujube Based on BPDF Models. Agriculture. 2025; 15(13):1334. https://doi.org/10.3390/agriculture15131334
Chicago/Turabian StyleDi, Yabei, Jinlong Yu, Huaping Luo, Huaiyu Liu, Lei Kang, and Yuesen Tong. 2025. "Study on Outdoor Spectral Inversion of Winter Jujube Based on BPDF Models" Agriculture 15, no. 13: 1334. https://doi.org/10.3390/agriculture15131334
APA StyleDi, Y., Yu, J., Luo, H., Liu, H., Kang, L., & Tong, Y. (2025). Study on Outdoor Spectral Inversion of Winter Jujube Based on BPDF Models. Agriculture, 15(13), 1334. https://doi.org/10.3390/agriculture15131334






