Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm
Abstract
1. Introduction
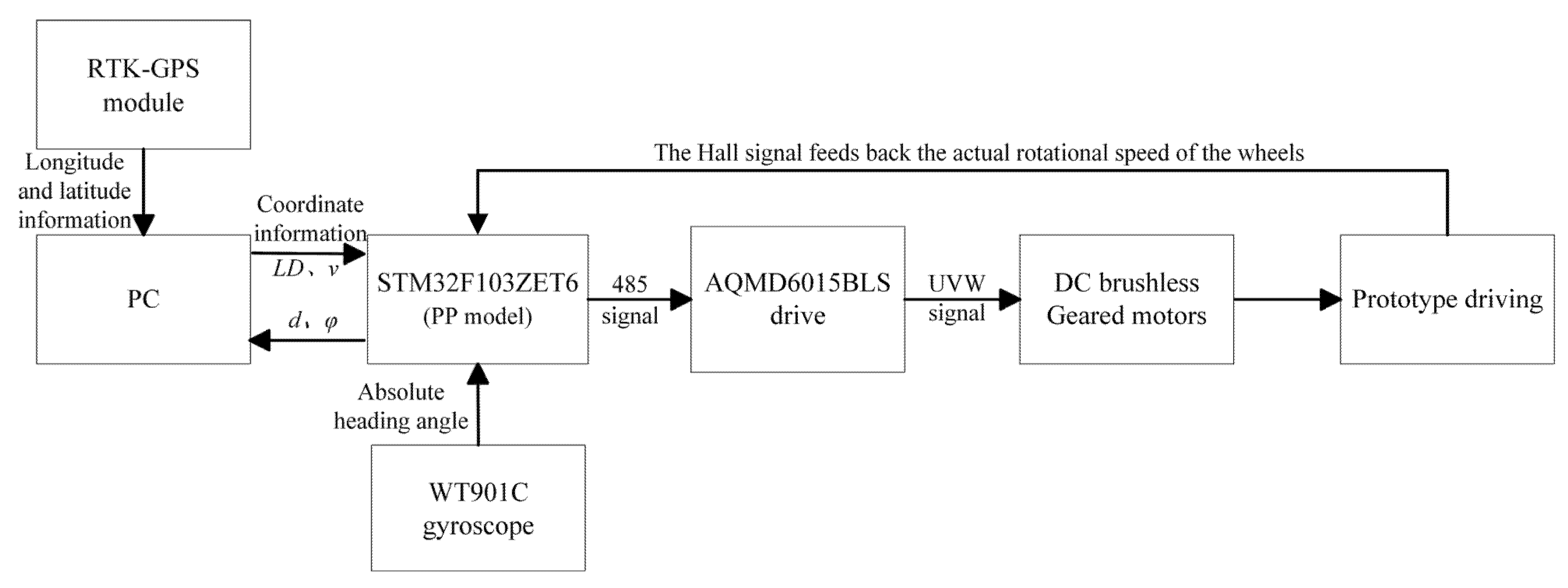
2. Experimental Platform
3. Path Tracking Quality Analysis
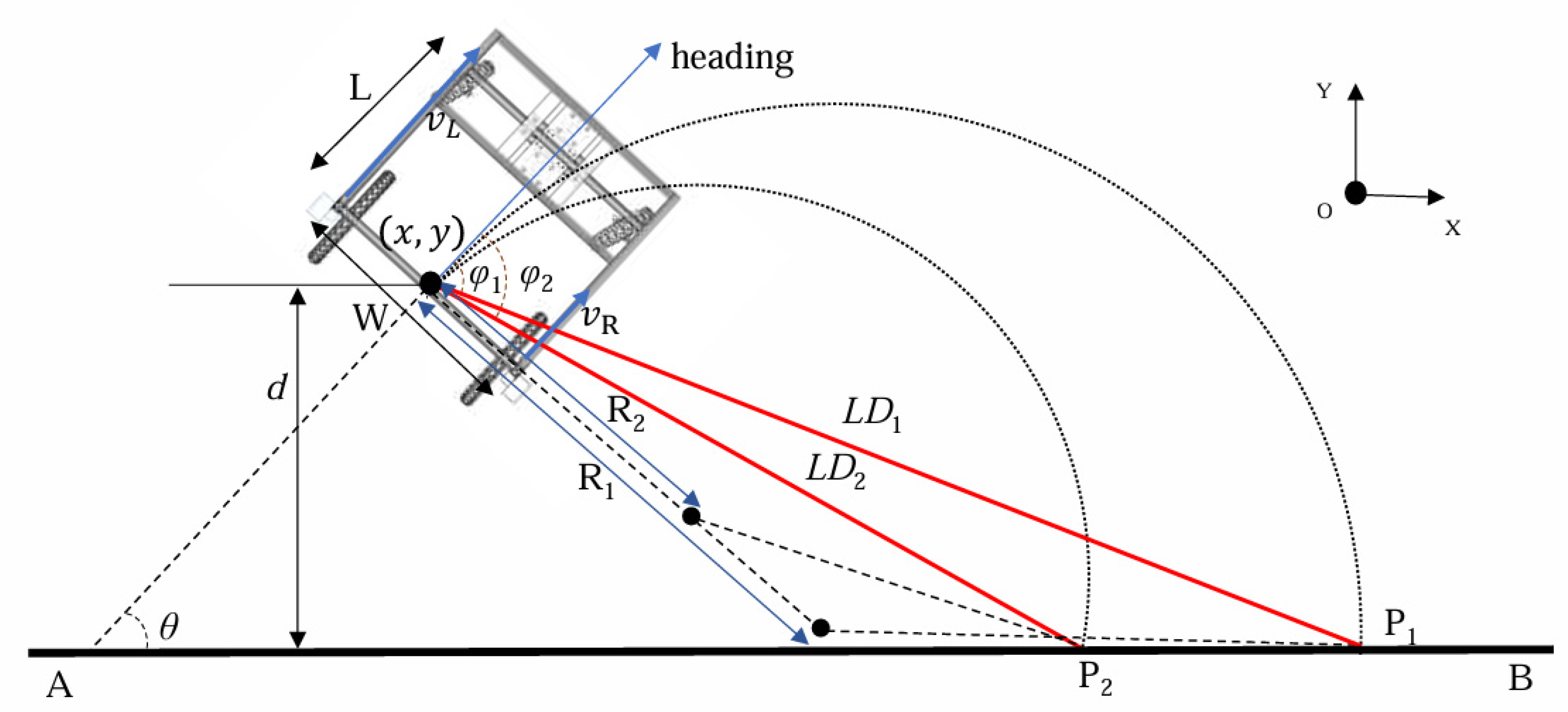
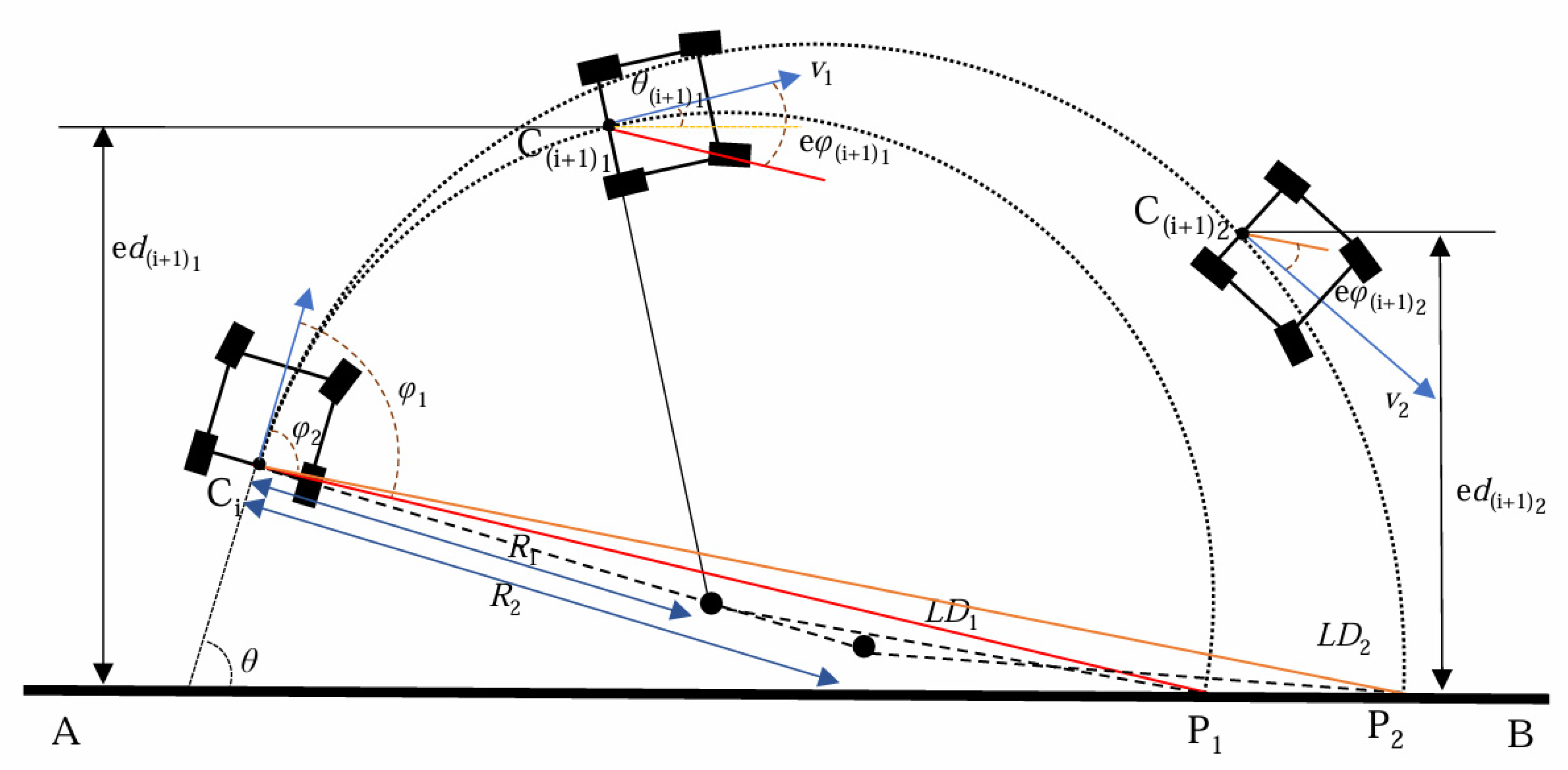
3.1. Influence of Look-Ahead Distance in the Pure Pursuit Model
3.2. The Impact of Speed on Tracking Quality
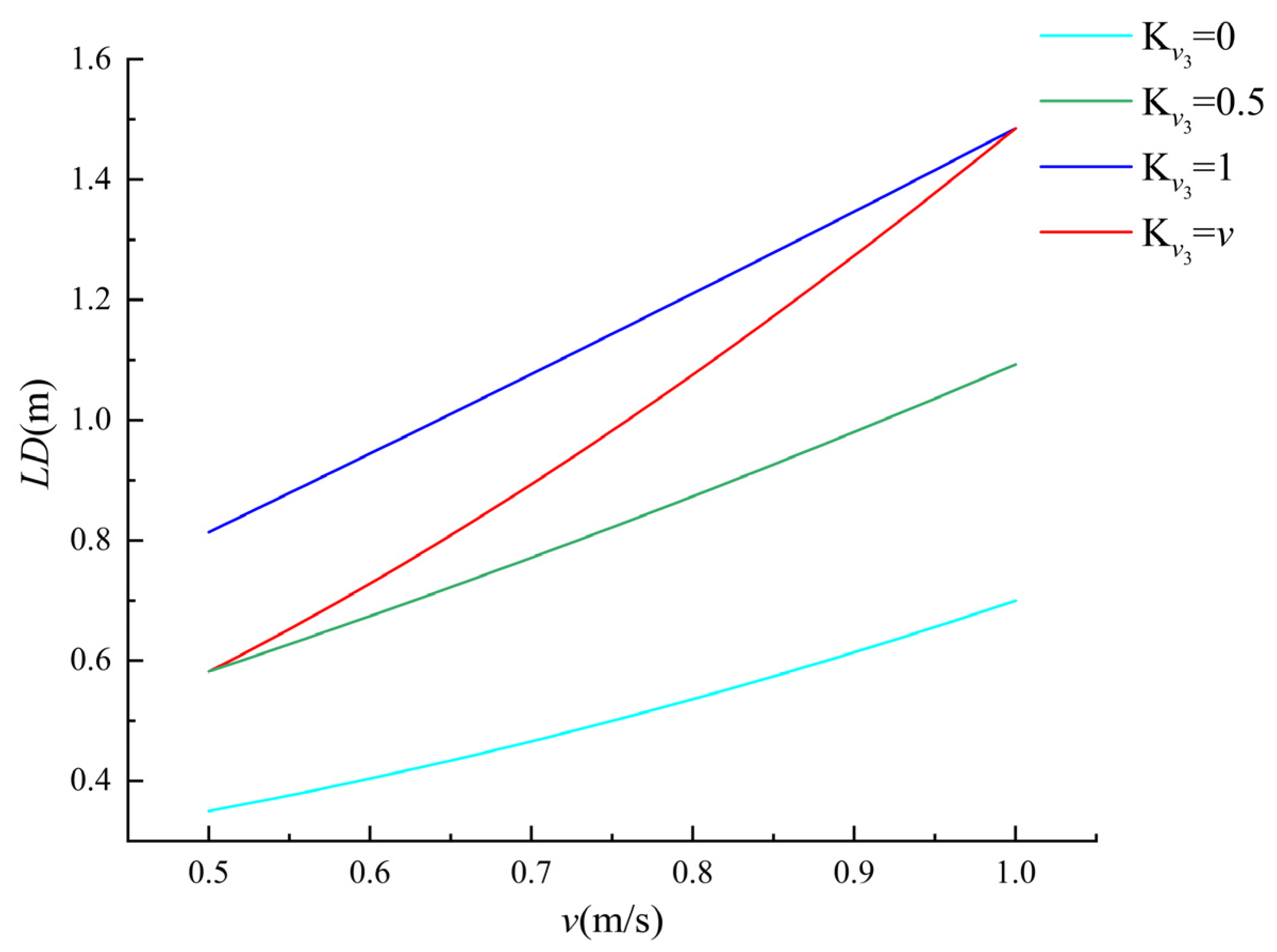
3.3. The Relationship Between Speed and Look-Ahead Distance
4. ISSA-PP Algorithm
4.1. Schematic Flow of the Algorithm
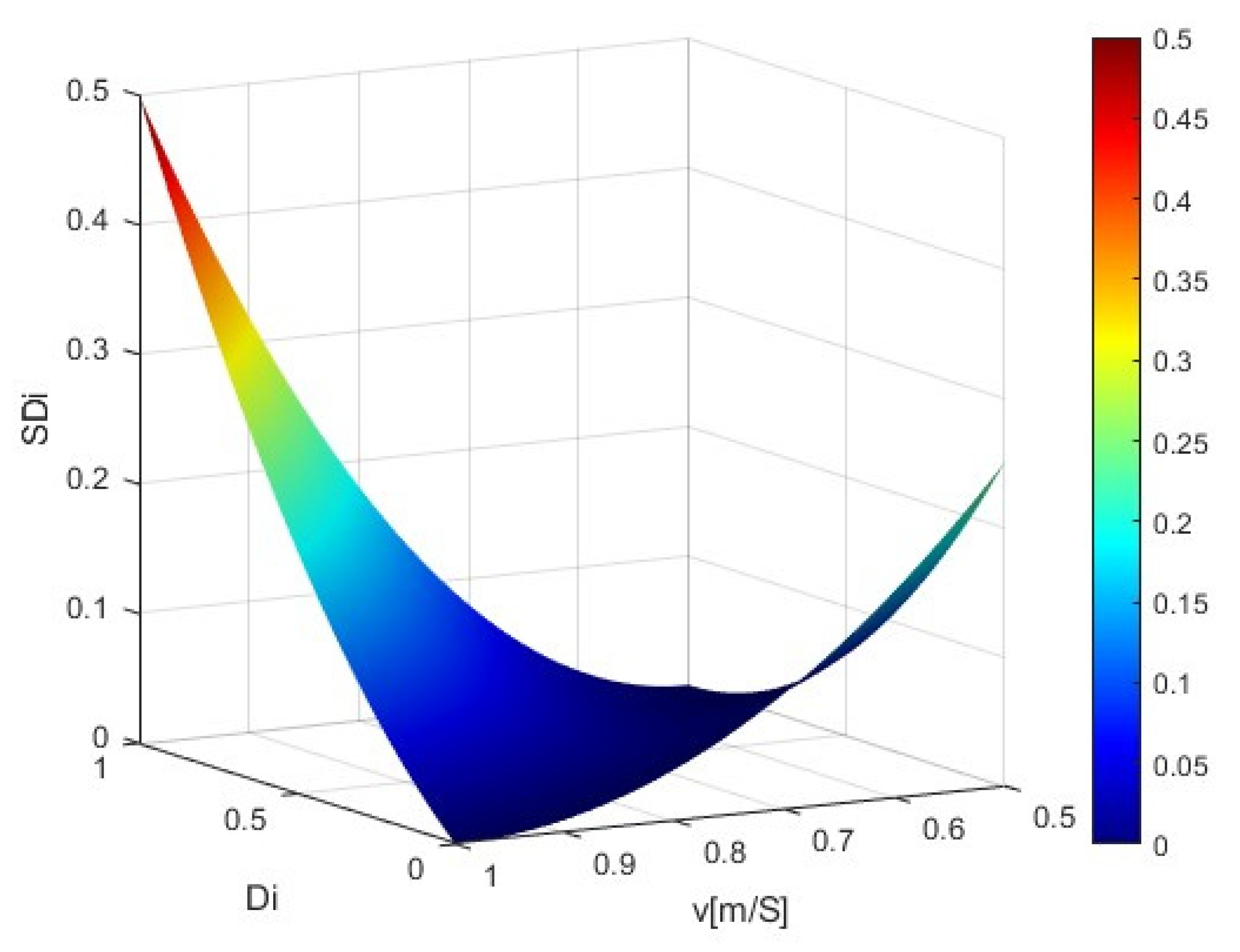
4.2. Design of the Fitness Function
4.3. Dynamic v and LD Acquisition Process
5. Improved Sparrow Search Algorithm
5.1. Introduction of Random Variable Tent Chaotic Mapping
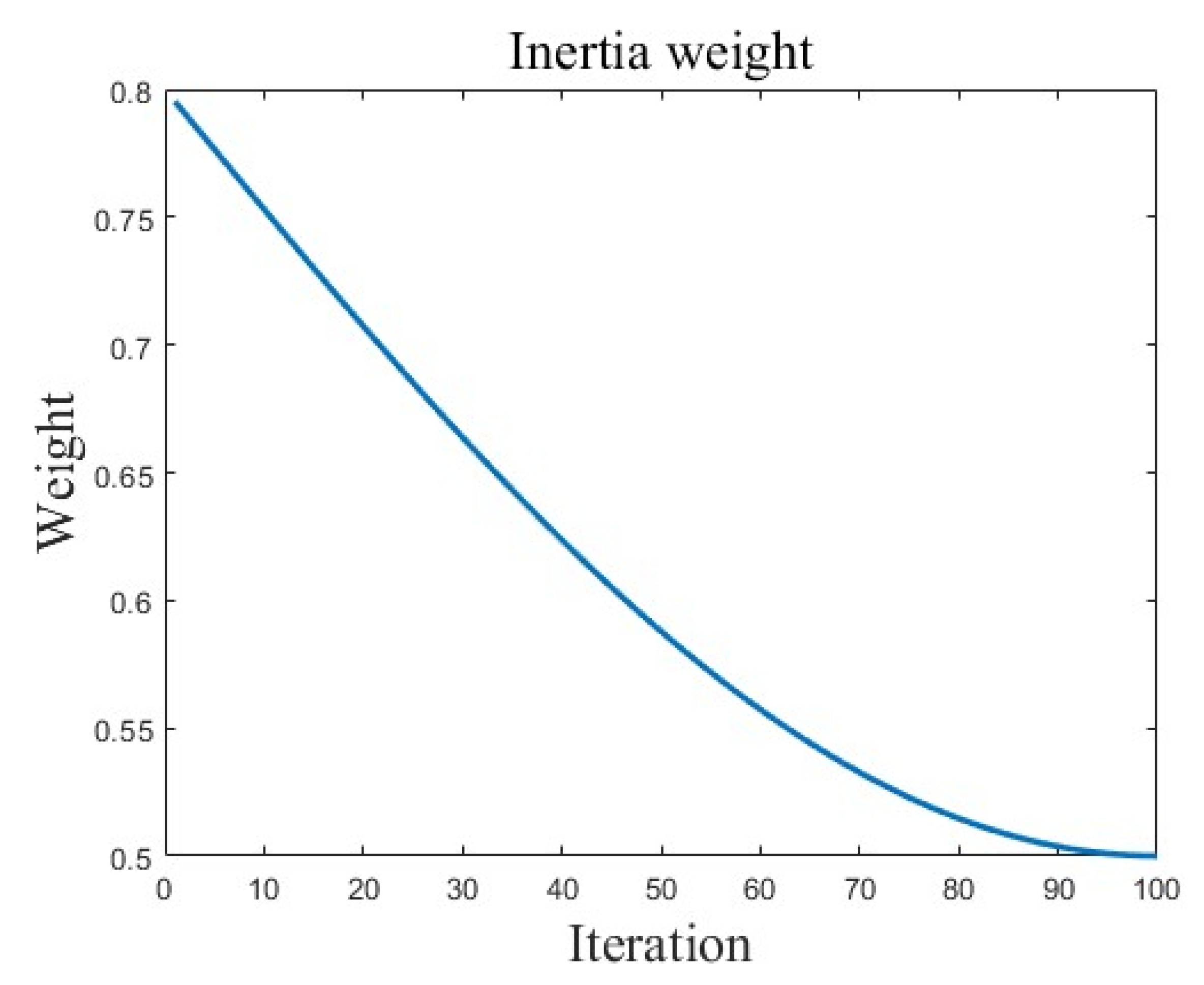
5.2. Dynamic Proportion and Inertia Weight
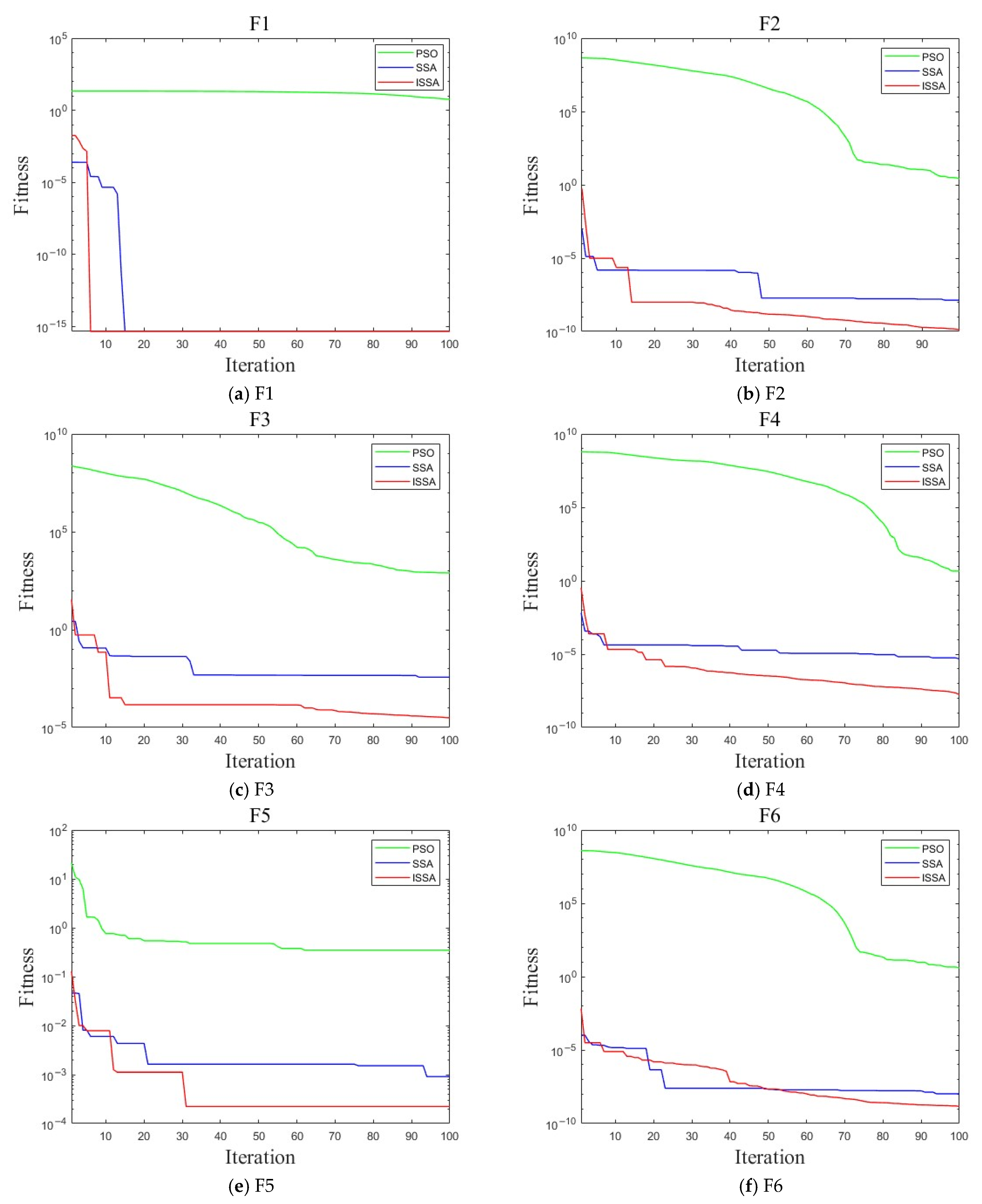
5.3. Overall Performance Simulation Test of ISSA
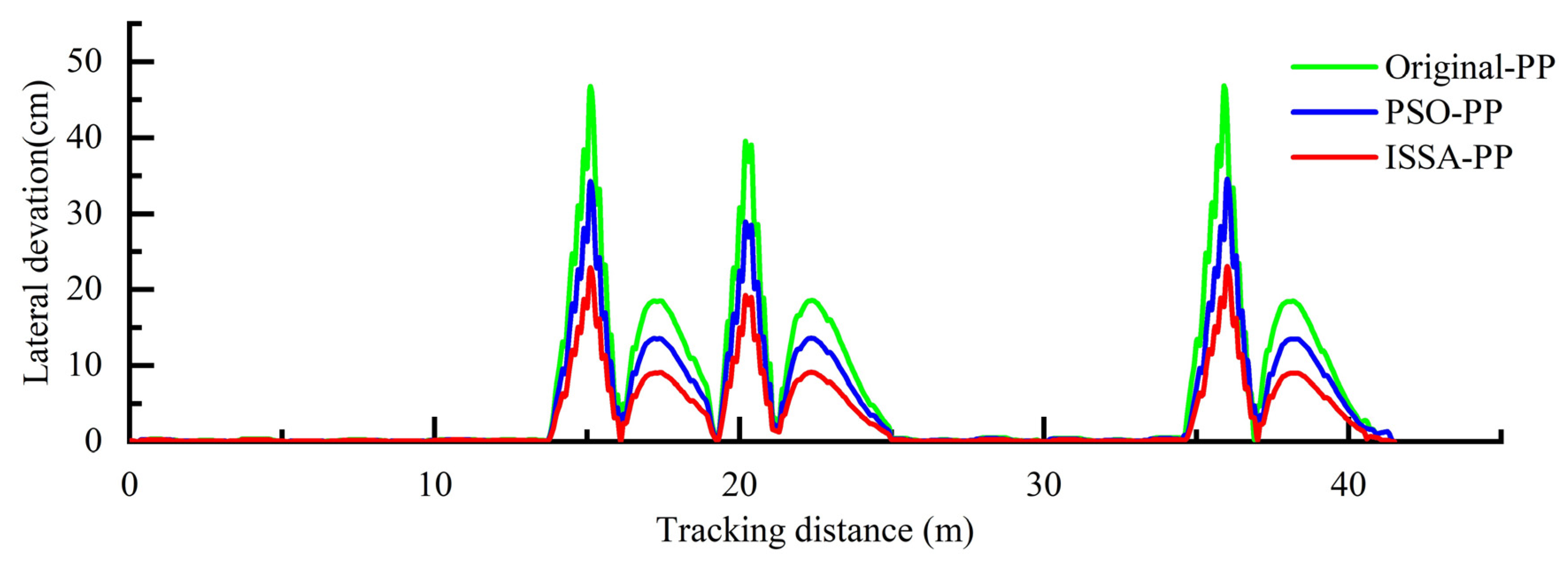
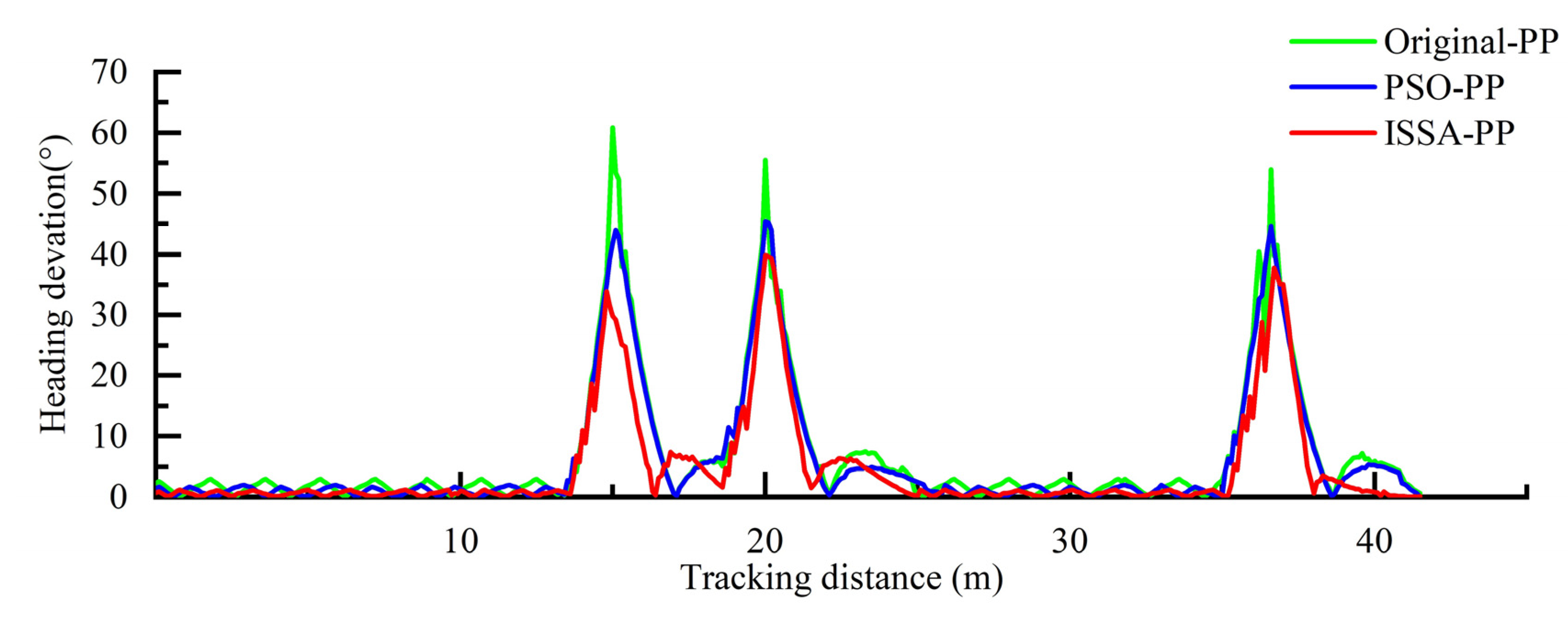
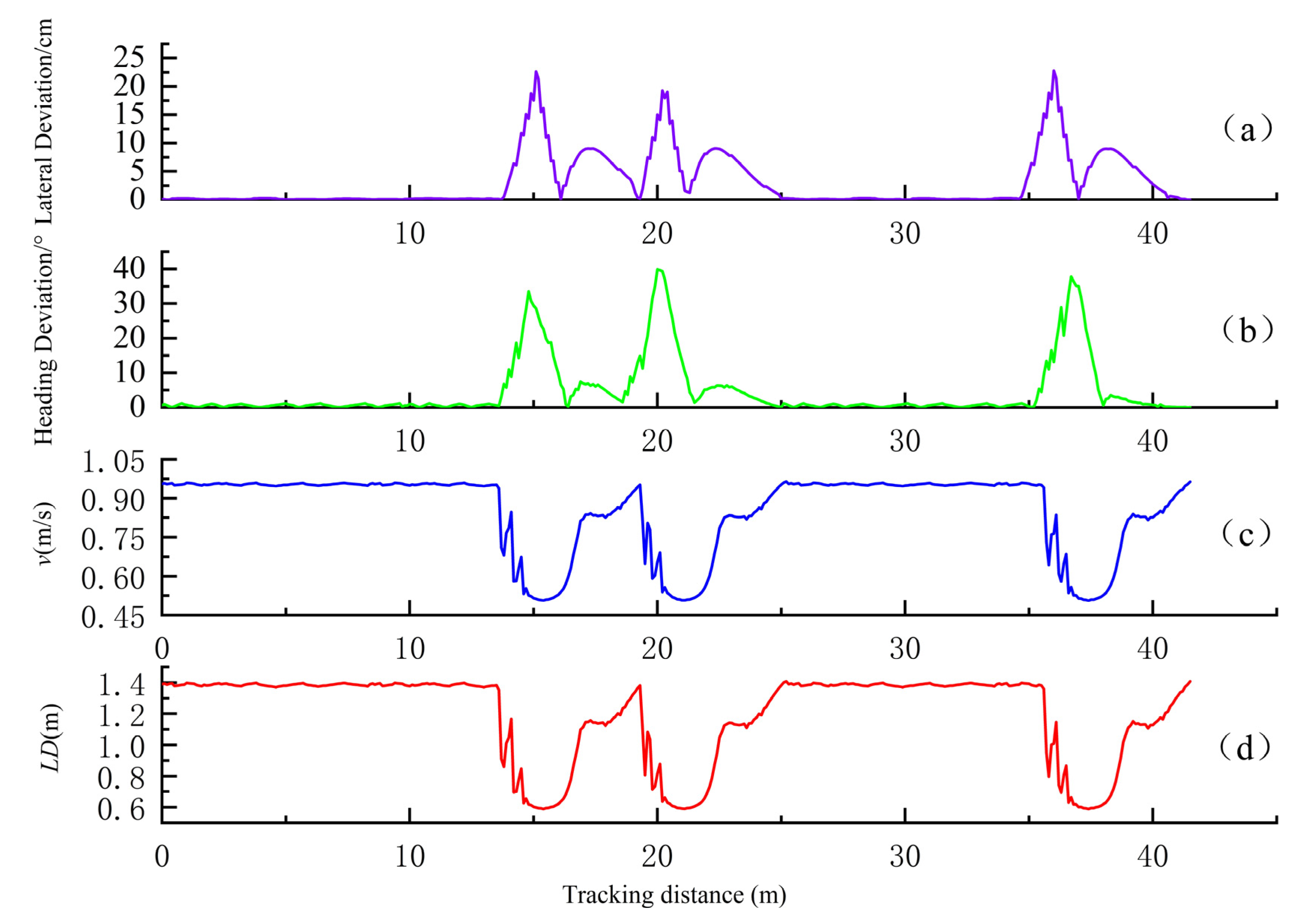
6. Experiment and Results Analysis
6.1. Experiment Design
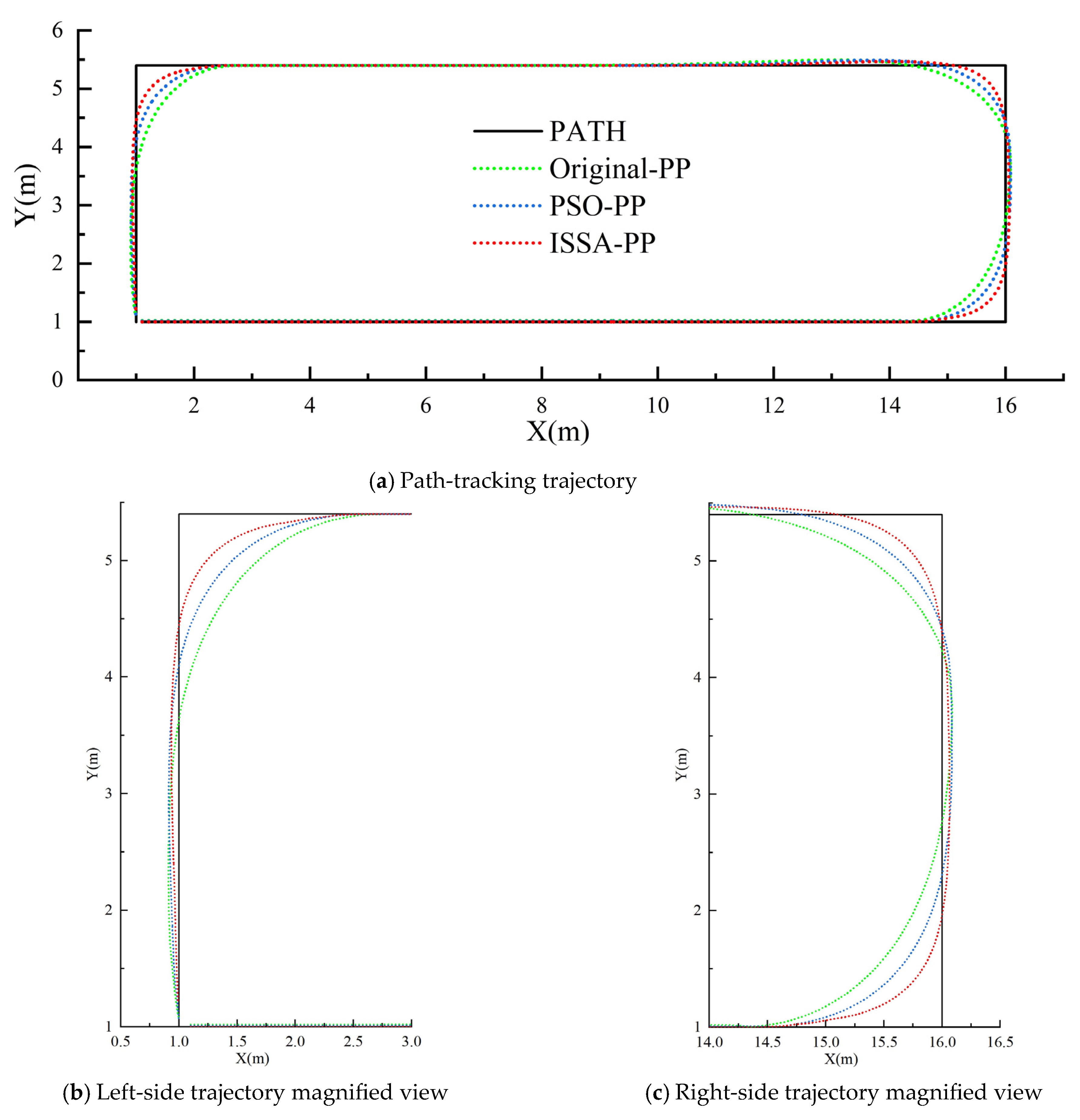
6.2. Experiment Results
6.3. Data Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, Z.; Zhao, C.; Zhang, T. Agricultural machinery automatic navigation technology. iScience 2024, 27, 108714. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Jin, Y.; Faheem, M.; Gao, W.; Liu, J.; Jiang, H.; Cai, L.; Li, Y. Research progress of autonomous navigation technology for multi-agricultural scenes. Comput. Electron. Agric. 2023, 211, 107963. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; Du, Y.; Zhu, Z.; Mao, E.; Song, Z. Method on automatic navigation control of tractor based on speed adaptation. Trans. Chin. Soc. Agric. Eng. 2017, 33, 48–55. [Google Scholar]
- Zhang, W.; Gai, J.; Zhang, Z.; Tang, L.; Liao, Q.; Ding, Y. Double-DQN based path smoothing and tracking control method for robotic vehicle navigation. Comput. Electron. Agric. 2019, 166, 104985. [Google Scholar] [CrossRef]
- Li, Z.; Chen, L.; Zheng, Q.; Dou, X.; Yang, L. Control of a path following caterpillar robot based on a sliding mode variable structure algorithm. Biosyst. Eng. 2019, 186, 293–306. [Google Scholar] [CrossRef]
- Nguyen, P.T.T.; Yan, S.W.; Liao, J.F.; Kuo, C.H. Autonomous mobile robot navigation in sparse LiDAR feature environments. Appl. Sci. 2021, 11, 5963. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Luo, X. Design of GNSS automatic navigation operation system for Leivol ZP9500 upland gap sprayer. J. Agric. Eng. 2018, 34, 15–21. [Google Scholar]
- Monot, N.; Moreau, X.; Benine-Neto, A.; Rizzo, A.; Aioun, F. Automated vehicle lateral guidance using multi-PID steering control and look-ahead point reference. Int. J. Veh. Auton. Syst. 2021, 16, 38–55. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Y.; Wang, J. Fuzzy observer-based transitional path-tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3078–3088. [Google Scholar] [CrossRef]
- Macenski, S.; Singh, S.; Martín, F.; Ginés, J. Regulated pure pursuit for robot path tracking. Auton. Robot. 2023, 47, 685–694. [Google Scholar] [CrossRef]
- Petrinec, K.; Kovacic, Z.; Marozin, A. Simulator of multi-AGV robotic industrial environments. In Proceedings of the IEEE International Conference on Industrial Technology, Maribor, Slovenia, 10–12 December 2003; Volume 2, pp. 979–983. [Google Scholar]
- Xu, L.; Yang, Y.; Chen, Q.; Fu, F.; Yang, B.; Yao, L. Path tracking of a 4WIS–4WID agricultural machinery based on variable look-ahead distance. Appl. Sci. 2022, 12, 8651. [Google Scholar] [CrossRef]
- Wu, Y.; Xie, Z.; Lu, Y. Steering wheel AGV path tracking control based on improved pure pursuit model. J. Phys. Conf. Ser. 2021, 2093, 012005. [Google Scholar] [CrossRef]
- Wang, R.; Li, Y.; Fan, J.; Wang, T.; Chen, X. A novel pure pursuit algorithm for autonomous vehicles based on salp swarm algorithm and velocity controller. IEEE Access 2020, 8, 166525–166540. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wen, X.; Zhang, G.; Ma, Q.; Cheng, S.; Qi, J.; Xu, L.; Chen, L. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 194, 106760. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Han, K.; Choi, S.B. Vehicle path tracking control using pure pursuit with MPC-based look-ahead distance optimization. IEEE Trans. Veh. Technol. 2023, 73, 53–66. [Google Scholar] [CrossRef]
- Fathy, A.; Alanazi, T.M.; Rezk, H.; Yousri, D. Optimal energy management of micro-grid using sparrow search algorithm. Energy Rep. 2021, 8, 758–773. [Google Scholar] [CrossRef]
- Zhao, W.; Liang, T. Optimization of terminal area arrival flight sorting based on an improved sparrow search algorithm. Sci. Prog. 2024, 107, 368504241238078. [Google Scholar] [CrossRef]
- Zhu, Y.; Yousefi, N. Optimal parameter identification of PEMFC stacks using adaptive sparrow search algorithm. Int. J. Hydrogen Energy 2021, 46, 9541–9552. [Google Scholar] [CrossRef]
- Yao, Y.; Lei, S.; Guo, Z.; Li, Y.; Ren, S.; Liu, Z.; Guan, Q.; Luo, P. Fast optimization for large scale logistics in complex urban systems using the hybrid sparrow search algorithm. Int. J. Geogr. Inf. Sci. 2023, 37, 1420–1448. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A survey on sparrow search algorithms and their applications. Int. J. Syst. Sci. 2024, 55, 814–832. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Liao, X. Some properties of the logistic map over the finite field and its application. Signal Process. 2018, 153, 231–242. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- Jiao, B.; Lian, Z.; Gu, X. A dynamic inertia weight particle swarm optimization algorithm. Chaos Solitons Fractals 2008, 37, 698–705. [Google Scholar] [CrossRef]
- Liu, J.; Mei, Y.; Li, X. An analysis of the inertia weight parameter for binary particle swarm optimization. IEEE Trans. Evol. Comput. 2015, 20, 666–681. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, T.; Song, Y.; Qian, F. Color feature-based object tracking through particle swarm optimization with improved inertia weight. Sensors 2018, 18, 1292. [Google Scholar] [CrossRef]





| Method | Logistic | Tent | IRV Tent | Completely Uniform Distribution |
|---|---|---|---|---|
| Expectation | 0.7510 | 0.7356 | 0.7468 | 0.7450 |
| Variance | 0.0185 | 0.0178 | 0.0197 | 0.0206 |
| Test Function | Algorithm | Best Value | Average | Optimization Time/s |
|---|---|---|---|---|
| ISSA | 4.45 × 10−16 | 2.95 × 10−13 | 0.056 | |
| SSA | 4.45 × 10−16 | 3.44 × 10−10 | 0.075 | |
| PSO | 1.92 | 49.48 | 0.136 | |
| ISSA | 2.69 × 10−10 | 9.86 × 10−8 | 0.086 | |
| SSA | 1.57 × 10−6 | 8.23 × 10−6 | 0.102 | |
| PSO | 4.03 | 3.09 × 107 | 0.085 | |
| ISSA | 1.23 × 10−5 | 8.39 × 10−5 | 0.021 | |
| SSA | 9.36 × 10−4 | 3.09 × 10−3 | 0.033 | |
| PSO | 102.82 | 3.66 × 10−5 | 0.137 | |
| ISSA | 4.34 × 10−7 | 3.13 × 10−6 | 0.193 | |
| SSA | 9.36 × 10−6 | 7.75 × 10−4 | 0.244 | |
| PSO | 100.58 | 2.91 × 106 | 0.377 | |
| ISSA | 6.58 × 10−5 | 1.96 × 10−4 | 0.058 | |
| SSA | 7.32 × 10−4 | 8.67 × 10−4 | 0.071 | |
| PSO | 0.48 | 8.63 | 0.088 | |
| ISSA | 1.09 × 10−9 | 3.65 × 10−6 | 0.058 | |
| SSA | 6.34 × 10−9 | 7.58 × 10−9 | 0.093 | |
| PSO | 71.8 | 4.05 × 106 | 0.073 |
| Experiment Number | Evaluation Metrics | ISSA-PP | PSO-PP | Original-PP |
|---|---|---|---|---|
| 1 | Average Lateral Deviation/cm | 3.09 | 4.64 | 6.33 |
| Average Heading Deviation/° | 4.68 | 6.21 | 6.81 | |
| Average Stabilization Distance/m | 4.72 | 6.92 | 9.33 | |
| Navigation time/s | 46.07 | 52.36 | 51.92 | |
| 2 | Average Lateral Deviation/cm | 3.18 | 4.84 | 6.56 |
| Average Heading Deviation/° | 4.78 | 6.51 | 6.88 | |
| Average Stabilization Distance/m | 4.53 | 6.88 | 9.17 | |
| Navigation time/s | 47.32 | 52.49 | 52.66 | |
| 3 | Average Lateral Deviation/cm | 3.12 | 4.76 | 6.37 |
| Average Heading Deviation/° | 4.92 | 6.38 | 6.97 | |
| Average Stabilization Distance/m | 4.87 | 7.01 | 9.43 | |
| Navigation time/s | 45.79 | 51.97 | 51.24 | |
| Average value | Average Lateral Deviation/cm | 3.13 | 4.75 | 6.42 |
| Average Heading Deviation/° | 4.78 | 6.37 | 6.89 | |
| Average Stabilization Distance/m | 4.71 | 6.94 | 9.31 | |
| Navigation time/s | 46.40 | 52.27 | 51.94 |
| Evaluation Metrics | Algorithm | N | MEAN | SD | F | p |
|---|---|---|---|---|---|---|
| Lateral Deviation/cm | ISSA-PP | 1392 | 3.13 | 5.755 | 72.34 | <0.001 |
| PSO-PP | 1569 | 4.75 | 7.057 | |||
| Original-PP | 1560 | 6.42 | 11.198 | |||
| Heading Deviation/° | ISSA-PP | 1392 | 4.78 | 7.60 | 18.27 | <0.001 |
| PSO-PP | 1569 | 6.37 | 10.60 | |||
| Original-PP | 1560 | 6.89 | 17.10 |
| Evaluation Metrics | Comparison Group | MEAN Difference | SE | t | p | 1-β | Cohen’s d | 95% CI |
|---|---|---|---|---|---|---|---|---|
| Lateral Deviation /cm | ISSA-PP vs. PSO-PP | 1.62 | 0.25 | 6.48 | <0.001 | >0.99 | 0.41 | [1.13,2.11] |
| ISSA-PP vs. Original-PP | 3.29 | 0.32 | 10.28 | <0.001 | >0.99 | 0.83 | [2.66,3.92] | |
| Heading Deviation /° | ISSA-PP vs. PSO-PP | 1.59 | 0.34 | 4.68 | <0.001 | 0.98 | 0.34 | [0.92,2.26] |
| ISSA-PP vs. Original-PP | 2.11 | 0.49 | 4.31 | <0.001 | 0.99 | 0.45 | [1.15,3.07] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, J.; Yao, L.; Zhou, J.; Yang, Z.; Xu, L.; Yao, L. Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm. Agriculture 2025, 15, 1215. https://doi.org/10.3390/agriculture15111215
Wen J, Yao L, Zhou J, Yang Z, Xu L, Yao L. Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm. Agriculture. 2025; 15(11):1215. https://doi.org/10.3390/agriculture15111215
Chicago/Turabian StyleWen, Junhao, Liwen Yao, Jiawei Zhou, Zidong Yang, Lijun Xu, and Lijian Yao. 2025. "Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm" Agriculture 15, no. 11: 1215. https://doi.org/10.3390/agriculture15111215
APA StyleWen, J., Yao, L., Zhou, J., Yang, Z., Xu, L., & Yao, L. (2025). Path Tracking Control of Agricultural Automatic Navigation Vehicles Based on an Improved Sparrow Search-Pure Pursuit Algorithm. Agriculture, 15(11), 1215. https://doi.org/10.3390/agriculture15111215






