Estimation of Genetic Parameters and Prediction for Body Weight of Angus Cattle

Abstract

With the growing global population, the demand for beef is increasing, making the genetic improvement of beef cattle crucial for sustainable production. This study aimed to estimate genetic parameters using different models and predict body weight in Angus cattle to enhance the accuracy of genetic evaluation and support optimal breeding and selection programs. We used the inclusion or exclusion of maternal genetic effects, maternal permanent environmental effects, and the presence or absence of covariance between maternal and direct genetic effects to distinguish between the six animal models. The variance components and genetic parameters of 13,607 weight records from Angus cattle were estimated using the Average Information Restricted Maximum Likelihood (AI-REML) method. The best estimated model was selected based on the Akaike Information Criterion (AIC) and Likelihood Ratio Test (LRT). The results of this study revealed that, in addition to individual genetic effects, maternal genetic effects had a significant impact on unbiased and accurate genetic parameter estimates of body weight in Angus cattle. The total heritability estimated with the best model for body weight at birth (BW0), 3 months (BW3), 6 months (BW6), 12 months (BW12), and 18 months (BW18) was 0.215 ± 0.007, 0.340 ± 0.021, 0.239 ± 0.035, 0.362 ± 0.044, and 0.225 ± 0.048, respectively. The maternal heritability ranges from 0.017~0.438 and significantly affects Angus cattle throughout their growth and development stages, with the effect decreasing with increasing age. Positive correlations were observed between body weights at different months of age, ranging from 0.061 to 0.828. BW6 has a high positive genetic correlation with later age weight, and BW6 is a good predictor of later age weight. Thus, it is possible to optimize breeding programs and accelerate genetic progress by selecting for higher 6-month-old live weights for early Angus selection. In addition, our results emphasize the importance of considering maternal effects in genetic evaluation to improve the efficiency and accuracy of selection programs and thereby contribute to sustainable genetic improvement in beef cattle.

1. Introduction

Animal breeding in the economy of a country is considered one of the most important economic branches and is of special importance. Animal breeding is a very profitable job, and it is considered a means of raising the economy of countries. Most of the people of the world are engaged in cattle breeding and use their products. In addition, cattle breeding has an important role [1]. The demand for beef as an important food source is increasing as the world’s population grows, and to meet production needs, genetic improvement accomplished by estimating the breeding value of economically important traits in beef cattle is a sustainable solution to increase production on farms [2,3]. However, accurate estimation of genetic parameters for economic traits is a prerequisite for scientific breeding programs, and selecting a reasonable model is an important means of improving the accuracy of genetic parameter estimation. The animal model is considered to be the preferred model for a wide range of applications that can take advantage of all the relatives in the dataset [4]. Animal models can be further divided into direct genetic effect, maternal genetic effect, and maternal permanent environmental effect models [5,6]. In the selection of beef cattle for growth traits, in addition to systematic environmental effects, the effects of direct additive genetic effects, maternal genetic effects, and permanent environmental effects are also considered, In particular, where there is a conflict between direct additive genetic effects and maternal genetic effects, and omitting maternal genetic effects from the model leads to an overestimation of total heritability [7]. Rumph et al. [8] estimated genetic parameters for different seasonal maturity weights; they concluded that a model that included maternal genetic and maternal permanent environmental effects, and direct genetic and direct permanent environmental effects, best fit the estimates of genetic parameters. It has also been shown that maternal effects have a significant effect on growth traits in beef cattle both before and after weaning [9].

The Ningxia region has a typical continental semi-humid and semi-arid climate, and this unique natural condition provides a unique advantage for beef cattle breeding. In recent years, Angus cattle, as a high-quality beef cattle breed, have been imported to the Ningxia region in large quantities, and have quickly adapted to the local growing environment, becoming the core force to promote the development of the regional beef cattle industry. However, the growth performance and genetic potential of Angus cattle may be affected to some extent by the combined effect of multiple factors, such as changes in feeding environment, adjustments in feeding methods, and genetic drift. To scientifically exploit their genetic potential and optimize the quality of the breeding stock, it is particularly important to develop an accurate breeding program. Genetic parameters, as the core basis of the breeding program, directly determine the accuracy of the breeding results.

In this study, we initially estimated the variance components and genetic parameters associated with body weight in Angus cattle. This analysis utilized an extensive dataset comprising 13,607 body weight records collected from Angus cattle across various growth stages. We employed six distinct animal models, which either included or excluded maternal genetic effects, maternal permanent environmental effects, and the covariance between maternal effects and direct genetic effects. The optimal model was identified using the Akaike Information Criterion (AIC), addressing the deficiency in practical breeding insights for Angus cattle under specific climatic conditions in Ningxia, China. This approach offers a more precise and effective foundation for Angus cattle breeding programs. Furthermore, it enhances the global knowledge base of beef cattle genetics and introduces a refined genetic evaluation methodology that applies to other regions and breeds.

2. Materials and Methods

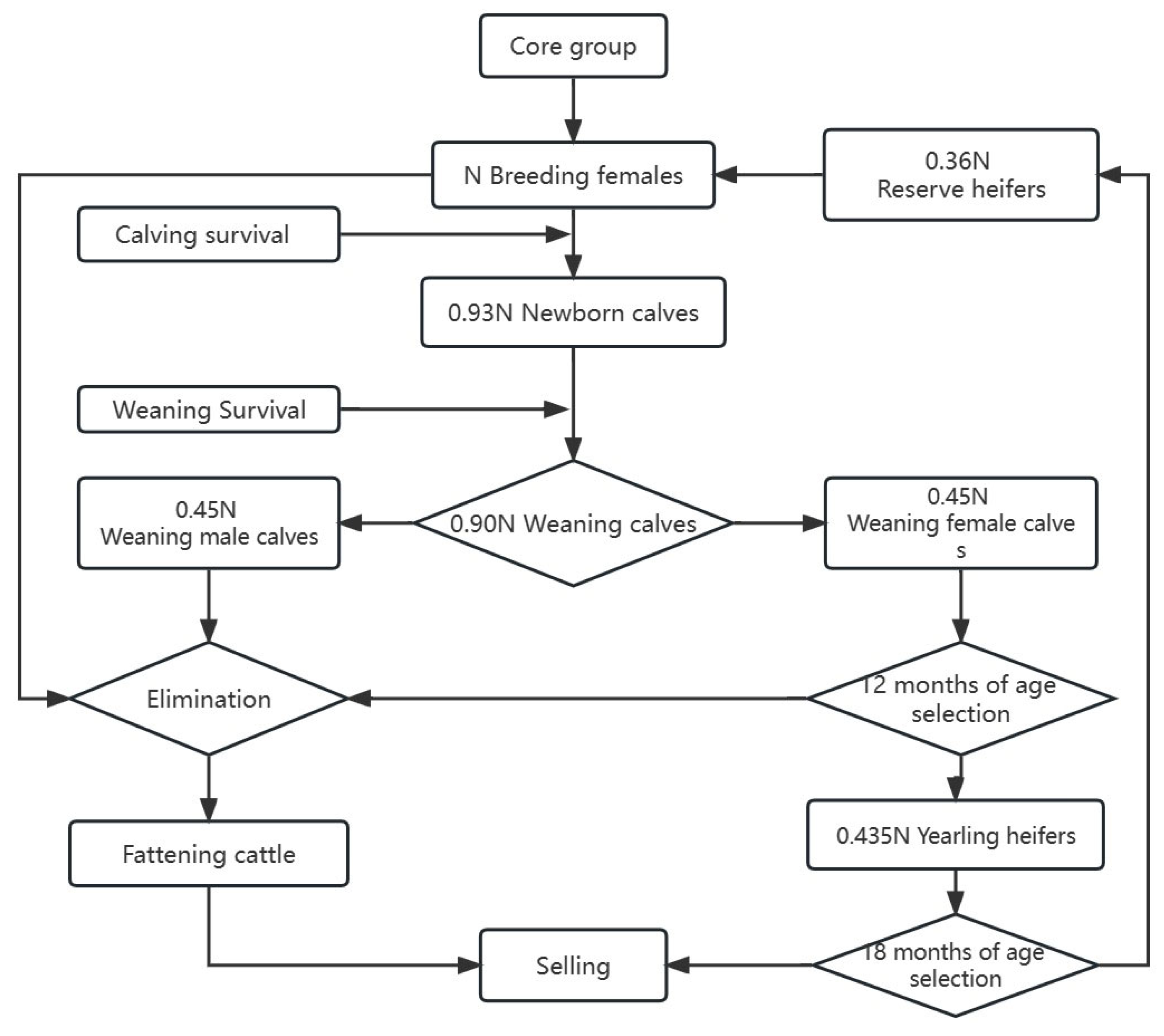
2.1. Data Sources and Animal Management

The data for this study were collected by the animal husbandry extension station of Ningxia and stored in the Ningxia beef cattle breeding data collection system database. The use of data is authorized by the animal husbandry extension station (China). The cattle come from eight core herd selection farms of Angus cattle in the Ningxia region. The region has a temperate continental arid and semi-arid climate with large annual and monthly temperature differences, with the highest temperatures in July, averaging 24 °C, and the lowest temperatures in January, averaging −9 °C. The herd uses an open-core herd selection program (Figure 1). The animal husbandry extension station invites tenders for the purchase of imported purebred frozen semen to breed the females of the core herd and provides some semen to the production herd, from which excellent breeding animals are regularly selected to replenish the core herd. The male calves in the core herd go directly into the fattening herd after weaning, the female calves are selected at 12 and 18 months of age in turn, and the eliminated females go into the fattening herd. In addition, animals are fed different concentrations of concentrate depending on their body weight, with 30%, 25%, and 20% of concentrate added to the diet for weaning ~350 kg, 350–500 kg, and >500 kg, respectively. Free-range feeding, with drinking water and dry lick mineral blocks in each enclosure, was employed.

2.2. Data Collection and Statistical Analysis

Our research uses data from 2016~2024. Measurement and collection of birth weight (BW0), 3-month weight (BW3), 6-month weight (BW6), 12-month weight (BW12), and 18-month weight (BW18) of Angus cattle. We herd cattle onto a platform weighbridge to measure the weight, with a movable pen to properly restrict their range of motion. The protocol was approved by the laboratory animal welfare and ethics review committee of Ningxia University, approval code NXU-2016-011. The phenotype records outside the mean ± 3SD were removed. We also eliminated bulls when they had an offspring number less than 10. In the population used for the study, 3519 animals had at least one phenotypic record, 4482 individuals were present in the pedigree, and both parents of the animals with phenotypic records were known. There were 2412 dams in the pedigree, and they all had progeny records, a minimum of one and a maximum of seven, with an average number of 2.19 progeny, of which 790 dams had their phenotypic records. All 86 males had recorded offspring, with a minimum of 10 and a maximum of 509, with an average offspring number of 99.82. The results of descriptive statistics for each trait are presented in

Table 1. Results of descriptive statistics for the weight of Angus cattle by growth stage.

Traits	Number of Records	Mean	Standard Deviation	Coefficient of Variation	Number of Sires	Number of Dams	Number of Dams with Records
BW0	3493	32.63	4.84	14.74	78	2356	538
BW3	3002	119.50	24.19	19.50	63	2192	386
BW6	2931	188.53	33.61	17.83	53	2236	496
BW12	2323	235.48	63.68	19.56	45	1721	785
BW18	1858	561.93	68.91	15.84	36	1206	162

.

2.3. Methods and Models for Estimating Genetic Parameters

The inclusion or exclusion of maternal genetic effects, maternal permanent environmental effects, and the presence of covariates between maternal and direct genetic effects distinguished the six animal models. The estimation of genetic parameters for traits was conducted using the AI-REML algorithm of the DMU software (Aarhus University, Aarhus, Denmark, Version 6). All models include direct additive genetic effects, which are the only random effects in Model 1. Model 2 includes parental permanent environmental effects. Model 3 includes maternal genetic effects. Model 4 is the same as Model 3, and there is covariance between the direct additive genetic effect and the maternal genetic effect. Model 5 includes maternal genetic effects and maternal permanent environmental effects; Model 6 is the same as Model 5 and takes into account the correlation between direct additive genetic effects and maternal genetic effects. The models for each trait were as follows:

$$\begin{array}{cc}\text{Model 1:} y=Xb+Z_{1}a+e\hfill & \\ \text{Model 2:} y=Xb+Z_{1}a+Z_{3}c+e\hfill & \\ \text{Model 3:} y=Xb+Z_{1}a+Z_{2}m+e\hfill & \hfill {\sigma }_{a,m}=0\\ \text{Model 4:} y=Xb+Z_{1}a+Z_{2}m+e\hfill & \hfill {\sigma }_{a,m}\ne 0\\ \text{Model 5:} y=Xb+Z_{1}a+Z_{2}m+Z_{3}c+e\hfill & \hfill {\sigma }_{a,m}=0\\ \text{Model 6:} y=Xb+Z_{1}a+Z_{2}m+Z_{3}c+e\hfill & \hfill {\sigma }_{a,m}\ne 0\end{array}$$

where $y$ is the vector of observations for each trait; $b$ is a vector of fixed effects (group-year effect: 8 groups and 9 birth years for a total of 14 effect levels; year-season effect: 9 birth years and 4 seasons for a total of 36 effect levels; sex effect: 2 effect levels for males and females); $a,m,c$ and $e$ are direct additive genetic effect vectors, maternal genetic effect vectors, maternal permanent environmental effect vectors, and residual effect vectors, respectively; $X,Z_1,Z_2$ and $Z_3$ are structural matrices for fixed effects, direct additive genetic effects, maternal genetic effects, and maternal permanent environmental effects, respectively.

Total heritability is calculated according to the following equation [10]:

$$h_T^2=\left({\sigma }_a^2+0.5{\sigma }_m^2+1.5{\sigma }_{a,m}\right)/{\sigma }_p^2$$

${\mathsf{\sigma }}_{\mathrm{p}}^2={\mathsf{\sigma }}_{\mathrm{a}}^2+{\mathsf{\sigma }}_{\mathrm{m}}^2+{\mathsf{\sigma }}_{\mathrm{a},\mathrm{m}}+{\mathsf{\sigma }}_{\mathrm{c}}^2+{\mathsf{\sigma }}_{\mathrm{e}}^2,{ h}_T^2$ is total heritability, ${\sigma }_a^2$ is direct additive genetic variances, ${\sigma }_m^2$ is maternal additive genetic variance, ${\sigma }_{a,m}$ is covariance between the direct genetic effect and the maternal genetic effect, ${\sigma }_c^2$ is parent permanent environment variance, ${\sigma }_e^2$ is residual variance, and ${\sigma }_p^2$ is phenotypic variance.

The Akaike Information Criterion (AIC) was used to determine the best animal model for genetic parameter estimation [11].

$$\mathrm{A}\mathrm{I}\mathrm{C}=2\mathrm{k}-2\mathrm{l}\mathrm{n}\left({\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{X}}\right)$$

${\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{X}}$ is the maximum likelihood, and $\mathrm{k}$ is the number of parameters.

3. Results and Discussion

3.1. Variance Components and Heritability

Table 2. Variance components and heritability estimates for live weight of Angus cattle estimated using different models.

Model	${\mathit{\sigma }}_{\mathit{a}}^2$	${\mathit{\sigma }}_{\mathit{m}}^2$	${\mathit{\sigma }}_{\mathit{a}\mathit{m}}$	${\mathit{\sigma }}_{\mathit{c}}^2$	${\mathit{\sigma }}_{\mathit{e}}^2$	${\mathit{\sigma }}_{\mathit{p}}^2$	${\mathit{h}}_{\mathit{a}}^2$	${\mathit{h}}_{\mathit{m}}^2$	${\mathit{C}}^2$	${\mathit{h}}_{\mathit{e}}^2$	${\mathit{h}}_{\mathit{T}}^2$	ram
BW0
1	11.001				7.885	18.886	0.582 ± 0.017			0.418 ± 0.017	0.582 ± 0.012
2	8.134			3.322	6.988	18.444	0.441 ± 0.014		0.180 ± 0.013	0.379 ± 0.015	0.441 ± 0.012
3	8.123	3.284			7.064	18.472	0.440 ± 0.018	0.178 ± 0.009		0.382 ± 0.016	0.529 ± 0.016
4	12.709	8.241	−8.524		6.373	18.798	0.676 ± 0.014	0.438 ± 0.015		0.339 ± 0.011	0.215 ± 0.007	−0.969
5	8.071	0.945		2.427	6.995	18.438	0.438 ± 0.011	0.051 ± 0.019	0.132 ± 0.015	0.379 ± 0.015	0.463 ± 0.015
6	12.709	8.241	−8.524	0.000	6.373	18.798	0.676 ± 0.013	0.438 ± 0.015	0.000 ± 0.000	0.339 ± 0.010	0.215 ± 0.007	−0.969
BW3
1	123.588				164.726	288.314	0.429 ± 0.019			0.571 ± 0.022	0.429 ± 0.030
2	125.259			0.000	162.658	287.917	0.435 ± 0.021		0.000 ± 0.000	0.565 ± 0.030	0.435 ± 0.028
3	121.886	4.959			160.649	287.495	0.424 ± 0.021	0.017 ± 0.017		0.559 ± 0.025	0.433 ± 0.024
4	307.850	108.600	−167.986		175.822	424.286	0.726 ± 0.027	0.256 ± 0.022		0.414 ± 0.026	0.340 ± 0.021	−0.919
5	121.886	4.959		0.000	160.649	287.495	0.424 ± 0.024	0.017 ± 0.019	0.000 ± 0.000	0.559 ± 0.026	0.433 ± 0.024
6	307.850	108.600	−167.986	0.000	175.822	424.286	0.726 ± 0.027	0.256 ± 0.025	0.000 ± 0.000	0.414 ± 0.023	0.340 ± 0.020	−0.919
BW6
1	91.406				261.656	353.062	0.259 ± 0.042			0.741 ± 0.056	0.259 ± 0.0
2	95.452			0.000	256.893	352.345	0.271 ± 0.045		0.000 ± 0.000	0.729 ± 0.051	0.271 ± 0.0
3	95.452	0.000			256.893	352.345	0.271 ± 0.044	0.000 ± 0.000		0.729 ± 0.063	0.271 ± 0.0
4	247.984	71.223	−128.721		187.660	378.146	0.656 ± 0.051	0.188 ± 0.028		0.496 ± 0.043	0.239 ± 0.035	−0.917
5	95.452	0.000		0.000	256.893	352.345	0.271 ± 0.047	0.000 ± 0.000	0.000 ± 0.000	0.729 ± 0.050	0.271 ± 0.048
6	247.984	71.223	−128.721	0.000	187.660	378.146	0.656 ± 0.051	0.188 ± 0.028	0.000 ± 0.000	0.496 ± 0.043	0.239 ± 0.057	−0.917
BW12
1	785.542				1029.232	1814.774	0.433 ± 0.066			0.567 ± 0.055	0.433 ± 0.039
2	785.542			0.000	1029.231	1814.774	0.433 ± 0.054		0.000 ± 0.000	0.567 ± 0.050	0.433 ± 0.061
3	766.657	41.628			1005.516	1813.801	0.423 ± 0.039	0.023 ± 0.019		0.554 ± 0.043	0.434 ± 0.072
4	1293.711	248.986	−491.143		831.320	1882.873	0.687 ± 0.064	0.105 ± 0.025		0.350 ± 0.062	0.362 ± 0.044	−0.865
5	766.657	41.628		0.000	1005.516	1813.801	0.423 ± 0.078	0.023 ± 0.044	0.000 ± 0.000	0.554 ± 0.082	0.434 ± 0.058
6	1293.711	248.986	−491.143	0.000	831.320	1882.873	0.687 ± 0.059	0.132 ± 0.052	0.000 ± 0.000	0.442 ± 0.049	0.362 ± 0.046	−0.865
BW18
1	1371.163				2481.217	3852.380	0.356 ± 0.059			0.644 ± 0.044	0.356 ± 0.067
2	1324.442			1.273	2473.359	3799.075	0.349 ± 0.061		0.000 ± 0.000	0.651 ± 0.058	0.349 ± 0.082
3	1364.411	0.000			2481.941	3846.352	0.355 ± 0.056	0.000 ± 0.000		0.645 ± 0.043	0.355 ± 0.075
4	2069.838	526.834	−957.769		2341.229	3980.132	0.419 ± 0.042	0.107 ± 0.017		0.474 ± 0.066	0.225 ± 0.048	−0.833
5	1324.442	0.000		1.273	2473.359	3799.075	0.349 ± 0.034	0.000 ± 0.000	0.000 ± 0.000	0.651 ± 0.044	0.349 ± 0.055
6	2007.014	479.849	−899.738	1.989	2336.090	3925.204	0.511 ± 0.091	0.122 ± 0.025	0.001 ± 0.000	0.595 ± 0.037	0.229 ± 0.063	−0.833

shows the variance components and genetic parameters for each trait estimated by the different single-trait models. The heritability of the traits estimated by the different models differed. Models 1, 2, 3, and 5 estimated approximately the same heritability of Angus cattle for BW0, BW3, BW6, BW12, and BW18. However, when the covariance between individual and maternal additive genetic effects was considered in the models (Models 4 and 6), the direct and maternal heritability estimates for the traits increased, and the total heritability estimates decreased. This may be caused by the negative correlation between maternal genetic effects and direct additive genetic effects. Maternal genetic effects included the intrauterine environment, breast milk, etc. Direct additive genetic effects are more related to the individual’s own growth and development genes. From the point of view of energy resource allocation, there is a balance between the mother’s provision of resources to her offspring and her own other physiological activities. If the mother devotes a large amount of resources to the expression of genes related to her own growth and development (direct additive genetic effects), there may be a relative reduction in the resources that can be allocated to the fetus or young, resulting in a negative correlation. This negative correlation is a relatively common phenomenon in animal breeding [12,13]. Our results show that the inverse relationship between the direct and maternal genetic effects decreases with increasing age, but never disappears. It needs to be fully considered in genetic evaluation and breeding decisions to avoid biased estimation of genetic parameters and unsatisfactory breeding results caused by ignoring this relationship.

The C² at the neonatal stage explained 13.2% to 18.0% of the total phenotypic variation, but the influence of maternal environmental effects on body weight disappeared after weaning, suggesting that maternal uterine space and maternal ability to provide nutrition to the fetus were important determinants of birth weight. In the study by Vargas Jurado et al. [14]. it was similarly found that maternal permanent environment effects had a greater influence on the estimation of genetic parameters of newborn weight. The h_m² represents the maternal genetic component inherited from the mother to the child and represents the ability to be a mother. In our study, σc² for BW18 estimated by Model 6 is 1.989, even though the C² of BW3-BW18 is zero. On the one hand, the variation in data quantity and quality across different growth stages might play a role. BW18 data may have more complex environmental influences or greater measurement errors compared to the earlier weights. As animals age, they are exposed to a wider range of environmental conditions, management practices, and potential health issues, which could introduce more variability captured by the parent permanent environmental effect. On the other hand, the model fitting process and parameter estimation algorithm might also contribute. Model 6, being the most complex model, may have different convergence properties and sensitivity to the data structure at various growth stages. The estimation of σc² for BW18 might reflect the model’s adaptation to the specific characteristics of the later growth phase data.

As the estimates of the genetic parameters varied between models, we looked for the model with the lowest AIC value. The results obtained for the model with the lowest AIC value (Model 4) indicate that there is an influence on weight traits in Angus cattle not only via individual genetic effects but also via maternal genetic effects and covariance between individual and maternal genetic effects (

Table 3. −2lnL values and AIC information standard values for different animal models.

Model	Number of Parameters	BW0		BW3		BW6		BW12		BW18
		−2lnL	AIC	−2lnL	AIC	−2lnL	AIC	−2lnL	AIC	−2lnL	AIC
1	2	12,369.300	12,373.300	12,369.300	12,373.300	17,353.990	17,357.990	17,353.990	17,357.990	20,078.055	20,082.055
2	3	12,369.300	12,375.300	12,369.300	12,375.300	17,154.936	17,160.936	17,154.936	17,160.936	19,628.659	19,634.659
3	3	12,365.441	12,371.441	12,365.441	12,371.441	17,154.936	17,160.936	17,154.936	17,160.936	19,628.738	19,634.738
4	4	12,336.133	12,344.133	12,336.133	12,344.133	17,109.369	17,117.369	17,109.369	17,117.369	19,610.121	19,618.121
5	4	12,365.441	12,373.441	12,365.441	12,373.441	17,154.936	17,162.936	17,154.936	17,162.936	19,628.659	19,636.659
6	5	12,336.133	12,346.133	12,336.133	12,346.133	17,109.369	17,119.369	17,109.369	17,119.369	19,609.962	19,619.962

). The direct heritability values estimated by Model 4 were all high, with values of 0.676 ± 0.014, 0.726 ± 0.027, 0.656 ± 0.051, 0.687 ± 0.064, and 0.419 ± 0.042 for BW0, BW3, BW6, BW12, and BW18, respectively. Heritability is strongly influenced by population and environmental factors, and although different breeds, growing environments, feeding management programs, and fitted models can lead to biases in heritability estimates, general comparisons can still be made. Goshu [15] estimated the direct and maternal heritability for Horro cattle BW12 at 0.77 ± 0.12 and 0.26 ± 0.09, respectively, using a model that included direct and maternal genetic effects covariates. Rumph et al. [8] estimated a direct heritability of 0.79 ± 0.08 and 0.75 ± 0.08 for Hereford cattle weaning weight and pre-breeding weight, respectively, taking into account direct and maternal genetic effects and their permanent environmental effects in their model. Costa et al. [16] estimated a heritability of 0.44 ± 0.11 and 0.43 ± 0.07 for Angus cattle weaning weight and BW12, respectively, using the same model as this study. Estrada-León et al. [17] estimated the direct heritability of BW0 and weaning weight in Brahman cattle to be 0.41 ± 0.09 and 0.43 ± 0.09, respectively. Normally, a heritability above 0.4 is considered high heritability, 0.2 to 0.4 is medium heritability, and below 0.2 is low heritability [18]. These findings are in agreement with the results of this study that beef cattle weight is a highly heritable trait.

The total heritability of BW0, BW3, BW6, BW12, and BW18 estimated by Model 4 with the lowest AIC values was 0.215 ± 0.007, 0.340 ± 0.021, 0.239 ± 0.035, 0.362 ± 0.044, and 0.225 ± 0.048, respectively. Next, we compared the results with other studies. Estrada-León et al. [17] reported total heritability estimates of BW0 and weaning weight for Brahman cattle were 0.33 and 0.30, respectively. The total heritability for the BW0, BW6, BW12, and BW18 of Sahiwal cattle estimated using the Bayesian method was 0.22 ± 0.0052, 0.47 ± 0.0037, 0.30 ± 0.0025, 0.65 ± 0.0021, and 0.65 ± 0.0021, respectively [19]. In addition to this, there is still some direct heritability estimated using simple animal models that are close to the total heritability results of this study. As reported by Lopes et al. [20], the additive direct heritability of weight at 120, 210, 365, and 450 days of age for Nellore cattle was 0.28 ± 0.013, 0.32 ± 0.002, 0.31 ± 0.002, and 0.50 ± 0.026, respectively. Boligon et al. [21] also reported that the heritability estimates of BW3 and BW12 were 0.33 ± 0.02 and 0.37 ± 0.03 in Nellore cattle. Vargas et al. [22] estimated a direct heritability of 0.25 ± 0.05, 0.13 ± 0.04, 0.17 ± 0.05, and 0.28 ± 0.06 for Brahman cattle weight at 120, 210, 365, and 550 days of age, respectively. In summary, it can be seen that our findings are basically consistent with those of other studies, but there are differences with some of them. We analyzed in depth the possible factors of differences between different studies, including the methods of data collection, the characteristics and sizes of the samples, the modeling and computational methods, the environmental conditions to which the animals were exposed, and many other aspects. Given the considerable covariance between direct and maternal genetic effects in this study, resulting in an overestimation of direct heritability, we recommend using total heritability for the selection of Angus cattle. Eler et al. [23] also concluded that when there is a high negative correlation between direct and maternal, the economic response to long-term selection by considering direct and maternal covariates is greater than selection based on direct genetic effects alone. This not only reduces bias in the estimation of genetic parameters but also leads to more accurate genetic assessment and prediction of the expected genetic gain in body weight at each stage.

In our study, the maternal heritability estimated using the best model for BW0, BW3, BW6, BW12, and BW18 was 0.438 ± 0.015, 0.256 ± 0.022, 0.188 ± 0.028, 0.105 ± 0.025, and 0.107 ± 0.017, respectively, significantly affecting Angus cattle throughout their growth and development, but the contribution of maternal genetic variation to total phenotypic variation steadily decreased post-weaning. For maternal heritability, Lopes et al. [20] found a considerable effect on body weight from 120 to 450 days of age (0.25~0.32). Herrera-Ojeda et al. and Fitzmaurice et al. [24,25] found similar results to ours, with an effect of maternal heritability on both pre- and post-weaning body weight, and this effect decreases progressively with age from 0.31 for BW0 to 0.14 for BW12. These studies all emphasize the importance of maternal genetic effects in the growth of animals. Therefore, maternal genetic effects should not be ignored when analyzing body weight data.

3.2. Genetic and Phenotypic Correlations

Positive correlations were found between body weights at different months of age (

Table 4. Genetic correlations ± standard errors (above diagonal) and phenotypic correlations ± standard errors (below diagonal) between the body weight at different age classes in Angus cattle.

Traits	BW0	BW3	BW6	BW12	BW18
BW0		0.110 ± 0.062	0.061 ± 0.049	0.113 ± 0.030	0.160 ± 0.043
BW3	0.165 ± 0.057		0.417 ± 0.038	0.688 ± 0.041	0.704 ± 0.029
BW6	0.029 ± 0.028	0.337 ± 0.048		0.504 ± 0.026	0.828 ± 0.033
BW12	0.074 ± 0.035	0.396 ± 0.034	0.598 ± 0.062		0.785 ± 0.025
BW18	0.136 ± 0.017	0.499 ± 0.022	0.552 ± 0.020	0.755 ± 0.032

), but the lowest genetic and phenotypic correlations were found between BW0 and other months of age, with genetic correlations ranging from 0.061 to 0.160 and phenotypic correlations ranging from 0.029 to 0.165. Kamprasert et al. [26] also found a low correlation between BW0 and the weight measured at other ages. Bertipaglia et al. [27] estimated correlations ranging from −0.06 to 0.42 between 60 and 550 days of age for body weight. It is evident that the choice of initial weight has a small effect on later weight. The genetic and phenotypic correlations between weight traits ranged from low to high with increasing age and had the same pattern. For example, the genetic correlation between BW3 and BW6, BW12, and BW18 ranged from 0.417 to 0.704; the correlation between BW6 and BW12 and BW18 was 0.504 and 0.828, respectively; and the correlation between BW12 and BW18 was 0.785. The highly positive genetic and phenotypic correlations between body weight at 120–550 days of age reported by Vargas et al. [22] support our findings. In previous studies, researchers have observed similar genetic and phenotypic correlations using multivariate analysis [16,28]. The growth of beef cattle is a continuous process, and theoretically, early body weight has some influence on later body weight on a genetic basis. However, many studies, including the present study, found that although early body weight was positively correlated with late body weight, the correlation was low. The reason for this may be analyzed as the different rates and patterns of body weight growth in different stages of beef cattle. In the early stage of growth, the rate of body weight growth is faster, and the correlation may be low because of the large differences in body weight between stages. In contrast, in the later stages of growth, body weight growth gradually leveled off, and the relative relationship between body weights at each stage was more stable, and the correlation was higher.

3.3. Regression Model for Early Growth Live Weight to Predict Late Growth Live Weight

To enable the possibility of the early selection of Angus cattle, we use early growth stage weights to predict weights at the later growth stage.

Table 5. Regression model for early live weights of Angus cattle to predict later live weights.

Predicted Traits	Model	Regression Equation	Determination Coefficient
BW18	1: BW0	Y = −256.495 + 25.092BW0	0.630
	2: BW3	Y = 72.509 + 3.631BW3	0.596
	3: BW6	Y = −117.452 + 3.348BW6	0.797
	4: BW12	Y = −1.415 + 1.585BW12	0.746
	5: BW0 + BW3	Y = −251.826 + 16.293BW0 + 2.167BW3	0.765
	6: BW0 + BW3 + BW6	Y = −174.789 + 4.960BW0 + 0.894BW3 + 2.263BW6	0.810
	7: BW0 + BW3 + BW6 + BW12	Y = −187.472 + 4.448BW0 + 1.008BW3 + 2.981BW6−0.371BW12	0.811
	8: BW3 + BW6 + BW12	Y = −141.586 + 0.865BW3 + 3.730BW6−0.472BW12	0.807
	9: BW3 + BW6	Y = −118.011 + 0.693BW3 + 2.902BW6	0.804
	10: BW6 + BW12	Y = −125.403 + 3.667BW6−0.160BW12	0.797
BW12	1: BW0	Y = −102.988 + 13.966BW0	0.657
	2: BW3	Y = 65.309 + 2.141BW3	0.697
	3: BW6	Y = −49.663 + 1.989BW6	0.947
	5: BW0 + BW3	Y = −99.984 + 8.303BW0 + 1.394BW3	0.844
	7: BW0 + BW3 + BW6	Y = −34.163−1.379BW0 + 0.307BW3 + 1.933BW6	0.955
	9: BW3 + BW6	Y = −34.045 + 5.008BW3 + 0.562BW6	0.876

shows the different linear regression models for predicting BW18 and BW12. The coefficient of determination R² was used to test the predictive effect of the models. For BW18, we observed that both regression Model 6 (R² = 0.810) and regression Model 7 (R² = 0.811) were highly predictive, and, given the early selection, we chose regression Model 6 as the predictive model for live weight at 18 months of age. For BW12, regression Models 3, 5, 7, and 9 all had high predictability (R² ≥ 0.844), with predictor BW6 explaining 94.7% of the variability in BW12. Therefore, we considered Model 3 as the best model for predicting BW12 in Angus cattle. In summary, BW6 is a critical predictor of late body weight. Therefore, indirect selection for optimal later growth can be achieved by selecting a higher 6-month live weight. In this study, we comprehensively analyzed the genetic parameters of different growth stages of Angus cattle. The results showed that BW6 has a high positive genetic correlation with later age weights, which makes BW6 an effective early selection indicator. Considering the total heritability of BW6 is 0.239 ± 0.035, even though it is lower than BW3 and BW12, its high genetic correlation with later age weights makes it a crucial indicator for predicting later growth performance. Additionally, from an economic perspective, selecting BW6 as an early selection indicator can effectively shorten the rearing cycle and reduce costs without affecting long-term genetic progress. Thus, we recommend incorporating BW6 as one of the key selection indicators in practical breeding programs to effectively predict and select for the later growth performance of Angus cattle.

4. Conclusions

The aim of this study was to improve the breeding program for Angus cattle. Six animal models were evaluated using the AI-REML method, and the best model was selected. It was found that maternal genetic effects had a significant influence on assessing body weight in Angus cattle and that this effect diminished with increasing age. The total heritability derived from the best model (Model 4) was 0.215 ± 0.007 for BW0, 0.340 ± 0.021 for BW3, 0.239 ± 0.035 for BW6, 0.362 ± 0.044 for BW12, and 0.225 ± 0.048 for BW18. It was also found that there was a positive correlation between body weights at different stages. The regression model for prediction of later body weights by body weights at early growth stages showed that BW6 had the highest R² value (0.947) in predicting body weights at 12 months of age (BW12), whereas the combined model (which consisted of BW0, BW3, and BW6) demonstrated a higher predictive ability (R² = 0.811). These findings will assist in the early selection and optimization of breeding programs for Angus cattle by facilitating a more accurate genetic evaluation and prediction of the expected genetic gain.