Critical Flow Velocity Analysis of Multi-Span Viscoelastic Micro-Bending Irrigation Pipelines
Abstract
1. Introduction
2. Materials and Methods
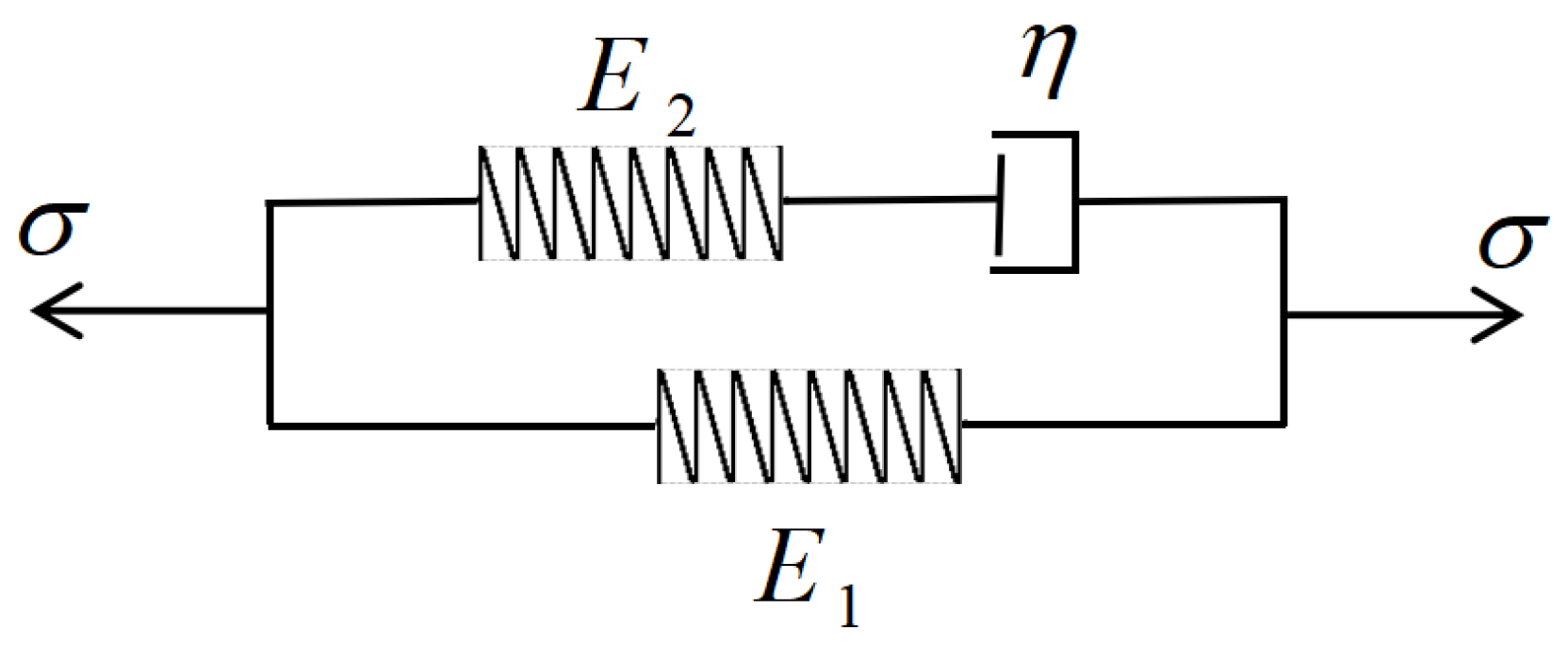
2.1. Viscoelastic Model of Pipeline-Wall Material
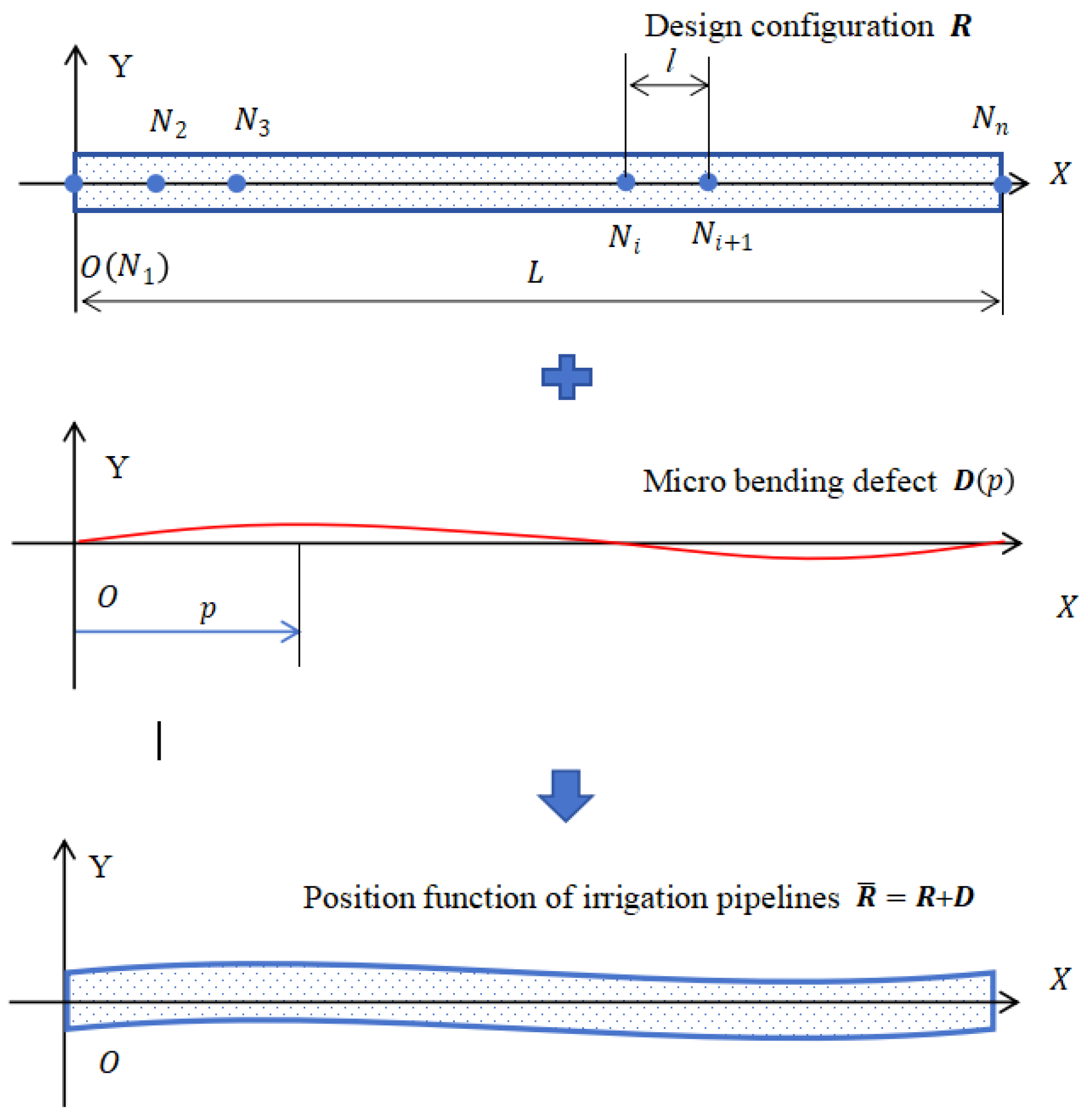
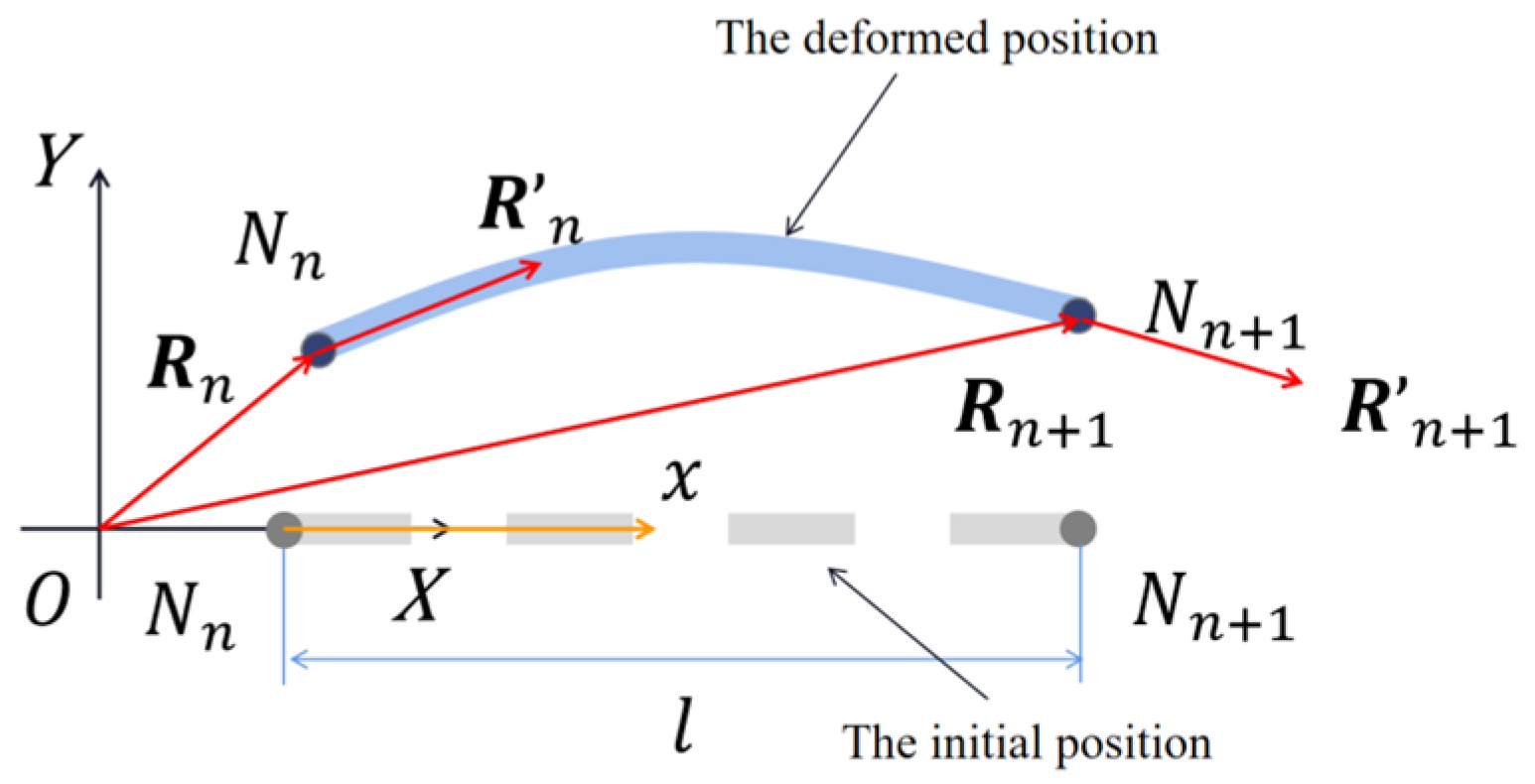
2.2. Dynamic Model of Irrigation Pipeline
2.3. Verification
2.3.1. Theoretical Verification
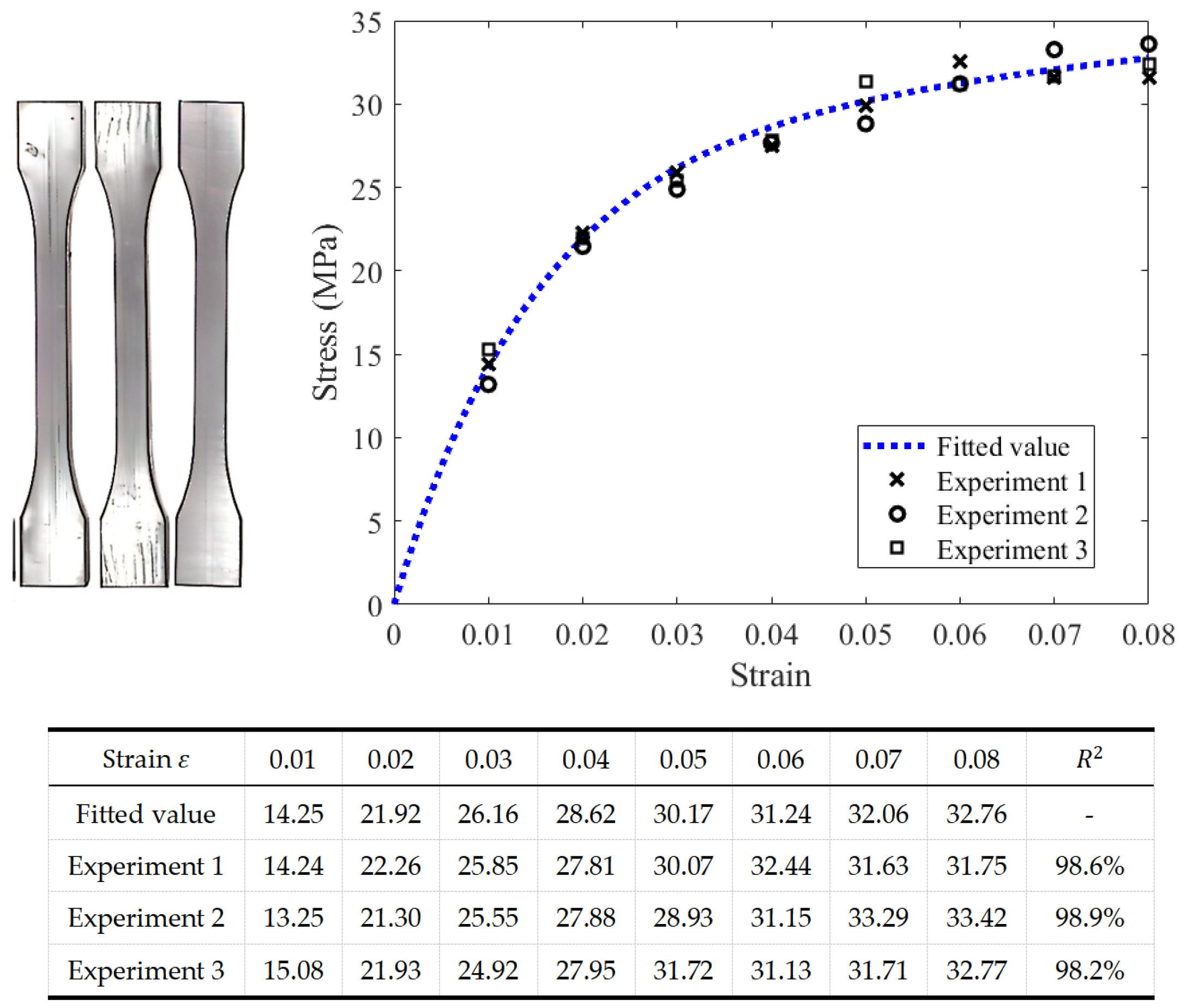
2.3.2. Experimental Verification
3. Stability Analysis and Improvement
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANCF | Absolute Nodal Coordinate Formulation |
Appendix A
References
- Wang, H.; Zhao, J.; Zhang, L.; Yu, S. Application of Disturbance Observer-Based Fast Terminal Sliding Mode Control for Asynchronous Motors in Remote Electrical Conductivity Control of Fertigation Systems. Agriculture 2024, 14, 168. [Google Scholar] [CrossRef]
- Jia, W.; Wei, Z.; Tang, X.; Zhang, Y.; Shen, A. Intelligent control technology and system of on-demand irrigation based on multiobjective optimization. Agronomy 2023, 13, 1907. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Z.; Zhang, J.; Ma, K. Application effect of different oxygenation methods with mulched drip irrigation system in Xinjiang. Agric. Water Manag. 2023, 275, 108024. [Google Scholar] [CrossRef]
- El-Sayed, T.A.; El-Mongy, H.H. Free vibration and stability analysis of a multi-span pipe conveying fluid using exact and variational iteration methods combined with transfer matrix method. Appl. Math. Model. 2019, 71, 173–193. [Google Scholar] [CrossRef]
- Amabili, M.; Garziera, R. Vibrations of circular cylindrical shells with nonuniform constraints, elastic bed and added mass; Part I: Empty and fluid-filled shells. J. Fluids Struct. 2000, 14, 669–690. [Google Scholar] [CrossRef]
- Pellicano, F.; Amabili, M. Dynamic instability and chaos of empty and fluid-filled circular cylindrical shells under periodic axial loads. J. Sound Vib. 2006, 293, 227–252. [Google Scholar] [CrossRef]
- Tsyss, V.G.; Sergaeva, M.Y. Simulating of the composite cylindrical shell of the pipe of the supply pipelines based on ANSYS package. Procedia Eng. 2016, 152, 332–338. [Google Scholar] [CrossRef][Green Version]
- Lee, U.; Jang, H.I. Go, Stability and dynamic analysis of oil pipelines by using spectral element method. J. Loss Prev. Process Ind. 2009, 22, 873–878. [Google Scholar] [CrossRef]
- Sınır, B.G.; Demir, D.D. The analysis of nonlinear vibrations of a pipe conveying an ideal fluid. Eur. J. Mech. B-Fluids 2015, 52, 38–44. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y. Vibration analysis of conveying fluid pipe via He’s variational iteration method. Appl. Math. Model. 2017, 43, 409–420. [Google Scholar] [CrossRef]
- Chernik, V.V. Analysis of dynamics and controllability of a system described by the equation of a pipeline with a moving fluid. IFAC-PapersOnLine 2018, 51, 156–161. [Google Scholar] [CrossRef]
- Khudayarov, B.A.; Komilova, K.M.; Turaev, F.Z. Numerical study of the effect of viscoelastic properties of the material and bases on vibration fatigue of pipelines conveying pulsating fluid flow. Eng. Fail. Anal. 2020, 115, 104635. [Google Scholar] [CrossRef]
- Nejadi, M.M.; Mohammadimehr, M.; Mehrabi, M. Free vibration and stability analysis of sandwich pipe by considering porosity and graphene platelet effects on conveying fluid flow. Alex. Eng. J. 2021, 60, 1945–1954. [Google Scholar] [CrossRef]
- Sutar, S.; Madabhushi, R.; Chellapilla, K.R.; Poosa, R.B. Determination of natural frequencies of fluid conveying pipes using Muller’s method. J. Inst. Eng. Ser. C 2019, 100, 449–454. [Google Scholar] [CrossRef]
- Sharififard, E.; Azizipour, M.; Ahadiyan, J.; Haghighi, A. Determinatin of creep function coefficients of viscoelastic pipes using a transient-guided machine learning model. AQUA-Water Infrastruct. Ecosyst. Soc. 2024, 73, 2132–2149. [Google Scholar] [CrossRef]
- Azizipour, M.; Sharififard, E.; Haghighi, A.; Ahadiyan, J. Optimization of creep function parameters of viscoelastic pipelines based on transient pressure signal. J. Hydraul. Struct. 2024, 10, 97–114. [Google Scholar] [CrossRef]
- Sinir, B.G. Bifurcation and chaos of slightly curved pipes. Math. Comput. Appl. 2010, 15, 490–502. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Soltani, P. Nonlinear flow-induced vibration of a SWCNT with a geometrical imperfection. Comput. Mater. Sci. 2012, 53, 105–116. [Google Scholar] [CrossRef]
- Zhen, Y.; Gong, Y.; Tang, Y. Nonlinear vibration analysis of a supercritical fluid-conveying pipe made of functionally graded material with initial curvature. Compos. Struct. 2021, 268, 113980. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.; Fan, B.; Yong, X. Vibration characteristics of functionally graded fractional derivative viscoelastic fluid–conveying pipe with initial geometric defects. J. Eng. Mech. 2024, 150, 7419. [Google Scholar] [CrossRef]
- Chupakhin, A.; Mamontov, A.; Vasyutkin, S. Asymptotic representation of vorticity and dissipation energy in the flux problem for the navier–stokes equations in curved pipes. Axioms 2024, 13, 65. [Google Scholar] [CrossRef]
- Li, B.H.; Gao, H.S.; Zhai, H.B.; Liu, Y.S.; Yue, Z.F. Free vibration analysis of multi-span pipe conveying fluid with dynamic stiffness method. Nucl. Eng. Des. 2011, 241, 666–671. [Google Scholar] [CrossRef]
- Sollund, H.A.; Vedeld, K.; Hellesland, J.; Fyrileiv, O. Dynamic response of multi-span offshore pipelines. Mar. Struct. 2014, 39, 174–197. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y. Random vibration response of three-dimensional multi-span hydraulic pipeline system with multipoint base excitations. Thin-Walled Struct. 2014, 166, 108124. [Google Scholar] [CrossRef]
- Xu, W.; Jia, K.; Ma, Y.; Wang, Y.; Song, Z. Multispan classification methods and interaction mechanism of submarine pipelines undergoing vortex-induced vibration. Appl. Ocean Res. 2022, 120, 103027. [Google Scholar] [CrossRef]
- Wen, H.B.; Yang, Y.; Li, Y. Study on the stability of multi-span U-shaped pipe conveying fluid with complex constraints. Int. J. Press. Vessel. Pip. 2023, 203, 104911. [Google Scholar] [CrossRef]
- Oke, W.A.; Khulief, Y.A.; Owolabi, T.O.; Ikumapayi, O.M. Dynamic analysis of a multi-span pipe conveying fluid using wavelet based finite element method. Arab. J. Sci. Eng. 2024, 49, 14663–14682. [Google Scholar] [CrossRef]
- Fan, B.; Wang, Z.M. Vibration analysis of radial tire using the 3D rotating hyperelastic composite REF based on ANCF. Appl. Math. Model. 2024, 126, 206–231. [Google Scholar] [CrossRef]
- Liu, D.; Ai, S.; Sun, L.; Soares, C.G. ALE-ANCF modeling of the lowering process of a J-lay pipeline coupled with dynamic positioning. Ocean Eng. 2023, 269, 113552. [Google Scholar] [CrossRef]
- Yuan, J.R.; Ding, H. Three-dimensional dynamic model of the curved pipe based on the absolute nodal coordinate formulation. Mech. Syst. Signal Process. 2023, 194, 110275. [Google Scholar] [CrossRef]
- Xing, H.; He, Y.; Dai, H.; Wang, L. Design of simply support for fluid-conveying pipe with complex configurations based on absolute node coordinate formulation. Chin. J. Theor. Appl. Mech. 2024, 56, 482–493. (In Chinese) [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Abaei, A.R.; Ilkhani, M.R. Free vibrations of functionally graded viscoelastic cylindrical panel under various boundary conditions. Compos. Struct. 2015, 126, 1–15. [Google Scholar] [CrossRef]
- Irschik, H.; Holl, H.J. The equations of Lagrange written for a non-material volume. Acta Mech. 2002, 153, 231–248. [Google Scholar] [CrossRef]
- Fan, B.; Wang, Z.M.; Wang, Q.B. Nonlinear forced transient response of rotating ring on the elastic foundation by using adaptive ANCF curved beam element. Appl. Math. Model. 2022, 108, 748–769. [Google Scholar] [CrossRef]
- Wu, J.S.; Shih, P.Y. The dynamic analysis of a multispan fluid-conveying pipe subjected to external load. J. Sound Vib. 2001, 239, 201–215. [Google Scholar] [CrossRef]
- Wang, Z.M.; Liu, Y.Z. Transverse vibration of pipe conveying fluid made of functionally graded materials using a symplectic method. Nucl. Eng. Des. 2016, 298, 149–159. [Google Scholar] [CrossRef]







| Name | Symbol | Value | Unit |
|---|---|---|---|
| Density | 960 | kg/m3 | |
| Elastic modulus | 55.7 | MPa | |
| 1869.1 | Mpa | ||
| Damping constant | 284.5 | Mpa·s/m |
| Name | Symbol | Value | Unit |
|---|---|---|---|
| Sectional radius | 26 | mm | |
| 24 | mm | ||
| Length | 2 | m | |
| Flow velocity | 0.2 | m/s |
| Elemental Number | Mode Order | ||
|---|---|---|---|
| 1st | 2nd | 3rd | |
| 5 | 9.59, 9.61 | 26.03, 26.10 | 49.98, 50.21 |
| 10 | 9.01, 9.07 | 24.72, 24.77 | 48.75, 48.97 |
| 15 | 8.94, 8.97 | 23.29, 23.30 | 46.82, 46.83 |
| 20 | 8.94, 8.97 | 23.30, 23.30 | 46.82, 46.83 |
| Model | (m/s) | Mode Order (rad/s) | ||||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | ||
| PM | 0 | 29.44 | 83.31 | 161.80 | 249.92 | 270.55 |
| Model in Ref. [35] | 29.87 | 84.62 | 167.52 | 259.28 | 273.98 | |
| R.E | 1.44% | 1.55% | 3.41% | 3.61% | 1.25% | |
| PM | 20 | 28.88 | 82.28 | 161.44 | 252.77 | 269.61 |
| Model in Ref. [35] | 27.85 | 83.64 | 166.95 | 258.90 | 273.63 | |
| R.E | 4.83% | 1.62% | 3.30% | 2.37% | 1.47% | |
| Name | Symbol | Value | Unit |
|---|---|---|---|
| Sectional radius | 26 × 10−3 | m | |
| 24 × 10−3 | m | ||
| Length | 10 | m | |
| Interval length | 2 | m | |
| Displacement | ∆Q | 8 × 10−4 | m3/s |
| Model | 1st Order | 2nd Order | 3rd Order | |
|---|---|---|---|---|
| Experiment | 2.37 | 6.07 | 12.34 | |
| MBP model | 2.17 | 5.92 | 11.97 | |
| RE | 8.43% | 2.47% | 3.00% | |
| MSP model | 2.13 | 5.84 | 11.88 | |
| 10.01% | 3.79% | 3.72% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Fan, B.; Cao, J.; Xiao, S.; Cao, Y. Critical Flow Velocity Analysis of Multi-Span Viscoelastic Micro-Bending Irrigation Pipelines. Agriculture 2025, 15, 1214. https://doi.org/10.3390/agriculture15111214
Wu S, Fan B, Cao J, Xiao S, Cao Y. Critical Flow Velocity Analysis of Multi-Span Viscoelastic Micro-Bending Irrigation Pipelines. Agriculture. 2025; 15(11):1214. https://doi.org/10.3390/agriculture15111214
Chicago/Turabian StyleWu, Sihao, Bo Fan, Jianhua Cao, Suwei Xiao, and Yuhe Cao. 2025. "Critical Flow Velocity Analysis of Multi-Span Viscoelastic Micro-Bending Irrigation Pipelines" Agriculture 15, no. 11: 1214. https://doi.org/10.3390/agriculture15111214
APA StyleWu, S., Fan, B., Cao, J., Xiao, S., & Cao, Y. (2025). Critical Flow Velocity Analysis of Multi-Span Viscoelastic Micro-Bending Irrigation Pipelines. Agriculture, 15(11), 1214. https://doi.org/10.3390/agriculture15111214





