Surface Reconstruction and Volume Calculation of Grain Pile Based on Point Cloud Information from Multiple Viewpoints
Abstract
1. Introduction
1.1. Grain Silo Management and 3D Grain Pile Reconstruction Technologies
1.2. Challenges in 3D Reconstruction of Grain Piles
1.3. Surface Reconstruction and Volume Calculation Methods for Grain Piles
- Surface continuity enhancement
- 2.
- Balancing measurement efficiency and accuracy
- 3.
- Correction of intersection region misalignment
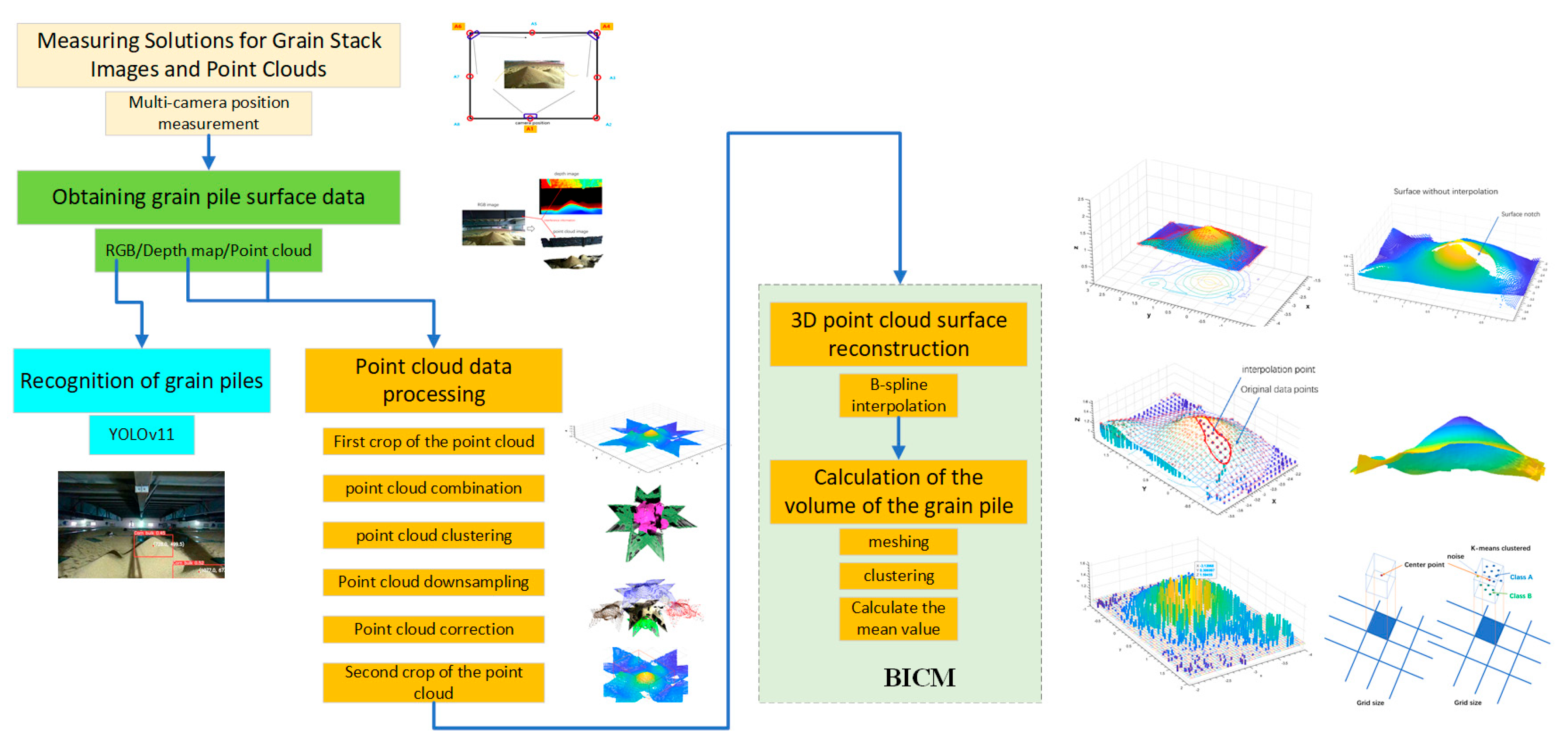
2. Materials and Methods
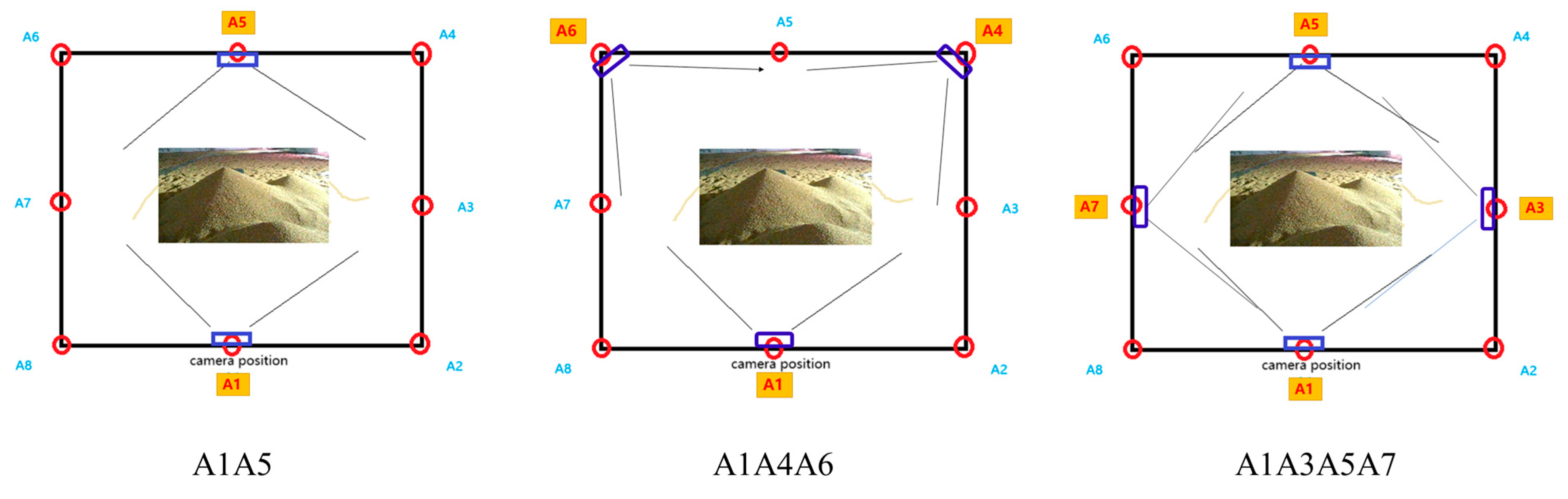
2.1. Measurement Solutions for Images and Point Clouds
2.2. Recognition of Grain Piles
2.3. Processing of 3D Point Cloud Data
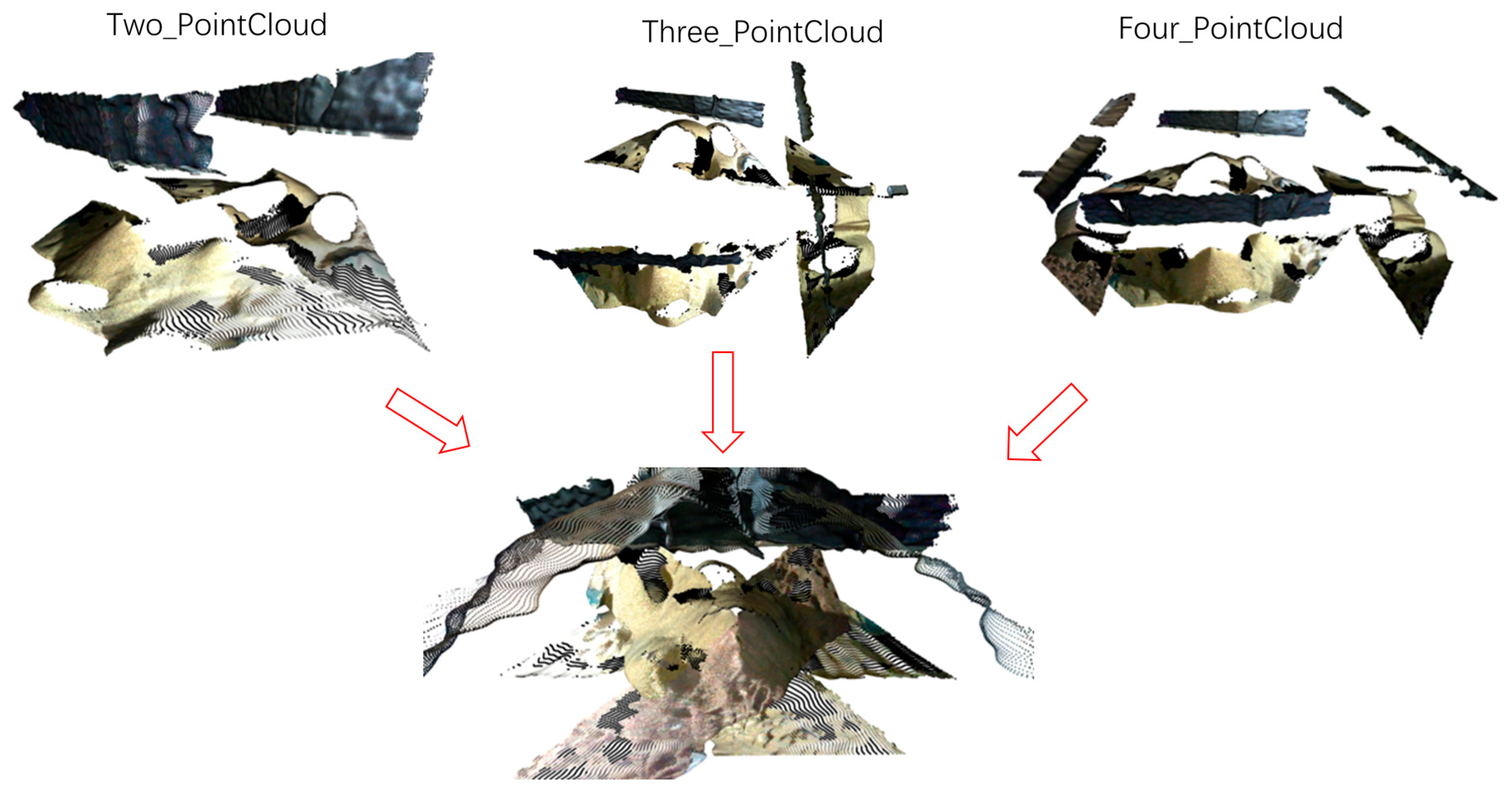
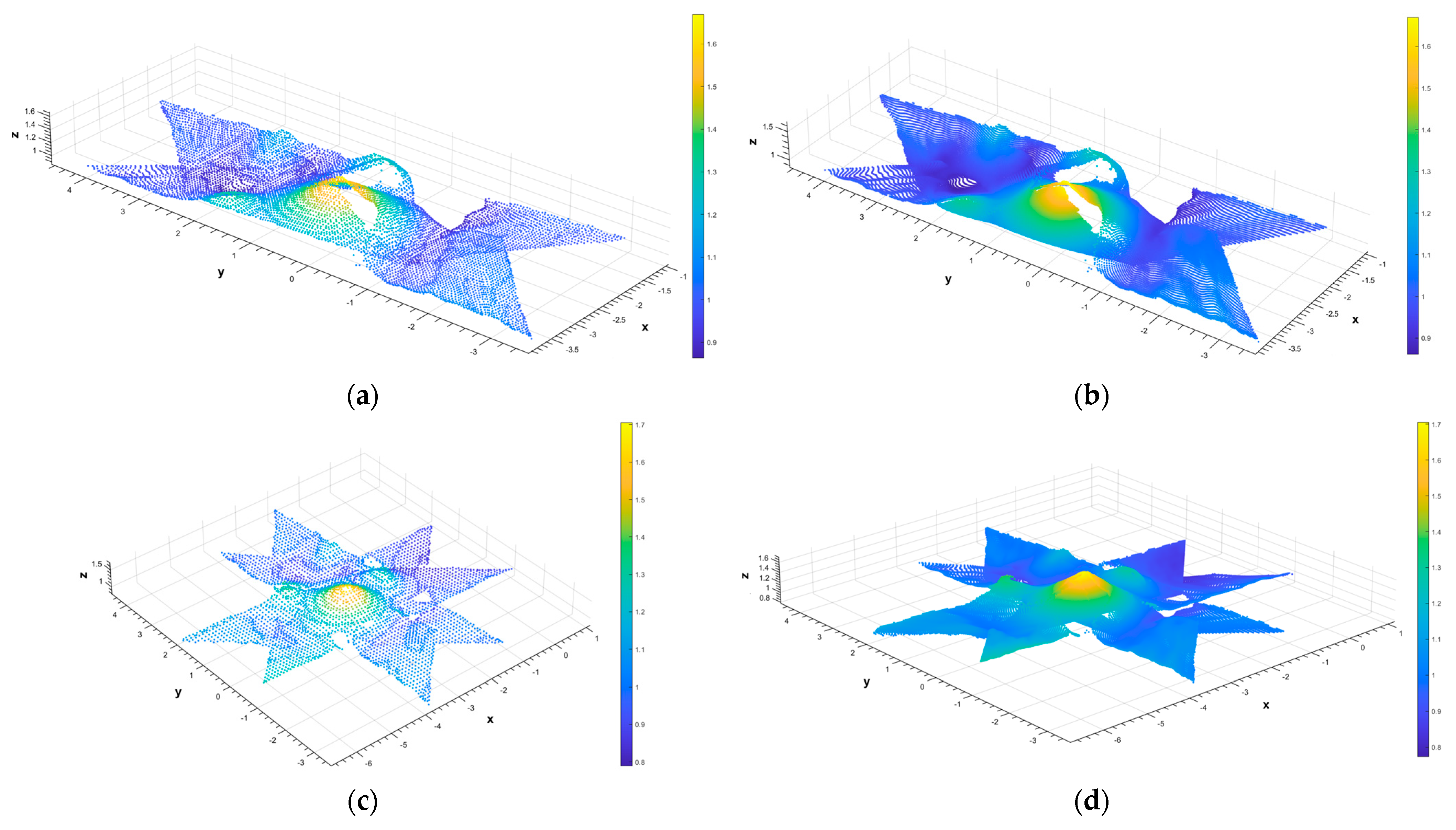
2.3.1. Multi-Angle Point Cloud Combination and Initial Cropping
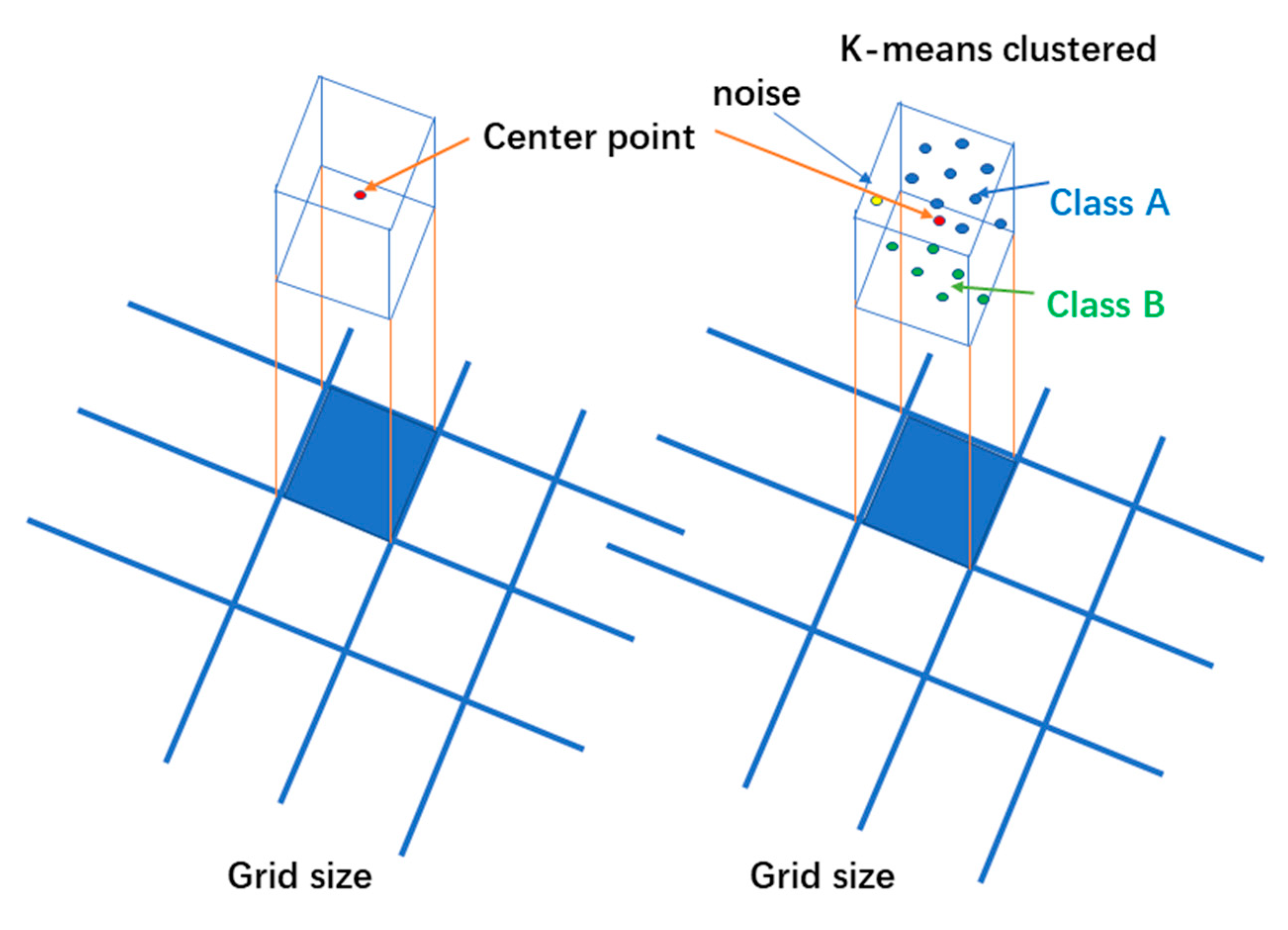
2.3.2. Combined Point Cloud Clustering
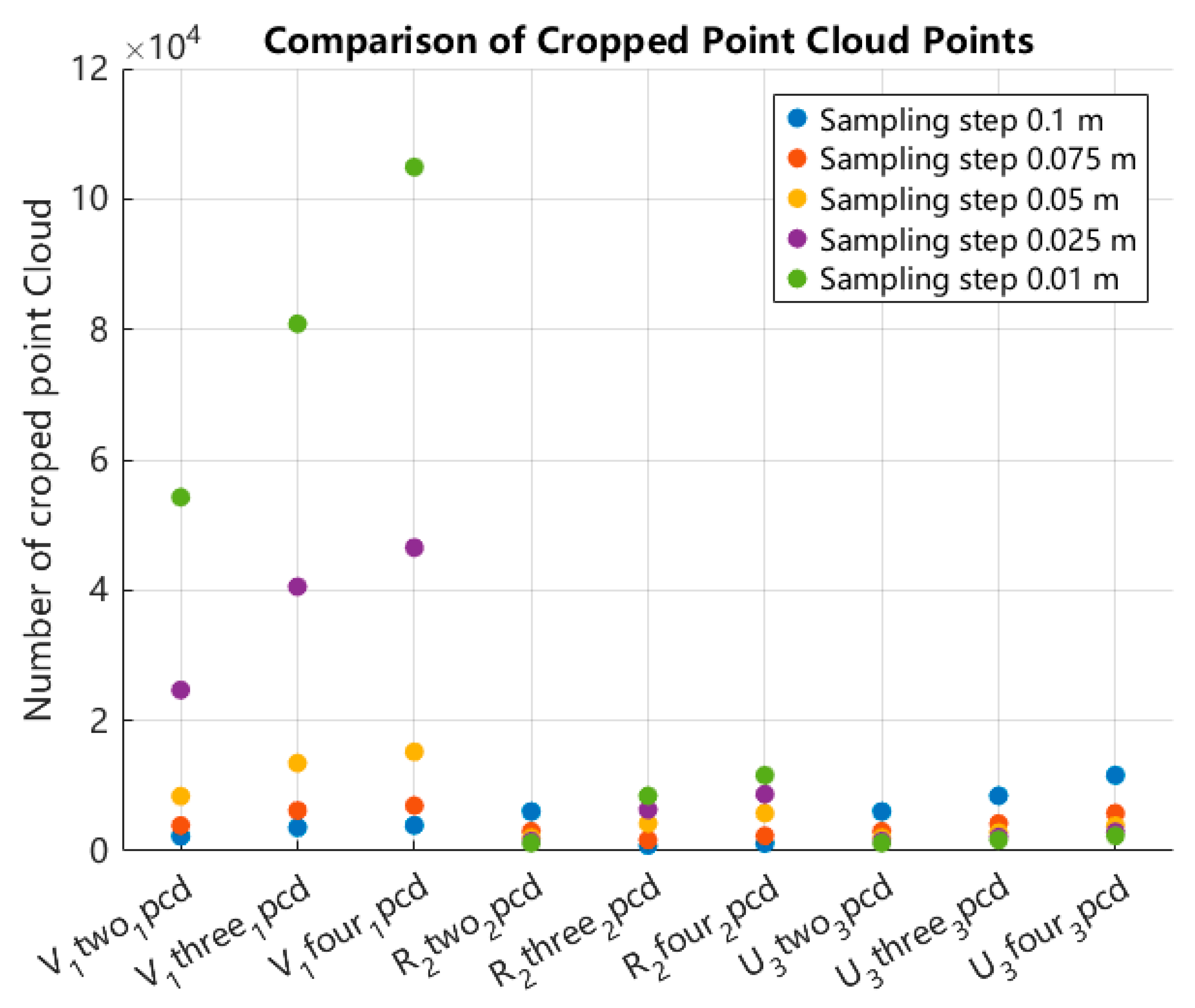
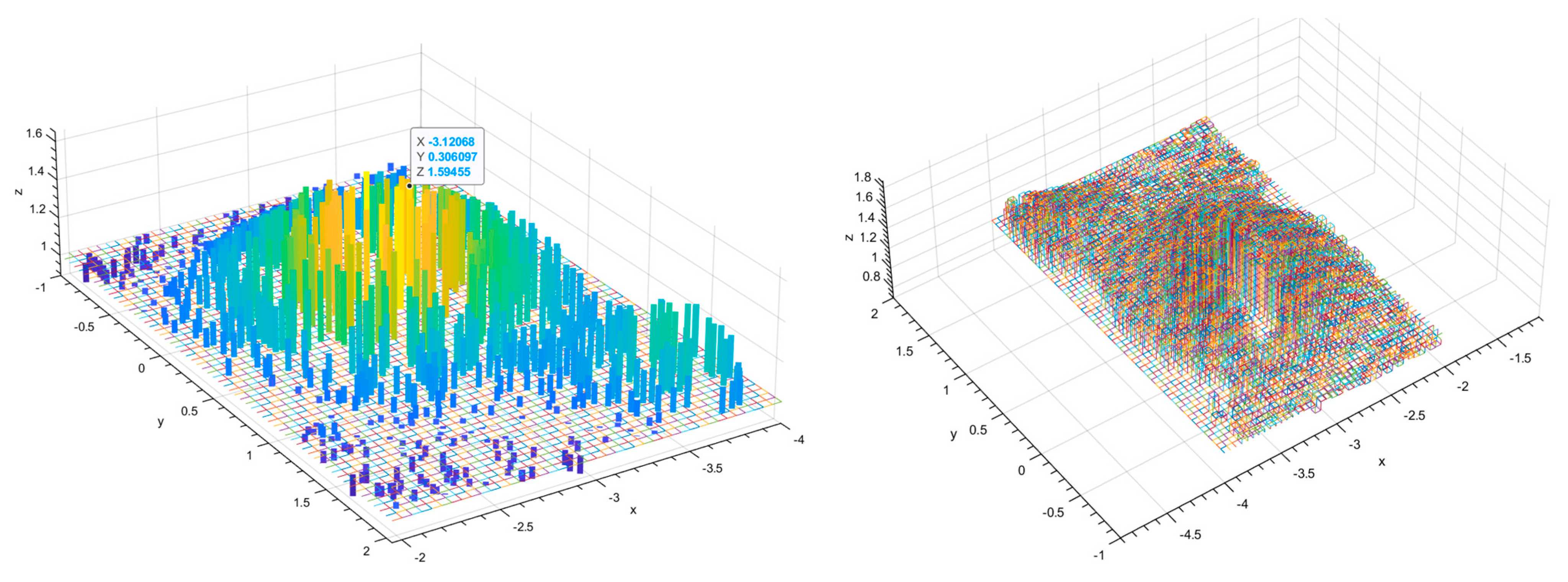
2.3.3. Point Cloud Down-Sampling Processing
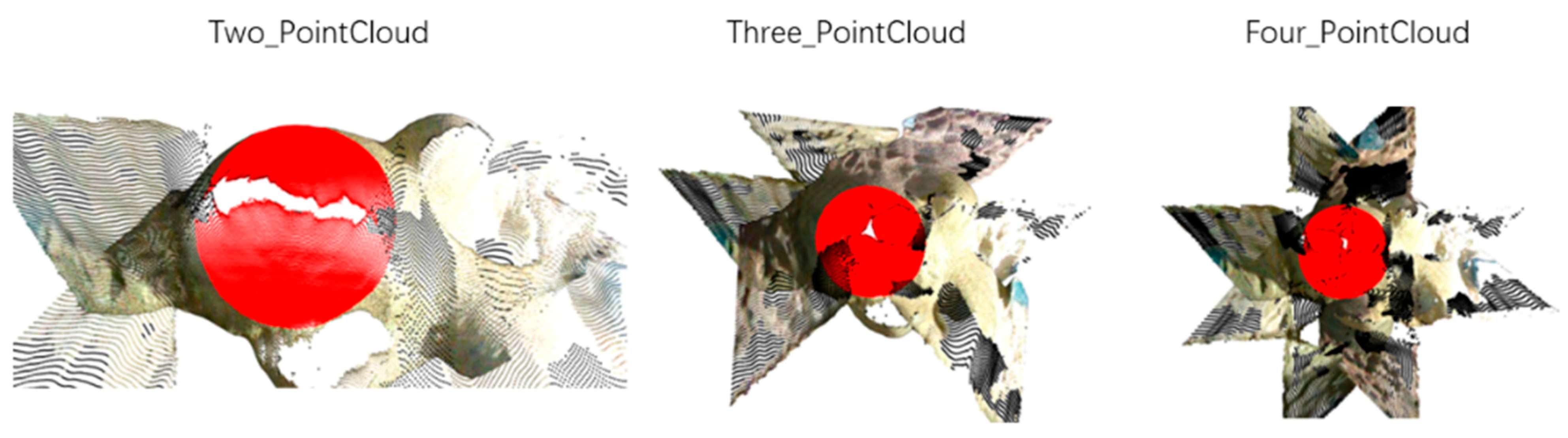
2.3.4. Correction of Point Cloud Position
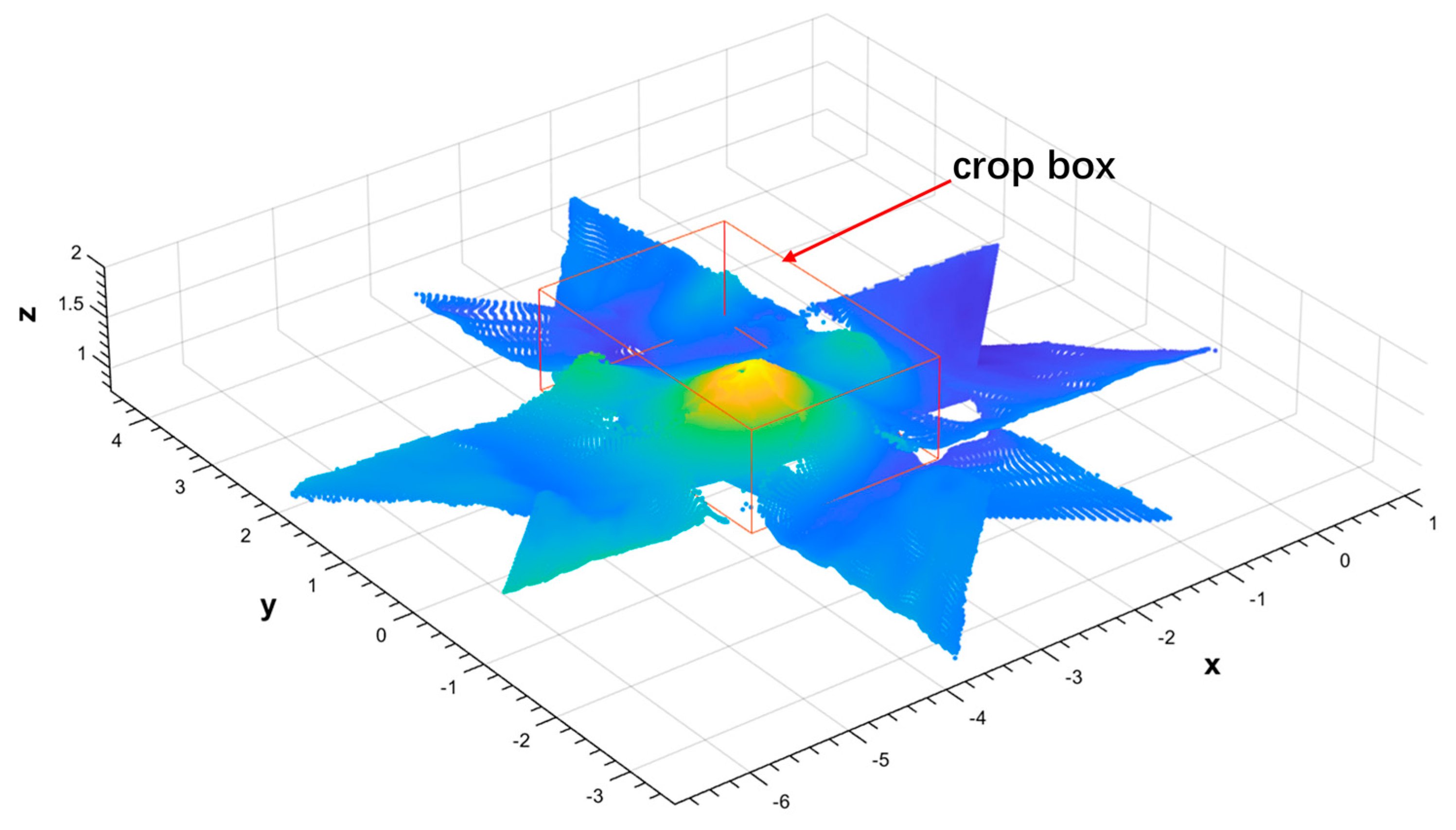
2.3.5. Second Cropping of the Point Cloud
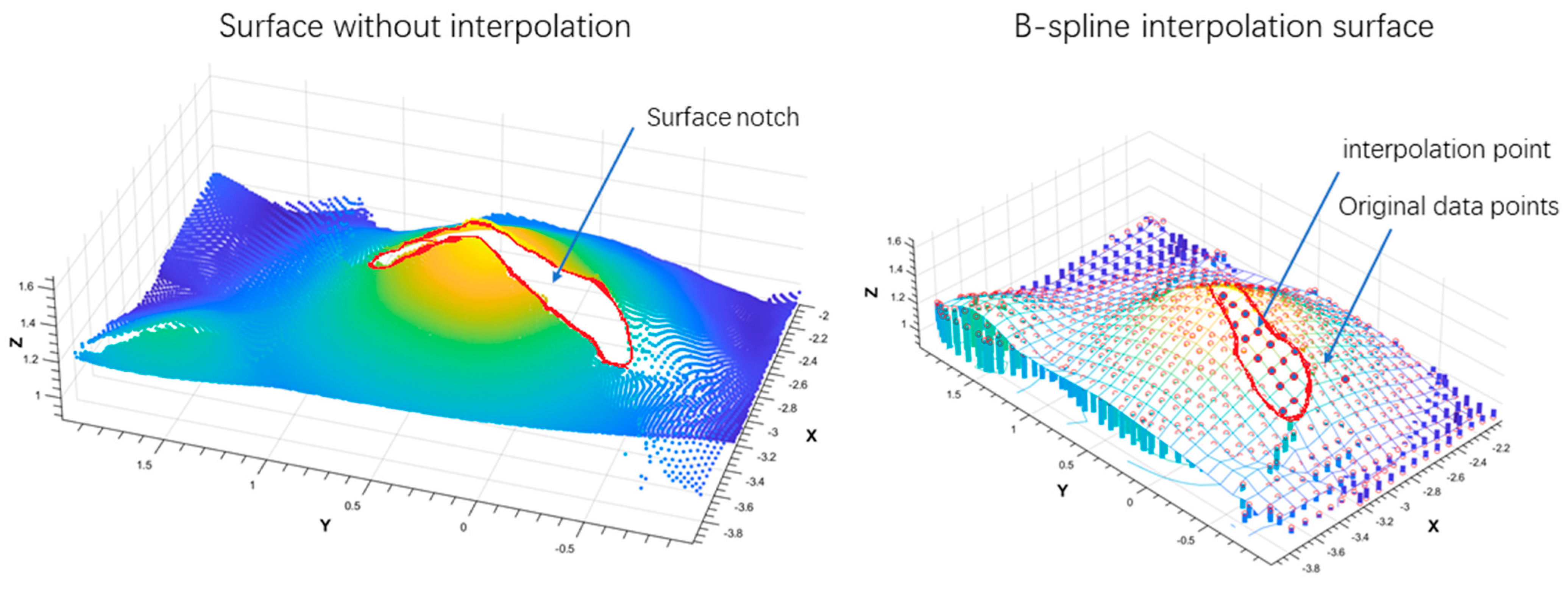
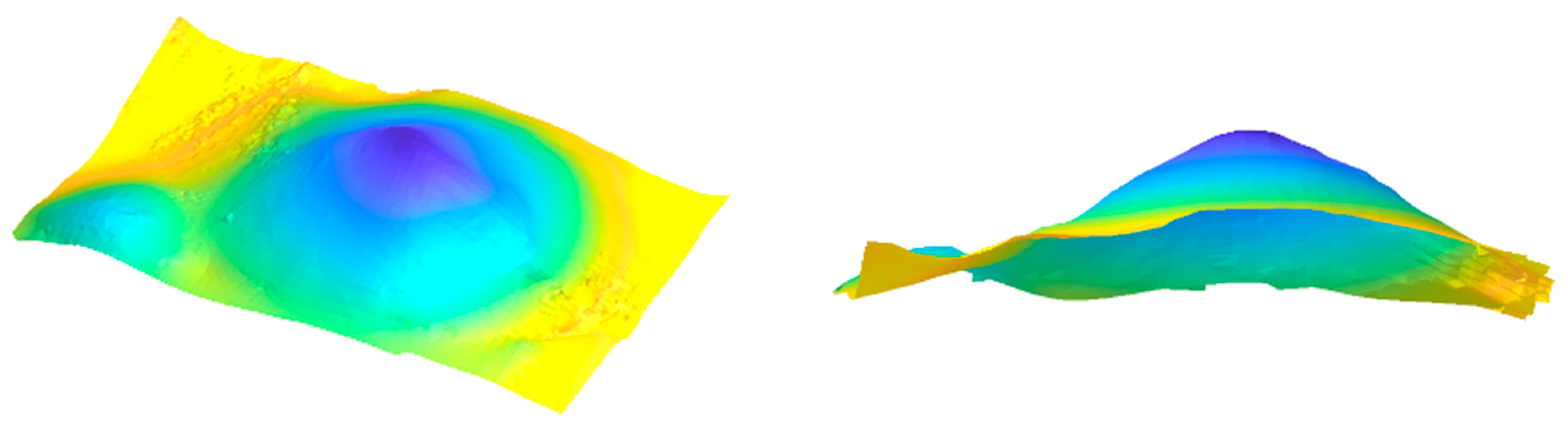
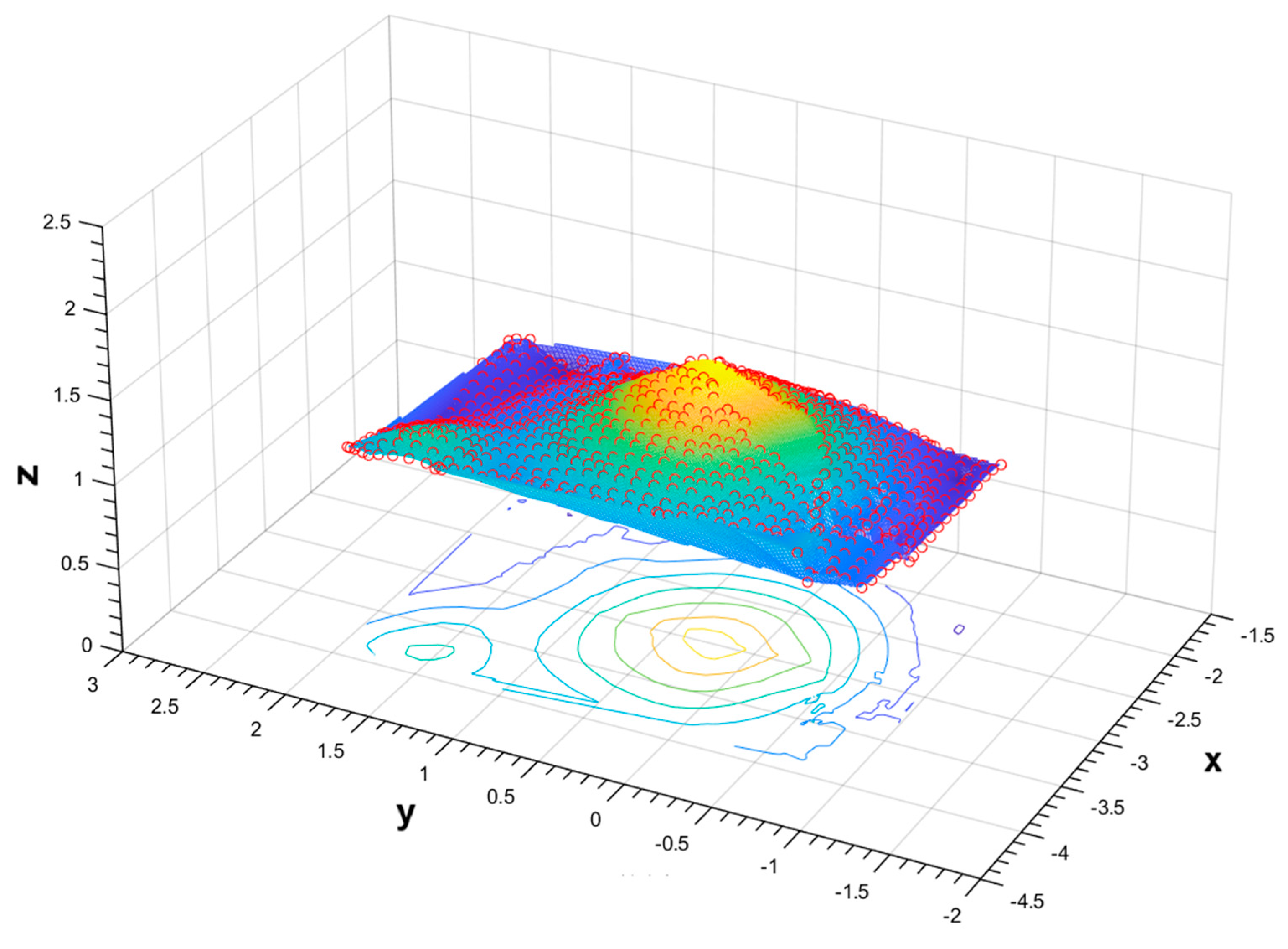
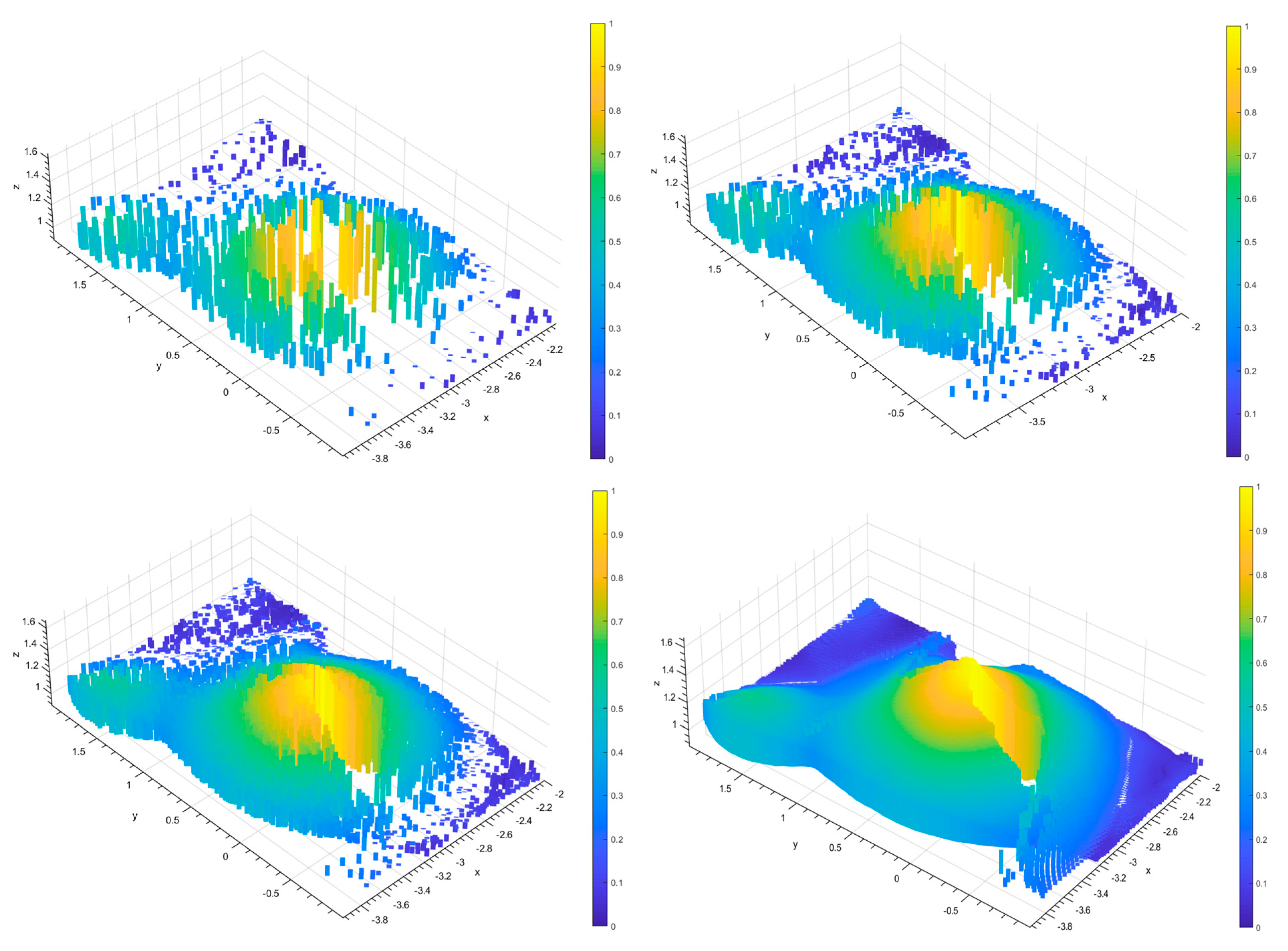
2.3.6. D Surface Reconstruction of Grain Piles
- is a known function value at the grid point ;
- is the ith B-spline basis function in the x direction of order p;
- is the jth B-spline basis function in the y direction of order q.
2.4. Volume Calculation of the Grain Pile
| Algorithm 1: CM(D, ε, MinPts) |
| 1. Initialize all points as unvisited. 2. Create an empty list clusters[] to store clusters. 3. For each point p in D: a. If p is unvisited: i. Mark p as visited. ii. Find all points in N_ε(p). iii. If |N_ε(p)| < MinPts: Mark P as noise (outlier). iv. Else: Create a new cluster C. Add p to C. Expand C with all points in N_ε(p). For each point q in N_ε(p), if q is a core point, expand the cluster recursively. 4. If the number of clusters > 2: cluster = sort (clusters) cluster = clusters[0 1] 5. If the number of clusters <= 2: a. For each cluster C: Calculate the centroid (mean position) of the cluster: i. centroid_C = (1/|C|) ∗ Σ (x_i, y_i) for all points (x_i, y_i) in C. ii. Assign the centroid_C as the representative position of the cluster. 6. Return all clusters and their centroids. |
3. Results
4. Discussion
5. Conclusions
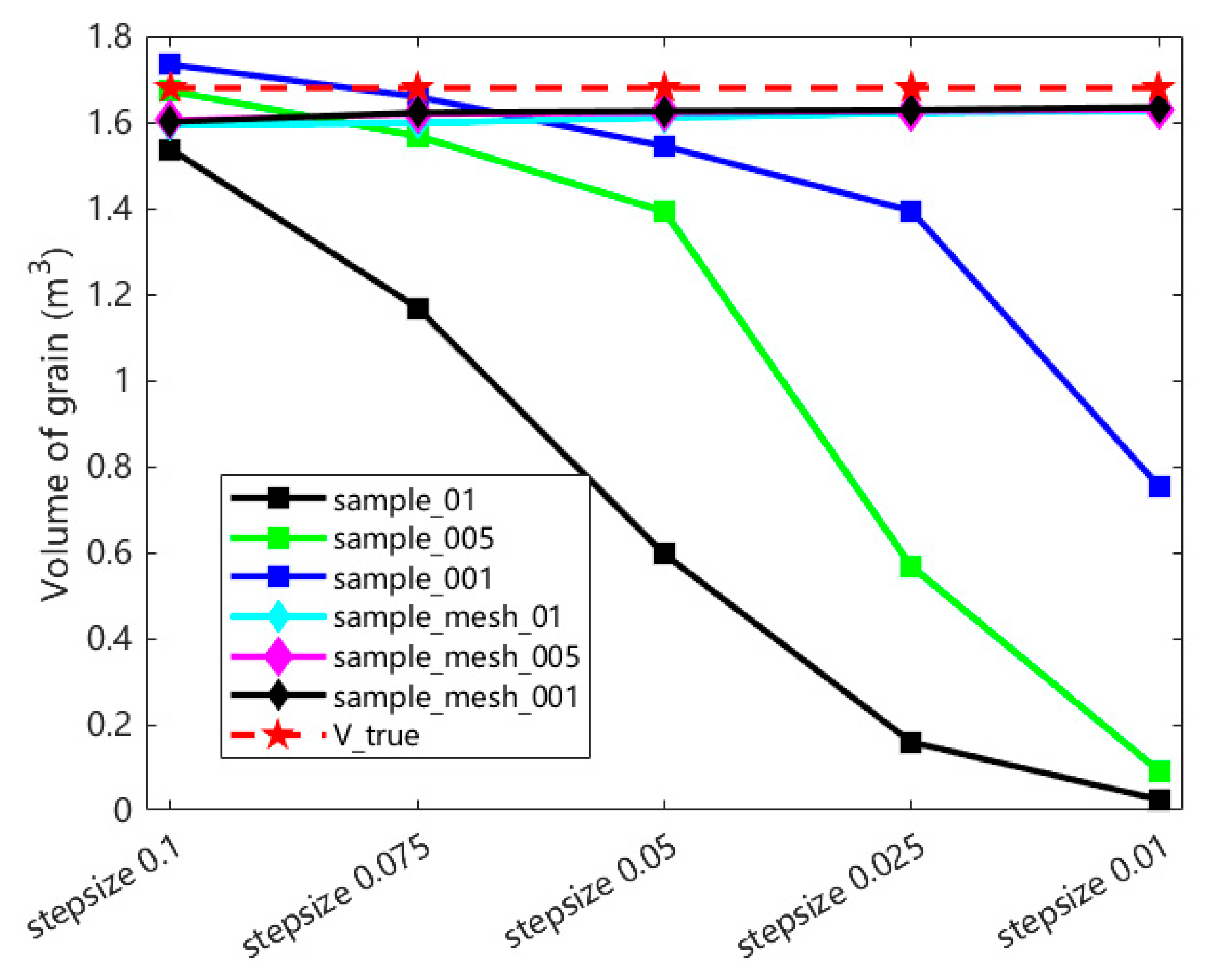
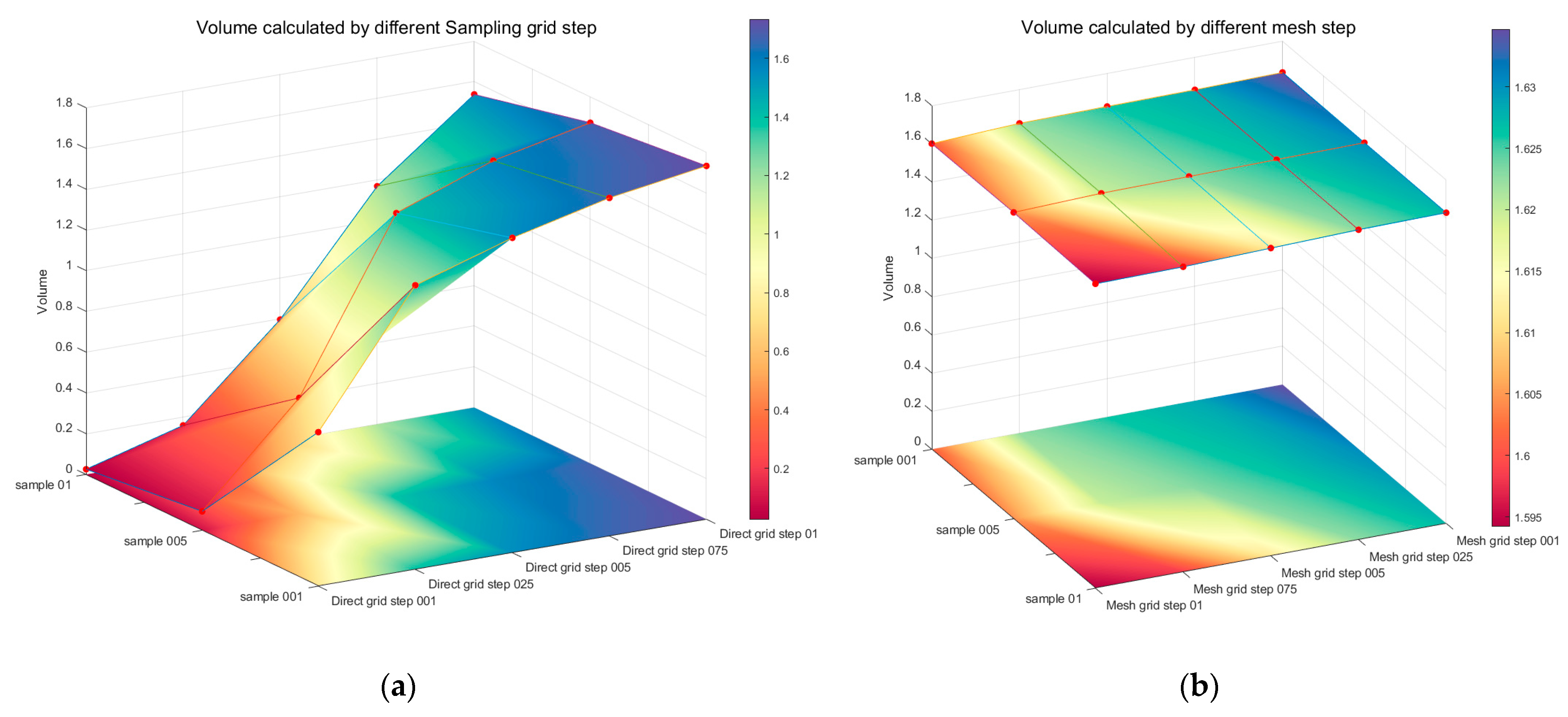
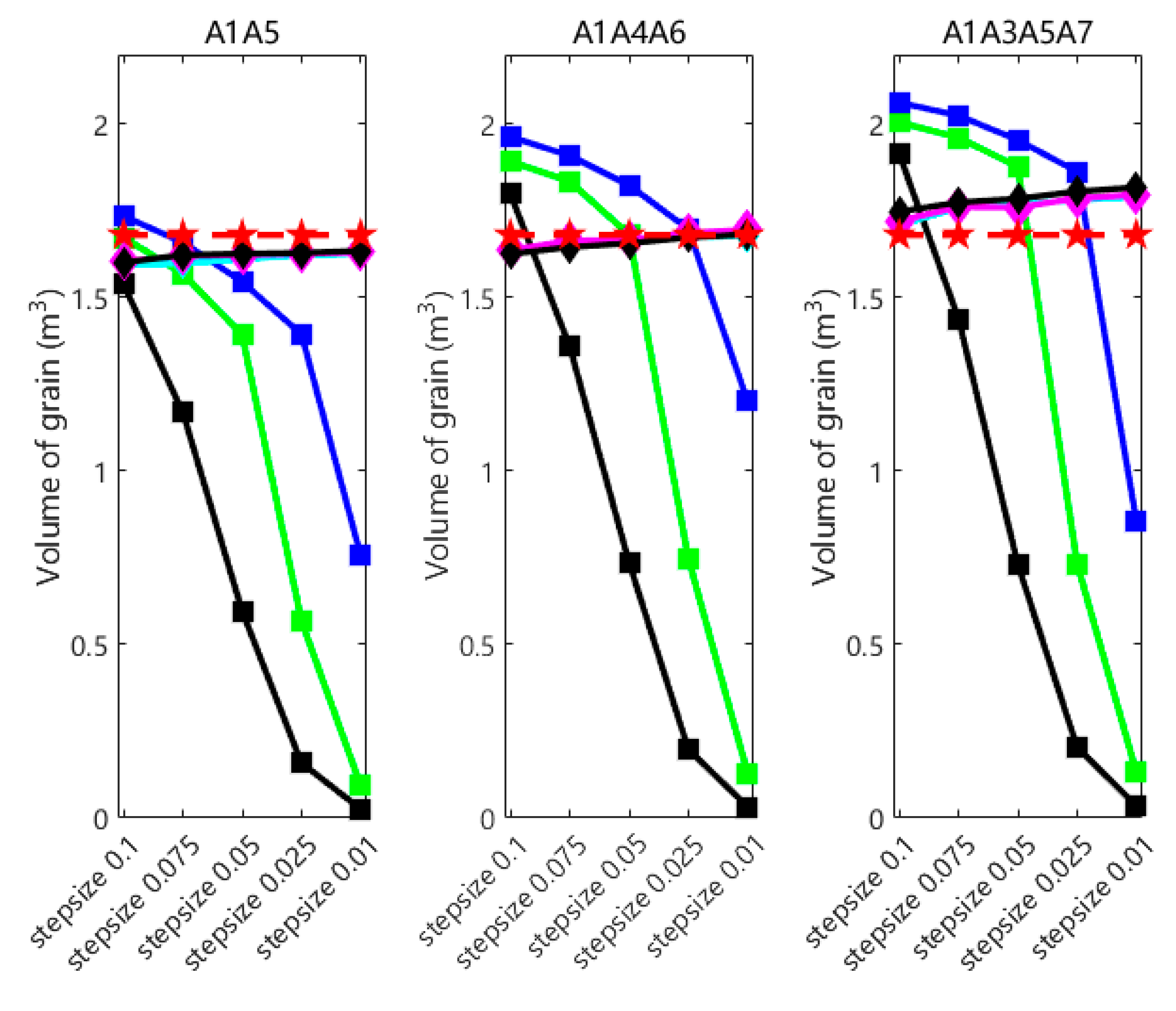
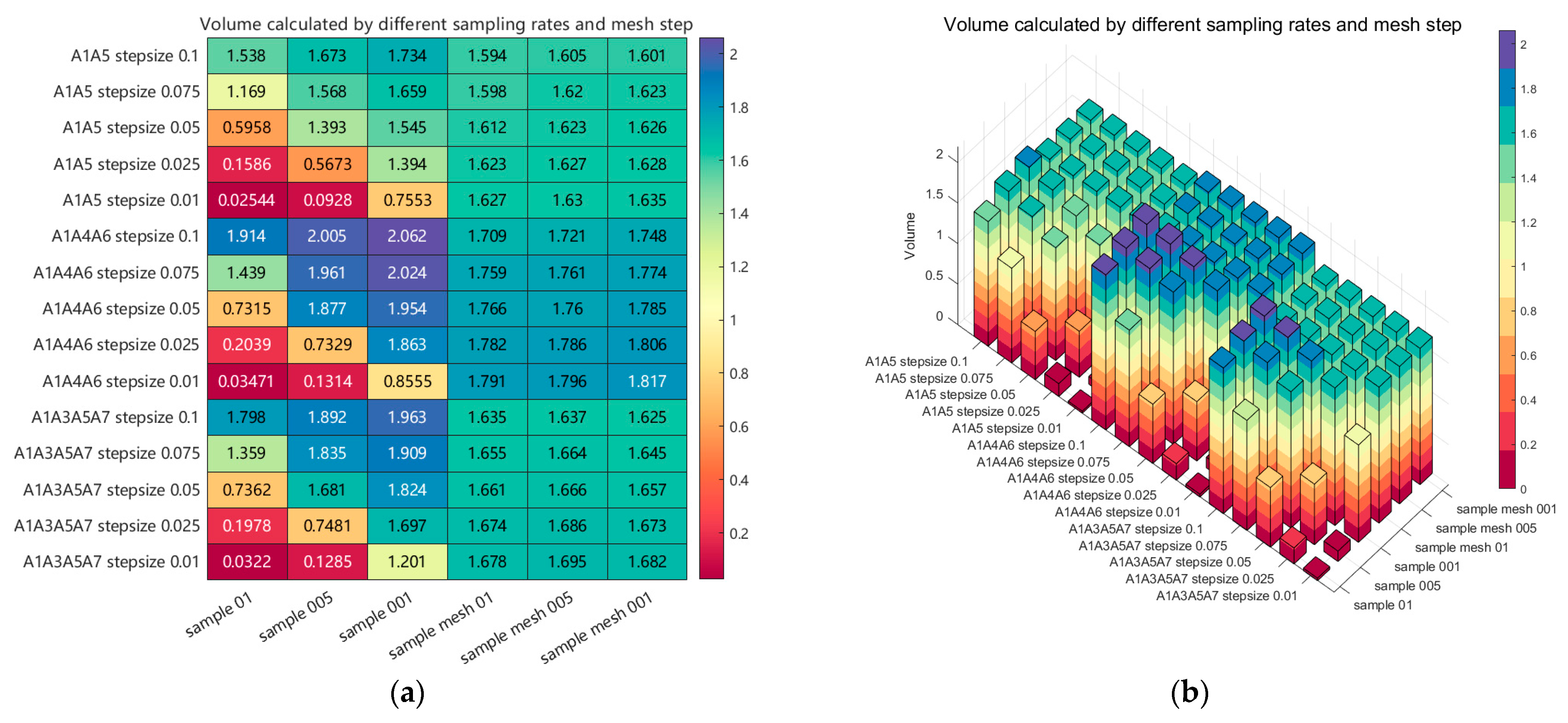
- Through comparisons of grain pile point clouds obtained by combining 2, 3, and 4 different camera viewpoints, each sampled at step (in meters) lengths of 0.1, 0.075, 0.05, 0.025, and 0.01, and calculating the volume using the BICM method, a maximum error of 6.29%, a minimum error of 1.13%, and an overall average error of 3.39% were achieved. These results demonstrate that the BICM method is an efficient and stable approach for grain pile volume calculation. Therefore, considering measurement efficiency and the minimization of equipment and computational resource usage, it is feasible to achieve a volume calculation error within 5% by employing two opposing viewpoint measurements combined with the BICM method for processing.
- The proposed BICM method effectively addresses the issue of significant surface gaps on grain piles by applying B-spline interpolation fitting. It reconstructs smooth and continuous 3D surfaces, successfully overcoming the discontinuities and surface defects caused by the integration of point clouds from multiple camera viewpoints. With its efficient and reliable surface completion performance, the BICM method exhibits strong potential for practical applications in engineering scenarios.
- By comparing the effects of different sampling step lengths and grid interpolation step lengths on the surface fitting and volume calculation of the grain pile, the relationship between grid interpolation step length and volume calculation accuracy was identified. Specifically, the sampling step length should be matched to the grid interpolation step length, with the optimal configuration determined to be 0.01 m for both.
- The BICM method enables real-time reconstruction of the 3D model of grain surfaces and grain piles in grain silos, providing essential data for the intelligent management of grain storage, as well as generating 3D maps to support motion planning for robots operating within the silos.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Jianyao, Y.; Zhang, Q.; Ge, L.; Chen, J. Technical Methods of National Security Supervision: Grain Storage Security as an Example. J. Saf. Sci. Resil. 2023, 4, 61–74. [Google Scholar] [CrossRef]
- Duysak, H.; Yigit, E. Machine Learning Based Quantity Measurement Method for Grain Silos. Measurement 2020, 152, 107279. [Google Scholar] [CrossRef]
- Yariv, L.; Kasten, Y.; Moran, D.; Galun, M.; Atzmon, M.; Basri, R.; Lipman, Y. Multiview Neural Surface Reconstruction by Disentangling Geometry and Appearance. Adv. Neural Inf. Process. Syst. 2020, 33, 2492–2502. [Google Scholar]
- Pan, Z.; Hou, J.; Yu, L. Optimization Algorithm for High Precision RGB-D Dense Point Cloud 3D Reconstruction in Indoor Unbounded Extension Area. Meas. Sci. Technol. 2022, 33, 055402. [Google Scholar] [CrossRef]
- Lutz, É.; Coradi, P.C. Applications of New Technologies for Monitoring and Predicting Grains Quality Stored: Sensors, Internet of Things, and Artificial Intelligence. Measurement 2022, 188, 110609. [Google Scholar] [CrossRef]
- Xu, Y.; Nan, L.; Zhou, L.; Wang, J.; Wang, C.C.L. HRBF-Fusion: Accurate 3D Reconstruction from RGB-D Data Using On-the-Fly Implicits. ACM Trans. Graph. 2022, 41, 1–19. [Google Scholar] [CrossRef]
- Kurtser, P.; Lowry, S. RGB-D Datasets for Robotic Perception in Site-Specific Agricultural Operations—A Survey. Comput. Electron. Agric. 2023, 212, 108035. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Lu, G. Improving RGB-D-Based 3D Reconstruction by Combining Voxels and Points. Vis. Comput. 2023, 39, 5309–5325. [Google Scholar] [CrossRef]
- Vila, O.; Boada, I.; Coll, N.; Fort, M.; Farres, E. Automatic Silo Axis Detection from RGB-D Sensor Data for Content Monitoring. ISPRS J. Photogramm. Remote Sens. 2023, 203, 345–357. [Google Scholar] [CrossRef]
- Huang, T. Fast Neural Distance Field-Based Three-Dimensional Reconstruction Method for Geometrical Parameter Extraction of Walnut Shell from Multiview Images. Comput. Electron. Agric. 2024, 224, 109189. [Google Scholar] [CrossRef]
- Yu, S.; Liu, X.; Tan, Q.; Wang, Z.; Zhang, B. Sensors, Systems and Algorithms of 3D Reconstruction for Smart Agriculture and Precision Farming: A Review. Comput. Electron. Agric. 2024, 224, 109229. [Google Scholar] [CrossRef]
- Hu, K.; Ying, W.; Pan, Y.; Kang, H.; Chen, C. High-Fidelity 3D Reconstruction of Plants Using Neural Radiance Fields. Comput. Electron. Agric. 2024, 220, 108848. [Google Scholar] [CrossRef]
- Hamidpour, P.; Araee, A.; Baniassadi, M. Transfer Learning-Based Techniques for Efficient 3D-Reconstruction of Functionally Graded Materials. Mater. Des. 2024, 248, 113415. [Google Scholar] [CrossRef]
- Lyu, X.; Sun, Y.-T.; Huang, Y.-H.; Wu, X.; Yang, Z.; Chen, Y.; Pang, J.; Qi, X. 3DGSR: Implicit Surface Reconstruction with 3D Gaussian Splatting. ACM Trans. Graph. 2024, 43, 1–12. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Kwon, S. Volume Estimation Method for Irregular Object Using RGB-D Deep Learning. Electronics 2025, 14, 919. [Google Scholar] [CrossRef]
- Miranda, J.C.; Arnó, J.; Gené-Mola, J.; Lordan, J.; Asín, L.; Gregorio, E. Assessing Automatic Data Processing Algorithms for RGB-D Cameras to Predict Fruit Size and Weight in Apples. Comput. Electron. Agric. 2023, 214, 108302. [Google Scholar] [CrossRef]
- Yang, M.; Cho, S.-I. High-Resolution 3D Crop Reconstruction and Automatic Analysis of Phenotyping Index Using Machine Learning. Agriculture 2021, 11, 1010. [Google Scholar] [CrossRef]
- Yang, T.; Ye, J.; Zhou, S.; Xu, A.; Yin, J. 3D Reconstruction Method for Tree Seedlings Based on Point Cloud Self-Registration. Comput. Electron. Agric. 2022, 200, 107210. [Google Scholar] [CrossRef]
- Wu, Z.; Li, H.; Lu, C.; He, J.; Wang, Q.; Liu, D.; Cui, D.; Li, R.; Wang, Q.; He, D. Development and Evaluations of an Approach with Full Utilization of Point Cloud for Measuring the Angle of Repose. Comput. Electron. Agric. 2023, 209, 107799. [Google Scholar] [CrossRef]
- Xie, P.; Du, R.; Ma, Z.; Cen, H. Generating 3D Multispectral Point Clouds of Plants with Fusion of Snapshot Spectral and RGB-D Images. Plant Phenomics 2023, 5, 0040. [Google Scholar] [CrossRef]
- Yang, D.; Yang, H.; Liu, D.; Wang, X. Research on Automatic 3D Reconstruction of Plant Phenotype Based on Multi-View Images. Comput. Electron. Agric. 2024, 220, 108866. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Shi, Y.; Xiong, M.; Ren, D.; Wu, L.; Zou, X. Efficient Three-Dimensional Reconstruction and Skeleton Extraction for Intelligent Pruning of Fruit Trees. Comput. Electron. Agric. 2024, 227, 109554. [Google Scholar] [CrossRef]
- Zhu, Y.; Cao, S.; Song, T.; Xu, Z.; Jiang, Q. 3D Reconstruction and Volume Measurement of Irregular Objects Based on RGB-D Camera. Meas. Sci. Technol. 2024, 35, 125010. [Google Scholar] [CrossRef]
- Hu, H.; Song, A. Digital Image Correlation Calculation Method for RGB-D Camera Multi-View Matching Using Variable Template. Measurement 2025, 240, 115617. [Google Scholar] [CrossRef]
- Wei, P.; Yan, L.; Xie, H.; Qiu, D.; Qiu, C.; Wu, H.; Zhao, Y.; Hu, X.; Huang, M. LiDeNeRF: Neural Radiance Field Reconstruction with Depth Prior Provided by LiDAR Point Cloud. ISPRS J. Photogramm. Remote Sens. 2024, 208, 296–307. [Google Scholar] [CrossRef]
- Shi, C.; Tang, F.; Wu, Y.; Ji, H.; Duan, H. Accurate and Complete Neural Implicit Surface Reconstruction in Street Scenes Using Images and LiDAR Point Clouds. ISPRS J. Photogramm. Remote Sens. 2025, 220, 295–306. [Google Scholar] [CrossRef]
- Qin, K.; Li, J.; Zlatanova, S.; Wu, H.; Gao, Y.; Li, Y.; Shen, S.; Qu, X.; Yang, Z.; Zhang, Z.; et al. Novel UAV-Based 3D Reconstruction Using Dense LiDAR Point Cloud and Imagery: A Geometry-Aware 3D Gaussian Splatting Approach. Int. J. Appl. Earth Obs. Geoinf. 2025, 140, 104590. [Google Scholar] [CrossRef]
- Vulpi, F.; Marani, R.; Petitti, A.; Reina, G.; Milella, A. An RGB-D Multi-View Perspective for Autonomous Agricultural Robots. Comput. Electron. Agric. 2022, 202, 107419. [Google Scholar] [CrossRef]
- Qi, H.; Wang, C.; Li, J.; Shi, L. Loop Closure Detection with CNN in RGB-D SLAM for Intelligent Agricultural Equipment. Agriculture 2024, 14, 949. [Google Scholar] [CrossRef]
- Vélez, S. Integrated Framework for Multipurpose UAV Path Planning in Hedgerow Systems Considering the Biophysical Environment. Crop Prot. 2025, 187, 106992. [Google Scholar] [CrossRef]
- Conti, A.; Poggi, M.; Cambareri, V.; Oswald, M.R.; Mattoccia, S. ToF-Splatting: Dense SLAM Using Sparse Time-of-Flight Depth and Multi-Frame Integration. arXiv 2025, arXiv:2504.16545. [Google Scholar]
- Storch, M. Comparative Analysis of UAV-Based LiDAR and Photogrammetric Systems for the Detection of Terrain Anomalies in a Historical Conflict Landscape. Sci. Remote Sens. 2025, 11, 100191. [Google Scholar] [CrossRef]
- Zhang, N.; Canini, K.; Silva, S.; Gupta, M. Fast Linear Interpolation. J. Emerg. Technol. Comput. Syst. 2021, 17, 1–15. [Google Scholar] [CrossRef]
- Klančar, G.; Zdešar, A.; Krishnan, M. Robot Navigation Based on Potential Field and Gradient Obtained by Bilinear Interpolation and a Grid-Based Search. Sensors 2022, 22, 3295. [Google Scholar] [CrossRef]
- Li, D.; Cheng, B.; Xiang, S. Direct Cubic B-Spline Interpolation: A Fuzzy Interpolating Method for Weightless, Robust and Accurate DVC Computation. Opt. Lasers Eng. 2024, 172, 107886. [Google Scholar] [CrossRef]
- Essanhaji, A.; Errachid, M. Lagrange Multivariate Polynomial Interpolation: A Random Algorithmic Approach. J. Appl. Math. 2022, 2022, 8227086. [Google Scholar] [CrossRef]
- Supajaidee, N.; Chutsagulprom, N.; Moonchai, S. An Adaptive Moving Window Kriging Based on K-Means Clustering for Spatial Interpolation. Algorithms 2024, 17, 57. [Google Scholar] [CrossRef]












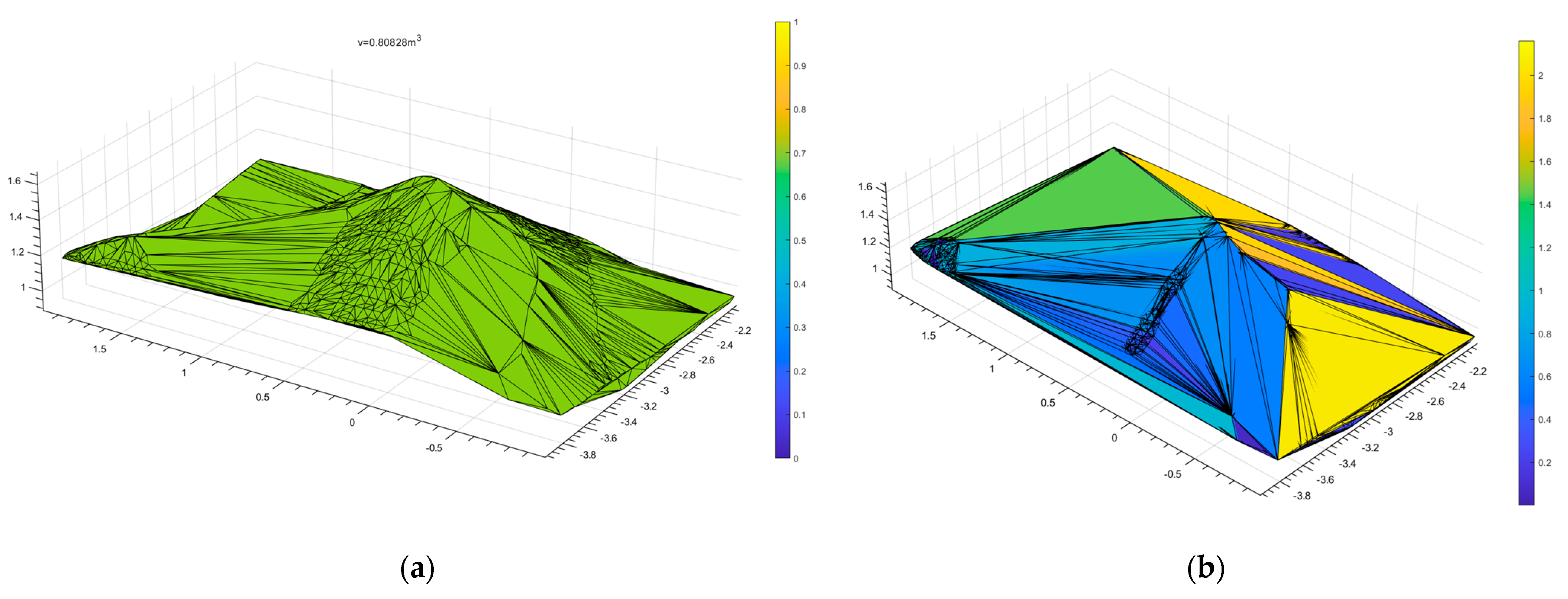
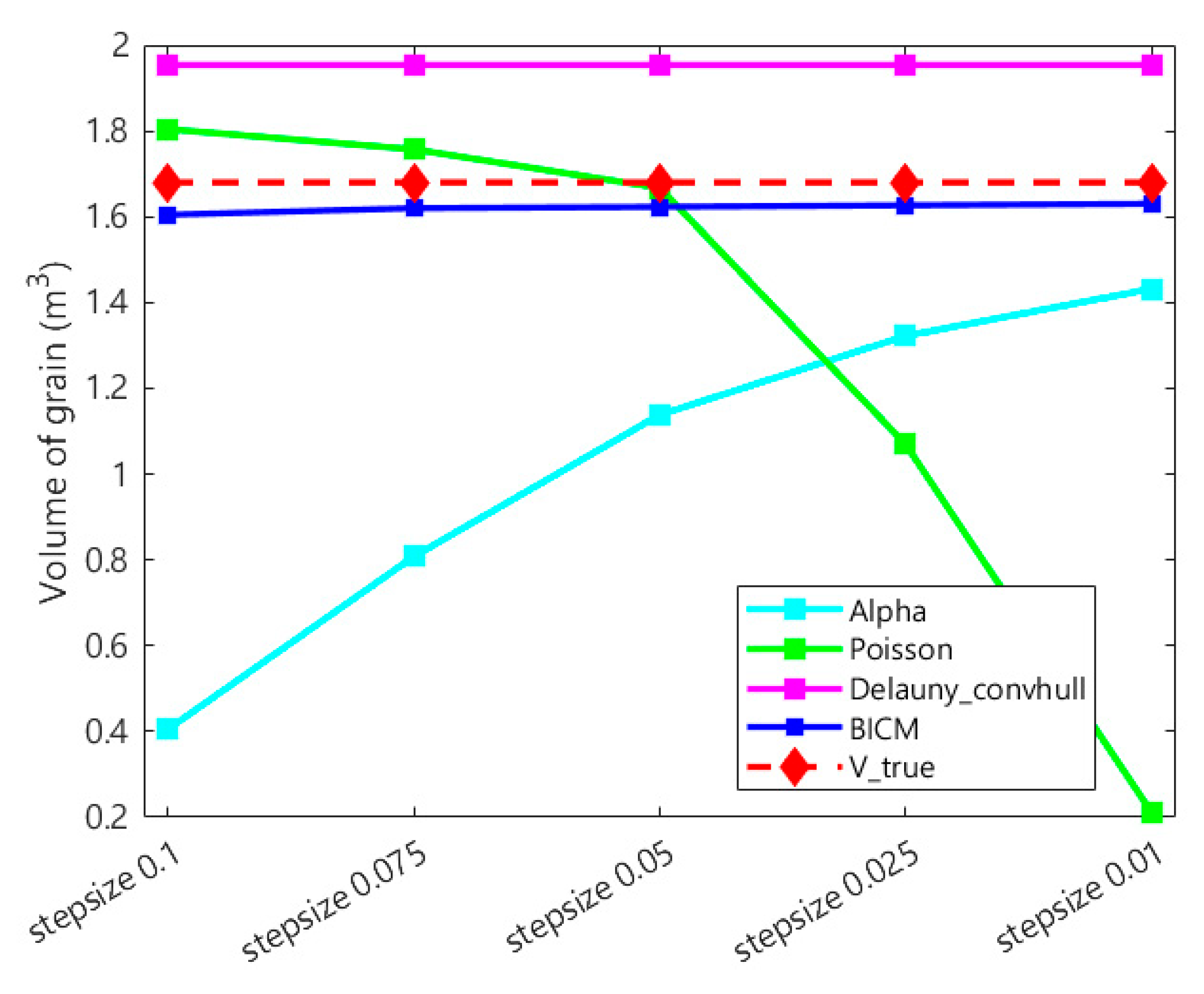
| Mesh Interpolation Step | Alpha | Poisson | Delaunay_Convhull | BICM |
|---|---|---|---|---|
| grid_0.1 | 0.4057 | 1.804 | 1.9538 | 1.6046 |
| grid_0.075 | 0.8083 | 1.757 | 1.9538 | 1.6199 |
| grid_0.05 | 1.1383 | 1.6671 | 1.9538 | 1.623 |
| grid_0.025 | 1.3221 | 1.0694 | 1.9538 | 1.6266 |
| grid_0.01 | 1.4318 | 0.21215 | 1.9538 | 1.6301 |
| true volume | 1.680 | |||
| maximum error | 73.81% | 36.35% | 16.29% | 4.48% |
| minimum error | 14.78% | 0.77% | 16.29% | 2.97% |
| average error | 39.21% | 27.89% | 16.29% | 3.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Ran, C.; Yu, Z.; Han, F.; Wu, W. Surface Reconstruction and Volume Calculation of Grain Pile Based on Point Cloud Information from Multiple Viewpoints. Agriculture 2025, 15, 1208. https://doi.org/10.3390/agriculture15111208
Yang L, Ran C, Yu Z, Han F, Wu W. Surface Reconstruction and Volume Calculation of Grain Pile Based on Point Cloud Information from Multiple Viewpoints. Agriculture. 2025; 15(11):1208. https://doi.org/10.3390/agriculture15111208
Chicago/Turabian StyleYang, Lingmin, Cheng Ran, Ziqing Yu, Feng Han, and Wenfu Wu. 2025. "Surface Reconstruction and Volume Calculation of Grain Pile Based on Point Cloud Information from Multiple Viewpoints" Agriculture 15, no. 11: 1208. https://doi.org/10.3390/agriculture15111208
APA StyleYang, L., Ran, C., Yu, Z., Han, F., & Wu, W. (2025). Surface Reconstruction and Volume Calculation of Grain Pile Based on Point Cloud Information from Multiple Viewpoints. Agriculture, 15(11), 1208. https://doi.org/10.3390/agriculture15111208







