Study on the Interactions Process of Coupled Model of Furrow Opener–Soil–Pot Seedling Based on Discrete Approach

Abstract

The upright state of pot seedlings in the process of rice mechanized throwing operations has an important influence on the growth rate and yield of rice, and pot seedling uprightness is affected by the influence of soil backfilling during trenching. Due to the complexity of the furrow opener–soil–pot seedling interaction mechanism in the rice pot seedling planting process, the soil backfilling process is difficult to observe. In order to improve the uprightness of pot seedling planting, this paper constructs a soil model and a soil–pot seedling model step by step, based on the discrete element method (DEM), as well as a coupled model of the pot seedling planting system to study the process of furrow opener–soil–pot seedling planting, the reliability of which is then verified. The results showed that the simulation results of the constructed soil model and soil–pot seedling model deviated from the actual calibration results by <6%, and the model could accurately simulate the pot seedling throwing process. The simulation analysis of the trenching process revealed that the soil backfilling process during trenching showed a three-stage evolution pattern of “backfilling-covering-stabilizing”; in addition, the forward speed of the machine was 0.8 m/s, and the falling speed of the seedling discharge cylinder was 3.5 m/s, which made it possible for the model to simulate the pot seedling throwing process accurately. In addition, when the pot seedling with a forward speed of 0.8 m/s and a drop speed of 3.5 m/s fell into the trench after 0.15 s of trenching, its lateral and longitudinal uprightness were 67.0 ± 1.2° and 65.2 ± 1.5°, respectively. After optimization of the structure of the trenchers, the width, depth, and length of the main body were 40 mm, 37.87 mm, and 32.32 mm, respectively, and the lateral and longitudinal uprightness of the pot seedlings increased to 70.0 ± 1.0° and 69.4 ± 0.8, respectively. The coupled model bench validation test showed that its reliability error was <5%. The coupled model provides technical support for the design and parameter optimization of rice planting equipment.

1. Introduction

Rice seedling pot throwing is an efficient rice planting technology that plays a significant role in rice production [1]. However, existing rice seedling pot throwing machinery still faces issues such as floating of the pot seedlings after transplanting and low uprightness, which lead to prolonged seedling growth periods [2,3,4]. Therefore, it is necessary to conduct research on the mechanism of the pot seedling throwing process. However, this process is complex, involving interactions between machinery, pot seedlings (pot soil, stems, and leaves), and paddy field soil. Moreover, due to the difficulty in observing and detecting the interaction mechanisms within the paddy field soil, there is a lack of relevant theoretical guidance for optimizing the working and structural parameters of rice seedling pot throwing machinery [5]. Therefore, employing the DEM to construct a coupling model of the furrow opener–soil–pot seedling system and exploring the interactions between the furrow opener and soil, as well as between the soil and pot seedling, can lay a theoretical foundation for improving the uprightness of pot seedlings and optimizing the operational parameters of throwing machinery.

The coupled modeling of furrow opener–soil–pot seedling systems is based on paddy soil models, with the the DEM serving as the primary methodology for simulating the external dimensions and contact characteristics of research subjects [6]. Using the draw plate method, in combination with soil simulation parameters of paddy fields calibrated by the collapse test, the operation process of the furrow opener can be analyzed and the optimization of the furrow opener parameters can be carried out [7]. Puncture tests further calibrate bonding parameters of hole-tray seedling potting soil [8,9]. EDEM 2022.2 software can simplify the whole hole-pot seedling process into a model composed of potting soil and stalks, and the pot seedling–soil complex can be modeled and shear characterization studied [10]. The discrete element coupling model can also effectively simulate the dynamic performance of mechanical operations [11,12,13,14,15]. Researchers have conducted comprehensive investigations across diverse scenarios: Zhu et al. [16] developed a machine–straw–soil coupling dynamics model to analyze rotary tillage processes; Lin Jianxin [17] established a spade cultivator–multiphase medium interaction model based on soil and straw property measurements from rice stubble fields; Wan et al. [18,19] constructed a licorice-soil–oscillating harvester coupling model to study system behavior linked to licorice distribution and soil characteristics. These findings collectively demonstrate the feasibility of developing a potting–soil–opener coupled model using the DEM.

However, synthesizing the above studies, it was found that the current research on coupled machinery–soil–plant system modeling mostly focuses on harvesting and tillage directions, and the simulation research on the dynamic response of pot seedlings in the process of throwing planting is still lacking. To this end, this study analyzes the mechanics of the seedling falling process, obtains the factors affecting seedling uprightness, calibrates paddy soil and seedlings, establishes the furrow opener–soil–pot seedling coupling model, reveals the dynamic evolution of the soil backfilling law in the process of rice pot seedling throwing, and clarifies the influence of the working parameters of the seedling throwing device and the structural parameters of the furrow opener in the coupling system on the uprightness of the seedling. It thus provides a theoretical basis for improving the uprightness of pot seedlings. The accuracy of the model is further verified through the comparative analysis of the results of the throwing stand test and the simulated throwing test. This study is expected to provide a reference for improving the uprightness of pot seedlings and provide technical support for the design and parameter optimization of rice throwing equipment.

2. Materials and Methods

2.1. Rice Pot Seedling Mechanized Planting Upright Process

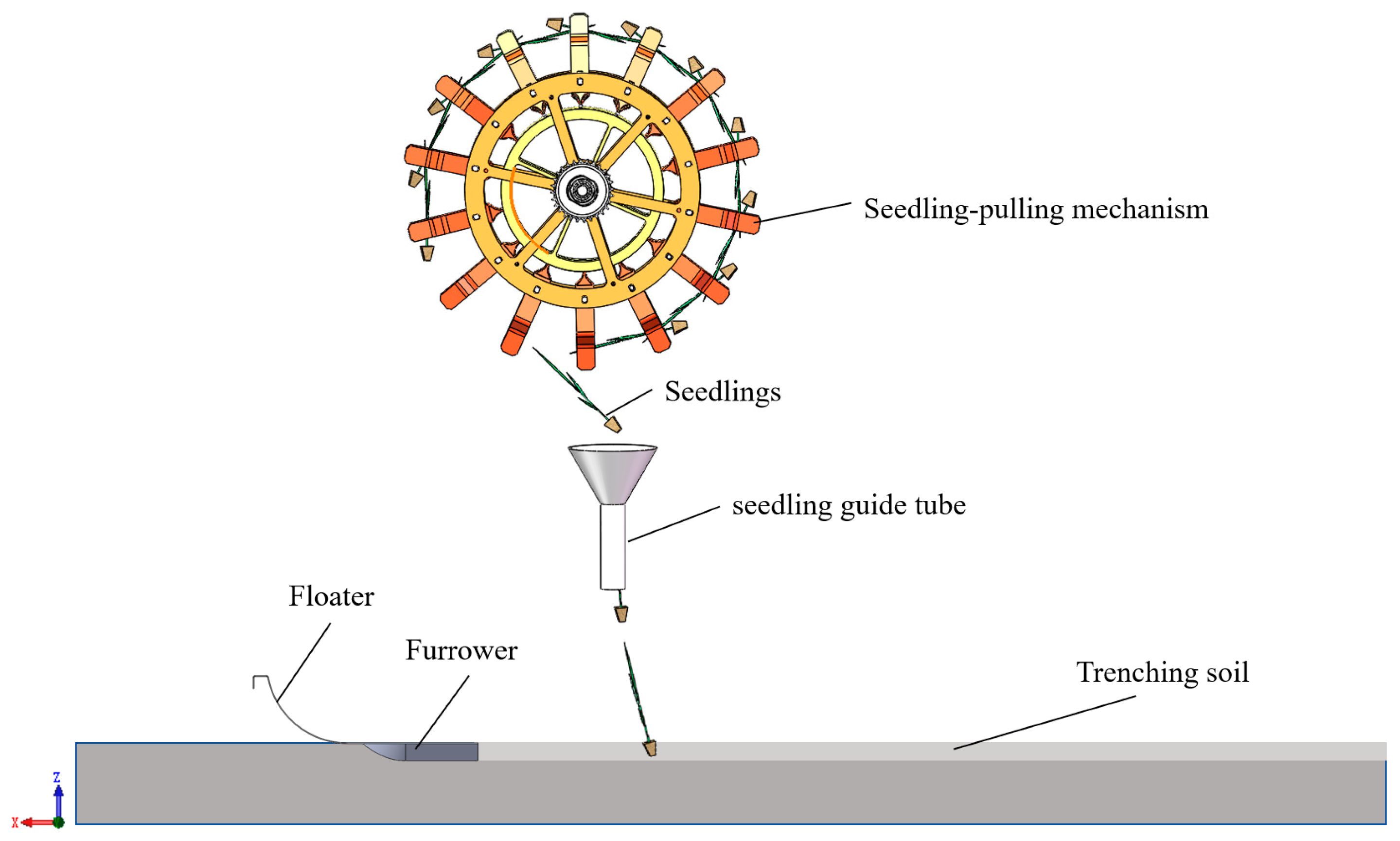
The rice pot seedling mechanical throwing system comprises a seedling extraction mechanism, furrow opener, rice pot seedlings, and paddy soil (Figure 1), with its operational quality governed by extraction mechanism parameters, furrow opener–paddy soil interaction dynamics, and seedling intrinsic properties. The rice throwing process involves three sequential phases—seedling extraction, soil furrowing, and seedling embedment—where soil furrowing and seedling extraction operate synchronously. During the embedment phase, seedlings rapidly settle onto the furrow bed under the combined action of seedling guide tube initial velocity and gravitational acceleration, achieving seedling uprightness through paddy soil backflow effects. To address the limitations in visualizing the dynamics of the pot seedling after exiting the seedling transfer tube, a DEM-based coupled model was developed using collapse test calibration parameters, enabling mechanistic analysis of correlations among seedling-throwing device kinematics, soil rheological characteristics, and seedling uprightness metrics. These findings provide theoretical foundations for furrow opener structural optimization and operational parameter regulation in high-speed rice throwing systems.

2.2. Mechanical Characterization of Rice Potted Seedling Trenching and Establishment

In order to investigate the factors affecting the uprightness of rice potted seedling planting, the process of rice potted seedling planting uprightness was analyzed. Center-of-mass dynamics were used to analyze the evolution of forces and velocities in the air and soil entry phases of the rice potted seedling after exiting the seedling transport cylinder, which can provide theoretical support for subsequent experiments [20].

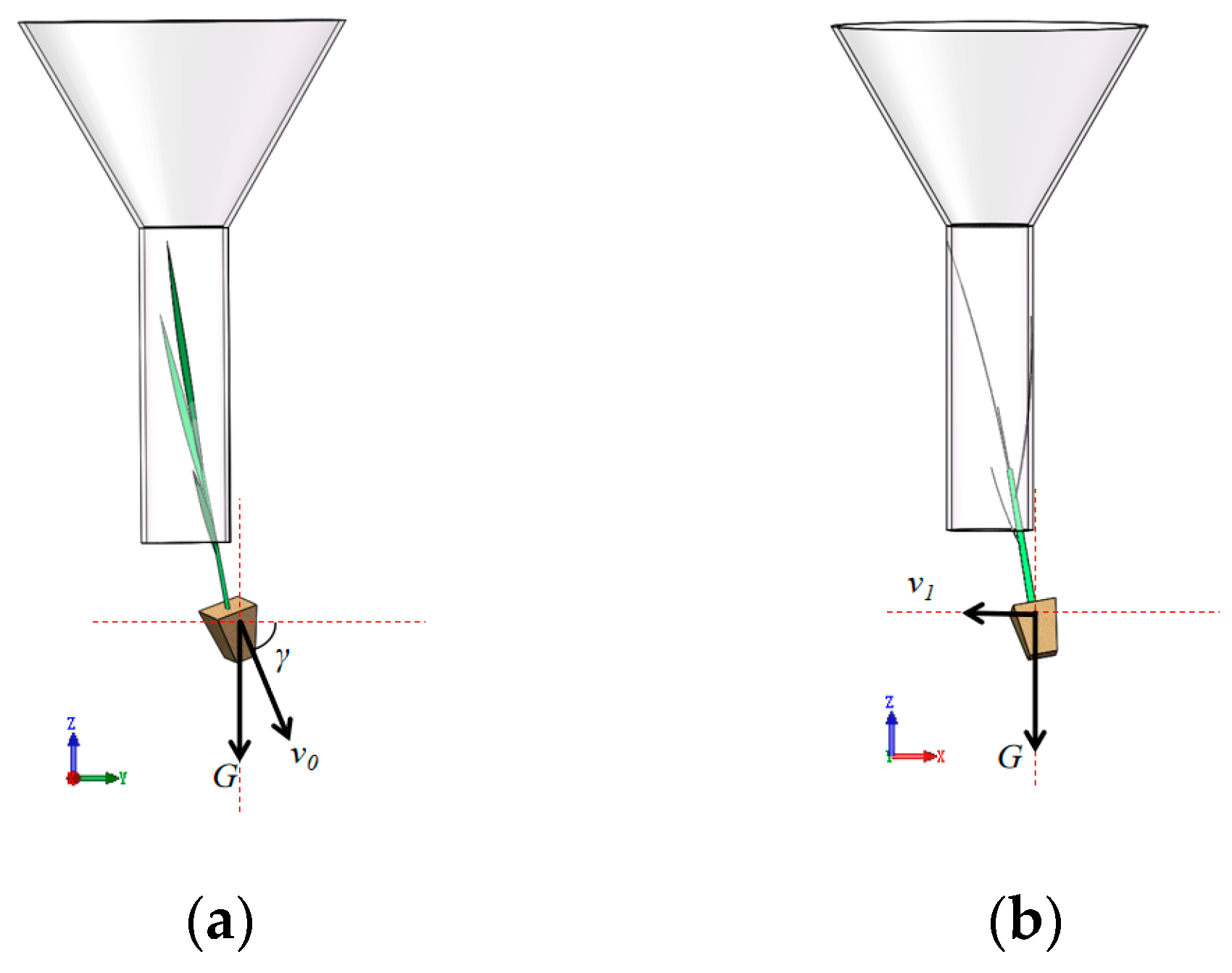
2.2.1. Rice Pot Seedlings Aerial Down Stage

During the airborne descent phase of rice pot seedlings (neglecting air resistance), the seedlings are subjected solely to gravitational force G (with gravitational acceleration g). Their kinematic behavior is characterized by a velocity component in the YOZ plane, with speed v₀ and angle γ, and forward velocity v₁ in the XOZ plane, as illustrated in Figure 2.

The velocity of the pot seedling before it falls into the soil and the value of the displacement deviation on the Y-axis can be given by Equations (1) and (2):

$$\left\{\begin{array}{l}{v}_{2Y}=v_0\mathit{cos}\gamma \\ v_{2Z}=v_0\mathit{sin}\gamma +gt\\ v_2=\sqrt{{v_{2Y}}^2+{v_{2Z}}^2}\end{array}\right.$$

(1)

$$\left\{\begin{array}{l}t={\displaystyle \frac{-v_0\mathit{sin}\gamma +\sqrt{{(v_0\mathit{sin}\gamma )}^2+2g{L}_h}}{g}}\\ \Delta L=v_{2Y}t\end{array}\right.$$

(2)

where v_2Y is the speed of the pot seedling in the Y-axis, m/s; v_2z is the speed in the Z-axis, m/s; v₂ is the falling speed before falling into the soil, m/s; t is the falling time in the air after coming out of the seedling guide tube, s; L_h is the distance from the bottom of the seedling guide tube to the surface of the mud, m; g is the acceleration of gravity, m/s²; and ΔL is the displacement deviation value of the pot seedling in the Y-axis, m.

Combined with the high-speed photographic observation test of the attitude of the seedling throwing movement in the previous period, the instantaneous speed of the seedling in the plane of YOZ from the seedling transmission cylinder v₀ is in the range of 1.84–2.40 m/s; the forward speed of v₁ in the plane of XOZ is in the range of 0.80–1.20 m/s, and the angle of the initial speed v₀ with the Y-axis γ is in the range of 75.34–84.42°. And combined with the previous research and the design requirements of the machine, it can be seen that the distance L_h between the mouth of the rice transfer cylinder and the mud surface of the rice planting machine is 280 mm, and the value of v₂ is in the range of 2.72–3.51 m/s.

2.2.2. Rice Pot Seedling In-Soil Stage

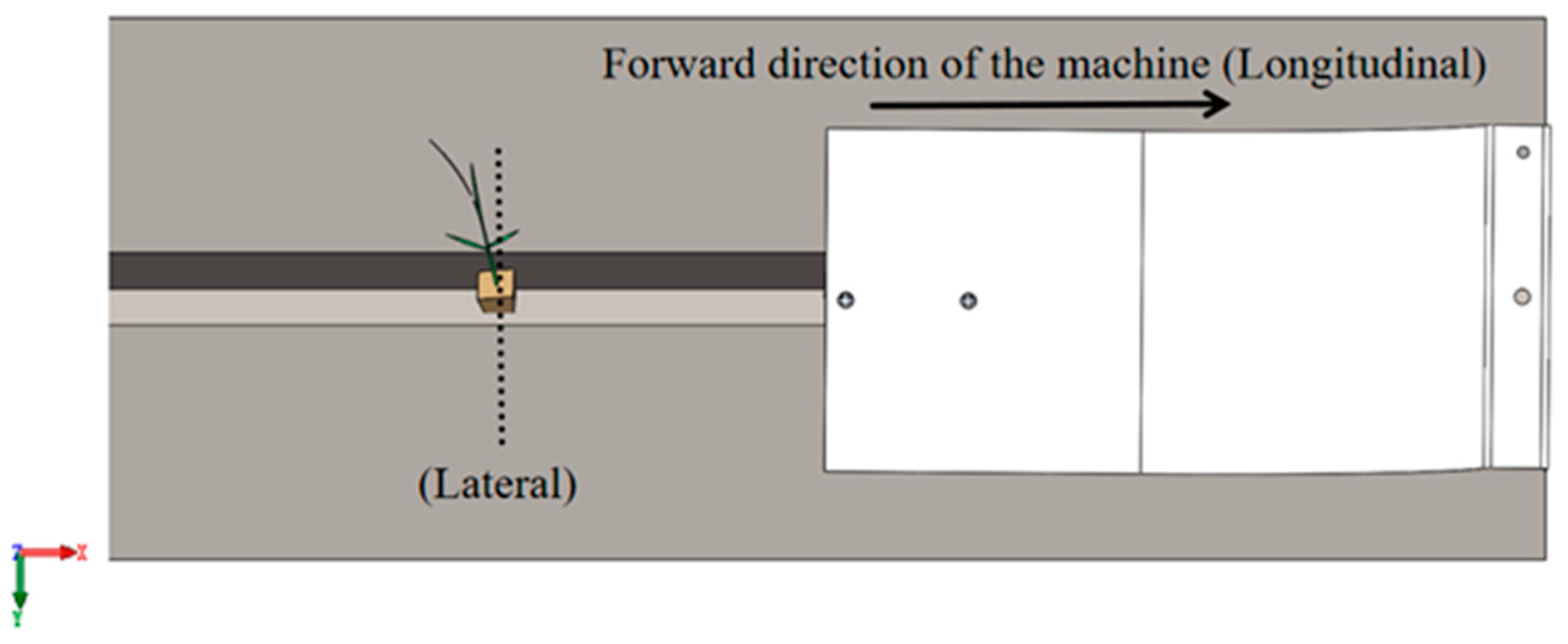
When the rice seedling falls into the trench, its top view is shown in Figure 3. The paddy soil slows down the rice seedling’s movement in the forward speed direction (longitudinal) due to soil backfilling, and it will be squeezed by the soil to slow down the rice seedling’s movement in the forward speed transversal direction (transversal), as shown in Figure 4.

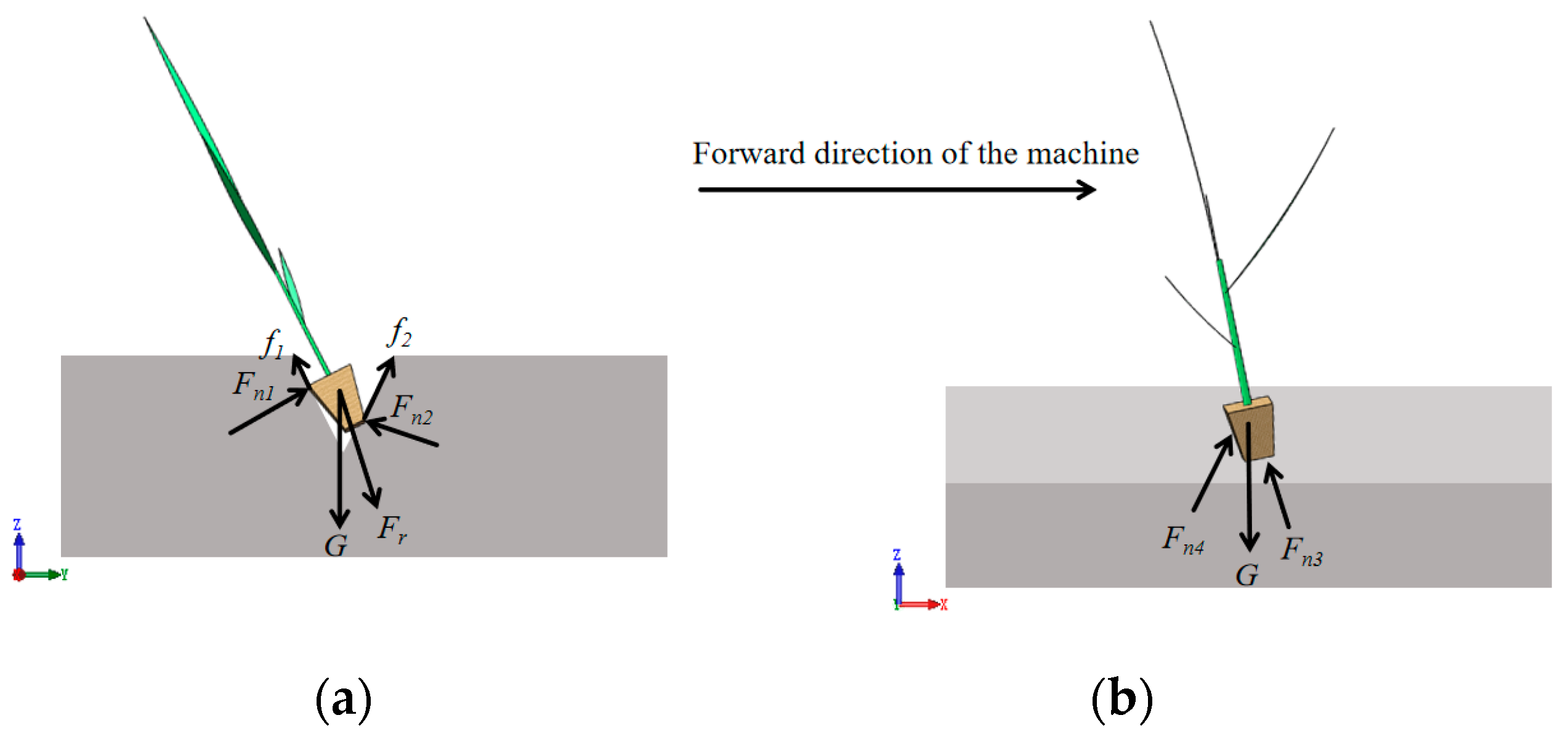
Establishment of force equations for pot seedlings in the soil (3):

$$\left\{\begin{array}{l}{\displaystyle \sum M_Z=G{l}_G+F_r{l}_{Fr}+F_{n1}{l}_{Fn1}+F_{n2}{l}_{Fn2}+f_1{l}_{f1}+f_2{l}_{f2}+F_{n3}{l}_{Fn3}+F_{n4}{l}_{Fn4}}\\ F_r=m{v}_2^{2}r\end{array}\right.$$

(3)

where M_Z is the total torque of the pot seedling, N·m; G is the gravity force of the pot seedling, N; m is the mass of the pot seedling, g; F_r is the centrifugal force, N; F_n is the normal force, N; f_n is the friction force, N; l_G is the force arm of gravity, m; l_Fr is the force arm of the centrifugal force, m; l_Fn is the force arm of the normal force, m; l_fn is the force arm of the friction force, m; and r is the radius of centrifugal force, m.

Mechanical analysis showed that the rice seedling was synergistically regulated by transverse and longitudinal mechanics during soil entry. In the YOZ plane, squeezing forces F_n1 and F_n2 collectively suppressed transverse tilting through clamping effects. Simultaneously, in the XOZ plane, supporting forces F_n3 and F_n4, enhanced by paddy soil backflow, significantly reduced the total torque M_Z. This torque reduction (M_Z→0) directly contributed to longitudinal stabilization. Under multi-force coupling, soil forces exhibited a negative correlation with seedling uprightness, and parametric influences on seedling uprightness could be analyzed through anisotropic force quantification.

2.3. Rice Potting-Soil-Furrow Opener Coupling Model

2.3.1. Modeling Approach

(1)

Soil tank modeling: Based on the pre-test data, the paddy soil that is favorable for pot seedlings erection was selected, and its paddy soil environment was the soil without bright water just after plowing, and its parameters such as water content, density and particle size distribution were determined. Based on the particle size distribution, the radius of the filled soil particles was 1 mm. According to the gradient of soil water content, the soil trench was divided into the surface layer (0–20 mm) and the deep layer (20–60 mm). Meanwhile, in order to avoid the interference of the side wall and cover the range of trenching, the size of the simulated soil trench was set to be 1000 mm (length) × 300 mm (width) × 60 mm (depth).

(2)

Rice pot seedling modeling: Pot seedlings were selected at the period of three leaves and one heart, and their geometrical forms were determined through dimensional measurements and three-dimensional modeling, and the spatial coordinates of the filled particles were generated in the EDEM software.

(3)

Trenching model simplification: The trench furrow opener and the floating plate were simulated according to homogeneous leveling, and their 3D models were assembled and converted to STL format and imported into EDEM software.

(4)

Multi-step coupled modeling: The key to establishing a coupling model of furrow opener–soil–pot seedling systems using the discrete element method is to integrate multiple models constructed step by step, as shown in Figure 5. Step 1: generation of soil trench particles—successively set the particle factory at the heights of 40 mm and 60 mm to generate the bottom and surface soil particles, and save the initial state file as “zero time” after the completion of the generation. Step 2: setting up the motion of trenching—position the model of the furrow opener to the front of the soil trench, and assign the translation speed. Step 3: pot seedling falling simulation, trenching within the soil trench, and translation speed assignment—when trenching to the middle of the soil trench, set the particle factory 5 mm above the end of the trench, and define the falling time, speed, and angle based on the soil backfilling characteristics and pot seedlings mechanical analysis. Step 4: simulation parameter setting—set the Rayleigh time step size of 20%, the data storage frequency of 0.01 s, and the total simulation length to 0.5 s after contact parameter calibration.

2.3.2. Calibration and Validation of Model Parameters

Accurate model parameters can precisely simulate the mechanical and behavioral characteristics of the furrow opener–soil–pot seedling system [21]. In the coupled model, the driving parameters of the furrow opener model are consistent with the forward speed of the planting mechanism. The model parameters to be determined are the intrinsic parameters of the soil, pot seedling, and furrow opener; and the model parameters of soil particle–soil particle, soil particle–pot seedling particle, soil particle–furrow opener, and soil particle–floating plate interactions [15,22,23].

(1)

Calibration and validation of soil model parameters

In this study, the densities of soil at different depths were 1537.37 kg/m³ and 1557.87 kg/m³, respectively, using direct measurements, and the ranges of soil–soil and furrow opener–soil contact parameters were determined according to the relevant literature on paddy field soils [24] and the GEMM database, where the furrow opener material was ABS. 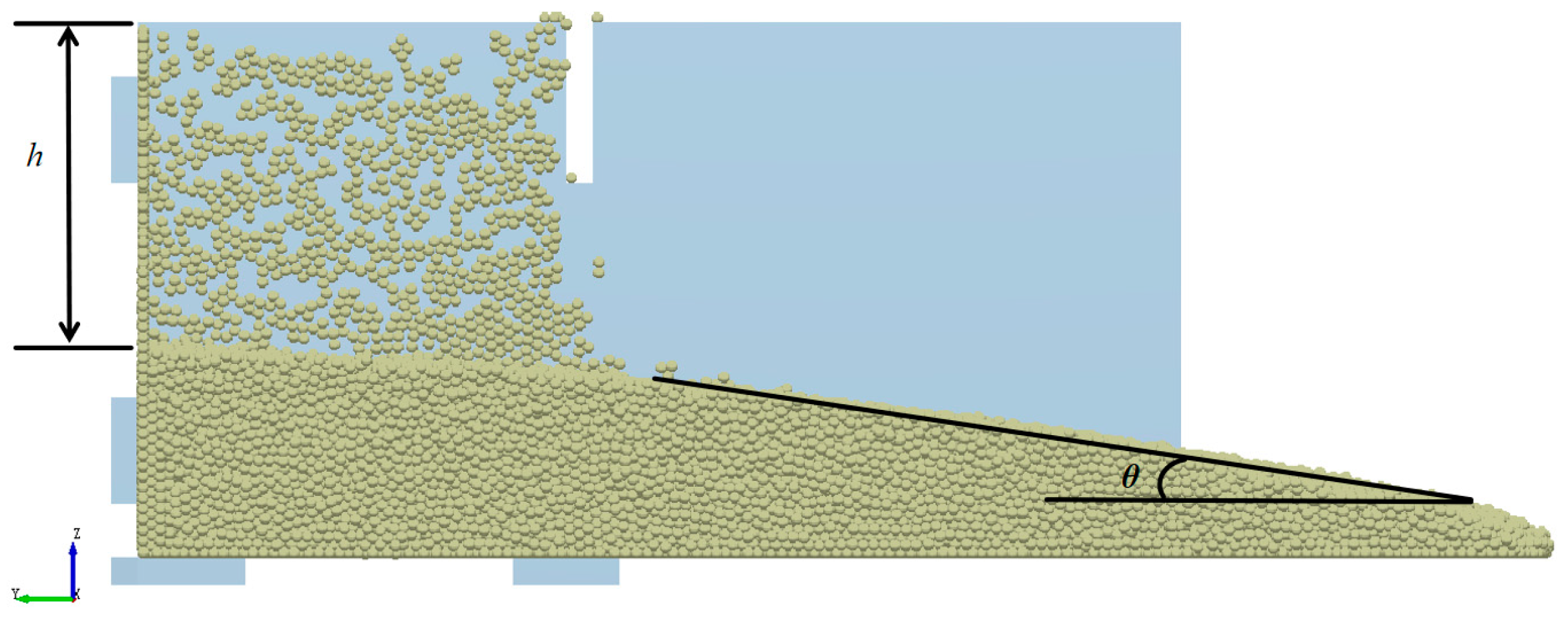The “Hertz-Mindlin with JKR” contact model was used to simulate the viscosity of soil particles in paddy fields [25]. 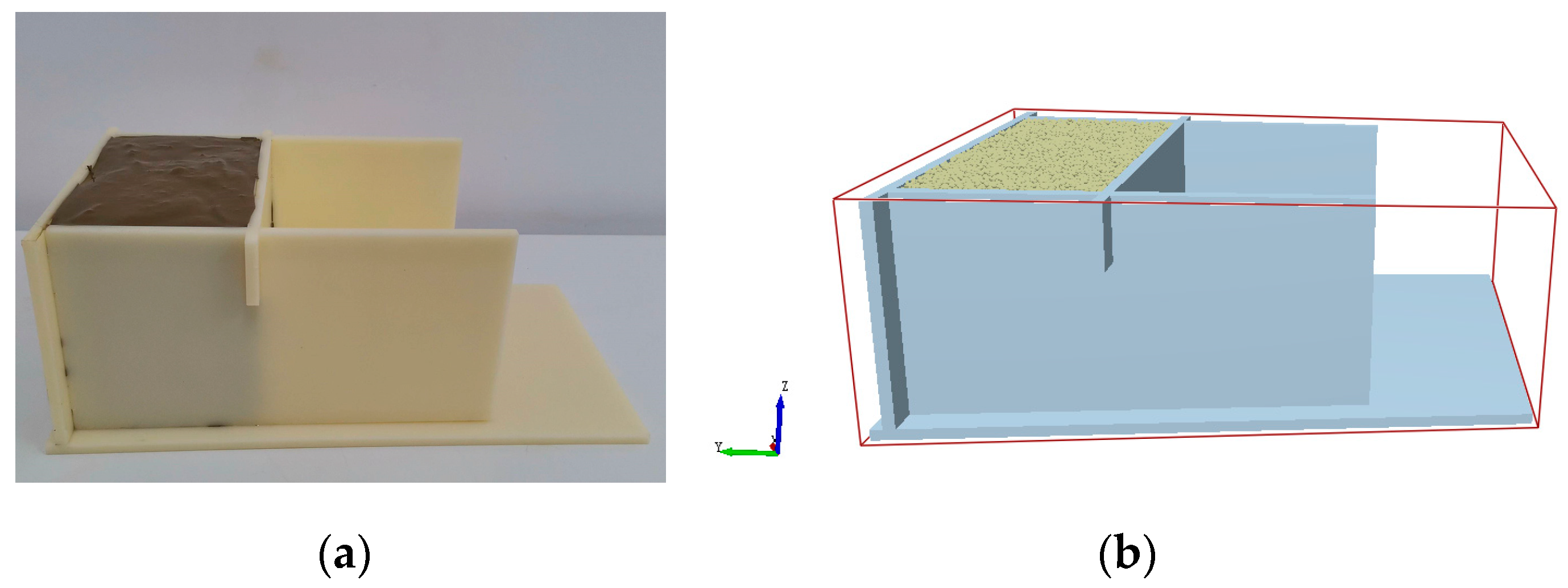The optimal parameter solutions of the soil–furrow opener model were determined by using the pumping plate method as shown in Figure 6, calibrating the soil at different depths, and taking the soil accumulation angle θ and the degree of collapse h as the target values as shown in Figure 7, as shown in

Table 1. Simulation parameters of the soil.

0–20 mm Soil Parameters	Value	20–60 mm Soil Parameters	Value
Soil Poisson’s ratio	0.300	Soil Poisson’s ratio	0.300
Shear modulus of soil, MPa	0.832	Shear modulus of soil, MPa	4.331
Soil–soil recovery coefficient	0.055	Soil–soil recovery coefficient	0.055
Soil–soil static friction coefficient	0.150	Soil–soil static friction coefficient	0.150
Soil–soil dynamic friction coefficient	0.125	Soil–soil dynamic friction coefficient	0.125
Soil–soil surface energy, J/m2	0.020	Soil–soil surface energy, J/m2	0.098
Soil–ABS recovery coefficient	0.350	Soil–ABS recovery coefficient	0.350
Soil–ABS static friction coefficient	0.300	Soil–ABS static friction coefficient	0.300
Soil–ABS dynamic friction coefficient	0.450	Soil–ABS dynamic friction coefficient	0.450
Soil–ABS surface energy, J/m2	1.250	Soil–ABS surface energy, J/m2	0.501

, where the contact parameters between the surface and deeper soils are the same as those between the deeper soils.

To further verify the accuracy of the two-layer soil model, the two-layer soil was mixed and compared with the actual collapse test through simulation [26,27], and the process is shown in Figure 8. The calibrated parameters were imported into EDEM software, and the relative errors of the simulated and actual test double-layer soil model collapse degree were obtained at 0.85%, and the relative error of the expansion degree was 5.93%. The results of parameter validation show that the model parameters are accurate and can effectively simulate soil rheology.

(2)

Calibration and validation of soil–pot seedling model parameters

In order to calibrate the soil–potting soil contact parameters, the stem and leaf were simplified into an equivalent mass rigid body model (a stem and leaf mass of 4.62 g and potting soil mass of 0.34 g), and the pot seedling drop test was carried out based on the range of soil–soil contact parameters (Figure 9). By setting the drop height to 300 mm, the average depths of pot seedlings in the surface layer (0–20 mm) and the deep layer (20–60 mm) were measured to be 16.10 mm and 14.80 mm, respectively, and the optimal contact parameters were determined by combining data from the literature [28], as shown in

Table 2. Potting soil–soil contact parameters.

0–20 mm Soil and Potting Soil	Value	20–60 mm Soil and Potting Soil	Value
Soil–potting soil restoration coefficient	0.095	Soil–potting soil restoration coefficient	0.040
Soil–potting soil static friction coefficient	0.178	Soil–potting soil static friction coefficient	0.157
Soil–potting soil dynamic friction coefficient	0.121	Soil–potting soil dynamic friction coefficient	0.113
Soil–potting soil surface energy, J/m2	0.064	Soil– potting soil surface energy, J/m2	0.064

. The test was conducted in two layers of soil, and the test showed that the relative error of the potting depth in the simulated two-layer soil model was 1.38% compared to the actual test.

2.4. Simulation and Bench Test of Trenching and Upright Planting of Rice Pot Seedlings

2.4.1. Experimentation with Different Out-of-Tube Postures of Pot Seedlings

The detachment attitude of the pot seedling out of the seedling guide tube was selected as the main test factor, and the test factors and levels were determined with the results of high-speed photographic observation of the pot seedling’s throwing motion attitude in the previous period and the results of the mechanical analysis of the pot seedling in the process of opening the furrow and standing up the seedling, as shown in

Table 3. Attitude test factor-level table.

Number	Experimental Factors
	Falling Speed/v2 (m/s)	Forward Speed/v1 (m/s)	Soil Backfilling Time/T (s)
1	2.5	0.8	0–0.15
2	3.0	1.0	0.15–0.30
3	3.5	1.2	0.30–0.45

. When conducting a single-factor test for one factor, the other two factors were maintained at their intermediate levels, and the test was repeated three times. The data selected were the mean values of these repetitions.

Based on the analysis of pot seedling uprightness and mechanical response, the mechanism of detachment attitude on the effect of seedling standing was systematically investigated. The experimental indexes included the following:

(1)

Soil kinematic velocities: real-time extraction of velocity field distributions using the EDEM particle vector mode;

(2)

Lateral uprightness: angle between the furrow opener forward transverse plane, potting center axis, and horizontal plane (Figure 10a);

(3)

Longitudinal uprightness: angle between the center axis of the pot seedling and the horizontal plane in the plane of the forward direction of the furrow opener (Figure 10b).

2.4.2. Testing of Different Furrow Opener Structural Parameters

The structural parameters of the opener were selected as the main test factors to analyze the uprightness of the pot seedling, in which the selection of the width, depth, and body length structural parameters of the opener was based on the width of the tube opening of the seedling guide tube, the required planting depth of the pot seedling, and the installation position of the opener, respectively. Experimental factors and levels are shown in

Table 4. Level table of structural parameter factors of furrow opener.

Number	Experimental Factors
	Furrow Opener Width /LK (mm)	Furrow Opener Depth /LS (mm)	Furrow Opener Body Length /LC (mm)
1	40	30	25
2	50	40	50
3	60	50	75
4	-	-	100

. Similarly, the effect of the structural parameters of the trenching opener on the effect of pot seedling uprightness was explored with an analysis of potting uprightness and stress, using a one-factor test and orthogonal test, with the same test indexes as above.

2.4.3. Simulation Verification Bench Test

Verification of the optimal parameters of the simulation was carried out through bench tests on a test soil tank, and the three-dimensional modeling of the rice pot seedling uprightness test device was first carried out using SolidWorks 2019 three-dimensional drawing software, as shown in Figure 11a. The test device, shown in Figure 11b, consists of a frame, screw, conveyor belt, seedling delivery cylinder, floating plate, and furrow opener. When working, the test stand moves forward under the drive of the motor of the soil trough, and the furrow opener at the lower end of the stand carries out the furrowing operation; at the same time, the conveyor belt at the upper end conveys the pot seedling to the specified position and then falls into the furrowed soil after it is righted by the seedling delivery cylinder. In order to meet the initial conditions for inserting pot seedlings into the soil, the conveyor belt is set at a distance of 400 mm from the bottom of the seedling tube, with the bottom of the seedling tube at a distance of 280 mm from the mud surface; the distance between the seedling tube and the furrow opener is kept within 120 mm, and the forward speed of the platform is set to 0.8 m/s. The other main tools required for the test are a DH-190 automatic moisture meter, high-precision digital display angle tape, a ruler, a JJ1000 electronic balance, and so on.

3. Results

3.1. Rice Pot Seedling Furrowing Process into the Soil

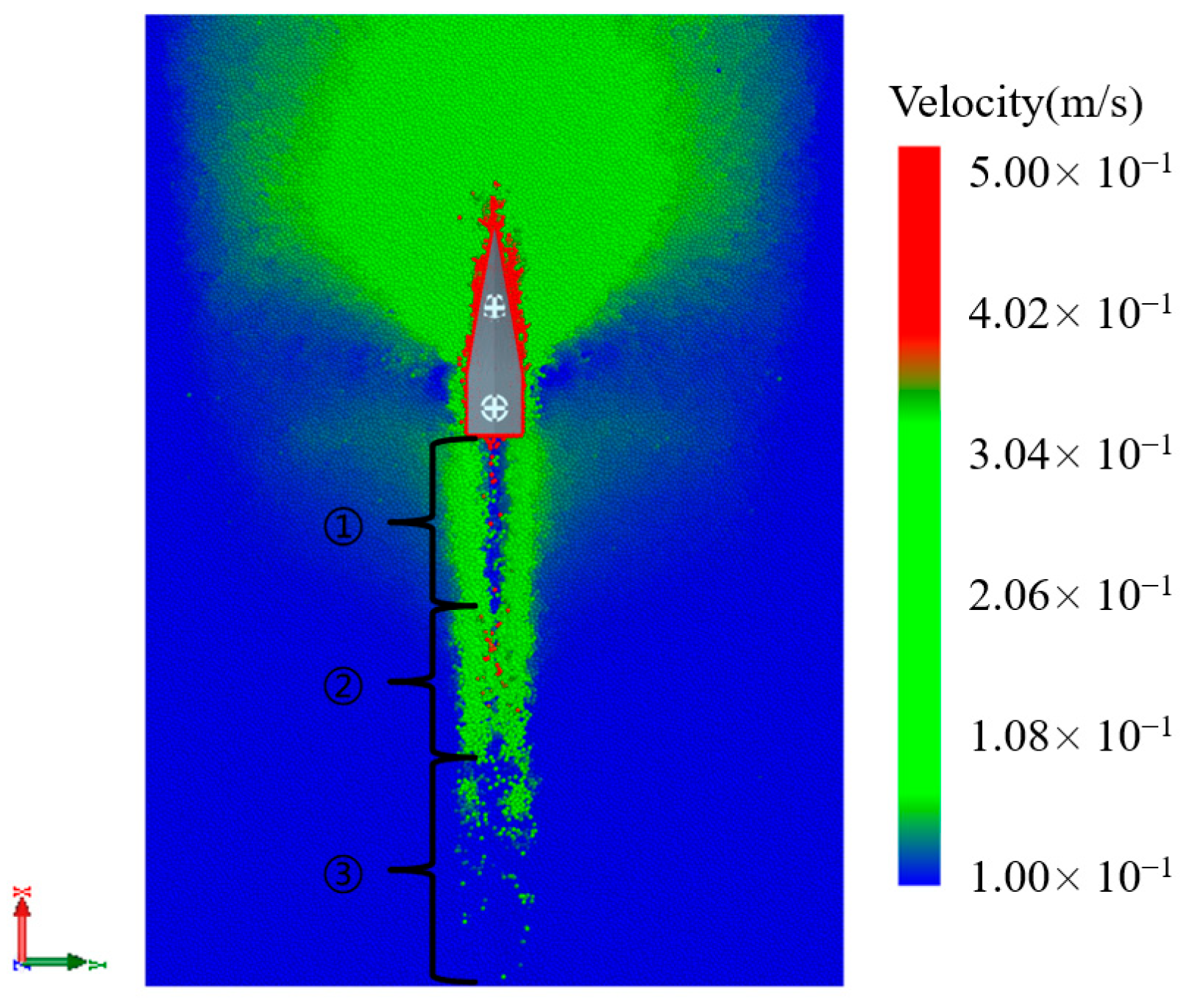
The simulation results show that soil disturbance during the operation of trenching is mainly concentrated in the edge curve area, which confirms that it is the core action site. The soil backfilling process presents three stages with dynamic characteristics (Figure 12): ① Sidewall backfilling stage (0–0.15 s)—when the trenchers have just passed, the soil particles squeezed inside the trench can be released, migrating to the center of the trenching movement; the closer the particles are squeezed against the mud surface, the faster the soil backfilling occurs. ② Covering deposition stage (0.15–0.30 s)—as soil particles flow back, they slowly cover the bottom of the trench. ③ Stabilized formation stage (>0.30 s)—soil particle speed decreases to the point that they no longer move, and the trench type is fixed. The evolution law provides a theoretical basis for the optimal design of the trenching edge.

3.2. Factors Affecting Rice Potting Uprightness

3.2.1. Effect of Pot Seedling Disengagement Posture on Pot Seedling Uprightness

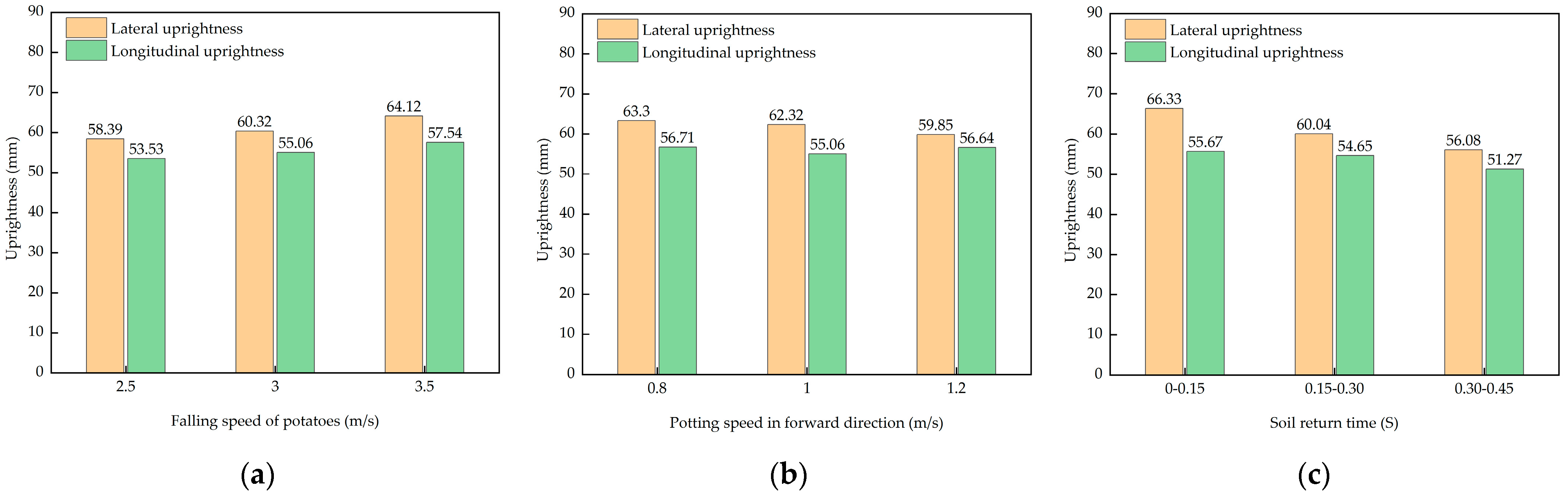
Impact of falling speed: As shown in Figure 13a, the uprightness of pot seedlings is positively correlated with falling speed (2.5–3.5 m/s), reaching maximum values for both lateral and longitudinal uprightness (73.12°, 67.54°) at 3.5 m/s. The falling speed primarily affects the lateral uprightness of the pot seedlings. An analysis based on Formula (3) reveals that the greater the speed, the deeper the pot seedlings descend, increasing soil resistance against the seedlings and reducing the torque on the seedlings after they enter the soil, which impedes the tilting movement of the seedlings and enhances their uprightness.

Impact of forward speed: As shown in Figure 13b, the uprightness of pot seedlings is negatively correlated with the forward speed (0.8–1.2 m/s), with the lateral and longitudinal uprightness being optimal at 0.8 m/s (73.30°, 66.71°). The forward speed primarily affects the longitudinal uprightness of pot seedlings. In the direction of forward speed, due to the trenching process pushing soil particles forward, the number of particles supporting the pot soil at the same height in this direction is significantly lower than on both sides of the trench. Therefore, under low-speed conditions, the rotational movement of pot seedlings is smaller, the deviation is less, and the uprightness of the pot seedlings is higher.

Impact of soil backfilling time: As shown in Figure 13c, the uprightness of pot seedlings was negatively correlated with soil backfilling time (0–0.30 s), and pot seedlings had the highest degree of uprightness (72.33°, 67.67°) when they fell in the “sidewall backfilling stage” (0–0.15 s). At this stage, the soil particles were not completely backfilling to the bottom of the trench, and the force released from the soil particles extruded by the openers increased the force on the pot seedlings, which further reduced the rotation of the pot seedlings; then (>0.15 s), the backfilling was weakened, and the resistance was reduced, resulting in an increase in the amount of deflection and a decrease in uprightness.

As can be seen from the analysis of orthogonal tests carried out in

Table 5. Orthogonal simulation test results and analysis table.

Number		Factor			Lateral Uprightness (°)	Longitudinal Uprightness (°)
		v2 (m/s)	v1 (m/s)	T (s)
1		1 (2.5)	1 (0.8)	1 (0–0.15)	72.66	62.76
2		1	2 (1.0)	2 (0.15–0.30)	70.63	59.90
3		1	3 (1.2)	3 (0.30–0.45)	71.70	51.01
4		2 (3.0)	1	2	73.67	66.38
5		2	2	3	71.90	64.3
6		2	3	1	71.14	61.61
7		3 (3.5)	1	3	72.52	68.24
8		3	2	1	74.36	64.88
9		3	3	2	70.85	61.44
Lateral Uprightness (°)	K1	214.99	218.85	218.16
	K2	216.71	216.89	215.15
	K3	217.73	213.69	216.12
	R	2.74	5.16	3.01
Longitudinal Uprightness (°)	K1	173.67	197.38	189.25
	K2	192.29	189.08	187.72
	K3	194.56	174.06	183.55
	R	20.89	23.32	5.7

, R_VQ > R_T > R_VX; that is, the degree of influence of test factors on the measure of pot seedling uprightness is in the order of V_Q (forward speed) > T (reflux time period) > V_X (drop speed). Moreover, when the falling speed is 3.5 m/s, the soil reflux period is 0–0.15 s. When the pot seedlings fall into the trench, and the forward speed is 0.8 m/s, the pot seedlings fall into the trench with the best uprightness, and the effect of seedling erection is good.

3.2.2. Influence of Furrow Opener Structural Parameters on Pot Seedling Uprightness

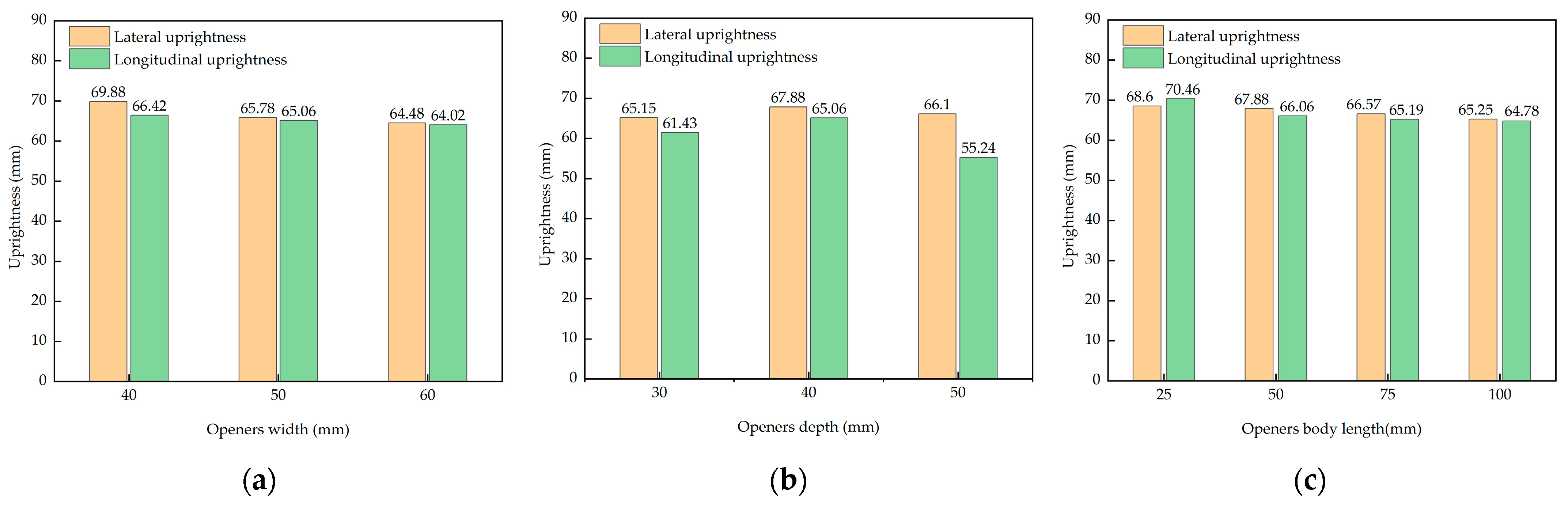
Impact of width: As shown in Figure 14a, there was a significant negative correlation between the width of openers and the uprightness of pot seedlings. At a width of 40 mm, the horizontal and vertical uprightness reached maximum values (69.88°, 66.42°). The smaller the width of the openers, the narrower the trench opened, resulting in a greater clamping effect of soil particles on the potting soil in all directions, which impedes the tilting movement of the pot seedlings and increases the uprightness of the pot seedlings.

Impact of depth: As shown in Figure 14b, uprightness showed a nonlinear response with increasing depth, and the lateral and vertical uprightness values were optimal at 40 mm (67.88°, 64.06°). At the same width, the deeper the trench, the steeper the trench slope, which in turn leads to inconsistent backfilling. This can be seen in the trenching depth of 40 mm, where the trench is the shallowest and the backfilling effect is the most significant, resulting in the largest soil particle entrapment in the potting soil.

Impact of main body length: As shown in Figure 14c, the main body length was negatively correlated with uprightness, which was the greatest at 25 mm (68.60° in the lateral direction and 70.46° in the longitudinal direction). The shorter the length of the openers, the shorter the soil particle backfilling time and, at the same time, the more soil particles are backfilled, increasing the effect of potting soil clamping.

To further characterize the effect of the structural parameters of the openers on the uprightness of the pot seedlings, a Box–Behnken test was conducted to investigate the most favorable opener parameters for pot seedling uprightness. The results are shown in

Table 6. Orthogonal simulation test and results.

Number	Experimental Factors			Lateral Uprightness (°)	Longitudinal Uprightness (°)
	LK	LS	LC
1	0 (50)	−1 (30)	−1 (25)	70.11	68.12
2	0	−1	1 (75)	66.86	61.12
3	−1 (40)	0 (40)	1	66.61	67.54
4	1 (60)	−1	0 (50)	66.11	65.62
5	0	1 (50)	1	63.61	63.01
6	1	1	0	64.64	63.87
7	0	1	−1	68.75	63.34
8	−1	1	0	68.06	68.08
9	0	0	0	67.88	68.06
10	−1	−1	0	69.16	66.15
11	1	0	−1	67.48	66.7
12	−1	0	−1	70.17	68.25
13	0	0	0	68.21	67.97
14	1	0	1	63.03	63.81
15	0	0	0	68.31	69.4

below.

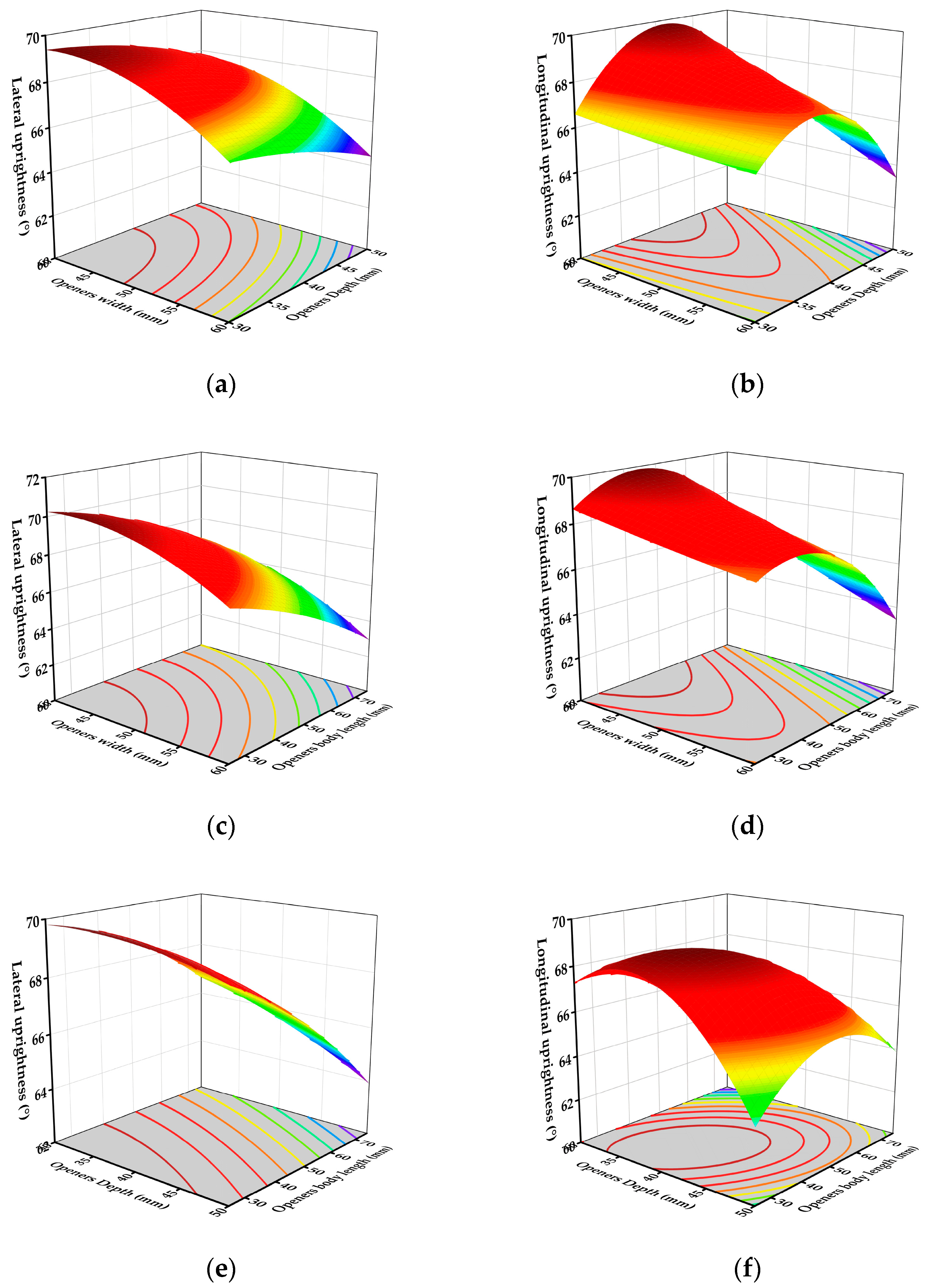
Response surface analysis based on Design-Expert 12 showed that the interaction of the structural parameters of the furrow opener significantly (p < 0.05) affected pot seedling uprightness:

Width–depth interaction (Figure 15a,b): lateral uprightness decreases with increasing width or depth, reaching a maximum at 40 mm (width) × 30 mm (depth); longitudinal uprightness is optimal at 40 mm (width) × 40 mm (depth), with increasing depth triggering nonlinear decay.

Width–body length interaction (Figure 15c,d): lateral uprightness is highest at 40 mm (width) × 25 mm (length), with both increasing width and length weakening the entrapment effect; longitudinal uprightness peaks at 40 mm (width) × 55 mm (length), with too long a length leading to delayed particle coverage.

Depth–body length interaction (Figure 15e,f): the maximum value of lateral uprightness was located at 40 mm (depth) × 25 mm (length), with increasing depth or length exacerbating soil support dispersion; longitudinal uprightness was optimal at 35 mm (depth) × 35 mm (length), with excessively long ends weakening the efficiency of dynamic reflux.

Conclusion: The structural parameters of the furrow opener need to be synergistically optimized to maximize uprightness at a width of 40 mm, a depth of 35–40 mm, and a body length of 25–35 mm.

In order to obtain the best planting results of the furrow opener for pot seedlings, the parameters of width, depth, and length of the furrow opener were optimized using the DesignExpert 12 software, with the goal of optimizing the uprightness of pot seedlings. The constraints are shown in Equation (4). When the width of the furrow opener is 40 mm, the depth is 37.87 mm, and the body length is 32.32 mm, the average lateral uprightness of the pot seedlings can reach about 70°, and the longitudinal uprightness can reach 69.4°.

$$s.t\left\{\begin{array}{l}\mathit{max}{Z}_1,\mathit{max}{Z}_2\\ 40\le L_K\le 60\\ 30\le L_S\le 50\\ 25\le L_C\le 75\end{array}\right.$$

(4)

3.3. Bench Test Results

By comparing the results of the simulation test with those of the validation test, it was found that the uprightness bias of the pot seedling in the bench test and the simulation test was the same, as shown in Figure 16. And the relative error between the actual value and the simulation value is less than 5%, and the rice seedling has a high degree of uprightness after falling into the trench in the test, and the lateral and longitudinal degree of uprightness can reach about 70°.

4. Discussion

The basic principle of seedling throwers is to let the pot seedling fall into the field by its own gravity. In this process, the falling attitude of the seedling and the soil backfilling state have a significant impact on the planting effect [26]. Nowadays, there is a problem of low pot seedling uprightness with commercially available seedling throwers, and at present, research on seedling throwers mostly focuses on the macroscopic level, meaning that understanding of the mechanism of machinery–soil–pot seedling interactions in the process of rice planting and the observation of soil reflux dynamics are also still problematic [2,3,4,5].

In this study, EDEM discrete element simulation software was used as a platform, which can accurately simulate the flow characteristics of soil and can also set up the falling attitude of the pot seedling, so that the pot seedling is not restricted by space and time during the falling process [12,13,14,15]. Based on the above advantages, a more in-depth study on the effect of pot seedling throwing uprightness can be carried out.

From the relative error of 0.85% between the simulation and the actual test two-layer soil model collapse, it can be seen that the constructed soil model can simulate the field soil. When the furrow opener opens the furrow, the furrow soil backfilling shows the three-stage evolution law of “backfilling-covering-stabilizing”, which is due to the flow characteristics of the soil after the furrow opener, resulting in the movement of the soil to heal the furrow pattern. When the falling speed of the pot seedling was 3.5 m/s, the soil backfilling period was 0–0.15 s when falling into the trench, and the advancing speed was 0.8 m/s, the horizontal and vertical uprightness of pot seedling after falling into the trench could reach 67.0 ± 1.2° and 65.2 ± 1.5°. This is because, with the quicker falling speed and faster movement into the trench, both sides of the soil rapidly return to cover the stage, thus hindering the pot seedling’s left and right tilt; at the same time, the slower forward speed will lead to a smaller tilt angle of pot seedlings in the longitudinal direction. With a furrow opener width of 40 mm, depth of 37.87 mm, and body length of 32.32 mm, the pot seedling could achieve 70.0 ± 1.0° lateral uprightness and 69.4 ± 0.8° longitudinal uprightness. This is because the narrow grooves all support the pot seedlings in the vertical direction, increasing the left and right clamping forces hindering pot seedling sink and lateral offset; different-depth grooves’ soil mobility is not the same, because soil mobility at different depths is not consistent; and the longer the length of the furrow opener, the longer the soil reflux time and the slower its dynamic clamping effect. In the above results, although rice pot seedling uprightness has a better effect, the results are based on the simulation test and bench test, and there is still a more significant difference compared to real field operation.

In order to further improve rice potting uprightness, future research will focus on the following aspects:

(1)

Consider the effect of field-specific conditions on pot seedling throwing. In order to further study the quality of pot seedling throwing, further research is needed to take into account the influence of soil changes in paddy fields and rice stubble in the field.

(2)

Research on soil furrow openers in paddy fields. Although a V-type furrow opener is proposed in this study, its furrow opening effect is affected by different soil environments, and its adaptability needs to be further improved.

(3)

Research on furrow-opening and seedling-supporting devices for planting implements. Although the furrow opener can improve the uprightness of rice pot seedlings, adding a seedling support device can further improve the uprightness of pot seedlings.

5. Conclusions

In this study, a coupling model of the furrow opener–soil–pot seedling system was constructed based on the discrete element method, with contact parameters calibrated to verify its accuracy, and the experiment was carried out using the method of synergistic analysis of soil backfilling dynamics and upright planting of rice pot seedlings, which provided an accurate simulation and analysis of the falling process of pot seedlings throwing and optimized the soil opener in paddy fields, providing a guide to improve the uprightness of pot seedling throwing. The main conclusions are as follows:

(1)

The mechanism of open furrow soil backfilling is revealed: the open furrow disturbance is concentrated in the edge region, and the return process is divided into three stages—backfilling (0–0.15 s), covering (0.15–0.30 s), and stabilizing (>0.30 s), which realize the migration of particles, accumulation, and the fixation of furrow shape, respectively.

(2)

Analysis of pot seedlings into the soil: lateral clamping force and longitudinal impact force together reduce the total torque to zero, where the optimal operating parameters of 3.5 m/s drop speed, 0.8 m/s forward speed, and 0.15 s drop time difference achieve lateral and longitudinal uprightness of 67.0 ± 1.2° and 65.2 ± 1.5°, respectively.

(3)

Optimize the structural parameters of the furrow opener: when the width of the furrow opener is 40 mm, the depth is 37.87 mm, and the length of the body is 32.32 mm, the degree of uprightness is improved to 70.0 ± 1.0° (lateral) and 69.4 ± 0.8° (longitudinal).

(4)

Model validation: the error between bench test and simulation results is <5%, and the optimized uprightness of the pot seedling has a significant increase compared to the standard of pot seedling uprightness during throwing (uprightness > 30°), which confirms the reliability of the model and provides theoretical support for the design and parameter regulation of high-speed rice-planting equipment.