Flow Control of Tractor Multi-Channel Hydraulic Tester Based on AMESim and PSO-Optimized Fuzzy-PID
Abstract
1. Introduction
- (1)
- Modeling level: A dynamic torque equation for the ball valve considering the friction coefficient is established, and a modified transfer function model integrating hydraulic fluid force and damping effects is derived to improve the modeling accuracy and dynamic response analysis capability of the hydraulic control system.
- (2)
- Simulation level: On the co-simulation platform of AMESim2020.1 and MATLAB/Simulink, a PSO-based multi-objective fitness function is constructed to perform Pareto-optimal searching for fuzzy quantization factors and PID parameters, thereby enhancing the precision and efficiency of control parameter optimization.
- (3)
- Engineering application level: A hardware-in-the-loop (HIL) testing platform based on the OLE for process control (OPC) protocol is developed to address parameter transfer issues between the simulation environment and real vehicle working conditions, thereby improving the adaptability and reliability of the control strategy in engineering applications.
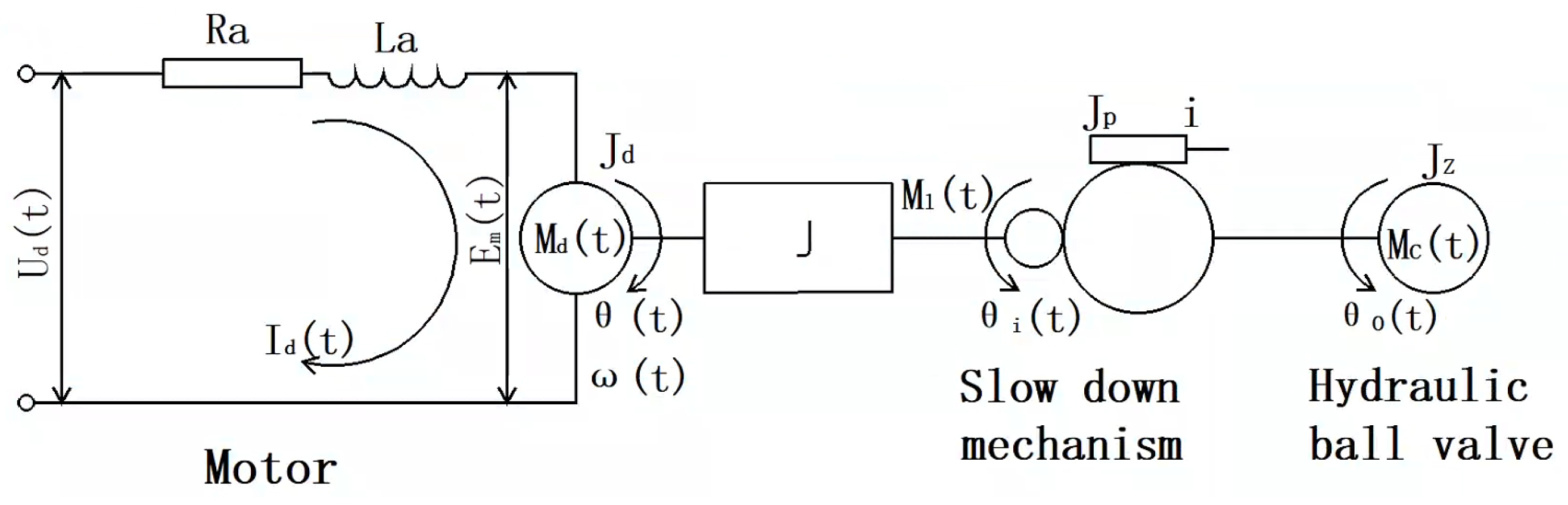
2. Structure and Working Principle of YYSCT-250-3
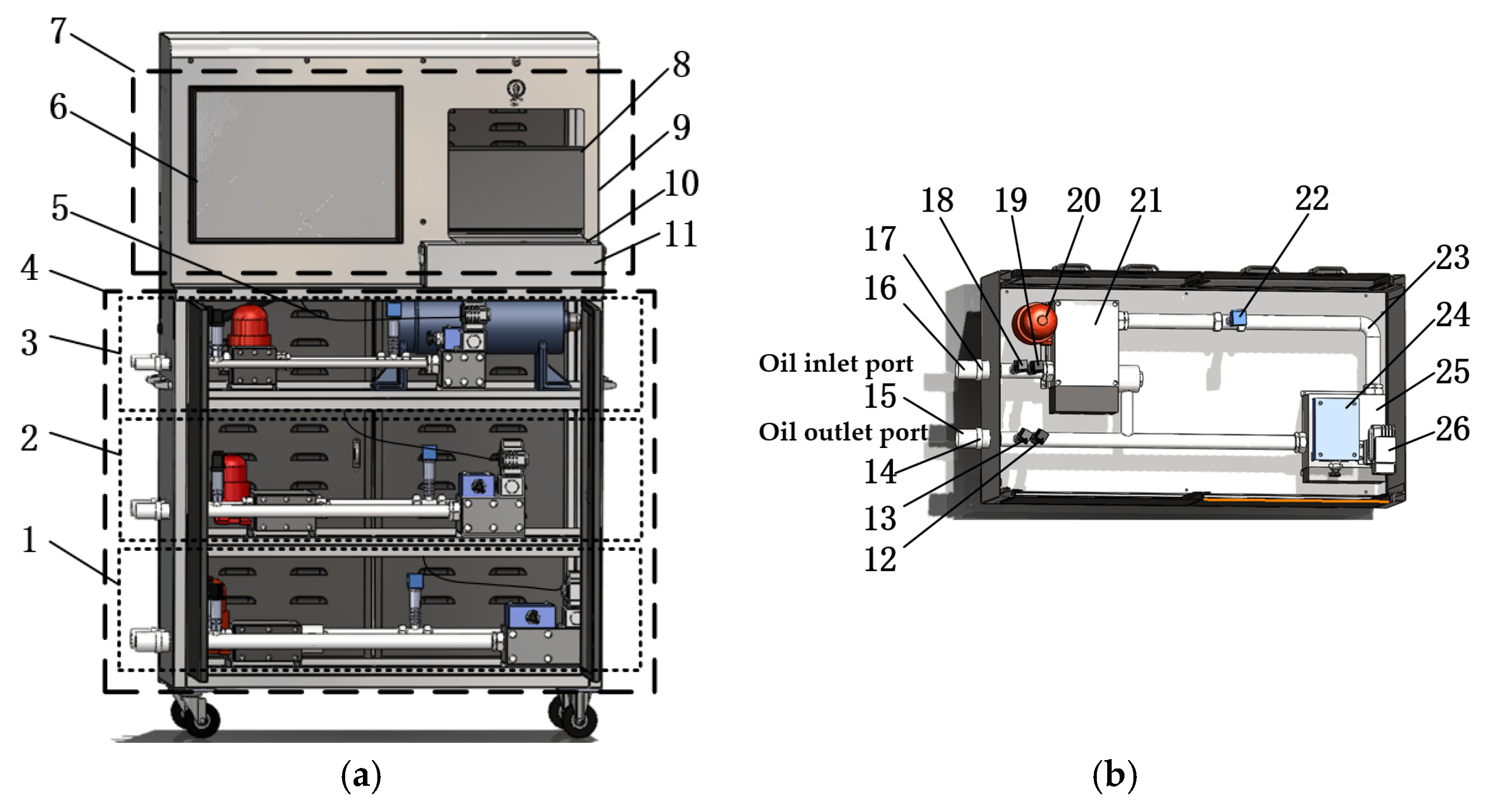
2.1. Structure of YYSCT-250-3
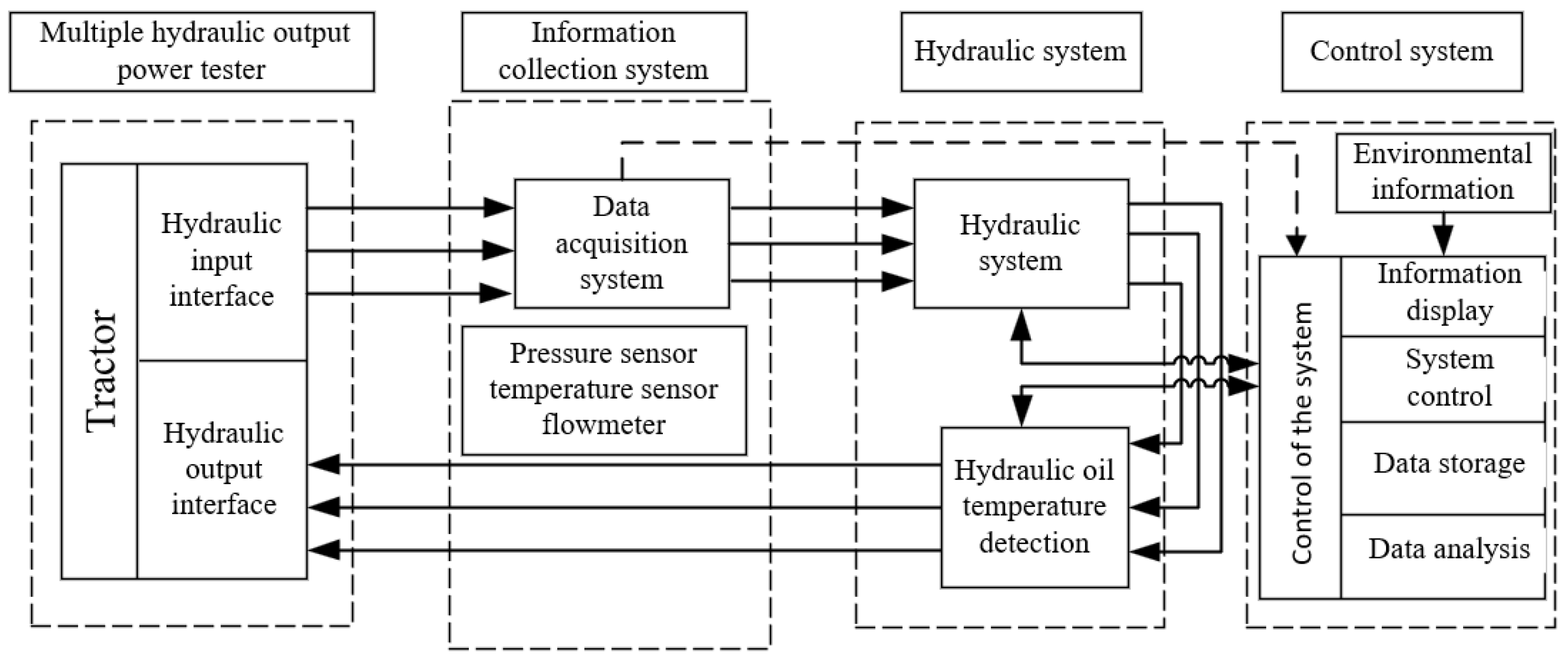
2.2. Composition of Hydraulic Output Power Tester Parameter Detection
2.3. Working Principle of YYSCT-250-3
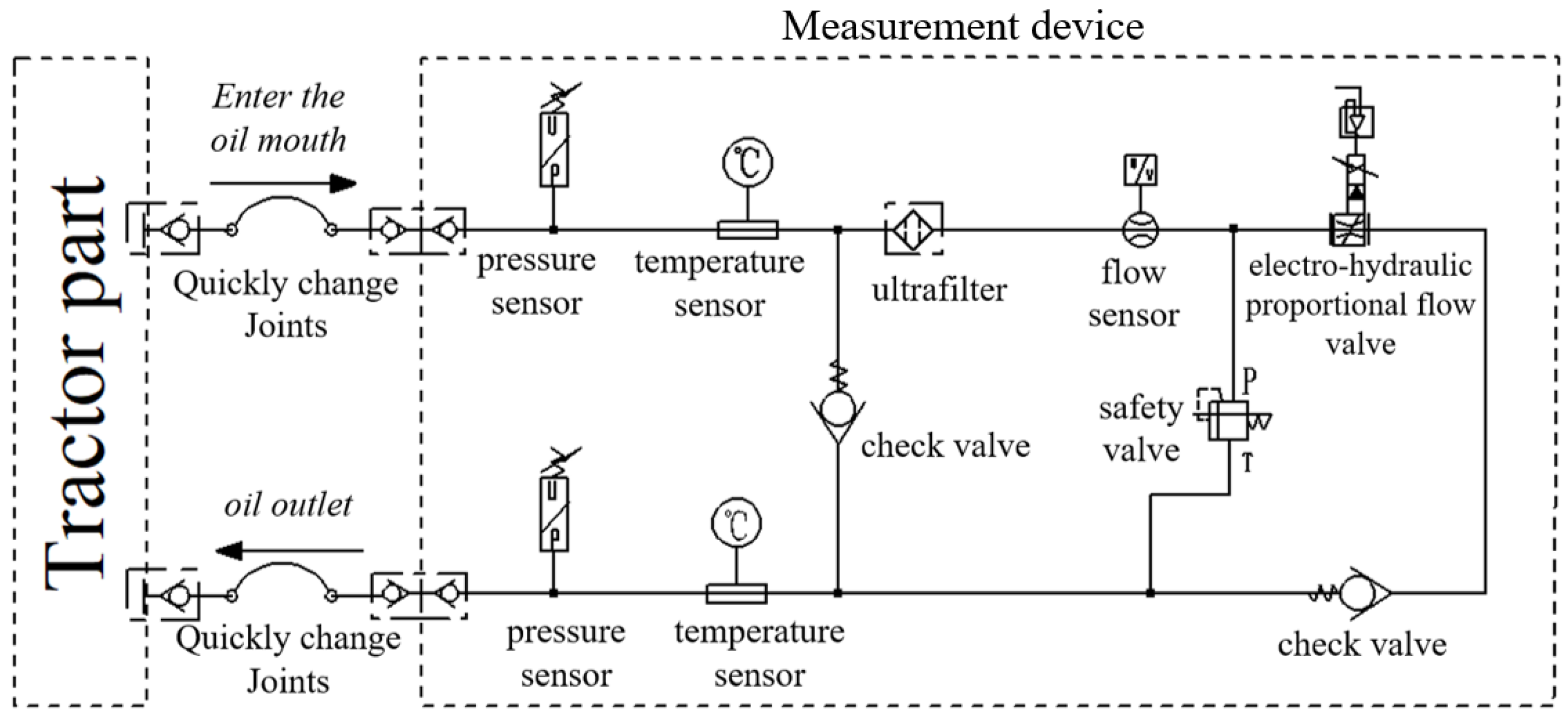
3. Working Principle and Transfer Function Model of Electro-Hydraulic Proportional Flow Valve
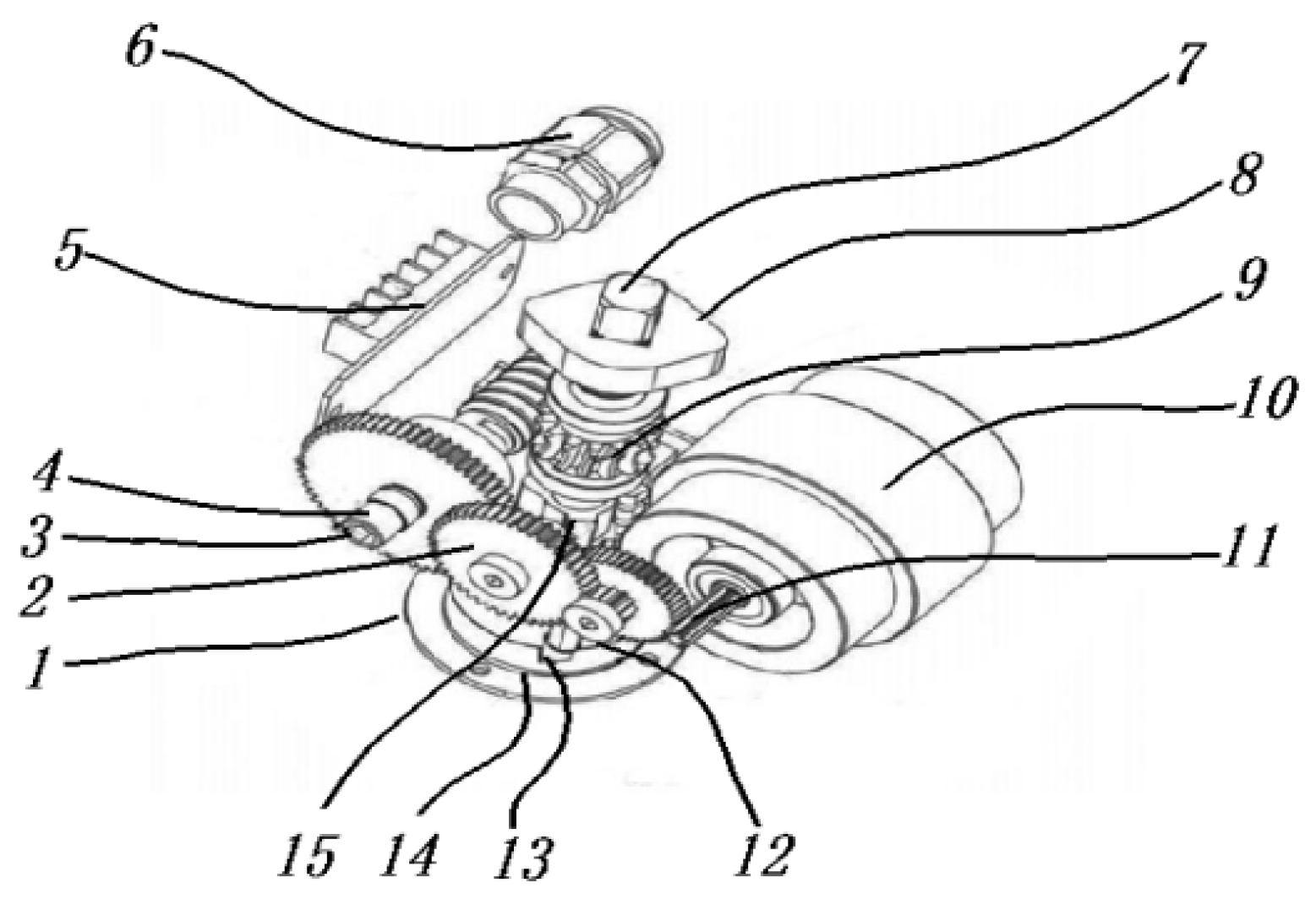
3.1. Working Principle of Electro-Hydraulic Proportional Flow Valve
3.2. Construction of the Transfer Function Model for Electro-Hydraulic Proportional Flow Valve
3.3. Parameter Selection for Electric Actuator
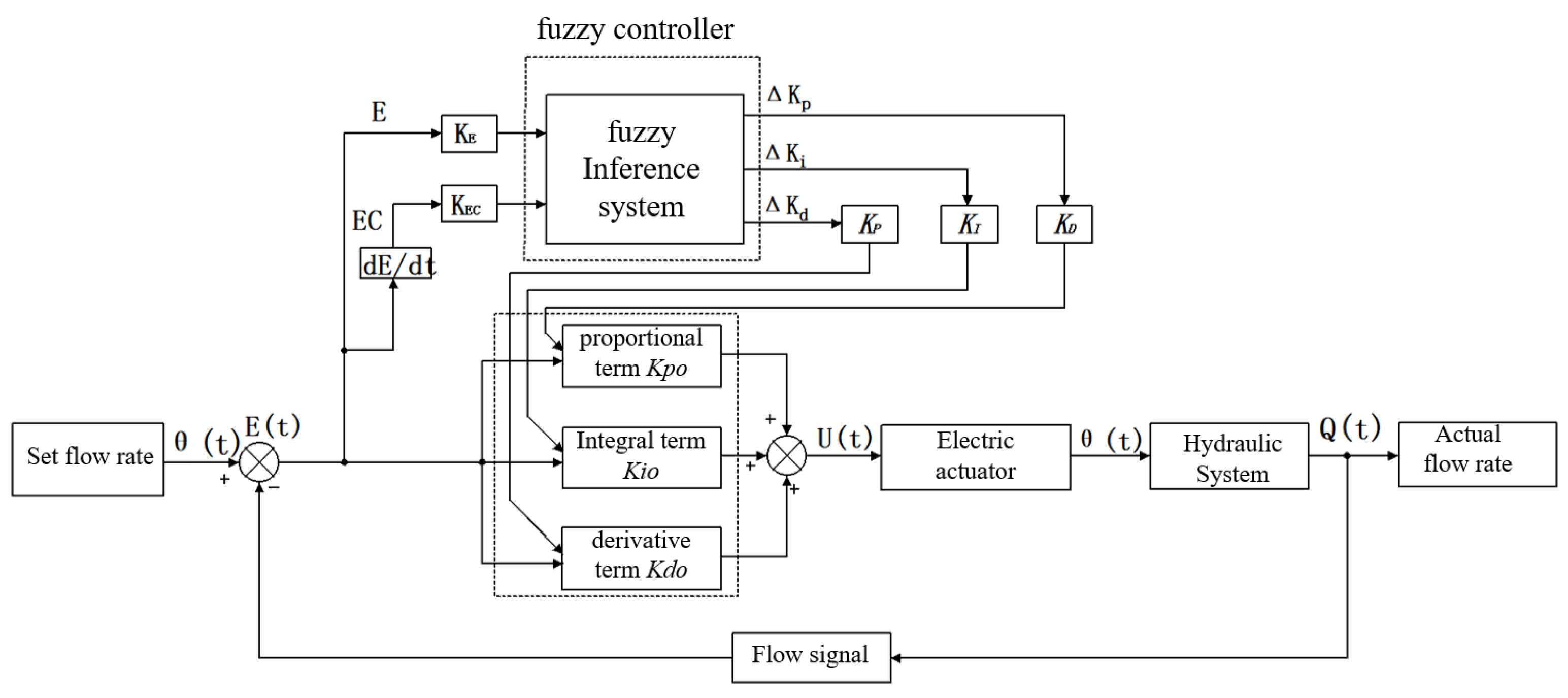
4. Design of Electro-Hydraulic Proportional Flow Controller
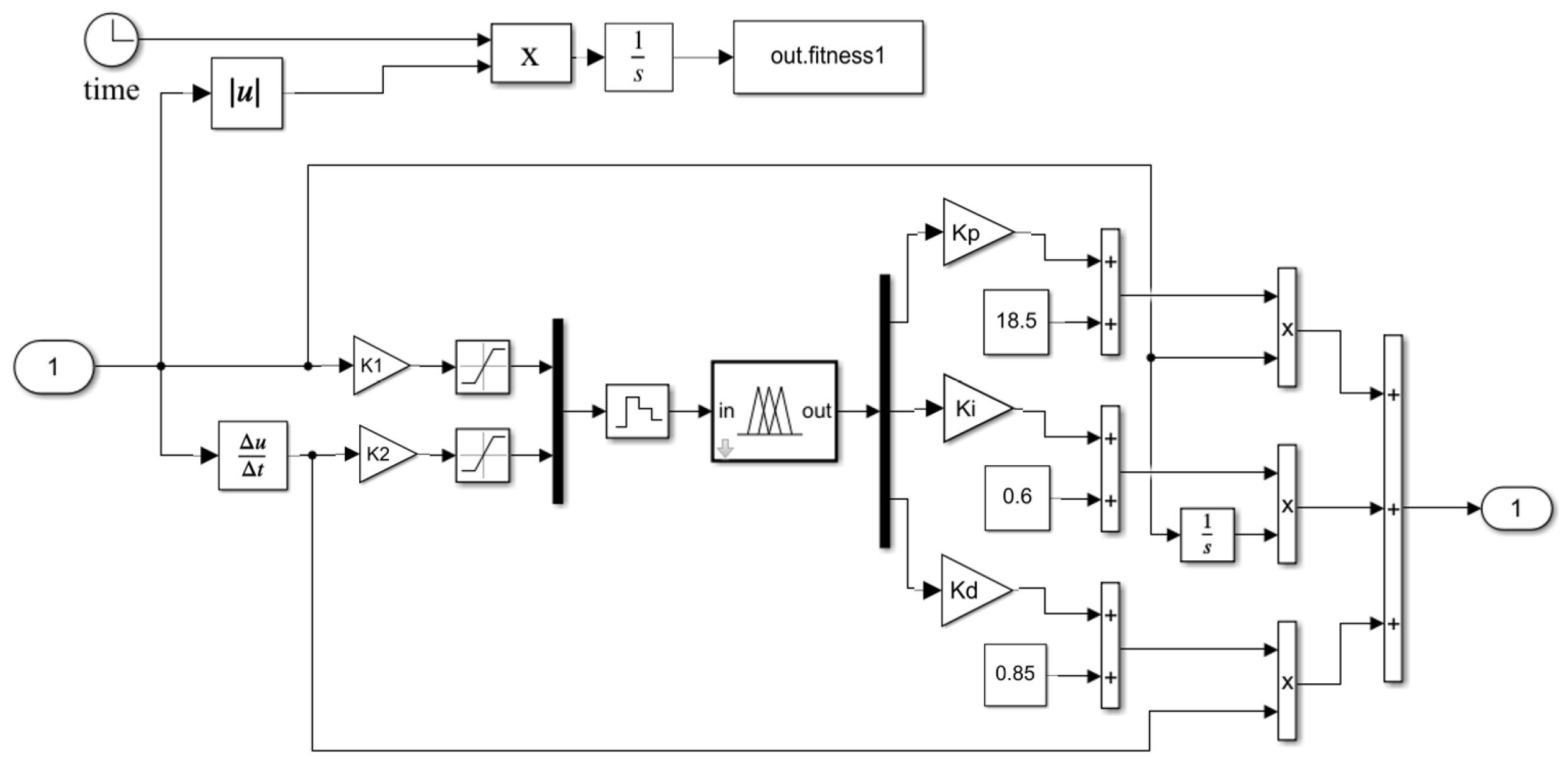
4.1. Fuzzy-PID Controller Design
4.2. Establishment and Fuzzification of Fuzzy Controller Input and Output Variables
4.3. Determination of Membership Functions and Establishment of Fuzzy Control Rules
4.4. PSO-Optimized Fuzzy-PID Control for Flow Valve
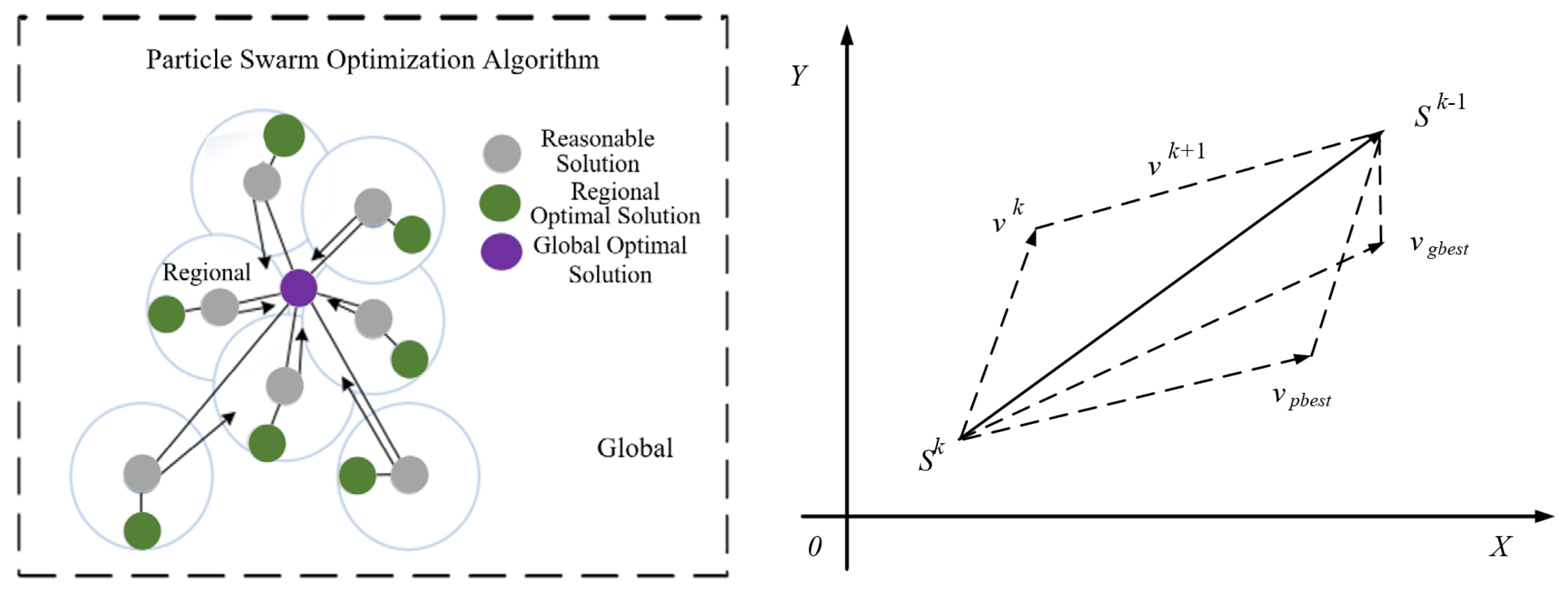
4.4.1. Selection of Objective Function
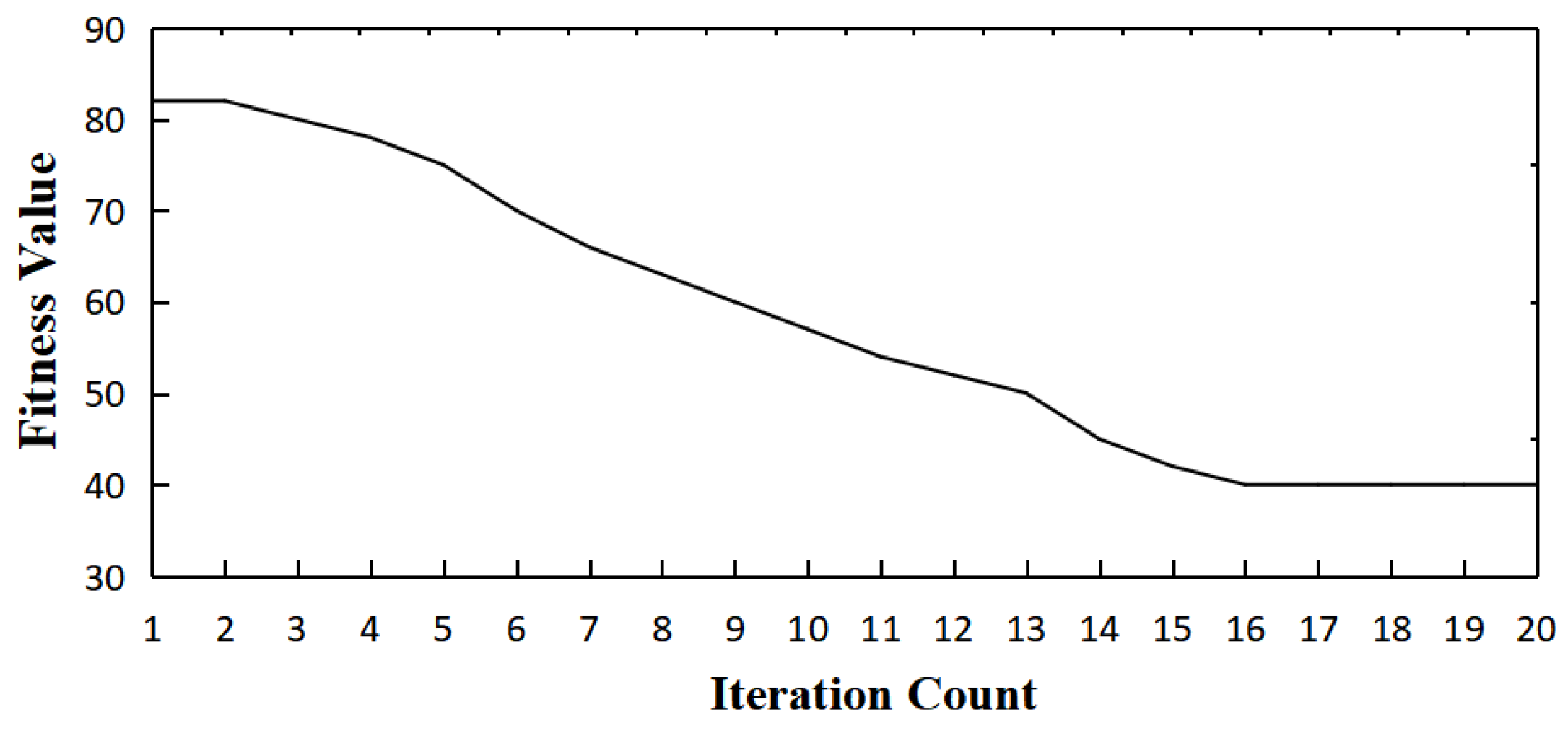
4.4.2. PSO Parameter Settings and Iteration Process
5. Simulation Analysis and Experimental Study of Electro-Hydraulic Proportional Flow Valve Flow Control
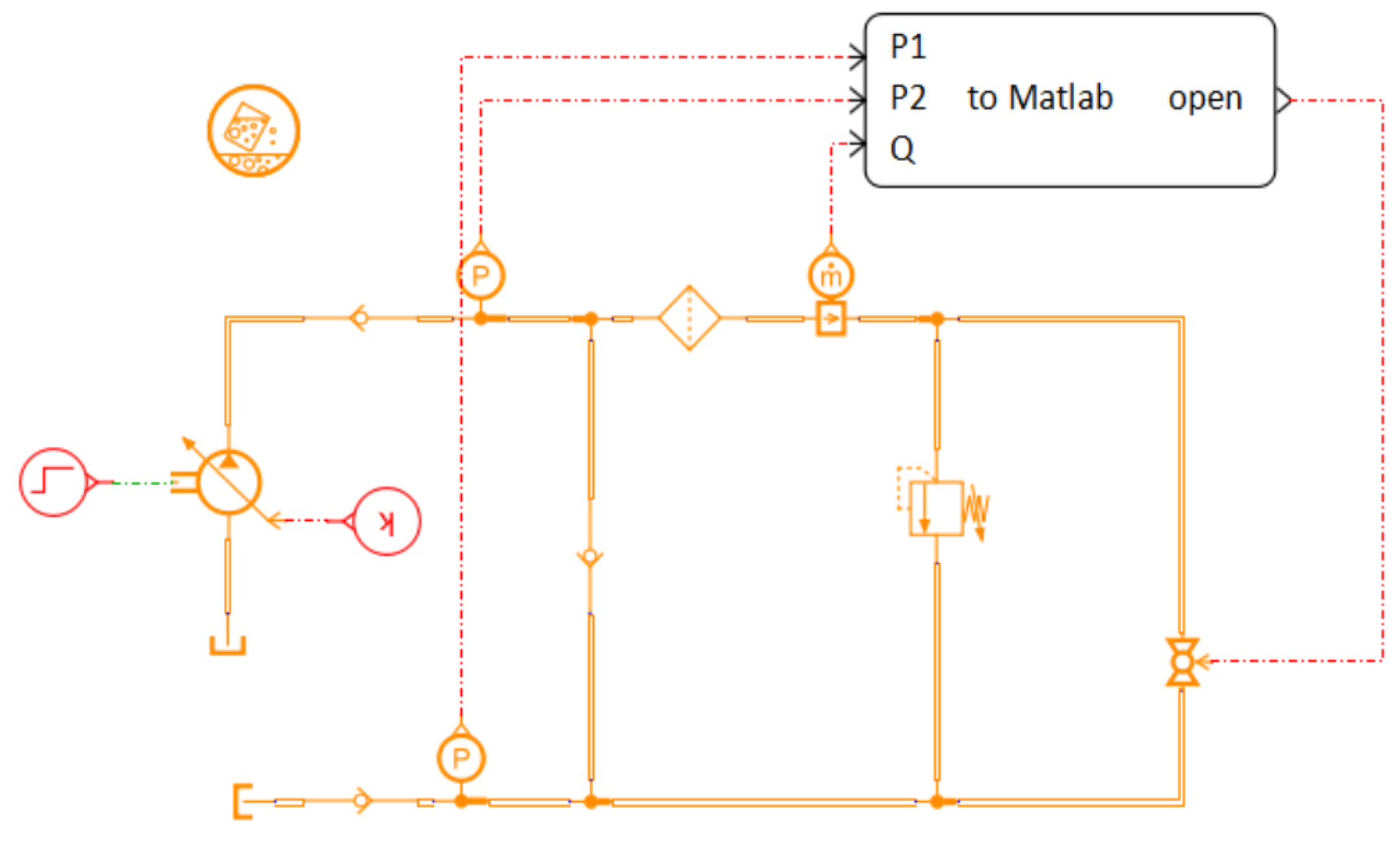
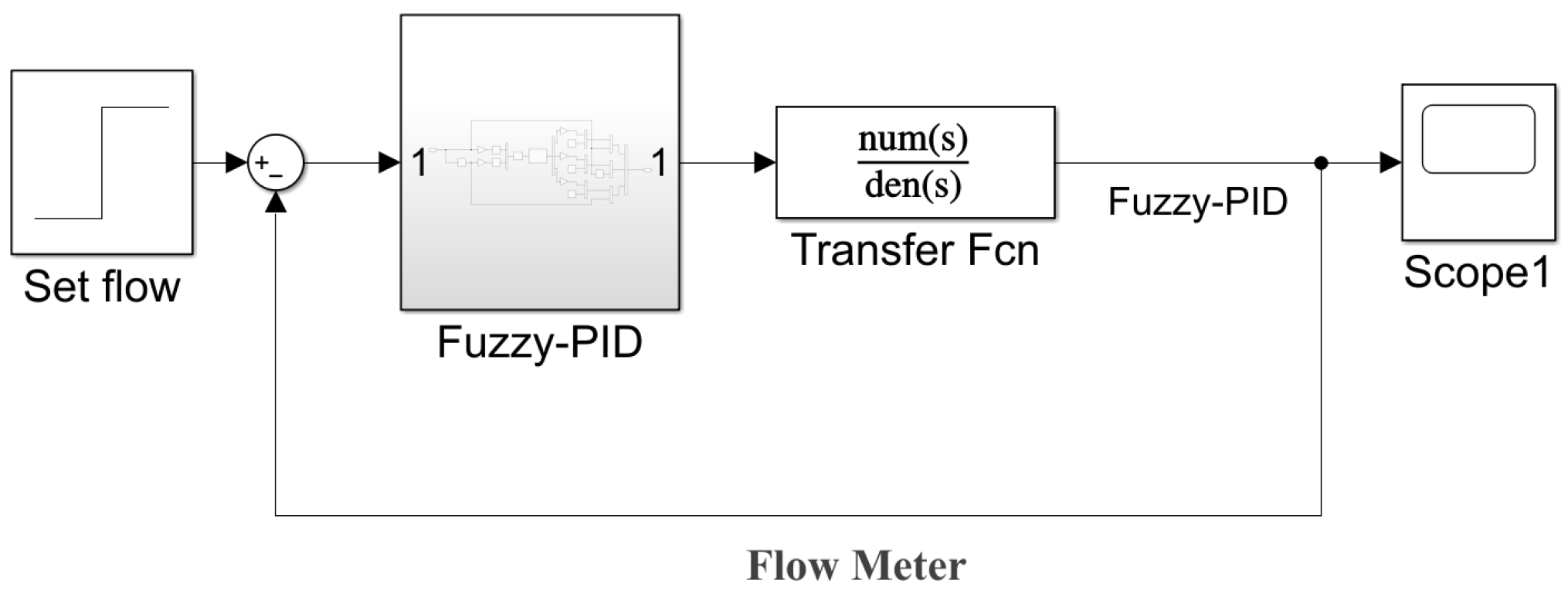
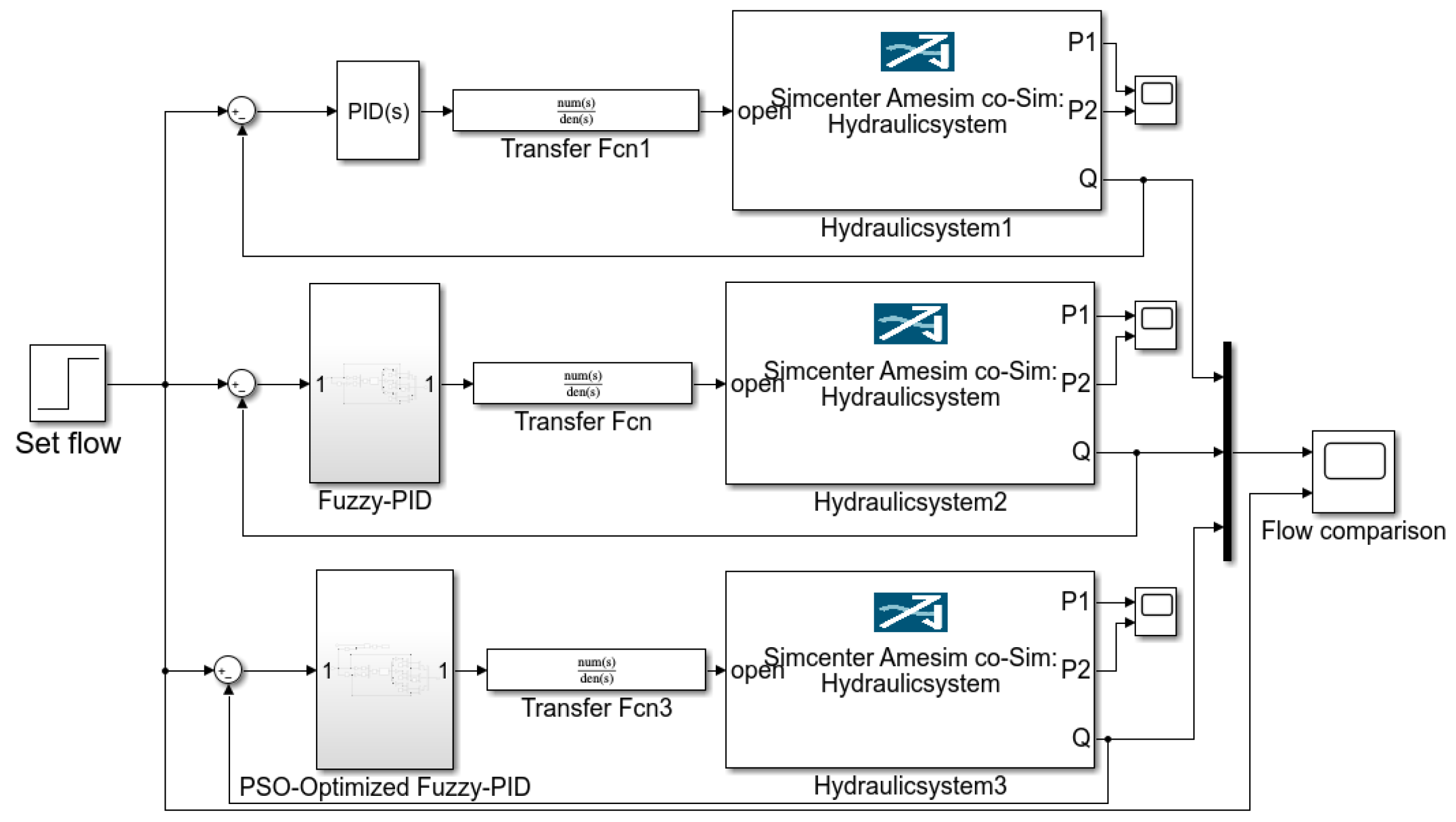
5.1. Establishment of Hydraulic Control System Co-Simulation Model
5.2. Simulation Model of Electro-Hydraulic Proportional Flow Control System
5.3. Stability and Robustness Analysis of the PSO-Optimized Fuzzy-PID Controller
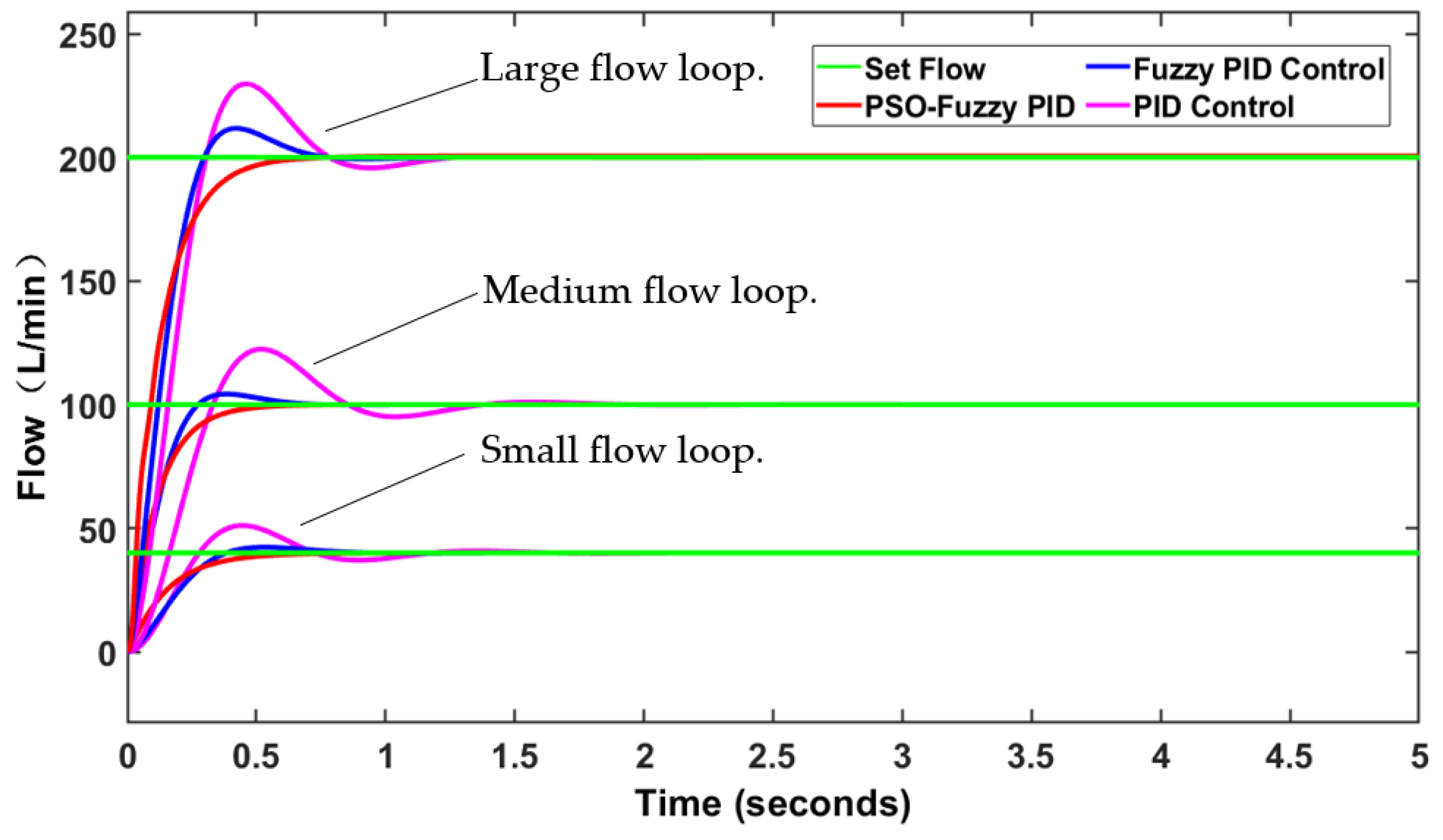
5.4. Analysis of Hydraulic Simulation Results for Different Flow Rate Loop Sections
5.5. Test and Result Analysis
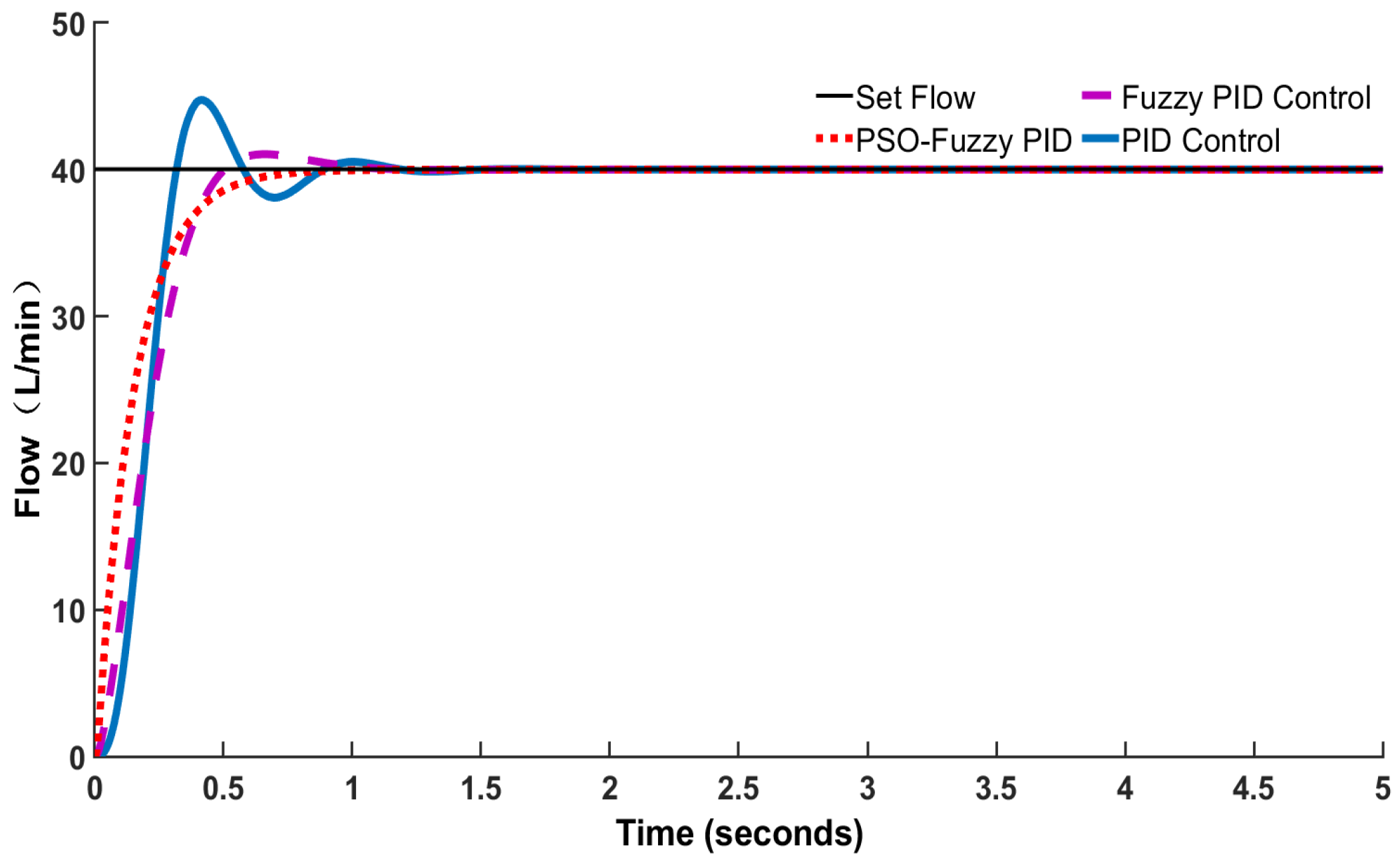
5.5.1. Low Flow Rate YYSCT-250-3 Test
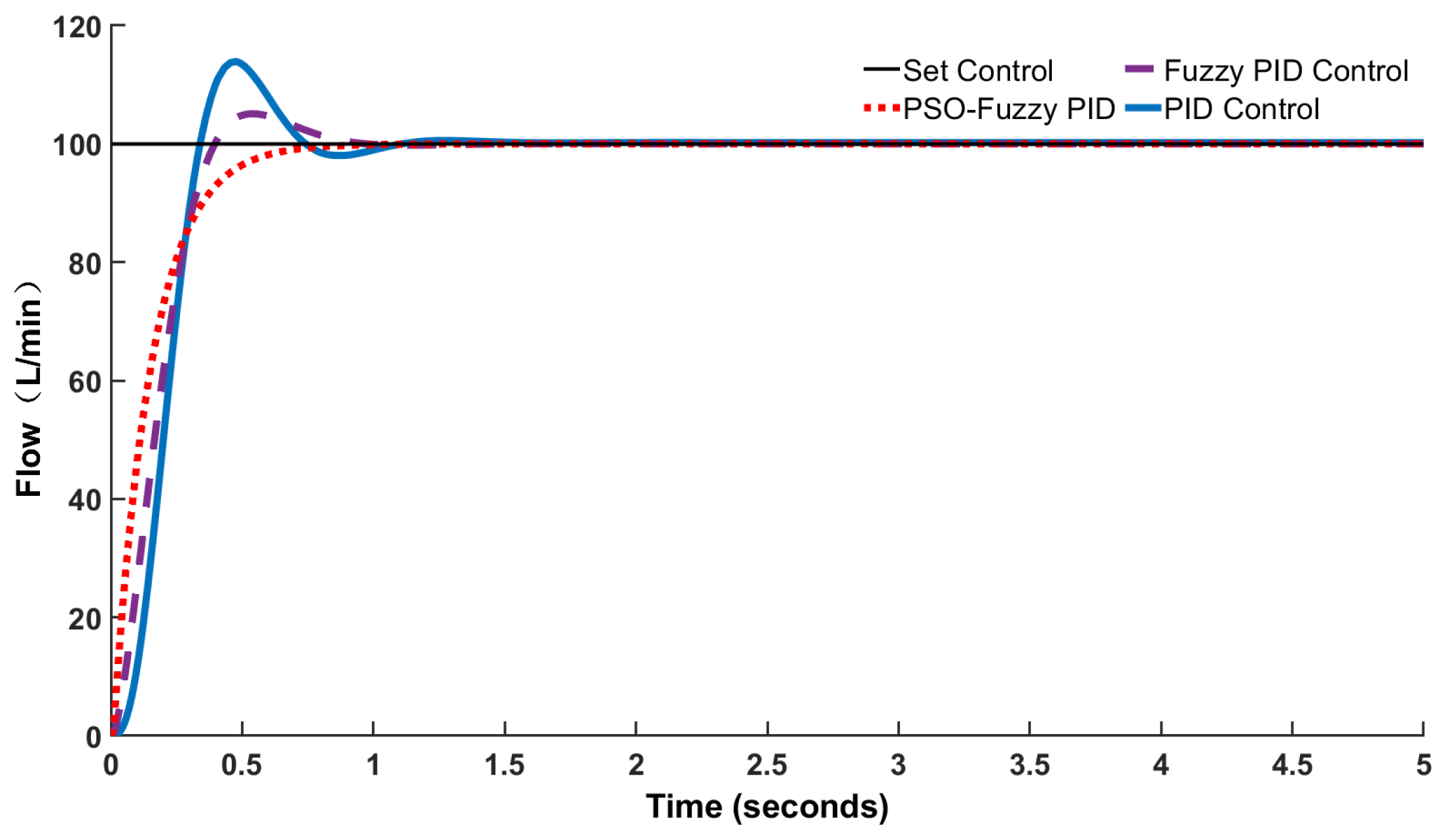
5.5.2. Medium Flow Rate YYSCT-250-3 Test
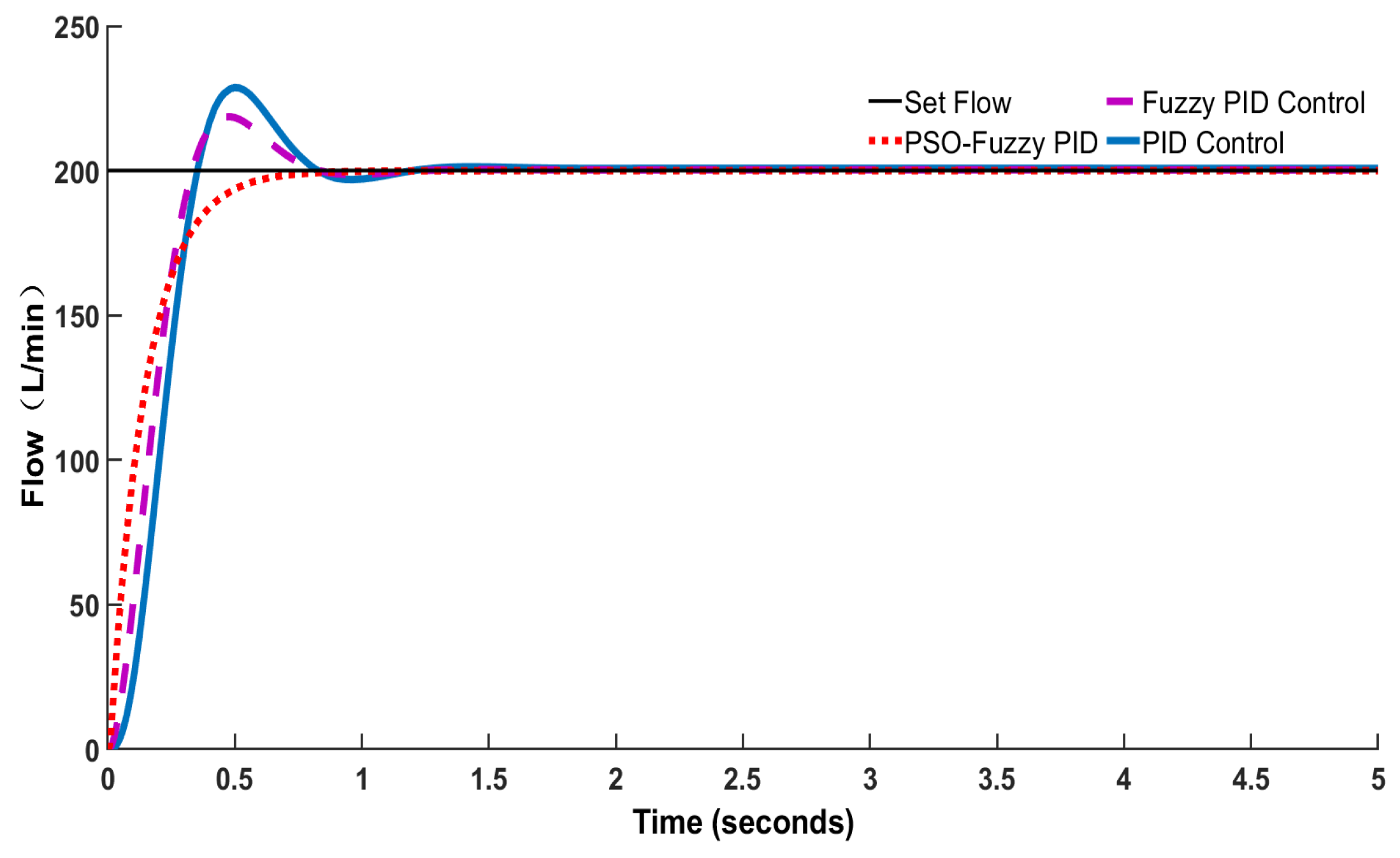
5.5.3. High Flow Rate YYSCT-250-3 Test
6. Conclusions
- (1)
- This work is the first to systematically analyze the nonlinear coupling mechanism between hydraulic damping and friction effects and to establish a modified transfer function model incorporating spool resistance torque and fluid pulsation dynamics. Experimental results show that the prediction error converges within ±0.5%, significantly improving modeling accuracy under complex conditions. The model reveals the mechanical–fluid interaction mechanism from a multi-physics coupling perspective and provides a theoretical foundation for high-precision flow regulation.
- (2)
- The PSO-based multi-objective fitness function within the AMESim–MATLAB co-simulation framework overcomes the empirical dependency of traditional Fuzzy-PID control. Tests show that, under 40 L/min conditions, the system overshoot is reduced by 78.9% compared to segmented PID [3] (from 1.42% to 0.3%), and the number of convergence iterations is 37% lower than that of GA-optimized control [18] (from 32 to 20), demonstrating the algorithm’s global optimization efficiency and control robustness in complex hydraulic systems.
- (3)
- The hardware-in-the-loop (HIL) testing platform based on the OPC protocol resolves the parameter transfer gap between simulation and real-vehicle conditions. Under steady-state flow conditions (40–200 L/min), the absolute control error is within ±0.5 L/min (relative error ≤ ±1.0%), showing superior accuracy and consistency over traditional Fuzzy-PID methods [7]. The modular plug-and-play design offers a standardized technical interface for the intelligent upgrade of agricultural hydraulic systems.
- (4)
- The current model does not account for viscosity changes under extreme oil temperatures (<−20 °C or >60 °C). Future work will incorporate temperature–viscosity compensation to enhance environmental adaptability. In addition, advanced control methods such as adaptive robust control (ARC) and model predictive control (MPC) will be introduced to improve real-time control accuracy and expand the theoretical and technical scope of intelligent control in agricultural hydraulics. In addition, online self-tuning mechanisms and machine-vision-based flow detection will be introduced to establish a more intelligent, closed-loop adaptive control system.
- (5)
- In terms of scalability, future work will explore coordinated control strategies for multi-channel hydraulic circuits to mitigate power oscillations caused by uneven flow distribution. The proposed friction–flow coupling model shows potential for lifespan prediction, expanding the theoretical perspective of condition monitoring. The PSO-Fuzzy-PID approach also demonstrates good transferability to scenarios such as combine harvester drive control and precision irrigation distribution. Future research will integrate emerging technologies such as digital twins and edge computing to promote the evolution of agricultural hydraulic systems toward adaptive, high-reliability, and low-energy solutions.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gu, L.C.; Qi, Z.L.; Li, J.B. Application study of fuzzy and PID control in flow control of hydraulic power source at variable speed. Mech. Des. Manuf. 2021, 4, 29–33. [Google Scholar]
- Ma, F.; Miao, J.; Fan, G.; Li, S.; Ye, F.; Luo, Y. Design and Experiment of a Profiling Soil Covering Device for Sugarcane Planter in Hilly Areas. Trans. Chin. Soc. Agric. Eng. 2025, X, 1–11. [Google Scholar]
- Wang, H.; Liu, Y.H.; Zhou, L.M.; Zhou, H.Y.; Niu, K.; Xu, M.H. Design and Experiment of a Segmented PID Control System for Fertilizer Flow in a Fertilizer Seeder. Trans. Chin. Soc. Agric. Mach. 2023, 54, 32–40+94. [Google Scholar]
- Ketelsen, S.; Padovani, D.; Andersen, T.O.; Ebbesen, M.K.; Schmidt, L. Classification and Review of Pump-Controlled Differential Cylinder Drives. Energies 2019, 12, 1293. [Google Scholar] [CrossRef]
- Sun, C.; Dong, X.; Wang, M.; Li, J. Sliding mode control of electro-hydraulic position servo system based on adaptive reaching law. Appl. Sci. 2022, 12, 6897. [Google Scholar] [CrossRef]
- Li, M.S.; Ye, J.; Xie, B.; Yang, S.; Zeng, B.G.; Liu, J. Design and Experiment of a Hydraulic Proportional Flow Valve for Tractor Hydraulic Chassis. Trans. Chin. Soc. Agric. Mach. 2018, 49, 397–403. [Google Scholar]
- Mao, W.; Ji, Z.K.; Wei, H.L.; Peng, X.W. Application Research of Fuzzy PID Composite Control in Electro-Hydraulic Proportional Servo Systems. Hydraul. Pneum. 2019, 1, 95–99. [Google Scholar] [CrossRef]
- Li, H.T.; Li, W.; Hu, C.Y.; Wang, R.; Luo, K.K. Fault-Tolerant Control Method for Electro-Hydraulic Servo Systems Based on Fuzzy PID Signal Compensation. Gas Turbine Technol. 2021, 34, 15–22. [Google Scholar]
- Li, W.J.; Gong, G.F.; Liu, J.; Zhang, Y.K.; Yang, H.Y. Simulation of Train Braking Electro-Hydraulic System Based on High-Frequency Solenoid Valve Pressure Control. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 340–348. [Google Scholar]
- Wrat, G.; Bhola, M.; Ranjan, P.; Mishra, S.K.; Das, J. Energy Saving and Fuzzy-PID Position Control of Electro-Hydraulic System by Leakage Compensation through Proportional Flow Control Valve. ISA Trans. 2020, 101, 269–280. [Google Scholar] [CrossRef]
- Huang, K.W.; Qin, X.P.; Zhan, J.; She, Y.; Wu, F.; Miao, D.; Yang, S.M. Fuzzy PID Control for Hydraulic Steering of Heavy-Duty AGV. Hydraul. Pneum. 2021, 45, 108–115. [Google Scholar]
- Chen, Z.G.; Hu, S.C.; Li, X.Q. Variable amplitude hydraulic control system based on fuzzy PID. Chin. Hydraul. Pneum. 2021, 45, 156–162. [Google Scholar]
- Luo, Q.Z.; An, A.M.; Zhang, H.C.; Meng, F.C. Non-Linear Performance Analysis and Voltage Control of MFC Based on Feedforward Fuzzy Logic PID Strategy. J. Cent. South Univ. 2019, 26, 3359–3371. [Google Scholar] [CrossRef]
- Ghasemi, A.; Azimi, M.M. Adaptive fuzzy PID control based on nonlinear disturbance observer for quadrotor. J. Vib. Control 2022, 29, 965–2977. [Google Scholar] [CrossRef]
- Peng, H.; Wang, J.Z.; Shen, W.; Li, D.Y. Application of Dual Fuzzy Control with Compensation Factor in Electro-Hydraulic Servo Valve-Controlled Asymmetric Cylinder Systems. J. Mech. Eng. 2017, 53, 184–192. [Google Scholar] [CrossRef]
- Niu, B. Research on Performance of Intelligent Control Valve Based on PID Fuzzy Control. Supervisor: Fan, Y.G. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2023. [Google Scholar]
- Hou, Y.; Fan, J. Research on Hydraulic Drive Active Heaving Compensation Predictive Control Based on Neural Network PID Control. J. Mach. Tools Hydraul. 2020, 48, 145–148. [Google Scholar]
- Mounce, S.; Shepherd, W.; Ostojin, S.; Abdel-Aal, M.; Schellart, A.; Shucksmith, J.; Tait, S. Optimisation of a fuzzy logic-based local real-time control system for mitigation of sewer flooding using genetic algorithms. J. Hydroinform. 2020, 22, 281–295. [Google Scholar] [CrossRef]
- Liu, B. Speed Tracking Control of Vehicle Hydraulic Transmission Based on IPSO Fuzzy PID. Automot. Maint. 2024, 3, 26–28. [Google Scholar]
- Shen, Z.; Cheng, H.; Li, H. Design of an Electro-hydraulic Proportional Position Control System for Sugarcane Topper Cutter Based on Fuzzy PID Method. Trans. Chin. Soc. Agric. Mach. 2025, Online First, 1–13. Available online: http://kns.cnki.net/kcms/detail/11.1964.s.20241010.1555.002.html (accessed on 22 February 2025).
- Li, Y.; Li, Y.Z. Fuzzy PID parameter optimization of valve controlled hydraulic cylinder based on improved ant colony algorithm. Mach. Des. Manuf. 2018, 7, 143–146. [Google Scholar]
- Wu, C.W.; Zhu, Y.C.; Gao, Q. Fuzzy adaptive PID control of pneumatic position servo system using high-speed on/off valves. Chin. Hydraul. Pneum. 2021, 45, 47–53. [Google Scholar]
- Zhang, J.; Zhang, C.Y.; Zhang, S.H.; Hu, Z.Q. Multi-Cylinder Position Synchronization Control Based on Mean Coupling. Hydraul. Pneum. 2021, 2, 50–55. [Google Scholar]
- Zhao, S. Research on the hydraulic servo flow control method based on LADRC. J. Eng. Mech. Control 2022, 20, 45–52. [Google Scholar]
- Yao, Y.F.; Chen, X.G.; Ji, C.; Chen, J.C.; Zhang, H.; Pan, F. Design and Experiment of a Monomer Actuator for Corn Precision Planters Based on Fuzzy PID Control. Trans. Chin. Soc. Agric. Eng. 2022, 38, 12–21. [Google Scholar]
- Qi, W.; Yang, B.; Chao, Y. Research on Synchronization of Hydraulic Fracturing Pumps Based on Fuzzy RBF. Mach. Tool Hydraul. 2023, 51, 44–50. [Google Scholar]
- Mao, W.; Zheng, Y.S.; Wang, D.R.; Sun, J.; Dou, X.Z. Analysis of Flow Characteristics of V-Ball Valves with Different Cone Angles. Hydraul. Pneum. 2021, 45, 165–171. [Google Scholar]
- Yi, P.F.; Ma, S.W.; Zhang, J.P.; Li, Y.F.; Ren, L. Transient Flow Characteristics Analysis of PVC Ball Valves Based on Dynamic Mesh Simulation. J. Water Resour. Archit. Eng. 2022, 20, 130–135+141. [Google Scholar]
- Xiao, M.H.; Ma, Y.; Wang, C.; Chen, J.; Zhu, Y.; Bartos, P.; Geng, G. Design and Experiment of Fuzzy-PID Based Tillage Depth Control System for a Self-Propelled Electric Tiller. Int. J. Agric. Biol. Eng. 2023, 16, 116–125. [Google Scholar] [CrossRef]
- Chen, L.J.; Peng, Z.Q.; Sun, J.Q.; Gao, W.; Hua, Z.; Ai, C. Adaptive Compensation Control for Nonlinear Position of Pilot-Operated Electro-Hydraulic Proportional Valves. Hydraul. Pneum. 2021, 45, 64–71. [Google Scholar]
- Solovjev, D.S. Improving the electroplating coating uniformity based on fuzzy control of the setting value using the combined defuzzification method with the presence of stochastic influences. Solid State Phenom. 2022, 6653, 112–120. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Q.; Bai, J.; Xu, X.; Yao, Y.; Fang, W. A Temperature Control Method for Microaccelerometer Chips Based on Genetic Algorithm and Fuzzy PID Control. Micromachines 2021, 12, 1511. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.D.; Zhang, Y.C. Research on speed control of hydraulic drive spindle based on fuzzy adaptive PID controller. Chin. J. Eng. Mach. 2020, 18, 516–520. [Google Scholar]
- Tian, M.; Platinum, B.; Li, J.H.Q. A fertilization control system based on genetic algorithm. J. Agric. Eng. 2021, 37, 21–30. [Google Scholar]
- Hao, W.; Jiyun, Z.; Chao, C.; Yunfei, W.; He, Z. Modeling and simulation analysis of a novel proportional water flow valve with a digital pilot stage. Proc. Inst. Mech. Eng. Part E 2024, 09544089231224325. [Google Scholar] [CrossRef]

| Parameters | Units | Values |
|---|---|---|
| Overall dimensions (door closed state) | mm | 1200 × 700 × 1800 |
| Supply voltage | Hz | 220 VAC/50 Hz |
| Weight | kg | 350 |
| Low flow | L/min | ~100 |
| Medium flow | L/min | ~166 |
| High flow | L/min | ~250 |
| Hydraulic input/output port pressure | MPa | (0~40) MPa, accuracy: 0.5% FS |
| Hydraulic oil temperature | °C | (0~150) °C, accuracy: ±0.5 °C |
| Parameters | NT-5-50 N·m | NT-10-100 N·m |
|---|---|---|
| Motor shaft moment of inertia (J) | 6.01 × 10−4 kg·m2 | 1.2 × 10−3 kg·m2 |
| Friction coefficient (f) | 1.4 × 10−5 N·m·s/rad | 2.8 × 10−5 N·m·s/rad |
| Stator resistance (Ra) | 2.12 Ω | 1.56 Ω |
| Gear reduction ratio (i) | 100 | 100 |
| Motor back-EMF constant (Ke) | 0.126 V/rad | 0.25 V/rad |
| Electrical inductance (La) | 4.2 mH | 4.52 mH |
| Torque constant (Km) | 15.9 N·m/A | 8.7 N·m/A |
| Moment of inertia of the load ball valve (Jz) | 1.0 × 10−5 kg·m2 | 7.7 × 10−5 kg·m2 |
| EC\E | NB | NM | NS | Z0 | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| NB | ZO/NB/NS | ZO/NB/NS | PS/NB/NS | PS/NM/NS | PM/ZO/NS | PM/ZO/NS | PM/ZO/NS |
| NM | ZO/NB/NS | ZO/NB/NS | PS/NM/NS | PS/NM/NS | PM/NS/NS | PM/ZO/NS | PM/ZO/NS |
| NS | ZO/NM/NS | ZO/NM/NS | PS/ZO/NS | PS/NS/NS | PM/ZO/ZO | PM/PS/ZO | PM/PS/ZO |
| Z0 | ZO/ZO/NS | ZO/NS/NS | PS/ZO/ZO | PS/ZO/ZO | PM/PS/ZO | PM/PM/PS | PM/PM/PS |
| PS | PS/NM/NS | PS/NS/NS | PS/ZO/ZO | PS/PS/ZO | PM/PS/ZO | PM/PM/PS | PM/PB/PS |
| PM | PS/NM/PS | PS/ZO/PS | PM/PS/PS | PM/PM/PS | PB/PM/PS | PB/PB/PS | PB/PB/PS |
| PB | PS/ZO/PS | PS/ZO/PM | PM/ZO/PM | PM/PM/PM | PB/PB/PM | PB/PB/PB | PB/PB/PM |
| Name | n | c1, c2 | N | D | t |
|---|---|---|---|---|---|
| Parameter | 0.9 | 2 | 50 | 5 | 20 |
| Parameter-Tuning Results | Ke | Kec | Kp | Ki | Kd | ITAE |
|---|---|---|---|---|---|---|
| PSO-Optimized Parameter Values | 0.12 | 0.006 | 9.16 | 0.08 | 0.5 | 0.041 |
| Number of Runs (i) | ITAE(i) | Number of Runs (i) | ITAE(i) | Number of Runs (i) | ITAE(i) | Number of Runs (i) | ITAE(i) |
|---|---|---|---|---|---|---|---|
| 1 | 0.0417 | 6 | 0.0408 | 11 | 0.0404 | 16 | 0.0409 |
| 2 | 0.0409 | 7 | 0.0414 | 12 | 0.0412 | 17 | 0.0411 |
| 3 | 0.0405 | 8 | 0.0406 | 13 | 0.0408 | 18 | 0.0406 |
| 4 | 0.0411 | 9 | 0.0410 | 14 | 0.0408 | 19 | 0.0415 |
| 5 | 0.0413 | 10 | 0.0407 | 15 | 0.0413 | 20 | 0.0410 |
| Category | Overshoot | Response Time | Settling Time | |
|---|---|---|---|---|
| Low-flow loop | PID | 17.6% | 0.48 s | 1.64 s |
| Fuzzy-PID | 6.2% | 0.51 s | 0.85 s | |
| PSO-optimized Fuzzy-PID | 0.1% | 0.68 s | 0.76 s | |
| Medium-flow loop | PID | 22.3% | 0.62 s | 1.71 s |
| Fuzzy-PID | 5.8% | 0.43 s | 0.78 s | |
| PSO-optimized Fuzzy-PID | 0.1% | 0.58 s | 0.69 s | |
| High-flow loop | 13.00% | 0.54 s | 1.16 s | 13.00% |
| 4.00% | 0.46 s | 0.69 s | 4.00% | |
| 0.06% | 0.44 s | 0.51 s | 0.06% | |
| Flow Specifications (L/min) | Controlling Means | Overshoot (%) | Settling Time (s) | Response Time (s) |
|---|---|---|---|---|
| Low flow 40 L/min | PID | 9.0 | 1.00 | 0.30 |
| Fuzzy-PID | 2.4 | 0.88 | 0.30 | |
| PSO-Fuzzy PID | 0 | 0.80 | 0.30 | |
| Medium flow 100 L/min | PID | 16.9 | 1.10 | 0.32 |
| Fuzzy-PID | 7.8 | 0.90 | 0.32 | |
| PSO-Fuzzy PID | 0 | 0.78 | 0.32 | |
| High flow 200 L/min | PID | 14.6 | 1.40 | 0.35 |
| Fuzzy-PID | 11.5 | 0.92 | 0.35 | |
| PSO-Fuzzy PID | 0 | 0.82 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Bai, X.; Lu, Y.; Deng, X.; Lu, Z. Flow Control of Tractor Multi-Channel Hydraulic Tester Based on AMESim and PSO-Optimized Fuzzy-PID. Agriculture 2025, 15, 1190. https://doi.org/10.3390/agriculture15111190
Li Q, Bai X, Lu Y, Deng X, Lu Z. Flow Control of Tractor Multi-Channel Hydraulic Tester Based on AMESim and PSO-Optimized Fuzzy-PID. Agriculture. 2025; 15(11):1190. https://doi.org/10.3390/agriculture15111190
Chicago/Turabian StyleLi, Qinglun, Xuefeng Bai, Yang Lu, Xiaoting Deng, and Zhixiong Lu. 2025. "Flow Control of Tractor Multi-Channel Hydraulic Tester Based on AMESim and PSO-Optimized Fuzzy-PID" Agriculture 15, no. 11: 1190. https://doi.org/10.3390/agriculture15111190
APA StyleLi, Q., Bai, X., Lu, Y., Deng, X., & Lu, Z. (2025). Flow Control of Tractor Multi-Channel Hydraulic Tester Based on AMESim and PSO-Optimized Fuzzy-PID. Agriculture, 15(11), 1190. https://doi.org/10.3390/agriculture15111190






