Morphological Estimation of Primary Branch Inclination Angles in Jujube Trees Based on Improved PointNet++

Abstract

The segmentation of jujube tree branches and the estimation of primary branch inclination angles (IAs) are crucial for achieving intelligent pruning. This study presents a primary branch IA estimation algorithm for jujube trees based on an improved PointNet++ network. Firstly, terrestrial laser scanners (TLSs) are used to acquire jujube tree point clouds, followed by preprocessing to construct a point cloud dataset containing open center shape (OCS) and main trunk shape (MTS) jujube trees. Subsequently, the Chebyshev graph convolution module (CGCM) is integrated into PointNet++ to enhance its feature extraction capability, and the DBSCAN algorithm is optimized to perform instance segmentation of primary branch point clouds. Finally, the generalized rotational symmetry axis (ROSA) algorithm is used to extract the primary branch skeleton, from which the IAs are estimated using weighted principal component analysis (PCA) with dynamic window adjustment. The experimental results show that compared to PointNet++, the improved network achieved increases of 1.3, 1.47, and 3.33% in accuracy (Acc), class average accuracy (CAA), and mean intersection over union (mIoU), respectively. The correlation coefficients between the primary branch IAs and their estimated values for OCS and MTS jujube trees were 0.958 and 0.935, with root mean square errors of 2.38° and 4.94°, respectively. In summary, the proposed method achieves accurate jujube tree primary branch segmentation and IA measurement, providing a foundation for intelligent pruning.

1. Introduction

Dormant pruning is a key aspect of fruit tree management, effectively controlling the shape of trees, optimizing nutrient distribution, reducing the risk of pests and diseases, and improving the yield and quality of fruit [1,2,3]. However, existing pruning practices primarily rely on manual labor, which is costly and inefficient. With the advancement of urbanization and the worsening shortage of agricultural labor, intelligent pruning technology has become an inevitable choice for orchard management [4,5]. Intelligent pruning relies on the precise 3D modeling of fruit tree structures and the extraction of branch information [6]. The complex orchard environment, irregular morphology of trees, and interfering factors such as lighting, weeds, leaves, and weather make branch information extraction highly challenging [7]. In recent years, the rapid development of point cloud technology and artificial intelligence has provided new approaches to address these challenges [8,9].

Branch IA measurement is a critical step in achieving intelligent pruning, and the acquisition of primary branch instances directly affects the accuracy of IA measurement approaches [10]. Mo et al. [11] proposed a partition-based segmentation method using high-resolution Digital Orthophoto Maps and trained the model on the Litchi-Citrus dataset, achieving a best Average Precision (AP) of 96.25% on the test set. Pérez-Borrero et al. [12] proposed an efficient strawberry instance segmentation method by optimizing the network architecture and regional grouping algorithm, achieving an inference speed of 10 fps and segmentation accuracy comparable to that of Mask R-CNN [13]. Ling et al. [14] addressed data quality and model performance issues in jujube branch detection by replacing the YOLOv8 backbone with GhostNetv2 for lightweight improvement, achieving an accuracy of 92.3% (a 2.4% increase over the baseline model). Although these studies have successfully distinguished individual branch instances using RGB images, the lack of 3D information makes it difficult to extract fruit tree structural data from 2D images, limiting their application in the context of dormant pruning.

With the rapid development of terrestrial laser scanners (TLSs) and computer technology, the acquisition of 3D point cloud data has become more efficient, and point cloud segmentation approaches have also advanced rapidly [15,16]. Existing point cloud segmentation methods can be broadly categorized into two types: machine learning-based methods and deep learning-based methods. Machine learning methods, such as Euclidean clustering [17] and support vector machines [18], typically rely on manually designed features [19,20,21]. Qiu et al. [22] combined the Laplacian skeletonization algorithm with the DBSCAN clustering algorithm to achieve point cloud segmentation and structural phenotypic feature extraction for apple trees. Itakura et al. [23] used FPFH features and k-means clustering for leaf and branch point classification, then segmented each branch instance with a region-growing algorithm. However, in real canopy environments, variations in lighting and complex backgrounds reduce the robustness of machine learning algorithms, making it difficult to accurately distinguish each primary branch instance in dormant fruit tree point clouds [7].

The segmentation of fruit tree point clouds and the extraction of branch information using deep learning techniques remain challenging tasks [24,25]. In 2017, Qi et al. [26] proposed the PointNet network to address the rotation invariance and disorder of point clouds, which can efficiently segment point clouds by independently processing each point and using max pooling to aggregate global features. Building on this, they introduced the PointNet++ algorithm, enabling part segmentation of individual objects and addressing challenges relating to local feature extraction [27]. Since then, researchers have used improved PointNet++ models to address various complex plant point cloud segmentation scenarios. For example, Guo et al. [25] integrated the ASAP attention module into PointNet++, achieving a semantic segmentation Acc of 0.95 and an Intersection over Union of 0.86. Sun et al. [28] used the PointNet++ part segmentation approach to merge the primary branches of apple trees, achieving 93.64% accuracy in branch count estimation and a 12.00% mean absolute percentage error in branch length estimation. However, applying PointNet++ for jujube tree point cloud segmentation and branch IA extraction remains challenging. The combination of deep learning and traditional clustering algorithms [25,29] has become a key approach for processing 3D plant data and extracting phenotypic parameters, enhancing the efficiency and accuracy of branch information extraction to support fruit tree pruning.

In summary, branch segmentation and primary branch inclination estimation of jujube trees based on TLS point clouds pose unaddressed challenges, relating to uneven point cloud density, complex tree structures, and large variations in branch curvature. To address the abovementioned issues, this study proposes a jujube tree primary branch IA estimation method based on an improved PointNet++ network. The main contributions of this work are summarized as follows: (1) the CGCM is introduced into PointNet++ to enhance the nonlinear feature extraction capability of the resulting model; (2) a residual feature fusion mechanism is incorporated to integrate shallow geometric features with deep semantic features, ensuring the effective transmission of high-level semantics; (3) a density-adaptive DBSCAN optimization strategy is proposed to dynamically adjust the epsilon neighborhood radius (eps), enhancing the branch instance segmentation performance of the model; (4) primary branch skeletons are extracted using the ROSA algorithm and primary branch IAs are accurately estimated through a weighted PCA method with dynamic window adjustment.

2. Materials and Methods

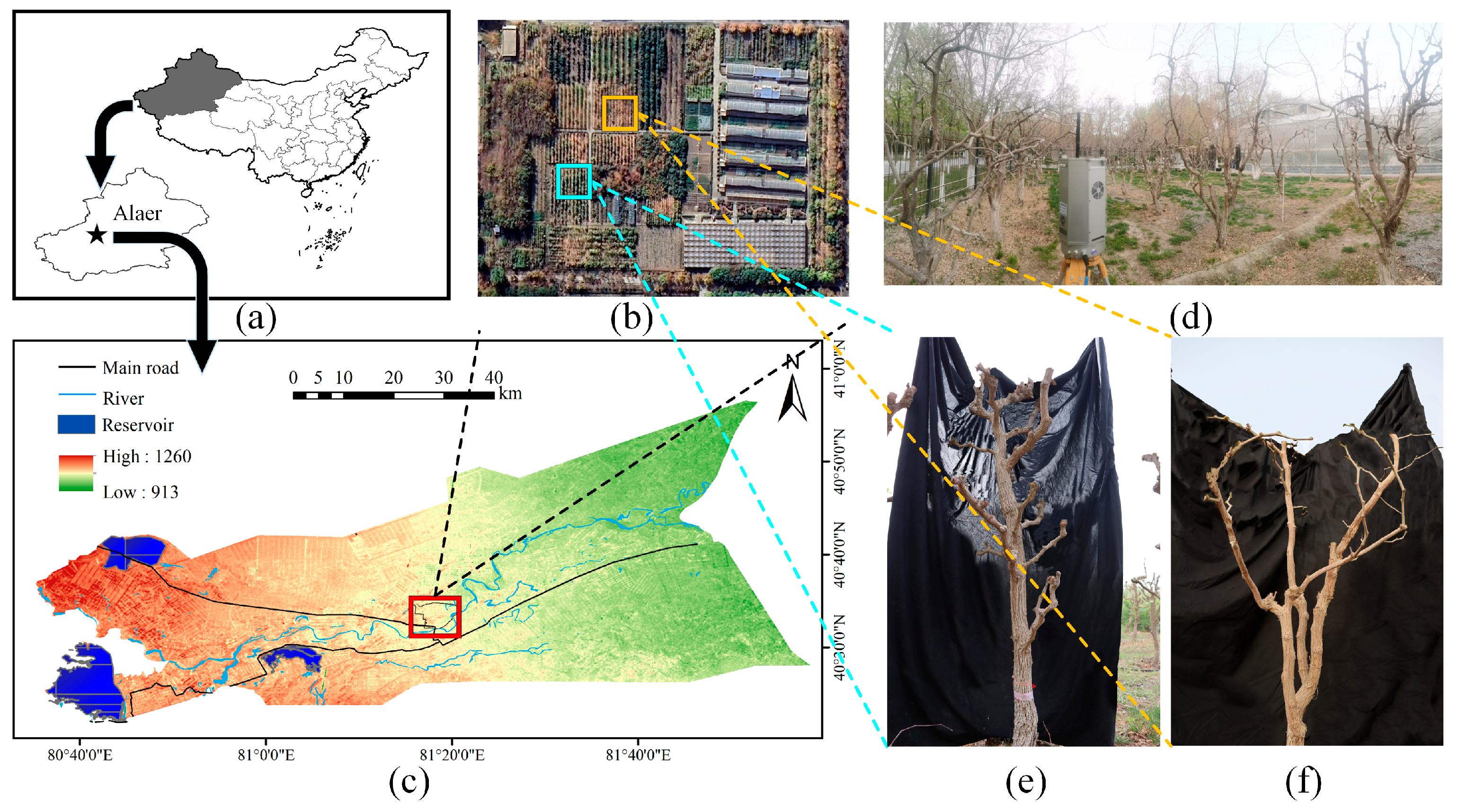
2.1. Experimental Site

To acquire jujube tree data during the dormant period, the experiment was conducted at the horticultural experimental station of Tarim University (40°54′ N, 81°3′ E) in Alar City, Xinjiang Uygur Autonomous Region. This region features a typical temperate continental climate, with an average annual precipitation of less than 50 mm and a diurnal temperature difference of 15–20 °C, meeting the environmental requirements for jujube tree dormancy. The sampled jujube trees were 8 years old, planted at a spacing of 3 m × 4 m, and comprised two types of cultivated tree structures. In the open center shape (OCS), 3–5 primary branches emerged at a height of 60–80 cm above the ground, with no central trunk retained. In the main trunk shape (MTS), a central trunk was preserved, with branches distributed in a spiral pattern, forming a spindle-shaped canopy. Figure 1 illustrates the experimental site, the jujube orchard environment, and the typical tree structures of the two jujube types.

2.2. Jujube Tree Dataset

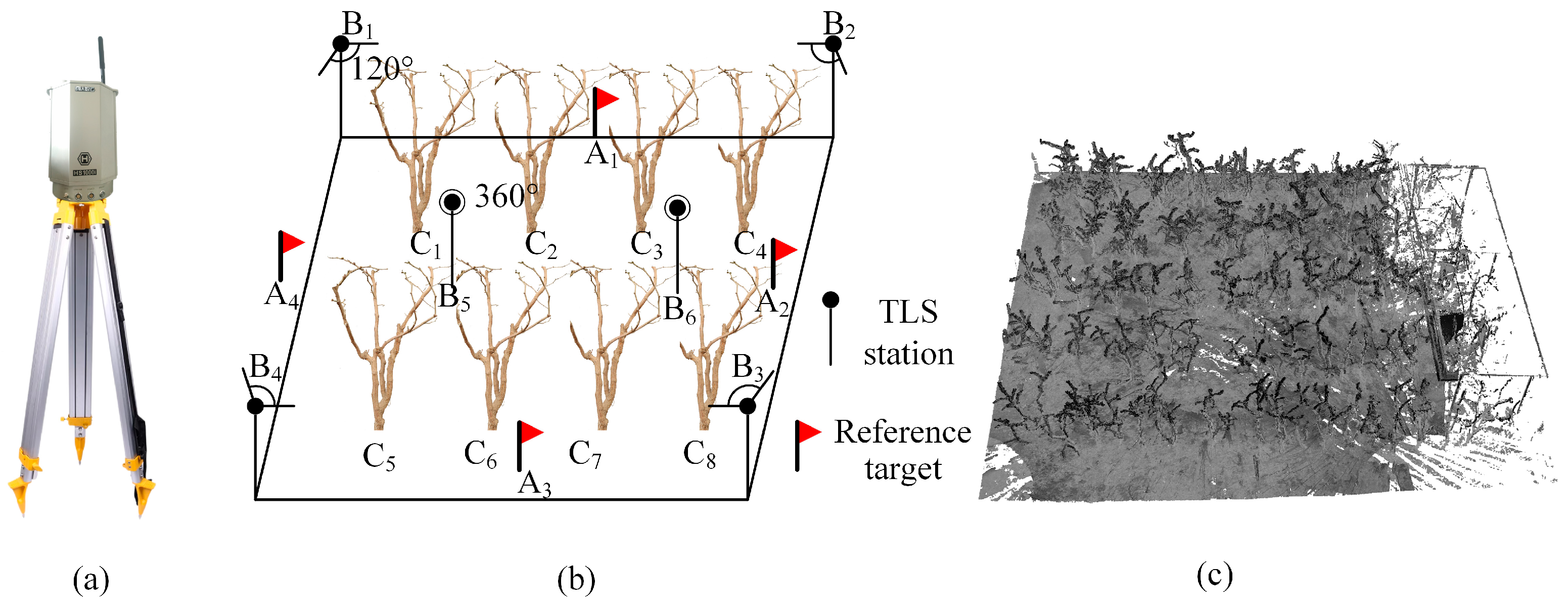
2.2.1. Jujube Tree Point Cloud Acquisition

Multi-station coordinated scanning of dormant jujube trees was conducted using the HS 1000i TLS (Wuhan Hi-Cloud Technology Co., Ltd., Wuhan, China; wavelength: 980 nm; ranging accuracy: 5 mm @ 40 m). The system setup is shown in Figure 2a. The TLS was configured with a pulse frequency of 100 kHz, vertical and horizontal resolutions of 0.0576° and 0.0128°, respectively, and a maximum range of 30 m per station. Six TLS stations were deployed to fully cover two rows of jujube trees (Figure 2b). Four peripheral stations (B₁–B₄) were positioned at the corners surrounding the tree group (C₁–C₈) to perform 120° sector scans for capturing of the outer point clouds. Two central stations (B₅–B₆) were symmetrically placed on either side of the central axis of the tree rows to perform 360° full-circle scans in order to capture the inner point clouds. Four spherical targets (A₁–A₄) were placed at the midpoints of the lines connecting each pair of adjacent peripheral stations. Multi-station point cloud registration was performed using the Iterative Closest Point algorithm. Rigid transformations were solved through least-squares optimization to align the scan data from each station with the target point clouds, resulting in a high-density 3D point cloud of jujube trees (Figure 2c).

2.2.2. Point Cloud Preprocessing

Raw point cloud data typically contain a large amount of noise and redundant information, such as ground points, buildings, and sensor noise, which must be removed through multi-stage filtering to improve the quality of the data (Figure 3). The specific process in this study is as follows: ground points are first removed using the Cloth Simulation Filtering (CSF) algorithm, which simulates the process of cloth draping and sinking to separate ground points from the jujube tree point cloud. As shown in Equation (1), the cloth is controlled by the elasticity coefficient ($k_s$) and the bending coefficient ($k_b$), gradually fitting the ground points during the sinking process. Ground points are identified by calculating the distance change ($\Delta l_i$) and angle change ($\Delta {\theta }_i$) between the cloth and the point cloud points. Finally, the ground points are labeled and removed, while the remaining points are retained as the jujube tree point cloud, as illustrated in Figure 3a.

$$\mathrm{E}={\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left(k_s·\Delta l_i+k_b·\Delta {\theta }_i\right)$$

(1)

$$d_i>\mu +\alpha ·\sigma$$

(2)

Then, the Statistical Outlier Removal (SOR) algorithm is used to clean noise and outliers in the jujube tree point cloud, as shown in Figure 3b. The method calculates the average distance ($d_i$) between each point and its k nearest neighbors, removing outliers that exceed a predefined threshold. This criterion is expressed in Equation (2), where $\mu$ represents the mean of the average distances for all points, $\sigma$ is the standard deviation of the distance distribution, and $\alpha$ is a user-defined deviation multiplier.

To support the training of deep learning models, the obtained single-tree jujube point clouds were then standardized and annotated, as shown in Figure 4. First, the 3D coordinates (x, y, z) were retained, and normal vectors (N_x, N_y, N_z) were calculated through neighborhood point analysis to provide enhanced geometric features. Then, manual annotation was performed using the open-source software CloudCompare v2.13.alpha, classifying the point cloud into trunk, primary branches, and secondary branches. Finally, data standardization was conducted through centroid translation, size normalization, and normal vector orientation correction.

2.2.3. Jujube Tree Dataset Overview

The jujube tree point cloud dataset constructed in this study was acquired using a TLS and built following the ShapeNet dataset standards [30]. It includes 78 jujube tree samples (42 MTS and 36 OCS), including raw point clouds, semantic labels, and metadata configuration files. Statistics obtained for the data show that MTS jujube trees had 5–18 primary branches per tree, for a total of 353 primary branches and 130 secondary branches. Meanwhile, the OCS jujube trees had 2–6 primary branches per tree, for a total of 118 primary branches and 311 secondary branches. To ensure model generalization and fair evaluation, the dataset was randomly divided into a training set of 62 trees and a test set of 16 trees. The dataset preserved the complete 3D topological structure of the jujube tree branches and, after pre-processing, could be fed into segmentation networks to support branch segmentation tasks for different tree structures.

2.3. Point Cloud Segmentation

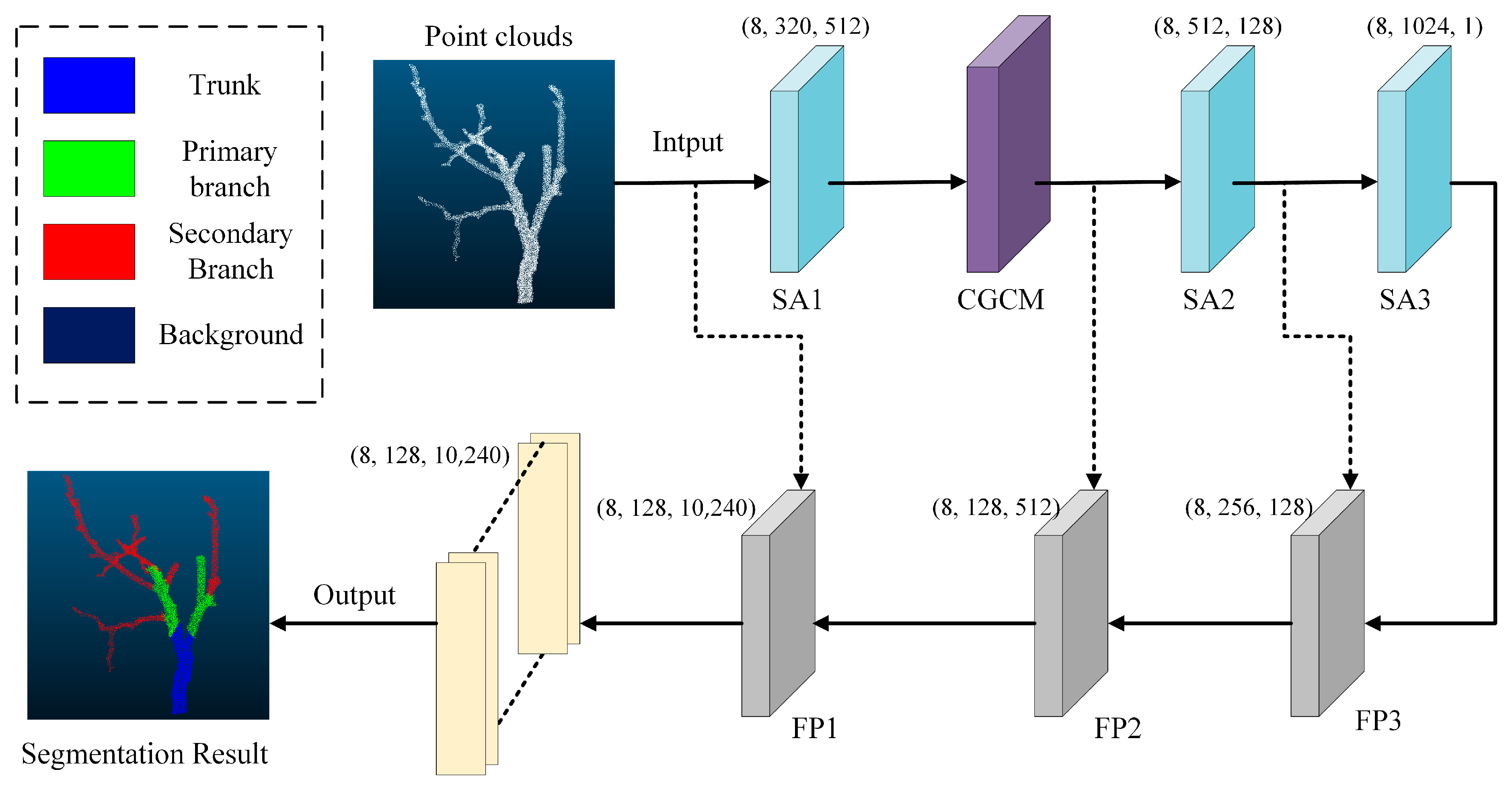
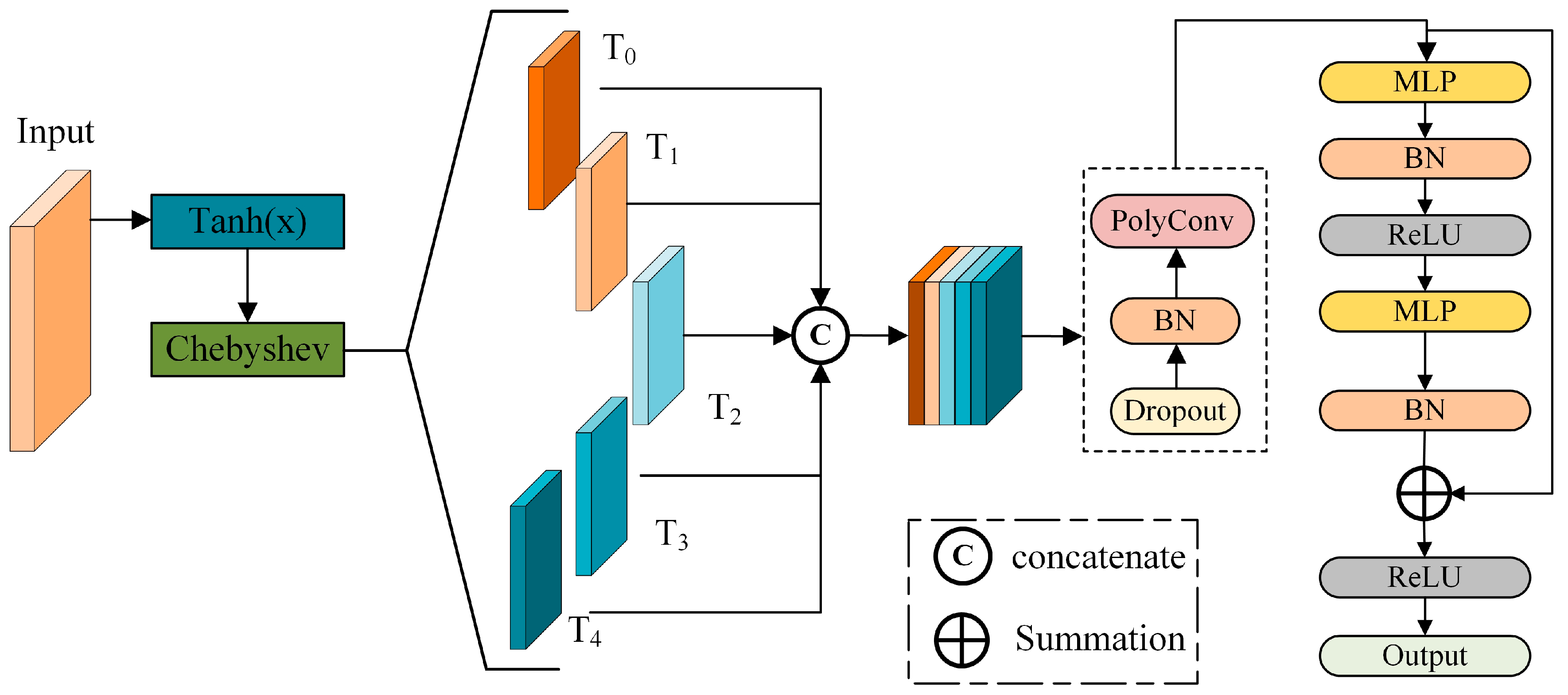
2.3.1. Improvement of the PointNet++

As a classic point cloud processing network, PointNet++ employs a Set Abstraction (SA) layer that relies on an MLP to extract local features. However, the core component (i.e., the MLP) is limited by its linear combination nature, making it less effective in handling the complex nonlinear topological structures formed by intersecting jujube tree branches. Defferrard et al. [31] have proposed a spectral convolution based on Chebyshev polynomials, enabling localized filtering and effectively handling complex features in nonlinear structural data. Motivated by this approach, the Chebyshev Graph Convolution Module (CGCM) is proposed and embedded into the SA feature extraction process of PointNet++, forming the CGCM-PointNet++ network. The detailed architecture is shown in Figure 5.

Traditional spectral graph convolution requires eigendecomposition of the Laplacian matrix, which results in high computational complexity. In contrast, the CGCM approximates the graph Fourier transform through polynomial expansion, thus avoiding explicit eigendecomposition and reducing computational complexity while maintaining rotational invariance. The detailed architecture of the CGCM is shown in Figure 6. The module is constructed based on the normalized Laplacian matrix ($\tilde{L}$), as shown in Equation (3):

$$\tilde{L}=D^{-1/2}(D-A)D^{-1/2}$$

(3)

where $A$ is the adjacency matrix constructed using the K-Nearest Neighbors (KNN) algorithm and $D$ is the degree matrix, which is a diagonal matrix with each diagonal element $D_{\mathrm{ii}}$ representing the degree of node $i$.

Chebyshev polynomial basis functions of orders 0 to 4 are recursively generated using the recurrence relation shown in Equation (4):

$$T_n(\tilde{L})=2\tilde{L}{T}_{n-1}(\tilde{L})-T_{n-2}(\tilde{L}),\hspace{1em}{T}_0=I,T_1=\tilde{L}$$

(4)

where $T_n\left(\tilde{L}\right)$ represents the $n$-th order Chebyshev polynomial based on the normalized Laplacian matrix ($\tilde{L}$), and $I$ is the identity matrix.

The output features of each polynomial order are concatenated along the channel dimension and processed using the weighted aggregation rule defined in Equation (5).

$$F_{\mathrm{poly}}={\sum }_{n=0}^4{W}_n·T_n(\tilde{L})F_{\mathrm{in}}$$

(5)

where ${\mathrm{F}}_{\mathrm{in}}$ denotes the input graph feature matrix, typically with dimensions ${\mathrm{R}}^{\mathrm{N}\times \mathrm{C}}$, where $\mathrm{N}$ is the number of nodes in the graph and $\mathrm{C}$ is the number of input feature channels; ${\mathrm{W}}_{\mathrm{n}}$ is a learnable weight matrix corresponding to the $\mathrm{n}$-th order Chebyshev polynomial, used to weight features of different orders and adaptively extract important information from the graph; and ${\mathrm{F}}_{\mathrm{poly}}$ represents the output feature matrix after the Chebyshev polynomial graph convolution operation. Finally, the graph features $F_{\mathit{poly}}$ produced via Chebyshev polynomial graph convolution are added to the features $F_{\mathit{MLP}}$ extracted using the two-layer MLP in the residual branch. This sum is then passed through a ReLU activation to obtain the final output ($F_{\mathit{out}}$), as shown in Equation (6):

$$F_{\mathit{out}}=\mathit{ReLU}\left(F_{\mathit{poly}}+F_{\mathit{MLP}}\right)$$

(6)

This residual architecture integrates the basic semantic features extracted by the MLP with the higher-order geometric features modeled by the graph convolution, enhancing the ability to capture nonlinear features in jujube tree point clouds while preserving the integrity of the fundamental semantic information.

2.3.2. Instance Segmentation of Point Clouds

The DBSCAN clustering algorithm has been widely used for point cloud instance segmentation due to its robustness to noise and the advantage of not requiring a predefined number of clusters [32,33]. In this study, a deep learning-based semantic segmentation method was employed to classify jujube tree point clouds into trunk, primary branch, and secondary branch categories, allowing for the assignment of corresponding semantic labels. Leveraging semantic priors, DBSCAN performs instance segmentation specifically on the primary branch category, thus enhancing the segmentation accuracy. However, DBSCAN relies on a fixed eps value, which can lead to adjacent clusters with small inter-cluster distances being incorrectly grouped into a single instance when applied to jujube tree point clouds with uneven density distribution, thereby affecting the segmentation accuracy. To address this issue, an adaptive eps adjustment strategy based on KNN statistics is introduced, which dynamically adjusts the neighborhood radius according to the local density characteristics of the point cloud data. The strategy first computes the $k$-nearest neighbor distance for each point, defined as follows:

$$d_k(x_i)={\displaystyle \frac{1}{k}}{\sum }_{j=1}^{k}d(x_i,x_{\left(j\right)})$$

(7)

where $x_{\left(j\right)}$ denotes the $j$-th nearest neighbor of point $x_i$, and $d_k\left(x_i\right)$ represents the distance metric between $x_i$ and $x_{\left(j\right)}$.

After obtaining the average $k$-nearest neighbor distance ($d_k\left(x\right)$) for each point, a suitable eps value is determined using a quantile-based approach. As shown in Equation (8), $P_q$ represents the $q$-th quantile of $d_k\left(x_i\right)$ meaning that in the ordered set of all $d_k\left(x\right)$ values, a proportion $q$ of the points have $k$-nearest neighbor distances less than or equal to this value.

$$\epsilon =P_q\left(d_k\left(x\right)\right)$$

(8)

For example, when $q$ = 85%, eps is set to the 85th percentile of $d_k\left(x\right)$, meaning that 85% of the points have k-nearest neighbor distances less than or equal to this value. In dense regions of the point cloud, the $k$-nearest neighbor distances are small, resulting in smaller eps values, which helps to avoid incorrect merging of separate instances. In sparse regions, the $k$-nearest neighbor distances are larger, leading to larger eps values, which allows previously disconnected points to be grouped into the same cluster, effectively addressing the issue of uneven density.

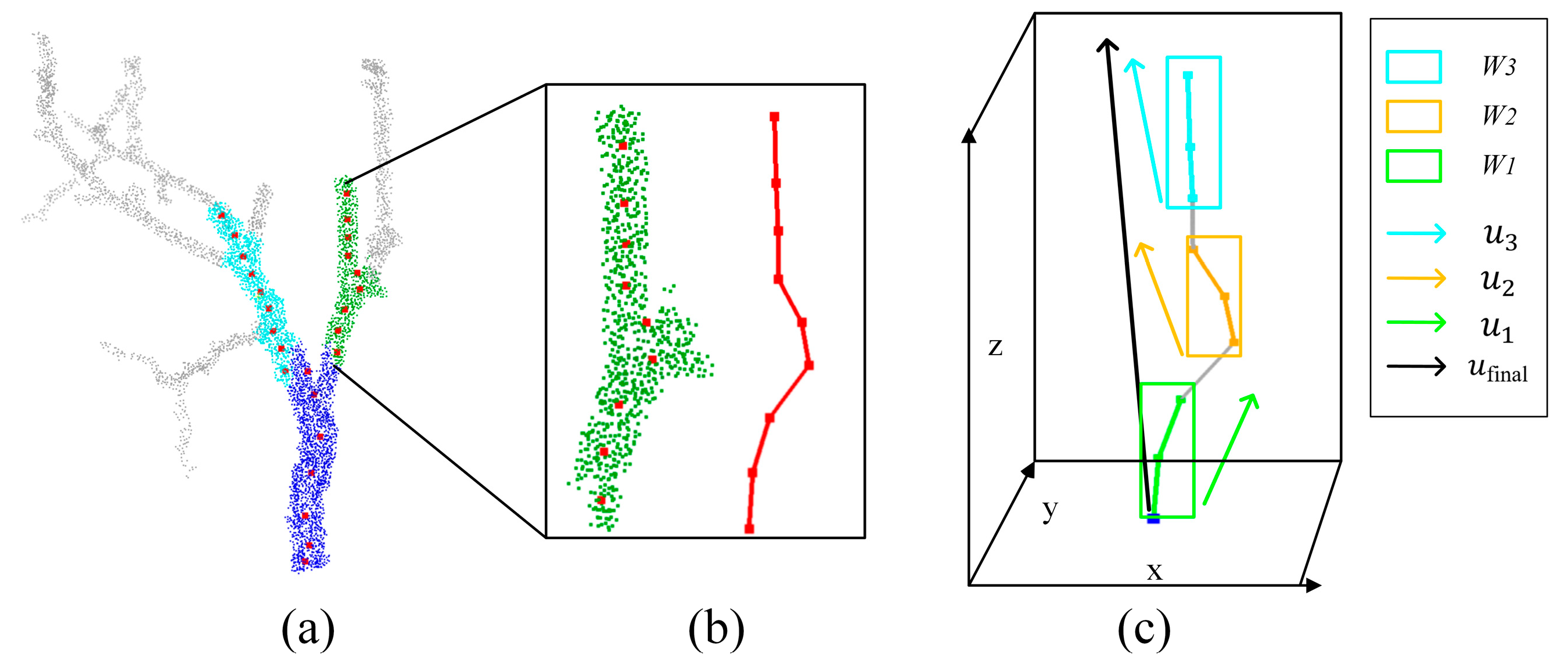
2.4. Estimation of Primary Branch Inclination Angles

The curved growth of branches results in significant variations in curvature, which can cause deviations in principal direction estimation when using the PCA method, thereby affecting the accuracy of inclination estimation. To address this issue, this study proposes a primary branch IA estimation method that integrates ROSA [34] skeleton extraction with sliding-window weighted PCA. First, the ROSA algorithm is applied to the primary branch point cloud instance to extract a sequence of skeleton points (Figure 7a). Then, a depth-first search algorithm is used to traverse the topology constructed from the skeleton to determine the primary branch path (Figure 7b). To improve the accuracy of path selection, a directional continuity scoring strategy is introduced during the search process, as defined in Equation (9):

$$S_p={\sum }_{i=1}^{N_p-1}{\displaystyle \frac{v_i·v_{i+1}}{\Vert v_i\Vert \Vert v_{i+1}\Vert }}+\lambda N_p$$

(9)

where $v_i=p_{i+1}-p_i$ is the vector between adjacent points, $\lambda$ is the weighting factor for path length, and $N_p$ is the number of points in the path. The depth-first search algorithm maximizes the scoring function ($S_p$) to ensure that the primary branch path satisfies both directional continuity and spatial extensibility.

To address the curved characteristics of jujube primary branches, a dynamic window adjustment mechanism is designed to apply smaller windows in regions with significant curvature variation and larger windows in straighter regions. The average curvature within each window is calculated according to Equation (10):

$$\kappa ={\displaystyle \frac{1}{m-2}}{\sum }_{i=1}^{m-2}(1-\mathit{cos}{\theta }_i)$$

(10)

where $\mathit{cos}{\theta }_i$ represents the cosine of the angle between vectors formed by three consecutive points ($p_{i-1},p_i{,p}_{i+1}$), serving as an indicator of local curvature variation. When $\kappa$ > 0.3, the window is reduced to 30% of its original length; otherwise, it is expanded to 70%, enabling adaptive processing across regions with different curvature levels.

In the inclination angle calculation stage, as shown in Figure 7c, PCA is performed on the point cloud within each window. The first principal component direction vector $u_j$, which corresponds to the largest variance, is selected, and the global principal direction $u_{\mathrm{final}}$ is obtained as a weighted average using the weights ${\omega }_j$, as defined in Equation (11):

$$u_{\mathit{final}}={\displaystyle \frac{\sum {\omega }_j{u}_j}{\sum {\omega }_j}}, {\omega }_j=|W_j|·\Vert w_j^L-w_j^1\Vert$$

(11)

where $W_j$ is the number of points in the $j$-th window, and $w_j^1$ and $w_j^L$ denote the first and last points of the window, respectively, which are used to measure the spatial extent of the window.

The final primary branch inclination angle $\alpha$ is calculated as the angle between the global principal direction and the vertical direction, as defined in Equation (12).

$$\alpha =\mathit{arccos}\left(r\right)\times {\displaystyle \frac{180}{\pi }}, r={\displaystyle \frac{\left|u_z\right|}{\sqrt{u_x^2+u_y^2+u_z^2}}}$$

(12)

where $r$ represents the normalized component of the global principal direction along the vertical axis, reflecting the cosine of the angle between the principal direction and the vertical direction. The inclination angle ($\alpha$) is then computed using the arccosine function and converted to degrees. Combining dynamic window adjustment with a weighted principal component analysis strategy, this method effectively adapts to regions with varying curvature, improving the accuracy and stability of the primary branch IA estimate.

2.5. Evaluation Metrics

2.5.1. Point Cloud Semantic Segmentation

To evaluate the performance of the CGCM-PointNet++ network in the jujube tree branch segmentation task, four metrics were adopted: Acc, CAA, mIoU, and cross-entropy loss function (Loss). $\mathit{Acc}$ measures the consistency between predicted values ($p_i$) and ground truth labels ($y_i$) across all samples. $\mathit{CAA}$ is computed as the average of per-class accuracies (${\mathit{Acc}}_j$), reflecting the network’s performance balanced across different categories. $\mathit{mIoU}$ quantifies the overlap between the predicted and actual regions using the intersection-over-union metric. During training, the $\mathit{Loss}$ function is used to minimize the discrepancy between $p_i$ and $y_i$, thereby enhancing the network’s performance. The specific calculation methods for $\mathit{Acc}$, $\mathit{CAA}$, $\mathit{mIoU}$, and $\mathit{Loss}$ are provided in the following equations.

$$\mathit{Acc}={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m}{f}_i, f_i=\left\{\begin{array}{cc}1& y_i=p_i\\ 0& y_i\ne p_i\end{array}\right.$$

(13)

$$\mathit{CAA}={\displaystyle \frac{1}{c}}{\displaystyle \sum _{j=1}^c}{\mathit{Acc}}_j$$

(14)

$$\mathit{mIoU}={\displaystyle \frac{1}{c}}{\displaystyle \sum _{j=1}^c}{\displaystyle \frac{T{P}_j}{T{P}_j+F{P}_j+F{N}_j}}$$

(15)

$$\mathit{Loss}={\displaystyle \sum _{i=1}^m}\left(y_i\mathit{log}(p_i)+(1-y_i)\mathit{log}(1-p_i)\right)$$

(16)

2.5.2. Primary Branch Inclination Estimation

The jujube tree IA extraction performance was evaluated using the coefficient of determination (R²—Equation (17)) and root mean square error (RMSE—Equation (18)). $R^2$ measures the goodness of fit between predicted and true values, with values closer to 1 indicating better fit, while $\mathit{RMSE}$ quantifies the prediction error, with smaller values indicating lower error.

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^N{(y_i-\stackrel{-}{y})}^2}}$$

(17)

$$\mathit{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}$$

(18)

where $N$ represents the total number of samples, $y_i$ represents the ground truth of the $i$-th sample, $\widehat{y}$ is the predicted value for the $i$-th sample, and $\stackrel{-}{y}$ is the mean of all true values.

2.5.3. DBSCAN Clustering

To evaluate the performance of the DBSCAN clustering algorithm, four commonly used evaluation metrics were selected: Adjusted Rand Index (ARI), Normalized Mutual Information (NMI), Fowlkes–Mallows Index (FMI), and Completeness. $\mathit{ARI}$ evaluates the consistency of sample pairs by adjusting the $\mathit{RI}$ for chance, reflecting how well pairs of samples are grouped together. $\mathit{NMI}$ assesses the amount of information shared between the predicted clusters and the ground truth labels based on mutual information $I(U,L)$ and entropies $H\left(U\right)$ and $H\left(L\right)$. $\mathit{FMI}$ computes the geometric mean of precision and recall using true positives ($\mathit{TP}$), false positives ($\mathit{FP}$), and false negatives ($\mathit{FN}$), indicating the trade-off between accuracy and completeness of the clustering. $\mathit{Completeness}$ measures whether all samples from the same class are assigned to the same cluster, based on the conditional entropy $H\left(U\right|L)$, and reflects the integrity of clustering results. Higher values of $\mathit{ARI}$, $\mathit{NMI}$, $\mathit{FMI}$, and $\mathit{Completeness}$ indicate better performance. The specific calculation methods are provided in the following equations.

$$\mathit{ARI}={\displaystyle \frac{\mathit{RI}-E\left[\mathit{RI}\right]}{\mathit{max}\left(\mathit{RI}\right)-E\left[\mathit{RI}\right]}}$$

(19)

$$\mathit{NMI}={\displaystyle \frac{2·I(U,L)}{H\left(U)+H\right(L)}}$$

(20)

$$FMI={\displaystyle \frac{TP}{\sqrt{(TP+FP)·(TP+FN)}}}$$

(21)

$$\mathit{Completeness}=1-{\displaystyle \frac{H\left(U\right|L)}{H\left(U\right)}}$$

(22)

3. Results

3.1. Semantic Segmentation of Jujube Tree Branches

3.1.1. Network Training

All experiments were conducted on a Dell server running the Ubuntu 20.04 operating system, equipped with a GeForce RTX 3060Ti 22GB GPU (driver version 470.141). The experimental environment was supported by CUDA 11.3 and cuDNN 8.2.0. Model development was carried out using the PyTorch 1.11.0 deep learning framework and trained within the Python 3.8 environment using PyCharm 2022.

The CGCM-PointNet++ model was trained for 300 epochs with the following parameter settings: batch size of 8, an initial learning rate of 0.001, weight decay of 1 × 10⁻⁴, a learning rate decay factor of 0.5, and a decay step size of 20 epochs. As shown in Figure 8, both Acc and Loss of CGCM-PointNet++ exhibited favorable trends during training. In the first 50 epochs, Acc increased rapidly while Loss decreased sharply. The model then gradually converged, with Acc stabilizing above 95% and Loss decreasing to around 0.1.

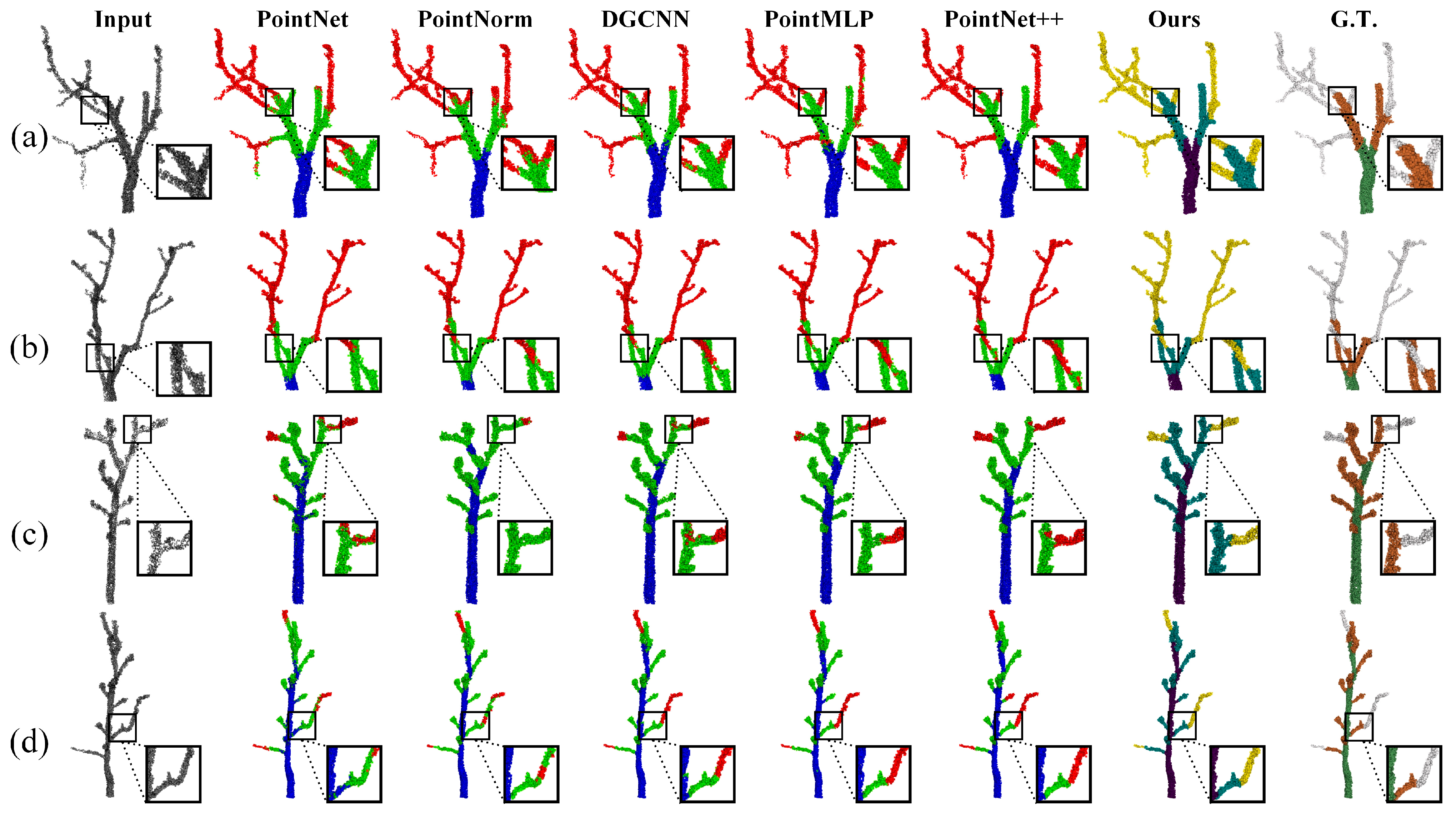
3.1.2. Comparison of Semantic Segmentation of Branches

In this study, six point cloud segmentation models were evaluated on the jujube tree point cloud dataset: PointNet [26], PointNet++ [27], DGCNN [35], PointNorm [36], PointMLP [37], and CGCM-PointNet++. As shown in

Table 1. Comparison of test results on the dataset using different segmentation networks.

Model	Acc	CAA	mIoU	Ocs_mIoU	Mts_mIoU
PointNet	84.47	83.18	69.6	75.0	64.3
PointNorm	87.69	85.28	72.7	73.7	71.7
DGCNN	90.06	87.8	80.0	75.0	69.0
PointMLP	94.76	94.35	88.7	89.3	88.2
PointNet++	95.94	95.79	90.5	88.1	93.0
Ours	97.27	97.26	93.83	95.2	92.47

, CGCM-PointNet++ achieved the best performance, with Acc, CAA, and mIoU reaching 97.27, 97.26, and 93.83%, respectively. These represent respective improvements of 1.33, 1.47, and 3.33% over the baseline PointNet++. This was further validated in specific canopy structure scenarios. For OCS jujube trees, the CGCM-PointNet++ achieved an OCS_mIoU of 95.2%, representing a 7.1% improvement over PointNet++. Although the MTS_mIoU for MTS jujube trees reached 92.47%, which was 0.53% lower than that of PointNet++, it still significantly outperformed PointNet (64.3%) and PointMLP (88.2%).

Compared with the other networks, PointNet performed the worst due to its reliance on a single global feature pooling mechanism, which limits its ability to model local geometric structures. Although PointNorm demonstrated adaptability to different tree structures (with only a 2.0% difference between OCS_mIoU and MTS_mIoU), its overall performance remained limited, with Acc at 87.69% and mIoU at 72.7%. DGCNN achieved an Acc of 90.06%, but its performance gap across different tree structures reached 6.0%. PointMLP achieved an Acc of 94.76%, but its mIoU (88.7%) still fell short compared to that of CGCM-PointNet++ (93.83%). Notably, CGCM-PointNet++ demonstrated stronger adaptability across different tree structures, with a performance gap of 2.73%, which was 2.17% lower than that of PointNet++ (4.9%). In summary, CGCM-PointNet++ demonstrated superior performance in both segmentation accuracy and adaptability to tree-like structures, which can be attributed to the integration of the CGCM module into the SA layers of PointNet++.

The visualization results of tree point cloud segmentation (Figure 9) demonstrate that CGCM-PointNet++ outperformed the other networks in jujube branch segmentation. The structures of the trunk, primary branches, and secondary branches were complete, with no obvious over-segmentation or incorrect segmentation, and were highly consistent with the ground truth (G.T.). In OCS jujube trees (Figure 9a,b), PointNet and DGCNN exhibited incorrect segmentation at the distal ends of primary and secondary branches, and point cloud adhesion occurred at their junctions, resulting in a noticeable boundary blur. PointNorm performed even worse in these regions (Figure 9a). PointMLP exhibited over-segmentation at the junction between the trunk and primary branches, where the base of some secondary branches was incorrectly classified as an extension of the primary branch (Figure 9b). PointNet++ showed incorrect segmentation at the junction between secondary and primary branches, with some secondary branch points mistakenly assigned to the primary branch region (Figure 9b). In MTS jujube trees, PointNet, PointNorm, DGCNN, and PointMLP all exhibited varying degrees of over-segmentation and incorrect segmentation (Figure 9c,d). Although PointNet++ achieved an mIoU of 93%, local patches of incorrect segmentation were still present within the primary branches (Figure 9c). In contrast, CGCM-PointNet++ maintained strong segmentation performance across both tree structure scenarios, with only slight over-segmentation at the junctions between primary and secondary branches, and its error range was significantly smaller than those of other networks.

3.2. Instance Segmentation of Jujube Tree Branches

Five methods were used to evaluate the instance segmentation performance based on the semantic segmentation results of the CGCM-PointNet++ network: Gaussian Mixture Model (GMM) [38], K-Means [39], Spectral Clustering (SC) [40], Mean-Shift [41], and DBSCAN [32]. To address the issue in which DBSCAN struggles to distinguish closely spaced instances in jujube tree point clouds due to density variations, this study introduces an adaptive eps strategy to improve the clustering performance. As shown in

Table 2. Instance segmentation results for different clustering algorithms.

Method	ARI	NMI	FMI	Completeness
Mean-Shift	0.459	0.717	0.584	0.772
SC	0.810	0.856	0.846	0.869
GMM	0.846	0.890	0.873	0.878
K-Means	0.861	0.910	0.884	0.898
DBSCAN	0.982	0.989	0.986	0.999

, the DBSCAN algorithm with the adaptive eps strategy demonstrated significant advantages across all four evaluation metrics: ARI (0.982), NMI (0.989), FMI (0.986), and Completeness (0.999). Mean-Shift showed noticeably lower performance in ARI (0.459) and Completeness (0.772) compared to the other algorithms, indicating its limited ability to effectively distinguish instances. SC, GMM, and K-Means all achieved ARI, NMI, and FMI scores above 0.8, demonstrating a certain level of clustering capability. However, their overall performance remained lower than that of the DBSCAN algorithm with the adaptive eps strategy.

Figure 10 illustrates the performance of the different clustering algorithms in primary branch instance segmentation of jujube trees, where different colors represent distinct individual instances. The DBSCAN algorithm with adaptive eps achieved the best segmentation results, showing a significant advantage in distinguishing closely spaced primary branch instances. For OCS jujube trees (Figure 10a,b), when the spacing between primary branch instances was relatively large, SC, K-Means, GMM, and DBSCAN all performed well. However, when the instances were closely spaced, SC, K-Means, and Mean-Shift exhibited severe incorrect segmentation, while GMM showed over-segmentation at the instance junctions. For MTS jujube trees (Figure 10c,d), the Mean-Shift, SC, K-Means, and GMM algorithms exhibited similar issues: they had difficulty distinguishing primary branch instances with small inter-instance distances, and multiple instances were incorrectly mixed within a single primary branch. In contrast, the DBSCAN algorithm with adaptive eps consistently avoided these problems, achieving accurate and complete segmentation of primary branch instances and overall superior performance compared to the other algorithms.

3.3. Skeleton Extraction of Jujube Tree Branches

The ROSA algorithm was used to extract skeletons from primary branch instances of jujube trees, and the results are shown in Figure 11. For OCS jujube trees (Figure 11a,c), it accurately captured the topological structure of the primary branches. Similarly, for MTS jujube trees (Figure 11b,d), it demonstrated high precision in reconstructing the complete branch morphology. The matching results between primary branch instances and the extracted skeletons (Figure 11e,f) further verify the accuracy of the proposed algorithm. Overall, the ROSA algorithm was found to effectively extract primary branch skeletons under different tree structures, providing reliable support for subsequent IA estimation.

3.4. Estimation of the Inclination Angle of Primary Branches

This study proposes a jujube primary branch inclination angle estimation method that combines dynamic window adjustment with weighted PCA. The accuracy of the proposed method was evaluated by comparing manually measured values with the estimated results. The experimental results demonstrate that the proposed method achieved high accuracy in estimating primary branch IAs for both OCS (Figure 12a) and MTS (Figure 12b) jujube trees. For OCS jujube trees, the primary branch inclination angle estimation achieved an R² of 0.958 and an RMSE of 2.38°; for MTS jujube trees, the R² was 0.935 and the RMSE was 4.94°. Additionally, both tree structures exhibited narrow 95% confidence intervals (red shaded areas) and 95% prediction intervals (blue shaded areas), indicating low variability in the estimation results and strong stability. The data points were uniformly distributed around the fitted curve without evident outliers, further validating the accuracy and reliability of the proposed method in primary branch IA estimation.

3.5. Ablation Experiments

The CGCM module consists of three submodules: a polynomial term (Poly), Chebyshev graph convolution (ChebPoly), and a residual block (ResBlock). To evaluate the contribution of each submodule within CGCM-PointNet++, ablation experiments were conducted, the results of which are presented in

Table 3. Performance comparison of different submodule combinations.

Model	Poly	ChebPoly	ResBlock	Acc	CAA	mIoU	Ocs_mIoU	Mts_mIoU
PointNet++	✗	✗	✗	95.94	95.79	90.54	92.97	88.10
PolyNet	✓	✗	✗	96.50	96.40	92.2	93.02	91.42
PolyResNet	✓	✗	✓	96.78	96.67	92.78	93.29	92.26
ChebPolyNet	✓	✓	✗	96.93	96.59	92.52	93.42	91.62
CGCM-PointNet++	✓	✓	✓	97.27	97.26	93.83	95.20	92.47

. When no submodules were introduced, the baseline model PointNet++ achieved an Acc of 95.94% and a mean mIoU of 90.54%, indicating certain limitations in handling complex geometric structures. Incorporating the Poly submodule, the constructed PolyNet had an improved Acc of 96.50%, suggesting that the polynomial transformation enhances the model’s ability to extract nonlinear features. With the further addition of the ResBlock to form PolyResNet, the Acc increased to 96.78%, demonstrating the effectiveness of the residual structure in feature propagation and model stability. Incorporating both the Poly and ChebPoly submodules, the constructed ChebPolyNet achieved an Acc of 96.93%, validating the advantage of ChebPoly in terms of high-order feature modeling. Finally, the CGCM-PointNet++ model, constructed by incorporating the Poly, ChebPoly, and ResBlock submodules, achieved the best performance, with an Acc of 97.27% and an mIoU of 93.83%. This result confirms the synergistic effects of the three components: Poly enhances nonlinear feature representation, ChebPoly further strengthens high-order feature processing, and ResBlock ensures effective deep feature propagation.

4. Discussion

4.1. Analysis of Point Cloud Data Acquisition

High-quality acquisition of point cloud data forms the foundation for plant structural modeling and phenotypic parameter extraction and constitutes a critical prerequisite for subsequent high-precision point cloud segmentation and estimation of primary branch IA. In this study, TLS was employed for data acquisition. By performing multi-station scans and using spherical targets for registration, the three-dimensional phenotypic information of jujube trees was captured efficiently and accurately. Compared with 2D imaging methods that depend on natural or artificial illumination [42], TLS is insensitive to environmental lighting variations, operates stably under diverse illumination conditions, and is well suited to complex natural environments such as orchards and forested areas. Compared with the approximately 3 min per plant required by conventional binocular reconstruction [43], our multi-station TLS method acquired data from 78 jujube trees in 43 min, averaging about 33 s per tree, demonstrating strong field applicability and time-efficiency advantages. Additionally, to enhance data quality, the CSF and SOR were applied in combination to eliminate redundant ground points and outlier noise, providing robust support for subsequent segmentation, skeleton extraction, and IA estimation.

4.2. Analysis of Point Cloud Segmentation

Accurate segmentation of jujube tree branches and extraction of branch instances are critical for primary branch IA estimation. In this study, we propose a novel approach that integrates CGCM-PointNet++ with an optimized DBSCAN algorithm to extract jujube branch instances. The CGCM-PointNet++ model enhances semantic segmentation performance on jujube tree point clouds, while the optimized DBSCAN algorithm mitigates cluster over-segmentation and erroneous merging under uneven point-cloud density distributions. Our results align with those of Liu et al. [44], who incorporated a Transformer attention module into the PointNet++ model to enhance feature-extraction accuracy and applied the HDBSCAN algorithm for organ-level segmentation of cotton plant point clouds, successfully isolating leaves, bolls, and branches and extracting their phenotypic parameters. Similarly, Guo et al. [25] proposed a novel approach that combines ASAP-PointNet with an optimized DBSCAN algorithm for organ-level segmentation of cabbage point clouds. They demonstrated that the ASAP-PointNet model significantly improves semantic segmentation performance on cabbage point clouds, while the optimized DBSCAN algorithm effectively addresses challenges such as overlapping leaves and color similarity.

4.3. Analysis of Inclination Angle Estimation

Skeleton information, as a simplified representation of a model’s topological and geometric structure, can intuitively capture the morphological characteristics of branched plant architectures and has become a fundamental basis for extracting plant phenotypic information [45,46]. Wang et al. [47] applied a Laplacian-based skeletonization algorithm, first denoising the point cloud with a multi-pass filtering scheme before extracting the skeleton, and then obtained directional vectors for both the stem and the petiole to compute the angle between them for leaf IA. Compared with their approach, the ROSA algorithm employed in this study demonstrates superior robustness in skeleton topology reconstruction, particularly in preserving branch detail integrity and trunk continuity. Furthermore, by integrating a weighted PCA method with a dynamically adjustable window, we reduce the estimation bias introduced by significant local branch curvature variations in conventional PCA, thereby improving the stability and accuracy of primary branch IA estimation.

4.4. Analysis of Experimental Results

The proposed CGCM-PointNet++ model achieved an OA of 97.27%, CAA of 97.26%, and mIoU of 93.83% on the jujube tree point cloud test set, and likewise demonstrated outstanding performance in the ablation experiments. The DBSCAN algorithm with adaptive eps exhibited significant advantages, confirming its efficacy in branch instance segmentation. The ROSA algorithm efficiently extracted the primary branch skeleton across different tree architectures. In primary branch IA estimation, OCS and MTS jujube trees both showed high agreement with manual measurements, yielding R² values of 0.958 and 0.935 and RMSE of 2.38° and 4.94°, respectively, thereby validating the accuracy of the proposed IA estimation method. In summary, this study offers a feasible technical pathway for fruit tree structural modeling and extraction of key phenotypic parameters, and provides a research basis for digital orchard management and intelligent pruning.

5. Conclusions

The segmentation of jujube tree branches and the estimation of primary branch IAs are critical for achieving intelligent pruning, as the results directly impact the effectiveness of the pruning task. However, in this context, branch segmentation and primary branch IA estimation based on TLS point clouds pose several challenges, relating to uneven point cloud density, complex jujube tree structures, and significant branch curvature variations. To address these challenges, this study proposed a primary branch IA estimation method based on an improved PointNet++ network, which was shown to successfully achieve accurate segmentation of jujube tree branches and precise estimation of primary branch IAs. First, jujube tree point cloud data were acquired using TLS scanning, and CloudCompare was used for point cloud annotation, normal vector calculation, and normalization, resulting in a dataset suitable for training a segmentation network. Next, the PointNet++ network was improved by integrating the CGCM module into the SA layer to enhance its feature extraction capability for jujube tree point clouds. Instance segmentation of primary branch point clouds was then achieved using the DBSCAN algorithm with an adaptive eps strategy. Finally, the ROSA algorithm was used to extract primary branch skeleton points, allowing the inclination angles to be estimated using a weighted PCA method with dynamic window adjustment. From the experimental results, the improved PointNet++ achieved an Acc of 97.27%, a CAA of 97.26%, and an mIoU of 93.83%. In primary branch IA estimation, the results for OCS and MTS jujube trees showed high consistency with manual measurements, with R² values of 0.958 and 0.935, and RMSE values of 2.38 and 4.94°, respectively. In summary, the proposed method enables accurate jujube tree branch segmentation and IA measurement, offering a solid theoretical foundation and technical support for intelligent pruning.