CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards
Abstract
1. Introduction
2. Materials and Methods
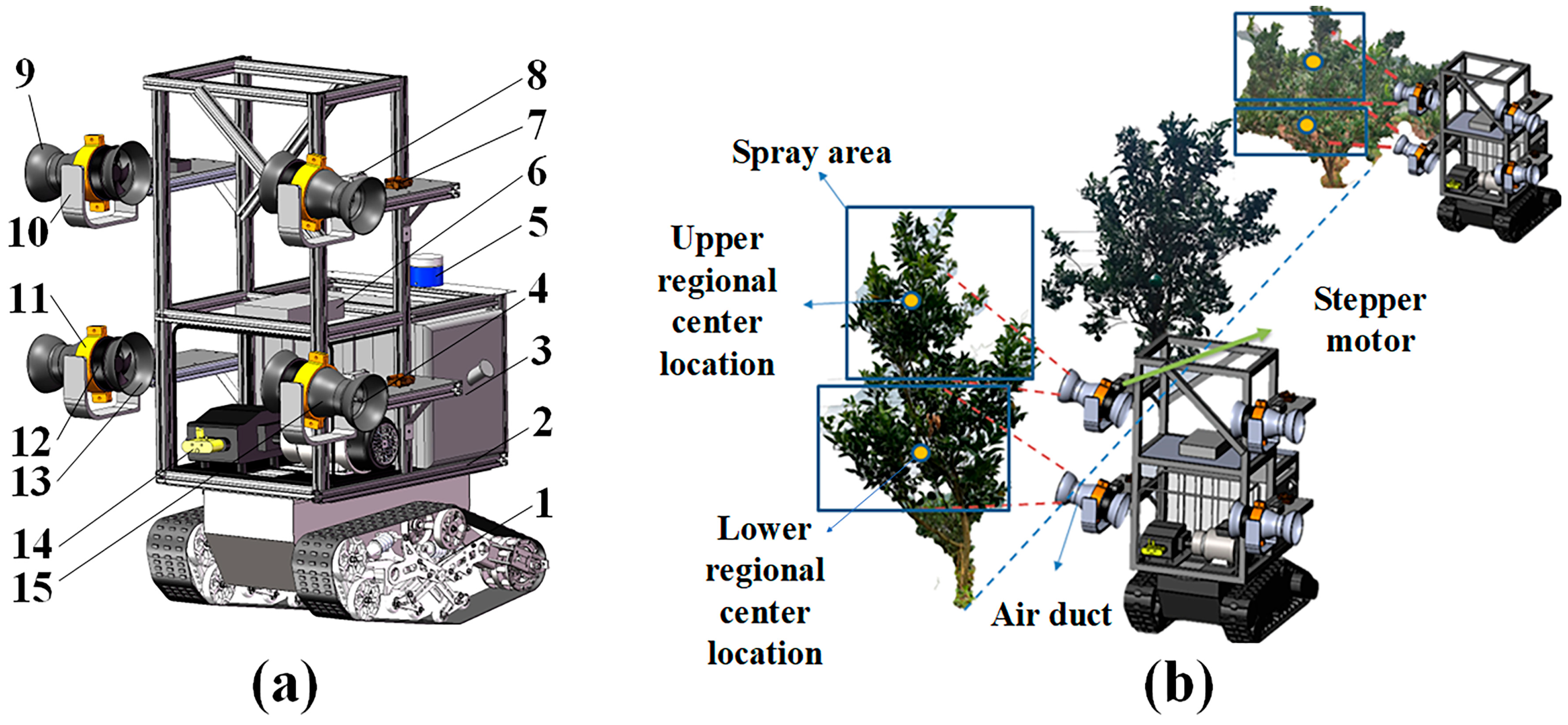
2.1. Overall Structure and Working Principle of the Orchard Sprayer
2.2. Determination of Axial Fan Parameters
2.2.1. Calculation of Fan Airflow Capacity
2.2.2. Calculation of Fan Outlet Airflow Velocity
2.3. Simulation Parameters for the Sprayer Airflow Field
2.3.1. Governing Questions and Models
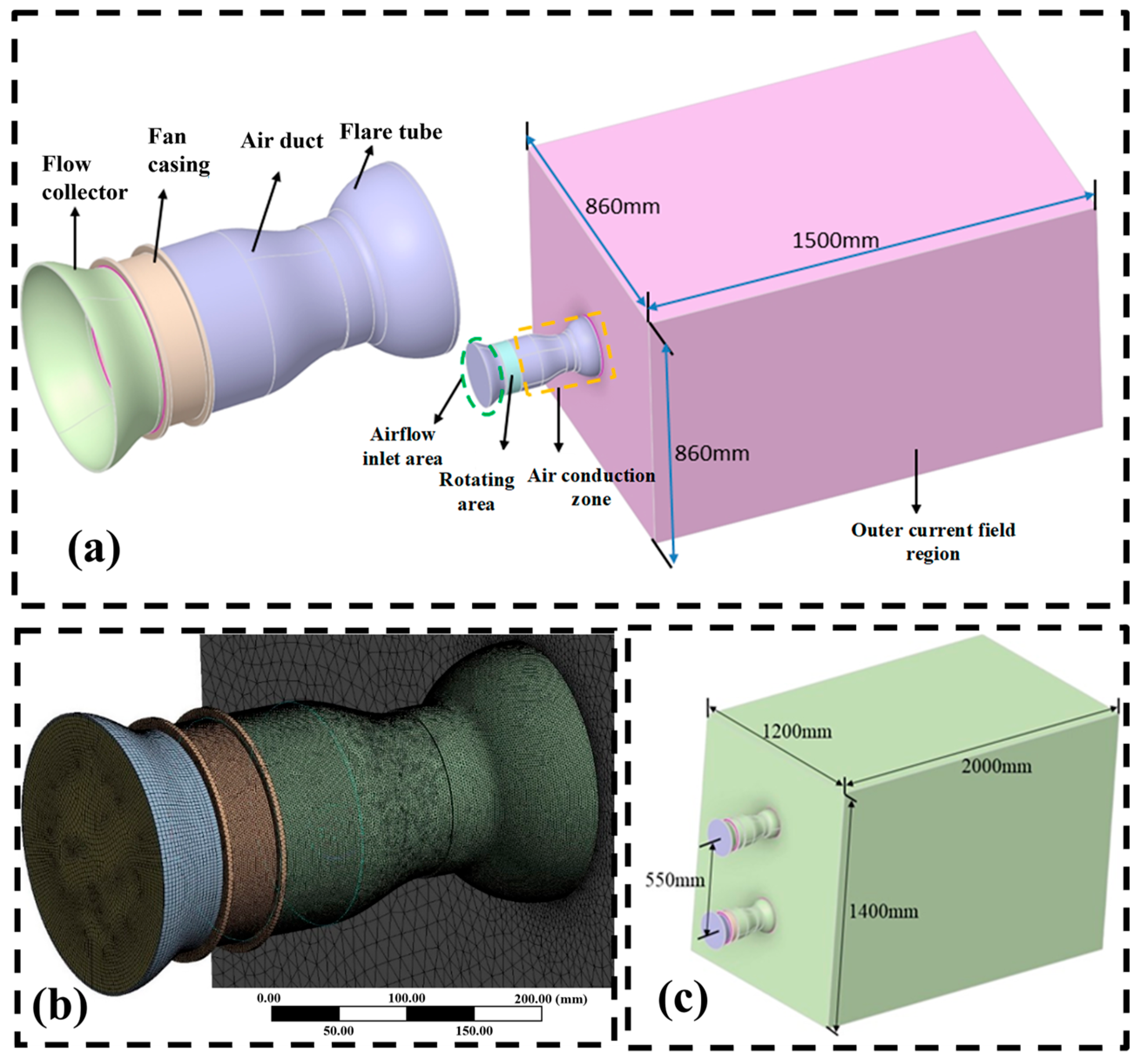
2.3.2. Computational Domain and Boundary Conditions
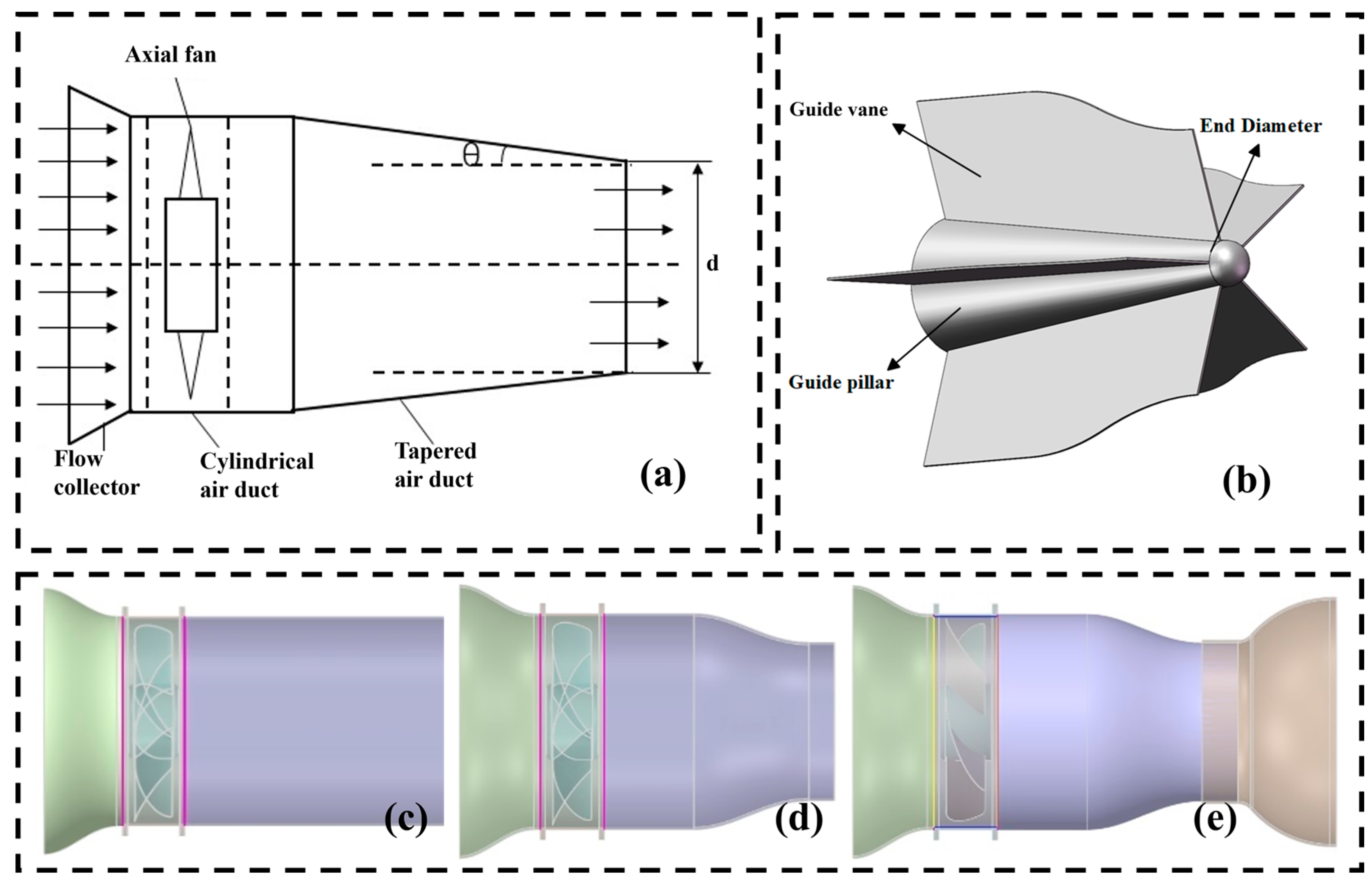
2.3.3. Model Construction of the Air Duct and Rectifier
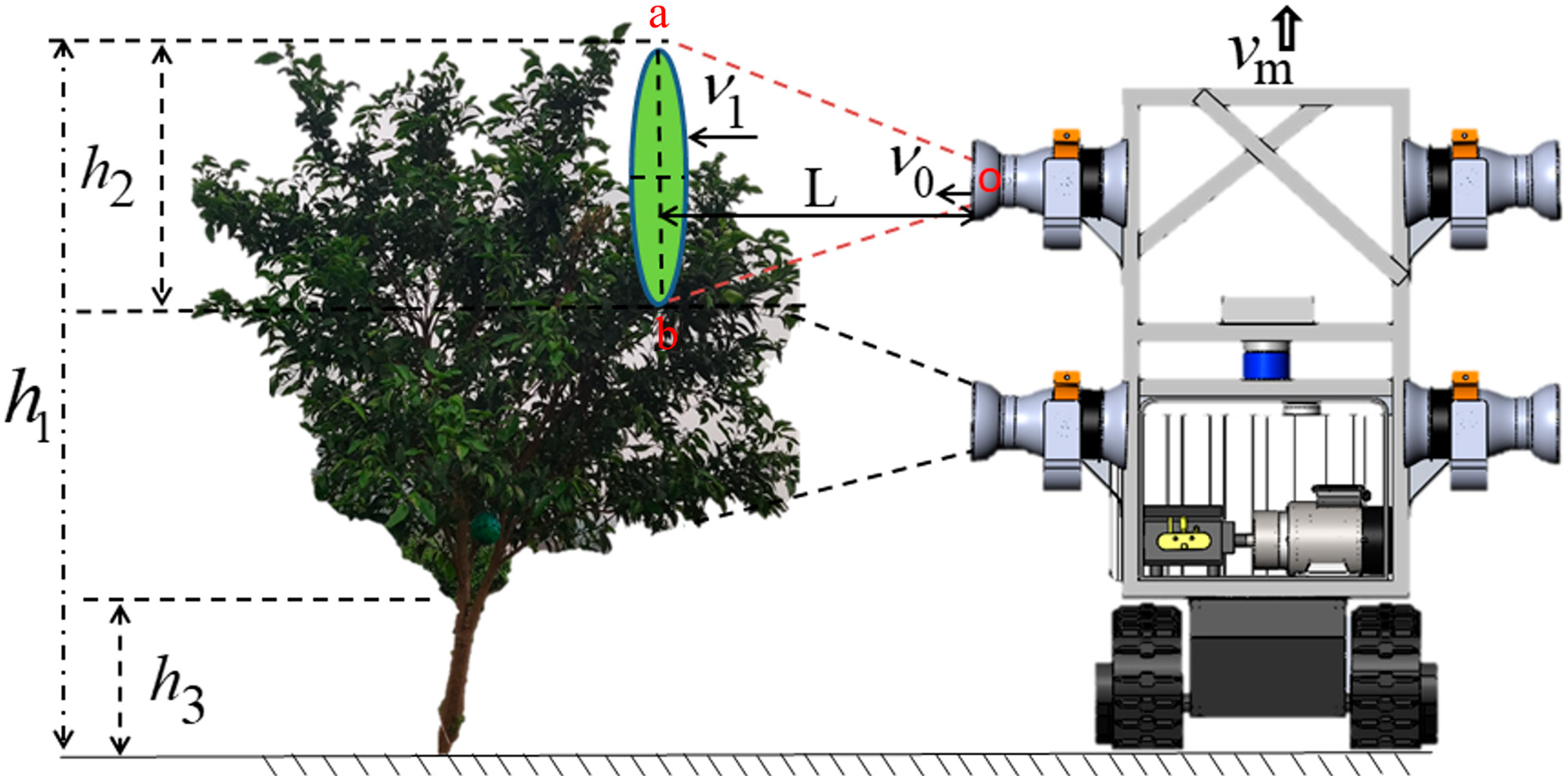
2.4. Air Speed Verification and Boundary Measurement
2.5. Simulation Experiment
2.5.1. Optimization of Air-Assisted Spraying Components Simulation
2.5.2. Air-Assisted Spray Flow Field Pattern Experiment
- (1)
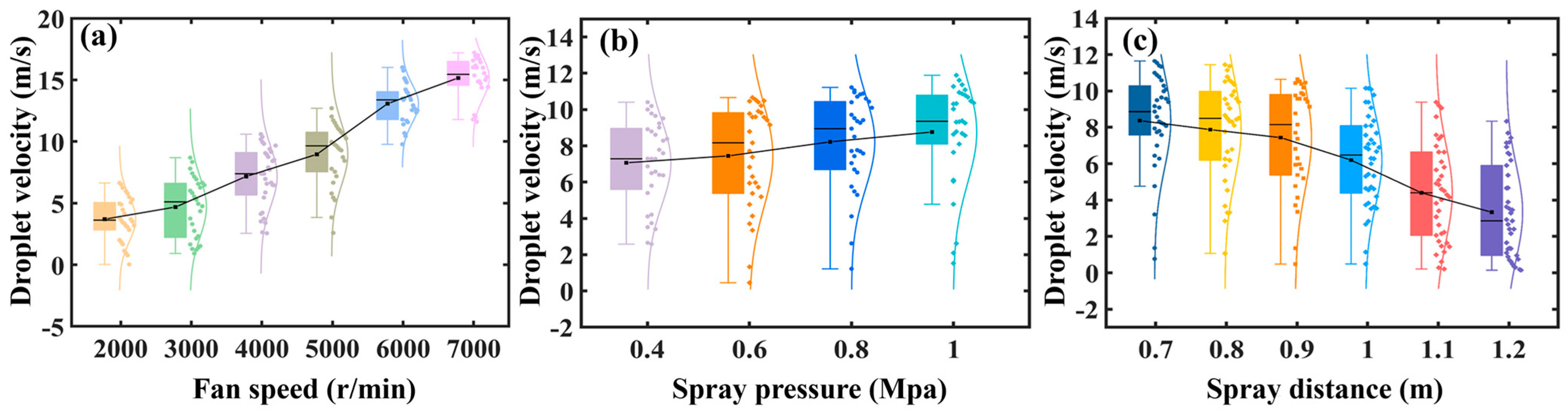
- Effect of different fan speed on droplet movement. Set the spray pressure to 0.4 MPa and the spray distance to 0.9 m to investigate the droplet deposition characteristics at axial fan speeds of 2000 r/min, 3000 r/min, 4000 r/min, 5000 r/min, 6000 r/min, and 7000 r/min.
- (2)
- Effect of different spray pressure on droplet movement. Set the axial fan speed to 4000 r/min and the spray distance to 0.9 m to investigate the droplet deposition characteristics at spray pressures of 0.4 MPa, 0.6 MPa, 0.8 MPa, and 1.0 MPa.
- (3)
- Effect of different spray distance on droplet movement. Set the axial fan speed to 4000 r/min and the spray pressure to 0.6 MPa to investigate the droplet deposition characteristics in the vertical plane at spray distances of 0.7 m, 0.8 m, 0.9 m, 1.0 m, 1.1 m, and 1.2 m.
2.6. Evaluation of Droplet Deposition
3. Results and Discussion
3.1. Air Speed Verification and Analysis
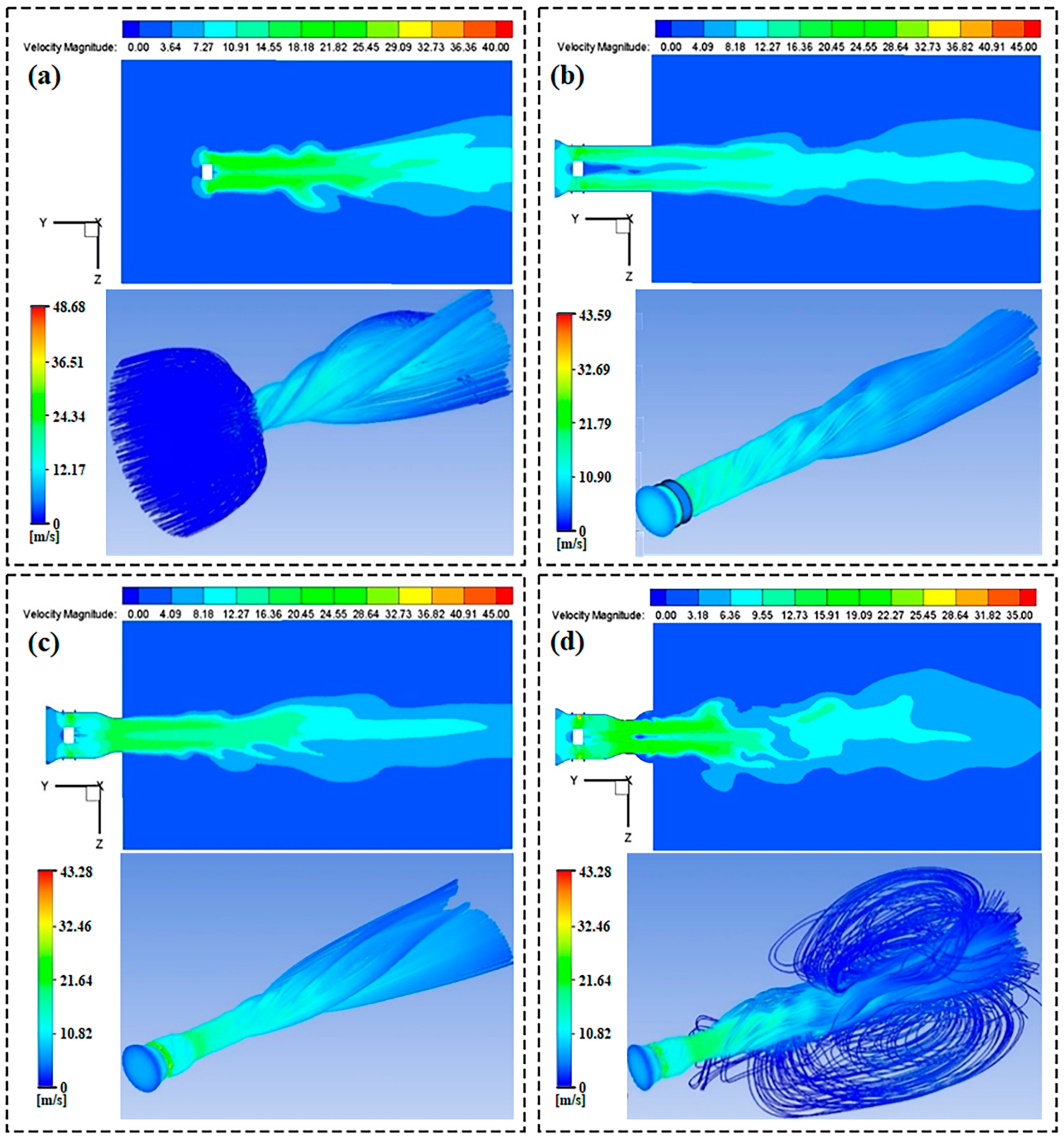
3.2. The Impact of the Air Duct on the Flow Field
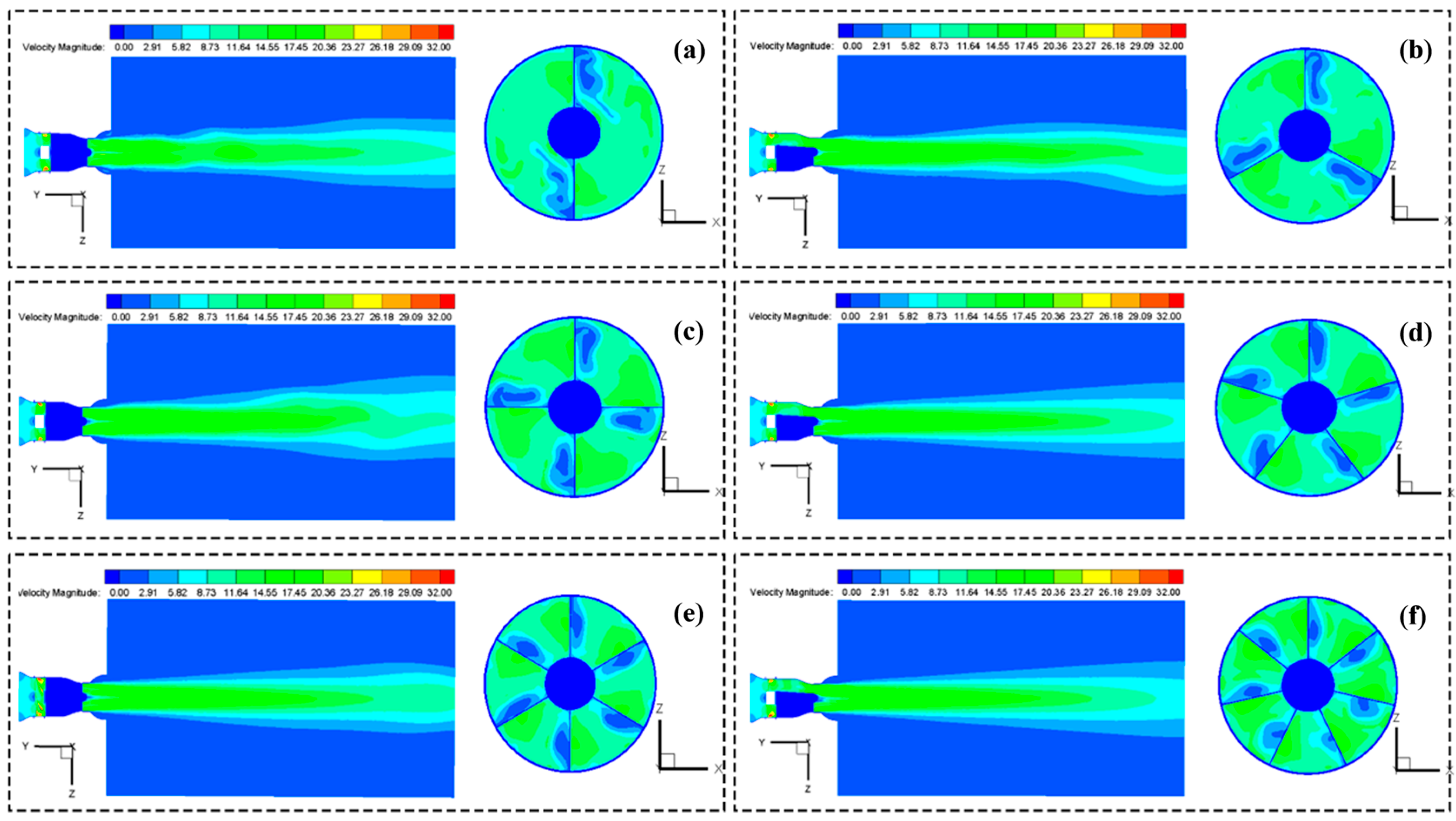
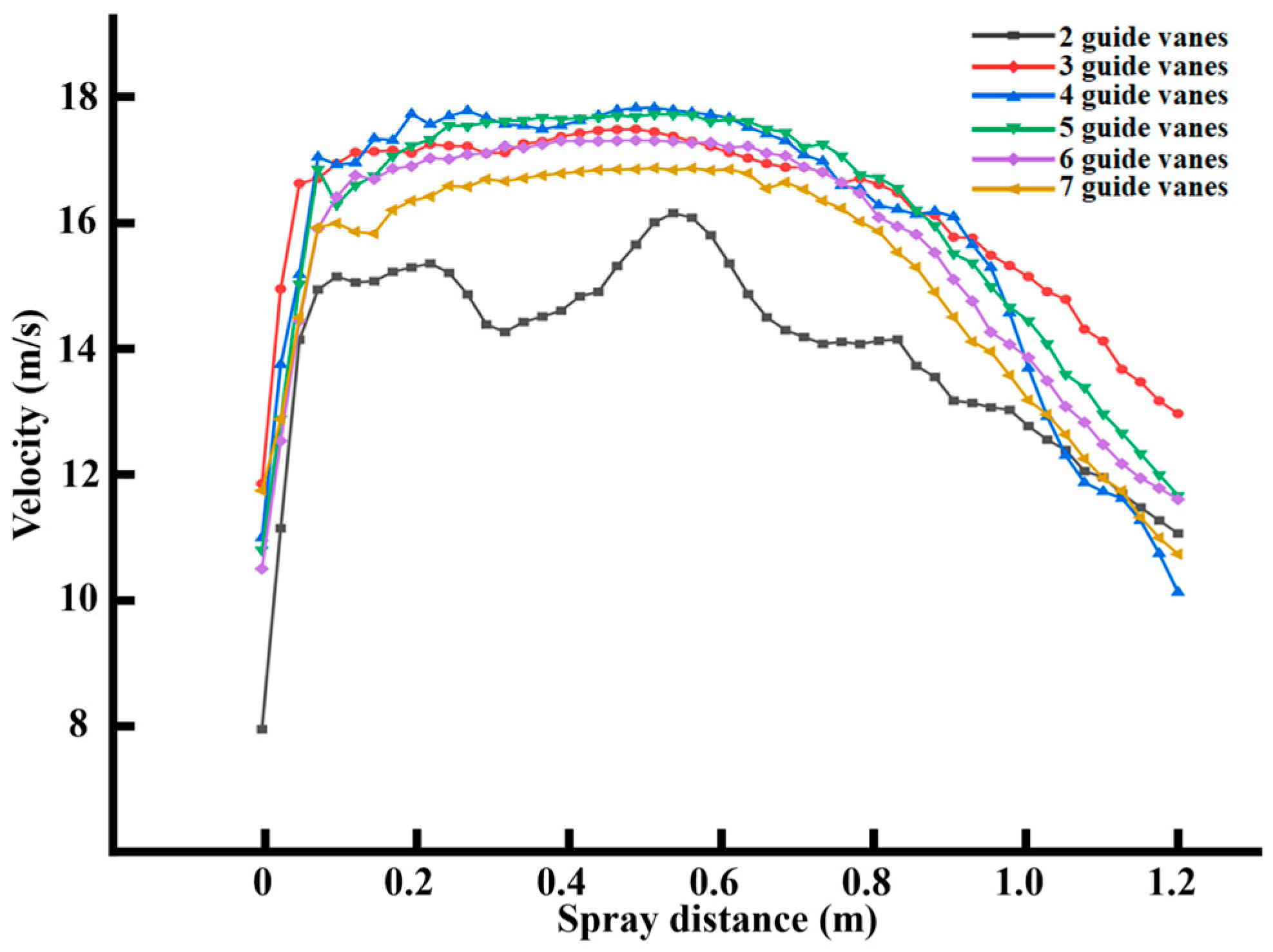
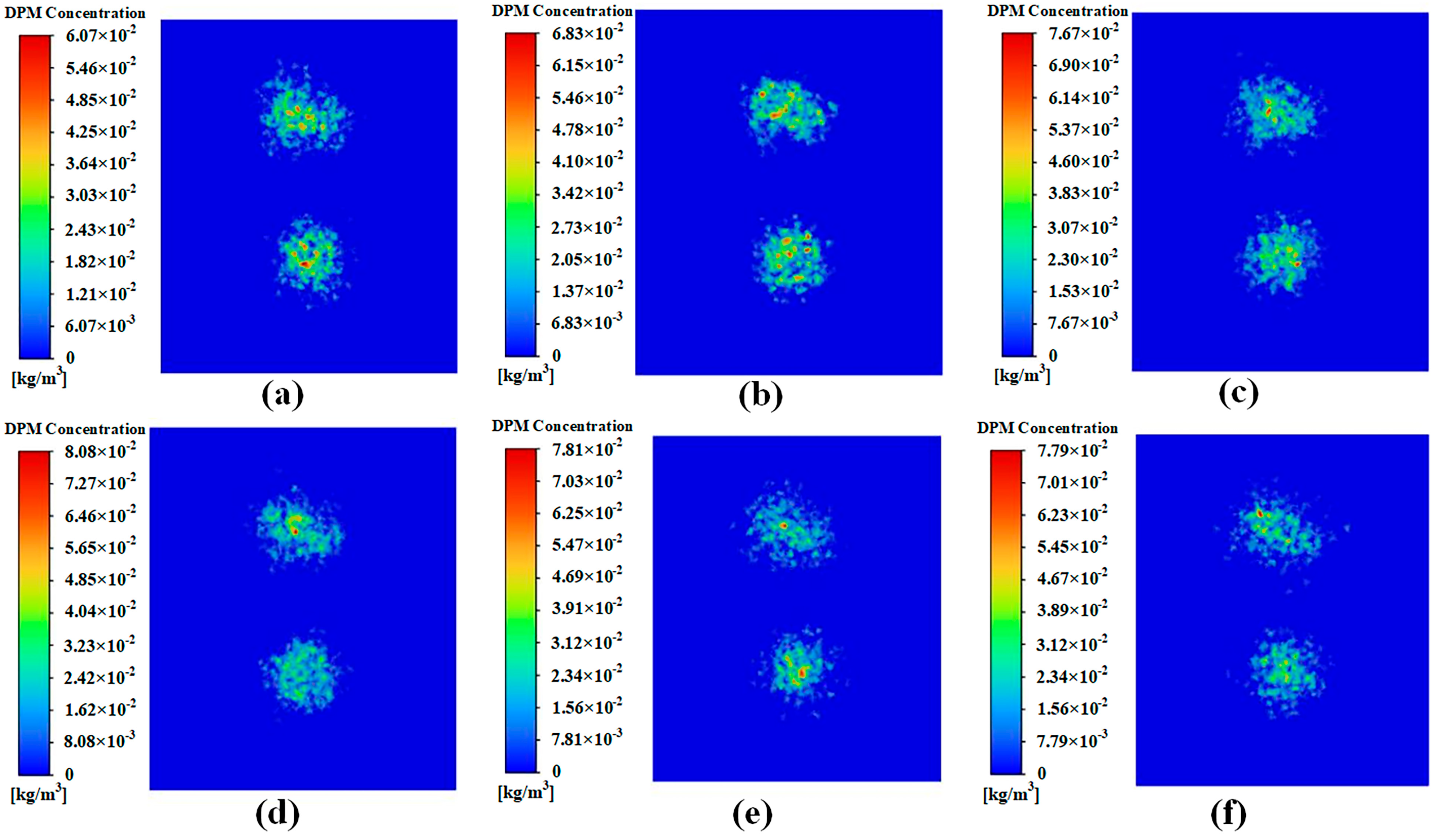
3.3. The Impact of the Number of Guide Vanes on the Flow Field
3.4. Effect of Different Fan Speed on Droplet Movement
3.5. Effect of Different Spray Pressure on Droplet Movement
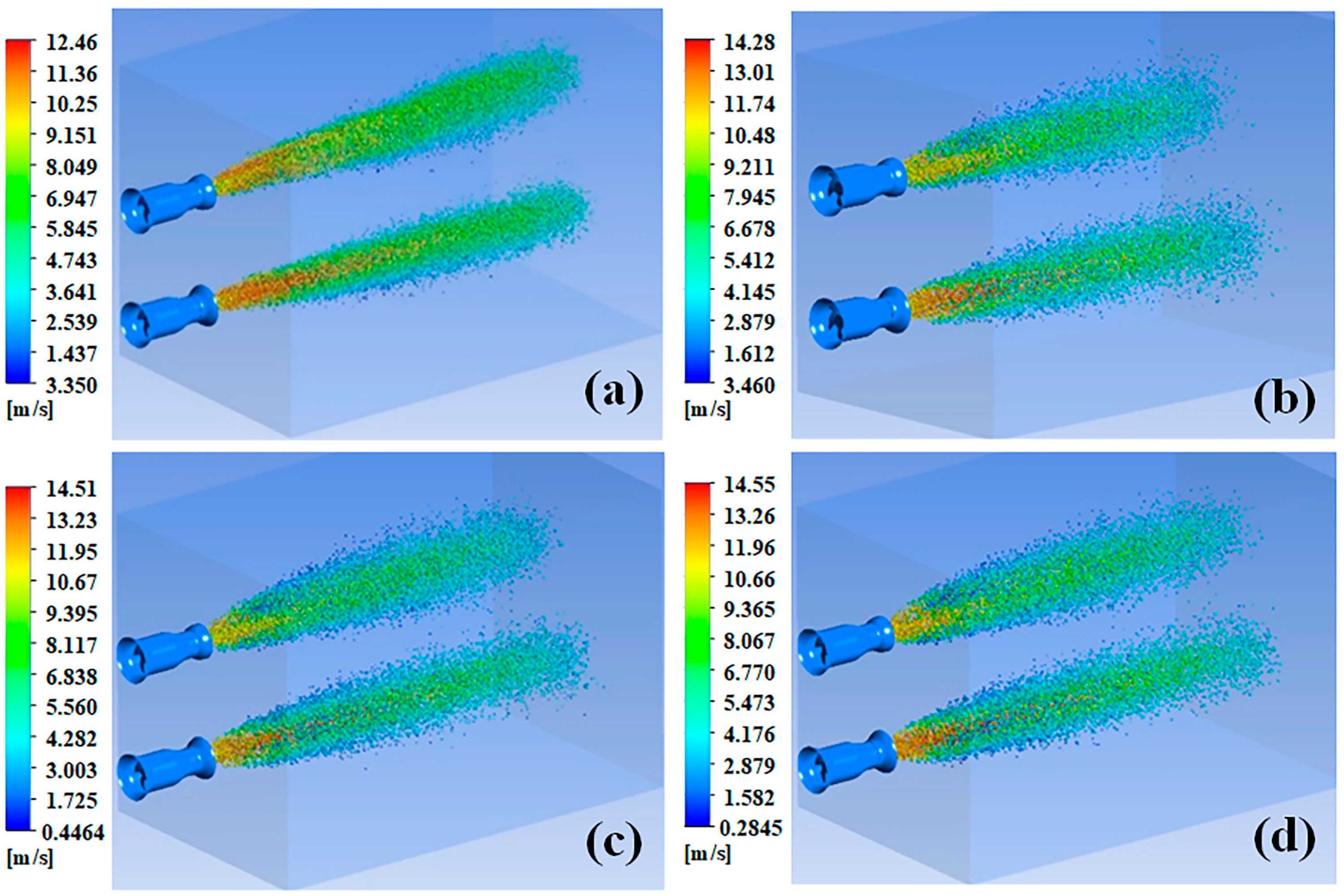
3.6. Effect of Different Spray Distance on Droplet Movement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ou, M.; Wang, M.; Zhang, J.; Gu, Y.; Jia, W.; Dai, S. Analysis and Experiment Research on Droplet Coverage and Deposition Measurement with Capacitive Sensor. Comput. Electron. Agric. 2024, 218, 108743. [Google Scholar] [CrossRef]
- Qin, W.; Chen, X.; Chen, P. “H” Sprayer Effect on Liquid Deposition on Cucumber Leaves and Powdery Mildew Prevention in the Shed. Front. Plant Sci. 2023, 14, 1175939. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.J.; Chen, B.T.; Lyu, H.T.; Kang, F.; Jiang, S.J. Research Progress of Orchard Plant Protection Mechanization Technology and Equipment in China. Trans. Chin. Soc. Agric. Eng. 2020, 36, 110–124. [Google Scholar]
- Changyuan, Z.; Chunjiang, Z.; Xiu, W.; Wei, L.; Ruixiang, Z. Nozzle Test System for Droplet Deposition Characteristics of Orchard Air-Assisted Sprayer and Its Application. Int. J. Agric. Biol. Eng. 2014, 7, 122–129. [Google Scholar]
- Salcedo, R.; Pons, P.; Llop, J.; Zaragoza, T.; Campos, J.; Ortega, P.; Gallart, M.; Gil, E. Dynamic Evaluation of Airflow Stream Generated by a Reverse System of an Axial Fan Sprayer Using 3D-Ultrasonic Anemometers. Effect of Canopy Structure. Comput. Electron. Agric. 2019, 163, 104851. [Google Scholar] [CrossRef]
- Liao, J.; Luo, X.; Wang, P.; Zhou, Z.; O’Donnell, C.C.; Zang, Y.; Hewitt, A.J. Analysis of the Influence of Different Parameters on Droplet Characteristics and Droplet Size Classification Categories for Air Induction Nozzle. Agronomy 2020, 10, 256. [Google Scholar] [CrossRef]
- Mozzanini, E.; Bhalekar, D.G.; Grella, M.; Hoheisel, G.-A.; Samy, S.; Balsari, P.; Gioelli, F.; Khot, L.R. Cleaning Performance Evaluation of Pneumatic Spray Delivery Based Solid Set Canopy Delivery System. J. ASABE 2024, 67, 1049–1063. [Google Scholar] [CrossRef]
- Morales-Rodríguez, P.A.; Cano Cano, E.; Villena, J.; López-Perales, J.A. A Comparison between Conventional Sprayers and New UAV Sprayers: A Study Case of Vineyards and Olives in Extremadura (Spain). Agronomy 2022, 12, 1307. [Google Scholar] [CrossRef]
- Fan, G.; Wang, S.; Bai, P.; Wang, D.; Shi, W.; Niu, C. Research on Droplets Deposition Characteristics of Anti-Drift Spray Device with Multi-Airflow Synergy Based on CFD Simulation. Appl. Sci. 2022, 12, 7082. [Google Scholar] [CrossRef]
- Bahlol, H.Y.; Chandel, A.K.; Hoheisel, G.-A.; Khot, L.R. The Smart Spray Analytical System: Developing Understanding of Output Air-Assist and Spray Patterns from Orchard Sprayers. Crop Prot. 2020, 127, 104977. [Google Scholar] [CrossRef]
- Jianping, L.I.; Yongliang, B.; Peng, H.U.O.; Pengfei, W.; Chunlin, X.U.E.; Xin, Y. Design and Experimental Optimization of Spray Device for Air-Fed Annular Nozzle of Sprayer. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2021, 52, 79–88. [Google Scholar]
- Salcedo, R.; Fonte, A.; Grella, M.; Garcerá, C.; Chueca, P. Blade Pitch and Air-Outlet Width Effects on the Airflow Generated by an Airblast Sprayer with Wireless Remote-Controlled Axial Fan. Comput. Electron. Agric. 2021, 190, 106428. [Google Scholar] [CrossRef]
- Salcedo, R.; Sánchez, E.; Zhu, H.; Fàbregas, X.; García-Ruiz, F.; Gil, E. Evaluation of an Electrostatic Spray Charge System Implemented in Three Conventional Orchard Sprayers Used on a Commercial Apple Trees Plantation. Crop Prot. 2023, 167, 106212. [Google Scholar] [CrossRef]
- Duga, A.; Ruysen, K.; Dekeyser, D.; Nuyttens, D.; Bylemans, D.; Nicolaï, B.; Verboven, P. CFD Based Analysis of the Effect of Wind in Orchard Spraying. Chem. Eng. Trans. 2015, 44, 289–294. [Google Scholar]
- Hu, Y.; Chen, Y.; Wei, W.; Hu, Z.; Li, P. Optimization Design of Spray Cooling Fan Based on CFD Simulation and Field Experiment for Horticultural Crops. Agriculture 2021, 11, 566. [Google Scholar] [CrossRef]
- Ran, S.S.; Bing, X.H.; Shan, L.H.; Sheng, H.T.; Zong, S.D.; Hua, L.Y. Numerical Simulation and Experiment of Structural Optimization for Air-Blast Sprayer. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2013, 44, 73–78. [Google Scholar] [CrossRef]
- Huang, C.-H.; Gau, C.-W. An Optimal Design for Axial-Flow Fan Blade: Theoretical and Experimental Studies. J. Mech. Sci. Technol. 2012, 26, 427–436. [Google Scholar] [CrossRef]
- Khot, L.R.; Ehsani, R.; Albrigo, G.; Larbi, P.A.; Landers, A.; Campoy, J.; Wellington, C. Air-Assisted Sprayer Adapted for Precision Horticulture: Spray Patterns and Deposition Assessments in Small-Sized Citrus Canopies. Biosyst. Eng. 2012, 113, 76–85. [Google Scholar] [CrossRef]
- Jing, S.; Ren, L.; Zhang, Y.; Han, X.; Gao, A.; Liu, B.; Song, Y. A Simulation and Experiment on the Optimization Design of an Air Outlet Structure for an Air-Assisted Sprayer. Agriculture 2023, 13, 2277. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Li, C.; Lan, H.; He, Y.; Tang, Z.; Tang, Y. Performance Analysis and Testing of a Multi-Duct Orchard Sprayer. Agronomy 2023, 13, 1815. [Google Scholar] [CrossRef]
- Fan, S.; Gao, G.; Shen, H. Optimization of Diversion Device and Experiment on Air-Assisted Sprayers in Orchards. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2492, p. 012007. [Google Scholar]
- Guo, Z.; Zhang, J.; Chen, L.; Wang, Z.; Wang, H.; Wang, X. Study on Deposition Characteristics of the Electrostatic Sprayer for Pesticide Application in Greenhouse Tomato Crops. Agriculture 2024, 14, 1981. [Google Scholar] [CrossRef]
- Xue, X.; Zeng, K.; Li, N.; Luo, Q.; Ji, Y.; Li, Z.; Lyu, S.; Song, S. Parameters Optimization and Performance Evaluation Model of Air-Assisted Electrostatic Sprayer for Citrus Orchards. Agriculture 2023, 13, 1498. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Q.; Zhou, H.; Zhang, C.; Jiang, X.; Lv, X. CFD Analysis and RSM-Based Design Optimization of Axial Air-Assisted Sprayer Deflectors for Orchards. Crop Prot. 2024, 184, 106794. [Google Scholar] [CrossRef]
- Hong, S.-W.; Zhao, L.; Zhu, H. SAAS, a Computer Program for Estimating Pesticide Spray Efficiency and Drift of Air-Assisted Pesticide Applications. Comput. Electron. Agric. 2018, 155, 58–68. [Google Scholar] [CrossRef]
- Cui, H.; Wang, C.; Yu, S.; Xin, Z.; Liu, X.; Yuan, J. Two-Stage CFD Simulation of Droplet Deposition on Deformed Leaves of Cotton Canopy in Air-Assisted Spraying. Comput. Electron. Agric. 2024, 224, 109228. [Google Scholar] [CrossRef]
- Wang, J.; Lan, X.; Chen, P.; Liang, Q.; Liao, J.; Ma, C. Field Evaluation of Spray Quality and Environmental Risks of Unmanned Aerial Spray Systems in Mango Orchards. Crop Prot. 2024, 182, 106718. [Google Scholar] [CrossRef]
- Patel, M.K.; Praveen, B.; Sahoo, H.K.; Patel, B.; Kumar, A.; Singh, M.; Nayak, M.K.; Rajan, P. An Advance Air-Induced Air-Assisted Electrostatic Nozzle with Enhanced Performance. Comput. Electron. Agric. 2017, 135, 280–288. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, L.; Xue, X.; Ding, W.; Sun, Z.; Zhou, Q.; Cui, L. Design and Experiment of 3WQ-400 Double Air-Assisted Electrostatic Orchard Sprayer. Trans. Chin. Soc. Agric. Eng. 2016, 32, 45–53. [Google Scholar]
- Dai, S.; Ou, M.; Du, W.; Yang, X.; Dong, X.; Jiang, L.; Zhang, T.; Ding, S.; Jia, W. Effects of Sprayer Speed, Spray Distance, and Nozzle Arrangement Angle on Low-Flow Air-Assisted Spray Deposition. Front. Plant Sci. 2023, 14, 1184244. [Google Scholar] [CrossRef]
- Endalew, A.M.; Debaer, C.; Rutten, N.; Vercammen, J.; Delele, M.A.; Ramon, H.; Nicolaï, B.M.; Verboven, P. A New Integrated CFD Modelling Approach towards Air-Assisted Orchard Spraying. Part I. Model Development and Effect of Wind Speed and Direction on Sprayer Airflow. Comput. Electron. Agric. 2010, 71, 128–136. [Google Scholar] [CrossRef]
- Mashhadi, H.; Raeini, M.G.N.; Asoodar, M.A.; Mehdizadeh, S.A. Effect of Pressure and Nozzle Diameter on Spray Quality and Droplet Size in Handheld Gun Sprayers. Results Eng. 2025, 26, 104709. [Google Scholar] [CrossRef]
- Lan, X.; Wang, J.; Chen, P.; Liang, Q.; Zhang, L.; Ma, C. Risk Assessment of Environmental and Bystander Exposure from Agricultural Unmanned Aerial Vehicle Sprayers in Golden Coconut Plantations: Effects of Droplet Size and Spray Volume. Ecotoxicol. Environ. Saf. 2024, 282, 116675. [Google Scholar] [CrossRef]
- Dou, H.; Zhai, C.; Zhang, Y.; Chen, L.; Gu, C.; Yang, S. Research on Decoupled Air Speed and Air Volume Adjustment Methods for Air-Assisted Spraying in Orchards. Front. Plant Sci. 2023, 14, 1250773. [Google Scholar] [CrossRef]
- Williams, P.T.; Baker, A.J. Incompressible Computational Fluid Dynamics and the Continuity Constraint Method for the Three-Dimensional Navier-Stokes Equations. Numer. Heat Transf. 1996, 29, 137–273. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Gao, C.; Qi, L.; Wu, Y.; Feng, J.; Yang, Z. Design and Testing of a Self-Propelled Air-Blowing Greenhouse Sprayer. In Proceedings of the 2017 ASABE Annual International Meeting; American Society of Agricultural and Biological Engineers, Spokane, WA, USA, 16–19 July 2017; p. 1. [Google Scholar]
- Sørensen, J.N. Aerodynamic Aspects of Wind Energy Conversion. Annu. Rev. Fluid Mech. 2011, 43, 427–448. [Google Scholar] [CrossRef]
- Hong, S.-W.; Zhao, L.; Zhu, H. CFD Simulation of Airflow inside Tree Canopies Discharged from Air-Assisted Sprayers. Comput. Electron. Agric. 2018, 149, 121–132. [Google Scholar] [CrossRef]
- Yao, Y.; Li, F.; Xiang, J.; Song, L.; Li, J. Experimental Study on the Aerodynamic Performance of Variable Geometry Low-Pressure Turbine Adjustable Guide Vanes. Proc. Inst. Mech. Eng. Part A J. Power Energy 2023, 237, 669–686. [Google Scholar] [CrossRef]
- Dalgamoni, H.N.; Yong, X. Numerical and Theoretical Modeling of Droplet Impact on Spherical Surfaces. Phys. Fluids 2021, 33, 052112. [Google Scholar] [CrossRef]
- Lv, Q.; Li, J.; Guo, P.; Tang, P. Experimental Study on the Impact Forces of a Water Droplet Colliding with a Surface Carrying a Deposited Droplet. Exp. Therm. Fluid Sci. 2023, 145, 110883. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| End diameter of flare tube (mm) | 220 |
| Length of tapering air duct (mm) | 190 |
| End diameter of tapering air duct (mm) | 125 |
| Maximum diameter of tapering air duct (mm) | 170 |
| Diameter of axial fan (mm) | 162 |
| Number of axial fan blades (unit) | 5 |
| Length of fan casing (mm) | 60 |
| Diameter at the air inlet of the flow collector (mm) | 220 |
| Length of flow collector (mm) | 35 |
| Taper angle of air duct (°) | 17 |
| Parameters | Value |
|---|---|
| Dimensions (mm) | 172 × 160 × 51 |
| Power (W) | 135 |
| Speed range (r/min) | 1000–9000 |
| Operating voltage (V) | 32–72 DC |
| Airflow (m3/s) | 0.264 |
| Maximum wind pressure (Pa) | 400 |
| (1) Fan Speed | (2) Spray Pressure | (3) Spray Distance | |
|---|---|---|---|
| Condition | Spray pressure = 0.4 MPa Spray distance = 0.9 m | Fan speed = 4000 r/min Spray distance = 0.9 m | Fan speed = 4000 r/min Spray pressure = 0.6 MPa |
| Value | {2000, 3000, 4000, 5000, 6000, 7000}/(r/min) | {0.4, 0.6, 0.8, 1.0}/(MPa) | {0.7, 0.8, 0.9, 1.0, 1.1, 1.2}/(m) |
| Mounted | Distance from Air Outlet (m) | Air Velocity (m/s) | Results | Relative Error (%) | |||
|---|---|---|---|---|---|---|---|
| I | II | III | Average (m/s) | Simulation (m/s) | |||
| Integrated | 0.1 | 15.07 | 15.05 | 15.06 | 15.06 | 13.16 | 14.44% |
| 0.3 | 14.22 | 14.25 | 14.22 | 14.23 | 14.95 | −4.82% | |
| 0.5 | 13.08 | 13.08 | 13.05 | 13.07 | 14.48 | −9.74% | |
| 0.7 | 11.46 | 11.44 | 11.45 | 11.45 | 13.69 | −16.36% | |
| 0.9 | 10.65 | 10.63 | 10.61 | 10.63 | 12.96 | −17.98% | |
| 1.1 | 9.78 | 9.77 | 9.79 | 9.78 | 12.23 | −20.03% | |
| Independent | 0.1 | 16.34 | 16.35 | 16.33 | 16.34 | 15.57 | 4.95% |
| 0.3 | 16.03 | 16.07 | 16.04 | 16.05 | 16.94 | −5.27% | |
| 0.5 | 15.01 | 15.03 | 15.02 | 15.02 | 16.18 | −7.17% | |
| 0.7 | 13.23 | 13.27 | 13.29 | 13.26 | 15.87 | −16.43% | |
| 0.9 | 12.16 | 12.19 | 12.18 | 12.18 | 14.92 | −18.39% | |
| 1.1 | 10.09 | 10.06 | 10.07 | 10.07 | 12.58 | −19.93% | |
| Fan speed (r/min) | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 |
| Droplet deposition (µL·cm−2) | 0.96 | 1.92 | 3.72 | 2.96 | 1.45 | 0.87 |
| Spray pressure (MPa) | 0.4 | 0.6 | 0.8 | 1.0 |
| Droplet deposition (µL·cm−2) | 3.72 | 5.11 | 4.03 | 3.47 |
| Distance from air outlet (m) | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 |
| Droplet deposition (µL·cm−2) | 2.75 | 3.77 | 5.23 | 4.59 | 2.51 | 1.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Li, Y.; Chen, L.; Wang, K. CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards. Agriculture 2025, 15, 1103. https://doi.org/10.3390/agriculture15101103
Huang X, Li Y, Chen L, Wang K. CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards. Agriculture. 2025; 15(10):1103. https://doi.org/10.3390/agriculture15101103
Chicago/Turabian StyleHuang, Xiangfei, Yunwu Li, Lang Chen, and Kechao Wang. 2025. "CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards" Agriculture 15, no. 10: 1103. https://doi.org/10.3390/agriculture15101103
APA StyleHuang, X., Li, Y., Chen, L., & Wang, K. (2025). CFD-Based Flow Field Characteristics of Air-Assisted Sprayer in Citrus Orchards. Agriculture, 15(10), 1103. https://doi.org/10.3390/agriculture15101103





