Determining the Vibration Parameters for Coffee Harvesting Through the Vibration of Fruit-Bearing Branches: Field Trials and Validation

Abstract

In order to explore the optimal vibration parameters for the selective harvesting of coffee fruits, a high-velocity dynamic photography monitoring system was developed to analyze the vibration-assisted harvesting process. This system identified the optimal vibration position on coffee branches and facilitated theoretical energy transfer analysis, obtaining a mathematical formula for calculating the total kinetic energy of coffee branches. A single-factor experiment was conducted with the vibration position as the experimental factor and the total kinetic energy of coffee branches as the response variable. The results showed that the total kinetic energy of the branches was the highest at Vibration Position 2 (the position between the third and the fourth Y-shaped bud tips on the branch). Therefore, Vibration Position 2 was determined as the optimal vibration position. Further analysis established a mathematical model linking coffee cherry motion parameters to theoretical detachment force. A factorial experiment was conducted with vibration frequency and amplitude as test factors, using detachment rates of green, semi-ripe, and ripe cherries as indicators. The results showed that at 55 Hz and 10.10 mm amplitude, the detachment rate of ripe cherries was highest (83.33%), while green and semi-ripe cherries detached at 16.67% and 33.33%, respectively. A field validation experiment, with Vibration Position 2, 55 Hz frequency, 10.10 mm amplitude, and 1 s vibration duration, yielded actual detachment rates of 15.86%, 35.17%, and 89.50% for green, semi-ripe, and ripe cherries, respectively. The error margins compared with the theoretical values were all below 10%. These results confirm the feasibility of optimizing vibration harvesting parameters through high-velocity photography dynamic analysis.

1. Introduction

Arabica coffee (Coffea arabica L.) is the most widely cultivated coffee variety, accounting for over 80% of global planting area and production [1]. In 2022, Yunnan Province contributed 98% of China’s total coffee planting area and 99% of its coffee production [2,3]. The high-altitude mountainous climate of Yunnan provides the optimal conditions for high-quality coffee cultivation. However, reliance on manual harvesting remains a major challenge that significantly restricts the development of the coffee industry [4].

Vibration harvesting is the most commonly used method for tree fruit collection, and optimizing the vibration parameters is essential for improving harvesting efficiency and fruit quality [4,5,6,7]. However, owing to the prolonged maturation period and significant growth variation in coffee cherries, vibration harvesting often causes premature fruit drop, affecting both coffee quality and economic returns. Therefore, determining the optimal vibration parameters for coffee harvesting machines is crucial for advancing the coffee harvesting technology and equipment.

Extensive studies have been conducted from various perspectives to achieve precise vibration harvesting of tree fruit. Ping [8] investigated the vibration harvesting theory of goji berries and demonstrated the feasibility of using high-velocity photography to analyze vibration parameters. Fu et al. [9] conducted harvesting experiments on sea buckthorn using a self-developed vibration harvester and suggested that different vibration parameter combinations significantly affected harvesting performance. Hu et al. [10] performed structural simulations of a jujube harvester using ADAMS and ANSYS to identify the optimal vibration parameters for jujube harvesting. San [11] adopted a high-velocity video analysis software to obtain the velocity and acceleration data of apricots during vibration and established a mathematical model of the apricot motion. Jakob et al. [12] studied the adhesion characteristics between fruits and branches, demonstrating that the adhesion force decreased as the fruit ripened, providing guidance for optimizing vibration parameters. Jaime Buitrago-Osorio et al. [13] studied the physical and mechanical properties of coffee berries, and the relationship between the color of coffee berries and their mechanical properties was discovered. The coffee berries were classified into four colors.

The aforementioned studies investigated the vibration parameters, binding force characteristics, and motion dynamics of fruit and forest fruit harvesters, enabling one-time mechanized harvesting of certain fruits and forest products. However, for fruits and forest fruits with extended maturation periods that require batch harvesting, the selective harvesting of ripe fruits while retaining unripe fruits remains a significant challenge that urgently needs to be addressed.

To achieve the selective harvesting of coffee berries, this study designed a two-axis adaptive vibration test bench, built a high-speed photography dynamic monitoring system, and conducted high-speed photography dynamic analysis experiments. Based on the physical parameters of the coffee branches and the characteristics of vibration energy transfer, a kinetic energy transfer equation for coffee branches was established. A quantitative comparison of the kinetic energy transfer effects of coffee branches at different vibration positions was conducted, and the vibration position with the best kinetic energy transfer effect was selected as the optimal vibration position, thereby achieving the goal of improving the harvesting efficiency of coffee berries. Based on the motion characteristics of coffee branches with fruits, a mathematical model between the motion parameters of coffee fruits and the theoretical detachment force was established. Through factorial experiments, the selective harvesting effects under different combinations of amplitudes and frequencies were analyzed, and the optimal combination of vibration frequency and amplitude for the selective harvesting of coffee fruits was obtained, thus enhancing the selective harvesting effect of coffee berries. The field test results further verified the accuracy of the high-speed photography dynamic analysis experiments, which provided a solution for the selective harvesting of coffee berries.

2. Measurement of Physical Characteristics of Experimental Samples

2.1. Measurement of Physical Characteristics of Coffee Branches

The physical characteristics of coffee branches and cherries are essential for analyzing branch kinetic energy and fruit detachment forces. Arabica coffee branches from the Baoshan Xinjia Mountain Specialty Coffee Estate were selected as research subjects. Each branch contained six Y-shaped bud nodes, which served as connection points between the coffee cherries pedicels and branches. The branch structure is shown in Figure 1, and its detailed structural characteristics are shown in Figure 2. To ensure accuracy and repeatability, 50 coffee branches were randomly selected as test samples. To minimize the impact of sample variability on the subsequent experimental results, a scale with 1 mm precision was used to measure branch lengths, and all sample branches were uniformly trimmed to a length of 495 mm.

The diameters of the roots and ends of 20 coffee branches were measured using the Shang Gong digital display vernier caliper 300 (Country: China; City: Shanghai; Equipment Manufacturer: Shanghai Shushi Tool Business Department; Precision: 0.01 mm). The density of 20 branches was measured by using the Shanghai Ruifang MDY-2 liquid densitometer (Country: China; City: Shanghai; Equipment Manufacturer: Shanghai Fangrui Instrument Co., Ltd. Precision: 0.001 g/cm³). The measurement results are listed in

Table 1. Physical parameter measurements of coffee branches.

Physical Parameters	Results
	Value	Standard Deviation
Accuracy range R1/mm	13.67	0.71
Diameter at the tip R2/mm	6.82	0.52
Density ρ/g·cm−3	0.682	0.084

.

By analyzing the data in Table 1, it is found that the diameters of the roots of the coffee branches are all larger than those of the ends, and the diameters of the coffee branches change relatively uniformly. Therefore, the coffee branch can be regarded as a conical cylinder with a uniformly changing diameter.

2.2. Measurement of Physical Characteristics of Coffee Cherries and Pedicels

As coffee cherry maturity is closely associated with color, the academic community classified them into three maturity stages based on color: unripe, semi-ripe, and ripe [4,14,15] (Figure 3).

Coffee cherries exhibit varying physical characteristics at different maturity stages, with size and mass increasing as they mature [16,17]. To analyze these variations, 50 samples were randomly selected for each stage (unripe, semi-ripe, and ripe). A vernier caliper with an accuracy of 0.03 mm was used to measure the pedicel length (L₁) and the major axis length of the coffee cherry (L₂) (Figure 4). Assuming that coffee cherries can be uniformly dense ellipsoidal bodies, their center of mass was considered to be at the midpoint (M) of the major axis. Based on this assumption, the distance from the pedicel base to the coffee cherry’s center of mass (L_b) and the total length of the coffee cherry and pedicel (L_a) were calculated. Additionally, an electronic scale with an accuracy of 0.01 g was applied to measure the mass of each sample. The physical properties of coffee cherries and pedicels are listed in

Table 2. Physical characteristics of coffee berries across maturity stages.

Physical Parameters	Unripe		Semi-Ripe		Ripe
	Average Value	Standard Deviation	Average Value	Standard Deviation	Average Value	Standard Deviation
Fruit Pedicel Length L1/mm	6.21	1.60	6.31	1.55	6.37	1.35
Coffee Cherry Length L2/mm	18.36	1.54	18.49	1.34	18.62	1.41
Distance from Pedicel Base to Centroid Lb/mm	15.31	1.37	15.43	1.09	15.62	1.12
Distance from Pedicel Base to Fruit Apex La/mm	24.57	3.14	24.80	2.89	24.99	2.76
Coffee Cherry Mass m/g	1.53	0.24	1.58	0.21	1.62	0.17

Note: The color of ripe fruits is red, the color of semi-ripe fruits is yellowish orange, and the color of unripe fruits is green.

.

2.3. Measurement of Coffee Cherry and Pedicel Detachment Force

The detachment force between coffee cherries and their pedicels can be a critical factor in determining the optimal vibration frequency and amplitude for harvesting machines. In this study, 50 coffee cherry samples with pedicels were randomly selected at each maturity stage (unripe, semi-ripe, and ripe). The actual detachment force was measured using a texture anal‘yzer TA Type-XT Plus (Country: China; City: Xiamen; Equipment Supplier: Xiamen Chaoji Instrument and Equipment Co., Ltd.), and the measurement accuracy was enhanced using a specialized clamp designed for coffee cherries (Figure 5).

During the measurement, the coffee cherry clamp was secured to the base of the texture analyzer, firmly holding the pedicel. An upward force was gradually applied at a constant rate until the pedicel detached from the cherry. The maximum detachment force recorded for each test was documented, and the results are presented in

Table 3. Average value and standard deviation of detachment force between coffee cherries and pedicel.

Parameter/N	Results
	Average Value	Standard Deviation
Unripe Cherry Detachment Force/N	4.77	0.51
Semi-Ripe Cherry Detachment Force/N	3.71	0.62
Ripe Cherry Detachment Force/N	2.89	0.38

.

The measurement results demonstrated a clear numerical gradient in the detachment force across different maturity stages, with the unripe cherries exhibiting the highest detachment force, followed by the semi-ripe cherries, and the ripe cherries having the lowest. This finding confirmed the feasibility of the selective vibration harvesting of coffee cherries.

3. High-Velocity Photographic Dynamic Monitoring System

3.1. Two-Axis Adaptive Vibration Test Bench

3.1.1. Structure and Working Principle of the Two-Axis Adaptive Vibration Test Bench

The two-axis adaptive vibration test bench comprised a stopper assembly, foot supports, mounting base, adjustable-parameter vibrator, linear guide system, locking device, linear guide slider, lifting mechanism, and quick-locking mechanism. The structural layout is shown in Figure 6.

During the experiment, the coffee branch root was secured to a test bench using a quick clamping device. The linear guide slider was adjusted horizontally to position the vibration action point directly below the vibration fork, whereas the lifting device was used vertically to align the branch’s vibration point with the center of the vibration fork, ensuring precise vibration positioning. Among them, the adjustment stroke in the horizontal direction is 0–550 mm, and the adjustment stroke in the vertical direction is 0–200 mm. By modifying the parameters of the adjustable vibrator, different amplitudes and frequencies of the excitation forces can be applied to the branch to satisfy experimental requirements. The working principle of the two-axis adaptive vibration test bench is illustrated in Figure 7.

3.1.2. Structure and Working Principle of the Adjustable-Parameter Vibrator

The adjustable-parameter vibrator comprised a 4260 motor, motor base, spring coupling, eccentric shaft, 3210A bearing and housing, 693ZZ bearing, reciprocating shaft frame, reciprocating shaft, linear bearing, rocker arm, S7000 bearing housing, and vibration fork. The overall structural layout is illustrated in Figure 8.

During the experiment, the vibration frequency was controlled by adjusting the velocity control knob, whereas the amplitude was regulated by replacing the eccentric shafts with different eccentric distances. The adjustable-parameter vibrator involved five eccentric shafts (Figure 9), and their corresponding amplitudes are listed in

Table 4. Comparison of eccentric axles and amplitudes.

Eccentricity/mm	Amplitude/mm
2.00	3.26
2.50	6.74
3.00	10.10
3.50	13.48
4.00	16.84

.

3.2. Construction and Working Principle of High-Velocity Photography Dynamic Monitoring System

The high-velocity photography dynamic monitoring system comprised a personal computer, a 5F01 high-velocity camera, a supplementary light, a two-axis adaptive vibration test platform, a control board, and a 24 V power supply. Its structure is shown in Figure 10. The two-axis adaptive vibration test platform served as the testing unit, and the supplementary light and high-velocity camera formed the test shooting unit. A personal computer was used as the data analysis unit. The high-velocity camera, model 5F01, was manufactured by Hefei Fuhuang Junda High-Tech Information Technology Co., Ltd. (Hefei, China), and operated with a shooting accuracy of 2000 FPS.

During testing, the two-axis adaptive vibration test platform applied excitation forces to the sample, whereas the supplementary light enhanced the brightness in the shooting area. The high-velocity camera captured dynamic video of the vibrating sample and transmitted the data to a personal computer via a high-velocity interface (USB 3.0) for storage. Motion analysis was conducted using the High-Velocity Video Target Tracking and Measurement Software V1.0 [5,18]. During the analysis, the bearing seat of the branch compression device was selected as a calibration reference. The specific size was set in the image, and the target was defined. Motion analysis was then performed to yield the relevant motion parameters of the coffee cherries and branch [19].

4. High-Velocity Photography Dynamic Analysis Test

The high-velocity photography dynamic analysis test consisted of two main parts: (1) analyzing the optimal vibration position on the coffee branch and (2) determining the optimal combination of vibration frequency and amplitude parameters. Figure 11 illustrates the on-site test setup. Based on the working characteristics of the harvesting machine, the indices of vibration frequency, amplitude, and vibration position were selected as the research variables. Preliminary tests established a vibration frequency range of 50–70 Hz, an amplitude range of 3.26–13.48 mm, and a vibration duration of 1 s. The vibration position was set at the midpoint between two adjacent Y-shaped buds. The analysis of the optimal vibration position focused on quantitatively evaluating the total energy accumulated in the branch at different vibration positions under an excitation force [20,21]. A test for the optimal combination of vibration frequency and amplitude assessed how different parameter combinations could influence the harvesting efficiency of coffee cherries at three maturity levels [22,23]. Through detailed analysis and comprehensive evaluation of the test data, the optimal vibration parameters for coffee harvesting were determined.

4.1. Analysis of the Optimal Vibration Position on Coffee Branches

4.1.1. Vibration Energy Transmission Analysis

Under the action of the excitation force generated by the adjustable-parameter vibrator, the branches exhibited regular vibrations. When an excitation force is applied to different positions along the branches, significant differences arise in the kinetic energy transfer effect [24]. To quantitatively investigate this phenomenon, a study focusing on the maximum total kinetic energy of the branches was conducted. A mathematical equation was established to calculate the maximum total kinetic energy of coffee branches during vibration. The optimal vibration position for achieving the most effective kinetic energy transfer was determined by comparing the total kinetic energy values at different vibration positions.

In Section 2.1, the diameters at the root and end of the coffee branches were measured. The results showed that the diameter at the end was smaller than that at the root, with uniform tapering from the root to the end. Therefore, the coffee branches were simplified to conical cylinders with uniformly varying diameters. Based on this simplified model, the diameter change rate (K) of coffee branches was determined as follows:

$$K={\displaystyle \frac{R_1-R_2}{0.495}}$$

(1)

By substituting the root diameter of 13.67 mm and the tip diameter of 6.82 mm into Formula (1), the diameter change rate of the branch was calculated to be −0.0138. Consequently, the linear equation for the sample branch diameter can be derived as follows:

$$R\left(l\right)=-0.0138l+0.01367$$

(2)

where $l$ represents the length from a certain point on the branch to the base of the branch (m).

The coffee branch has an approximately circular structure and can be considered as a conical body when calculating its mass. The density of the measured coffee branches is 0.682 g·cm⁻³. In conclusion, the differential equation for the mass of the branches can be obtained as follows:

$$dm={\displaystyle \frac{\rho \mathsf{\pi }}{4}}\left(0.01367-0.0138l\right)dl$$

(3)

where

• $\rho$ denotes the density of the coffee sample branch (kg/m³).
• $dl$ denotes the length differential of the coffee branch at position $l$.

Using High-Velocity Video Target Tracking and Measurement Software V1.0, the motion video of the vibrating branch was analyzed to determine the maximum velocity of the velocity markers at the same moment. The data were processed using MATLAB 2023b, and a binomial fitting method was applied to derive the velocity equation of the vibrating branch. By substituting the mass differential equation and velocity equation into the kinetic energy integral formula and integrating over the entire branch length, the total kinetic energy of the coffee branch at the moment of maximum velocity $E$ is obtained:

$$E={\displaystyle \frac{1}{2}}{\int }_0^{0.495}{v\left(l\right)}^{2}dm$$

(4)

4.1.2. Vibration Position Test Results and Analysis

A vibration position analysis test was performed to determine the optimal vibration position on the coffee branches to enhance the harvester efficiency. A high-velocity photography dynamic monitoring system was used as the test equipment, and branches measuring 495 mm in length with uniform thickness and no coffee cherries were selected as the test samples. The vibration frequency was set at 60 Hz (midpoint of the 50–70 Hz range), amplitude at 6.74 mm (midpoint of the 3.26–13.48 mm range), and the vibration duration was fixed at 1 s. The vibration position served as the test variable, and the total kinetic energy (EEE) of the branch was used as the evaluation indicator in a single-factor test. As shown in Figure 12, the velocity markers and vibration positions were assigned on the branch, where the red dots represent 12 velocity markers evenly spaced at 45 mm intervals, numbered 1 to 12 from left to right, and the green squares indicate five vibration positions located between the first and sixth Y-shaped buds, numbered 1 to 5. The test was conducted on five groups, with six samples per group. After each test group, High-Velocity Video Target Tracking and Measurement Software V1.0 was used to analyze the high-velocity video, recording the maximum velocity value of each velocity marker at the same moment once the branch reached a stable vibration state. The test results are listed in

Table 5. Experimental results of velocity analysis at velocity marker points.

Vibration Position	Average Velocity of Velocity Marker Point/m·s−1
	1	2	3	4	5	6	7	8	9	10	11	12
1	0.000	0.851	1.250	1.699	2.130	2.610	3.100	3.391	3.460	3.387	2.350	3.390
2	0.000	0.823	1.403	2.395	3.620	5.061	4.960	4.214	3.540	3.369	1.510	5.059
3	0.000	0.829	1.280	1.680	2.110	2.474	2.640	2.472	2.350	2.471	3.012	3.294
4	0.000	0.838	1.736	2.513	3.160	3.349	3.240	3.040	2.950	3.234	4.362	4.833
5	0.000	0.835	1.620	2.504	3.526	4.167	2.580	1.177	1.862	2.680	3.240	2.503

.

To establish the mathematical relationship between the branch velocity marker positions and their corresponding velocities, MATLAB was used to perform the binomial regression analysis on the velocity data from Table 5. After multiple attempts, a sixth-order polynomial fitting equation was identified as the optimal model. The velocity curve equations for the five vibration positions are presented in

Table 6. Equation of binomial fitted velocity curve for coffee branches.

Vibration Position	Velocity Curve Equation
1	$v\left(l\right)=-4161l^6+8269l^5-5985l^4+1944l^3-292.7l^2+28.58l-0.0002645$
2	$v\left(l\right)=-63,700l^6+93,280l^5-49,580l^4+11,460l^3-1098 \ast l^2+50.88l-0.01779$
3	$v\left(l\right)=-20,160l^6+29,820l^5-16,270l^4+4042l^3-474.3 \ast l^2+33.83l-0.008802$
4	$v\left(l\right)=-19,490l^6+25,490l^5-11,450l^4+2057l^3-161.1 \ast l^2+23.58l-0.008455$
5	$v\left(l\right)=-47,940l^6+59,420l^5-24,880l^4+3860l^3-163.9 \ast l^2+15.73l+0.04807$

. The correlation coefficients, $R^2$, of these equations ranged from 0.9902 to 0.9997, with all significance levels (PPP) below 0.01, indicating that the regression models met the significance requirements and accurately described the velocity variations at different positions on the branch.

The total kinetic energy of the branch was calculated by substituting the velocity equations in Table 6 into the total kinetic energy formula (Equation (6)) and performing integration using MATLAB [24]. The results indicated that the total kinetic energy was 0.0866 J at Vibration Position 1, 0.1626 J at Position 2, 0.0660 J at Position 3, 0.1174 J at Position 4, and 0.0959 J at Position 5. Ranking the vibration positions by the total kinetic energy from highest to lowest, Position 2 exhibited the highest energy transfer efficiency, followed by Positions 4, 1, 5, and 3. These findings revealed that applying the excitation force at Vibration Position 2 yielded the maximum total kinetic energy, making it the optimal vibration position for the coffee harvesting process.

4.2. Analysis of Optimal Vibration Frequency and Amplitude Parameter Combinations

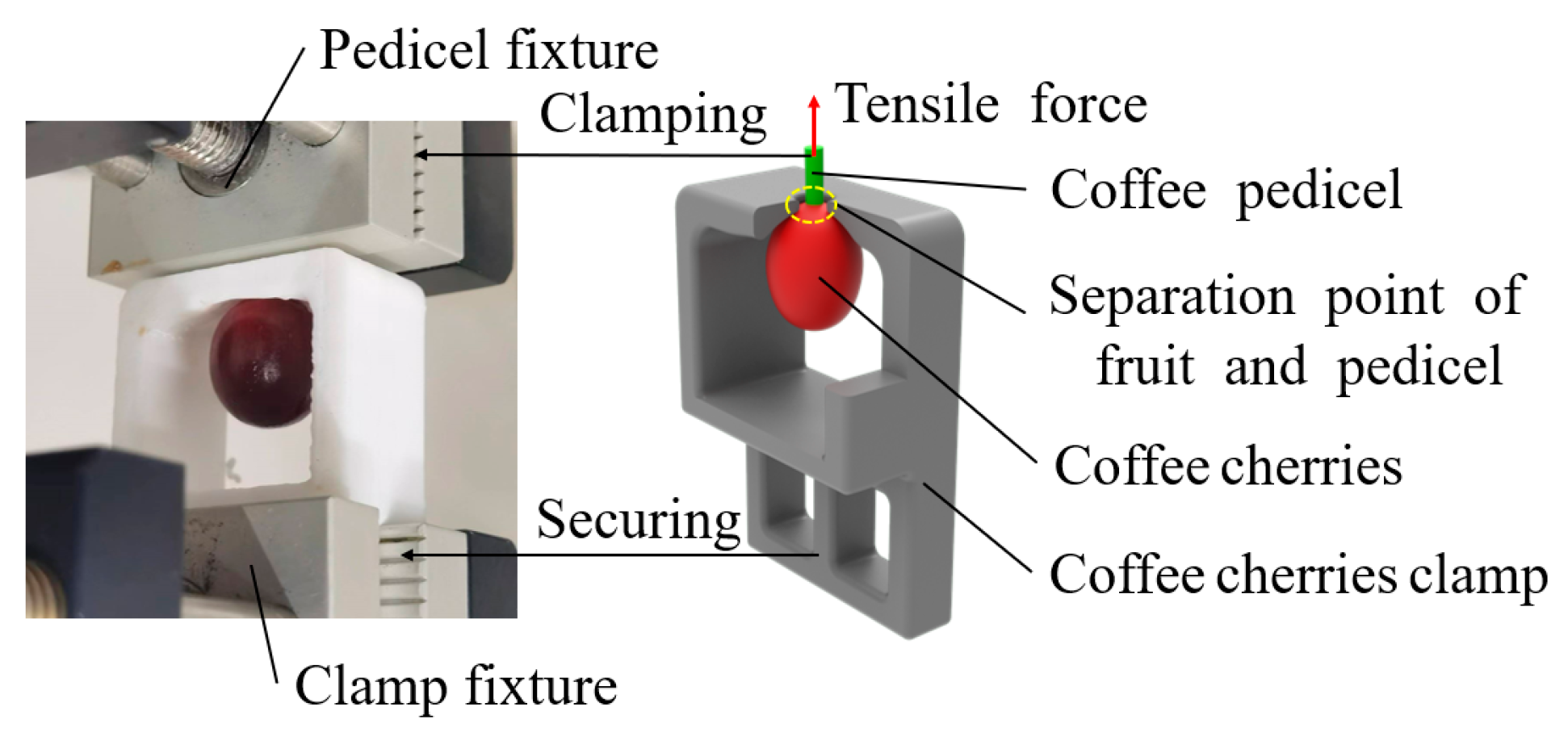
4.2.1. Coffee Cherries Motion Analysis

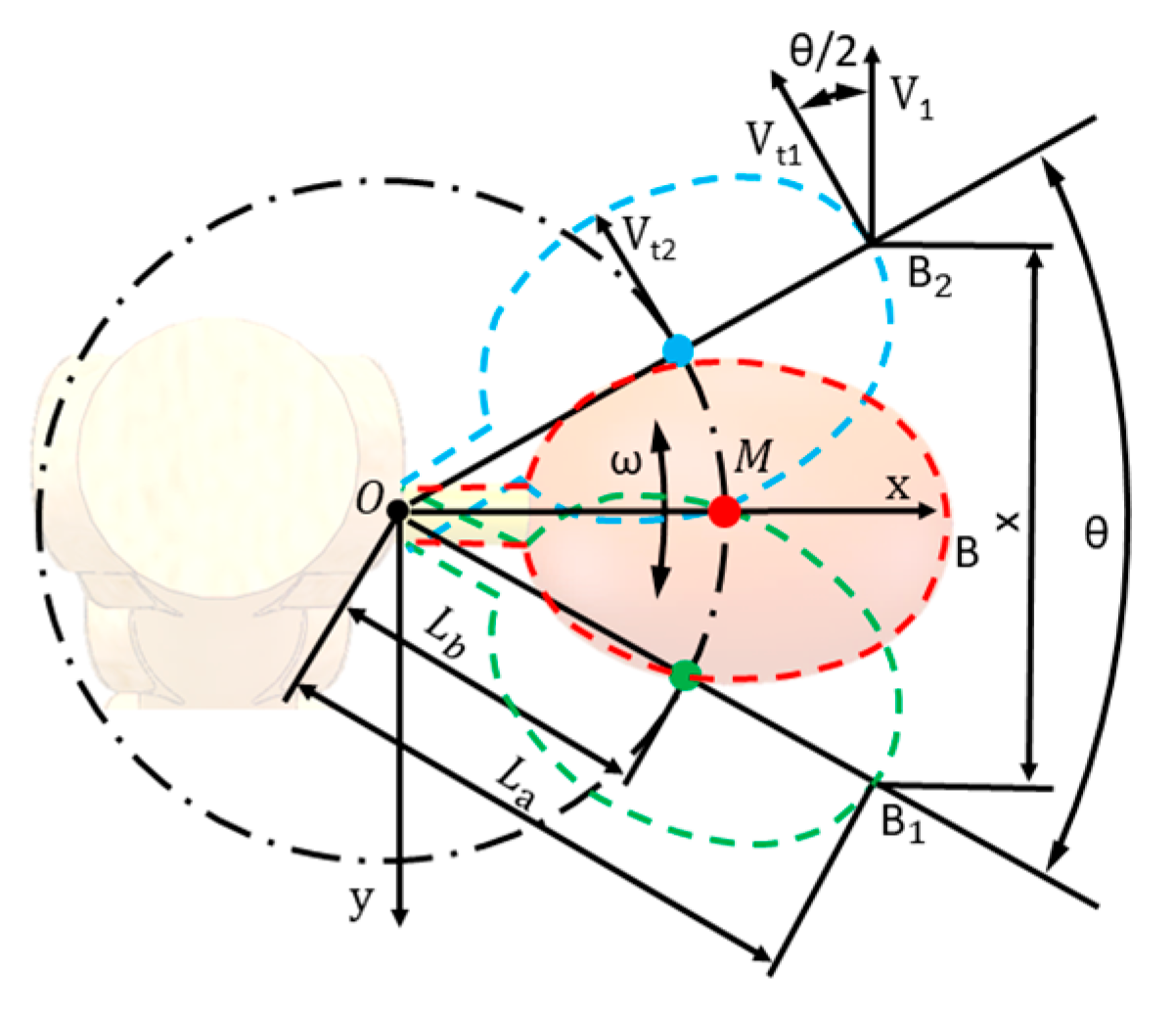
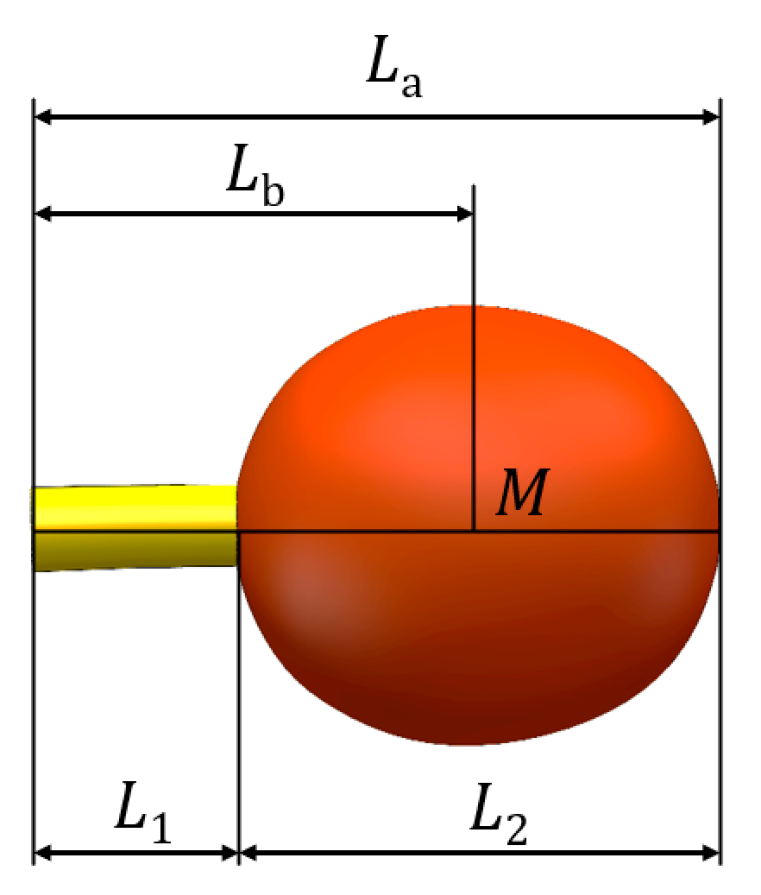
The analysis of the high-velocity dynamic video revealed that the coffee cherries underwent two extreme positions and one intermediate transition position during its motion (Figure 13). States 1 and 3 represent the moments when the fruit reaches its maximum velocity, with these extreme positions being symmetrically related to the connection point, $O$, between the branch and fruit stem, as illustrated in Figure 14. In State 1, the fruit velocity ($V_1$) was positive, whereas in State 3, $V_1$ became negative. However, at these two extreme positions, the absolute velocity values were nearly equal.

Because the coffee cherry’s stem is a flexible structure, it can exert a tensile force that constrains the movement of the fruit under external vibration. High-velocity video analysis confirmed this interaction, indicating that the stem remained under constant tension during the motion. Consequently, the long axis of the fruit remained collinear with the stem throughout its movement.

Based on this observation, when the coffee cherries reached their maximum velocity, their instantaneous motion could be inferred to be circular, with the connection point O as the center and $L_b$ as the radius. This analysis established a relative motion relationship between the coffee cherries, stem, and branch (Figure 14).

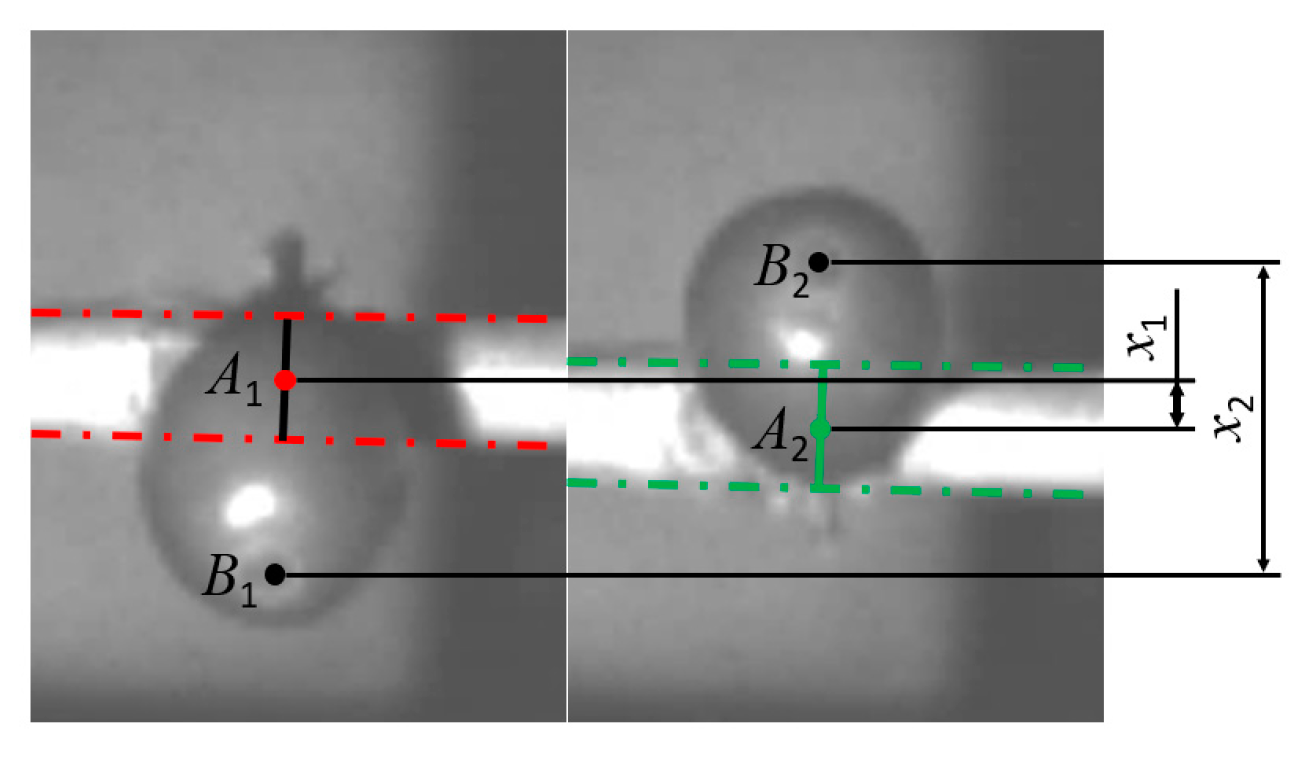
The analysis of the high-velocity camera footage facilitated the identification of the moment when the velocity of the marker point of the coffee cherries reached its maximum. The displacement relationship between the root of the fruit peduncle and velocity marker point at this moment is illustrated in Figure 15.

Using the extreme displacement relationships of the coffee cherries shown in Figure 14 and Figure 15, the maximum movement displacement ($x$) of the coffee cherries relative to the branch at the peak velocity can be determined as follows:

$$x=x_1-x_2$$

(5)

where

• x₂ represents the displacement of the coffee cherries’ velocity marker point (m).
• x₁ denotes the displacement of the pedicel base at the connection point with the branch (m).

Using the pedicel length (L₁) and long-axis length (L₂) data from Table 2 for the three maturity stages of coffee cherries, along with the coffee cherries motion relationship diagram, the angle ($\theta$) between the fruit in State 1 and State 2 can be determined as follows:

$$\Theta =arctan{\displaystyle \frac{x}{2L_a}}$$

(6)

Using High-Velocity Video Tracking Software V1.0 to analyze the high-velocity dynamic video, the velocity ($v_1$) of the coffee cherries at their maximum velocity was obtained. Combined with the coffee cherries motion relationship diagram shown in Figure 14, the linear velocity ($v_{t1}$) of the marker point on the coffee cherries can be determined as follows:

$$v_{t1}={\displaystyle \frac{v_1}{cos\Theta /2}}$$

(7)

The angular velocity of the coffee cherries at the moment of maximum velocity, ω is

$$\omega ={\displaystyle \frac{v_1}{L_a}}$$

(8)

The linear velocity of the coffee cherries center of mass, $v_{t2}$, is as follows:

$$v_{t2}=\omega \times L_b$$

(9)

The centripetal acceleration at the center of mass M of the coffee cherries, $a_t$, is as follows:

$$a_t={\displaystyle \frac{{v_{t2}}^2}{L_b}}$$

(10)

At the maximum velocity, the coffee cherries underwent instantaneous circular motion and experienced centrifugal force. Detachment occurred when the centrifugal force exceeded the binding force between the pedicel and fruit. The theoretical detachment force (F_n) of a coffee cherry can be calculated as follows:

$$F_n=m\times {\left({\displaystyle \frac{2v_1}{\left(2L_1+L_2\right)\times \mathit{cos}\frac{{\mathit{tan}}^{-1}\frac{2x_2-x_1}{2L_1+L_2}}{2}}}\right)}^2\times L_b$$

(11)

4.2.2. Test Results and Analysis of Vibration Frequency and Amplitude Parameters

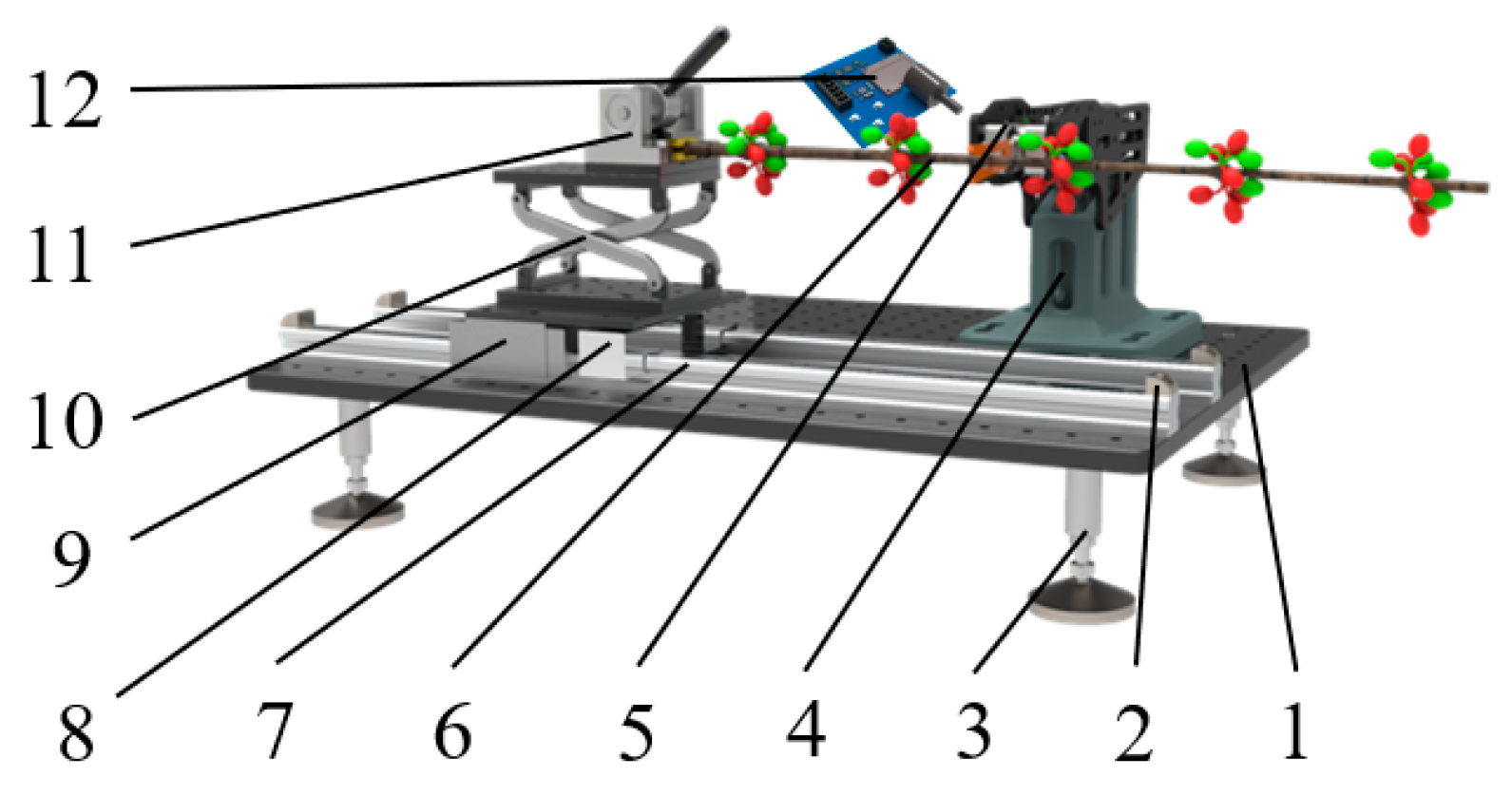
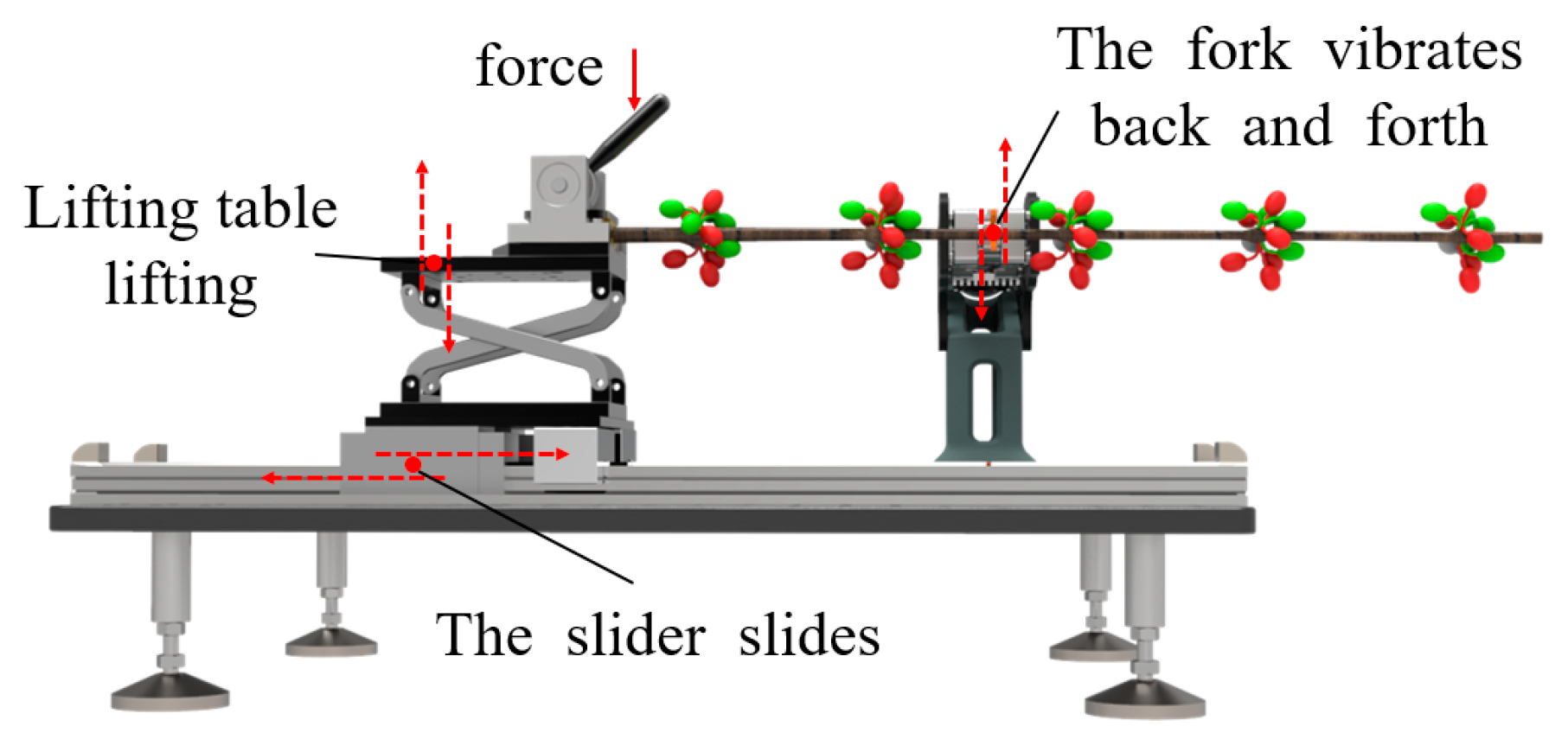
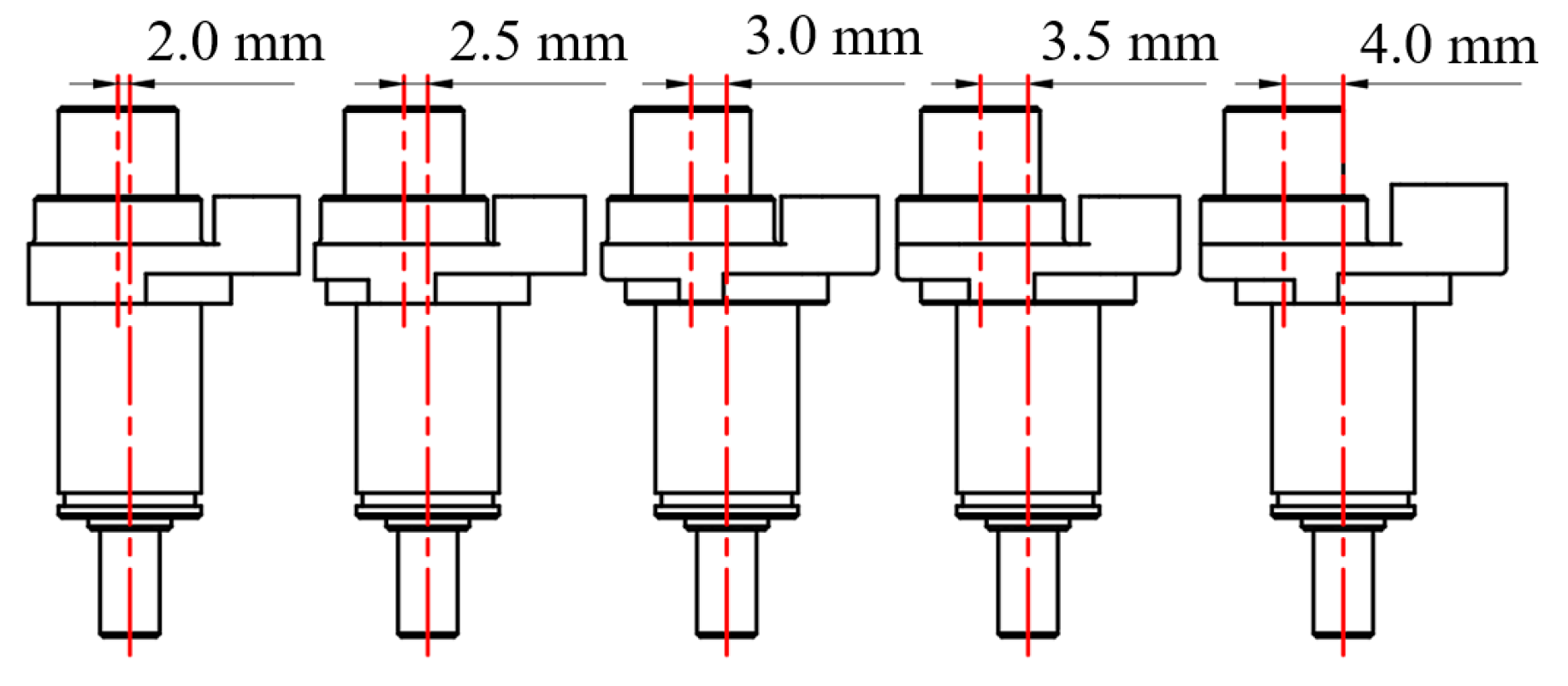
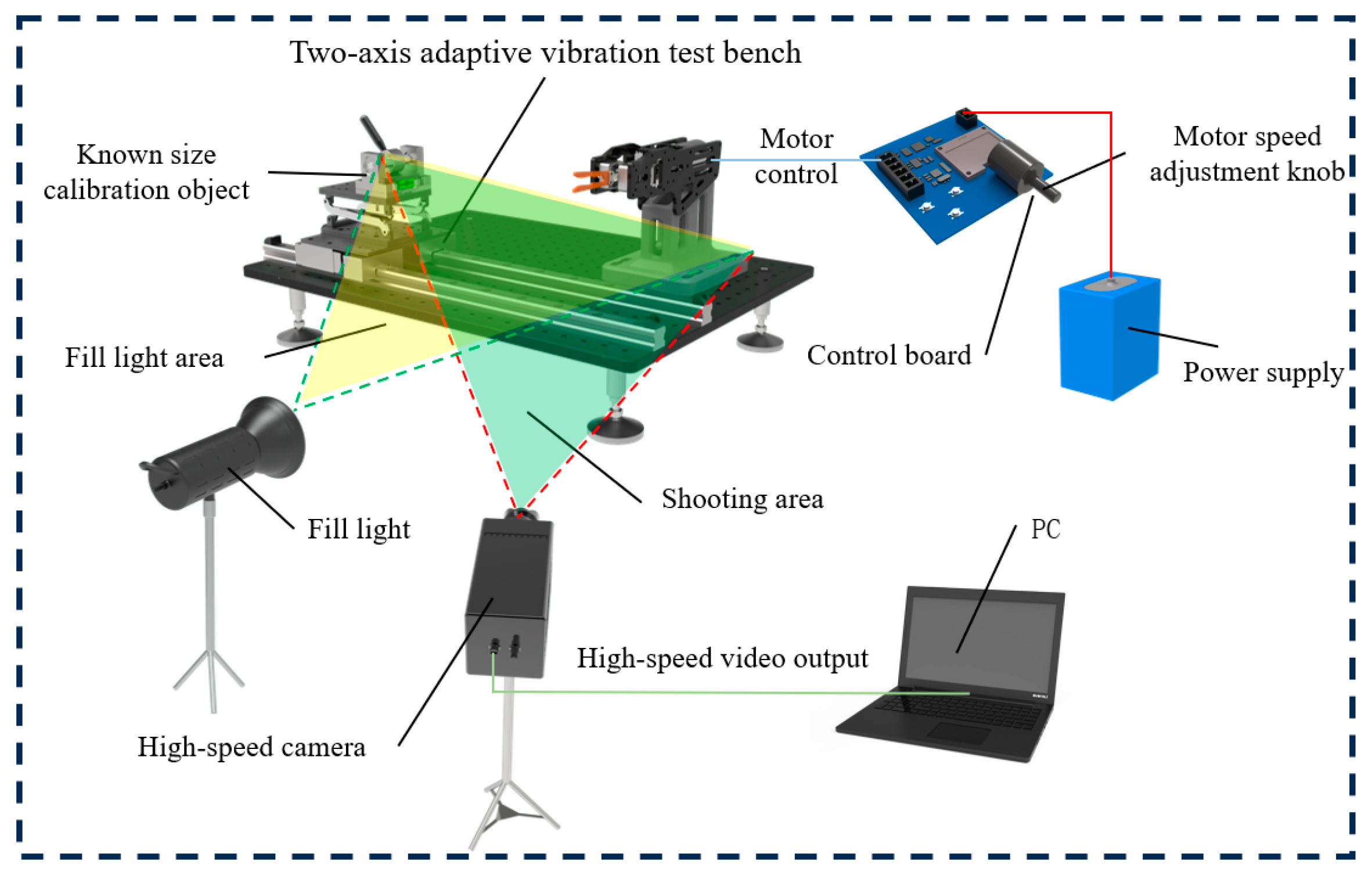
The test for determining the optimal combination of vibration frequency and amplitude aimed to identify the optimal vibration parameters. A high-velocity dynamic monitoring system was used as the test equipment, and coffee branches with uniform thickness and consistent maturity with the attached fruits were selected as test samples. To ensure consistency, branch length was standardized at 495 mm with six Y-shaped nodes, each bearing one unripe (green) fruit, one half-ripe fruit, and one ripe fruit.

The excitation force was applied at Vibration Position 2 for 1 s, with the vibration frequency and amplitude selected as the test factors, and the theoretical detachment rate of the fruits at different maturity levels was used as the evaluation index. A factorial experiment was designed with 25 groups, with each testing six samples. Before each test, the positions of green, half-ripe, and ripe fruits were recorded and marked with green, yellow, and red dots, respectively (Figure 16).

After the test, a high-velocity video analysis was performed using the high-velocity video target-tracking measurement software V1.0. The fruit tips were marked at their recorded positions for green, half-ripe, and ripe fruits, and the velocity (v₁), displacement (x₁), and displacement (x₂) at the connection point between the fruit stem and the branch were recorded. These data were then substituted into the theoretical detachment force calculation formula (Equation (11)) to determine the theoretical detachment force for each maturity level. The experimental design and calculation results for the theoretical detachment force of green, half-ripe, and ripe fruits are presented in

Table 7. Calculated results of theoretical detachment forces for green fruits.

Test Number	Vibration Frequency/Hz	Amplitude/mm	Theoretical Detachment Force/N						Theoretical Detachment Quantity
			Unripe Fruit 1	Unripe Fruit 2	Unripe Fruit 3	Unripe Fruit 4	Unripe Fruit 5	Unripe Fruit 6	n1
1	50	3.26	0.55	1.02	0.98	1.46	1.81	0.69	0
2	55	3.26	0.56	1.00	1.06	1.71	2.09	0.77	0
3	60	3.26	0.55	1.06	1.06	1.94	2.24	0.82	0
4	65	3.26	0.58	1.07	1.08	2.18	2.41	0.89	0
5	70	3.26	0.57	1.16	1.09	2.34	2.73	0.87	0
6	50	6.74	0.72	1.50	1.63	2.44	2.69	0.90	0
7	55	6.74	0.71	1.55	1.67	2.77	3.32	1.13	0
8	60	6.74	0.67	1.51	1.57	2.91	3.65	1.13	0
9	65	6.74	0.74	1.48	1.67	3.13	3.94	1.55	0
10	70	6.74	0.74	1.55	1.64	3.44	4.51	2.42	1
11	50	10.10	0.9	2.17	2.40	3.53	4.47	2.58	1
12	55	10.10	0.96	2.35	2.41	3.74	4.90	3.20	1
13	60	10.10	0.93	2.44	2.57	3.94	5.29	3.91	1
14	65	10.10	1.00	2.40	2.70	4.94	5.90	3.92	2
15	70	10.10	0.93	2.45	2.64	5.59	6.17	3.43	2
16	50	13.48	1.16	2.21	2.53	5.19	6.33	3.31	2
17	55	13.48	1.13	2.43	2.86	5.86	7.97	3.70	2
18	60	13.48	1.19	2.74	3.20	6.60	9.28	3.65	2
19	65	13.48	1.21	2.95	3.55	7.92	11.09	3.44	2
20	70	13.48	1.16	3.40	3.90	8.81	12.74	3.29	2
21	50	16.84	1.40	3.23	3.65	8.30	12.10	1.81	2
22	55	16.84	1.44	3.53	3.71	10.65	15.46	1.79	2
23	60	16.84	1.42	3.87	4.19	12.34	17.71	1.74	2
24	65	16.84	1.39	4.20	4.70	15.66	22.20	1.54	3
25	70	16.84	1.44	4.70	5.18	19.56	28.03	1.48	4

,

Table 8. Calculated results of theoretical detachment forces for semi-ripe fruits.

Test Number	Vibration Frequency/Hz	Amplitude/mm	Theoretical Detachment Force/N						Theoretical Detachment Quantity
			Semi-Ripe Fruits 1	Semi-Ripe Fruits 2	Semi-Ripe Fruits 3	Semi-Ripe Fruits 4	Semi-Ripe Fruits 5	Semi-Ripe Fruits 6	n2
1	50	3.26	0.56	1.04	1.00	1.49	1.85	0.70	0
2	55	3.26	0.57	1.02	1.08	1.74	2.13	0.78	0
3	60	3.26	0.56	1.08	1.08	1.99	2.28	0.83	0
4	65	3.26	0.59	1.10	1.10	2.23	2.46	0.90	0
5	70	3.26	0.58	1.18	1.11	2.39	2.79	0.89	0
6	50	6.74	0.73	1.53	1.66	2.49	2.75	0.92	0
7	55	6.74	0.72	1.59	1.70	2.83	3.39	1.15	1
8	60	6.74	0.69	1.55	1.60	2.97	3.73	1.15	1
9	65	6.74	0.75	1.52	1.71	3.20	4.03	1.59	2
10	70	6.74	0.76	1.58	1.68	3.51	4.61	2.47	2
11	50	10.10	0.94	2.22	2.45	3.61	4.57	2.63	2
12	55	10.10	0.98	2.40	2.46	3.82	5.00	2.96	2
13	60	10.10	0.95	2.49	2.62	4.03	5.41	3.99	3
14	65	10.10	1.02	2.45	2.76	5.04	6.03	4.00	3
15	70	10.10	0.95	2.50	2.69	5.71	6.30	3.50	3
16	50	13.48	1.18	2.25	2.58	5.31	6.46	3.38	3
17	55	13.48	1.16	2.48	2.92	5.99	8.14	3.78	3
18	60	13.48	1.22	2.80	3.27	6.74	9.48	3.73	4
19	65	13.48	1.24	3.02	3.63	8.09	11.33	3.51	4
20	70	13.48	1.18	3.48	3.98	9.00	13.02	3.36	5
21	50	16.84	1.43	3.30	3.73	8.47	12.36	1.85	4
22	55	16.84	1.47	3.61	3.79	10.88	15.79	1.83	4
23	60	16.84	1.45	3.95	4.28	12.61	18.09	1.78	4
24	65	16.84	1.42	4.29	4.80	15.99	22.68	1.57	4
25	70	16.84	1.47	4.80	5.29	19.98	28.64	1.52	4

and

Table 9. Calculated results of the theoretical detachment force for ripe fruits.

Test Number	Vibration Frequency/Hz	Amplitude/mm	Theoretical Detachment Force/N						Theoretical Detachment Quantity
			Ripe Fruit 1	Ripe Fruit 2	Ripe Fruit 3	Ripe Fruit 4	Ripe Fruit 5	Ripe Fruit 6	n3
1	50	3.26	0.57	1.07	1.03	1.53	1.9	0.72	0
2	55	3.26	0.59	1.05	1.11	1.78	2.18	0.8	0
3	60	3.26	0.58	1.11	1.11	2.03	2.33	0.85	0
4	65	3.26	0.60	1.12	1.13	2.28	2.51	0.92	1
5	70	3.26	0.59	1.21	1.13	2.44	2.85	0.91	1
6	50	6.74	0.75	1.57	1.70	2.55	2.81	0.94	2
7	55	6.74	0.74	1.62	1.74	2.9	3.47	1.18	2
8	60	6.74	0.7	1.58	1.64	3.04	3.81	1.18	2
9	65	6.74	0.77	1.55	1.75	3.27	4.12	1.62	2
10	70	6.74	0.78	1.61	1.71	3.59	4.71	2.52	3
11	50	10.10	0.96	2.27	2.50	3.69	4.67	2.93	3
12	55	10.10	1.00	2.51	2.63	3.90	5.11	3.34	5
13	60	10.10	0.98	2.55	2.68	4.12	5.53	4.08	5
14	65	10.10	1.05	2.50	2.82	5.16	6.17	4.09	5
15	70	10.10	0.97	2.56	2.75	5.84	6.44	3.58	5
16	50	13.48	1.21	2.31	2.64	5.42	6.61	3.46	4
17	55	13.48	1.18	2.54	2.98	6.12	8.32	3.86	5
18	60	13.48	1.25	2.86	3.34	6.89	9.69	3.81	5
19	65	13.48	1.27	3.08	3.71	8.27	11.60	3.59	5
20	70	13.48	1.21	3.55	4.07	9.20	13.30	3.43	5
21	50	16.84	1.46	3.37	3.81	8.66	12.60	1.90	4
22	55	16.84	1.5	3.69	3.88	11.10	16.10	1.87	4
23	60	16.84	1.49	4.04	4.37	12.90	18.50	1.82	4
24	65	16.84	1.45	4.38	4.91	16.30	23.20	1.61	4
25	70	16.84	1.50	4.91	5.41	20.40	29.30	1.55	4

, respectively.

The theoretical detachment rate calculation formulas for green, semi-ripe, and ripe coffee cherries were as follows:

$${\eta }_1={\displaystyle \frac{n_1}{6}}\times 100\%$$

(12)

$${\eta }_2={\displaystyle \frac{n_2}{6}}\times 100\%$$

(13)

$${\eta }_3={\displaystyle \frac{n_3}{6}}\times 100\%$$

(14)

where

• η₁ represents the theoretical shedding rate of green fruits (%).
• ${\eta }_2$ represents the theoretical detachment rate of semi-ripe coffee cherries (%).
• ${\eta }_3$ denotes the theoretical detachment rate of ripe coffee cherries (%).
• n₁ denotes the number of green coffee cherries for which the theoretical detachment force exceeded the actual detachment force.
• n₂ denotes the number of semi-ripe coffee cherries for which the theoretical detachment force exceeded the actual detachment force.
• n₃ denotes the number of ripe coffee cherries for which the theoretical detachment force exceeded the actual detachment force.

The actual detachment force ranges for green, half-ripe, and ripe coffee cherries were 4.26–5.28, 3.09–4.33, and 2.51–3.27 N, respectively. Based on different theoretical detachment force thresholds, the detachment conditions at various maturity levels were determined as follows: when the theoretical detachment force exceeded 4.26 N, all green, half-ripe, and ripe fruits were detached; when it exceeded 3.09 N, only half-ripe and ripe fruits were detached; and when it exceeded 2.51 N, only ripe fruits were detached. The theoretical detachment numbers for each fruit type were recorded in Table 7, Table 8 and Table 9 by comparing the theoretical detachment forces in Table 7, Table 8 and Table 9 with the actual detachment force ranges. These values were then substituted into Formulas (12)–(14) to calculate the theoretical detachment rates for each maturity level; the results are presented in

Table 10. Calculated results of theoretical detachment rates for green, semi-ripe, and ripe fruits.

Test Number	Theoretical Detachment Rate/%
	Unripe Fruit	Semi-Ripe Fruits	Ripe Fruit
1	0.00	0.00	0.00
2	0.00	0.00	0.00
3	0.00	0.00	0.00
4	0.00	0.00	16.67
5	0.00	0.00	16.67
6	0.00	0.00	33.33
7	0.00	16.67	33.33
8	0.00	16.67	33.33
9	0.00	33.33	33.33
10	16.67	33.33	50.00
11	16.67	33.33	50.00
12	16.67	33.33	83.33
13	16.67	50.00	83.33
14	33.33	50.00	83.33
15	33.33	50.00	83.33
16	33.33	50.00	83.33
17	33.33	50.00	83.33
18	33.33	66.67	83.33
19	33.33	66.67	83.33
20	33.33	83.33	83.33
21	33.33	66.67	66.67
22	33.33	66.67	66.67
23	33.33	66.67	66.67
24	50.00	66.67	66.67
25	66.67	66.67	66.67

.

Based on the data in Table 10, the theoretical detachment rates for green, half-ripe, and ripe fruits are plotted in Figure 17. The figure revealed that as the amplitude increased from 3.26 to 16.84 mm, the theoretical detachment rate of green fruits gradually increased. Similarly, the detachment rates of the half-ripe and ripe fruits exhibited stage-wise growth as the amplitude increased from 3.26 to 13.48 mm. However, when the amplitude exceeded 13.48 mm and reached 16.84 mm, the detachment rates of half-ripe and ripe fruits began to decline. This suggested that while a moderate increase in amplitude continuously enhanced the harvesting rate of green fruits, half-ripe and ripe fruits had an optimal amplitude beyond which the detachment rate decreased.

When the amplitude was 3.26 mm, the theoretical detachment rates for green and ripe fruits remained at zero, indicating that these maturity stages could not detach. When the amplitude increased and the vibration frequency reached 65 Hz, the theoretical detachment rate of the ripe fruit suddenly increased to 16.67%. However, this remained too low to meet coffee-harvesting requirements. As the amplitude increased to 6.74 mm, the detachment rates for green, half-ripe, and ripe fruits increased significantly, reaching maximum theoretical harvesting rates of 16.67% for green fruit, 33.33% for half-ripe fruit, and 50.00% for ripe fruit. Despite this increase, the detachment rate of ripe fruits remained insufficient to meet the harvesting requirements.

At an amplitude of 10.10 mm, the theoretical harvesting rates for all three fruit maturity stages showed significant improvement, with maximum detachment rates of 33.33% for green fruit, 50.00% for half-ripe fruit, and 83.33% for ripe fruit. At this point, the ripe fruit detachment rate reached 83.33%, meeting coffee-harvesting requirements. When the amplitude increased to 13.48 mm, the detachment rate for green fruit remained unchanged, whereas that for half-ripe fruit increased significantly to 83.33%, and the rate for ripe fruit remained at 83.33%. The high detachment rate of half-ripe fruits exceeded the acceptable harvesting requirements. At an amplitude of 16.84 mm, the detachment rate for green fruit increased to 66.67%, whereas the rates for ripe and half-ripe fruits decreased to 66.67%. Although the harvesting rates of green and half-ripe fruits were high, the decrease in ripe fruit detachment made this amplitude unsuitable for coffee harvesting.

A further analysis of Figure 17 indicated that at an amplitude of 10.10 mm and a vibration frequency of 55 Hz, the theoretical detachment rate for green fruit was at its minimum of 16.67%, for half-ripe fruit it was at its minimum of 33.33%, and for ripe fruit it was at its maximum of 83.33%. At this point, the detachment rates for green and half-ripe fruits remained below 33.33%, whereas the rate for ripe fruit reached its statistical maximum, meeting the coffee-harvesting requirements. Therefore, the optimal vibration parameters for coffee harvesting were the frequency of 55 Hz and the amplitude of 10.10 mm (The optimal vibration parameters are highlighted in green in the figure).

5. Field Harvest Verification

To validate the accuracy of the optimal vibration parameters obtained through high-velocity photography dynamic analysis, a field harvesting test was conducted at the test site shown in Figure 18. Coffee branches with uniform length, thickness, fruit quantity, and maturity as well as similar Y-shaped bud spacing with six Y-shaped buds were selected. The total number of coffee cherries and fruits at each maturity stage was recorded. The vibration frequency was set to 55 Hz, the amplitude to 10.10 mm, and the excitation force was applied at Vibration Position 2. Thirty validation trials were conducted while ensuring the normal operation of the test equipment. After each trial, the number of remaining green, half-ripe, and ripe fruits on the branches was recorded and the number of detached fruits at each maturity stage was calculated. The results were averaged to determine the actual detachment rates at each maturity stage (

Table 11. Results of actual detachment rate from field validation test.

Ripeness	Actual Picking Rate/%	Theoretical Picking Rate/%	Relative Accuracy/%
Unripe fruit	15.86	16.67	4.86
Half-ripe fruit	35.17	33.33	5.52
Ripe fruit	89.65	83.33	7.58

).

The relative error between the theoretical and actual detachment rates was less than 10%, indicating that the mathematical model for the theoretical detachment force of coffee cherries was reliable. The larger error in the ripe fruit detachment rate was primarily due to the unclear boundaries between the ripe and half-ripe stages, leading to statistical inconsistencies. In the future, more precise criteria for distinguishing coffee cherries’ maturity stages should be established to enhance the accuracy of test results.

6. Conclusions

In this study, coffee berries were classified into three levels of maturity according to their color, which is one level less than the four levels of maturity in previous studies. This increases the distinguishability between coffee berries of different maturity levels and helps to improve the accuracy of data statistics during the experiment. The measurement results for the physical parameters of coffee berries show that there are significant differences in the size and mass of green fruits, semi-ripe fruits, and ripe fruits. As the maturity of coffee berries increases, the length and mass of coffee berries gradually increase, while the length of the fruit stalks remains relatively stable, which is consistent with the results of previous studies. The binding forces of two coffee varieties, Catuai and Arabica, are as follows: The binding force of ripe Catuai coffee fruits is (3.56–5.82 N), and that of green fruits is (9.89–11.92 N), with a minimum difference in binding force of 6.06 N. In this study, the binding force of ripe Arabica coffee fruits is (2.41–3.27 N), that of semi-ripe fruits is (3.09–4.33 N), and that of green fruits is (4.26–5.28 N). There is an overlapping phenomenon in the range of binding forces. From the perspective of selective harvesting, it is more difficult to achieve the selective harvesting of Arabica coffee than that of Catuai coffee.

The results for the experiment on the combination of vibration frequency and amplitude parameters show that when the amplitude is 10.10 mm and the vibration frequency is 55 Hz, the harvesting effect of coffee berries is the best. The corresponding theoretical detachment rate of ripe fruits is 83.33%, and the theoretical detachment rates of green fruits and semi-ripe fruits remain at the relatively low levels of 16.67% and 33.33%, respectively. The optimal vibration frequency is determined to be 55 Hz, and the optimal amplitude is 10.10 mm. The results of the field harvesting verification experiment show that when the vibration position is two, the vibration frequency is 55 Hz, the amplitude is 10.10 mm, and the vibration time is 1 s, the actual harvesting rates of green fruits, semi-ripe fruits, and ripe fruits are 15.86%, 35.17%, and 89.65%, respectively. Compared with the harvesting rate of ripe Catuai coffee fruits (92.22%) and that of green fruits (8.33%) in previous studies, the harvesting rate of ripe Arabica coffee fruits in this study is 89.65%, the harvesting rate of semi-ripe fruits is 35.17%, and the harvesting rate of green fruits is 15.86%. All of these rates are higher than those of Catuai coffee. The main reason is that there is an overlap in the range of binding forces of Arabica coffee at different maturity levels, which requires a higher level of selective harvesting.

Although our study has met the requirements for the selective harvesting of Arabica coffee, there are still some deficiencies. When collecting the motion parameters of coffee berries and branches through high-speed photography, due to the mutual occlusion between coffee berries and branches, some data are lost, which affects the experimental accuracy. In the next stage of our research, we will use spatial high-speed photography technology to collect the motion parameters of coffee berries and branches to avoid the problem of data loss caused by occlusion. In addition, we will also enrich the collection of physical parameters of coffee berries and branches, and expand the research method to the multi-body dynamics simulation research of agricultural materials, so as to provide more valuable information for the research on the selective harvesting of coffee berries.