Estimation of Leaf Chlorophyll Content of Maize from Hyperspectral Data Using E2D-COS Feature Selection, Deep Neural Network, and Transfer Learning
Abstract
1. Introduction
2. Materials and Methods
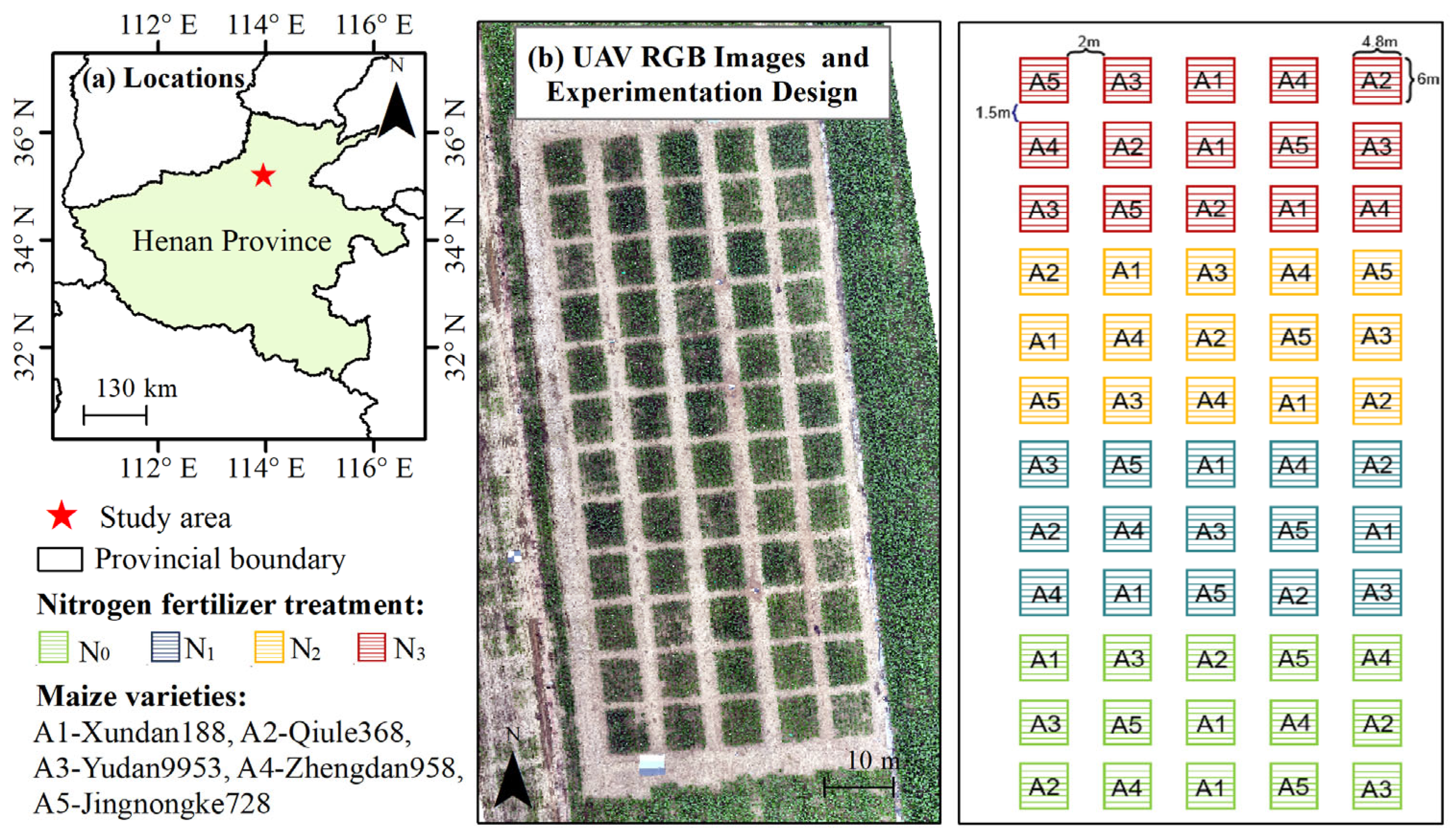
2.1. Study Area and Data
2.1.1. Study Area
2.1.2. UAV-Canopy Hyperspectral Data
2.1.3. Leaf Chlorophyll Content and Other Data
2.2. Overview of Methods
- Dataset collection: UAV hyperspectral systems and spectrophotometers were used to obtain a total of 120 canopy spectral data (Section 2.1.2) and leaf chlorophyll data (Section 2.1.3) over two fertility stages. The PROSAIL model was used to simulate leaf spectral data (Section 2.3).
- Band selection: To identify bands that are sensitive to LCC and resistant to structural effects, the E2D-COS method (Section 2.4) was used and analyzed in combination with radiative transfer model simulation data (Section 2.3).
- Model pre-training: The simulated spectral data was employed to pre-train the DNN model to learn the potential knowledge of spectral versus vegetation traits, i.e., to get the model weights of the pre-trained model (Section 2.5.1 and Section 3.3.1).
- Model fine-tuning based on transfer learning: The weights of the pre-trained model are used as initial values for the model, which is again de-trained based on the field measured spectral data to fine-tune the part parameters of model (Section 2.5.2 and Section 3.3.2).
- Comparison of other methods: This study compared the performance of (1) the Mazie-LCNet trained on simulated and field measured data, (2) LCNet model trained on simulated dataset, (3) an Maize-LCNet-Field trained on field measured data, and (4) traditional statistical regression methods in estimating the maize LCC (Section 2.5.3 and Section 3.3.3).
2.3. Maize Canopy Spectral Simulation Using PROSAIL
2.4. Enhanced Two-Dimensional Correlation Spectral Analysis (E2D-COS)
2.4.1. Spectral Response Enhancement
- ✓
- Spectral Normalization
- ✓
- First Derivative of the Spectrum
- ✓
- Response Relationship Computation
- ✓
- Enhanced Dynamic Spectrum Computation
2.4.2. Two-Dimensional Correlation Spectral Analysis
2.5. Modeling Methods
2.5.1. Deep Neural Network
2.5.2. Transfer Learning
2.5.3. Comparison of Methods
- LCNet: Pre-trained models trained on simulated data (n = 6666) directly estimate the field validation dataset (n = 20) to evaluate their performance.
- Maize-LCNet-field methods: DNN trained on field data (n = 40) directly estimate the field validation dataset (n = 20) to evaluate their performance.
- PLSR/SVM-field methods: Based on the spectral data measured in the field (n = 40), linear and non-linear machine learning algorithms (PLSR and SVM) are used to train the model and verify its accuracy.
2.6. Assessing Accuracy
3. Results
3.1. Sensitive Bands of LCC
3.1.1. Characteristics of the Simulated Spectral Data
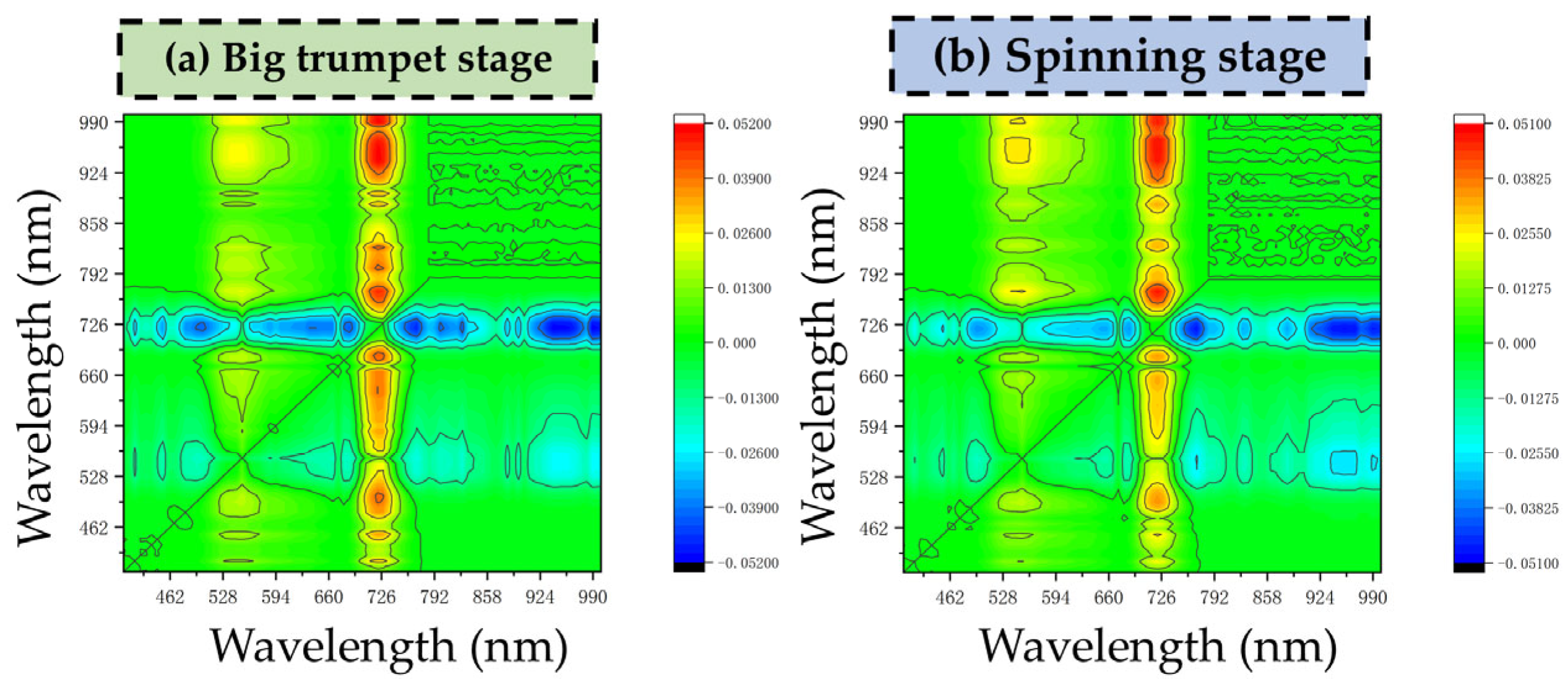
3.1.2. Enhanced Two-Dimensional Correlation Spectral Analysis of Canopy LCCs
3.2. Screening Results for Structural Interference Signature Bands
3.2.1. Enhanced Two-Dimensional Correlation Spectral Analysis of LAI
- ✓
- The synchronous E2D-COS maps of the big trumpet stage with various LAIs
- ✓
- The synchronous E2D-COS maps of the spinning stage with various LAIs
3.2.2. Enhanced Two-Dimensional Correlation Spectral Analysis of LA
- ✓
- The synchronous E2D-COS maps of the big trumpet stage with various LADs
- ✓
- The synchronous E2D-COS maps of the spinning stage with various LADs
3.3. LCC Estimation Result
3.3.1. Pre-Training Based on Simulated Hyperspectral Reflectance Dataset
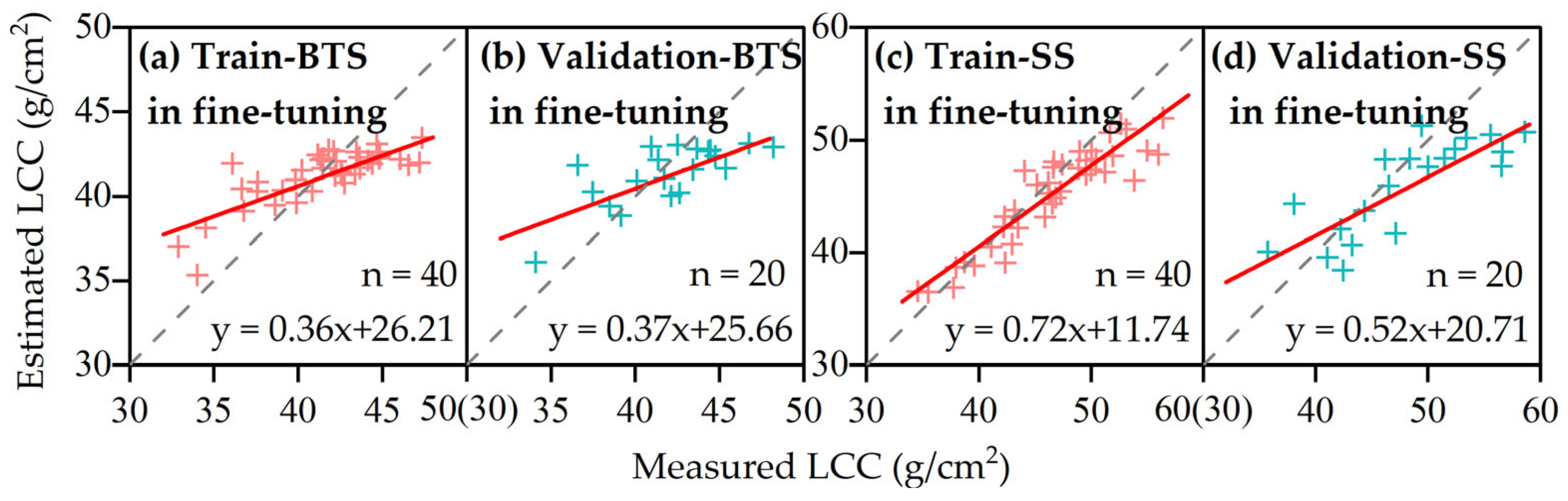
3.3.2. LCC Estimation Based on Transfer Learning
3.3.3. Estimation Results from Comparative Experiments
4. Discussion
4.1. Advantages of the Estimation Method
4.2. Optimized Bands for Maize Chlorophyll Estimation
4.3. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanaka, A.; Ito, H. Chlorophyll degradation and its physiological function. Plant Cell Physiol. 2024, 66, 139–152. [Google Scholar] [CrossRef]
- Gao, F.; Guo, J.; Shen, Y. Advances from chlorophyll biosynthesis to photosynthetic adaptation, evolution and signaling. Plant Stress 2024, 12, 100470. [Google Scholar] [CrossRef]
- Singhal, G.; Choudhury, B.U.; Singh, N.; Goswami, J. An enhanced chlorophyll estimation model with a canopy structural trait in maize crops: Use of multi-spectral UAV images and machine learning algorithm. Ecol. Inform. 2024, 83, 102811. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, S.; Li, X.; Cunha, M.; Jayavelu, S.; Cammarano, D.; Fu, Y. Machine learning-based approaches for predicting SPAD values of maize using multi-spectral images. Remote Sens. 2022, 14, 1337. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, P.; Liu, S.; Wang, C.; Liu, J. Evaluation of the methods for estimating leaf chlorophyll content with SPAD chlorophyll meters. Remote Sens. 2022, 14, 5144. [Google Scholar] [CrossRef]
- Khan, M.S.; Yadav, P.; Semwal, M.; Prasad, N.; Verma, R.K.; Kumar, D. Predicting canopy chlorophyll concentration in citronella crop using machine learning algorithms and spectral vegetation indices derived from UAV multispectral imagery. Ind. Crops Prod. 2024, 219, 119147. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Martins, G.B.; de Almeida, T.M.H.; da Silva Ribeiro, R.; da Veiga Júnior, V.F.; Paz, I.d.S.R.; de Siqueira, M.F.; Kurtz, B.C. Estimating aboveground biomass of tropical urban forests with UAV-borne hyperspectral and LiDAR data. Urban For. Urban Green. 2024, 96, 128362. [Google Scholar] [CrossRef]
- Jiazheng, L.; Beibei, L.; Xiang, C.; Feng, S.; Juting, C.; Jing, W.; Qian, Z.; Xiefeng, Y. Monitoring of Leaf Chlorophyll Content in Flue-Cured Tobacco Based on Hyperspectral Remote Sensing of Unmanned Aerial Vehicle. Smart Agric. 2023, 5, 68. [Google Scholar]
- Angel, Y.; McCabe, M.F. Machine learning strategies for the retrieval of leaf-chlorophyll dynamics: Model choice, sequential versus retraining learning, and hyperspectral predictors. Front. Plant Sci. 2022, 13, 722442. [Google Scholar] [CrossRef]
- Afsar, M.M.; Iqbal, M.S.; Bakhshi, A.D.; Hussain, E.; Iqbal, J. MangiSpectra: A Multivariate Phenological Analysis Framework Leveraging UAV Imagery and LSTM for Tree Health and Yield Estimation in Mango Orchards. Remote Sens. 2025, 17, 703. [Google Scholar] [CrossRef]
- Fei, S.; Xiao, S.; Zhu, J.; Xiao, Y.; Ma, Y. Dual sampling linear regression ensemble to predict wheat yield across growing seasons with hyperspectral sensing. Comput. Electron. Agric. 2024, 216, 108514. [Google Scholar] [CrossRef]
- Sherstneva, O.; Abdullaev, F.; Kior, D.; Yudina, L.; Gromova, E.; Vodeneev, V. Prediction of biomass accumulation and tolerance of wheat seedlings to drought and elevated temperatures using hyperspectral imaging. Front. Plant Sci. 2024, 15, 1344826. [Google Scholar] [CrossRef] [PubMed]
- Wieme, J.; Mollazade, K.; Malounas, I.; Zude-Sasse, M.; Zhao, M.; Gowen, A.; Argyropoulos, D.; Fountas, S.; Van Beek, J. Application of hyperspectral imaging systems and artificial intelligence for quality assessment of fruit, vegetables and mushrooms: A review. Biosyst. Eng. 2022, 222, 156–176. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Zheng, H.; Zhou, K.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Estimation of area-and mass-based leaf nitrogen contents of wheat and rice crops from water-removed spectra using continuous wavelet analysis. Plant Methods 2018, 14, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Townsend, P.A.; Naber, M.R.; Bethke, P.C.; Hills, W.B.; Wang, Y. Hyperspectral imagery to monitor crop nutrient status within and across growing seasons. Remote Sens. Environ. 2021, 255, 112303. [Google Scholar] [CrossRef]
- Chen, R.; Feng, H.; Yang, F.; Li, C.; Yang, G.; Pei, H.; Pan, L.; Chen, P. Estimation of leaf area index of winter wheat based on hyperspectral data of unmanned aerial vehicles. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1785–1788. [Google Scholar]
- Manikandan, G.; Pragadeesh, B.; Manojkumar, V.; Karthikeyan, A.; Manikandan, R.; Gandomi, A.H. Classification models combined with Boruta feature selection for heart disease prediction. Inform. Med. Unlocked 2024, 44, 101442. [Google Scholar] [CrossRef]
- Ji, T.; Liu, X. Establishing a Hyperspectral Model for the Chlorophyll and Crude Protein Content in Alpine Meadows Using a Backward Feature Elimination Method. Agriculture 2024, 14, 757. [Google Scholar] [CrossRef]
- Gao, D.; Qiao, L.; An, L.; Sun, H.; Li, M.; Zhao, R.; Tang, W.; Song, D. Diagnosis of maize chlorophyll content based on hybrid preprocessing and wavelengths optimization. Comput. Electron. Agric. 2022, 197, 106934. [Google Scholar] [CrossRef]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2014; Volume 37. [Google Scholar]
- Pudjihartono, N.; Fadason, T.; Kempa-Liehr, A.W.; O’Sullivan, J.M. A review of feature selection methods for machine learning-based disease risk prediction. Front. Bioinform. 2022, 2, 927312. [Google Scholar] [CrossRef]
- Zouhri, H.; Idri, A.; Ratnani, A. Evaluating the impact of filter-based feature selection in intrusion detection systems. Int. J. Inf. Secur. 2024, 23, 759–785. [Google Scholar] [CrossRef]
- Gong, H.; Li, Y.; Zhang, J.; Zhang, B.; Wang, X. A new filter feature selection algorithm for classification task by ensembling pearson correlation coefficient and mutual information. Eng. Appl. Artif. Intell. 2024, 131, 107865. [Google Scholar] [CrossRef]
- Zhang, Y.; Hui, J.; Qin, Q.; Sun, Y.; Zhang, T.; Sun, H.; Li, M. Transfer-learning-based approach for leaf chlorophyll content estimation of winter wheat from hyperspectral data. Remote Sens. Environ. 2021, 267, 112724. [Google Scholar] [CrossRef]
- Park, Y.; Jin, S.; Noda, I.; Jung, Y.M. Continuing progress in the field of two-dimensional correlation spectroscopy (2D-COS), part II. Recent noteworthy developments. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 284, 121750. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Noda, I.; Jung, Y.M. Diverse Applications of Two-Dimensional Correlation Spectroscopy (2D-COS). Appl. Spectrosc. 2025, 79, 36–68. [Google Scholar] [CrossRef]
- Thieme, A.; Jennewein, J.; Hively, W.; Lamb, B.; Whitcraft, A.; Mirsky, S.; Reberg-Horton, S.; Justice, C. Multispectral red-edge indices accurately estimate nitrogen content in winter cereal cover crops. Agron. J. 2025, 117, e70011. [Google Scholar] [CrossRef]
- dos Santos Luciano, A.C.; Picoli, M.C.A.; Duft, D.G.; Rocha, J.V.; Leal, M.R.L.V.; Le Maire, G. Empirical model for forecasting sugarcane yield on a local scale in Brazil using Landsat imagery and random forest algorithm. Comput. Electron. Agric. 2021, 184, 106063. [Google Scholar] [CrossRef]
- Wang, C.; Yang, C.; Zhang, J.; Kuai, J.; Xie, J.; Wu, W.; Zuo, Q.; Yan, M.; Du, H.; Ma, N. A PROSAIL model with a vegetation index lookup table optimized with in-situ statistics for rapeseed leaf area index estimation using diverse unmanned aerial vehicle sensors in the Yangtze River Basin. Comput. Electron. Agric. 2023, 215, 108418. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, H.; Qi, J.; Sun, Z.; Han, S.; Feng, H.; Jiang, J.; Xu, W.; Li, Z.; Yang, G. Estimating canopy-scale chlorophyll content in apple orchards using a 3D radiative transfer model and UAV multispectral imagery. Comput. Electron. Agric. 2022, 202, 107401. [Google Scholar] [CrossRef]
- Bhadra, S.; Sagan, V.; Sarkar, S.; Braud, M.; Mockler, T.C.; Eveland, A.L. PROSAIL-Net: A transfer learning-based dual stream neural network to estimate leaf chlorophyll and leaf angle of crops from UAV hyperspectral images. ISPRS J. Photogramm. Remote Sens. 2024, 210, 1–24. [Google Scholar] [CrossRef]
- Zhao, D.; Yang, G.; Xu, T.; Yu, F.; Zhang, C.; Cheng, Z.; Ren, L.; Yang, H. Dynamic Maize True Leaf Area Index Retrieval with KGCNN and TL and Integrated 3D Radiative Transfer Modeling for Crop Phenotyping. Plant Phenomics 2025, 7, 100004. [Google Scholar] [CrossRef]
- Jiao, Q.; Sun, Q.; Zhang, B.; Huang, W.; Ye, H.; Zhang, Z.; Zhang, X.; Qian, B. A random forest algorithm for retrieving canopy chlorophyll content of wheat and soybean trained with PROSAIL simulations using adjusted average leaf angle. Remote Sens. 2021, 14, 98. [Google Scholar] [CrossRef]
- Lu, B.; Proctor, C.; He, Y. Investigating different versions of PROSPECT and PROSAIL for estimating spectral and biophysical properties of photosynthetic and non-photosynthetic vegetation in mixed grasslands. GISci. Remote Sens. 2021, 58, 354–371. [Google Scholar] [CrossRef]
- Ma, Y.; Song, X.; Zhang, J.; Pan, D.; Feng, H.; Yang, G.; Qiu, C.; Sun, H.; Zheng, C.; Li, P. Inversion of biophysical parameters of potato based on an active learning pool-based sampling strategy. Int. J. Remote Sens. 2025, 46, 320–339. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, W.; He, Y.; Wanger, T.C.; Cen, H. Combining transfer learning and hyperspectral reflectance analysis to assess leaf nitrogen concentration across different plant species datasets. Remote Sens. Environ. 2022, 269, 112826. [Google Scholar] [CrossRef]
- de França e Silva, N.R.; Chaves, M.E.D.; Luciano, A.C.d.S.; Sanches, I.D.A.; de Almeida, C.M.; Adami, M. Sugarcane yield estimation using satellite remote sensing data in empirical or mechanistic modeling: A systematic review. Remote Sens. 2024, 16, 863. [Google Scholar] [CrossRef]
- Wang, D.; Cao, W.; Zhang, F.; Li, Z.; Xu, S.; Wu, X. A review of deep learning in multiscale agricultural sensing. Remote Sens. 2022, 14, 559. [Google Scholar] [CrossRef]
- Pichler, M.; Hartig, F. Machine learning and deep learning—A review for ecologists. Methods Ecol. Evol. 2023, 14, 994–1016. [Google Scholar] [CrossRef]
- Avacharmal, R.; Pamulaparthyvenkata, S.; Pandiya, D.K.; Prakash, R.K.; Ranjan, P.; Balakrishnan, A.; Maheswaran, S. Comprehensive investigation on Deep learning models: Applications, Advantages, and Challenges. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024; pp. 1–6. [Google Scholar]
- Yue, J.; Yang, H.; Feng, H.; Han, S.; Zhou, C.; Fu, Y.; Guo, W.; Ma, X.; Qiao, H.; Yang, G. Hyperspectral-to-image transform and CNN transfer learning enhancing soybean LCC estimation. Comput. Electron. Agric. 2023, 211, 108011. [Google Scholar] [CrossRef]
- Hu, B.; Huang, h.; JI, Y.; Zhao, X.; Qi, J.; Zhang, L.; Zhang, G. Evaluation of the optimum concentration of chlorophyll for determination of chlorophyll content by spectrophotometert. Pratacultural Sci. 2018, 35, 1965–1974. [Google Scholar]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Raya-Sereno, M.D.; Camino, C.; Pancorbo, J.L.; Alonso-Ayuso, M.; Gabriel, J.L.; Beck, P.; Quemada, M. Assessing wheat genotype response under combined nitrogen and water stress scenarios coupling high-resolution optical and thermal sensors with radiative transfer models. Eur. J. Agron. 2024, 154, 127102. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, C.; Xiang, S.; Chen, L.; Yu, X.; Li, H.; Li, Z.; Guo, X.; Zhang, H.; Huang, X. A Hybrid Method of PROSAIL RTM for the Retrieval Canopy LAI and Chlorophyll Content of Moso Bamboo (Phyllostachys Pubescens) Forests From Sentinel-2 MSI Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 3125–3143. [Google Scholar] [CrossRef]
- Zhang, S.; Tian, J.; Lu, X.; Tian, Q.; He, S.; Lin, Y.; Li, S.; Zheng, W.; Wen, T.; Mu, X. Monitoring of chlorophyll content in local saltwort species Suaeda salsa under water and salt stress based on the PROSAIL-D model in coastal wetland. Remote Sens. Environ. 2024, 306, 114117. [Google Scholar] [CrossRef]
- Li, D.; Wu, Y.; Berger, K.; Kuang, Q.; Feng, W.; Chen, J.M.; Wang, W.; Zheng, H.; Yao, X.; Zhu, Y. Estimating canopy nitrogen content by coupling PROSAIL-PRO with a nitrogen allocation model. Int. J. Appl. Earth Obs. Geoinf. 2024, 135, 104280. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Liu, S.; Jin, X.; Nie, C.; Wang, S.; Yu, X.; Cheng, M.; Shao, M.; Wang, Z.; Tuohuti, N.; Bai, Y. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, A.; Gupta, P.; Chowdary, V. Machine learning applications for precision agriculture: A comprehensive review. IEEe Access 2020, 9, 4843–4873. [Google Scholar] [CrossRef]
- Joshi, A.; Pradhan, B.; Gite, S.; Chakraborty, S. Remote-sensing data and deep-learning techniques in crop mapping and yield prediction: A systematic review. Remote Sens. 2023, 15, 2014. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2024, 301, 113924. [Google Scholar] [CrossRef]
- Tong, X.-Y.; Xia, G.-S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- Shen, Z.; Ramirez-Lopez, L.; Behrens, T.; Cui, L.; Zhang, M.; Walden, L.; Wetterlind, J.; Shi, Z.; Sudduth, K.A.; Baumann, P. Deep transfer learning of global spectra for local soil carbon monitoring. ISPRS J. Photogramm. Remote Sens. 2022, 188, 190–200. [Google Scholar] [CrossRef]
- Jagota, M.; Ye, C.; Albors, C.; Rastogi, R.; Koehl, A.; Ioannidis, N.; Song, Y.S. Cross-protein transfer learning substantially improves disease variant prediction. Genome Biol. 2023, 24, 182. [Google Scholar] [CrossRef] [PubMed]
- Rossel, R.A.V.; Shen, Z.; Lopez, L.R.; Behrens, T.; Shi, Z.; Wetterlind, J.; Sudduth, K.A.; Stenberg, B.; Guerrero, C.; Gholizadeh, A. An imperative for soil spectroscopic modelling is to think global but fit local with transfer learning. Earth-Sci. Rev. 2024, 254, 104797. [Google Scholar] [CrossRef]
- Wu, B.; Ye, H.; Huang, W.; Wang, H.; Luo, P.; Ren, Y.; Kong, W. Monitoring the vertical distribution of maize canopy chlorophyll content based on multi-angular spectral data. Remote Sens. 2021, 13, 987. [Google Scholar] [CrossRef]
- Chatterjee, S.; Baath, G.S.; Sapkota, B.R.; Flynn, K.C.; Smith, D.R. Enhancing LAI estimation using multispectral imagery and machine learning: A comparison between reflectance-based and vegetation indices-based approaches. Comput. Electron. Agric. 2025, 230, 109790. [Google Scholar] [CrossRef]
- Dou, S.; Zhang, W.; Deng, Y.; Zhang, C.; Mei, Z.; Yan, J.; Li, M. Comparison of Citrus Leaf Water Content Estimations Based on the Continuous Wavelet Transform and Fractional Derivative Methods. Horticulturae 2024, 10, 177. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, S.; Miao, H.; Song, Z.; Yu, J.; Guo, S.; Chang, Q. Ground-Based Hyperspectral Estimation of Maize Leaf Chlorophyll Content Considering Phenological Characteristics. Remote Sens. 2024, 16, 2133. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.; Guga, S.; Li, K.; Zhi, F.; Guo, Y.; Zhang, J.; Bao, Y. Retrieving SPAD values of summer maize using UAV hyperspectral data based on multiple machine learning algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]










| Parameters | Units | Big Trumpet Stage | Spinning Stage | ||
|---|---|---|---|---|---|
| Transfer Learning | Bands Selection | Transfer Learning | Bands Selection | ||
| Leaf structure index (N) | unitless | 1.2–1.6 (0.2) | 1.5 | 1.2–1.8 (0.3) | 1.7 |
| Chlorophyll a + b content (Chl) | μg/cm2 | 20–90 (2) | |||
| Carotenoid content (Car) | μg/cm2 | Cab/5 | |||
| Equivalent water thickness (Cw) | cm | 0.015–0.025 (0.002) | 0.018 | 0.02–0.035 (0.002) | 0.022 |
| Dry matter content (Cm) | g/cm2 | 0.003–0.009 (0.001) | 0.008 | 0.006–0.012 (0.002) | 0.012 |
| Leaf area index (LAI) | m2/m2 | 2–5 (0.5) | 1.0–8.0 (1) | 2.5–5 (0.5) | 1.0–8.0 (1) |
| Average leaf inclination angle (LA) | Deg (°) | 10–60 (10) | 10–80 (10) | 10–60 (10) | 10–80 (10) |
| Solar zenith angle (SZA) | Deg (°) | 45 | |||
| Observer zenith angle (OZA) | Deg (°) | 0 | |||
| Model | Stage | Train (n = 6667) | Validation (n = 3334) | ||
|---|---|---|---|---|---|
| R2 | RMSE (g/cm2) | R2 | RMSE (g/cm2) | ||
| Pre-trained LCNet | Big trumpet stage | 0.94 | 4.33 | 0.94 | 4.31 |
| Spinning stage | 0.97 | 3.07 | 0.97 | 3.04 | |
| Model | Stage | Train (n = 40) | Validation (n = 20) | ||
|---|---|---|---|---|---|
| R2 | RMSE (g/cm2) | R2 | RMSE (g/cm2) | ||
| Maize-LCNet | Big trumpet stage | 0.63 | 2.49 | 0.54 | 2.53 |
| Spinning stage | 0.84 | 2.67 | 0.65 | 4.39 | |
| Growth Stage | Accuracy Indicators | LCNet | Maize-LCNet-Field | PLSR-Field | SVM-Field | |
|---|---|---|---|---|---|---|
| Big trumpet stage | Validation | R2 | 0.09 | 0.48 | 0.51 | 0.45 |
| RMSE (g/cm2) | 3.61 | 3.59 | 2.52 | 2.55 | ||
| Spinning stage | Validation | R2 | 0.17 | 0.54 | 0.62 | 0.55 |
| RMSE (g/cm2) | 65.84 | 4.96 | 3.87 | 4.23 | ||
| Comparison | Big Trumpet Stage | Spinning Stage | ||
|---|---|---|---|---|
| t | p-Value | t | p-Value | |
| Maize-LCNet vs. LCNet | 0.468 | 0.645 | 2.421 | 0.026 |
| Maize-LCNet vs. Maize-LCNet-field | 4.289 | 0.000 | 49.619 | 0.000 |
| Maize-LCNet vs. PLSR-field | −3.772 | 0.045 | 2.256 | 0.036 |
| Maize-LCNet vs. SVM-field | −4.330 | 0.000 | −0.285 | 0.779 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Ren, L.; Yang, G.; Cheng, Z.; Zhao, D.; Zhang, C.; Feng, H.; Hu, H.; Yang, H. Estimation of Leaf Chlorophyll Content of Maize from Hyperspectral Data Using E2D-COS Feature Selection, Deep Neural Network, and Transfer Learning. Agriculture 2025, 15, 1072. https://doi.org/10.3390/agriculture15101072
Chen R, Ren L, Yang G, Cheng Z, Zhao D, Zhang C, Feng H, Hu H, Yang H. Estimation of Leaf Chlorophyll Content of Maize from Hyperspectral Data Using E2D-COS Feature Selection, Deep Neural Network, and Transfer Learning. Agriculture. 2025; 15(10):1072. https://doi.org/10.3390/agriculture15101072
Chicago/Turabian StyleChen, Riqiang, Lipeng Ren, Guijun Yang, Zhida Cheng, Dan Zhao, Chengjian Zhang, Haikuan Feng, Haitang Hu, and Hao Yang. 2025. "Estimation of Leaf Chlorophyll Content of Maize from Hyperspectral Data Using E2D-COS Feature Selection, Deep Neural Network, and Transfer Learning" Agriculture 15, no. 10: 1072. https://doi.org/10.3390/agriculture15101072
APA StyleChen, R., Ren, L., Yang, G., Cheng, Z., Zhao, D., Zhang, C., Feng, H., Hu, H., & Yang, H. (2025). Estimation of Leaf Chlorophyll Content of Maize from Hyperspectral Data Using E2D-COS Feature Selection, Deep Neural Network, and Transfer Learning. Agriculture, 15(10), 1072. https://doi.org/10.3390/agriculture15101072








