Experimental Study of Liquid Jet Atomization and Penetration in Subsonic Crossflows
Abstract
1. Introduction
2. Materials and Methods
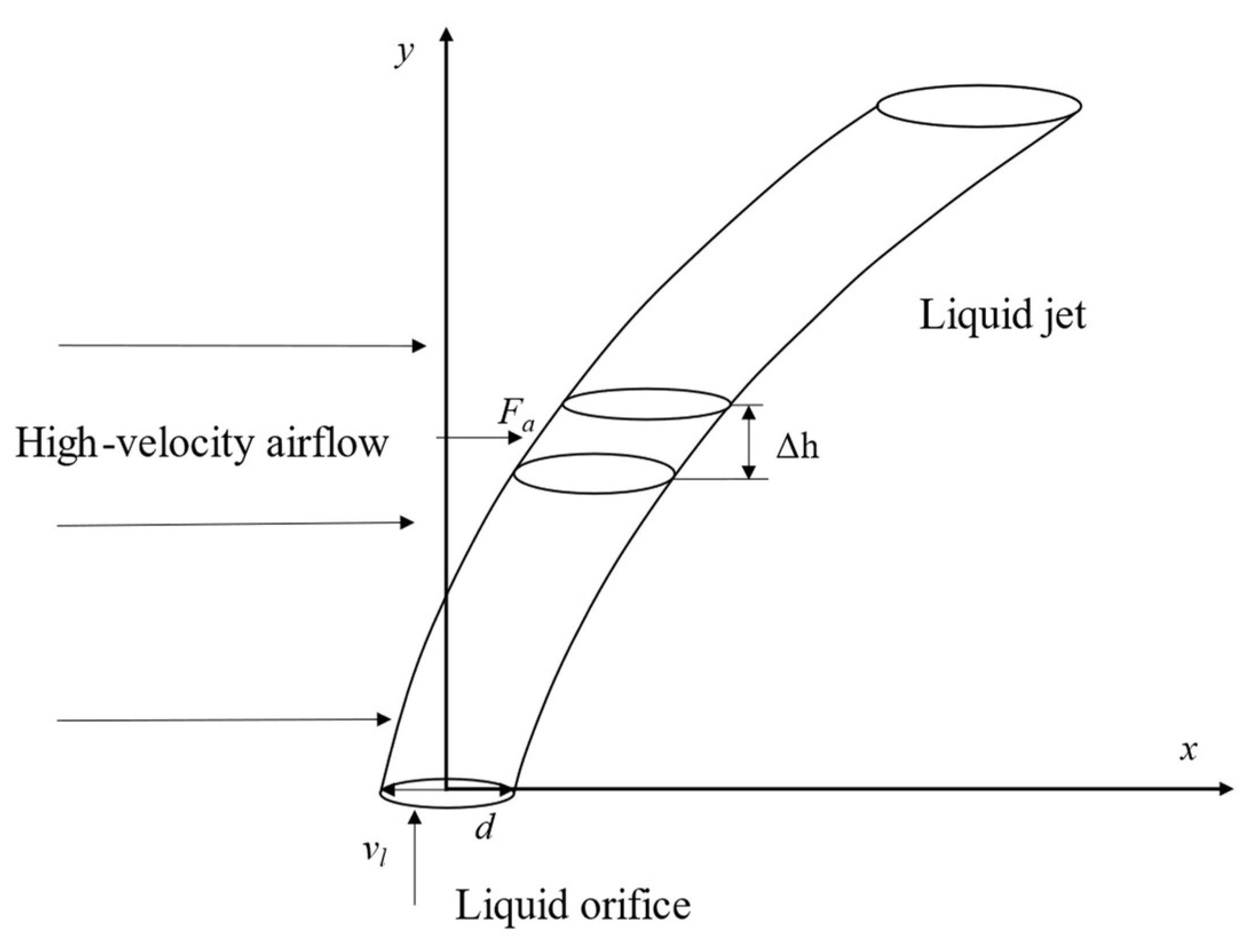
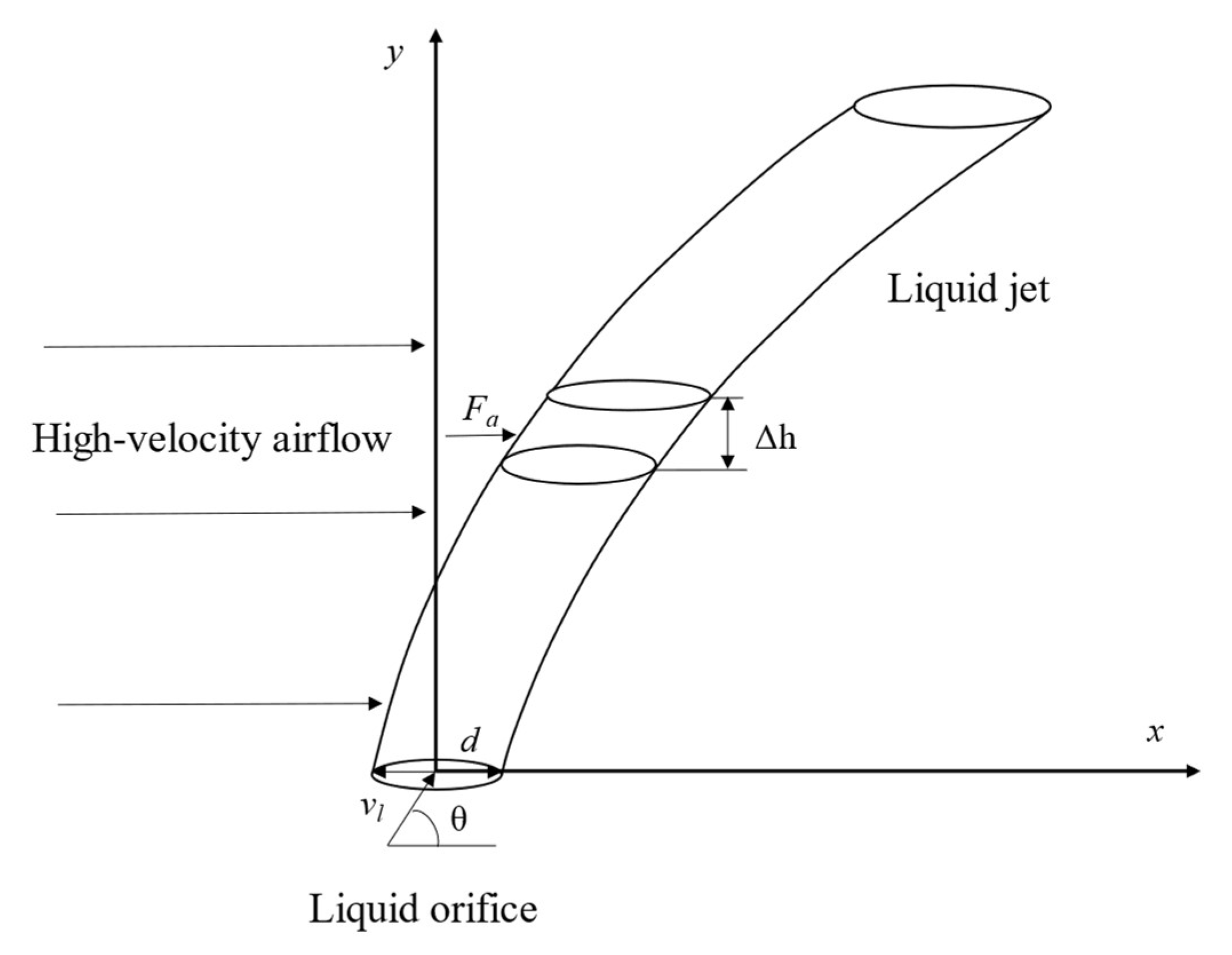
2.1. Theoretical Analysis
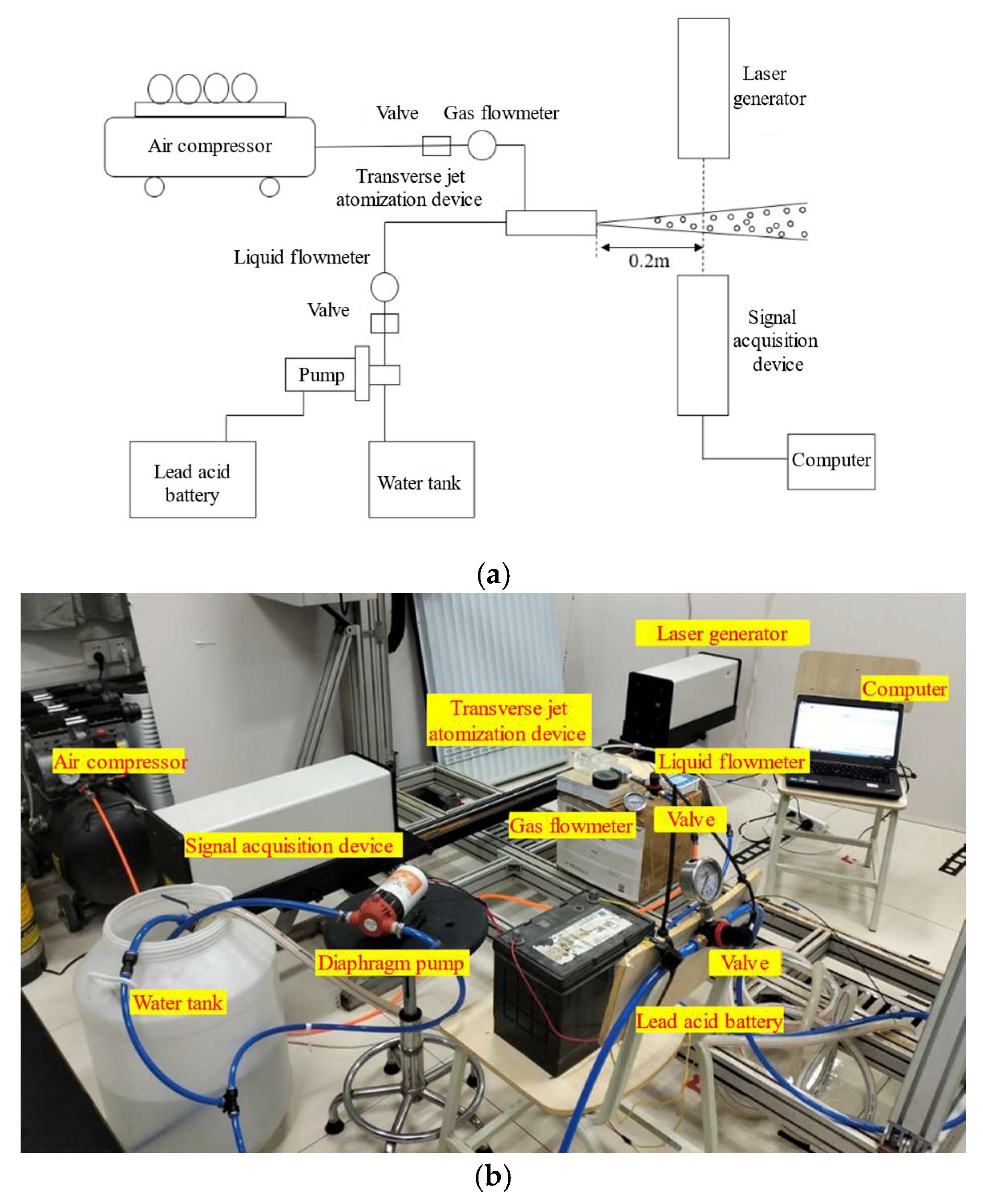
2.2. Experimental Setup
2.2.1. Visualization of Charged Droplet Generation
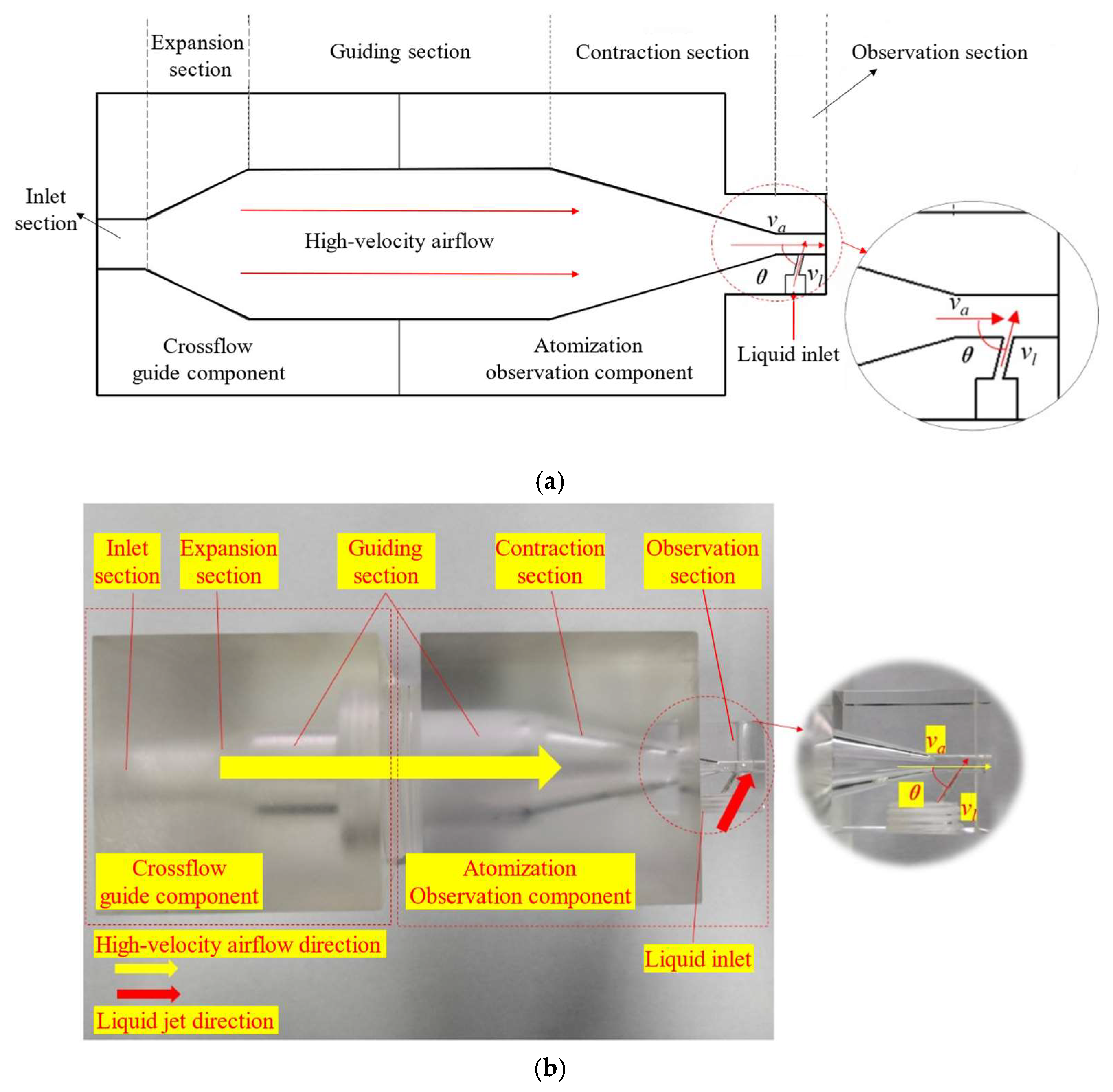
2.2.2. Visualization Test System
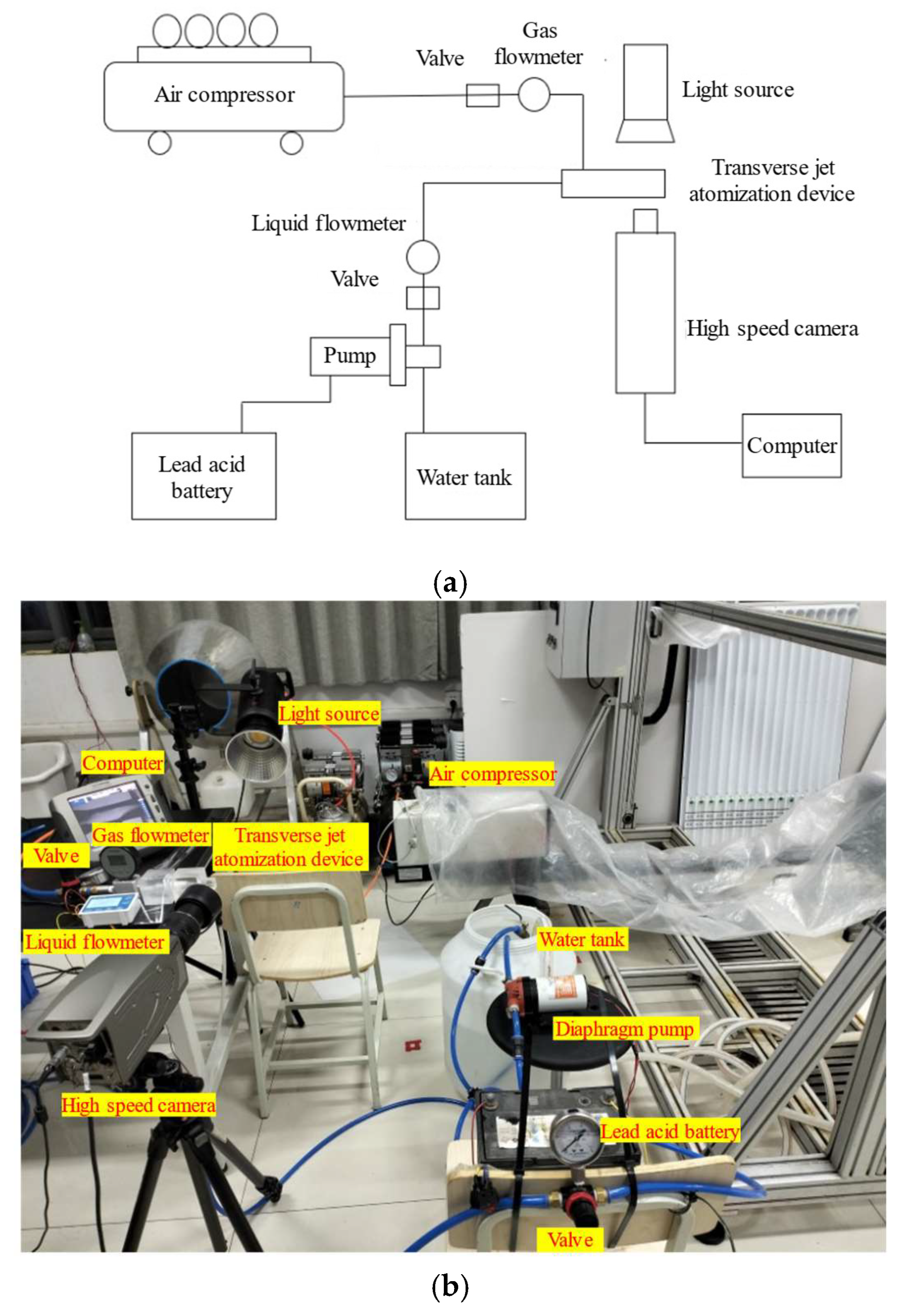
2.2.3. Transverse Jet Atomization Test System
2.3. Experimental Design
2.4. Data Process
3. Results and Discussion
3.1. Results and Analysis of Visualization Test
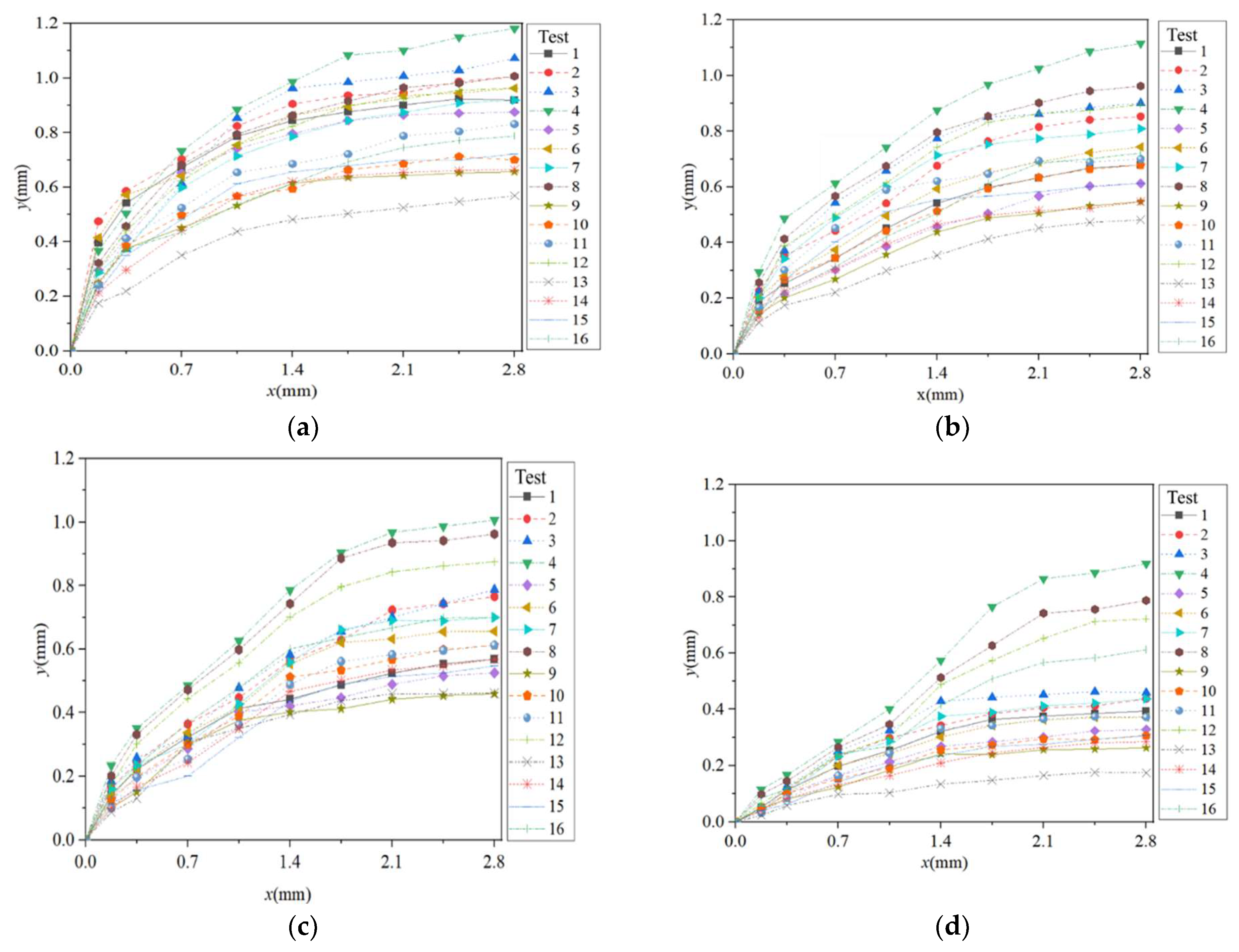
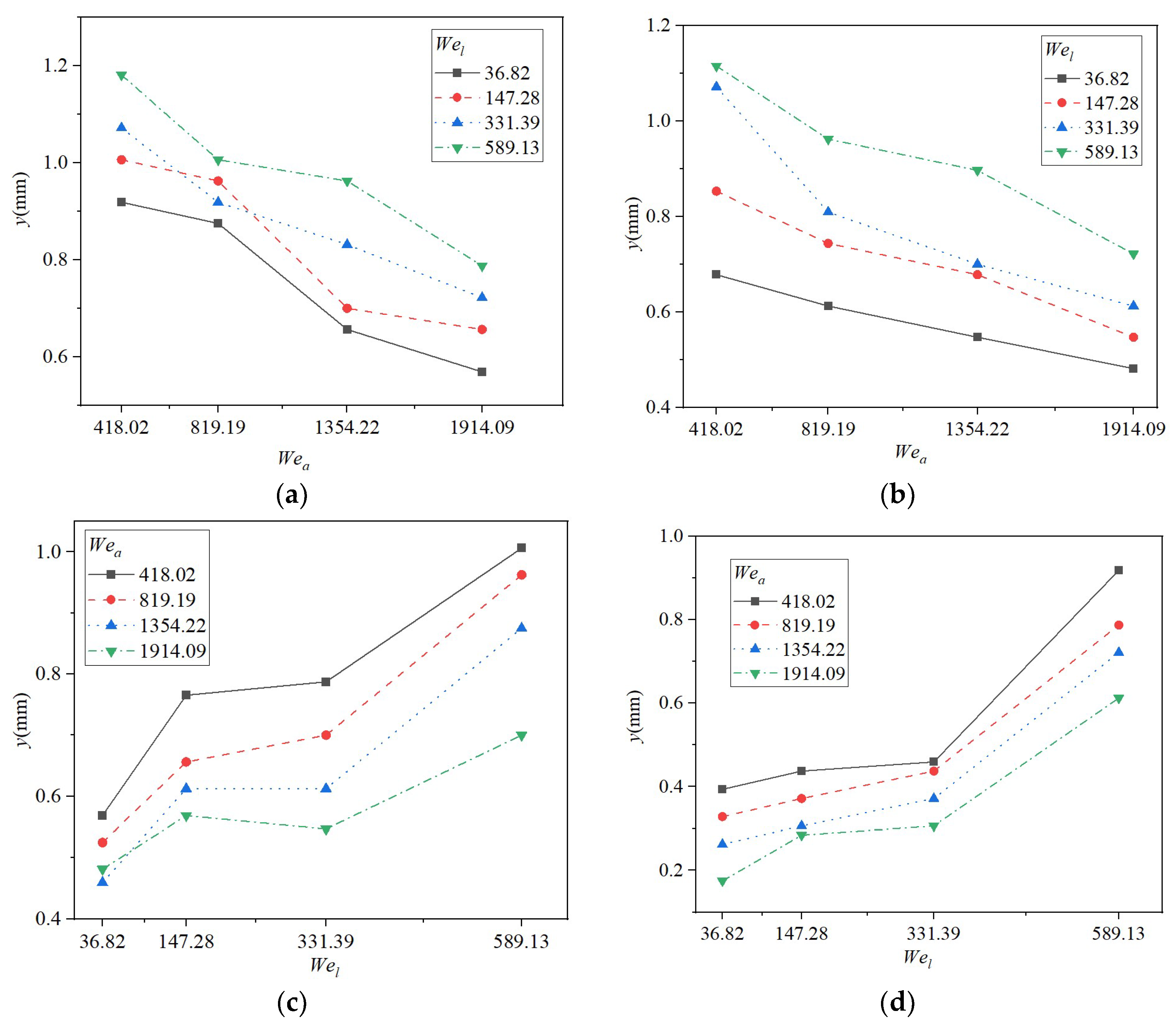
3.1.1. Effect of Weber Number on Penetration Depth
3.1.2. Effect of Incidence Angle on Penetration Depth
3.2. Model Construction and Validation
3.2.1. Penetration Depth Model at an Incidence Angle of 90°
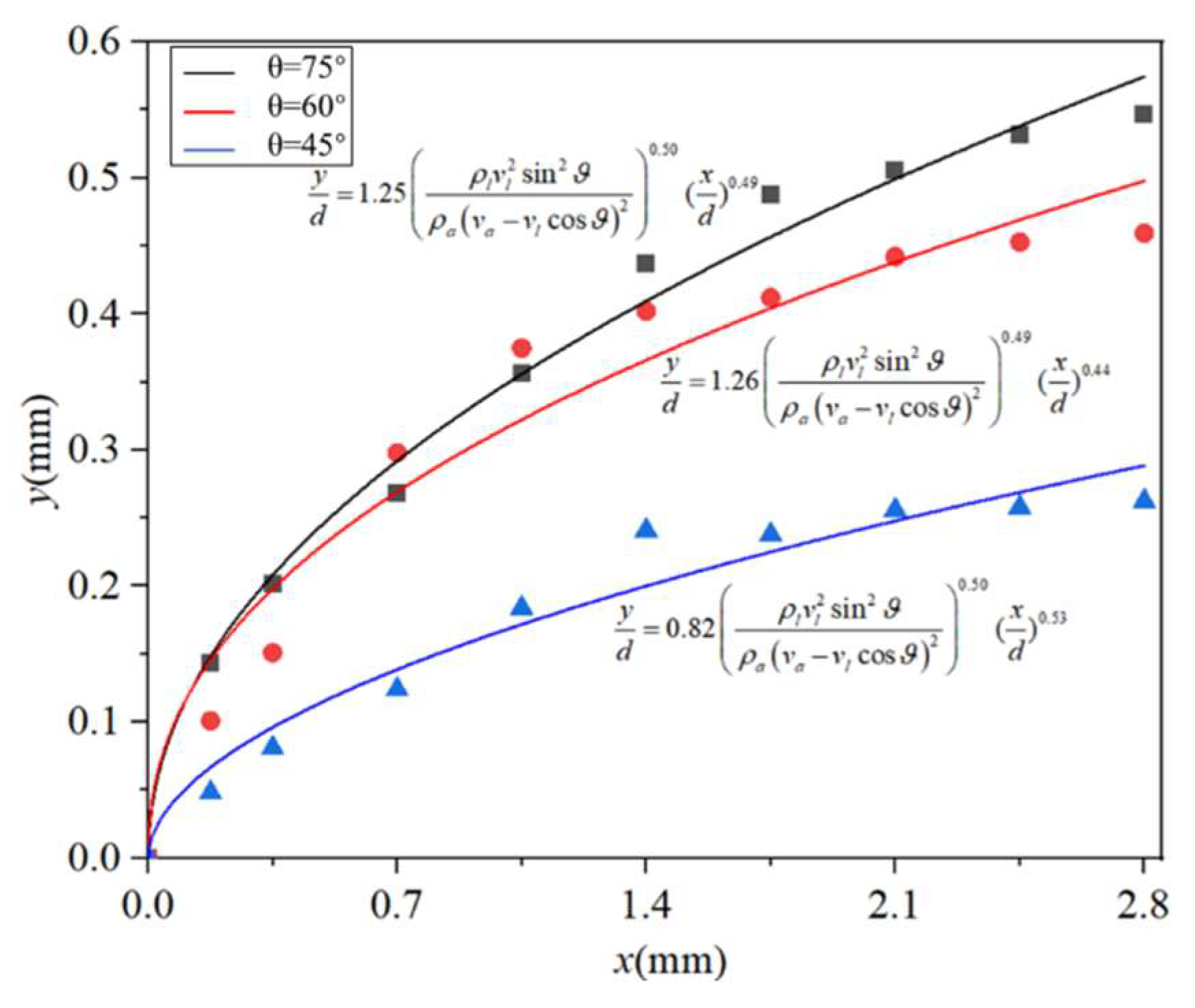
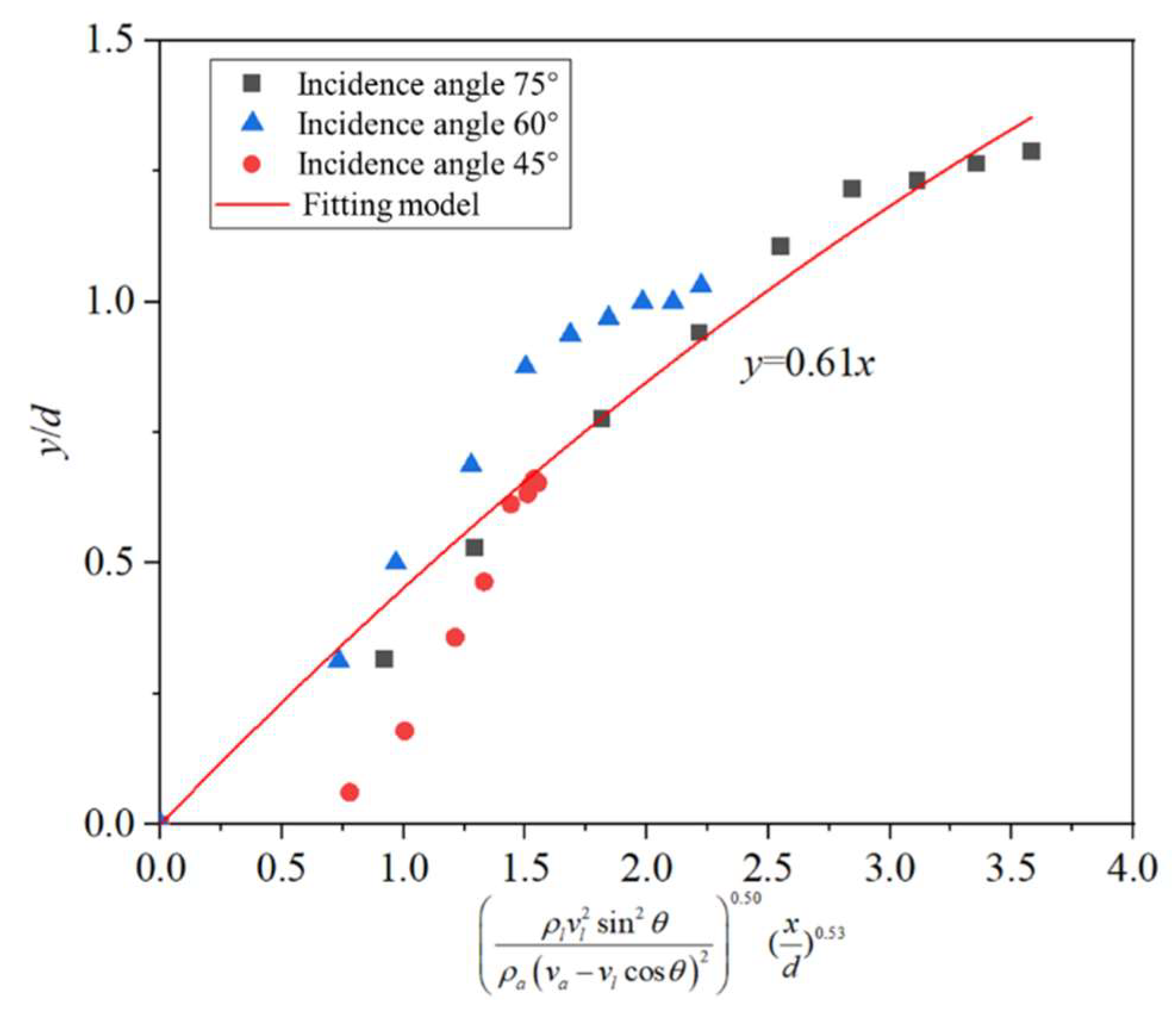
3.2.2. Penetration Depth Model at an Incidence Angle of θ
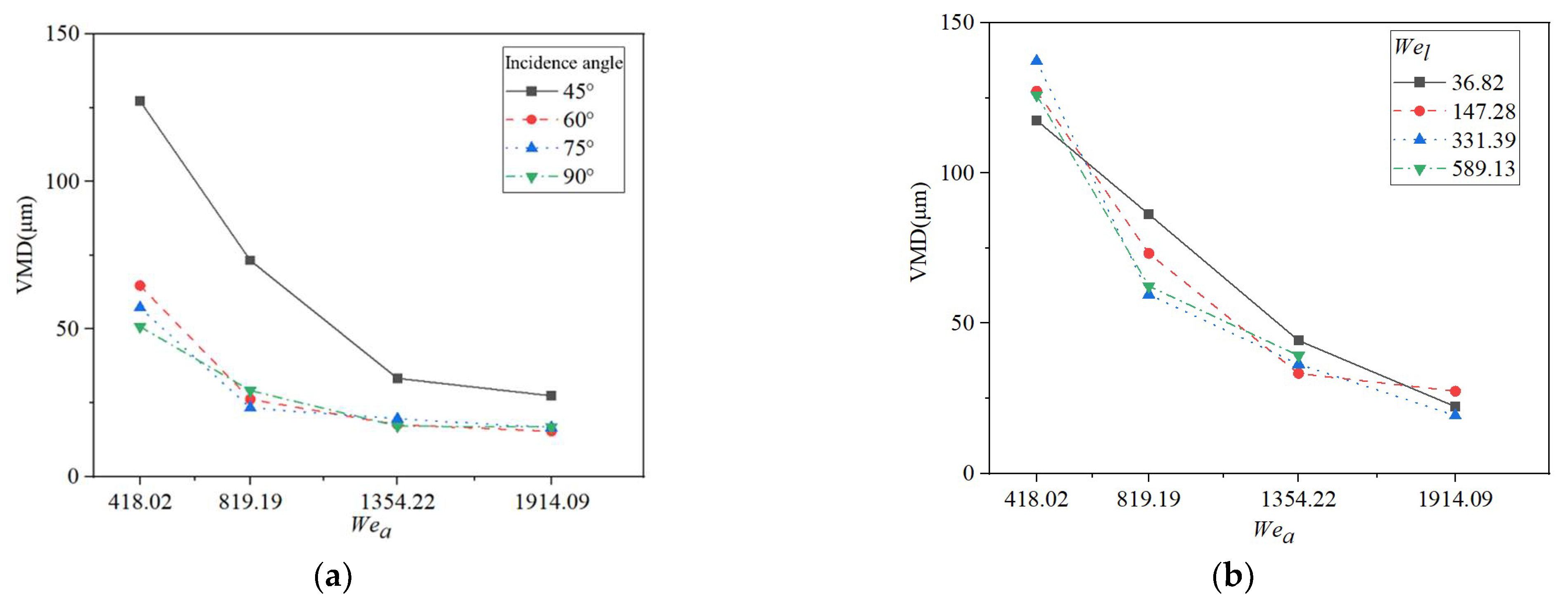
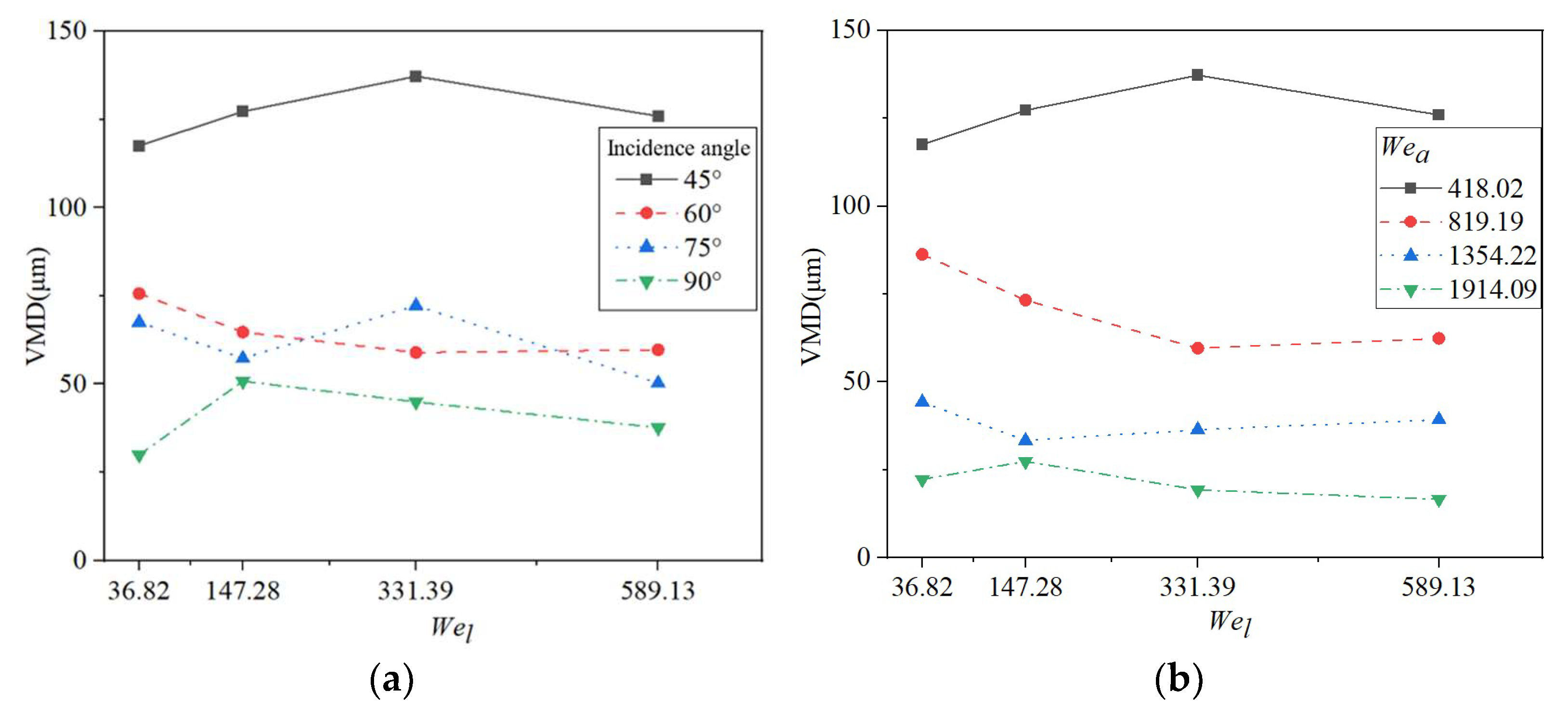
3.3. Results and Analysis of Atomization Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peters, J. An Experimental Study of the Primary Breakup of a Liquid Jet in a Turbulent Low Speed Crossflow. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2023. [Google Scholar]
- Yue, J.; Chao, C.; Hong, L.; Xiang, Q. Influences of nozzle parameters and low-pressure on jet breakup and droplet characteristics. Int. J. Agric. Biol. Eng. 2016, 9, 22–32. [Google Scholar]
- Zhou, D.; Chang, J.; Tang, C.; He, L. Review on research progress in liquid jet in crossflow. Int. Commun. Heat Mass Transf. 2023, 148, 107003. [Google Scholar] [CrossRef]
- Fu, Q.F.; Yao, M.W.; Yang, L.J.; Xie, L. Atomization model of liquid jets exposed to subsonic crossflows. AIAA J. 2020, 58, 2347–2351. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Hua, L.; Zhang, D.; Issaka, Z. Experimental study on jet breakup morphologies and jet characteristic parameters of non-circular nozzles under low-intermediate pressures. Appl. Eng. Agric. 2019, 35, 617–632. [Google Scholar] [CrossRef]
- Lee, I.C.; Kang, Y.S.; Moon, H.J.; Jang, S.P.; Kim, J.K.; Koo, J. Spray jet penetration and distribution of modulated liquid jets in subsonic cross-flows. J. Mech. Sci. Technol. 2010, 24, 1425–1431. [Google Scholar] [CrossRef]
- Inamura, T. Trajectory of a liquid jet traversing subsonic airstreams. J. Propuls. Power 2000, 16, 155–157. [Google Scholar] [CrossRef]
- Kasmaiee, S.; Tadjfar, M.; Kasmaiee, S. Pressure swirl nozzles with different discharge orifice shapes injecting into transverse airflow. Phys. Fluids 2025, 37, 013357. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Hua, L.; Zhang, D. Three-dimensional flow breakup characteristics of a circular jet with different nozzle geometries. Biosyst. Eng. 2020, 193, 216–231. [Google Scholar] [CrossRef]
- Xiang, Q.; Qureshi, W.A.; Tunio, M.H.; Solangi, K.A.; Xu, Z.; Lakhiar, I.A. Low-pressure drop size distribution characterization of impact sprinkler jet nozzles with and without aeration. Agric. Water Manag. 2021, 243, 106458. [Google Scholar] [CrossRef]
- Dighe, S.; Gadgil, H. Effect of transverse acoustic forcing on the characteristics of impinging jet atomization. At. Sprays 2019, 29, 79–103. [Google Scholar] [CrossRef]
- Nishimoto, S.; Nakaya, S.; Lee, J.; Tsue, M. Effects of the penetration height of ethylene transverse jets on flame stabilization behavior in a Mach 2 supersonic crossflow. Proc. Combust. Inst. 2023, 39, 3117–3126. [Google Scholar] [CrossRef]
- Thomas, R.H.; Schetz, J.A. Distributions across the plume of transverse liquid and slurry jets in supersonic airflow. AIAA J. 1985, 23, 1892–1901. [Google Scholar] [CrossRef][Green Version]
- Amini, G.; Dolatabadi, A. Capillary instability of elliptic liquid jets. Phys. Fluids 2011, 23, 084109. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Chen, C.; Xiang, Q. Calculation and verification of formula for the range of sprinklers based on jet breakup length. Int. J. Agric. Biol. Eng. 2018, 11, 49–57. [Google Scholar] [CrossRef]
- Xie, M.; Wang, W.; Yu, B.; He, M.; Wu, S.; Huang, X.; Liu, H. Primary breakup model development for trajectory prediction of liquid jets in subsonic crossflow. Phys. Fluids 2024, 36, 033357. [Google Scholar] [CrossRef]
- Kong, L.; Lan, T.; Chen, J.; Wang, K.; Sun, H. Breakup processes and droplet characteristics of liquid jets injected into low-speed air crossflow. Processes 2020, 8, 676. [Google Scholar] [CrossRef]
- Wu, R.; Sun, C.; Gui, Y. Numerical analysis of atomization characteristics of fuel-jet in crossflow. AIP Adv. 2024, 14, 085115. [Google Scholar] [CrossRef]
- Liao, J.; Luo, X.; Wang, P.; Zhou, Z.; O’donnell, C.C.; Zang, Y.; Hewitt, A.J. Analysis of the influence of different parameters on droplet characteristics and droplet size classification categories for air induction nozzle. Agronomy 2020, 10, 256. [Google Scholar] [CrossRef]
- Hussain, Z.; Liu, J.; Chauhdary, J.N.; Zhao, Y. Evaluating the effect of operating pressure, nozzle size and mounting height on droplet characteristics of rotating spray plate sprinkler. Irrig. Sci. 2024, 1–16. [Google Scholar] [CrossRef]
- Liu, H.; Guo, Y.; Lin, W. Numerical simulations of spray jet in sup ersonic crossflows using an Eulerian approach with an SMD model. Int. J. Multiph. Flow 2016, 82, 49–64. [Google Scholar] [CrossRef]
- Yu, S.; Yin, B.; Bi, Q.; Jia, H.; Chen, C. The influence of elliptical and circular orifices on the transverse jet characteristics at supersonic crossflow. Acta Astronaut. 2021, 185, 124–131. [Google Scholar] [CrossRef]
- Tunio, M.H.; Gao, J.; Qureshi, W.A.; Sheikh, S.A.; Chen, J.; Chandio, F.A.; Lakhiar, I.A.; Solangi, K.A. Effects of droplet size and spray interval on root-to-shoot ratio, photosynthesis efficiency, and nutritional quality of aeroponically grown butterhead lettuce. Int. J. Agric. Biol. Eng. 2022, 15, 79–88. [Google Scholar]
- Gong, C.; Li, D.; Kang, C. Effect of oil-based emulsion on air bubbles in the spray sheet produced through the air-induction nozzle. Pest Manag. Sci. 2022, 78, 5347–5357. [Google Scholar] [CrossRef]
- Wu, M.; Ou, M.; Zhang, Y.; Jia, W.; Dai, S.; Wang, M.; Dong, X.; Wang, X.; Jiang, L. Development and Evaluation of a Monodisperse Droplet-Generation System for Precision Herbicide Application. Agriculture 2024, 14, 1885. [Google Scholar] [CrossRef]
- Jalili, B.; Jalili, P.; Ommi, F.; Ganji, D.D. Experimental study on the nozzle-shape effect on liquid jet characteristics in gaseous crossflow. Front. Mech. Eng. 2023, 9, 1207894. [Google Scholar] [CrossRef]
- Jalili, B.; Jalili, P. Numerical analysis of airflow turbulence intensity effect on liquid jet trajectory and breakup in two-phase cross flow. Alex. Eng. J. 2023, 68, 577–585. [Google Scholar] [CrossRef]
- Kumar, R.; Mukhopadhyay, S. Liquid Jet in Cross Flow Modeling Under Different Weber Numbers. In Proceedings of the ICTEA: International Conference on Thermal Engineering, Tashkent, Uzbekistan, 28 May–1 June 2024; Volume 1. [Google Scholar]
- Mashayek, A.; Jafari, A.; Ashgriz, N. Improved model for the penetration of liquid jets in subsonic crossflows. AIAA J. 2008, 46, 2674–2686. [Google Scholar] [CrossRef]
- Pourrousta, M.; Larimi, M.M.; Biglarian, M.; Hedayati, P. Liquid Jet Breakup and Penetration in a Gas Cross-Flow-An Experimental Study. Exp. Tech. 2024, 48, 449–459. [Google Scholar] [CrossRef]
- Kasmaiee, S.; Tadjfar, M. Influence of injection angle on liquid jet in crossflow. Int. J. Multiph. Flow 2022, 153, 104128. [Google Scholar] [CrossRef]
- Kasmaiee, S.; Tadjfar, M.; Kasmaiee, S.; Ahmadi, G. Linear stability analysis of surface waves of liquid jet injected in transverse gas flow with different angles. Theor. Comput. Fluid Dyn. 2024, 38, 107–138. [Google Scholar] [CrossRef]
- Chang, J.; He, L.; Chen, L.; Shen, Z.; Chuah, L.F.; Bokhari, A.; Klemeš, J.J.; Han, N. Numerical simulation of liquid jet atomization in subsonic crossflow. Energy 2022, 257, 124676. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Le, J. Review of atomization characteristics of liquid jets in crossflow. Phys. Fluids 2024, 36, 021302. [Google Scholar] [CrossRef]






| (L/min) | (L/min) | θ (°) |
|---|---|---|
| 50 | 0.045 | 45 |
| 70 | 0.090 | 60 |
| 90 | 0.135 | 75 |
| 110 | 0.180 | 90 |
| Case Number | (L/min) | (m/s) | (L/min) | (m/s) | |||
|---|---|---|---|---|---|---|---|
| 1 | 50 | 92.60 | 418.02 | 0.045 | 1.95 | 36.82 | 0.38 |
| 2 | 50 | 92.60 | 418.02 | 0.090 | 3.90 | 147.28 | 1.51 |
| 3 | 50 | 92.60 | 418.02 | 0.135 | 5.85 | 331.39 | 3.40 |
| 4 | 50 | 92.60 | 418.02 | 0.180 | 7.80 | 589.13 | 6.04 |
| 5 | 70 | 129.63 | 819.19 | 0.045 | 1.95 | 36.82 | 0.19 |
| 6 | 70 | 129.63 | 819.19 | 0.090 | 3.90 | 147.28 | 0.77 |
| 7 | 70 | 129.63 | 819.19 | 0.135 | 5.85 | 331.39 | 1.73 |
| 8 | 70 | 129.63 | 819.19 | 0.180 | 7.80 | 589.13 | 3.08 |
| 9 | 90 | 166.67 | 1354.22 | 0.045 | 1.95 | 36.82 | 0.12 |
| 10 | 90 | 166.67 | 1354.22 | 0.090 | 3.90 | 147.28 | 0.47 |
| 11 | 90 | 166.67 | 1354.22 | 0.135 | 5.85 | 331.39 | 1.05 |
| 12 | 90 | 166.67 | 1354.22 | 0.180 | 7.80 | 589.13 | 1.86 |
| 13 | 110 | 203.70 | 1914.09 | 0.045 | 1.95 | 36.82 | 0.08 |
| 14 | 110 | 203.70 | 1914.09 | 0.090 | 3.90 | 147.28 | 0.33 |
| 15 | 110 | 203.70 | 1914.09 | 0.135 | 5.85 | 331.39 | 0.74 |
| 16 | 110 | 203.70 | 1914.09 | 0.180 | 7.80 | 589.13 | 1.32 |
| Case Number | Simplified Penetration Depth Curve Model | R2 | Modified Penetration Depth Curve Model | R2 |
|---|---|---|---|---|
| 1 | 0.856 | 0.987 | ||
| 2 | 0.846 | 0.994 | ||
| 3 | 0.955 | 0.960 | ||
| 4 | 0.968 | 0.989 | ||
| 5 | 0.910 | 0.968 | ||
| 6 | 0.879 | 0.992 | ||
| 7 | 0.960 | 0.983 | ||
| 8 | 0.946 | 0.984 | ||
| 9 | 0.894 | 0.981 | ||
| 10 | 0.916 | 0.985 | ||
| 11 | 0.952 | 0.986 | ||
| 12 | 0.956 | 0.985 | ||
| 13 | 0.966 | 0.983 | ||
| 14 | 0.926 | 0.965 | ||
| 15 | 0.924 | 0.969 | ||
| 16 | 0.979 | 0.995 |
| Test | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| R2 | 0.961 | 0.961 | 0.947 | 0.988 | 0.966 | 0.973 | 0.982 | 0.984 |
| Test | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| R2 | 0.971 | 0.98 | 0.986 | 0.985 | 0.981 | 0.965 | 0.968 | 0.992 |
| Test | Incidence Angle of 75° | Incidence Angle of 60° | Incidence Angle of 45° | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.87 | 0.49 | 0.48 | 0.992 | 0.82 | 0.48 | 0.45 | 0.992 | 0.65 | 0.52 | 0.57 | 0.972 |
| 2 | 0.55 | 0.54 | 0.47 | 0.990 | 0.50 | 0.35 | 0.56 | 0.994 | 0.35 | 0.62 | 0.56 | 0.970 |
| 3 | 0.41 | 0.53 | 0.43 | 0.979 | 0.33 | 0.48 | 0.55 | 0.992 | 0.26 | 0.46 | 0.55 | 0.939 |
| 4 | 0.36 | 0.52 | 0.44 | 0.995 | 0.34 | 0.49 | 0.52 | 0.987 | 0.29 | 0.38 | 0.81 | 0.979 |
| 5 | 1.06 | 0.50 | 0.50 | 0.996 | 1.07 | 0.49 | 0.45 | 0.985 | 0.76 | 0.51 | 0.56 | 0.978 |
| 6 | 0.67 | 0.48 | 0.47 | 0.993 | 0.65 | 0.52 | 0.52 | 0.976 | 0.43 | 0.54 | 0.57 | 0.967 |
| 7 | 0.52 | 0.57 | 0.42 | 0.977 | 0.44 | 0.43 | 0.55 | 0.972 | 0.33 | 0.94 | 0.57 | 0.959 |
| 8 | 0.45 | 0.53 | 0.43 | 0.991 | 0.46 | 0.48 | 0.53 | 0.984 | 0.36 | 0.25 | 0.79 | 0.983 |
| 9 | 1.25 | 0.50 | 0.49 | 0.990 | 1.26 | 0.49 | 0.44 | 0.956 | 0.82 | 0.50 | 0.53 | 0.958 |
| 10 | 0.77 | 0.49 | 0.49 | 0.993 | 0.76 | 0.51 | 0.53 | 0.983 | 0.46 | 0.51 | 0.55 | 0.973 |
| 11 | 0.59 | 0.23 | 0.40 | 0.962 | 0.48 | 0.69 | 0.59 | 0.974 | 0.36 | 0.59 | 0.62 | 0.949 |
| 12 | 0.53 | 0.54 | 0.46 | 0.982 | 0.54 | 0.47 | 0.53 | 0.984 | 0.42 | 0.41 | 0.63 | 0.982 |
| 13 | 1.26 | 0.51 | 0.53 | 0.992 | 1.48 | 0.50 | 0.48 | 0.952 | 0.62 | 0.51 | 0.56 | 0.980 |
| 14 | 0.78 | 0.48 | 0.44 | 0.982 | 0.81 | 0.52 | 0.58 | 0.977 | 0.48 | 0.53 | 0.60 | 0.988 |
| 15 | 0.62 | 0.36 | 0.40 | 0.959 | 0.50 | 0.58 | 0.60 | 0.972 | 0.34 | 0.55 | 0.61 | 0.973 |
| 16 | 0.45 | 0.33 | 0.58 | 0.991 | 0.53 | 0.32 | 0.51 | 0.976 | 0.45 | 0.80 | 0.73 | 0.981 |
| Test | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| θ | 75° | 0.988 | 0.985 | 0.991 | 0.983 | 0.995 | 0.988 | 0.957 | 0.973 |
| 60° | 0.981 | 0.993 | 0.964 | 0.987 | 0.985 | 0.976 | 0.972 | 0.984 | |
| 45° | 0.971 | 0.969 | 0.938 | 0.925 | 0.977 | 0.965 | 0.957 | 0.935 | |
| Test | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| θ | 75° | 0.987 | 0.991 | 0.933 | 0.974 | 0.992 | 0.969 | 0.927 | 0.987 |
| 60° | 0.944 | 0.983 | 0.971 | 0.984 | 0.947 | 0.975 | 0.967 | 0.942 | |
| 45° | 0.958 | 0.973 | 0.940 | 0.924 | 0.980 | 0.982 | 0.966 | 0.963 | |
| Incidence Angle (°) | Wel | Wea | |||
|---|---|---|---|---|---|
| 418.02 | 819.19 | 1354.22 | 1914.09 | ||
| 45 | 36.82 | 117.55 | 86.28 | 44.25 | 22.26 |
| 147.28 | 127.27 | 73.25 | 33.30 | 27.37 | |
| 331.39 | 137.25 | 59.58 | 36.37 | 19.28 | |
| 589.13 | 125.97 | 62.35 | 39.24 | 16.58 | |
| 60 | 36.82 | 75.65 | 32.87 | 16.74 | 14.35 |
| 147.28 | 64.76 | 26.21 | 17.56 | 15.37 | |
| 331.39 | 58.91 | 39.07 | 17.17 | 14.26 | |
| 589.13 | 59.74 | 36.81 | 30.38 | 16.37 | |
| 75 | 36.82 | 67.54 | 34.26 | 21.25 | 12.85 |
| 147.28 | 57.26 | 23.25 | 19.57 | 16.59 | |
| 331.39 | 72.25 | 27.26 | 16.36 | 14.29 | |
| 589.13 | 50.27 | 32.59 | 20.17 | 17.64 | |
| 90 | 36.82 | 29.93 | 18.39 | 16.89 | 14.36 |
| 147.28 | 50.83 | 29.17 | 17.12 | 16.85 | |
| 331.39 | 44.95 | 30.64 | 17.23 | 15.26 | |
| 589.13 | 37.68 | 27.73 | 17.66 | 14.37 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, M.; Dai, S.; Ye, R.; Ou, M.; Wang, G.; Hu, C.; Fan, X.; Jia, W. Experimental Study of Liquid Jet Atomization and Penetration in Subsonic Crossflows. Agriculture 2025, 15, 1037. https://doi.org/10.3390/agriculture15101037
Wu M, Dai S, Ye R, Ou M, Wang G, Hu C, Fan X, Jia W. Experimental Study of Liquid Jet Atomization and Penetration in Subsonic Crossflows. Agriculture. 2025; 15(10):1037. https://doi.org/10.3390/agriculture15101037
Chicago/Turabian StyleWu, Minmin, Shiqun Dai, Rui Ye, Mingxiong Ou, Guanqun Wang, Chao Hu, Xurui Fan, and Weidong Jia. 2025. "Experimental Study of Liquid Jet Atomization and Penetration in Subsonic Crossflows" Agriculture 15, no. 10: 1037. https://doi.org/10.3390/agriculture15101037
APA StyleWu, M., Dai, S., Ye, R., Ou, M., Wang, G., Hu, C., Fan, X., & Jia, W. (2025). Experimental Study of Liquid Jet Atomization and Penetration in Subsonic Crossflows. Agriculture, 15(10), 1037. https://doi.org/10.3390/agriculture15101037





