Combining Multitemporal Sentinel-2A Spectral Imaging and Random Forest to Improve the Accuracy of Soil Organic Matter Estimates in the Plough Layer for Cultivated Land
Abstract
1. Introduction
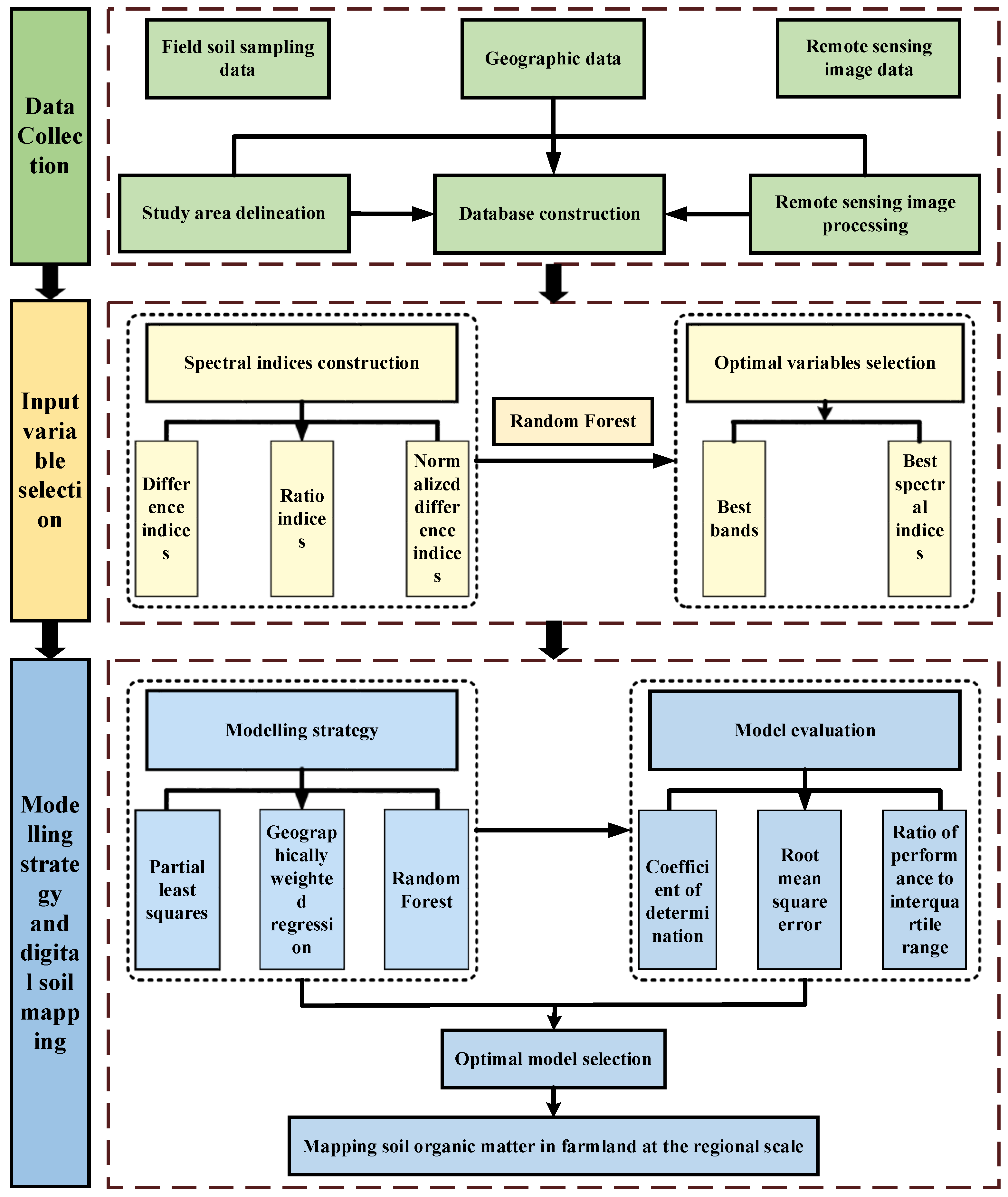
2. Materials and Methods
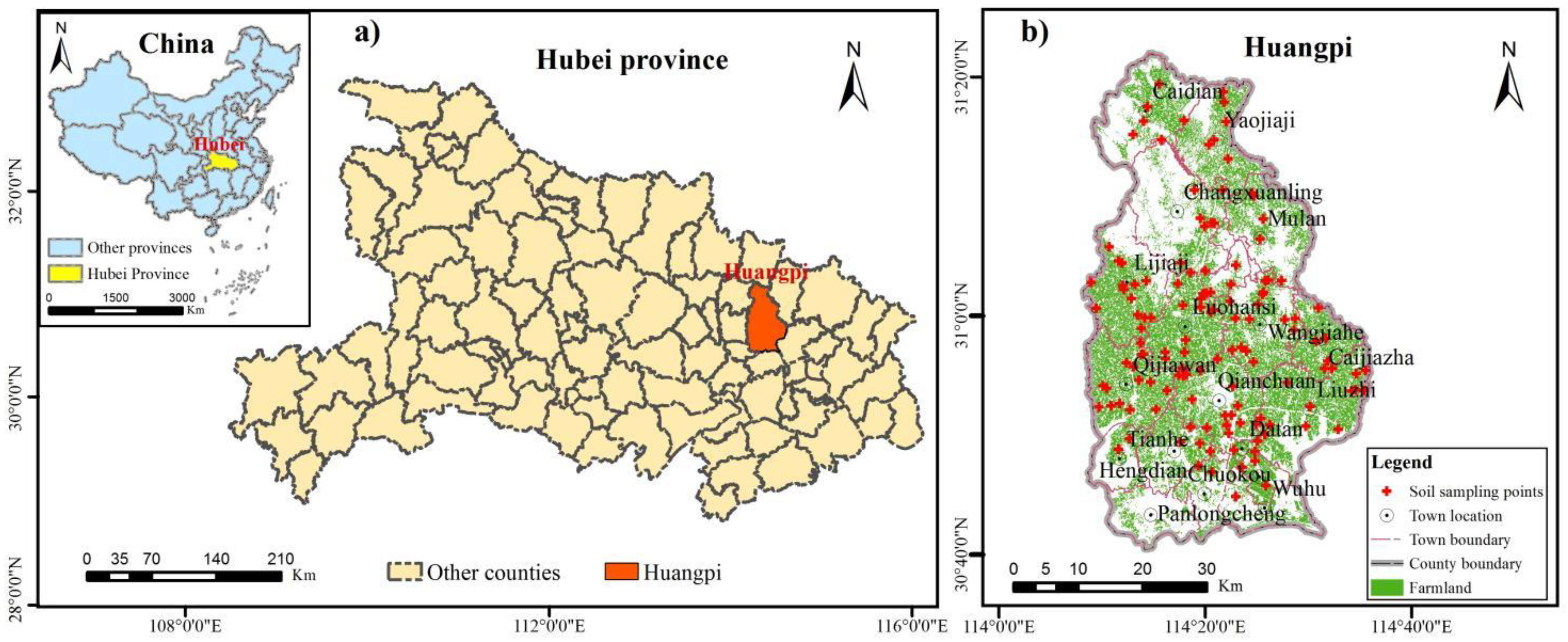
2.1. Study Area
2.2. Soil Sampling and Analysis
2.3. Satellite Remote Sensing Image Collection and Processing
2.4. Spectral Indices Construction
2.5. Optimal Variables Selection
2.6. Modelling Strategy
2.6.1. Partial Least Squares
2.6.2. Geographically Weighted Regression
2.6.3. Random Forest
2.7. Statistical Analysis and Model Evaluation
3. Results
3.1. SOM Content of the Soil Sampling Points
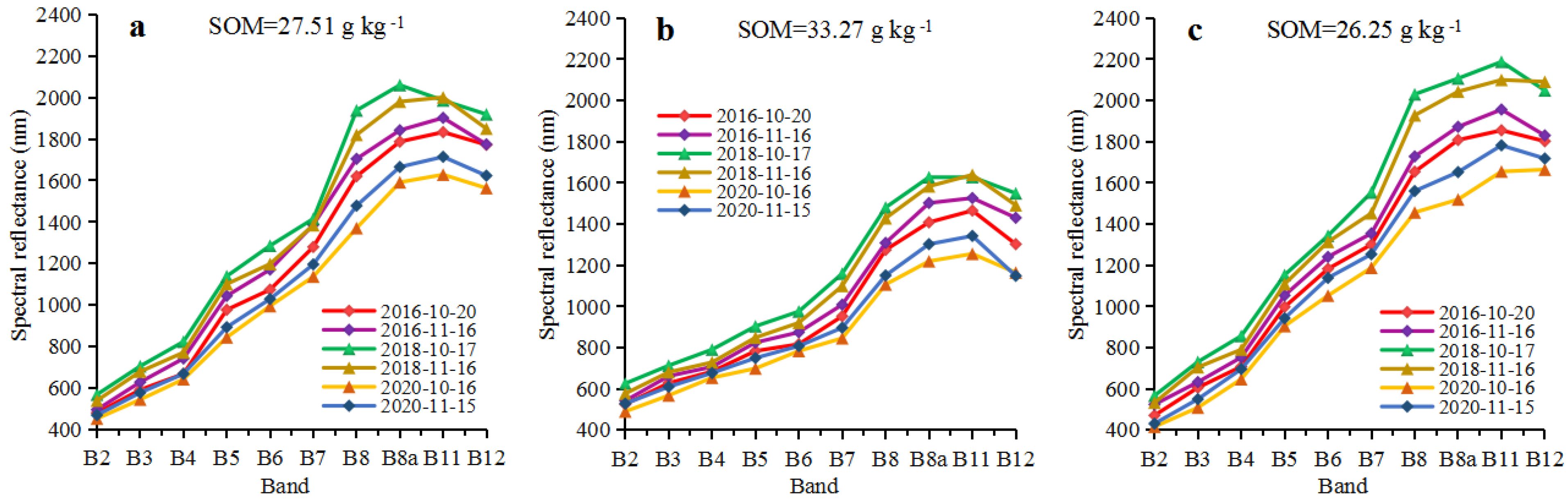
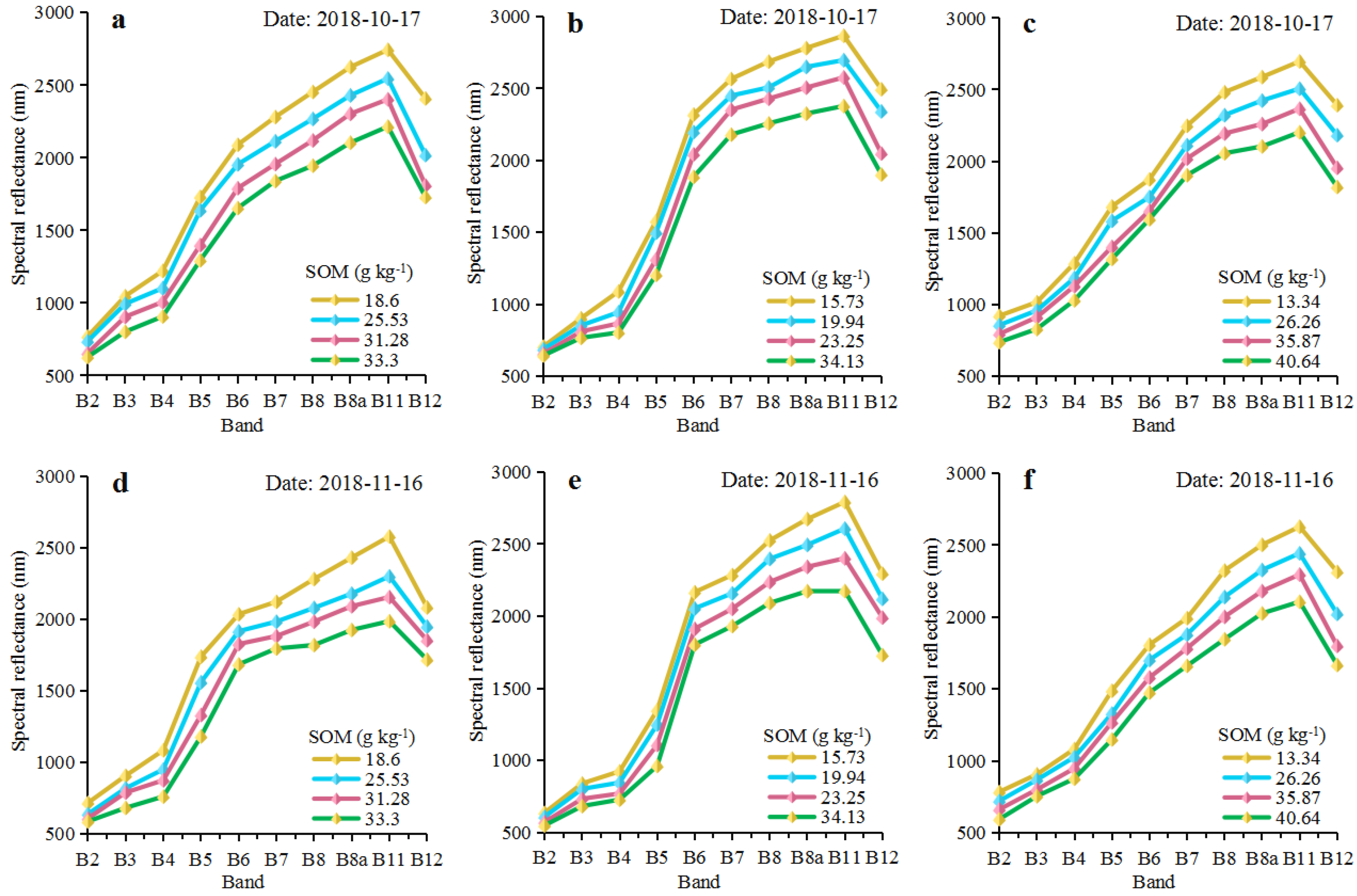
3.2. Characterization of the Soil Spectral Reflectance from Satellite Images
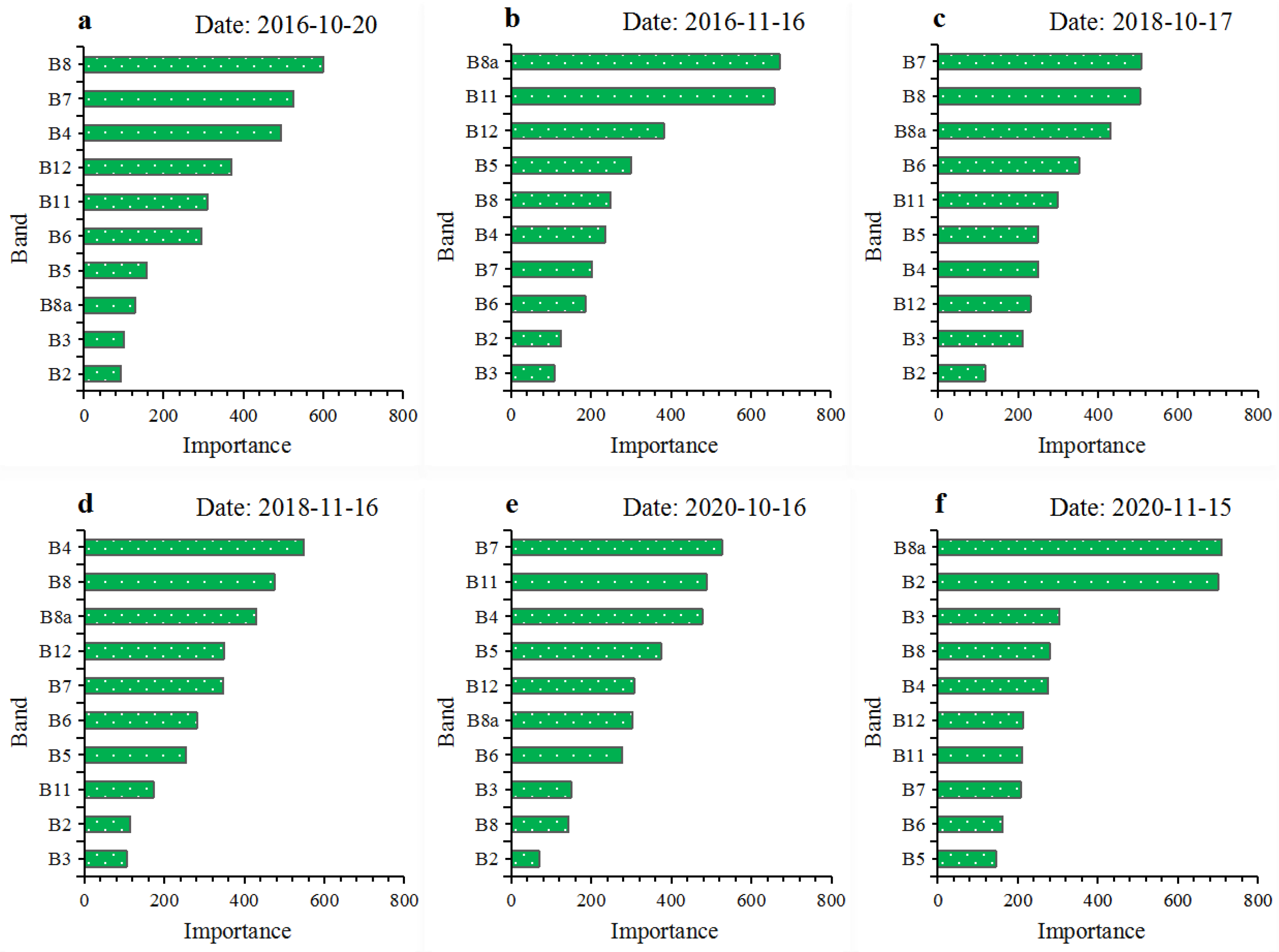
3.3. Selection of the Optimal Prediction Variables
3.3.1. Optimal Prediction Variables for the Single-Temporal Images
3.3.2. Optimal Prediction Variables for the Double-Temporal Images
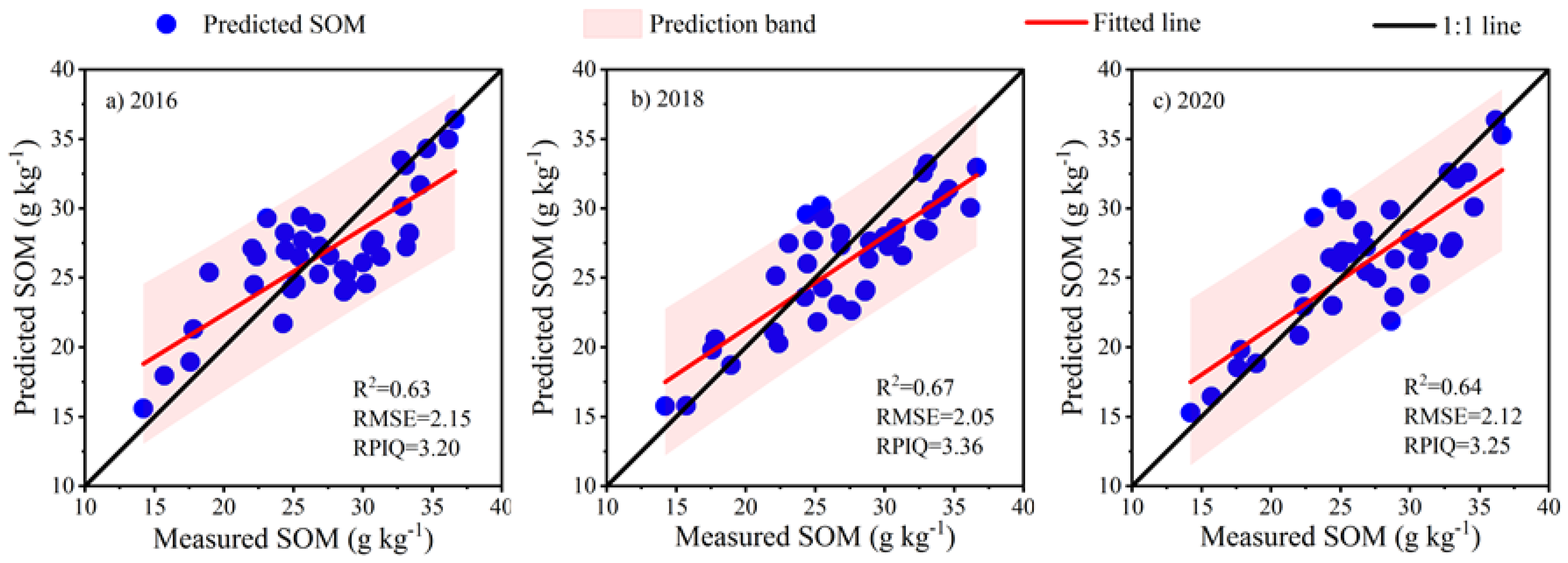
3.4. Analysis of the SOM Estimation Model for the Single-Temporal Images
3.5. Analysis of the SOM Estimation Model for the Double-Temporal Images
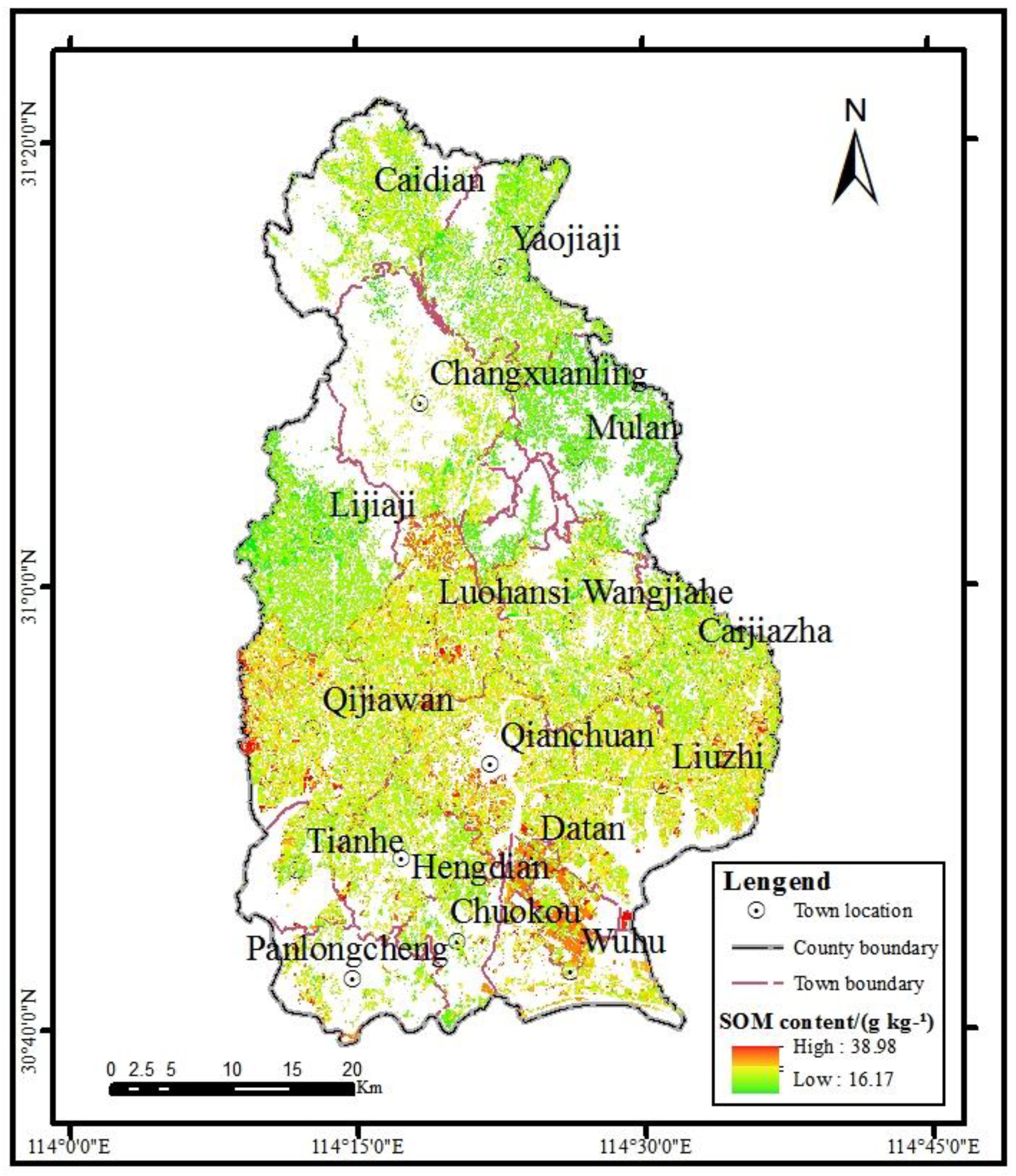
3.6. SOM Mapping in the Plough Layer for the Cultivated Land throughout the Study Area
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Wu, C.; Liu, G.; Huang, C.; Liu, Q. Soil Quality Assessment in Yellow River Delta: Establishing a Minimum Data Set and Fuzzy Logic Model. Geoderma 2019, 334, 82–89. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, X.; Wang, Y.; Men, Z.; Liu, H. Regional Soil Organic Matter Mapping Models Based on the Optimal Time Window, Feature Selection Algorithm and Google Earth Engine. Soil Tillage Res. 2022, 219, 105325. [Google Scholar] [CrossRef]
- Lin, L.; Han, S.; Zhao, P.; Li, L.; Zhang, C.; Wang, E. Influence of Soil Physical and Chemical Properties on Mechanical Characteristics under Different Cultivation Durations with Mollisols. Soil Tillage Res. 2022, 224, 105520. [Google Scholar] [CrossRef]
- Bradford, M.; Wood, S.; Addicott, E.; Fenichel, E.; Fields, N.; Gonzlez-Rivero, J.; Jevon, F.; Maynard, D.; Oldfield, E.; Polussa, A.; et al. Quantifying Microbial Control of Soil Organic Matter Dynamics at Macrosystem Scales. Biogeochemistry 2021, 156, 19–40. [Google Scholar] [CrossRef]
- Buckeridge, K.; Creamer, C.; Whitaker, J. Deconstructing the Microbial Necromass Continuum to Inform Soil Carbon Sequestration. Funct. Ecol. 2022, 36, 1396–1410. [Google Scholar] [CrossRef]
- Liu, J.; Xie, J.; Meng, T.; Dong, H. Organic Matter Estimation of Surface Soil Using Successive Projection Algorithm. Agron. J. 2022, 114, 1944–1951. [Google Scholar] [CrossRef]
- Lu, M.; Liu, Y.; Liu, G. Precise Prediction of Soil Organic Matter in Soils Planted with a Variety of Crops through Hybrid Methods. Comput. Electron. Agric. 2022, 200, 107246. [Google Scholar] [CrossRef]
- Wang, Z.; Du, Z.; Li, X.; Bao, Z.; Zhao, N.; Yue, T. Incorporation of High Accuracy Surface Modeling into Machine Learning to Improve Soil Organic Matter Mapping. Ecol. Indic. 2021, 129, 107975. [Google Scholar] [CrossRef]
- Song, Y.Q.; Yang, L.A.; Li, B.; Hu, Y.M.; Wang, A.L.; Zhou, W.; Cui, X.S.; Liu, Y.L. Spatial Prediction of Soil Organic Matter Using a Hybrid Geostatistical Model of an Extreme Learning Machine and Ordinary Kriging. Sustainability 2017, 9, 754. [Google Scholar] [CrossRef]
- Hong, Y. Application of Fractional-Order Derivative in the Quantitative Estimation of Soil Organic Matter Content through Visible and near-Infrared Spectroscopy. Geoderma 2018, 337, 758–769. [Google Scholar] [CrossRef]
- Asrar, G. Theory and Applications of Optical Remote Sensing. Trans. Inst. Br. Geogr. 1989, 18, 159–160. [Google Scholar]
- Zhai, M. Inversion of Organic Matter Content in Wetland Soil Based on Landsat 8 Remote Sensing Image. J. Vis. Commun. Image Represent. 2019, 64, 102645. [Google Scholar] [CrossRef]
- Fu, C.; Xiong, H.; Tian, A. Study on the Effect of Fractional Derivative on the Hyperspectral Data of Soil Organic Matter Content in Arid Region. J. Spectrosc. 2019, 2019, 7159317. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Sun, Q.; Yang, G.; Zhang, C. Hyperspectral Inversion of Soil Organic Matter Content in Cultivated Land Based on Wavelet Transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Sun, M.; Li, Q.; Jiang, X.; Ye, T.; Li, X.; Niu, B. Estimation of Soil Salt Content and Organic Matter on Arable Land in the Yellow River Delta by Combining UAV Hyperspectral and Landsat-8 Multispectral Imagery. Sensors 2022, 22, 3990. [Google Scholar] [CrossRef]
- Castaldi, F.; Casa, R.; Castrignano, A.; Pascucci, S.; Palombo, A.; Pignatti, S. Estimation of Soil Properties at the Field Scale from Satellite Data: A Comparison between Spatial and Non-Spatial Techniques. Eur. J. Soil Sci. 2014, 65, 842–851. [Google Scholar] [CrossRef]
- Li, X.; Zhang, F.; Wang, X.P. Study on Differential-Based Multispectral Modeling of Soil Organic Matter in Ebinur Lake Wetland. Spectrosc. Spectr. Anal. 2019, 039, 535–542. [Google Scholar]
- Wang, X.; Zhang, F.; Kung, H.T.; Johnson, V.C. New Methods for Improving the Remote Sensing Estimation of Soil Organic Matter Content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in Northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, M.; Yang, H.; Zhang, X.; Meng, X.; Li, H.; Tang, H. Invertion of Cultivated Soil Organic Matter Content Combining Multi-Spectral Remote Sensing and Random Forest Algorithm. Trans. Chin. Soc. Agric. Eng. 2020, 36, 134–140. [Google Scholar]
- Dou, X.; Wang, X.; Liu, H.; Zhang, X.; Cui, Y. Prediction of Soil Organic Matter Using Multi-Temporal Satellite Images in the Songnen Plain, China. Geoderma 2019, 356, 113896. [Google Scholar] [CrossRef]
- Yu, Q.; Yao, T.; Lu, H.; Feng, W.; Xue, Y.; Liu, B. Improving Estimation of Soil Organic Matter Content by Combining Landsat 8 OLI Images and Environmental Data: A Case Study in the River Valley of the Southern Qinghai-Tibet Plateau. Comput. Electron. Agric. 2021, 185, 106144. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of Multivariate Methods for Estimating Selected Soil Properties from Intact Soil Cores of Paddy Fields by Vis-NIR Spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Ma, Y.; Jiang, Q.G.; Meng, Z.G.; Liu, H.X. Black Soil Organic Matter Content Estimation Using Hybrid Selection Method Based on RF and GABPSO. Spectrosc. Spectr. Anal. 2018, 38, 181–187. [Google Scholar]
- Xie, S.; Li, Y.; Wang, X.; Liu, Z.; Ma, K.; Ding, L. Research on Estimation Models of the Spectral Characteristics of Soil Organic Matter Based on the Soil Particle Size. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 260, 119963. [Google Scholar] [CrossRef]
- Yang, M.; Xu, D.; Chen, S.; Li, H.; Shi, Z. Evaluation of Machine Learning Approaches to Predict Soil Organic Matter and PH Using Vis-NIR Spectra. Sensors 2019, 19, 263. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Zhang, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Cheng, H.; Liu, Y. Rapid Identification of Soil Organic Matter Level via Visible and Near-Infrared Spectroscopy: Effects of Two-Dimensional Correlation Coefficient and Extreme Learning Machine. Sci. Total Environ. 2018, 644, 1232–1243. [Google Scholar] [CrossRef]
- Chen, D.; Chang, N.; Xiao, J.; Zhou, Q.; Wu, W. Mapping Dynamics of Soil Organic Matter in Croplands with MODIS Data and Machine Learning Algorithms. Sci. Total Environ. 2019, 669, 844–855. [Google Scholar] [CrossRef]
- Zhang, S.; Lu, X.; Nie, G.; Li, Y.; Shao, Y.; Tian, Y.; Fan, L.; Zhang, Y. Estimation of Soil Organic Matter in Coastal Wetlands by SVM and BP Based on Hyperspectral Remote Sensing. Spectrosc. Spectr. Anal. 2020, 40, 556–561. [Google Scholar]
- Jiao, C.; Zheng, G.; Xie, X.; Cui, X.; Shang, G. Prediction of Soil Organic Matter Using Visible-Short Near-Infrared Imaging Spectroscopy. Spectrosc. Spectr. Anal. 2020, 40, 3277–3281. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Q.; Siew, C. Extreme Learning Machine: Theory and Applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Kadiyala, A.; Kumar, A. Applications of Python to Evaluate the Performance of Decision Tree-Based Boosting Algorithms. Environ. Prog. Sustain. Energy 2018, 37, 618–623. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping Soil Organic Matter Contents at Field Level with Cubist, Random Forest and Kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Nowkandeh, S.M.; Noroozi, A.A.; Homaee, M. Estimating Soil Organic Matter Content from Hyperion Reflectance Images Using PLSR, PCR, MinR and SWR Models in Semi-Arid Regions of Iran. Environ. Dev. 2018, 25, 23–32. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Wang, Y.; Zhang, B.; Wang, Z.; Li, L. A Comparative Assessment of Geostatistical, Machine Learning, and Hybrid Approaches for Mapping Topsoil Organic Carbon Content. ISPRS Int. J. Geo-Inf. 2019, 8, 174. [Google Scholar] [CrossRef]
- FAO. World Reference Base for Soil Resources; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total Carbon, Organic Carbon and Organic Matter. In Methods of Soil Analysis: Part 2 Chemical and Microbial Properties; Academic Press: Cambridge, MA, USA, 1982; pp. 552–553. [Google Scholar]
- Zhu, C.; Zhang, Z.; Wang, H.; Wang, J.; Yang, S. Assessing Soil Organic Matter Content in a Coal Mining Area through Spectral Variables of Different Numbers of Dimensions. Sensors 2020, 20, 1795. [Google Scholar] [CrossRef]
- Lin, C.; Zhu, A.; Wang, Z.; Wang, X.; Ma, R. The Refined Spatiotemporal Representation of Soil Organic Matter Based on Remote Images Fusion of Sentinel-2 and Sentinel-3. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102094. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Xie, L.; Li, H.; Yue, T. Hyperspectral Inversion of Soil Heavy Metals in Three-River Source Region Based on Random Forest Model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Scornet, E. Random Forests and Kernel Methods. IEEE Trans. Inf. Theory 2016, 62, 1485–1500. [Google Scholar] [CrossRef]
- Molinaro, A.; Simon, R.; Pfeiffer, R. Prediction Error Estimation: A Comparison of Resampling Methods. Bioinformatics 2005, 21, 3301–3307. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Yang, C.; Zhou, M. Partial Least Squares Improved Multivariate Adaptive Regression Splines for Visible and Near-Infrared-Based Soil Organic Matter Estimation Considering Spatial Heterogeneity. Appl. Sci. 2021, 11, 566. [Google Scholar] [CrossRef]
- Rasoolimanesh, S.M.; Ringle, C.M.; Sarstedt, M.; Olya, H. The Combined Use of Symmetric and Asymmetric Approaches: Partial Least Squares-Structural Equation Modeling and Fuzzy-Set Qualitative Comparative Analysis. Int. J. Contemp. Hosp. Manag. 2021, 33, 1571–1592. [Google Scholar] [CrossRef]
- Sun, W.; Liu, S.; Zhang, X.; Li, Y. Estimation of Soil Organic Matter Content Using Selected Spectral Subset of Hyperspectral Data. Geoderma 2022, 409, 115653. [Google Scholar] [CrossRef]
- Li, H.D.; Xu, Q.S.; Liang, Y.Z. LibPLS: An Integrated Library for Partial Least Squares Regression and Linear Discriminant Analysis. Chemom. Intell. Lab. Syst. 2018, 176, 34–43. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.; Leng, P.; Yang, Q.; Duan, S. Hyperspectral Estimation of Soil Organic Matter Content Using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef]
- Li, Z.; Fotheringham, A.S. Computational Improvements to Multi-Scale Geographically Weighted Regression. Int. J. Geogr. Inf. Sci. 2020, 34, 1378–1397. [Google Scholar] [CrossRef]
- Comber, A. Hyper-Local Geographically Weighted Regression: Extending GWR through Local Model Selection and Local Bandwidth Optimization. J. Spat. Inf. Sci. 2018, 17, 63–84. [Google Scholar] [CrossRef]
- Costa, E.M.; Tassinari, W.; Pinheiro, H.; Beutler, S.J.; Anjos, L.D. Mapping Soil Organic Carbon and Organic Matter Fractions by Geographically Weighted Regression. J. Environ. Qual. 2018, 47, 718–725. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Finke, P. Comparing the Efficiency of Digital and Conventional Soil Mapping to Predict Soil Types in a Semi-Arid Region in Iran. Geomorphology 2017, 285, 186–204. [Google Scholar] [CrossRef]
- Zhang, X.; Dou, X.; Xie, Y.; Liu, H.; Wang, N.; Wang, X.; Pan, Y. Remote Sensing Inversion Model of Soil Organic Matter in Farmland by Introducing Temporal Information. Trans. Chin. Soc. Agric. Eng. 2018, 34, 143–151. [Google Scholar]
- Bao, Y.; Meng, X.; Ustin, S.; Wang, X.; Tang, H. Vis-SWIR Spectral Prediction Model for Soil Organic Matter with Different Grouping Strategies. Catena 2020, 195, 104703. [Google Scholar] [CrossRef]
- Said, E.; Baroudy, A.; El-Beshbeshy, T.; Emam, M.; Lasaponara, R. Vis-NIR Spectroscopy and Satellite Landsat-8 OLI Data to Map Soil Nutrients in Arid Conditions: A Case Study of the Northwest Coast of Egypt. Remote Sens. 2020, 12, 3716. [Google Scholar]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Zhang, X. Remote Sensing of the Terrestrial Carbon Cycle: A Review of Advances over 50 Years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Chen, S.; Zou, S.; Mao, Y.; Liang, W.; Ding, H. Inversion of Soil Organic Matter Content in Wetland Using Multispectral Data Based on Soil Spectral Reconstruction. Spectrosc. Spectr. Anal. 2018, 38, 912–917. [Google Scholar]
- Qiao, M.; He, X.; Cheng, X.; Li, P.; Luo, H.; Zhang, L.; Tian, Z. Crop Yield Prediction from Multi-Spectral, Multi-Temporal Remotely Sensed Imagery Using Recurrent 3D Convolutional Neural Networks. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102436. [Google Scholar] [CrossRef]
- Biney, J.K.M.; Saberioon, M.; Boruvka, L.; Houska, J.; Vasat, R.; Chapman Agyeman, P.; Coblinski, J.A.; Klement, A. Exploring the Suitability of UAS-Based Multispectral Images for Estimating Soil Organic Carbon: Comparison with Proximal Soil Sensing and Spaceborne Imagery. Remote Sens. 2021, 13, 308. [Google Scholar] [CrossRef]
- Xie, S.; Ding, F.; Chen, S.; Wang, X.; Li, Y.; Ma, K. Prediction of Soil Organic Matter Content Based on Characteristic Band Selection Method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 273, 120949. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Liu, H.; Song, K.; Wang, L.; Meng, X. Prediction of Soil Organic Matter Using VNIR Spectral Parameters Extracted from Shape Characteristics. Soil Tillage Res. 2022, 216, 105241. [Google Scholar] [CrossRef]
- Jin, X.; Song, K.; Du, J.; Liu, H.; Wen, Z. Comparison of Different Satellite Bands and Vegetation Indices for Estimation of Soil Organic Matter Based on Simulated Spectral Configuration. Agric. For. Meteorol. 2017, 244, 57–71. [Google Scholar] [CrossRef]
- Tang, S.; Du, C.; Nie, T. Inversion Estimation of Soil Organic Matter in Songnen Plain Based on Multispectral Analysis. Land 2022, 11, 608. [Google Scholar] [CrossRef]
- Tziachris, P.; Aschonitis, V.; Chatzistathis, T.; Papadopoulou, M. Assessment of Spatial Hybrid Methods for Predicting Soil Organic Matter Using DEM Derivatives and Soil Parameters. Catena 2019, 174, 206–216. [Google Scholar] [CrossRef]
- Nikou, M.; Tziachris, P. Prediction and Uncertainty Capabilities of Quantile Regression Forests in Estimating Spatial Distribution of Soil Organic Matter. ISPRS Int. J. Geo-Inf. 2022, 11, 130. [Google Scholar] [CrossRef]
| Soil Spectral Indices Computed Using Single-Temporal Images | Equation | Soil Spectral Indices Computed Using Multi-Temporal Images | Equation |
|---|---|---|---|
| Dataset | Number | Min | Max | Median | 1st Qu a | 3rd Qu b | Mean | SDc | CV (%) d | SKe | KUf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Whole dataset | 134 | 13.79 | 40.64 | 25.55 | 21.56 | 30.06 | 25.86 | 5.84 | 22.58 | 0.18 | −0.41 |
| Calibration dataset | 94 | 13.79 | 40.64 | 25.14 | 20.55 | 28.56 | 25.30 | 5.89 | 23.29 | 0.43 | −0.12 |
| Validation dataset | 40 | 14.20 | 36.63 | 27.24 | 24.28 | 31.17 | 27.18 | 5.56 | 20.47 | −0.45 | −0.27 |
| Year | Single Band | Spectral Indices | |
|---|---|---|---|
| 2016 | Variables | B8_1020, B11_1116, B8a_1116, B7_1020, B4_1020, B12_1020, B11_1020 | D1020-1116_48a, R1020-1116_411, ND1020-1116_411 |
| Importance | 410.53 328.09, 306.77, 272.36, 256.80, 173.78, 156.68 | 80.30, 61.39, 57.65 | |
| 2018 | Variables | B8_1017, B6_1017, B7_1017, B4_1116, B8a_1017, B11_1017, B5_1017 | D1116-1017_48, D1017-1116_74, D1116-1017_411 |
| Importance | 444.74, 397.53, 394.66, 337.85, 277.09, 211.02, 195.84 | 63.82, 49.69, 48.22 | |
| 2020 | Variables | B11_1016, B8_1115, B7_1016, B4_1016, B5_1016, B8a_1016, B4_1115 | D1115-1016_84, D1115-1016_47, D1016-1115_48 |
| Importance | 361.97, 334.69, 333.94, 296.43, 278.03, 226.30, 210.70 | 65.64, 43.06, 41.89 | |
| Modelling Strategies | Year | Full Spectrum | Optimum Bands and Spectral Indices | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | ||||||||
| R2cal | RMSEcal | R2val | RMSEval | RPIQval | R2cal | RMSEcal | R2val | RMSEval | RPIQval | ||
| PLS | 2016 | 0.43 | 2.84 | 0.40 | 2.91 | 2.13 | 0.54 | 2.53 | 0.47 | 2.89 | 2.38 |
| 2018 | 0.49 | 2.55 | 0.45 | 2.74 | 2.26 | 0.61 | 2.26 | 0.53 | 2.43 | 2.83 | |
| 2020 | 0.47 | 2.66 | 0.44 | 2.83 | 2.19 | 0.57 | 2.46 | 0.51 | 2.51 | 2.74 | |
| GWR | 2016 | 0.51 | 2.67 | 0.48 | 2.57 | 2.42 | 0.60 | 2.27 | 0.56 | 2.42 | 2.85 |
| 2018 | 0.54 | 2.54 | 0.50 | 2.79 | 2.47 | 0.63 | 2.16 | 0.59 | 2.37 | 2.91 | |
| 2020 | 0.52 | 2.67 | 0.50 | 2.76 | 2.49 | 0.61 | 2.27 | 0.58 | 2.35 | 2.93 | |
| RF | 2016 | 0.59 | 2.31 | 0.53 | 2.39 | 2.88 | 0.65 | 2.08 | 0.63 | 2.15 | 3.20 |
| 2018 | 0.61 | 2.1 | 0.55 | 2.28 | 3.02 | 0.68 | 1.89 | 0.67 | 2.05 | 3.36 | |
| 2020 | 0.59 | 2.2 | 0.54 | 2.16 | 3.19 | 0.66 | 1.98 | 0.64 | 2.12 | 3.25 | |
| Contents/(g kg−1) | Area/km2 | Percentage/% |
|---|---|---|
| 16.17~22.47 | 96.28 | 10.14 |
| 22.47~25.36 | 230.46 | 24.27 |
| 25.36~28.12 | 388.53 | 40.91 |
| 28.12~32.50 | 147.31 | 15.51 |
| 32.50~38.98 | 87.08 | 9.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhou, Y. Combining Multitemporal Sentinel-2A Spectral Imaging and Random Forest to Improve the Accuracy of Soil Organic Matter Estimates in the Plough Layer for Cultivated Land. Agriculture 2023, 13, 8. https://doi.org/10.3390/agriculture13010008
Wang L, Zhou Y. Combining Multitemporal Sentinel-2A Spectral Imaging and Random Forest to Improve the Accuracy of Soil Organic Matter Estimates in the Plough Layer for Cultivated Land. Agriculture. 2023; 13(1):8. https://doi.org/10.3390/agriculture13010008
Chicago/Turabian StyleWang, Li, and Yong Zhou. 2023. "Combining Multitemporal Sentinel-2A Spectral Imaging and Random Forest to Improve the Accuracy of Soil Organic Matter Estimates in the Plough Layer for Cultivated Land" Agriculture 13, no. 1: 8. https://doi.org/10.3390/agriculture13010008
APA StyleWang, L., & Zhou, Y. (2023). Combining Multitemporal Sentinel-2A Spectral Imaging and Random Forest to Improve the Accuracy of Soil Organic Matter Estimates in the Plough Layer for Cultivated Land. Agriculture, 13(1), 8. https://doi.org/10.3390/agriculture13010008






