An Aquatic Product Price Forecast Model Using VMD-IBES-LSTM Hybrid Approach
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Variational Modal Decomposition
3.2. Bald Eagle Search Algorithm (BES)
- Select the search space.
- Search for prey in a selected space.
- Swoop to capture prey.
3.3. Improved Bald Eagle Search Algorithm (IBES)
- (1)
- Population initialization strategy based on Tent mapping.
- (2)
- Local search strategy based on levy flight.
- Set the parameters of the algorithm. The parameters that are initially set are mainly the number of populations, the maximum number of iterations T, the dimension D, the upper limit UB, and the lower limit LB of the solution space.
- Initialize the population using the Tent mapping strategy, the maximum number of iterations and other parameters.
- Calculate the fitness values and rank them.
- Select the search space.
- Search for prey in the selected space.
- Swoop to capture prey.
- Calculate fitness values and update bald eagle position.
- Calculate the inertia weighting factors and use roulette wheel selection to levy flight variation on the selected individual sparrows.
- Determine whether the stopping condition is satisfied. Exit and output the results if the stopping condition is met, otherwise, repeat Steps 2–9.
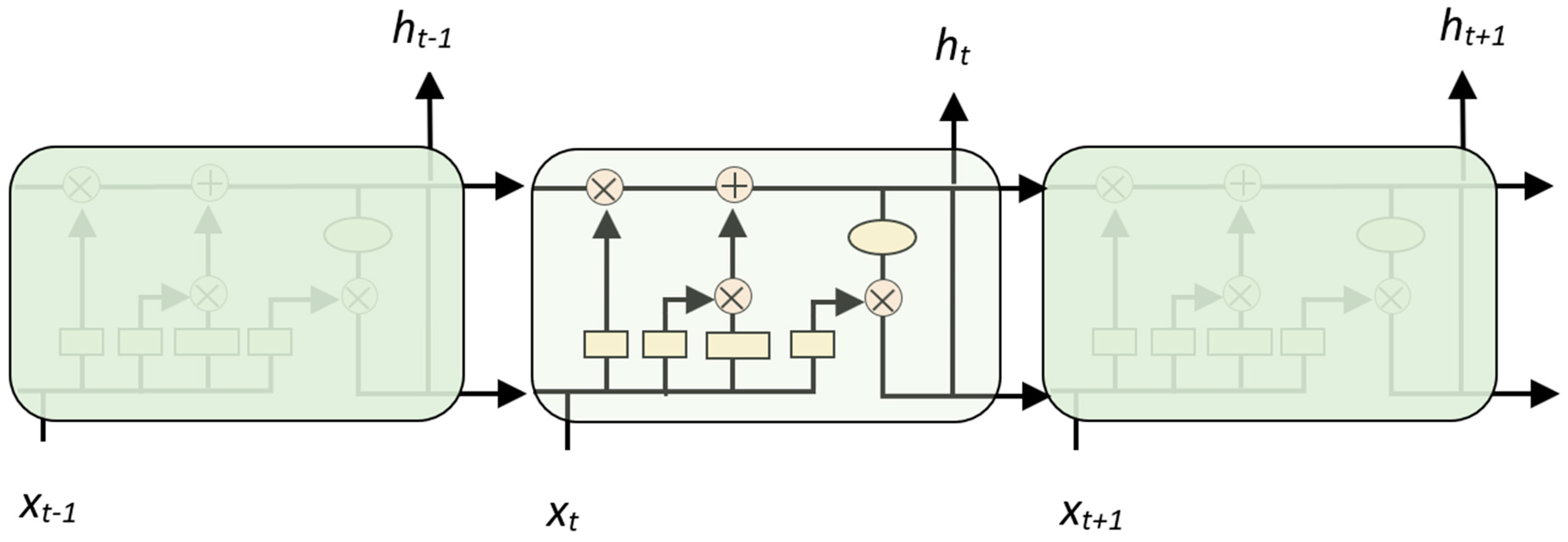
3.4. LSTM
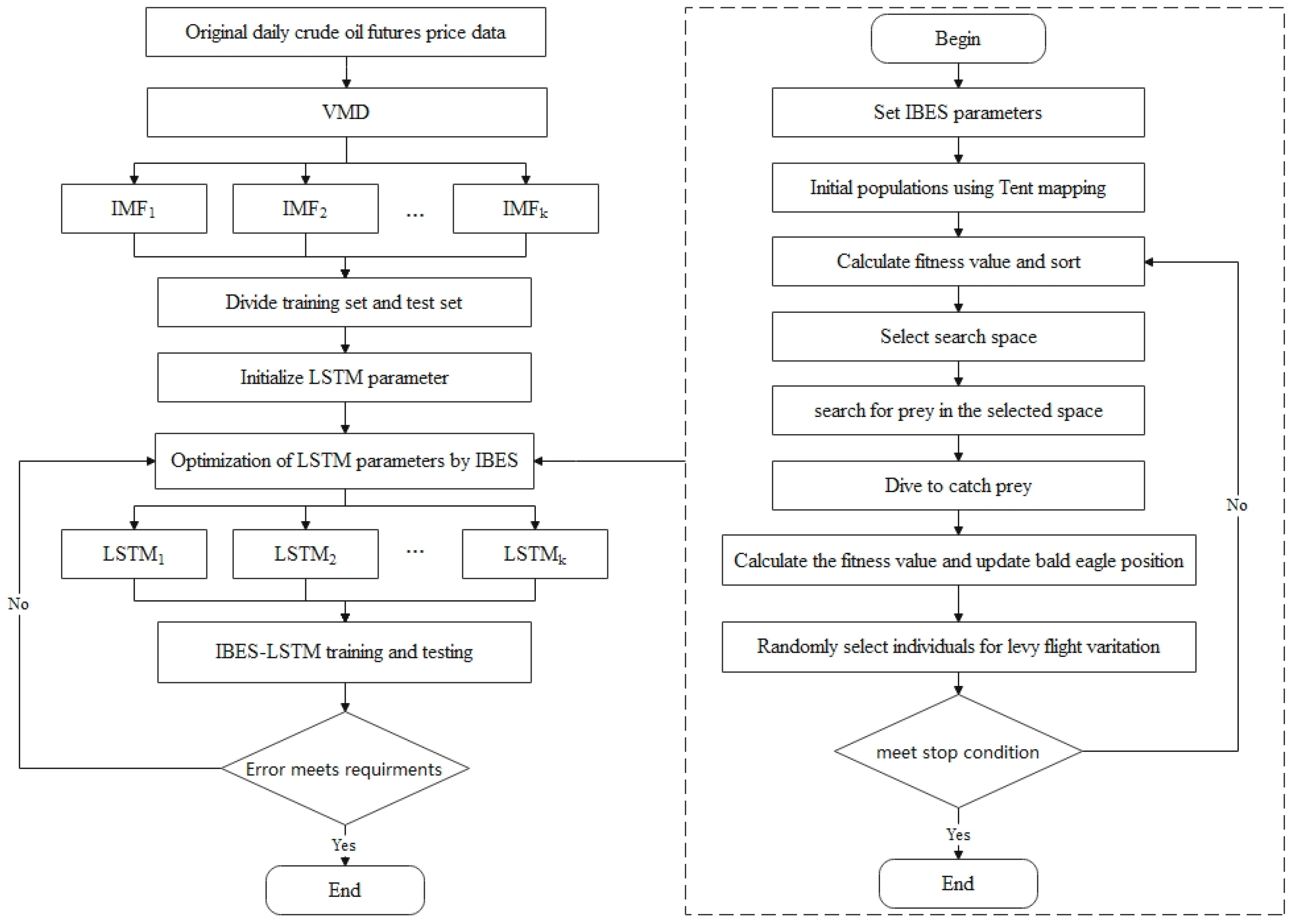
3.5. Hybrid Model of Aquatic Products Prices Forecasting
- The data pre-processing stage. First, the original aquatic product time series with strong non-linearity is decomposed into a series of IMF components using variational modal decomposition.
- Optimization based on IBES. The time window step, the number of hidden layer units, the learning rate and the number of training times in the LSTM model are used as the optimization objects of the improved bald eagle search algorithm, and the parameters of the IBES algorithm (maximum number of iterations, number of populations, upper limit, lower limit, etc.) are initialized.
- Use the hybrid model to do prediction and evaluation. The LSTM network model is constructed using the optimal time window step, number of hidden layer units, learning rate and training times, and the model is trained and subsequently predicted for the test set.
- The prediction results that are obtained from the sub-series test set are added by simple linear summation to obtain the final prediction results. The flow chat is shown below (Figure 2).
3.6. Error Evaluation Criteria
4. Computational Experiments and Analyses
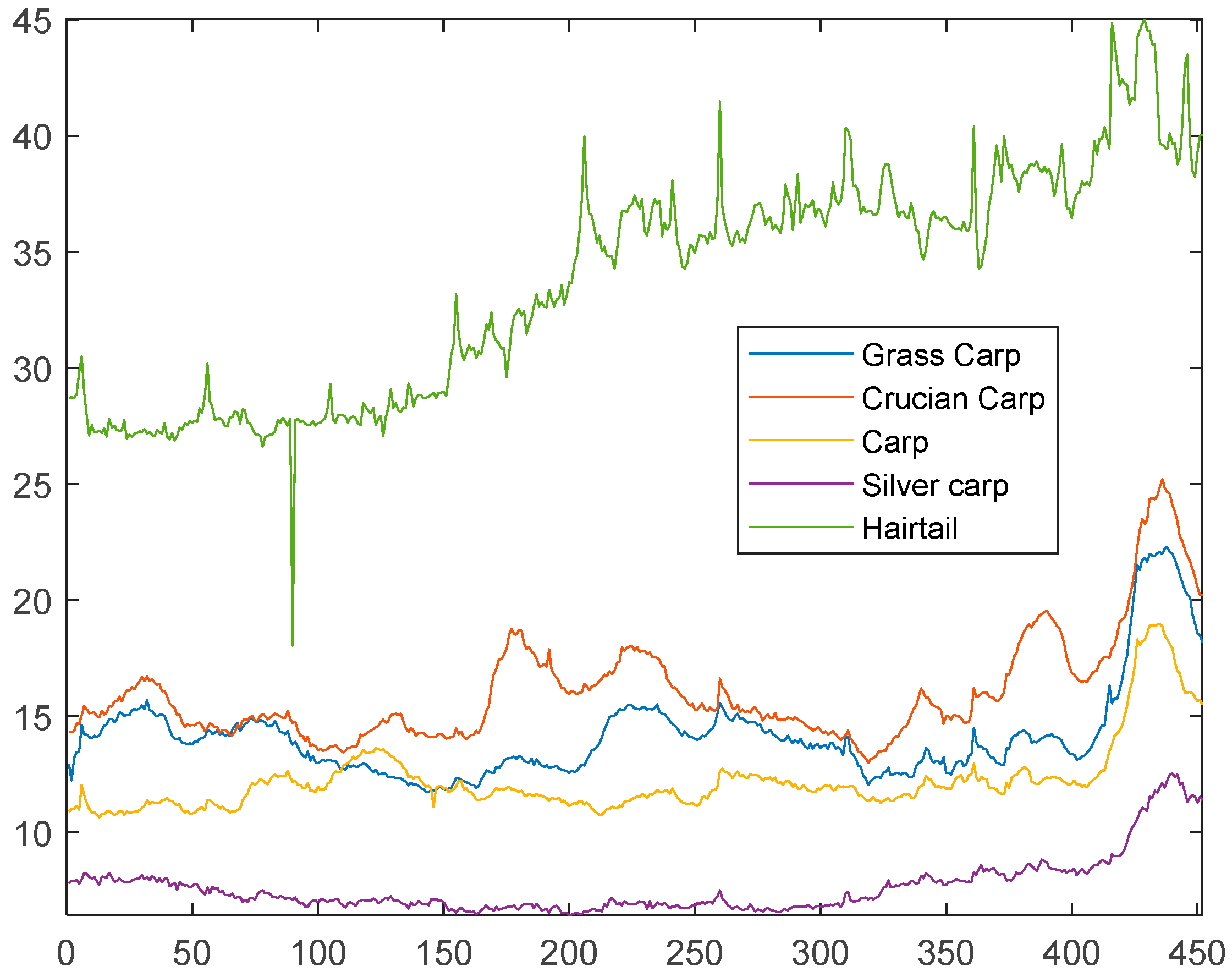
4.1. Data Source and Descriptive Analysis
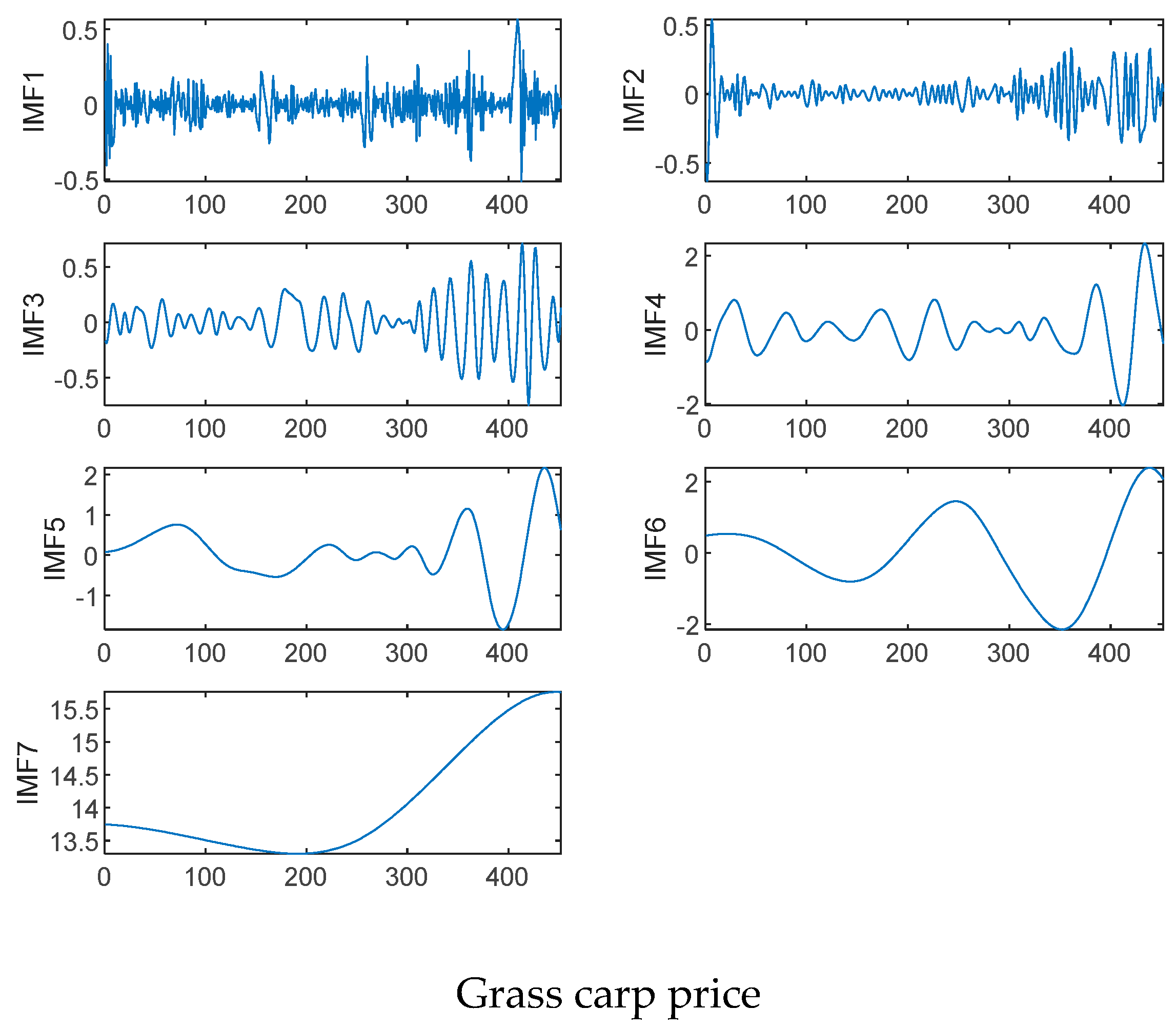
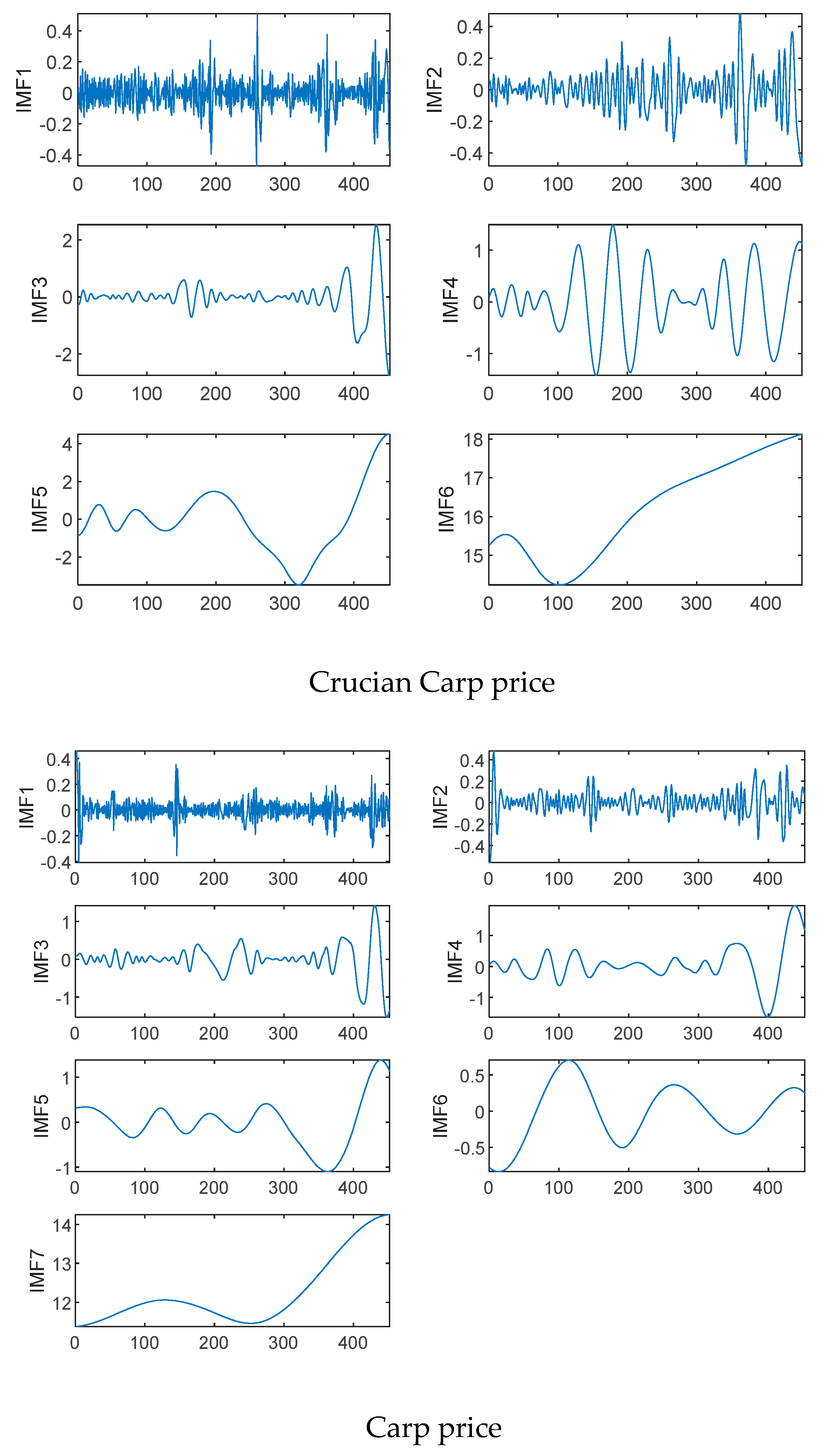
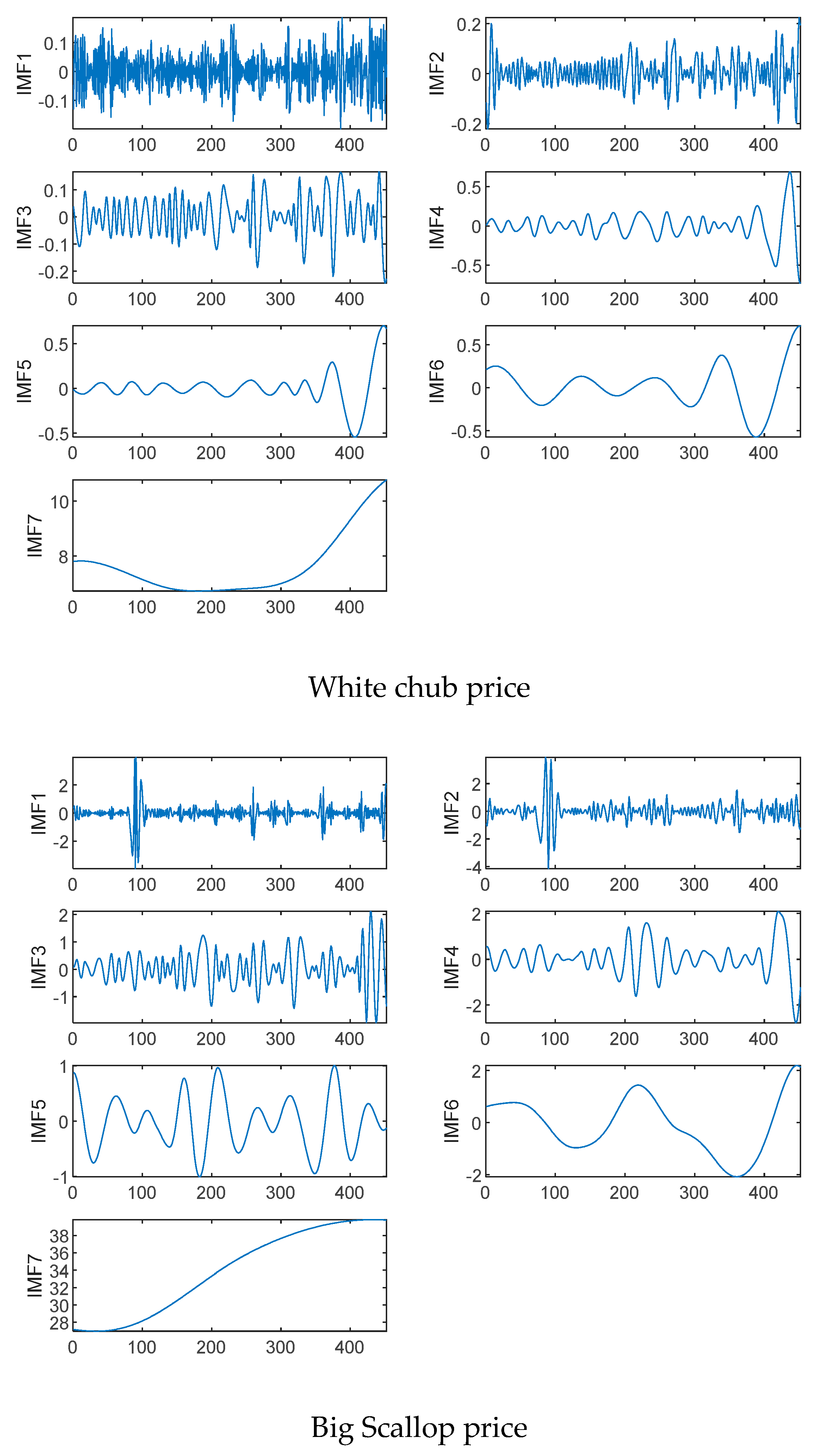
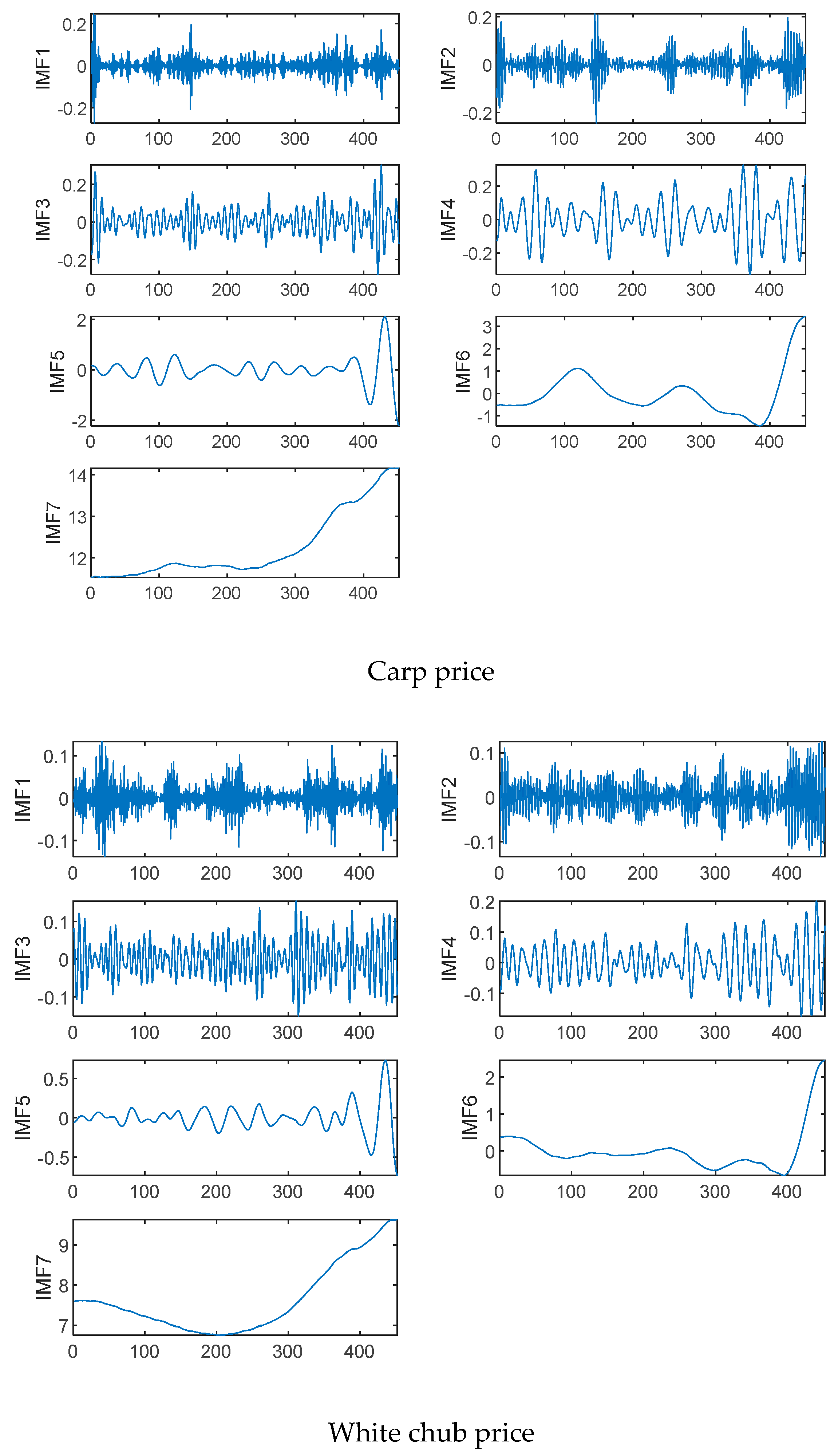
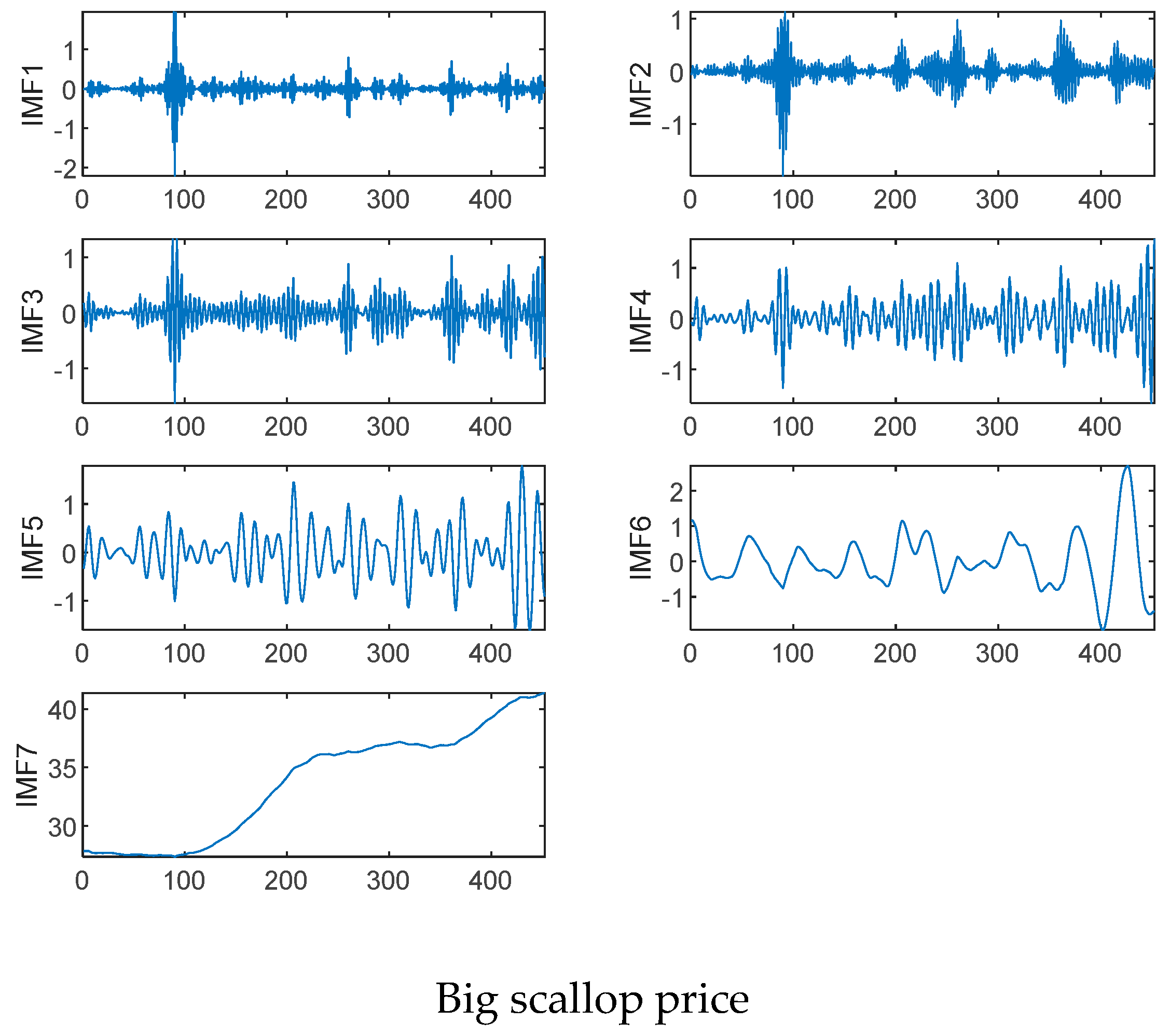
4.2. VMD Results
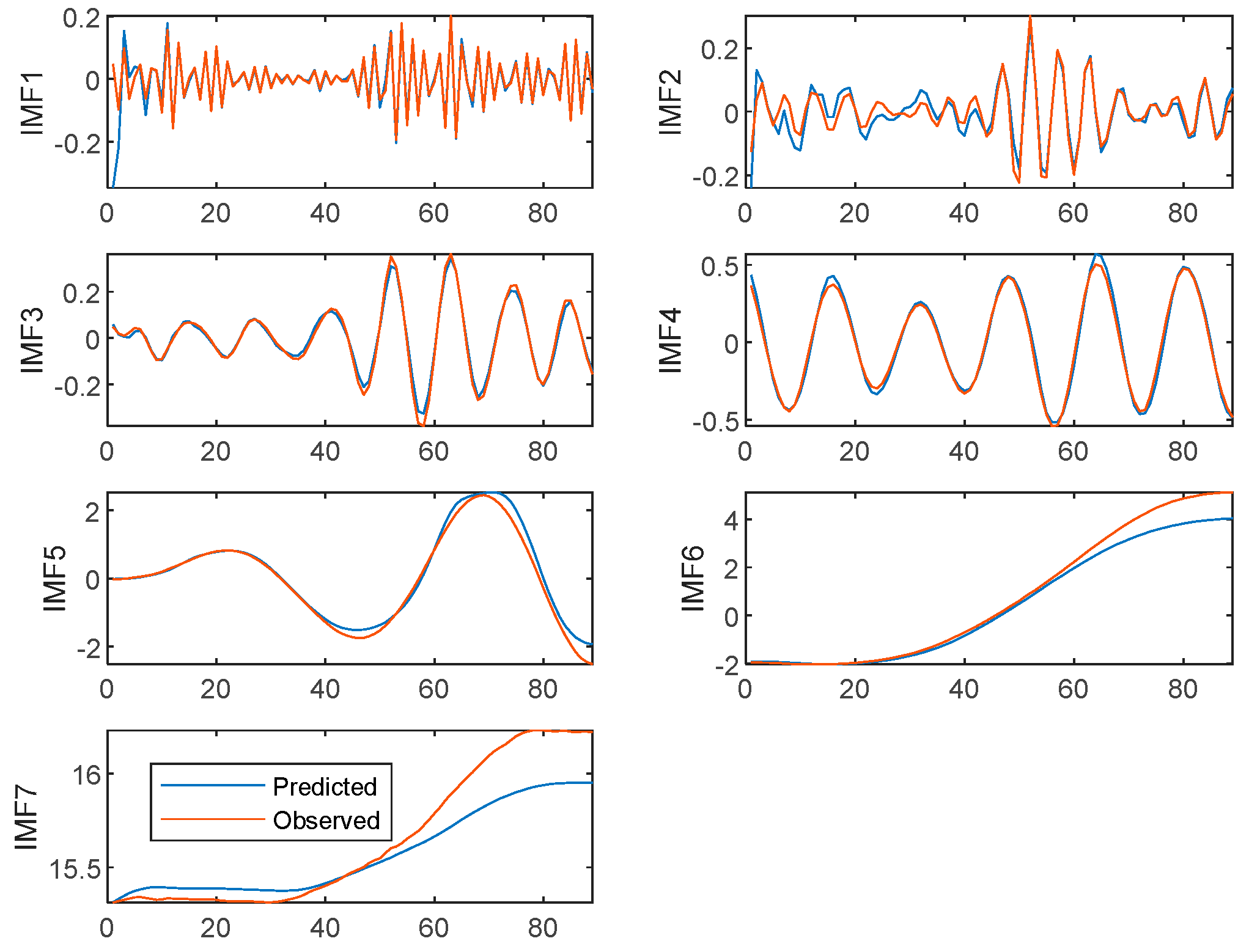
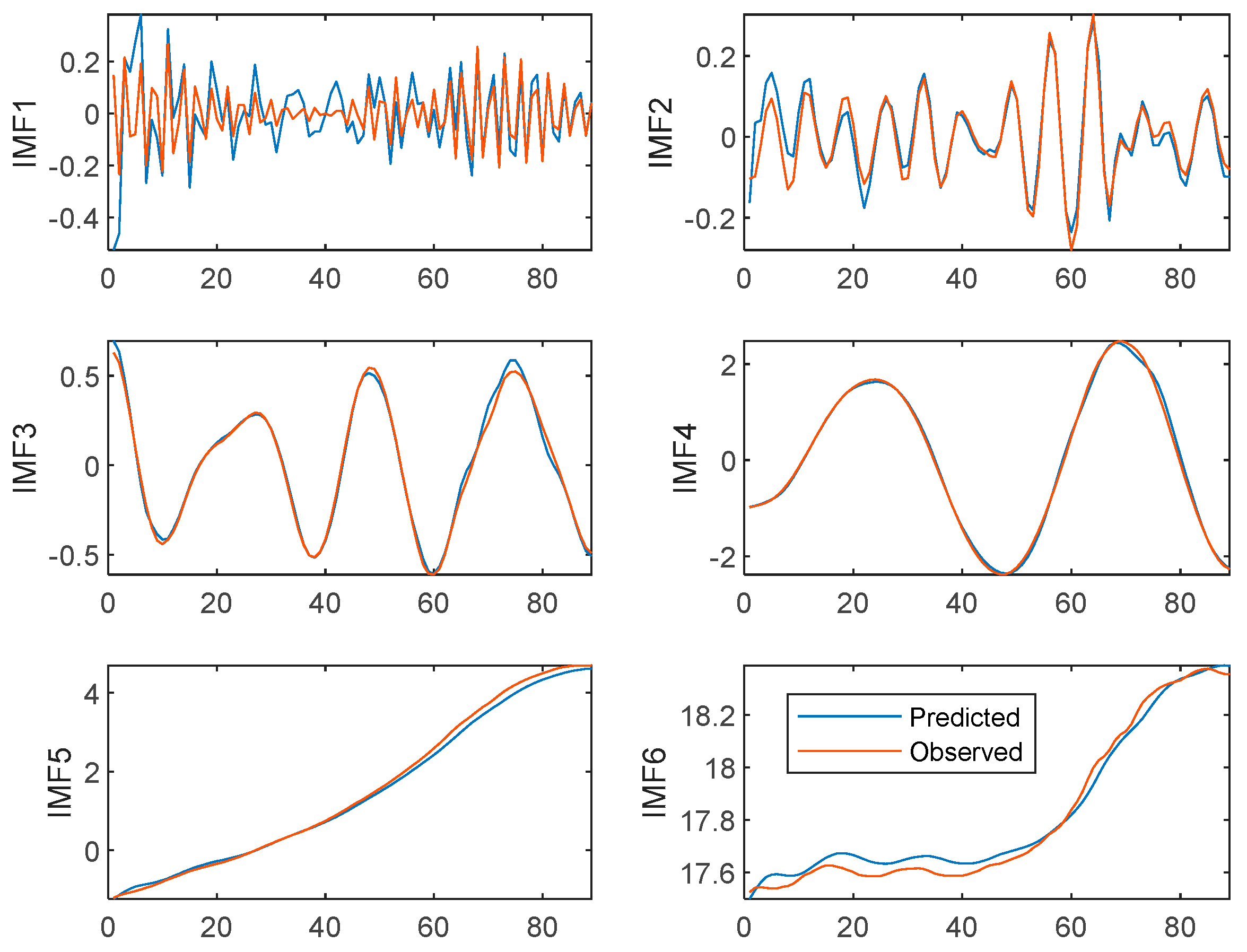
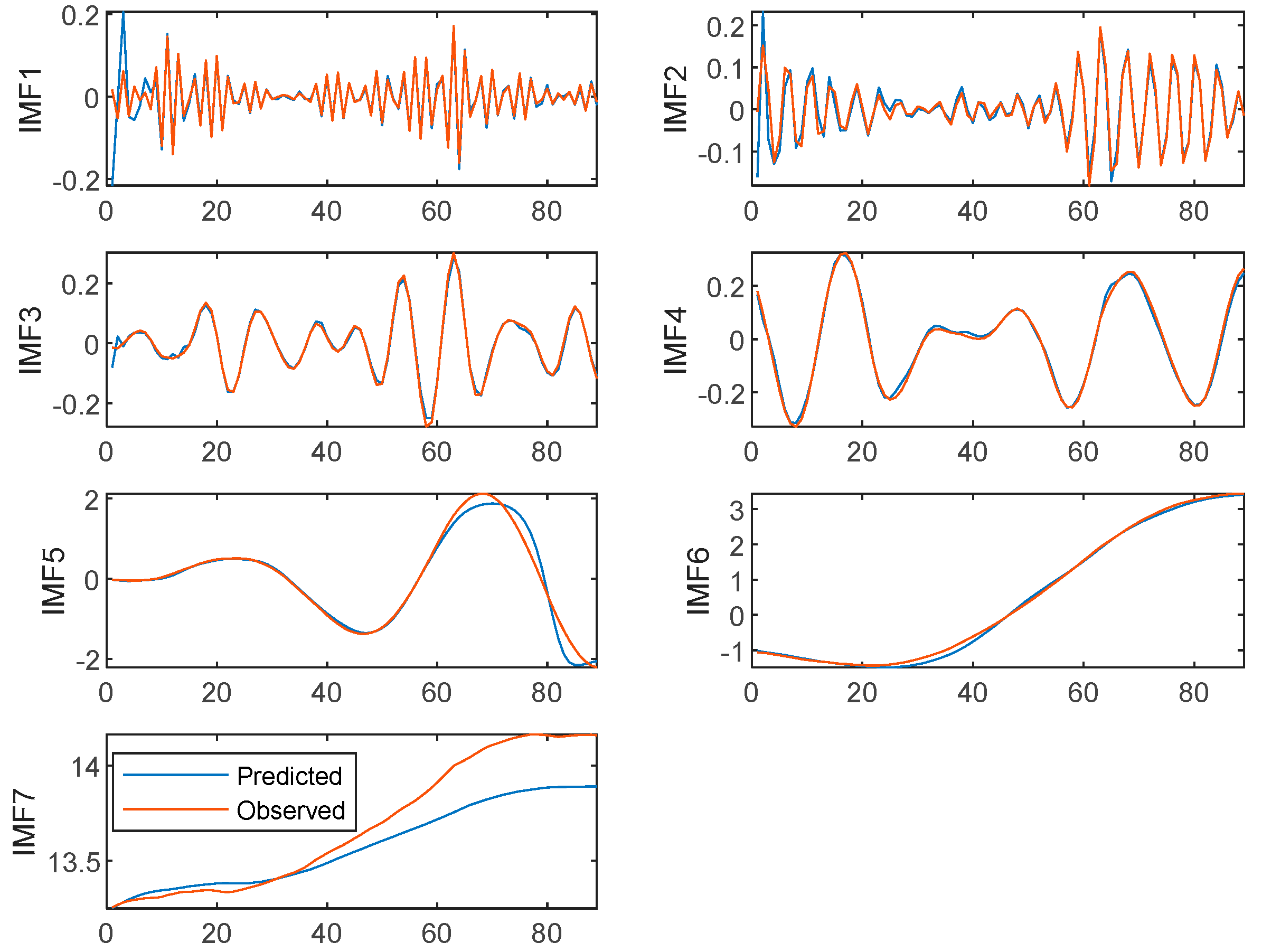
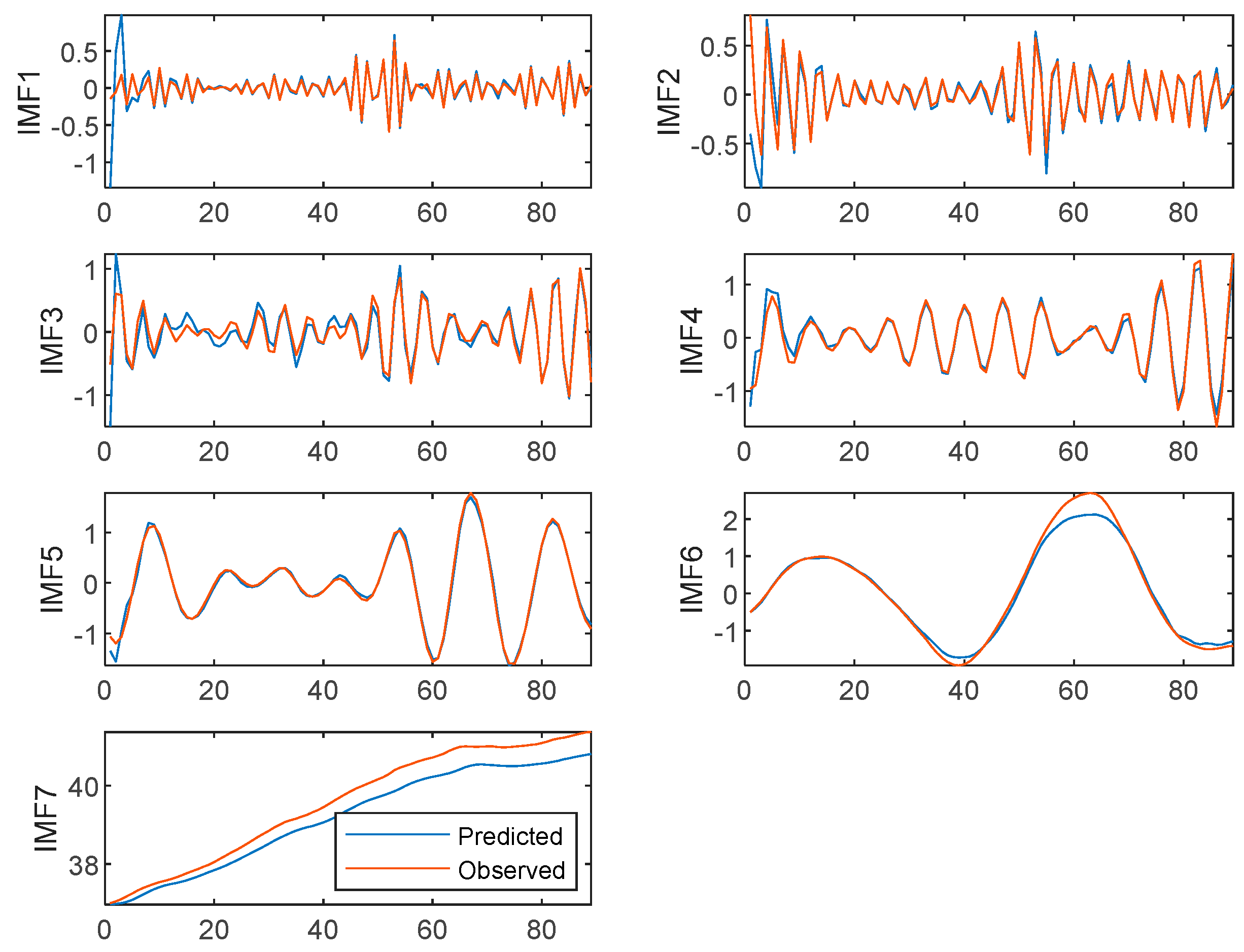
4.3. Aquatic Product Price Forecasting Results Based on VMD-IBES-LSTM Model
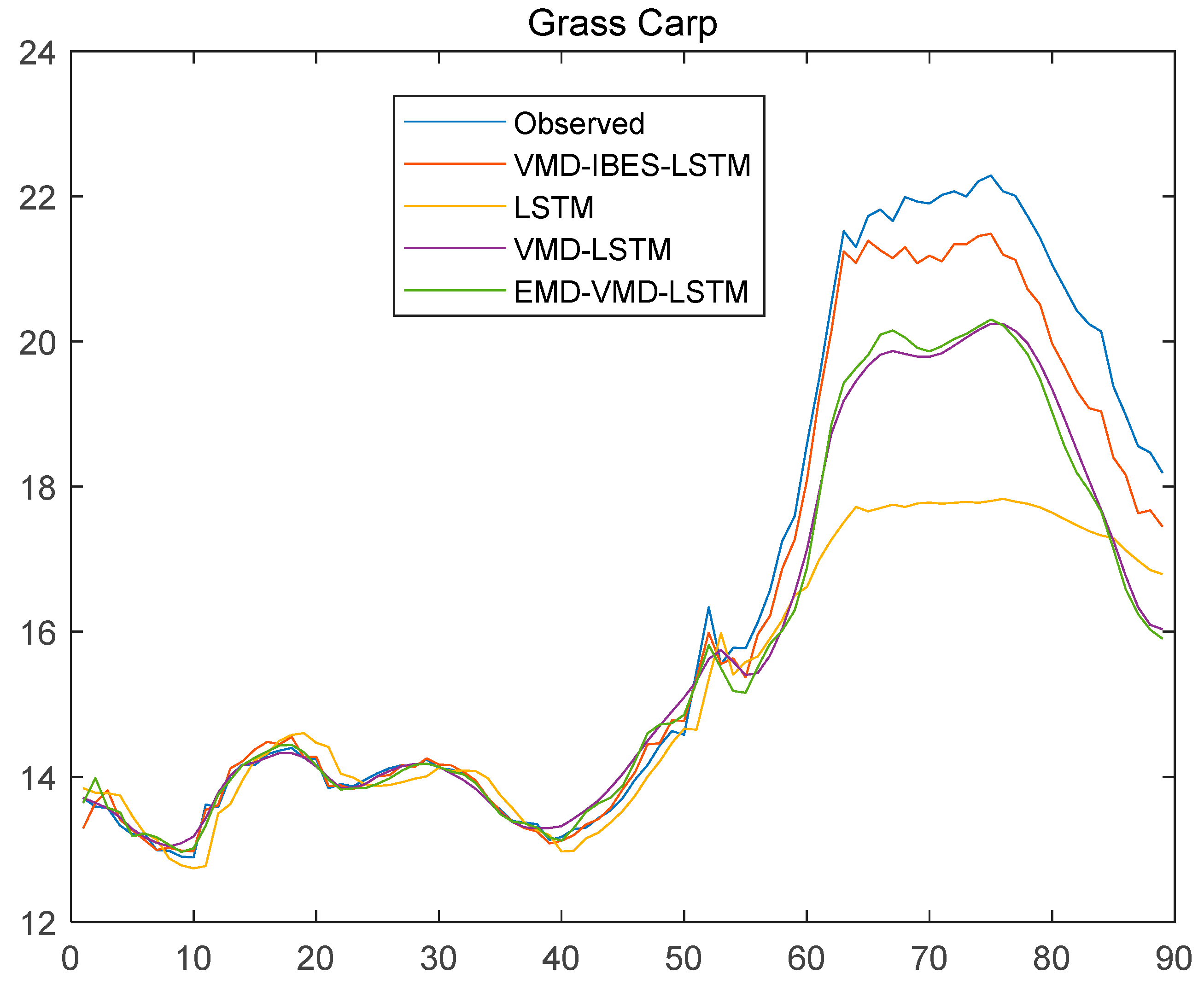
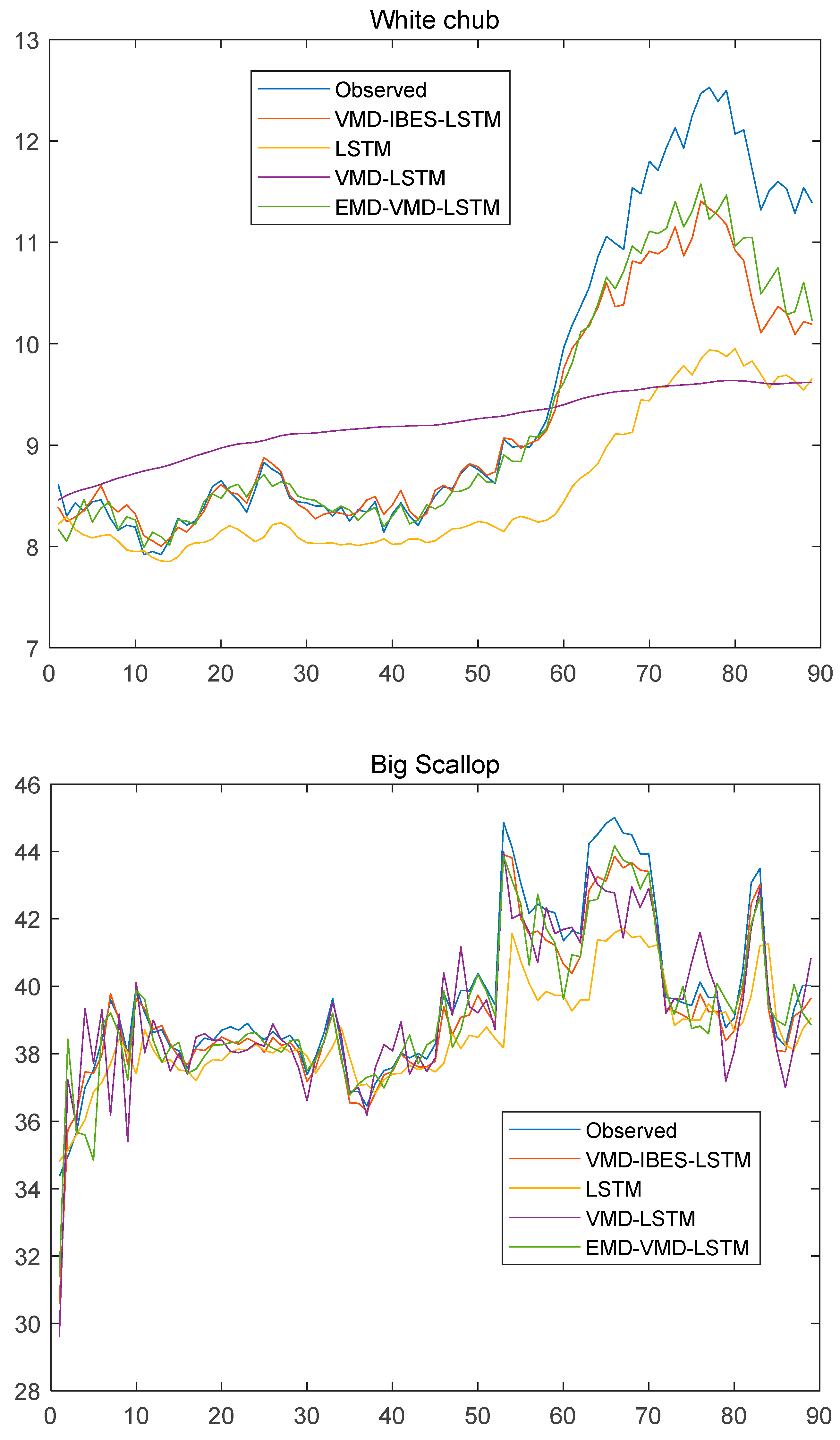
4.4. Comparative Results and Discussion
- LSTM: The learning rate is 0.3%, the number of iterations is 100, the number of cells in the hidden layer is 200, the solver is set to adam, the gradient threshold is set to 1, and the mini-batch size is 32.
- CNN-LSTM: the maximum number of iterations is 100 and the learning rate is 0.003.
- BiLSTM: the number of iterations is 100. The number of cells in the hidden layer is 200. The learning rate is 0.3%.
- MOGWO: We set the smoothness and accuracy of the model as the objective function. Set the size of the repository to 30, the maximum number of iterations to 100, and the number of grey wolves to 100. Set the grid expansion parameter to 0.1. Set the leader Selection Pressure Parameter to 4.
- The error analysis for each comparison model is shown in the Table 4 as below.
5. Discussion
- (1)
- The variational modal decomposition is used to decompose the fish price dataset into several IMF components, which can effectively reduce the non-linearity and non-smoothness of the dataset and improve the accuracy of the model.
- (2)
- An improved optimization algorithm is used to optimise each hyperparameter of the LSTM. In LSTM, the choice of parameters has an extremely important impact on the accuracy of the model. In previous studies, although scholars have proposed models that are based on the idea of “decomposition-prediction-integration” that can effectively improve the accuracy of prediction, less attention has been paid to the selection of parameters. The bald eagle search algorithm has received a lot of attention because of its advantages such as strong merit-seeking ability and difficulty in falling into local optimality. Thus, in this study, an improved bald eagle search algorithm was selected to optimize the hyperparameters of the LSTM.
- (3)
- A long short-term memory network was used to predict the individual IMF components. Compared with the traditional recurrent neural network, LSTM can effectively overcome the problem of gradient explosion and gradient disappearance with an increasing number of iterations of the traditional recurrent neural network. Thus, the VMD-IBES-LSTM model that was proposed in this study is effective and competitive.
- Data collection standards should be improved. The cross-fertilization of agricultural data and information technology should be strengthened and a unified system of data collection standards, including data collection and storage, should be established. A unified standard system should be formed through standardized data types, classifications, storage, interfaces, etc.
- Information analysis should be strengthened. First, we should actively study the analysis models, both to strengthen the study of the adaptability of existing models, such as time series, autoregressive models, moving average models, mixed autoregressive-moving average models, vector autoregressive models, etc., and to study new models that are based on existing data. Secondly, we should strengthen the cross analysis of different disciplines. Agricultural monitoring and early warning is a multidisciplinary field that requires both economic analysis and the integrated use of information technology, computer technology, database technology, and agricultural technology. Third, special analyses should be carried out in conjunction with different target groups. It is necessary to take full account of the economic operation of agriculture, taking into account reasonable fluctuations in the prices of agricultural products, as well as the returns of producers and the benefits to consumers. At the same time, technology is actively used to liberate manpower and increase labor productivity.
- The construction of the agricultural Internet of Things should be strengthened to improve the efficiency of agricultural products production. The agricultural Internet of Things is the application of Internet of Things technology in agricultural production, It is a specific application of agricultural production, management, and services, using various types of sensing devices to collect information about the agricultural production process, logistics of agricultural products, and animals and plants. It uses various sensing devices to collect information about the agricultural production process, the logistics of agricultural products, and the plants and animals themselves, and to transmit them through wireless sensor networks, mobile communication wireless networks, and the Internet. The information that was obtained is fused and processed through wireless sensor networks, mobile communication wireless networks, and internet transmission, and finally, through intelligent operation terminals, the process monitoring, scientific decision-making, and real-time services are realized for the pre-production, production, and post-production of agricultural products.
- (1)
- In this study, LSTM is used to predict fish prices. While there are many improved versions of LSTM, including Bi-LSTM, Adaptive Neuro-Fuzzy Inference System (ANFIS), etc., the above methods can be compared with the model that was proposed in this study.
- (2)
- The improved bald eagle search algorithm that was proposed in this study can also be combined with other optimisation algorithms (e.g., gravitational search algorithm, etc.) to subsequently optimize the parameters of the machine learning prediction model.
- (3)
- There are still some errors in the accuracy of the model that was proposed in this paper. The reasons for this are mainly the following. Price fluctuations of aquatic products are closely related to a variety of factors, such as the supply and demand of aquatic products, policy changes, consumer preferences, etc. In subsequent studies, consideration can be given to adding the above-mentioned influencing factors to further improve the accuracy of the model.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fabinyi, M.; Liu, N. The social context of the chinese food system: An ethnographic study of the beijing seafood market. Sustainability 2016, 8, 244. [Google Scholar] [CrossRef]
- Sun, Y.; Lian, F.; Guo, W.Y.; Yang, Z.Z. The spatial evolution and optimization of supply channels for marine products consumed in China. Marit. Policy Manag. 2022, 8, 1–23. [Google Scholar] [CrossRef]
- Fabinyi, M. Historical, cultural and social perspectives on luxury seafood consumption in China. Environ. Conserv. 2012, 39, 83–92. [Google Scholar] [CrossRef]
- Miao, M.; Liu, H.; Chen, J. Factors affecting fluctuations in China’s aquatic product exports to Japan, the USA, South Korea, Southeast Asia, and the EU. Aquacult. Int. 2021, 29, 2507–2533. [Google Scholar] [CrossRef]
- Wang, R.; Li, C.; Fu, W.; Tang, G. Deep learning method based on gated recurrent unit and variational mode decomposition for short-term wind power interval prediction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3814–3827. [Google Scholar] [CrossRef]
- Huang, Y.; Dai, X.; Wang, Q.; Zhou, D. A hybrid model for carbon price forecasting using GARCH and long short-term memory network. Appl. Energy 2021, 285, 116485. [Google Scholar] [CrossRef]
- Lin, Y.; Lu, Q.; Tan, B.; Yu, Y. Forecasting energy prices using a novel hybrid model with variational mode decomposition. Energy 2022, 246, 123366. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. A novel carbon price prediction model combines the secondary decomposition algorithm and the long short-term memory network. Energy 2020, 207, 118294. [Google Scholar] [CrossRef]
- Liang, Y.; Lin, Y.; Lu, Q. Forecasting gold price using a novel hybrid model with ICEEMDAN and LSTM-CNN-CBAM. Expert Syst. Appl. 2022, 206, 117847. [Google Scholar] [CrossRef]
- Huang, Y.; Deng, Y. A new crude oil price forecasting model based on variational mode decomposition. Knowl.-Based Syst. 2021, 213, 106669. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, C.; Huang, K.; Gui, W. Non-ferrous metals price forecasting based on variational mode decomposition and LSTM network. Knowl.-Based Syst. 2020, 188, 105006. [Google Scholar] [CrossRef]
- Rezaei, H.; Faaljou, H.; Mansourfar, G. Stock price prediction using deep learning and frequency decomposition. Expert Syst. Appl. 2021, 169, 114332. [Google Scholar] [CrossRef]
- Duran, N.M.; Maciel, E.D.S.; Galvao, J.A.; Savay-da-Silva, L.K.; Sonati, J.G.; Oetterer, M. Availability and consumption of fish as convenience food—Correlation between market value and nutritional parameters. Food Sci. Technol.-Brazil 2018, 37, 65–69. [Google Scholar] [CrossRef][Green Version]
- Nam, J.; Sim, S. Forecast accuracy of abalone producer prices by shell size in the republic of korea: Modified diebold–mariano tests of selected autoregressive models. Aquacult. Econ. Manag. 2017, 22, 474–489. [Google Scholar] [CrossRef]
- Mazliana, M.; Raja, R.P.; Ho, M.K. Forecasting Prices of Fish and Vegetable using Web Scraped Price Micro Data. Int. J. Rec. Eng. 2019, 7, 251–256. [Google Scholar]
- Hasan, M.R.; Dey, M.M.; Engle, C.R. Forecasting monthly catfish (ictalurus punctatus.) pond bank and feed prices. Aquacult. Econ. Manag. 2019, 23, 86–110. [Google Scholar] [CrossRef]
- Gordon, D.V. A short-run ARDL-bounds model for forecasting and simulating the price of lobster. Mar. Resour. Econ. 2020, 35, 43–63. [Google Scholar] [CrossRef]
- Guillen, J.; Maynou, F. Characterisation of fish species based on ex-vessel prices and its management implications: An application to the spanish mediterranean. Fish. Res. 2015, 167, 22–29. [Google Scholar] [CrossRef]
- Nguyen, H.T.K.; Thu, T.T.N.; Lebailly, P.; Azadi, H. Economic challenges of the export-oriented aquaculture sector in Vietnam. J. Appl. Aquac. 2019, 31, 367–383. [Google Scholar] [CrossRef]
- Li, H.; Gao, X.; Cheng, K. The application of wavelet neural network in prediction of the fish price. Appl. Mech. Mater. 2014, 687, 1945–1949. [Google Scholar] [CrossRef]
- Duan, Q.; Zhang, L.; Wei, F.; Xiao, X.; Wang, L. Forecasting model and validation for aquatic product price based on time series GA-SVR. Trans. Chin. Soc. Agric. Eng. 2017, 33, 308–314. [Google Scholar]
- Bloznelis, D. Short term salmon price forecasting. J. Forecast. 2018, 37, 151–169. [Google Scholar] [CrossRef]
- Yuan, H.; Chen, Y.; Ju, J. A CBR Based Prediction Method for Web Aquatic Products Prices. Int. J. Comput. Int. Sys. 2007, 195–200. [Google Scholar]
- Shi, J.; Leau, Y.B.; Li, K.; Park, Y.J.; Yan, Z. Optimization and Decomposition Methods in Network Traffic Prediction Model: A Review and Discussion. IEEE Access 2020, 8, 202858–202871. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Angayarkanni, S.A.; Sivakumar, R.; Ramana Rao, Y.V. Hybrid Grey Wolf: Bald Eagle search optimized support vector regression for traffic flow forecasting. J. Amb. Intel. Hum. Comp. 2021, 12, 1293–1304. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Z.F.; Tseng, M.L.; Zheng, S.J.; Lim, M.K. Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107504. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S. An Optimization Method for an Integrated Energy System Scheduling Process Based on NSGA-II Improved by Tent Mapping Chaotic Algorithms. Processes 2020, 8, 426. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a long short-term memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yuan, P.; Wang, L.; Cheng, D. An adaptive daily runoff forecast model using VMD-LSTM-PSO hybrid approach. Hydrol. Sci. J. 2021, 66, 1488–1502. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Predicting flood susceptibility using LSTM neural networks. J. Hydrol. 2021, 594, 125734. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, M.; Yu, R.; Wang, T. Research on simulation and state prediction of nuclear power system based on LSTM neural network. Sci. Technol. Nucl. Install. 2021, 2021, 8839867. [Google Scholar] [CrossRef]
- Fukuoka, R.; Suzuki, H.; Kitajima, T.; Kuwahara, A.; Yasuno, T. Wind Speed Prediction Model Using LSTM and 1D-CNN. J. Signal Process. 2018, 22, 207–210. [Google Scholar] [CrossRef]
- Ehsan, M.A.; Shahirinia, A.; Zhang, N.; Oladunni, T. Wind Speed Prediction and Visualization Using Long Short-Term Memory Networks (LSTM). In Proceedings of the 10th International Conference on Information Science and Technology (ICIST), Bath, London, and Plymouth, UK, 9–15 September 2020; pp. 234–240. [Google Scholar]
- Troiano, L.; Villa, E.M.; Loia, V. Replicating a Trading Strategy by Means of LSTM for Financial Industry Applications. IEEE Trans. Ind. Inform. 2018, 14, 3226–3234. [Google Scholar] [CrossRef]
- Sundermeyer, M.; Schlüter, R.; Ney, H. LSTM Neural Networks for Language Modeling. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association, Portland, OR, USA, 9–13 September 2012. [Google Scholar]
- Wu, S.; Feng, F.; Zhu, J.; Wu, C.; Zhang, G. A method for determining intrinsic mode function number in variational mode decomposition and its application to bearing vibration signal processing. Shock. Vib. 2020, 2020, 8304903. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Research on ship-radiated noise denoising using secondary variational mode decomposition and correlation coefficient. Sensors 2017, 18, 48. [Google Scholar] [CrossRef]
- Zhang, K.; Cao, H.; Thé, J.; Yu, H. A hybrid model for multi-step coal price forecasting using decomposition technique and deep learning algorithms. Appl. Energy 2022, 306, 118011. [Google Scholar] [CrossRef]
- Bai, L.; Liu, Z.; Wang, J. Novel hybrid extreme learning machine and multi-objective optimization algorithm for air pollution prediction. Appl. Math. Model. 2022, 106, 177–198. [Google Scholar] [CrossRef]


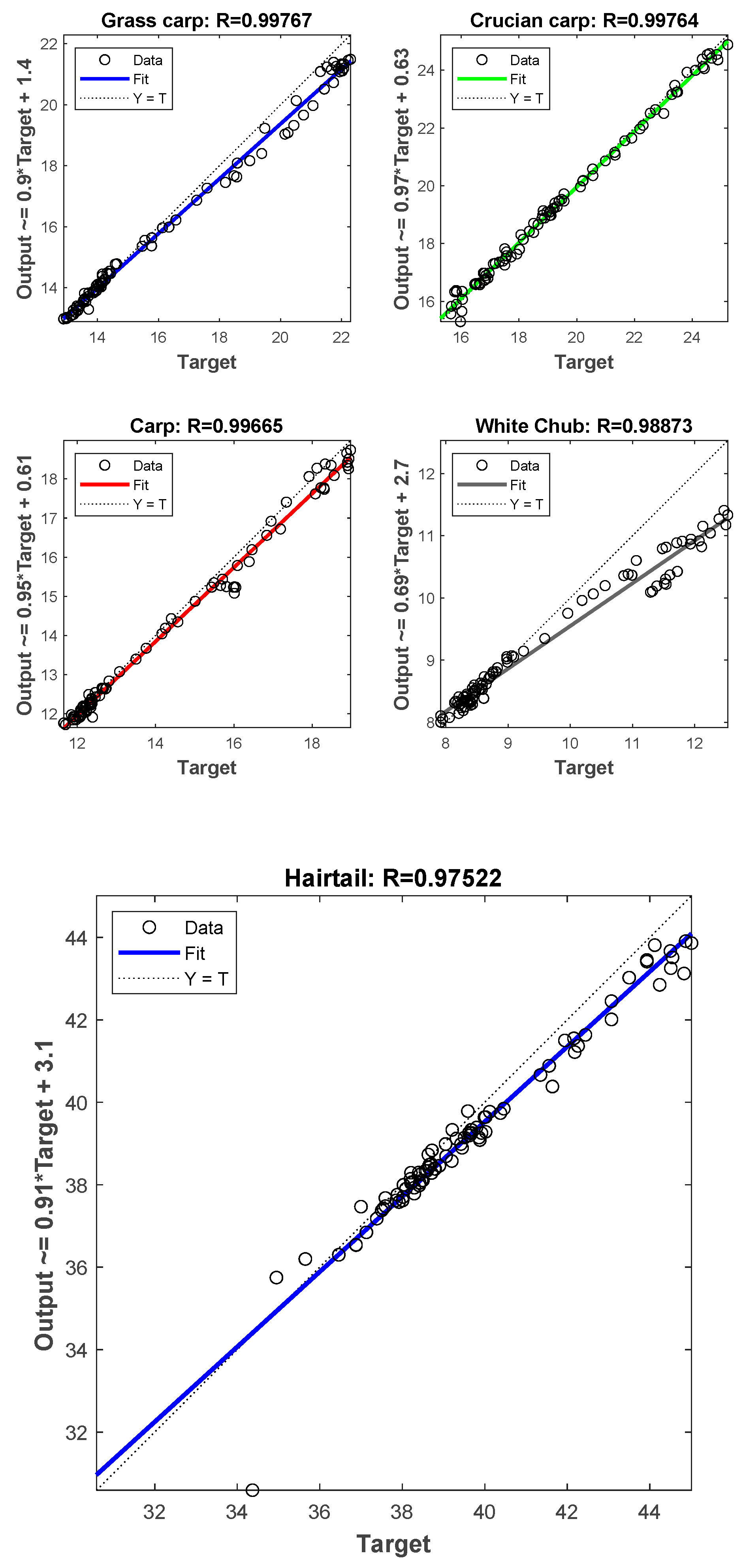

| Minimum Value | Maximum Value | Mean | Standard Deviation | |
|---|---|---|---|---|
| Grass carp | 11.73 | 22.29 | 14.2 | 2.08 |
| Crucian carp | 12.99 | 25.22 | 16.1 | 2.34 |
| Carp | 10.64 | 18.98 | 12.25 | 1.57 |
| White Chub | 6.43 | 12.53 | 7.63 | 1.23 |
| Big Scallop | 18.04 | 45.01 | 33.7 | 4.9 |
| Grass Carp | Crucian CARP | Carp | White Chub | Big Scallop | |
|---|---|---|---|---|---|
| Grass Carp | 1 | 0.83 | 0.78 | 0.81 | 0.43 |
| Crucian carp | 1 | 0.73 | 0.78 | 0.56 | |
| Carp | 1 | 0.79 | 0.47 | ||
| White Chub | 1 | 0.45 | |||
| Big Scallop | 1 |
| MSE | RMSE | MAE | MAPE | ||
|---|---|---|---|---|---|
| Grass Carp | IMF1 | 0.0020 | 0.0447 | 0.0150 | 0.3840 |
| IMF2 | 0.0010 | 0.0316 | 0.0240 | 1.2040 | |
| IMF3 | 0.0003 | 0.0173 | 0.0140 | 0.2390 | |
| IMF4 | 0.0001 | 0.0100 | 0.0273 | 0.3378 | |
| IMF5 | 0.0440 | 0.2098 | 0.1401 | 0.2438 | |
| IMF6 | 0.2473 | 0.4973 | 0.3250 | 0.1741 | |
| IMF7 | 0.0235 | 0.1532 | 0.1136 | 0.0071 | |
| Crucian carp | IMF1 | 0.0130 | 0.1140 | 0.0731 | 6.2650 |
| IMF2 | 0.0011 | 0.03317 | 0.0250 | 1.112 | |
| IMF3 | 0.0009 | 0.0300 | 0.0213 | 0.4643 | |
| IMF4 | 0.0049 | 0.0700 | 0.0499 | 0.1003 | |
| IMF5 | 0.0138 | 0.1175 | 0.0948 | 0.0842 | |
| IMF6 | 0.0014 | 0.0374 | 0.0330 | 0.0019 | |
| Carp | IMF1 | 0.0010 | 0.0316 | 0.0121 | 0.5859 |
| IMF2 | 0.0007 | 0.0265 | 0.0146 | 1.1712 | |
| IMF3 | 0.0001 | 0.0100 | 0.0074 | 0.5499 | |
| IMF4 | 0.0002 | 0.0140 | 0.0100 | 0.3814 | |
| IMF5 | 0.0333 | 0.1824 | 0.1044 | 0.2633 | |
| IMF6 | 0.0058 | 0.07622 | 0.0589 | 0.0724 | |
| IMF7 | 0.0269 | 0.1640 | 0.1227 | 0.0088 | |
| White chub | IMF1 | 0.0017 | 0.0412 | 0.0297 | 3.2284 |
| IMF2 | 0.0009 | 0.0300 | 0.0239 | 0.9942 | |
| IMF3 | 0.0010 | 0.0316 | 0.0285 | 1.0449 | |
| IMF4 | 0.0001 | 0.0100 | 0.0085 | 0.1973 | |
| IMF5 | 0.0009 | 0.0300 | 0.0212 | 0.3164 | |
| IMF6 | 0.2717 | 0.5212 | 0.2926 | 1.9635 | |
| IMF7 | 0.0026 | 0.0510 | 0.0427 | 0.0046 | |
| Hairtail | IMF1 | 0.0293 | 0.1712 | 0.0590 | 0.9651 |
| IMF2 | 0.0254 | 0.1594 | 0.0629 | 0.4858 | |
| IMF3 | 0.0267 | 0.1634 | 0.1055 | 1.8694 | |
| IMF4 | 0.0150 | 0.1225 | 0.0741 | 0.6865 | |
| IMF5 | 0.0060 | 0.0775 | 0.0513 | 0.2352 | |
| IMF6 | 0.0378 | 0.1944 | 0.1277 | 0.3146 | |
| IMF7 | 0.1669 | 0.4085 | 0.3791 | 0.0095 |
| VMD-IBES-LSTM | LSTM | BPNN | CNN-LSTM | BiLSTM | CNN-BiLSTM | Bayes-BiLSTM | VMD-LSTM | EMD-VMD-LSTM | MOGWO-LSSVM | CEEMD-CNN-LSTM | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grass carp | MSE | 0.230 | 4.260 | 5.700 | 7.540 | 20.970 | 8.539 | 3.507 | 1.430 | 1.460 | 1.358 | 6.281 |
| RMSE | 0.480 | 2.064 | 2.390 | 2.750 | 4.570 | 2.922 | 1.873 | 1.196 | 1.208 | 1.165 | 2.506 | |
| MAE | 0.016 | 0.065 | 5.040 | 0.080 | 0.180 | 0.088 | 0.058 | 0.041 | 0.040 | 0.037 | 0.110 | |
| MAPE | 0.320 | 1.310 | 1.690 | 1.690 | 3.340 | 1.804 | 1.168 | 0.801 | 0.804 | 0.739 | 1.993 | |
| Crucian carp | MSE | 0.046 | 0.880 | 2.750 | 5.860 | 10.670 | 5.717 | 0.142 | 0.160 | 0.710 | 1.716 | 2.921 |
| RMSE | 0.214 | 0.940 | 1.660 | 2.420 | 3.270 | 2.391 | 0.377 | 0.400 | 0.843 | 1.310 | 1.709 | |
| MAE | 0.008 | 0.036 | 1.460 | 0.070 | 0.160 | 0.071 | 0.014 | 0.015 | 0.028 | 0.049 | 0.053 | |
| MAPE | 0.157 | 0.720 | 1.330 | 1.570 | 3.070 | 1.582 | 0.276 | 0.304 | 0.600 | 1.013 | 1.157 | |
| Carp | MSE | 0.083 | 1.320 | 5.040 | 4.390 | 9.540 | 3.714 | 3.577 | 0.086 | 0.709 | 1.343 | 4.889 |
| RMSE | 0.288 | 1.150 | 2.240 | 2.100 | 3.100 | 1.927 | 1.891 | 0.293 | 0.842 | 1.159 | 2.211 | |
| MAE | 0.012 | 0.044 | 3.900 | 0.080 | 0.120 | 0.068 | 0.118 | 0.013 | 0.028 | 0.041 | 0.112 | |
| MAPE | 0.190 | 0.730 | 1.500 | 1.290 | 2.000 | 1.168 | 1.296 | 0.200 | 0.596 | 0.700 | 1.751 | |
| White chub | MSE | 0.240 | 1.630 | 6.020 | 3.600 | 6.360 | 3.577 | 0.282 | 0.253 | 0.242 | 1.589 | 2.403 |
| RMSE | 0.489 | 1.280 | 2.450 | 1.900 | 2.520 | 1.891 | 0.531 | 0.503 | 0.492 | 1.261 | 1.550 | |
| MAE | 0.032 | 0.091 | 1.200 | 0.120 | 0.230 | 0.118 | 0.034 | 0.033 | 0.039 | 0.082 | 0.118 | |
| MAPE | 0.350 | 0.960 | 2.160 | 1.300 | 2.310 | 1.296 | 0.365 | 0.362 | 0.318 | 0.887 | 1.227 | |
| Big Scallop | MSE | 0.470 | 2.820 | 4.540 | 7.420 | 142.700 | 7.107 | 6.520 | 1.326 | 0.814 | 3.665 | 5.108 |
| RMSE | 0.680 | 1.680 | 2.130 | 2.720 | 11.950 | 2.666 | 2.55 | 1.152 | 0.902 | 1.914 | 2.260 | |
| MAE | 0.012 | 0.030 | 1.690 | 0.050 | 0.260 | 0.049 | 0.042 | 0.020 | 0.016 | 0.035 | 0.049 | |
| MAPE | 0.490 | 2.220 | 1.630 | 2.100 | 10.670 | 2.016 | 1.740 | 0.794 | 0.65 | 1.426 | 1.972 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Hu, Y.; Wu, D.; Yang, Z. An Aquatic Product Price Forecast Model Using VMD-IBES-LSTM Hybrid Approach. Agriculture 2022, 12, 1185. https://doi.org/10.3390/agriculture12081185
Wu J, Hu Y, Wu D, Yang Z. An Aquatic Product Price Forecast Model Using VMD-IBES-LSTM Hybrid Approach. Agriculture. 2022; 12(8):1185. https://doi.org/10.3390/agriculture12081185
Chicago/Turabian StyleWu, Junhao, Yuan Hu, Daqing Wu, and Zhengyong Yang. 2022. "An Aquatic Product Price Forecast Model Using VMD-IBES-LSTM Hybrid Approach" Agriculture 12, no. 8: 1185. https://doi.org/10.3390/agriculture12081185
APA StyleWu, J., Hu, Y., Wu, D., & Yang, Z. (2022). An Aquatic Product Price Forecast Model Using VMD-IBES-LSTM Hybrid Approach. Agriculture, 12(8), 1185. https://doi.org/10.3390/agriculture12081185






