Wheat Water Deficit Monitoring Using Synthetic Aperture Radar Backscattering Coefficient and Interferometric Coherence
Abstract
:1. Introduction
2. Materials and Methods
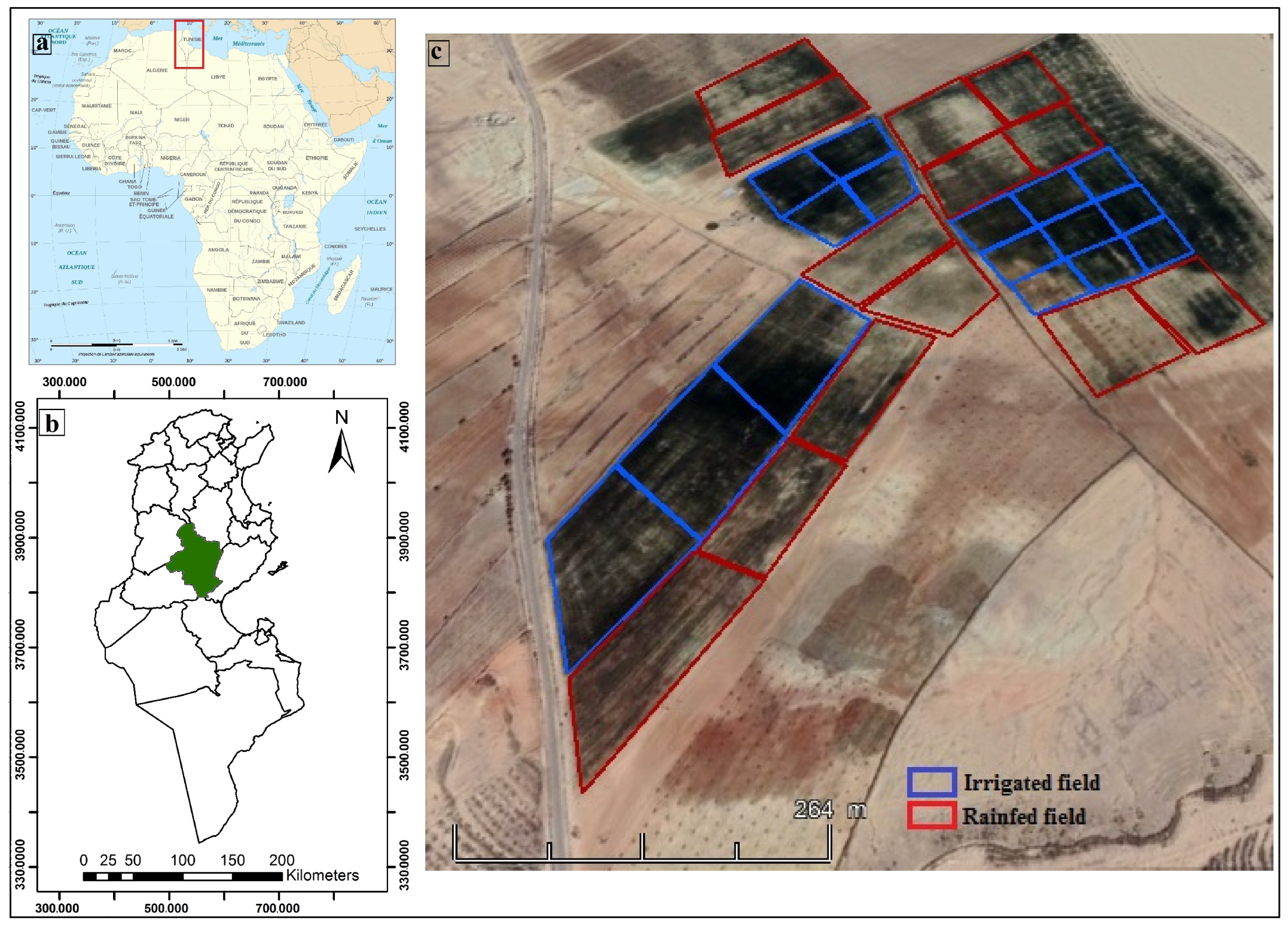
2.1. Study Area
2.2. Field Data Measurement
2.2.1. Plant Height Measurements
2.2.2. LAI Measurements
2.3. Reference Evapotranspiration ET0
2.4. Actual and Potential Evapotranspiration
2.5. Water Stress Index (Ks)
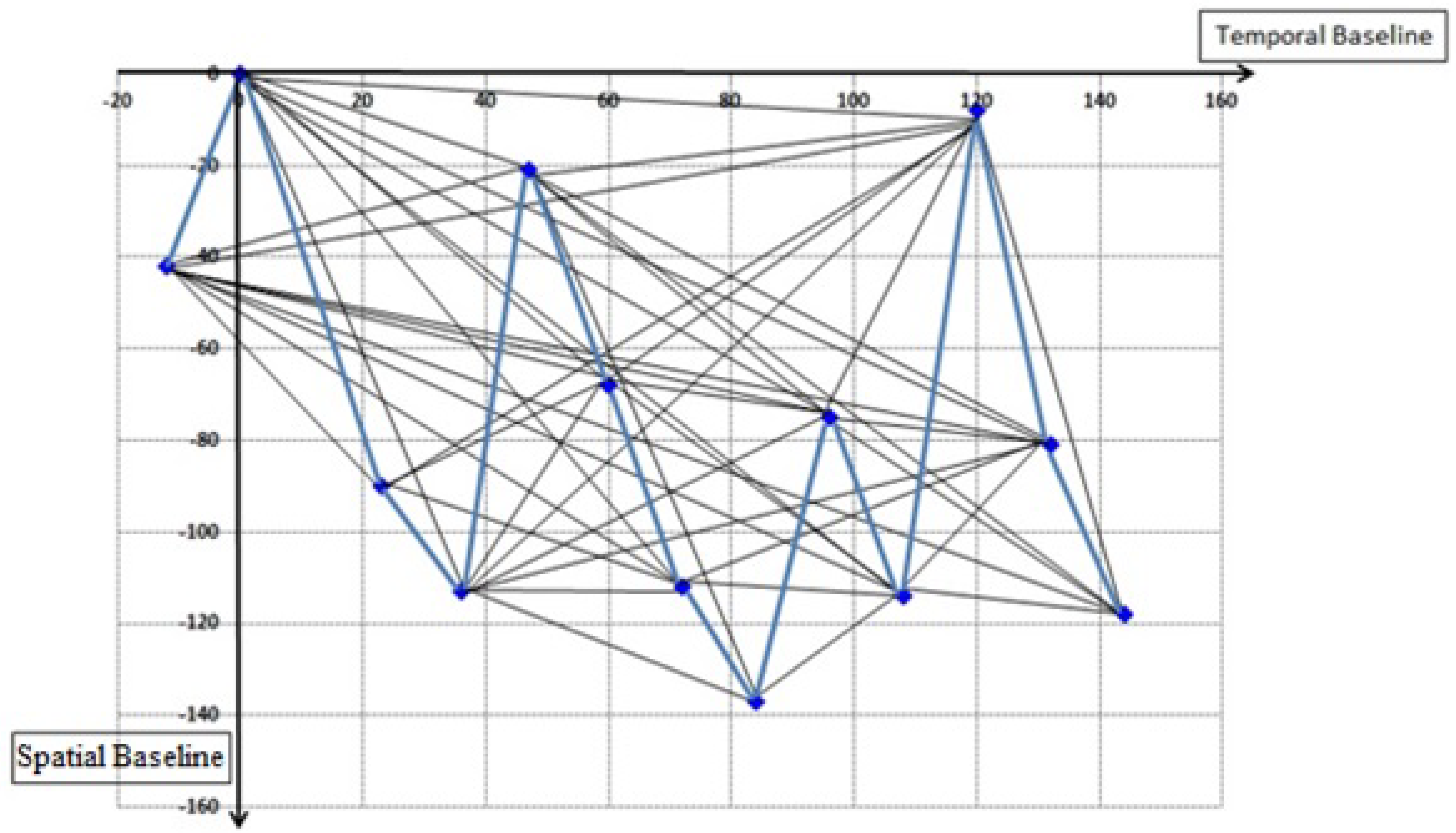
2.6. Remote Sensing Data
3. Methodology
4. Experimental Results
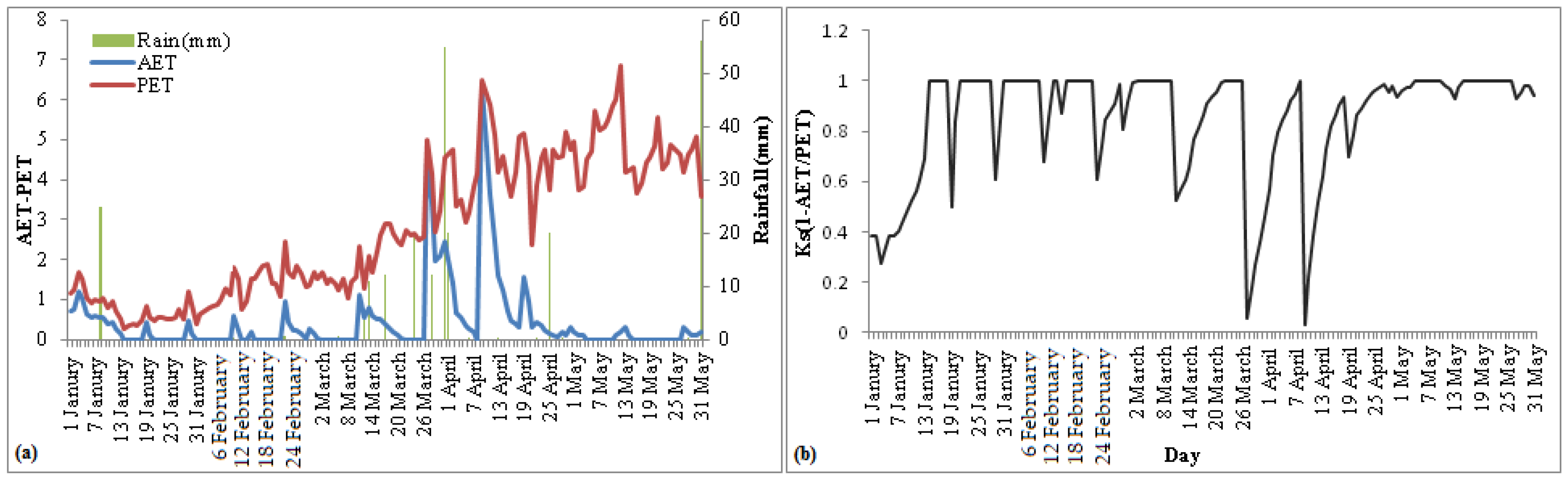
4.1. Temporal Variation of Actual and Potential Evapotranspiration and Water Stress Coefficient
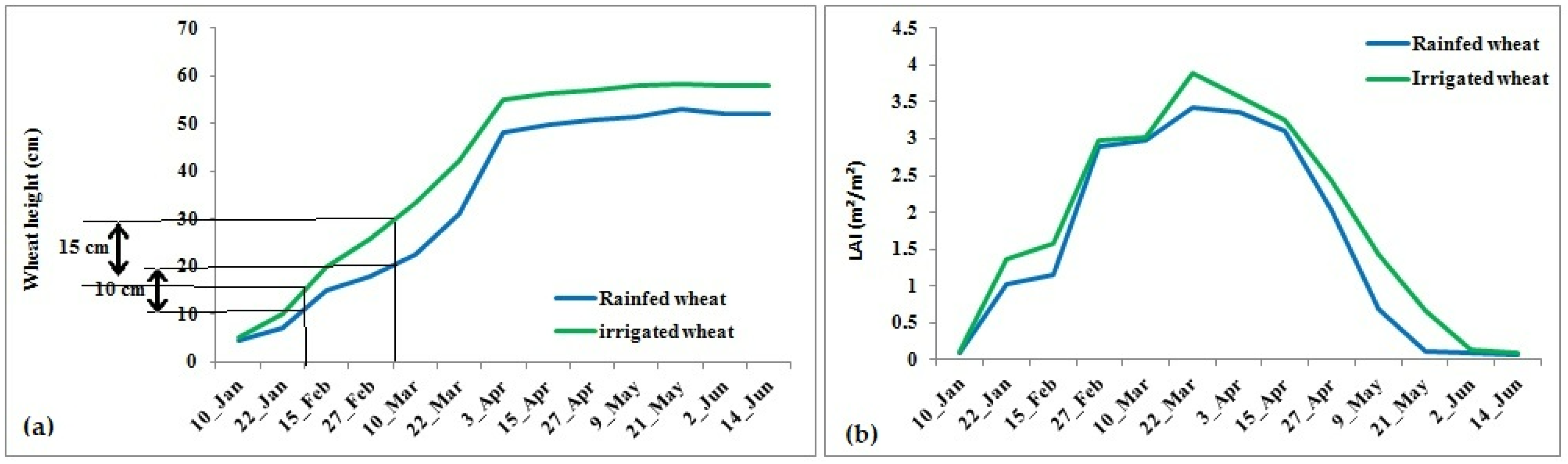
4.2. Temporal Variation of Height and LAI
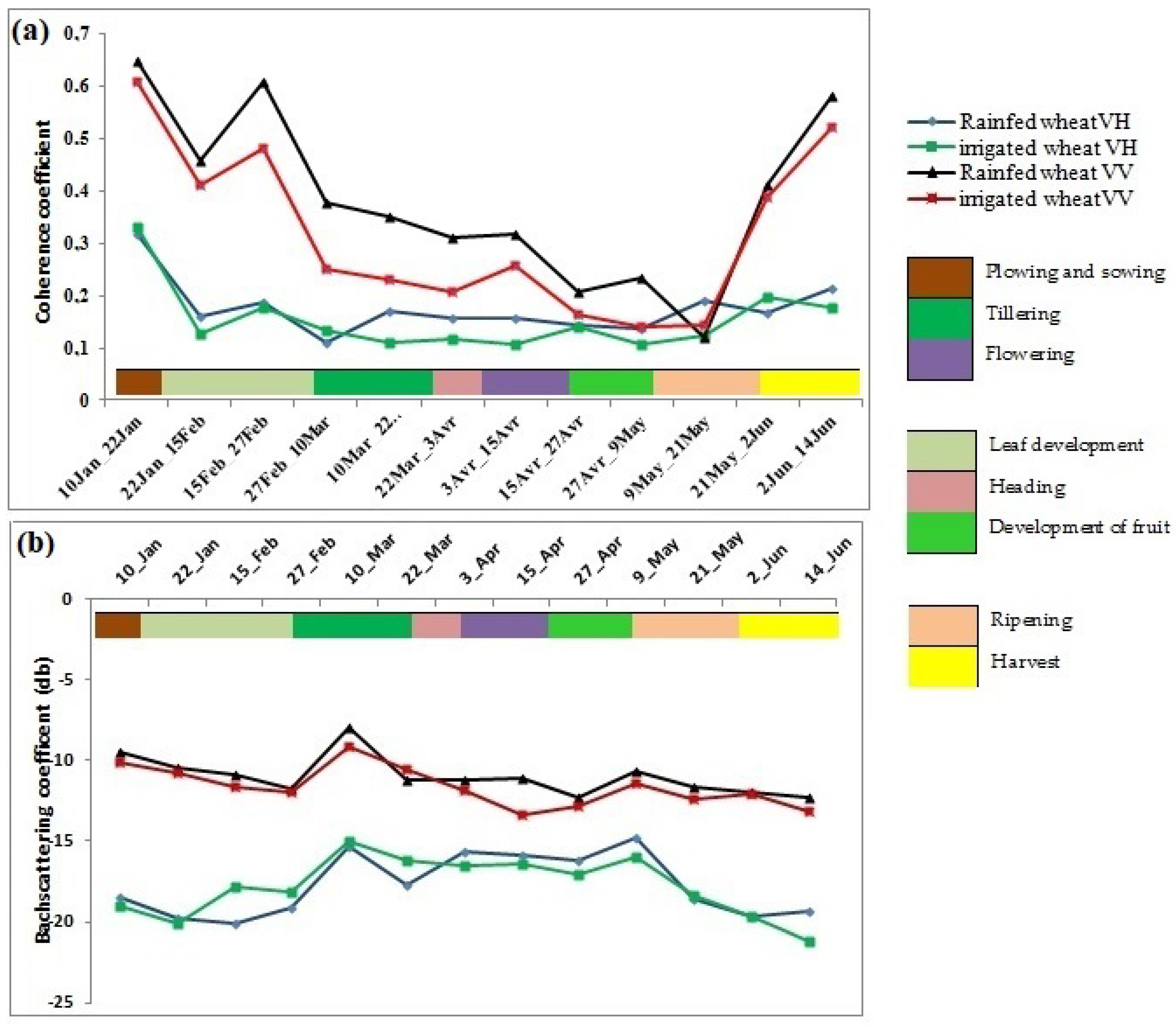
4.3. InSAR Coherence and Backscatter Analysis and Their Relation with Crop Growth
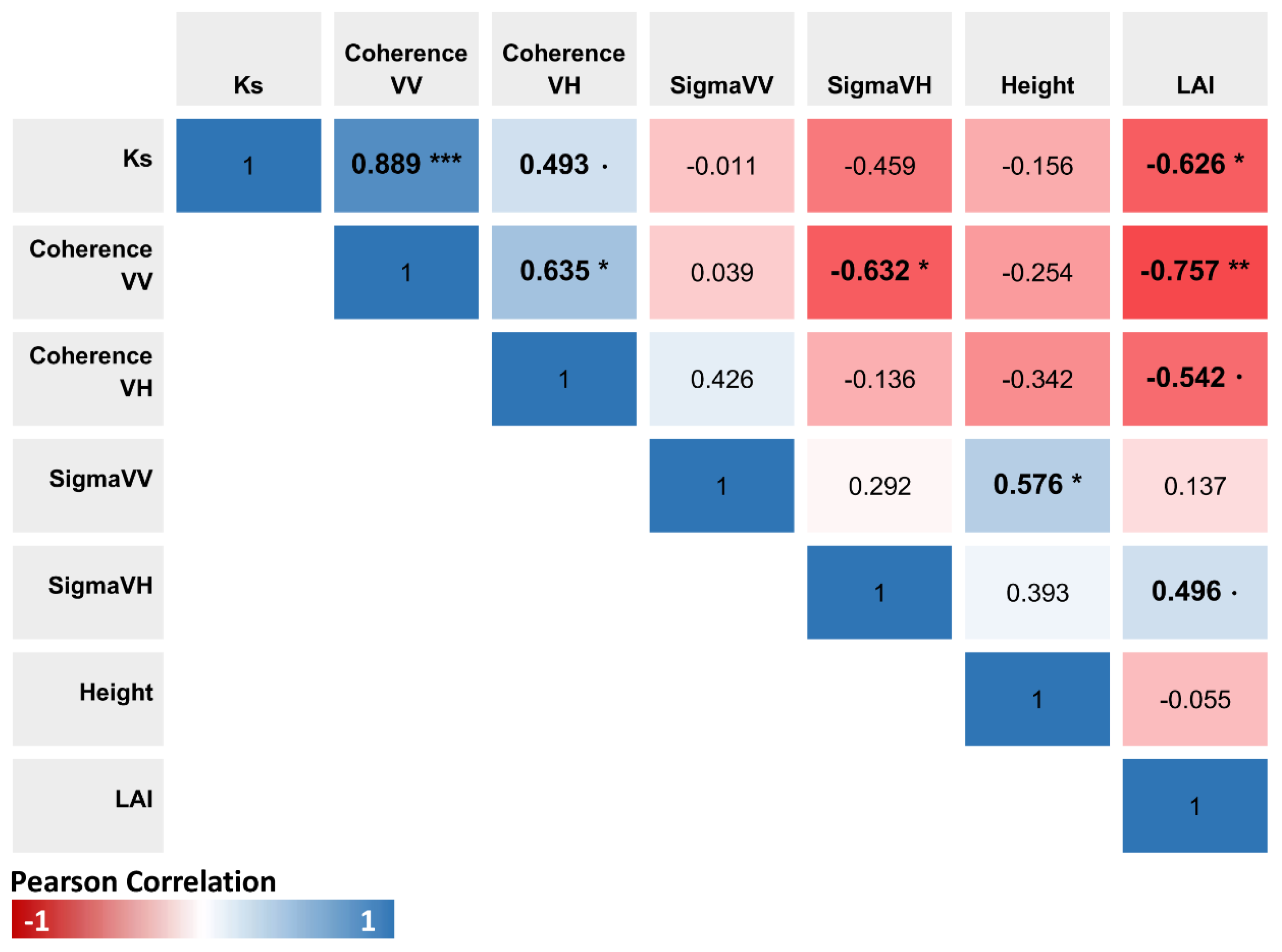
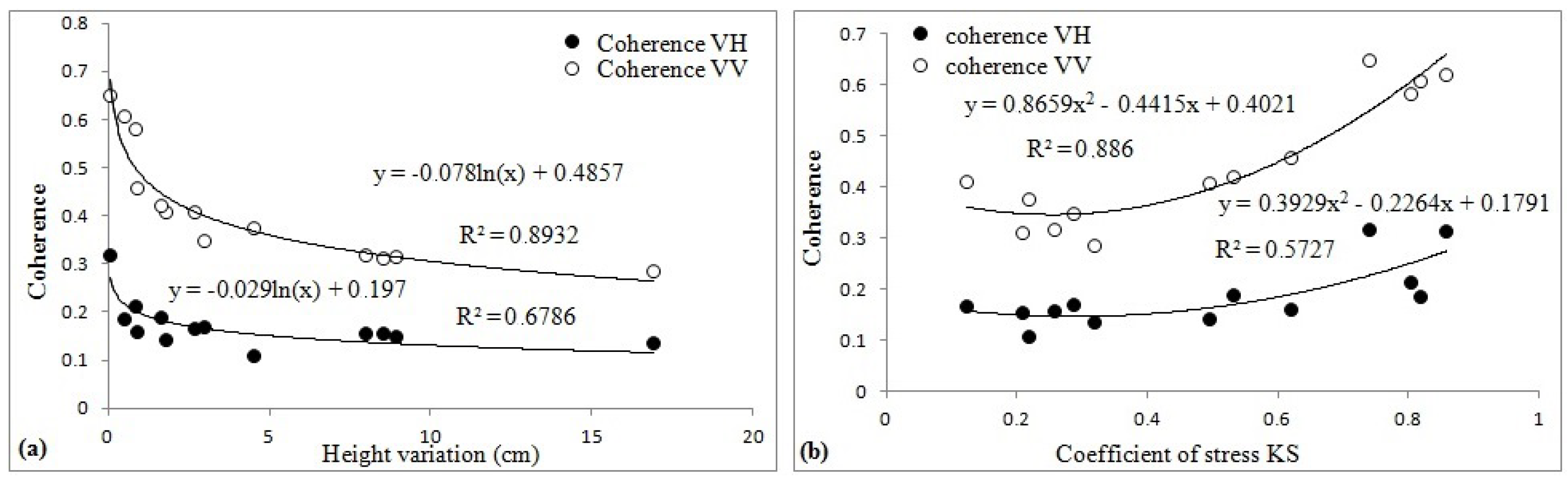
4.4. Detection of Water Deficit Using Interferometric Coherence
- The first two models considered Ks as a function of the SAR backscatter and the InSAR coherence data.
- The other two models integrated also the interaction between both Ks with crop height and Ks with LAI values.
5. Discussion
5.1. Variation of the InSAR Coherence and SAR Backscattering Coefficient as a Function of the Wheat Growth Stages
5.2. Estimation of the Water Stress Coefficient Ks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dellal, I.; McCarl, B.A. The economic impacts of drought on agriculture: The case of Turkey. Options Méditerranéennes 2010, 95, 169–174. [Google Scholar]
- Elias, E.; Manthey, F.; Stack, R.; Kianian, S. Breeding efforts to develop Fusarium head blight resistant durum wheat in North Dakota. In Proceedings of the 2005 National Fusarium Head Blight Forum, Milwaukee, WI, USA, 11–13 December 2005; pp. 25–26. [Google Scholar]
- Slama, A.; Ben Salem, M.; Ben Naceur, M.; Zid, E. Les céréales en Tunisie: Production, effet de la sécheresse et mécanismes de résistance. Sécheresse 2005, 16, 225–229. [Google Scholar]
- Bachta, M.S. L’agriculture, l’agroalimentaire, la pêche et le développement rural en Tunisie. In Les Agricultures Méditerranéennes: Analyses par Pays; CIHEAM: Montpellier, France, 2008; pp. 75–94. [Google Scholar]
- González-Dugo, M.; Moran, M.; Mateos, L.; Bryant, R. Canopy temperature variability as an indicator of crop water stress severity. Irrig. Sci. 2006, 24, 233–240. [Google Scholar] [CrossRef]
- Ihuoma, S.O.; Madramootoo, C.A. Recent advances in crop water stress detection. Comput. Electron. Agric. 2017, 141, 267–275. [Google Scholar] [CrossRef]
- Luquet, D. Suivi de l’état Hydrique des Plantes par Infrarouge Thermique: Analyse Expérimentale et Modélisation 3D de la Variabilité des Températures au Sein d’une Culture en Rang de Cotonniers. Ph.D. Thesis, INA-PG, Paris, France, 2002. [Google Scholar]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I. Derivation of a shortwave infrared water stress index from MODIS near-and shortwave infrared data in a semiarid environment. Remote Sens. Environ. 2003, 87, 111–121. [Google Scholar] [CrossRef]
- Schlemmer, M.R.; Francis, D.D.; Shanahan, J.; Schepers, J.S. Remotely measuring chlorophyll content in corn leaves with differing nitrogen levels and relative water content. Agron. J. 2005, 97, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.; Kharrou, M.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Hadria, R.; Duchemin, B.; Lahrouni, A.; Khabba, S.; Er-Raki, S.; Dedieu, G.; Chehbouni, A.; Olioso§, A. Monitoring of irrigated wheat in a semi-arid climate using crop modelling and remote sensing data: Impact of satellite revisit time frequency. Int. J. Remote Sens. 2006, 27, 1093–1117. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining satellite remote sensing data with the FAO-56 dual approach for water use mapping in irrigated wheat fields of a semi-arid region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef] [Green Version]
- Kotchi, S.O. Détection du Stress Hydrique par Thermographie Infrarouge: Application à la Culture de la Pomme de Terre. Master’s Thesis, Faculté de Foresterie et Géomatique Université Laval Québec, Québec, QC, Canada, 2004. [Google Scholar]
- Lili, Z.; Duchesne, J.; Nicolas, H.; Rivoal, R.; de Breger, P. Détection infrarouge thermique des maladies du blé d’hiver 1. Eppo Bull. 1991, 21, 659–672. [Google Scholar] [CrossRef]
- Courault, D.; Clastre, P.; Guinot, J.; Seguin, B. Analyse des sécheresses de 1988 à 1990 en France à partir de l’analyse combinée de données satellitaires NOAA-AVHRR et d’un modèle agrométéorologique. Agronomie 1994, 14, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Moran, M.; Clarke, T.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Brown, S.C.; Quegan, S.; Morrison, K.; Bennett, J.C.; Cookmartin, G. High-resolution measurements of scattering in wheat canopies-implications for crop parameter retrieval. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1602–1610. [Google Scholar] [CrossRef] [Green Version]
- Amri, R.; Zribi, M.; Lili-Chabaane, Z.; Wagner, W.; Hasenauer, S. Analysis of C-band scatterometer moisture estimations derived over a semiarid region. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2630–2638. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.; Fung, A. Microwave dielectric properties of natural earth materials. Microw. Remote Sens. 1986, 3, 2017–2027. [Google Scholar]
- Zribi, M. Développement de Nouvelles Méthodes de Modélisation de la Rugosité Pour la Rétrodiffusion Hyperfréquence de la Surface du sol. Ph.D. Thesis, CGU, Toulouse, France, 1995. [Google Scholar]
- Adragna, F.; Et Nicolas, J. Traitement des images de Radar à Synthèse d’Ouverture (RSO). In Sous la Direction de Henri Maître; Hermes Science Europe Publication: Paris, France, 2001; Volume 328. [Google Scholar]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar] [CrossRef] [Green Version]
- McNairn, H.; Brisco, B. The application of C-band polarimetric SAR for agriculture: A review. Can. J. Remote Sens. 2004, 30, 525–542. [Google Scholar] [CrossRef]
- Moran, M.S.; Alonso, L.; Moreno, J.F.; Mateo, M.P.C.; De La Cruz, D.F.; Montoro, A. A RADARSAT-2 quad-polarized time series for monitoring crop and soil conditions in Barrax, Spain. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1057–1070. [Google Scholar] [CrossRef]
- Vereecken, H.; Weihermüller, L.; Jonard, F.; Montzka, C. Characterization of crop canopies and water stress related phenomena using microwave remote sensing methods: A review. Vadose Zone J. 2012, 11, vzj2011-0138ra. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F.; Marais-Sicre, C. Monitoring wheat and rapeseed by using synchronous optical and radar satellite data—From temporal signatures to crop parameters estimation. Adv. Remote Sens. 2013, 2, 33222. [Google Scholar] [CrossRef] [Green Version]
- Hajj, M.E.; Baghdadi, N.; Belaud, G.; Zribi, M.; Cheviron, B.; Courault, D.; Hagolle, O.; Charron, F. Irrigated grassland monitoring using a time series of terraSAR-X and COSMO-skyMed X-Band SAR Data. Remote Sens. 2014, 6, 10002–10032. [Google Scholar] [CrossRef] [Green Version]
- Le Toan, T.; Laur, H.; Mougin, E.; Lopes, A. Multitemporal and dual-polarization observations of agricultural vegetation covers by X-band SAR images. IEEE Trans. Geosci. Remote Sens. 1989, 27, 709–718. [Google Scholar] [CrossRef]
- Mattia, F.; Le Toan, T.; Picard, G.; Posa, F.I.; D’Alessio, A.; Notarnicola, C.; Gatti, A.M.; Rinaldi, M.; Satalino, G.; Pasquariello, G. Multitemporal C-band radar measurements on wheat fields. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1551–1560. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-Wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Fontanelli, G.; Paloscia, S.; Zribi, M.; Chahbi, A. Sensitivity analysis of X-band SAR to wheat and barley leaf area index in the Merguellil Basin. Remote Sens. Lett. 2013, 4, 1107–1116. [Google Scholar] [CrossRef] [Green Version]
- Wiseman, G.; McNairn, H.; Homayouni, S.; Shang, J. RADARSAT-2 polarimetric SAR response to crop biomass for agricultural production monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4461–4471. [Google Scholar] [CrossRef]
- Nasirzadehdizaji, R.; Cakir, Z.; Sanli, F.B.; Abdikan, S.; Pepe, A.; Calò, F. Sentinel-1 interferometric coherence and backscattering analysis for crop monitoring. Comput. Electron. Agric. 2021, 185, 106118. [Google Scholar] [CrossRef]
- Khabbazan, S.; Vermunt, P.; Steele-Dunne, S.; Ratering Arntz, L.; Marinetti, C.; van der Valk, D.; Iannini, L.; Molijn, R.; Westerdijk, K.; van der Sande, C. Crop monitoring using Sentinel-1 data: A case study from The Netherlands. Remote Sens. 2019, 11, 1887. [Google Scholar] [CrossRef] [Green Version]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Sieber, J.; Yates, D.; Huber Lee, A.; Purkey, D. WEAP: A demand priority and preference driven water planning model: Part 1, model characteristics. Water Int. 2005, 30, 487–500. [Google Scholar]
- Farg, E.; Arafat, S.; Abd El-Wahed, M.; El-Gindy, A. Estimation of evapotranspiration ETc and crop coefficient Kc of wheat, in south Nile Delta of Egypt using integrated FAO-56 approach and remote sensing data. Egypt. J. Remote Sens. Space Sci. 2012, 15, 83–89. [Google Scholar] [CrossRef] [Green Version]
- Kameli, A.; Lösel, D. Growth and sugar accumulation in durum wheat plants under water stress. New Phytol. 1996, 132, 57–62. [Google Scholar] [CrossRef] [PubMed]
- Tardieu, F.; Dreyer, E. Regulation of gaseous exchanges in plants under drought stress. In L’eau dans l’espace Rural Production Végétale et Qualité de l’eau; Institut National de la Recherche Agronomique (INRA): Paris, France, 1997; pp. 41–59. ISBN 9782738007087. [Google Scholar]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Engdahl, M.E.; Borgeaud, M.; Rast, M. The use of ERS-1/2 tandem interferometric coherence in the estimation of agricultural crop heights. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1799–1806. [Google Scholar] [CrossRef]
- Manavalan, R. Review of synthetic aperture radar frequency, polarization, and incidence angle data for mapping the inundated regions. J. Appl. Remote Sens. 2018, 12, 021501. [Google Scholar]
- Cookmartin, G.; Saich, P.; Quegan, S.; Cordey, R.; Burgess-Allen, P.; Sowter, A. Modeling microwave interactions with crops and comparison with ERS-2 SAR observations. IEEE Trans. Geosci. Remote Sens. 2000, 38, 658–670. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Kouyate, F.; Brisco, B.; Williams, T.L. Textural infornation in SAR images. IEEE Trans. Geosci. Remote Sens. 1986, 235–245. [Google Scholar] [CrossRef]
- Fieuzal, R.; Baup, F.; Marais-Sicre, C. Sensitivity of TerraSAR-X, RADARSAT-2 and ALOS satellite radar data to crop variables. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3740–3743. [Google Scholar]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Gorrab, A.; Ameline, M.; Albergel, C.; Baup, F. Use of sentinel-1 multi-configuration and multi-temporal series for monitoring parameters of winter wheat. Remote Sens. 2021, 13, 553. [Google Scholar] [CrossRef]
- Han, D.; Liu, S.; Du, Y.; Xie, X.; Fan, L.; Lei, L.; Li, Z.; Yang, H.; Yang, G. Crop water content of winter wheat revealed with Sentinel-1 and Sentinel-2 imagery. Sensors 2019, 19, 4013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Shirbeny, M.; Ali, A.; Mohamed, E.; Abutaleb, K.; Bauomy, E. Monitoring of actual evapotranspiration using remotely sensed data under modern irrigation systems. J. Geograph Environ. Earth Sci. Int. 2017, 12, 1–12. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; Volume 2. [Google Scholar]
- Gens, R.; Van Genderen, J.L. Review Article SAR interferometry—Issues, techniques, applications. Int. J. Remote Sens. 1996, 17, 1803–1835. [Google Scholar] [CrossRef]
- Massonnet, D.; Holzer, T.; Vadon, H. Land subsidence caused by the East Mesa geothermal field, California, observed using SAR interferometry. Geophys. Res. Lett. 1997, 24, 901–904. [Google Scholar] [CrossRef]
- Ouchi, K. Recent trend and advance of synthetic aperture radar with selected topics. Remote Sens. 2013, 5, 716–807. [Google Scholar] [CrossRef] [Green Version]
- Ulaby, F.; Allen, C.; Eger Iii, G.; Kanemasu, E. Relating the microwave backscattering coefficient to leaf area index. Remote Sens. Environ. 1984, 14, 113–133. [Google Scholar] [CrossRef]


| Equation | RMSE | ||
|---|---|---|---|
| Model 1 | = | ||
| Model 2 | = | ||
| Model 3 | = | ||
| Model 4 | = |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbouchi, M.; Chaabani, C.; Cheikh M’Hamed, H.; Abdelfattah, R.; Lhissou, R.; Chokmani, K.; Ben Aissa, N.; Annabi, M.; Bahri, H. Wheat Water Deficit Monitoring Using Synthetic Aperture Radar Backscattering Coefficient and Interferometric Coherence. Agriculture 2022, 12, 1032. https://doi.org/10.3390/agriculture12071032
Barbouchi M, Chaabani C, Cheikh M’Hamed H, Abdelfattah R, Lhissou R, Chokmani K, Ben Aissa N, Annabi M, Bahri H. Wheat Water Deficit Monitoring Using Synthetic Aperture Radar Backscattering Coefficient and Interferometric Coherence. Agriculture. 2022; 12(7):1032. https://doi.org/10.3390/agriculture12071032
Chicago/Turabian StyleBarbouchi, Meriem, Chayma Chaabani, Hatem Cheikh M’Hamed, Riadh Abdelfattah, Rachid Lhissou, Karem Chokmani, Nadhira Ben Aissa, Mohamed Annabi, and Haithem Bahri. 2022. "Wheat Water Deficit Monitoring Using Synthetic Aperture Radar Backscattering Coefficient and Interferometric Coherence" Agriculture 12, no. 7: 1032. https://doi.org/10.3390/agriculture12071032
APA StyleBarbouchi, M., Chaabani, C., Cheikh M’Hamed, H., Abdelfattah, R., Lhissou, R., Chokmani, K., Ben Aissa, N., Annabi, M., & Bahri, H. (2022). Wheat Water Deficit Monitoring Using Synthetic Aperture Radar Backscattering Coefficient and Interferometric Coherence. Agriculture, 12(7), 1032. https://doi.org/10.3390/agriculture12071032









