Analysis on Regional Differences and Spatial Convergence of Digital Village Development Level: Theory and Evidence from China
Abstract
1. Introduction
2. Materials and Methods
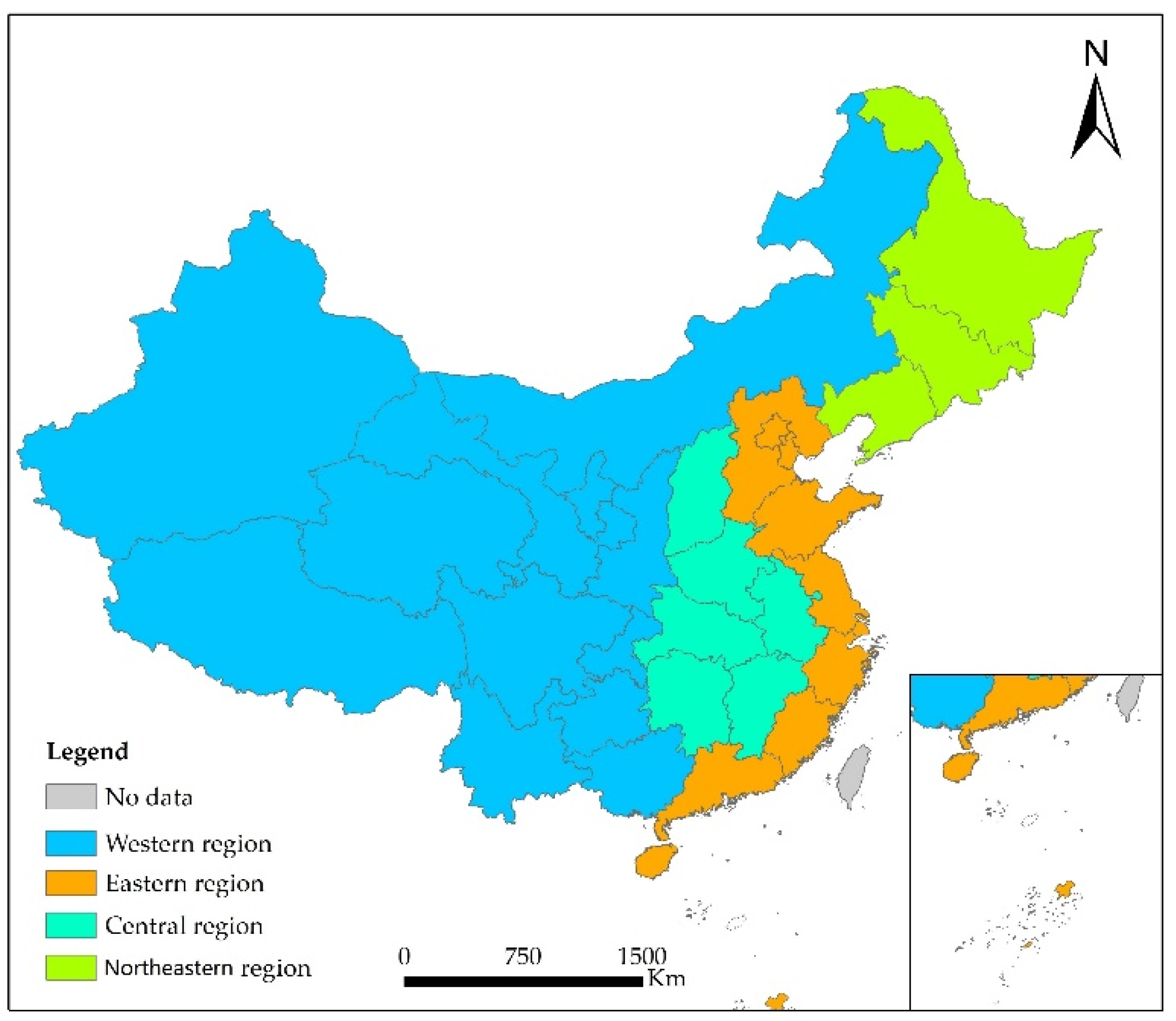
2.1. Data Source
2.2. Methods
2.2.1. Construction and Evaluation Method of DVI
The Evaluation Index System of DVI
The Value of the DVI Evaluation Method
2.2.2. Decomposition of Dagum Gini Coefficient
2.2.3. Spatial Autocorrelation Analysis
2.2.4. Spatial Convergence Model
-Convergence Model
-Convergent Spatial Autoregressive Model (SAR)
Spatial Error Model with -Convergence (SEM)
3. Results
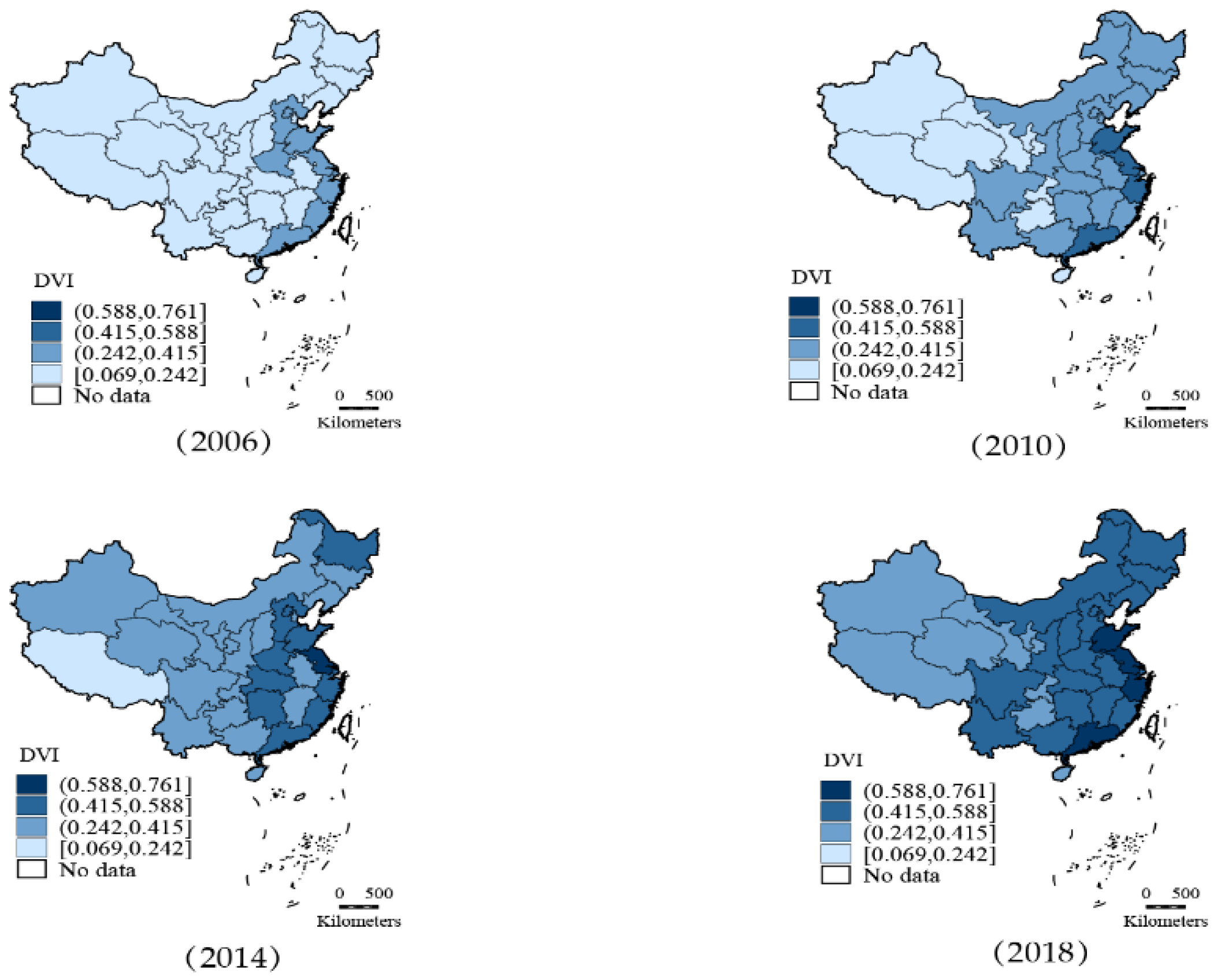
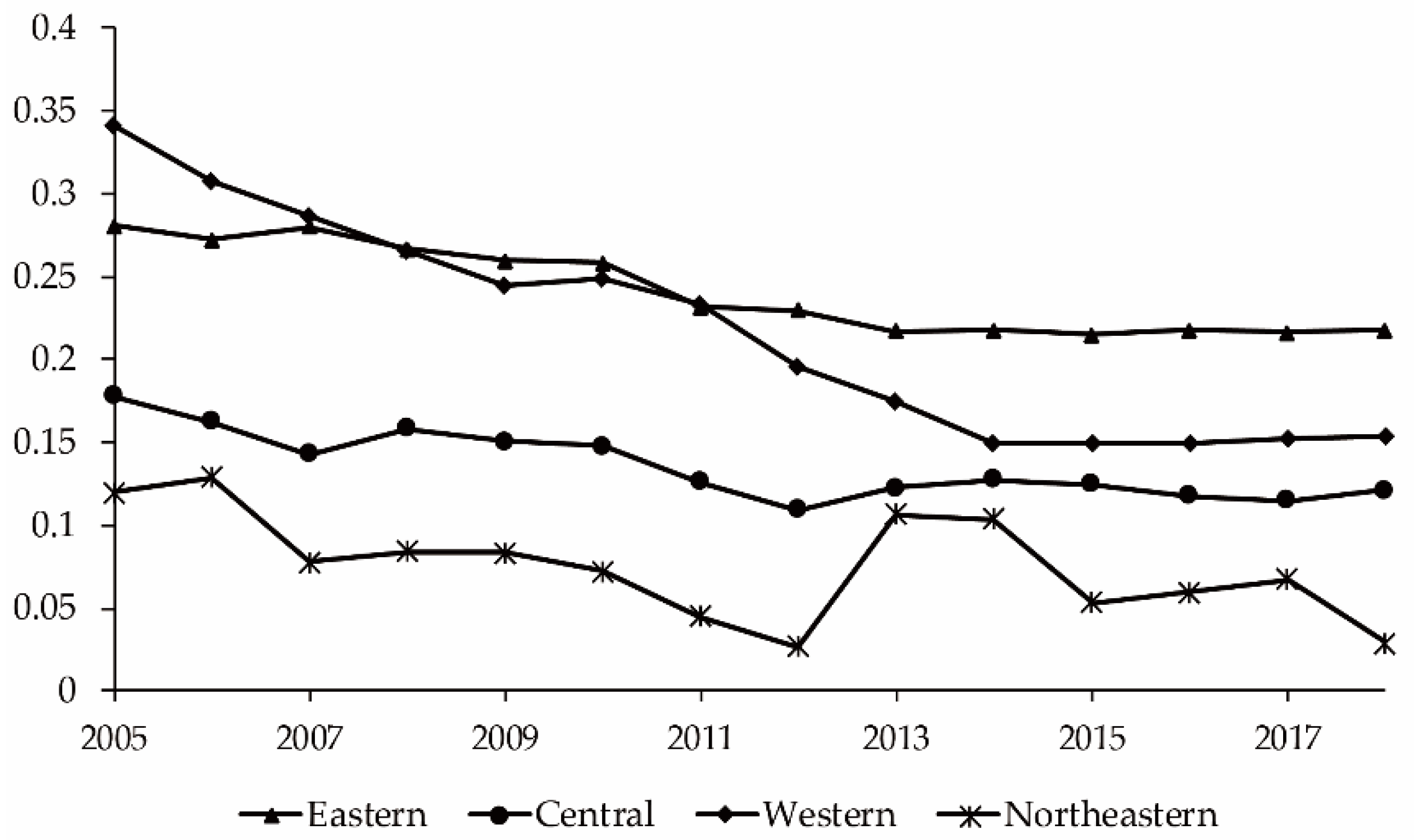
3.1. General Description of DVI in China and Four Major Regions
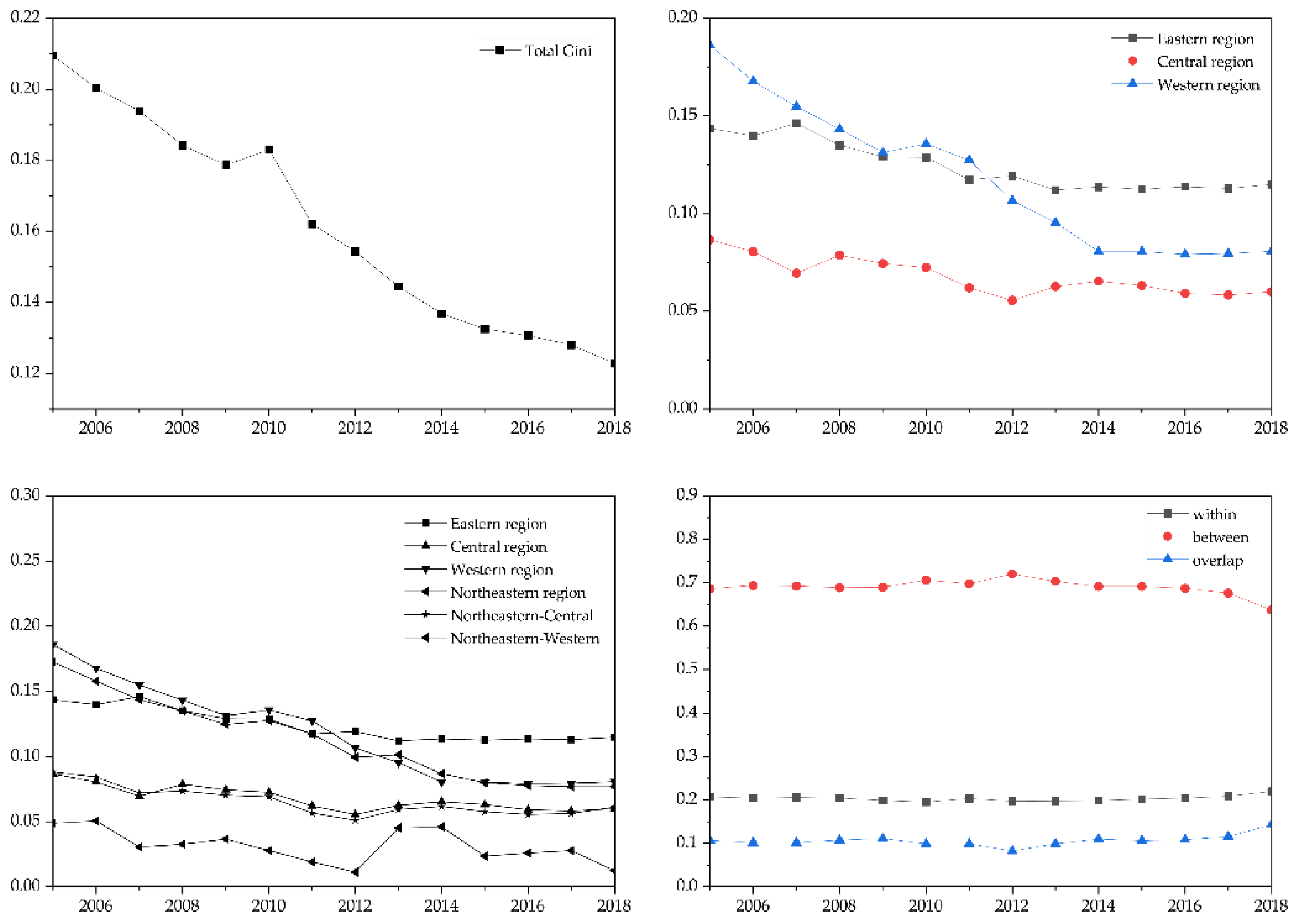
3.2. Regional Difference Decomposition of DVI
3.3. Convergence Analysis of DVI
3.3.1. -Convergence Analysis of DVI in China
3.3.2. -Convergence analysis of DVI in China
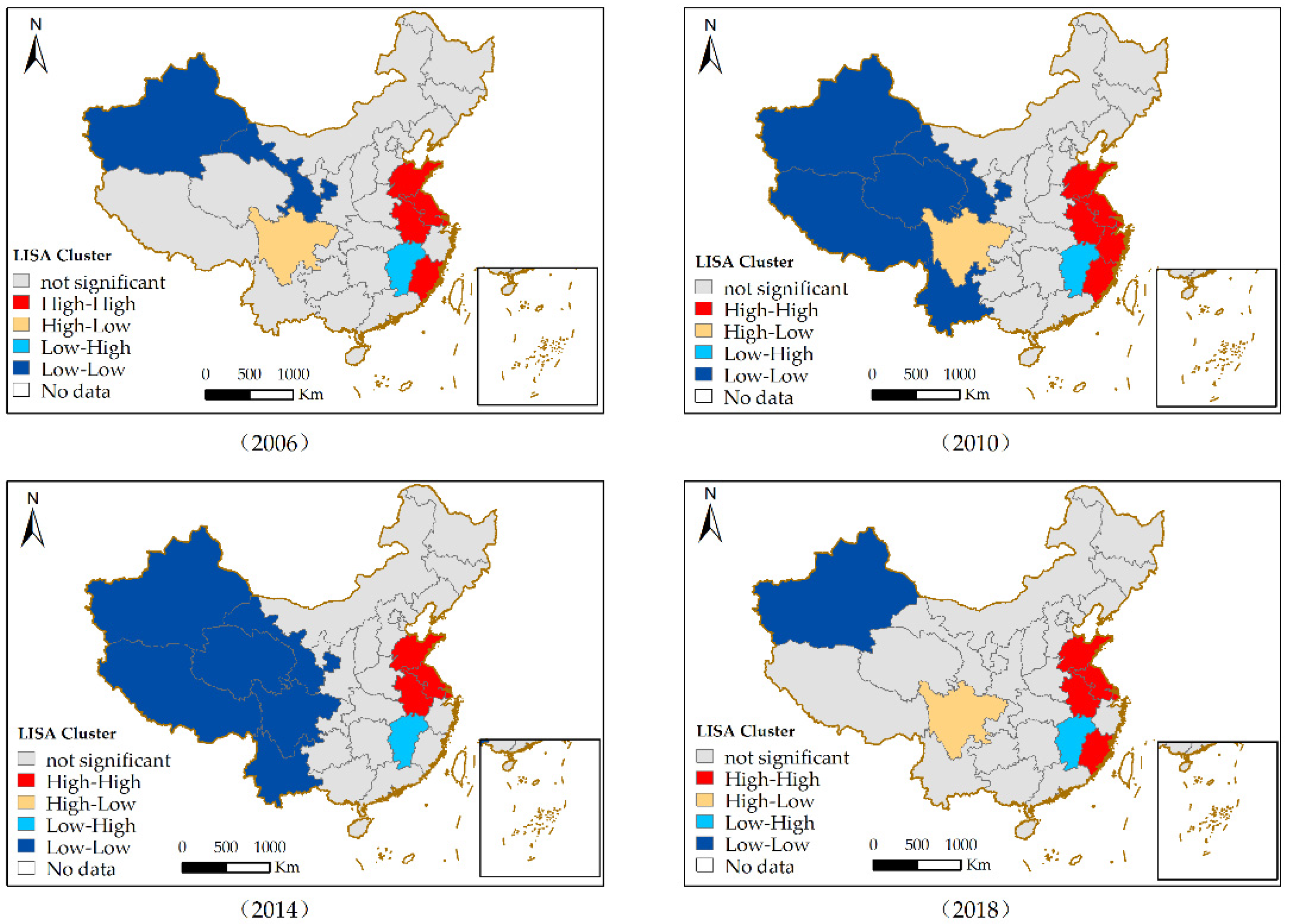
Spatial Correlation Test
Absolute -Convergence Analysis
Conditional -Convergence Analysis
4. Discussion
5. Conclusions and Policy Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Litan, R.E.; Rivlin, A.M. Projecting the Economic Impact of the Internet. Am. Econ. Rev. 2001, 91, 313–317. [Google Scholar] [CrossRef]
- Kim, D. A 2020 Perspective on “A Dynamic Model for the Evolution of the next Generation Internet—Implications for Network Policies”: Towards a Balanced Perspective on the Internet’s Role in the 5G and Industry 4.0 Era. Electron. Commer. Res. Appl. 2020, 41, 100966. [Google Scholar] [CrossRef]
- Maurseth, P.B. The Effect of the Internet on Economic Growth: Counter-Evidence from Cross-Country Panel Data. Econ. Lett. 2018, 172, 74–77. [Google Scholar] [CrossRef]
- Gabellone, F.; Lanorte, A.; Masini, N.; Lasaponara, R. From Remote Sensing to a Serious Game: Digital Reconstruction of an Abandoned Medieval Village in Southern Italy. J. Cult. Herit. 2017, 23, 63–70. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Z.; Zhang, H.; Zhao, M. Agricultural High-Quality Development: Digital Empowerment and Implementation Path. Chin. Rural Econ. 2019, 420, 2–15. [Google Scholar]
- Bonati, L.; Polese, M.; D’Oro, S.; Basagni, S.; Melodia, T. Open, Programmable, and Virtualized 5G Networks: State-of-the-Art and the Road Ahead. Comput. Netw. 2020, 182, 107516. [Google Scholar] [CrossRef]
- Varghese, P. Exploring Other Concepts of Smart-Cities within the Urbanising Indian Context. Procedia Technol. 2016, 24, 1858–1867. [Google Scholar] [CrossRef][Green Version]
- Lawson, P. Telecommunications Regulation: Creating Order & Opportunity in UK Digital Terrestrial Television Whitespace. Comput. Law Secur. Rev. 2014, 30, 375–391. [Google Scholar] [CrossRef]
- Ydersbond, I.M.; Auvinen, H.; Tuominen, A.; Fearnley, N.; Aarhaug, J. Nordic Experiences with Smart Mobility: Emerging Services and Regulatory Frameworks. Transp. Res. Procedia 2020, 49, 130–144. [Google Scholar] [CrossRef]
- Visvizi, A.; Lytras, M.D. Sustainable Smart Cities and Smart Villages Research: Rethinking Security, Safety, Well-Being, and Happiness. Sustainability 2019, 12, 215. [Google Scholar] [CrossRef]
- Visvizi, A.; Lytras, M.D. Rescaling and Refocusing Smart Cities Research: From Mega Cities to Smart Villages. JSTPM 2018, 9, 134–145. [Google Scholar] [CrossRef]
- Bielska, A.; Stańczuk-Gałwiaczek, M.; Sobolewska-Mikulska, K.; Mroczkowski, R. Implementation of the Smart Village Concept Based on Selected Spatial Patterns—A Case Study of Mazowieckie Voivodeship in Poland. Land Use Policy 2021, 104, 105366. [Google Scholar] [CrossRef]
- Berghel, H. Digital Village: Predatory Disintermediation. Commun. ACM 2000, 43, 23–29. [Google Scholar] [CrossRef]
- Tang, N.; Marshall, W.F. Centrosome Positioning in Vertebrate Development. J. Cell Sci. 2012, 125, 4951–4961. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wu, J.; Li, D. Research on Micro Measurement Model of Digital Village Based on Entropy Weight Method. J. Libr. Inf. Sci. Agric. 2020, 34, 68–76. [Google Scholar]
- Zhang, H.; Du, K.; Jin, B. Research on the Evaluation of Digital Rural Development Readiness under the Strategy of Rural Revitalization. J. Univ. Financ. Econ. 2020, 33, 51–60. [Google Scholar] [CrossRef]
- Fang, Y. Construction and Analysis of Digital Village Evaluation Index System. Shanxi Agric. Econ. 2020, 275, 21–23. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, M.Y. Spatial-Temporal Characteristics and Determinants of Land Urbanization Quality in China: Evidence from 285 Prefecture-Level Cities. Sustain. Cities Soc. 2018, 38, 70–79. [Google Scholar] [CrossRef]
- Cui, Y.; Khan, S.U.; Deng, Y.; Zhao, M. Spatiotemporal Heterogeneity, Convergence and Its Impact Factors: Perspective of Carbon Emission Intensity and Carbon Emission per Capita Considering Carbon Sink Effect. Environ. Impact Assess. Rev. 2022, 92, 106699. [Google Scholar] [CrossRef]
- Shen, F. The Endogenous Development Model of Digital Village: Practical Logic, Operation Mechanism and Optimization Strategy. E-Government 2021, 226, 57–67. [Google Scholar]
- Wang, Y.; Wang, H. The Impact of Digital Village on Rural Residents’ Online Shopping. China Bus. Mark. 2021, 35, 9–18. [Google Scholar]
- Ranade, P.; Londhe, S.; Mishra, A. Smart Villages through Information Technology—Need of Emerging India. IPASJ Int. J. Inf. Technol. 2015, 3, 1–6. [Google Scholar]
- Daniel, S.; Doran, M.A. GeoSmartCity: Geomatics Contribution to the Smart City. In Proceedings of the International Conference on Digital Government Research: From E-government to Smart Government, Quebec City, QC, Canada, 17–20 June 2013. [Google Scholar] [CrossRef]
- Guo, H.; Chen, X. Building a “Digital Village” to Promote Rural Revitalization. Hangzhou Wkly. 2018, 47, 10–11. [Google Scholar]
- Irwansyah. The Social Contractual Utilitarianism of a Digital Village in Rural Indonesia. Technol. Soc. 2020, 63, 101354. [Google Scholar] [CrossRef]
- Shang, L.; Heckelei, T.; Gerullis, M.K.; Börner, J.; Rasch, S. Adoption and Diffusion of Digital Farming Technologies—Integrating Farm-Level Evidence and System Interaction. Agric. Syst. 2021, 190, 103074. [Google Scholar] [CrossRef]
- Wu, H.-W.; Li, E.; Sun, Y.; Dong, B. Research on the Operation Safety Evaluation of Urban Rail Stations Based on the Improved TOPSIS Method and Entropy Weight Method. J. Rail Transp. Plan. Manag. 2021, 20, 100262. [Google Scholar] [CrossRef]
- Tian, R.; Shao, Q.; Wu, F. Four-Dimensional Evaluation and Forecasting of Marine Carrying Capacity in China: Empirical Analysis Based on the Entropy Method and Grey Verhulst Model. Mar. Pollut. Bull. 2020, 160, 111675. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Q.; Wang, L.; Liang, L. Regional Environmental Efficiency in China: An Empirical Analysis Based on Entropy Weight Method and Non-Parametric Models. J. Clean. Prod. 2020, 276, 124147. [Google Scholar] [CrossRef]
- Zhao, J.; Ji, G.; Tian, Y.; Chen, Y.; Wang, Z. Environmental Vulnerability Assessment for Mainland China Based on Entropy Method. Ecol. Indic. 2018, 91, 410–422. [Google Scholar] [CrossRef]
- Dagum, C. A New Approach to the Decomposition of the Gini Income Inequality Ratio. Empir. Econ. 1997, 22, 515–531. [Google Scholar] [CrossRef]
- Thomson, E.M.; Bradley, B.A.; Lee, R.L.; Wotherspoon, L.M.; Wood, C.M.; Cox, B.R. Generalised Parametric Functions and Spatial Correlations for Seismic Velocities in the Canterbury, New Zealand Region from Surface-Wave-Based Site Characterisation. Soil Dyn. Earthq. Eng. 2020, 128, 105834. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vu, T.D. Identification of Multivariate Geochemical Anomalies Using Spatial Autocorrelation Analysis and Robust Statistics. Ore Geol. Rev. 2019, 111, 102985. [Google Scholar] [CrossRef]
- Jha, R.K.; Gundimeda, H.; Andugula, P. Assessing the Social Vulnerability to Floods in India: An Application of Superefficiency Data Envelopment Analysis and Spatial Autocorrelation to Analyze Bihar Floods. In Economic Effects of Natural Disasters; Elsevier: Amsterdam, The Netherlands, 2021; pp. 559–581. ISBN 978-0-12-817465-4. [Google Scholar]
- Melecky, L. Spatial Autocorrelation Method for Local Analysis of The EU. Procedia Econ. Financ. 2015, 23, 1102–1109. [Google Scholar] [CrossRef]
- Ren, H.; Shang, Y.; Zhang, S. Measuring the Spatiotemporal Variations of Vegetation Net Primary Productivity in Inner Mongolia Using Spatial Autocorrelation. Ecol. Indic. 2020, 112, 106108. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, K.; Zhu, Y.; Liu, W. Spatial and Temporal Differentiation and Influencing Factors of Environmental Governance Performance in the Yangtze River Delta, China. Sci. Total Environ. 2021, 801, 149699. [Google Scholar] [CrossRef]
- Tepanosyan, G.; Sahakyan, L.; Zhang, C.; Saghatelyan, A. The Application of Local Moran’s I to Identify Spatial Clusters and Hot Spots of Pb, Mo and Ti in Urban Soils of Yerevan. Appl. Geochem. 2019, 104, 116–123. [Google Scholar] [CrossRef]
- Das Majumdar, D.; Biswas, A. Quantifying Land Surface Temperature Change from LISA Clusters: An Alternative Approach to Identifying Urban Land Use Transformation. Landsc. Urban Plan. 2016, 153, 51–65. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Sadovskaya, V. Spatial Variation and Hotspot Detection of COVID-19 Cases in Kazakhstan, 2020. Spat. Spatio-Temporal Epidemiol. 2021, 39, 100430. [Google Scholar] [CrossRef]
- Banerjee, A.; Singh, A.K.; Chaurasia, H. An Exploratory Spatial Analysis of Low Birth Weight and Its Determinants in India. Clin. Epidemiol. Glob. Health 2020, 8, 702–711. [Google Scholar] [CrossRef]
- Seya, H.; Tsutsumi, M.; Yamagata, Y. Income Convergence in Japan: A Bayesian Spatial Durbin Model Approach. Econ. Model. 2012, 29, 60–71. [Google Scholar] [CrossRef]
- He, S.; Jiang, L. Identifying Convergence in Nitrogen Oxides Emissions from Motor Vehicles in China: A Spatial Panel Data Approach. J. Clean. Prod. 2021, 316, 128177. [Google Scholar] [CrossRef]
- Baumont, C.; Ertur, C.; Le Gallo, J. Spatial Convergence Clubs and the European Regional Growth Process,1980–1995. In European Regional Growth; Fingleton, B., Ed.; Advances in Spatial Science; Springer: Berlin/Heidelberg, Germany, 2003; pp. 131–158. ISBN 978-3-642-05571-3. [Google Scholar]
- Boots, B.; Haining, R. Spatial Data Analysis in the Social and Environmental Sciences. Trans. Inst. Br. Geogr. 1993, 18, 287. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, L.; Jiang, L.; Liu, M.; Wang, J.; Shi, K.; Duan, X. Dynamic Spatial Analysis of NO2 Pollution over China: Satellite Observations and Spatial Convergence Models. Atmos. Pollut. Res. 2021, 12, 89–99. [Google Scholar] [CrossRef]
- Jiang, L.; He, S.; Zhou, H. Spatio-Temporal Characteristics and Convergence Trends of PM2.5 Pollution: A Case Study of Cities of Air Pollution Transmission Channel in Beijing-Tianjin-Hebei Region, China. J. Clean. Prod. 2020, 256, 120631. [Google Scholar] [CrossRef]
- Hao, Y.; Peng, H. On the Convergence in China’s Provincial per Capita Energy Consumption: New Evidence from a Spatial Econometric Analysis. Energy Econ. 2017, 68, 31–43. [Google Scholar] [CrossRef]
- Gong, Y.; Hu, J.; Boelhouwer, P.J. Spatial Interrelations of Chinese Housing Markets: Spatial Causality, Convergence and Diffusion. Reg. Sci. Urban Econ. 2016, 59, 103–117. [Google Scholar] [CrossRef]
- Mishra, V.; Smyth, R. Conditional Convergence in Australia’s Energy Consumption at the Sector Level. Energy Econ. 2017, 62, 396–403. [Google Scholar] [CrossRef]
- Akram, V.; Rath, B.N.; Sahoo, P.K. Stochastic Conditional Convergence in per Capita Energy Consumption in India. Econ. Anal. Policy 2020, 65, 224–240. [Google Scholar] [CrossRef]
- Gotway, C.A.; Haining, R. Spatial Data Analysis in the Social and Environmental Sciences. Technometrics 1992, 34, 499. [Google Scholar] [CrossRef]
- Kassouri, Y.; Okunlola, O.A. Analysis of Spatio-Temporal Drivers and Convergence Characteristics of Urban Development in Africa. Land Use Policy 2021, 112, 105868. [Google Scholar] [CrossRef]
- Bartesaghi-Koc, C.; Osmond, P.; Peters, A. Innovative Use of Spatial Regression Models to Predict the Effects of Green Infrastructure on Land Surface Temperatures. Energy Build. 2022, 254, 111564. [Google Scholar] [CrossRef]
- Espoir, D.K.; Sunge, R. CO2 Emissions and Economic Development in Africa: Evidence from a Dynamic Spatial Panel Model. J. Environ. Manag. 2021, 300, 113617. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Liu, Y. Poverty Alleviation through Land Assetization and Its Implications for Rural Revitalization in China. Land Use Policy 2021, 105, 105418. [Google Scholar] [CrossRef]
- Yin, X.; Chen, J.; Li, J. Rural Innovation System: Revitalize the Countryside for a Sustainable Development. J. Rural Stud. 2019; in press. [Google Scholar] [CrossRef]
- Wu, H.; Ba, N.; Ren, S.; Xu, L.; Chai, J.; Irfan, M.; Hao, Y.; Lu, Z.-N. The Impact of Internet Development on the Health of Chinese Residents: Transmission Mechanisms and Empirical Tests. Socio-Econ. Plan. Sci. 2021, 101178. [Google Scholar] [CrossRef]
- Zhu, W.; Shang, F. Rural Smart Tourism under the Background of Internet Plus. Ecol. Inform. 2021, 65, 101424. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, W.; Ruan, W. Spatial Spillover and Impact Factors of the Internet Finance Development in China. Phys. A Stat. Mech. Its Appl. 2019, 527, 121390. [Google Scholar] [CrossRef]
- Song, Z.; Wang, C.; Bergmann, L. China’s Prefectural Digital Divide: Spatial Analysis and Multivariate Determinants of ICT Diffusion. Int. J. Inf. Manag. 2020, 52, 102072. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, T.; Lan, F.; Wang, M. ICT and Socio-Economic Development: Evidence from a Spatial Panel Data Analysis in China. Telecommun. Policy 2021, 45, 102173. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Q.; Gao, S.; Huang, J. The Spatial Aggregation of Rural E-Commerce in China: An Empirical Investigation into Taobao Villages. J. Rural Stud. 2020, 80, 403–417. [Google Scholar] [CrossRef]
- Wu, H.; Hao, Y.; Ren, S.; Yang, X.; Xie, G. Does Internet Development Improve Green Total Factor Energy Efficiency? Evidence from China. Energy Policy 2021, 153, 112247. [Google Scholar] [CrossRef]
- Li, H.; Yuan, Y.; Zhang, X.; Li, Z.; Wang, Y.; Hu, X. Evolution and Transformation Mechanism of the Spatial Structure of Rural Settlements from the Perspective of Long-Term Economic and Social Change: A Case Study of the Sunan Region, China. J. Rural Stud. 2019, S0743016718301487. [Google Scholar] [CrossRef]
- Cheng, L. China’s Rural Transformation under the Link Policy: A Case Study from Ezhou. Land Use Policy 2021, 103, 105319. [Google Scholar] [CrossRef]
- Xu, W.; Pan, Z.; Wang, G. Market Transition, Labor Market Dynamics and Reconfiguration of Earning Determinants Structure in Urban China. Cities 2018, 79, 113–123. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Li, Y. Rural Regional System and Rural Revitalization Strategy in China. Acta Geogr. Sin. 2019, 74, 2511–2528. [Google Scholar] [CrossRef]
- Wong, S.W.; Dai, Y.; Tang, B.; Liu, J. A New Model of Village Urbanization? Coordinative Governance of State-Village Relations in Guangzhou City, China. Land Use Policy 2021, 109, 105500. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, M.; Xiao, Y. Urbanization for Rural Development: Spatial Paradigm Shifts toward Inclusive Urban-Rural Integrated Development in China. J. Rural Stud. 2019, 71, 94–103. [Google Scholar] [CrossRef]
- Chen, K.; Long, H.; Liao, L.; Tu, S.; Li, T. Land Use Transitions and Urban-Rural Integrated Development: Theoretical Framework and China’s Evidence. Land Use Policy 2020, 92, 104465. [Google Scholar] [CrossRef]
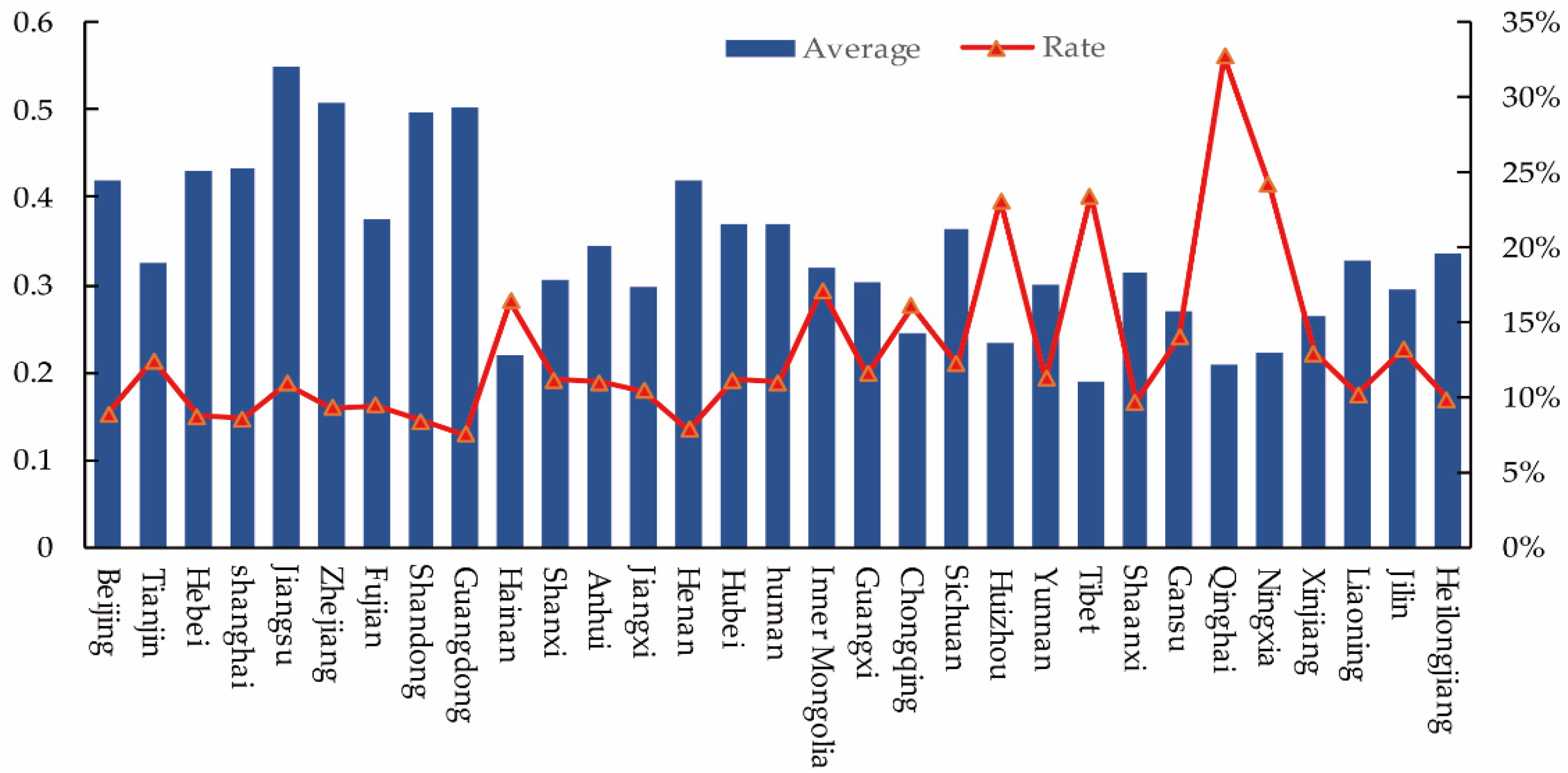
| Primary Indicators | Secondary Indicators | Unit | Weight (%) |
|---|---|---|---|
| Main development ability (31.9591%) | Per capita disposable income of rural residents | Yuan/person | 9.7124 |
| Consumption level of rural residents | Yuan/person | 6.9659 | |
| Average education level of rural residents | Year | 7.5285 | |
| Per capita expenditure on transportation and communication of rural residents | Yuan/person | 7.7523 | |
| Infrastructure construction (40.9690%) | Length of long-distance optical cable line | Km | 6.1673 |
| Length of rural delivery route of long-distance optical cable line (one way) | Km | 10.0915 | |
| Proportion of administrative villages with Internet broadband services | % | 2.5326 | |
| Proportion of postal administrative villages | % | 2.8889 | |
| Total power of agricultural machinery | Ten thousand kw | 8.4360 | |
| Rural power consumption | Ten thousand kw/h | 7.5282 | |
| Average weekly delivery times in rural areas | Times | 3.3245 | |
| Information environment (27.0719%) | Internet penetration rate | % | 8.0714 |
| Number of color TV sets per 100 rural households | Set | 2.9976 | |
| Mobile phone ownership per 100 rural households | Department | 7.0624 | |
| Computer ownership per 100 rural households | Set | 8.9405 |
| Year | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moran’s I | 0.306 | 0.313 | 0.315 | 0.303 | 0.318 | 0.374 | 0.336 | 0.360 | 0.352 | 0.350 | 0.326 | 0.309 | 0.291 | 0.253 |
| Z-value | 2.839 | 2.900 | 2.918 | 2.812 | 2.931 | 3.397 | 3.094 | 3.308 | 3.240 | 3.221 | 3.031 | 2.904 | 2.756 | 2.421 |
| p-value | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.000 | 0.001 | 0.000 | 0.001 | 0.001 | 0.001 | 0.002 | 0.003 | 0.008 |
| Test Method | Statistic | p-Value | Test Method | Statistic | p-Value |
|---|---|---|---|---|---|
| Lagrange multiplier (error) | 69.781 | 0.000 | Robust Lagrange multiplier (error) | 28.816 | 0.000 |
| Lagrange multiplier (lag) | 42.207 | 0.000 | Robust Lagrange multiplier (lag) | 1.241 | 0.265 |
| Model | SAR | SEM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Regions | National | Eastern | Central | Western | Northeastern | National | Eastern | Central | Western | Northeastern |
| −0.0166 *** (0.0055) | −0.0347 *** (0.0076) | −0.0046 (0.0139) | −0.0039 (0.0064) | −0.0488 *** (0.0136) | −0.0351 *** (0.0086) | −0.0466 *** (0.0091) | −0.0063 (0.0164) | −0.0157 (0.0119) | −0.0542 *** (0.0143) | |
| 0.3911 *** (0.0431) | 0.2212 *** (0.0447) | 0.1171 *** (0.0362) | 0.4742 *** (0.0421) | 0.0624 * (0.0353) | ||||||
| 0.4161 *** (0.0418) | 0.2378 *** (0.0423) | 0.1209 *** (0.0428) | 0.4848 *** (0.0417) | 0.0872 *** (0.0230) | ||||||
| LogL | 1343.4135 | 433.8977 | 269.2690 | 530.4190 | 117.4042 | 1345.4145 | 434.3711 | 269.2926 | 530.7026 | 117.4802 |
| 0.0033 | 0.0983 | 0.0008 | 0.0002 | 0.0701 | 0.0223 | 0.1032 | 0.0011 | 0.0001 | 0.0728 | |
| Test Method | Statistic | p-Value | Test Method | Statistic | p-Value |
|---|---|---|---|---|---|
| Lagrange multiplier (error) | 51.579 | 0.000 | Robust Lagrange multiplier (error) | 8.707 | 0.003 |
| Lagrange multiplier (lag) | 48.259 | 0.000 | Robust Lagrange multiplier (lag) | 5.387 | 0.020 |
| Model | SAR | SEM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Regions | National | Eastern | Central | Western | Northeastern | National | Eastern | Central | Western | Northeastern |
| −0.2332 *** (0.0419) | −0.2460 *** (0.0773) | −0.4911 *** (0.0802) | −0.2145 *** (0.0623) | −0.6787 *** (0.1696) | −0.2529 *** (0.0438) | −0.2450 *** (0.0749) | −0.4714 *** (0.0741) | −0.2098 *** (0.0582) | −0.6944 *** (0.1709) | |
| 0.3238 *** (0.0462) | 0.1873 *** (0.0425) | 0.1108 *** (0.0409) | 0.4274 *** (0.0486) | −0.0524 (0.0966) | ||||||
| 0.3440 *** (0.0451) | 0.1829 *** (0.0442) | 0.1461 ** (0.0695) | 0.4413 *** (0.0467) | −0.1103 * (0.0668) | ||||||
| Ln DEN | 0.0288 ** (0.0115) | 0.0107 (0.0294) | 0.1102 *** (0.0321) | 0.0499 ** (0.0227) | −0.2178 ** (0.0917) | 0.0252 ** (0.0100) | 0.0048 (0.0300) | 0.1230 *** (0.0278) | 0.0517 ** (0.0245) | −0.2321 ** (0.1019) |
| Ln STR | 0.0207 ** (0.0083) | 0.0258 (0.0214) | 0.0146 (0.0101) | 0.0146 (0.0164) | 0.1143 *** (0.0379) | 0.0169 ** (0.0081) | 0.0231 (0.0214) | 0.0105 (0.0122) | 0.0114 (0.0141) | 0.1222 *** (0.0428) |
| Ln URB | 0.0118 (0.0108) | −0.0099 (0.0403) | 0.1656 *** (0.0362) | 0.0651 *** (0.00232) | −0.3658 ** (0.1616) | 0.0140 (0.0121) | −0.0222 (0.0435) | 0.1696 *** (0.0416) | 0.0556 *** (0.0217) | −0.4087 ** (0.1931) |
| Ln ECO | 0.0321 *** (0.0067) | 0.0368*** (0.0132) | 0.0538 *** (0.0101) | 0.0162 ** (0.0075) | 0.0959 *** (0.0276) | 0.0330 *** (0.0070) | 0.0369 *** (0.0136) | 0.0538 *** (0.0094) | 0.0176 ** (0.0086) | 0.1012 *** (0.0315) |
| Ln OPE | −0.0025 (0.0027) | 0.0006 (0.0072) | −0.0222 ** (0.0095) | 0.0014 (0.0030) | 0.0481 *** (0.0169) | −0.0035 (0.0027) | −0.0014 (0.0083) | −0.0223 ** (0.0098) | 0.0016 (0.0025) | 0.0487 *** (0.0136) |
| Ln GOV | −0.0036 * (0.0021) | −0.0038 (0.0049) | −0.0252 *** (0.0029) | −0.0001 (0.0030) | −0.0068 (0.0068) | −0.0022 (0.0025) | −0.0031 (0.0055) | −0.0267 *** (0.0044) | 0.0022 (0.0036) | −0.0097 (0.0093) |
| LogL | 1380.1760 | 443.7616 | 286.5129 | 542.8184 | 129.2942 | 1380.0814 | 443.1522 | 286.6016 | 541.2971 | 129.4549 |
| 0.2141 | 0.2466 | 0.3568 | 0.2146 | 0.4940 | 0.2083 | 0.2352 | 0.3541 | 0.1643 | 0.4958 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Singh Chandel, R.B.; Xia, X. Analysis on Regional Differences and Spatial Convergence of Digital Village Development Level: Theory and Evidence from China. Agriculture 2022, 12, 164. https://doi.org/10.3390/agriculture12020164
Li X, Singh Chandel RB, Xia X. Analysis on Regional Differences and Spatial Convergence of Digital Village Development Level: Theory and Evidence from China. Agriculture. 2022; 12(2):164. https://doi.org/10.3390/agriculture12020164
Chicago/Turabian StyleLi, Xiaojing, Raj Bahadur Singh Chandel, and Xianli Xia. 2022. "Analysis on Regional Differences and Spatial Convergence of Digital Village Development Level: Theory and Evidence from China" Agriculture 12, no. 2: 164. https://doi.org/10.3390/agriculture12020164
APA StyleLi, X., Singh Chandel, R. B., & Xia, X. (2022). Analysis on Regional Differences and Spatial Convergence of Digital Village Development Level: Theory and Evidence from China. Agriculture, 12(2), 164. https://doi.org/10.3390/agriculture12020164






